Abstract
Chromatographic separation processes need efficient simulation methods, especially for nonlinear adsorption isotherms such as the Langmuir isotherms which imply the formation of concentration shocks. The focus of this paper is on the space–time conservation element/solution element (CE/SE) method. This is an explicit method for the solution of systems of partial differential equations. Numerical stability of this method is guaranteed when the Courant–Friedrichs–Lewy condition is satisfied. To investigate the accuracy and efficiency of this method, it is compared with the classical cell model, which corresponds to a first-order finite volume discretization using a method of lines approach (MOL). The evaluation is done for different models, including the ideal equilibrium model and a mass transfer model for different adsorption isotherms—including linear and nonlinear Langmuir isotherms—and for different chromatographic processes from single-column operation to more sophisticated simulated moving bed (SMB) processes for the separation of binary and ternary mixtures. The results clearly show that CE/SE outperforms MOL in terms of computational times for all considered cases, ranging from 11-fold for the case with linear isotherm to 350-fold for the most complicated case with ternary center-cut eight-zone SMB with Langmuir isotherms, and it could be successfully applied for the optimization and control studies of such processes.
1. Introduction
Chromatographic separation processes are used for the separation of temperature-sensitive mixtures and mixtures of components with very similar physical properties, making them difficult to separate via other cheaper methods. These types of processes are frequently used in the chemical and the pharmaceutical industries ranging from small-scale batch separations of highly valuable pharmaceutically active compounds to large-scale continuous separations of isomer mixtures in the petroleum industries [1].
Mathematical modeling of such processes usually leads to a system of partial differential equations (PDEs) [1]. These mathematical models are used for the design, optimization, and control of chromatographic processes. Depending on the modeling assumptions, different types of models are available and frequently used including equilibrium models, which assume thermodynamic equilibrium between the solid and the fluid phase, or mass transfer models with finite mass transfer resistance between both phases.
For negligible axial dispersion, the equilibrium model admits an analytical solution for piecewise constant initial and boundary conditions and for certain types of linear and nonlinear adsorption isotherms including the well-known Langmuir isotherm. This analytical approach is the core of the so-called equilibrium theory [2,3], which has become an important tool for the conceptual design of chromatographic processes [4,5,6,7,8]. For the mass transfer models, analytical solutions are only possible under further restrictions [9,10,11]. Thus, in both cases, the numerical solution of the underlying PDE system is an important tool for the validation of the analytical results and to overcome the limitations posed by the analytical treatment.
In general, the numerical simulation of chromatographic columns is challenging due to the occurrence of steep concentration fronts, which was the subject of many papers [12,13,14]. For the real-time control and the optimization of the chromatographic processes, fast and reliable methods are required. In practice, the method of lines (MOL) [15] is often used for the solution of the PDE system using finite differences (FDs), finite elements (FEM), or finite volumes (FVM) for the spatial discretization. The simplest choice is a first-order finite volume discretization leading to the popular cell models (CELL), which can then be solved with some standard integrators. The efficiency and accuracy can be further enhanced, with more advanced high-resolution schemes and adaptive grids [13,14,16]. For a recent review of the available numerical methods and simulation tools with many references, the reader is referred to Chapter 6.4 of [1].
An interesting alternative is the so-called space–time conservation element/solution element (CE/SE) method which was originally developed by Chang [17,18,19] for similar problems in fluid dynamics. Later, the CE/SE method was also successfully applied to chromatographic problems by Jørgensen and coworkers [12,20]. Focus was on a mass transfer model for binary simulated moving bed (SMB) processes with linear and nonlinear adsorption isotherms. It was shown [12] that the solutions obtained using the CE/SE method are comparable in accuracy with a MOL approach using a fifth-order high-resolution weighted essentially non-oscillatory (WENO) discretization scheme but need a significantly shorter calculation time. More recently, results were extended in [21] by combining the CE/SE method with a continuous prediction technique. Again, focus was on the mass transfer model for binary SMB processes with linear and nonlinear adsorption isotherms, and again it was shown for a benchmark problem that the CE/SE method is very fast compared to an MOL and a wavelet collocation approach. This motivated us to investigate possible applications of the CE/SE method to the other important class of mathematical models of chromatographic columns, i.e., equilibrium models, and to extend its field of application to a challenging class of ternary SMB processes, i.e., so-called center-cut separations, where the process objective is to isolate a component with intermediate affinity to the solid phase from a mixture of at least three components. This type of separation process plays an important role in the separation of natural products and in biotechnology [22]. In addition, to the best of our knowledge, the first dynamic simulation of a substantially nonlinear eight-zone SMB process is presented, which is much more challenging than the linear [23] or the weakly nonlinear [24] cases which were previously considered [23].
The outline of the paper is as follows: first, the different mathematical models of chromatographic process are presented in Section 2, and the CE/SE method is described in Section 3. Subsequently, numerical studies are shown in which the cell model (MOL) and CE/SE method are compared in terms of efficiency for different process configurations, models, and isotherms in Section 4; lastly, discussion and conclusions are presented in Section 5.
2. Mathematical Models of Chromatographic Processes
The starting point is the linear driving force (LDF) model of a single chromatographic column, which assumes a finite mass transfer resistance between the solid and the fluid phase. In the present paper, it is used for the modeling of single-column batch processes and multi-column continuous simulated moving bed (SMB) processes. It consists of three equations—one partial differential equation (PDE), one ordinary differential equation (ODE), and one algebraic equation (AE) for each of the components and each of the columns.
where ε is the column void fraction, v is the liquid phase velocity (m·s−1), Dax is the axial dispersion coefficient (m2·s−1), km is the mass transfer coefficient between the two phases (s−1), C is the liquid-phase concentration (g·L−1), q is the solid-phase concentration (g·L−1), q* is the solid-phase concentration at the interphase boundary in equilibrium with the liquid phase (g·L−1), t and z are time and spatial coordinates, respectively, (s) and (m), and i and k are the component and column indices, respectively. This model formulation assumes isothermal operation, a constant void fraction, and a constant mobile-phase velocity inside each of the columns. The apparent axial dispersion coefficient Dax lumps together all effects leading to band broadening in addition to the finite mass transfer resistance, which is known to have a similar effect [2]. Below, only the limiting case when Dax 0 is considered which is valid for efficient columns with a high number of theoretical stages N. The algebraic equation describes the thermodynamic equilibrium between the solid and the liquid phase and represents the adsorption isotherm. In the present work, two types of adsorption isotherms are used:
where the former is linear, and the latter is the well-known Langmuir isotherm. H denotes the adsorption Henry coefficient, b is the retention factor (L·g−1), and r is the component index. In the limiting case where the mass transfer is instantaneous (i.e., km,i and ) and there is negligible dispersion, the ideal equilibrium model [1] is obtained.
The loading of an empty column is now considered as a test scenario. For the present isotherms, this scenario is more challenging than the regeneration step due to the occurrence of steep concentration fronts and is, therefore, used as a benchmark problem. Frequently applied pulse injections can be considered as a combination of loading and regeneration steps and are, therefore, also included to some extent. The initial conditions (ICs) are zero, i.e., we start every simulation with empty columns.
Boundary conditions (BCs) are of the Dirichlet type,
where is the liquid-phase concentration just before the column inlet. For the SMB processes, these BCs follow from the material balances of the in- and outlet ports as later discussed in detail.
3. Conservation Element/Solution Element (CE/SE) Method
The most distinctive feature of the CE/SE method developed by Chang [17,18,19] is that time and space are treated in the same manner through the so-called conservation element and solution element. It is based on the integral formulation of the conservation laws and can resolve the typical steep concentration fronts of nonlinear chromatography. It is an explicit time-marching method for the solution of PDEs, i.e., the value of the quantity of interest or so-called state variable (liquid-phase C and solid-phase q concentrations in chromatography) in the current time instant and its spatial derivative only depend on their values at the previous time instants (Figure 1a).
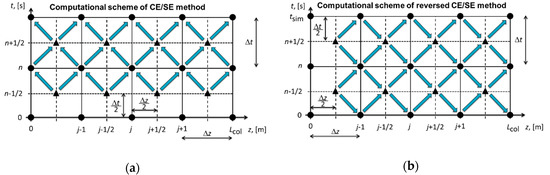
Figure 1.
Computational schemes of the conservation element/solution element (CE/SE) method: (a) standard CE/SE method; (b) reversed CE/SE method.
The model in Equation (1) with Dax 0 can be presented in the following vector form (the indices are omitted for simplicity):
where u is vector of state variables, f is vector of fluxes, and p is vector of source terms. Equation (1) can then be written in the following form:
Equation (10) is the PDE formulation which is solved using the CE/SE method. For the detailed derivation of the CE/SE method, the reader is referred to [12,17,18,19,20,21]. Here, only the final equations of the fully discretized scheme in space and time are presented. The state variable u at the j-th spatial point and n-th time instant is
where is
In the last equation, uz and ft are the discrete analogues of the derivatives and . The current value of is calculated from the already available values of and at the previous time instant. The different versions of the CE/SE method only differ in the way the spatial derivative uz of the state variables is calculated. In the current work, the proposition of [21] is used.
The definition of the function W0 is
with [18]. In this study, . and are the values of calculated from left and right of the point with coordinates (j, n), respectively, and are given by
where
where ut is the numerical analogue of and is
Since the CE/SE method is a fully discrete explicit scheme, the Courant–Friedrichs–Lewy condition has to be fulfilled to guarantee numerical stability. This condition gives the relationship between the spatial and time step sizes through the Courant–Friedrichs–Lewy (CFL) number,
In practice, we specify or and the CFL number and then calculate the other unspecified step or .
4. Results
To compare the cell model (MOL) and CE/SE methods for the simulation of chromatographic processes in terms of computational efficiency, several examples were considered. All simulations were carried out on a desktop personal computer (PC) with Intel Core i7 6700 central processing unit (CPU) (3.4 GHz), with 8 GB random-access memory (RAM) on MathWorks MATLAB R2017a under the Microsoft Windows 8.1 operating system.
4.1. Single Column with the Ideal Equilibrium Model
First, the focus was placed on the equilibrium model without axial dispersion which can be used for the simulation of highly efficient columns. In practice, column efficiency is often specified in terms of number of theoretical stages N corresponding to the number of grid points of the first order finite volume MOL formulation. For N and a step input, discontinuities travel through the column during the loading of an empty bed for the linear and the Langmuir isotherms considered in this paper. For a linear isotherm, these are contact discontinuities, and, for the Langmuir isotherm, these are self-sharpening shock waves [2].
In practical situations, the number of theoretical plates can be high but will be finite. In the remainder, N is fixed and, therefore, so is the number of grid points of the MOL formulation. The number of grid points for the CE/SE method is adapted accordingly to meet the given column efficiency. For comparison, the analytical solution for N is also given.
The first scenario is concerned with the loading of a single column with a binary system described by Langmuir isotherms. Table 1 summarizes all simulation parameters. Feed concentrations of the two components serve as boundary conditions for the PDE system Equation (6).

Table 1.
Simulation parameters and reversed CE/SE method parameters for Example 1 (single-column binary process with Langmuir isotherms described by the ideal equilibrium model).
As already mentioned, the CE/SE method formulation is given by Equation (10), while the ideal chromatographic model is of type
For nonlinear isotherms, the model in Equation (19) can only be directly converted to the type in Equation (10) in special cases. A detailed discussion for Langmuir isotherms is given in Appendix A. A possible alternative is to interchange the spatial and the time coordinates, i.e., instead of propagating in time, the solution procedure propagates in space (Figure 1b). This particular use of the CE/SE method is called the reversed CE/SE method. The CFL number is then formulated as
The algorithm is as follows:
- (i)
- Specify the simulation time tsim;
- (ii)
- Specify the number of time steps Nt, i.e., the number of conservation elements;
- (iii)
- Calculate the time step size ;
- (iv)
- Specify (;
- (v)
- Calculate the spatial step size from Equation (20);
- (vi)
- Continue with the reversed CE/SE method.
For the solution obtained via the MOL, the integration in time was done using the built-in MATLAB ODE solver ode45 which uses the Runge–Kutta method [25]. Doubled computational time was found using ode23, which is also a Runge–Kutta method but of lower order. As an alternative for stiff systems, the ode15s solver was also used but it was threefold slower than ode45. This indicates that the present system is nonstiff.
The concentration profiles along the column calculated by the two numerical methods are shown in Figure 2a for three time instants—0, 5, and 10 s. Additionally, the analytical solution of the system in Equation (4) obtained via the method of characteristics for N is shown [26]. It can be seen that both MOL and reversed CE/SE methods resolved the concentration shocks with the same number of points. For MOL, the number of points refers to the number of finite volumes in space, while, for the reversed CE/SE method, the number of points refers to the number of elements in time. The corresponding number of elements in space followed from the given number of elements in time and the given number from Equation (20). The computational time of the MOL (ode45) simulation was 7.85 s, which was the reference time for all of the simulations in the current work. The reversed CE/SE method was much more efficient (approximately 34-fold) as shown in Figure 2b, even with the chosen number of 0.4, which is rather conservative.
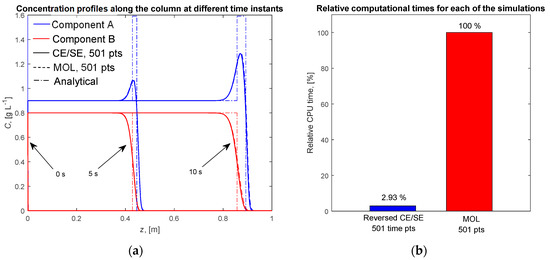
Figure 2.
Single-column binary chromatographic process with Langmuir isotherms—ideal equilibrium model. (a) Concentration profiles along the column calculated using the two numerical methods and the analaytical solution. (b) Comparison of the computational times for each of the numerical methods.
4.2. Single Column with the LDF Model
Unfortunately, the reversed formulation of the CE/SE method, as well as the other methods discussed in Appendix A, can only be used for single-column simulations because the feed concentrations, i.e., the boundary conditions are known a priori at all time steps. However, this is not true anymore for SMB processes and control problems. That is why, for systems with nonlinear Langmuir isotherms, the mass-transfer model in Equation (1) was used. The LDF chromatographic model corresponded to Equation (10), and the original formulation of the CE/SE method could be used for simulations. Interchanging of space and time coordinates was not required. It is worth noting that the LDF model represents a system of semi-linear transport equations compared to the equilibrium model, which is quasi-linear and, therefore, represents a nonlinear system of transport equations [27]. Thus, the LDF model has a simpler mathematical structure, but the number of equations is doubled.
The parameters for this example were the same as those for Example 1 presented in Table 1. Additional parameters were the mass transfer coefficients. Here, the same value was assumed for both components. The value of km and the CE/SE method parameters are given in Table 2. The values of the mass transfer coefficients were chosen to be high enough such that physical mass transfer was negligible.

Table 2.
Simulation parameters and CE/SE method parameters for Example 2 (single-column binary process with Langmuir isotherms described by the linear driving force (LDF) model).
The results of the CE/SE and MOL simulations are shown in Figure 3a together with the analytical solution for and . It can be seen that the orginal CE/SE method formulation could resolve the concentration fronts very well with a small number of spatial points, i.e., 101 points, whereas MOL needed more than 2000 points to achieve a similar accuracy. In both cases, the number of points refers to the spatial discretization. Therefore, the computational times of the two methods differed significantly (Figure 3b), and the CE/SE method was more than 55 times faster than MOL. Again, ode45 was the solver used for MOL. For the LDF model, computational times for ode45 and ode23 were found to be very similar. In particular, ode45 or ode23 was about 280-fold faster than ode15s, indicating that the LDF model was considerably less stiff than the equilibrium one. Therefore, in the remainder of the study, unless stated otherwise, ode45 was used for MOL.
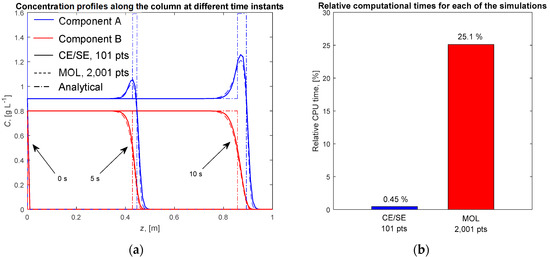
Figure 3.
Single-column binary chromatographic process with Langmuir isotherms—LDF model. (a) Concentration profiles along the column calculated by two numerical methods and the analaytical solution. (b) Comparison of the computational times for each of the numerical methods.
For lower values of the mass transfer coefficients, km,i concentration fronts were less steep compared to those in Figure 3a. In consequence, a lower number of grid points was required to resolve the fronts in both cases (CE/SE and MOL), leading to lower computational times.
4.3. Binary SMB Process with the LDF Model
The dynamical model of the SMB processes includes the PDE system in Equation (1) to describe each chromatographic column, as well as the nodal material balances which define the boundary conditions for the system in Equation (1). These equations are shown below.
- − Desorbent node
- − Extract node
- − Feed node
- − Raffinate node
The process configuration for the binary SMB process is shown in Figure 4a. In this case study, each zone had only one chromatographic column. The simulation parameters and the operating conditions are presented in Table 3. The operating point, i.e., the m values, was close to the optimal operating point for this system according to the triangle theory [4]. The m values are dimensionless flowrate ratios of liquid and solid phases. For the SMB process, these are defined as
where tsw is the switching time (s), Vcol is the column volume (m3), and p is the zone index. From these values, the internal flowrates Qint (m3·s−1) in each zone of the SMB plant could be calculated.
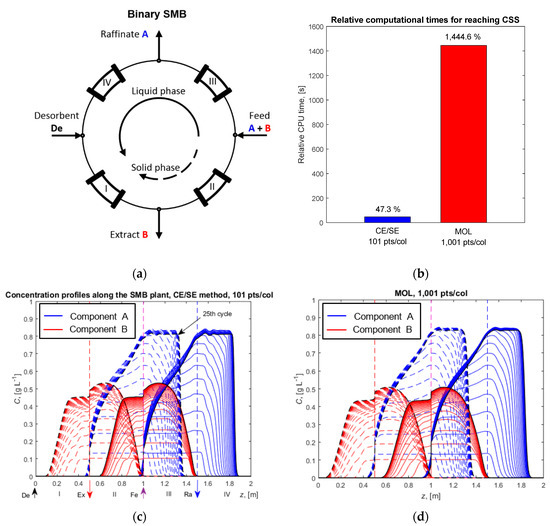
Figure 4.
Binary SMB chromatographic process with Langmuir isotherms—LDF model. (a) Process configuration. (b) Comparison of the computational times for each of the methods. (c) Concentration profiles along the SMB plant calculated using the CE/SE method. (d) Concentration profiles along the SMB plant calculated using MOL. Dashed curves in (c,d) are at the beginning of each cycle, while solid curves are at the end.

Table 3.
Simulation parameters for Example 3 (binary SMB process with Langmuir isotherms described by the LDF model).
After several column switchings, a cyclic steady state (CSS) was reached. In this particular example, this cyclic steady state was reached after 25 cycles. Figure 4c,d show the concentration profiles of the two components inside the SMB plant during this startup. Dashed–dotted curves are the profiles at the beginning of every cycle just after the column switching, while the solid curves correspond to the profiles at end of the cycle. With the chosen values for the isotherm parameters Hi and bi, the component A (blue) had lower affinity to the solid phase and flowed out of the raffinate port, while the component B (red) had higher affinity to the solid phase and flowed out from the extract port.
For the simulation with the CE/SE method, the value of the CFL number was selected as 0.4. To satisfy the CFL condition in each zone of the SMB, the value of the time step size was calculated from the highest liquid velocity in the system, i.e., in zone I.
The number of spatial points was 101 per column, and the CSS was reached after 47% relative computational time. To achieve similar accuracy with the MOL, 10 times more spatial discretization points per column were needed. This led to the much slower performance of the MOL simulation (Figure 4b).
For MOL in Figure 4b,d, ode45 was used. Again, the performance of ode23 was similar (1002% compared to 1444.6% for ode45). In contrast, ode15s needed 580-fold more computational time than the simulation with ode45.
4.4. Ternary Center-Cut Eight-Zone SMB Process with Linear Isotherms and the Ideal Equilibrium Model
Ternary SMB processes, called center-cut separations, play an important role in biotechnology and pharmaceutical industries for the isolation of desired key components that have medium affinity to the solid phase in comparison to the other fractions in the mixture. There are several configurations for ternary center-cut separation—cascade of two SMB units, eight-zone SMB, Japan Organo process, etc. [28]. Eight-zone SMB processes can be used with raffinate or with extract recycle [23]. In the present work, an eight-zone SMB process with raffinate recycle and both linear and Langmuir isotherms was investigated.
Since, for systems with linear isotherms, the ideal equilibrium model Equation (4) can be converted directly to form Equation (10), it was used as a first example. The process configuration is shown in Figure 5a. Again, each zone had one column. The nodal material balances for the eight-zone SMB with raffinate recycle are as follows:
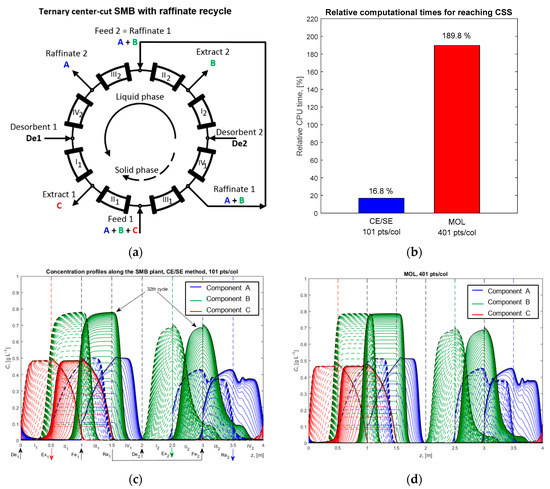
Figure 5.
Ternary center-cut eight-zone SMB chromatographic process with raffinate recycle with linear isotherms—ideal equilibrium model. (a) Process configuration. (b) Comparison of the computational times for each of the methods. (c) Concentration profiles along the SMB plant calculated using CE/SE method. (d) Concentration profiles along the SMB plant calculated using MOL. Dashed curves in (c,d) are at the beginning of each cycle, while solid curves are at the end.
- − First desorbent node
- − First extract node
- − First feed node
- − First raffinate node
- − Second desorbent node
- − Second extract node
- − Second feed node
- − Second raffinate node
Table 4 summarizes the simulation parameters and the operating conditions, which were taken from [22]. Component C (red) had the highest affinity to the solid phase and flowed out through the first extract port together with some amount of the middle component B (green). The outlet mixture from the first raffinate port, which contained the components A (blue, the component with the lowest affinity to the solid phase) and B, was fed to the second subunit where it was separated. Component B flowed out from the second extract port, while component A flowed out from the second raffinate port. Simulation results show that CSS was reached after 32 cycles, and the concentration profiles are shown in Figure 5c,d. For the CE/SE method simulation, the CFL number was 0.8 and the number of spatial discretization points per column was 101. For the MOL, 401 such points were needed per column, and the mass matrix for systems with linear isotherms is constant and, therefore, was calculated once at the beginning of the simulation, leading to a very fast computational time. As result, the CE/SE method was only 11-fold faster than MOL (Figure 5b).

Table 4.
Simulation parameters for Example 4 (ternary center-cut eight-zone SMB process with linear isotherms described by the ideal equilibrium model).
Finally, it is worth mentioning that, for linear isotherms and for N , a new analytical solution approach is available, which was applied to binary and ternary center-cut SMB processes and which is even orders of magnitude faster than the CE/SE method [29].
4.5. Ternary Center-Cut Eight-Zone SMB Process with Langmuir Isotherms and the LDF Model
Lastly, a study of a ternary system with Langmuir isotherms was performed. The process configuration was the same as in Figure 5a, i.e., ternary eight-zone center-cut SMB with raffinate recycle. The nodal material balances were those in Equations (31)–(46). Physical parameters of the chromatographic columns are presented in Table 4 (first column), while the operating conditions and the parameters of the participating components are listed in Table 5. The operating conditions were calculated with the methodology presented in [30] for a true moving bed process (TMB) with little adjustments to take the SMB process into account; to the best of our knowledge, this is the first simulation of ternary eight-zone SMB with Langmuir isotherms in the nonlinear concentration range. Calculations for the nonlinear case were based on the LDF model.

Table 5.
Simulation parameters for Example 5 (ternary center-cut eight-zone SMB process with Langmuir isotherms described by the LDF model).
Concentration profiles along the SMB plant are shown in Figure 6a,b. Target component B was obtained as a pure component from the extract port of the second SMB subunit. The cyclic steady state was reached after around 60 cycles. The CFL number for the CE/SE method was 0.4, and the number of spatial discretization points was 101 per column. On the other hand, MOL needed 10-fold more spatial points per column to achieve a similar accuracy to CE/SE. This led to enormous computational time for the MOL method (around 2.5 h) in comparison to the CE/SE simulation (Figure 6c), which is 350-fold greater than that by CE/SE.
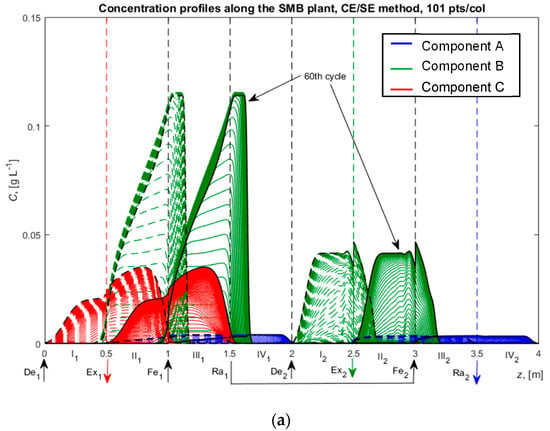
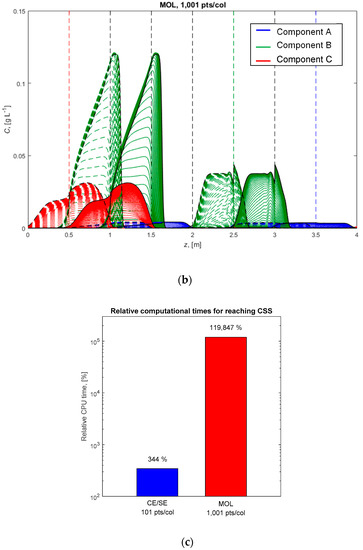
Figure 6.
Ternary center-cut eight-zone SMB chromatographic process with raffinate recycle with Langmuir isotherms—LDF model. (a) Concentration profiles along the SMB plant calculated using CE/SE method. (b) Concentration profiles along the SMB plant calculated using MOL. (c) Comparison of the computational times for each of the methods. Dashed curves in (a,b) are at the beginning of each cycle, while solid curves are at the end.
5. Discussion and Conclusions
This paper focused on the numerical simulation of chromatographic processes using the explicit space–time CE/SE method. For a systematic evaluation of the method, different models with linear and nonlinear isotherms and different process configurations including single-column, binary, and ternary eight-zone SMB processes were investigated.
For the first time, the application of the CE/SE method to the popular equilibrium model was also considered. It was shown that application of the CE/SE method requires reformulation of the equilibrium model equations. For linear isotherms, this reformulation is easy to achieve and straightforward. For nonlinear isotherms, reformulation is more involved. In particular, two different approaches were proposed, namely, (i) the reversed space–time formulation, which can be applied to any nonlinear adsorption isotherm, and (ii) an inversion-based approach, which applies only to the important but limited class of nonlinear Langmuir isotherms. In either case, reformulation is only possible for single-column processes. For the reversed method, the solution procedure propagates in space instead of time. Therefore, the temporal evolution of the boundary conditions needs to be known before the start of the simulation, which is not possible for multicolumn processes with recycle. For the inversion-based method, discussed in detail in Appendix A, an adjusted time was introduced, which depended on the linear velocity of the column and would be different from column to column in a multicolumn process, thus preventing simultaneous integration of multicolumn processes in time. Consequently, the LDF model was used for the simulation of nonlinear multicolumn processes since reformulation is not required for the LDF model.
In all cases, the CE/SE method was shown to be much more efficient than the popular cell model, which represents a method of lines approach using a first-order finite volume discretization (MOL) in combination with established time integrators from MATLAB such as the Runge–Kutta method ode45. Computational efficiency of the two methods was measured in terms of computational times for same resolution of the concentration profiles. The largest reduction in computation times was found for processes with steep fronts and with nonlinear Langmuir adsorption isotherms. In particular, the CE/SE method was found to be about 350-fold faster than MOL with ode45 for a ternary eight-zone SMB process with raffinate recycle for a challenging center-cut separation. This opens new possibilities for an efficient computational evaluation of different processes for ternary center-cut separations with nonlinear adsorption isotherms. The main focus in this field has so far been on processes with linear adsorption isotherms described by the true moving bed approximation [23].
In our future work, we also intend to use the CE/SE method for model-based control of binary and ternary SMB processes following the approach in [31,32,33].
Author Contributions
Conceptualization, V.P.C.; formal analysis, V.P.C.; funding acquisition, A.K.; investigation, V.P.C.; methodology, V.P.C.; project administration, A.V.W. and A.K.; software, V.P.C.; supervision, A.V.W. and A.K.; validation, V.P.C.; visualization, V.P.C.; writing—original draft, V.P.C.; writing—review and editing, A.V.W. and A.K. All authors read and agreed to the published version of the manuscript.
Funding
The financial support of the International Max Planck Research School for Advanced Methods in Process and Systems Engineering—IMPRS ProEng Magdeburg through the European Regional Development Fund (ERDF) is greatly acknowledged.
Acknowledgments
Valentin Plamenov Chernev would like to thank to Heorhii Marhiiev from Donetsk National Technical University in Pokrovsk (DonNTU), Ukraine for the fruitful discussions related to the CE/SE method during his stay in Magdeburg.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analysis, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Nomenclature
| bi,k | retention factor in the Langmuir isotherm expression (L·g−1) |
| Ci,k | liquid phase concentration (g·L−1) |
| Courant–Friedrichs–Lewy number | |
| Courant–Friedrichs–Lewy number in the reversed CE/SE method | |
| Dax | axial dispersion coefficient (m2·s−1) |
| Dcol | column diameter (m) |
| Dpipe | pipe diameter (m) |
| f | vector of fluxes |
| Hi,k | adsorption Henry coefficient |
| mass transfer coefficient (s−1) | |
| Lcol | column length (m) |
| m | dimensionless flowrate ratio of liquid and solid phases |
| N | number of theoretical stages of the cell model |
| Ncol | number of columns in the SMB plant |
| Ncomp | number of components |
| Nt | number of time steps |
| Nz | number of spatial steps |
| p | vector of source terms |
| qi,k | solid phase concentration (g·L−1) |
| solid phase concentration at the interphase in equilibrium with the liquid phase (g·L−1) | |
| Q | volumetric flowrate (m3·s−1) |
| t | time coordinate (s) |
| tsim | simulation time (s) |
| tsw | switching time (s) |
| u | vector of state variables |
| Vcol | column volume (m3) |
| vk | liquid phase velocity (m·s−1) |
| z | spatial coordinate (m) |
| Δt | time step size (s) |
| Δz | spatial step size (m) |
| ε | column void fraction |
| τ | adjusted time |
| A, B, C | different components |
| De | desorbent stream |
| Ex | extract stream |
| Fe | feed stream |
| i, r | component indices |
| in | column inlet |
| int | internal flowrate |
| j | spatial coordinate index |
| k | column index |
| n | time coordinate index |
| out | column outlet |
| p | zone index |
| Ra | raffinate stream |
Appendix A. Direct Conversion of the Equilibrium Model to the Form Given by Equation (10)
As already mentioned above, the CE/SE method applies to PDEs of the type shown in Equation (10). In contrast to this, the equilibrium model of chromatography is given by
with and . In the case of a linear isotherm, shown in Equation (2), its derivative is constant, and Equation (A1) can be easily rearranged to the form in Equation (10). For nonlinear isotherms, an inversion of the function is required and the corresponding system of PDEs can then be solved for f instead of u according to
which is again equivalent to the form given by Equation (10).
For the single-component Langmuir isotherm, inversion leads to the solution of a single quadratic equation, which can be solved explicitly for the unique positive solution to bring the model to the form given by Equation (10). For the multicomponent Langmuir isotherm, inversion leads to the solution of a system of quadratic equations, which is much more involved. However, the problem can be simplified by transformation of the equilibrium model to a simpler form by using an adjusted time [34]. With this adjusted time, the equilibrium model reads
In a second step, the well-known inverse of the Langmuir isotherm [2] (p. 252) is applied,
and Equation (A3), together with Equation (A4), is solved for q. For the Langmuir isotherm, this is always possible for any number of components.
References
- Schmidt-Traub, H.; Schulte, M.; Seidel-Morgenstern, A. Preparative Chromatography, 3rd ed.; Wiley-VCH Verlag: Weinheim, Germany, 2020. [Google Scholar]
- Rhee, H.-K.; Aris, R.; Amundson, N.R. First-Order Partial Differential Equations: Volume II—Theory and Application of Hyperbolic Systems of Quasilinear Equations; Prentice Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Mazzotti, M.; Rajendran, A. Equilibrium theory-based analysis of nonlinear waves in separation processes. Ann. Rev. Chem. Biomol. Eng. 2013, 4, 119–141. [Google Scholar] [CrossRef] [PubMed]
- Mazzotti, M.; Storti, S.; Morbidelli, M. Optimal operation of simulated moving bed units for nonlinear chromatographic separations. J. Chromatogr. A 1997, 769, 3–24. [Google Scholar] [CrossRef]
- Migliorini, C.; Mazzotti, M.; Morbidelli, M. Continuous chromatographic separation through simulated moving beds under linear and nonlinear conditions. J. Chromatogr. A 1998, 827, 161–173. [Google Scholar] [CrossRef]
- Kaspereit, M.; Seidel-Morgenstern, A.; Kienle, A. Design of simulated moving bed processes under reduced purity requirements. J. Chromatogr. A 2007, 1162, 2–13. [Google Scholar] [CrossRef]
- Sainio, T.; Kaspereit, M. Analysis of steady state recycling chromatography using equilibrium theory. Sep. Purif. Technol. 2009, 6, 9–18. [Google Scholar] [CrossRef]
- Siitonen, J.; Sainio, T. Unified design of chromatographic separation processes. Chem. Eng. Sci. 2015, 122, 436–451. [Google Scholar] [CrossRef]
- Rhee, H.-K.; Aris, R.; Amundson, N.R. Shock layer in two solute chromatography: Effect of axial dispersion and mass transfer. Chem. Eng. Sci. 1974, 29, 2049–2060. [Google Scholar] [CrossRef]
- Mazzotti, M.; Storti, G.; Morbidelli, M. Shock layer analysis in multicomponent chromatography and countercurrent adsorption. Chem. Eng. Sci. 1994, 49, 1337–1355. [Google Scholar] [CrossRef]
- Marquardt, W. Traveling waves in chemical processes. Int. Chem. Eng. 1990, 30, 585–606. [Google Scholar]
- Lim, Y.I.; Chang, S.-C.; Jørgensen, S.B. A novel partial differential algebraic equation (PDAE) solver: Iterative space-time conservation element/solution element (CE/SE) method. Comput. Chem. Eng. 2004, 28, 1309–1324. [Google Scholar] [CrossRef]
- Von Lieres, E.; Andersson, J. A fast and accurate solver for the general rate model of column liquid chromatography. Comp. Chem. Eng. 2010, 34, 1180–1191. [Google Scholar] [CrossRef]
- Javeed, S.; Qamar, S.; Seidel-Morgenstern, A.; Warnecke, G. Efficient and accurate numerical simulation of nonlinear chromatographic processes. Comput. Chem. Eng. 2011, 35, 2294–2305. [Google Scholar] [CrossRef]
- Vande Wouwer, A.; Saucez, P.; Vilas, C. Simulation of ODE/PDE Models with MATLAB, OCTAVE and SCILAB. Scientific and Engineering Applications; Springer International Publishing Switzerland: Cham, Switzerland, 2014; pp. 125–202. [Google Scholar]
- Köhler, R.; Mohl, K.D.; Schramm, H.; Zeitz, M.; Kienle, A.; Mangold, M.; Stein, E.; Gilles, E.-D. Methods of lines within the simulation environment DIVA© for chemical processes. In Adaptive Method of Lines; Vande Wouwer, A., Saucez, P., Schiesser, W.E., Eds.; CRC Press: New York, NY, USA, 2001; pp. 371–406. [Google Scholar]
- Chang, S.-C. New Developments in the Method of Space-Time Conservation Element and Solution Element: Applications to the Euler and Navier-Stokes Equations; NASA TM 106226; The SAO/NASA Astrophysics Data System: Cleveland, OH, USA, 1993. [Google Scholar]
- Chang, S.-C. The method of space-time conservation element and solution element—A new approach for solving the Navier–Stokes and Euler equations. J. Comp. Phys. 1995, 119, 295–324. [Google Scholar] [CrossRef]
- Chang, S.-C. Courant number insensitive CE/SE schemes. In Proceedings of the 38th AIAA Joint Propulsion Conference, Indianapolis, Indiana, 7–10 July 2002; AIAA-2002-3890. AIAA: Indianapolis, IN, USA, 2012. [Google Scholar]
- Lim, Y.I.; Jørgensen, S.B. A fast and accurate numerical method for solving simulated moving bed (SMB) chromatographic separation problems. Chem. Eng. Sci. 2004, 59, 1931–1947. [Google Scholar] [CrossRef]
- Yao, C.; Tang, S.; Lu, Y.; Yao, H.-M.; Tade, M.O. Combination of space-time conservation element/solution element method and continuous prediction technique for accelerated simulation of simulated moving bed chromatography. Chem. Eng. Process 2015, 96, 54–61. [Google Scholar] [CrossRef]
- Keßler, L.C.; Seidel-Morgenstern, A. Theoretical study of multicomponent continuous countercurrent chromatography based on connected 4-zone units. J. Chromatogr. A 2006, 1126, 323–337. [Google Scholar] [CrossRef]
- Da Silva, F.V.S.; Seidel-Morgenstern, A. Evaluation of center-cut separations applying simulated moving bed chromatography with 8 zones. J. Chromatogr. A 2016, 1456, 123–136. [Google Scholar] [CrossRef]
- Kiwala, D.; Mendrella, J.; Antos, D.; Seidel-Morgenstern, A. Center-cut separation of intermediately. adsorbing target component by 8-zone simulated moving bed chromatography with internal recycle. J. Chromatogr. A 2016, 1453, 19–33. [Google Scholar] [CrossRef]
- MATLAB R2017a (Version 9.2.0); The MathWorks Inc.: Natick, MA, USA, 2017.
- Guiochon, G.; Lin, B. Modeling for Preparative Chromatography, 1st ed.; Academic Press: San Diego, CA, USA, 2003. [Google Scholar]
- Rhee, H.-K.; Aris, R.; Amundson, N.R. First-Order Partial Differential Equations: Volume I—Theory and Application of Single Equations; Prentice Hall: Englewood Cliffs, NJ, USA, 1986. [Google Scholar]
- Agrawal, G.; Kawajiri, Y. Comparison of various ternary simulated moving bed separation schemes by multi-objective optimization. J. Chromatogr. A 2012, 1238, 105–113. [Google Scholar] [CrossRef]
- Pishkari, R.; Kienle, A. Fast and accurate simulation of simulated moving bed chromatographic processes with linear adsorption isotherms. Comp. Aided Chem. Eng. 2020, 48, 487–492. [Google Scholar]
- Nicolaos, A.; Muhr, L.; Gotteland, P.; Nicoud, R.M.; Bailly, M. Application of equilibrium theory to ternary moving bed configurations (4 + 4, 5 + 4, 8 and 9 zones) II. Langmuir case. J. Chromatogr. A 2001, 908, 87–109. [Google Scholar] [CrossRef]
- Suvarov, P.; Vande Wouwer, A.; Kienle, A.; Nobre, C.; De Weireld, G. Cycle to cycle adaptive control of simulated moving bed chromatographic separation processes. J. Proc. Control 2014, 24, 357–367. [Google Scholar] [CrossRef]
- Suvarov, P.; Vande Wouwer, A.; Lee, J.-W.; Seidel-Morgenstern, A.; Kienle, A. Control of incomplete separation in simulated moving bed chromatographic processes. In Proceedings of the 11th IFAC Symposium on Dynamics and Control of Process Systems, including Biosystems, Trondheim, Norway, 6–8 June 2016. [Google Scholar]
- Suvarov, P.; Lee, J.-W.; Vande Wouwer, A.; Seidel-Morgenstern, A.; Kienle, A. Online estimation of optimal operating conditions for simulated moving bed chromatographic processes. J. Chrom. A 2019, 1602, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Helfferich, F.G.; Klein, G. Multicomponent Chromatography: Theory of Interference; Marcel Dekker: New York, NY, USA, 1970. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).