Initiator Feeding Policies in Semi-Batch Free Radical Polymerization: A Monte Carlo Study
Abstract
1. Introduction
2. Model Development
2.1. Kinetic Model
2.2. Monte Carlo Simulation
3. Results and Discussion
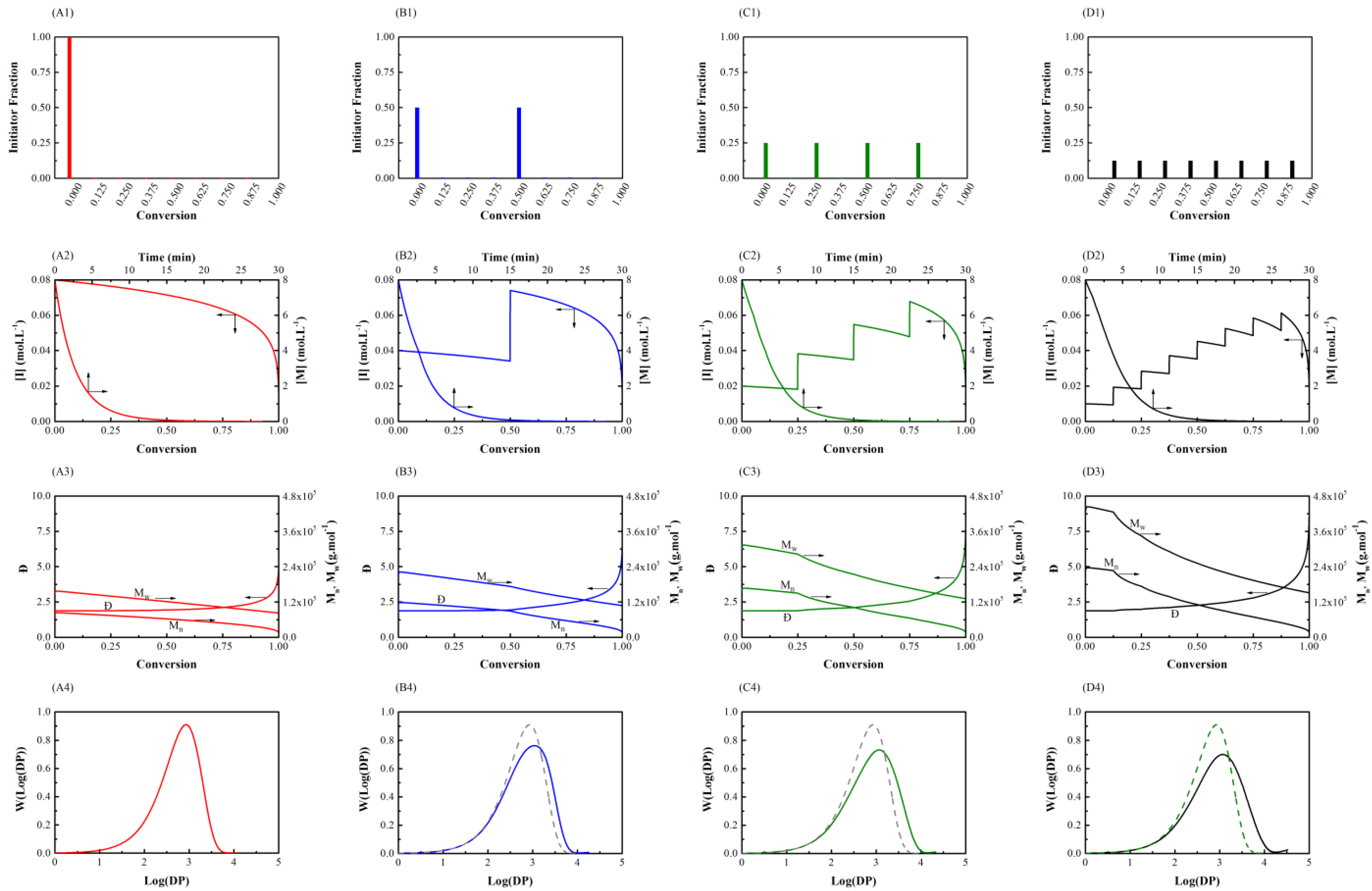
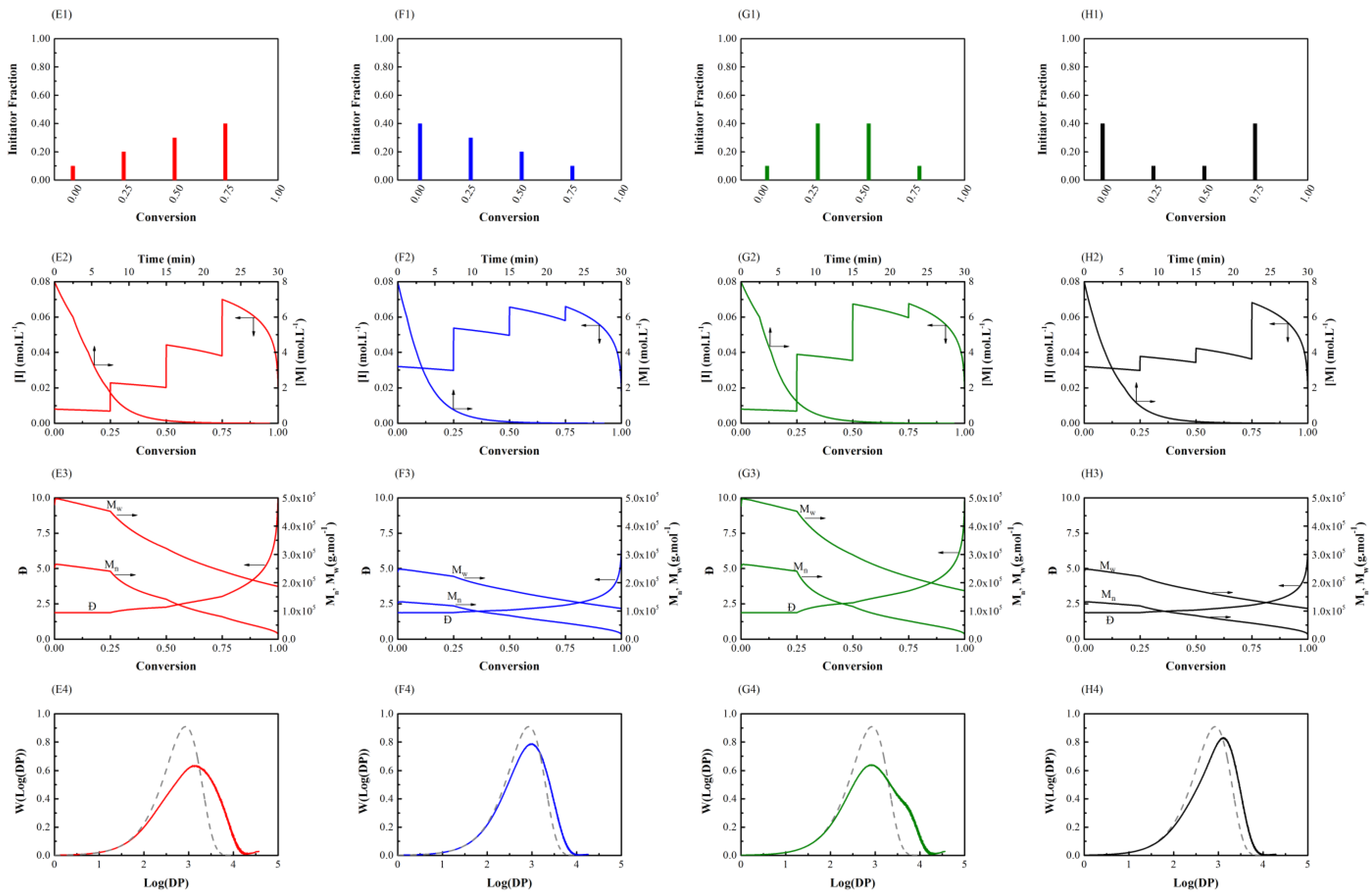
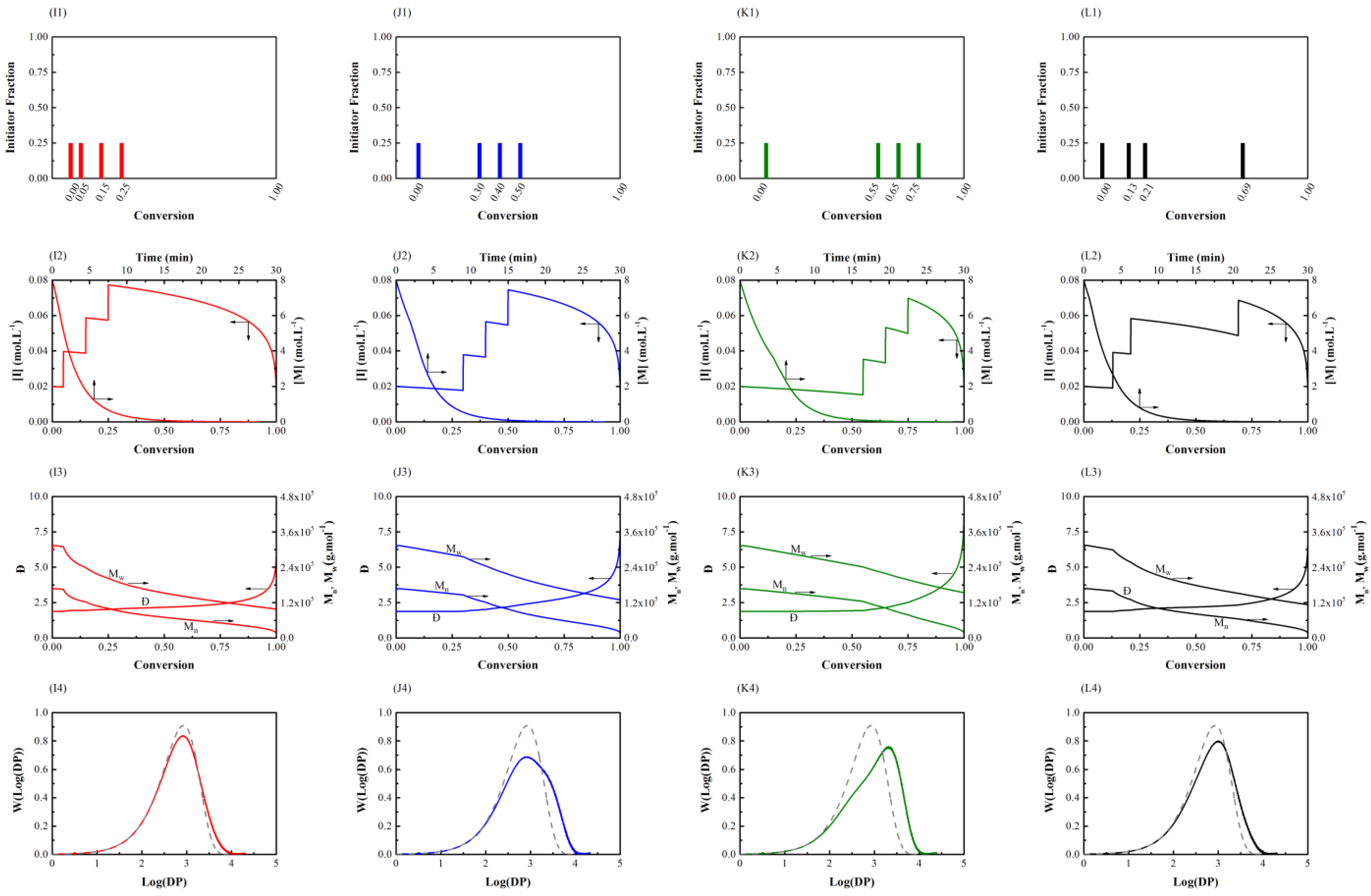
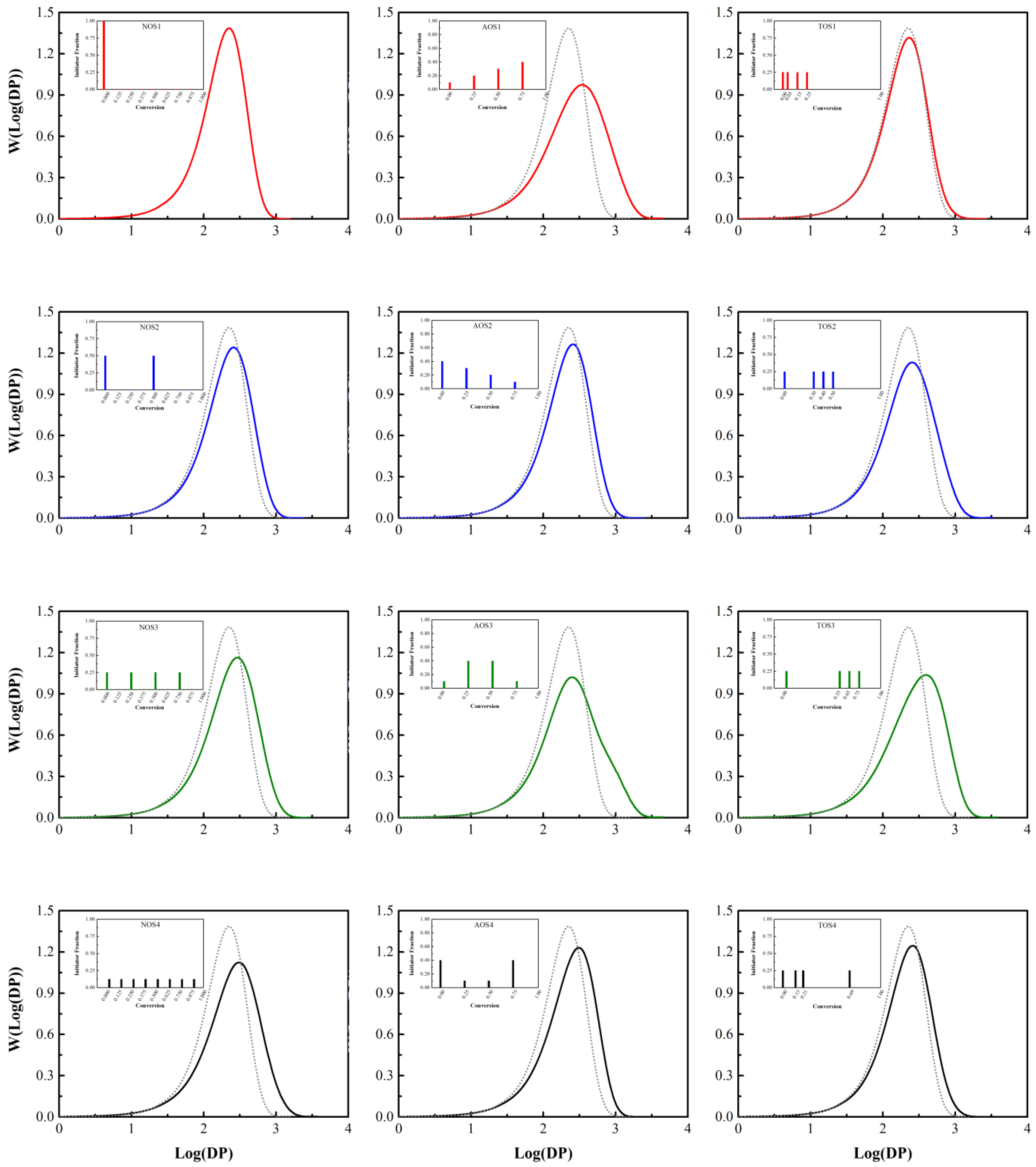
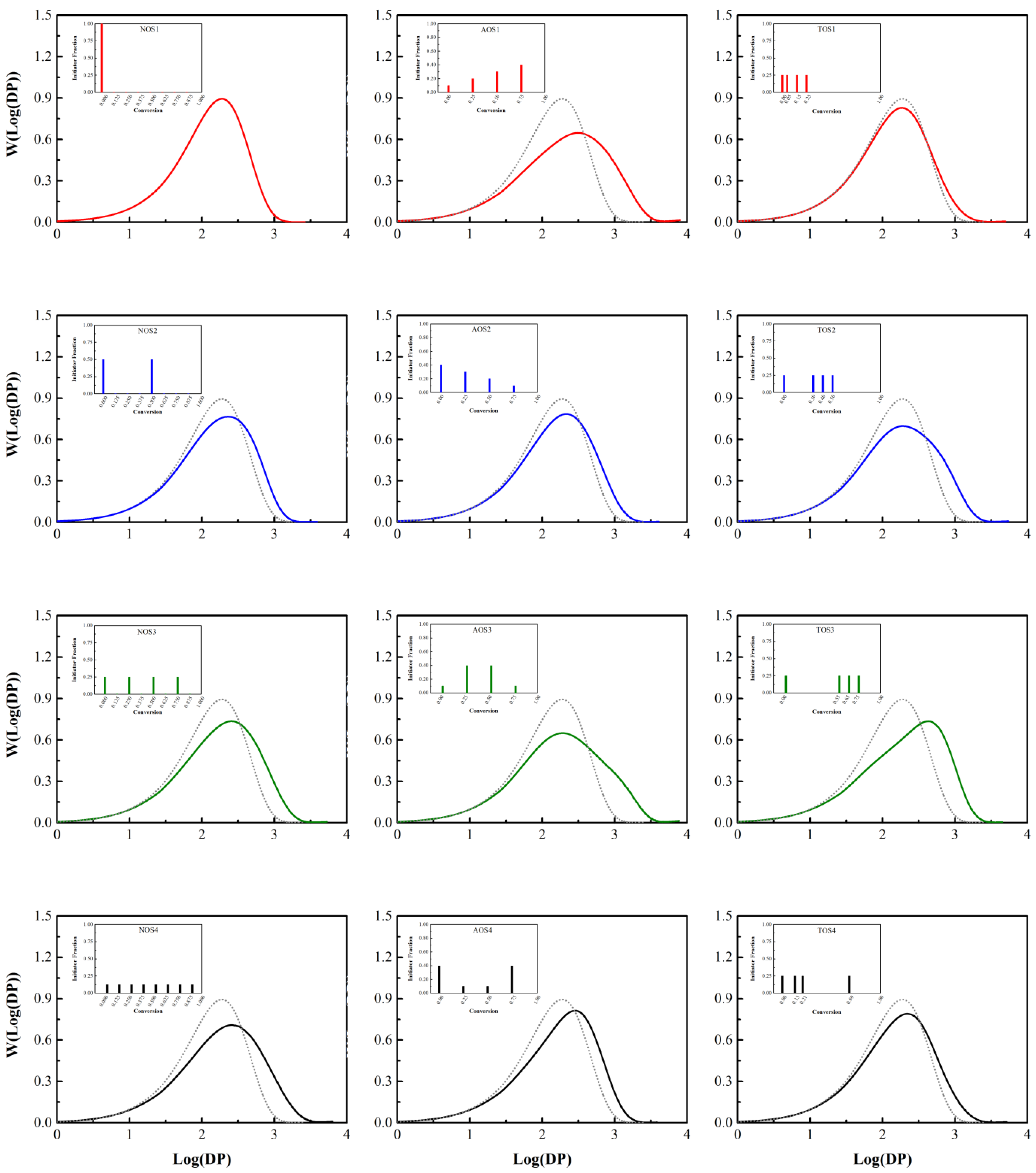
3.1. Initiator Feeding Policies
3.2. General Free Radical Polymerization
3.3. Styrene Free Radical Polymerization in Solution
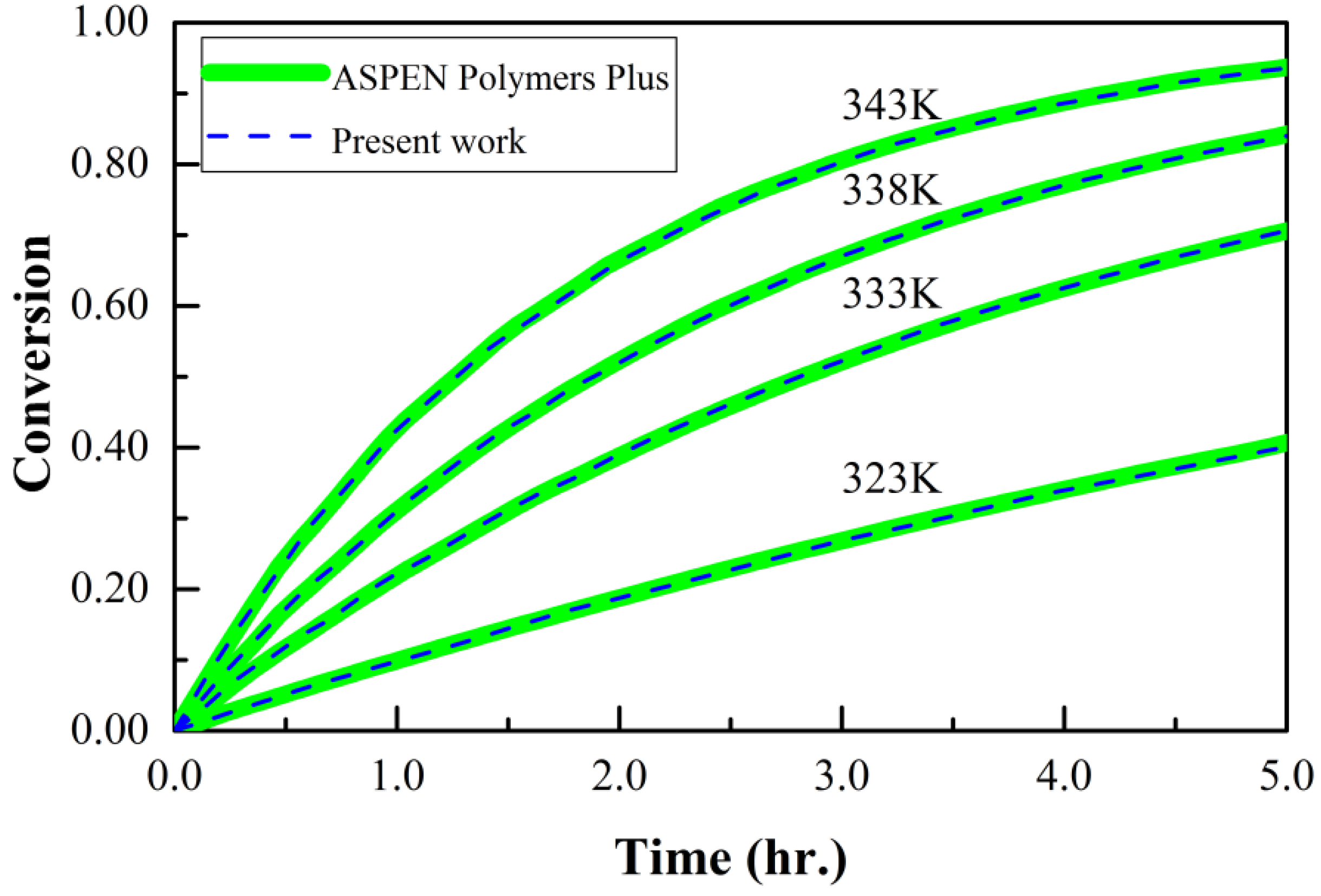
3.4. Free Radical Polymerization of Methyl Methacrylate in Solution
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chiefari, J.; Chong, Y.K.B.K.B.; Ercole, F.; Krstina, J.; Jeffery, J.; Le, T.P.T.P.T.; Mayadunne, R.T.A.T.A.; Meijs, G.F.F.; Moad, C.L.L.; Moad, G.; et al. Living Free-Radical Polymerization by Reversible Addition—Fragmentation Chain Transfer: The RAFT Process. Macromolecules 1998, 31, 5559–5562. [Google Scholar] [CrossRef]
- Noble, B.B.; Coote, M.L. First principles modelling of free-radical polymerisation kinetics. Int. Rev. Phys. Chem. 2013, 32, 467–513. [Google Scholar] [CrossRef]
- Wang, D.; Wang, W.-J.; Li, B.-G.; Zhu, S. Semibatch RAFT polymerization for branched polyacrylamide production: Effect of divinyl monomer feeding policies. AIChE J. 2013, 59, 1322–1333. [Google Scholar] [CrossRef]
- Lowe, A.B.; McCormick, C.L. Homogeneous controlled free radical polymerization in aqueous media. Aust. J. Chem. 2002, 55, 367–379. [Google Scholar] [CrossRef]
- Aydin, M.; Arsu, N.; Yagci, Y.; Jockusch, S.; Turro, N.J. Mechanistic study of photoinitiated free radical polymerization using thioxanthone thioacetic acid as one-component type II photoinitiator. Macromolecules 2005, 38, 4133–4138. [Google Scholar] [CrossRef]
- Crowley, T.J.; Choi, K.Y. Experimental studies on optimal molecular weight distribution control in a batch-free radical polymerization process. Chem. Eng. Sci. 1998, 53, 2769–2790. [Google Scholar] [CrossRef]
- Crowley, T.J.; Choi, K.Y. Discrete optimal control of molecular weight distribution in a batch free radical polymerization process. Ind. Eng. Chem. Res. 1997, 36, 3676–3684. [Google Scholar] [CrossRef]
- Kiparissides, C.; Krallis, A.; Meimaroglou, D.; Pladis, P.; Baltsas, A. From Molecular to Plant-Scale Modeling of Polymerization Processes: A Digital High-Pressure Low-Density Polyethylene Production Paradigm. Chem. Eng. Technol. 2010, 33, 1754–1766. [Google Scholar] [CrossRef]
- Wang, R.; Luo, Y.; Li, B.; Sun, X.; Zhu, S. Design and Control of Copolymer Composition Distribution in Living Radical Polymerization Using Semi-Batch Feeding Policies: A Model Simulation. Macromol. Theory Simul. 2006, 15, 356–368. [Google Scholar] [CrossRef]
- Zhang, M.; Ray, W.H. Modeling of “living” free-radical polymerization processes.I. Batch, semibatch, and continuous tank reactors. J. Appl. Polym. Sci. 2002, 86, 1630–1662. [Google Scholar] [CrossRef]
- Colombani, D. Chain-growth control in free radical polymerization. Prog. Polym. Sci. 1997, 22, 1649–1720. [Google Scholar] [CrossRef]
- Hamielec, A.E.; MacGregor, J.F.; Penlidis, A. Multicomponent free-radical polymerization in batch, semi-batch and continuous reactors. In Makromolekulare Chemie. Macromolecular Symposia; Hüthig & Wepf Verlag: Basel, Switzerland, 1987; Volume 10, pp. 521–570. [Google Scholar]
- Goto, A.; Fukuda, T. Effects of radical initiator on polymerization rate and polydispersity in nitroxide-controlled free radical polymerization. Macromolecules 1997, 30, 4272–4277. [Google Scholar] [CrossRef]
- Wang, R.; Luo, Y.; Li, B.-G.; Zhu, S. Control of gradient copolymer composition in ATRP using semibatch feeding policy. AIChE J. 2007, 53, 174–186. [Google Scholar] [CrossRef]
- Diaz-Camacho, F.; Lopez-Morales, S.; Vivaldo-Lima, E.; Saldivar-Guerra, E.; Vera-Graziano, R.; Alexandrova, L. Effect of Regime of Addition of Initiator on TEMPO-Mediated Polymerization of Styrene. Polym. Bull. 2004, 52, 339. [Google Scholar] [CrossRef]
- Roa-Luna, M.; Diaz-Barber, M.P.; Vivaldo-Lima, E.; Lona, L.M.F.; McManus, N.T.; Penlidis, A.; Macromol, J. Assessing the Importance of Diffusion-Controlled Effects on Polymerization Rate and Molecular Weight Development in Nitroxide-Mediated Radical Polymerization of Styrene. Sci. Pure Appl. Chem. 2007, 44, 192. [Google Scholar] [CrossRef]
- Mastan, E.; Zhu, S. Method of moments: A versatile tool for deterministic modeling of polymerization kinetics. Eur. Polym. J. 2015, 68, 139–160. [Google Scholar] [CrossRef]
- Mastan, E.; Li, X.; Zhu, S. Modeling and theoretical development in controlled radical polymerization. Prog. Polym. Sci. 2015, 45, 71–101. [Google Scholar] [CrossRef]
- Arzamendi, G.; Asua, J.M. Monomer addition policies for copolymer composition control in semicontinuous emulsion copolymerization. J. Appl. Polym. Sci. 1989, 38, 2019–2036. [Google Scholar] [CrossRef]
- Guiping, C.; Zhongnan, Z.; Huihui, L.; Minghua, Z. Molecular weight distribution of polystyrene produced in a starved feed reactor. Chinese J. Chem. Eng. 1999, 7, 205–213. [Google Scholar]
- Pinto, J.M.; Giudici, R. Optimization of a cocktail of initiators for suspension polymerization of vinyl chloride in batch reactors. Chem. Eng. Sci. 2001, 56, 1021–1028. [Google Scholar] [CrossRef]
- Li, X.; Wang, W.-J.; Weng, F.; Li, B.-G.; Zhu, S. Targeting copolymer composition distribution via model-based monomer feeding policy in semibatch RAFT mini-emulsion copolymerization of styrene and butyl acrylate. Ind. Eng. Chem. Res. 2014, 53, 7321–7332. [Google Scholar] [CrossRef]
- Meimaroglou, D.; Kiparissides, C. Review of Monte Carlo methods for the prediction of distributed molecular and morphological polymer properties. Ind. Eng. Chem. Res. 2014, 53, 8963–8979. [Google Scholar] [CrossRef]
- Brandão, A.L.T.; Soares, J.B.P.; Pinto, J.C.; Alberton, A.L. When polymer reaction engineers play dice: Applications of Monte Carlo models in PRE. Macromol. React. Eng. 2015, 9, 141–185. [Google Scholar] [CrossRef]
- Bruns, W.; Motoc, I.; O’Driscoll, K.F. Monte Carlo Applications in Polymer Science; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 27. [Google Scholar]
- Khubi-Arani, Z.; Salami-Kalajahi, M.; Najafi, M.; Roghani-Mamaqani, H.; Haddadi-Asl, V.; Ghafelebashi-Zarand, S.M. Simulation of styrene free radical polymerization over bi-functional initiators using Monte Carlo simulation method and comparison with mono-functional initiators. Polym. Sci. Ser. B 2010, 52, 184–192. [Google Scholar] [CrossRef]
- Tobita, H.; Hatanaka, K. Branched structure formation in free radical polymerization of vinyl acetate. J. Polym. Sci. Part B Polym. Phys. 1996, 34, 671–681. [Google Scholar] [CrossRef]
- Prescott, S.W. Chain-length dependence in living/controlled free-radical polymerizations: Physical manifestation and Monte Carlo simulation of reversible transfer agents. Macromolecules 2003, 36, 9608–9621. [Google Scholar] [CrossRef]
- Pintos, E.; Sarmoria, C.; Brandolin, A.; Asteasuain, M. Modeling of RAFT Polymerization Processes Using an Efficient Monte Carlo Algorithm in Julia. Ind. Eng. Chem. Res. 2016, 55, 8534–8547. [Google Scholar] [CrossRef]
- Mohammadi, Y.; Najafi, M.; Haddadi-Asl, V. Comprehensive study of free radical copolymerization using a Monte Carlo simulation method, 1. Macromol. Theory Simul. 2005, 14, 325–336. [Google Scholar] [CrossRef]
- Najafi, M.; Haddadi-Asl, V.; Mohammadi, Y. Application of the Monte Carlo simulation method to the investigation of peculiar free-radical copolymerization reactions: Systems with both reactivity ratios greater than unity (rA > 1 and rB > 1). J. Appl. Polym. Sci. 2007, 106, 4138. [Google Scholar] [CrossRef]
- Najafi, M.; Roghani-Mamaqani, H.; Haddadi-Asl, V.; Salami-Kalajahi, M. A simulation of kinetics and chain length distribution of styrene FRP and ATRP: Chain-length-dependent termination. Adv. Polym. Technol. 2011, 30, 257–268. [Google Scholar] [CrossRef]
- Saeb, M.R.; Mohammadi, Y.; Ahmadi, M.; Khorasani, M.M.; Stadler, F.J. A Monte Carlo-based feeding policy for tailoring microstructure of copolymer chains: Reconsidering the conventional metallocene catalyzed polymerization of $α$-olefins. Chem. Eng. J. 2015, 274, 169–180. [Google Scholar] [CrossRef]
- Salami-Kalajahi, M.; Najafi, M.; Haddadi-Asl, V. Application of Monte Carlo simulation method to polymerization kinetics over Ziegler--Natta catalysts. Int. J. Chem. Kinet. 2009, 41, 45–56. [Google Scholar] [CrossRef]
- Najafi, M.; Roghani-Mamaqani, H.; Salami-Kalajahi, M.; Haddadi-Asl, V. A comprehensive Monte Carlo simulation of styrene atom transfer radical polymerization. Chinese J. Polym. Sci. 2010, 28, 483–497. [Google Scholar] [CrossRef]
- Fu, Y.; Cunningham, M.F.; Hutchinson, R.A. Modeling of Nitroxide-Mediated Semibatch Radical Polymerization. Macromol. React. Eng. 2007, 1, 243–252. [Google Scholar] [CrossRef]
- Ellis, M.F.; Taylor, T.W.; Gonzalez, V.; Jensen, K.F. Estimation of the molecular weight distribution in batch polymerization. AIChE J. 1988, 34, 1341–1353. [Google Scholar] [CrossRef]
- Buback, M.; Sandmann, J. Pressure and temperature dependence of the decomposition rate of aliphatic tert-butyl peroxyesters. Zeitschrift für Phys. Chemie 2000, 214, 583. [Google Scholar] [CrossRef]
- Buback, M.; Wittkowski, L. Acid-Induced Decomposition of Di-tert-butyl Peroxide in n-Heptane Solution up to High Temperatures and Pressures. Zeitschrift für Phys. Chemie 1999, 210, 61–81. [Google Scholar] [CrossRef]
- Hui, A.W.; Hamielec, A.E. Thermal polymerization of styrene at high conversions and temperatures. An experimental study. J. Appl. Polym. Sci. 1972, 16, 749–769. [Google Scholar] [CrossRef]
- Buback, M.; Gilbert, R.G.; Hutchinson, R.A.; Klumperman, B.; Kuchta, F.-D.; Manders, B.G.; O’Driscoll, K.F.; Russell, G.T.; Schweer, J. Critically evaluated rate coefficients for free-radical polymerization, 1. Propagation rate coefficient for styrene. Macromol. Chem. Phys. 1995, 196, 3267–3280. [Google Scholar] [CrossRef]
- Buback, M.; Kuchta, F.-D. Variation of the propagation rate coefficient with pressure and temperature in the free-radical bulk polymerization of styrene. Macromol. Chem. Phys. 1995, 196, 1887–1898. [Google Scholar] [CrossRef]
- Brandrup, J.; Immergut, E.H.; Grulke, E.A. Polymer Handbook, 4th ed.; Wiley: New York, NY, USA, 1999; ISBN 0471166286. [Google Scholar]
- Chen, C.-Y.; Wu, Z.-Z.; Kuo, J.-F. Determination of the mode of termination in free-radical copolymerization. Polym. Eng. Sci. 1987, 27, 553–557. [Google Scholar] [CrossRef]
- Schmidt, A.D.; Ray, W.H. The dynamic behavior of continuous polymerization reactors—I: Isothermal solution polymerization in a CSTR. Chem. Eng. Sci. 1981, 36, 1401–1410. [Google Scholar] [CrossRef]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Matsumoto, M.; Nishimura, T. Mersenne twister: A 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans. Model. Comput. Simul. 1998, 8, 3–30. [Google Scholar] [CrossRef]
- AspenTech Methyl Methacrylate Polymerization in Ethyl Acetate. Aspen Polymer Plus User Guide. Examples Application Case B (3rd ed.). 1981. Available online: https://sites.chemengr.ucsb.edu/~ceweb/courses/che184b/aspenplus/PolymersPlusUserGuideVolume2.pdf (accessed on 10 September 2020).
| Case 1: General Free Radical Polymerization | |
| Initiator decomposition | |
| Chain initiation | |
| Propagation | |
| Termination by combination | |
| Termination by disproportionation | |
| Case 2: Free Radical Polymerization of Styrene | |
| Chemical Initiation | |
| Thermal Initiation | |
| Propagation | |
| Termination by combination | |
| Termination by disproportionation | |
| Chain transfer to monomer | |
| Chain transfer to solvent | |
| Case 3: Free Radical Polymerization of Methyl Methacrylate | |
| Chemical Initiation | |
| Propagation | |
| Termination by disproportionation | |
| Chain transfer to monomer | |
| Chain transfer to solvent | |
| Parameters | Value/Expression | References |
|---|---|---|
| Case 1: General Free Radical Polymerization | ||
| f | 0.50 | This work |
| kd (s−1) | 10−3 | This work |
| ki (L.mol−1.s−1) | 104 | This work |
| Kp (L.mol−1.s−1) | 104 | This work |
| ktc (L.mol−1.s−1) | 108 | This work |
| ktd (L.mol−1.s−1) | 108 | This work |
| Case 2: Free Radical Polymerization of Styrene | ||
| f | 0.50 | [38,39] |
| kd (s−1) | 6.78 × 1015 exp(−17,714.0 / T) | [38,39] |
| kthermal (L2.mol−2.s−1) | 2.19 × 105 exp(−13,800.0 / T) | [40] |
| Kp (L.mol−1.s−1) | 4.266 × 107 exp(−3910.0 / T) | [41] |
| kt,0 (L.mol−1.s−1) | 3.82 × 109 exp(−958.0 / T) | [42] |
| KtrM (L.mol−1.s−1) | 2.31 × 106 exp(−6377.0 / T) | [40] |
| KtrS (L.mol−1.s−1) | 1.8 | [43] |
| Kt (L.mol−1.s−1) | [10] | |
| ktc (L.mol−1.s−1) | 0.01kt | [44] |
| ktd (L.mol−1.s−1) | 0.99kt | [44] |
| Note: wp is the polymer weight fraction. | ||
| Case 3: Free Radical Polymerization of Methyl Methacrylate | ||
| f | 0.50 | [45] |
| kd (s−1) | 1.2525 × 1014 exp(−14,770.0 / T) | [43] |
| Kp (L.mol−1.s−1) | 4.92 × 105 exp(−2191.0 / T) | [45] |
| ktrM (L.mol−1.s−1) | 7.177 × 109 exp(−9036.0 / T) | [43] |
| ktrS (L.mol−1.s−1) | 4.673 × 108 exp(−7902.0 / T) | [43] |
| ktd (L.mol−1.s−1) | 9.8 × 107 exp(−353.0 / T) | [45] |
| Number of Shots | Initiator Fraction |
| NOS-1 | One step (1.000) |
| NOS-2 | Two steps (0.500, 0.500) |
| NOS-3 | Four steps (0.250, 0.250, 0.250, 0.250) |
| NOS-4 | Eight steps (0.125, 0.125, 0.125, 0.125, 0.125, 0.125, 0.125, 0.125) |
| Amount of Shots | Initiator Fraction |
| AOS-1 | (0.10, 0.20, 0.30, 0.40) |
| AOS-2 | (0.40, 0.30, 0.20, 0.10) |
| AOS-3 | (0.10, 0.40, 0.40, 0.10) |
| AOS-4 | (0.40, 0.10, 0.10, 0.40) |
| Time of Shots | Conversion of Each Shot (Initiator Fraction is Equal to 0.25 for Each Step) |
| TOS-1 | (0.00, 0.05, 0.15, 0.25) |
| TOS-2 | (0.00, 0.30, 0.40, 0.50) |
| TOS-3 | (0.00, 0.55, 0.65, 0.75) |
| TOS-4 | (0.00, random, random, random) |
| Policy | Reaction Time at Conversion 100% (min) | Đ | Unreacted Initiator (%) | |
|---|---|---|---|---|
| Number of Shots | ||||
| NOS-1 | 42 | 22,000 | 2.1 | 3.5 |
| NOS-2 | 39 | 27,000 | 2.4 | 6.7 |
| NOS-3 | 39 | 31,000 | 2.7 | 9.3 |
| NOS-4 | 39 | 34,000 | 2.9 | 11 |
| Amount of Shots | ||||
| AOS-1 | 42 | 41,000 | 3.4 | 12.3 |
| AOS-2 | 39 | 27,000 | 2.4 | 6.6 |
| AOS-3 | 43 | 37,000 | 3.2 | 8.3 |
| AOS-4 | 37 | 30,000 | 2.6 | 10.6 |
| Time of Shots | ||||
| TOS-1 | 44 | 24,000 | 2.3 | 3.7 |
| TOS-2 | 40 | 30,000 | 2.7 | 7.4 |
| TOS-3 | 41 | 38,000 | 3.2 | 12.8 |
| TOS-4 | 40 | 27,000 | 2.5 | 6.4 |
| Policy | Reaction Time at Conversion 100% (min) | Đ | Unreacted Initiator (%) | |
|---|---|---|---|---|
| Number of Shots | ||||
| NOS-1 | 1700 | 19,000 | 4.2 | 7.4 |
| NOS-2 | 1650 | 24,500 | 5.3 | 9.5 |
| NOS-3 | 1600 | 30,000 | 6.2 | 11.2 |
| NOS-4 | 1600 | 33,000 | 7.0 | 12.5 |
| Amount of Shots | ||||
| AOS-1 | 1600 | 40,000 | 8.4 | 13.3 |
| AOS-2 | 1600 | 25,000 | 5.4 | 9.5 |
| AOS-3 | 1650 | 37,000 | 7.9 | 11.0 |
| AOS-4 | 1600 | 27,000 | 5.7 | 11.6 |
| Time of Shots | ||||
| TOS-1 | 1700 | 22,000 | 4.9 | 8.1 |
| TOS-2 | 1650 | 29,000 | 6.3 | 9.9 |
| TOS-3 | 1600 | 34,000 | 7.2 | 13.1 |
| TOS-4 | 1630 | 25,500 | 5.5 | 9.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seyedi, A.; Najafi, M.; Russell, G.T.; Mohammadi, Y.; Vivaldo-Lima, E.; Penlidis, A. Initiator Feeding Policies in Semi-Batch Free Radical Polymerization: A Monte Carlo Study. Processes 2020, 8, 1291. https://doi.org/10.3390/pr8101291
Seyedi A, Najafi M, Russell GT, Mohammadi Y, Vivaldo-Lima E, Penlidis A. Initiator Feeding Policies in Semi-Batch Free Radical Polymerization: A Monte Carlo Study. Processes. 2020; 8(10):1291. https://doi.org/10.3390/pr8101291
Chicago/Turabian StyleSeyedi, Ali, Mohammad Najafi, Gregory T. Russell, Yousef Mohammadi, Eduardo Vivaldo-Lima, and Alexander Penlidis. 2020. "Initiator Feeding Policies in Semi-Batch Free Radical Polymerization: A Monte Carlo Study" Processes 8, no. 10: 1291. https://doi.org/10.3390/pr8101291
APA StyleSeyedi, A., Najafi, M., Russell, G. T., Mohammadi, Y., Vivaldo-Lima, E., & Penlidis, A. (2020). Initiator Feeding Policies in Semi-Batch Free Radical Polymerization: A Monte Carlo Study. Processes, 8(10), 1291. https://doi.org/10.3390/pr8101291









