Numerical Modeling of Thermal Flows in Entrance Channels for Polymer Extrusion: A Parametric Study
Abstract
1. Introduction
2. Mathematical Model of Temperature Distribution of the Casson Fluid Flow
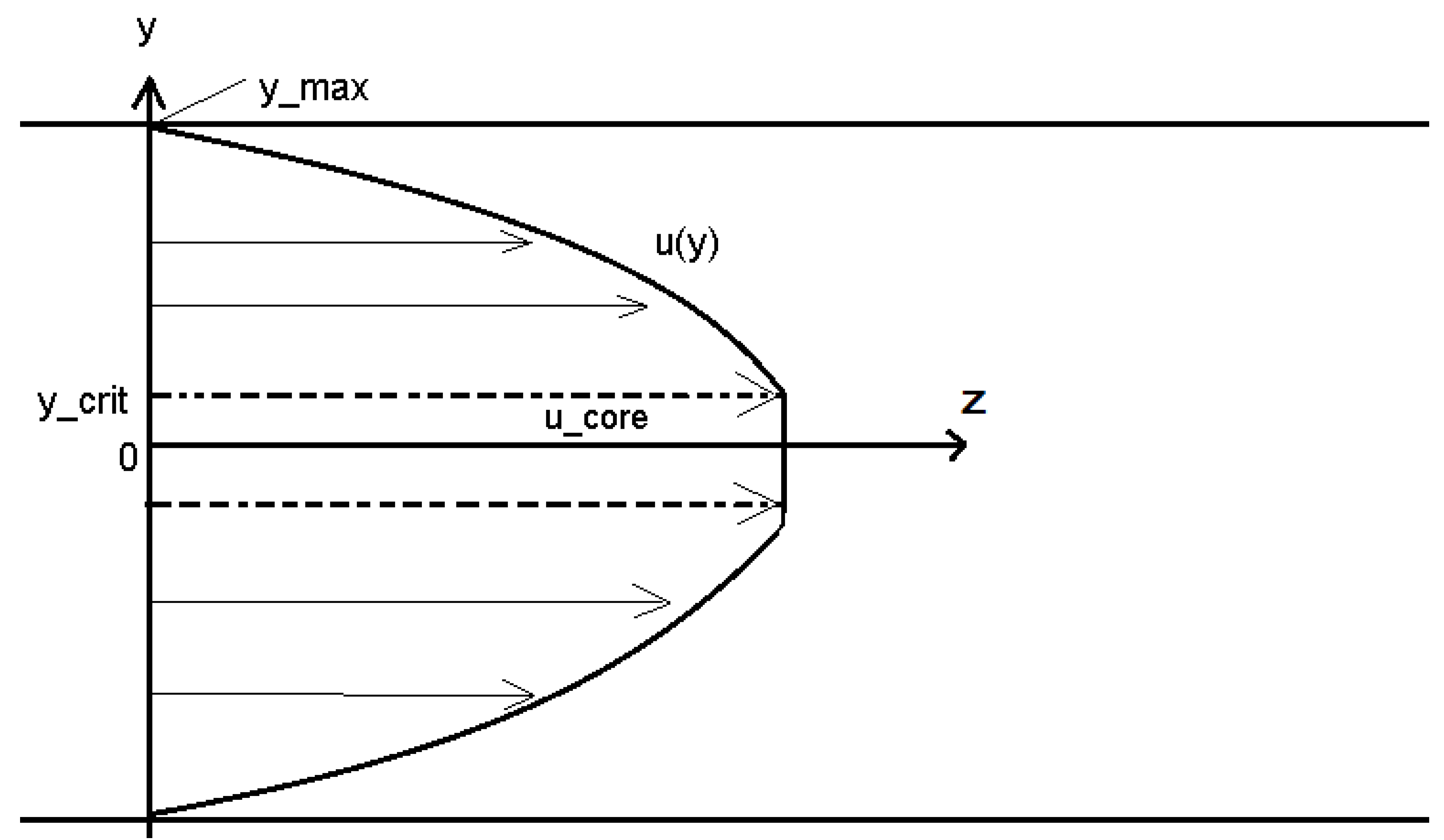
2.1. Derivation of the Velocity Profile
2.2. Temperature Distribution of the Flow in Parallel-Plate Channel
2.3. Temperature Distribution of the Flow in Circular Tube Channel
Finite Element Model
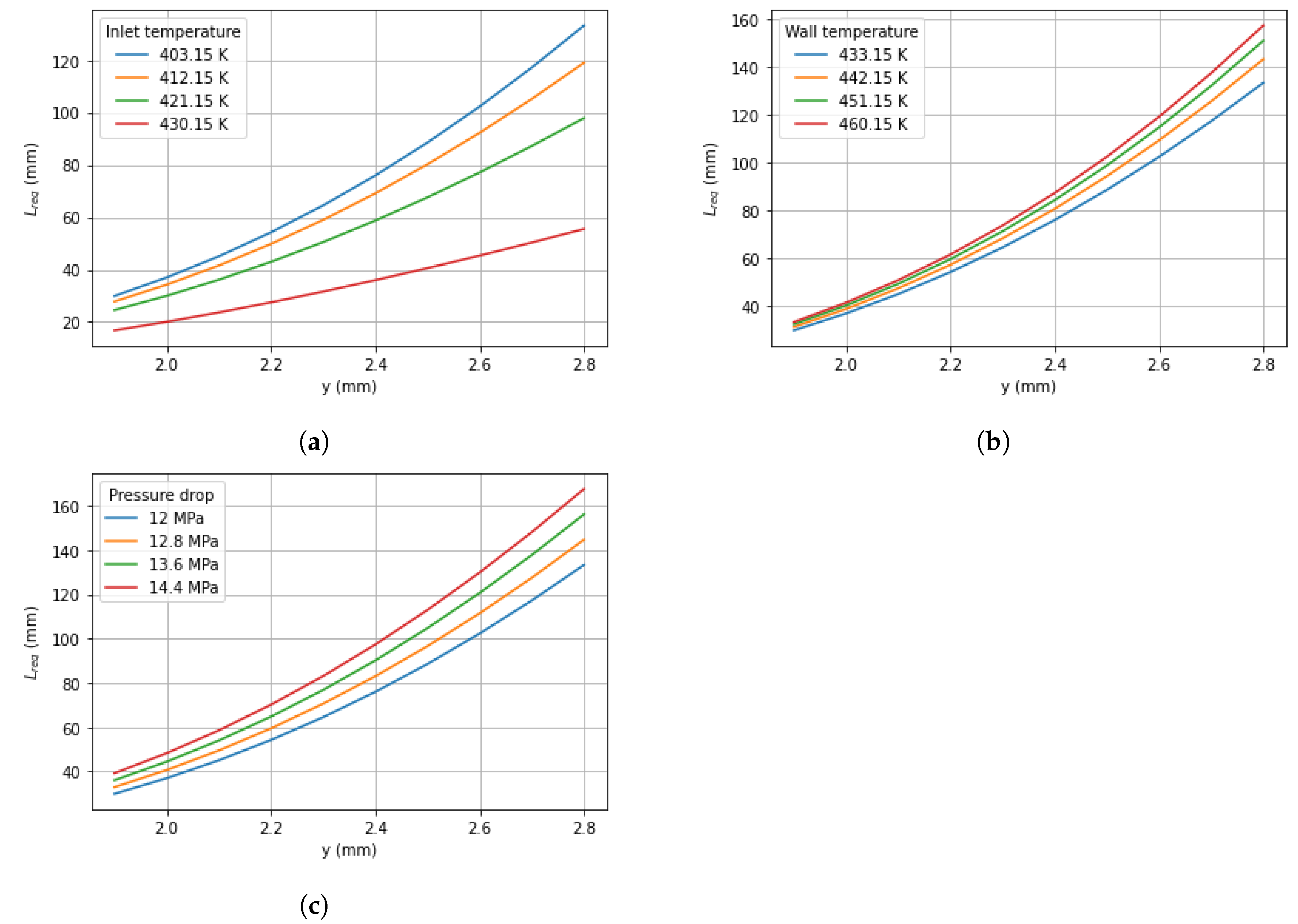
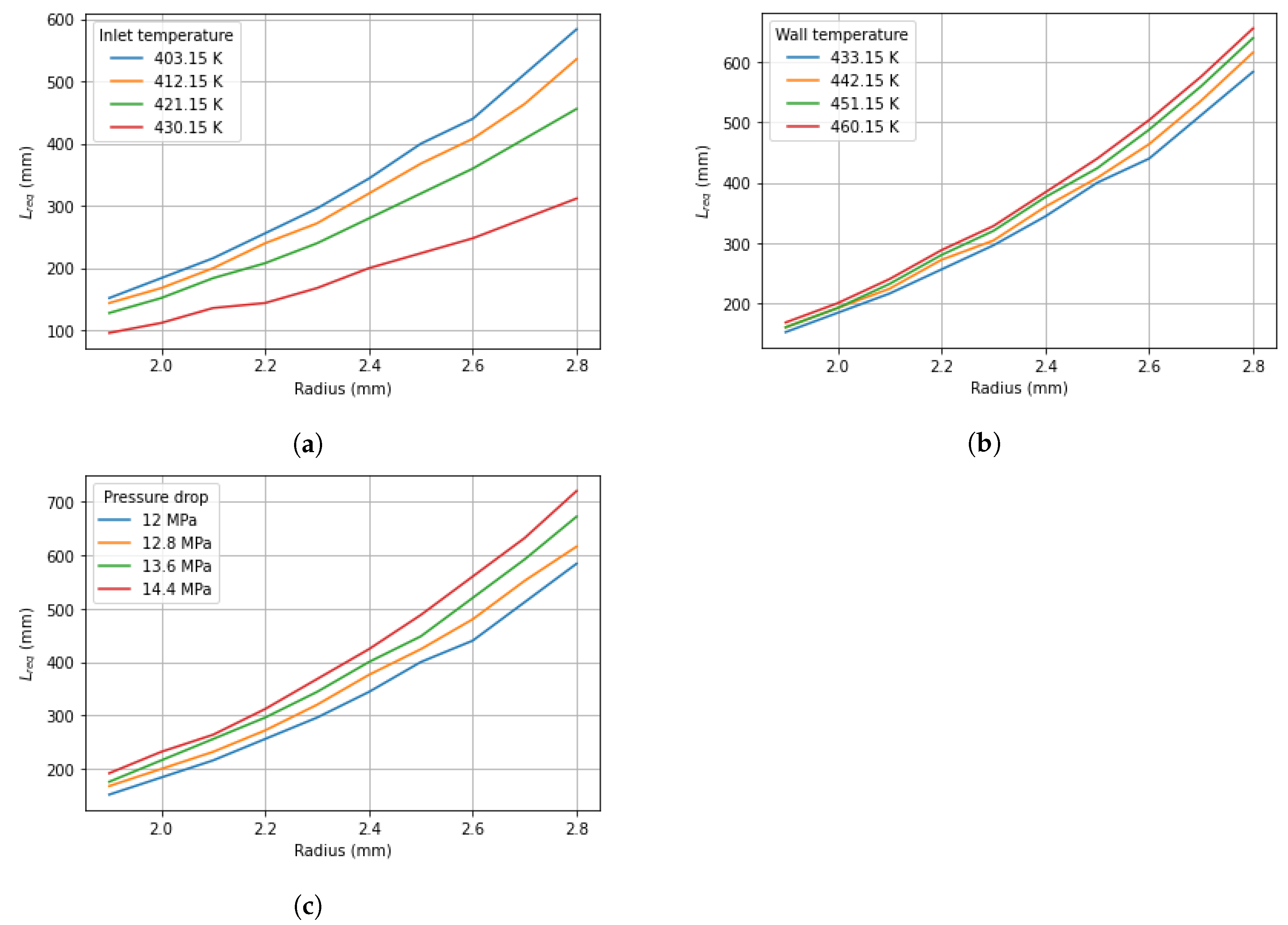
3. Description of the Parametric Study
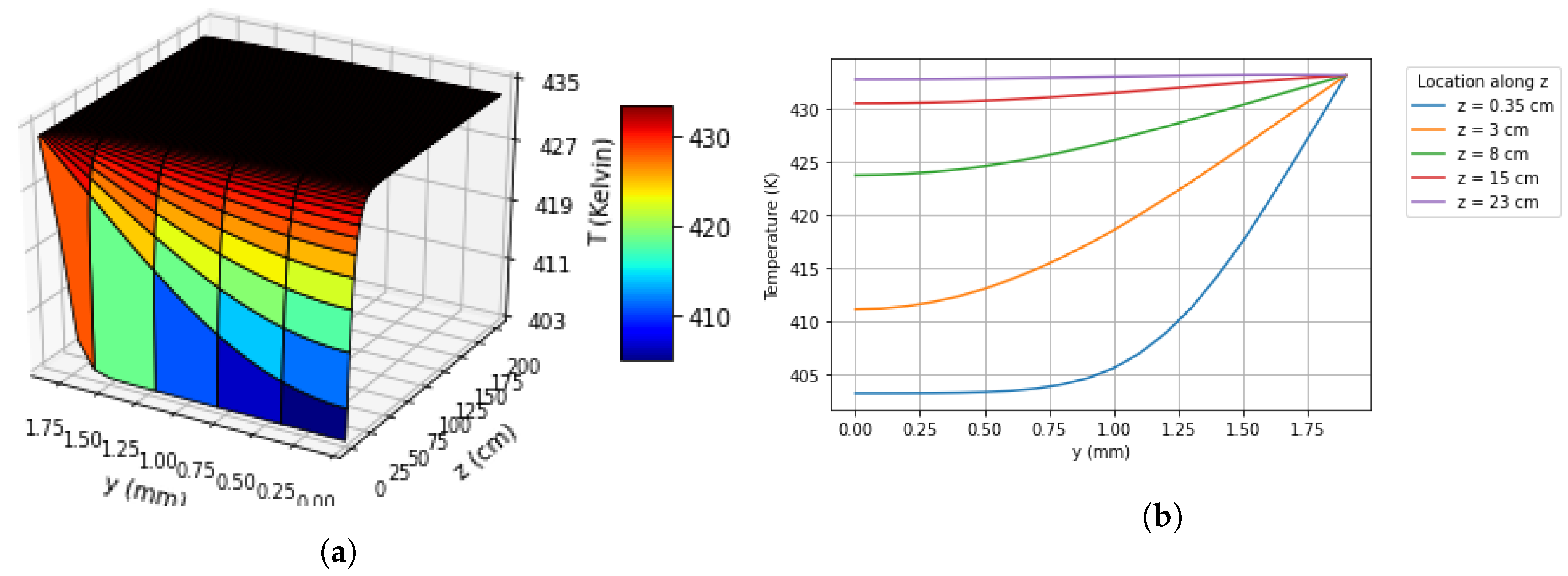
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Constants and variables | |
| ,g | pressure drop in the channel |
| Casson viscosity | |
| shear rate in circular tube | |
| shear rate in parallel-plate | |
| element domain | |
| boundary domain | |
| fluid density | |
| shear stress | |
| Casson yield stress | |
| wall stress constant | |
| specific heat capacity of the fluid | |
| increment in y | |
| increment in z | |
| k | fluid thermal conductivity |
| L | distance from the inlet to exit |
| optimal length of the channel to reach the steady state | |
| for inlet pressure, for pressure at exit | |
| Q | flow rate |
| dimensional, and non-dimensional radial coordinates of the circular tube | |
| maximum radius of the circular tube | |
| critical radius of the circular tube | |
| T | temperature of the fluid |
| temperature of the fluid at or for , and at for | |
| temperature of the fluid at the inlet | |
| wall temperature | |
| u | velocity of the fluid flow |
| y | axis coordinate perpendicular to z in parallel-plate |
| , | critical length from the center to the critical point along y in parallel-plate |
| distance from the center to the wall in parallel-plate | |
| dimensional, and non-dimensional axial coordinates in the direction of the flow | |
| F,{F} | local and global load vectors |
| K,K | local and global stiffness matrices |
| W | vector of three linear shape functions |
| Superscripts and subscripts | |
| evaluation of the entity referring to the particular element | |
| p | evaluation of the corresponding function at the particular point |
| T | matrix transpose |
| J | Jacobian matrix |
References
- Morris, P.J.T. Polymer Pioneers; University of Pennsylvania Press: Philadelphia, PA, USA, 1989. [Google Scholar]
- Razeghiyadaki, A.; Zhang, D.; Wei, D.; Perveen, A. Optimization of Polymer Extrusion Die Based on Response Surface Method. Processes 2020, 8, 1043. [Google Scholar] [CrossRef]
- Yilmaz, O.; Polat, Y.; Kocabas, H. Optimum Design of a Flat Coat-Hanger Die for Spunbond Nonwoven Production Process. In Proceedings of the 3rd International Scientific Conference on Engineering “Manufacturing and Advanced Technologies”, Mostar, Herzegovina, 18–20 September 2014. [Google Scholar]
- Maier, C.; Calafut, T. Polypropylene; William Andrew: New York, NY, USA, 1998. [Google Scholar]
- Igali, D.; Perveen, A.; Wei, D.; Zhang, D.; Mentbayeva, A. 3D FEM Study of the Flow Uniformity of Flat Polypropylene Film/Sheet Extrusion Dies. Key Eng. Mater. 2020, 841, 375–380. [Google Scholar] [CrossRef]
- NPTEL. Available online: https://nptel.ac.in/courses/112/106/112106153/ (accessed on 9 September 2020).
- A Guide to Polyolefin Sheet Extrusion. Available online: https://www.yumpu.com/en/document/read/11672189/a-guide-to-polyolefin-sheet-extrusion-lyondellbasell (accessed on 9 September 2020).
- Winter, H.H.; Fritz, H.J. Design of dies for the extrusion of sheets and annular parisons: The distribution problem. Polym. Eng. Sci. 1986, 26, 543–553. [Google Scholar] [CrossRef]
- Ellahi, R.; Hameed, M. Numerical analysis of steady non-Newtonian flows with heat transfer analysis, MHD and nonlinear slip effects. Int. J. Numer. Methods Heat Fluid Flow 2012, 22, 24–38. [Google Scholar] [CrossRef]
- Gauthier, F.; Goldsmith, H.L.; Mason, S.G. Particle motions in Non-Newtonian media. II. Poiseuille flow. Trans. Soc. Rheol. 1971, 15, 297–330. [Google Scholar] [CrossRef]
- Chhabra, R.P.; Richardson, J.F. Non-Newtonian Flow and Applied Rheology: Engineering Applications; Butterworth-Heinemann: Oxford, UK, 2011. [Google Scholar]
- Biswas, D. Blood Flow Models: A Comparative Study; Mittal Publications: Delhi, India, 2002. [Google Scholar]
- Rao, M.A. Rheology of Fluid and Semisolid Foods: Principles and Applications; Springer: New York, NY, USA, 2010. [Google Scholar]
- Karger-Kocsis, J. Polypropylene Structure; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Wilkes, J.O. Fluid Mechanics for Chemical Engineers with Microfluidics and CFD; Pearson: London, UK, 2005; pp. 272–320. [Google Scholar]
- Gee, R.E.; Lyon, J.B. Nonisothermal flow of viscous non-newtonian fluids. Ind. Eng. Chem. 1957, 49, 956–960. [Google Scholar] [CrossRef]
- Catherine, O. A Short Review of Flow Simulation Techniques for Extrusion Die Design. In Proceedings of the SPE International Polyolefins Conference, Houston, TX, USA, 27 February 2017. [Google Scholar]
- Wei, D.; Luo, H. Finite element solutions of heat transfer in molten polymer flow in tubes with viscous dissipation. Int. J. Heat Mass Transf. 2003, 46, 3097–3108. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Casson fluid flow and heat transfer over a nonlinearly stretching surface. Chin. Phys. B 2013, 22, 074701. [Google Scholar] [CrossRef]
- Khan, M.I.; Waqas, M.; Hayat, T.; Alsaedi, A. A comparative study of Casson fluid with homogeneous-heterogeneous reactions. J. Colloid Interface Sci. 2017, 498, 85–90. [Google Scholar] [CrossRef] [PubMed]
- Michaelides, E.; Crowe, C.T.; Schwarzkopf, J.D. Multiphase Flow Handbook; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Nandy, S.K. Analytical solution of MHD stagnation-point flow and heat transfer of Casson fluid over a stretching sheet with partial slip. Int. Sch. Res. Not. 2013, 2013, 108264. [Google Scholar] [CrossRef]
- Ullah, I.; Alkanhal, T.A.; Shafie, S.; Nisar, K.S.; Khan, I. MHD Slip flow of Casson fluid along a nonlinear permeable stretching cylinder saturated in a porous medium with chemical reaction, viscous dissipation, and heat generation/absorption. Symmetry 2019, 11, 531. [Google Scholar] [CrossRef]
- Lungu, M.; Petrovan, S.; Rusu, M.; Apetroaiei, A.; Lungu, A. Application of rheological models for the description of the flow characteristics of some polymer systems. Acta Polym. 1992, 43, 214–218. [Google Scholar] [CrossRef]
- Matveenko, V.N.; Kirsanov, E.A. Structural viscosity and structural elasticity of polymer melts. Russ. J. Appl. Chem. 2018, 91, 839–865. [Google Scholar] [CrossRef]
- Vlachopoulos, J.; Polychronopoulos, N.D. Chapter 4: Flat Film and Sheet Dies; Smithers Rapra: London, UK, 2012. [Google Scholar]
- Adewale, F.J.; Lucky, A.P.; Oluwabunmi, A.P.; Boluwaji, E.F. Selecting the most appropriate model for rheological characterization of synthetic based drilling mud. Int. J. Appl. Eng. Res. 2017, 12, 7614–7629. [Google Scholar]
- Engineering Toolbox. Available online: https://www.engineeringtoolbox.com (accessed on 9 September 2020).
- Technical Data on Extrusion Dies. Available online: https://figshare.com/articles/dataset/01-Die_-_CF3-B-ETP_-_Manual_1_pdf/12981113 (accessed on 9 September 2020).
- Typical Engineering Properties of Polypropylene. Available online: https://www.ineos.com/globalassets/ineos-group/businesses/ineos-olefins-and-polymers-usa/products/technical-information--patents/ineos-engineering-properties-of-pp.pdf (accessed on 9 September 2020).
- Cebeci, T. Convective Heat Transfer; Springer: New York, NY, USA, 2002. [Google Scholar]
- Segerlind, L.J. Applied Finite Element Analysis; John Wiley: New York, NY, USA, 1984. [Google Scholar]
- Karkri, M.; Jarny, Y.; Mousseau, P. Estimation of the Initial Temperature Profile in the Channel of an Experimental Extrusion Die. In Proceedings of the 5th International Conference on Inverse Problems in Engineering: Theory and Practice, Cambridge, UK, 1–15 July 2005. [Google Scholar]
- Andreozzi, A.; Buonomo, B.; Pasqua, A.; Ercole, D.; Manca, O. Heat Transfer Behaviors of Parallel Plate Systems in Sensible Thermal Energy Storage. In Proceedings of the 72nd Conference of the Italian Thermal Machines Engineering Association, Lecce, Italy, 6–8 September 2017. [Google Scholar]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amangeldi, M.; Wei, D.; Perveen, A.; Zhang, D. Numerical Modeling of Thermal Flows in Entrance Channels for Polymer Extrusion: A Parametric Study. Processes 2020, 8, 1256. https://doi.org/10.3390/pr8101256
Amangeldi M, Wei D, Perveen A, Zhang D. Numerical Modeling of Thermal Flows in Entrance Channels for Polymer Extrusion: A Parametric Study. Processes. 2020; 8(10):1256. https://doi.org/10.3390/pr8101256
Chicago/Turabian StyleAmangeldi, Medeu, Dongming Wei, Asma Perveen, and Dichuan Zhang. 2020. "Numerical Modeling of Thermal Flows in Entrance Channels for Polymer Extrusion: A Parametric Study" Processes 8, no. 10: 1256. https://doi.org/10.3390/pr8101256
APA StyleAmangeldi, M., Wei, D., Perveen, A., & Zhang, D. (2020). Numerical Modeling of Thermal Flows in Entrance Channels for Polymer Extrusion: A Parametric Study. Processes, 8(10), 1256. https://doi.org/10.3390/pr8101256





