A Confidence Interval-Based Process Optimization Method Using Second-Order Polynomial Regression Analysis
Abstract
1. Introduction
2. Process Modeling Using Second-Order Polynomial Regression
2.1. Second-Order Polynomial Regression Analysis
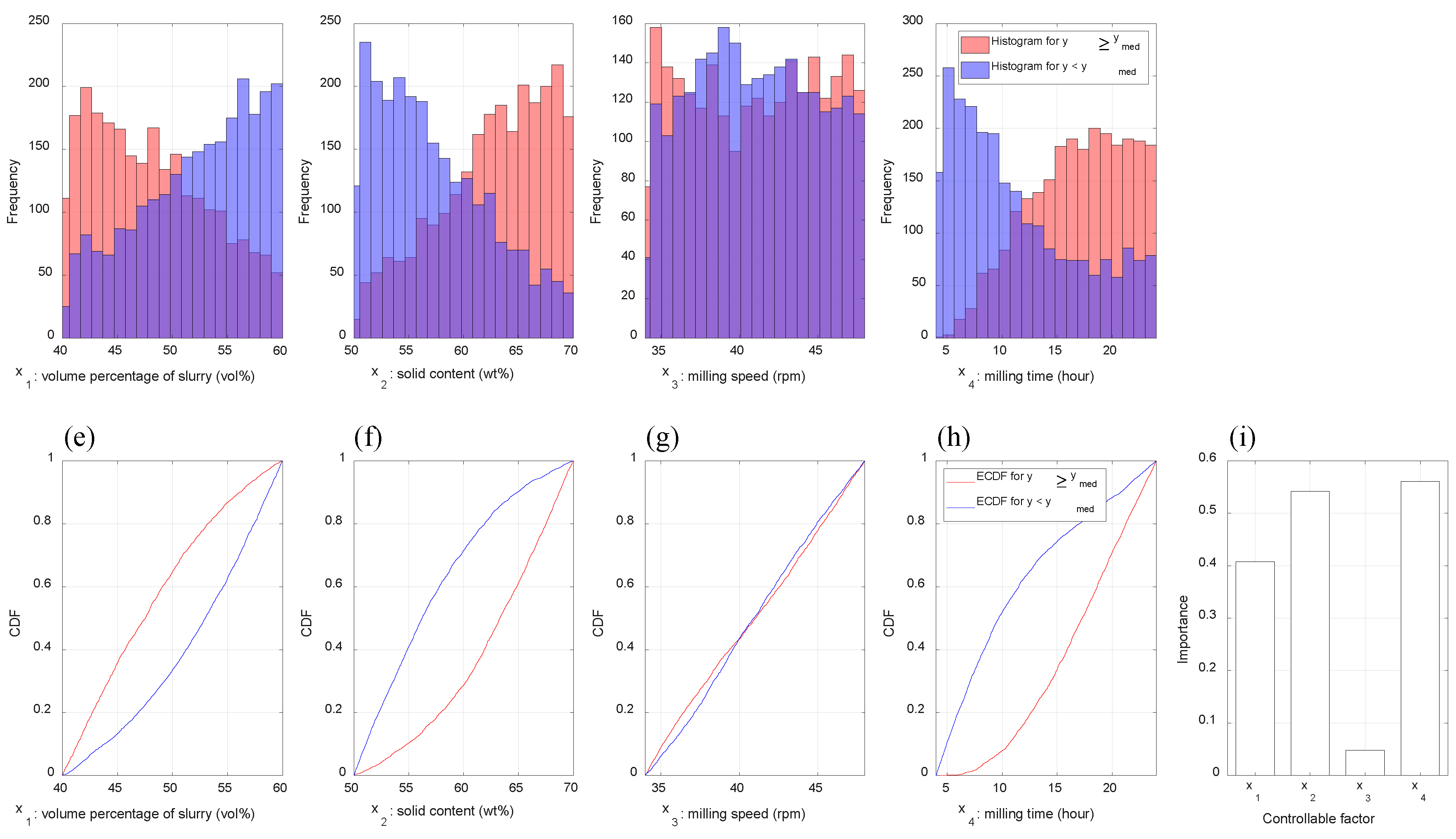
2.2. Importance Estimation of Input Variables
- Step 1:
- Generate N uniform random vectors x(1), ..., x(N) with p dimensions; the jth element of these vectors follows uniform distribution over the interval [−1, 1].
- Step 2:
- Calculate N outputs by substituting the N vectors x(1), ..., x(N) in the constructed model, and then obtain the median ymed of , i = 1, ..., N.
- Step 3:
- Divide the N vectors x(1), ..., x(N) into two sets Xlarger and Xsmaller as follows: Xlarger = {x(i)| ≥ ymed, i = 1, ..., N} and Xsmaller = {x(i)| < ymed, i = 1, ..., N}.
- Step 4:
- Estimate two cumulative distribution functions (CDFs) for each input variable empirically on the basis of the vectors belonging to Xlarger, and Xsmaller, respectively; that is, xj, j = 1, ..., p, has two estimated CDFs related with Xlarger, and Xsmaller, respectively.
- Step 5:
- Calculate the total area of the region(s) surrounded by the two CDFs of each input variable by numerical integration techniques.
3. Process Optimization
3.1. Particle Swarm Optimization
3.2. Proposed Method: Confidence Interval-Based Process Optimization
| Algorithm 1. The proposed CI-based process optimization procedure. |
| 1: Input: Experiment dataset gathered from a target process, D = {(xi; yi)|i = 1,..., n} 2: α ← significant level for CI 3: ytarget ← target value for a quality characteristic 4: L ← the number of repetitions of optimization algorithm 5: L’ ← the number of solutions to be recommended, where L’ < L 6: Construct 2nd-order polynomial regression model based on the dataset D 7: Define objective function F(x) formulating process optimization problem; for example, 8: For l from 1 to L 9: Find a solution by applying optimization algorithm to F(x); here, different solutions are found each time because of its stochastic mechanism 10: Obtain CI for using Equation (2), and then calculate its length, i.e., 11: end 12: Sort Wl, l = 1,..., L, in ascending order, i.e., 13: return |
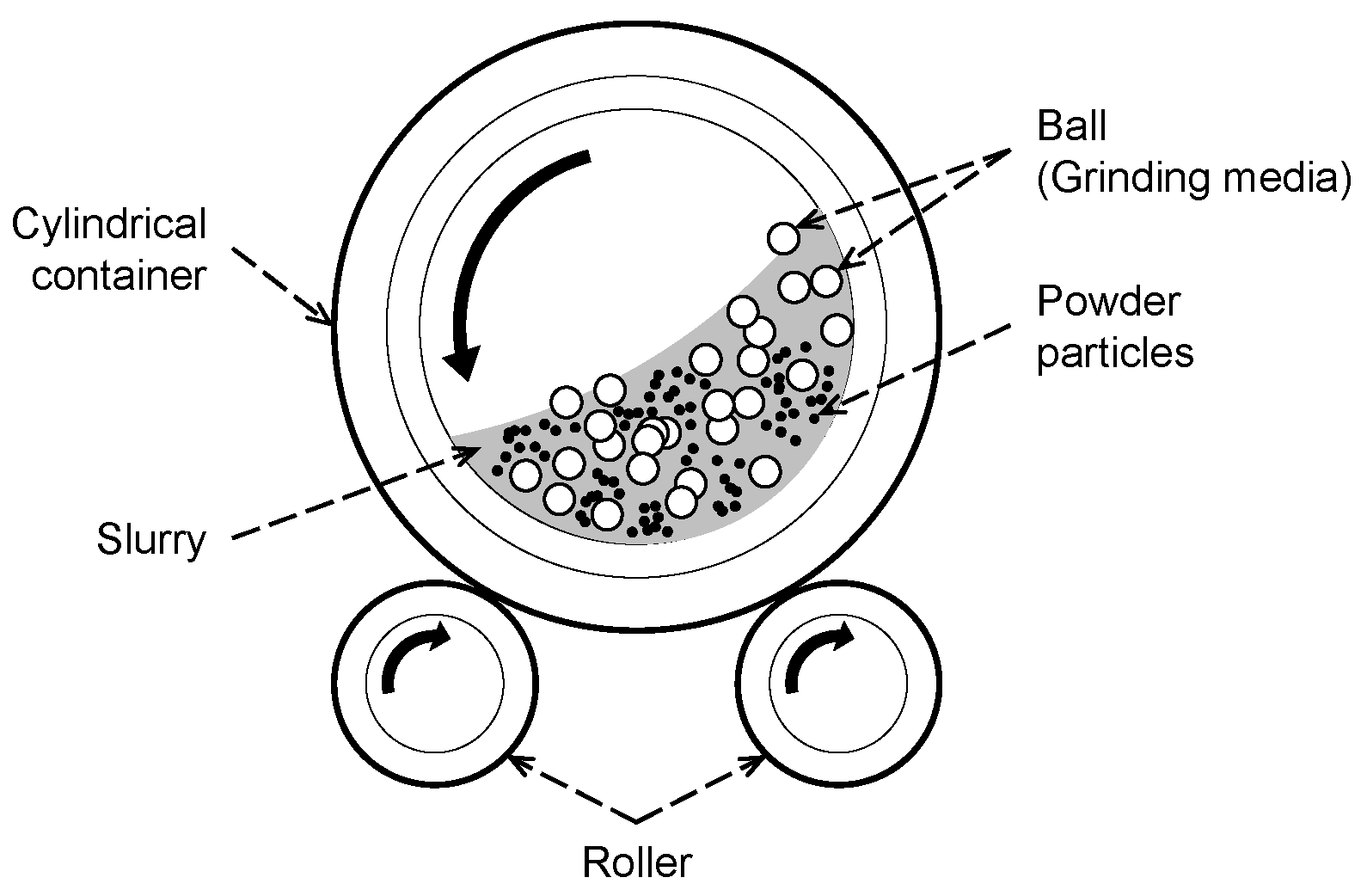
4. Description of the Target Process: Ball Mill
5. Experimental Results and Discussion
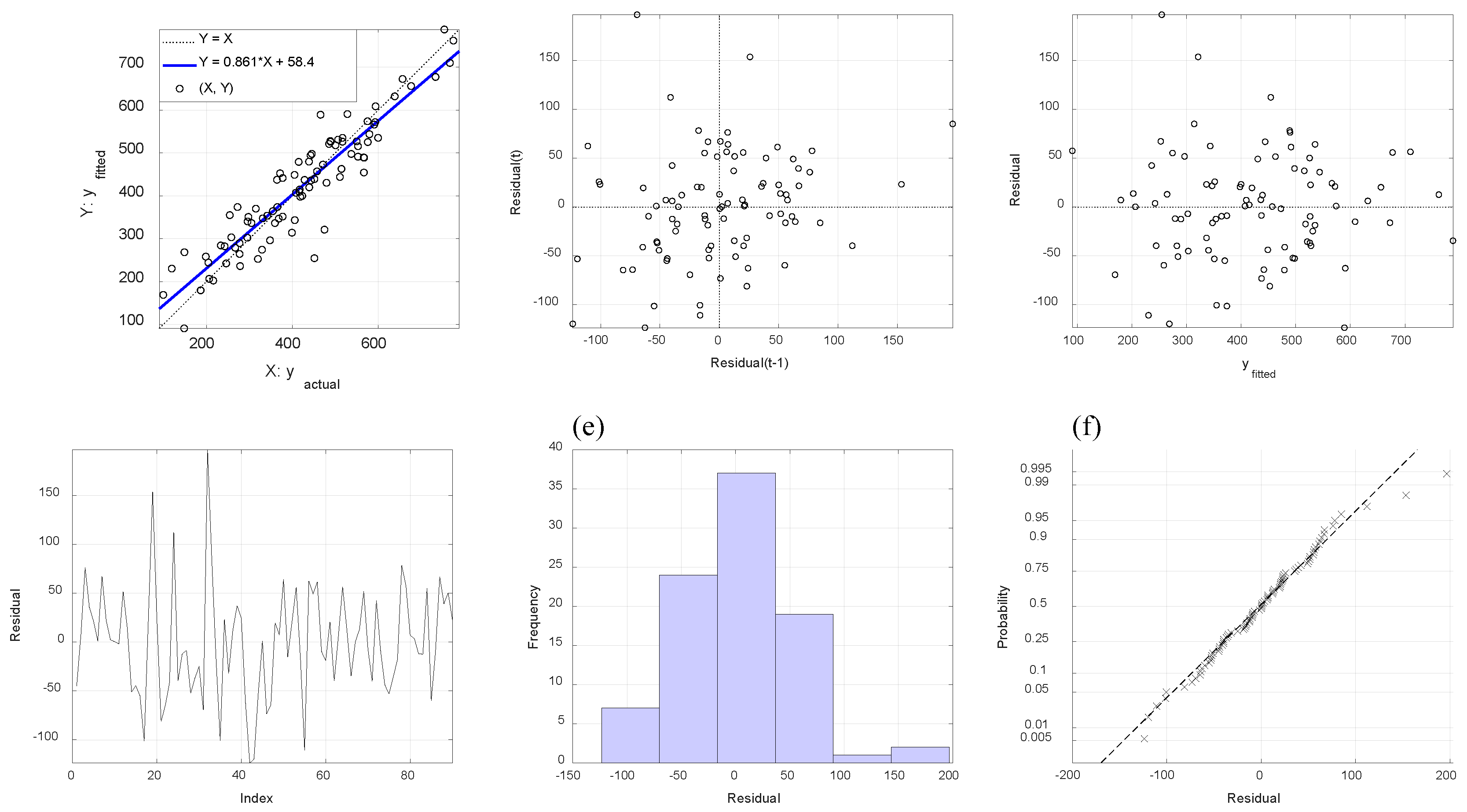
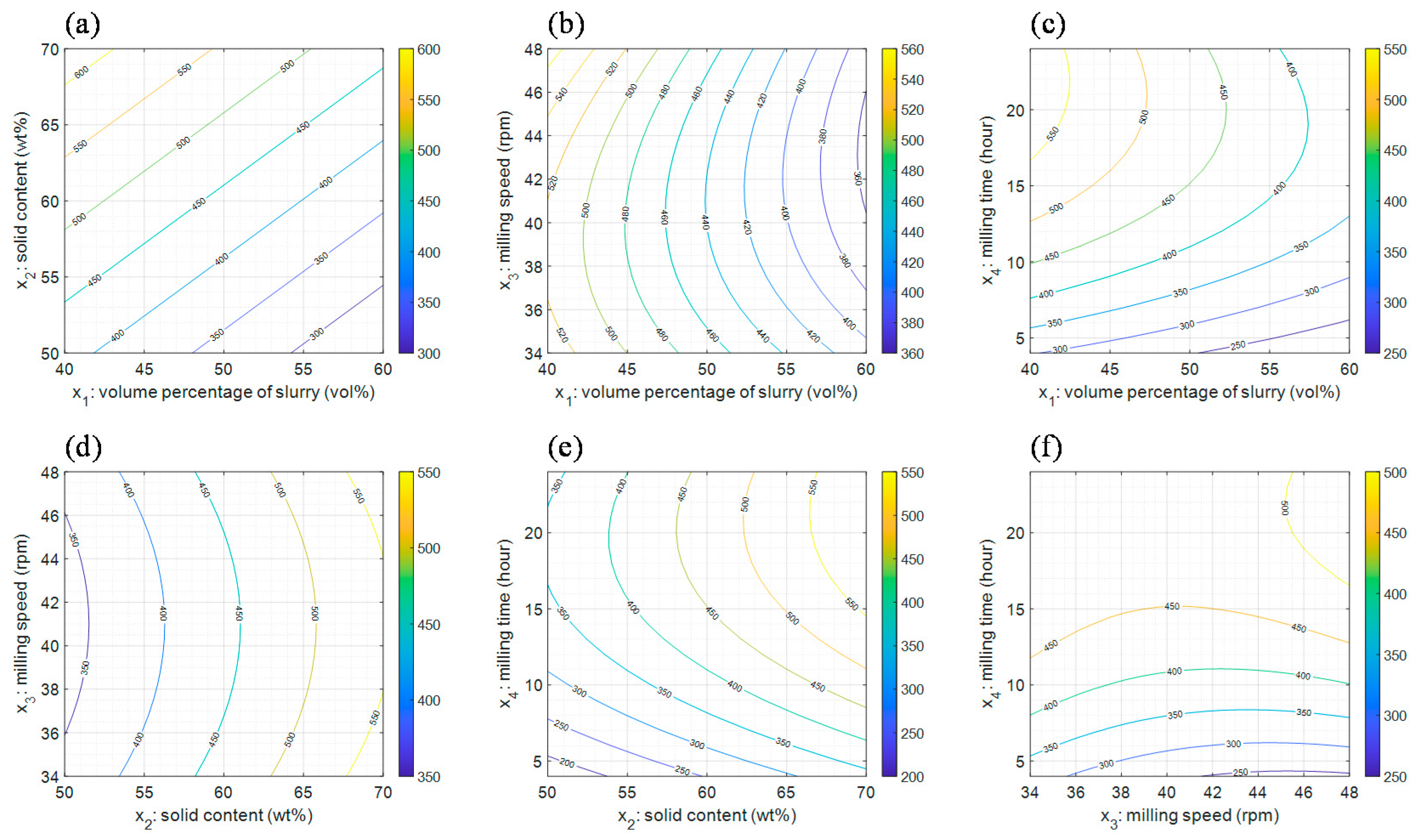
5.1. Results of Second-Order Polynomial Regression Analysis
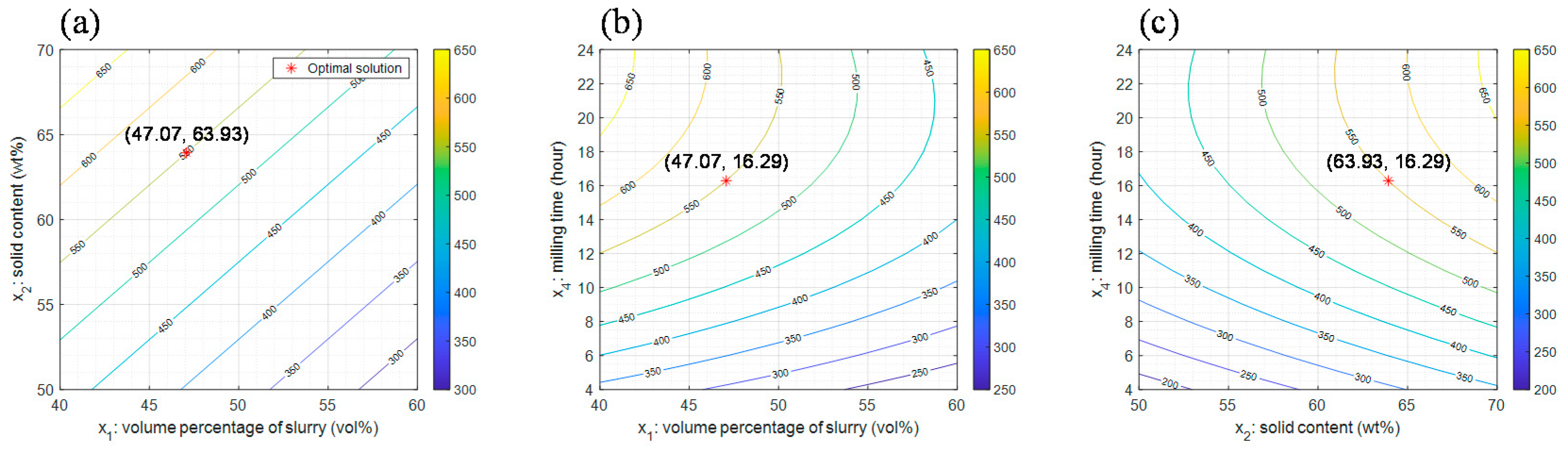
5.2. Results of Confidence Interval-Based Process Optimization
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rao, R.V. Advanced Modeling and Optimization of Manufacturing Processes: International Research and Development; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Castillo, E.D. Process Optimization: A Statistical Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Dejaegher, B.; Heyden, Y.V. Experimental designs and their recent advances in set-up, data interpretation, and analytical applications. J. Pharm. Biomed. Anal. 2011, 56, 141–158. [Google Scholar] [CrossRef] [PubMed]
- Draper, N.R.; Smith, H. Applied Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Ebadnejad, A.; Karimi, G.R.; Dehghani, H. Application of response surface methodology for modeling of ball mills in copper sulphide ore grinding. Powder Technol. 2013, 245, 292–296. [Google Scholar] [CrossRef]
- Parida, M.K.; Joardar, H.; Fout, A.K.; Routaray, I.; Mishra, B.P. Multiple response optimizations to improve performance and reduce emissions of Argemone Mexicana biodiesel-diesel blends in a VCR engine. Appl. Thermal Eng. 2019, 148, 1454–1466. [Google Scholar] [CrossRef]
- Adesina, O.A.; Abdulkareem, F.; Yusuff, A.S.; Lala, M.; Okewale, A. Response surface methodology approach to optimization of process parameter for coagulation process of surface water using Moringa oleifera seed. S. Afr. J. Chem. Eng. 2019, 28, 46–51. [Google Scholar] [CrossRef]
- Costa, N.; Garcia, J. Using a multiple response optimization approach to optimize the coefficient of performance. Appl. Thermal Eng. 2016, 96, 137–143. [Google Scholar] [CrossRef]
- Chen, Z.; Shi, Y.; Lin, X.; Yu, T.; Zhao, P.; Kang, C.; He, X.; Li, H. Analysis and optimization of process parameter intervals for surface quality in polishing Ti-6Al-4V blisk blade. Results Phys. 2019, 12, 870–877. [Google Scholar] [CrossRef]
- Li, Y.X.; Xu, Q.Y.; Guo, R.T.; Wang, Z.Y.; Liu, X.Y.; Shi, X.; Qiu, Z.Z.; Qin, H.; Jia, P.Y.; Qin, Y.; et al. Removal of NO by using sodium persulfate/limestone slurry: Modeling by response surface methodology. Fuel 2019, 254. [Google Scholar] [CrossRef]
- Aggarwal, A.; Singh, H.; Kumar, P.; Singh, M. Optimizing power consumption for CNC turned parts using response surface methodology and Taguchi’s technique-a comparative analysis. J. Mater. Process. Technol. 2008, 200, 373–384. [Google Scholar] [CrossRef]
- Mohanty, S.; Mishra, A.; Nanda, B.K.; Routara, B.C. Multi-objective parametric optimization of nano powder mixed electrical discharge machining of AlSiCp using response surface methodology and particle swarm optimization. Alexandria Eng. J. 2018, 57, 609–619. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Z.; Mei, Q.; Duan, J. Application of particle swarm optimization combined with response surface methodology to transverse flux permanent magnet motor optimization. IEEE Trans. Magn. 2017, 53, 1–7. [Google Scholar] [CrossRef]
- Hasanien, H.M. Particle swarm design optimization of transverse flux linear motor for weight reduction and improvement of thrust force. IEEE Trans. Ind. Electron. 2010, 58, 4048–4056. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Talbi, E.G. Metaheuristics: From Design to Implementation; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Richerson, D.W.; Lee, W.E. Modern Ceramic Engineering Properties, Processing, and Use in Design; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Deng, B.; Shi, Y.; Yu, T.; Kang, C.; Zhao, P. Multi-response parameter interval sensitivity and optimization for the composite tape winding process. Materials 2018, 11, 220. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; He, Z.; Niu, Z.; Li, Z.S. A hybrid intelligent optimization approach to improving quality for serial multistage and multi-response coal preparation production systems. J. Manuf. Syst. 2018, 47, 199–216. [Google Scholar] [CrossRef]
- Bera, S.; Mukherjee, I. A multistage and multiple response optimization approach for serial manufacturing system. Eur. J. Oper. Res. 2016, 248, 444–452. [Google Scholar] [CrossRef]
- Precup, R.E.; David, R.C. Nature-inspired Optimization Algorithms for Fuzzy Controlled Servo Systems; Butterworth-Heinemann: Oxford, UK, 2019. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L. A novel hybrid bat algorithm with harmony search for global numerical optimization. J. Appl. Math. 2013. [Google Scholar] [CrossRef]
- Haber, R.E.; Beruvides, G.; Quiza, R.; Hernandez, A. A simple multi-objective optimization based on the cross-entropy method. IEEE Access 2017, 5, 22272–22281. [Google Scholar] [CrossRef]
- Tharwat, A.; Hassanien, A.E. Quantum-behaved particle swarm optimization for parameter optimization of support vector machine. J. Classif. 2019, 36, 576–598. [Google Scholar] [CrossRef]
- Engelbrecht, A.P. Computational Intelligence: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of ICNN’95-International Conference on Neural Networks; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Ratnaweera, A.; Halgamuge, S.K.; Watson, H.C. Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients. IEEE Trans. Evol. Comput. 2004, 8, 240–255. [Google Scholar] [CrossRef]
- Del Valle, Y.; Venayagamoorthy, G.K.; Mohagheghi, S.; Hernandez, J.C.; Harley, R.G. Particle swarm optimization: Basic concepts, variants and applications in power systems. IEEE Trans. Evol. Comput. 2008, 12, 171–195. [Google Scholar] [CrossRef]
- Kwak, J.S. Application of Taguchi and response surface methodologies for geometric error in surface grinding process. Int. J. Mach. Tools Manuf. 2005, 45, 327–334. [Google Scholar] [CrossRef]
- Castaño, F.; Beruvides, G.; Villalonga, A.; Haber, R.E. Self-tuning method for increased obstacle detection reliability based on internet of things LiDAR sensor models. Sensors 2018, 18, 1508. [Google Scholar] [CrossRef] [PubMed]

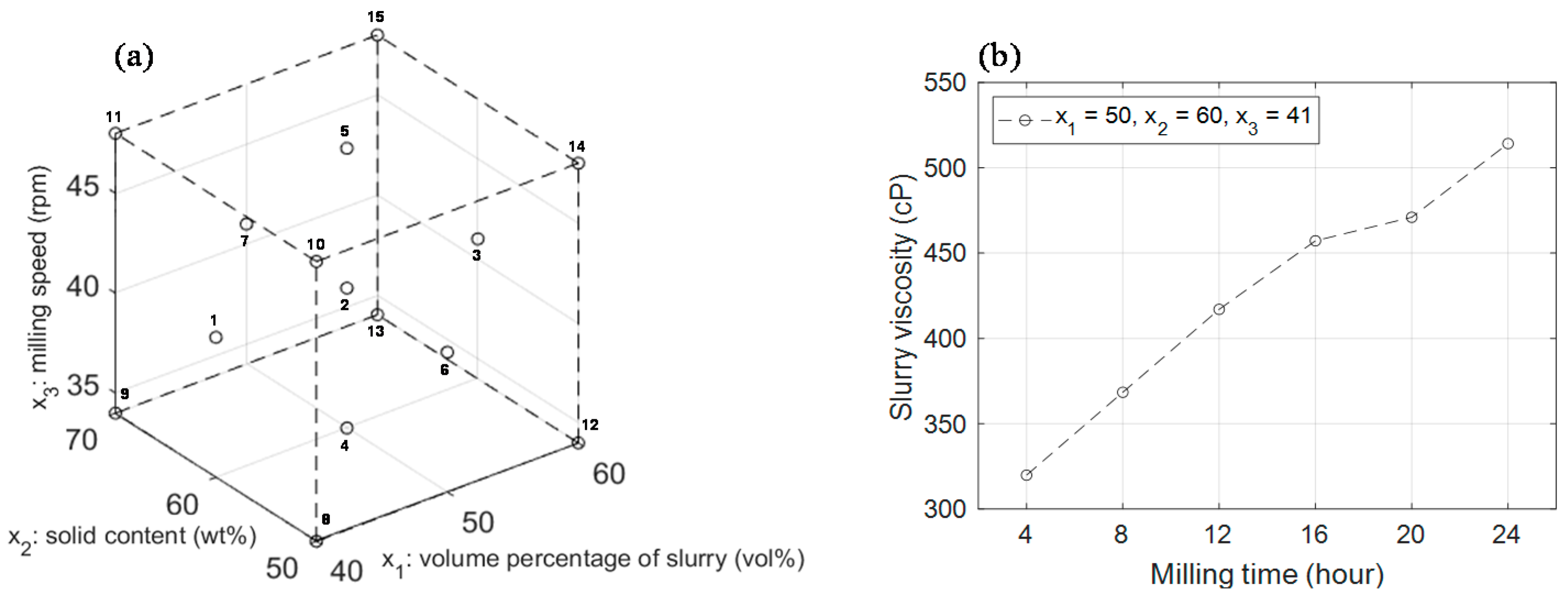




| Controllable Factor | Level | ||
|---|---|---|---|
| −1 | 0 | 1 | |
| x1: slurry volume (vol%) | 40 | 50 | 60 |
| x2: solid content (wt%) | 50 | 60 | 70 |
| x3: milling speed (rpm) | 34 | 41 | 48 |
| Test ID | x1 | x2 | x3 | Slurry Viscosity (cP) | |||||
|---|---|---|---|---|---|---|---|---|---|
| After 4 h | After 8 h | After 12 h | After 16 h | After 20 h | After 24 h | ||||
| Test 1 | 40 | 60 | 41 | 258.0 | 416.4 | 565.8 | 579.3 | 592.8 | 574.8 |
| Test 2 | 50 | 60 | 41 | 319.8 | 368.4 | 417.0 | 457.2 | 471.0 | 514.2 |
| Test 3 | 60 | 60 | 41 | 216.0 | 233.4 | 295.8 | 315.0 | 272.4 | 377.4 |
| Test 4 | 50 | 60 | 34 | 474.6 | 423.0 | 371.4 | 414.6 | 438.6 | 566.4 |
| Test 5 | 50 | 60 | 48 | 204.6 | 341.4 | 428.4 | 442.2 | 489.0 | 506.4 |
| Test 6 | 50 | 50 | 41 | 99.6 | 451.2 | 399.0 | 331.2 | 254.4 | 359.4 |
| Test 7 | 50 | 70 | 41 | 304.8 | 451.2 | 552.6 | 590.4 | 528.0 | 465.6 |
| Test 8 | 40 | 50 | 34 | 148.8 | 297.6 | 408.0 | 364.2 | 377.4 | 439.2 |
| Test 9 | 40 | 70 | 34 | 443.3 | 599.4 | 593.6 | 676.2 | 733.0 | 656.4 |
| Test 10 | 40 | 50 | 48 | 119.4 | 405.6 | 479.4 | 552.6 | 516.6 | 516.6 |
| Test 11 | 40 | 70 | 48 | 418.2 | 488.2 | 638.2 | 766.4 | 774.6 | 753.4 |
| Test 12 | 60 | 50 | 34 | 206.4 | 277.2 | 348.0 | 295.2 | 242.4 | 278.4 |
| Test 13 | 60 | 70 | 34 | 364.8 | 405.0 | 445.2 | 485.4 | 500.4 | 567.0 |
| Test 14 | 60 | 50 | 48 | 148.2 | 186.6 | 246.0 | 267.0 | 277.2 | 329.4 |
| Test 15 | 60 | 70 | 48 | 198.6 | 354.6 | 510.6 | 537.0 | 575.4 | 549.6 |
| Coefficient | Estimate | Standard Error | t-Statistic | p-Value |
|---|---|---|---|---|
| β0 | 439.00 | 15.10 | 29.08 | 0.0000 |
| β1 | −80.80 | 7.75 | −10.43 | 0.0000 |
| β2 | 105.08 | 7.75 | 13.57 | 0.0000 |
| β3 | 3.01 | 7.75 | 0.39 | 0.6989 |
| β4 | 105.01 | 9.26 | 11.34 | 0.0000 |
| β12 | −10.91 | 8.66 | −1.26 | 0.2115 |
| β13 | −19.32 | 8.66 | −2.23 | 0.0286 |
| β14 | −30.38 | 11.34 | −2.68 | 0.0091 |
| β23 | −5.55 | 8.66 | −0.64 | 0.5233 |
| β24 | 21.31 | 11.34 | 1.88 | 0.0640 |
| β34 | 38.42 | 11.34 | 3.39 | 0.0011 |
| β11 | −3.70 | 15.27 | −0.24 | 0.8091 |
| β22 | 3.82 | 15.27 | 0.25 | 0.8031 |
| β33 | 29.92 | 15.27 | 1.96 | 0.0538 |
| β44 | −81.38 | 15.84 | −5.14 | 0.0000 |
| ns | tmax | w(0) | w(tmax) | c1min | c1max | c2min | c2max |
|---|---|---|---|---|---|---|---|
| 20 | 200 | 0.9 | 0.4 | 0.5 | 2.5 | 0.5 | 2.5 |
| Order | x1 | x2 | x3 | x4 | CI | Length |
|---|---|---|---|---|---|---|
| 1 | 47.07 | 63.93 | 45.59 | 16.29 | [528.63, 571.37] | 42.73 |
| 2 | 46.41 | 61.80 | 44.66 | 19.29 | [527.83, 572.17] | 44.34 |
| 3 | 50.53 | 66.91 | 34.83 | 17.13 | [527.74, 572.26] | 44.52 |
| 4 | 48.38 | 65.23 | 35.07 | 19.36 | [527.70, 572.30] | 44.60 |
| 5 | 50.00 | 62.60 | 48.00 | 18.94 | [527.63, 572.37] | 44.75 |
| 6 | 44.30 | 60.71 | 45.52 | 17.06 | [527.44, 572.56] | 45.12 |
| 7 | 49.92 | 66.38 | 34.16 | 16.40 | [527.16, 572.84] | 45.67 |
| 8 | 46.17 | 63.57 | 48.00 | 14.32 | [526.69, 573.31] | 46.63 |
| 9 | 48.10 | 65.21 | 35.59 | 20.29 | [526.68, 573.32] | 46.64 |
| 10 | 47.75 | 65.28 | 37.37 | 19.10 | [526.67, 573.33] | 46.65 |
| Order | x1 | x2 | x3 | x4 | CI | Length |
|---|---|---|---|---|---|---|
| 1 | 49.13 | 61.62 | 34.54 | 16.27 | [480.23, 519.77] | 39.54 |
| 2 | 47.52 | 61.56 | 35.00 | 14.87 | [480.08, 519.92] | 39.83 |
| 3 | 48.65 | 61.69 | 34.53 | 15.38 | [480.01, 519.99] | 39.98 |
| 4 | 51.15 | 61.61 | 44.95 | 19.51 | [479.39, 520.61] | 41.22 |
| 5 | 47.57 | 59.92 | 45.10 | 16.56 | [479.18, 520.82] | 41.64 |
| 6 | 49.02 | 65.43 | 34.96 | 11.66 | [479.07, 520.93] | 41.86 |
| 7 | 51.34 | 65.18 | 46.18 | 14.20 | [479.02, 520.98] | 41.97 |
| 8 | 51.95 | 61.87 | 47.80 | 16.75 | [478.97, 521.03] | 42.06 |
| 9 | 49.32 | 61.09 | 34.00 | 17.95 | [478.64, 521.36] | 42.72 |
| 10 | 48.56 | 61.56 | 37.42 | 19.87 | [478.63, 521.37] | 42.75 |
| Order | x1 | x2 | x3 | x4 | CI | Length |
|---|---|---|---|---|---|---|
| 1 | 48.46 | 57.58 | 35.03 | 14.71 | [430.31, 469.69] | 39.38 |
| 2 | 50.32 | 62.94 | 36.25 | 11.07 | [430.17, 469.83] | 39.65 |
| 3 | 52.68 | 60.31 | 46.15 | 15.49 | [430.12, 469.88] | 39.77 |
| 4 | 53.64 | 60.34 | 35.50 | 18.25 | [429.68, 470.32] | 40.64 |
| 5 | 48.25 | 61.67 | 36.81 | 11.37 | [429.42, 470.58] | 41.16 |
| 6 | 47.11 | 56.06 | 46.66 | 14.36 | [429.20, 470.80] | 41.60 |
| 7 | 49.02 | 57.46 | 45.16 | 15.60 | [429.05, 470.95] | 41.89 |
| 8 | 46.63 | 59.84 | 45.36 | 12.04 | [428.94, 471.06] | 42.12 |
| 9 | 50.21 | 60.35 | 37.04 | 13.90 | [428.90, 471.10] | 42.20 |
| 10 | 48.37 | 62.18 | 47.88 | 10.79 | [428.73, 471.27] | 42.54 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Yang, S.; Kim, J.; Lee, Y.; Lim, K.-T.; Kim, S.; Ryu, S.-S.; Jeong, H. A Confidence Interval-Based Process Optimization Method Using Second-Order Polynomial Regression Analysis. Processes 2020, 8, 1206. https://doi.org/10.3390/pr8101206
Yu J, Yang S, Kim J, Lee Y, Lim K-T, Kim S, Ryu S-S, Jeong H. A Confidence Interval-Based Process Optimization Method Using Second-Order Polynomial Regression Analysis. Processes. 2020; 8(10):1206. https://doi.org/10.3390/pr8101206
Chicago/Turabian StyleYu, Jungwon, Soyoung Yang, Jinhong Kim, Youngjae Lee, Kil-Taek Lim, Seiki Kim, Sung-Soo Ryu, and Hyeondeok Jeong. 2020. "A Confidence Interval-Based Process Optimization Method Using Second-Order Polynomial Regression Analysis" Processes 8, no. 10: 1206. https://doi.org/10.3390/pr8101206
APA StyleYu, J., Yang, S., Kim, J., Lee, Y., Lim, K.-T., Kim, S., Ryu, S.-S., & Jeong, H. (2020). A Confidence Interval-Based Process Optimization Method Using Second-Order Polynomial Regression Analysis. Processes, 8(10), 1206. https://doi.org/10.3390/pr8101206




