Abstract
As interest in the modularization and intensification of chemical processes continues to grow, more research must be directed towards the modeling and analysis of these units. Intensified process units such as polymer membrane reactors pose unique challenges pertaining to design and operation that have not been fully addressed. In this work, a novel approach for modeling membrane reactors is developed in AVEVA’s Simcentral Simulation Platform. The produced model allows for the simulation of polymer membrane reactors under nonisothermal and countercurrent operation for the first time. This model is then applied to generate an operability mapping to study how operating points translate to overall unit performance. This work demonstrates how operability analyses can be used to identify areas of improvement in membrane reactor design, other than just using operability mapping studies to identify optimal input conditions. The performed analysis enables the quantification of the Pareto frontier that ultimately leads to design improvements that both increase overall performance and decreases the cost of the unit.
1. Introduction
Modular equipment is an emerging technology that offers many potential benefits in terms of increased safety, flexibility, and ease of modification [1]. However, to take advantage of or access the benefits of modular plants, traditional processes must be significantly reduced in size for easier transportation and assembly. This design philosophy goes against the long-standing tradition of building massive chemical plants to take advantage of economies of scale. These modular plants cannot simply be smaller versions of traditional processes, but they must also be more efficient than their traditional counterparts.
This concept of increased efficiency of process units gave rise to the technologies associated with process intensification. Process intensification (PI) is defined as “any chemical engineering development that leads to substantially smaller, cleaner, and more energy efficient technologies.” [1] In many cases, this is achieved by combining multiple phenomena in a single process unit (i.e., reactive distillation, reactive crystallization, [2] and membrane reactors) rather than performing step-by-step unit operations. Although PI can greatly improve the efficiency of the unit, intensified processes pose challenges to modeling and in the control/operations of these units.
As combinations of phenomena are introduced in a unit, the complexity of the resulting problem grows. In the case of a membrane reactor, reaction kinetics, heat duty, and membrane permeation must all be considered at every point along the reactor. For some cases, the problem can be simplified by making isothermal assumptions to remove the heat duty or enthalpy from permeation, cocurrent operation to avoid boundary value problems, and utilization of membrane materials such as palladium where only one component is capable of permeating into or out of the process. These simplifications greatly reduce the time required to run online optimization or modeling studies, but at the cost of a loss in accuracy.
These aforementioned phenomena are so interdependent, that the removal of any one of them can result in very different results. These simplifying assumptions may lead to a gap in understanding of the behavior of membrane reactors.
The first objective in this research is to present a modeling methodology that addresses these issues in which the fundamental phenomena present are broken down into individual blocks that are assembled to create the complex behavior of a membrane reactor. This method provides a reliable way of simulating a countercurrent, nonisothermal, and bidirectional-permeation membrane reactor model.
Second, with the use of this model, operability analysis [3,4] is performed for a polymer membrane reactor for the first time. The operability concept is used to study the relationship between unit performance and operational decisions. This analysis helps with improving the understanding of the benefits and drawbacks of polymer membranes and provides a direction for future work in the design of membrane materials.
Third, the operability analyses are also employed to drive future membrane reactor design decisions. Others have used operability analysis previously to improve membrane reactor design [3,4,5,6], but this proposed approach differs in a key way. Prior work in operability either looked at how design changes could be used to improve a nominal operating point or what the optimal nominal point of a given design would be. In this work, operability is used to identify the Pareto frontier for optimization in order to drive design decisions for overall performance improvement.
These three contributions form the necessary foundation for future work in developing an effective mixed-integer algorithm for determining an optimum modular design that improves unit operability. The outline of the rest of this paper is as follows. First, the membrane reactor modeling, simulation, and operability analysis approaches are introduced. These approaches are then employed for simulating the polymer membrane reactor unit and performing the operability mapping for identifying the Pareto frontier and redesigning the membrane reactor. The paper is closed with conclusions and some directions for future work.
2. Modeling, Simulation, and Operability Approach
2.1. Membrane Reactor Modeling Approach
For this study, a water-gas shift membrane reactor (WGS-MR) system in a shell and tube reactor is considered as shown in Figure 1. The membrane reactor model is developed as a one-dimensional, nonisothermal, single tube, and countercurrent unit. The unit is assumed to be operated at steady-state using pressure-driven flow calculations in the AVEVA SimCentral Simulation Platform (AVEVA Group plc. Cambridge, UK) The process side, which is a packed bed, is modeled using the Ergun Equation (1), while the sweep gas side uses the Colbrooke Equation (2) for modeling the pressure drop.
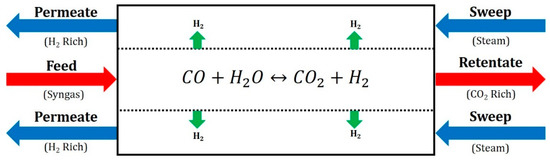
Figure 1.
Schematic of the polymer membrane which consists of a tube packed with catalyst surrounded by a polymer membrane to allow simultaneous reaction and permeation.
Ergun equation, tube:
where μ is the fluid’s viscosity, Dp is the catalyst particle diameter, ε is the void fraction of the catalyst, vs is the superficial velocity of the fluid, and is the fluid density.
Colebrook equation, shell:
where Dh is the hydraulic diameter of the shell side and f is the Darcy friction factor that can be obtained by solving the implicit formula:
On the tube side of the reactor, the water-gas shift reaction and membrane permeation take place, whereas only membrane permeation contributes to changes in the mole balance of the shell side. Therefore, the mole balance can be described by Equations (4) and (5) below, assuming plug-flow operation.
Mole balance, tube:
where is the molar flow rate in the tube, is the species reaction rate, is the cross sectional area of a single tube, is the molar flux across the membrane, and is the diameter of a single tube. The subscript i denotes the species and z is the reactor axial coordinate. For the water-gas shift reaction, for i = CO, H2O, for i = CO2, H2, and for N2. The reaction rate, , is assumed to be for the low-temperature water-gas shift. (Cu/ZnO/Al2O3) catalyst and is modeled using the reaction provided in Reference [7].
Mole balance, shell:
where is the flowrate in the shell. For this study, counter-current operation is used, and thus, a negative sign is required. The molar flux of a polymer membrane can be captured using a Fickian diffusion model with the partial pressure gradient of each component as the driving force:
in which is the permeance, δ is the membrane thickness, and and are the partial pressures of species i on the tube and shell sides, respectively. For the case of the considered polybenzimidazole-based polymer membrane, the permeance values selected for this study come from References [8,9,10,11] and are shown in Table 1.

Table 1.
Component permeance (Qi,o) and permeability (Pi,o) values used reported in gas permeation units (GPU) and barrer, respectively, as well as the ideal selectivities (αH2/i) of hydrogen relative to other components in the syngas.
Hence, in this case, all the species that are present are capable of crossing through the membrane. This is important to consider for later as the sweep gas, steam, is three times more permeable than the hydrogen through the polymer membrane whereas the other species permeabilities are very low, but not negligible.
Lastly, the energy balances for each side of the reactor are considered for the calculation of their temperatures. In a membrane reactor, there are three factors that contribute to changes in temperature: reactions, heat duty, and the Joules-Thomson effect as material permeates from one side of the membrane to the other. Considering a thin control volume along the length of the membrane reactor, these three effects can be modeled with the following energy balances:
Energy balance, tube:
Energy balance, shell:
in which the central term accounts for the Joule-Thomson effect caused by material leaving or entering each side through the membrane. pt is the total tube pressure, ps is the total shell pressure, and is the isothermal Joule-Thomson coefficient for species i at constant temperature (where is the temperature of the side species i originated). The last term in the balance accounts for the heat duty across the membrane where U is the overall heat transfer coefficient, which is assumed to have a value of 30 W/m2-K for gas-to-gas convective heat transfer [12]. Normally, this value would change as a function of mass flowrate of the tube and shell sides; however, the dominating terms for heat duty on the lab scale reactor studied are the heat transfer area and the temperature gradient so potential U variations are expected to have a minimal effect when compared to the heats of reaction and Joule-Thomson effects. Finally, the temperature change due to the reaction is accounted for by the change in composition in the expanded form of the first term.
2.2. Block-Based Modeling and Simulation Approach
To simulate the polymer membrane reactor, a model was developed using AVEVA’s equation-oriented SimCentral Simulation Platform [13] employing a block-based phenomena concept. This method allows for the simulation of complex membrane systems that may take too long in other platforms to calculate all the operating conditions required for a reasonable operability analysis to take place.
The model is constructed by discretizing along the length of the membrane reactor and modeling each of the produced sections using a model element referred to as “MemElem.” MemElem is further broken down into submodels, where each of which captures the various phenomena that occur in a membrane reactor. A block diagram of how these submodels are connected to each other within the MemElem model is provided in Figure 2.
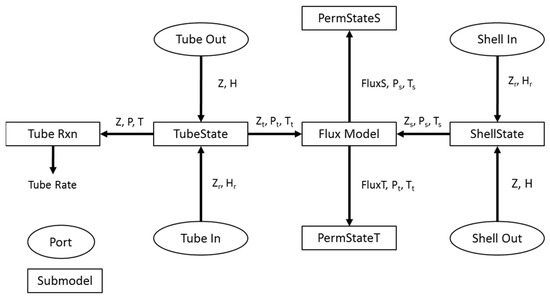
Figure 2.
The submodel structure for the MemElem model.
For a thin slice along the length of a membrane reactor, the tube and shell sides of the reactor can be assumed to operate as a continuous stirred-tank reactor (CSTR), where the outlets are equal to the current state of the reactor, depicted in Figure 2 as “TubeState” and “ShellState.” These state submodels determine the thermodynamic state on each side of the reactor and send that information (in this case the molar composition (Z), pressure, and temperature) to the other submodels. The other submodels handle the calculations of the membrane permeation (Flux Model, PermStateS, and PermStateT) and reaction kinetics (Tube Rxn). The results from all the submodels are used by the MemElem model to calculate the mass and energy balances. Lastly, these thin sections of membrane can be combined in series to produce the full membrane reactor structure as seen in Figure 3.
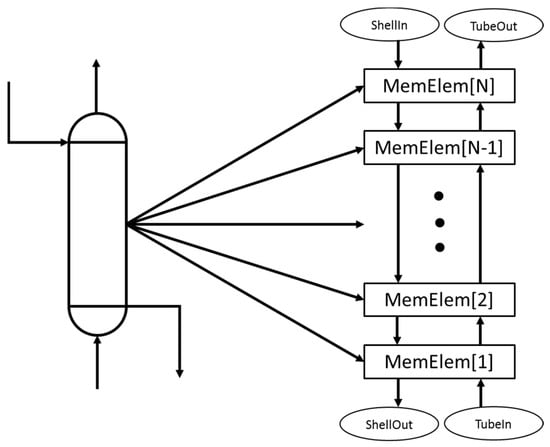
Figure 3.
Each MemElem submodel [1, 2, …, N − 1, N] is combined in series to complete the calculation of the full polymer membrane reactor unit.
This methodology allows for the simulation of countercurrent, nonisothermal, and bidirectional permeation of a polymer membrane system quickly enough that it can be solved in real-time in a dynamic simulation using an Intel® Core™ i7-4790 CPU @ 3.60GHz processor. Although for the purposes of this analysis, all simulations will be performed at steady-state conditions, the dynamic simulation and control of this reactor will be subject of subsequent studies.
By dividing the model into blocks that are dedicated to each of the phenomena that occur in the membrane reactor unit, additional features and unit customization are available to the user. By adding or removing blocks from the model, MemElem is thus capable of simulating a membrane reactor, membrane separator, packed-bed reactor, or heat exchanger. For example, if a user is interested in using MemElem to simulate a stand-alone packed-bed reactor with heat transfer, they would remove the Flux Model, PermStateS, and PermStateT blocks (see blocks in Figure 2). The potential benefits of being able to do this customization are covered in more depth in the Results section.
Although a block-based phenomena approach to modeling and simulating membrane reactor systems in an equation-oriented modeling environment provides the ability for conducting mixed-integer design optimizations, control studies, etc., the initialization process for this approach is challenging and the swapping in and out of the blocks may cause the model to become unsolved if the transition between solutions is discontinuous.
In equation-oriented modeling, it is necessary that the solver can find a unique solution at every step of the initialization process. This means two conditions should remain true throughout the initialization process: (1) the system of equations that describe the model must have a finite number of solutions; (2) the transition between intermediate solutions should be either continuous or smooth. If the system has infinitely many solutions, the solver will be unable to find a solution because the system is indeterminate. This can be a problem for the PermStateS and PermStateT blocks, which require N + 2 independent thermodynamic properties to be uniquely defined. During the initialization process, there is no material permeating across the membrane; therefore, there is no unique solution for what the N component mole fractions of the permeating material are and the PermState blocks can become unsolved. Arbitrary values could be sent to the PermState submodels so they remain solved, but this can lead to the second issue described above. If the provided arbitrary values are very different from the actual values in the final solution, the solver is unlikely to arrive at a solution, especially if the system is in countercurrent mode. Because the initialization approach is the most challenging barrier in the modeling of the countercurrent, nonisothermal, polymer membrane reactor, a comprehensive description of the developed approach is a necessary point of discussion.
This process begins by flowing the contents of the tube and shell side cocurrently with specified pressure drops for each side and no heat or mass transfer interactions between the two sides. This allows the TubeState and ShellState submodels in Figure 2 to solve for initial solutions for the thermodynamic states of the tube and shell side and gives MemElem the opportunity to establish an initial mass and energy balance for the system. Once the model is filled with initial values, the goal is then to introduce each element of the desired model in such a way that the two conditions mentioned above can be satisfied. The elements that need to be added to the initial model are: (1) pressure drop; (2) reaction kinetics; (3) countercurrent operation; (4) membrane permeation and heat transfer. This order of adding elements in steps 1–4 was determined to be the most effective in initializing the block-based modeling approach as each step provides the best possible guess for the next element to be added to the model.
Lastly, a series of “contact” variables, C, are implemented that facilitate the transition from step 3 to step 4. The standard formula used for these contact variables is of the form:
where S is the solution used by the model, S1 represents an initial solution, and S2 represents a desired solution. By switching the value of the contact variable from 0 to 1, the value of S will switch from S1 to S2 continuously rather than discretely, making the model much easier for the solver to determine a solution. This same concept has also been applied at the block level of the model where contact variables can remove entire blocks from the model. This feature, combined with the fact that the block-based approach allows for simulating multiple unit operations by adding or removing blocks, creates a design space for a membrane reactor model using this MemElem concept that is homotopic. That is to say, every possible topological design for the unit is connected to every other design through a continuous deformation. This is especially appealing for a mixed-integer optimization problem, as the solution space can now be continuous and the transitions can take place without having to reinitialize the model.
This initialization procedure makes this model very useful for conducting operability analyses where many operating conditions must be simulated in quick succession. To demonstrate this, two performance metrics are selected for the membrane reactor unit. Reactor performance is assessed using the metrics of H2 recovery (RH2) and CO2 capture (CCO2) defined as follows:
To achieve the different values for RH2 and CCO2, the process flowrate and sweep gas flowrate are manipulated with the use of two flow control valves, FC1 and FC2, as shown in Figure 4.
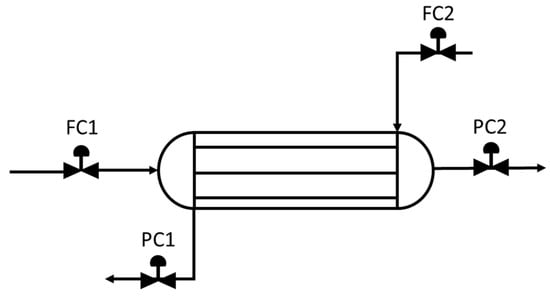
Figure 4.
Depiction of the membrane reactor and control valves present in the simulation.
The valves are sized assuming they are 50% open at the nominal operating point. The manual positions of FC1 and FC2 are then varied between 10–100% open and the values of hydrogen recovery and carbon capture are recorded to produce the operability mapping in Section 3.2 below.
2.3. Operability Analysis
Operability ultimately serves as the interface between design and control [14]. Traditionally, when creating a plant, the unit will undergo a design phase for the pieces of equipment before it undergoes a design phase for the control system. However, as the interest in intensified processes grows, the literature has identified that “process design, operation, and control should be considered simultaneously, or in other terms, they should be fully integrated” [15] for intensified processes. Because operability can provide the interface between design and control, any intensified process (such as the polymer membrane reactor unit considered in this work) should undergo such an analysis to identify the control challenges upfront and to determine if any design changes can be implemented to mitigate these challenges. Set-point operability is used in this research to measure the performance of the membrane reactor design, as defined in the operability analysis for square systems [14]. The mapping of inputs () of a model (M) to its outputs () can be formulated the following way:
in which are the state variables and and are equality and inequality process constraints, respectively. Additionally, and represent time derivatives associated with and , respectively, and and are nonlinear process maps.
Using the operability mapping concept, there are two sets of inputs and outputs that are important in this analysis:
Available Input Set (AIS): The set of all operational inputs or manipulated variables that are available to produce change to the output of the process and is defined as:
For this study, the AIS for the polymer membrane reactor consists of the sweep gas flowrate and the syngas flow rate into the membrane unit.
Achievable Output Set (AOS): This set consists of all possible outputs that can be achieved, given the available input set and is mathematically defined as:
For the purposes of this study, the AOS consists of the achievable hydrogen recovery and carbon capture for the unit to analyze how the polymer membrane reactor performs under different operating conditions. In this study, the ideal performance for any membrane would be 100% recovery of hydrogen and 100% capture of CO2, thus, high performance in these two outputs is desired. A schematic visual depiction of these spaces is provided in Figure 5.
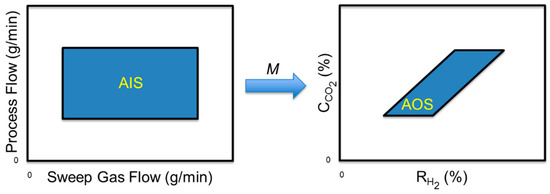
Figure 5.
Example of an available input set (AIS) being mapped to an achievable output set (AOS) with the use of a process model (M).
Because the AOS corresponds to the set of all the outputs that can be achieved given the entire set of inputs, the ideal objective is to improve the design until the entire AOS meets some desired output specifications. In the ideal case, all the available inputs would map to a desired region of the output space. In the opposite case, if the unit is designed considering only the nominal operating point, a control system could face significant challenges, as the window for effective control shrinks significantly, making process disturbances much more difficult to reject. Therefore, the goal of the operability analyses in this paper is to determine design changes that can expand the AOS, and therefore, move the membrane reactor closer to the ideal case as described above.
3. Results
3.1. Simulation of the Polymer Membrane Reactor Model
The operating conditions for this study are taken from Reference [8]. The reactor utilizes as process stream a syngas feed that has undergone the necessary removal of impurities, while the chosen sweep gas is steam. The inlet composition of these streams can be found in Table 2.

Table 2.
Molar composition of inlet streams, given in mole fraction.
The syngas feed enters the tube side of the reactor at 300 °C, 47.63 atm, and with a volumetric flow rate of 400 cm3/min. The sweep gas enters the shell as pure, saturated steam at 25.86 atm and a volumetric flowrate of 400 cm3/min. The reactor consists of a single tube (1.02 cm diameter) and shell (6.12 cm diameter) arrangement with a total reactor length of 300 cm. A membrane thickness of 100 nm is selected to reflect an industrially relevant thickness [9,10,11]. Under these conditions, a simulation was run using the block-based phenomena modeling approach and compared to the simulation data from Radcliffe et al. [8] for validation. The results of such comparison are shown in Table 3. In future work, the authors will pursue the additional validation of the model with experimental data.

Table 3.
Comparison between the block-based proposed approach and literature [8].
Using the nominal conditions described above, profiles for the permeation rates of hydrogen and steam are produced as shown in Figure 6.
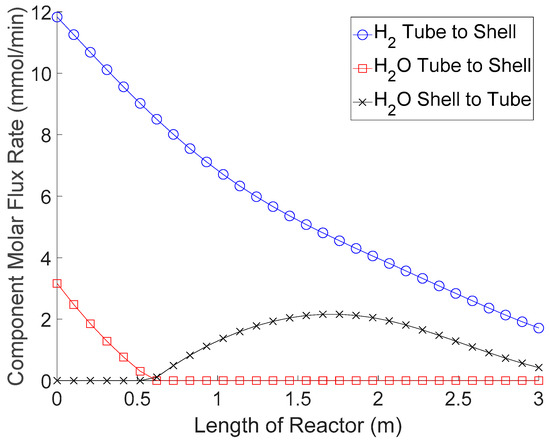
Figure 6.
Profile of the permeation rates for hydrogen and steam down the length of the polymer membrane reactor.
Although the other components, CO2, CO, and N2, are also permeating through the membrane, they are permeating at a much lower rate than H2 and H2O, depicted in Figure 6. This result shows an interesting characteristic of the polymer membrane. For about the first sixth of the reactor, H2O (steam) is being removed from the tube side along with the H2 product. However, for the remainder of the reactor, steam is being injected into the tube side of the reactor. During this time, the sweep gas enters the catalytic tube side, reacts to become hydrogen, and then permeates back to the shell side as a product. This is a nice property for an equilibrium-limited reaction such as WGS, because not only is the membrane removing a main product, but it is also providing steam injection for enhanced conversion. This would be a useful property for cases where the CO/H2O ratio of the feed becomes greater than one and there is insufficient steam to convert all the CO to CO2.
Temperature is also an important factor to consider as WGS is known to produce a significant amount of heat and becomes equilibrium limited as the temperature increases. The temperature profiles for the tube and shell sides at the nominal operating condition and for a syngas feed at 200 °C can be seen in Figure 7.
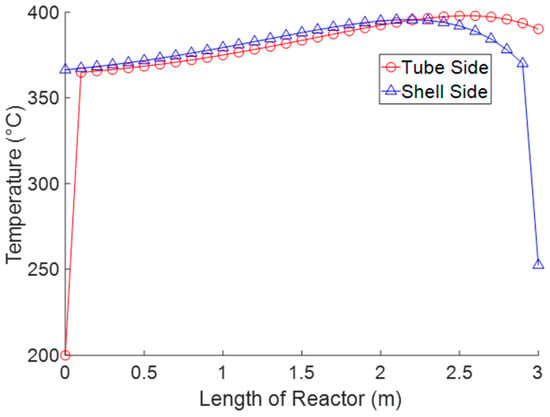
Figure 7.
Temperature profiles of the tube and shell sides for nonisothermal operations.
It is important to note in Figure 7 the temperature spike at the beginning of the reactor. The conditions at the inlet of the reactor lie very far to the left of equilibrium. This is evidenced by the fact that steam is permeating out of the tube side at the beginning of the process. The reaction rates are much greater than in a normal WGS reactor because H2 product is being removed, thus, also removing a major equilibrium limitation, but also introducing a large temperature spike. This problem of excess heat in polymer membrane reactors was reported by Singh et al. [11] who stated that “syngas operating temperatures in the vicinity of the water-gas shift (WGS) reactors ranges from 200 to 500 °C, depending on the WGS stage and catalyst used.” This illustrates the importance of including the nonisothermal reactor operation in the modeling approach, as the reactor inlet temperature for our past study [8] leads to reactor temperatures that exceed the glass transition temperature (Tg = 450 °C) and would eventually cause degradation of the polymer membrane material.
These simulation results indicate many research pathways for the design of membrane reactors. Most membrane reactor models require simplifications to the problem in order to produce results in a tractable manner, especially when performing an operability analysis (or online optimization) that requires many simulations to be run to produce the output space for further analysis. However, these simplifications are harder to justify in the design and simulation of intensified processes. The purpose of combining phenomena such as mass transfer and kinetics is to see how the performance of the unit can be improved by having them work in tandem. However, as shown earlier with the temperature profile in Figure 7, there are also difficult challenges that arise when combining them. As more phenomena are combined in these process units, the more interdependent they become, and the more difficult it is to design the equipment to meet the desired output specifications [2,15,16].
Isothermal operation is often assumed for a few reasons. The reaction rate, equilibrium, and the membrane permeance are all affected by the temperature in the reactor. When this is coupled with the interdependence that the phenomena have with each other, it creates a very complex behavior and difficult calculation before even considering how the tube side of the membrane reactor might interact with the shell side for heat transfer calculations.
The difficulty in solving for the state of the tube or shell side of the membrane reactor is a reason the Joule-Thomson is normally not considered. In most cases, the Joule-Thomson effect has a minor impact on the accuracy of the temperature and requires accurate knowledge of the temperature at a given point in the reactor to calculate accurately. Many membranes, such as palladium-based membranes, are highly selective to only H2, and therefore, do not need to consider this effect. Because of this, it is normally not worthwhile from a modeling perspective unless other nonisothermal factors are being considered in the model. However, in the case of polymer membranes with a high selectivity for H2O permeation and nearly a 22 atm difference in pressure across the membrane wall, the Joules-Thomson effect may be more important to include.
The stated complexities are also the reason for avoiding countercurrent operation in membrane reactor simulation. The significant dependency on the states of each side of the reactor creates a very difficult boundary-value problem, where even slight changes to the conditions of one side of the reactor can lead to dramatically different solutions overall. In most traditional unit operations such as heat exchangers and reactors, the profiles will still have similar shapes, but will shift, compress, or contract as unit operations are varied. However, with the membrane reactor model, different operating points lead to dramatically different behaviors, and because of this, countercurrent operation is generally avoided.
Lastly, membranes such as the polybenzimidazole are able to have multiple components permeating in both directions simultaneously. This only becomes difficult when combined with countercurrent operation as this allows for a circulation effect to occur in the membrane reactor. For example, steam flows countercurrently to the tube side, permeates to the tube side, reacts to become hydrogen, flows cocurrently within the tube, and then permeates back to the shell side before leaving the reactor. Given all these aforementioned challenges, the proposed model of the comprehensive nonisothermal, countercurrent membrane reactor with bidirectional permeation is thus one of the significant contributions of this work.
3.2. Operability Analysis of Polymer Membrane Reactors
Once a reliable modeling approach is established, an operability analysis is conducted using the process model to see the behavior of the polymer membrane at various operating conditions. The results of this operability mapping can be found in Figure 8.
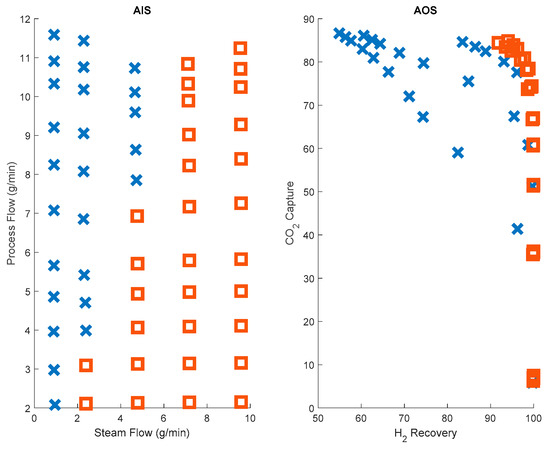
Figure 8.
Input-output mapping of the polymer membrane reactor. For ease of understanding, parts of the mapping region (shown using the x and ◻ markings) are marked differently to see how the inputs are mapped to the output space.
This operability mapping in Figure 8 provides a good representation of the challenges caused by the nonlinearity of the system. It appears that if the flowrate of sweep gas increases to much more than that of the syngas (process flow), then the output becomes very constrained in terms of achievability (indicated by the square markers in Figure 8). This contrasts with the opposite mode of operation (sweep gas flow rate is much less than the syngas flowrate), where the two-dimensional input space is still mapped to another two-dimensional output space.
The achievable output set (AOS) also appears to form a Pareto front. The use of input-output mapping was also demonstrated by Messac and Mattson for generating Pareto points through physical programming [17]. Employing this concept in an operability framework proves to be a useful tool in identifying both operational shortcomings and potential design solutions for the polymer membrane reactor. To show this, an analysis is conducted to identify which points in the output space fit the definition of a Pareto optimal point. A point is considered to be Pareto optimal if one objective cannot be improved without degrading another objective. This analysis is performed using a MATLAB script that checks each point in the output set for Pareto optimality. Since the ideal membrane output would be 100% CO2 capture with 100% H2 recovery, a “best compromise” point is defined here as the Pareto optimal point with the shortest Euclidean distance between itself, and the ideal output point. This analysis is performed in MATLAB using the pdist function with the ‘Euclidean’ norm option. The result of this analysis is shown in Figure 9.
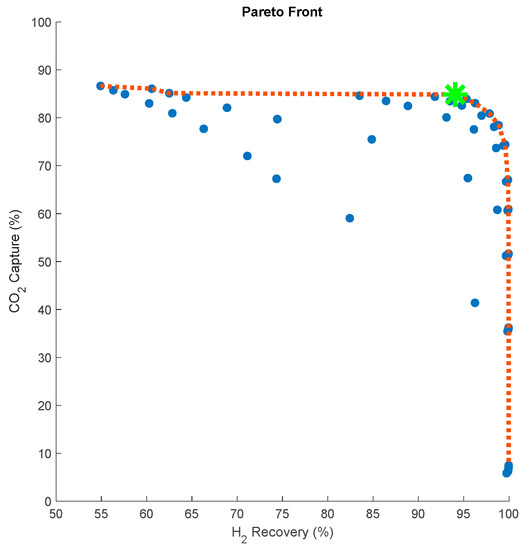
Figure 9.
AOS points with the Pareto frontier included and the “best compromise” marked by a star.
This Pareto frontier in Figure 9, by definition, characterizes the best performance this polymer membrane reactor design can achieve, given the available inputs. To see how this operability analysis can help drive future design decisions, three operating points are selected from the Pareto front for further analysis based on where they are located in the output space; (i) high CO2 capture, low H2 recovery; (ii) low CO2 capture, high H2 recovery; (iii) a “best compromise” point (shown as a green star in Figure 9). The points at each end of the Pareto front were selected and for the purpose of easier comparison, the H2 and H2O fluxes associated with these points were calculated, shown in Figure 10.
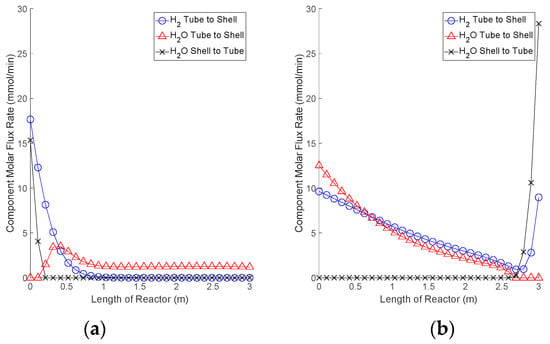
Figure 10.
(a) Flux profile with the highest H2 recovery. (b) Flux profile with the highest CO2 capture.
The profiles in Figure 10 explain how the high CO2 capture or high H2 recovery is achieved. In Figure 10a, the process reaches an equilibrium within the first third of the reactor due to a relatively high flowrate of sweep gas. Slightly manipulating the sweep gas flowrate at this condition would reduce the permeation, but the membrane reactor would still reach this equilibrium. This results in very good H2 recovery, but poor CO2 capture as CO2 continues to permeate out of the tube side despite the H2 recovery process already being finished. Conversely, Figure 10b shows that steam injection is occurring at the end of the membrane reactor, leaving little room left in the reactor for the sweep gas to capture the newly produced H2 product. This low sweep gas flowrate means that very little CO2 will escape from the reactor, leading to optimum CO2 capture, but at the cost of reducing H2 recovery.
The operating points selected for the simulations in Figure 10 show what is happening at the extreme ends of the Pareto frontier. For the next simulation, the best compromise point is selected from the elbow of the Pareto front to see how the polymer membrane reactor can achieve both high H2 recovery and CO2 capture. The results of this simulation are shown in Figure 11.
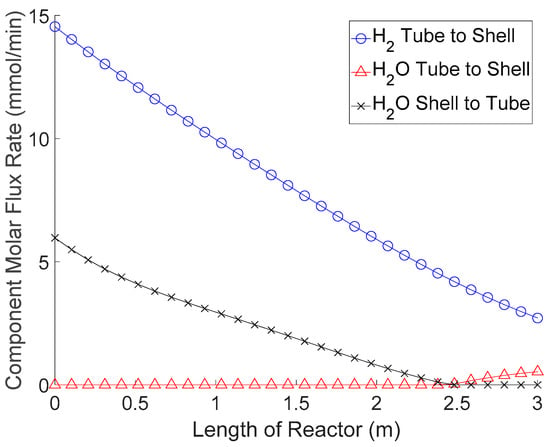
Figure 11.
Flux profile for the “best compromise” operating condition (syngas-to-steam ratio = 0.92).
Unlike the simulation in Figure 10a, the process did not hit an equilibrium point where all potential H2 recovery is completed. This means that although CO2 is still being lost to the shell side, H2 is also being recovered. Another improvement is that the steam injection process is completed before reaching the end of the membrane reactor. Taking what was learned from Figure 10b, this avoids hydrogen being formed at the end of the membrane reactor and not having space remaining to be captured. There are three lessons to be learned from this analysis; (i) steam injection appears to be beneficial at the beginning of the reactor; (ii) the end of the reactor should be primarily used for H2 recovery; (iii) CO2 continues to permeate out of the tube side at all points of the reactor (an undesired feature).
By further analyzing the Pareto frontier in Figure 9, the polymer membrane reactor does not struggle to recover H2 but seems to be limited in its ability to capture CO2. Therefore, the goal should be to push the Pareto front upward by improving the CO2 capture of the unit. However, as previously mentioned, there is no operational change that can achieve this improvement. Therefore, a design change must be proposed to improve the process in this direction.
3.3. Redesign of the Polymer Membrane Reactor
The first two points learned from the operability analysis above focus on improving H2 recovery and should remain features of any new design decision. The third point deals with CO2 permeating out of the tube side, reducing the CO2 capture of the unit and should be the focus of the design change. CO2 permeation is increased by an increase in sweep gas flow in the presence of the membrane. Because sweep gas flow is needed for the H2 recovery to occur, one obvious choice is to strategically remove the polymer membrane from certain areas of the reactor. Because membrane is needed at the beginning of the membrane reactor for the steam injection and at the end for H2 recovery, the only place left is to remove it from the center of the reactor. The proposed redesign to avoid the issue of unnecessary CO2 permeation is shown in Figure 12.
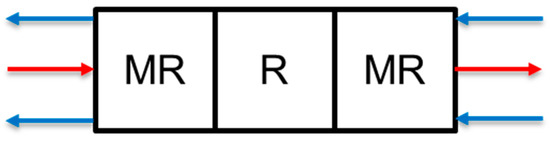
Figure 12.
Proposed redesign of the polymer membrane reactor with membrane being removed from the center of the unit (MR = polymer membrane reactor, R = Reactor).
To simulate this redesign, the contact variables along with the block-based modeling approach described above can be used to allow for the removal of membrane without the need to reinitialize the model. Figure 13 shows the block-diagram representation for the packed-bed reactor section of the unit.
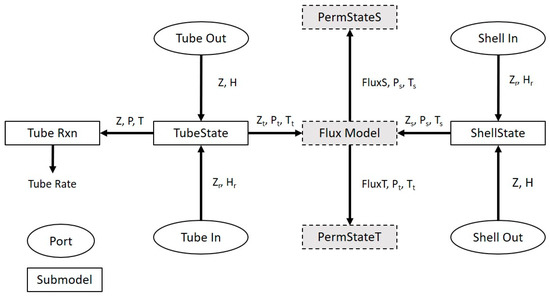
Figure 13.
Diagram representing how removal of the Flux, PermStateT, and PermStateS submodels leads to the MemElem model of a packed-bed reactor.
The input space from the original operability analysis is applied to this new design modeled and simulated in the AVEVA SimCentral Simulation Platform. An example, using the best compromise operating point along with the new design, produces the flux profiles found in Figure 14.
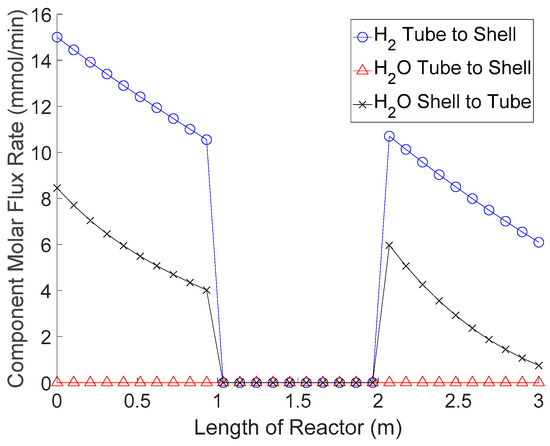
Figure 14.
Flux profiles for the modified membrane reactor design with the membrane tube being replaced by a non-permeative tube.
For this new design, in Figure 14, steam injection is still taking place in the beginning of the membrane reactor and is almost complete by the end of the reactor while H2 is being recovered at the end of the membrane reactor as desired. Additionally, it is important to compare the flux of CO2 in both designs (in Figure 11 versus Figure 14) with the desire for reducing the CO2 lost to the shell side. This comparison is shown in Figure 15.

Figure 15.
(a) Flux profile for the original design showing the continuous permeation of CO2 out of the reactor. (b) Flux profile for the modified design where the polymer membrane was replaced with non-permeative tubes in the center.
By removing the polymer membrane from the center of the reactor, less CO2 can permeate to the sweep gas, thus improving the capture percentage while maintaining a similar H2 recovery. The Pareto analysis was conducted again on this new design and compared to the original design as shown in Figure 16.
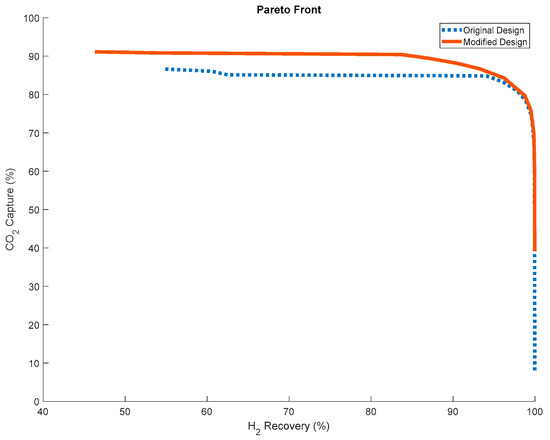
Figure 16.
Comparison of the Pareto fronts for the original and modified designs.
Note that not only this new design change pushes the maximum CO2 capture closer to 100%, it also increased the minimum possible CO2 capture from 5.8% to 38.1%. Moreover, this design potentially brings economic benefits, as the amount of membrane material required to achieve the outputs is reduced. This study shows that operability analyses can provide insights for improving the design of membrane reactors in terms of performance targets and/or cost.
4. Conclusions and Future Work
This paper introduced a new modeling and operability analysis method for polymer membrane reactor studies. The modeling approach presented aimed to reduce the number of simplifying assumptions as much as possible to capture the complex behavior of polymer membranes. As a result, the following features were included in the membrane model for the study where normally some combination of them would be excluded: (i) nonisothermal operation—heat transfer across the tube wall, Joule-Thomson cooling and heating, heat of reaction, and thermal inertia for dynamic calculations; (ii) countercurrent operation; (iii) simultaneous, bidirectional permeation of multiple components.
Although this study is performed assuming steady-state operations, it should be noted that the polymer membrane reactor model also runs reliably in a dynamic simulation where additional features such as thermal inertia from the membrane materials can be considered. The hope is to continue to push these bounds in future work to further study the interdependence of phenomena and improve the overall operation of intensified equipment.
This modeling approach allowed for the first operability analysis of a polymer membrane reactor. In this work, an operability analysis showed a few important considerations when operating a polymer-based membrane reactor (1) nearly half of the available input space was mapped to a one-dimensional curve in the output space; and (2) although such reactors are able to recover H2 effectively, it comes at the cost of lower CO2 capture.
The first point is an undesirable feature of many membrane reactors and leads to problems for those who have worked in operability. If one is interested in which inputs are required to achieve a desired output, it is impossible to perform back calculations if more than one input can achieve that output. This fact would also be relevant for control studies associated with membrane. The second point highlights the tradeoff of switching to a polymer-based membrane rather than a more expensive palladium membrane, but also provides an objective for improving polymer membrane design.
This work also presented a new contribution for operability analyses. This type of analysis has always been useful for seeing how inputs translate to the output space. The use of operability to determine the Pareto front was employed in this study to motivate design changes to the WGS polymer membrane reactor unit. By applying this concept to the operability analysis, a best tradeoff point can be selected and compared to other operating points to determine possible design changes to improve the operability of the system. Although the process of running the analysis, diagnosing the problem areas, and using this info to develop a new design had a logical thought process applied to it, it is still an empirical approach. Future work will focus on the development of a mathematical optimization algorithm using the block-based modeling approach, and the operability and Pareto analyses shown in this work to design equipment with the objective of improving or expanding the entire output set given an available input set.
Author Contributions
This paper is a collaborative work among the authors. B.A.B. performed all simulations and wrote manuscript. F.V.L. helped with the paper writing and oversaw all technical aspects of the research work. All authors have read and agreed to the published version of the manuscript.
Funding
The authors gratefully acknowledge the financial support from AVEVA.
Acknowledgments
The authors thank Cal Depew, Ralph Cos, Richard Pelletier, and Larry Balcom of AVEVA for their technical guidance and advice on the membrane model.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Roy, S.; Eng, P. Consider Modular Plant Design. AIChE CEP Magazine. 2017, 113, 28–31. [Google Scholar]
- Schembecker, G.; Tlatlik, S. Process synthesis for reactive separations. Chem. Eng. Process. Process Intensif. 2003, 42, 179–189. [Google Scholar] [CrossRef]
- Carrasco, J.C.; Lima, F.V. Novel operability-based approach for process design and intensification: Application to a membrane reactor for direct methane aromatization. AIChE J. 2017, 63, 975–983. [Google Scholar] [CrossRef]
- Carrasco, J.C.; Lima, F.V. Bilevel and parallel programing-based operability approaches for process intensification and modularity. AIChE J. 2018, 64, 3042–3054. [Google Scholar] [CrossRef]
- Gazzaneo, V.; Lima, F.V. Multilayer Operability Framework for Process Design, Intensification, and Modularization of Nonlinear Energy Systems. Ind. Eng. Chem. Res. 2019, 58, 6069–6079. [Google Scholar] [CrossRef]
- Fouty, N.J.; Carrasco, J.C.; Lima, F.V. Modeling and Design Optimization of Multifunctional Membrane Reactors for Direct Methane Aromatization. Membranes 2017, 7, 48. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.; Stenger, H.G. Water gas shift reaction kinetics and reactor modeling for fuel cell grade hydrogen. J. Power Sour. 2003, 124, 432–439. [Google Scholar] [CrossRef]
- Radcliffe, A.J.; Singh, R.P.; Berchtold, K.A.; Lima, F.V. Modeling and Optimization of High-Performance Polymer Membrane Reactor Systems for Water–Gas Shift Reaction Applications. Processes 2016, 4, 8. [Google Scholar] [CrossRef]
- Li, X.; Singh, R.P.; Dudeck, K.W.; Berchtold, K.A.; Benicewicz, B.C. Influence of polybenzimidazole main chain structure on H2/CO2 separation at elevated temperatures. J. Membr. Sci. 2014, 461, 59–68. [Google Scholar] [CrossRef]
- Berchtold, K.A.; Singh, R.P.; Young, J.S.; Dudeck, K.W. Polybenzimidazole composite membranes for high temperature synthesis gas separations. J. Membr. Sci. 2012, 415–416, 265–270. [Google Scholar] [CrossRef]
- Singh, R.P.; Dahe, G.J.; Dudeck, K.W.; Welch, C.F.; Berchtold, K.A. High Temperature Polybenzimidazole Hollow Fiber Membranes for Hydrogen Separation and Carbon Dioxide Capture from Synthesis Gas. Energy Procedia 2014, 63, 153–159. [Google Scholar] [CrossRef]
- Turton, R.; Bailie, R.; Whiting, W.; Shaeiwitz, J.; Bhattacharyya, D. Analysis, Synthesis, and Design of Chemical Processes, 4th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2012. [Google Scholar]
- AVEVA. Simcentral Simulation Platform: Process Simulation Reinvented; AVEVA: Cambridge, UK, 2019. [Google Scholar]
- Lima, F.V.; Jia, Z.; Ierapetritou, M.; Georgakis, C. Similarities and differences between the concepts of operability and flexibility: The steady-state case. AIChE J. 2010, 56, 702–716. [Google Scholar] [CrossRef]
- Nikačević, N.M.; Huesman, A.E.M.; van den Hof, P.M.J.; Stankiewicz, A.I. Opportunities and challenges for process control in process intensification. Chem. Eng. Process. Process Intensif. 2012, 52, 1–15. [Google Scholar] [CrossRef]
- Baldea, M. From Process Integration to Process Intensification. Comput. Chem. Eng. 2015, 81, 104–114. [Google Scholar] [CrossRef]
- Messac, A.; Mattson, C.A. Generating Well-Distributed Sets of Pareto Points for Engineering Design Using Physical Programming. Optim. Eng. 2002, 3, 431–450. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).