Abstract
Entropy generation and dual solutions are rarely studied in the literature. An analysis is attempted here. More exactly, the present paper looks at the impact of radiation of a micropolar fluid on mixed convective flow containing the titanium alloy Ti6Al4V nanoparticle along with a Riga plate. The study of dual-nature solution for the entropy generation along a Riga surface was not being explored in the literature; therefore, the current model focuses on the dual solutions of this complex nature model. Riga surface is identified as an actuator of electromagnetic in which electrodes are accumulated alternatively. This array produces the behavior of electromagnetic hydrodynamic in the flow field. The transmuted leading equations were worked out through the formula of 3-stage Lobatto IIIA. Influences of exercising enormous parameters on temperature distribution, velocity, and micro rotation fields are portrayed and argued. More than one solution is achieved in opposing flow, while in the phenomenon of assisting flow result is unique. Moreover, due to the micropolar parameter, the separation of the boundary layer is decelerating. It is determined that the entire structure produces the dual-nature solution of the phenomenon of stagnation point flow, and the temperature profile behavior shows the significant enhancement in the thermal conductivity due to the addition of the nanoparticle. The results exposed that liquid velocity is enhanced, and micro rotation is decelerated, by improving the values of Hartmann numbers in both solutions, whereas the temperature field is decelerated in the first solution and accelerated in the second solution.
1. Introduction
The topic of non-Newtonian liquid is a defying and inspiring area, as it encloses plenty of imperative problems from the processing of biomedical food, petroleum, polymer, and chemical industries. Models of non-Newtonian liquids are relatively valuable to exemplify the flow of commonly used liquids, existing naturally or processed, like slurries, motor oils, volcano lava, biological liquids, paste, and polymer liquids. The dilute suspensions macro-molecules rigid through motion were grasped by micropolar fluid and their individual body moment and stress which are related to spin inertia. The theory of micropolar fluid was introduced by Eringen [1]; it describes a group of fluids that demonstrated certain characters of microscopic occurring from micro-rotation and the local formation of the liquid components. These liquids include dilute suspensions of rigid macro-molecules through motions of individuals that carry the stress and moment of the body which are affecting through spin inertia. Mohammadein and Gorla [2] investigated the impact of viscous dissipation on liquid motion of micropolar liquid from an expanded sheet with heat generation. The time-dependent mixed convective flow near a stagnation-point involving non-Newtonian micropolar liquid through a vertical surface was examined by Lok et al. [3]. They discussed the assisting flow, as well as opposing flow, of the cases of small-time and large-time solutions. Aman et al. [4] scrutinized the impacts of slips on mixed convective flow toward a stagnation point through a vertical sheet. They observed that the multiple solutions are attained for a certain amount of buoyancy constraint for opposing flow only, while the solution is unique in the case of assisting flow. Turkyilmazoglu [5] discussed the characteristic of heat transfer involving micropolar fluid from a permeable stretching sheet. Analytic solution of unsteady flow of micropolar liquid by Newtonian heating was found by Hussanan et al. [6]. Waqas et al. [7] explored the influence of magnetohydrodynamics (MHD) flow of micropolar liquid through moving sheet along forced convection, thermal radiation, and heat flux. Das and Duari [8] inspected the influence of chemical reaction on the liquid movement of micropolar liquid containing nanomaterial from an overextended sheet. Combined possessions of MHD and viscous dissipation on liquid flow of micropolar liquid containing nanofluid to a stretched surface were scrutinized by Hsiao [9]. Recently, the analytical solution of micropolar liquid through mass and heat transfer by Newtonian heating was explored by Hussanan et al. [10].
A metallic liquid or solid that may be compiled from a combination of homogenous/ non-homogenous of two or more metalloid either nonmetals or metal nanometer size elements are known as a mixture. In modern times, they can be utilized in order to convey the definite physical character of mixtures. The examples of alloys are gold, steel brass, solder, and phosphor bronze. Alloys have been used in a variety of applications, e.g., technologies in aerospace science and advanced powder, processes of a hip-joint substitute, implantation through surgery, and many biological treatments. In addition, alloys are employed in the handling of fabrication systems, production of hot and cold rolled sheets, and many more. These alloys also maintain the savings weight in model of smaller strengthen the place of aerospace type steel and aluminum. More about alloys and their applications can be seen in [11,12,13]. Afterward, many researchers [14,15,16,17,18] showed the theoretical, as well as experimental, explorations with different effects and geometries on flow of titanium alloys. In addition, in the equipment of heat transfer, liquids are frequently used as heat transporters [19,20].
In equipment of heat transfer, liquids are frequently used as heat transporters. For example, heat transfer liquid shows a vital responsibility in numerous manufacturing applications in engineering, such as polymer, microelectronic, and automotive industries. In the heat-transfer process, thermal conductivity of liquids is significant in the equipment of the transfer rate of heat at the surface [21,22]. However, the regular heat transported of solutions, such as oil, toluene, and water, is generally insufficient for the rate of transferring heat. The thermal conductivity of a metallic solid like gold is greater compared to regular liquid, like oil. Thus, metallic fluids have extra thermal conductivity associated with nonmetallic fluids. As a result, several researchers endeavored to dispense metallic solid/liquid particles in regular liquids, to improve the heat-transfer rate and thermal conductivity. Maxwell [23] showed that the thermal conductivity of nanoparticles improved due to solid particles of volume fraction, taking into account the spherical particles in the analysis of flow. However, when micro and mini-sized particles merge with the regular fluids, the liquid flows can have blockage problems. Consequently, extremely small amount of particles is required to dispense in the solutions, to make them free of blockage troubles. Choi [24] was the first one who utilized the concept of nanofluid that submits to the liquid in which extremely small-sized (<50 nm) particles dispersed into regular liquids. However, the present technology is adequate to assemble nanoparticles of 10nm. Afterward, Pop and Khan [25] discussed the boundary layer flow containing nanoliquid from stretched surface. Mabood et al. [26] found that water-based Al2O3 nanoparticles give a wider velocity boundary layer compared to water base copper nanoparticles. Nonlinear radiative heat transfer containing water-based copper and silver nanoparticles on mixed convective flow was investigated by Hayat et al. [27]. Du and Tang [28] scrutinized the properties of plasmonic optical nanoliquids involving gold nanoparticles, taking into account of different sizes and shapes. Recently, Zaib et al. [29] argued the effects of binary chemical reaction and activation energy on flow of Williamson nanoliquid through a plate with energy condition.
Flow of electrically conducting liquid, for example electrolytes, fluid rails and plasma, etc. can be managed through pertaining MHD. These flows have remarkable applications in geophysics, sensors and engineering etc. Magnetic and electric fields are required to direct and control the liquid flow. These kinds of flow are described as EMHD flow. Riga plate is one of the devices is utilized in this regard. The influence of EMHD (Electro–magneto–hydrodynamic) has an important character in act of momentum and the consequence detected in micro-coolers, thermal reactor, chromatography of liquid and controlling the flow in network of fluids. In 1861, Gallites and Lilausis [30] considered Riga surface to produce and pertained electric and magnetic fields in order to manage fluid flow which accordingly creates Lorentz force equivalent to the wall. Magyari and Pantokratoras [31] examined the flow from a Riga plate enclosing low electrical conductivity. From a Riga plate, the entropy analysis was scrutinized by Abbas et al. [32], in the presence of nanomaterials’ fluid flow. The impact of chemical reaction on squeezing flow from a convectively heated Riga surface was examined by Hayat et al. [33]. Recently, Iqbal et al. [34] utilized Keller box procedure to obtain the numerical solution of melting heat-transfer flow comprising nanomaterial through the Riga surface with irregular thickness.
The idea of entropy generation is incredibly imperative to examine the problems of heat transfer. Minimization of entropy cohort has been widely wrapped by Bejan [35] particularly, in the fields of freezing, heat transfer, conversion of thermal solar power, and storage. The minimization technique of entropy generation is utilized to improve the devices of thermal manufacturing for efficiency of higher energy. Aiboud and Sauoli [36] discussed the influence of entropy generation in viscoelastic electrically conducting flow from a wide elastic sheet. The effect of velocity slip on flow toward a convectively heated vertical surface was presented by Butt et al. [37]. Noghrehabadiet al. [38] investigated the heat generation/absorption effects on fluid flow comprising nanofluid through a stretched sheet with entropy generation. Abolbashari et al. [39] scrutinized the entropy generation on the slip flow of Casson nanofluid induced by convectively heated stretched sheet. Entropy generation involving non-Newtonian Jeffrey liquid in the presence of nanomaterials induced by stretched sheet with zero flux was surveyed by Rehman et al. [40]. Recently, Azhar et al. [41] discussed the entropy generation through an unsteady MHD fractional flow of Couette liquid in a rotating frame with exponentially heating walls.
The configuration of micropolar liquid with titanium alloy nanomaterial composes the more complex mixture compared to regular nanoliquids. Therefore, we planned to explore the mixed convective flow containing micropolar titanium alloy nanomaterial from a vertical Riga plate through an entropy generation with thermal radiation. Exercising via the formula of three-stage Lobatto IIIA computationally on the established similarity equations, to find more than one result (dual solutions). The influences of the significant parameters have argued in detail through the help of the tables and the graphs.
2. Construction of Problem
The contemplate of a steady mixed convective flow near a stagnation-point involving micropolar liquid comprising water-based titanium alloy nanomaterial from a Riga plate with thermal radiation and entropy generation is scrutinized. We have considered the Cartesian coordinates x-y system, where x is taken along the Riga surface and y is normal to it. We deem that the ambient velocity and temperature are taken to be linearly and with , respectively, where , c, and b correspondingly stand for the ambient temperature and positive constants. Additionally, an irregular array of electrodes gathered with the permanent magnets on the surface of the plate presented in (Figure 1), using Riga plate. These arrays generate a resistive-type force known as the Lorentz force. This force is parallel to the plate’s surface and declines exponentially in the horizontal way to the surface, after exercising via the Boussinesq approximation, along with a boundary layer approximation. The condition in the model was used to create the following leading system of equations (Equations (1) to (4)) [42,43].
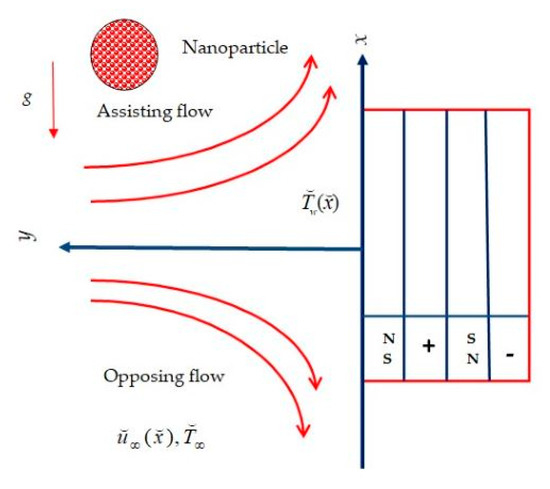
Figure 1.
Physical diagram of the problem.
The physical conditions of the boundary are as follows:
In the aforementioned equations, and are axes direction, and the velocity component is represented by and , respectively. , and , are the nanofluid thermal expansion, acceleration caused by gravity, the applied current density in the electrodes, electrodes and magnets width, magnetization of the permanents magnets, vortex viscosity, nanofluid density, and nanofluid dynamic viscosity, respectively. Furthermore, stands for the micro gyration parameter; is used for the micro inertia density, shows the thermal diffusivity, presents the spin gradient viscosity, displays the temperature; and is the micro rotation vector. Thus, by the well-known interpretation that the parameter varies in the closed interval , whereas by special imposed condition signifies the strong concentration, suggests as weak concentration, and the turbulent flow is found for the value .
Using the Rosseland approximation, the radiative heat flux can be calculated as follows:
where and denotes the constant of Stefan–Boltzmann and the coefficient of mean absorption. It is acknowledged that the flow is tiny in comprising the temperature differences, in showing that the mathematical formulation of may be articulated as a degree one function of temperature. Thus, by exercising the Taylors series for about a point and vanished the higher order term, we get Equation (7):
The standard of nanoparticles equations for , , , , ,, and are as follows:
where stands for the nanoliquid volume fraction; and portray the thermal conductivity of regular liquid and nanoliquid; and show the density of nanoliquid and the base fluid; and and represent the thermal expansion of nanoliquid and base fluid coefficients, respectively.
We utilize the transformation called the similarity, as mentioned below, in Equation (9):
By applying Equation (9), Equations (2) to (5), by utilizing Equations (6) to (8) are transmuted to the following equations:
Along the renewed boundary conditions, we get the following calculations:
In overhead equations, dimensionless constant parameters and numbers are as follows: micropolar is , buoyancy is , Grashof is , Reynolds is radiation is , modified Hartmann is , dimensionless is , and Prandtl is .
The skin friction coefficient and the Nusselt number are calculated as follows:
Using Equations (8) and (9), we attain the following:
3. Entropy Analysis
Analysis of entropy generation with micropolar fluid holding titanium alloy nanomaterial with thermal radiation is engraved as follows:
Volumetric entropy number is characterized as follows:
In dimensionless form, we get Equation (8):
where is the dimensionless difference of temperature, is the Brinkman number, and is the characteristic length based Reynolds number.
4. Results and Discussions
The transmuted mixed convective problem described in Equations (10) to (12) through boundary condition in Equation (13) has been computed numerically via the formula of three-stage Lobatto IIIA. The influences of physical parameters on velocity and micro-rotation profiles, temperature distribution, along with the corresponding and , is established and portrayed graphically via Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21 and Figure 22. Now, at this point, we can take the value of the micro gyration parameter is equal to 0.5. The feature properties of the regular and particle fluids are exemplified in Table 1. The authenticity of our computational results were invoked in Table 2 and Table 3 for and , and we found a tremendous agreement as compared to old one.
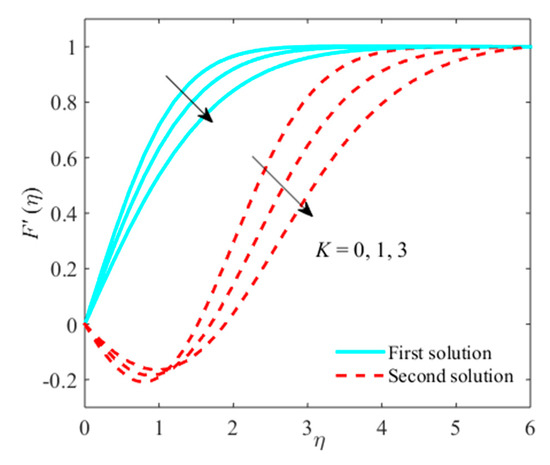
Figure 2.
Impact of on when .
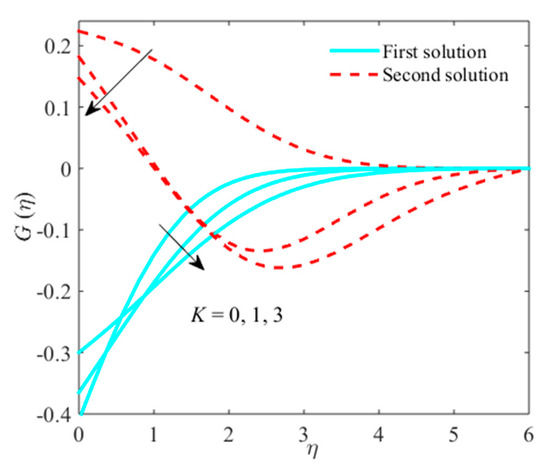
Figure 3.
Impact of on when .
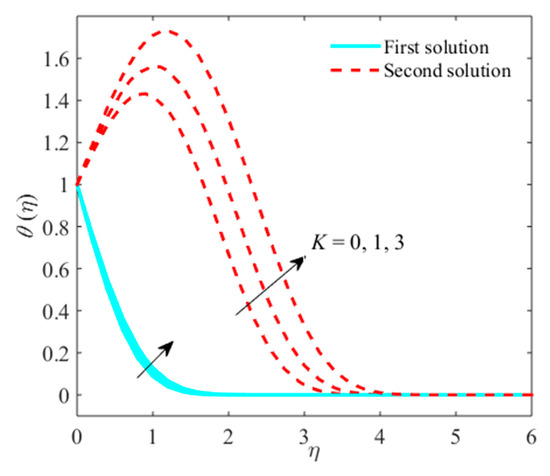
Figure 4.
Impact of on when .

Figure 5.
Impact of on when .
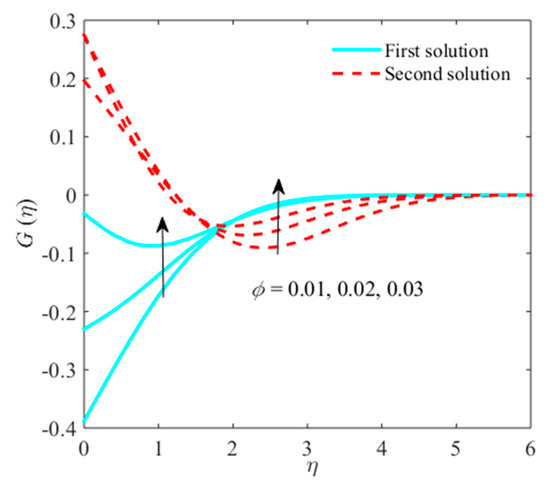
Figure 6.
Impact of on when .
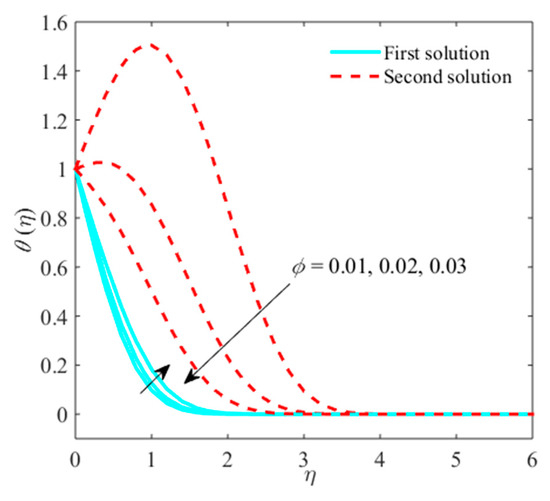
Figure 7.
Impact of on when .
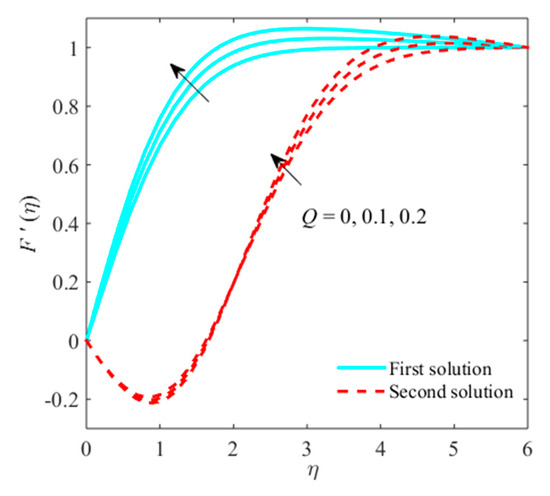
Figure 8.
Impact of on when .
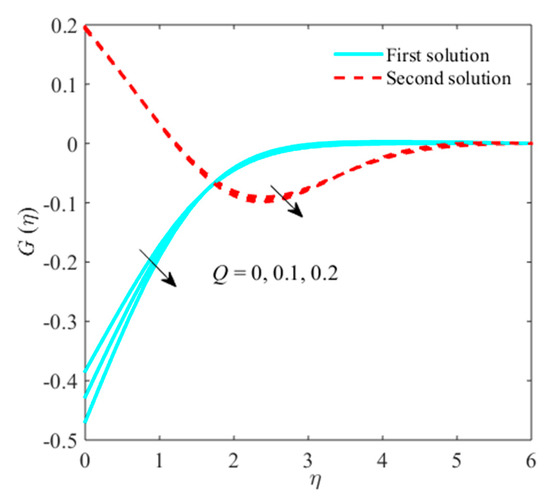
Figure 9.
Impact of on when .
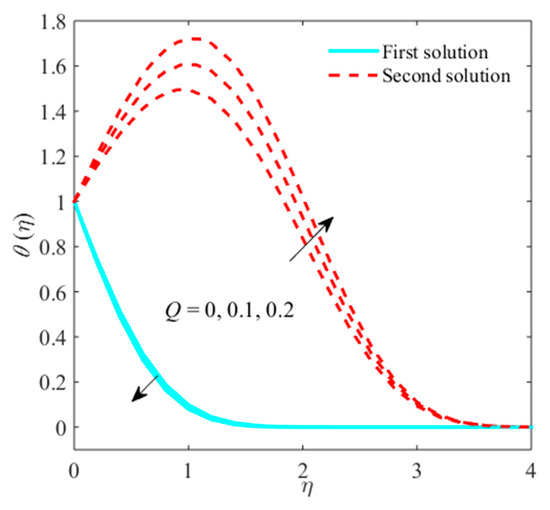
Figure 10.
Impact of on when .
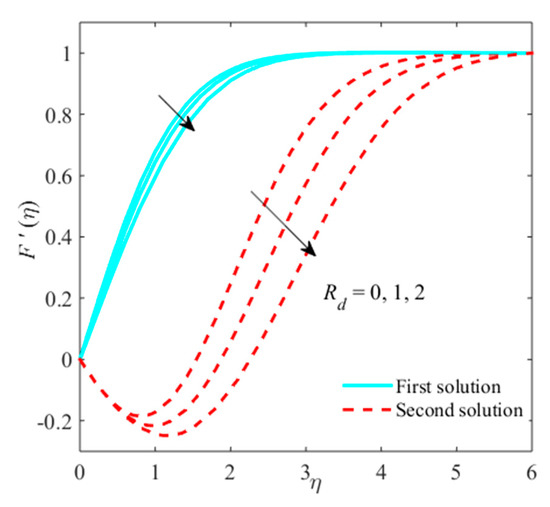
Figure 11.
Impact of on when .
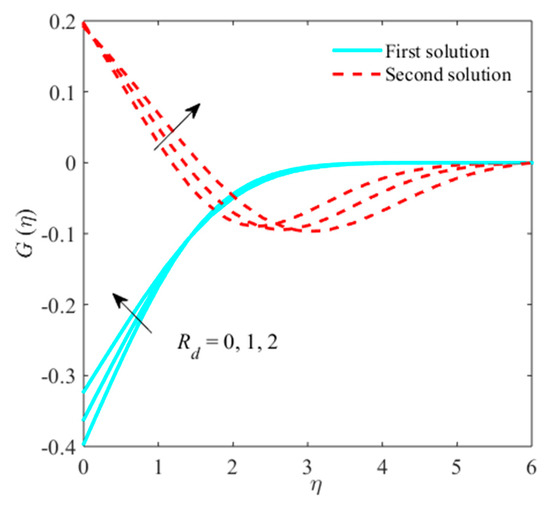
Figure 12.
Impact of on when .
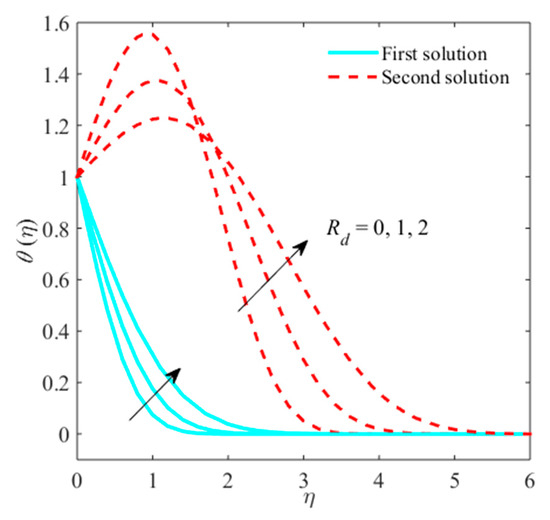
Figure 13.
Impact of on when .
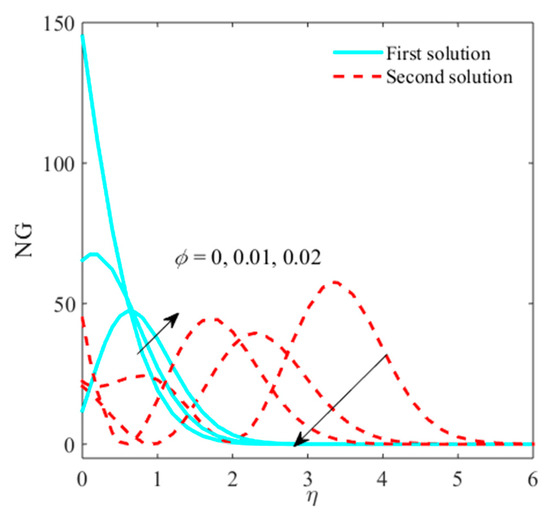
Figure 14.
Impact of on when .
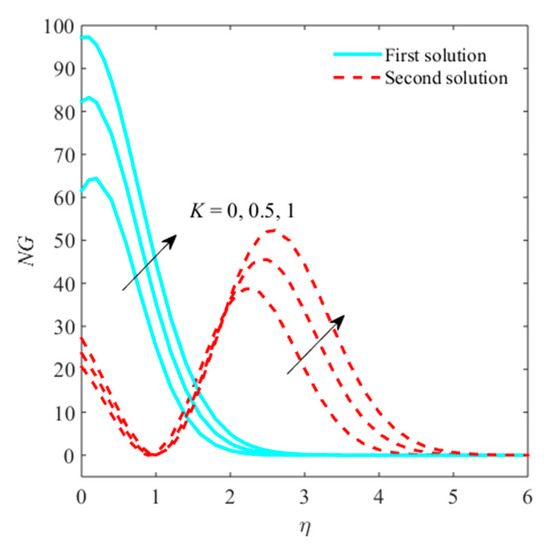
Figure 15.
Impact of on when .
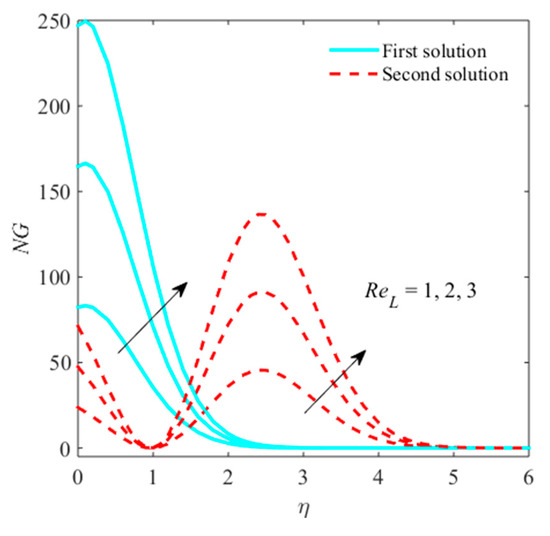
Figure 16.
Impact of on when .
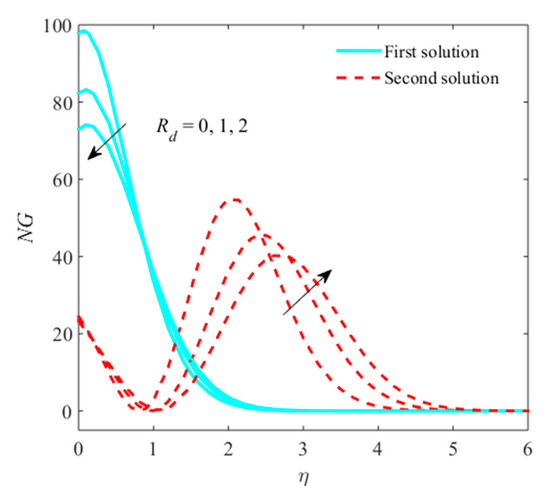
Figure 17.
Impact of on when .
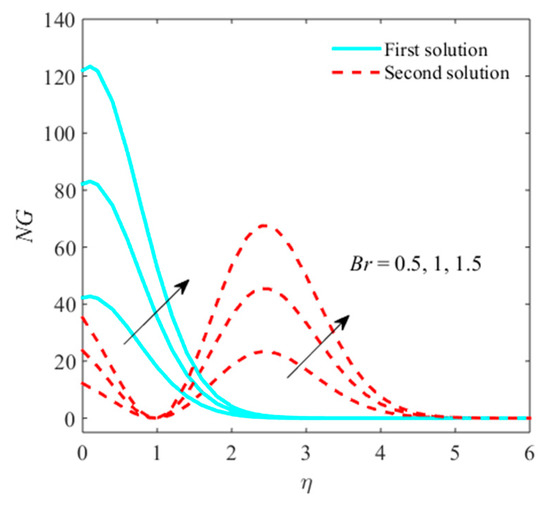
Figure 18.
Impact of on when .
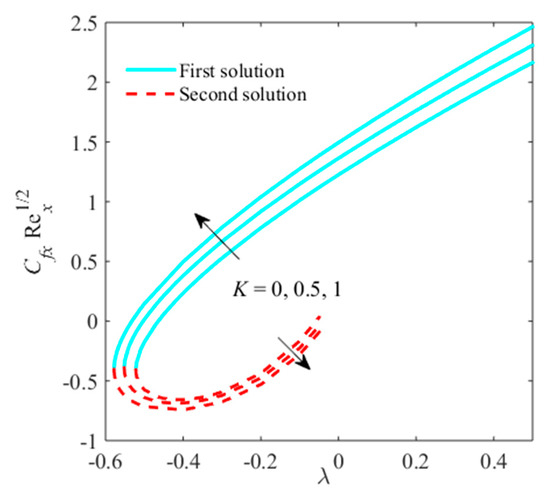
Figure 19.
Impact of on when .
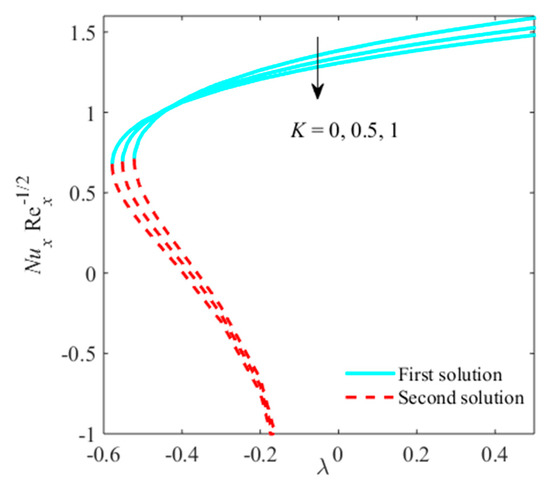
Figure 20.
Impact of on when .
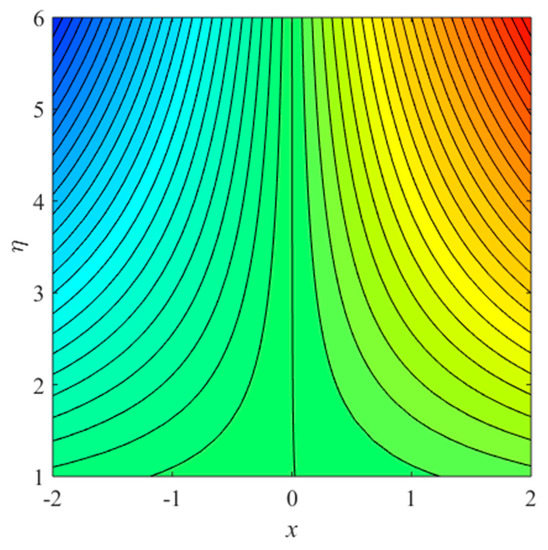
Figure 21.
Streamline patterns for first solution when .
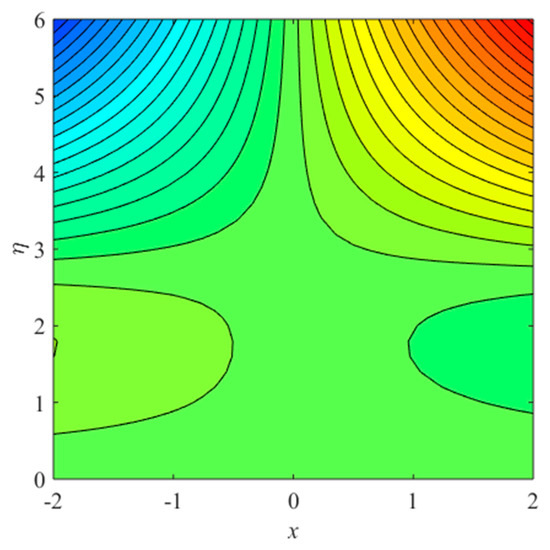
Figure 22.
Streamline patterns for second solution when .

Table 1.
Thermophysical properties of base fluid and Ti6Al4V.

Table 2.
Comparison of when .

Table 3.
Comparison of when .
Figure 2, Figure 3 and Figure 4 observe the impression of micropolar parameter on micro rotation, velocity profiles, and temperature distribution. The larger values of decline and micro-rotation fields in the upper-branch solution, as well as in the second-branch solution, while the temperature distribution augments for in both solutions. Physically, due to escalating viscosity, microelements therefore continuously encourage and slowdown in the flow nearby the plate. From these plots, the significant growth in the behavior of thermal and momentum boundary layer thicknesses is noticed as grows in first and second solutions. It is also perceived that the plots are larger in non-viscous liquid compared to viscous liquid .
Figure 5, Figure 6 and Figure 7 are enlisted in pursuit of the stimulation of on liquid , micro rotation, and temperature fields. Figure 5 explains that the liquid velocity shrinks when rises in the first solution, while the graph shows escalating behavior in the second solution. Physically, it indicates that the raises the , which consequently shrinks the momentum boundary layer. However, the graph of micro rotation (Figure 6) displays a decreasing trend with the enhancement of in both branches. In contrast, the temperature (Figure 7) and boost-up thermal boundary layer due to in upper solution while in lower solution reverse trend is examined. This means that improves the element-to-element distribution. Physically, as the of titanium alloy nanomaterial grows the thermal conductivity, it improves the thermal boundary layer by making it finer in the upper branch. The variations in the material, size, shape, and concentration nanoparticles, allow for alteration to boost up the energy of absorption, using via the volume of fluid, since the depends on the magnitude of the particle. Escalating the results in raising the coefficient of heat transfer.
Another significant factor in our study is the modified Hartman number, , which is portrayed in Figure 8, Figure 9 and Figure 10. Figure 8 captures that the liquid velocity enhances from mounting the values of in both branches. This means that various selected choices of outcomes which augment internal or external forces called adhesive and cohesive forces. Due to these forces, the momentum of the flow is increased, and thus, as a result, the velocity expands. On the other hand, the micro-rotation plot shows the opposite behavior when increases, as shown in Figure 9. Figure 10 elucidates that the liquid temperature moderates with higher choices of in upper solution and develops in lower branch. Physically, outer/inner forces present an additional resistance to stop the flow of fluid particles. Therefore, more heat is formed, which, in turn, enhances the second branch solution for the temperature distribution.
Figure 11, Figure 12 and Figure 13 are organized to examine the stimulus of on , micro rotation, and temperature fields. An anticipated result from these outcomes is that the momentum, thermal boundary layers, and micro rotation thicknesses increase as radiation parameter grows. Physically, it shows that the radiation impact is augmented due to more heat of flux as a result the higher temperature, which is observed within the boundary layer region. Moreover, at all times, it is susceptible to preserve the minimum thermal radiation to achieve a higher rate of heat transfer, which leads toward additional cooling.
The impacts of , micropolar parameter, Reynolds number, and radiation parameter on entropy generation are sketched in Figure 14, Figure 15, Figure 16 and Figure 17. Figure 14 explains that the entropy generation confirms the growing behavior due to in first outcome, while, in second outcome, the generation of entropy shrinks. Figure 15 shows that the entropy generation improves with superior behavior in both branches of solution due to boost-up . It is imperative to observe that plot of entropy generation is larger in , not equal to zero compared to equal to zero. Figure 16 reveals that the entropy generation is caused by enhancing the Reynolds number. Physically, the entropy formed from all irreversibility mechanisms, and thus entropy enhances due to the Reynolds number. Figure 17 depicts that, for a larger radiation parameter, the entropy generation is enhanced. For the superior belief of systems, internal energy augments, making it accountable for rising the entropy generation. The intention of Brinkman number is to find the rate of heat releasing through molecular conduction to viscous heating. The greater amount of heat discharges involved liquid particle layers, which are accountable for enhancing the entropy generation, as shown in Figure 18.
Figure 19 and Figure 20 are set to view the effect of micropolar on the and the versus mixed convective parameter . The (dual) more than one solution is accomplished for the case of opposing flow , while the solution is unique in the case of assisting flow . The multiple solutions exist in some range where the critical values are found, and their values are mentioned in the graphs for (say ), and no solution exists in the range . is the point where both solutions are combined or the same. Computationally, we tackled our problem and found the values of are −0.5219, −0.5520, and −0.5783 for the different values of equal to 0, 0.5, 1, respectively. Therefore, the values of grow with bigger values of . The separation of the boundary layer is decaying due to micropolar parameters. In addition, the values of skin friction in the first branch enhance as and rise, while the opposite trend is scrutinized in the second solution. Physically, assisting flow generated an auspicious pressure slope that augmented the movement of fluid, which successively boosted the shear stress at the surface of the plate. In spite of this, the values of the Nusselt number shows a declining behavior with mounting values of in uphill and downhill solution, because an adverse velocity slope yields by opposing flow, which delays the run of fluid.
Figure 21 and Figure 22 explain the patterns of streamlines in first and second solutions. Figure 21 indicates that the flow pattern of lines is symmetric, fuller, and simple from an axis in uphill solution, due to equal forces of opposing and assisting flows. Alternatively, Figure 22 demonstrates that the streamlines are somewhat complex in upper solution and part the flows in the double region.
5. Concluding Remarks
Here, the impact of thermal radiation on mixed convection flow of micropolar liquid comprising titanium alloy nanomaterial over a Riga plate with entropy generation is discussed. More than one solution is obtained in opposing flow by using the formula of three-stage Lobatto IIIA. The key points monitored from the current flow problem are enlisted below:
- ➢
- The dual solutions are attained in opposing flow only.
- ➢
- Increasing the micropolar parameter decreases the liquid velocity and micro rotation and raises the temperature distribution within the region of boundary layer in both branches.
- ➢
- Micropolar parameter impedes the boundary layer separation.
- ➢
- Velocity and micro rotation fields augment for escalating values of in the second solution, while in the first solution, the reverse behavior is seen. Temperature field rises in the upper solution and falloffs in the lower solution due to
- ➢
- The results exposed that liquid velocity is accelerated and micro rotation is decelerated by modified Hartmann number in both solutions, whereas temperature field is decelerated in the uphill solution and accelerated in the downhill solution.
- ➢
- Radiation parameter enhances the temperature and micro rotation fields and reduces the liquid velocity in both solutions.
- ➢
- Increasing behavior is observed for an entropy generation in both solutions via , , and . In contrast, an entropy generation augments due to and declines due to in the first solution.
Author Contributions
A.Z. and U.K. conceived and designed the model; I.K. performed the formulation; A.H.S. and E.-S.M.S. analyzed the data; A.Z. contributed reagents/materials/analysis tools; U.K. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded from the Project number (RSP-2019/33), King Saud University, Riyadh, Saudi Arabia.
Acknowledgments
Researchers Supporting Project number (RSP-2019/33), King Saud University, Riyadh, Saudi Arabia.
Conflicts of Interest
Authors do not have any conflict of interest.
Nomenclature
| positive constants | |
| skin friction coefficient | |
| specific heat of fluid [J kg−1 K−1] | |
| electrodes and magnets width | |
| acceleration caused by gravity [ms−2] | |
| Grashof number | |
| applied current density in the electrodes | |
| micro inertia per unit mass [m2] | |
| micropolar parameter | |
| absorption coefficient | |
| thermal conductivity of regular liquid [W m−1 K−1] | |
| thermal conductivity of nanoliquid [W m−1 K−1] | |
| magnetization of thepermanents magnets | |
| micro rotation vector [ms−1] | |
| micro gyration parameter | |
| Nusselt number | |
| Prandtl number | |
| radiative heat flux [W m−2] | |
| radiation parameter | |
| local Reynolds number | |
| temperature [T] | |
| free stream temperature [T] | |
| fluid temperature at wall [T] | |
| free stream velocity [ms−1] | |
| velocity components [ms−1] | |
| Cartesian coordinates [m] | |
| Greek symbols | |
| modified Hartmann number | |
| thermal diffusivity [m2 s−1] | |
| nanofluid thermal expansion [K−1] | |
| spin−gradient viscosity [kg m s−1] | |
| vortex viscosity [kg m−1 s−1] | |
| mixed convective parameter | |
| nanofluid dynamic viscosity [kg m−1 s−1] | |
| volume fraction of nanoliquid | |
| dimensionless temperature | |
| kinematic viscosity [m2 s−1] | |
| density [kg m−3] | |
| density of nanoliquid [kg m−3] | |
| density of base fluid [kg m−3] | |
| stream function [m2 s−1] | |
| dimensionless parameter | |
| Stefan–Boltzmann constant [Wm−2K−4] | |
| similarity variable | |
| Subscripts | |
| condition at wall | |
| condition at free stream | |
| Superscripts | |
| ‘ | derivative w.r.t. |
References
- Eringen, A.C. Theory of micropolar fluids. J. Appl. Math. Mech. 1966, 16, 1–18. [Google Scholar] [CrossRef]
- Mohammadein, A.A.; Gorla, R.S.R. Heat transfer in a micropolar fluid over a stretching sheet with viscous dissipation and internal heat generation. Int. J. Numer. Methods Heat Fluid Flow 2001, 11, 50–58. [Google Scholar] [CrossRef]
- Lok, Y.Y.; Amin, N.; Pop, I. Unsteady mixed convection flow of a micropolar fluid near the stagnation point on a vertical surface. Int. J. Thermal Sci. 2006, 45, 1149–1157. [Google Scholar] [CrossRef]
- Aman, F.; Ishak, A.; Pop, I. Mixed convection boundary layer flow near stagnation-point on vertical surface with slip. Appl. Math. Mech. Engl. Ed. 2011, 32, 1599–1606. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Flow of a micropolar fluid due to a porous stretching sheet and heat transfer. Int. J. Non-Linear Mech. 2016, 83, 59–64. [Google Scholar] [CrossRef]
- Hussanan, A.; Salleh, M.Z.; Khan, I.; Tahar, R.M. Unsteady free convection flow of a micropolar fluid with Newtonian heating: Closed form solution. Therm. Sci. 2017, 21, 2313–2326. [Google Scholar] [CrossRef][Green Version]
- Waqas, H.; Hussain, S.; Sharif, H.; Khalid, S. MHD forced convective flow of micropolar fluids past a moving boundary surface with prescribed heat flux and radiation. Br. J. Math. Comput. Sci. 2017, 21, 1–14. [Google Scholar] [CrossRef]
- Das, K.; Duari, P.R. Micropolar nanofluid flow over a stretching sheet with chemical reaction. Int. J. Appl. Comput. Math. 2017, 3, 3229–3239. [Google Scholar] [CrossRef]
- Hsiao, K.L. Micropolar nanofluid flow with MHD and viscous dissipation effects towards a stretching sheet with multimedia feature. Int. J. Heat Mass Transf. 2017, 112, 983–990. [Google Scholar] [CrossRef]
- Hussanan, A.; Salleh, M.Z.; Khan, I.; Tahar, R.M. Heat and mass transfer in a micropolar fluid with Newtonian heating: An exact analysis. Neural Comput. Appl. 2018, 29, 59–67. [Google Scholar] [CrossRef]
- Makinde, O.D.; Aziz, A. Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Therm. Sci. 2011, 50, 1326–1332. [Google Scholar] [CrossRef]
- Hogan, C. Density of states of an insulating ferromagnetic alloy. Phys. Rev. 1969, 188, 870. [Google Scholar] [CrossRef]
- Parayanthal, P.; Pollak, F.H. Raman scattering in alloy semiconductors: Spatial correlation model. Phys. Rev. Lett. 1984, 52, 1822–1825. [Google Scholar] [CrossRef]
- Žitňanský, M.; Čaplovič, L. Effect of the thermomechanical treatment on the structure of titanium alloy Ti6Al4V. J. Mater. Process. Technol. 2004, 157, 643–649. [Google Scholar] [CrossRef]
- Zhu, X.J.; Tan, M.J.; Zhou, W. Enhanced super plasticity in commercially pure titanium alloy. Scr. Mater. 2005, 52, 651–655. [Google Scholar] [CrossRef]
- Hao, Y.L.; Li, S.J.; Sun, B.B.; Sui, M.L.; Yang, R. Ductile titanium alloy with low Poisson’s ratio. Phys. Rev. Lett. 2007, 98, 216405. [Google Scholar] [CrossRef]
- Balazic, M.; Kopac, J.; Jackson, M.J.; Ahmed, W. Review: Titanium and titanium alloy applications in medicine. Int. J. Nano Biomater. 2007, 1, 3–34. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Sekhar, K.R.; Ibrahim, S.M.; Lorenzini, G.; Reddy, G.V.; Lorenzini, E. Variable viscosity on unsteady dissipative Carreau fluid over a truncated cone filled with titanium alloy nanoparticles. Contin. Mech. Thermodyn. 2017, 29, 699–713. [Google Scholar] [CrossRef]
- Kassai, M.; Poleczky, L.; Al-Hyari, L.; Kajtar, L.; Nyers, J. Investigation of the Energy Recovery Potentials in Ventilation Systems in Different Climates. Facta Univ. Ser. Mech. Eng. 2018, 16, 203–217. [Google Scholar] [CrossRef]
- Gao, H.; Guo, L.J.; Zhang, X.M. Liquid-solid separation phenomena of two-phase turbulent flow in curved pipes. Int. J. Heat Mass Transf. 2002, 45, 4995–5005. [Google Scholar] [CrossRef]
- Kassai, M.; Ge, G.; Simonson, C.J. Dehumidification performance investigation of run-around membrane energy exchanger system. Therm. Sci. 2016, 20, 1927–1938. [Google Scholar] [CrossRef]
- Shi, D.P.; Luo, Z.H.; Zheng, Z.W. Numerical simulation of liquid-solid two-phase flow in a tubular loop polymerization reactor. Powder Technol. 2010, 198, 135–143. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism, 2nd ed.; Clarendon Press: Oxford, UK, 1873; Volume 1. [Google Scholar]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles, developments and applications of non-Newtonian flows. In Proceedings of the 1995 International Mechanical Engineering Congress and Exhibition, San Francisco, CA, USA, 12–17 November 1995; Volume 66, pp. 99–105. [Google Scholar]
- Khan, W.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Mabood, F.; Shateye, S.; Rashidi, M.M.; Momoniat, E.; Freidoonimehr, N. MHD stagnation point flow heat and mass transfer of nanofluids in porous medium with radiation, viscous dissipation and chemical reaction. Adv. Powder Technol. 2016, 27, 742–749. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Imtiaz, M.; Alsaedi, A. Comparative study of silver and copper water nanofluids with mixed convection and non-linear thermal radiation. Int. J. Heat Mass Transf. 2016, 102, 723–732. [Google Scholar] [CrossRef]
- Du, M.; Tang, G.H. Plasmonic nanofluids based on gold nanorods/nanoellipsoids/nanosheets for solar energy harvesting. Sol. Energy 2016, 137, 393–400. [Google Scholar] [CrossRef]
- Zaib, A.; Abelman, S.; Chamkha, A.J.; Rashidi, M.M. Entropy generation in a Williamson nanofluid near a stagnation point over a moving plate with binary chemical reaction and activation energy. Heat Transf. Res. 2018, 49, 1131–1149. [Google Scholar] [CrossRef]
- Gailitis, A.; Lielausis, O. On a possibility to reduce the hydrodynamic resistance of a plate in an electrolyte. Appl. Magnetohydrodyn. Rep. Phys. Inst. Riga 1961, 12, 143–146. [Google Scholar]
- Pantokratoras, A.; Magyari, E. EMHD free-convection boundary-layer flow from a Riga-plate. J. Eng. Math. 2009, 64, 303–315. [Google Scholar] [CrossRef]
- Abbas, T.; Ayub, M.; Bhatti, M.M.; Rashidi, M.M.; Ali, M.E.l. Entropy generation on nanofluid flow through a horizontal Riga plate. Entropy 2016, 18, 223. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.; Imtiaz, M.; Alsaedi, A. Squeezing flow past a Riga plate with chemical reaction and convective conditions. J. Mol. Liq. 2017, 225, 569–576. [Google Scholar] [CrossRef]
- Iqbal, Z.; Azhar, E.; Mehmood, Z.; Maraj, E.N. Melting heat transport of nanofluidic problem over a Riga plate with erratic thickness: Use of Keller Box scheme. Res. Phys. 2017, 7, 3648–3658. [Google Scholar] [CrossRef]
- Bejan, A. A study of entropy generation in fundamental convective heat transfer. J. Heat Transf. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Aiboud, S.; Saouli, S. Entropy analysis for viscoelastic magneto-hydrodynamic flow over a stretching surface. Int. J. Non-linear Mech. 2010, 45, 482–489. [Google Scholar] [CrossRef]
- Butt, A.S.; Munawar, S.; Ali, A.; Mehmood, A. Entropy generation in hydrodynamic slip flow over a vertical plate with convective boundary. J. Mech. Sci. Technol. 2012, 26, 2977–2984. [Google Scholar] [CrossRef]
- Noghrehabadi, A.; Saffarian, M.R.; Pourrajab, R.; Ghalambaz, M. Entropy analysis for nanofluid flow over a stretching sheet in the presence of heat generation/absorption and partial slip. J. Mech. Sci. Technol. 2013, 27, 927–937. [Google Scholar] [CrossRef]
- Abolbashari, M.H.; Freidoonimehr, N.; Nazari, F.; Rashidi, M.M. Analytical modeling of entropy generation for Casson nano-fluid flow induced by a stretching surface. Adv. Powder Technol. 2015, 26, 542–552. [Google Scholar] [CrossRef]
- Rehman, S.U.; Haq, R.U.; Khan, Z.H.; Lee, C. Entropy generation analysis for non-Newtonian nanofluid with zero normal flux of nanoparticles at the stretching surface. J. Taiwan Inst. Chem. Eng. 2016, 63, 226–235. [Google Scholar] [CrossRef]
- Azhar, W.A.; Vieru, D.; Fetecau, C. Entropy generation due to fractional Couette flow in a rotating channel with exponential heating of walls. Heat Transf. Res. 2018, 49, 1507–1526. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.; Khan, M.I.; Alsaedi, A.; Ayub, M. Electromagneto squeezing rotational flow of carbon (C)-water (H2O) kerosene oil nanofluid past a Riga plate: A numerical study. PLoS ONE 2017, 12, e0180976. [Google Scholar] [CrossRef]
- Zaib, A.; Haq, R.U.; Chamkha, A.J.; Rashidi, M.M. Impact of partial slip on mixed convective flow towards a Riga plate comprising micropolar TiO2-kerosene/water nanoparticles. Int. J. Numer. Meth. Heat Fluid Flow 2019, 29, 1647–1662. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).