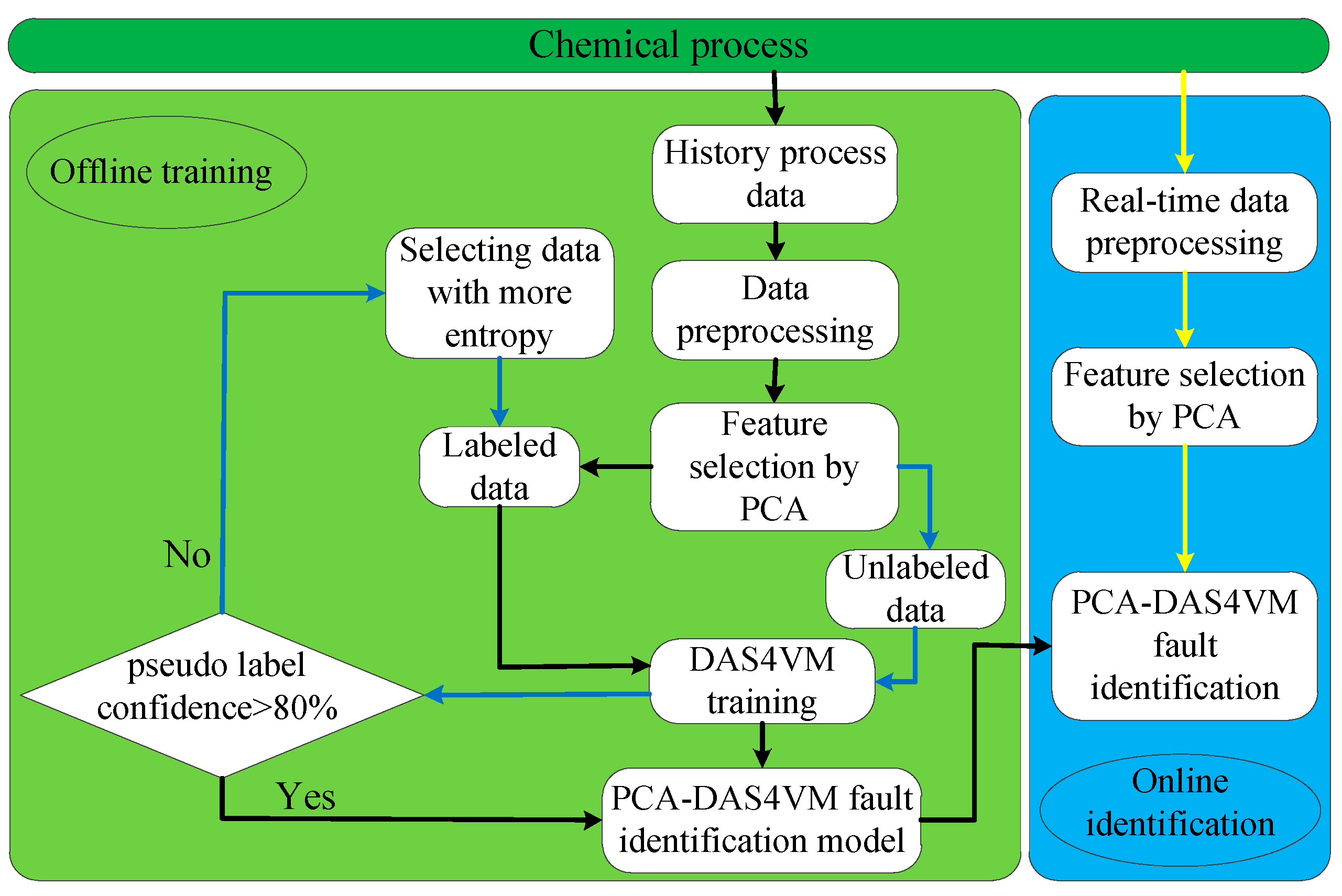
3.3. Identification Results and Discussion
In recent years, many researchers have made various optimization efforts for supervising SVM and have achieved remarkable results. For example, Gao et al. [
23] used grid search to determine the optimal SVM parameters. Yuan et al. [
24] optimized SVM parameters with the cuckoo algorithm. Xiao [
25] trained KNN and SVM on the same training set, and then used the integrated model of KNN and SVM to predict the test dataset. KNN predict the test dataset through labels of k nearest neighbors data, SVM predict the test dataset based on hyperplane. However, these methods are still limited to supervised learning, resulting in poor generalization performance, a low industrial fault diagnosis rate (FDR), and a high false positive rate (FPR). Therefore, this paper proposes a fault identification method PCA-DAS4VM based on a graphical scenario object model, which improves the identification accuracy of traditional SVM due to its full use of the unlabeled data distribution information. In order to better prove the effectiveness of the proposed method, the PCA-DAS4VM proposed in this paper is compared with the DAS4VM and PCA-S4VM fault identification methods when applied to the TE process. In these methods, the DAS4VM directly recognizes raw process data, and the PCA-S4VM model is based on S4VM to identify key process data selected by PCA.
In order to clearly show the performance of the proposed method, this paper defines a confusion matrix (
Table 4), F1 score (Equation (13)), fault diagnosis rate (FDR) (Equation (14)), false positive rate (FPR) (Equation (15)), and accuracy (Equation (16)) as comparing criterions.
where TN represents a normal condition diagnosed as normal, FP represents a fault condition diagnosed as normal, FN represents normal conditions diagnosed as a fault, and TP represents a fault condition diagnosed as a fault.
Semi-supervised learning is usually sensitive to the number of labeled data and unlabeled data. This paper uses the S4VM parameters recommended by Li et al. [
26], as shown in
Table 5. The parameter “a” is recommended by Yin et al. [
14]. The amount of labeled data and unlabeled data are determined based on experience and experiments. Since the amount of labeled data and unlabeled data directly affect the accuracy of the identification model, the influence of the number of labeled data and unlabeled data on the identification accuracy is discussed with the average identification accuracy of 20 kinds of TE faults as criterion, as shown in
Figure 8 and
Figure 9.
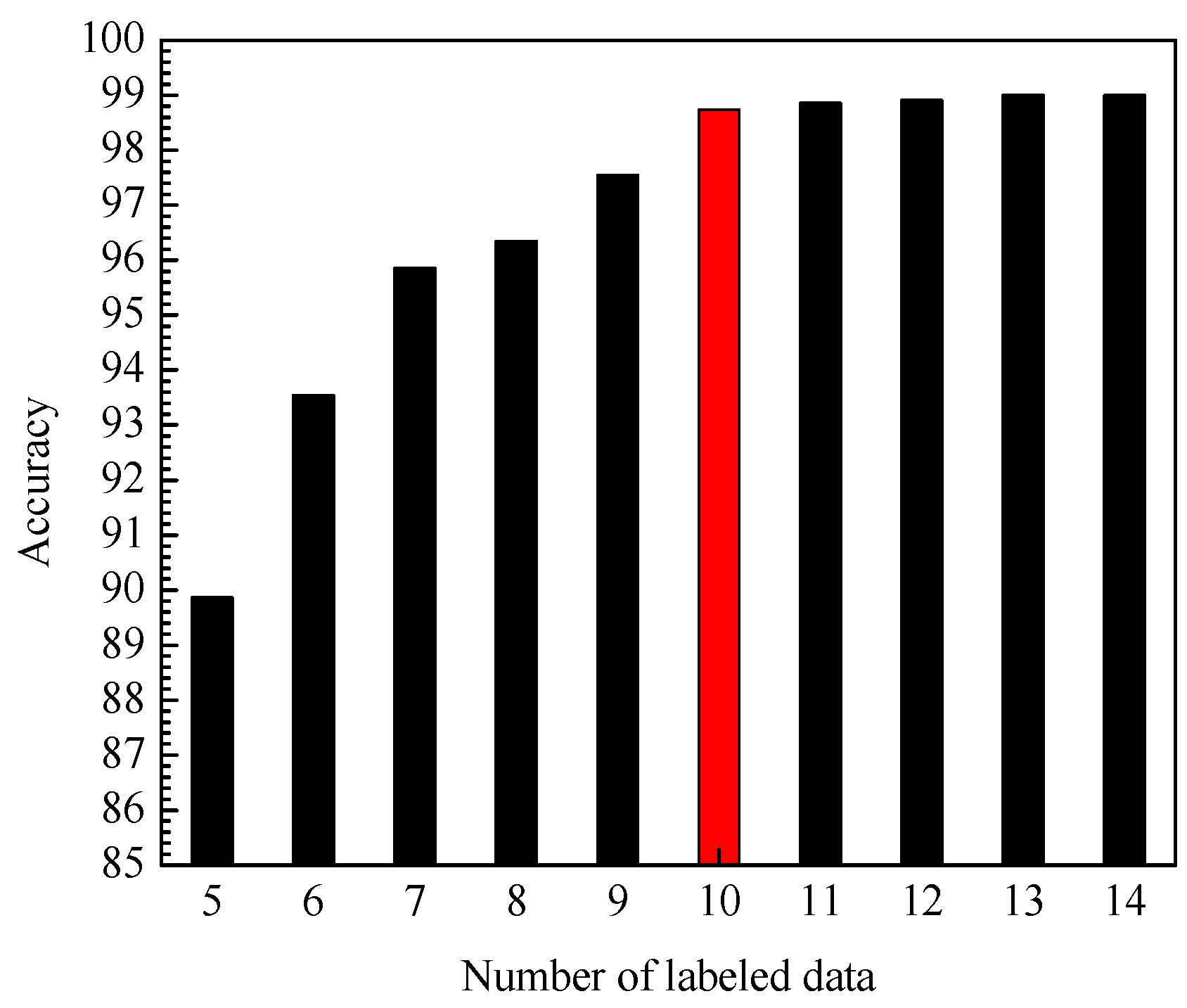
First, under the condition that the training set contains 960 unlabeled data, the impact of the amount of labeled data in the training set on the accuracy of the identification model is tested. It can be seen from
Figure 8 that with the increasing number of labeled data, the average identification accuracy of PCA-DAS4VM is gradually improved. However, the number of labeled data increases slowly after more than 10, so this article uses 10 labeled data (especially denoted by red color in
Figure 8). Secondly, under the condition that the training set contains 10 labeled data, the impact of the number of unlabeled data in the training set on the accuracy of the identification model is tested. All of the number of unlabeled data for each condition is 960. It can be seen from
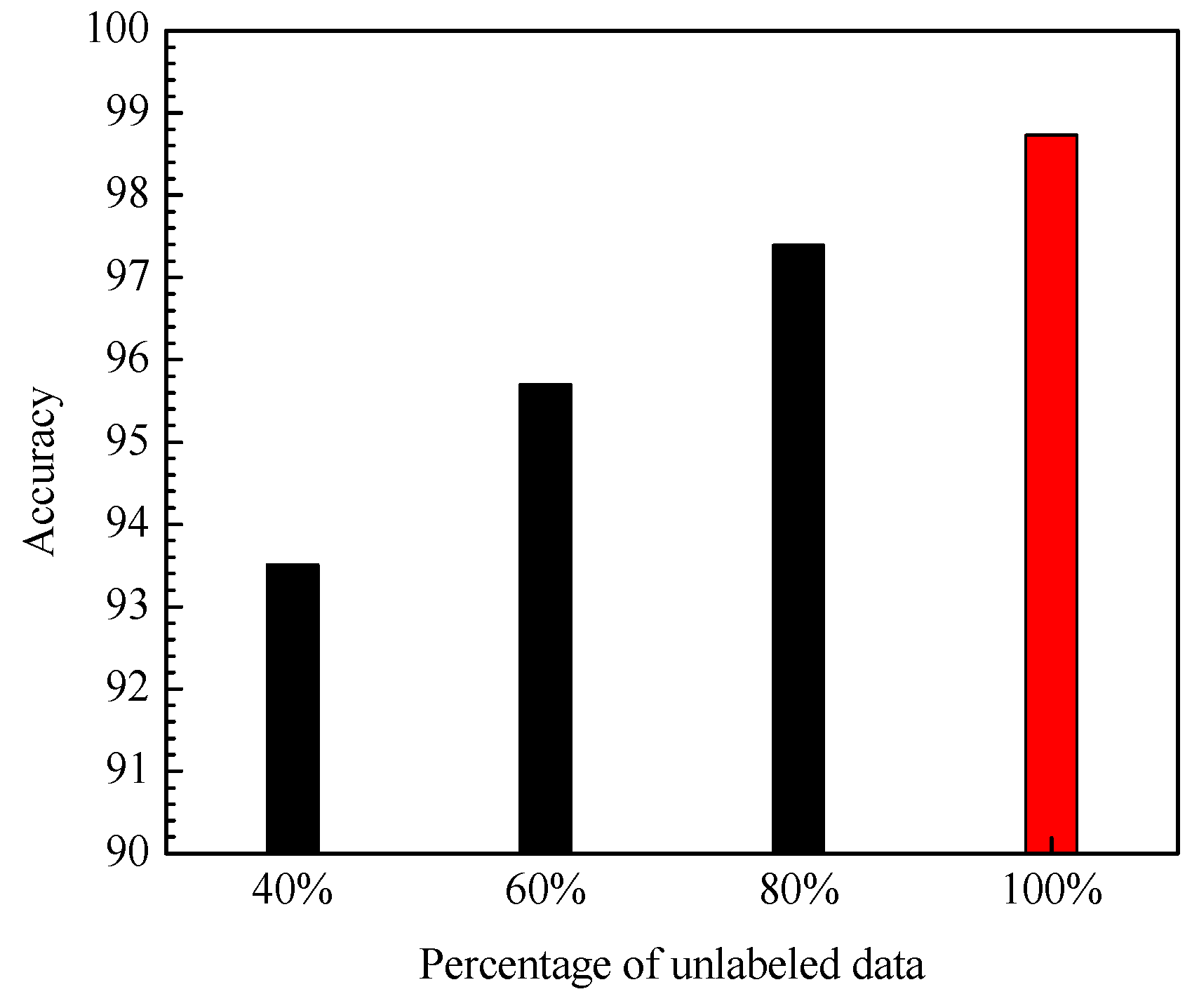
Figure 9 that with the increasing percentage of unlabeled data, the average identification accuracy of PCA-DAS4VM is gradually improved, so this paper uses the 100% (960) unlabeled data to train PCA-DAS4VM (especially denoted by red color in
Figure 9). Therefore, the training set of PCA-DAS4VM contains 10 labeled data and 960 unlabeled data.
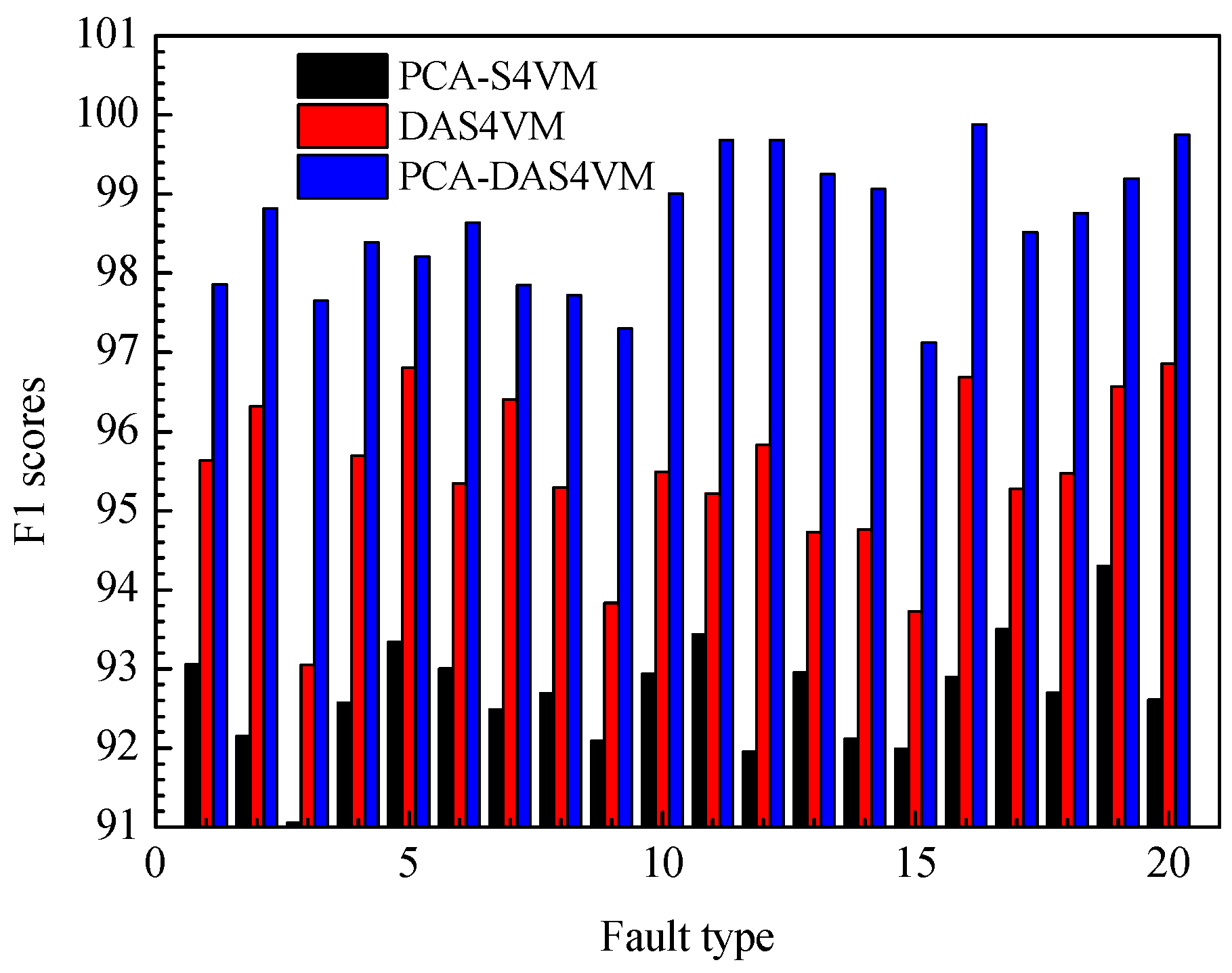
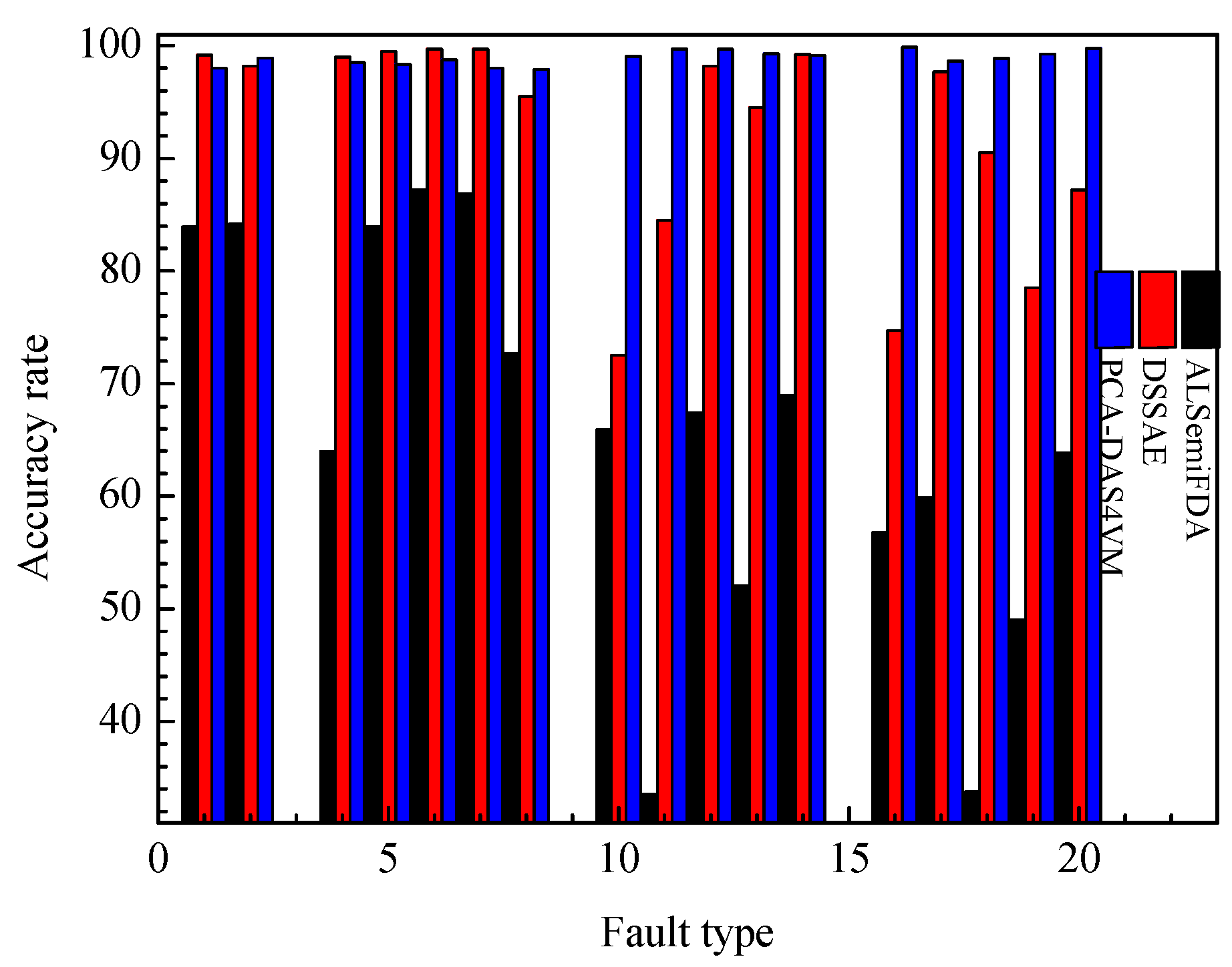
The F1 scores for PCA-S4VM, DAS4VM, and PCA-DAS4VM using 20 types of faults in the TE process are compared in
Figure 10. It can be seen from
Figure 10 that compared with other identification methods, PCA-DAS4VM has the highest F1 score. Compared with PCA-S4VM and DAS4VM, the average F1 scores of PCA-DAS4VM are enhanced by approximately 6.01% and 3.21%, respectively. The identification performance of PCA-DAS4VM is stable around 98%, further proving the reliability and stability of the S4VM. For the four types of faults in the TE process, PCA-S4VM and PCA-DAS4VM have higher identification accuracy for drift type faults, with average F1 scores of 92.96% and 99.25%. DAS4VM has higher identification accuracy for step type faults, with an average F1 score of 95.61%.
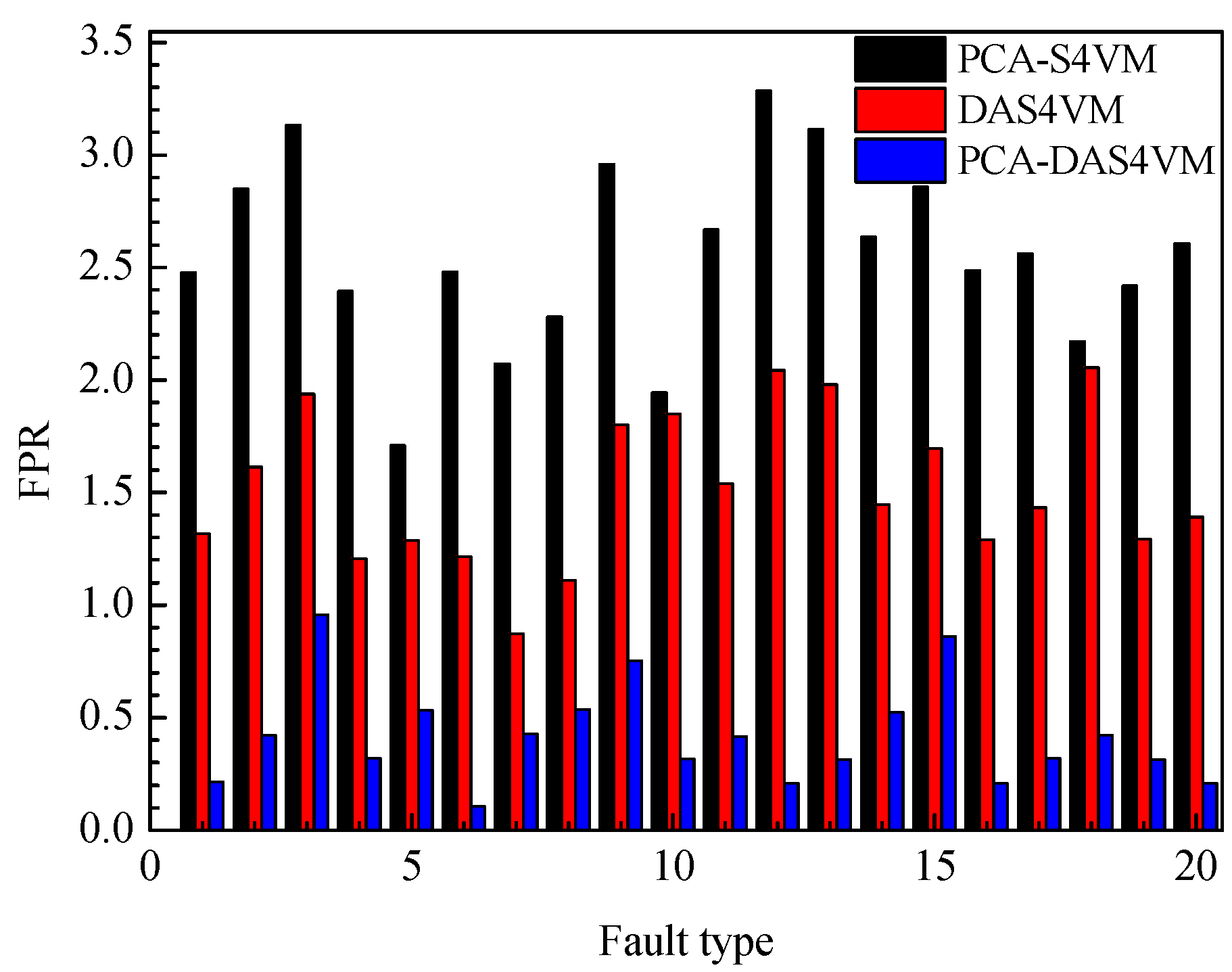
To further illustrate the effectiveness of PCA-DAS4VM for industrial processes, the FPR for the model PCA-S4VM, DAS4VM, and PCA-DAS4VM are compared in
Figure 11. In
Figure 11, the average FPR for PCA-DAS4VM is only 0.42%, 507.14% less than that of PCA-S4VM and 261.90% less than that of DAS4VM. For the four types of faults in the TE process, PCA-S4VM and DAS4VM have lower FPRs for step type faults, with an average FPR of 2.44% and 1.35%. PCA-DAS4VM has a lower FPR for drift type faults, with an average FPR of 0.31%.
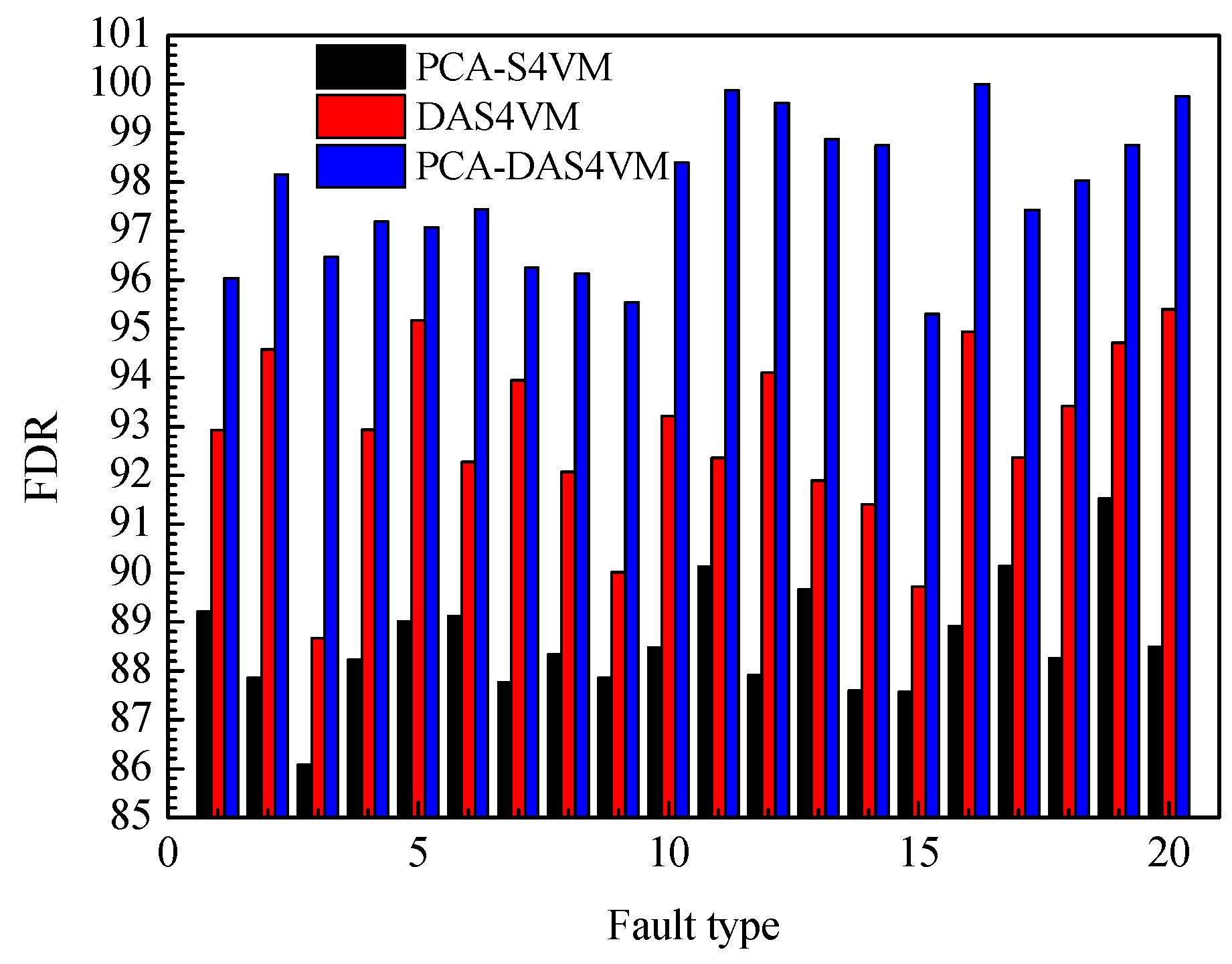
The FDR for PCA-S4VM, DAS4VM, and PCA-DAS4VM are compared in
Figure 12. The average FDR for PCA-DAS4VM is 9.35% higher than that of PCA-S4VM and 5.05% than that of DAS4VM. For the four types of faults in the TE process, PCA-S4VM and PCA-DAS4VM have higher FDRs for drift type faults, with an average FDR of 89.66% and 98.88%. DAS4VM has a higher FDR for step type faults, with an average FDR of 92.93%.
The core work of this paper is to train and test the identification models in the offline phase. In order to compare the performance of each identification model more clearly, this article compares the average computation time of each identification model for the 20 TE process faults. As can be seen from
Table 6, the average computation time of PCA-DAS4VM is 130.35 s (tested on a Core i5, 8 GB memory computer) because it has high modeling complexity. PCA-DAS4VM reduces the computing time by 53.53% compared with DAS4VM. Although PCA-DAS4VM adds 17.95% more computing time than PCA-S4VM, PCA-DAS4VM is still recommended as it has better identification performance.
In order to better demonstrate the effectiveness of the PCA-DAS4VM method, this method is also compared with those typical semi-supervised learning methods such as ALSemiFDA [
14] and DSSAE [
15]. The accuracy rate of each method when applied to TE process is shown in
Figure 13. It can be concluded that the accuracy rate of the PCA-DAS4VM method is 33.76% and 6.74% higher than that of ALSemiFDA and DSSAE, respectively.
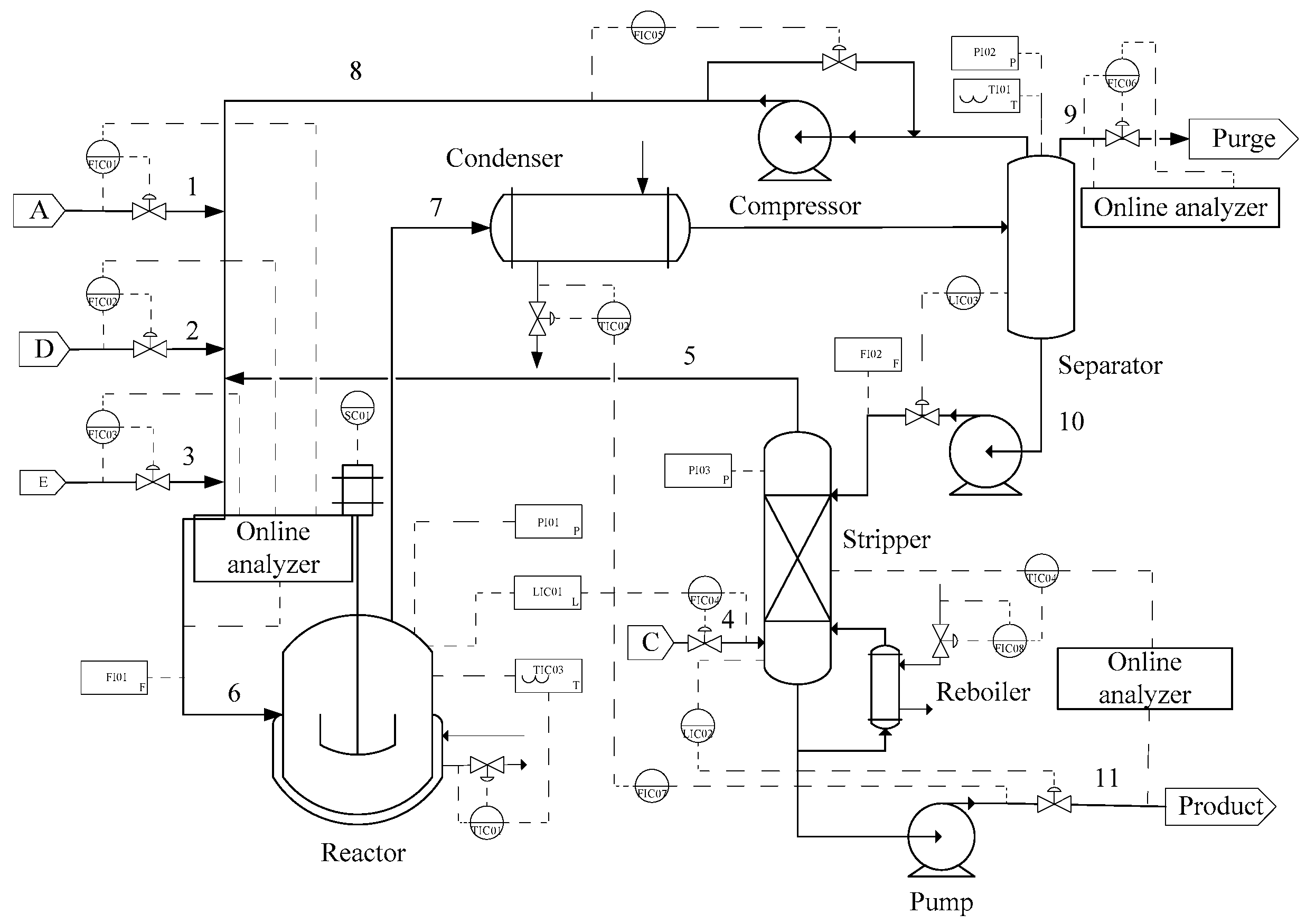
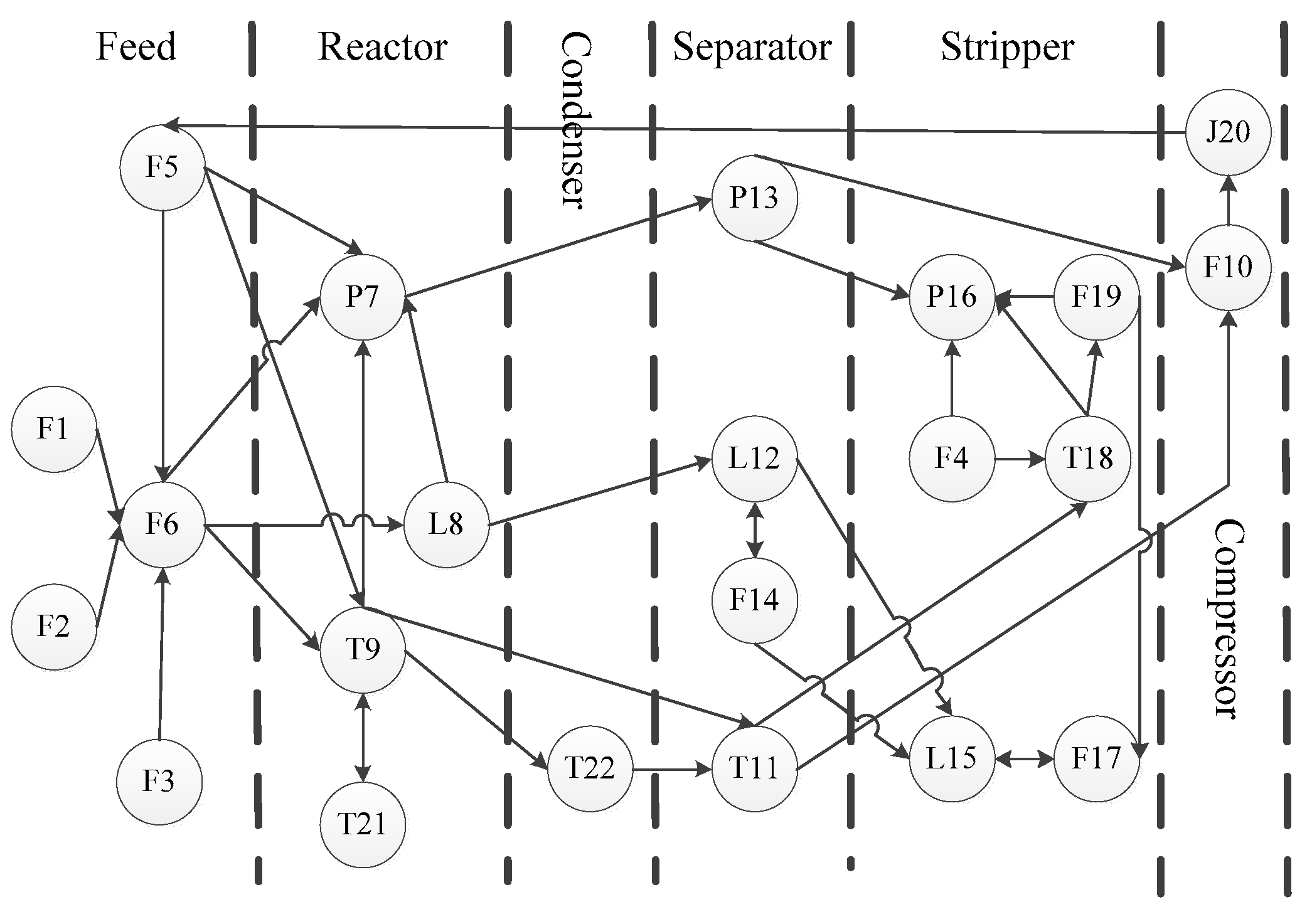
For fault diagnosis, the TE process is divided into five parts for analysis: Reactor, condenser, separator, recycle compressor, and stripper. The graphical scenarios object model of TE process based on ontology is established (
Figure 14) where the circle point represents 22 continuous measurement variables (
Table 2) of the TE process, and the connection lines indicate mutual influence between variables (also called events). The mutual influence includes four relations: Control relation, reaction relation, type relation, and position relation [
27].
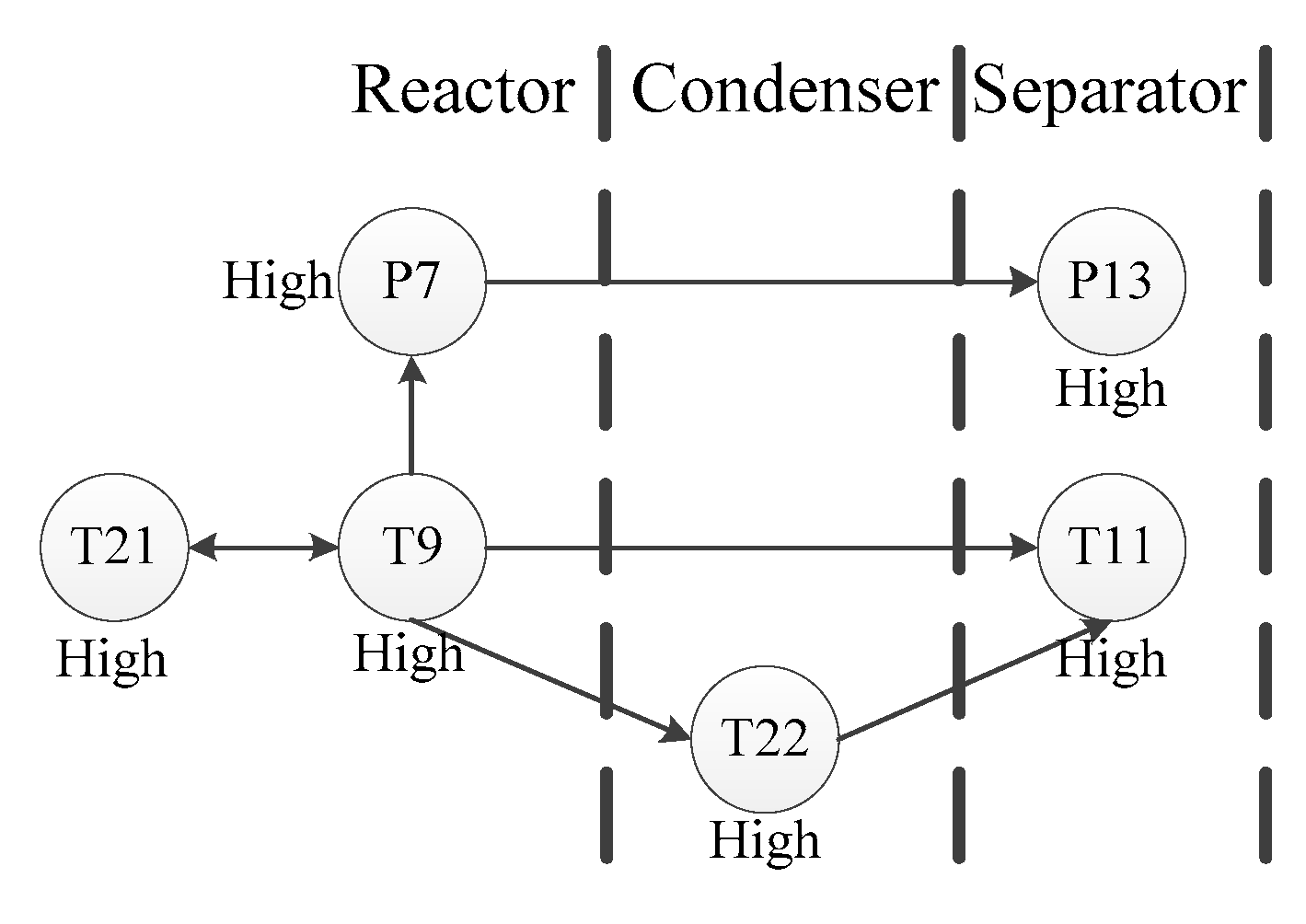
This scenario object model is used to monitor the continuous measurement variables in the TE process, starting with the key events of the initial alarm, and then reversely reasoning the possible root nodes. Take fault 4 as an example. The reactor temperature in fault 4 is the first variable to have a high alarm. As the reaction is an exothermic reaction, three direct causes possibly affecting the reactor temperature are found: Recycle flow abnormality, reactor feed rate abnormality, and reactor cooling water temperature abnormality. This fault leads to four direct consequences: High reactor cooling water outlet temperature, high condenser cooling water outlet temperature, high product separator temperature, and high reactor pressure. The graphical scenario object model of fault 4 is shown in
Figure 15.
After analysis, we find that the circulating flow rate and the reactor feed flow rate have no deviation, so the abnormal temperature of the reactor cooling water most likely causes the reactor temperature anomaly. Therefore, the root cause of fault 4 is the abnormal temperature of the reactor cooling water.