A Wind Farm Active Power Dispatch Strategy Considering the Wind Turbine Power-Tracking Characteristic via Model Predictive Control
Abstract
1. Introduction
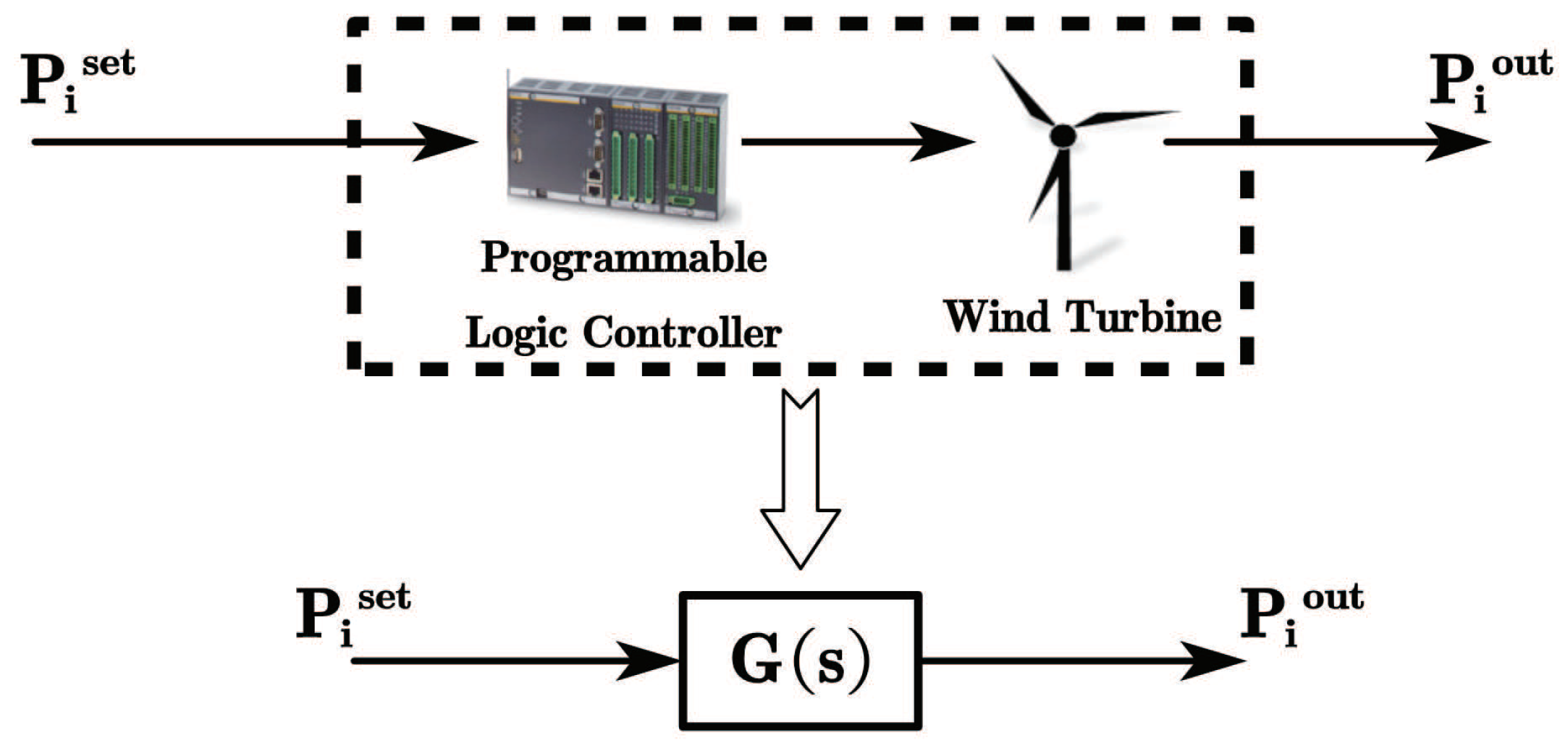
2. Modeling the Wind Turbine Power-Tracking Characteristic
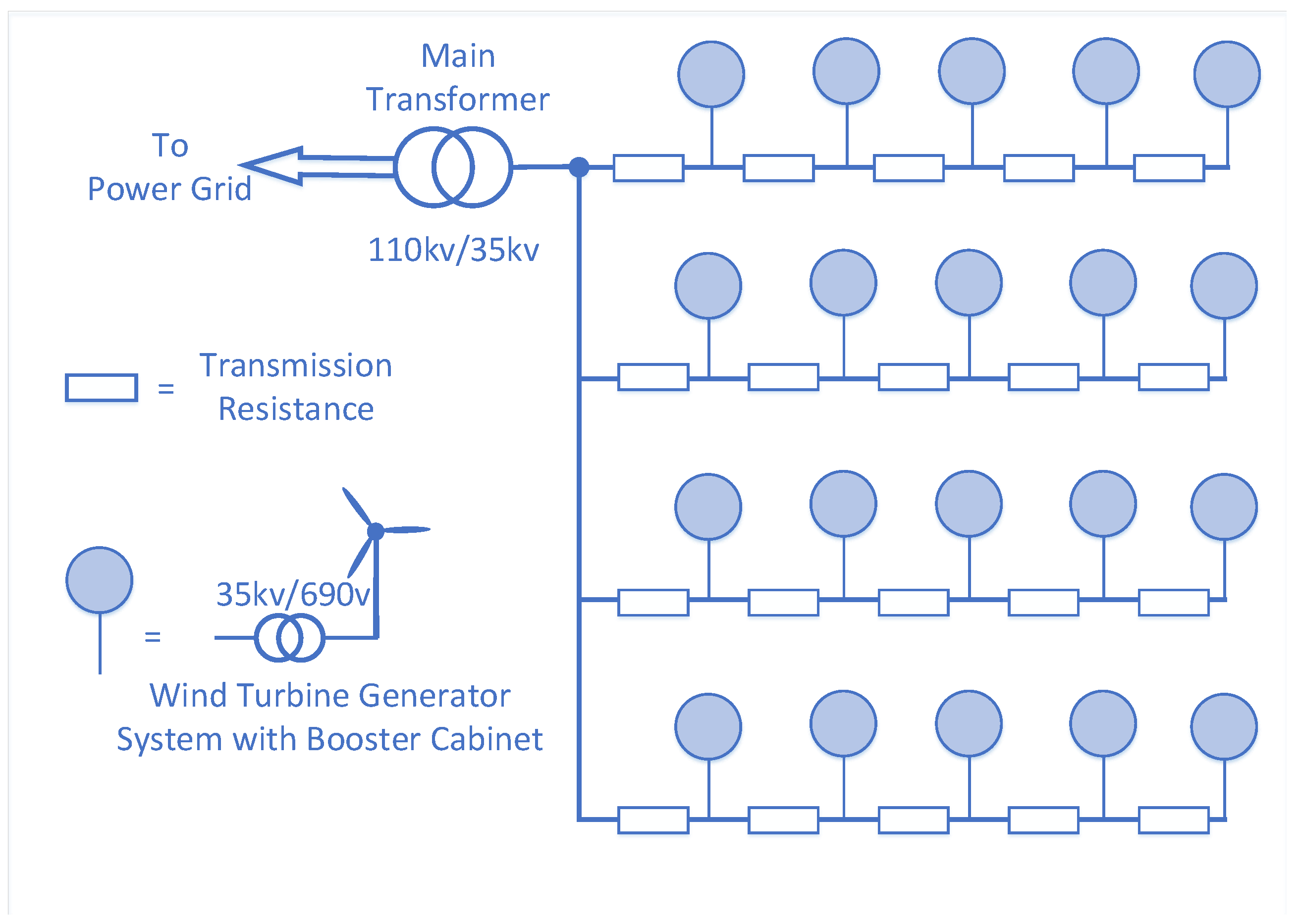
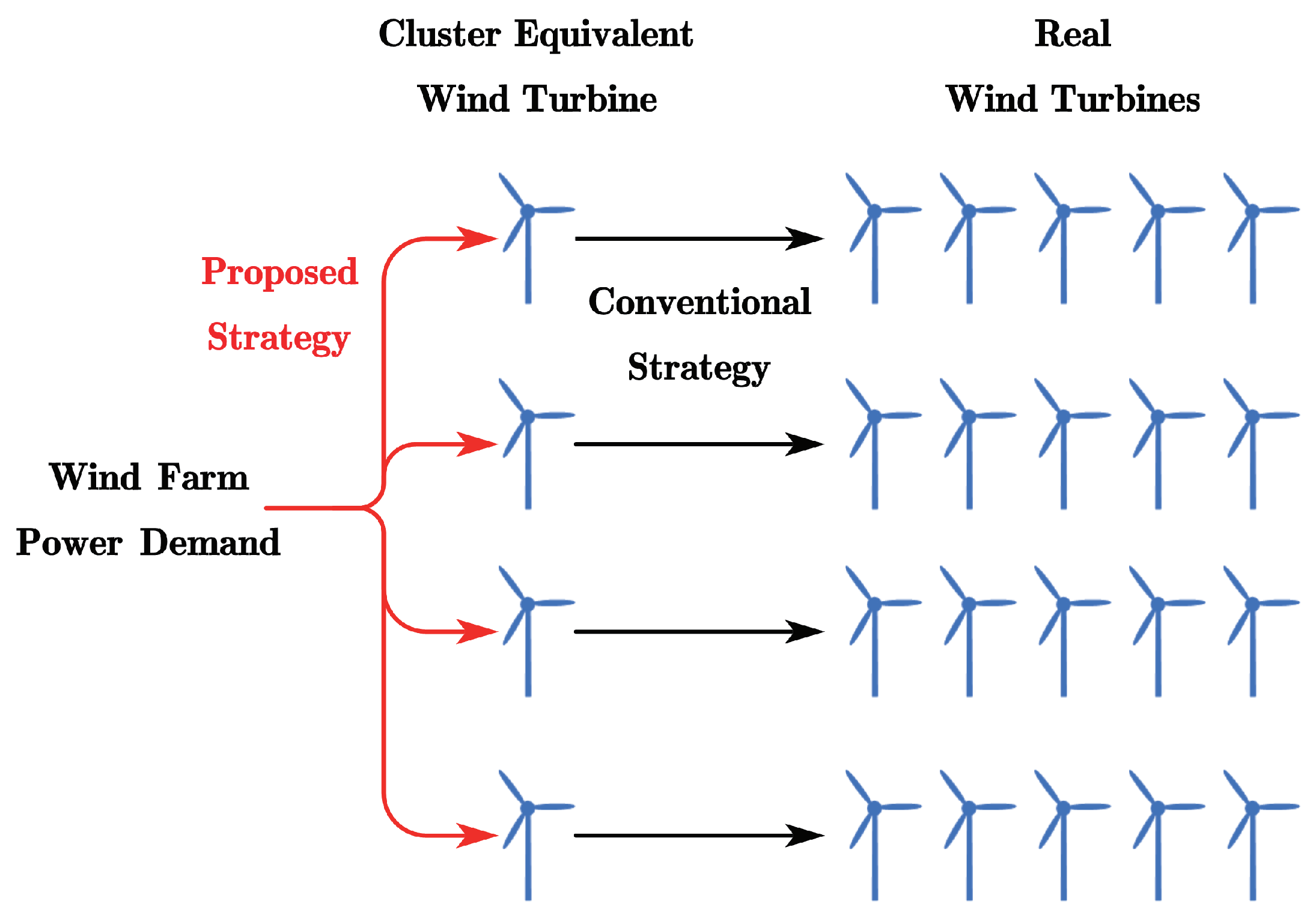
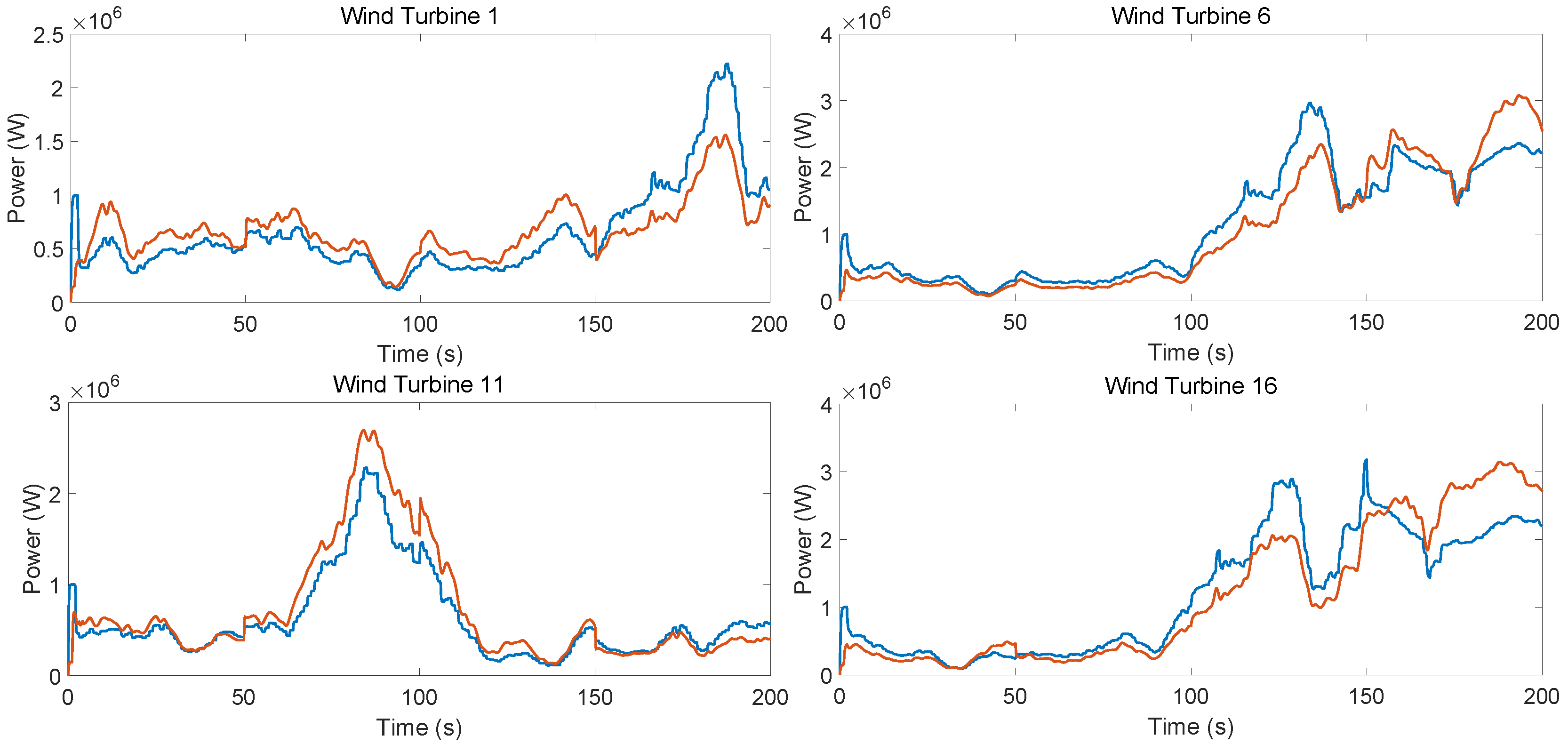
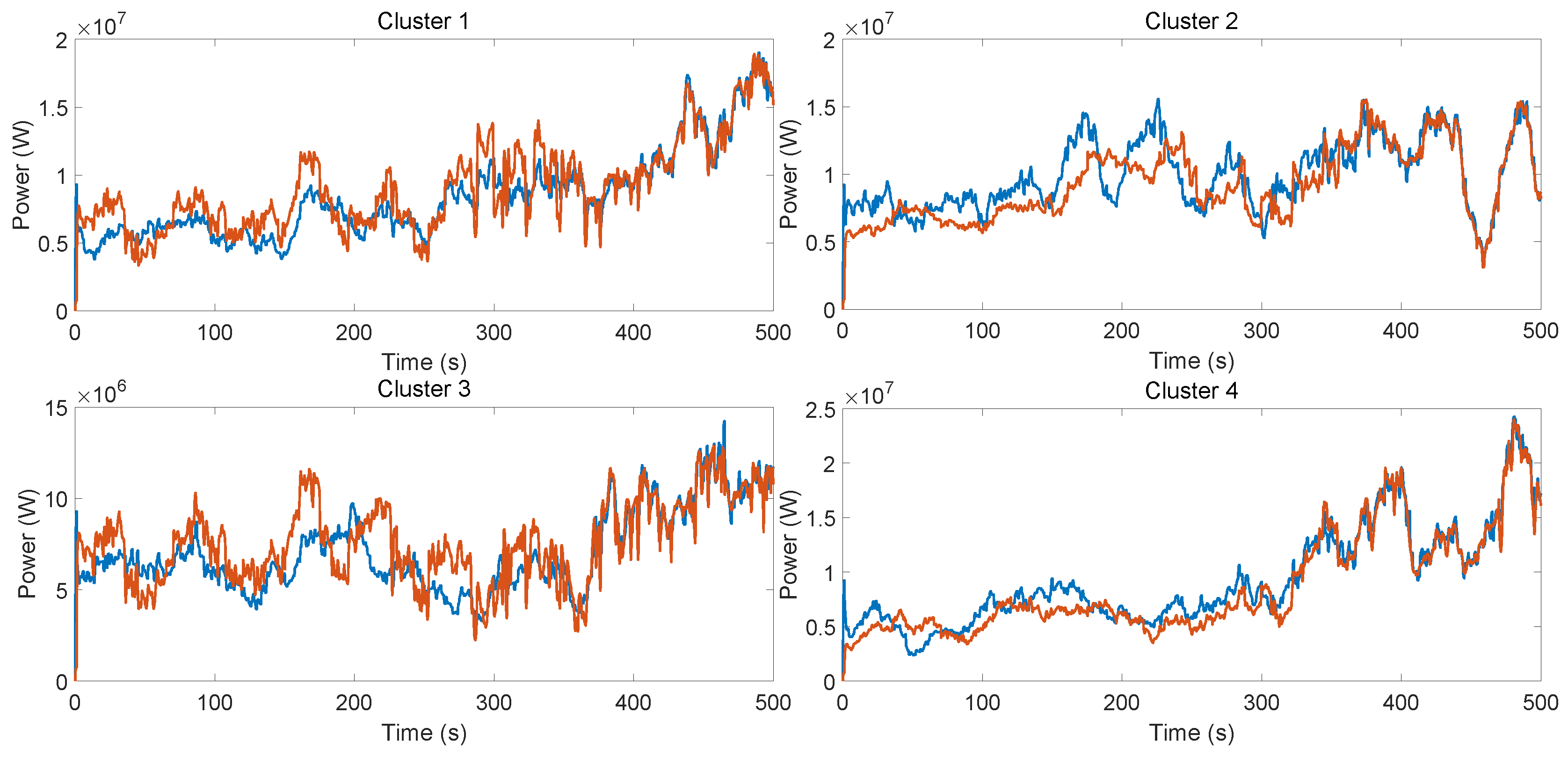
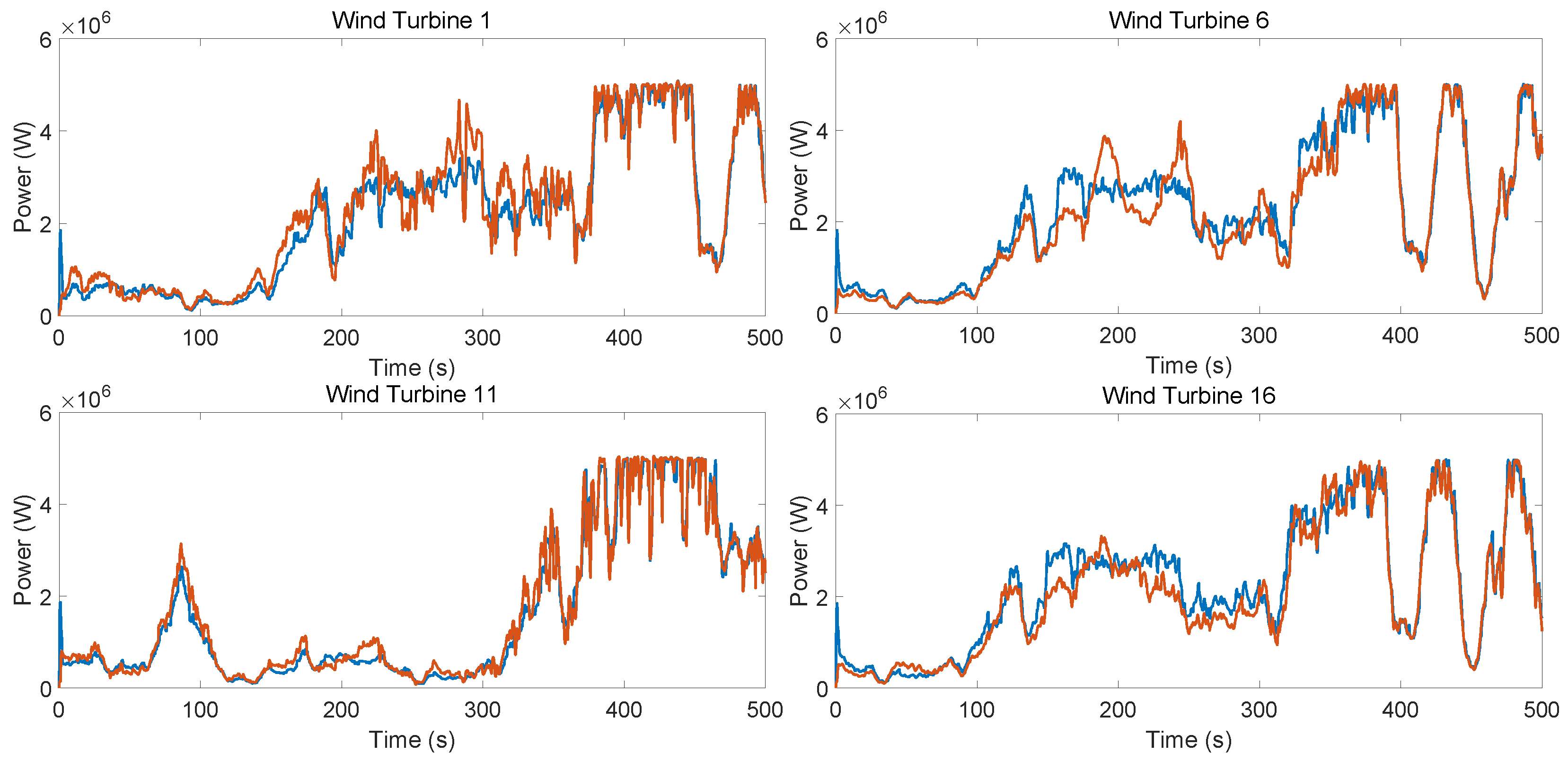
3. Wind Farm Clustering and Equivalent Modeling Based on Topology
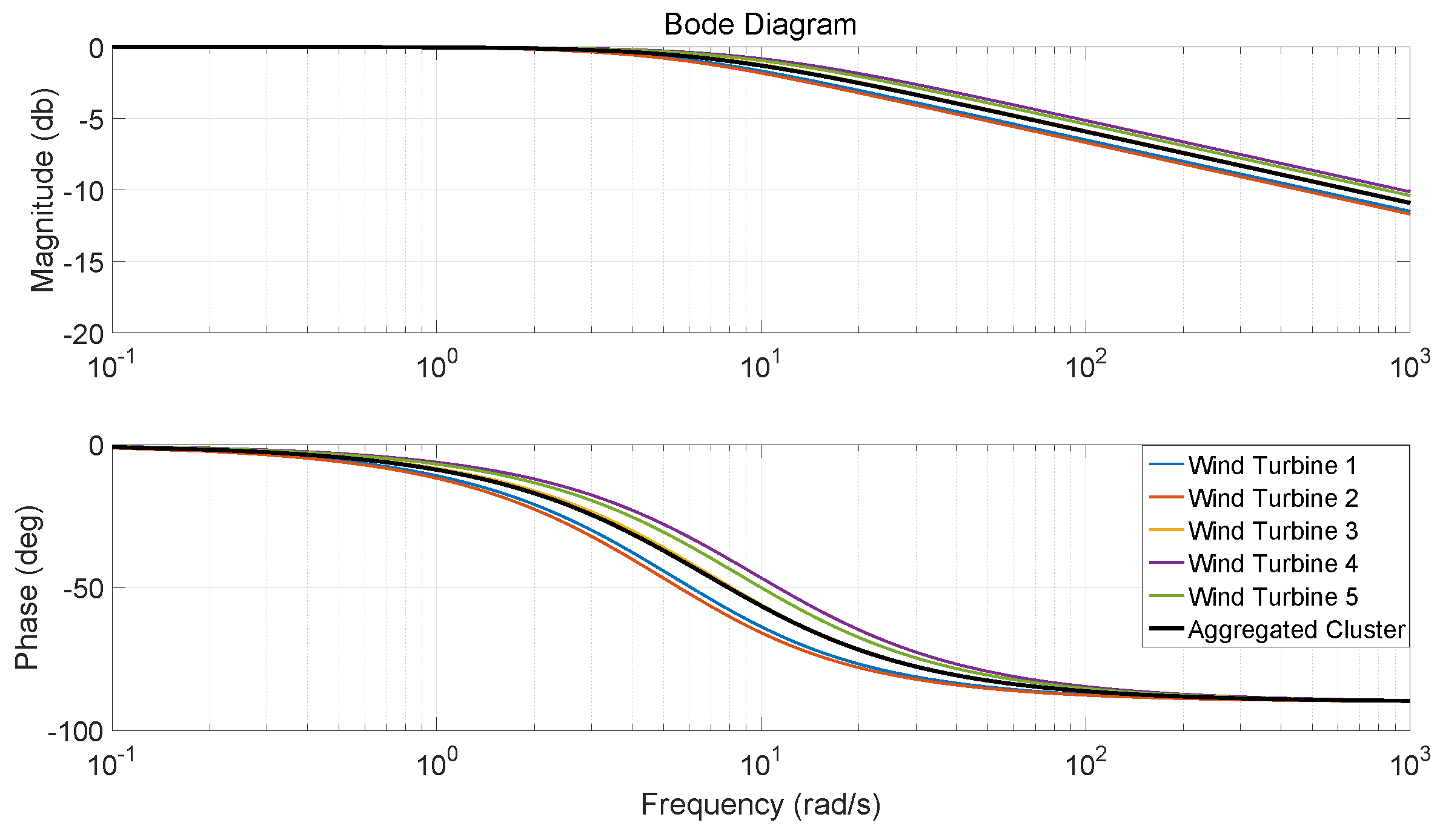
- Step 1. The wind turbine power-tracking model is analyzed for its frequency-domain performance using the Bode diagram. The magnitude of the ith wind turbine is denoted by , and the phase is denoted by .
- Step 2. Repeat Step 1 until all the wind turbines in the cluster are analyzed.
- Step 3. The cluster’s frequency-domain performance is calculated as
- Step 4. Plot all magnitudes and phase performances of the studied cluster in one Bode diagram.
- Step 5. Choose the wind turbine model that is closest to the cluster’s magnitude and phase performance as the cluster’s power-tracking model.
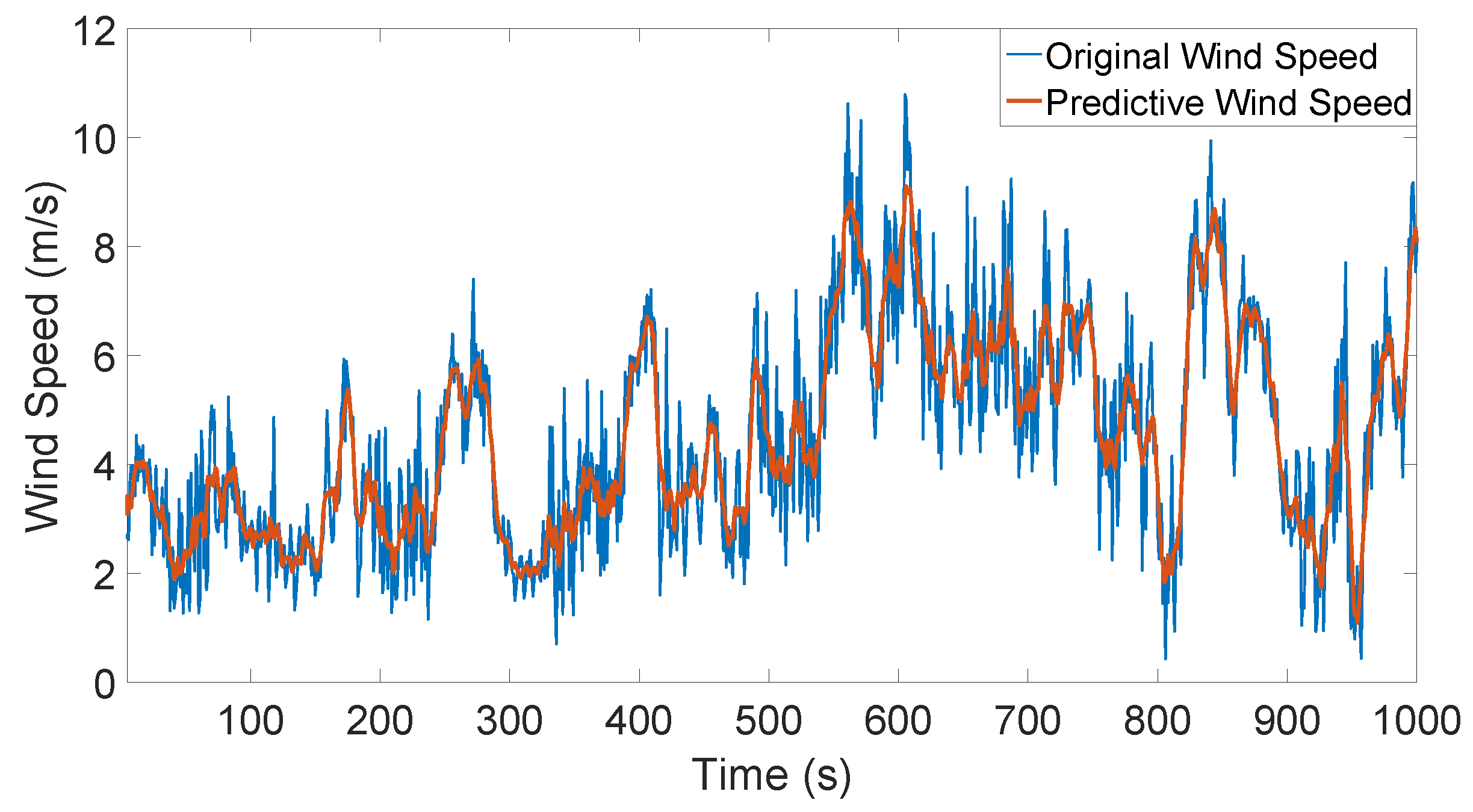
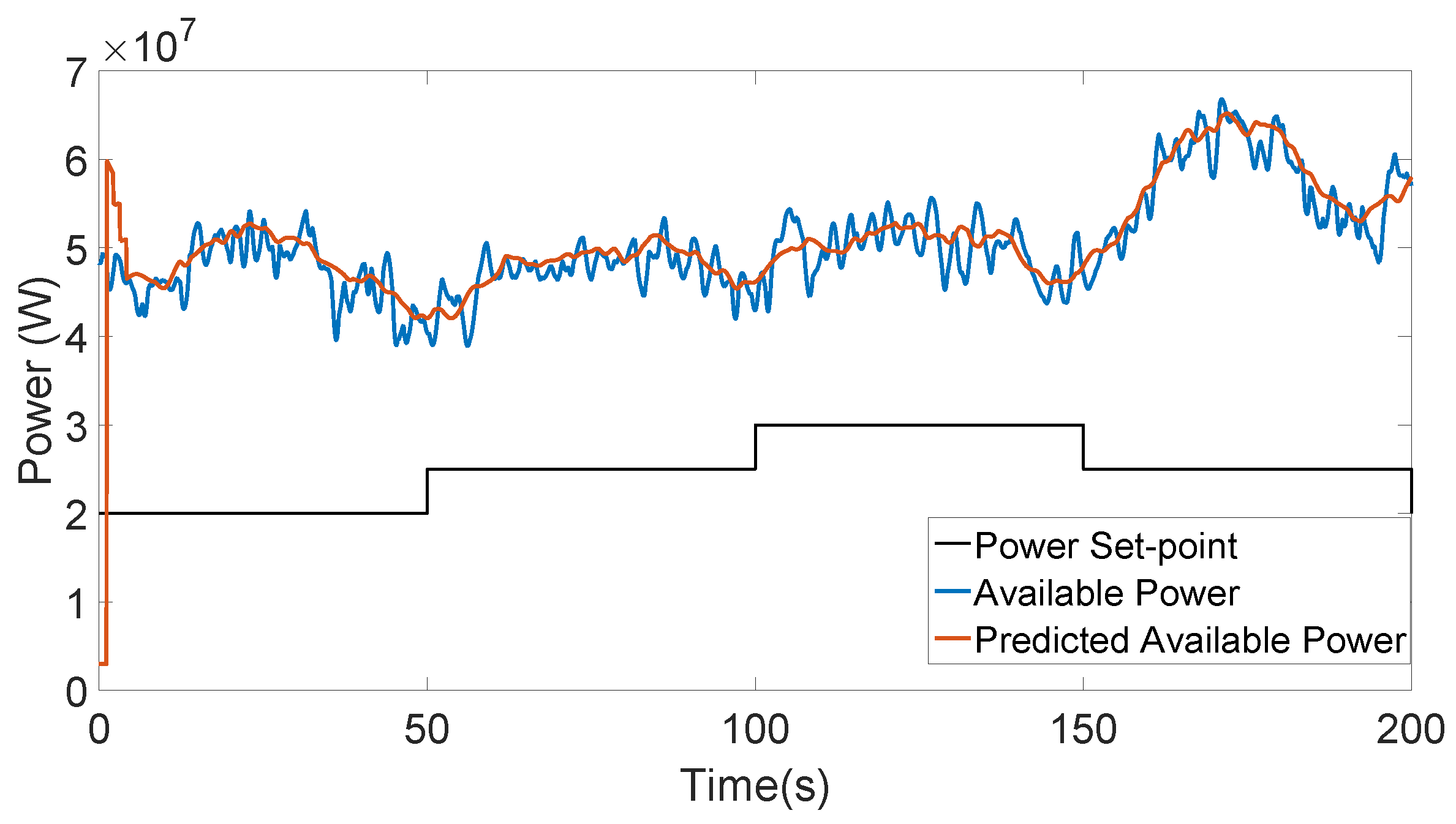
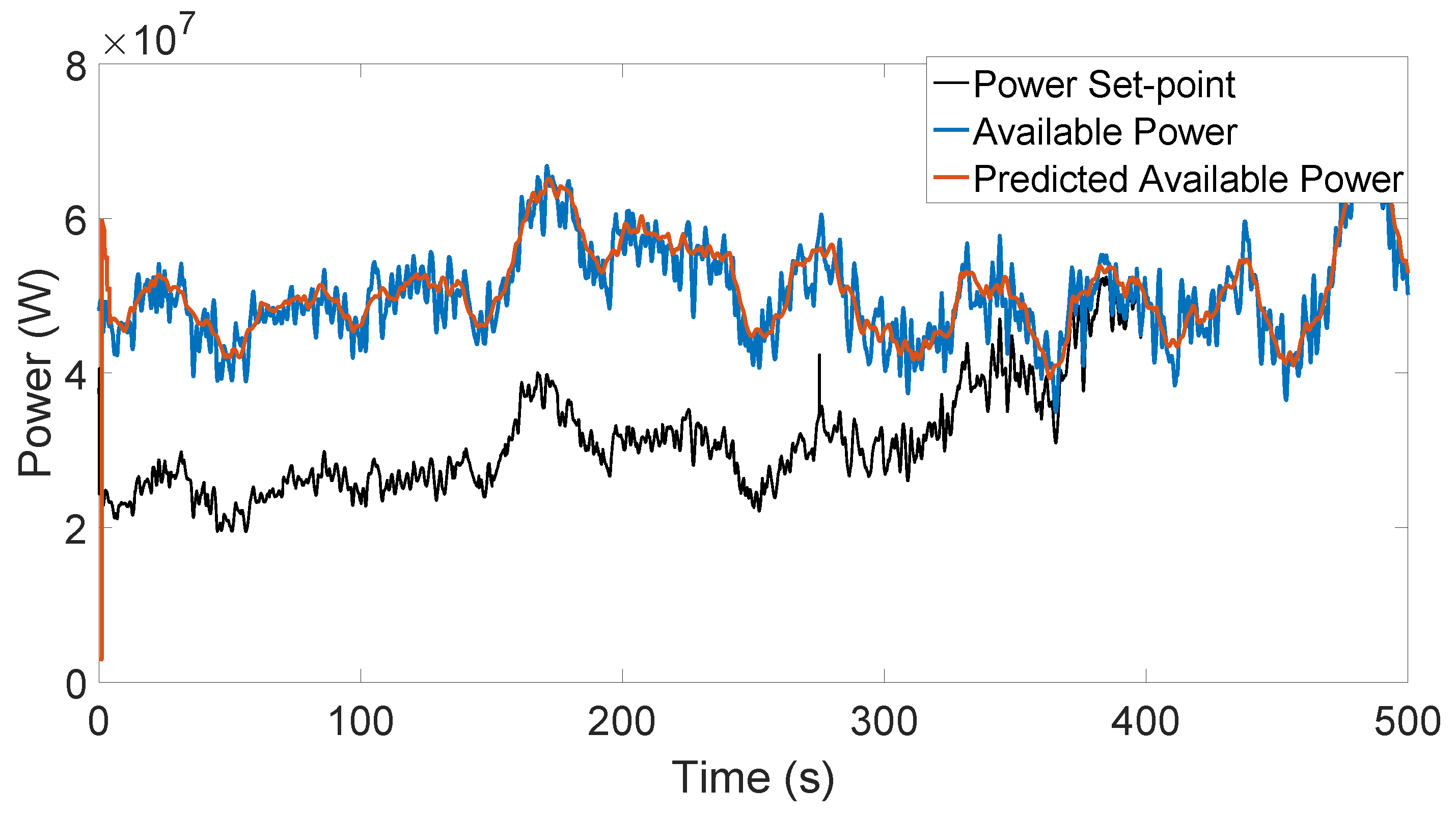
4. Ultra Short-Term Wind Speed Prediction
5. Wind Farm Active Power Dispatch Strategy
5.1. Conventional Strategy
5.2. Wind Farm Active Power Dispatch Structure
5.3. Wind Farm Power-Tracking Predictive Model
5.4. Cost Function
5.5. Constraints
5.6. Industrial Application-Related Information
6. Simulation Tests
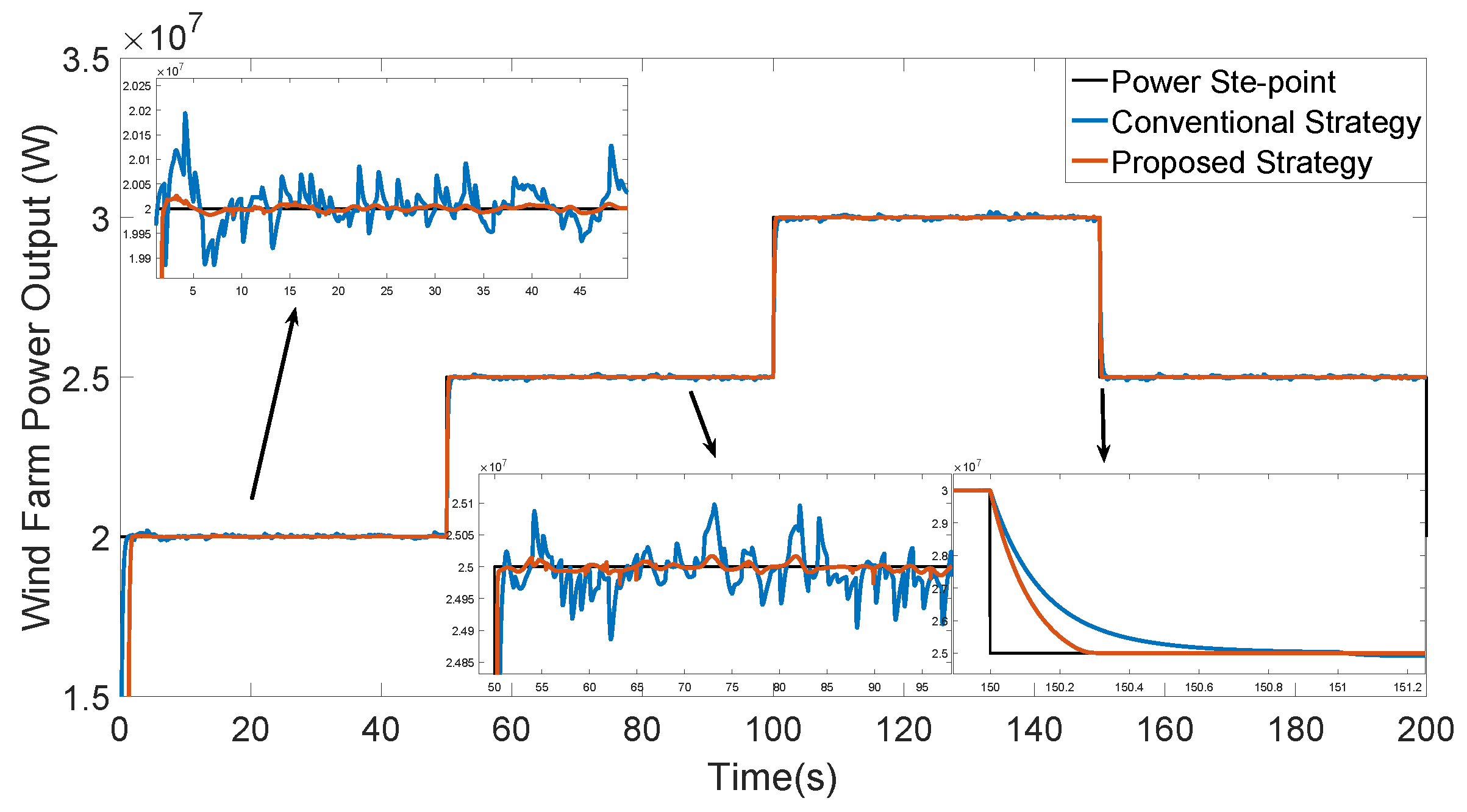
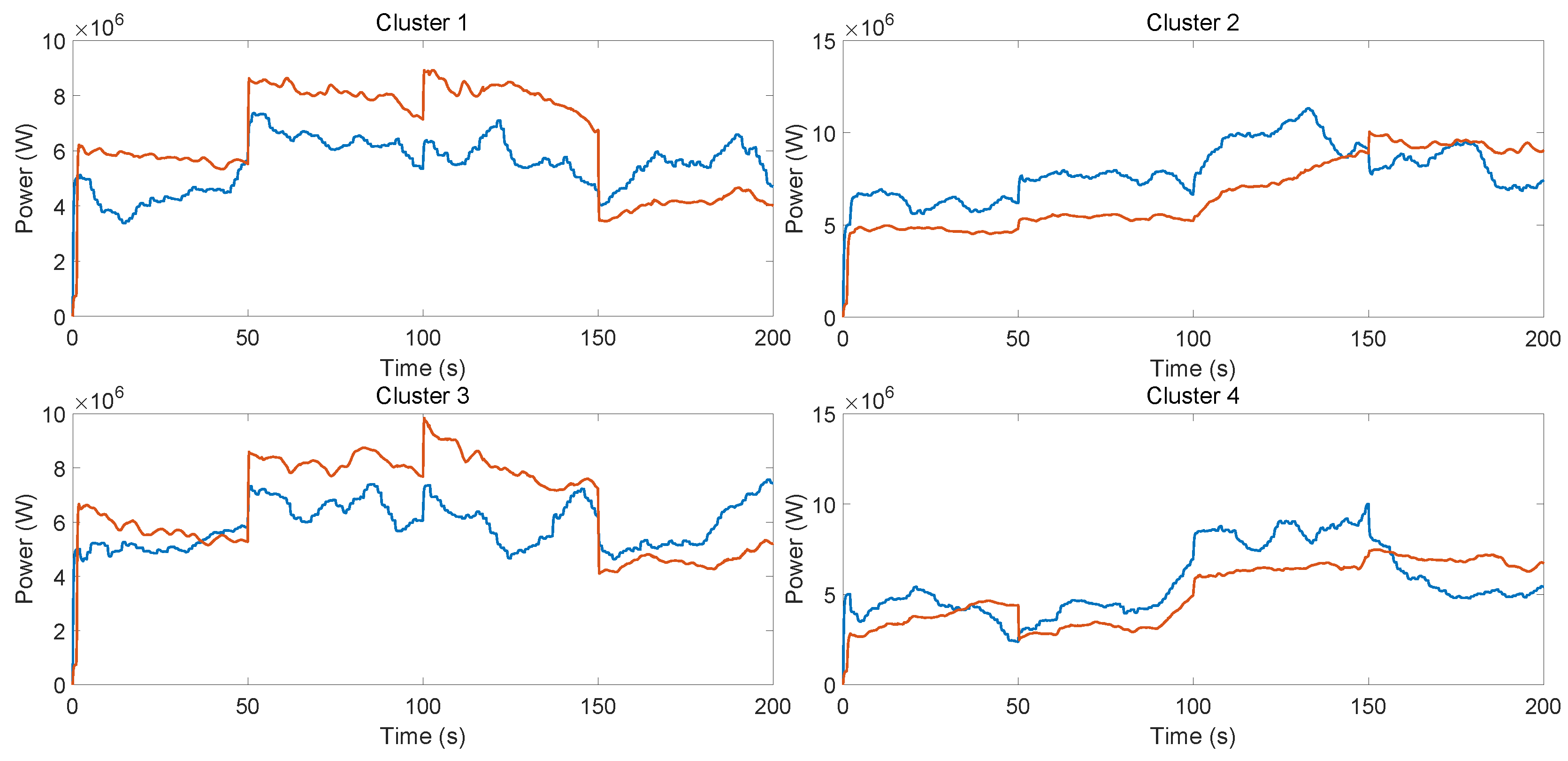
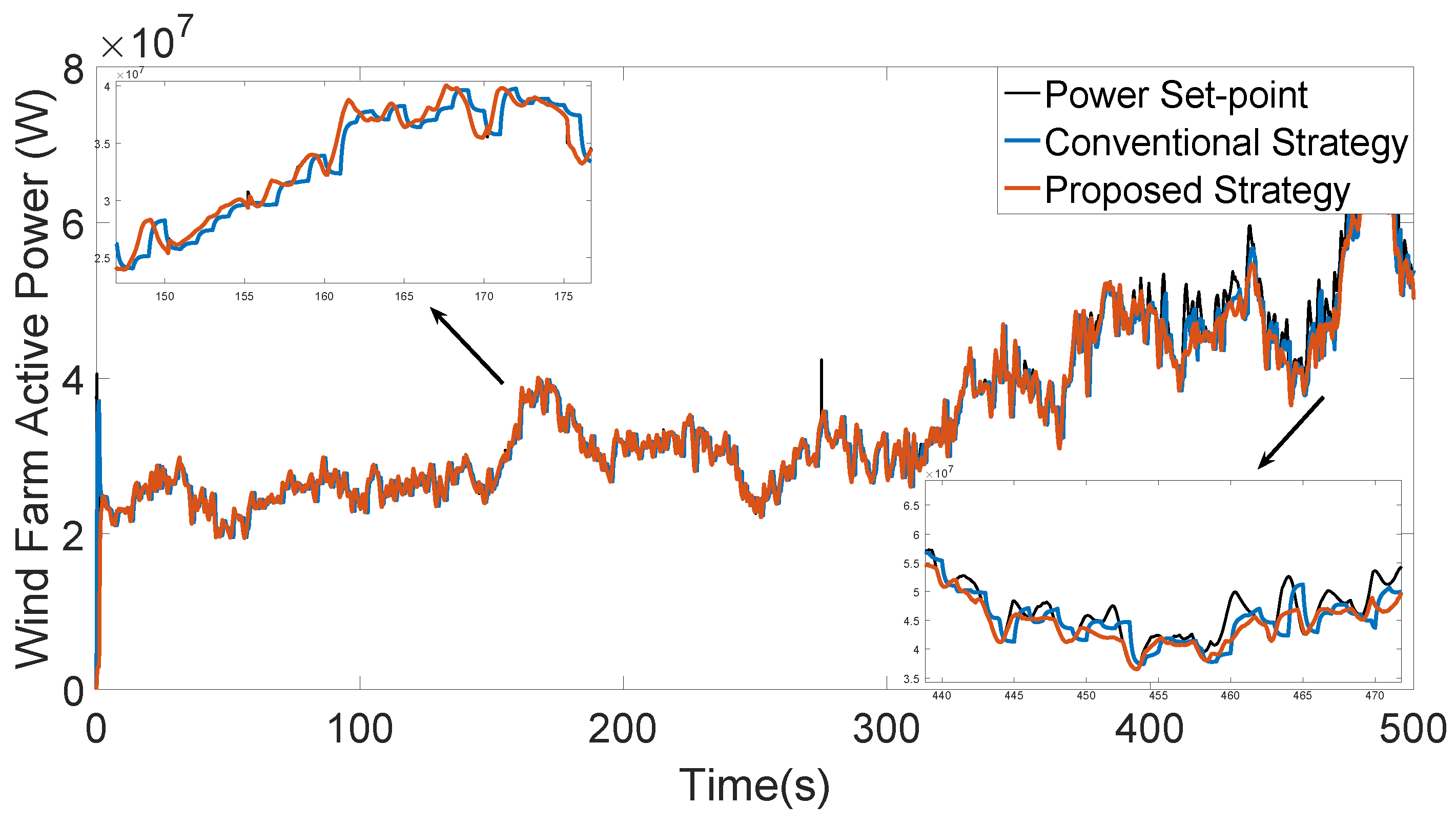
6.1. Step Set-Point Test
6.2. Time-Varying Set-Point Test
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- GWEC. Global Wind Report 2017. Available online: http://gwec.net/publications/global-wind-report-2/ (accessed on 25 April 2018).
- Cai, W.; Liu, C.; Lai, K.H.; Li, L.; Cunha, J.; Hu, L. Energy performance certification in mechanical manufacturing industry: A review and analysis. Energy Convers. Manag. 2019, 186, 415–432. [Google Scholar] [CrossRef]
- Chehouri, A.; Younes, R.; Ilinca, A.; Perron, J. Review of performance optimization techniques applied to wind turbines. Appl. Energy 2015, 142, 361–388. [Google Scholar] [CrossRef]
- Kumar, D.; Chatterjee, K. A review of conventional and advanced MPPT algorithms for wind energy systems. Renew. Sustain. Energy Rev. 2016, 55, 957–970. [Google Scholar] [CrossRef]
- Boukhezzar, B.; Lupu, L.; Siguerdidjane, H.; Hand, M. Multivariable control strategy for variable speed, variable pitch wind turbines. Renew. Energy 2007, 32, 1273–1287. [Google Scholar] [CrossRef]
- Yin, X.X.; Lin, Y.G.; Li, W.; Gu, Y.J.; Lei, P.F.; Liu, H.W. Adaptive back-stepping pitch angle control for wind turbine based on a new electro-hydraulic pitch system. Int. J. Control 2015, 88, 2316–2326. [Google Scholar] [CrossRef]
- Rodriguez-Amenedo, J.L.; Arnalte, S.; Burgos, J.C. Automatic generation control of a wind farm with variable speed wind turbines. IEEE Trans. Energy Convers. 2002, 17, 279–284. [Google Scholar] [CrossRef]
- Horiuchi, N.; Kawahito, T. Torque and power limitations of variable speed wind turbines using pitch control and generator power control. In Proceedings of the 2001 Power Engineering Society Summer Meeting. Conference Proceedings (Cat. No. 01CH37262), Vancouver, BC, Canada, 15–19 July 2001; Volume 1, pp. 638–643. [Google Scholar]
- Knudsen, T.; Bak, T.; Svenstrup, M. Survey of wind farm control—Power and fatigue optimization. Wind Energy 2015, 18, 1333–1351. [Google Scholar] [CrossRef]
- Sun, Y.Z.; Zhang, Z.S.; Li, G.J.; Lin, J. Review on frequency control of power systems with wind power penetration. In Proceedings of the 2010 International Conference on Power System Technology, Hangzhou, China, 24–28 October 2010; pp. 1–8. [Google Scholar]
- Aho, J.; Buckspan, A.; Laks, J.; Fleming, P.; Jeong, Y.; Dunne, F.; Churchfield, M.; Pao, L.; Johnson, K. A tutorial of wind turbine control for supporting grid frequency through active power control. In Proceedings of the American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 3120–3131. [Google Scholar]
- Badihi, H.; Zhang, Y.; Hong, H. Active power control design for supporting grid frequency regulation in wind farms. Annu. Rev. Control 2015, 40, 70–81. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, Q.; Guo, Q.; Sun, H.; Xue, Y. Distributed Model Predictive Control of a Wind Farm for Optimal Active Power ControlPart I: Clustering-Based Wind Turbine Model Linearization. IEEE Trans. Sustain. Energy 2015, 6, 831–839. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, Q.; Guo, Q.; Sun, H.; Xue, Y. Distributed Model Predictive Control of a Wind Farm for Optimal Active Power ControlPart II: Implementation With Clustering-Based Piece-Wise Affine Wind Turbine Model. IEEE Trans. Sustain. Energy 2015, 6, 840–849. [Google Scholar] [CrossRef]
- Spudić, V.; Conte, C.; Baotić, M.; Morari, M. Cooperative distributed model predictive control for wind farms. Optim. Control Appl. Methods 2015, 36, 333–352. [Google Scholar] [CrossRef]
- Guo, Y.; Gao, H.; Wu, Q.; Zhao, H.; Østergaard, J.; Shahidehpour, M. Enhanced voltage control of VSC-HVDC-connected offshore wind farms based on model predictive control. IEEE Trans. Sustain. Energy 2018, 9, 474–487. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, J.; Lin, Z.; Duan, Z. Closed-loop active power control of wind farm based on frequency domain analysis. Electr. Power Syst. Res. 2019, 170, 13–24. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, J.; Lin, Z.; Qu, C. Variable-Constrained Model Predictive Control of Coordinated Active Power Distribution for Wind-Turbine Cluster. Appl. Sci. 2019, 9, 112. [Google Scholar] [CrossRef]
- Nanahara, T.; Asari, M.; Sato, T.; Yamaguchi, K.; Shibata, M.; Maejima, T. Smoothing effects of distributed wind turbines. Part 1. Coherence and smoothing effects at a wind farm. Wind Energy 2004, 7, 61–74. [Google Scholar] [CrossRef]
- Nanahara, T.; Asari, M.; Maejima, T.; Sato, T.; Yamaguchi, K.; Shibata, M. Smoothing effects of distributed wind turbines. Part 2. Coherence among power output of distant wind turbines. Wind Energy 2004, 7, 75–85. [Google Scholar] [CrossRef]
- Bilgili, M.; Sahin, B.; Yasar, A. Application of artificial neural networks for the wind speed prediction of target station using reference stations data. Renew. Energy 2007, 32, 2350–2360. [Google Scholar] [CrossRef]
- Li, G.; Shi, J. On comparing three artificial neural networks for wind speed forecasting. Appl. Energy 2010, 87, 2313–2320. [Google Scholar] [CrossRef]
- Khodayar, M.; Kaynak, O.; Khodayar, M.E. Rough deep neural architecture for short-term wind speed forecasting. IEEE Trans. Ind. Inform. 2017, 13, 2770–2779. [Google Scholar] [CrossRef]
- Dalto, M.; Matuško, J.; Vašak, M. Deep neural networks for ultra-short-term wind forecasting. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 1657–1663. [Google Scholar]
- Jang, J.S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Petković, D.; Ćojbašić, Ž.; Nikolić, V.; Shamshirband, S.; Kiah, M.L.M.; Anuar, N.B.; Wahab, A.W.A. Adaptive neuro-fuzzy maximal power extraction of wind turbine withcontinuously variable transmission. Energy 2014, 64, 868–874. [Google Scholar] [CrossRef]
- Petković, D.; Ćojbašić, Ž.; Nikolić, V. Adaptive neuro-fuzzy approach for wind turbine power coefficient estimation. Renew. Sustain. Energy Rev. 2013, 28, 191–195. [Google Scholar] [CrossRef]
- Jonkman, J.M.; Buhl, M.L. SciTech Connect: FAST User’s Guide—Updated August 2005; FAST User’s Guide; National Renewable Energy Lab: Golden, CO, USA, 2005. [Google Scholar]
| Cluster Number | Closest Wind Turbine | |
|---|---|---|
| 1 | No. 3 | 0.1339 |
| 2 | No. 8 | 0.2240 |
| 3 | No. 12 | 0.1328 |
| 4 | No. 16 | 0.2053 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Kong, D.; Xu, Q.; Wang, X.; Zhao, X.; Li, Y.; Han, H.; Wang, W.; Chen, Z. A Wind Farm Active Power Dispatch Strategy Considering the Wind Turbine Power-Tracking Characteristic via Model Predictive Control. Processes 2019, 7, 530. https://doi.org/10.3390/pr7080530
Li W, Kong D, Xu Q, Wang X, Zhao X, Li Y, Han H, Wang W, Chen Z. A Wind Farm Active Power Dispatch Strategy Considering the Wind Turbine Power-Tracking Characteristic via Model Predictive Control. Processes. 2019; 7(8):530. https://doi.org/10.3390/pr7080530
Chicago/Turabian StyleLi, Wei, Dean Kong, Qiang Xu, Xiaoyu Wang, Xiang Zhao, Yongji Li, Hongzhi Han, Wei Wang, and Zhenyu Chen. 2019. "A Wind Farm Active Power Dispatch Strategy Considering the Wind Turbine Power-Tracking Characteristic via Model Predictive Control" Processes 7, no. 8: 530. https://doi.org/10.3390/pr7080530
APA StyleLi, W., Kong, D., Xu, Q., Wang, X., Zhao, X., Li, Y., Han, H., Wang, W., & Chen, Z. (2019). A Wind Farm Active Power Dispatch Strategy Considering the Wind Turbine Power-Tracking Characteristic via Model Predictive Control. Processes, 7(8), 530. https://doi.org/10.3390/pr7080530





