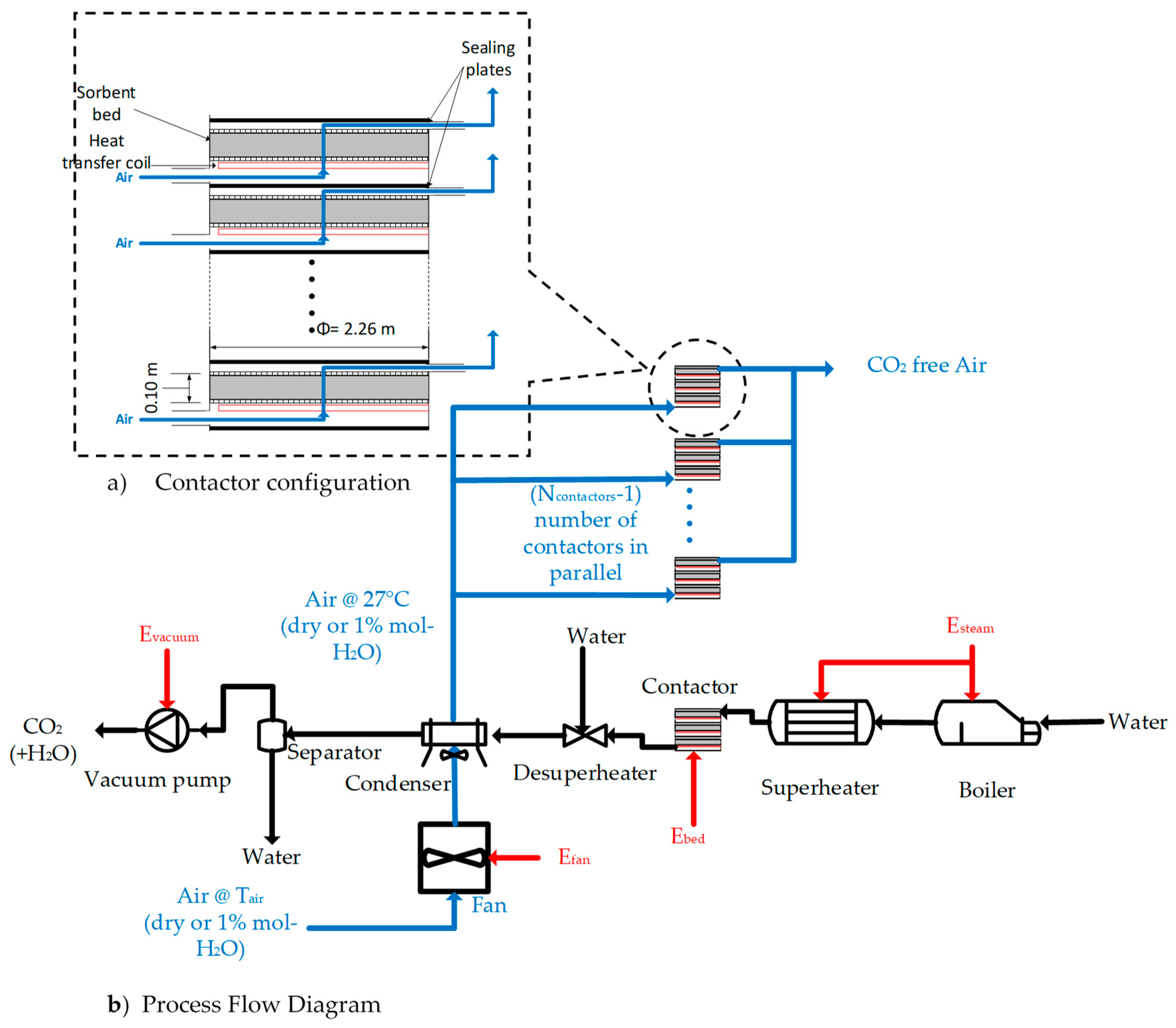
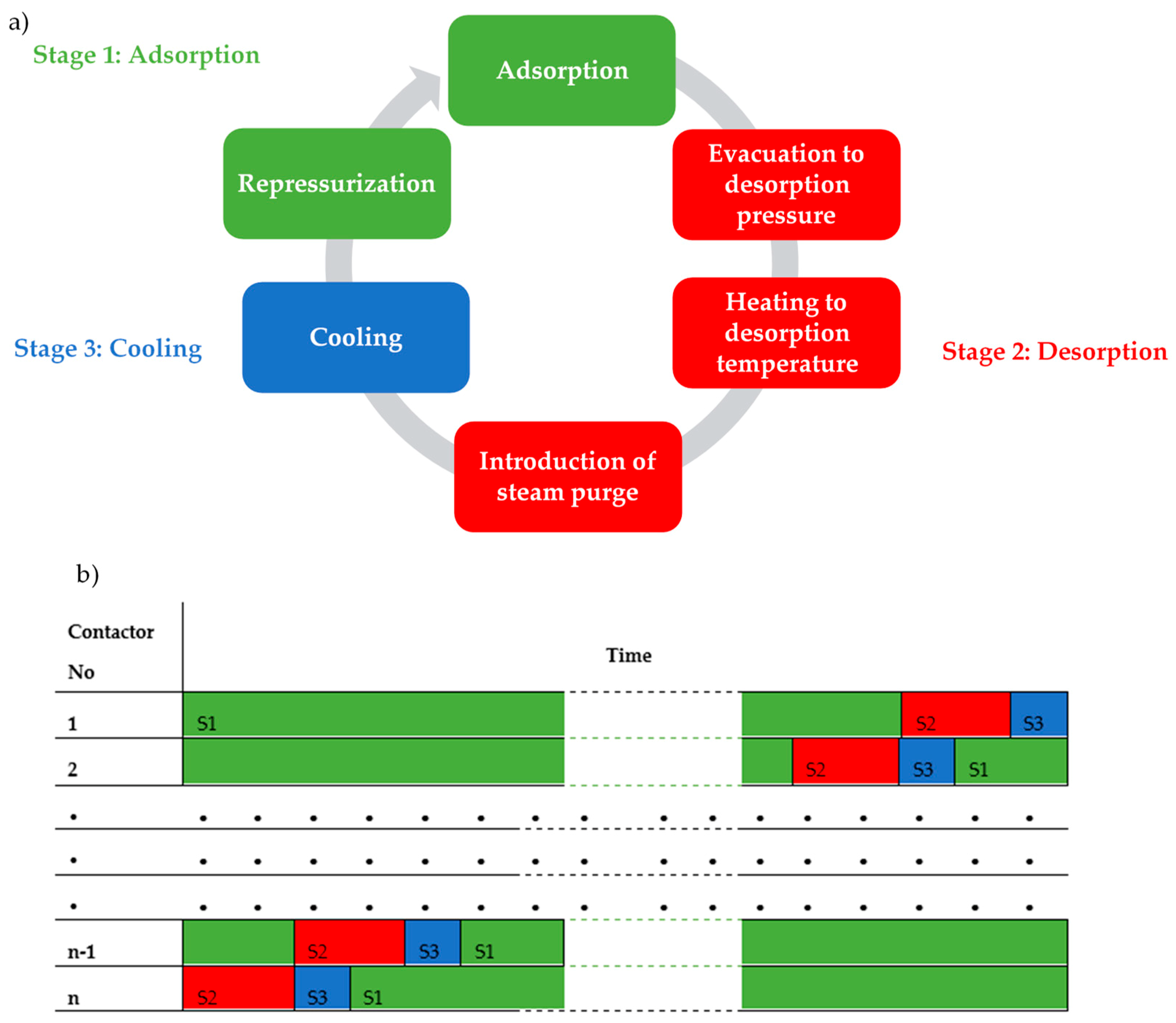
1. Introduction
The increase in anthropogenic CO
2 emissions has been identified as a main cause of global climate change. Close to half [
1] of these emissions are accounted for by diffuse sources such as motor vehicles, homes and offices. Capturing these emissions at the source would require the fitting of capture systems to each of these, which would neither be economical, nor practical. Alternatively, the effect of these emissions could be compensated for with “Direct Air Capture” (DAC) systems, i.e., processes which capture CO
2 directly from the atmosphere. The captured CO
2 could either be sequestered or utilized for application in various industries [
2]. The technologies evaluated for DAC include absorption with aqueous hydroxide solutions, adsorption with solid inorganic bases, and adsorption with solid-supported amines (SSA). A review of the studies done on DAC has been detailed in Sanz-Pérez et al. [
3]. Of these technologies, adsorption with SSA has presented itself to be promising for DAC.
SSAs are a group of sorbents made of various amines, physically or chemically supported on porous solid materials. They are well suited for DAC applications, due to their high uptake capacity and selectivity, resilience to moisture which is present in air, and the possibility of regeneration under relatively mild conditions. While significant research has been done on SSA for DAC, its focus has mainly been on sorbent development. There have only been a few reports [
4,
5,
6,
7,
8,
9] on the energy requirements and the cost of capture of such systems, and there is significant discrepancy between their results. These reports [
4,
5,
6,
7,
8,
9] evaluated DAC systems which used temperature concentration swing adsorption (TCSA) [
5,
6], temperature vacuum swing adsorption (TVSA) [
9] and steam-assisted temperature vacuum swing adsorption (S-TVSA) [
4,
7,
8] type processes. For TCSA, after the CO
2 is adsorbed on to the sorbent, the sorbent is heated and purged with a gas (steam in Krekel et al. [
5] and Zhang et al. [
6]) to effect desorption. In TVSA, desorption is achieved by heating the sorbent and applying a vacuum. S-TVSA is a hybrid of the two approaches, where in addition to applying heat and a vacuum, a steam purge is also used.
In two of the early studies, Kulkarni and Sholl [
7] and Zhang et al. [
6] carried out an economic analysis based only on the operating cost of the processes. They reported costs of CO
2 capture of 43–494 [
7] and 91–227 [
6] USD tonne
−1. Krekel et al. [
5] expanded on the work carried out by Zhang et al. [
6], and reported that once the capital expenses are included, the cost of capture would be increased significantly to 792–1200 USD tonne
−1. Sinha et al. [
4] estimated a cost of capture of 60–190 USD tonne
−1.
Several companies are active in the field of DAC with SSA. The most well-known of these are Climeworks [
10] and Global Thermostat [
11]. The cost of capture reported for the operations of first-generation DAC system by Climeworks was estimated to be 600 USD tonne
−1 [
12]. This is an important benchmark, as it is based on a commercially operating system, as opposed to results of studies which are sensitive to the scope and assumptions used. Climeworks has further expressed their confidence in reducing this cost down to 200 USD tonne
−1 by 2021, and down to 100 USD tonne
−1 by 2030 [
12]. Similarly, Global Thermostat expects a cost of capture of 100 USD tonne
−1 for their first commercial DAC process [
12]. Carbon Engineering [
13] is another company which is developing a DAC process, although they focus on an aqueous hydroxide-based process. The projected cost of capture with this process has been reported to be 94–232 USD tonne
−1 [
14], but this process requires very high temperatures for regeneration of the sorbent.
In comparison, removing CO
2 from air via afforestation and forest management has a cost of capture of 15–50 USD tonne
−1 [
15]. However, this approach carries a large land requirement, which would compete with the land available for food production. Moreover, the land available also enforces an upper limit on the scale at which CO
2 can be removed. In comparison, CO
2 removal by DAC faces less stringent limitations on the degree of possible scaling. However, it is important to stress that DAC is not envisioned to be an alternative for good forest management practices, but rather as a technology to supplement the rate of CO
2 removal by the natural carbon cycle.
The energy requirements of the DAC processes in prior works, is largely accounted for by the thermal energy required for the desorption process. This mainly consists of the sensible heat required to heat up the sorbent to the desorption temperature, and the large heat of desorption for CO
2. When adsorption is considered under humid conditions, the heat of desorption of water, which gets co-adsorbed on SSA, adds to the thermal energy demand [
9]. Another big contributor to the energy consumption is that needed for pushing air through the air-sorbent contactors. Due to the low concentration of CO
2 in air, large amounts of air need to be processed to capture the CO
2. This results in large energy requirements, even for low pressure drop contactor configurations as are described in some studies [
4,
7].
It was previously reported [
16] that branched polyethyleneimine (PEI) loaded mesocellular foam (MCF) silica sorbent in pelletized form is promising for CO
2 adsorption under DAC conditions. The study identified that while low temperatures were better for the thermodynamics of the reaction between the CO
2 and amine sites, the uptake of CO
2 was limited by diffusional resistances in the sorbent. In contrast, higher temperatures allowed for better diffusion of CO
2, but the thermodynamics were less favored. The amount of CO
2 adsorbed by the sorbent was determined by the combined effect of these two factors. Due to the large diffusional resistances of the sorbent studied, the highest uptake was achieved under relatively warm conditions (46 °C). The study further identified that low levels of moisture in the gas (0.5 to 2% mol-H
2O), enhanced the CO
2 uptake by up to 53%.
The same sorbent was evaluated using a S-TVSA adsorption/desorption cycle [
17]. It was identified that substantial CO
2 desorption could be achieved with mild vacuum levels (12 to 56 kPa abs), and temperatures (70 to 100 °C). This indicated that the process could benefit from a reduced electrical energy demand for vacuum generation and a lower capital cost owing to the use of smaller vacuum pumps. It was further noted that as desorption is possible at relatively low temperatures, the thermal energy requirement could be supplied with low grade heat. The desorption conditions (pressure, temperature, steam flow rate) were seen to have a significant effect on the desorption performance. Moreover, it was identified that while the presence of moisture enhanced CO
2 adsorption, it also resulted in a significant uptake of H
2O, which increased the thermal energy demand for the desorption stage.
Building on this prior work, the present study aimed to (1) identify operating conditions which yield the lowest cost of DAC, (2) determine the relative effects of varying operating conditions on its technoeconomic performance and (3) identify promising directions for research on sorbent development that could foster further cost reduction for DAC.
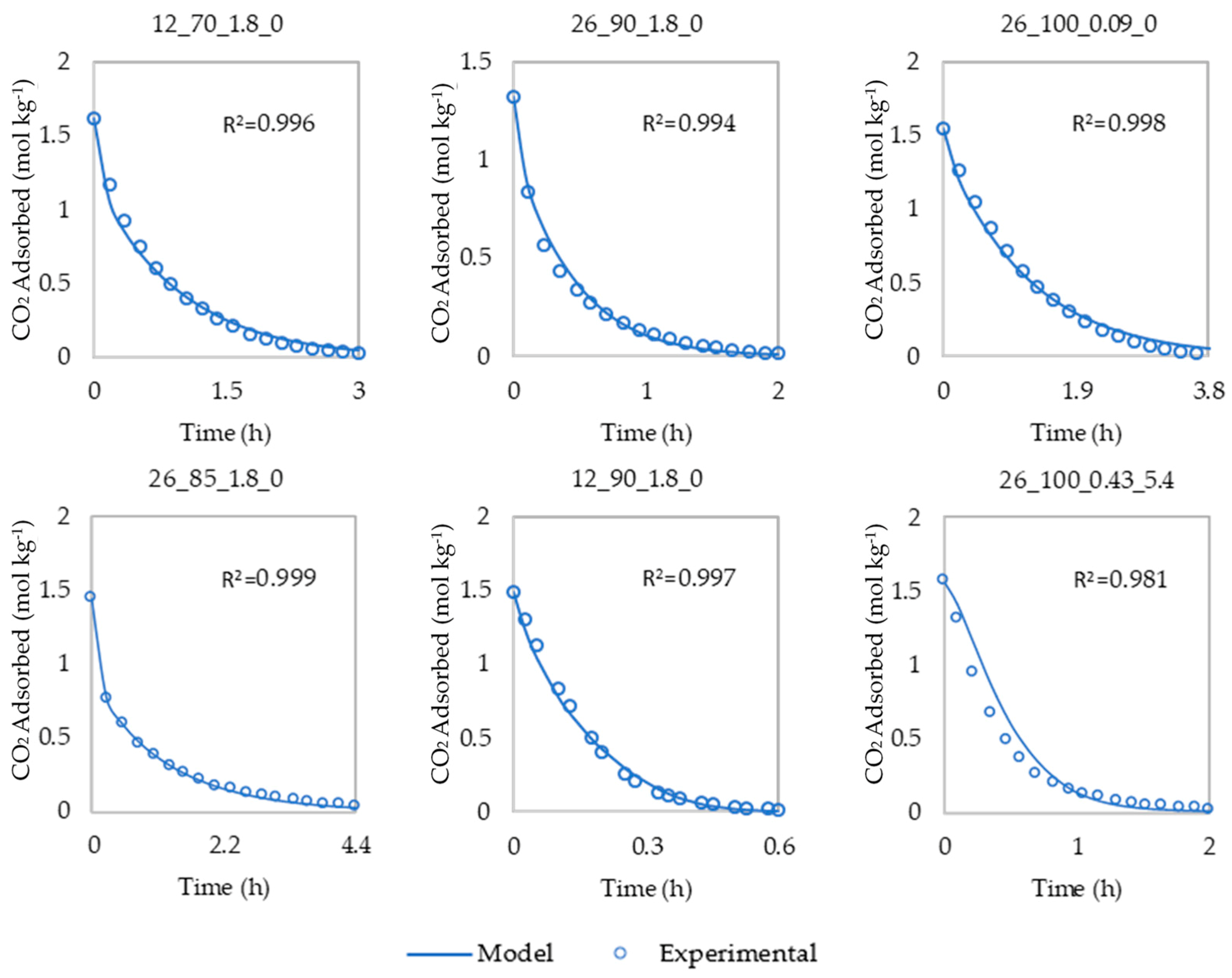
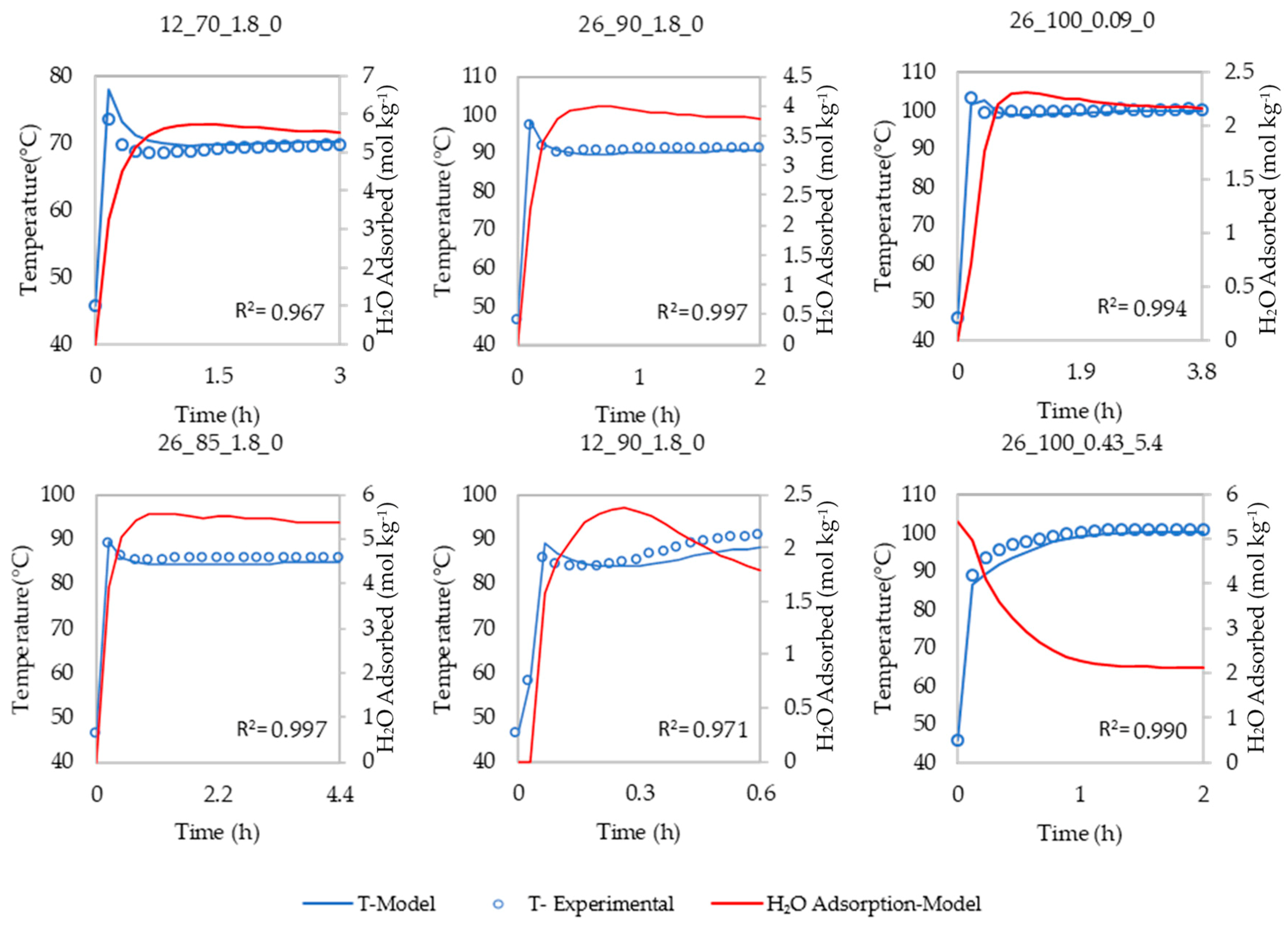
To address the first two aims, a DAC technoeconomic model was developed based on the results of laboratory scale experimental data [
17]. Next, the process model was subjected to a Multi-Objective Optimization (MOO) to minimize the cost of capture, while simultaneously maximizing the amount of CO
2 captured. In contrast to prior studies [
4,
5,
6,
7] which fixed on particular process conditions, the present study considers a range of conditions, seeking to minimize the cost. Moreover, adsorption from dry versus and humid air was compared, to evaluate the effect of the water, which co-adsorbs, on the process. Previous technoeconomic studies do not appear to have addressed this aspect [
4,
5,
6,
7]. The final aim was addressed through the use of case studies exploring the relative effect that sorbent modifications could have on the cost of capture.
5. Discussion
5.1. Influence of Process Conditions
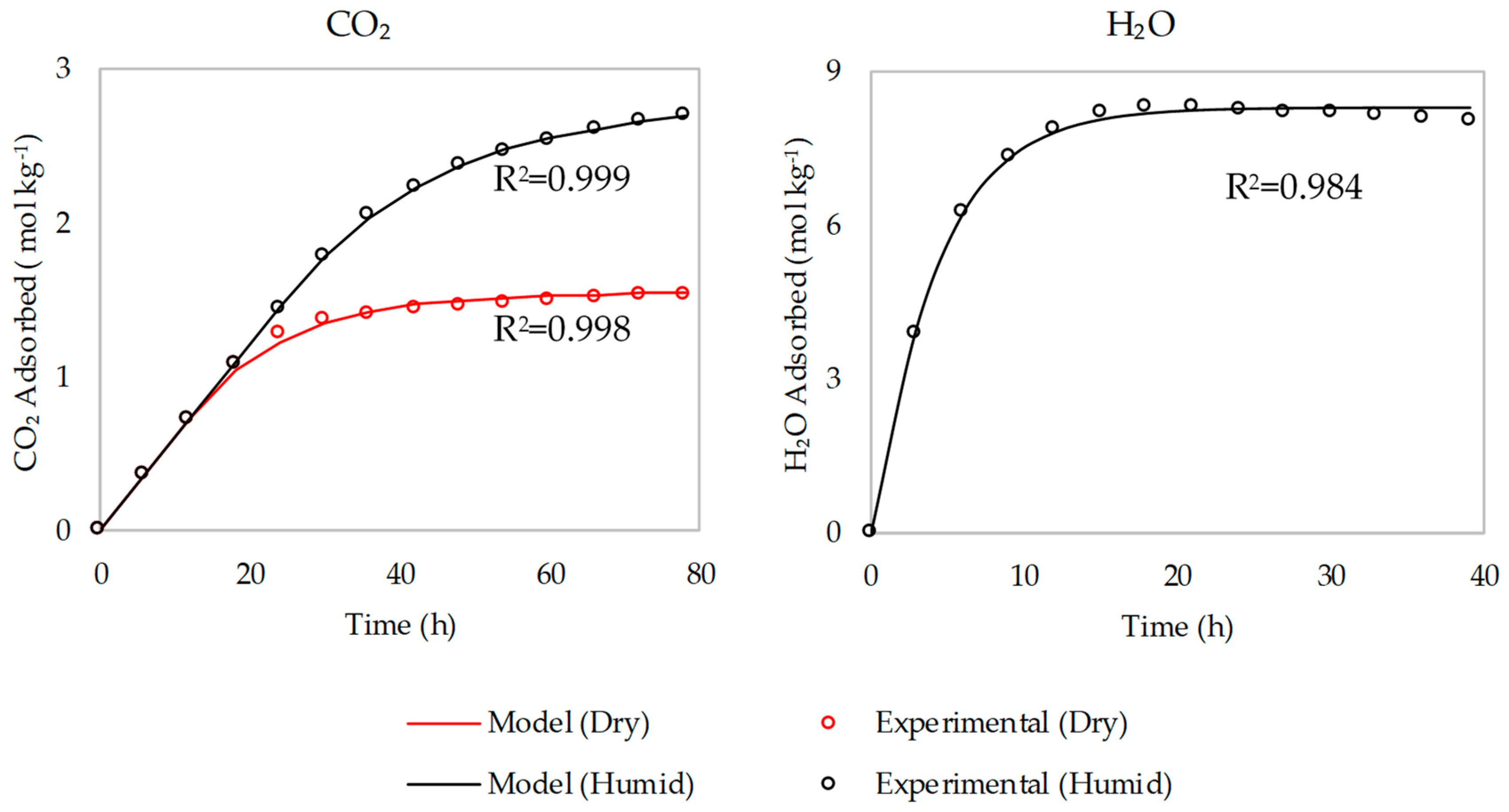
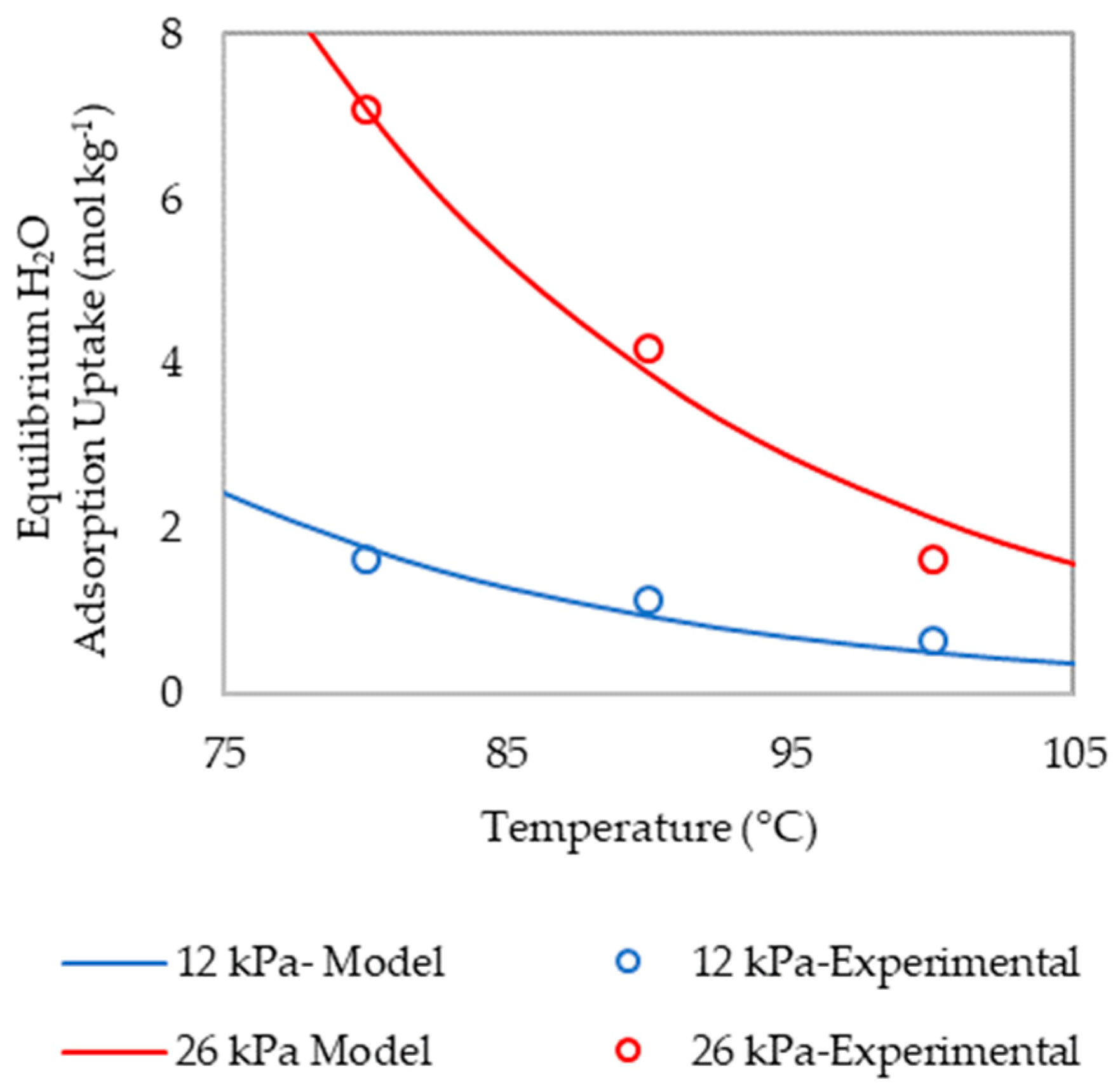
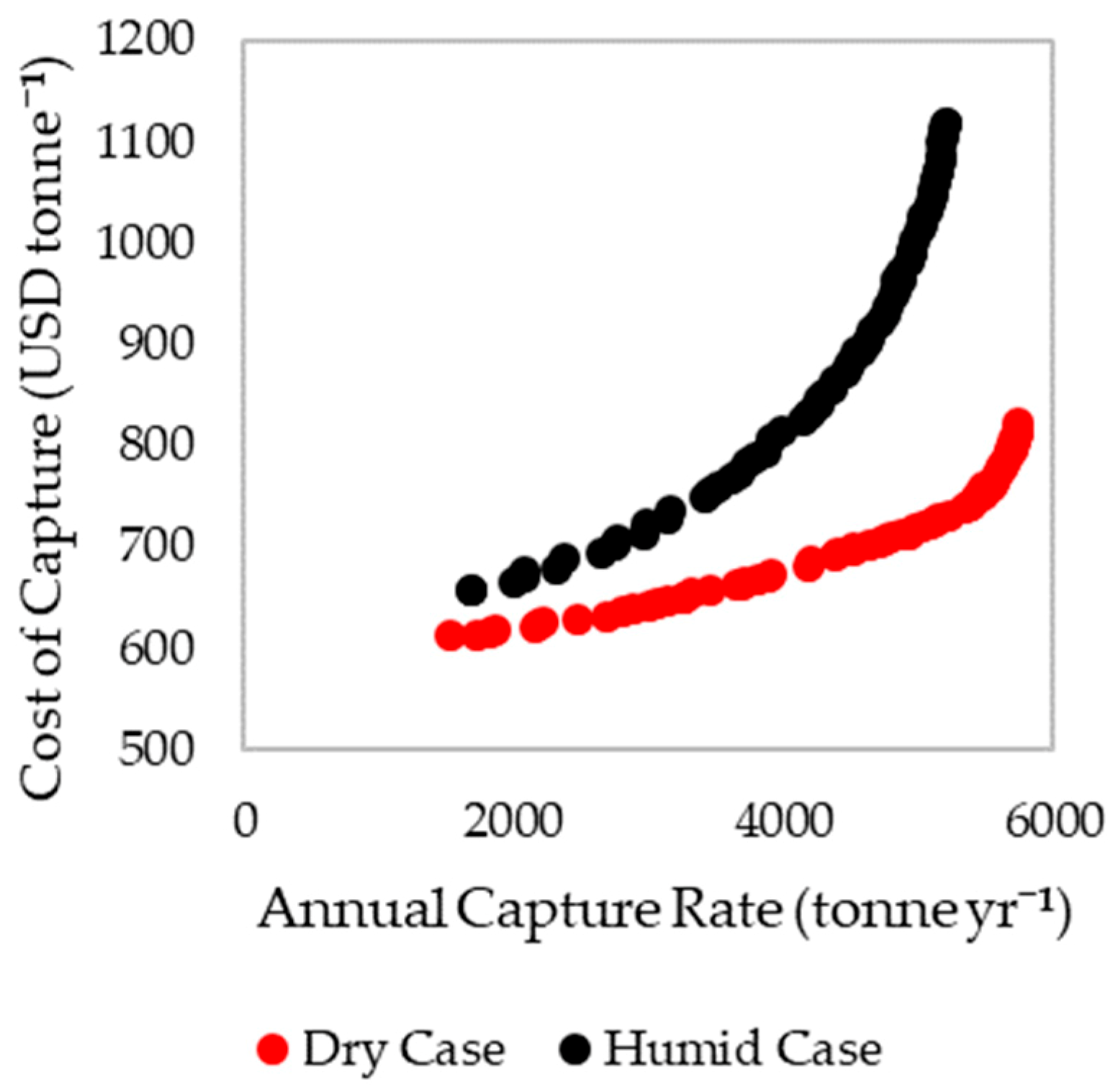
It can be noted that the cost of capturing under humid conditions is higher than that under dry conditions for all the capture rates in the Pareto fronts (
Figure 7). The presence of moisture allows the process to take advantage of the improved CO
2 adsorption capacities of the sorbent [
16] as indicated by the higher
and
in the humid case. However, this also leads to a longer
and
, which increases
. This reduces the annual capture rate, and so increases the cost of capture (see Equations (12) and (13)).
In the humid case, the process is restricted from using smaller
and
, due to the large amount of water adsorbed. As the water adsorption/desorption is significantly faster than that of CO
2 (see
Figure 3), at lower
and
(shorter
and
) values, there is a much higher proportion of H
2O adsorbed in comparison to CO
2. This in turn translates to a proportionately higher cost of thermal energy consumed for desorbing the H
2O. And as the thermal energy accounts for a large fraction of the cost, this has a significant impact on the economics of the process. These results indicate that using a sorbent with a reduced affinity for water may improve the economics of the process.
When comparing the process conditions which yielded the lowest cost scenario, both the humid and the dry case had a similar adsorption air flow rate (), desorption temperature () and desorption pressure (). At high , the rate at which CO2 can be captured is increased, which can reduce the cycle time. However, this is done at the compromise of higher pressure drops across the contactors resulting in an increased electrical energy consumption.
The preferred
Td was identified as 100 °C which is the upper limit used for the optimization. This is due to the faster desorption kinetics presented at higher temperatures [
17], which leads to shorter cycle times. The upper limit for this study was set at 100 °C, as solid supported amines have been reported to undergo degradation at high temperatures [
32]. However, the sorbent in this study was previously reported [
17] to be stable at temperatures up to 100 °C, under the desorption conditions evaluated here. In the case of
Pd, the preferred value is a balance between benefitting from the faster desorption rates (shorter cycle times) offered by the lower pressures [
17] and the increased expenses for electrical energy.
The identification of the preferred steam flow rate,
, is similar to that of
Pd. The preferred value is a balance between benefitting from the faster desorption rates (shorter
) offered by the faster steam flow rates [
17] at the compromise of increased cost of thermal energy. In both cases, the steam flow rate with the lowest cost was the close to its lower bounds, indicating that benefit of shorter
is not justified by the higher energy cost. This can be attributed to the fact that thermal energy demand has the one of the biggest impacts on the economics of the process (see
Figure 10).
When comparing the energy requirements, the electrical energy consumption was similar for both cases. However, the humid case needed more thermal energy to heat up the sorbent during the desorption. This is because the energy consumed by the water being desorbed from the sorbent, cools it down [
17]. Therefore, more heat needs to be provided in the humid case, to maintain the desired desorption temperature.
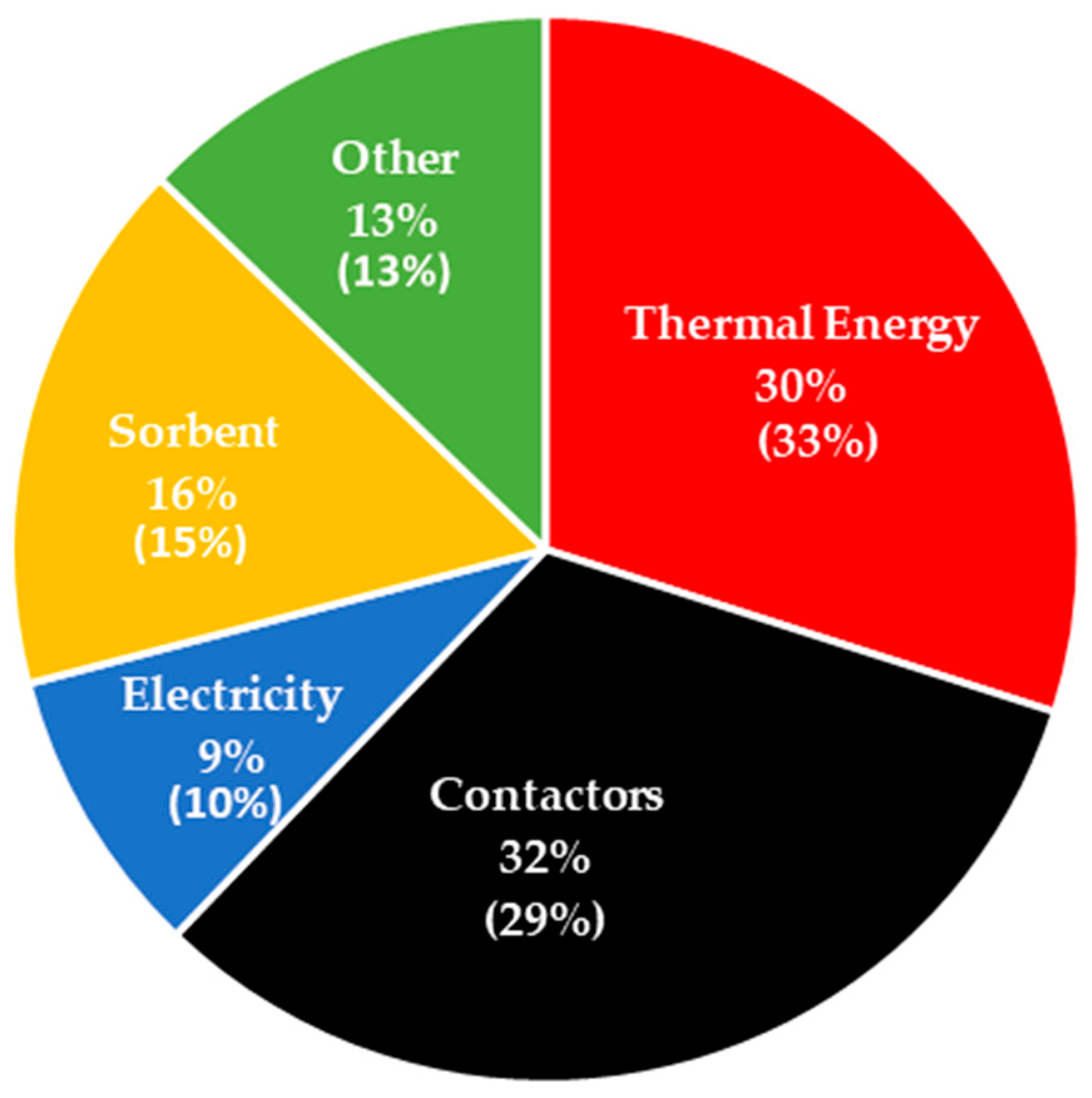
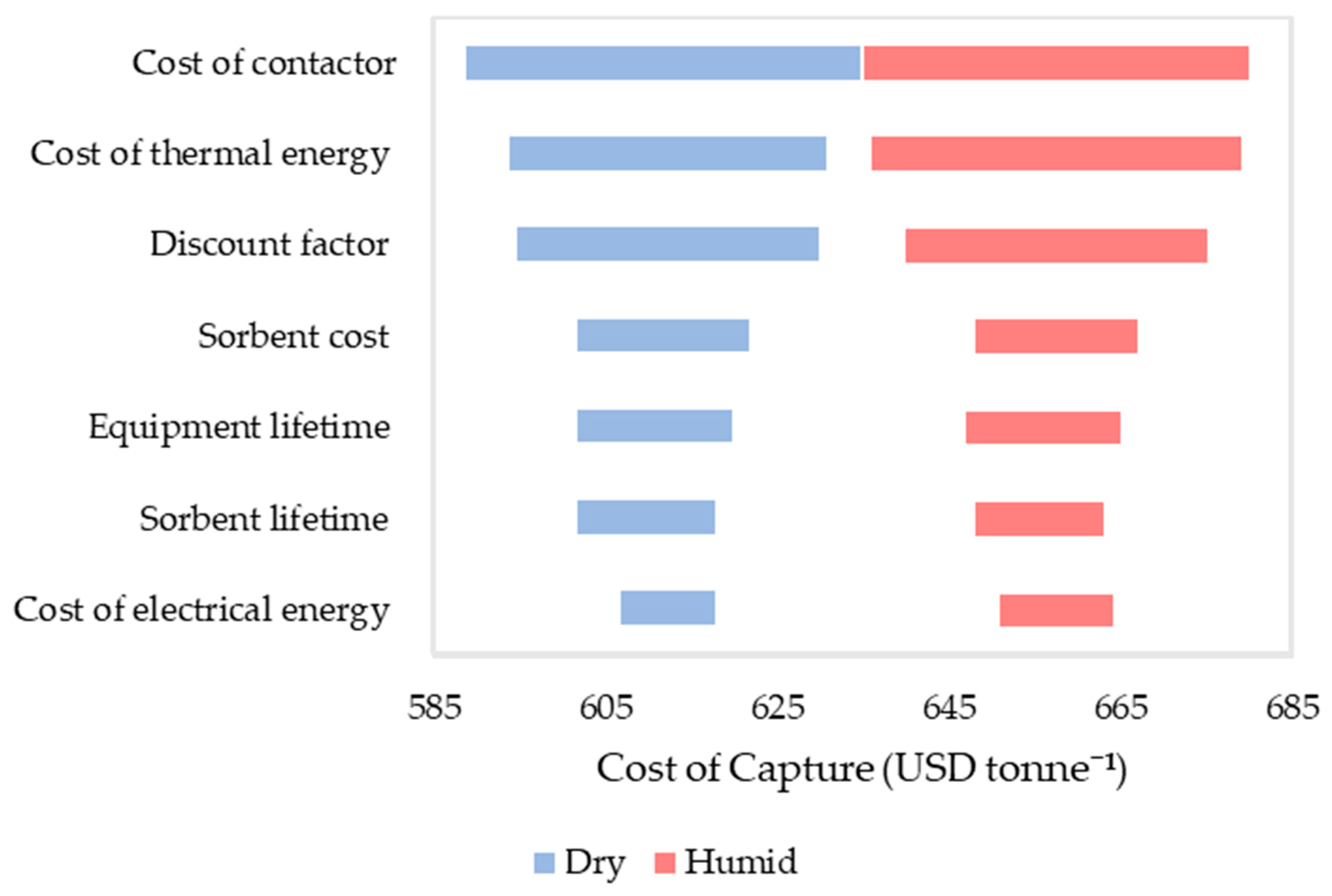
From
Figure 11, it can be seen that both cases display similar sensitivities to the values studied. The final result was seen to be relatively insensitive to the values studied, as the cost was seen to vary by <±4% for a variation of ±10% in the parameters. The cost of thermal energy and the contactor were identified to be the variables which most affected the cost of capture. This is consistent with the fact that thermal energy and the cost of the contactor are the two largest contributions to the cost (see
Figure 10). The discount factor was also seen to have a large impact on the cost of capture and a value of 10% is conservative for the current economic conditions.
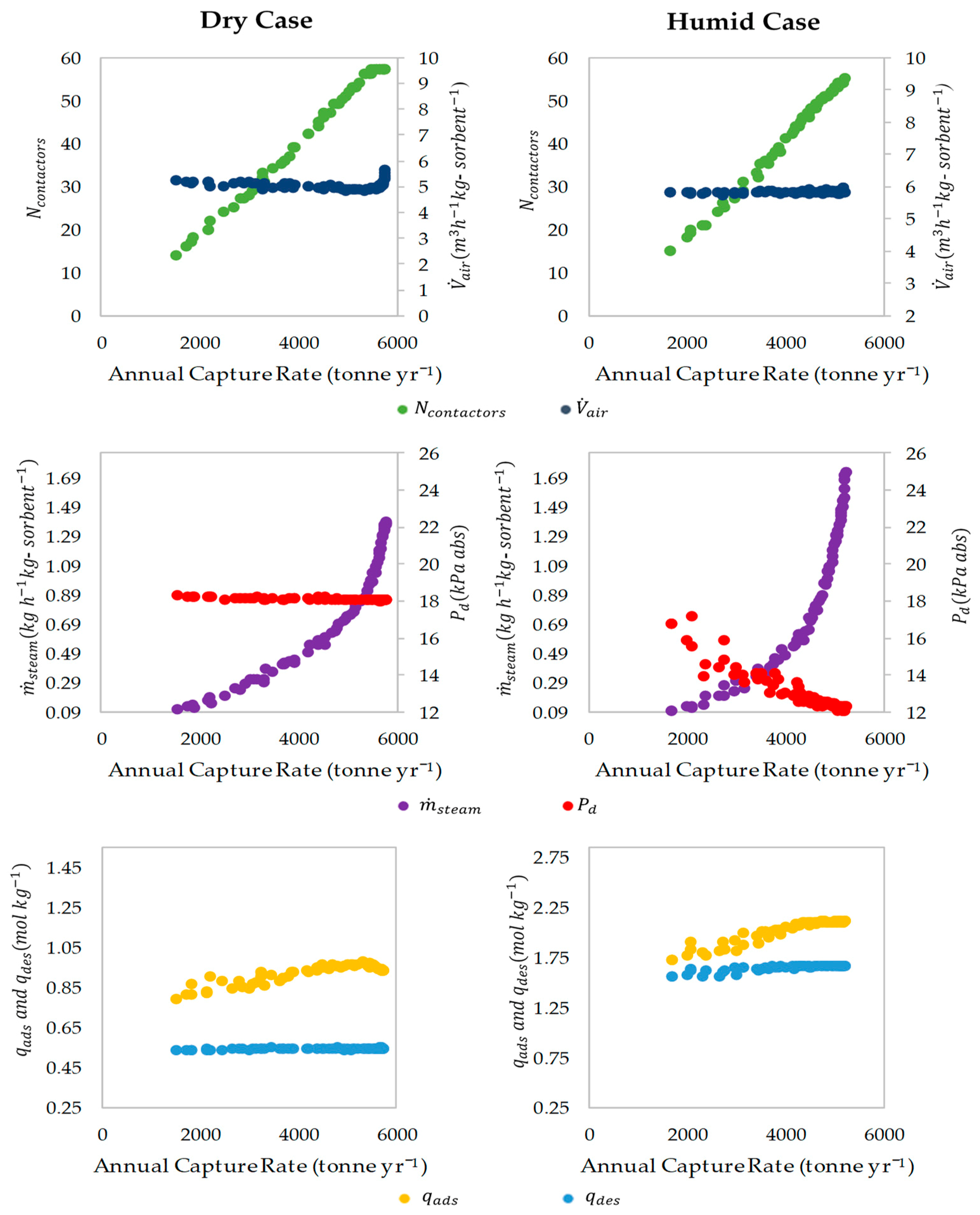
5.2. Pareto Non-Dominated Fronts
In both cases, the cost of capture increases as the capture rate increases. As seen in the Pareto plots of the variables (
Figure 8), the increase in the capture rate is achieved mainly by using a higher
which increases the amount of CO
2 captured. However, to increase
, either
needs to be increased or
needs to be decreased to satisfy the inequality constraint in Equation (14). This is fulfilled by increasing
, which shortens
by improving the CO
2 desorption kinetics.
is also decreased for the humid case, which can be attributed to the comparatively longer
, which demands a greater increase in the kinetics to satisfy the inequality constraint in Equation (14). Furthermore,
is increased to increase the
and
is kept relatively constant which shortens
when used in combination with higher
, and lower
. These changes to the process conditions (except
) increase the annual capture rate while incurring additional expenses as explained in
Section 5.1. The increases in the thermal energy demand and the contactors are particularly significant as they are the two biggest contributors to the economics of the process.
, can be seen to be relatively constant for most of the Pareto front. This can be expected since it is selected based on the compromise between the positive effect of a shorter and the negative of a higher energy requirement for high flow rates. It is likely that the balance between the two does not significantly vary for the different points in the Pareto plot. In the dry case, there is a steep increase in at the higher capture rate end which coincides with a steep increase in the cost. This highlights that while slightly higher capture rates can be achieved with higher , it is accompanied by a significant increase in the cost.
5.3. Temperature and RH of the Incoming Air to the Process
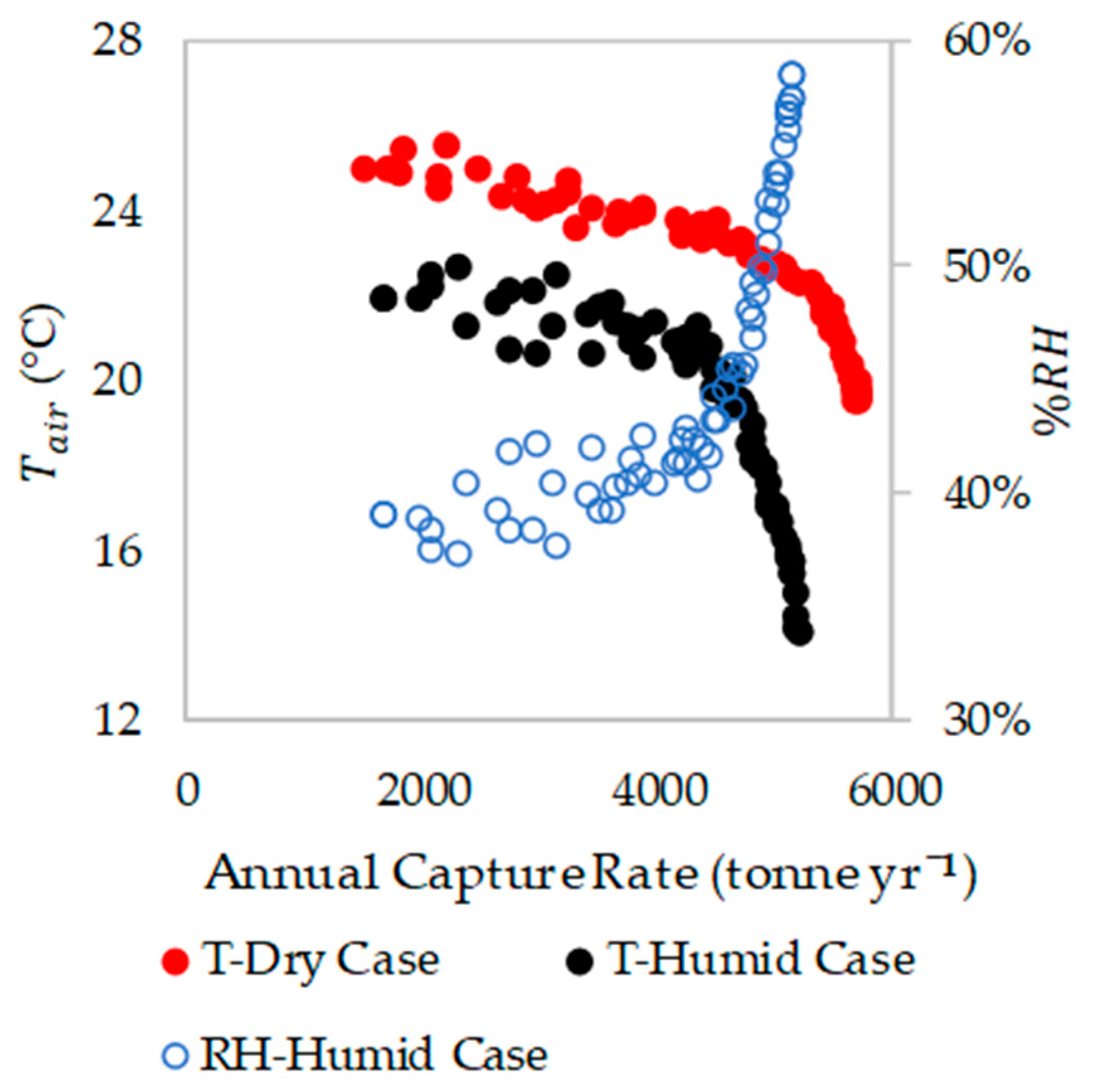
For the lowest cost cases, the incoming air temperature,
, was calculated to be 25 °C for the dry case and 22 °C for the humid case (see
Figure 9). The RH of the humid case was calculated to be 39%. It is noted that, while the dry case yielded a lower cost, it is unrealistic to expect completely dry conditions anywhere in the world. However, the conditions calculated for the humid case are far more realistic and can be expected of regions with sub-tropical climates.
can be seen to reduce with increases in the capture rate (see
Figure 9). This can be attributed to the higher steam flow rates available at the higher capture rate/higher cost end of the Pareto fronts. It is also apparent that the humid case allows for significantly lower temperatures. This is owing to the water which gets desorbed from the sorbent which condenses, releasing additional thermal energy. These results indicate that the process could operate in colder climates with higher humidity, at the compromise of a higher cost of capture. It is also noteworthy that when operating at a higher moisture level than 1% mol-H
2O, lower
may be achieved due to the increased adsorption of water, although this would also likely lead to a higher cost of capture.
5.4. Comparison to Results of Other Studies
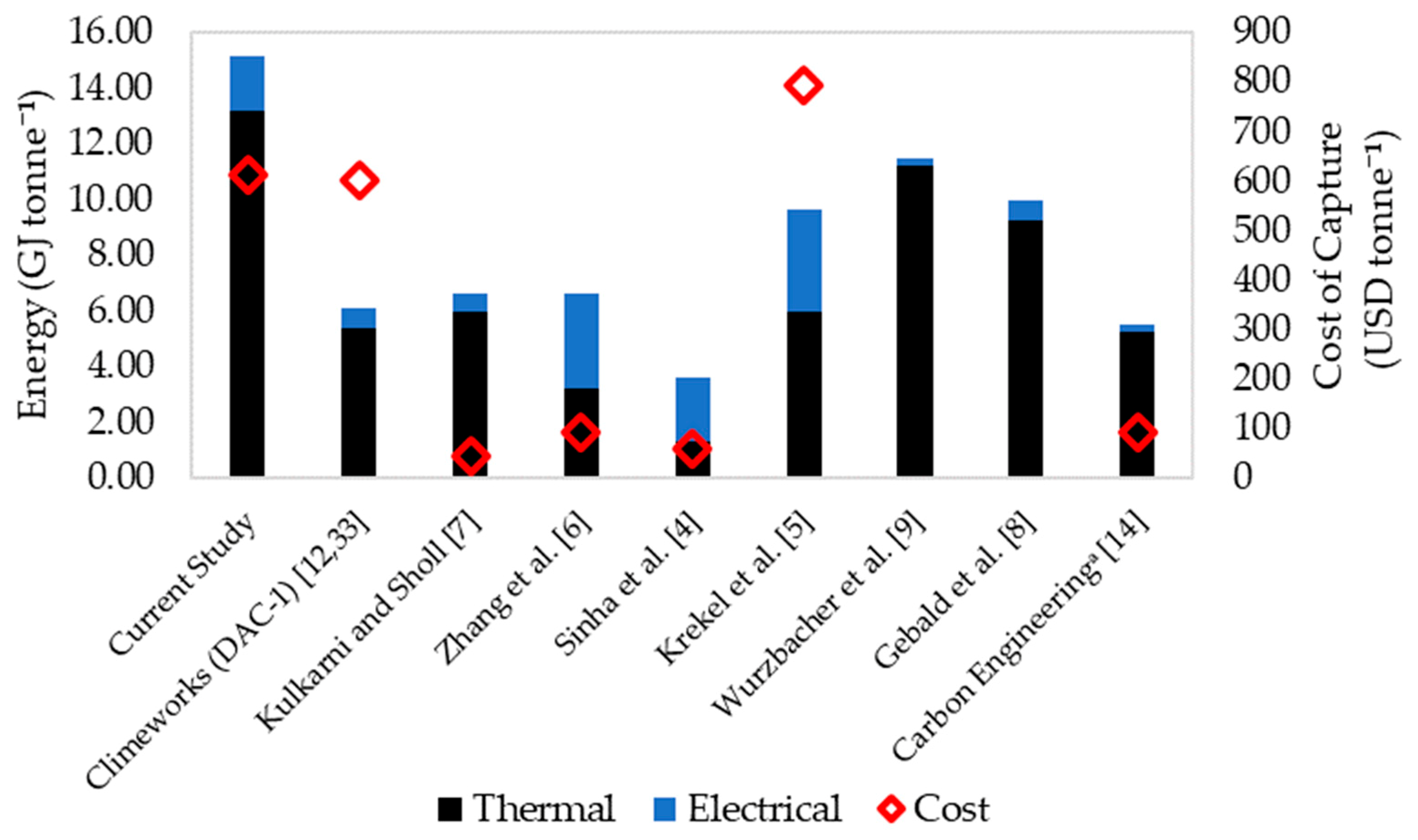
The cost and energy data for the lowest cost case described in the current study is presented alongside data found for other DAC processes [
4,
5,
6,
7,
8,
9,
12,
14,
33] in
Figure 12. The data are that of the lowest cost case described in the respective studies.
It is evident that the cost of capture presented in the current study is in the upper end of the range of costs reported for similar processes. However, it can be noted that the cost in the current study is similar to that reported by Climeworks based on the actual performance of their first-generation DAC system (DAC-1) [
12]. In comparison, the other values depicted in
Figure 12 are subjective to the scope of the respective study and the assumptions that were used. For example, Kulkarni and Sholl [
7] and Zhang et al. [
6] did not include the capital expenses of the equipment in their studies. Krekel et al. [
5] expanded on the work carried out by Zhang et al. [
6], and reported that once the capital expenses are included, the cost of capture is increased significantly. Moreover, the costs of capture depicted in
Figure 12 for Zhang et al. [
6] and Krekel et al. [
5] are based on scenarios where the energy is supplied with fossil fuels, as opposed to the low carbon solar energy used here. Krekel et al. [
5] reported that the cost of capture increases from 792 to 1333 USD tonne
−1 when the emissions from energy generation are considered. They further reported that if wind energy is used, a capture cost of 824 USD tonne
−1 can be achieved. Zhang et al. [
6] estimated an increase from 91 to 225 USD tonne
−1 for a system utilizing wind and nuclear energy.
The large difference between the results of this study and that of the Sinha et al. [
4] is in part due to the two main differences. Firstly, the cash flow was not discounted [
4]. The second reason is due to the nature of the sorbent used. Sinha et al. [
4] evaluated a monolithic sorbent which was assumed to be self-contained. In comparison, the pelletized sorbent in the current study needs to be contained in contactors which contribute to about a third of the total cost. This may indicate the advantage that monolithic sorbents have over pelletized ones. Furthermore, Sinha et al. [
4] also did not consider the CO
2 emissions from energy generation in their calculations.
Apart from these, another major reason for the higher cost reported in the current study is the slower kinetics of the sorbent evaluated. It was previously reported [
16] that the large loading of PEI in this sorbent resulted in a large CO
2 uptake capacity although at the sacrifice of significant mass transfer limitations, which resulted in a slow uptake rate of CO
2. The effect of this is evident here, where long cycle times are required for the process (7.51 h for the dry case). In comparison, for other studies, the reported cycle times are in the range of 1.27 [
4] to 4 h [
7]. These long cycle times result in a lower annual capture rate and hence a larger cost. Furthermore, it should be noted that the subject sorbent was shown to provide better adsorption performance at the higher temperature of 46 °C [
16]; thus, it may be that further improvements in the process economics could be achieved by tailoring the design of sorbent material so that its optimum sorption performance occurs at the intended adsorption temperature.
The slow kinetics also have a large effect on the energy requirement of the process. As seen in
Table 3, the thermal energy requirement is dominated by the energy for steam generation, and for longer desorption times, larger amounts of steam are needed to desorb the CO
2. This would explain the larger thermal energy requirement of the process in comparison to the other studies depicted in
Figure 12. However, the electrical energy requirement of the process is in close agreement with most of the values reported in literature. While Wurzbacher et al. [
9] and Gebald et al. [
8] reported much lower values, they only evaluated the desorption stage and did not include the energy needed to pump the air through contactors during adsorption.
It is difficult to make direct comparisons with the costs reported by Carbon Engineering [
14], as this corresponds to a completely different type of process. However, it is noted that the need for very high temperatures (900 °C) for the regeneration of the sorbent, may make the process more reliant on fossil fuel-based energy. In comparison, the processes using SSA could more easily be powered with relatively inexpensive low carbon energy sources like solar thermal hot water systems.
5.5. Case Studies
In this section, the effect of five different scenarios on the cost of capture is evaluated. The scenarios were selected based on the main cost drivers and the limitations of the process identified in the previous sections. For these evaluations, the MOO was repeated with the respective changes described below for each scenario.
Case study A: Thermal energy from waste heat utilization—This scenario was chosen because the main contributor to the cost of the capture was identified to be the thermal energy requirement. Moreover, the low temperatures (≤100 °C) used for the desorption process makes it possible for integration with waste heat sources. It was assumed that this energy could be achieved free of charge.
Case study B: Hypothetical sorbent with faster kinetics—This scenario addresses the limitation of slow mass transfer kinetics of the sorbent (longer cycle times). Here a hypothetical sorbent, with improved mass transfer kinetics of CO
2 is used. Potential means of achieving this include using additives which improve CO
2 diffusion in the amine phase [
34,
35,
36,
37] and using support materials with high surface areas [
38] and/or large pore sizes [
39] to better disperse the amines and thus improve their accessibility to the CO
2. To carry out the evaluation,
in Equation (1) and
in Equation (3) were multiplied by a factor of 2, to emulate a sorbent with twice as faster CO
2 mass transfer kinetics.
Case study C: Hypothetical sorbent with faster kinetics but lower CO
2 uptake capacity—This scenario considers an iteration of case study B. It is possible that the improvements made to the kinetics would come at the expense of a smaller CO
2 uptake capacity. For example, it has been reported in literature that lower PEI loadings (% wt) on the sorbent results in lower uptake capacities and faster kinetics [
40,
41]. For this scenario, a hypothetical sorbent where the kinetics are increased by a factor of 2, at the compromise of a halved equilibrium capacity, is evaluated. To carry out the evaluation,
in Equation (1) and
in Equation (3) were multiplied by a factor of 2, and
in Equation (1) was multiplied by 0.5.
Case study D: Combination of case studies A and B, where a sorbent with superior kinetics is used with waste heat utilization.
Case study E: Hypothetical sorbent with lower H
2O uptake capacity—As mentioned earlier, while adsorbing from humid air enhances the CO
2 uptake, a proportionately higher amount of water is also adsorbed. This results in a higher energy requirement for desorption of water. It has been reported [
42] that the water uptake by PEI-silica sorbents could be reduced by using hydrophobic silica as the support material. The study [
42] further demonstrated that the benefit of enhanced CO
2 capacities when adsorbing in the presence of moisture could be retained, in spite of the reduction of the water uptake. Modifications to the amine such as reducing the proportion of primary amines [
43] and introduction of methyl groups [
44] have also been reported to reduce the water uptake by these sorbents. For this scenario, a hypothetical sorbent, with half the water uptake capacity is evaluated. To carry out the evaluation,
in Equation (1) and
in Equation (5) were multiplied by a factor of 0.5.
For case studies B–E, the current study does not attempt to identify exactly how the sorbent may be developed to meet the specified criteria but simply aims to estimate the impact each modification would have on the economics of the process. The results of this exercise are meant to be taken as a guide, for identifying the direction future research into sorbent development may head towards.
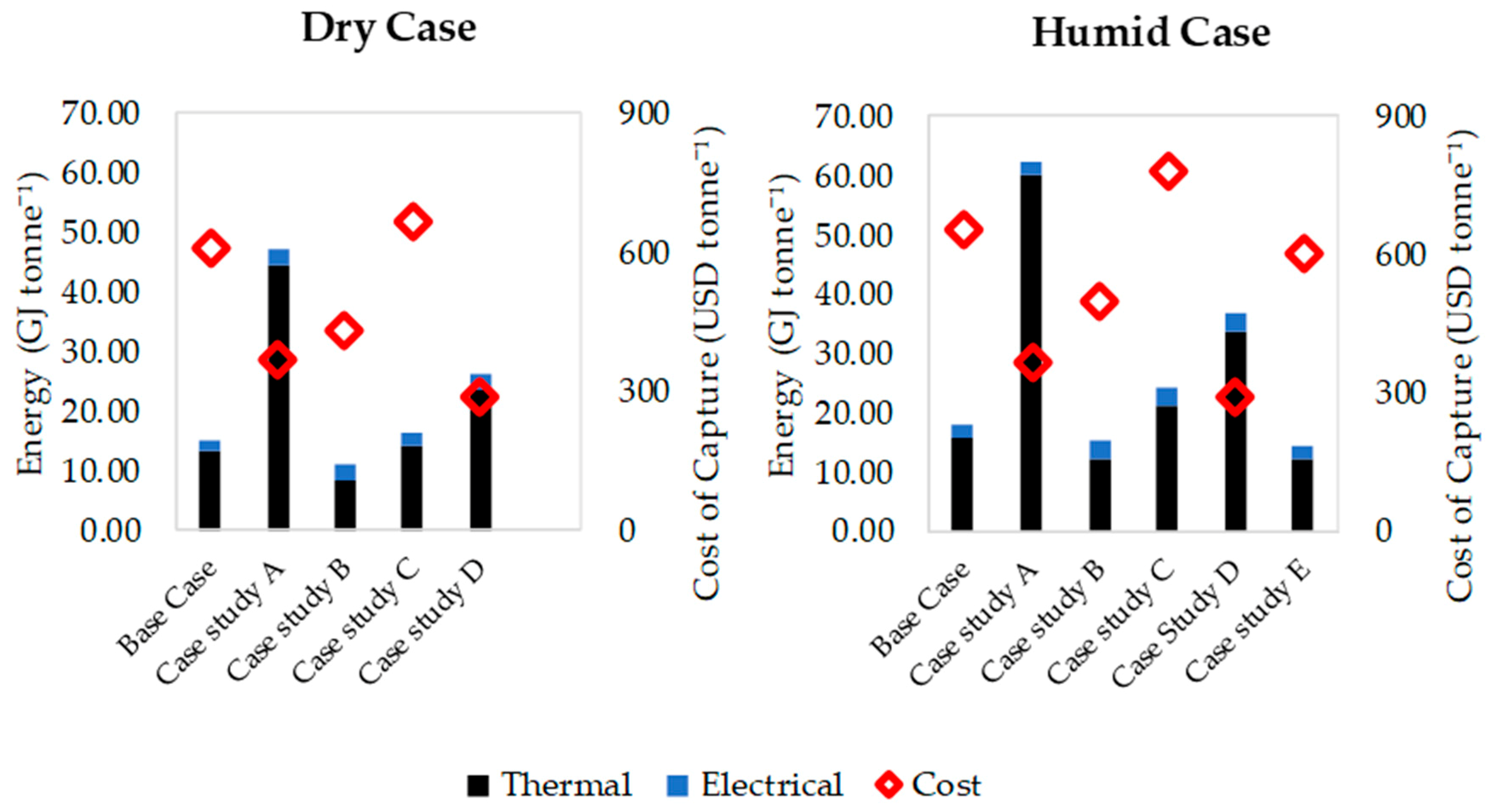
The results of the case studies are depicted in
Figure 13. From the results, it is evident that using waste heat to provide the thermal energy yields the biggest reduction (~ 42%) in the cost of capture. This reduction is an effect of two things. Firstly, the large contribution of the thermal energy to the cost is eliminated. Secondly, the process takes advantage of the free thermal energy and utilizes higher
to increase the capture rate. This is evident in the thermal energy demands which are more than 3-fold higher than that of the base case. The higher
facilitates faster desorption which reduces
, which in turn lowers the cost of capture. While the reductions are attractive, it should also be noted that the utilization of waste heat would restrict the locations where DAC systems could be operated to areas such as industrial parks. DAC systems with waste heat utilization would also likely be more practical for carbon capture and utilization projects rather than carbon capture and sequestration projects. This is because sequestration sites would likely be located far away from industrial sites, which would require the transportation of CO
2, incurring additional costs. In comparison, the utilization could be done at the same site the capture is done.
When comparing cases B to E, it can be seen that developing sorbents with improved CO2 mass transfer kinetics would have the biggest impact on reducing the cost (~27% reduction). With faster kinetics, shorter could be achieved, which reduces the cost of capture. The thermal energy demand can also be seen to reduce as hypothesized. However, case study C shows that the improvements to the kinetics of the sorbent should not be made at the expense of the CO2 uptake capacity. Case study D shows that combining faster sorbents with waste heat utilization could lower the cost of capture by ~54%. Finally, case study E shows that an 8% reduction in cost can be achieved by using less hygroscopic sorbents, which can be attributed to the reduced thermal energy requirement. Although the costs for these case studies are still quite high, these give an indication of the relative impact each modification could have on the economics of the process.
6. Conclusions
A process model was proposed, for a DAC process employing a S-TVSA cycle, and validated with laboratory experimental results. To evaluate the technoeconomic performance of the process, the model was subjected to a MOO with the objectives of minimizing the cost of capture and maximizing the amount of CO2 captured. A minimum cost of capture of 612 USD tonne−1 was calculated for a process with air entering at 25 °C under dry conditions, and a cost of 657 USD tonne−1 was calculated for air entering at 22 °C and 39% RH. The humid case yielded higher costs than the dry case, as an effect of the additional energy required to desorb the water that gets co-adsorbed on the sorbent. While the dry case yielded the lower cost, it is noted that the humid case is more realistic for practical DAC systems, and that the inlet air conditions correspond to that typical of subtropical climates. It was observed that the capture rate of the process could be increased (at the expense of a higher cost of capture) by increasing the number of contactors, using more aggressive desorption conditions and changing the cycle times. The process variables which had the most effect on the results were identified as the steam flow rate and the number of contactors. The relatively higher costs calculated here, in comparison to the results of prior studies, were identified to be a result of the differences in the assumptions and scope of the respective studies, and the slower kinetics of the sorbent evaluated in the current study. It was identified that using a sorbent with two-fold faster kinetics could reduce the cost by ~27% and that the utilization of waste heat could produce a ~42% reduction in cost. A combination of both would allow the cost to be reduced by ~54%.
In summary, the process evaluated in this study does not appear to be economically feasible in the current state. However, the study identified several avenues which could lead to improvements. Of these, the improvements in sorbent design suggested here could realistically be achieved even with the current state of the technology. However, further research is needed for areas such as the development of low-cost contactors. If a combination of these improvements is achieved, this DAC process has the potential to be economically feasible and a valuable tool for combatting climate change in the future.