Towards the Grand Unification of Process Design, Scheduling, and Control—Utopia or Reality?
Abstract
1. Introduction
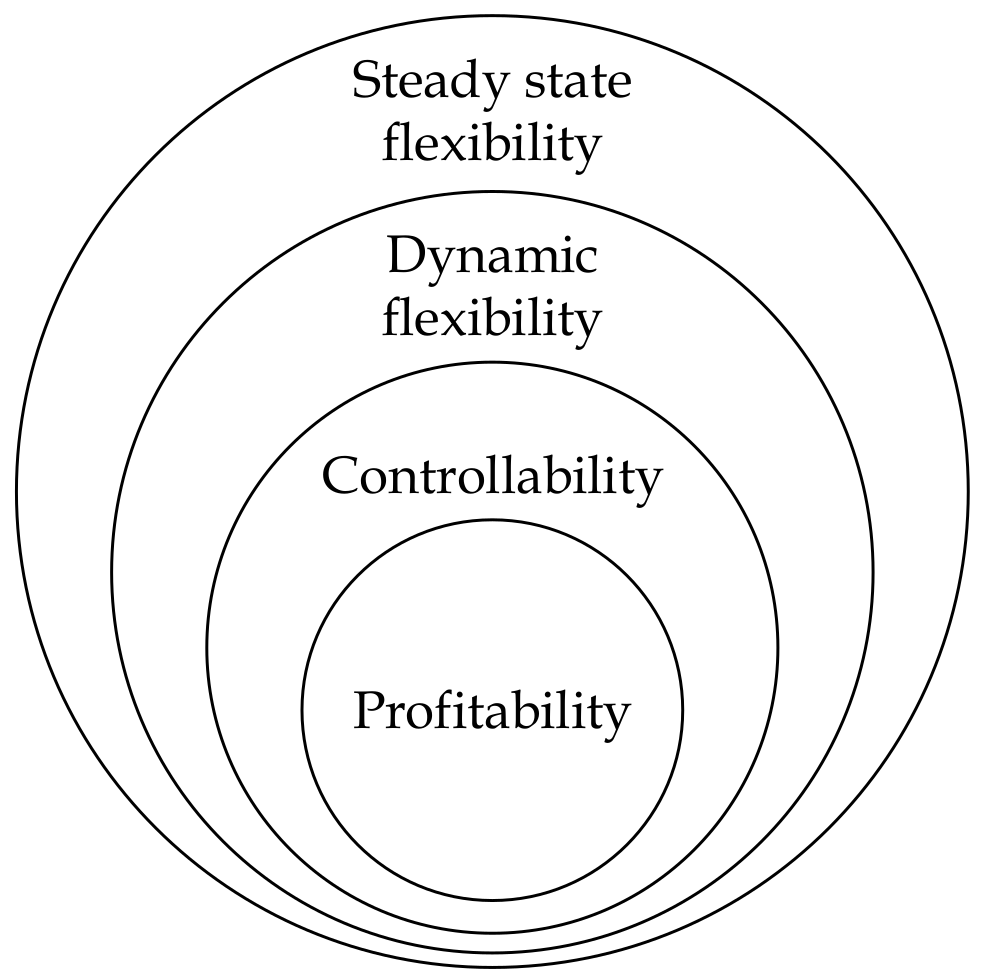
- Flexibility analysis and flexibility index. The early stages for design optimization under uncertainty. The studies here analyze the steady-state feasibility of a nominal process design under a set of unknown process parameters and unrealized operating decisions, as we will discuss in Section 2.
- Dynamic resilience and controllability analysis. Here, the researchers investigate the dynamic response of a system in closed loop, its interdependence with process design, and attempt to develop the “perfect controller” simultaneously the process that the controller can act on. Such attempts will be demonstrated in Section 3.
- Complete integration of design, control, and operational policies. The focus of the most recent studies in the field. The goal is to model tractable dynamic design optimization problems that account for the scheduling and control decisions to guarantee the operability and even profitability of the operation under all foreseeable conditions. These approaches will be discussed in Section 4.
2. Early Efforts in Design Optimization under Uncertainty
3. Integration of Process Control in Design Optimization
4. Towards the Grand Unification of Process Design, Scheduling, and Control
5. Current Challenges and Future Directions
5.1. The Need for an Industrial Benchmark Problem
- A high-fidelity model that describes the dynamics of the process. The model should feature appropriate design variables to exhibit the dynamic consequences of scaling up/down the process. Furthermore, considering the reduction in capital investment that the multipurpose and multiproduct operating units provide, the process should comprise such units to examine the scheduling/design and scheduling/control trade-offs. Recent research that consider process design, scheduling, and closed-loop control problems simultaneously [3,5,6] have studied only a single processing unit, which reflects a limited fraction of the overall benefit that the grand unification can provide.
- Cost relations for investment, utility, and raw materials. A functional form of the investment cost with respect to the capacity of the process is required to have standardized comparable results. Also, utility costs and raw materials may vary significantly, which inevitably impacts the optimal scheduling decisions. For instance, grid electricity costs are known to exhibit considerable differences during the day and night times. Thus, operational loads in energy intensive processes may fluctuate heavily. The impact of such changes in operating levels on design and control decisions were discussed in Section 3.
- Product demand and availability of the utility, raw materials, and operating units over a time horizon. Production allocation and timing is a key aspect of scheduling problem, which are heavily dictated by the product demand and availability of resources. However, it is not a trivial practice to estimate the future of these quantities. Therefore, probability distributions of these components will be beneficial to determine their expected values, while being able to take into account their worst-case scenarios.
5.2. Robust Advanced Control and Scheduling Strategies
5.3. Considering Flowsheet Optimization, Process Intensification, and Modular Design Opportunities
5.4. Theoretical and Algorithmic Developments in MIDO
5.5. Software Development
Author Contributions
Funding
Conflicts of Interest
References
- Sargent, R.W.H. Integrated design and optimization of processes. Chem. Eng. Prog. 1967, 63, 71–78. [Google Scholar]
- Terrazas-Moreno, S.; Flores-Tlacuahuac, A.; Grossmann, I.E. Simultaneous design, scheduling, and optimal control of a methyl-methacrylate continuous polymerization reactor. AIChE J. 2008, 54, 3160–3170. [Google Scholar] [CrossRef]
- Patil, B.P.; Maia, E.; Ricardez-sandoval, L.A. Integration of Scheduling, Design, and Control of Multiproduct Chemical Processes Under Uncertainty. AIChE J. 2015, 61. [Google Scholar] [CrossRef]
- Koller, R.W.; Ricardez-Sandoval, L.A. A dynamic optimization framework for integration of design, control and scheduling of multi-product chemical processes under disturbance and uncertainty. Comput. Chem. Eng. 2017, 106, 147–159. [Google Scholar] [CrossRef]
- Koller, R.W.; Ricardez-Sandoval, L.A.; Biegler, L.T. Stochastic back-off algorithm for simultaneous design, control, and scheduling of multiproduct systems under uncertainty. AIChE J. 2018, 64, 2379–2389. [Google Scholar] [CrossRef]
- Burnak, B.; Diangelakis, N.A.; Katz, J.; Pistikopoulos, E.N. Integrated process design, scheduling, and control using multiparametric programming. Comput. Chem. Eng. 2019, 125, 164–184. [Google Scholar] [CrossRef]
- Takamatsu, T.; Hashimoto, I.; Ohno, H. Optimal Design of a Large Complex System from the Viewpoint of Sensitivity Analysis. Ind. Eng. Chem. Process Des. Dev. 1970, 9, 368–379. [Google Scholar] [CrossRef]
- Nishida, N.; Ichikawa, A.; Tazaki, E. Synthesis of Optimal Process Systems with Uncertainty. Ind. Eng. Chem. Process Des. Dev. 1974, 13, 209–214. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Sargent, R.W.H. Optimum design of chemical plants with uncertain parameters. AIChE J. 1978, 24, 1021–1028. [Google Scholar] [CrossRef]
- Kwak, B.M.; Haug, E.J. Optimum design in the presence of parametric uncertainty. J. Optim. Theory Appl. 1976, 19, 527–546. [Google Scholar] [CrossRef]
- Halemane, K.P.; Grossmann, I.E. Optimal process design under uncertainty. AIChE J. 1983, 29, 425–433. [Google Scholar] [CrossRef]
- Swaney, R.E.; Grossmann, I.E. An index for operational flexibility in chemical process design. Part I: Formulation and theory. AIChE J. 1985, 31, 621–630. [Google Scholar] [CrossRef]
- Swaney, R.E.; Grossmann, I.E. An index for operational flexibility in chemical process design. Part II: Computational algorithms. AIChE J. 1985, 31, 631–641. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Floudas, C.A. Active constraint strategy for flexibility analysis in chemical processes. Comput. Chem. Eng. 1987, 11, 675–693. [Google Scholar] [CrossRef]
- Floudas, C.A.; Grossmann, I.E. Synthesis of flexible heat exchanger networks with uncertain flowrates and temperatures. Comput. Chem. Eng. 1987, 11, 319–336. [Google Scholar] [CrossRef]
- Shimizu, Y. A plain approach for dealing with flexibility problems in linear systems. Comput. Chem. Eng. 1989, 13, 1189–1191. [Google Scholar] [CrossRef]
- Shimizu, Y. Application of flexibility analysis for compromise solution in large-scale linear systems. J. Chem. Eng. Jpn. 1989, 22, 189–194. [Google Scholar] [CrossRef][Green Version]
- Bansal, V.; Perkins, J.D.; Pistikopoulos, E.N. Flexibility analysis and design of linear systems by parametric programming. AIChE J. 2000, 46, 335–354. [Google Scholar] [CrossRef]
- Pistikopoulos, E.N.; Grossmann, I.E. Optimal retrofit design for improving process flexibility in linear systems. Comput. Chem. Eng. 1988, 12, 719–731. [Google Scholar] [CrossRef]
- Pistikopoulos, E.N.; Grossmann, I.E. Stochastic optimization of flexibility in retrofit design of linear systems. Comput. Chem. Eng. 1988, 12, 1215–1227. [Google Scholar] [CrossRef]
- Pistikopoulos, E.N.; Grossmann, I.E. Optimal retrofit design for improving process flexibility in nonlinear systems—I. Fixed degree of flexibility. Comput. Chem. Eng. 1989, 13, 1003–1016. [Google Scholar] [CrossRef]
- Pistikopoulos, E.N.; Grossmann, I.E. Optimal retrofit design for improving process flexibility in nonlinear systems—II. Optimal level of flexibility. Comput. Chem. Eng. 1989, 13, 1087–1096. [Google Scholar] [CrossRef]
- Pistikopoulos, E.N.; Grossmann, I.E. Evaluation and redesign for improving flexibility in linear systems with infeasible nominal conditions. Comput. Chem. Eng. 1988, 12, 841–843. [Google Scholar] [CrossRef]
- Raspanti, C.; Bandoni, J.; Biegler, L. New strategies for flexibility analysis and design under uncertainty. Comput. Chem. Eng. 2000, 24, 2193–2209. [Google Scholar] [CrossRef]
- Kreisselmeier, G.; Steinhauser, R. Systematic Control Design by Optimizing a Vector Performance Index. In Computer Aided Design of Control Systems; Cuenod, M., Ed.; Pergamon: Oxford, UK, 1980; pp. 113–117. [Google Scholar] [CrossRef]
- Chen, C.; Mangasarian, O.L. A class of smoothing functions for nonlinear and mixed complementarity problems. Comput. Optim. Appl. 1996, 5, 97–138. [Google Scholar] [CrossRef]
- Pistikopoulos, E.N.; Mazzuchi, T.A. A novel flexibility analysis approach for processes with stochastic parameters. Comput. Chem. Eng. 1990, 14, 991–1000. [Google Scholar] [CrossRef]
- Straub, D.A.; Grossmann, I.E. Integrated stochastic metric of flexibility for systems with discrete state and continuous parameter uncertainties. Comput. Chem. Eng. 1990, 14, 967–985. [Google Scholar] [CrossRef]
- Straub, D.A.; Grossmann, I.E. Design optimization of stochastic flexibility. Comput. Chem. Eng. 1993, 17, 339–354. [Google Scholar] [CrossRef]
- Dimitriadis, V.D.; Pistikopoulos, E.N. Flexibility Analysis of Dynamic Systems. Ind. Eng. Chem. Res. 1995, 34, 4451–4462. [Google Scholar] [CrossRef]
- Zhou, H.; Li, X.; Qian, Y.; Chen, Y.; Kraslawski, A. Optimizing the Initial Conditions to Improve the Dynamic Flexibility of Batch Processes. Ind. Eng. Chem. Res. 2009, 48, 6321–6326. [Google Scholar] [CrossRef]
- Mohideen, M.J.; Perkins, J.D.; Pistikopoulos, E.N. Optimal design of dynamic systems under uncertainty. AIChE J. 1996, 42, 2251–2272. [Google Scholar] [CrossRef]
- Mohideen, M.J.; Perkins, J.D.; Pistikopoulos, E.N. Optimal synthesis and design of dynamic systems under uncertainty. Comput. Chem. Eng. 1996, 20, S895–S900. [Google Scholar] [CrossRef]
- Mohideen, M.J.; Perkins, J.D.; Pistikopoulos, E.N. Robust stability considerations in optimal design of dynamic systems under uncertainty. J. Process Control 1997, 7, 371–385. [Google Scholar] [CrossRef]
- Pretoro, A.D.; Montastruc, L.; Manenti, F.; Joulia, X. Flexibility analysis of a distillation column: Indexes comparison and economic assessment. Comput. Chem. Eng. 2019, 124, 93–108. [Google Scholar] [CrossRef]
- Zhu, Y.; Legg, S.; Laird, C.D. Optimal design of cryogenic air separation columns under uncertainty. Comput. Chem. Eng. 2010, 34, 1377–1384. [Google Scholar] [CrossRef]
- Huang, W.; Li, X.; Yang, S.; Qian, Y. Dynamic flexibility analysis of chemical reaction systems with time delay: Using a modified finite element collocation method. Chem. Eng. Res. Des. 2011, 89, 1938–1946. [Google Scholar] [CrossRef]
- Konukman, A.E.S.; Çamurdan, M.C.; Akman, U. Simultaneous flexibility targeting and synthesis of minimum-utility heat-exchanger networks with superstructure-based MILP formulation. Chem. Eng. Process. Process Intensif. 2002, 41, 501–518. [Google Scholar] [CrossRef]
- Konukman, A.E.S.; Akman, U. Flexibility and operability analysis of a HEN-integrated natural gas expander plant. Chem. Eng. Sci. 2005, 60, 7057–7074. [Google Scholar] [CrossRef]
- Escobar, M.; Trierweiler, J.O.; Grossmann, I.E. Simultaneous synthesis of heat exchanger networks with operability considerations: Flexibility and controllability. Comput. Chem. Eng. 2013, 55, 158–180. [Google Scholar] [CrossRef]
- Varvarezos, D.K.; Grossmann, I.E.; Biegler, L.T. An outer-approximation method for multiperiod design optimization. Ind. Eng. Chem. Res. 1992, 31, 1466–1477. [Google Scholar] [CrossRef]
- Pistikopoulos, E.; Ierapetritou, M. Novel approach for optimal process design under uncertainty. Comput. Chem. Eng. 1995, 19, 1089–1110. [Google Scholar] [CrossRef]
- Morari, M. Design of resilient processing plants—III: A general framework for the assessment of dynamic resilience. Chem. Eng. Sci. 1983, 38, 1881–1891. [Google Scholar] [CrossRef]
- Morari, M. Flexibility and resiliency of process systems. Comput. Chem. Eng. 1983, 7, 423–437. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Morari, M. Operability, Resiliency, and Flexibility: Process Design Objectives for a Changing World; Carnegie-Mellon University: Pittsburgh, PA, USA, 1983. [Google Scholar] [CrossRef]
- Morari, M.; Grimm, W.; Oglesby, M.J.; Prosser, I.D. Design of resilient processing plants—VII. Design of energy management system for unstable reactors—New insights. Chem. Eng. Sci. 1985, 40, 187–198. [Google Scholar] [CrossRef]
- Palazoglu, A.; Manousiouthakis, B.; Arkun, Y. Design of chemical plants with improved dynamic operability in an environment of uncertainty. Ind. Eng. Chem. Process Des. Dev. 1985, 24, 802–813. [Google Scholar] [CrossRef]
- Palazoglu, A.; Arkun, Y. A multiobjective approach to design chemical plants with robust dynamic operability characteristics. Comput. Chem. Eng. 1986, 10, 567–575. [Google Scholar] [CrossRef]
- Skogestad, S.; Morari, M. Design of resilient processing plants-IX. Effect of model uncertainty on dynamic resilience. Chem. Eng. Sci. 1987, 42, 1765–1780. [Google Scholar] [CrossRef]
- Colberg, R.D.; Morari, M.; Townsend, D.W. A Resilience target for heat exchanger network synthesis. Comput. Chem. Eng. 1989, 13, 821–837. [Google Scholar] [CrossRef]
- Perkins, J.D.; Wong, M.P.F. Assessing controllability of chemical plants. Chem. Eng. Res. Des. 1985, 63, 358–362. [Google Scholar]
- Rosenbrock, H.H. State-Space and Multivariable Theory; Studies in Dynamical Systems Series; Wiley Interscience Division: Hoboken, NJ, USA, 1970. [Google Scholar]
- Psarris, P.; Floudas, C.A. Improving dynamic operability in mimo systems with time delays. Chem. Eng. Sci. 1990, 45, 3505–3524. [Google Scholar] [CrossRef]
- Psarris, P.; Floudas, C.A. Dynamic operability of mimo systems with time delays and transmission zeroes—I. Assessment. Chem. Eng. Sci. 1991, 46, 2691–2707. [Google Scholar] [CrossRef]
- Psarris, P.; Floudas, C.A. Dynamic operability of mimo systems with time delays and transmission zeroes—II. Enhancement. Chem. Eng. Sci. 1991, 46, 2709–2728. [Google Scholar] [CrossRef]
- Barton, G.W.; Chan, W.K.; Perkins, J.D. Interaction between process design and process control: The role of open-loop indicators. J. Process Control 1991, 1, 161–170. [Google Scholar] [CrossRef]
- Narraway, L.T.; Perkins, J.D.; Barton, G.W. Interaction between process design and process control: Economic analysis of process dynamics. J. Process Control 1991, 1, 243–250. [Google Scholar] [CrossRef]
- Narraway, L.; Perkins, J. Selection of process control structure based on economics. Comput. Chem. Eng. 1994, 18, S511–S515. [Google Scholar] [CrossRef]
- Bahri, P.; Bandoni, J.; Barton, G.; Romagnoli, J. Back-off calculations in optimising control: A dynamic approach. Comput. Chem. Eng. 1995, 19, 699–708. [Google Scholar] [CrossRef]
- Walsh, S.; Perkins, J. Integrated Design of Effluent Treatment Systems. IFAC Proc. Vol. 1992, 25, 107–112. [Google Scholar] [CrossRef]
- Luyben, M.L.; Floudas, C.A. A Multiobjective Optimization Approach for Analyzing the Interaction of Design and Control. IFAC Proc. Vol. 1992, 25, 101–106. [Google Scholar] [CrossRef]
- Shah, N.; Pantelides, C.C.; Sargent, R.W.H. The Design and Scheduling of Multipurpose Batch Plants. IFAC Proc. Vol. 1992, 25, 203–208. [Google Scholar] [CrossRef]
- Kondili, E.; Pantelides, C.C.; Sargent, R.W.H. A general algorithm for short-term scheduling of batch operations—I. MILP formulation. Comput. Chem. Eng. 1993, 17, 211–227. [Google Scholar] [CrossRef]
- Thomaidis, T.V.; Pistikopoulos, E.N. Design of Flexible and Reliable Process Systems. IFAC Proc. Vol. 1992, 25, 235–240. [Google Scholar] [CrossRef]
- Walsh, S.; Perkins, J. Application of integrated process and control system design to waste water neutralisation. Comput. Chem. Eng. 1994, 18, S183–S187. [Google Scholar] [CrossRef]
- Narraway, L.T.; Perkins, J.D. Selection of process control structure based on linear dynamic economics. Ind. Eng. Chem. Res. 1993, 32, 2681–2692. [Google Scholar] [CrossRef]
- Luyben, M.L.; Floudas, C.A. Analyzing the interaction of design and control—1. A multiobjective framework and application to binary distillation synthesis. Comput. Chem. Eng. 1994, 18, 933–969. [Google Scholar] [CrossRef]
- Luyben, M.L.; Fluodas, C.A. Analyzing the interaction of design and control—2. reactor-separator-recycle system. Comput. Chem. Eng. 1994, 18, 971–993. [Google Scholar] [CrossRef]
- Bansal, V.; Perkins, J.D.; Pistikopoulos, E.; Ross, R.; van Schijndel, J.M.G. Simultaneous design and control optimisation under uncertainty. Comput. Chem. Eng. 2000, 24, 261–266. [Google Scholar] [CrossRef]
- Sandoval, L.A.R.; Budman, H.M.; Douglas, P.L. Simultaneous design and control of processes under uncertainty: A robust modelling approach. J. Process Control 2008, 18, 735–752. [Google Scholar] [CrossRef]
- Ricardez-Sandoval, L.A.; Budman, H.M.; Douglas, P.L. Application of Robust Control Tools to the Simultaneous Design and Control of Dynamic Systems. Ind. Eng. Chem. Res. 2009, 48, 801–813. [Google Scholar] [CrossRef]
- Ricardez-Sandoval, L.A.; Budman, H.M.; Douglas, P.L. Simultaneous design and control of chemical processes with application to the Tennessee Eastman process. J. Process Control 2009, 19, 1377–1391. [Google Scholar] [CrossRef]
- Kookos, I.K.; Perkins, J.D. Control structure selection based on economics: Generalization of the back-off methodology. AIChE J. 2016, 62, 3056–3064. [Google Scholar] [CrossRef]
- Mehta, S.; Ricardez-Sandoval, L.A. Integration of Design and Control of Dynamic Systems under Uncertainty: A New Back-Off Approach. Ind. Eng. Chem. Res. 2016, 55, 485–498. [Google Scholar] [CrossRef]
- Rafiei-Shishavan, M.; Mehta, S.; Ricardez-Sandoval, L.A. Simultaneous design and control under uncertainty: A back-off approach using power series expansions. Comput. Chem. Eng. 2017, 99, 66–81. [Google Scholar] [CrossRef]
- Rafiei, M.; Ricardez-Sandoval, L.A. Stochastic Back-Off Approach for Integration of Design and Control under Uncertainty. Ind. Eng. Chem. Res. 2018, 57, 4351–4365. [Google Scholar] [CrossRef]
- Kookos, I.K.; Perkins, J.D. An Algorithm for Simultaneous Process Design and Control. Ind. Eng. Chem. Res. 2001, 40, 4079–4088. [Google Scholar] [CrossRef]
- Malcolm, A.; Polan, J.; Zhang, L.; Ogunnaike, B.A.; Linninger, A.A. Integrating systems design and control using dynamic flexibility analysis. AIChE J. 2007, 53, 2048–2061. [Google Scholar] [CrossRef]
- Moon, J.; Kim, S.; Linninger, A.A. Integrated design and control under uncertainty: Embedded control optimization for plantwide processes. Comput. Chem. Eng. 2011, 35, 1718–1724. [Google Scholar] [CrossRef]
- Qin, S.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Brengel, D.D.; Seider, W.D. Coordinated design and control optimization of nonlinear processes. Comput. Chem. Eng. 1992, 16, 861–886. [Google Scholar] [CrossRef]
- Bemporad, A.; Morari, M.; Dua, V.; Pistikopoulos, E.N. The explicit linear quadratic regulator for constrained systems. Automatica 2002, 38, 3–20. [Google Scholar] [CrossRef]
- Sakizlis, V.; Perkins, J.D.; Pistikopoulos, E.N. Parametric Controllers in Simultaneous Process and Control Design Optimization. Ind. Eng. Chem. Res. 2003, 42, 4545–4563. [Google Scholar] [CrossRef]
- Diangelakis, N.A.; Burnak, B.; Katz, J.; Pistikopoulos, E.N. Process design and control optimization: A simultaneous approach by multi-parametric programming. AIChE J. 2017, 63, 4827–4846. [Google Scholar] [CrossRef]
- Diangelakis, N.A.; Pistikopoulos, E.N. A multi-scale energy systems engineering approach to residential combined heat and power systems. Comput. Chem. Eng. 2017, 102, 128–138. [Google Scholar] [CrossRef]
- Sanchez-Sanchez, K.B.; Ricardez-Sandoval, L.A. Simultaneous Design and Control under Uncertainty Using Model Predictive Control. Ind. Eng. Chem. Res. 2013, 52, 4815–4833. [Google Scholar] [CrossRef]
- Birewar, D.B.; Grossmann, I.E. Incorporating scheduling in the optimal design of multiproduct batch plants. Comput. Chem. Eng. 1989, 13, 141–161. [Google Scholar] [CrossRef]
- White, V.; Perkins, J.; Espie, D. Switchability analysis. Comput. Chem. Eng. 1996, 20, 469–474. [Google Scholar] [CrossRef]
- Bhatia, T.; Biegler, L.T. Dynamic Optimization in the Design and Scheduling of Multiproduct Batch Plants. Ind. Eng. Chem. Res. 1996, 35, 2234–2246. [Google Scholar] [CrossRef]
- Bhatia, T.K.; Biegler, L.T. Dynamic Optimization for Batch Design and Scheduling with Process Model Uncertainty. Ind. Eng. Chem. Res. 1997, 36, 3708–3717. [Google Scholar] [CrossRef]
- Baldea, M.; Harjunkoski, I. Integrated production scheduling and process control: A systematic review. Comput. Chem. Eng. 2014, 71, 377–390. [Google Scholar] [CrossRef]
- Mahadevan, R.; Doyle, F.J.; Allcock, A.C. Control-relevant scheduling of polymer grade transitions. AIChE J. 2002, 48, 1754–1764. [Google Scholar] [CrossRef]
- Chatzidoukas, C.; Perkins, J.; Pistikopoulos, E.; Kiparissides, C. Optimal grade transition and selection of closed-loop controllers in a gas-phase olefin polymerization fluidized bed reactor. Chem. Eng. Sci. 2003, 58, 3643–3658. [Google Scholar] [CrossRef]
- Flores-Tlacuahuac, A.; Grossmann, I.E. Simultaneous Cyclic Scheduling and Control of a Multiproduct CSTR. Ind. Eng. Chem. Res. 2006, 45, 6698–6712. [Google Scholar] [CrossRef]
- Terrazas-Moreno, S.; Flores-Tlacuahuac, A.; Grossmann, I.E. Simultaneous cyclic scheduling and optimal control of polymerization reactors. AIChE J. 2007, 53, 2301–2315. [Google Scholar] [CrossRef]
- Flores-Tlacuahuac, A.; Grossmann, I.E. Simultaneous Cyclic Scheduling and Control of Tubular Reactors: Single Production Lines. Ind. Eng. Chem. Res. 2010, 49, 11453–11463. [Google Scholar] [CrossRef]
- Flores-Tlacuahuac, A.; Grossmann, I.E. Simultaneous Cyclic Scheduling and Control of Tubular Reactors: Parallel Production Lines. Ind. Eng. Chem. Res. 2011, 50, 8086–8096. [Google Scholar] [CrossRef]
- Zhuge, J.; Ierapetritou, M.G. Integration of Scheduling and Control with Closed Loop Implementation. Ind. Eng. Chem. Res. 2012, 51, 8550–8565. [Google Scholar] [CrossRef]
- Gutiérrez-Limón, M.A.; Flores-Tlacuahuac, A.; Grossmann, I.E. MINLP Formulation for Simultaneous Planning, Scheduling, and Control of Short-Period Single-Unit Processing Systems. Ind. Eng. Chem. Res. 2014, 53, 14679–14694. [Google Scholar] [CrossRef]
- Du, J.; Park, J.; Harjunkoski, I.; Baldea, M. A time scale-bridging approach for integrating production scheduling and process control. Comput. Chem. Eng. 2015, 79, 59–69. [Google Scholar] [CrossRef]
- Baldea, M.; Du, J.; Park, J.; Harjunkoski, I. Integrated production scheduling and model predictive control of continuous processes. AIChE J. 2015, 61, 4179–4190. [Google Scholar] [CrossRef]
- Burnak, B.; Katz, J.; Diangelakis, N.A.; Pistikopoulos, E.N. Simultaneous Process Scheduling and Control: A Multiparametric Programming-Based Approach. Ind. Eng. Chem. Res. 2018, 57, 3963–3976. [Google Scholar] [CrossRef]
- Charitopoulos, V.M.; Papageorgiou, L.G.; Dua, V. Closed-loop integration of planning, scheduling and multi-parametric nonlinear control. Comput. Chem. Eng. 2019, 122, 172–192. [Google Scholar] [CrossRef]
- Loeblein, C.; Perkins, J.D. Structural design for on-line process optimization: I. Dynamic economics of MPC. AIChE J. 1999, 45, 1018–1029. [Google Scholar] [CrossRef]
- Zanin, A.C.; de Gouvêa, M.T.; Odloak, D. Integrating real-time optimization into the model predictive controller of the FCC system. Control Eng. Pract. 2002, 10, 819–831. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Amrit, R. Optimizing Process Economic Performance Using Model Predictive Control. In Nonlinear Model Predictive Control: Towards New Challenging Applications; Magni, L., Raimondo, D.M., Allgöwer, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 119–138. [Google Scholar] [CrossRef]
- Amrit, R.; Rawlings, J.B.; Angeli, D. Economic optimization using model predictive control with a terminal cost. Annu. Rev. Control 2011, 35, 178–186. [Google Scholar] [CrossRef]
- Würth, L.; Hannemann, R.; Marquardt, W. A two-layer architecture for economically optimal process control and operation. J. Process Control 2011, 21, 311–321. [Google Scholar] [CrossRef]
- Ellis, M.; Christofides, P.D. Selection of control configurations for economic model predictive control systems. AIChE J. 2014, 60, 3230–3242. [Google Scholar] [CrossRef]
- Jamaludin, M.Z.; Swartz, C.L.E. Dynamic real-time optimization with closed-loop prediction. AIChE J. 2017, 63, 3896–3911. [Google Scholar] [CrossRef]
- Li, H.; Swartz, C.L.E. Dynamic real-time optimization of distributed MPC systems using rigorous closed-loop prediction. Comput. Chem. Eng. 2019, 122, 356–371. [Google Scholar] [CrossRef]
- Simkoff, J.M.; Baldea, M. Production scheduling and linear MPC: Complete integration via complementarity conditions. Comput. Chem. Eng. 2019, 125, 287–305. [Google Scholar] [CrossRef]
- Downs, J.; Vogel, E. A plant-wide industrial process control problem. Comput. Chem. Eng. 1993, 17, 245–255. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Sargent, R.W.H. Optimum design of heat exchanger networks. Comput. Chem. Eng. 1978, 2, 1–7. [Google Scholar] [CrossRef]
- Nishida, N.; Stephanopoulos, G.; Westerberg, A.W. A review of process synthesis. AIChE J. 1981, 27, 321–351. [Google Scholar] [CrossRef]
- Papalexandri, K.P.; Pistikopoulos, E.N. Generalized modular representation framework for process synthesis. AIChE J. 1996, 42, 1010–1032. [Google Scholar] [CrossRef]
- Demirel, S.E.; Li, J.; Hasan, M.M.F. Systematic process intensification using building blocks. Comput. Chem. Eng. 2017, 105, 2–38. [Google Scholar] [CrossRef]
- Tula, A.K.; Babi, D.K.; Bottlaender, J.; Eden, M.R.; Gani, R. A computer-aided software-tool for sustainable process synthesis-intensification. Comput. Chem. Eng. 2017, 105, 74–95. [Google Scholar] [CrossRef]
- da Cruz, F.E.; Manousiouthakis, V.I. Process intensification of reactive separator networks through the IDEAS conceptual framework. Comput. Chem. Eng. 2017, 105, 39–55. [Google Scholar] [CrossRef]
- Tian, Y.; Pistikopoulos, E.N. Synthesis of Operable Process Intensification Systems—Steady-State Design with Safety and Operability Considerations. Ind. Eng. Chem. Res. 2019, 58, 6049–6068. [Google Scholar] [CrossRef]
- Demirel, S.E.; Li, J.; Hasan, M.M.F. Systematic process intensification. Curr. Opin. Chem. Eng. 2019. [Google Scholar] [CrossRef]
- Demirel, S.E.; Li, J.; Hasan, M.M.F. A General Framework for Process Synthesis, Integration, and Intensification. Ind. Eng. Chem. Res. 2019, 58, 5950–5967. [Google Scholar] [CrossRef]
- Tian, Y.; Demirel, S.E.; Hasan, M.M.F.; Pistikopoulos, E.N. An overview of process systems engineering approaches for process intensification: State of the art. Chem. Eng. Process. Process Intensif. 2018, 133, 160–210. [Google Scholar] [CrossRef]
- Baldea, M. From process integration to process intensification. Comput. Chem. Eng. 2015, 81, 104–114. [Google Scholar] [CrossRef]
- Tian, Y.; Pistikopoulos, E.N. Synthesis of operable process intensification systems: Advances and challenges. Curr. Opin. Chem. Eng. 2019. [Google Scholar] [CrossRef]
- Dias, L.S.; Ierapetritou, M.G. Optimal operation and control of intensified processes—Challenges and opportunities. Curr. Opin. Chem. Eng. 2019. [Google Scholar] [CrossRef]
- Pistikopoulos, E.N.; Diangelakis, N.A.; Oberdieck, R.; Papathanasiou, M.M.; Nascu, I.; Sun, M. PAROC—An integrated framework and software platform for the optimisation and advanced model-based control of process systems. Chem. Eng. Sci. 2015, 136, 115–138. [Google Scholar] [CrossRef]
- Diangelakis, N.; Burnak, B.; Pistikopoulos, E. A multi-parametric programming approach for the simultaneous process scheduling and control—Application to a domestic cogeneration unit. In Proceedings of the Chemical Process Control 2017, Tucson, AZ, USA, 8–12 January 2017; pp. 8–12. [Google Scholar]
- Pistikopoulos, E.N.; Diangelakis, N.A. Towards the integration of process design, control and scheduling: Are we getting closer? Comput. Chem. Eng. 2016, 91, 85–92. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burnak, B.; Diangelakis, N.A.; Pistikopoulos, E.N. Towards the Grand Unification of Process Design, Scheduling, and Control—Utopia or Reality? Processes 2019, 7, 461. https://doi.org/10.3390/pr7070461
Burnak B, Diangelakis NA, Pistikopoulos EN. Towards the Grand Unification of Process Design, Scheduling, and Control—Utopia or Reality? Processes. 2019; 7(7):461. https://doi.org/10.3390/pr7070461
Chicago/Turabian StyleBurnak, Baris, Nikolaos A. Diangelakis, and Efstratios N. Pistikopoulos. 2019. "Towards the Grand Unification of Process Design, Scheduling, and Control—Utopia or Reality?" Processes 7, no. 7: 461. https://doi.org/10.3390/pr7070461
APA StyleBurnak, B., Diangelakis, N. A., & Pistikopoulos, E. N. (2019). Towards the Grand Unification of Process Design, Scheduling, and Control—Utopia or Reality? Processes, 7(7), 461. https://doi.org/10.3390/pr7070461




