Modelling Hydration Swelling and Weakening of Montmorillonite Particles in Mudstone
Abstract
1. Introduction
2. Characterisation of Mudstone
2.1. Sample Collection
2.2. Characterisation
2.2.1. X-ray Powder Diffraction (XRD)
2.2.2. Field-Emission Scanning Electron Microscopy (FE-SEM)
2.2.3. Assumptions Used to Describe Mudstone
3. Experiments
4. Results
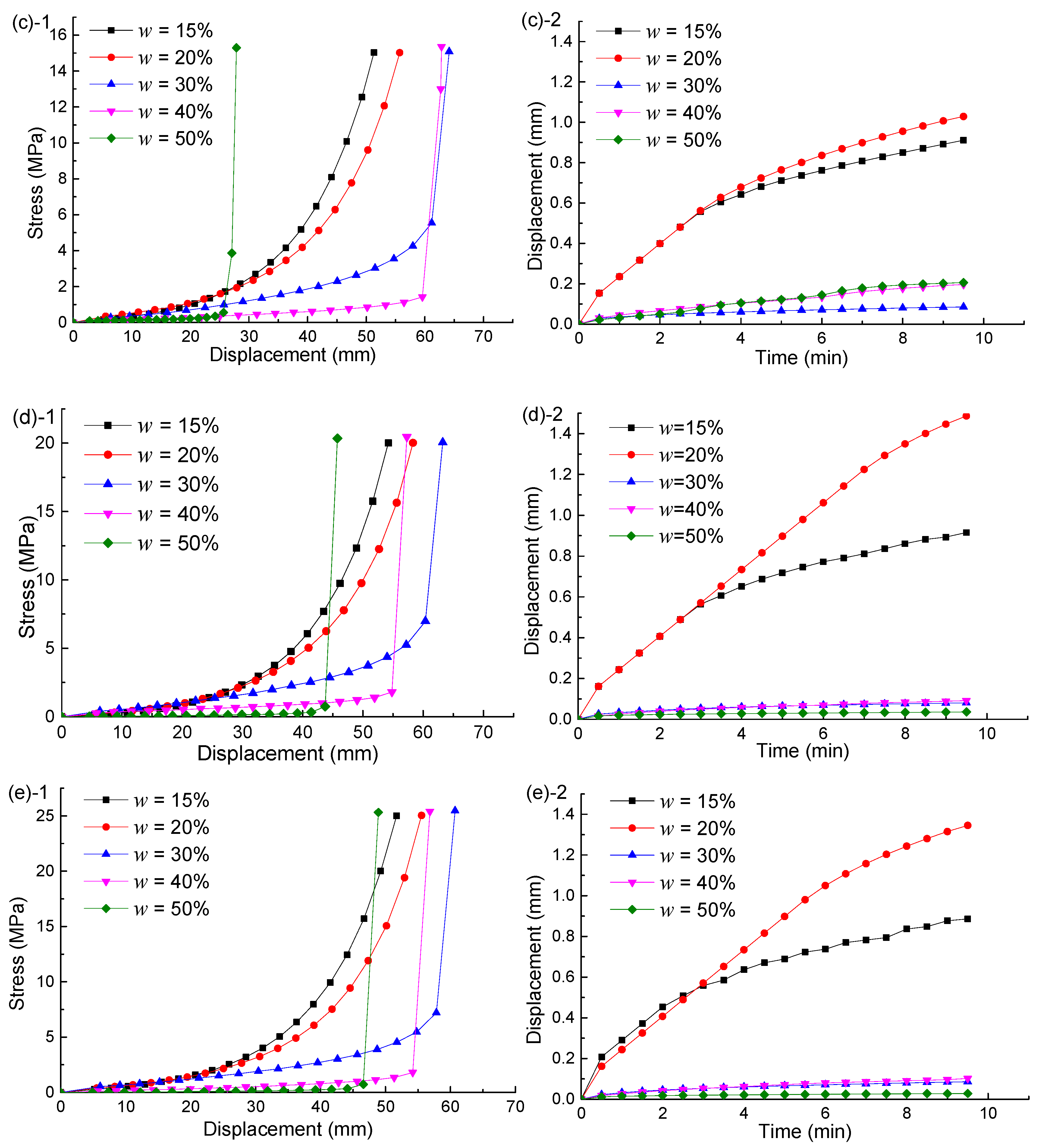
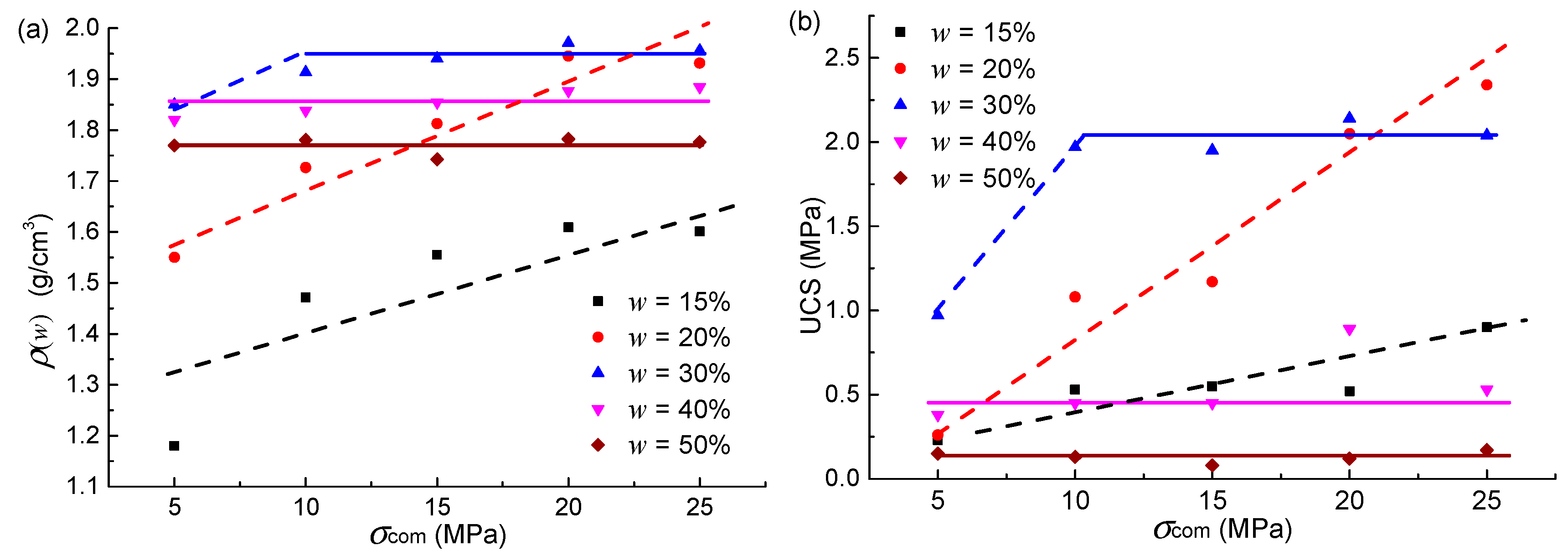
4.1. Compacted Testing Results
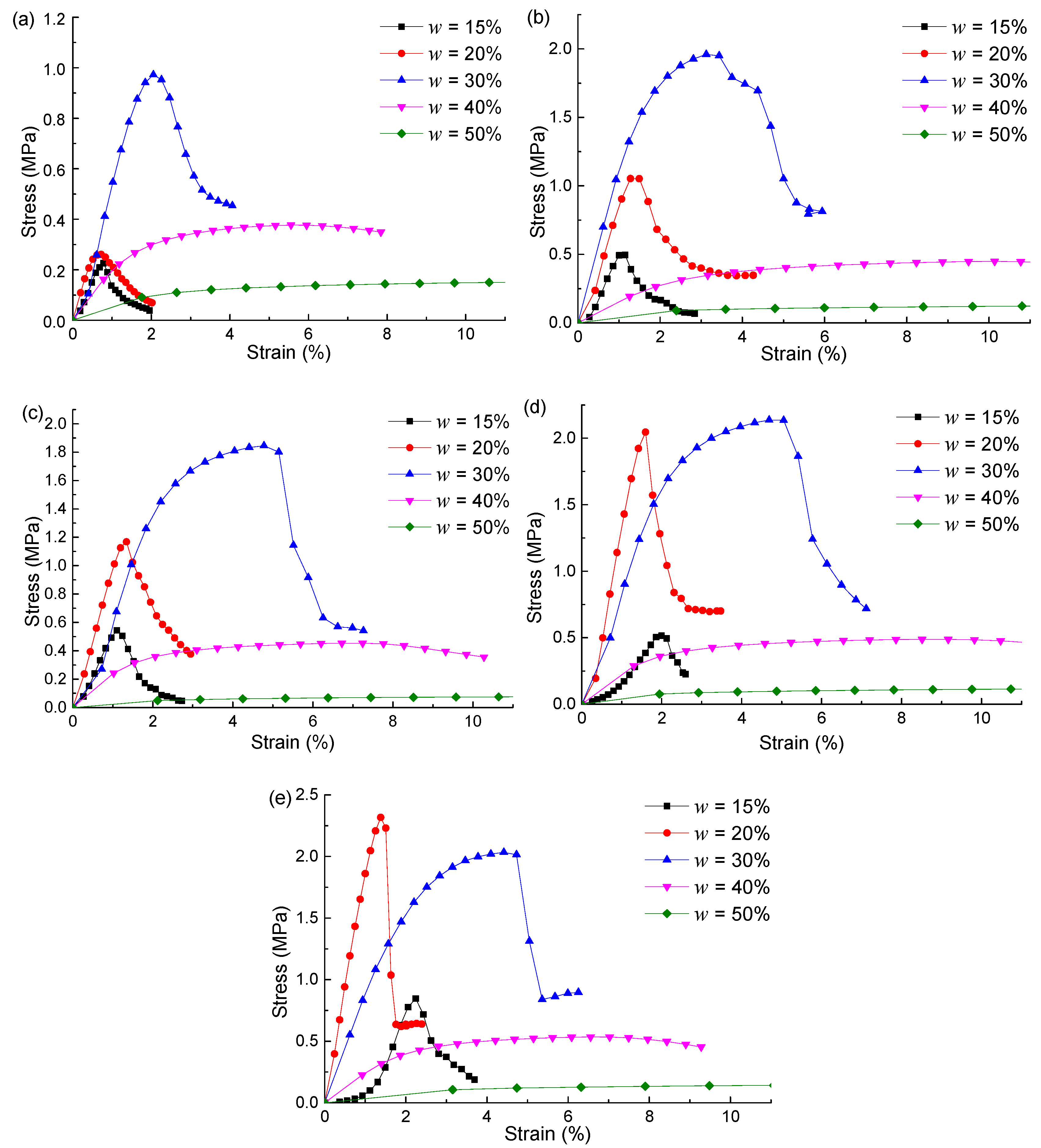
4.2. Uniaxial Compression Testing Results
5. Discussion
5.1. Integrated Specimens
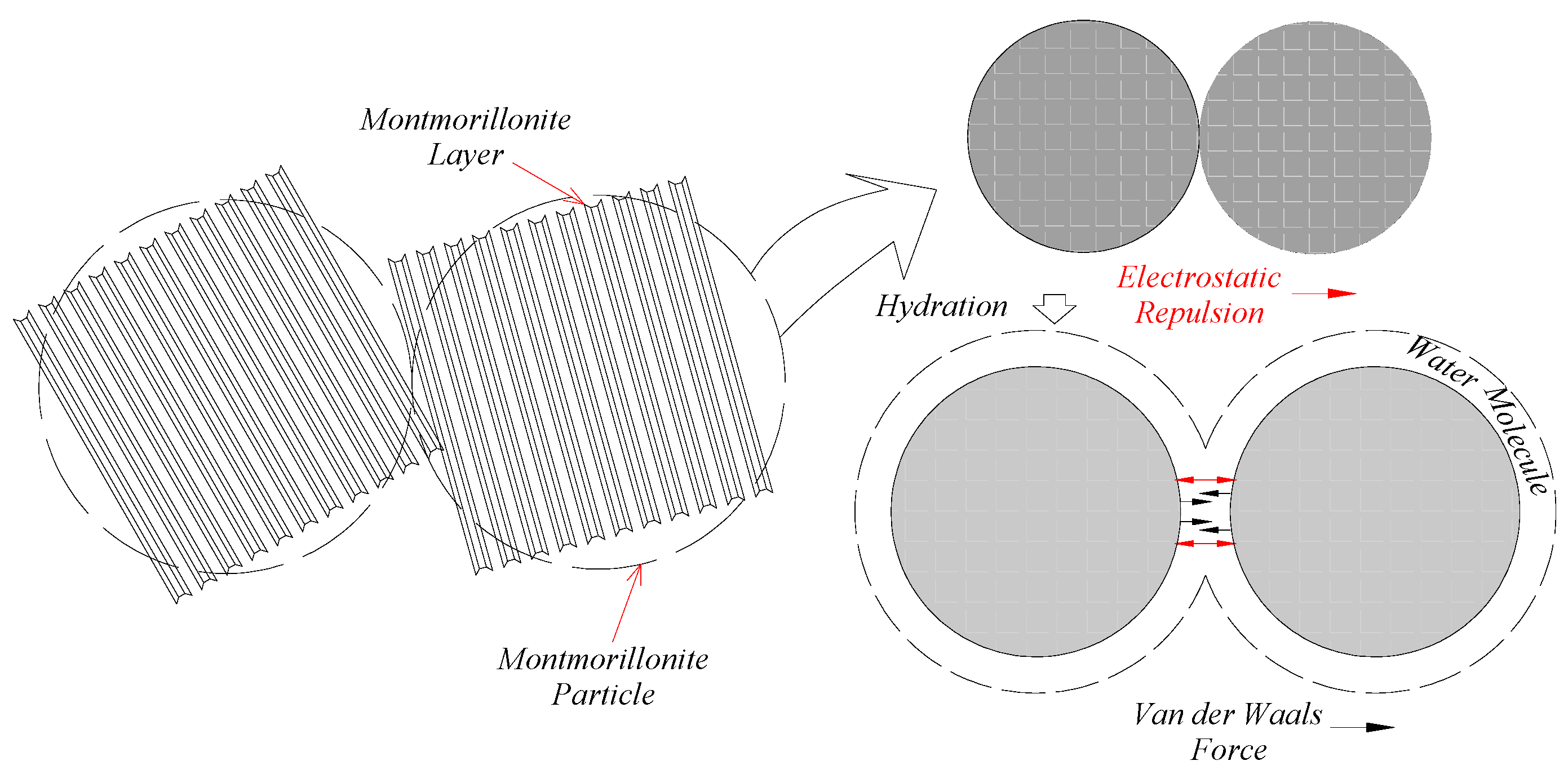
5.2. Hydration Swelling Model
5.3. Hydration Weakening Model
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, G.C.; Jiang, Z.H.; Feng, X.W.; Zhang, N.; Xu, X.L. Relation between molecular structure of montmorillonite and liquefaction of mudstone. RSC Adv. 2015, 5, 23481–23488. [Google Scholar] [CrossRef]
- Tetsuka, H.; Katayama, I.; Sakuma, H.; Kenji, T. Effects of humidity and interlayer cations on the frictional strength of montmorillonite. Earth Planets Space 2018, 70, 56. [Google Scholar] [CrossRef]
- Li, H.L.; Zhao, Y.L.; Song, S.X.; Hu, Y.; Nahmad, Y. Delamination of Na-montmorillonite particles in aqueous solutions and isopropanol under shear forces. J. Disper. Sci. Technol. 2017, 38, 1117–1123. [Google Scholar] [CrossRef]
- Zhou, C.Y.; Deng, Y.M.; Tan, X.S.; Liu, Z.Q.; Shang, W.; Zhan, S. Experimental research on the softening of mechanical properties of saturated soft rocks and application. Chin. J. Rock Mech. Eng. 2005, 24, 33–38. [Google Scholar]
- Ghorbani, A.; Zamora, M.; Cosenza, P. Effects of desiccation on the elastic wave velocities of clay-rocks. Int. J. Rock Mech. Min. Sci. 2009, 46, 1267–1272. [Google Scholar] [CrossRef]
- Yang, D.S.; Billiotte, J.; Su, K. Characterization of the hydromechanical behavior of argillaceous rocks with effective gas Permeability under deviatoric stress. Eng. Geol. 2010, 114, 116–122. [Google Scholar] [CrossRef]
- Yang, D.S.; Bornert, M.; Chanchole, S.; Wang, L.L.; Valli, P. Experimental investigation of the delayed behavior of unsaturated argillaceous rocks by means of digital image correlation techniques. Appl. Clay Sci. 2011, 54, 53–62. [Google Scholar] [CrossRef]
- Zhang, F.; Xie, S.Y.; Hu, D.W.; Shao, J.F.; Gatmiri, B. Effect of water content and structural anisotropy on mechanical property of claystone. Appl. Clay Sci. 2012, 69, 79–86. [Google Scholar] [CrossRef]
- Guéry, A.; Cormery, F.; Shao, J.F.; Kondo, D. A micromechanical model of elastoplastic and damage behavior of a cohesive geomaterial. Int. J. Solids Struct. 2008, 45, 1406–1429. [Google Scholar] [CrossRef]
- Robinet, J.C.; Sardini, P.; Coelho, D.; Parneix, J.C.; Prêt, D.; Sammartino, S.; Boller, E.; Altmann, S. Effects of mineral distribution at mesoscopic scale on solute diffusion in a clay-rich rock: Example of the Callovo-Oxfordian mudstone (Bure, France). Water Resour. Res. 2012, 48, W05554. [Google Scholar] [CrossRef]
- Armand, G.; Conil, N.; Talandier, J.; Seyedi, D. Fundamental aspects of the hydromechanical behaviour of Callovo-Oxfordian claystone: From experimental studies to model calibration and validation. Comput. Geotech. 2017, 85, 277–286. [Google Scholar] [CrossRef]
- Oohashi, K.; Hirose, T.; Takahashi, M.; Tanikawa, W. Dynamic weakening of smectite-bearing faults at intermediate velocities: Implications for subduction zone earthquakes. J. Geophys. Res. Solid Earth 2015, 120, 1572–1586. [Google Scholar] [CrossRef]
- Takahashi, M.; Mizoguchi, K.; Kitamura, K.; Masuda, K. Effects of clay content on the frictional strength and fluid transport property of faults. J. Geophys. Res. Solid Earth 2007, 112, B8. [Google Scholar] [CrossRef]
- Tembe, S.; Lockner, D.A.; Wong, T. Effect of clay content and mineralogy on frictional sliding behavior of simulated gouges: Binary and ternary mixtures of quartz, illite, and montmorillonite. J. Geophys. Res. Solid Earth 2010, 115, B3. [Google Scholar] [CrossRef]
- Matsumoto, S.; Shimada, H.; Sasaoka, T. Interaction between physical and chemical weathering of argillaceous rocks and the effects on the occurrence of acid mine drainage (AMD). Geosci. J. 2017, 21, 1–10. [Google Scholar] [CrossRef]
- He, M.C.; Zhou, L.; Li, D.J.; Wang, C.G.; Nie, W. Experimental research on hydrophilic characteristics of mudstone in deep well. Chin. J. Rock Mech. Eng. 2008, 27, 1113–1120. [Google Scholar]
- Chai, Z.Y.; Zhang, Y.T.; Zhang, X.Y. Experimental investigations on correlation with slake durability and mineral composition of mudstone. J. China Coal Soc. 2015, 40, 1188–1193. [Google Scholar]
- Mukherjee, K.; Mishra, A.K. Hydraulic and mechanical characteristics of compacted sand–bentonite: Tyre chips mix for its landfill application. Environ. Dev. Sustain. 2019, 21, 1411–1428. [Google Scholar] [CrossRef]
- Villar, M.V.; Antonio, L. Influence of dry density and water content on the swelling of a compacted bentonite. Appl. Clay Sci. 2009, 39, 38–49. [Google Scholar] [CrossRef]
- Xu, S.F.; Li, G.F.; Liu, J.Z.; Bian, M.D.; Wei, W.W.; Zhang, H.; Wang, Z. Deformation and hydraulic conductivity of compacted clay under waste differential settlement. Processes 2018, 6, 123. [Google Scholar] [CrossRef]
- Nilo, C.C.; Eduardo, J.B.M.; Rubén, A.Q.S.; Hugo, C.S.F.; Carlos, S.F.; Tiago, M.; Nuno, C. Effect of mellowing and coal fly ash addition on behavior of sulfate-rich dispersive clay after lime stabilization. J. Mater. Civ. Eng. 2019, 31, 04019071. [Google Scholar]
- Kumar, A.; Walia, B.S.; Mohan, J. Compressive strength of fiber reinforced highly compressible clay. Constr. Build. Mater. 2006, 20, 1063–1068. [Google Scholar] [CrossRef]
- Xu, X.L.; Zhang, N. Study of control process deformation behavior and of soft rock drift under rich condition. J. China Univ. Min. Technol. 2007, 36, 298–302. [Google Scholar]
- Li, S.Q.; Feng, T.; Wang, G.L.; Pan, C.L. Study on mechanism and control of soft rock roadway floor heave in Gequan Goal Ming. Chin. J. Rock Mech. Eng. 2005, 24, 1450–1455. [Google Scholar]
- Ruan, C.D.; Ward, C.R. Quantitative X-ray powder diffraction analysis of clay minerals in Australian coals using Rietveld methods. Appl. Clay Sci. 2002, 21, 227–240. [Google Scholar] [CrossRef]
- Mckissock, I.; Walker, E.L.; Gilkes, R.J.; Carter, D.J. The influence of clay type on reduction of water repellency by applied clays: A review of some West Australian work. J. Hydrol. 2000, 231, 323–332. [Google Scholar] [CrossRef]
- Cariou, S.; Dormieux, L.; Skoczylas, F. An original constitutive law for Callovo-Oxfordian argillite, a two-scale double-porosity material. Appl. Clay Sci. 2013, 80, 18–30. [Google Scholar] [CrossRef]
- Vesga, L.F.; Vallejo, L.E.; Lobo-Guerrero, S. DEM analysis of the crack propagation in brittle clays under uniaxial compression tests. Int. J. Numer. Anal. Met. 2008, 32, 1405–1415. [Google Scholar] [CrossRef]
- Bayesteh, H.; Mirghasemi, A.A. Numerical simulation of pore fluid characteristic effect on the volume change behavior of montmorillonite clays. Comput. Geotech. 2013, 48, 146–155. [Google Scholar] [CrossRef]
- He, M.C.; Xie, H.P.; Peng, S.P.; Jiang, Y.D. Study on rock mechanics in deep mining engineering. Chin. J. Rock Mech. Eng. 2005, 24, 2803–2813. [Google Scholar]
- Pintado, X.; Romero, E.; Suriol, A.; Lloret, A.; Madhusudhan, B.N. Small-stain shear stiffness of compacted bentonites for engineered barrier system. Geomech. Eng. Geol. Environ. 2019, 8, 1–12. [Google Scholar]
- Mašín, D.; Khalili, N. Swelling phenomena and effective stress in compacted expansive clays. Can. Geotech. J. 2016, 53, 134–147. [Google Scholar] [CrossRef]
- Zheng, Y.; Zaoui, A. How water and counterions diffuse into the hydrated montmorillonite. Solid State Ionics 2011, 203, 80–85. [Google Scholar] [CrossRef]
- Oueslati, W.; Rhaiem, H.B.; Amara, A.B.H. XRD investigations of hydrated homoionic montmorillonite saturated by several heavy metal cations. Desalination 2011, 271, 139–149. [Google Scholar] [CrossRef]
- Brice, F.; Ngouana, W.; Kalinichev, A.G. Structural arrangements of isomorphic substitutions in smectites: Molecular simulation of the swelling properties, interlayer structure, and dynamics of hydrated Cs-montmorillonite revisited with new clay models. J. Phys. Chem. C 2014, 118, 12758–12773. [Google Scholar]
- Salles, F.; Douillard, J.M.; Bildstein, O.; Gaudin, C.; Prelot, B.; Zajac, J.; Damme, H.V. Driving force for the hydration of the swelling clays: Case of montmorillonites saturated with alkaline-earth cations. J. Coll. Interface Sci. 2013, 395, 269–276. [Google Scholar] [CrossRef]
- Greathouse, J.A.; Cygan, R.T.; Fredrich, J.T.; Jerauld, G.R. Molecular dynamics simulation of diffusion and electrical conductivity in montmorillonite interlayers. J. Phys. Chem. C 2016, 120, 1640–1649. [Google Scholar] [CrossRef]
- Saiyouri, N.; Hicher, P.Y.; Tessier, D. Microstructural approach and transfer water modelling in highly compacted unsaturated swelling clays. Mech. Cohes-Fric Mater. 2000, 5, 41–60. [Google Scholar] [CrossRef]
- Li, G.X.; Zhang, B.Y.; Yu, Y.Z. Soil Mechanics; Tsinghua University Press: Beijing, China, 2013; pp. 28–31. [Google Scholar]

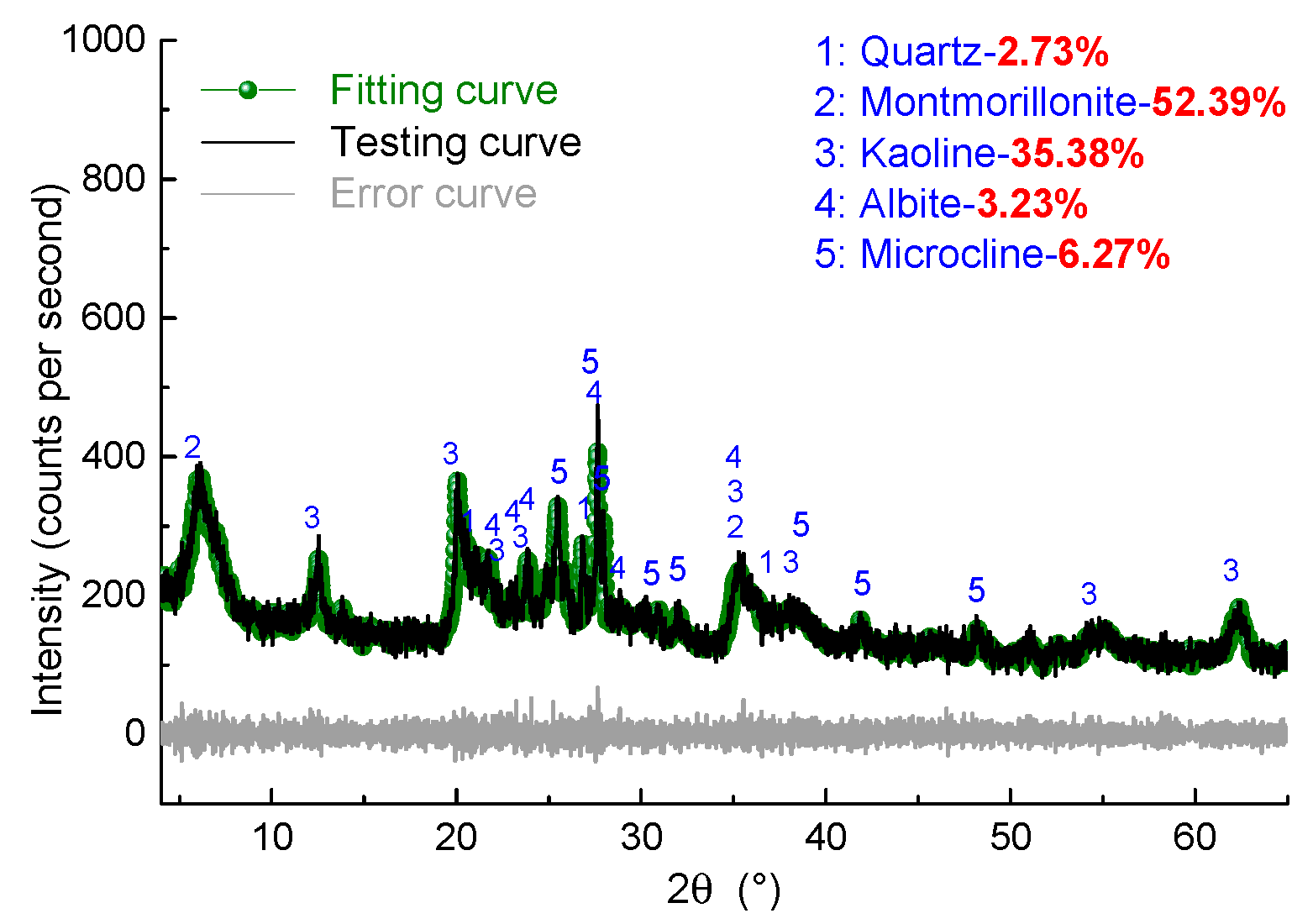

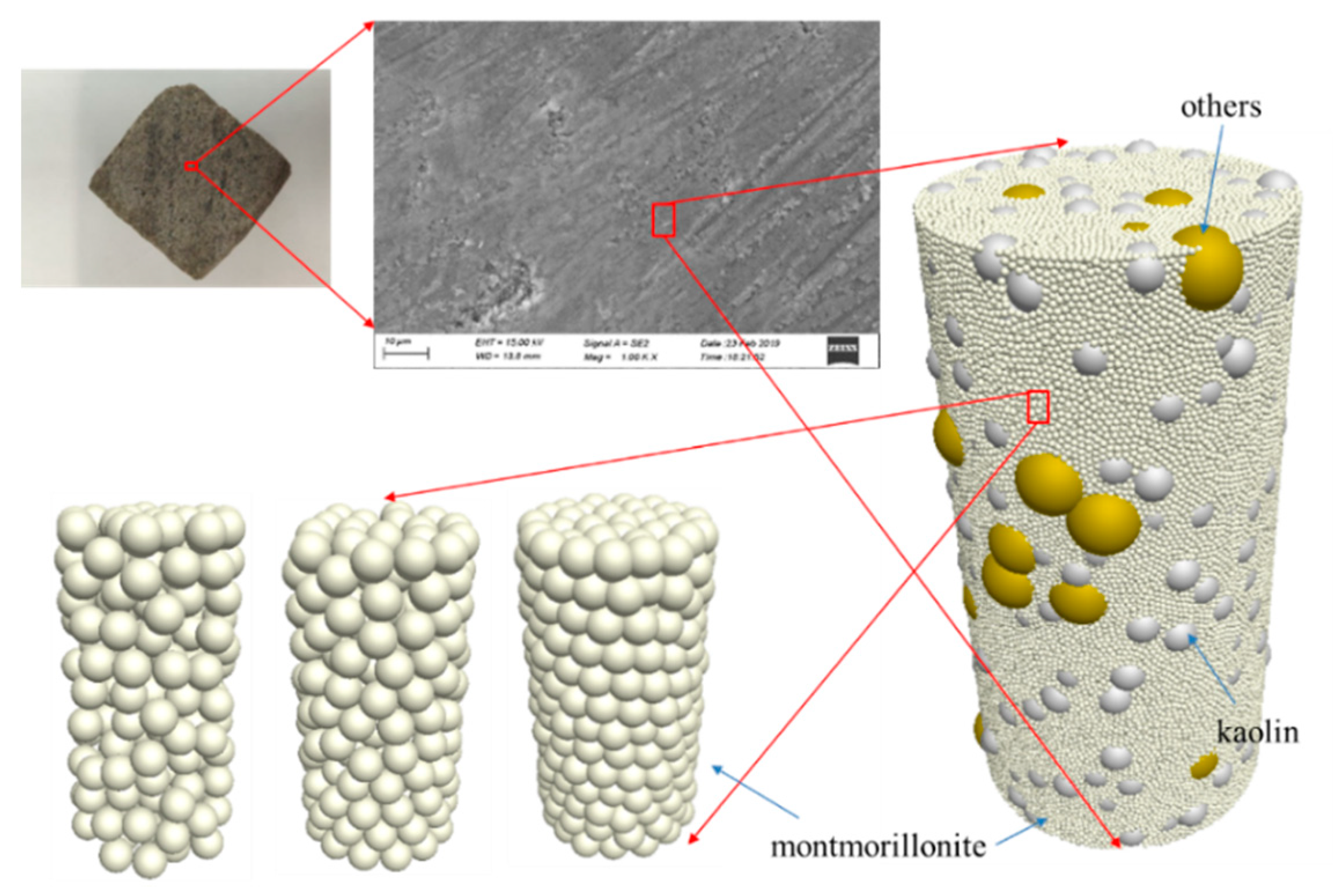

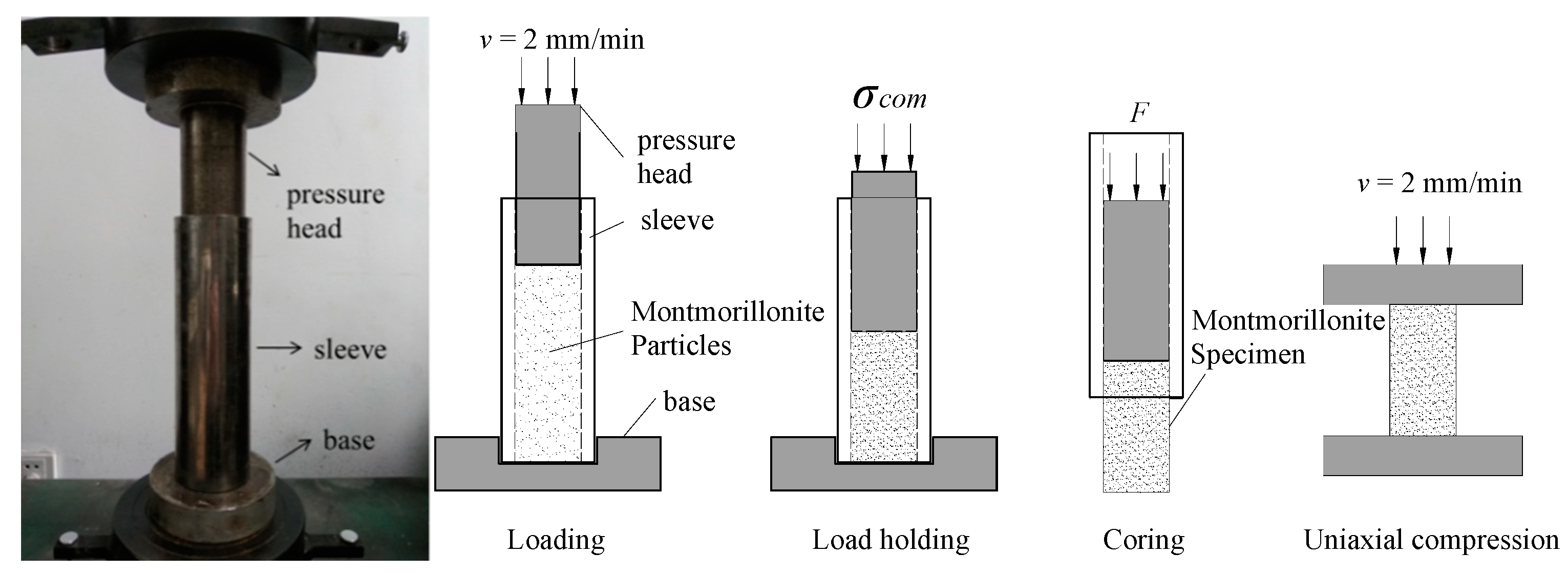
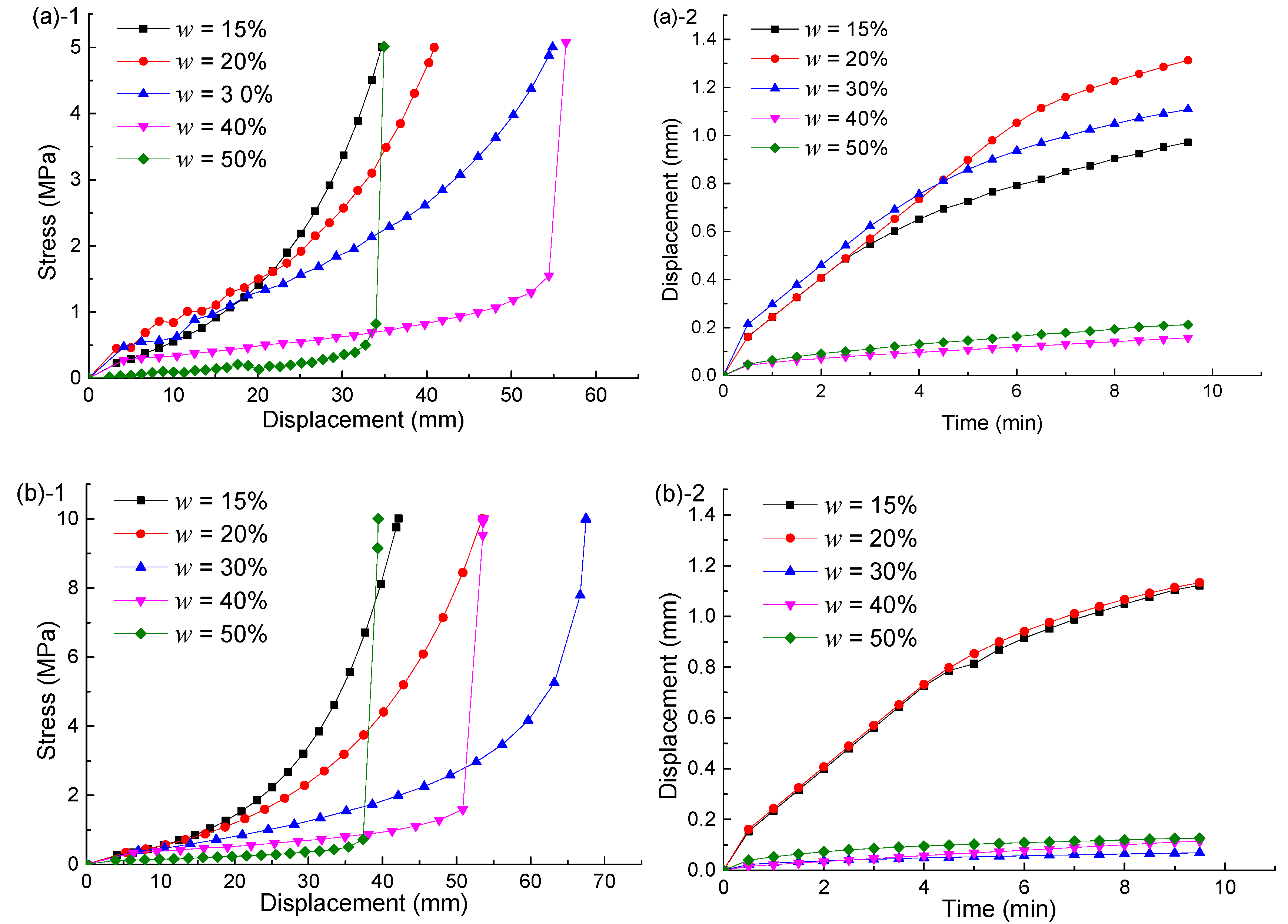



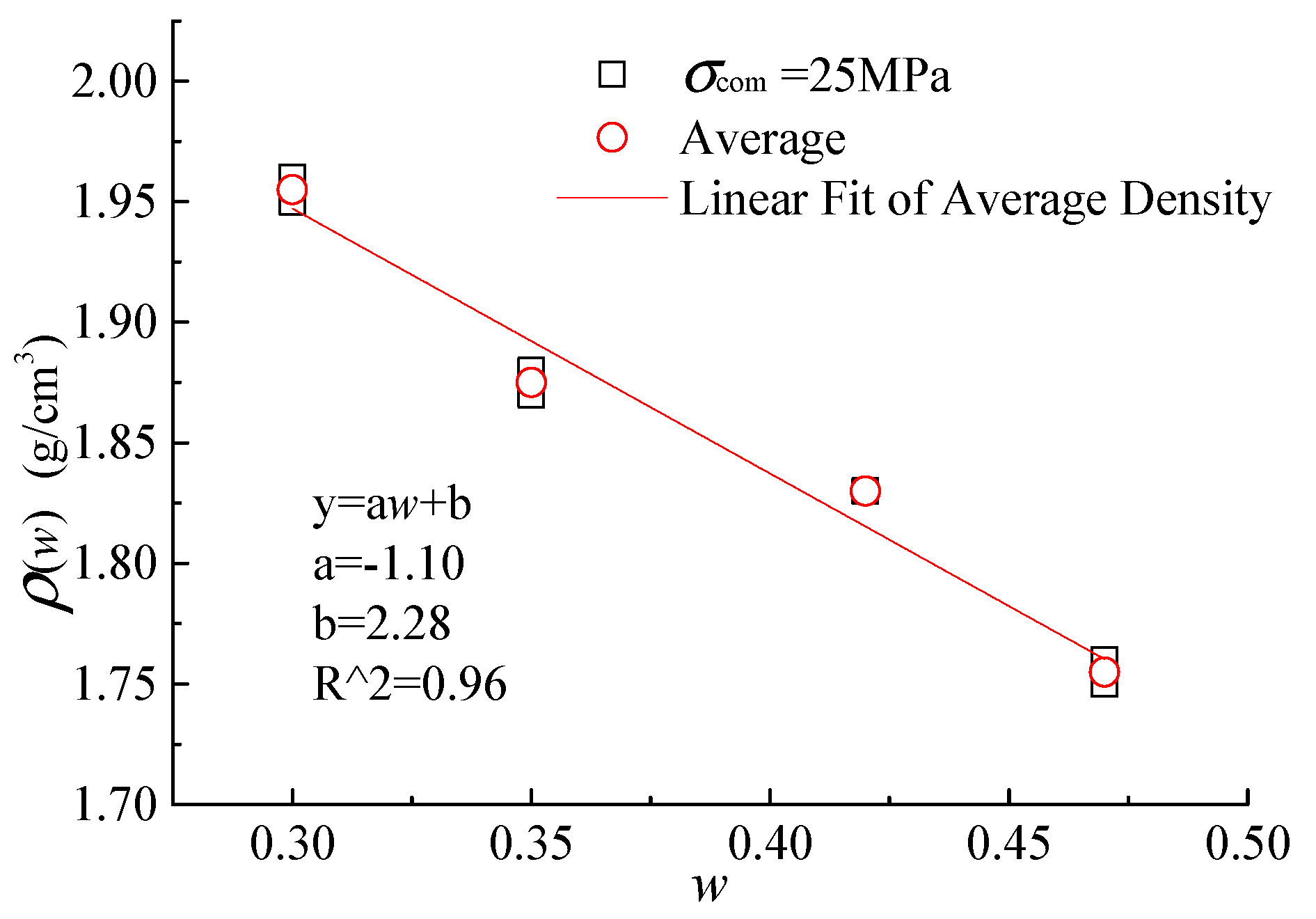
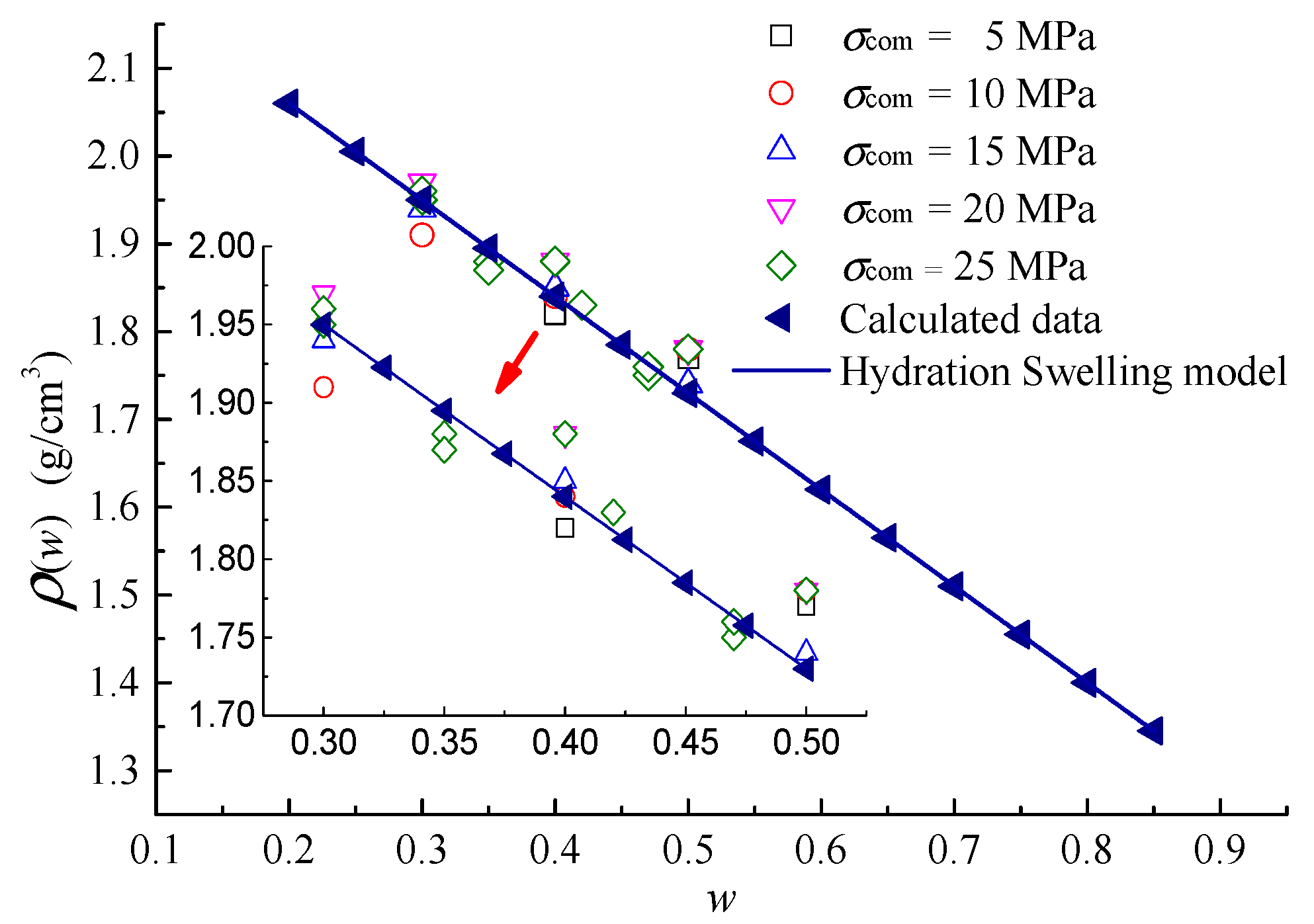

| w | (MPa) | (g/cm3) | (g/cm3) | MPa | MPa | ||
|---|---|---|---|---|---|---|---|
| 0.3 | 25 | 1.95 | 1.96 | 1.955 | 1.85 | 1.92 | 1.885 |
| 0.35 | 25 | 1.88 | 1.87 | 1.875 | 0.78 | 0.76 | 0.77 |
| 0.42 | 25 | 1.83 | 1.83 | 1.83 | 0.46 | 0.37 | 0.415 |
| 0.47 | 25 | 1.75 | 1.76 | 1.755 | 0.23 | 0.23 | 0.23 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, C.; Li, G.; Sun, Y.; He, J.; Rong, H. Modelling Hydration Swelling and Weakening of Montmorillonite Particles in Mudstone. Processes 2019, 7, 428. https://doi.org/10.3390/pr7070428
Sun C, Li G, Sun Y, He J, Rong H. Modelling Hydration Swelling and Weakening of Montmorillonite Particles in Mudstone. Processes. 2019; 7(7):428. https://doi.org/10.3390/pr7070428
Chicago/Turabian StyleSun, Changlun, Guichen Li, Yuantian Sun, Jintao He, and Haoyu Rong. 2019. "Modelling Hydration Swelling and Weakening of Montmorillonite Particles in Mudstone" Processes 7, no. 7: 428. https://doi.org/10.3390/pr7070428
APA StyleSun, C., Li, G., Sun, Y., He, J., & Rong, H. (2019). Modelling Hydration Swelling and Weakening of Montmorillonite Particles in Mudstone. Processes, 7(7), 428. https://doi.org/10.3390/pr7070428







