Irregularity Molecular Descriptors of Hourglass, Jagged-Rectangle, and Triangular Benzenoid Systems
Abstract
:1. Introduction
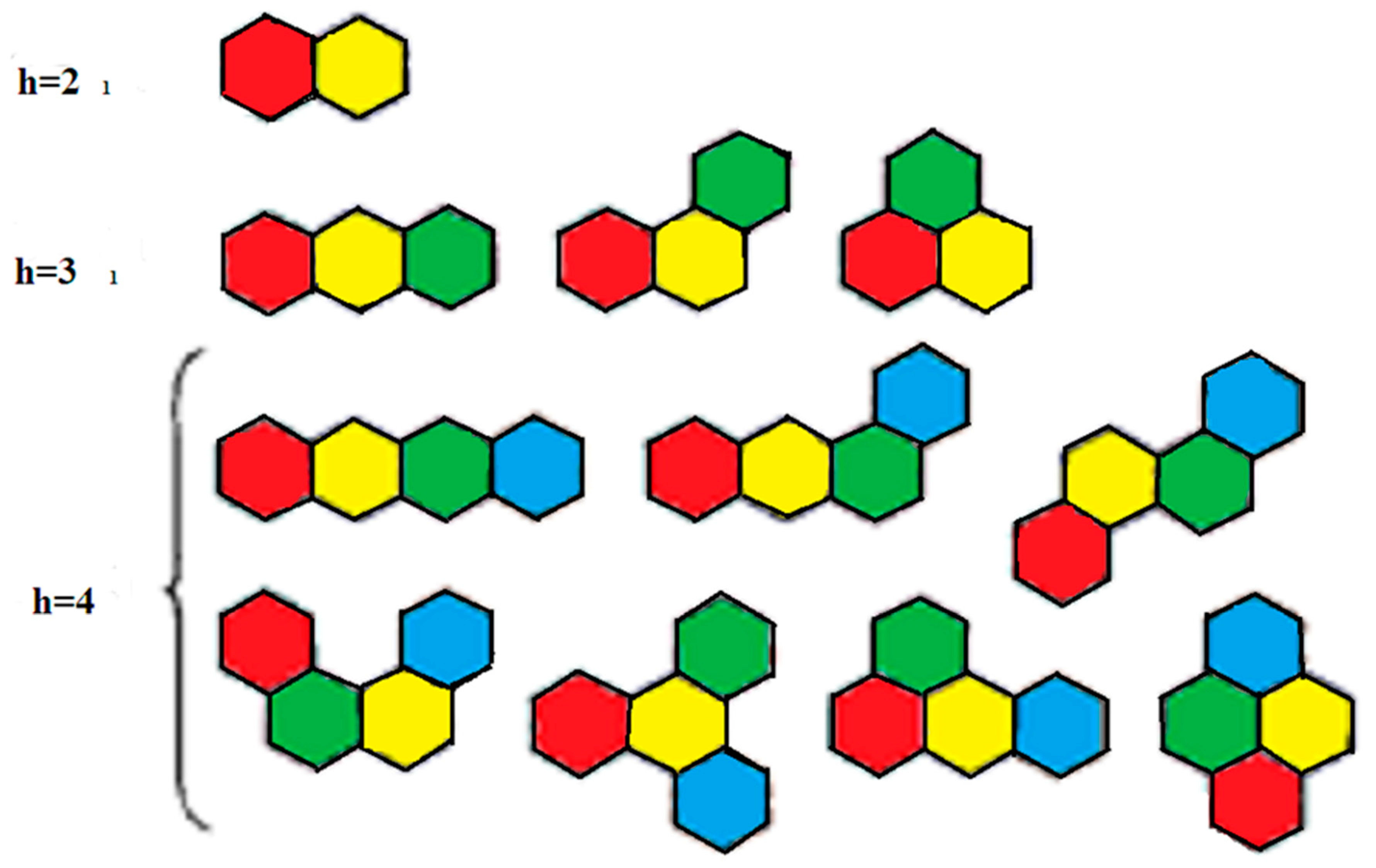
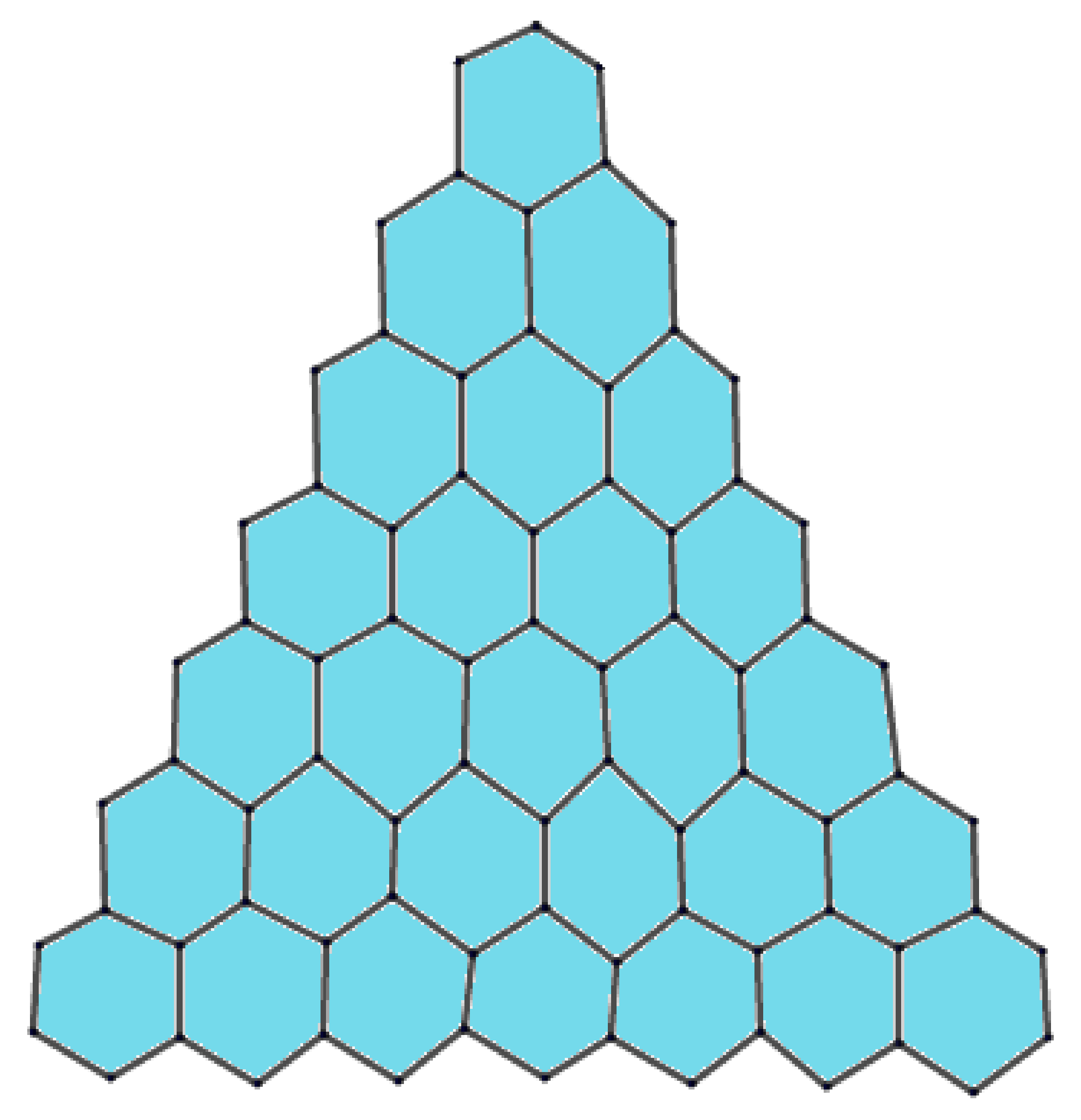
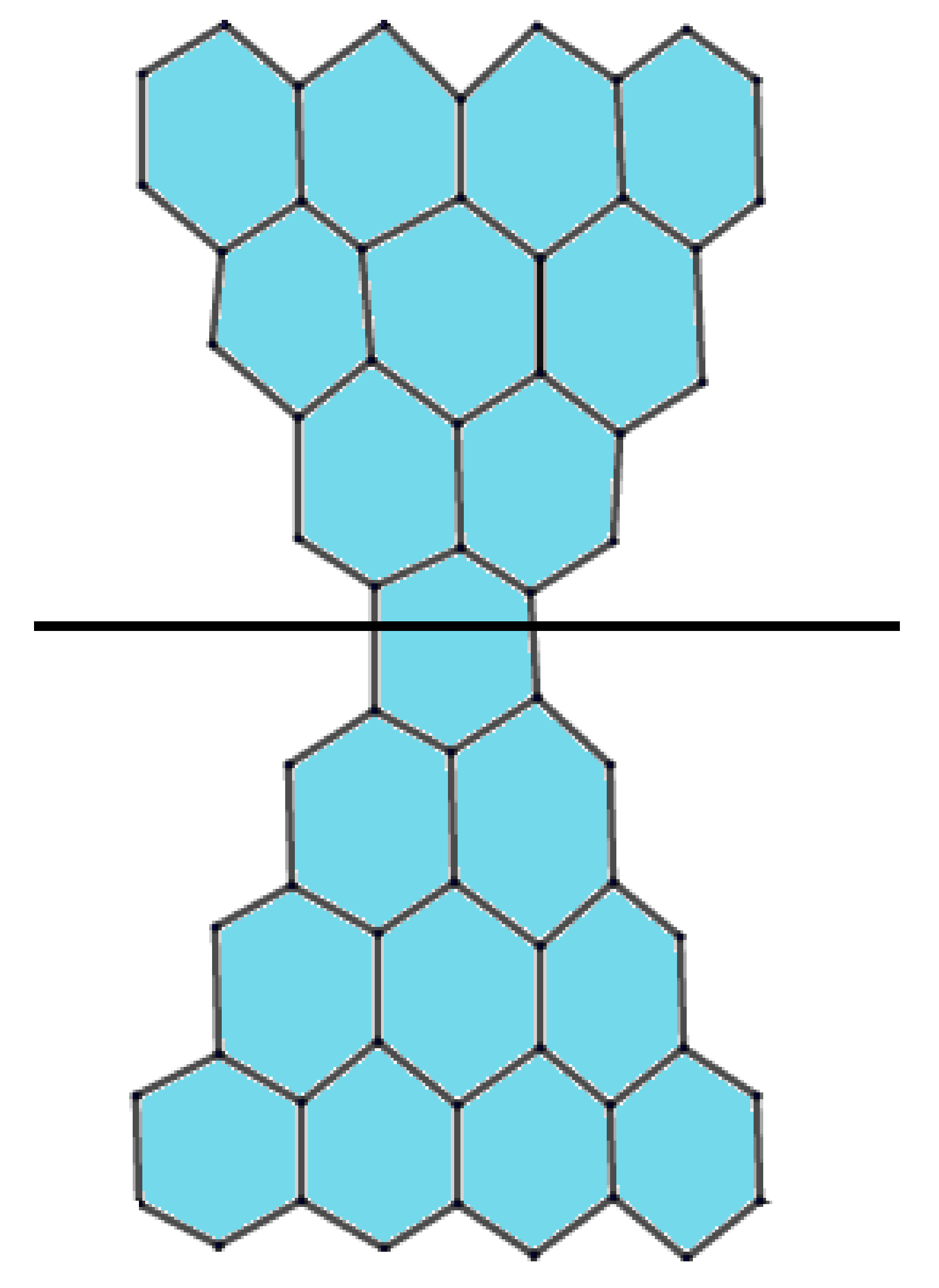
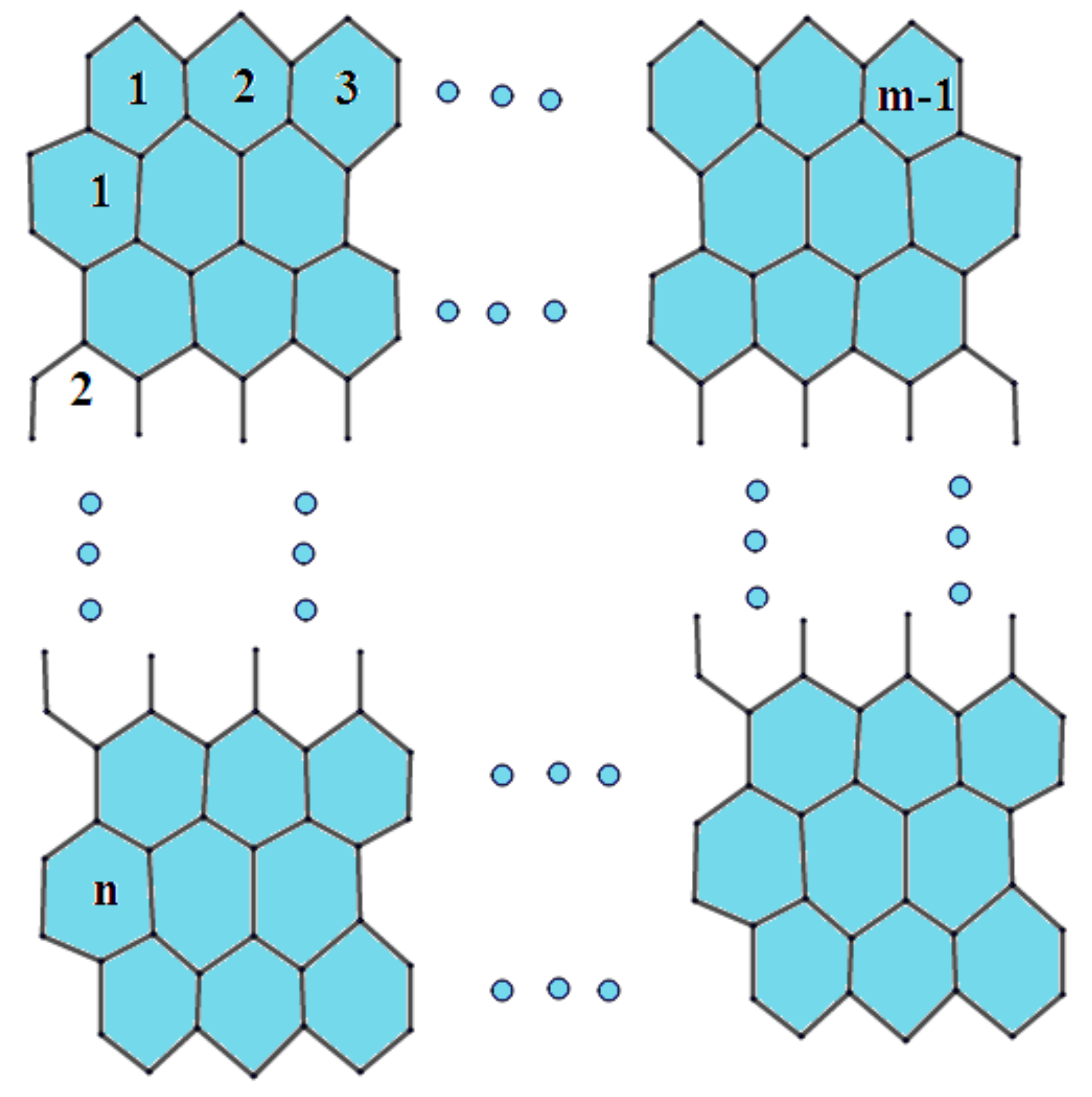
2. Preliminaries and Notations
3. Main Results
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
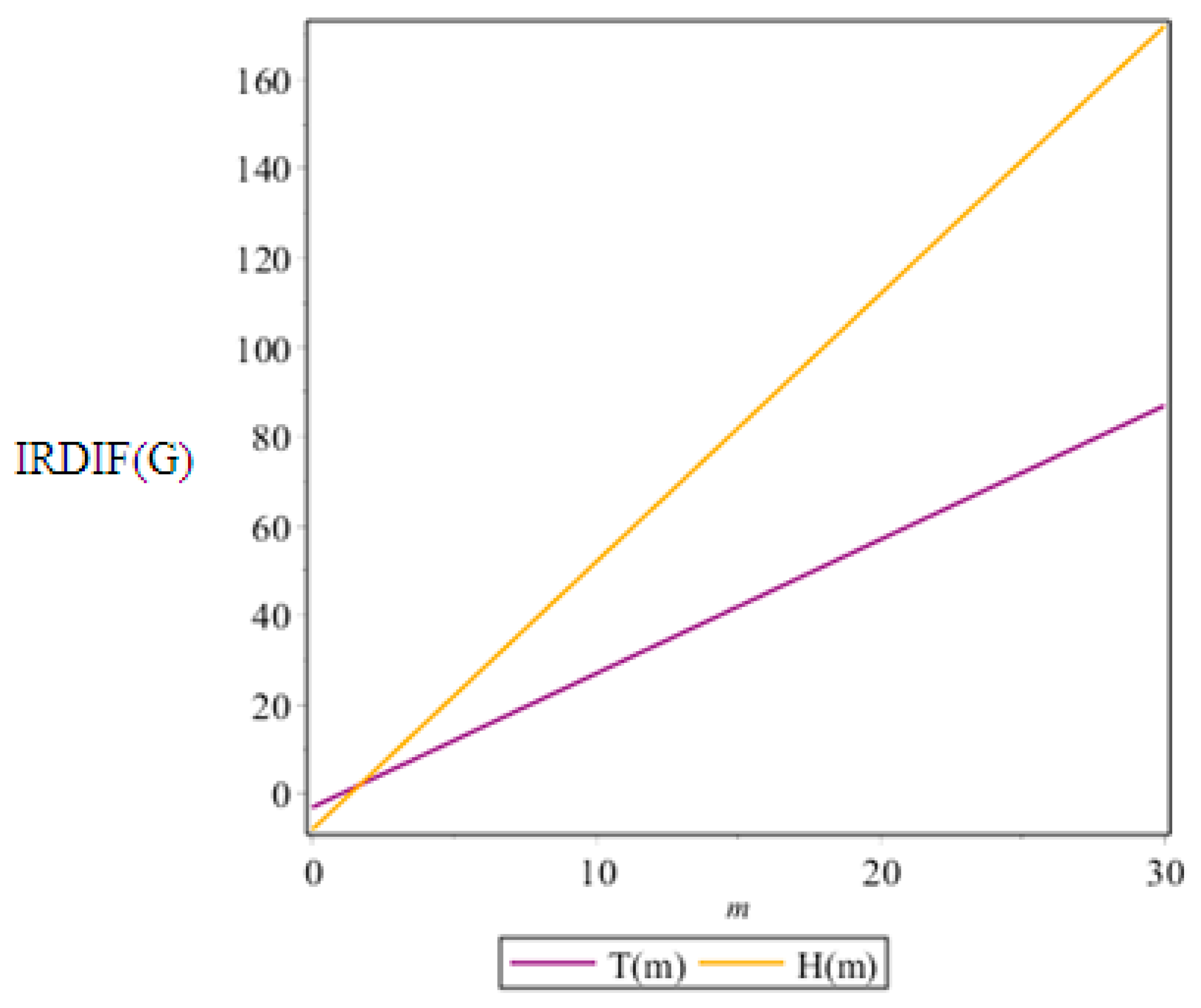
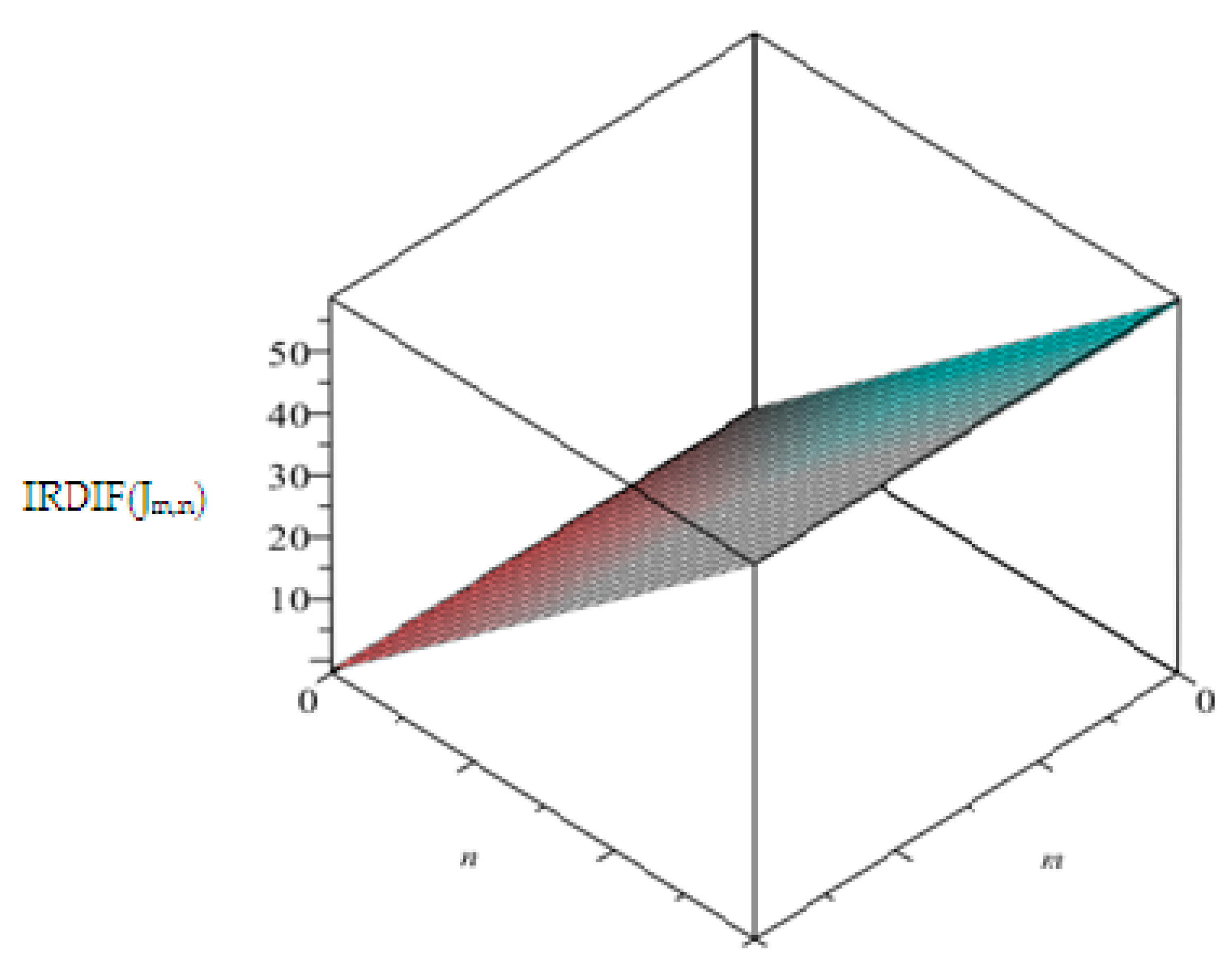
4. Graphical Analysis, Discussions, and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gutman, I.; Cyvin, S.V. Introduction to the Theory of Benzenoid Hydrocarbons; Springer: Berlin, Germany, 1989. [Google Scholar]
- Rucker, G.; Rucker, C. On topological indices, boiling points, and cyclo-alkanes. J. Chem. Inf. Comput. Sci. 1999, 39, 788–802. [Google Scholar] [CrossRef]
- Gutman, I.; Polansky, O.E. Mathematical Concepts in Organic Chemistry; Springer: New York, NY, USA, 1986. [Google Scholar]
- Randic, M. On the characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E. Atomic bond connectivity and the energetic of branched alkanes. Chem. Phys. Lett. 2008, 463, 422–425. [Google Scholar] [CrossRef]
- Kier, L.; Hall, L. Molecular Connectivity in Chemistry and Drug Research; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Kier, L.B.; Hall, L.H. Molecular Connectivity in Structure Activity Analysis; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Kwun, Y.C.; Ali, A.; Nazeer, W.; Ahmad Chaudhary, M.; Kang, S.M. M-Polynomials and Degree-Based Topological Indices of Triangular, Hourglass, and Jagged-Rectangle Benzenoid Systems. J. Chem. 2018. [Google Scholar] [CrossRef]
- Deng, H.; Yang, J.; Xia, F. A general modeling of some vertex-degree based topological indices in benzenoid systems and phenylenes. Compt. Math. Appl. 2011, 61, 3017–3023. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Zhang, F. The Clar covering polynomial of hexagonal systems. Discret. Appl. Math. 1996, 69, 147–167. [Google Scholar] [CrossRef]
- Munir, M.; Nazeer, W.; Rafique, S.; Kang, S.M. Mpolynomial and related topological indices of Nanostar dendrimers. Symmetry 2016, 8, 97. [Google Scholar] [CrossRef]
- Munir, M.; Nazeer, W.; Rafique, S.; Nizami, A.R.; Kang, S.M. M-polynomial and degree-based topological indices of titania nanotubes. Symmetry 2016, 8, 117. [Google Scholar] [CrossRef]
- Munir, M.; Nazeer, W.; Rafique, S.; Kang, S.M. M-Polynomial and Degree-Based Topological Indices of Polyhex Nanotubes. Symmetry 2016, 8, 149. [Google Scholar] [CrossRef]
- Munir, M.; Nazeer, W.; Shahzadi, S.; Kang, S.M. Some invariants of circulant graphs. Symmetry 2016, 8, 134. [Google Scholar] [CrossRef]
- Chartrand, G.; Erdos, P.; Oellermann, O. How to define an irregular graph. Coll. Math. J. 1988, 19, 36–42. [Google Scholar] [CrossRef]
- Majcher, Z.; Michael, J. Highly irregular graphs with extreme numbers of edges. Discr. Math. 1997, 164, 237–242. [Google Scholar] [CrossRef] [Green Version]
- Behzad, M.; Chartrand, G. No graph is perfect. Am. Math. Mon. 1947, 74, 962–963. [Google Scholar] [CrossRef]
- Horoldagva, B.; Buyantogtokh, L.; Dorjsembe, S.; Gutman, I. Maximum sizeof maximally irregular graphs. Match Commun. Math. Comput. Chem. 2016, 76, 81–98. [Google Scholar]
- Liu, F.; Zhang, Z.; Meng, J. The size of maximally irregular graphs and maximally irregular triangle–free graphs. Graphs Comb. 2014, 30, 699–705. [Google Scholar] [CrossRef]
- Collatz, L.; Sinogowitz, U. Spektren endlicher Graphen. Abh. Math. Sem. Univ. Hamburg 1957, 21, 63–77. [Google Scholar]
- Bell, F.K. A note on the irregularity of graphs. Linear Algebra Appl. 1992, 161, 45–54. [Google Scholar] [CrossRef] [Green Version]
- Albertson, M. The irregularity of a graph. Ars Comb. 1997, 46, 219–225. [Google Scholar]
- Vukičević, D.; Graovac, A. Valence connectivities versus Randić, Zagreb and modified Zagreb index: A linear algorithm to check discriminative properties of indices in acyclic molecular graphs. Croat. Chem. Acta 2004, 77, 501–508. [Google Scholar]
- Abdo, H.; Brandt, S.; Dimitrov, D. The total irregularity of a graph. Discr. Math. Theor. Comput. Sci. 2014, 16, 201–206. [Google Scholar]
- Abdo, H.; Dimitrov, D. The total irregularity of graphs under graph operations. Miskolc Math. Notes 2014, 15, 3–17. [Google Scholar] [CrossRef]
- Abdo, H.; Dimitrov, D. The irregularity of graphs under graph operations. Discuss. Math. Graph. Theory 2014, 34, 263–278. [Google Scholar] [CrossRef]
- Gutman, I. Topological Indices and Irregularity Measures. J. Bull. 2018, 8, 469–475. [Google Scholar]
- Reti, T.; Sharfdini, R.; Dregelyi-Kiss, A.; Hagobin, H. Graph irregularity indices used as molecular discriptors in QSPR studies. MATCH Commun. Math. Comput. Chem. 2018, 79, 509–524. [Google Scholar]
- Hu, Y.; Li, X.; Shi, Y.; Xu, T.; Gutman, I. On molecular graphs with smallest and greatest zeroth-Corder general randic index. MATCH Commun. Math. Comput. Chem. 2005, 54, 425–434. [Google Scholar]
- Caporossi, G.; Gutman, I.; Hansen, P.; Pavlovic, L. Graphs with maximum connectivity index. Comput. Biol. Chem. 2003, 27, 85–90. [Google Scholar] [CrossRef]
- Li, X.; Gutman, I. Mathematical aspects of Randic, Type molecular structure descriptors. In Mathematical Chemistry Monographs; University of Kragujevac and Faculty of Science Kragujevac: Kragujevac, Serbia, 2006. [Google Scholar]
- Das, K.; Gutman, I. Some properties of the second Zagreb Index. MATCH Commun. Math. Comput. Chem. 2004, 52, 103–112. [Google Scholar]
- Trinajstic, N.; Nikolic, S.; Milicevic, A.; Gutman, I. About the Zagreb Indices. Kemija u industriji: Časopis kemičara i kemijskih inženjera Hrvatske 2010, 59, 577–589. [Google Scholar]
- Milicevic, A.; Nikolic, S.; Trinajstic, N. On reformulated Zagreb indices. Mol. Divers. 2004, 8, 393–399. [Google Scholar] [CrossRef]
- Gupta, C.K.; Lokesha, V.; Shwetha, S.B.; Ranjini, P.S. On the symmetric division DEG index of graph. Southeast Asian Bull. Math. 2016, 40, 59–80. [Google Scholar]
- Balaban, A.T. Highly discriminating distance based numerical descriptor. Chem. Phys. Lett. 1982, 89, 399–404. [Google Scholar] [CrossRef]
- Furtula, B.; Graovac, A.; Vukičević, D. Augmented Zagreb index. J. Math. Chem. 2010, 48, 370–380. [Google Scholar] [CrossRef]
- Das, K.C. Atom–bond connectivity index of graphs. Discr. Appl. Math. 2010, 158, 1181–1188. [Google Scholar] [CrossRef]
- Estrada, E.; Torres, L.; Rodríguez, L.; Gutman, I. An atom–bond connectivity index: Modeling the enthalpy of formation of alkanes. Indian. J. Chem. 1998, 37, 849–855. [Google Scholar]
- Zahid, I.; Aslam, A.; Ishaq, M.; Aamir, M. Characteristic study of irregularity measures of some Nanotubes. Can. J. Phys. 2019. [Google Scholar] [CrossRef]
- Gao, W.; Aamir, M.; Iqbal, Z.; Ishaq, M.; Aslam, A. On Irregularity Measures of Some Dendrimers Structures. Mathematics 2019, 7, 271. [Google Scholar] [CrossRef]
- Gao, W.; Abdo, H.; Dimitrov, D. On the irregularity of some molecular structures. Can. J. Chem. 2017, 95, 174–183. [Google Scholar] [CrossRef] [Green Version]


| Number of Edges | Number of Indices |
|---|---|
| (2, 2) | |
| (2, 3) | |
| (3, 3) |
| Irregularity Indices | m = 1 | m = 2 | m = 3 | m = 4 | m = 5 |
|---|---|---|---|---|---|
| 0 | 3 | 6 | 9 | 12 | |
| 0 | 6 | 12 | 18 | 24 | |
| 0 | 2.4329 | 4.8658 | 7.2987 | 9.7316 | |
| 0 | 3 | 6 | 9 | 12 | |
| 0 | 2.44949 | 4.89898 | 7.34847 | 9.79796 | |
| 0 | 6 | 12 | 18 | 24 | |
| 0 | 2.40 | 4.80 | 7.20 | 9.60 | |
| 0 | 4.15888 | 8.31776 | 12.47664 | 16.63552 | |
| 0 | 0.101022 | 0.202044 | 0.303066 | 0.404088 | |
| 0 | 0.122465 | 0.244930 | 0.367395 | 0.489860 | |
| 0 | 0.60612 | 1.21224 | 1.81836 | 2.42448 | |
| 0 | 3 | 6 | 9 | 12 |
| Number of Edges | Number of Indices |
|---|---|
| (2, 2) | |
| (2, 3) | |
| (3, 3) |
| Irregularity Indices | m = 1 | m = 2 | m = 3 | m = 4 | m = 5 |
|---|---|---|---|---|---|
| −2 | 4 | 10 | 16 | 22 | |
| −4 | 8 | 20 | 32 | 44 | |
| −1.62186 | 3.4373 | 8.10932 | 12.97491 | 17.84050 | |
| −2 | 4 | 10 | 16 | 22 | |
| −1.62992 | 3.265984 | 8.164960 | 13.063936 | 16.962912 | |
| −4 | 8 | 20 | 32 | 44 | |
| −1.6 | 3.2 | 8.0 | 12.8 | 17.6 | |
| −2.772594 | 5.545165 | 13.862925 | 22.18068 | 30.498445 | |
| −0.067348 | 0.134696 | 0.336740 | 0.538784 | 0.740828 | |
| −0.08158 | 0.16342 | 0.40842 | 0.65342 | 0.89842 | |
| −0.40408 | 0.80816 | 2.02040 | 3.23264 | 4.44488 | |
| −2 | 4 | 10 | 16 | 22 |
| Number of Indices | |
|---|---|
| (2, 2) | 2 |
| (2, 3) | 4 |
| (3, 3) | ( |
| Irregularity Indices | m = 1 n = 1 | m = 2 n = 2 | m = 3 n = 3 | m = 4 n = 4 | m = 5 n = 5 |
|---|---|---|---|---|---|
| 2 | 6 | 10 | 14 | 18 | |
| 4 | 12 | 20 | 28 | 36 | |
| 1.6218043 | 4.865581 | 8.109302 | 11.353023 | 14.596743 | |
| 2 | 6 | 10 | 14 | 18 | |
| 1.632993 | 4.898979 | 8.164965 | 11.43095 | 14.696937 | |
| 4 | 12 | 20 | 28 | 36 | |
| 1.60 | 4.80 | 8 | 11.20 | 14.40 | |
| 1.386294 | 4.15888 | 6.931471 | 9.704060 | 12.476649 | |
| 0.067348 | 0.202044 | 0.336740 | 0.471436 | 0.606132 | |
| 0.0816439 | 0.244931 | 0.408219 | 0.571507 | 0.734795 | |
| 0.40408 | 1.21224 | 2.02040 | 2.82856 | 3.636772 | |
| 2 | 6 | 10 | 14 | 18 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussain, Z.; Rafique, S.; Munir, M.; Athar, M.; Chaudhary, M.; Ahmad, H.; Min Kang, S. Irregularity Molecular Descriptors of Hourglass, Jagged-Rectangle, and Triangular Benzenoid Systems. Processes 2019, 7, 413. https://doi.org/10.3390/pr7070413
Hussain Z, Rafique S, Munir M, Athar M, Chaudhary M, Ahmad H, Min Kang S. Irregularity Molecular Descriptors of Hourglass, Jagged-Rectangle, and Triangular Benzenoid Systems. Processes. 2019; 7(7):413. https://doi.org/10.3390/pr7070413
Chicago/Turabian StyleHussain, Zafar, Shazia Rafique, Mobeen Munir, Muhammad Athar, Maqbool Chaudhary, Haseeb Ahmad, and Shin Min Kang. 2019. "Irregularity Molecular Descriptors of Hourglass, Jagged-Rectangle, and Triangular Benzenoid Systems" Processes 7, no. 7: 413. https://doi.org/10.3390/pr7070413
APA StyleHussain, Z., Rafique, S., Munir, M., Athar, M., Chaudhary, M., Ahmad, H., & Min Kang, S. (2019). Irregularity Molecular Descriptors of Hourglass, Jagged-Rectangle, and Triangular Benzenoid Systems. Processes, 7(7), 413. https://doi.org/10.3390/pr7070413





