Thermodynamic vs. Kinetic Basis for Polymorph Selection
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Abramov, Y.A.; Pencheva, K. Thermodynamics and relative solubility prediction of polymorphic systems. In Chemical Engineering in the Pharmaceutical Industry; Ende, D.J.A., Ed.; Wiley: Hoboken, NJ, USA, 2010; pp. 477–490. [Google Scholar]
- Bauer, J.; Spanton, S.; Henry, R.; Quick, J.; Dziki, W.; Porter, W.; Morris, J. Ritonavir: An Extraordinary Example of Conformational Polymorphism. Pharm. Res. 2001, 18, 859–866. [Google Scholar] [CrossRef] [PubMed]
- Verma, V.; Hodnett, B.K. A Basis for the Kinetic Selection of Polymorphs during Solution Crystallization of Organic Compounds. CrystEngComm 2018, 20, 5551–5561. [Google Scholar] [CrossRef]
- Nyman, J.; Day, G.M. Static and lattice vibrational energy differences between polymorphs. CrystEngComm 2015, 17, 5154–5165. [Google Scholar] [CrossRef]
- Cruz-Cabeza, A.J.; Reutzel-Edens, S.M.; Bernstein, J. Facts and fictions about polymorphism. Chem. Soc. Rev. 2015, 44, 8619–8635. [Google Scholar] [CrossRef]
- Mealey, D.; Croker, D.M.; Rasmuson, A.C. Crystal nucleation of salicylic acid in organic solvents. CrystEngComm 2015, 17, 3961–3973. [Google Scholar] [CrossRef]
- Khamar, D.; Zeglinski, J.; Mealey, D.; Rasmuson, Å.C. Investigating the Role of Solvent–Solute Interaction in Crystal Nucleation of Salicylic Acid from Organic Solvents. J. Am. Chem. Soc. 2014, 136, 11664–11673. [Google Scholar] [CrossRef]
- Volmer, M. Kinetics of Phase Formation (Kinetik der Phasenbildung). In Die Chemische Reaktion; Bonhoeffer, K.F., Ed.; Central Air Documents; Wright-Patterson AFB: Dayton, OH, USA, 1939; Volume IV. [Google Scholar]
- Bernstein, J.; Davey Roger, J.; Henck, J.-O. Concomitant Polymorphs. Angew. Chem. Int. Ed. 1999, 38, 3440–3461. [Google Scholar] [CrossRef]
- Parsons, R.; Robinson, K.M.; Twomey, T.A.; Leiserowitz, L.; Roberts, K.J.; Chernov, A.A.; van der Eerden, J.P.; Bennema, P.; Frenken, J.W.M.; Sherwood, J.N.; et al. General discussion. Faraday Discuss. 1993, 95, 145–171. [Google Scholar] [CrossRef]
- Keller, A.; Goldbeck-Wood, G.; Hikosaka, M. Polymer crystallization: survey and new trends with wider implications for phase transformations. Faraday Discuss. 1993, 95, 109–128. [Google Scholar] [CrossRef]
- Teychené, S.; Biscans, B. Nucleation Kinetics of Polymorphs: Induction Period and Interfacial Energy Measurements. Cryst. Growth Des. 2008, 8, 1133–1139. [Google Scholar] [CrossRef]
- Black, J.F.B.; Cardew, P.T.; Cruz-Cabeza, A.J.; Davey, R.J.; Gilks, S.E.; Sullivan, R.A. Crystal nucleation and growth in a polymorphic system: Ostwald’s rule, p-aminobenzoic acid and nucleation transition states. CrystEngComm 2018, 20, 768–776. [Google Scholar] [CrossRef]
- Stranski, I.; Totomanow, D. Keimbildungsgeschwindigkeit und Ostwaldsche Stufenregel. Z. Phys. Chem. 1933, 163, 399–408. [Google Scholar] [CrossRef]
- Croker, D.; Hodnett, B.K. Mechanistic Features of Polymorphic Transformations: The Role of Surfaces. Cryst. Growth Des. 2010, 10, 2806–2816. [Google Scholar] [CrossRef]
- Kadam, S.S.; Kramer, H.J.M.; ter Horst, J.H. Combination of a Single Primary Nucleation Event and Secondary Nucleation in Crystallization Processes. Cryst. Growth Des. 2011, 11, 1271–1277. [Google Scholar] [CrossRef]
- Kulkarni, S.A.; Meekes, H.; ter Horst, J.H. Polymorphism Control through a Single Nucleation Event. Cryst. Growth Des. 2014, 14, 1493–1499. [Google Scholar] [CrossRef]
- Maher, A.; Hodnett, B.K.; Coughlan, N.; O’Brien, M.; Croker, D.M. Application of New Technology to a Mature Piroxicam Crystallization Process To Gain Process Understanding and Control, via Industrial–Academic Collaboration. Org. Process Res. Dev. 2018, 22, 306–311. [Google Scholar] [CrossRef]
- Verdurand, E.; Bebon, C.; Colson, D.; Klein, J.P.; Blandin, A.F.; Bossoutrot, J.M. Secondary nucleation and growth of organic crystals in industrial crystallization. J. Cryst. Growth 2005, 275, e1363–e1367. [Google Scholar] [CrossRef]
- De Souza, B.; Cogoni, G.; Tyrrell, R.; Frawley, P.J. Evidence of Crystal Nuclei Breeding in Laboratory Scale Seeded Batch Isothermal Crystallization Experiments. Cryst. Growth Des. 2016, 16, 3443–3453. [Google Scholar] [CrossRef]
- Steendam, R.R.E.; Keshavarz, L.; Blijlevens, M.A.R.; de Souza, B.; Croker, D.M.; Frawley, P.J. Effects of Scale-Up on the Mechanism and Kinetics of Crystal Nucleation. Cryst. Growth Des. 2018. [Google Scholar] [CrossRef]
- Anwar, J.; Khan, S.; Lindfors, L. Secondary Crystal Nucleation: Nuclei Breeding Factory Uncovered. Angew. Chem. Int. Ed. 2015, 54, 14681–14684. [Google Scholar] [CrossRef]
- Granberg, R.A.; Ducreux, C.; Gracin, S.; Rasmuson, Å.C. Primary nucleation of paracetamol in acetone–water mixtures. Chem. Eng. Sci. 2001, 56, 2305–2313. [Google Scholar] [CrossRef]
- Jiang, S.; ter Horst, J.H. Crystal Nucleation Rates from Probability Distributions of Induction Times. Cryst. Growth Des. 2011, 11, 256–261. [Google Scholar] [CrossRef]
- Mealey, D.; Zeglinski, J.; Khamar, D.; Rasmuson, A.C. Influence of solvent on crystal nucleation of risperidone. Faraday Discuss. 2015, 179, 309–328. [Google Scholar] [CrossRef] [PubMed]
- Cruz-Cabeza, A.J.; Davey, R.J.; Sachithananthan, S.S.; Smith, R.; Tang, S.K.; Vetter, T.; Xiao, Y. Aromatic stacking - a key step in nucleation. Chem. Commun. 2017, 53, 7905–7908. [Google Scholar] [CrossRef]
- Teychene, S.; Autret, J.M.; Biscans, B. Determination of solubility profiles of eflucimibe polymorphs: Experimental and modeling. J. Pharm. Sci. 2006, 95, 871–882. [Google Scholar] [CrossRef]
- Su, W.; Hao, H.; Glennon, B.; Barrett, M. Spontaneous Polymorphic Nucleation of d-Mannitol in Aqueous Solution Monitored with Raman Spectroscopy and FBRM. Cryst. Growth Des. 2013, 13, 5179–5187. [Google Scholar] [CrossRef]
- Renuka Devi, K.; Gnanakamatchi, V.; Srinivasan, K. Attainment of unstable β nucleation of glycine through novel swift cooling crystallization process. J. Cryst. Growth 2014, 400, 34–42. [Google Scholar] [CrossRef]
- Lu, J.; Wang, X.-J.; Yang, X.; Ching, C.-B. Polymorphism and Crystallization of Famotidine. Cryst. Growth Des. 2007, 7, 1590–1598. [Google Scholar] [CrossRef]
- Mirmehrabi, M.; Rohani, S.; Murthy, K.S.K.; Radatus, B. Polymorphic Behavior and Crystal Habit of an Anti-Viral/HIV Drug: Stavudine. Cryst. Growth Des. 2006, 6, 141–149. [Google Scholar] [CrossRef]
- Roelands, C.P.M.; Jiang, S.; Kitamura, M.; ter Horst, J.H.; Kramer, H.J.M.; Jansens, P.J. Antisolvent Crystallization of the Polymorphs of l-Histidine as a Function of Supersaturation Ratio and of Solvent Composition. Cryst. Growth Des. 2006, 6, 955–963. [Google Scholar] [CrossRef]
- Kitamura, M.; Hara, T.; Takimoto-Kamimura, M. Solvent Effect on Polymorphism in Crystallization of BPT Propyl Ester. Cryst. Growth Des. 2006, 6, 1945–1950. [Google Scholar] [CrossRef]
- Sun, Z.; Hao, H.; Xie, C.; Xu, Z.; Yin, Q.; Bao, Y.; Hou, B.; Wang, Y. Thermodynamic Properties of Form A and Form B of Florfenicol. Ind. Eng. Chem. Res. 2014, 53, 13506–13512. [Google Scholar] [CrossRef]
- Roelands, C.P.M.; ter Horst, J.H.; Kramer, H.J.M.; Jansens, P.J. The unexpected formation of the stable beta phase of l-glutamic acid during pH-shift precipitation. J. Cryst. Growth 2005, 275, e1389–e1395. [Google Scholar] [CrossRef]
- Shiau, L.-D. Modelling of the Polymorph Nucleation Based on Classical Nucleation Theory. Crystals 2019, 9, 69. [Google Scholar] [CrossRef]
- Jiang, S.; ter Horst, J.H.; Jansens, P.J. Concomitant Polymorphism of o-Aminobenzoic Acid in Antisolvent Crystallization. Cryst. Growth Des. 2008, 8, 37–43. [Google Scholar] [CrossRef]
- Su, W.; Hao, H.; Barrett, M.; Glennon, B. The Impact of Operating Parameters on the Polymorphic Transformation of d-Mannitol Characterized in Situ with Raman Spectroscopy, FBRM, and PVM. Org. Process Res. Dev. 2010, 14, 1432–1437. [Google Scholar] [CrossRef]
- Caridi, A.; Kulkarni, S.A.; di Profio, G.; Curcio, E.; ter Horst, J.H. Template-Induced Nucleation of Isonicotinamide Polymorphs. Cryst. Growth Des. 2014, 14, 1135–1141. [Google Scholar] [CrossRef]
- Arribas Bueno, R.; Crowley, C.M.; Hodnett, B.K.; Hudson, S.; Davern, P. Influence of Process Parameters on the Heterogeneous Nucleation of Active Pharmaceutical Ingredients onto Excipients. Org. Process Res. Dev. 2017, 21, 559–570. [Google Scholar] [CrossRef]
- Teychené, S.; Autret, J.M.; Biscans, B. Crystallization of Eflucimibe Drug in a Solvent Mixture: Effects of Process Conditions on Polymorphism. Cryst. Growth Des. 2004, 4, 971–977. [Google Scholar] [CrossRef]
- Espitalier, F.; Biscans, B.; Laguérie, C. Particle design Part A: Nucleation kinetics of ketoprofen. Chem. Eng. J. 1997, 68, 95–102. [Google Scholar] [CrossRef]
- Gracin, S.; Uusi-Penttilä, M.; Rasmuson, Å.C. Influence of Ultrasound on the Nucleation of Polymorphs of p-Aminobenzoic Acid. Cryst. Growth Des. 2005, 5, 1787–1794. [Google Scholar] [CrossRef]
- Eder, R.J.P.; Radl, S.; Schmitt, E.; Innerhofer, S.; Maier, M.; Gruber-Woelfler, H.; Khinast, J.G. Continuously Seeded, Continuously Operated Tubular Crystallizer for the Production of Active Pharmaceutical Ingredients. Cryst. Growth Des. 2010, 10, 2247–2257. [Google Scholar] [CrossRef]
- Lawton, S.; Steele, G.; Shering, P.; Zhao, L.H.; Laird, I.; Ni, X.W. Continuous Crystallization of Pharmaceuticals Using a Continuous Oscillatory Baffled Crystallizer. Org. Process Res. Dev. 2009, 13, 1357–1363. [Google Scholar] [CrossRef]
- Alvarez, A.J.; Singh, A.; Myerson, A.S. Crystallization of Cyclosporine in a Multistage Continuous MSMPR Crystallizer. Cryst. Growth Des. 2011, 11, 4392–4400. [Google Scholar] [CrossRef]
- Wong, S.Y.; Tatusko, A.P.; Trout, B.L.; Myerson, A.S. Development of Continuous Crystallization Processes Using a Single-Stage Mixed-Suspension, Mixed-Product Removal Crystallizer with Recycle. Cryst. Growth Des. 2012, 12, 5701–5707. [Google Scholar] [CrossRef]
- Alvarez, A.J.; Myerson, A.S. Continuous Plug Flow Crystallization of Pharmaceutical Compounds. Cryst. Growth Des. 2010, 10, 2219–2228. [Google Scholar] [CrossRef]
- Sultana, M.; Jensen, K.F. Microfluidic Continuous Seeded Crystallization: Extraction of Growth Kinetics and Impact of Impurity on Morphology. Cryst. Growth Des. 2012, 12, 6260–6266. [Google Scholar] [CrossRef]
- Wierzbowska, B.; Hutnik, N.; Piotrowski, K.; Matynia, A. Continuous Mass Crystallization of Vitamin C in l(+)-Ascorbic Acid−Ethanol−Water System: Size-Independent Growth Kinetic Model Approach. Cryst. Growth Des. 2011, 11, 1557–1565. [Google Scholar] [CrossRef]
- Ferguson, S.; Morris, G.; Hao, H.X.; Barrett, M.; Glennon, B. Characterization of the anti-solvent batch, plug flow and MSMPR crystallization of benzoic acid. Chem. Eng. Sci. 2013, 104, 44–54. [Google Scholar] [CrossRef]
- Quon, J.L.; Zhang, H.; Alvarez, A.; Evans, J.; Myerson, A.S.; Trout, B.L. Continuous Crystallization of Aliskiren Hemifumarate. Cryst. Growth Des. 2012, 12, 3036–3044. [Google Scholar] [CrossRef]
- Lai, T.-T.C.; Ferguson, S.; Palmer, L.; Trout, B.L.; Myerson, A.S. Continuous Crystallization and Polymorph Dynamics in the l-Glutamic Acid System. Org. Process Res. Dev. 2014, 18, 1382–1390. [Google Scholar] [CrossRef]
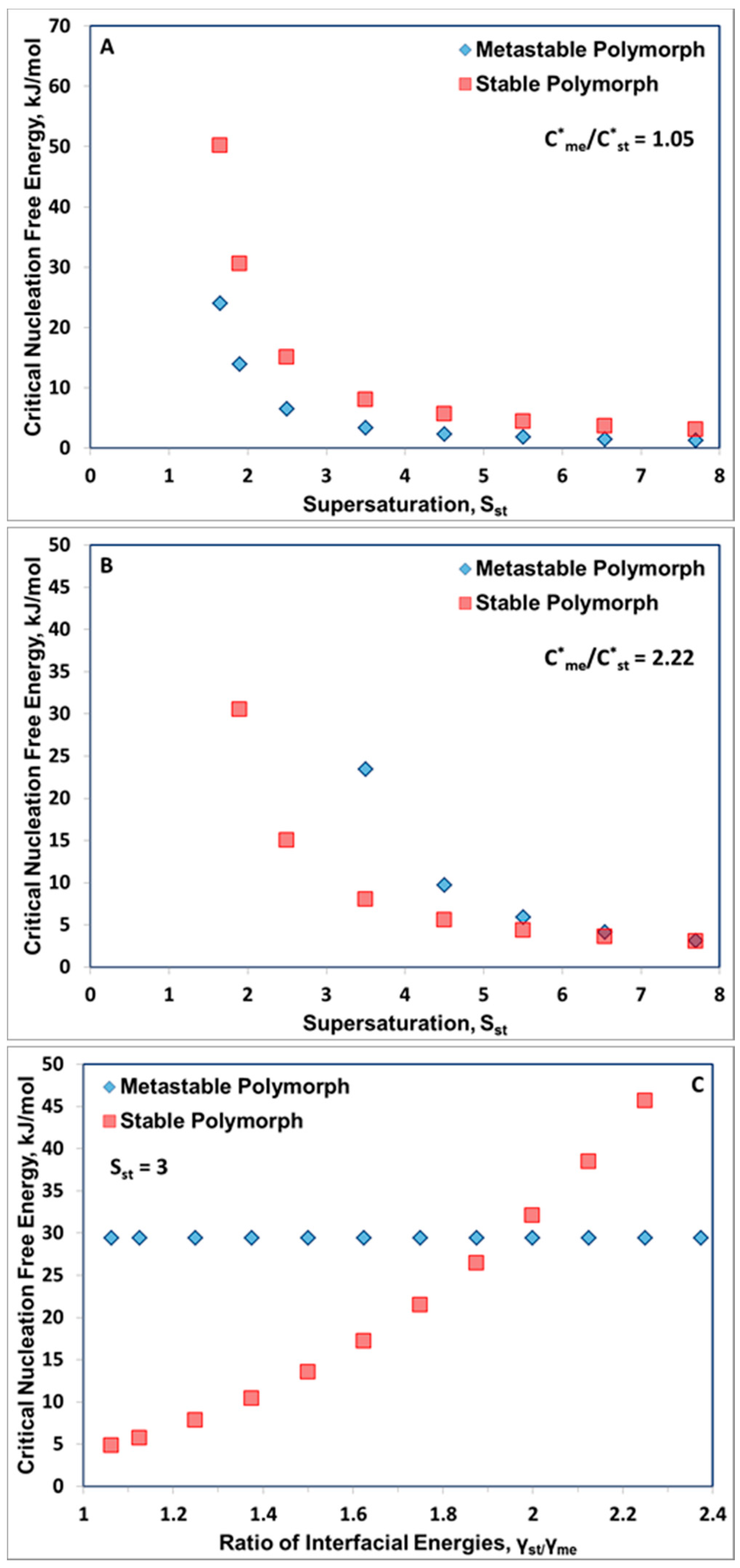
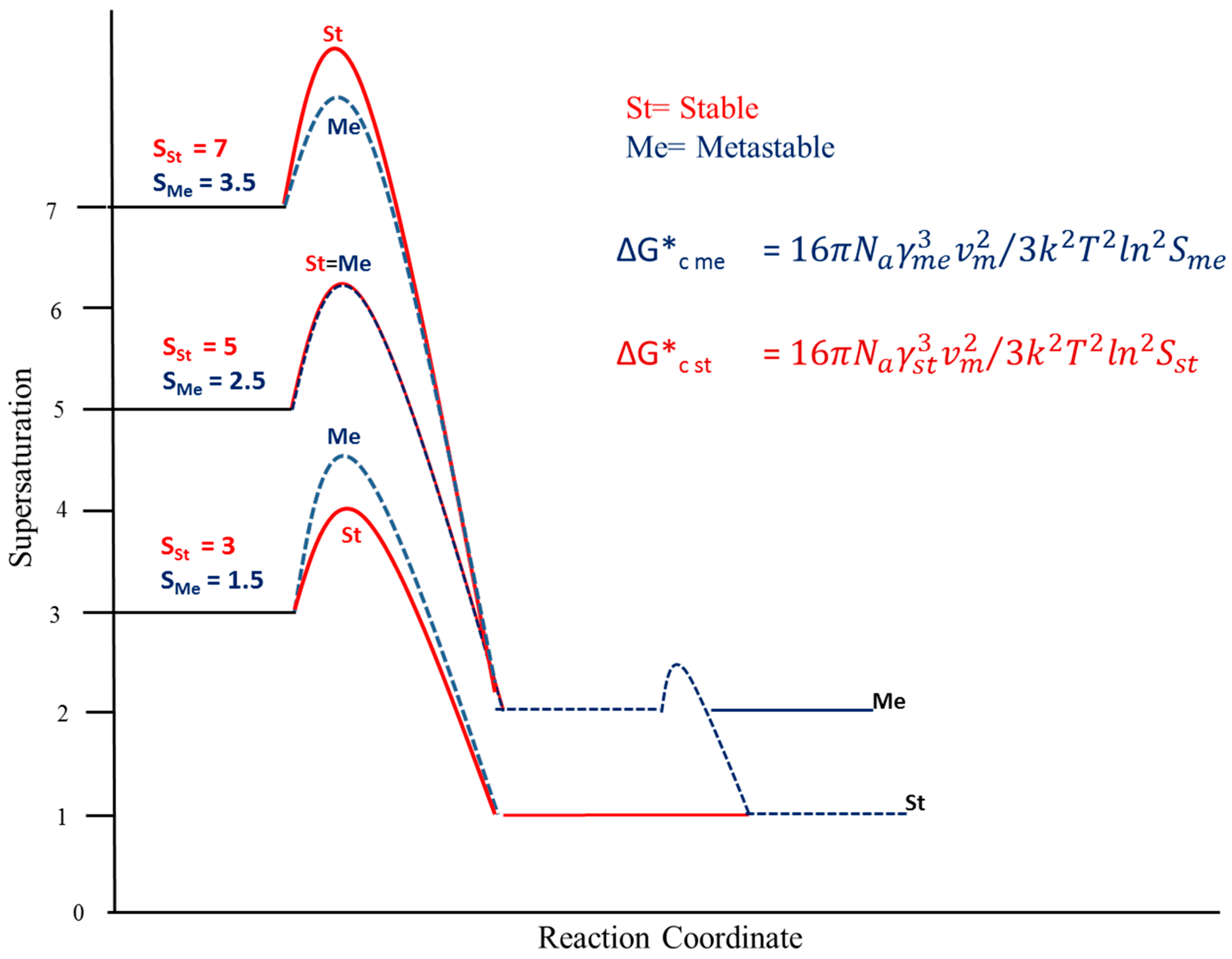
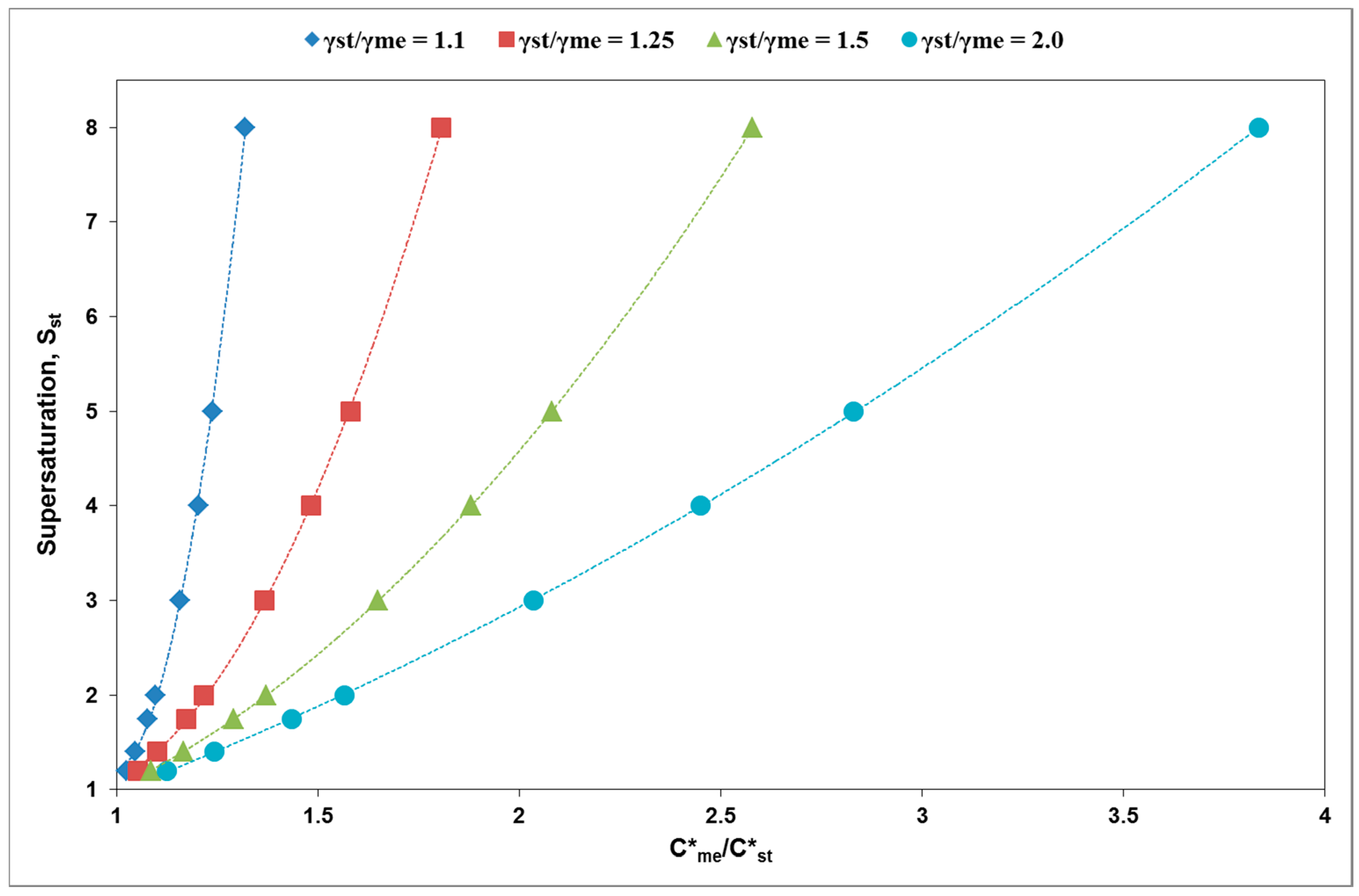
| γst/γme | C*me/C*st | Sst min (C/C*st) | Cmszw,me/C*st |
|---|---|---|---|
| 1.1 | 1.09 | 1.8 | 1.63 |
| 1.15 | 3.7 | 1.7 | |
| 1.33 | 8.0 | 2.0 | |
| 1.25 | 1.2 | 2 | 1.8 |
| 1.5 | 4 | 2.3 | |
| 1.8 | 8 | 2.7 | |
| 1.5 | 1.2 | 1.5 | 1.9 |
| 1.5 | 2.5 | 2.25 | |
| 2 | 5 | 3 | |
| 2.5 | 7.5 | 3.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hodnett, B.K.; Verma, V. Thermodynamic vs. Kinetic Basis for Polymorph Selection. Processes 2019, 7, 272. https://doi.org/10.3390/pr7050272
Hodnett BK, Verma V. Thermodynamic vs. Kinetic Basis for Polymorph Selection. Processes. 2019; 7(5):272. https://doi.org/10.3390/pr7050272
Chicago/Turabian StyleHodnett, Benjamin K., and Vivek Verma. 2019. "Thermodynamic vs. Kinetic Basis for Polymorph Selection" Processes 7, no. 5: 272. https://doi.org/10.3390/pr7050272
APA StyleHodnett, B. K., & Verma, V. (2019). Thermodynamic vs. Kinetic Basis for Polymorph Selection. Processes, 7(5), 272. https://doi.org/10.3390/pr7050272





