Monitoring the Process Based on Belief Statistic for Neutrosophic Gamma Distributed Product
Abstract
1. Introduction
2. The Neutrosophic Gamma Distribution
3. Designing of the Proposed Chart
3.1. The Proposed Chart
3.2. Neutrosophic Average Run Length for In-Control Process
3.3. Neutrosophic Average Run Length for Shifted Process
4. Advantages of the Proposed Chart
4.1. By NARL
4.2. By Simulation
5. Real Example
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gülbay, M.; Kahraman, C.; Ruan, D. α-Cut fuzzy control charts for linguistic data. Int. J. Intell. Syst. 2004, 19, 1173–1195. [Google Scholar] [CrossRef]
- Demirli, K.; Vijayakumar, S. Fuzzy logic based assignable cause diagnosis using control chart patterns. Inf. Sci. 2010, 180, 3258–3272. [Google Scholar] [CrossRef][Green Version]
- Montgomery, C.D. Introduction to Statistical Quality Control, 6th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2009. [Google Scholar]
- Cheng, C.-B. Fuzzy process control: Construction of control charts with fuzzy numbers. Fuzzy Sets Syst. 2005, 154, 287–303. [Google Scholar] [CrossRef]
- Gülbay, M.; Kahraman, C. An alternative approach to fuzzy control charts: Direct fuzzy approach. Inf. Sci. 2007, 177, 1463–1480. [Google Scholar] [CrossRef]
- Fallah Nezhad, M.S.; Akhavan Niaki, S.T. A new monitoring design for uni-variate statistical quality control charts. Inf. Sci. 2010, 180, 1051–1059. [Google Scholar] [CrossRef]
- Aksoy, H. Use of gamma distribution in hydrological analysis. Turk. J. Eng. Environ. Sci. 2000, 24, 419–428. [Google Scholar]
- Zhang, C.; Zhang, C.W.; Xie, M.; Liu, J.Y.; Goh, T.N. A control chart for the Gamma distribution as a model of time between events. Int. J. Prod. Res. 2007, 45, 5649–5666. [Google Scholar] [CrossRef]
- Aslam, M.; Arif, O.-H.; Jun, C.-H. A Control Chart for Gamma Distribution using Multiple Dependent State Sampling. Ind. Eng. Manag. Syst. 2017, 16, 109–117. [Google Scholar] [CrossRef]
- Chen, F.; Yeh, C.-H. Economic statistical design of non-uniform sampling scheme X bar control charts under non-normality and Gamma shock using genetic algorithm. Expert Syst. Appl. 2009, 36, 9488–9497. [Google Scholar] [CrossRef]
- Al-Oraini, H.A.; Rahim, M. Economic statistical design of X control charts for systems with Gamma (λ, 2) in-control times. Comput. Ind. Eng. 2002, 43, 645–654. [Google Scholar] [CrossRef]
- Bhaumik, D.K.; Gibbons, R.D. One-sided approximate prediction intervals for at least p of m observations from a gamma population at each of r locations. Technometrics 2006, 48, 112–119. [Google Scholar] [CrossRef]
- Khan, N.; Aslam, M.; Ahmad, L.; Jun, C.H. A Control Chart for Gamma Distributed Variables Using Repetitive Sampling Scheme. Pak. J. Stat. Oper. Res. 2017, 13, 47–61. [Google Scholar] [CrossRef][Green Version]
- Kaya, I.; Erdoğan, M.; Yıldız, C. Analysis and control of variability by using fuzzy individual control charts. Appl. Soft Comput. 2017, 51, 370–381. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophic logic-generalization of the intuitionistic fuzzy logic. arXiv, 2003; arXiv:math/0303009. [Google Scholar]
- Şentürk, S.; Erginel, N.; Kaya, İ.; Kahraman, C. Fuzzy exponentially weighted moving average control chart for univariate data with a real case application. Appl. Soft Comput. 2014, 22, 1–10. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Wang, J.-H.; Raz, T. On the construction of control charts using linguistic variables. Int. J. Prod. Res. 1990, 28, 477–487. [Google Scholar] [CrossRef]
- Raz, T.; Wang, J.-H. Probabilistic and membership approaches in the construction of control charts for linguistic data. Prod. Plan. Control 1990, 1, 147–157. [Google Scholar] [CrossRef]
- Taleb, H.; Limam, M. On fuzzy and probabilistic control charts. Int. J. Prod. Res. 2002, 40, 2849–2863. [Google Scholar] [CrossRef]
- Kanagawa, A.; Tamaki, F.; Ohta, H. Control charts for process average and variability based on linguistic data. Int. J. Prod. Res. 1993, 31, 913–922. [Google Scholar] [CrossRef]
- Erginel, N.; Sentürk, S.; Kahraman, C.; Kaya, I. Evaluating the packing process in food industry using fuzzy and [stilde] control charts. Int. J. Comput. Intell. Syst. 2011, 4, 509–520. [Google Scholar] [CrossRef]
- El-Shal, S.M.; Morris, A.S. A fuzzy rule-based algorithm to improve the performance of statistical process control in quality systems. J. Intell. Fuzzy Syst. 2000, 9, 207–223. [Google Scholar]
- Rowlands, H.; Wang, L.R. An approach of fuzzy logic evaluation and control in SPC. Qual. Reliab. Eng. Int. 2000, 16, 91–98. [Google Scholar] [CrossRef]
- Aslam, M. A New Sampling Plan Using Neutrosophic Process Loss Consideration. Symmetry 2018, 10, 132. [Google Scholar] [CrossRef]
- Senturk, S.; Erginel, N. Development of fuzzy and control charts using α-cuts. Inf. Sci. 2009, 179, 1542–1551. [Google Scholar] [CrossRef]
- Sentürk, S. Fuzzy regression control chart based on α-cut approximation. Int. J. Comput. Intell. Syst. 2010, 3, 123–140. [Google Scholar] [CrossRef]
- Kaya, İ.; Kahraman, C. Process capability analyses based on fuzzy measurements and fuzzy control charts. Expert Syst. Appl. 2011, 38, 3172–3184. [Google Scholar] [CrossRef]
- Broumi, S.; Smarandache, F. Correlation coefficient of interval neutrosophic set. In Applied Mechanics and Materials; Trans Tech Publication: Stafa-Zurich, Switzerland, 2013; pp. 511–517. [Google Scholar]
- Smarandache, F. Neutrosophic Logic-A Generalization of the Intuitionistic Fuzzy Logic. Multispace Multistruct. Neutrosophic Transdiscipl. 2010, 4, 396. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophy: Neutrosophic Probability, Set, and Logic: Analytic Synthesis & Synthetic Analysis; American Research Press: Rehoboth, DE, USA, 1998; p. 105. [Google Scholar]
- Smarandache, F. Introduction to Neutrosophic Statistics; Infinite Study: Hollywood, FL, USA, 2014. [Google Scholar]
- Chen, J.; Ye, J.; Du, S. Scale effect and anisotropy analyzed for neutrosophic numbers of rock joint roughness coefficient based on neutrosophic statistics. Symmetry 2017, 9, 208. [Google Scholar] [CrossRef]
- Chen, J.; Ye, J.; Du, S.; Yong, R. Expressions of rock joint roughness coefficient using neutrosophic interval statistical numbers. Symmetry 2017, 9, 123. [Google Scholar] [CrossRef]
- Aslam, M. A New Failure-Censored Reliability Test Using Neutrosophic Statistical Interval Method. Int. J. Fuzzy Syst. 2019, 1–7. [Google Scholar] [CrossRef]
- Aslam, M. Design of Sampling Plan for Exponential Distribution under Neutrosophic Statistical Interval Method. IEEE Access 2018, 6, 64153–64158. [Google Scholar] [CrossRef]
- Aslam, M. A new attribute sampling plan using neutrosophic statistical interval method. Complex Intell. Syst. 2019, 1–6. [Google Scholar] [CrossRef]
- Aslam, M.; Bantan, R.A.; Khan, N. Design of a New Attribute Control Chart Under Neutrosophic Statistics. Int. J. Fuzzy Syst. 2019, 21, 433–440. [Google Scholar] [CrossRef]
- Aslam, M.; Khan, N.; Khan, M. Monitoring the Variability in the Process Using Neutrosophic Statistical Interval Method. Symmetry 2018, 10, 562. [Google Scholar] [CrossRef]
- Aslam, M.; Bantan, R.A.; Khan, N. Design of a Control Chart for Gamma Distributed Variables under the Indeterminate Environment. IEEE Access 2019, 7, 8858–8864. [Google Scholar] [CrossRef]
- Aslam, M. Product Acceptance Determination with Measurement Error Using the Neutrosophic Statistics. Adv. Fuzzy Syst. 2019, 2019, 8953051. [Google Scholar] [CrossRef]
- Aslam, M.; Arif, O. Testing of Grouped Product for the Weibull Distribution Using Neutrosophic Statistics. Symmetry 2018, 10, 403. [Google Scholar] [CrossRef]
- Aslam, M.; Raza, M.A. Design of New Sampling Plans for Multiple Manufacturing Lines Under Uncertainty. Int. J. Fuzzy Syst. 2019, 21, 978–992. [Google Scholar] [CrossRef]
- Peng, X.; Dai, J. A bibliometric analysis of neutrosophic set: Two decades review from 1998 to 2017. Artif. Intell. Rev. 2018, 1–57. [Google Scholar] [CrossRef]
- Peng, X.; Dai, J. Approaches to single-valued neutrosophic MADM based on MABAC, TOPSIS and new similarity measure with score function. Neural Comput. Appl. 2018, 29, 939–954. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophic set-a generalization of the intuitionistic fuzzy set. J. Def. Resour. Manag. 2010, 1, 107. [Google Scholar]
- Smarandache, F. A geometric interpretation of the neutrosophic set-A generalization of the intuitionistic fuzzy set. arXiv, 2004; arXiv:math/0404520. [Google Scholar]
- Smarandache, F. n-Valued Refined Neutrosophic Logic and Its Applications to Physics. Available online: https://arxiv.org/pdf/1407.104 (accessed on 12 March 2019).
- Rivieccio, U. Neutrosophic logics: Prospects and problems. Fuzzy Sets Syst. 2008, 159, 1860–1868. [Google Scholar] [CrossRef]
- Wang, H.; Smarandache, F.; Zhang, Y.; Sunderraman, R. Single Valued Neutrosophic Sets. Available online: fs.unm.edu/SingleValuedNeutrosophicSets.pdf (accessed on 12 March 2019).
- Wang, H.; Smarandache, F.; Sunderraman, R.; Zhang, Y.Q. Interval Neutrosophic Sets and Logic: Theory and Applications in Computing: Theory and Applications in Computing. Available online: https://arxiv.org/abs/cs/0505014 (accessed on 12 March 2019).
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques—Part II: Fault diagnosis with knowledge-based and hybrid/active approaches. IEEE Trans. Ind. Electron. 2015, 62, 3768–3774. [Google Scholar] [CrossRef]
- Wilson, E.B.; Hilferty, M.M. The distribution of chi-square. Proc. Natl. Acad. Sci. USA 1931, 17, 684–688. [Google Scholar] [CrossRef]
- Ahmad, L.; Aslam, M.; Jun, C.-H. Designing of X-bar control charts based on process capability index using repetitive sampling. Trans. Inst. Meas. Control 2014, 36, 367–374. [Google Scholar] [CrossRef]
- Knoth, S. Accurate ARL Calculation for EWMA Control Charts Monitoring Normal Mean and Variance Simultaneously. Seq. Anal. 2007, 26, 251–263. [Google Scholar] [CrossRef]
- Li, Z.H.; Zou, C.; Gong, Z.; Wang, Z. The computation of average run length and average time to signal: An overview. J. Stat. Comput. Simul. 2014, 84, 1779–1802. [Google Scholar] [CrossRef]
- Lee, M.; Khoo, M.B. Optimal statistical design of a multivariate EWMA chart based on ARL and MRL. Commun. Stat. Simul. Comput. 2006, 35, 831–847. [Google Scholar] [CrossRef]
- Phanyaem, S.; Areepong, Y.; Sukparungsee, S. Numerical Integration of Average Run Length of CUSUM Control Chart for ARMA Process. Int. J. Appl. Phys. Math. 2014, 4, 232–235. [Google Scholar] [CrossRef]
- Busaba, J.; Sukparungsee, S.; Areepong, Y. Numerical approximations of average run length for AR (1) on exponential CUSUM. Comput. Sci. Telecommun. 2012, 19, 23. [Google Scholar]
- Aslam, M.; Khan, N.; Ahmad, L.; Jun, C.H.; Hussain, J. A mixed control chart using process capability index. Seq. Anal. 2017, 36, 278–289. [Google Scholar] [CrossRef]
- Ahmad, L.; Aslam, M.; Khan, N.; Jun, C.H. Double moving average control chart for exponential distributed life using EWMA. In AIP Conference Proceedings; AIP Publishing: New York, NY, USA, 2017. [Google Scholar]
- Ahmad, L.; Aslam, M.; Jun, C.-H. Coal Quality Monitoring With Improved Control Charts. Eur. J. Sci. Res. 2014, 125, 427–434. [Google Scholar]
- Aslam, M.; Khan, N.; Jun, C.-H. A control chart using belief information for a gamma distribution. Oper. Res. Decis. 2016, 26, 5–19. [Google Scholar]
- Santiago, E.; Smith, J. Control charts based on the exponential distribution: Adapting runs rules for the t chart. Qual. Eng. 2013, 25, 85–96. [Google Scholar] [CrossRef]
- Smarandache, F. Introduction to Neutrosophic Measure, Neutrosophic Integral, and Neutrosophic Probability. Available online: https://arxiv.org/abs/1311.7139 (accessed on 12 March 2019).
- Smarandache, F. Neutrosophic Precalculus and Neutrosophic Calculus: Neutrosophic Applications. Available online: https://arxiv.org/pdf/1509.07723 (accessed on 12 March 2019).
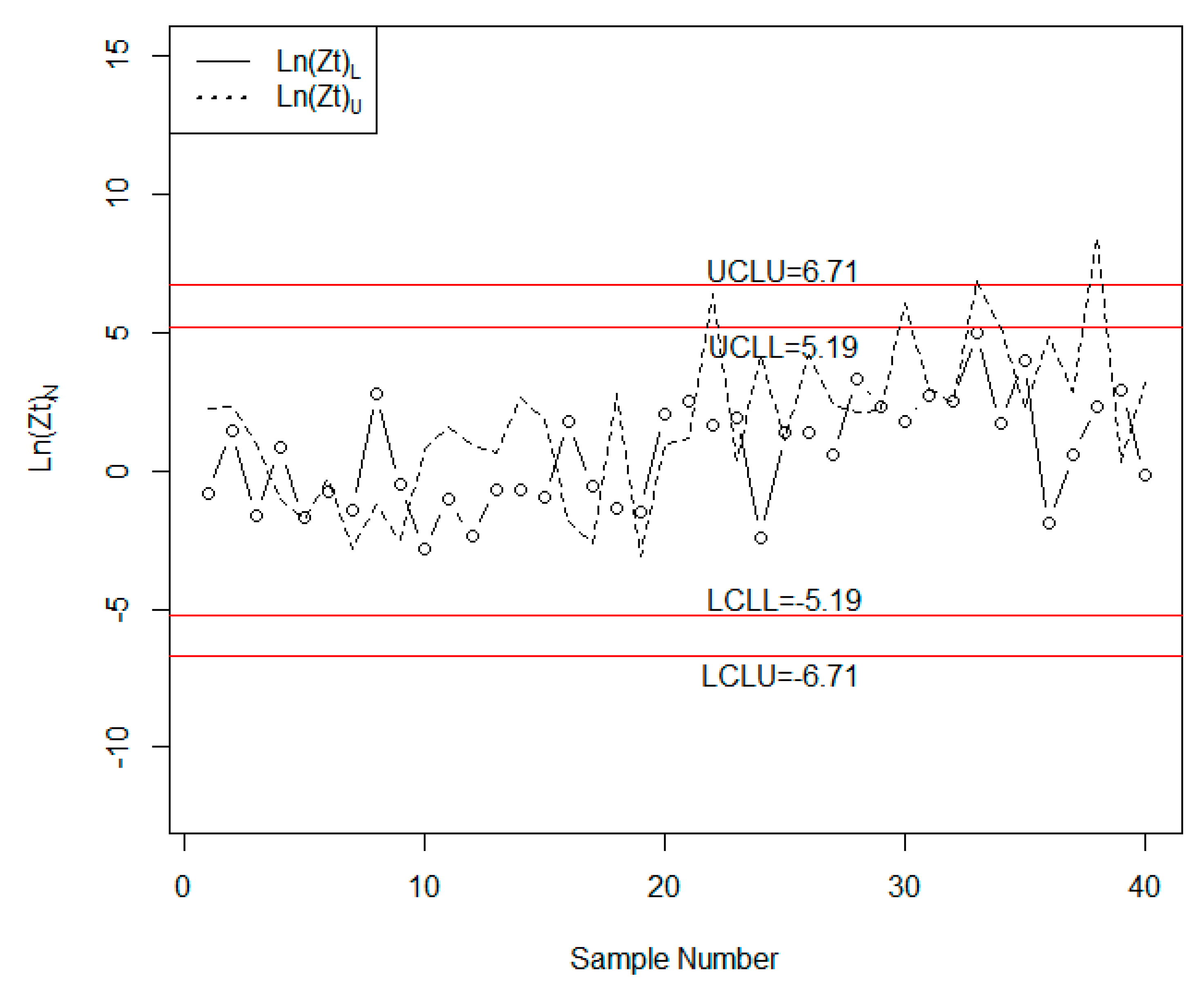
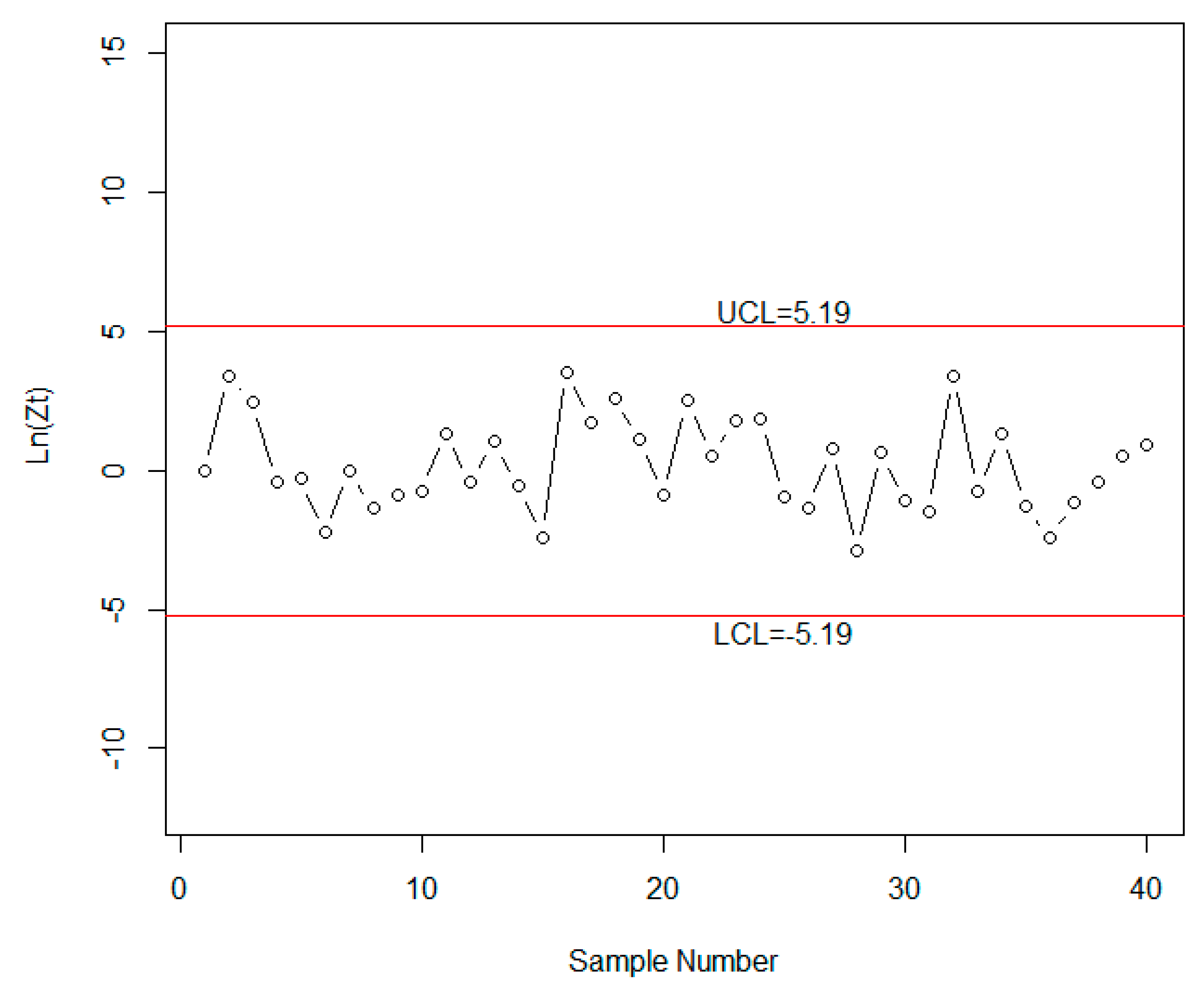
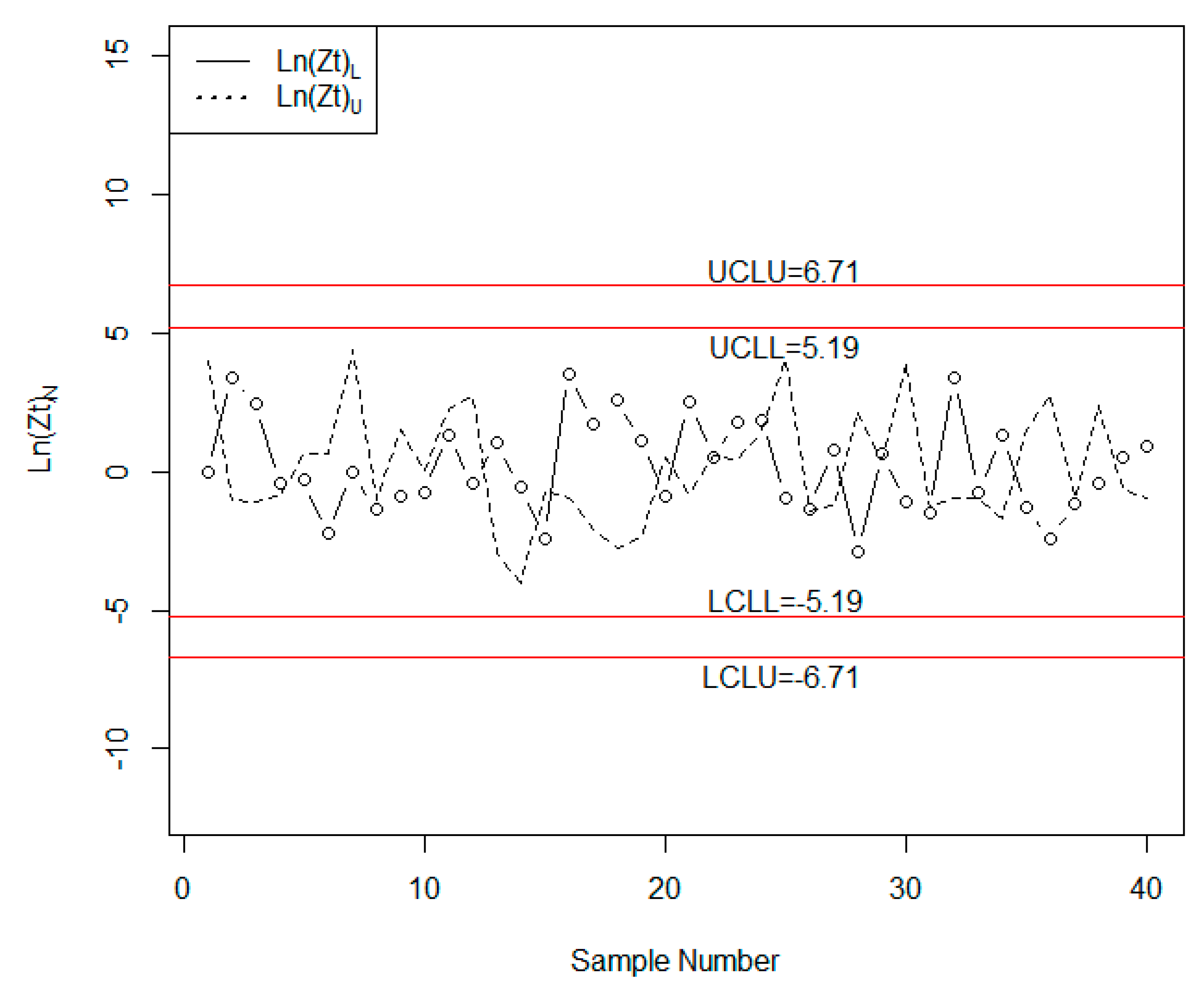
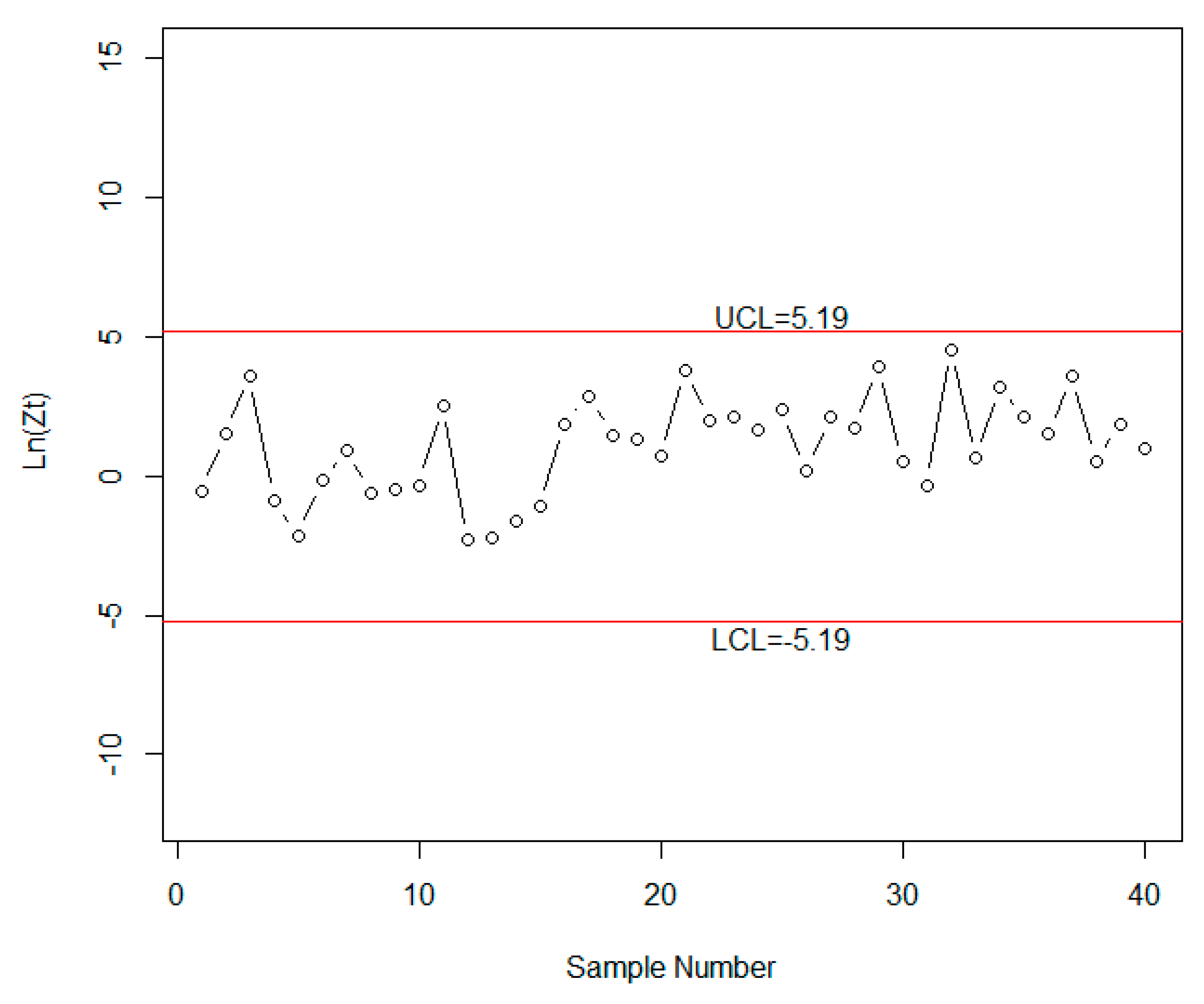
| [2.8071,2.8141] | [2.9354,2.9416] | [3.0003,3.0012] | |
| s | NARL | ||
| 4.00 | [1.28,1.06] | [1.32,1.07] | [1.34,1.07] |
| 3.00 | [1.76,1.24] | [1.88,1.28] | [1.95,1.31] |
| 2.80 | [1.98,1.34] | [2.13,1.40] | [2.22,1.43] |
| 2.50 | [2.50,1.58] | [2.75,1.68] | [2.89,1.73] |
| 2.25 | [3.27,1.97] | [3.67,2.13] | [3.91,2.22] |
| 2.00 | [4.75,2.74] | [5.48,3.05] | [5.92,3.22] |
| 1.90 | [5.74,3.28] | [6.71,3.70] | [7.29,3.93] |
| 1.80 | [7.13,4.05] | [8.47,4.66] | [9.28,4.98] |
| 1.70 | [9.18,5.24] | [11.1,6.12] | [12.26,6.61] |
| 1.60 | [12.32,7.12] | [15.19,8.51] | [16.96,9.28] |
| 1.50 | [17.4,10.34] | [21.93,12.67] | [24.76,13.98] |
| 1.40 | [26.08,16.27] | [33.74,20.51] | [38.61,22.94] |
| 1.30 | [41.89,28.25] | [55.90,36.86] | [64.99,41.90] |
| 1.20 | [72.12,54.92] | [99.88,74.68] | [118.35,86.58] |
| 1.10 | [127.96,115.71] | [185.0,165.6] | [224.15,196.69] |
| 1.00 | [200.02,204.41] | [300.17,306.26] | [370.82,371.83] |
| 0.80 | [152.58,98.67] | [227.95,143.72] | [281.15,172.31] |
| 0.75 | [119.34,67.59] | [177.29,97.32] | [218.11,116.09] |
| 0.70 | [90.73,45.44] | [134.07,64.61] | [164.56,76.64] |
| 0.60 | [49.26,19.71] | [71.88,27.17] | [87.73,31.78] |
| 0.50 | [24.63,8.22] | [35.26,10.86] | [42.65,12.45] |
| 0.40 | [11.21,3.44] | [15.56,4.26] | [18.55,4.75] |
| 0.30 | [4.64,1.60] | [6.10,1.82] | [7.09,1.95] |
| 0.25 | [2.91,1.22] | [3.68,1.32] | [4.19,1.37] |
| 0.15 | [1.27,1.00] | [1.4,1.01] | [1.49,1.01] |
| 0.10 | [1.03,1.00] | [1.05,1.00] | [1.07,1.00] |
| 0.05 | [1.00,1.00] | [1.00,1.00] | [1.00,1.00] |
| [2.8071,2.8164] | [2.9354,2.9436] | [2.9997,3.007] | |
| s | NARL | ||
| 4.00 | [1.01,1] | [1.01,1] | [1.01,1] |
| 3.00 | [1.07,1.02] | [1.08,1.03] | [1.09,1.03] |
| 2.80 | [1.11,1.04] | [1.13,1.05] | [1.14,1.05] |
| 2.50 | [1.23,1.1] | [1.27,1.12] | [1.29,1.13] |
| 2.25 | [1.43,1.22] | [1.5,1.26] | [1.54,1.28] |
| 2.00 | [1.86,1.5] | [2.01,1.59] | [2.1,1.64] |
| 1.90 | [2.17,1.71] | [2.38,1.83] | [2.5,1.9] |
| 1.80 | [2.63,2.02] | [2.93,2.21] | [3.1,2.31] |
| 1.70 | [3.34,2.52] | [3.8,2.81] | [4.07,2.97] |
| 1.60 | [4.51,3.36] | [5.25,3.83] | [5.69,4.1] |
| 1.50 | [6.58,4.88] | [7.87,5.72] | [8.64,6.22] |
| 1.40 | [10.58,7.92] | [13.06,9.6] | [14.57,10.61] |
| 1.30 | [19.27,14.85] | [24.68,18.73] | [28.06,21.11] |
| 1.20 | [40.86,33.47] | [54.79,44.29] | [63.76,51.16] |
| 1.10 | [99.7,91.45] | [141.65,128.72] | [169.75,153.39] |
| 1.00 | [200.01,205.94] | [300.2,308.26] | [370.01,379.03] |
| 0.80 | [63.82,47.69] | [91.14,66.87] | [109.64,79.63] |
| 0.75 | [39.6,27.68] | [55.57,37.96] | [66.28,44.72] |
| 0.70 | [24.4,16.13] | [33.57,21.58] | [39.66,25.12] |
| 0.60 | [9.26,5.74] | [12.14,7.23] | [14.01,8.17] |
| 0.50 | [3.69,2.34] | [4.54,2.74] | [5.07,2.98] |
| 0.40 | [1.71,1.27] | [1.94,1.36] | [2.08,1.42] |
| 0.30 | [1.09,1.01] | [1.14,1.02] | [1.16,1.03] |
| 0.25 | [1.02,1.00] | [1.03,1.00] | [1.03,1.00] |
| 0.15 | [1.00,1.00] | [1.00,1.00] | [1.00,1.00] |
| 0.10 | [1.00,1.00] | [1.00,1.00] | [1.00,1.00] |
| 0.05 | [1.00,1.00] | [1.00,1.00] | [1.00,1.00] |
| [2.8071,2.8142] | [2.9352,2.9392] | [2.9997,3.0056] | |
| s | NARL | ||
| 4.00 | [2.09,1.4] | [2.24,1.45] | [2.32,1.49] |
| 3.00 | [3.34,2.02] | [3.71,2.17] | [3.92,2.26] |
| 2.80 | [3.86,2.29] | [4.33,2.49] | [4.61,2.61] |
| 2.50 | [5.04,2.93] | [5.78,3.25] | [6.21,3.43] |
| 2.25 | [6.74,3.88] | [7.88,4.38] | [8.56,4.69] |
| 2.00 | [9.78,5.66] | [11.74,6.58] | [12.92,7.15] |
| 1.90 | [11.71,6.84] | [14.24,8.05] | [15.76,8.81] |
| 1.80 | [14.33,8.5] | [17.66,10.15] | [19.69,11.19] |
| 1.70 | [17.99,10.91] | [22.52,13.24] | [25.31,14.73] |
| 1.60 | [23.25,14.56] | [29.63,18] | [33.6,20.23] |
| 1.50 | [31.1,20.36] | [40.43,25.71] | [46.32,29.23] |
| 1.40 | [43.21,30.06] | [57.47,38.92] | [66.63,44.84] |
| 1.30 | [62.46,47.23] | [85.32,62.95] | [100.27,73.68] |
| 1.20 | [93.37,78.73] | [131.5,108.66] | [156.99,129.57] |
| 1.10 | [140.64,134.1] | [204.74,192.56] | [248.65,234.62] |
| 1.00 | [200.02,204.48] | [300.01,303.91] | [370.04,377.32] |
| 0.80 | [238.37,175.18] | [365.34,260.87] | [455.85,324.45] |
| 0.75 | [220.33,142.4] | [338.02,211.22] | [422.1,262.24] |
| 0.70 | [197.09,112.31] | [302.88,166.02] | [378.67,205.82] |
| 0.60 | [147.18,65.42] | [227.51,95.98] | [285.52,118.6] |
| 0.50 | [101.86,34.98] | [158.66,50.71] | [200.09,62.32] |
| 0.40 | [64.33,16.86] | [100.95,23.93] | [127.95,29.12] |
| 0.30 | [35.38,7.15] | [55.76,9.77] | [70.97,11.66] |
| 0.25 | [24.24,4.43] | [38.16,5.86] | [48.62,6.88] |
| 0.15 | [8.68,1.64] | [13.36,1.93] | [16.9,2.13] |
| 0.10 | [4.15,1.12] | [6.10,1.20] | [7.59,1.26] |
| 0.05 | [1.60,1.00] | [2.05,1.00] | [2.39,1.00] |
| [2.8071,2.8145] | [2.9354,2.9399] | [2.9998,3.0019] | |
| s | NARL | ||
| 4.00 | [1.18,1.07] | [1.21,1.08] | [1.22,1.08] |
| 3.00 | [1.55,1.27] | [1.64,1.32] | [1.68,1.34] |
| 2.80 | [1.72,1.38] | [1.83,1.44] | [1.90,1.47] |
| 2.50 | [2.13,1.64] | [2.32,1.74] | [2.42,1.80] |
| 2.25 | [2.76,2.05] | [3.06,2.22] | [3.24,2.32] |
| 2.00 | [3.97,2.87] | [4.53,3.20] | [4.86,3.39] |
| 1.90 | [4.78,3.43] | [5.54,3.88] | [5.98,4.14] |
| 1.80 | [5.95,4.25] | [7.00,4.89] | [7.62,5.25] |
| 1.70 | [7.68,5.50] | [9.20,6.43] | [10.10,6.97] |
| 1.60 | [10.37,7.48] | [12.67,8.94] | [14.06,9.79] |
| 1.50 | [14.79,10.84] | [18.49,13.27] | [20.77,14.71] |
| 1.40 | [22.54,17] | [28.94,21.4] | [32.96,24.07] |
| 1.30 | [37.13,29.36] | [49.22,38.19] | [56.97,43.67] |
| 1.20 | [66.38,56.51] | [91.46,76.54] | [107.95,89.33] |
| 1.10 | [123.82,117.26] | [178.57,166.92] | [215.76,199.71] |
| 1.00 | [200.02,204.72] | [300.15,304.57] | [370.2,372.66] |
| 0.80 | [133.37,103.02] | [197.81,149.39] | [242.69,180.6] |
| 0.75 | [100.03,71.35] | [147.26,102.35] | [180.06,123.11] |
| 0.70 | [73.11,48.45] | [106.83,68.69] | [130.19,82.17] |
| 0.60 | [36.85,21.38] | [52.88,29.45] | [63.9,34.75] |
| 0.50 | [17.23,9.02] | [24.08,11.93] | [28.73,13.8] |
| 0.40 | [7.48,3.76] | [10.03,4.69] | [11.73,5.28] |
| 0.30 | [3.10,1.71] | [3.89,1.96] | [4.40,2.11] |
| 0.25 | [2.02,1.28] | [2.42,1.39] | [2.67,1.46] |
| 0.15 | [1.09,1.00] | [1.14,1.01] | [1.18,1.01] |
| 0.10 | [1.00,1.00] | [1.01,1.00] | [1.01,1.00] |
| 0.05 | [1.00,1.00] | [1.00,1.00] | [1.00,1.00] |
| s | Control Chart [63] | The Proposed Chart | ||||
|---|---|---|---|---|---|---|
| ARLs | NARL | |||||
| 4.00 | 1.178764 | 1.206864 | 1.2224 | [1.18,1.07] | [1.21,1.08] | [1.22,1.08] |
| 3.00 | 1.550192 | 1.635354 | 1.68279 | [1.55,1.27] | [1.64,1.32] | [1.68,1.34] |
| 2.80 | 1.720708 | 1.833704 | 1.896919 | [1.72,1.38] | [1.83,1.44] | [1.90,1.47] |
| 2.50 | 2.133142 | 2.317927 | 2.422306 | [2.13,1.64] | [2.32,1.74] | [2.42,1.80] |
| 2.25 | 2.757243 | 3.061253 | 3.23504 | [2.76,2.05] | [3.06,2.22] | [3.24,2.32] |
| 2.00 | 3.967114 | 4.530703 | 4.858373 | [3.97,2.87] | [4.53,3.20] | [4.86,3.39] |
| 1.90 | 4.783924 | 5.539304 | 5.982269 | [4.78,3.43] | [5.54,3.88] | [5.98,4.14] |
| 1.80 | 5.950011 | 6.99735 | 7.617622 | [5.95,4.25] | [7.00,4.89] | [7.62,5.25] |
| 1.70 | 7.680794 | 9.193211 | 10.09918 | [7.68,5.50] | [9.20,6.43] | [10.10,6.97] |
| 1.60 | 10.37155 | 12.66559 | 14.058 | [10.37,7.48] | [12.67,8.94] | [14.06,9.79] |
| 1.50 | 14.79182 | 18.4856 | 20.76225 | [14.79,10.84] | [18.49,13.27] | [20.77,14.71] |
| 1.40 | 22.53872 | 28.93451 | 32.94814 | [22.54,17] | [28.94,21.4] | [32.96,24.07] |
| 1.30 | 37.12749 | 49.20506 | 56.94885 | [37.13,29.36] | [49.22,38.19] | [56.97,43.67] |
| 1.20 | 66.37585 | 91.41983 | 107.9055 | [66.38,56.51] | [91.46,76.54] | [107.95,89.33] |
| 1.10 | 123.8084 | 178.4871 | 215.6592 | [123.82,117.26] | [178.57,166.92] | [215.76,199.71] |
| 1.00 | 200 | 300 | 370.0001 | [200.02,204.72] | [300.15,304.57] | [370.2,372.66] |
| 0.80 | 133.3607 | 197.7073 | 242.5684 | [133.37,103.02] | [197.81,149.39] | [242.69,180.6] |
| 0.75 | 100.0185 | 147.1854 | 179.9717 | [100.03,71.35] | [147.26,102.35] | [180.06,123.11] |
| 0.70 | 73.10437 | 106.7805 | 130.1201 | [73.11,48.45] | [106.83,68.69] | [130.19,82.17] |
| 0.60 | 36.84876 | 52.85517 | 63.86527 | [36.85,21.38] | [52.88,29.45] | [63.9,34.75] |
| 0.50 | 17.23191 | 24.06818 | 28.71763 | [17.23,9.02] | [24.08,11.93] | [28.73,13.8] |
| 0.40 | 7.479311 | 10.02559 | 11.72831 | [7.48,3.76] | [10.03,4.69] | [11.73,5.28] |
| 0.30 | 3.097514 | 3.884251 | 4.398122 | [3.10,1.71] | [3.89,1.96] | [4.40,2.11] |
| 0.25 | 2.023985 | 2.417816 | 2.672091 | [2.02,1.28] | [2.42,1.39] | [2.67,1.46] |
| 0.15 | 1.090389 | 1.144401 | 1.180756 | [1.09,1.00] | [1.14,1.01] | [1.18,1.01] |
| 0.10 | 1.003689 | 1.008166 | 1.011881 | [1.00,1.00] | [1.01,1.00] | [1.01,1.00] |
| 0.05 | 1.000 | 1.000 | 1.000001 | [1.00,1.00] | [1.00,1.00] | [1.00,1.00] |
| Sr. # | B(k) | z(k) | ln(zk) |
|---|---|---|---|
| 1 | [0.496,0.982] | [0.985,54.568] | [−0.015,3.999] |
| 2 | [0.968,0.261] | [30.555,0.353] | [3.42,−1.04] |
| 3 | [0.922,0.252] | [11.788,0.338] | [2.467,−1.086] |
| 4 | [0.403,0.290] | [0.675,0.408] | [−0.393,−0.897] |
| 5 | [0.432,0.654] | [0.761,1.891] | [−0.274,0.637] |
| 6 | [0.096,0.652] | [0.106,1.872] | [−2.247,0.627] |
| 7 | [0.490,0.988] | [0.962,83.351] | [−0.039,4.423] |
| 8 | [0.204,0.264] | [0.256,0.358] | [−1.363,−1.028] |
| 9 | [0.287,0.820] | [0.403,4.546] | [−0.908,1.514] |
| 10 | [0.325,0.519] | [0.481,1.078] | [−0.732,0.075] |
| 11 | [0.795,0.904] | [3.885,9.443] | [1.357,2.245] |
| 12 | [0.396,0.941] | [0.656,15.825] | [−0.421,2.762] |
| 13 | [0.740,0.049] | [2.843,0.051] | [1.045,−2.974] |
| 14 | [0.361,0.017] | [0.564,0.017] | [−0.572,−4.048] |
| 15 | [0.084,0.331] | [0.091,0.496] | [−2.393,−0.701] |
| 16 | [0.972,0.278] | [34.857,0.385] | [3.551,−0.956] |
| 17 | [0.849,0.109] | [5.611,0.122] | [1.725,−2.101] |
| 18 | [0.932,0.06] | [13.683,0.064] | [2.616,−2.75] |
| 19 | [0.752,0.086] | [3.028,0.094] | [1.108,−2.364] |
| 20 | [0.293,0.621] | [0.414,1.64] | [−0.883,0.495] |
| 21 | [0.924,0.304] | [12.2,0.436] | [2.501,−0.829] |
| 22 | [0.631,0.636] | [1.709,1.748] | [0.536,0.558] |
| 23 | [0.859,0.611] | [6.108,1.572] | [1.810,0.452] |
| 24 | [0.863,0.812] | [6.296,4.306] | [1.840,1.460] |
| 25 | [0.279,0.983] | [0.388,59.465] | [−0.947,4.085] |
| 26 | [0.208,0.191] | [0.263,0.236] | [−1.337,−1.445] |
| 27 | [0.691,0.232] | [2.236,0.303] | [0.805,−1.195] |
| 28 | [0.052,0.896] | [0.055,8.661] | [−2.908,2.159] |
| 29 | [0.659,0.608] | [1.936,1.551] | [0.660,0.439] |
| 30 | [0.252,0.981] | [0.337,50.315] | [−1.087,3.918] |
| 31 | [0.186,0.221] | [0.229,0.283] | [−1.475,−1.262] |
| 32 | [0.968,0.286] | [29.788,0.4] | [3.394,−0.916] |
| 33 | [0.324,0.279] | [0.479,0.387] | [−0.736,−0.95] |
| 34 | [0.791,0.157] | [3.78,0.186] | [1.33,−1.684] |
| 35 | [0.217,0.812] | [0.277,4.321] | [−1.284,1.464] |
| 36 | [0.08,0.942] | [0.086,16.316] | [−2.449,2.792] |
| 37 | [0.246,0.273] | [0.327,0.376] | [−1.119,−0.979] |
| 38 | [0.398,0.914] | [0.66,10.644] | [−0.415,2.365] |
| 39 | [0.625,0.358] | [1.665,0.557] | [0.51,−0.586] |
| 40 | [0.720,0.286] | [2.569,0.400] | [0.944,−0.916] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aslam, M.; Bantan, R.A.R.; Khan, N. Monitoring the Process Based on Belief Statistic for Neutrosophic Gamma Distributed Product. Processes 2019, 7, 209. https://doi.org/10.3390/pr7040209
Aslam M, Bantan RAR, Khan N. Monitoring the Process Based on Belief Statistic for Neutrosophic Gamma Distributed Product. Processes. 2019; 7(4):209. https://doi.org/10.3390/pr7040209
Chicago/Turabian StyleAslam, Muhammad, Rashad A. R. Bantan, and Nasrullah Khan. 2019. "Monitoring the Process Based on Belief Statistic for Neutrosophic Gamma Distributed Product" Processes 7, no. 4: 209. https://doi.org/10.3390/pr7040209
APA StyleAslam, M., Bantan, R. A. R., & Khan, N. (2019). Monitoring the Process Based on Belief Statistic for Neutrosophic Gamma Distributed Product. Processes, 7(4), 209. https://doi.org/10.3390/pr7040209





