Application of Parameter Optimization to Search for Oscillatory Mass-Action Networks Using Python
Abstract
1. Introduction
2. Materials and Methods
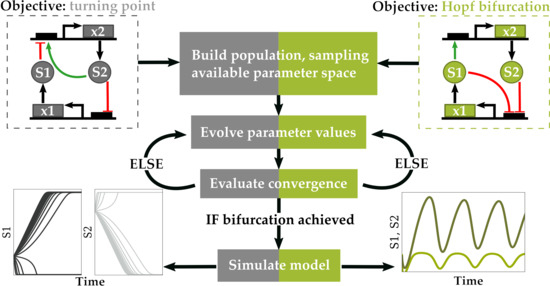
2.1. Objective Function
2.1.1. Optimization for Turning Point Bifurcations
2.1.2. Optimization for Oscillatory Systems
2.1.3. Steady State Solver
2.2. Parameter Selection and Value Assignment
2.3. Differential Evolution Algorithm
2.3.1. Initializing a Population
2.3.2. Recombination
2.3.3. Mutation
2.3.4. Selection
2.3.5. Termination
2.3.6. Conditions for Optimal Convergence
2.4. Local Optimization Algorithm
2.5. Random Network Generation
2.6. Machine Specifications
2.7. Data Repository
3. Results
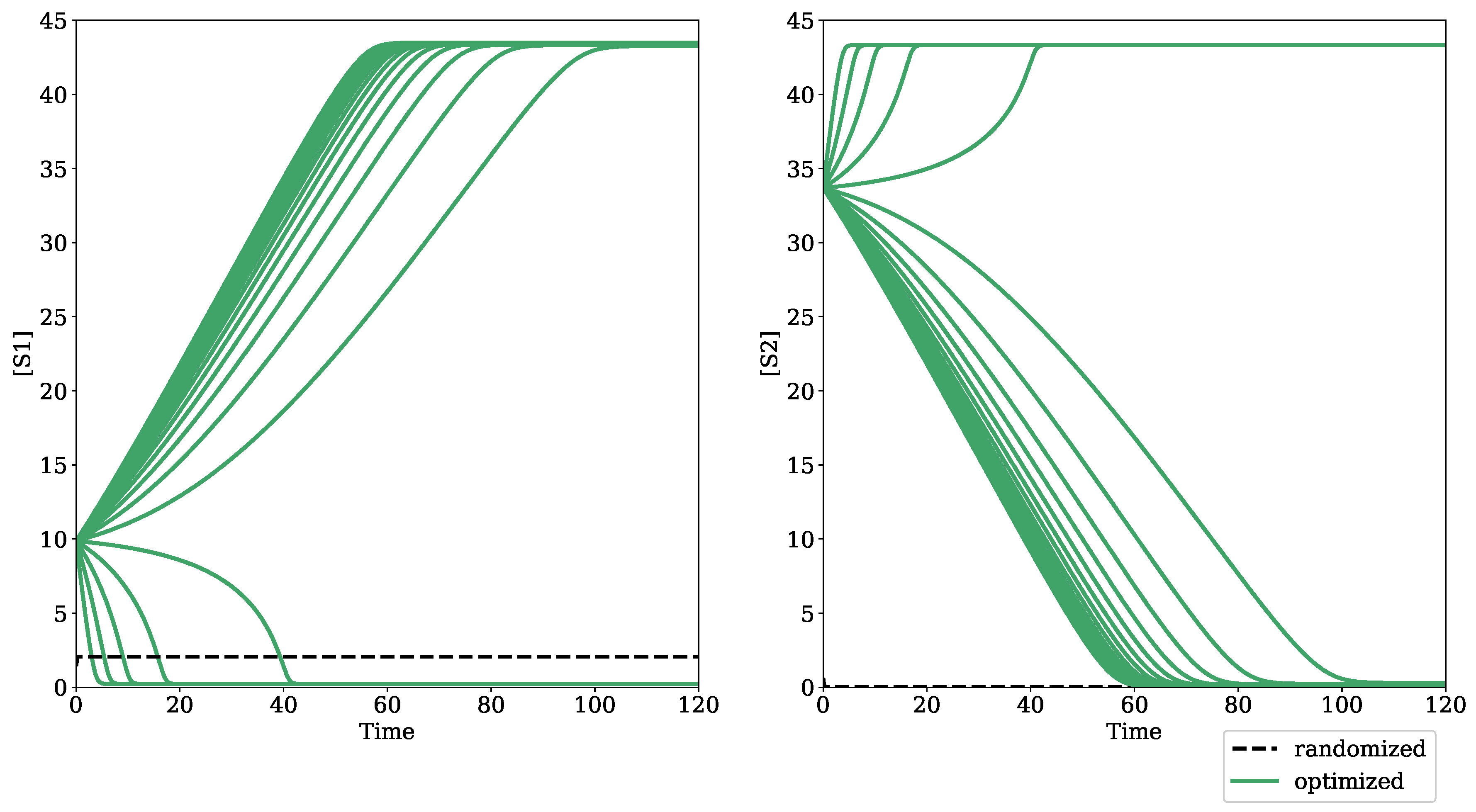
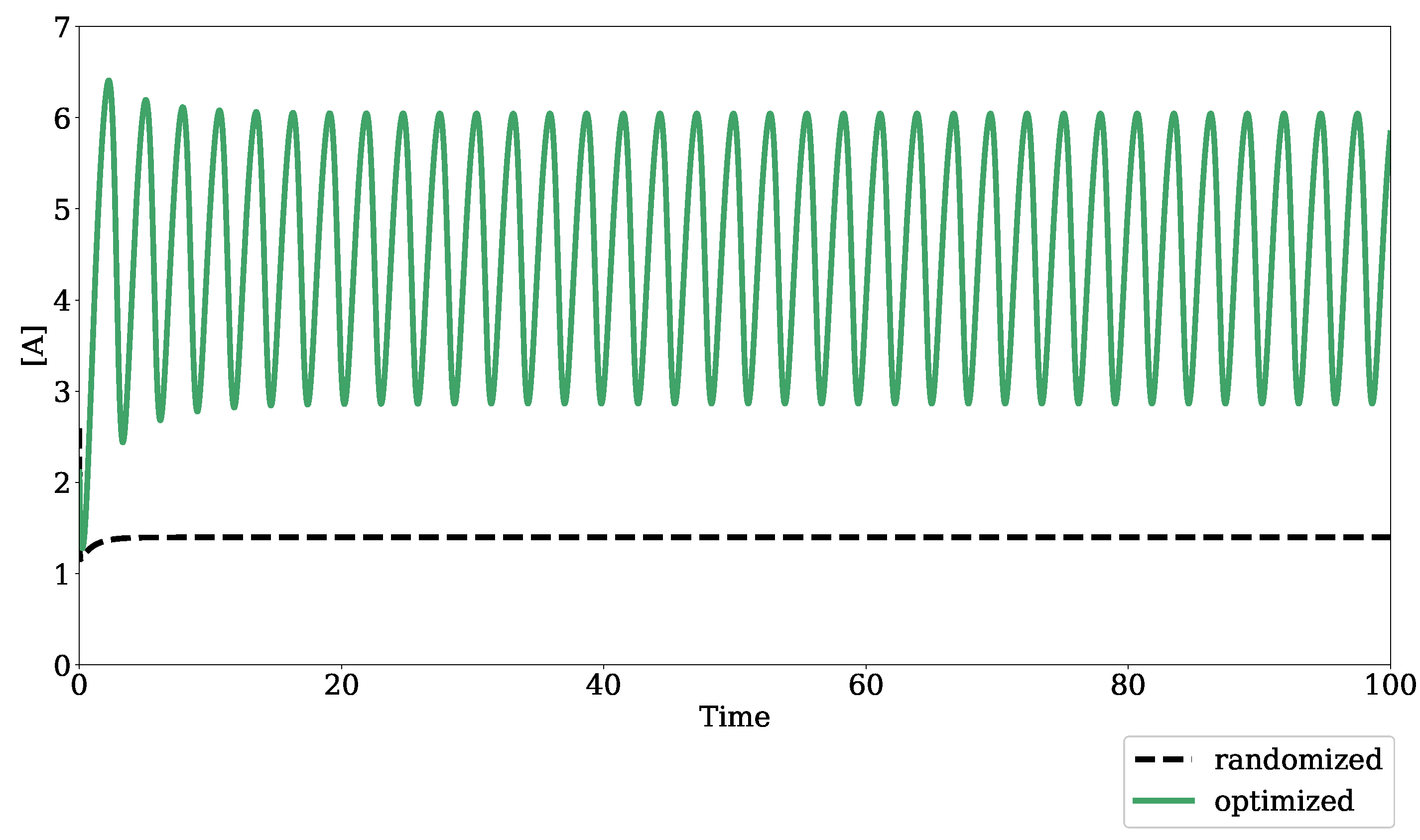
3.1. Testing Bifurcation–Evolution Software on Models from the BioModels Database
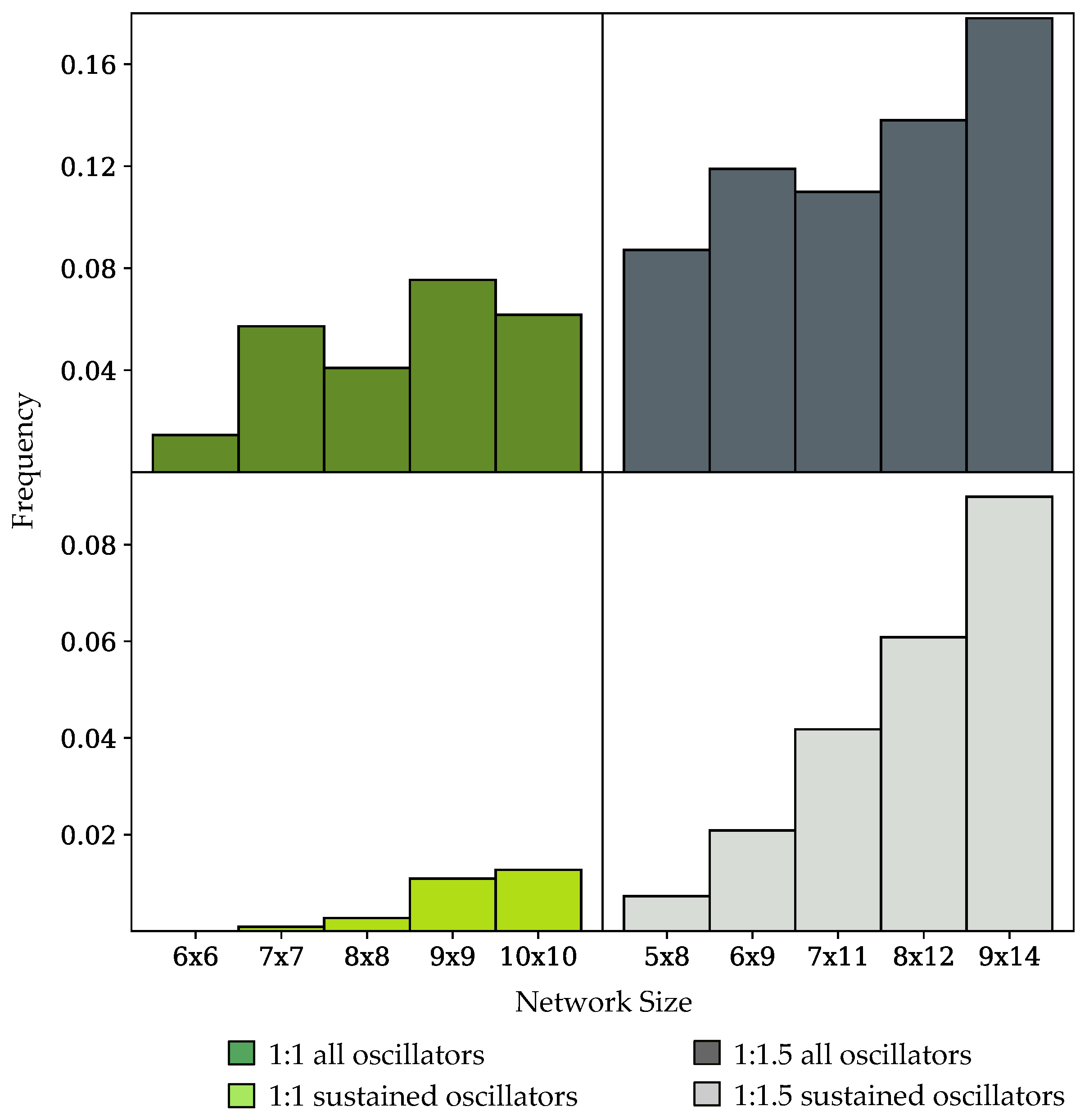
3.2. Oscillation Discovery in Randomly-Generated Networks
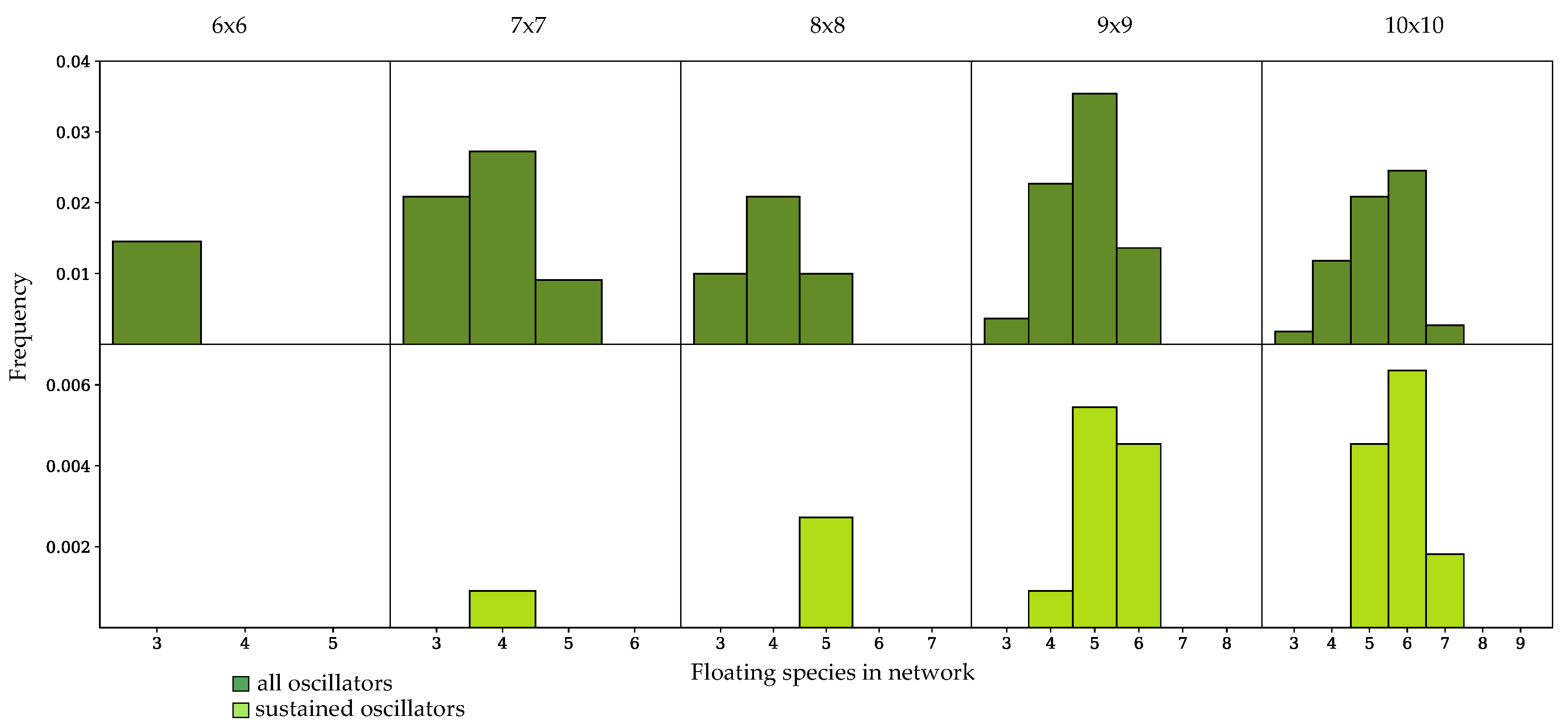
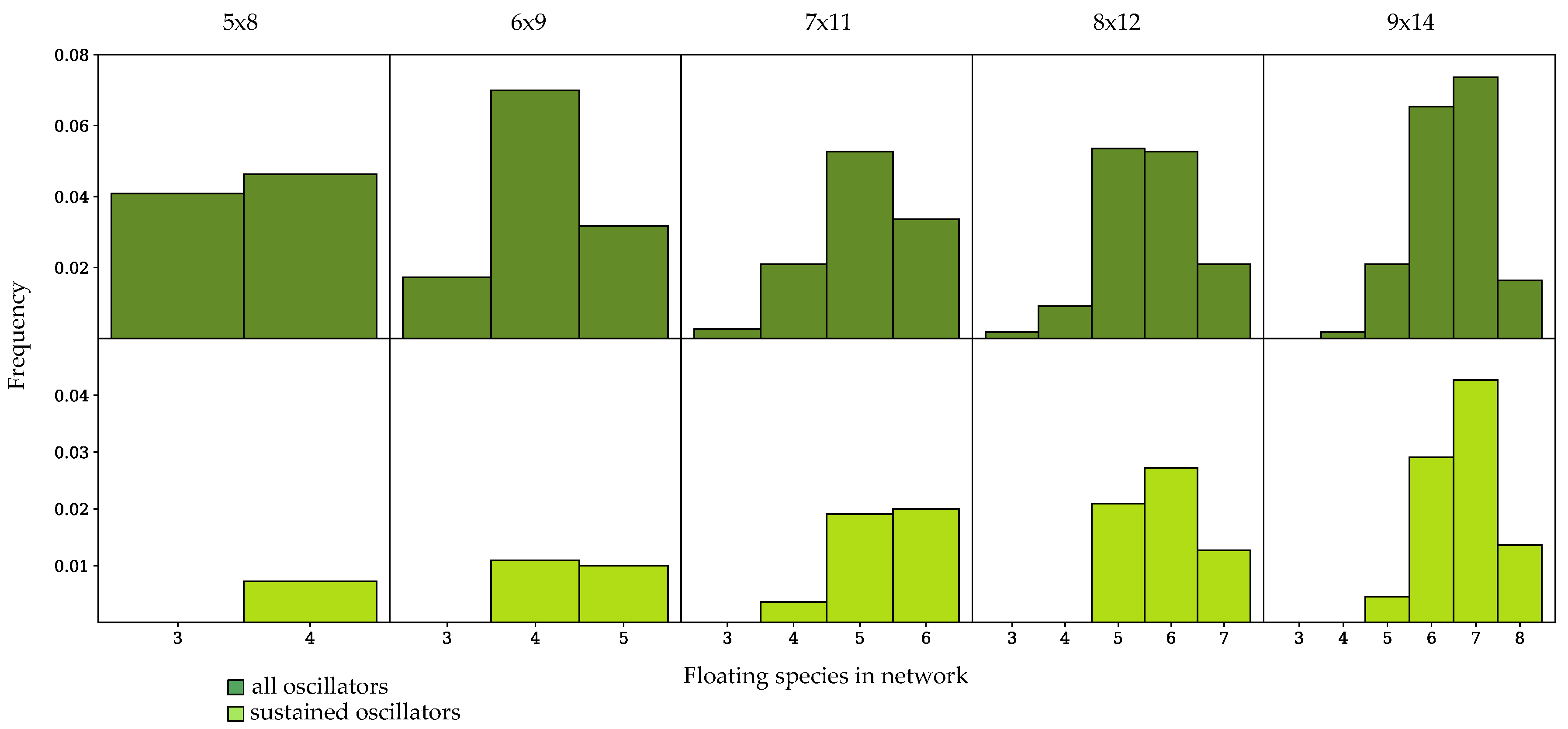
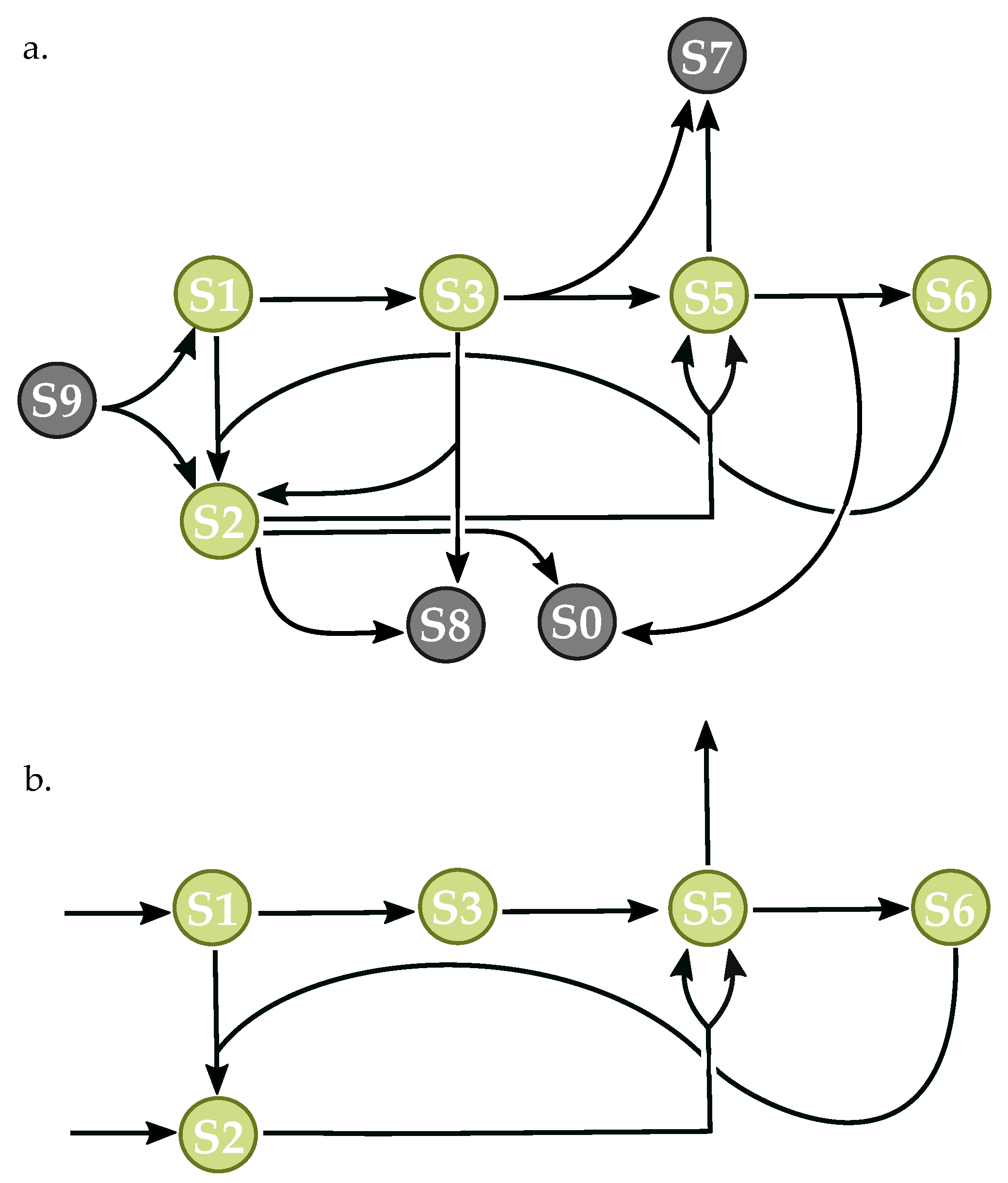
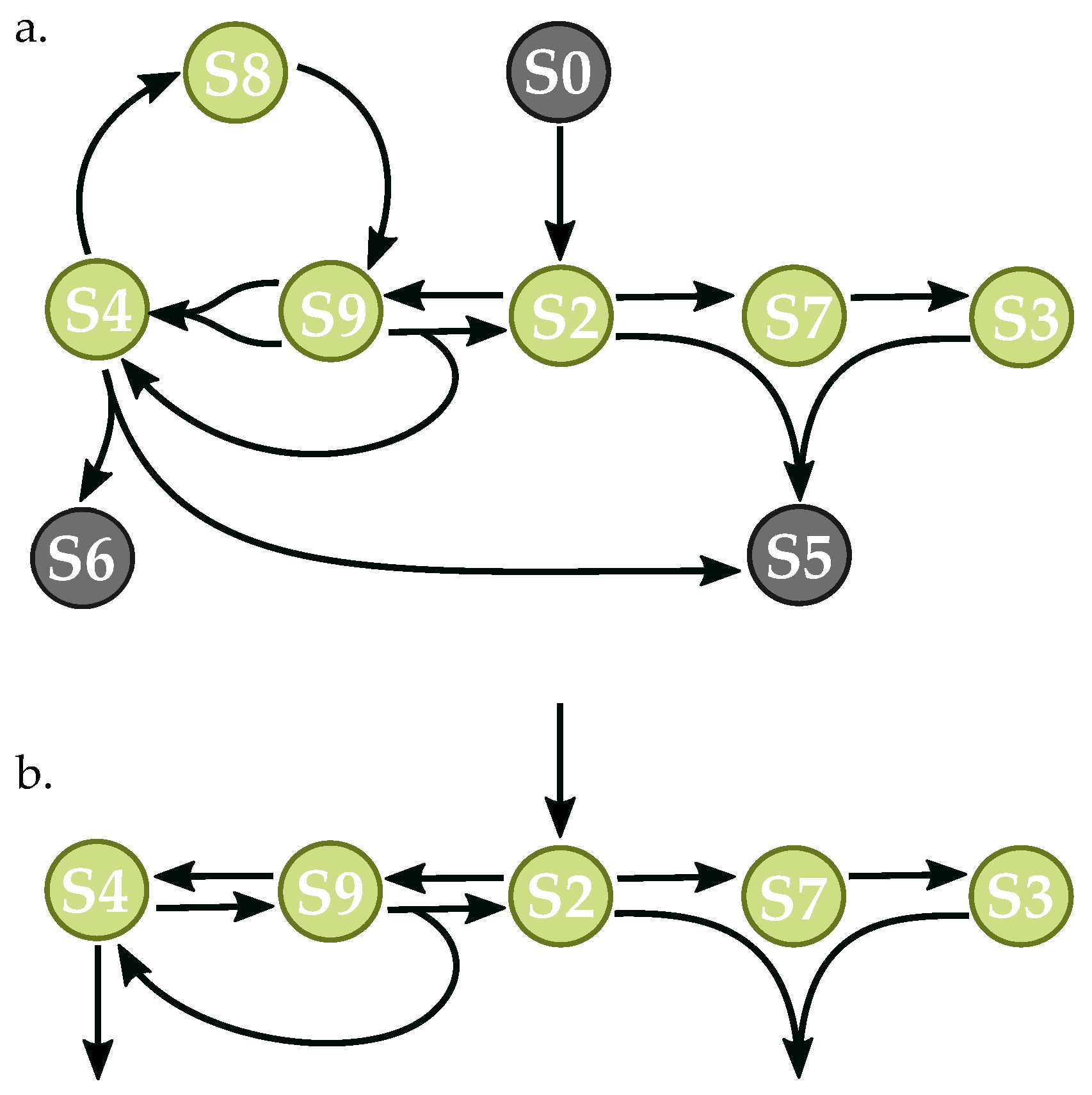
3.3. Components of Randomly-Generated Networks Responsible for Oscillation
4. Discussion
4.1. Algorithm Evaluation
4.2. Oscillator Frequency in Randomly-Generated Network Populations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Csikasz-Nagy, A. Computational systems biology of the cell cycle. Brief. Bioinform. 2009, 10, 424–434. [Google Scholar] [CrossRef] [PubMed]
- Pavlides, A.; Hogan, S.J.; Bogacz, R. Computational Models Describing Possible Mechanisms for Generation of Excessive Beta Oscillations in Parkinson’s Disease. PLoS Comput. Biol. 2015, 1, e1004609. [Google Scholar] [CrossRef] [PubMed]
- Zamora-Sillero, E.; Hafner, M.; Ibig, A.; Stelling, J.; Wagner, A. Efficient characterization of high-dimensional parameter spaces for systems biology. BMC Syst. Biol. 2011, 5, 142. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Gunawan, R. Parameter estimation of dynamic biological network models using integrated fluxes. BMC Syst. Biol. 2014, 8, 127. [Google Scholar] [CrossRef]
- Ashyraliyev, M.; Fomekong-Nanfack, Y.; Kaandorp, J.A.; Blom, J.G. Systems biology: Parameter estimation for biochemical models. FEBS J. 2009, 276, 886–902. [Google Scholar] [CrossRef] [PubMed]
- Chickarmane, V.; Paladugu, S.R.; Bergmann, F.; Sauro, H.M. Bifurcation discovery tool. Bioinformatics 2005, 21, 3688–3690. [Google Scholar] [CrossRef]
- Li, C.; Donizelli, M.; Rodriguez, N.; Dharuri, H.; Endler, L.; Chelliah, V.; Li, L.; He, E.; Henry, A.; Stefan, M.I.; et al. BioModels Database: An enhanced, curated and annotated resource for published quantitative kinetic models. BMC Syst. Biol. 2010, 4, 92. [Google Scholar] [CrossRef]
- Choi, K.; Medley, J.K.; Cannistra, C.; Konig, M.; Smith, L.; Stocking, K.; Sauro, H.M. Tellurium: A Python Based Modeling and Reproducibility Platform for Systems Biology. Biosystems 2018, 171, 74–79. [Google Scholar] [CrossRef]
- Somogyi, E.T.; Bouteiller, J.M.; Glazier, J.A.; König, M.; Medley, J.K.; Swat, M.H.; Sauro, H.M. libRoadRunner: A high performance SBML simulation and analysis library. Bioinformatics 2015, 31, 3315–3321. [Google Scholar] [CrossRef]
- Reich, J.G.; Selkov, E.E. Energy Metabolism of the Cell: A Theoretical Treatise; Academic Press: London, UK, 1981; p. 345. [Google Scholar]
- Sauro, H.M.; Ingalls, B. Conservation analysis in biochemical networks: Computational issues for software writers. Biophys. Chem. 2004, 109, 1–15. [Google Scholar] [CrossRef]
- Sauro, H.M. Systems Biology: An Introduction to Metabolic Control Analysis; Ambrosius Publishing: Seattle, WA, USA, 2018. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- scipy.optimize.differential_evolution—SciPy v1.1.0 Reference Guide. Available online: https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.differential_evolution.html (accessed on 5 November 2018).
- Broyden, C.G. The Convergence of a Class of Double-rank Minimization Algorithms 1. General Considerations. IMA J. Appl. Math. 1970, 6, 76–90. [Google Scholar] [CrossRef]
- Fletcher, R. A new approach to variable metric algorithms. Comput. J. 1970, 13, 317–322. [Google Scholar] [CrossRef]
- Goldfarb, D. A Family of Variable-Metric Methods Derived by Variational Means. Math. Comput. 1970, 24, 23. [Google Scholar] [CrossRef]
- Shanno, D.F. Conditioning of Quasi-Newton Methods for Function Minimization. Math. Comput. 1970, 24, 647. [Google Scholar] [CrossRef]
- Sauro, H.M. Systems Biology: Introduction to Pathway Modeling, 1st ed.; Ambrosius Publishing: Seattle, WA, USA, 2017. [Google Scholar]
- Wilhelm, T.; Heinrich, R. Smallest chemical reaction system with Hopfbifurcation. J. Math. Chem. 1995, 17, 1–14. [Google Scholar] [CrossRef]
- Leloup, J.; Goldbeter, A. Chaos and birhythmicity in a model for circadian oscillations of the PER and TIM proteins in drosophila. J. Theor. Biol. 1999, 198, 445–459. [Google Scholar] [CrossRef]
- Hervagault, O.; Canu, P. Bistability and Irreversible Transitions in a Simple Substrate Cyclet; Technical Report; University of Technology of Compiègne: Compiègne, France, 1987. [Google Scholar]
- Seno, M.; Iwamoto, K.; Sawada, K. Instability and Oscillatory Behavior of Membrane-Chemical Reaction Systems; Technical Report; University of Tokyo: Tokyo, Japan, 1978. [Google Scholar]
- Tyson, J.J.; Chen, K.C.; Novak, B. Sniffers, buzzers, toggles and blinkers: Dynamics of regulatory and signaling pathways in the cell. Curr. Opin. Cell Biol. 2003, 15, 221–231. [Google Scholar] [CrossRef]
- Edelstein, B.B. Biochemical Model With Multiple Steady States and Hysteresis. J. Theor. Biol. 1970, 29, 57–62. [Google Scholar] [CrossRef]
- Angeli, D.; Ferrell, J.E.; Sontag, E.D. Detection of multistability, bifurcations, and hysteresis in a large class of biological positive-feedback systems. Proc. Natl. Acad. Sci. USA 2004, 101, 1822–1827. [Google Scholar] [CrossRef]
- Nicolis, G.; Prigogine, I. Self-Organization in Nonequilibrium Systems; Wiley-Blackwell: Hoboken, NJ, USA, 1977; Volume 82, p. 672. [Google Scholar]
- Heinrich, R.; Rapoport, S.M.; Rapoport, T.A. Metabolic regulation and mathematical models. Proq. Biophys. Mol. Biol. 1977, 32, 1–82. [Google Scholar]
- Kholodenko, B.N. Negative feedback and ultrasensitivity can bring about oscillations in the mitogen-activated protein kinase cascades. Eur. J. Biochem. 2000, 267, 1583–1588. [Google Scholar] [CrossRef] [PubMed]
- Goldbeter, A. A minimal cascade model for the mitotic oscillator involving cyclin and cdc2 kinase. Proc. Natl. Acad. Sci. USA 1991, 88, 9107–9111. [Google Scholar] [CrossRef] [PubMed]
- François, P.; Hakim, V. Core genetic module: The mixed feedback loop. Phys. Rev. E 2005, 72, 031908. [Google Scholar] [CrossRef] [PubMed]
- Lavrentovich, M.; Hemkin, S. A mathematical model of spontaneous calcium(II) oscillations in astrocytes. J. Theor. Biol. 2008, 251, 553–560. [Google Scholar] [CrossRef] [PubMed]
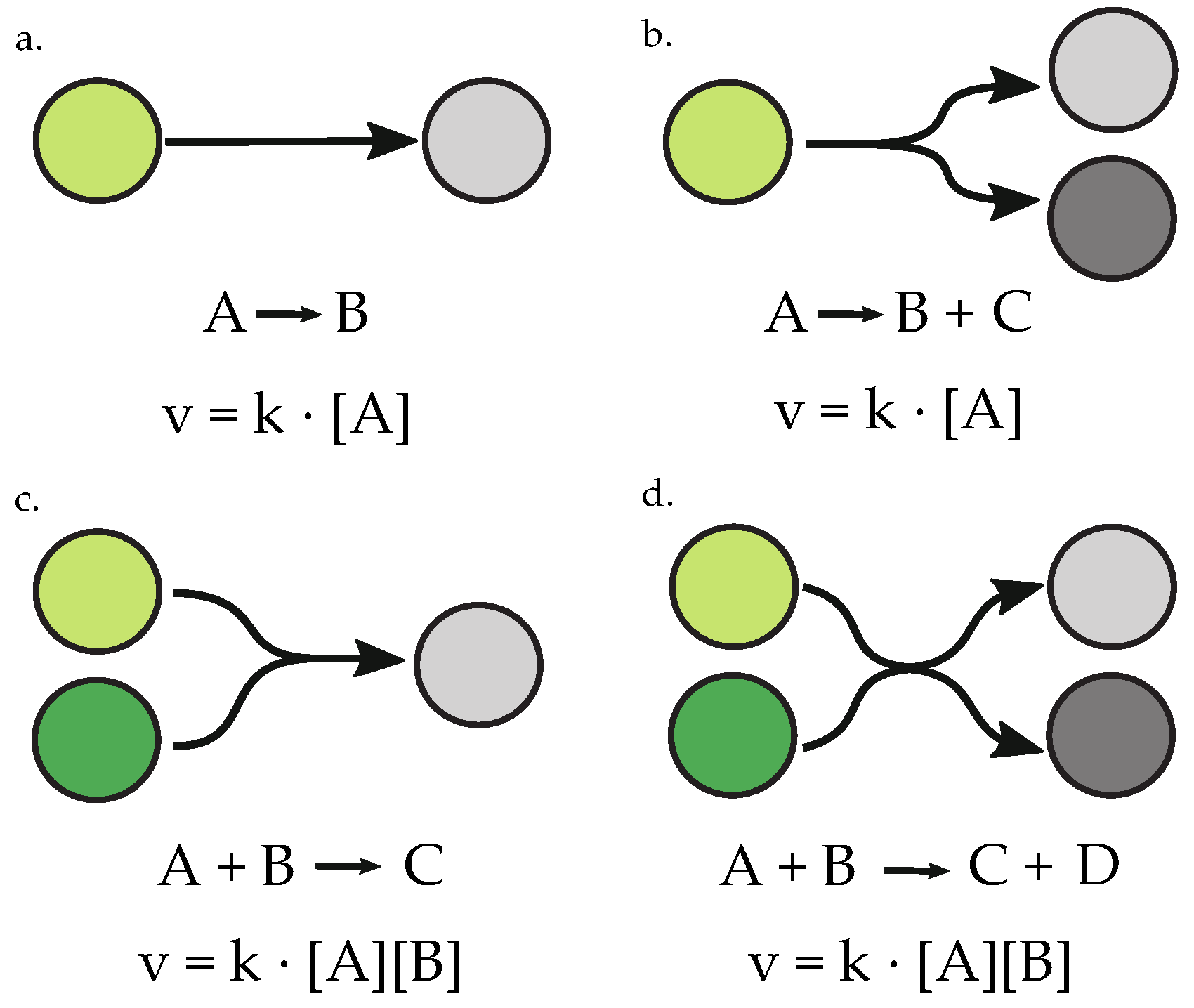
| Turning Point Model | Description | Runtime (s) |
|---|---|---|
| Tyson et al., 2003 (Figure 1e) [24] | Irreversible bistable switch | 9.10 |
| Tyson et al., 2003 (Figure 1f) [24] | Reversible bistable switch | 8.88 |
| Edelstein, 1970 [25] | Autocatalytic bistable switch | 17.70 |
| Hervagault and Canu, 1987 [22] | Bistable switch | 6.72 |
| Angeli et al., 2004 [26] | Bistable switch cdc2/wee1 | 8.16 |
| Oscillatory Model | Description | Runtime (s) |
| Tyson et al., 2003 (Figure 2a) [24] | Negative feedback oscillator | 1.24 |
| Tyson et al., 2003 (Figure 2b) [24] | Activator-inhibitor oscillator | 1.07 |
| Tyson et al., 2003 (Figure 2c) [24] | Substrate-depletion oscillator | 0.99 |
| Nicolis and Prigogine, 1977 [27] | Autocatalytic oscillator | 0.16 |
| Heinrich et al., 1977 [28] | Positive feedback oscillator | 0.16 |
| Seno et al., 1978 [23] | Modified Edelstein relaxation oscillator | 1.54 |
| Kholodenko, 2000 [29] | Mitogen-activated protein kinase feedback oscillator | 42.57 |
| Goldbeter, 1991 [30] | Mitotic oscillator | 1.20 |
| Francois et al., 2005 [31] | Mixed feedback loop oscillator | 6.18 |
| Lavrentovich and Hemkin, 2008 [32] | Spontaneous Ca oscillator | 1.70 |
| Species | Reactions | Oscillators |
|---|---|---|
| 5 | 8 | 0.7% |
| 6 | 6 | 0.0% |
| 6 | 9 | 2.0% |
| 7 | 7 | 0.1% |
| 7 | 11 | 4.2% |
| 8 | 8 | 0.3% |
| 8 | 12 | 6.1% |
| 9 | 9 | 1.1% |
| 9 | 14 | 9.0% |
| 10 | 10 | 1.3% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Porubsky, V.L.; Sauro, H.M. Application of Parameter Optimization to Search for Oscillatory Mass-Action Networks Using Python. Processes 2019, 7, 163. https://doi.org/10.3390/pr7030163
Porubsky VL, Sauro HM. Application of Parameter Optimization to Search for Oscillatory Mass-Action Networks Using Python. Processes. 2019; 7(3):163. https://doi.org/10.3390/pr7030163
Chicago/Turabian StylePorubsky, Veronica L., and Herbert M. Sauro. 2019. "Application of Parameter Optimization to Search for Oscillatory Mass-Action Networks Using Python" Processes 7, no. 3: 163. https://doi.org/10.3390/pr7030163
APA StylePorubsky, V. L., & Sauro, H. M. (2019). Application of Parameter Optimization to Search for Oscillatory Mass-Action Networks Using Python. Processes, 7(3), 163. https://doi.org/10.3390/pr7030163