Wind Power Short-Term Forecasting Hybrid Model Based on CEEMD-SE Method
Abstract
1. Introduction
- (1)
- Ensure the quality of input data of the forecasting model. Most wind power forecasting models only adopt a single data preprocessing method. Thus, the accuracy is limited due to the fact that the complexity of original data is not properly dealt with. This paper first analyses the correlation of indicators, eliminates the indicators with low correlation degree to reduce data redundancy, and then uses CEEMD to decompose wind power to improve the quality of input data of the forecasting model, and use sample entropy (SE), which was proposed by Richman [42] to classify and reconstruct subsequences to reduce the computational complexity.
- (2)
- Realize multi-step forecasting of wind power. The hybrid wind power forecasting model constructed in this paper comprises three parts: data preprocessing, optimization and forecasting. Reasonable multi-level forecasting model can be more supportive for decision-making.
- (3)
- Balance model forecasting accuracy and stationarity. This paper uses a variety of methods to enhance the forecasting accuracy of wind power and improve the stability of the model. The KELM model with faster training speed is used, and the parameters of the KELM model are optimized by the HS algorithm to improve the search performance.
- (4)
- Verify the performance of the forecasting model comprehensively. According to the real measured data of wind farms in China, the ultra-short-term and short-term forecasting of wind power are carried out by adopting the model respectively, and the comprehensive performance of the forecasting model is investigated by calculating four forecasting accuracy evaluation indicators, which confirms the feasibility of multi-scenario application of the model.
2. Materials and Methods
2.1. Pearson Correlation Coefficient
2.2. Complementary Ensemble Empirical Mode decomposition (EMD)
2.3. Sample Entropy Theory
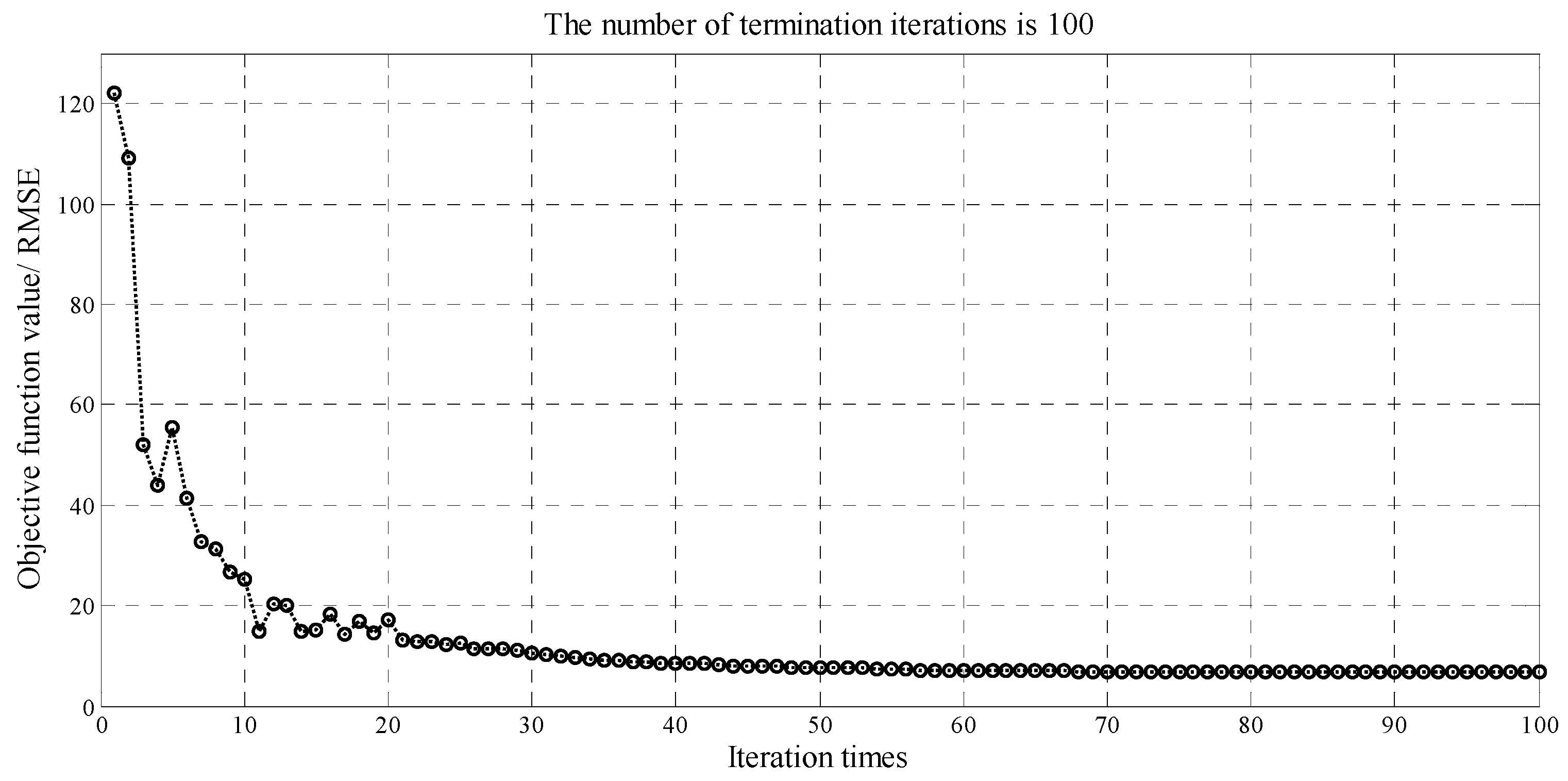
2.4. Harmony Search (HS) Algorithm
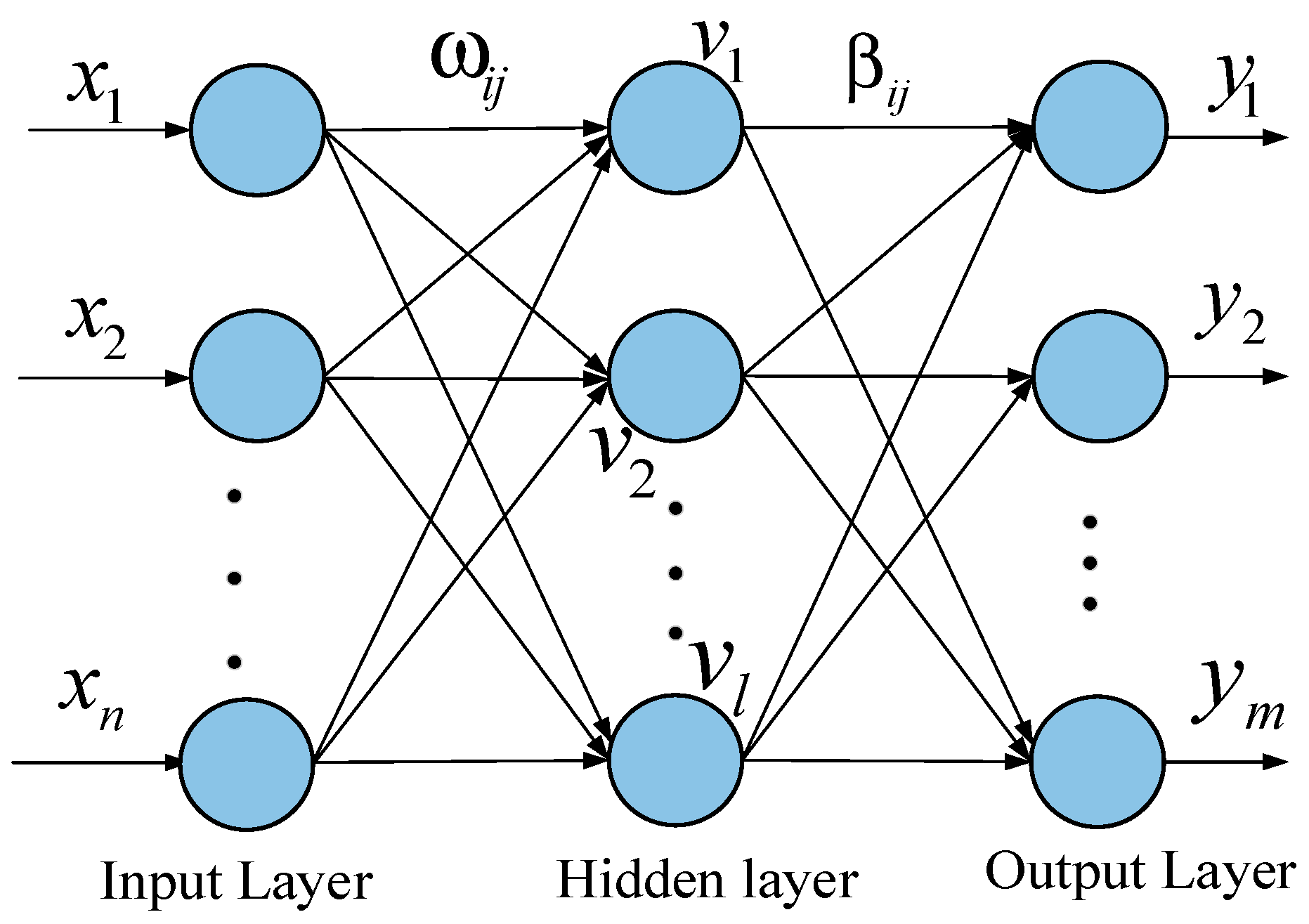
2.5. Extreme Learning Machine with Kernel
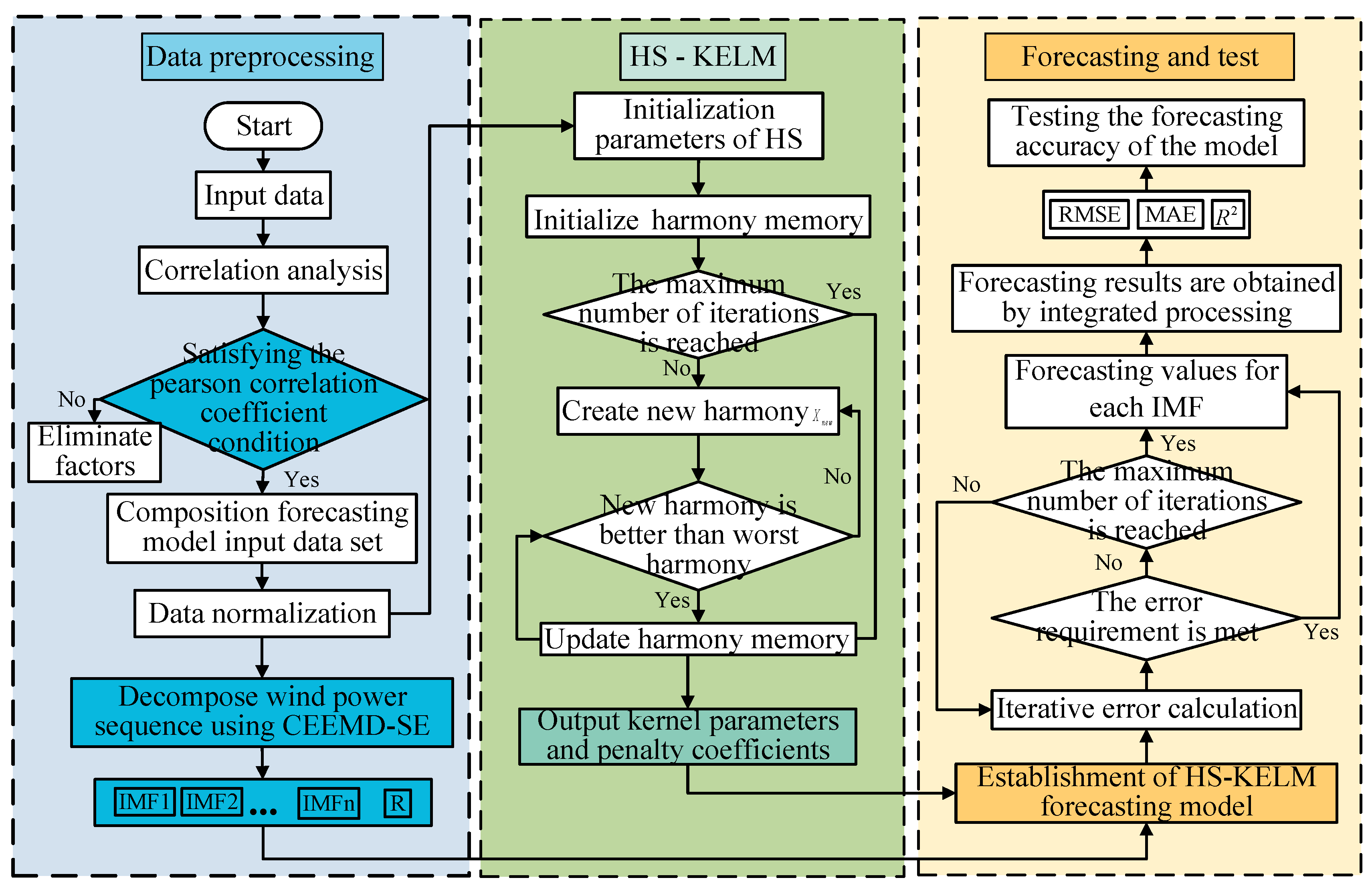
3. Wind Power Forecasting Model
3.1. Model Design
- (1)
- Screen the original data set through correlation analysis to obtain data indicators with high correlation, which can used as the input data of CEEMD-HS-KELM forecasting model;
- (2)
- Decompose the original wind power sequence through CEEMD method to obtain sub sequences components from high frequency to low frequency, which are intrinsic mode function and one approximately monotonous residual ;
- (3)
- Utilize SE theory to calculate the complexity of each subsequence and reconstruct the subsequence decomposed by CEEMD;
- (4)
- HS-KELM model is constructed for each subsequence and the forecast values of each subsequence are obtained;
- (5)
- Superimpose the wind power forecasting results of each subsequence to obtain the final forecasting results.
3.2. Evaluation Criteria
4. Short-Term Wind Power Forecasting
4.1. Data Set Screening
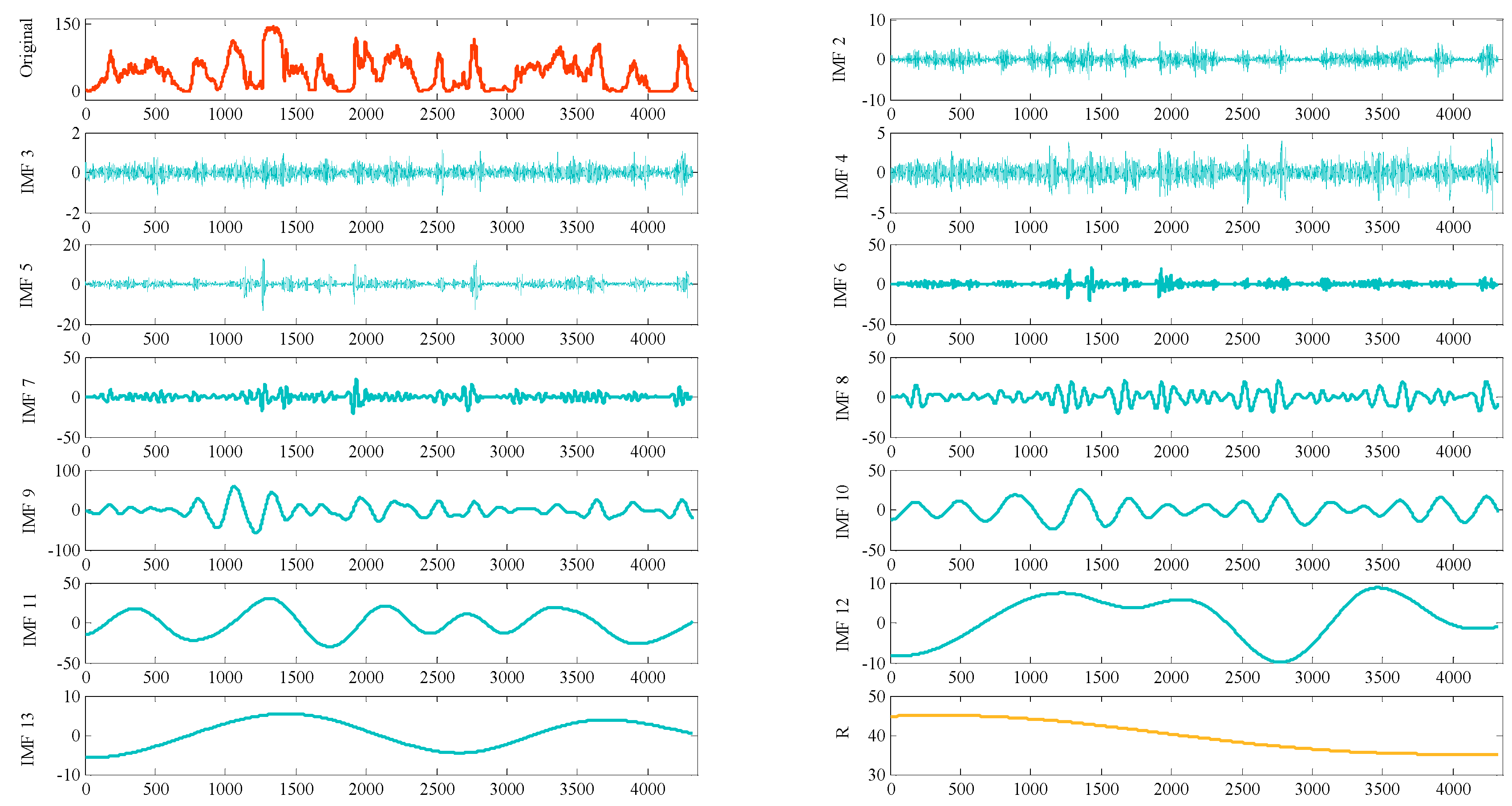
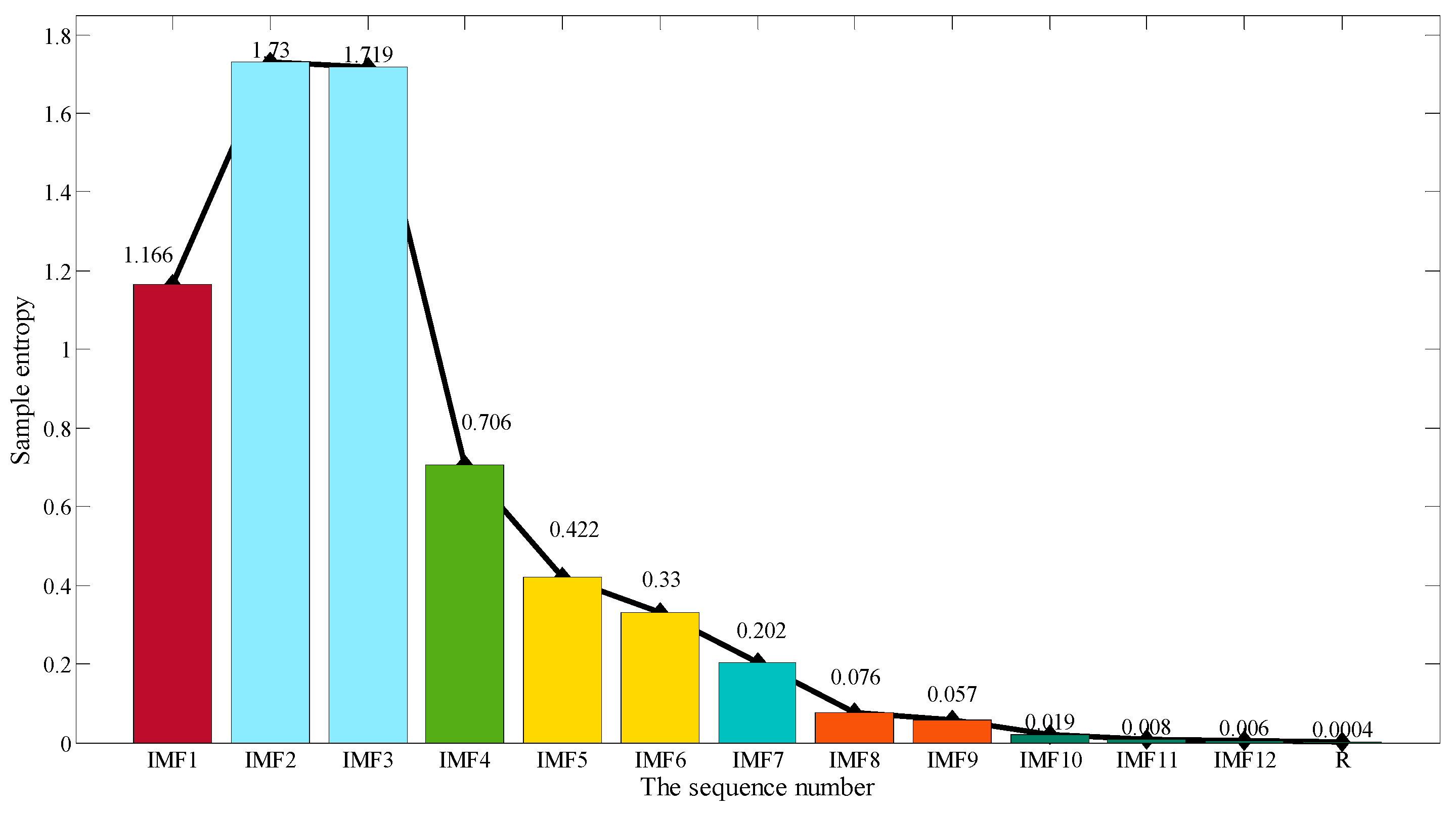
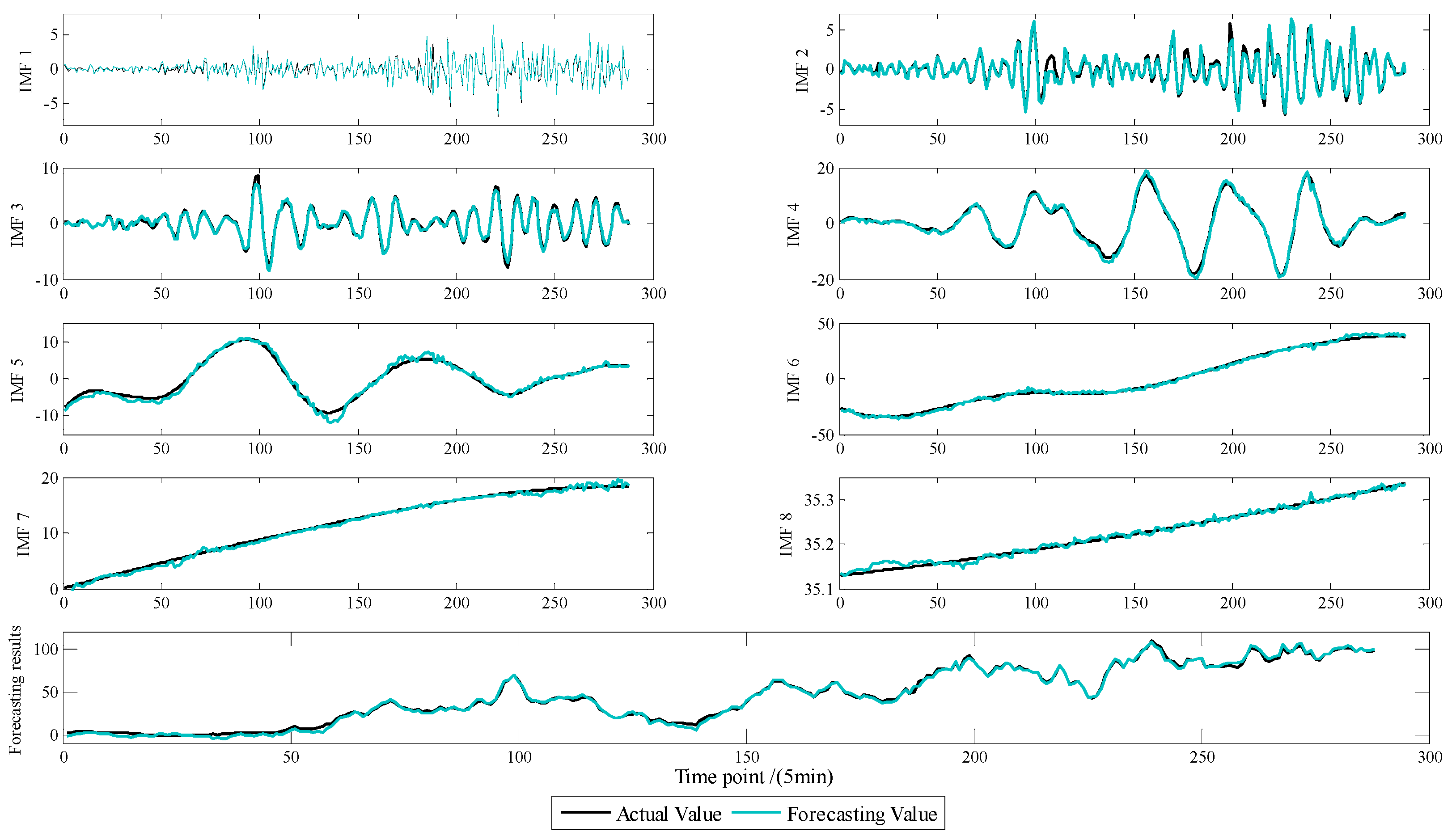
4.2. CEEMD Decomposition of Wind Power Sequence and Subsequence Reconstruction
4.3. Wind Power Forecasting by CEEMD-SE-HS-KELM Model
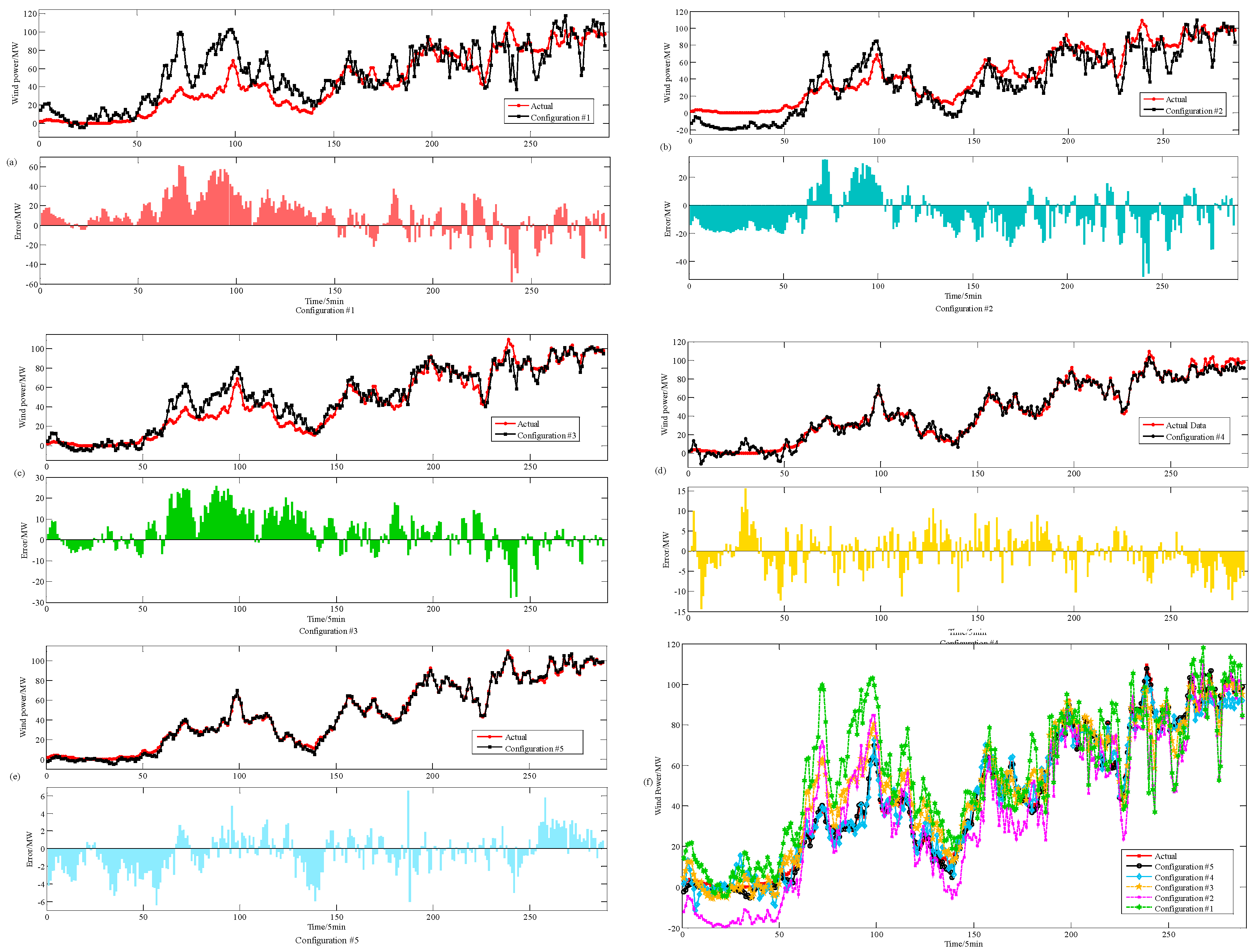
4.4. Comparative Analysis of Forecasting Models
- (1)
- Comparing EMD-SE-HS-KELM and CEEMD-SE-HS-KELM, the RMSE and MAE of the latter are improved by 53.63% and 24.36% respectively compared with EMD-SE-HS-KELM, which indicates that the hybrid model of data preprocessing based on CEEMD-HS has better processing effect.
- (2)
- Comparing HS-KELM and EMD-SE-HS-KELM, the RMSE and MAE of the latter are improved by 52.10% and 86.58%, respectively, compared with HS-KELM, which indicates that for non-stationary wind power series, pre-processing can effectively eliminate noise, ensure data quality and improve forecasting accuracy.
- (3)
- Comparing KELM and HS-KELM, the RMSE and MAE of the latter are improved by 37.67% and 45.23%, respectively, compared with KELM, which indicates that the parameters of KELM algorithm are optimized by HS algorithm, which effectively improves the search ability and the forecasting accuracy.
- (4)
- Compared with ELM, the RMSE and MAE of the KELM are improved by 25.02% and 24.06% respectively compared with ELM, which indicates that the forecasting accuracy of KELM algorithm is better than ELM model, and KELM has a stronger generalization ability.
5. Conclusions
- (1)
- KELM model has higher forecasting accuracy than ELM model, and has broad application prospects in wind power forecasting.
- (2)
- Compared with the single KELM model, HS can optimize the kernel parameters and penalty function of KELM to obtain higher forecasting accuracy, which indicates that HS-KELM model has stronger global search ability and more stable forecasting performance.
- (3)
- Compared with EMD-SE, the data preprocessing strategy based on CEMD-SE has better performance and effectively improves the forecasting accuracy. The hybrid model proposed in this paper can be well applied to short-term wind power forecasting.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| NWP | Numerical weather prediction |
| ANN | Artificial neural network |
| SVM | Support vector machine |
| LSSVM | Least squares support vector machine |
| PCA | Principal component analysis |
| WT | Wavelet transform |
| EMD | Empirical mode decomposition |
| EWT | Empirical wavelet transform |
| CEEMD | Complementary ensemble empirical mode decomposition |
| WAS | Wavelet neural network |
| DWT | Discrete wavelet transform |
| GARCH | Generalized autoregressive conditional heteroscedastic |
| MkRVR | Multi-kernel relevance vector regression |
| IMF | Intrinsic mode functions |
| MLFFNN | Multilayer feed-forward neural network |
| SVR | Support vector regression |
| RBF | Radial basis function |
| ANFIS | Adaptive neuro-fuzzy inference system |
| PSO | Particle swarm optimization |
| VMD | Variational mode decomposition |
| BA | Bat algorithm |
| ELM | Extreme learning machine |
| CSO | Crisscross optimization algorithm |
| KELM | Extreme learning machine with kernel |
| HS | Harmony search |
| SE | Sample entropy |
| HM | Harmony memory |
| HMS | Harmony memory size |
| HMCR | Harmony memory considering rate |
| PCR | Pitch adjusting rate |
| BW | Bandwidth |
| BPNN | Back propagation neural network |
| RMSE | Root mean square error |
| MAE | Mean absolute error |
| R2 | Determining factor |
References
- Cai, W.; Lai, K.-H.; Liu, C.; Wei, F.; Ma, M.; Jia, S.; Jiang, Z.; Lv, L. Promoting sustainability of manufacturing industry through the lean energy-saving and emission-reduction strategy. Sci. Total Environ. 2019, 665, 23–32. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Liu, C.; Lai, K.-H.; Li, L.; Cunha, J.; Hu, L. Energy performance certification in mechanical manufacturing industry: A review and analysis. Energy Convers. Manag. 2019, 186, 415–432. [Google Scholar] [CrossRef]
- Hong, C.; Lin, W.M.; Wen, B.Q. Review of wind speed and wind power prediction methods for wind farms. Power Syst. Clean Energy. 2011, 27, 60–66. [Google Scholar]
- Ren, Y.; Suganthan, P.N.; Srikanth, N. A novel empirical mode decomposition with support vector regression for wind speed forecasting. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1793–1798. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Wang, C.; Su, J.; Wang, J. Research and application based on the swarm intelligence algorithm and artificial intelligence for wind farm decision system. Renew. Energy 2019, 134, 681–697. [Google Scholar] [CrossRef]
- National Energy Administration. China Power Industry Annual Development Report: Renewable Energy Added Capacity Accounts for Over 50%. Available online: http://www.nea.gov.cn/2019-06/19/c_138155207.htm (accessed on 19 June 2019).
- Zhang, C.; Zhou, J.; Li, C.; Fu, W.; Peng, T. A compound structure of ELM based on feature selection and parameter optimization using hybrid backtracking search algorithm for wind speed forecasting. Energy Convers. Manag. 2017, 143, 360–376. [Google Scholar] [CrossRef]
- Tasnim, S.; Rahman, A.; Oo, A.M.T.; Haque, M.E. Wind power prediction in new stations based on knowledge of existing stations: A cluster based multi source domain adaptation approach. Knowl. Based Syst. 2018, 145, 15–24. [Google Scholar] [CrossRef]
- Wang, J.; Du, P.; Niu, T.; Yang, W. A novel hybrid system based on a new proposed algorithm-Multi-Objective Whale Optimization Algorithm for wind speed forecasting. Appl. Energy 2017, 208, 344–360. [Google Scholar] [CrossRef]
- Li, H.; Wang, J.; Lu, H.; Guo, Z. Research and application of a combined model based on variable weight for short term wind speed forecasting. Renew. Energy 2018, 116, 669–684. [Google Scholar] [CrossRef]
- Feng, S.L.; Wang, W.S.; Liu, C.; Dai, H.Z. Study on the physical approach to wind power prediction. Proc. CSEE 2010, 30, 1–6. [Google Scholar]
- Yang, W.; Wang, J.; Lu, H.; Niu, T.; Du, P. Hybrid wind energy forecasting and analysis system based on divide and conquer scheme: A case study in China. J. Clean. Prod. 2019, 222, 942–959. [Google Scholar] [CrossRef]
- Zhang, W.; Qu, Z.; Zhang, K.; Mao, W.; Ma, Y.; Fan, X. A combined model based on CEEMDAN and modified flower pollination algorithm for wind speed forecasting. Energy Convers. Manag. 2017, 136, 439–451. [Google Scholar] [CrossRef]
- Jiang, P.; Yang, H.; Heng, J. A hybrid forecasting system based on fuzzy time series and multi-objective optimization for wind speed forecasting. Appl. Energy 2019, 235, 786–801. [Google Scholar] [CrossRef]
- Hao, Y.; Tian, C. The study and application of a novel hybrid system for air quality early-warning. Appl. Soft Comput. 2019, 74, 729–746. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Wei, X. A hybrid wind speed forecasting model based on phase space reconstruction theory and Markov model: A case study of wind farms in northwest China. Energy 2015, 91, 556–572. [Google Scholar] [CrossRef]
- Sun, W.; Liu, M. Wind speed forecasting using FEEMD echo state networks with RELM in Hebei, China. Energy Convers. Manag. 2016, 114, 197–208. [Google Scholar] [CrossRef]
- Lahouar, A.; Slama, J.B.H. Hour-ahead wind power forecast based on random forests. Renew. Energy 2017, 109, 529–541. [Google Scholar] [CrossRef]
- Li, C.; Zhu, Z. Research and application of a novel hybrid air quality early-warning system: A case study in China. Sci. Total Environ. 2018, 626, 1421–1438. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L.; Shao, W.; Yu, M.; Ma, J.; Jin, C. Research and application of a hybrid wavelet neural network model with the improved cuckoo search algorithm for electrical power system forecasting. Appl. Energy 2017, 198, 203–222. [Google Scholar] [CrossRef]
- Li, G.; Shi, J.; Zhou, J. Bayesian adaptive combination of short-term wind speed forecasts from neural network models. Renew. Energy 2011, 36, 352–359. [Google Scholar] [CrossRef]
- Liu, D.; Niu, D.; Wang, H.; Fan, L. Short-term wind speed forecasting using wavelet transform and support vector machines optimized by genetic algorithm. Renew. Energy 2014, 62, 592–597. [Google Scholar] [CrossRef]
- Hu, J.; Wang, J.; Ma, K. A hybrid technique for short-term wind speed prediction. Energy 2015, 81, 563–574. [Google Scholar] [CrossRef]
- Zhou, J.; Shi, J.; Li, G. Fine tuning support vector machines for short-term wind speed forecasting. Energy Convers. Manag. 2011, 52, 1990–1998. [Google Scholar] [CrossRef]
- Li, H.; Wang, J.; Li, R.; Lu, H. Novel analysis-forecast system based on multi-objective optimization for air quality index. J. Clean. Prod. 2019, 208, 1365–1383. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2011, 42, 513–529. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhang, C.; Zhao, Y.; Gao, S. Wind speed prediction with RBF neural network based on PCA and ICA. J. Electr. Eng. 2018, 69, 148–155. [Google Scholar] [CrossRef]
- Huang, Y.; Shen, L.; Liu, H. Grey relational analysis, principal component analysis and forecasting of carbon emissions based on long short-term memory in China. J. Clean. Prod. 2019, 209, 415–423. [Google Scholar] [CrossRef]
- Qi, J.; Xu, C.Z.; Liu, Y.Q.; Han, S.; Li, L. Short-term wind power prediction method based on wind speed cloud model in similar day. Autom. Electr. Power Syst. 2018, 42, 53–59. [Google Scholar]
- Gilles, J. Empirical wavelet transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Naik, J.; Satapathy, P.; Dash, P. Short-term wind speed and wind power prediction using hybrid empirical mode decomposition and kernel ridge regression. Appl. Soft Comput. 2018, 70, 1167–1188. [Google Scholar] [CrossRef]
- Du, P.; Wang, J.Z.; Yang, W.D.; Niu, T. A novel hybrid model for short-term wind power forecasting. Appl. Soft Comput. 2019, 80, 93–106. [Google Scholar] [CrossRef]
- Jiang, P.; Wang, Y.; Wang, J. Short-term wind speed forecasting using a hybrid model. Energy 2017, 119, 561–577. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, G.; Peng, X.; Li, Y.; Yang, Q. A novel wind speed prediction method: Hybrid of correlation-aided DWT, LSSVM and GARCH. J. Wind Eng. Ind. Aerodyn. 2018, 174, 28–38. [Google Scholar] [CrossRef]
- Fei, S.W. A hybrid model of EMD and multiple-kernel RVR algorithm for wind speed prediction. Int. J. Electr. Power Energy Syst. 2016, 78, 910–915. [Google Scholar] [CrossRef]
- Khosravi, A.; Koury, R.; Machado, L.; Pabon, J. Prediction of wind speed and wind direction using artificial neural network, support vector regression and adaptive neuro-fuzzy inference system. Sustain. Energy Technol. Assess. 2018, 25, 146–160. [Google Scholar] [CrossRef]
- Wu, Q.; Lin, H.X. Short-term wind speed forecasting based on hybrid variational mode decomposition and least squares support vector machine optimized by bat algorithm model. Sustainability 2019, 11, 652. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, G.; Yang, Q.; Yan, Z.; Zhang, C. A novel probabilistic wind speed prediction approach using real time refined. Energy Convers. Manag. 2019, 185, 758–773. [Google Scholar] [CrossRef]
- Tian, C.; Hao, Y.; Hu, J. A novel wind speed forecasting system based on hybrid data preprocessing and multi-objective optimization. Appl. Energy 2018, 231, 301–319. [Google Scholar] [CrossRef]
- Yin, H.; Dong, Z.; Chen, Y.; Ge, J.; Lai, L.L.; Vaccaro, A.; Meng, A. An effective secondary decomposition approach for wind power forecasting using extreme learning machine trained by crisscross optimization. Energy Convers. Manag. 2017, 150, 108–121. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A: Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Lin, T.; Cai, R.Q.; Zhang, L.; Yang, X.; Liu, G.; Liao, W.J. Prediction intervals forecasts of wind power based on IBA-KELM. Renew. Energy Resour. 2018, 7, 23. [Google Scholar]
- Bapat, K.M.P.B. The Generalized Moore-Penrose Inverses. Linear Algebra Appl. 1992, 165, 59–69. [Google Scholar]
- Huang, G.-B. An insight into extreme learning machines: Random neurons, random features and kernels. Cogn. Comput. 2014, 6, 376–390. [Google Scholar] [CrossRef]
- Li, D. Kernel Function. In Encyclopedia of Microfluidics and Nanofluidics; Springer: Boston, MA, USA, 2008. [Google Scholar] [CrossRef]
- Hornero, R. Optimal parameters study for sample entropy-based atrial fibrillation organization analysis. Comput. Methods Programs Biomed. 2010, 99, 124–132. [Google Scholar]
- Kim, J.H.; Geem, Z.W.; Kim, E.S. Parameter estimation of the nonlinear muskingum model using harmony search. J. Am. Water Resour. Assoc. 2001, 37, 1131–1138. [Google Scholar] [CrossRef]
- Omran Mahamed, G.H.; Mahdavi, M. Global-best harmony search. Appl. Math. Comput. 2008, 198, 643–656. [Google Scholar]


| Indicators | Correlation | Indicators | Correlation | Indicators | Correlation | ||
|---|---|---|---|---|---|---|---|
| wind speed | 10 m | 0.788 | wind direction | 10 m | −0.391 | temperature | 0.227 |
| 30 m | 0.796 | 30 m | −0.308 | humidity | −0.51 | ||
| 50 m | 0.777 | 50 m | −0.025 | rainfall | 0.29 | ||
| 70 m | 0.764 | 70 m | 0.289 | pressure | −0.37 | ||
| hub height | 0.764 | hub height | 0.289 | - | |||
| New Subsequence Number | Initial Subsequence Number | New Subsequence Number | Initial Subsequence Number |
|---|---|---|---|
| 1 | 1 | 5 | 7 |
| 2 | 2,3 | 6 | 8,9 |
| 3 | 4 | 7 | 10,11,12 |
| 4 | 5,6 | 8 | R |
| Evaluation Index | ELM | KELM | HS-KELM | EMD-SE-HS-KELM | CEEMD-SE-HS-KELM |
|---|---|---|---|---|---|
| Configuration | #1 | #2 | #3 | #4 | #5 |
| RMSE | 20.84 | 15.63 | 9.74 | 4.67 | 2.16 |
| MAE | 9.29 | 7.05 | 3.86 | 0.52 | 0.39 |
| R2 | 1.12 | 1.05 | 0.96 | 1.03 | 1.01 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Niu, D.; Sun, L.; Zhen, H.; Liu, J.; De, G.; Xu, X. Wind Power Short-Term Forecasting Hybrid Model Based on CEEMD-SE Method. Processes 2019, 7, 843. https://doi.org/10.3390/pr7110843
Wang K, Niu D, Sun L, Zhen H, Liu J, De G, Xu X. Wind Power Short-Term Forecasting Hybrid Model Based on CEEMD-SE Method. Processes. 2019; 7(11):843. https://doi.org/10.3390/pr7110843
Chicago/Turabian StyleWang, Keke, Dongxiao Niu, Lijie Sun, Hao Zhen, Jian Liu, Gejirifu De, and Xiaomin Xu. 2019. "Wind Power Short-Term Forecasting Hybrid Model Based on CEEMD-SE Method" Processes 7, no. 11: 843. https://doi.org/10.3390/pr7110843
APA StyleWang, K., Niu, D., Sun, L., Zhen, H., Liu, J., De, G., & Xu, X. (2019). Wind Power Short-Term Forecasting Hybrid Model Based on CEEMD-SE Method. Processes, 7(11), 843. https://doi.org/10.3390/pr7110843





