Evaluating Production Process Efficiency of Provincial Greenhouse Vegetables in China Using Data Envelopment Analysis: A Green and Sustainable Perspective
Abstract
1. Introduction
2. Methodology and Data Source
2.1. Production Function of Vegetable Industry
2.2. Data Envelopment Analysis Model
- (1)
- If and , or if and , then decision unit j is weak DEA efficient.
- (2)
- If , , and , then decision unit j is DEA efficient.
- (3)
- If , then decision unit j is inefficient.
2.3. Data Source and DEA Model for Efficiency Evaluation of Greenhouse Vegetables
3. Results and Discussion
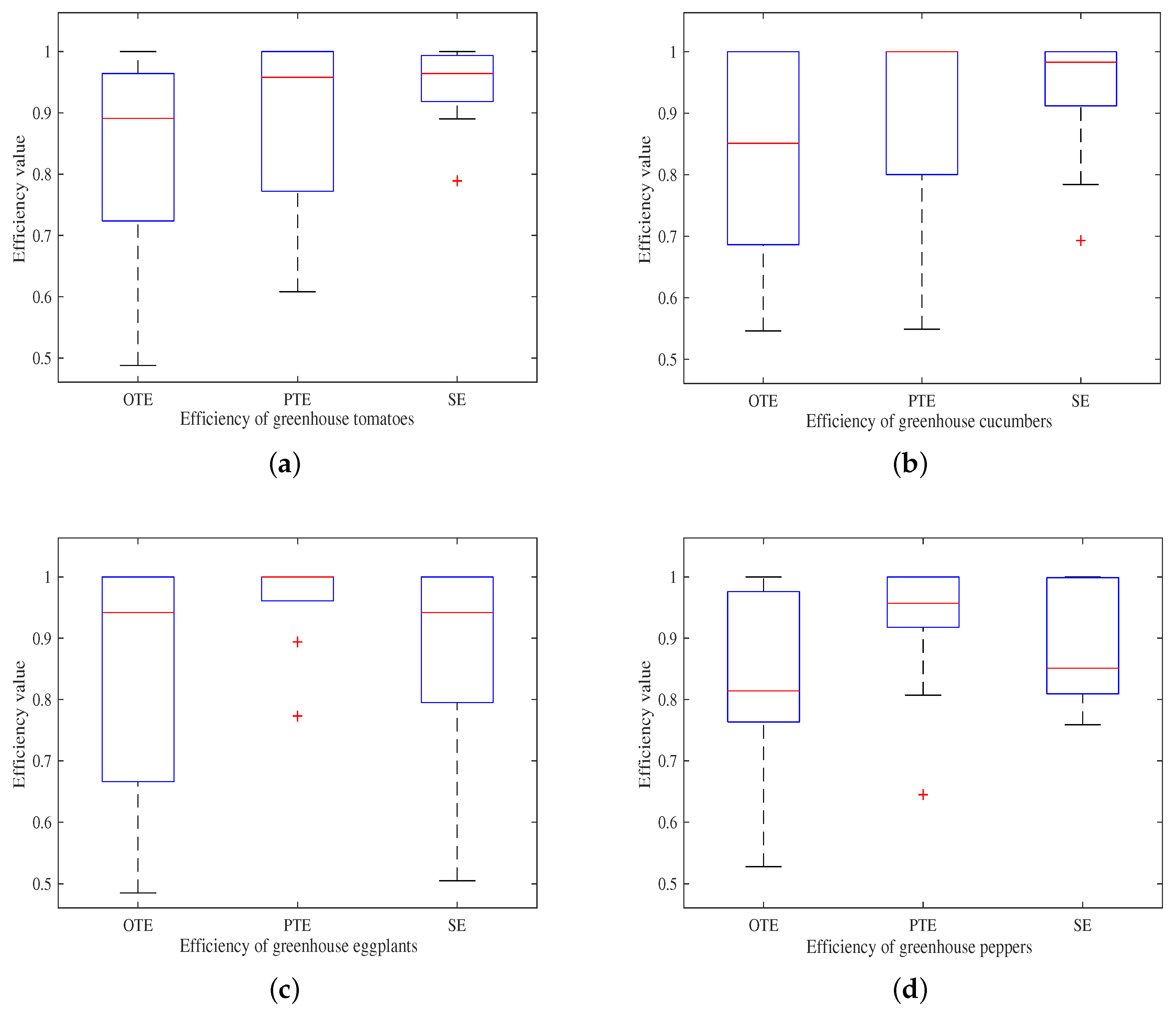
3.1. Comparative Analysis of Vegetable Efficiency in Greenhouses
3.2. Comparison and Analysis of the Efficiency of Greenhouse Vegetables at Provincial Level
3.3. Spatial Distribution Analysis of Efficiency
3.4. Analysis and Adjustment of Inefficient Provinces
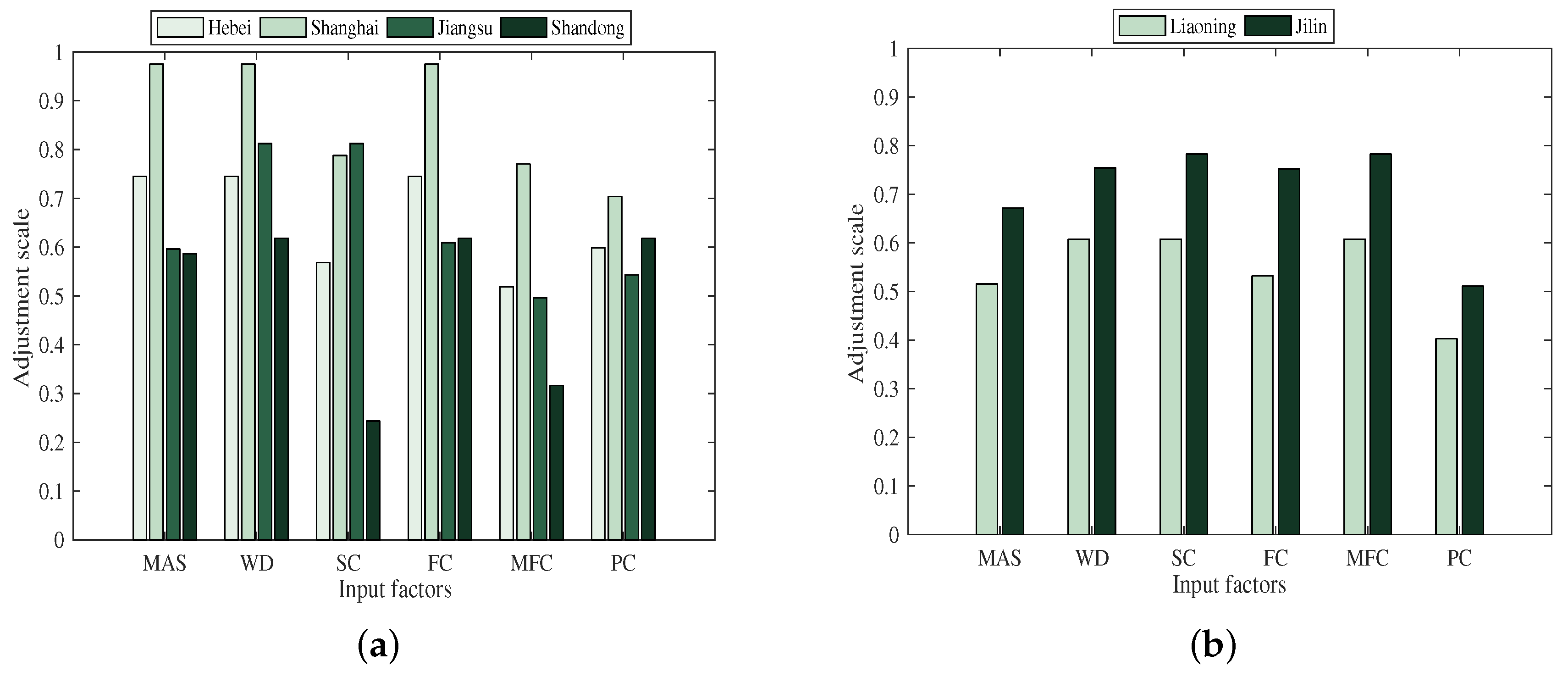
3.4.1. Analysis on the Adjustment of Efficiency Input in Eastern China
3.4.2. Analysis on the Adjustment of Efficiency Input in Northeast China
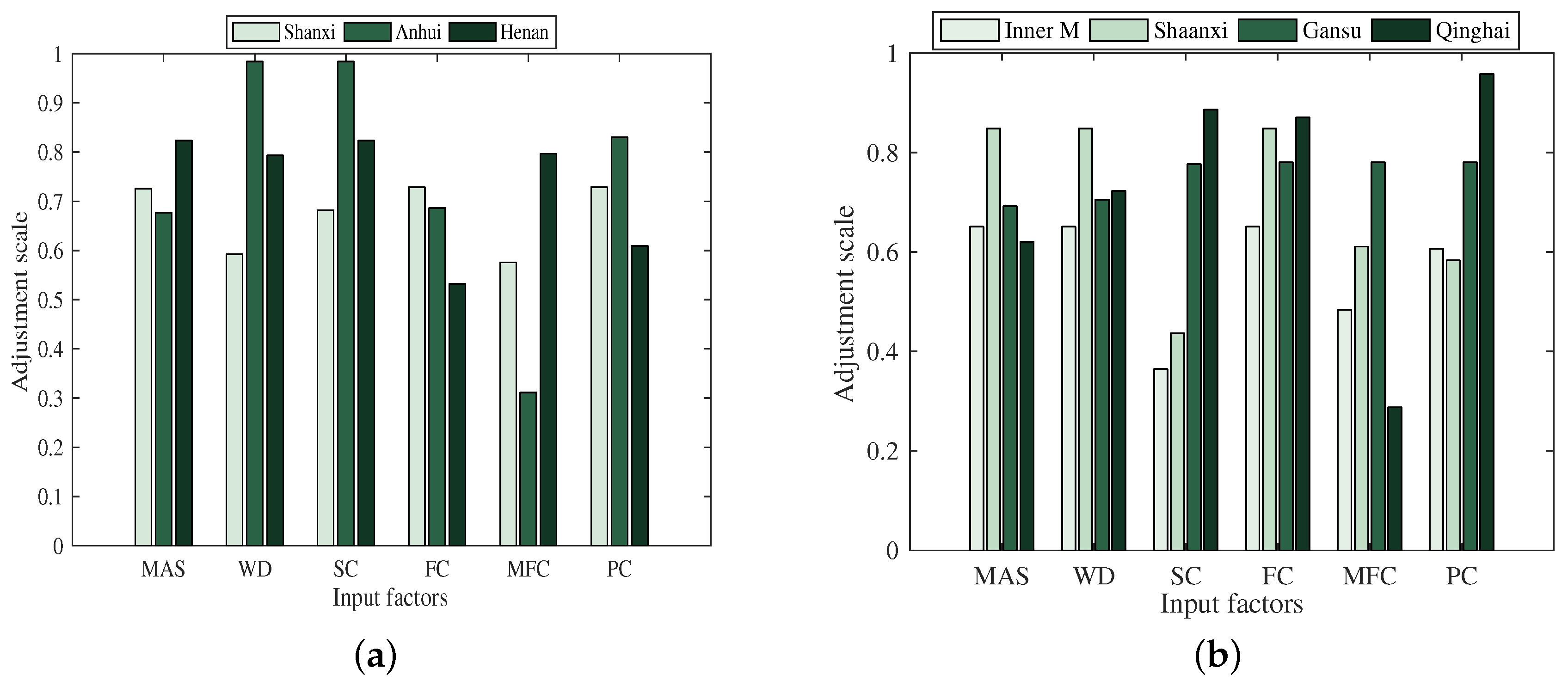
3.4.3. Analysis on the Adjustment of Efficiency Input in Central China
3.4.4. Analysis on the Adjustment of Efficiency Input in Western China
4. Conclusions and Policy Implication
- In the production of greenhouse tomatoes and cucumbers in China, the loss of PTE may lead to inefficiency in most provinces. For greenhouse tomatoes, among the 17 inefficient provinces, the PTE of 11 provinces is lower than the SE. For greenhouse cucumbers, among the 14 inefficient provinces, the PTE of 9 provinces is lower than the SE. The results show that the government should pay more attention to the improvement of the PTE of greenhouse tomatoes and cucumbers.
- In the production of greenhouse eggplants and peppers in China, the loss of SE may lead to inefficiency in most provinces. For greenhouse eggplants, among the six inefficient provinces, the SE of five provinces is lower than the PTE. For greenhouse peppers, among the eight inefficient provinces, the SE of six provinces is lower than the PTE. The results show that the government should pay more attention to improving the SE of greenhouse eggplants and peppers.
- From the perspective of input factors, fertilizers, farm manure and pesticides are inefficient in most parts of China. In particular, the overall use efficiency of farmyard manure is low, and chemical fertilizers and pesticides are seriously wasted. These results indicate that the government should pay more attention to the use of chemical fertilizers, farm manure, and pesticides to improve the use efficiency in the future. On the one hand, it helps to reduce the waste of resource. On the other hand, it is conducive to the development of green and sustainable agriculture.
- For provinces with DEA efficiency, such as Tianjin, Heilongjiang, and Hubei, on the basis of maintaining the existing production advantages, the supply and demand of greenhouse vegetable production should be balanced. For the provinces with high level of efficiency, such as Beijing, Sichuan, Shanghai, and Ningxia, the government should maintain the existing scale advantage in promoting vegetable production development at first. Thus, the government should focus on the introduction and application of advanced field technology and management mode to achieve higher utilization rate of input factors in greenhouse vegetable production.
- For the provinces with low level of efficiency, such as Shandong, Inner Mongolia, Shanxi, and Hebei, it is important to improve the PTE and find the appropriate scale suitable for the local. First, the government should increase support to these provinces and guide farmers to use chemical fertilizers and pesticides rationally. Second, the government should encourage and support the use of farm manure to reduce the use of chemical fertilizers.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, L.; Wang, Y.; Shah, S.A.A.; Zameer, H.; Solangi, Y.A.; Walasai, G.D.; Siyal, Z.A. Economic viability and environmental efficiency analysis of hydrogen production processes for the decarbonization of energy systems. Processes 2019, 7, 494. [Google Scholar] [CrossRef]
- Hafeez, G.; Islam, N.; Ali, A.; Ahmad, S.; Usman, M.; Alimgeer, K.S. A modular framework for optimal load scheduling under price-based demand response scheme in smart grid. Processes 2019, 7, 499. [Google Scholar] [CrossRef]
- Ruan, J.; Wang, Y.; Chan, F.T.S.; Hu, X.; Zhao, M.; Zhu, F.; Shi, B.; Shi, Y.; Lin, F. A life cycle framework of green IoT-based agriculture and its finance, operation, and management issues. IEEE Commun. Mag. 2019, 57, 90–96. [Google Scholar] [CrossRef]
- Ruan, J.; Jiang, H.; Li, X.; Shi, Y.; Chan, F.T.; Rao, W. A granular GA-SVM predictor for big data in agricultural cyber-physical systems. IEEE Trans. Ind. Inf. 2019, 57, 90–96. [Google Scholar] [CrossRef]
- Clark, M.; Tilman, D. Comparative analysis of environmental impacts of agricultural production systems, agricultural input efficiency, and food choice. Environ. Res. Lett. 2017, 12, 1–12. [Google Scholar] [CrossRef]
- Geng, Q.; Ren, Q.; Nolan, R.H.; Wu, P.; Yu, Q. Assessing China’s agricultural water use efficiency in a green-blue water perspective: A study based on data envelopment analysis. Ecol. Indic. 2019, 96, 329–335. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, S.; He, X.; Li, J. Efficiency change in North-East China agricultural sector: A DEA approach. Agric. Econ. 2015, 61, 522–532. [Google Scholar] [CrossRef]
- Pang, J.; Chen, X.; Zhang, Z.; Li, H. Measuring eco-efficiency of agriculture in China. Sustainability 2016, 8, 398. [Google Scholar] [CrossRef]
- Baráth, L.; Ferto, I. Productivity and convergence in European agriculture. J. Agric. Econ. 2017, 68, 228–248. [Google Scholar] [CrossRef]
- Toma, E.; Dobre, C.; Dona, I.; Cofas, E. DEA applicability in assessment of agriculture efficiency on areas with similar geographically patterns. Agric. Agric. Sci. Procedia 2015, 6, 704–711. [Google Scholar] [CrossRef]
- Raheli, H.; Rezaei, R.M.; Jadidi, M.R.; Mobtaker, H.G. A two-stage DEA model to evaluate sustainability and energy efficiency of tomato production. Inf. Process. Agric. 2017, 4, 342–350. [Google Scholar] [CrossRef]
- Cardozo, N.P.; de Oliveira Bordonal, R.; La Scala, N., Jr. Sustainable intensification of sugarcane production under irrigation systems, considering climate interactions and agricultural efficiency. J. Clean. Prod. 2018, 204, 861–871. [Google Scholar] [CrossRef]
- Grados, D.; Schrevens, E. Multidimensional analysis of environmental impacts from potato agricultural production in the Peruvian Central Andes. Sci. Total Environ. 2019, 663, 927–934. [Google Scholar] [CrossRef] [PubMed]
- Singbo, A.G.; Lansink, A.O.; Emvalomatis, G. Estimating shadow prices and efficiency analysis of productive inputs and pesticide use of vegetable production. Eur. J. Oper. Res. 2015, 245, 265–272. [Google Scholar] [CrossRef]
- Rajendran, S.; Afari-Sefa, V.; Karanja, D.K.; Musebe, R.; Romney, D.; Makaranga, M.A.; Samali, S.; Kessy, R.F. Technical efficiency of traditional African vegetable production: A case study of smallholders in Tanzania. J. Dev. Agric. Econ. 2015, 7, 92–99. [Google Scholar]
- Ajekiigbe, N.; Ayanwale, A.; Oyedele, D.; Adebooye, O. Technical efficiency in production of underutilized indigenous vegetables. Int. J. Veg. Sci. 2018, 24, 193–201. [Google Scholar] [CrossRef]
- Duan, N.; Guo, J.P.; Xie, B.C. Is there a difference between the energy and CO2 emission performance for China’s thermal power industry? A bootstrapped directional distance function approach. Appl. Energy 2016, 162, 1552–1563. [Google Scholar] [CrossRef]
- Riccardi, R.; Oggioni, G.; Toninelli, R. Efficiency analysis of world cement industry in presence of undesirable output: Application of data envelopment analysis and directional distance function. Energy Policy 2012, 44, 140–152. [Google Scholar] [CrossRef]
- Choi, Y.; Zhang, N.; Zhou, P. Efficiency and abatement costs of energy-related CO2 emissions in China: A slacks-based efficiency measure. Appl. Energy 2012, 98, 198–208. [Google Scholar] [CrossRef]
- Lee, T.; Yeo, G.T.; Thai, V.V. Environmental efficiency analysis of port cities: Slacks-based measure data envelopment analysis approach. Transp. Policy 2014, 33, 82–88. [Google Scholar] [CrossRef]
- Li, L.B.; Hu, J.L. Ecological total-factor energy efficiency of regions in China. Energy Policy 2012, 46, 216–224. [Google Scholar] [CrossRef]
- Zhang, N.; Zhou, P.; Kung, C.C. Total-factor carbon emission performance of the Chinese transportation industry: A bootstrapped non-radial Malmquist index analysis. Renew. Sustain. Energy Rev. 2015, 41, 584–593. [Google Scholar] [CrossRef]
- Zhou, G.; Chung, W.; Zhang, Y. Measuring energy efficiency performance of China’s transport sector: A data envelopment analysis approach. Expert Syst. Appl. 2014, 41, 709–722. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Yang, G.L. CO2 emissions reduction of Chinese light manufacturing industries: A novel RAM-based global Malmquist–Luenberger productivity index. Energy Policy 2016, 96, 397–410. [Google Scholar] [CrossRef]
- Wu, J.; Lv, L.; Sun, J.; Ji, X. A comprehensive analysis of China’s regional energy saving and emission reduction efficiency: From production and treatment perspectives. Energy Policy 2015, 84, 166–176. [Google Scholar] [CrossRef]
- Fei, R.; Lin, B. Energy efficiency and production technology heterogeneity in China’s agricultural sector: A meta-frontier approach. Technol. Forecast. Soc. Chang. 2016, 109, 25–34. [Google Scholar] [CrossRef]
- Fei, R.; Lin, B. The integrated efficiency of inputs–outputs and energy–CO2 emissions performance of China’s agricultural sector. Renew. Sustain. Energy Rev. 2017, 75, 668–676. [Google Scholar] [CrossRef]
- Li, N.; Jiang, Y.; Mu, H.; Yu, Z. Efficiency evaluation and improvement potential for the Chinese agricultural sector at the provincial level based on data envelopment analysis (DEA). Energy 2018, 164, 1145–1160. [Google Scholar] [CrossRef]
- Le, T.L.; Lee, P.P.; Peng, K.C.; Chung, R.H. Evaluation of total factor productivity and environmental efficiency of agriculture in nine East Asian countries. Agric. Econ. 2019, 65, 249–258. [Google Scholar]
- Wang, F.; Yu, C.; Xiong, L.; Chang, Y. How can agricultural water use efficiency be promoted in China? A spatial-temporal analysis. Resour. Conserv. Recycl. 2019, 145, 411–418. [Google Scholar] [CrossRef]
- Lampe, H.W.; Hilgers, D. Trajectories of efficiency measurement: A bibliometric analysis of DEA and SFA. Eur. J. Oper. Res. 2015, 240, 1–21. [Google Scholar] [CrossRef]
- Ahmad, Z.; Jun, M. Agricultural Production Structure Adjustment Scheme Evaluation and Selection Based on DEA Model for Punjab (Pakistan). J. Northeast Agric. Univ. (Engl. Ed.) 2015, 22, 87–91. [Google Scholar] [CrossRef]
- e Souza, G.D.S.; Gomes, E.G. Management of agricultural research centers in Brazil: A DEA application using a dynamic GMM approach. Eur. J. Oper. Res. 2015, 240, 819–824. [Google Scholar] [CrossRef]
- Zhu, N.; Hougaard, J.L.; Ghiyasi, M. Ranking production units by their impact on structural efficiency. J. Oper. Res. Soc. 2019, 70, 783–792. [Google Scholar] [CrossRef]
- Rahman, M.T.; Nielsen, R.; Khan, M.A.; Asmild, M. Efficiency and production environmental heterogeneity in aquaculture: A meta-frontier DEA approach. Aquaculture 2019, 509, 140–148. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Fenyves, V.; Tarnóczi, T.; Zsidó, K. Financial performance evaluation of agricultural enterprises with DEA method. Procedia Econ. Financ. 2015, 32, 423–431. [Google Scholar] [CrossRef]
- Adesemoye, A.O.; Kloepper, J.W. Plant–microbes interactions in enhanced fertilizer-use efficiency. Appl. Microbiol. Biotechnol. 2009, 85, 1–12. [Google Scholar] [CrossRef]
- Tilman, D.; Cassman, K.G.; Matson, P.A.; Naylor, R.; Polasky, S. Agricultural sustainability and intensive production practices. Nature 2002, 418, 671–677. [Google Scholar] [CrossRef]
- Idrees, M.; Batool, S.; Hussain, Q.; Ullah, H.; Al-Wabel, M.I.; Ahmad, M.; Kong, J. High-efficiency remediation of cadmium (Cd2+) from aqueous solution using poultry manure–and farmyard manure–derived biochars. Sep. Sci. Technol. 2016, 51, 2307–2317. [Google Scholar] [CrossRef]
- Vymazal, J.; Březinová, T. The use of constructed wetlands for removal of pesticides from agricultural runoff and drainage: A review. Environ. Int. 2015, 75, 11–20. [Google Scholar] [CrossRef] [PubMed]


| Variable Classification | Variable Names | Definitions | Units |
|---|---|---|---|
| Output | OVMP | Output value of main product | Kilogram |
| MSC | Material and service cost | Yuan | |
| SC | Seed cost | Yuan | |
| FC | Fertilizer cost | Yuan | |
| Inputs | FMC | Farmyard manure cost | Yuan |
| PC | Pesticide cost | Yuan | |
| WD | Working days | Day | |
| S | Acreage of greenhouse vegetables | m | |
| OV | Original value of an output or input variable | Kilogram or yuan or day | |
| Constraint variable | RM | Radial adjustment of an input variable | Kilogram or yuan or day |
| SM | Slack movement of an input variable | Kilogram or yuan or day | |
| PV | Target value of an output or input variable | Kilogram or yuan or day |
| Province | OTE | PTE | SE | SR |
|---|---|---|---|---|
| Beijing | 0.959 | 1.000 | 0.959 | |
| Tianjin | 1.000 | 1.000 | 1.000 | − |
| Hebei | 0.720 | 0.745 | 0.967 | |
| Shanxi | 0.728 | 0.729 | 0.998 | |
| Inner M | 0.628 | 0.651 | 0.964 | |
| Liaoning | 0.603 | 0.608 | 0.992 | |
| Jilin | 0.725 | 0.782 | 0.927 | |
| Heilongjiang | 1.000 | 1.000 | 1.000 | − |
| Shanghai | 0.891 | 0.975 | 0.914 | |
| Jiangsu | 0.788 | 0.812 | 0.970 | |
| Zhejiang | 0.920 | 1.000 | 0.920 | |
| Anhui | 0.929 | 0.984 | 0.944 | |
| Shandong | 0.488 | 0.618 | 0.789 | |
| Henan | 0.779 | 0.823 | 0.946 | |
| Hubei | 1.000 | 1.000 | 1.000 | − |
| Sichuan | 0.906 | 1.000 | 0.906 | |
| Shaanxi | 0.756 | 0.848 | 0.890 | |
| Gansu | 0.705 | 0.781 | 0.903 | |
| Qinghai | 0.949 | 0.958 | 0.990 | |
| Ningxia | 0.980 | 1.000 | 0.980 | |
| Xinjiang | 1.000 | 1.000 | 1.000 | − |
| Provinces | Item | OVMP/kg | MSC/Yuan | WD/d | SC/Yuan | FC/Yuan | FMC/Yuan | PC/Yuan |
|---|---|---|---|---|---|---|---|---|
| Hebei | OV | 5385.83 | 3199.96 | 61.4 | 399.1 | 476.45 | 425.39 | 258.27 |
| RM | 0 | −816.13 | −15.66 | −101.788 | −121.516 | −108.493 | −65.87 | |
| SM | 0 | 0 | 0 | −70.447 | 0 | −96.231 | −37.778 | |
| PV | 5385.83 | 2383.83 | 45.74 | 226.865 | 354.934 | 220.666 | 154.621 | |
| Shanxi | OV | 5494.79 | 3733.41 | 83.39 | 323.54 | 342.74 | 515.99 | 180.6 |
| RM | 0 | −1012.13 | −22.607 | −87.712 | −92.917 | −139.885 | −48.961 | |
| SM | 0 | −11.84 | −11.385 | −15.304 | 0 | −78.974 | 0 | |
| PV | 5494.79 | 2709.444 | 49.398 | 220.524 | 249.823 | 297.131 | 131.639 | |
| Inner M | OV | 5384.68 | 3704.19 | 68.07 | 636.82 | 584.67 | 433.84 | 266.01 |
| RM | 0 | −1292.45 | −23.751 | −222.197 | −204.001 | −151.374 | −92.815 | |
| SM | 0 | 0 | 0 | −182.395 | 0 | −72.588 | −11.777 | |
| PV | 5384.68 | 2411.736 | 44.319 | 232.227 | 380.669 | 209.878 | 161.418 | |
| Liaoning | OV | 5148.08 | 5559.37 | 71.11 | 329.09 | 591.24 | 368.22 | 408.8 |
| RM | 0 | −2181.35 | −27.902 | −29.126 | −231.987 | −144.48 | −160.402 | |
| SM | 0 | −511.446 | 0 | 0 | −44.596 | 0 | −83.724 | |
| PV | 5148.08 | 2866.577 | 43.208 | 199.964 | 314.657 | 223.74 | 164.674 | |
| Jilin | OV | 4484.96 | 2438.44 | 68.55 | 165.52 | 333.46 | 191.17 | 255.3 |
| RM | 0 | −530.439 | −14.912 | −36.006 | −72.538 | −41.586 | −55.536 | |
| SM | 355.543 | −270.354 | −1.93 | 0 | −10.141 | 0 | −69.356 | |
| PV | 4840.503 | 1637.647 | 51.708 | 129.514 | 250.78 | 149.584 | 130.408 | |
| Shanghai | OV | 4651.63 | 2132.19 | 48.79 | 193.17 | 298.41 | 210.83 | 206.49 |
| RM | 0 | −53.546 | −1.225 | −4.851 | −7.494 | −5.295 | −5.186 | |
| SM | 283.252 | 0 | 0 | −36.119 | 0 | −43.15 | −56.025 | |
| PV | 4934.882 | 2078.644 | 47.565 | 152.2 | 290.916 | 162.385 | 145.279 | |
| Jiangsu | OV | 4715.23 | 2752.13 | 66.11 | 152.82 | 347.68 | 344.18 | 221.79 |
| RM | 0 | −516.325 | −12.403 | −28.67 | −65.228 | −64.571 | −41.61 | |
| SM | 146.542 | −595.327 | 0 | 0 | −70.721 | −108.826 | −59.818 | |
| PV | 4861.772 | 1640.477 | 53.707 | 124.15 | 211.731 | 170.783 | 120.362 | |
| Anhui | OV | 4538.3 | 2412.29 | 49.23 | 140.46 | 457.91 | 369.43 | 176.76 |
| RM | 0 | −38.023 | −0.776 | −2.214 | −7.218 | −5.823 | −2.786 | |
| SM | 267.584 | −741.226 | 0 | 0 | −136.351 | −248.527 | −27.214 | |
| PV | 4805.884 | 1633.041 | 48.454 | 138.246 | 314.341 | 115.08 | 146.76 | |
| Shandong | OV | 4404.7 | 4148.17 | 68.61 | 769.7 | 589.55 | 492.77 | 290.14 |
| RM | 0 | −1584.34 | −26.205 | −293.978 | −225.172 | −188.208 | −110.816 | |
| SM | 520.407 | −131.078 | 0 | −288.368 | 0 | −148.647 | 0 | |
| PV | 4925.107 | 2432.748 | 42.405 | 187.354 | 364.378 | 155.915 | 179.324 | |
| Henan | OV | 5105.42 | 2664.3 | 65.01 | 193.99 | 406.89 | 286.88 | 204.75 |
| RM | 0 | −470.577 | −11.482 | −34.263 | −71.866 | −50.67 | −36.164 | |
| SM | 0 | 0 | −1.946 | 0 | −118.426 | −7.683 | −43.883 | |
| PV | 5105.42 | 2193.723 | 51.582 | 159.727 | 216.598 | 228.528 | 124.704 | |
| Shaanxi | OV | 4512.17 | 2244.62 | 60.49 | 314.83 | 275.67 | 293.67 | 220.67 |
| RM | 0 | −340.163 | −9.167 | −47.711 | −41.777 | −44.504 | −33.442 | |
| SM | 407.076 | 0 | 0 | −129.651 | 0 | −69.72 | −58.445 | |
| PV | 4919.246 | 1904.457 | 51.323 | 137.468 | 233.893 | 179.446 | 128.783 | |
| Gansu | OV | 5473.01 | 3259.06 | 73.93 | 295.34 | 451.16 | 278.32 | 232.8 |
| RM | 0 | −713.899 | −16.194 | −64.694 | −98.827 | −60.966 | −50.995 | |
| SM | 0 | −288.45 | −5.592 | −1.158 | 0 | 0 | 0 | |
| PV | 5473.01 | 2256.71 | 52.143 | 229.487 | 352.333 | 217.354 | 181.805 | |
| Qinghai | OV | 5781.85 | 3955.8 | 70.16 | 302.58 | 344.48 | 1092.73 | 138.07 |
| RM | 0 | −164.427 | −2.916 | −12.577 | −14.319 | −45.42 | −5.739 | |
| SM | 0 | −1336.75 | −16.504 | −21.657 | −30.038 | −732.328 | 0 | |
| PV | 5781.85 | 2454.629 | 50.74 | 268.346 | 300.124 | 314.982 | 132.331 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Y.; Jing, X.; Wang, Y.; Shi, Y.; Ruan, J. Evaluating Production Process Efficiency of Provincial Greenhouse Vegetables in China Using Data Envelopment Analysis: A Green and Sustainable Perspective. Processes 2019, 7, 780. https://doi.org/10.3390/pr7110780
Liang Y, Jing X, Wang Y, Shi Y, Ruan J. Evaluating Production Process Efficiency of Provincial Greenhouse Vegetables in China Using Data Envelopment Analysis: A Green and Sustainable Perspective. Processes. 2019; 7(11):780. https://doi.org/10.3390/pr7110780
Chicago/Turabian StyleLiang, Yuhu, Xu Jing, Yanan Wang, Yan Shi, and Junhu Ruan. 2019. "Evaluating Production Process Efficiency of Provincial Greenhouse Vegetables in China Using Data Envelopment Analysis: A Green and Sustainable Perspective" Processes 7, no. 11: 780. https://doi.org/10.3390/pr7110780
APA StyleLiang, Y., Jing, X., Wang, Y., Shi, Y., & Ruan, J. (2019). Evaluating Production Process Efficiency of Provincial Greenhouse Vegetables in China Using Data Envelopment Analysis: A Green and Sustainable Perspective. Processes, 7(11), 780. https://doi.org/10.3390/pr7110780







