Abstract
Computational effort and convergence problems can pose serious challenges when employing advanced thermodynamic models in process simulation and optimization. Data-based surrogate modeling helps to overcome these problems at the cost of additional modeling effort. The present work extends the range of methods for efficient data-based surrogate modeling of liquid–liquid equilibria. A new model formulation is presented that enables smaller surrogates with box-constrained input domains and reduced input dimensions. Sample data are generated efficiently by using numerical continuation. The new methods are demonstrated for the surrogate modeling and optimization of a process for the hydroformylation of 1-decene in a thermomorphic multiphase system.
1. Introduction
In chemical process design, advanced thermodynamic models offer increasing predictive accuracy for physical properties of mixtures. However, this correlates with increasingly complex models, which introduce serious challenges when used for process simulation and optimization. Problems may arise from embedded iterative solution procedures for the thermodynamic models, which may not converge to a valid solution or require a large number of iteration steps. The benefits of advanced thermodynamic models can be used by replacing them with surrogates that are computationally easy to handle [1].
The concept of surrogate modeling comprises a number of different approaches [2] that depend on the type of the original model and the desired properties of the surrogate. In chemical process engineering, data-driven surrogate modeling is usually employed [3]. This class of methods generally treats the original model as a black box with input–output data. The surrogate that replaces the original model is constructed such that it approximates the data and is easy to evaluate. These requirements define major steps of data-driven surrogate modeling.
In a first step, inputs and outputs have to be selected from the original model. This determines the properties of the input–output data and thereby affects both the accuracy and size of the surrogate model. A larger input dimension increases the size of the surrogate and necessitates more sample data. A difficult input domain may require modeling with an additional surrogate [4]. In addition, output multiplicities have to be treated with special methods [5].
Several data-driven surrogate models are available, e.g., polynomials, neural networks, and Gaussian processes [2]. The choice for the surrogate model structure is usually not trivial and a number of different models should be tried. Tools for automatically selecting a surrogate model structure are available (e.g., [6]).
Parameter fitting for surrogate models requires sample data that fully characterize the input–output behavior. The additional cost for sample generation is reduced by employing efficient sampling methods. Adaptive sampling approaches that employ exploration and exploitation strategies are preferred over one-shot methods in recent literature (see [3,4] for references).
Although various strategies are available for each aspect of surrogate modeling, there is still significant potential for improvements, especially when problem-specific features are taken into account.
The present contribution extends the methods of surrogate modeling for liquid–liquid phase equilibria (LLE). This includes efficient sample generation by employing a numerical continuation method and an efficient surrogate formulation that has a box-constrained input domain and a reduced input dimension compared to established formulations. In Section 2, LLE modeling is introduced briefly and a description of surrogate modeling of LLE is given that summarizes recent work on the topic. Section 3 describes the methods of sample data generation and surrogate modeling proposed in this work. A case study based on a process for the hydroformylation of 1-decene in a thermomorphic multiphase system is used in Section 4 to demonstrate the proposed methods. A short conclusion is given in Section 5.
2. Background
This section summarizes the required background for LLE modeling and recent work on surrogate modeling of LLE.
2.1. Liquid–Liquid Equilibrium Modeling
The liquid–liquid equilibrium is described by a two-phase flash model comprising component mass balance conditions
and thermodynamic equilibrium conditions
Here, is the mole amount, is the chemical potential, is the temperature and is the pressure in phase for component i. The mole amounts of the feed mixture are denoted by and the total number of components in the mixture is .
The conditions for equal chemical potential can be reformulated for liquid–liquid equilibria as the isoactivity conditions
with mole fractions , vectors of mole fractions , and activity coefficients .
Iterative procedures are usually utilized to find a solution of the implicit equilibrium model, evaluating the activity coefficients provided by the thermodynamic model in each iteration. Therefore, using advanced models such as the perturbed-chain statistical associating fluid theory (PC-SAFT) [7] or universal quasichemical functional-group activity coefficients (UNIFAC) [8] directly for flowsheet simulation and optimization is unfavorable in terms of convergence behavior and computational effort. Furthermore, excluding undesired trivial solutions of the equation system given above requires additional effort. The following section describes the technique of replacing such expensive calculations by data-driven surrogate models that are computationally easier to handle.
2.2. Surrogate Modeling of LLE
Surrogate modeling aims at replacing a function ,
with a surrogate function that is similar to the original function and exhibits favorable properties, e.g., much lower computational effort. More specifically, data-driven surrogate modeling generally uses samples to fit parameters of the surrogate such that some performance criterion is satisfied. If an approximation of the original function is desired, typical performance criteria include minimizing the mean squared error or mean absolute error with respect to the samples. Another performance criterion is the exact reproduction of the sample points , which can be used for instance in Kriging interpolation (e.g., [9]). In this sense, data-driven surrogate modeling is another name for nonlinear regression and interpolation methods. Applications for surrogate modeling include, but are not limited to, cases where the original function is expensive to evaluate, e.g., computational fluid dynamics simulations, or where a functional form may not be available, e.g., experimental results.
This section gives a summary of recent efforts [4,10] on using data-driven surrogate models for phase equilibrium calculations, particularly for LLE, to improve computational performance while preserving high model accuracy. For the sake of readability, some details of each approach are omitted here and we refer to the original publications for comprehensive descriptions. A broader overview on general surrogate modeling is available in the literature [2,3,11,12].
2.2.1. Selection of Inputs and Outputs
Distribution coefficients are introduced, which allows one to rewrite the equilibrium model as
In the model comprising Equations (7)–(10), is replaced by a surrogate . Kriging interpolation is used for the surrogates in [4,10]. The inputs of the surrogate are mole fractions of the feed mixture and the temperature. The outputs comprise the distribution coefficients. The pressure does not appear as an input since its influence on the liquid–liquid equilibrium is assumed to be negligible.
It should be emphasized that, given a feasible feed mixture and temperature, all quantities in Equations (7)–(10) can be calculated in a sequential fashion.
2.2.2. Description of the Input Domain X
A natural choice for the input domain, given molar fractions and the temperature as inputs, would be
However, the distribution coefficient model in Equations (7)–(10) is only valid within the miscibility gap of the mixture. Therefore, box constraints are not suitable to accurately describe the complete input domain X of the surrogate . Instead, the input domain can be defined by a classifier , which is less than zero only within the miscibility gap:
2.2.3. Sample Data and Surrogate Generation
The selection of sample locations for data generation can be categorized in one-shot space-filling designs, which select locations according to pre-defined strategies, and adaptive sampling approaches, which exploit information from available sampling data to select new sampling locations. In [10], sample values are calculated by evaluating the equilibrium model at pre-defined sample locations generated by a space-filling design. A major contribution of Nentwich and Engell [4] is a method of adaptively choosing new sample locations based on available sample data to improve the quality of the approximation compared to one-shot designs with the same number of samples. In principle, new sample locations are chosen by maximizing a weighted sum of the minimum distance to existing sample locations and the predicted variance, i.e., by exploration and exploitation strategies. The surrogate model needs to be updated in each iteration of this method.
In both references, the sample generation takes a substantial amount of time. For a constant sample density, the number of required samples scales exponentially with the dimension of the input domain. In addition, the equilibrium model is solved at each sample location independently, i.e., the solution algorithm needs to converge starting from an independent initial guess.
3. Methods
The literature approaches to surrogate modeling of LLE rely on a regression model for the distribution of components between phases and an additional classification model to determine whether a given set of input values lies in the two-phase region. This section describes new approaches aiming at extending the pool of methods for surrogate modeling of LLE. For this, a model reformulation that enables smaller surrogate models and a method for efficiently calculating sample data are presented.
3.1. Parameterization of Binodal Curves
The strategy for reducing the computational effort for surrogates in LLE modeling presented here comprises two ideas. First, instead of modeling the entire miscibility gap, only the binodal curve is described by a surrogate, which reduces the surrogate input dimension by one. As shown in Figure 1 for a ternary mixture, the binodal curve has one dimension fewer than the miscibility gap, i.e., it is a line instead of an area. Note that for more than three components , the set of equilibrium compositions is a -dimensional surface. For a constant sample density, the number of required sample points for a surrogate model depends exponentially on its input dimension. Reducing the number of inputs therefore improves computational tractability of the surrogate.
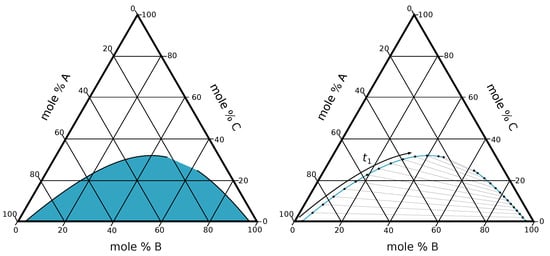
Figure 1.
Sample region for liquid-liquid equilibrium (LLE) calculations of a ternary mixture, (left) when modeling the entire miscibility gap and (right) when modeling the binodal curve. The parameterization variable determines the position on the binodal curve, i.e., the pair of equilibrium compositions on the endpoints of the tie line.
Second, instead of using molar fractions as inputs of the surrogate, the position on the binodal curve is introduced as a new coordinate, marked by in Figure 1. Each value of this coordinate corresponds to the endpoints of a tie line, i.e., the compositions of two phases in equilibrium. The parameterization variable can be defined from the border of the phase diagram to the critical point, if the data are available, or just on a section of the binodal curve. This removes the need for a complicated (surrogate) model of the input domain, since the parameterization of the binodal curve can be chosen such that box constraints are sufficient, i.e., .
Using these ideas, the equilibrium model is reformulated as follows.
Here, the parameterization variables for the binodal curve are denoted by . In the model comprising Equations (13) and (14), is replaced by a surrogate . The inputs of the surrogate are the temperature and variables for the parameterization of the binodal curve. The input domain for the surrogate functions reads simply
The outputs comprise independent mole fractions. We decided to include all molar fractions here, because eliminating one molar fraction by using the summation condition would make it harder to have the same error scaling for all components during surrogate fitting and it would increase the maximum error for the eliminated component in the final surrogate model.
In summary, the parameterization of binodal curves enables the generation of smaller surrogate models due to the reduction of the input dimension and the definition of the input domain by box constraints. The overall model is rendered implicit by this reformulation. Implicit models are generally harder to solve than explicit models. However, the reduced model size, and thereby the reduced number of nonlinear expressions that have to be evaluated, is favorable for the computational performance.
3.2. Numerical Continuation for Sample Calculation
Calculations of phase equilibria, especially for LLE, often require considerable computational effort due to iterative solution procedures and in some cases good initial guesses to calculate valid equilibrium compositions. Therefore, fast surrogates are employed for simulation and optimization. The original equilibrium model is only used during sample generation. However, the samples need to cover the entire miscibility gap to enable accurate surrogate modeling and their acquisition can take a considerable amount of time.
The computational cost of sample generation can be reduced by exploiting existing sample data. For instance, in [4], new sample locations are chosen such that they are most likely to improve the surrogate model, thus reducing the overall number of required sample points.
The basic idea followed in the present work is using numerical continuation methods (e.g., [13]) to improve convergence behavior of equilibrium calculations and thereby to reduce the computation time. Continuation methods are used to find solutions of an equation system that depend on a parameter, e.g., solutions of the equilibrium model depending on the feed composition. Varying this parameter, a prediction for the new solution is calculated based on previous solutions and then the prediction is corrected. Since initial guesses are improved using systematic predictions, the correction step converges more quickly to an accurate solution.
In an earlier work [14], the phase stability of an arbitrary point in the phase diagram is tested by tracking valid solutions of the equilibrium model from a known starting composition to the desired location using homotopy continuation. This strategy is adapted here to track solutions of the equilibrium model along the binodal curve by varying the feed composition.
We apply a dynamic method for minimization problems (e.g., [15]) to solve the equilibrium model for a given feed composition. The following ordinary differential equation system
converges to a valid solution if the initial guess of the phase compositions is sufficiently close to that solution. Mole fractions are calculated by and the activity coefficients are functions of composition and temperature. The scaling factor ensures consistent units on both sides of the equations.
In an effort to track solutions along the binodal curve, the feed composition is varied along a line with a constant phase ratio. This trajectory, depicted in Figure 2, starts from a point on the border of the phase diagram and covers the entire miscibility gap of a ternary mixture. For all feed compositions along the trajectory, corresponding points on the binodal curve are obtained by solving the equilibrium model using Equations (16) and (17). In comparison to the previous approaches in [4,10], this strategy only requires sampling on a line in the miscibility gap instead of sampling in the whole area. If the starting point does not lie on the border of the phase diagram, the line has to be tracked in both directions from the starting point.
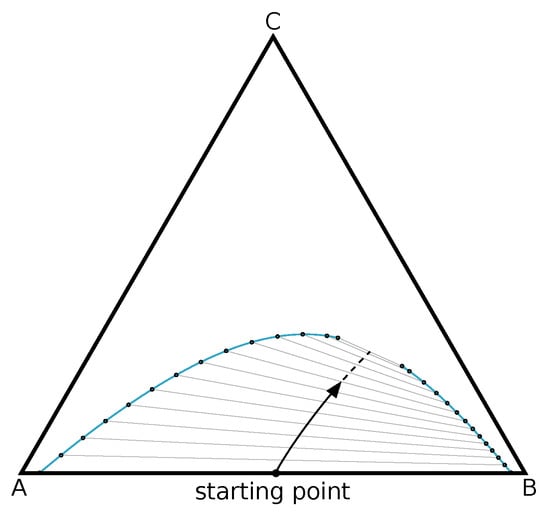
Figure 2.
Sampling of the binodal curve: Trajectory of the feed composition at a constant phase ratio of and corresponding equilibrium compositions on the binodal curve.
An efficient approach to characterize the overall phase behavior of a mixture by evaluating the convex envelope of the Gibbs energy, and thus to identify viable starting points within a miscibility gap, is given in [16].
The continuation method is implemented here by augmenting Equations (16) and (17) with additional expressions that offer convergence to the selected phase ratio and movement of the feed composition perpendicular to the current tie line. Each additional expression is chosen such that the dynamic it introduces is orders of magnitude slower than that of the equilibrium conditions. The resulting stiff ordinary differential equation system is solved using the MATLAB function ode15s [17].
In the case of mixtures with more than three components, the equilibrium compositions form a -dimensional surface instead of a one-dimensional curve. In the present work, the continuation method is adapted to this case by fixing the molar fractions of additional components to constant values and repeat the calculations for all sets of fixed values.
4. Results
This section demonstrates the application of the methods presented in the previous section to the modeling and optimization of a liquid–liquid extraction process.
4.1. Description of the Case Study
A multistage liquid–liquid extraction process adapted from [10] is used here as a case study for the methods presented above. In [10], the optimization of a process for the homogeneously catalyzed hydroformylation of 1-dodecene in a thermomorphic multiphase system is considered. The mixture is homogeneous at reaction conditions and biphasic at lower temperatures. This is used to separate the catalyst from the product in an extraction cascade and to recycle the catalyst back to the reactor. The extraction cascade considered here is highlighted in Figure 3, which shows a modified flowsheet of the overall process from [10].
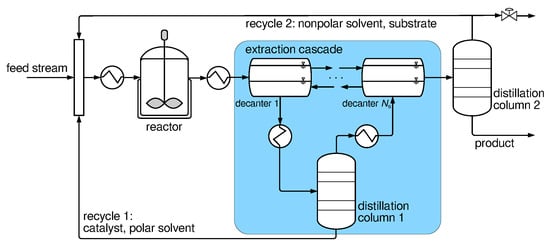
Figure 3.
Modified hydroformylation process adapted from [10]. The highlighted area marks the extraction cascade with extraction solvent recycle considered in the present work.
In the present work, the mixture consists of the polar solvent dimethylformamide, the nonpolar solvent dodecane, the product n-undecanal and the substrate 1-decene. As in [10], the mixture includes a catalyst, which is distributed between the two phases depending on their equilibrium composition. The catalyst concentration is higher in the more polar phase than in the less polar phase. Moreover, it is assumed that the catalyst has no influence on the phase equilibrium due to it having a very low concentration. Thus, the catalyst partition coefficient is modeled at infinite dilution and therefore it is added to the set of surrogate outputs, but not to the inputs. All extraction stages are operated at the same constant temperature , as suggested by the results in [10].
The resulting equation system for a single extraction stage reads
with denoting molar flows of component i in phase j and calculating the logarithmic partition coefficient for the catalyst between the less polar phase and the more polar phase . Table 1 lists the names of the components corresponding to the index i.

Table 1.
Component labels.
In the model consisting of Equations (18)–(21), and are replaced by a surrogate that comprises both the mole fractions and the logarithmic partition coefficient . With , the inputs of the surrogate are two parameterization variables and . The outputs are eight mole fractions for the equilibrium compositions in both phases as well as the catalyst partition coefficient.
The extraction cascade consists of stages, numbered from for the output stage of the more polar phase to for the output stage of the less polar phase . The stage is also the feed stage. Some of the polar solvent is separated using distillation column 1 and recycled to the extraction cascade at stage . The mass balances that describe the extraction cascade read
where is the distillate molar flow of distillation column 1 that recycles the extraction solvent and is the feed flow of the extraction cascade for component i.
The mass balances of the distillation column are replaced by the approximation that the distillate of column 1 contains only the polar solvent . The distillate flow is a degree of freedom for this process. A larger distillate flow is able to extract more catalyst, but requires, e.g., more heat for vaporization, a larger distillation column, and larger extraction stages.
The costs considered for this process comprise the catalyst that is retained in the nonpolar product stream, the investment for the decanter vessels, and the operation and investment for distillation column 1. The catalyst costs are proportional to the amount of catalyst that is lost. The investment costs for the distillation column and the decanter vessels are calculated based on [19]. The sizing of the column utilizes the Fenske–Underwood–Gilliland correlations [20,21,22,23] with mean mixture and component properties. A simplified cost function is generated by fitting a polynomial function to data obtained by evaluating the cost calculation for a set of different compositions of the column feed and different values of the distillate flow rate at a distillate purity of 99 % (see [24] for more details). The overall cost J in $ year for this process reads
with parameters given in Table 2.

Table 2.
Cost function parameters.
4.2. Data Generation
The method presented in Section 3.2 is used to generate sample data for . The activity coefficients are calculated utilizing a modified UNIFAC (Dortmund) model [8] with some parameters fit to experimental data as in [10]. Recall that, for four components, one molar fraction is required to be fixed to a constant value for each continuation run. Therefore, a set of binodal curves is calculated for different fixed values of the molar fraction of 1-dodecene in the less polar phase . Each continuation run is initialized at the boundary of the phase diagram with zero n-undecanal, i.e., . The starting point is calculated by solving the dynamic equation system using ode15s in MATLAB with an arbitrary initial guess for the molar fractions of the polar solvent and the nonpolar solvent. Beginning at the calculated starting point, the feed composition is continued along the line of a constant phase ratio of . The continuation is stopped when the condition is met, i.e., when the amount of polar solvent in the less polar phase is equal to that of the nonpolar solvent. This stopping criterion is chosen here because the extraction of catalyst is ineffective beyond that point due to low values of the partition coefficient. An example of the resulting binodal curves is shown in Figure 4.
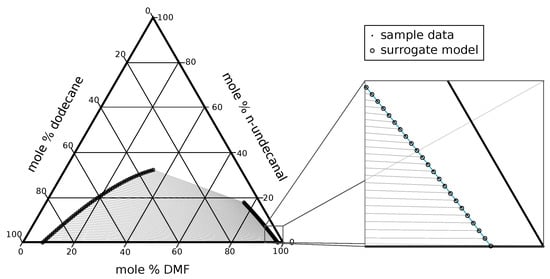
Figure 4.
Results of sample data generation and surrogate fitting. The binodal curve is shown for , i.e., for a mixture without 1-dodecene. The surrogate used for this figure has neurons in the hidden layer of the artificial neural network (ANN) (see Table 3).
The total number of 26 continuation runs produce more than samples with an accuracy of . The calculations require fewer than calls to the UNIFAC implementation of the activity coefficient model and a computation time of less than 1 min on a standard desktop computer without utilizing parallelization. For each binodal curve with a fixed value of , this corresponds to more than 1500 samples and less than 2 s of computation time. Calculating each starting point requires approximately 1000 function calls to the activity coefficient model and each binodal curve requires fewer than 5000 function calls. In other words, the continuation method required fewer than four function calls per sample point. Note that each evaluation of the right-hand-side of Equations (16) and (17) requires two function calls to the activity coefficient model, one for each phase.
The results from are used in COSMOtherm [25] to calculate the logarithmic partition coefficient of the catalyst using the same parameterization and catalyst COSMO input file as in [10]. Continuation is not available for COSMOtherm. Therefore, the logarithmic partition coefficient needs to be calculated separately for each phase composition, which takes a few seconds per sample point. To limit the computational effort, only 51 equally spaced sample points are used for each binodal curve.
The overall dataset used for the surrogate generation comprises sample locations on a regular grid for the input variables . The variables determine the equilibrium compositions of the two phases, i.e., the position on the two-dimensional binodal “curve”. The value of the molar fraction of 1-dodecene in the less polar phase is defined as . At each sample location, the output vector contains nine values, namely the phase compositions and the logarithmic catalyst partition coefficient:
with . Because the definition for makes interpolating redundant, only eight outputs are used for the surrogate model generation, which corresponds to 1326 × 8 = 10,608 sample values.
4.3. Surrogate Fitting
In the present work, the surrogate model is constructed as a sum of a second order polynomial function and a shallow artificial neural network (ANN) [26], i.e., an ANN with one hidden layer:
The polynomial function captures most of the information contained in the data using only simple expressions. The ANN is employed to further reduce the interpolation error of the surrogate model.
The second-order polynomial function
is fitted to the original data in three steps. First, for each output , all parameters of Equation (31) are determined by minimizing the sum of squared errors. Second, all terms with a low contribution to an output value are set to zero for that output value to reduce the number of nonlinear expressions, i.e.,
Third, the remaining parameter values are recalculated by minimizing the sum of squared errors. The polynomial function has a maximum of nonzero parameters.
Afterwards, the shallow ANN is fitted to the residual of the data . The model is fitted using the train command of MATLABs deep learning toolbox with the following options: the hyperbolic tangent as the activation function, the mean squared error as the performance function, data division using interleaved indices, Levenberg–Marquardt backpropagation, the regularization parameter equal to , and a minimum gradient equal to . The error weights for the outputs l are chosen proportionally to the inverse squared data range over all samples
with
The remaining options are at default values. The number of neurons in the hidden layer is varied from 5 to 15 to show the trade-off between the model accuracy and the number of parameters and nonlinear expressions.
The results of the parameter fitting are shown in Table 3 with the error metrics defined below. A part of the training algorithm relies on random number generation. The variations in model performance caused by this are not accounted for. The ANN training was executed once for each number of neurons in the hidden layer.

Table 3.
Performance metrics for the surrogate model. The sum of squared parameter values of the ANN is denoted by sumParANN.
The mean normalized error is the algebraic mean, over all outputs and samples , of the absolute error of an output value divided by the range of values for that output, i.e.,
The maximum normalized error is the maximum error of any output l over all samples k divided by the range of values for that output, i.e.,
The maximum normalized error offers a data-independent estimate of the surrogate quality, e.g., a surrogate with is not better than a constant function.
The error metric is the same as , but with the surrogate comprising only the polynomial function .
The surrogate fitting includes all molar fractions of a phase, although one of the molar fractions could be replaced by the summation condition. However, if the summation condition is used to replace one molar fraction, the worst case error for this quantity is the sum of absolute errors for all other molar fractions. This is increasingly relevant for a larger number of components. Including all molar fractions allows one to define suitable error weights for all quantities.
The results in Table 3 show that the surrogate can reproduce the data to a high degree of accuracy with a relatively low number of parameters. Based on the results for different numbers of neurons in the hidden layer, a surrogate model with is used for the following surrogate based optimization. The mean error over all sample data and surrogate outputs normalized by the data range for this surrogate model is and the maximum normalized error is . For 10608 sample values, this is achieved using 158 nonzero parameter values. There is no meaningful distinction between training set and validation set for this ratio of data points to number of parameters. The difference between surrogate model and sample data is also illustrated in Figure 4.
If only a second-order polynomial function is used as a surrogate, the maximum normalized error is .
4.4. Optimization
In this section, the surrogate model is tested for its suitability to be used in process optimization problems. The process model introduced in Section 4.1 is used as a case study. A mixture containing four components plus a catalyst is considered for the liquid–liquid extraction at a fixed temperature and pressure. The aim is to find the optimal extraction solvent recycle such that the costs, comprising energy, investment, and catalyst loss, are minimized. Surrogate models are employed for the liquid–liquid equilibrium in each extraction stage to keep the computational burden of the optimization problem low.
The original phase equilibrium model is replaced by the surrogate model and slack variables that account for regression errors
with the values of the slack variables lying between lower bounds and upper bounds
The values of the upper and lower bounds are estimated by the maximum error of the surrogate model at the sample points .
The optimization problem reads
with domains for all variables set to appropriate values and additional redundant constraints that enable tighter bounds for deterministic global optimization. The hyperbolic tangent is formulated as as suggested in [26]. The feed stream is given in Table 4. The number of stages is fixed to values between and .

Table 4.
Feed stream parameters.
The nonlinear programming (NLP) problem is implemented in GAMS 26.1.0 [27] using the deterministic global solver BARON 18.11.12 [28] with CONOPT 4.09 [29,30] as the nonlinear programming subsolver and CPLEX 12.8.0 [31] as the mixed-integer programming subsolver, and it is solved on the same standard desktop computer as used in Section 4.2. All options are at default values except for the relative optimality criterion, which is set to . The optimization is repeated for different numbers of stages . The computation time for global optimization is the total CPU time used as reported by BARON. Performance variability [32] is not accounted for: Each optimization problem is solved once. The time and the iterations required to find a local solution are determined by solving each problem with CONOPT and using the total time elapsed as reported by GAMS. Default values chosen by GAMS are used as initial guesses for all variables. Although this initial point is always infeasible, the selected solvers found feasible solutions in all observed cases.
The results in Table 5 show that the cost of the process falls steeply until a minimum is reached at . The cost increases slightly for . This behavior is due to large solvent recycles being required for good catalyst retention at low numbers of stages and the relatively small costs of increasing the number of stages. The overall optimum at resembles a trade-off between the cost for catalyst loss and solvent recycle on one hand and the investment cost for additional stages on the other hand. The solvent recycle for is an exception. The feed of the single stage already contains a large amount of the extraction solvent. Increasing the solvent amount further has only a marginal effect on catalyst retention, which does not compensate for the additional cost of solvent recycle at some point.

Table 5.
Optimization results.
The surrogate model implementation is significantly faster than the original model considering that we observed computation times of a few seconds for a single COSMOtherm evaluation. The computation times using BARON show that the surrogate model formulation is also suitable for small to medium sized deterministic global optimization problems. CONOPT was able to find a global solution for each of the considered cases. BARON requires the computation time to prove globality by converging the lower bound.
5. Conclusions
In this work, we introduce a new surrogate formulation that uses a parameterization of the binodal curve to reduce the input dimension and simplify the input domain. We also propose using numerical continuation methods for sampling of LLE data based on advanced thermodynamic models. The presented methods reduce the time required for sample data generation and allow for highly accurate reproduction of the data using smaller surrogate models.
Parameterization of complex input domains and sampling by numerical continuation are general strategies that may be extended to other applications in future work. Another possible improvement is replacing the activity coefficient model currently used for LLE calculations with more predictive equation of state models. The computation time of global optimization may be further reduced by employing reduced-space formulations of the optimization problem as in [26,33,34].
Author Contributions
Conceptualization, C.K.; methodology, C.K.; software, C.K., T.K., K.M. and S.L.; investigation, C.K.; writing—original draft preparation, C.K.; writing—review and editing, C.K., T.K., K.M., A.K. and S.L.; visualization, C.K. and T.K.; supervision, A.K. and K.S.; and funding acquisition, A.K. and K.S.
Funding
This research was funded by DFG grant number TRR 63.
Acknowledgments
This work is part of the Collaborative Research Center “Integrated Chemical Processes in Liquid Multiphase Systems”. Financial support by the Deutsche Forschungsgemeinschaft (DFG) is gratefully acknowledged through TRR 63.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nentwich, C.; Engell, S. Application of surrogate models for the optimization and design of chemical processes. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 1291–1296. [Google Scholar] [CrossRef]
- Asher, M.J.; Croke, B.F.W.; Jakeman, A.J.; Peeters, L.J.M. A review of surrogate models and their application to groundwater modeling. Water Resour. Res. 2015, 51, 5957–5973. [Google Scholar] [CrossRef]
- McBride, K.; Sundmacher, K. Overview of Surrogate Modeling in Chemical Process Engineering. Chem. Ing. Tech. 2019, 91, 228–239. [Google Scholar] [CrossRef]
- Nentwich, C.; Engell, S. Surrogate modeling of phase equilibrium calculations using adaptive sampling. Comput. Chem. Eng. 2019, 126, 204–217. [Google Scholar] [CrossRef]
- Keßler, T.; Kunde, C.; McBride, K.; Mertens, N.; Michaels, D.; Sundmacher, K.; Kienle, A. Global optimization of distillation columns using explicit and implicit surrogate models. Chem. Eng. Sci. 2019, 197, 235–245. [Google Scholar] [CrossRef]
- Boukouvala, F.; Floudas, C.A. ARGONAUT: AlgoRithms for Global Optimization of coNstrAined grey-box compUTational problems. Optim. Lett. 2017, 11, 895–913. [Google Scholar] [CrossRef]
- Gross, J.; Sadowski, G. Perturbed-Chain SAFT: An Equation of State Based on a Perturbation Theory for Chain Molecules. Ind. Eng. Chem. Res. 2001, 40, 1244–1260. [Google Scholar] [CrossRef]
- Weidlich, U.; Gmehling, J. A modified UNIFAC model. 1. Prediction of VLE, hE, and γ∞. Ind. Eng. Chem. Res. 1987, 26, 1372–1381. [Google Scholar] [CrossRef]
- Daya Sagar, B.; Cheng, Q.; Agterberg, F. (Eds.) Handbook of Mathematical Geosciences: Fifty Years of IAMG; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- McBride, K.; Kaiser, N.M.; Sundmacher, K. Integrated reaction-extraction process for the hydroformylation of long-chain alkenes with a homogeneous catalyst. Comput. Chem. Eng. 2017, 105, 212–223. [Google Scholar] [CrossRef]
- Forrester, A.I.; Keane, A.J. Recent advances in surrogate-based optimization. Prog. Aerosp. Sci. 2009, 45, 50–79. [Google Scholar] [CrossRef]
- Bhosekar, A.; Ierapetritou, M. Advances in surrogate based modeling, feasibility analysis, and optimization: A review. Comput. Chem. Eng. 2018, 108, 250–267. [Google Scholar] [CrossRef]
- Seydel, R. Practical Bifurcation and Stability Analysis, 3rd ed.; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Bausa, J.; Marquardt, W. Quick and reliable phase stability test in VLLE flash calculations by homotopy continuation. Comput. Chem. Eng. 2000, 24, 2447–2456. [Google Scholar] [CrossRef]
- Brown, A.A.; Bartholomew-Biggs, M.C. Some effective methods for unconstrained optimization based on the solution of systems of ordinary differential equations. J. Optim. Theory Appl. 1989, 62, 211–224. [Google Scholar] [CrossRef]
- Ryll, O.; Blagov, S.; Hasse, H. Convex envelope method for the determination of fluid phase diagrams. Fluid Phase Equilibria 2012, 324, 108–116. [Google Scholar] [CrossRef]
- MATLAB Release; The MathWorks, Inc.: Natick, MA, USA, 2018; Available online: https://www.mathworks.com/ (accessed on 14 October 2019).
- Privat, R.; Jaubert, J.N.; Privat, Y. A simple and unified algorithm to solve fluid phase equilibria using either the gamma-phi or the phi-phi approach for binary and ternary mixtures. Comput. Chem. Eng. 2013, 50, 139–151. [Google Scholar] [CrossRef]
- Douglas, J. Conceptual Design of Chemical Processes; McGraw-Hill Book Company: Singapore, 1988; p. 601. [Google Scholar]
- Fenske, M. Fractionation of Straight-Run Pennsylvania Gasoline. Ind. Eng. Chem. 1932, 24, 482–485. [Google Scholar] [CrossRef]
- Doherty, M.; Fidkowski, Z.; Malone, M.; Taylor, R. Perry’s Chemical Engineers’ Handbook; Chapter Distillation; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Gilliland, E. Multicomponent Rectification. Ind. Eng. Chem. 1940, 32, 1101–1106. [Google Scholar] [CrossRef]
- Eduljee, H. Equations replace Gilliland Plot. Hydrocarb. Process. 1975, 54, 120–122. [Google Scholar]
- Keßler, T.; Kunde, C.; Linke, S.; McBride, K.; Sundmacher, K.; Kienle, A. Systematic Selection of Green Solvents and Process Optimization for the Hydroformylation of Long-Chain Olefines. Process. Adv. Methods Process. Syst. Eng. 2019. forthcoming. [Google Scholar]
- COSMOtherm, C30, Release 1601; COSMOlogic GmbH & Co. KG: Leverkusen, Germany; Available online: http://www.cosmologic.de (accessed on 14 October 2019).
- Schweidtmann, A.M.; Mitsos, A. Deterministic Global Optimization with Artificial Neural Networks Embedded. J. Optim. Theory Appl. 2019, 180, 925–948. [Google Scholar] [CrossRef]
- General Algebraic Modeling System (GAMS), 26.1.0; GAMS Development Corporation: Fairfax, VA, USA. Available online: https://www.gams.com/ (accessed on 14 October 2019).
- Kılınç, M.R.; Sahinidis, N.V. Exploiting integrality in the global optimization of mixed-integer nonlinear programming problems with BARON. Optim. Methods Softw. 2018, 33, 540–562. [Google Scholar] [CrossRef]
- Drud, A.S. CONOPT-A Large-Scale GRG Code. ORSA J. Comput. 1994, 6, 207–216. [Google Scholar] [CrossRef]
- Drud, A.S. CONOPT: A GRG Code for Large Sparse Dynamic Nonlinear Optimization Problems. Math. Program. 1985, 31, 153–191. [Google Scholar] [CrossRef]
- CPLEX Optimizer; IBM Corporation: Armonk, NY, USA. Available online: https://www.cplex.com/ (accessed on 14 October 2019).
- Koch, T.; Achterberg, T.; Andersen, E.; Bastert, O.; Berthold, T.; Bixby, R.E.; Danna, E.; Gamrath, G.; Gleixner, A.M.; Heinz, S.; et al. MIPLIB 2010. Math. Program. Comput. 2011, 3, 103–163. [Google Scholar] [CrossRef]
- Bongartz, D.; Mitsos, A. Deterministic global flowsheet optimization: Between equation-oriented and sequential-modular methods. AIChE J. 2019, 65, 1022–1034. [Google Scholar] [CrossRef]
- Bongartz, D.; Mitsos, A. Deterministic global optimization of process flowsheets in a reduced space using McCormick relaxations. J. Glob. Optim. 2017, 69, 761–796. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).