1. Introduction
Gas separation techniques using membranes have many merits such as high efficiency, facile operation, and low energy cost. [
1,
2]. Traditionally, polymeric membranes are often used for this application while they suffer from the well-known problem of permeability–selectivity trade-off (e.g., the Robinson upper bound) [
3]. Recently, two-dimensional (2D) material membranes have been developed for gas separation because it exhibits the promising potential to overcome the permeability–selectivity trade-off problem. Therefore, in the past decade, they have gained enormous attention [
1,
2]. Typically, the 2D nanosheets assembled lamellar microporous inorganic membranes have interlayer galleries which can provide abundant molecular pathways [
4,
5]. For this attractive property, a variety of the 2D materials have been exploited to assemble lamellar membranes for gas separation. From the current published studies, the 2D materials include layered double hydroxides (LDH) [
6], graphene (GA) [
7,
8], MXene 2D materials [
2,
9], graphene oxide (GO) [
10,
11], tungsten disulfide (WS
2) [
12], molybdenum disulphide (MoS
2) [
13,
14], and metal-organic frameworks (MOFs) [
15,
16] have been receiving particular interest.
Generally, MXene 2D materials are a large family of 2D carbides and nitrides with the general formula of M
n+1X
nT
x, where M represents a transition metal, X is carbon and/or nitrogen, and T is referred to the surface termination [
17,
18]. Very recently, MXene-based 2D materials have been introduced to fabricate 2D lamellar membranes because of their tunable nanochannel width, excellent mechanical strength, and easy fabrication and integration [
2,
19,
20]. It has been reported that the assembled MXene 2D membranes exhibit a range of attractive characters in separation, e.g., precise ion sieving [
21], ultrafast water permeation [
22], and gas separation [
19,
20].
Even a promising potential for highly efficient gas separation has been proved experimentally, to fully clarify the gas transportation mechanism in 2D lamellar membranes, the insight into the theoretical and simulation clarification is scarce and the corresponding investigation is still needed to be conducted. Especially, there are only a few reports on theoretical simulation of gas separation through 2D lamellar nanochannels [
11,
23,
24] while the mechanism of transportation and separation of gas through 2D nanochannels is far away to be fully clarified. For example, Li et al. [
24] studied various gas transportations in MXene nanogalleries with molecular dynamic (MD) simulations and activated and Knudsen diffusion being observed for gas diffusion in through MD simulations. Nevertheless, Fan et al. [
20] found the gas transportation in MXene nanogalleries via the molecular sieving mechanism. Therefore, in order to optimize and promote the performance and the efficiency of the 2D MXene lamellar membranes, the gas transport mechanisms are still needed to be further clarified because they can efficiently provide the guidance for tuning the channel width of 2D lamellar membranes and gas molecule–channel wall interactions in gas transportation. That is due to the gas transportation mechanism in porous media is primarily related with pore diameter, pore geometry, and interconnectivity of the interlayer distance and defects in the 2D lamellar membranes structure [
25].
In this work, the related parameters were firstly determined theoretically and then the gas transport modeling to permeate through different nanochannels was developed to reveal the diffusion of different gas molecules (H2 and N2) in 2D MXene lamellar membranes. The simulation results are well consistent with the experimental results and their significance to the gas diffusion (e.g., permeance and selectivity) was discussed. The structural effects from MXene nanochannels formed during MXene nanosheets assembling on the transportation of different gas molecules (e.g., size and mass) were studied. Moreover, we provided the effects of temperature, pore diameter of structural defects, and the MXene thickness of the lamellar membrane on hydrogen and nitrogen permeances.
2. Experimental
The MXene lamellar membrane was prepared using the similar method illustrated previously [
20]. Briefly, Ti
3C
2T
x was synthesized by etching Ti
3AlC
2 powders using 50 wt% HF solution at a certain temperature followed with DMSO intercalation. The interlayer interaction became weak due to the removal of Al atom between layers, leading to a facile exfoliation to form MXene nanosheets under sonication. The suspended MXene nanosheets were deposited by filtration on the anodic aluminum oxide (AAO) support with a pore diameter of 200 nm (Whatman Co., Maidstone, UK) by a vacuum pump. The resultant MXene membrane was dried at 120 °C for 8 h in a vacuum oven to remove the water molecular between interlayers.
H
2 and N
2 gas permeances were derived from their gas mixture separation performance measurement through the MXene membrane supported on AAO [
20]. The gas mixture permeance was carried out in a home-made device as reported previously [
20]. The gas mixture containing 50 vol% H
2 and 50 vol% N
2 as the feed gas was supplied to the membrane feed side with a flow rate of 50 mL min
−1, while the argon sweep gas with a flow rate of 40 mL min
−1 at a standard pressure was supplied to the sweep side. The exit gas from the membrane sweep side was transferred to an online GC (6890N, Agilent Technologies, Inc, Waldbronn, Germany) with TCD to measure the permeated H
2 or N
2 concentration. The permeance and mixture selectivity or separation factor were defined by:
where
Fi is the permeance of the derived gas (
i) (mol m
−2s
−1Pa
−1),
Ni is the molar flux of the gas (
i) (mol m
−2 s
−1),
Pi1 and
Pi2 are the partial pressures of gas (
i) at the feed side and sweep side.
where
S is the mixture selectivity or separation factor y
i1,
yi2,
yj1 and
yj2, the volumetric fraction of the gas component
i or
j in the feed or permeated side gas mixtures, respectively. Experimental results are summarised in
Table 1.
The crystalline characteristics of MXene nanosheets and composite membranes were studied by XRD (Bruker D8 Advance with Cu-Kα radiation λ = 0.154 nm at 40 kV and 40 mA, in the 2 θ range 20–80° with a sacn step of 0.01°). The surface topology, cross-section, and microstructures of the MXene lamellar membrane were investigated by using a field emission scanning electron microscopy (SEM, FEI Sirion 200, Philips, The Netherlands).
3. Theoretical Models of Transport Mechanism
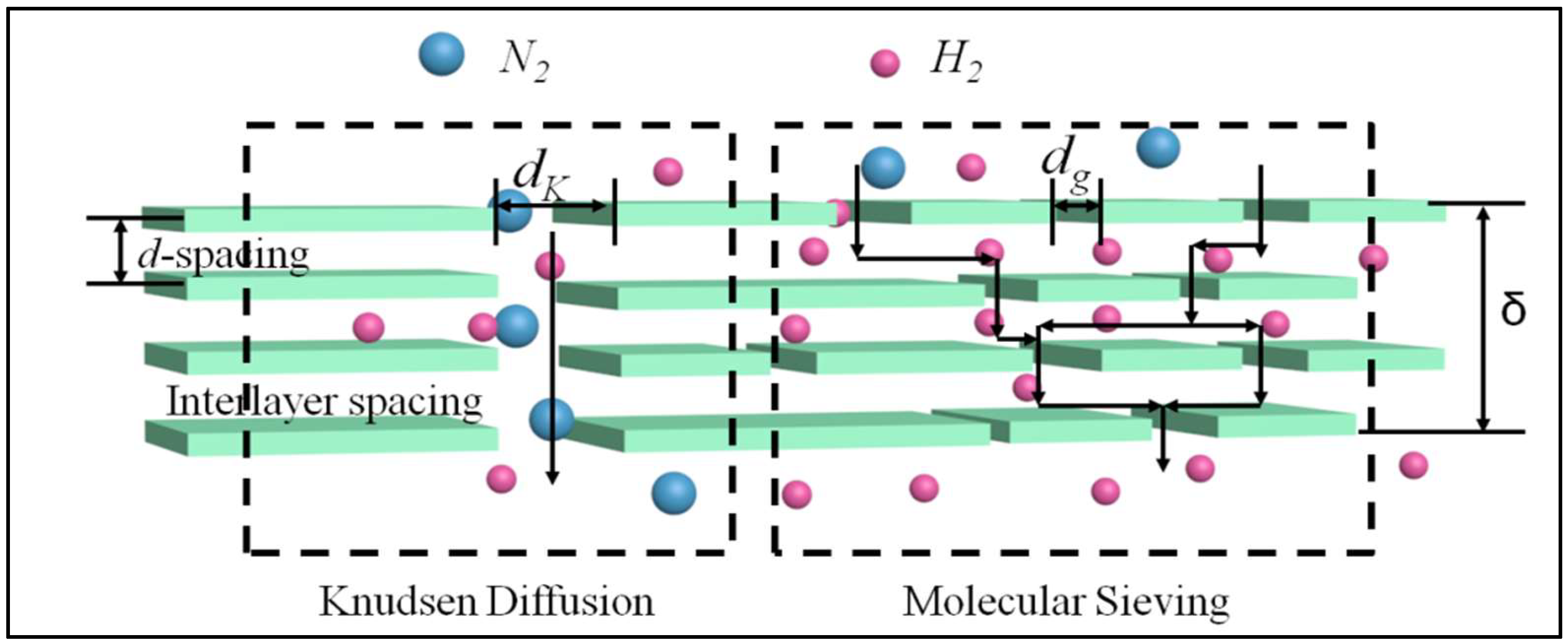
We propose the presence of two kinds of gas transport nanochannels as illustrated in
Figure 1. One is straight channels from structural defects and its width is assumed between 2 nm and the mean free path of transport gases (λ). Another nanochannel consists of randomly distributed nanoscale wrinkles and interlayer spacing between stacked MXene sheets and its width is between the kinetic diameter of gas molecular (
Φk) and 2 nm. Accordingly, two mathematical models of the gas transport mechanism for the permeation through the MXene lamellar membrane can be proposed based on the different nanochannels width using the following assumptions:
- (1)
One-dimensional transport model is used.
- (2)
There are two kinds of transport channels as illustrated in
Figure 1, which are the straight nanochannels (2 nm <
dp < λ) and tortuous nanochannels (
Φk <
dp < 2 nm). Their size remains unchanged with the temperature.
- (3)
The MXene/AAO lamellar membrane operates at a steady-state isothermal condition.
- (4)
The linear adsorption isotherm (or non-adsorption) for all gases on the surface of MXene lamellar membranes is neglected.
- (5)
The mass transfer resistance of gas within the porous AAO layer is neglected due to its much large pore size [
10,
26].
- (6)
Gas mixture (hydrogen and nitrogen) transport through the membrane is under ideal conditions on which the actual separation factor is equal to the ideal selectivity and pure gas permeance is equal to the mixture permeance.
The relevant schematic transport models for gas permeation through the MXene lamellar membranes are shown in
Figure 1. Here, H
2 (kinetic diameter of 2.89 Å) and N
2 (3.64 Å) diffuse through the MXene lamellar membrane based on our experimental results [
20], so the geometrical structure of nanochannels derived from the structural defects and interlayer spacing plays a significant role in the gas transportation. For gas permeation, two transport models were proposed corresponding to the nanochannels in order to explain the experimental results. The Knudsen diffusion is assumed to occur within the straight nanochannels with the lager pore diameter (2 nm <
dp < λ). The tortuous nanochannels are mainly composed of randomly distributed nanoscale wrinkles, inter-galleries, and interlayer spacing between stacked MXene sheets. Therefore, the gas transportation within tortuous nanochannels containing the interlayer spacing (
Φk <
dp < 2 nm) is mainly related to the molecular sieving.
Therefore, for MXene lamellar membranes, both Knudsen diffusion and molecular sieving contribute to the total mass transportation. The total permeance can be written by Equation (3) as follows:
Here, Ftotal, Fdefects, and Fint erlayer are the total gas permeance, the gas permeance through straight nanochannels of structural defects, and tortuous nanochannels containing interlayer spacing, respectively. FKn and Fg are the permeances contributed by the Knudsen diffusion and the molecular sieving, respectively.
3.1. Knudsen Diffusion (KD) Model
Typically, Knudsen diffusion dominates in the mesoporous nanochannels with the size range between 2 nm and the mean free path of transport gases (2 nm <
dp < λ), i.e., the average distance a molecule traversed by collisions, which is comparable or larger than transport channels, transport falls in Knudsen regime [
27]. The mass transport of gas may be described by Fick’s first law as Equation (4).
where
φ is the factor for structure geometrical effects by Equation (16).
R is the ideal gas constant,
T is the absolute temperature. Thus, the expression of Knudsen diffusion flux (
JK,i) for gas can be obtained in terms of pressure gradient. In this case,
DK is the Fick diffusion coefficient (Knudsen diffusivity), which may be expressed as the product of a geometric factor by diffusion pore diameter and the velocity of gas molecules by Equation (5):
where
dp is the diffusion pore diameter, the velocity of diffusing molecules is given by the kinetic theory of gases, and
M is the molecular weight of the diffusing gas. The geometric factor is 1/3 since only these molecules moving in the considered direction will be taken into account [
28]. The expression for Knudsen diffusion flux (
JK,i) obtained by combining Equations (4) and (5) is expressed as Equation (6).
The Knudsen diffusion permeance through a porous membrane can be determined after integration of Equation (6) over the membrane thickness (δ):
In order to obtain the diffusion pore diameter (
dp), Equation (7) was transformed to Equation (8) to reveal the gas permeance dependence on the temperature. Thus, the gas permeance in Knudsen regime is pressure-independent and decreases with temperature as indicated by Equation (8).
3.2. Molecular Sieving (MS) Model
The molecular sieving model was firstly used for zeolite, which can be illustrated by the kinetic theory of gases [
28]. In the small channels with the size range between kinetic diameter of gas molecular and 2 nm (
Φk <
dp < 2 nm), channel size changes into the molecular dimensions and molecules are no longer as free as these in Knudsen diffusion. For simplification purpose, the individual gas molecular adsorption difference is not considered. This is a reasonable assumption for these gases with less adsorption like He, H
2, and N
2 than CO
2. The molecular sieving flux can be expressed in terms of pressure gradient. As a result, the molecular sieving flux (
Js,i) can be written as:
where
Ds,i is the molecular sieving coefficient in the MXene laminates, which is given by Equation (10).
where
ls is the diffusion distance (the distance between two adjacent sites of the low energy regions),
Z is the number of adjacent sites [
28], and
Ea,g is the activation energy, which is required for molecules to surmount the attractive constrictions imposed by the nanochannels structure. However, the geometrical factor (1/
Z) is the probability of a molecule moving in the direction under consideration. The expression of molecular sieving flux (
Js,i) obtained by combining Equations (9) and (10) is shown as the following.
The gas permeance for molecular sieving through a microporous membrane is obtained after integration of Equation (12) over the membrane thickness δ:
Equation (12) reveals an exponential dependence of gas permeance on the temperature, which is different from that of the Knudsen diffusion model. Taking logs of the both sides of Equation (12) can obtain the activation energy
Ea,g and the diffusion distance
.The gas permeance tests at different temperatures were carried out, the activation energy Ea,g and the diffusion distance in the logarithmic plots can be regressed based on experimental data by Equation (13).
3.3. Diffusion Contribution to Total Transport
The fractional diffusion of Knudsen diffusion and molecular sieving, respectively can be expressed as the following Equations (14) and (15).
The relative individual diffusion contribution to total transport from Equations (3), (7), and (12) obtained using Equations (14) and (15) can be used to determine the rate-dominated diffusion process.
4. Results and Discussion
4.1. Morphology and Structure
The scanning electron microscopy (SEM) images of the cross-section of MXene (Ti
3C
2T
x), high magnification over the cross-section of MXene membrane, external surface of MXene membrane, and low magnification of the cross-section of MXene membrane are displayed as
Figure 2a–d, respectively.
As shown in
Figure 2a, the MXene membrane was assembled by the stacked 2D MXene nanosheets. Additionally, the nanosheets exhibit plicate feature on their surface. We can find there are structure defects and interlayer spacing in the bulky membrane, which can provide channels for the gas transportation. It is worth noting that the inner-sheet structural defect is assumed to be correlated with straight channels. The tortuous nanochannels consist of randomly distributed inter-galleries and nanoscale wrinkles between the stacked nanosheets. Here, the 2D MXene laminar membrane with 800-nm-thickness was assembled and supported on the AAO substrate (
Figure 2b), which shows similar morphology to that of other laminar materials such as GO membranes [
11]. MXene (Ti
3C
2Tx) nanosheets were deposited as an outer layer on top of a porous AAO support with a pore diameter of 200 nm using the vacuum impregnation method to form the supported MXene membrane (
Figure 2c,d).
From the XRD patterns in
Figure 3, the (002) plane at 6.6° can be used to determine the
d-spacing between the MXene nanosheets and the monolayer thickness, which were calculated to be ~13.4 Å and 10 Å, respectively. These data are inconsistent with the previous publications [
2,
20]. Moreover, the interlayer spacing of MXene membrane is estimated to be ~3.4 Å (
Figure 1), which is favorable to sieve small molecules such as hydrogen (kinetic diameter of 2.89 Å) and helium (2.60 Å).
The determination of geometrical effects in nanochannel structure is quite critical for the gas transport mechanisms model, and which can be described by [
16]:
where
φ is the geometrical effect of the porous structure (i.e., the ratio of the membrane porosity ε to the tortuosity factor
τ),
a is the thickness of monolayer thickness MXene lamellar which is ~10 Å,
d is the
d-spacing of MXene laminates which is about ~13.4 Å, and
τ is the tortuosity factor which can be approximated as the ratio of diffusion length to the MXene laminar thickness (Equation (17)).
In our work, the thickness of the MXene laminar membrane is 800 nm. The tortuosity factor τ can be estimated to be ~1 for straight nanochannels of inner-sheet structural defects. Moreover, the tortuosity factor τ (τ > 1) in tortuous nanochannels must be calculated using molecular sieving model.
4.2. The Experimental Nitrogen Permeance and the Parameters Regression of Knudsen Diffusion (KD) Model
There are two transport nanochannels in the MXene lamellar membrane, which are straight nanochannels from inner-sheet structural defects and tortuous nanochannels in wrinkles and inter-galleries contained interlayer spacing between stacked MXene sheets. Additionally, the gases transport mechanisms for the diffusion in porous membrane are primarily dependent on the transport channel width, geometry, and interconnectivity [
2,
25,
28]. Therefore, it is extremely critical to figure out the dimension of the nanochannels before we perform the modeling. To calculate the interlay spacing, the XRD measurement was conducted.
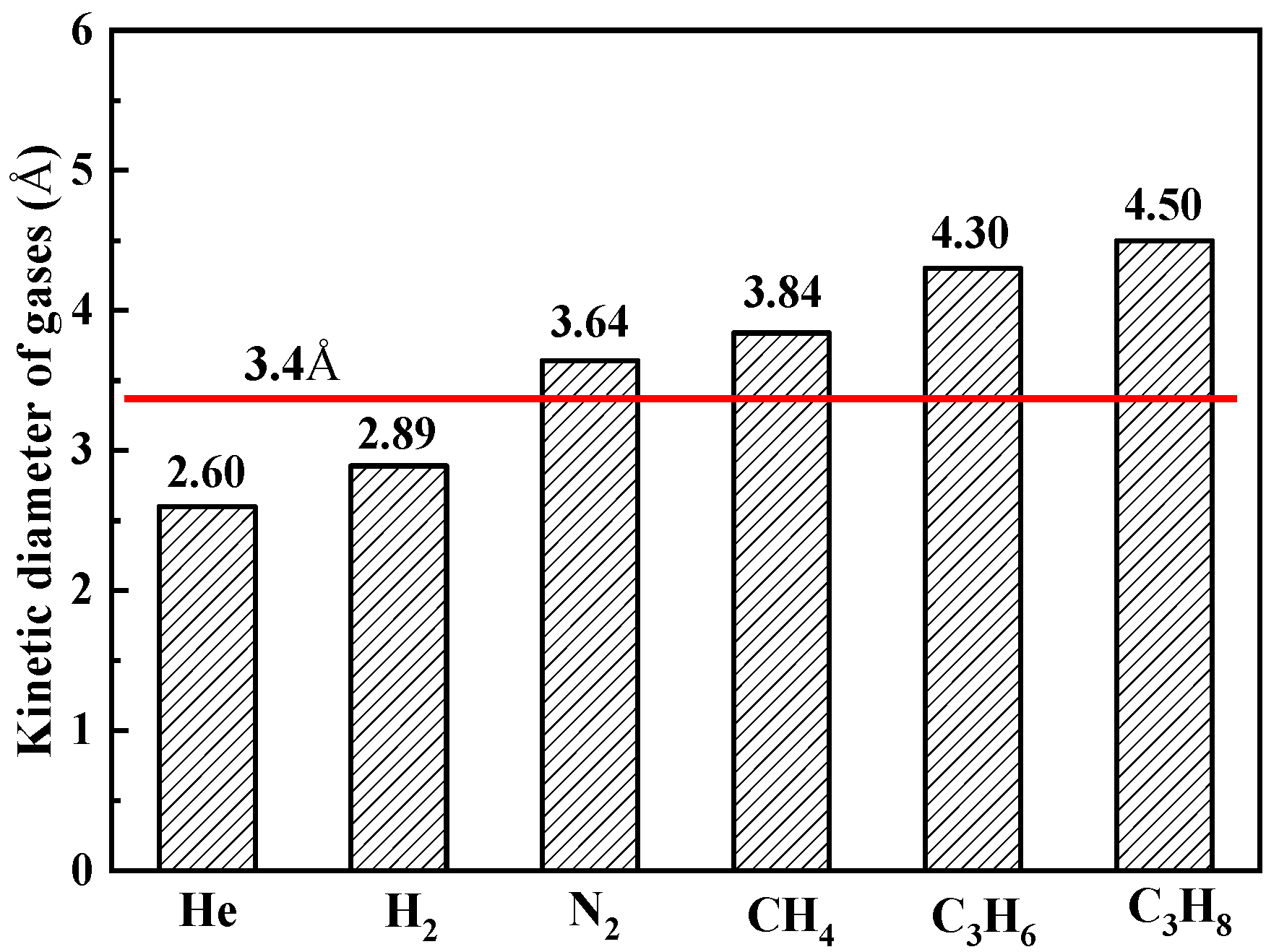
We can determine from the XRD results (
Figure 3) for MXene membranes that the interlayer spacing between the MXene sheets is 3.4 Å, which is smaller than the kinetic diameter of N
2 (3.64 Å), CH
4 (3.84 Å), C
3H
6 (4.30 Å), and C
3H
8 (4.50 Å) (
Figure 4). Since we assume that the width of straight nanochannels are larger than the kinetic diameters of these gases, therefore, for the transport permeance of N
2, CH
4, C
3H
6, and C
3H
8, Knudsen diffusion is the main process in the gas transportation in the straight channels. Since straight nanochannels flow dominates gas permeation, the Knudsen diffusion modeling was performed by the ordinary least squares method using MATLAB 7.0 (The Math Works Inc., Natick, MA, USA) [
29] to obtain the parameters in Equations (7) and (8) and the regression results were shown in
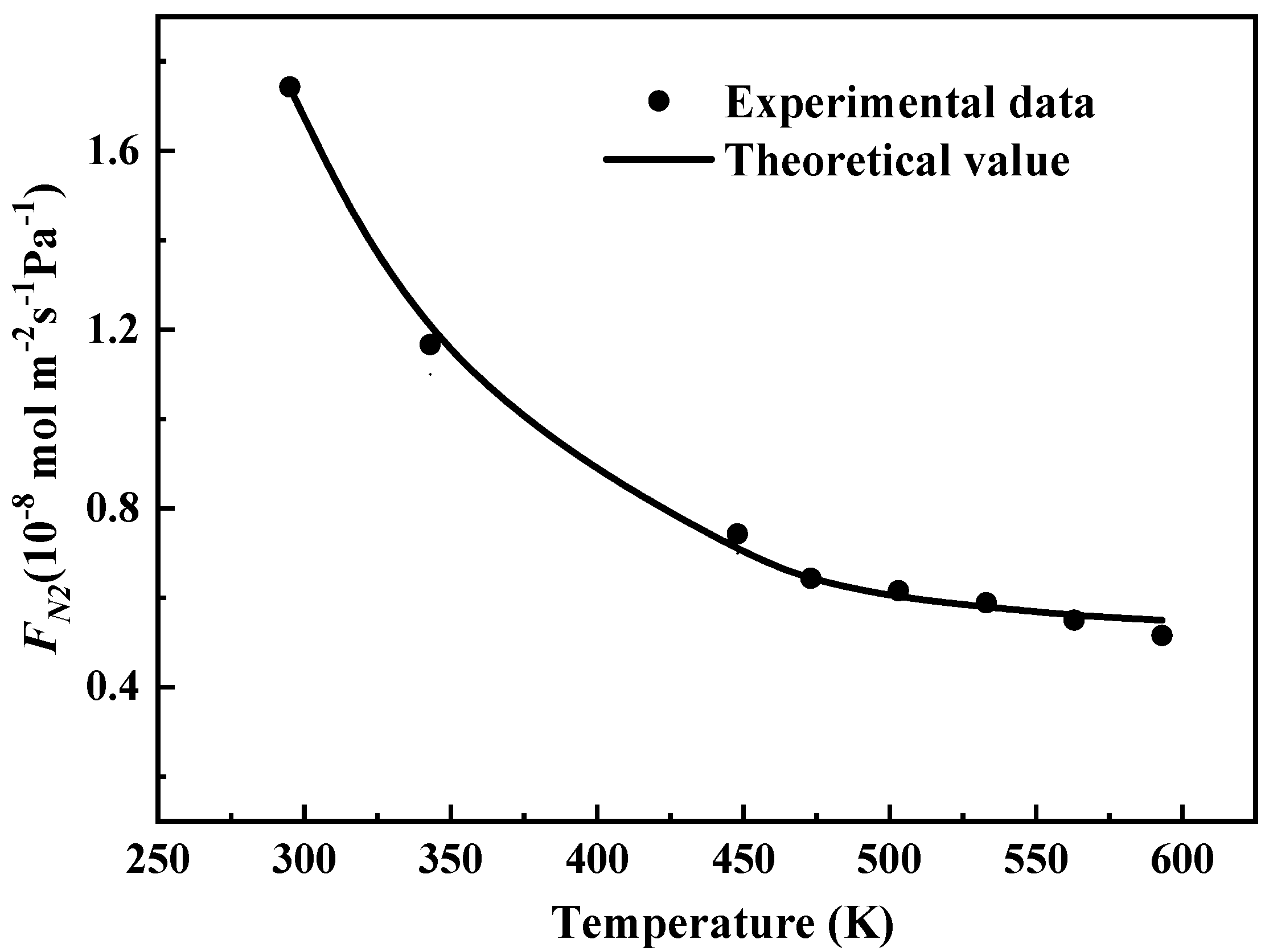
Figure 5. We can observe that the calculations using the Knudsen diffusion model with the obtained parameters can fit the experimental data well with the resultant correlation coefficient up to 0.9966.
The values for the model parameters φ and dp can be obtained from the regression. Since the tortuosity factor τ in Equation (17) can be estimated to ~1 in inner-sheet structural defects because of the straight diffusion channels. The geometrical effects (φ) of the porous structure derived from Equation (16) is 0.25, and the average diffusion pore diameter dp is 5.05 Å which is larger than the kinetic diameter of N2 (3.64 Å), CH4 (3.84 Å), C3H6 (4.30 Å), and C3H8 (4.50 Å). It can be concluded that the Knudsen diffusion through straight nanochannels for nitrogen is reasonable.
4.3. The Experimental Hydrogen Permeance and the Parameters Regression of Molecular Sieving (MS) Model
The interlayer spacing width between the MXene sheets is 3.4 Å which is larger than the kinetic diameter of He (2.60 Å) and H
2 (2.89 Å) (
Figure 4), thus it is favorable to separate them by molecular sieving diffusion. Therefore, hydrogen transport mechanism models in the MXene membrane are the combined Knudsen diffusion and molecular sieving, which correspond to the diffusion through straight nanochannels of structural defects, and tortuous nanochannels contained interlayer spacing between stacked MXene sheets, respectively. Hence, H
2 permeance is higher than N
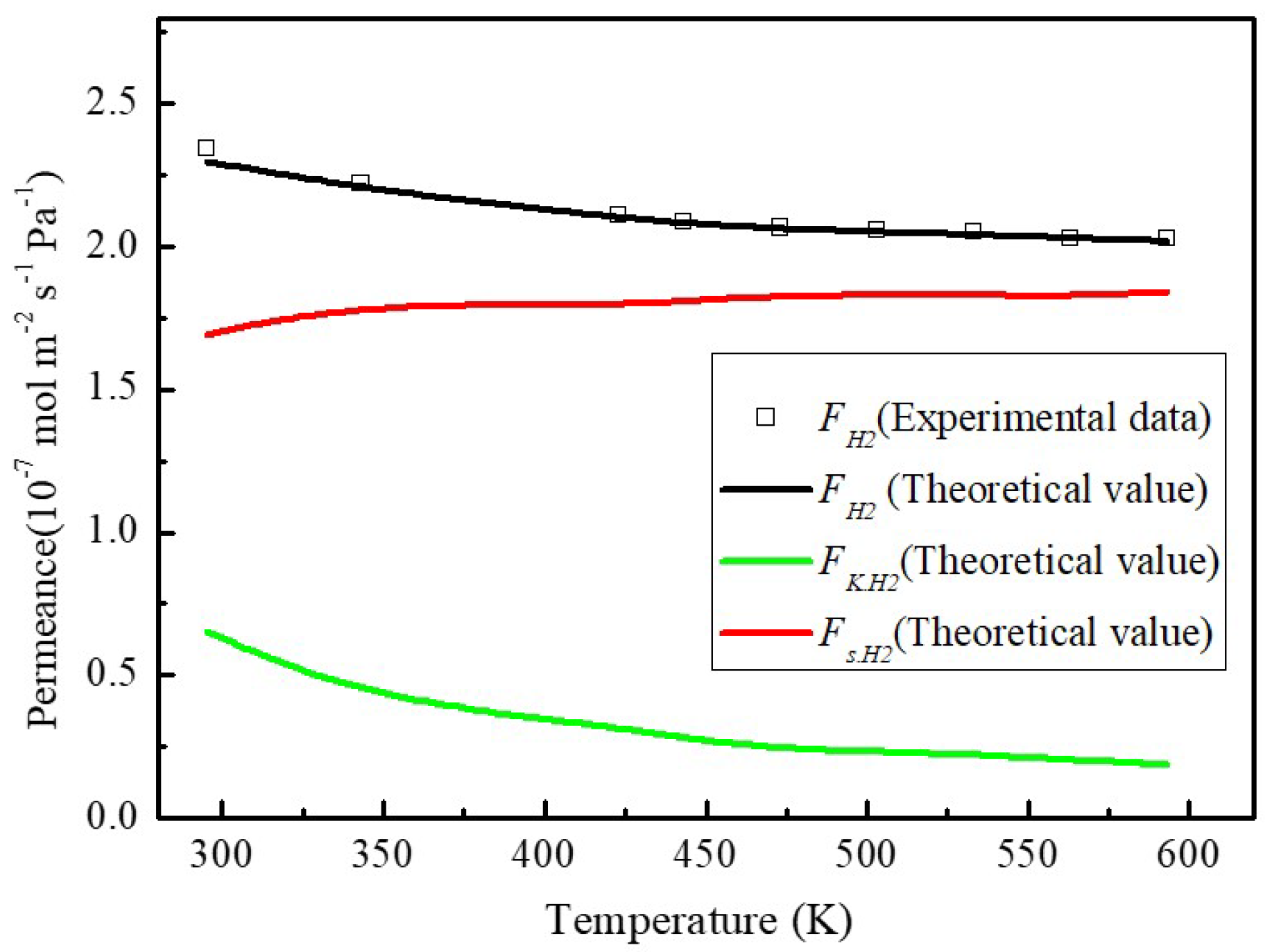
2 permeance in the temperature range of 295~593 K in experimental (
Table 1 and
Figure 6). For example, H
2 and N
2 permeances were 2.34 and 0.174 × 10
−7 mol m
−2 s
−1 Pa
−1, respectively, at 295 K. The calculated separation factor or selectivity of H
2/N
2 was ~13 based on the gas permeance, and it greatly exceeded the Knudsen selectivity of 3.74 for H
2/N
2 pairs. It indicates the promising potential application of the 2D MXene membrane to separate H
2 from its gas mixture. The modeling results show that molecular sieving plays a dominant role in the selectivity of gas separation.
Hydrogen permeances through the MXene lamellar membrane were obtained via the gas permeation test as a function of temperature between 22 °C (295.15 K) and 320 °C (593.15 K) using the mixture of hydrogen and nitrogen with a flow rate of 50 mL (STP) min−1 in the feed side of the membrane, and an argon sweep gas with a flow rate of 40 mL (STP) min−1 on the permeate side to remove the permeated hydrogen and nitrogen. The values for the model parameters φ, ls, and Ea,g can be obtained by Equations (12) and (13).
The calculated activation energies (
Ea,g) for H
2 permeance displayed in
Figure 6 is 20.54 kJ mol
−1. Although the geometrical effects of the porous structure (
φ) and diffusion distance (
ls) are difficult to be determined in Equation (12), by performing the ordinary least squares method using MATLAB 7.0 (The Math Works Inc., Natick, MA, USA) [
29] for regression, the value of multiple (
ls ×
φ) can be calculated to be 1.73 × 10
−12. In addition,
φ is the ratio of the membrane porosity
ε to the tortuosity factor
τ (see Equation (16)) and the tortuosity factor τ is difficult to be determined in Equation (17) as transport nanochannels from wrinkles and inter-galleries between stacked MXene sheets. The calculations using the model incorporating the obtained parameters fit the experimental data well with the resultant correlation coefficient of 0.9966.
Molecular sieving mechanism is also generally characterized by the activated diffusion [
24,
30]. Thus, the hydrogen permeance contributed from molecular sieving increased while that from Knudsen diffusion decreased with the temperature increment, so leading to the total permeance change with temperature variation.
4.4. Temperature Dependent Permeance and Relative Contribution to Total Gas Transport from Knudsen Diffusion and Molecular Sieving
To simulate the hydrogen or nitrogen gas permeance through the MXene lamellar membrane under the same conditions, we calculated the permeance using the models (Equations (7) and (12)) with the related regressed parameters and analyzed fractional diffusion to determine the rate dominates diffusion descripted by Equations (14) and (15) at different temperatures.
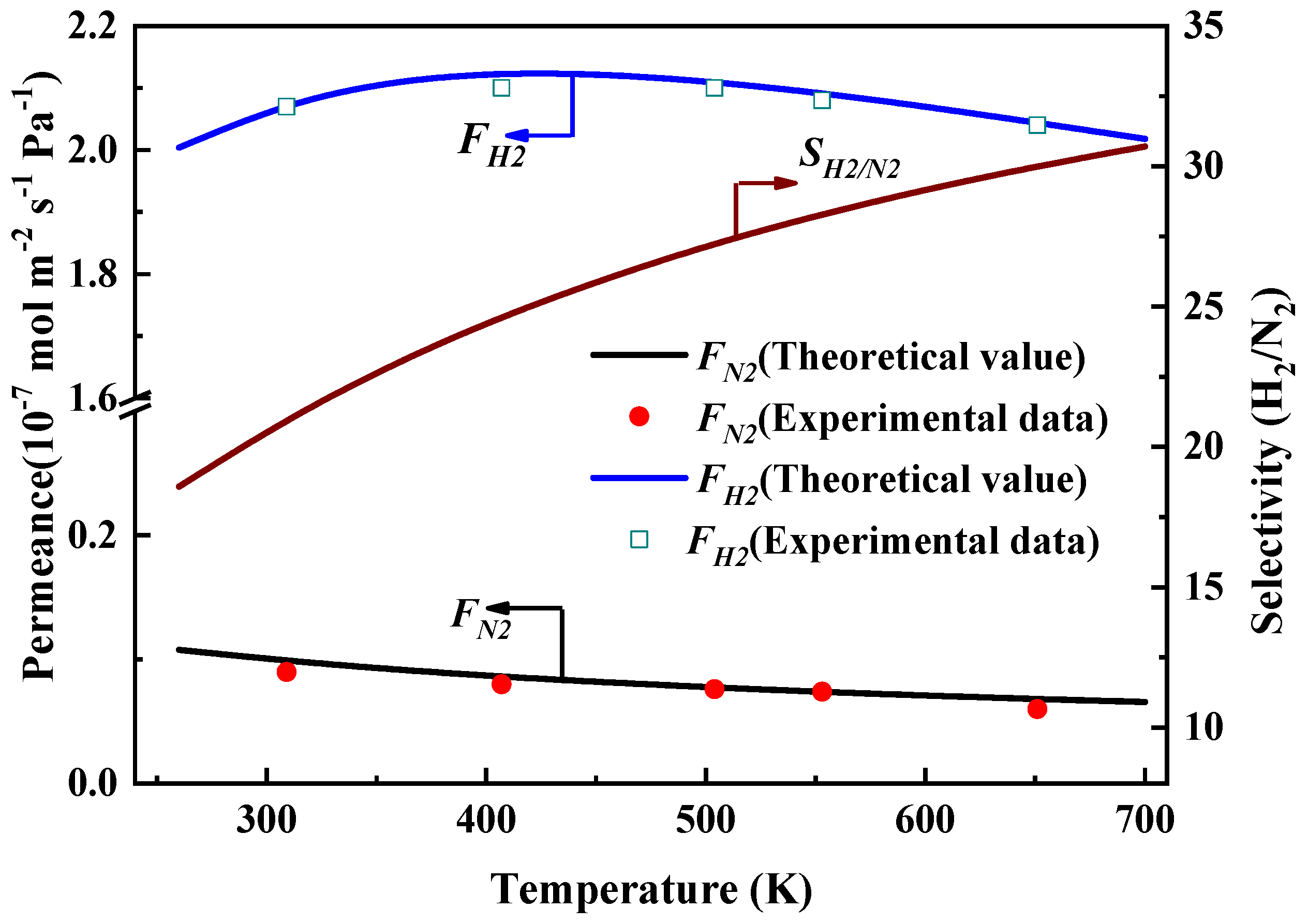
Figure 7 displays the gas permeance of hydrogen and nitrogen, and selectivity (H
2/N
2) between 260 and 700 K. We can see that the hydrogen permeances are higher than nitrogen. For example, the hydrogen and nitrogen permeance through the MXene lamellar membrane is 2.11 and 0.11 × 10
−7 mol m
−2s
−1Pa
−1 at 363 K, respectively. Moreover, the corresponding selectivity of H
2/N
2 is ~19 based on the gas permeance calculation. These results can be explained by the gas diffusion mechanism. The nitrogen transport is dominated by Knudsen diffusion through straight nanochannel of structural defects with the width of ~5.05 Å, while hydrogen transports based on Knudsen diffusion and molecular sieving through straight nanochannels of structural defects and tortuous nanochannels from interlayer spacing.
Meanwhile, we can also see that in
Figure 7 the nitrogen permeance decay upon the temperature increased in the range between 260 and 700 K. This trend can be ascribed to its Knudsen diffusion mechanism via which the permeance decreased with temperature as illustrated by Equation (7). Compared with nitrogen, the hydrogen permeance displays a different trend and reaches its maximum value of 2.12 × 10
−7 mol m
−2s
−1Pa
−1 at 408 K. However, the selectivity of H
2/N
2 is always enhanced. Such results can be interpreted by the joint effects of molecular sieving and Knudsen diffusion. From molecular sieving (Equation (12)), it reveals an exponential dependence of gas permeance on the temperature, which is obviously different from that of Knudsen diffusion. However, these trends are ascribed to the coverage of functional groups such as −OH and −O which will affect the adsorbed amount of hydrogen [
31,
32].
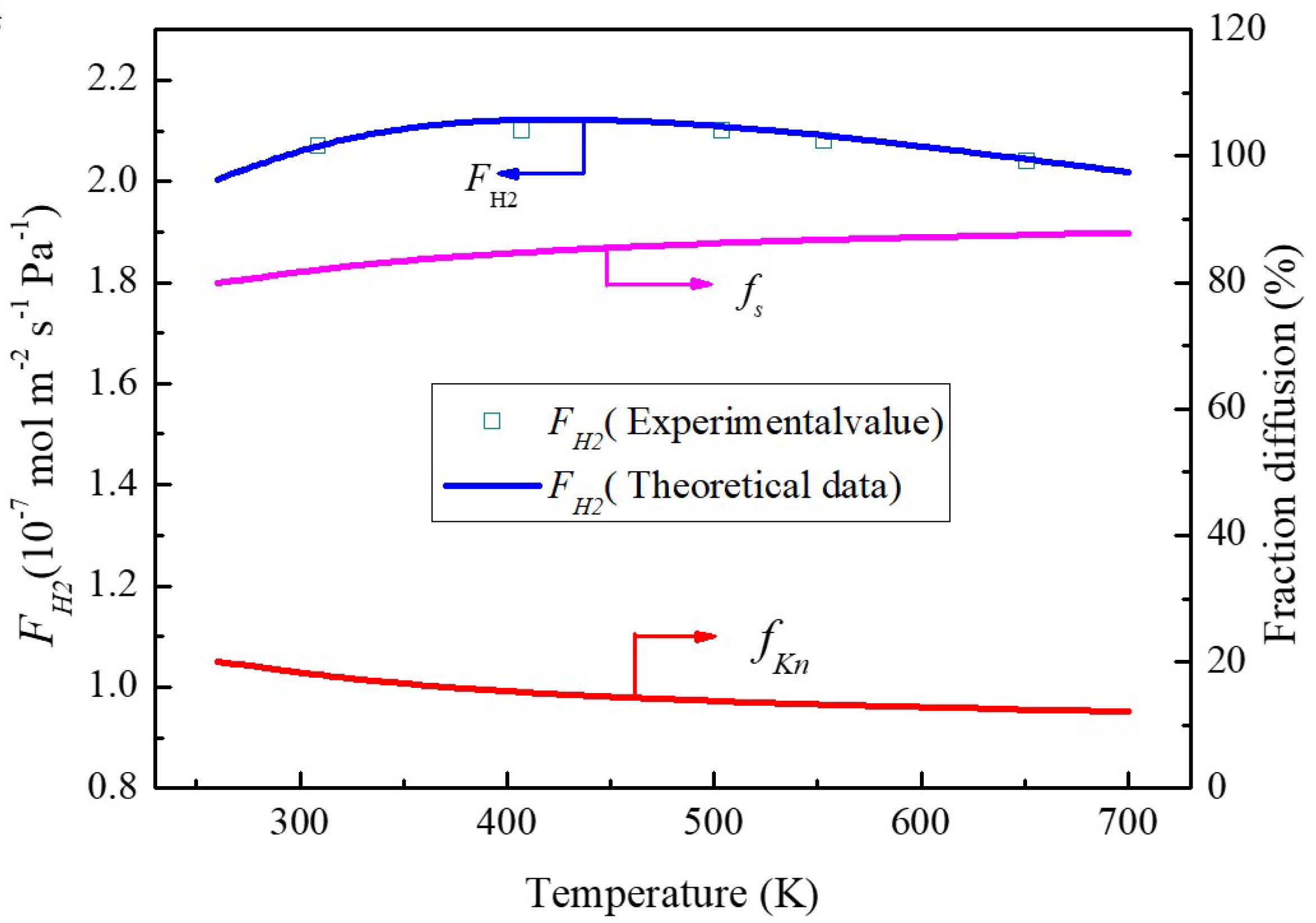
The effect of temperature on the fractional diffusion of Knudsen and molecular sieving for hydrogen permeance through the MXene membrane is depicted in
Figure 8. It is clear that the molecular sieving permeances are always higher than these of Knudsen diffusion between 260 and 700 K. Meanwhile, the fraction of molecular sieving increases steadily from ~80% to ~88%, and the Knudsen diffusion fraction slightly decreases from ~20% to ~12%. On average, the molecular sieving diffusion is about four times higher than the Knudsen diffusion, which indicates tortuous nanochannels containing interlayer spacing that dominates the whole transport channels.
Figure 8 also reveals that the increase of temperature will result in the decrease of Knudsen diffusion permeance which is consistent with Equation (7). However, the molecular sieving permeance increases steadily upon the increase of temperature which reveals that temperature is more readily affected in the exponent than those in pre-exponential coefficients in Equation (12).
4.5. The Effect of the Diffusion Pore Diameter of Straight Nanochannels on the Gas Permeance and Relative Contribution from Knudsen Diffusion and Molecular Sieving to Total Gas Transport
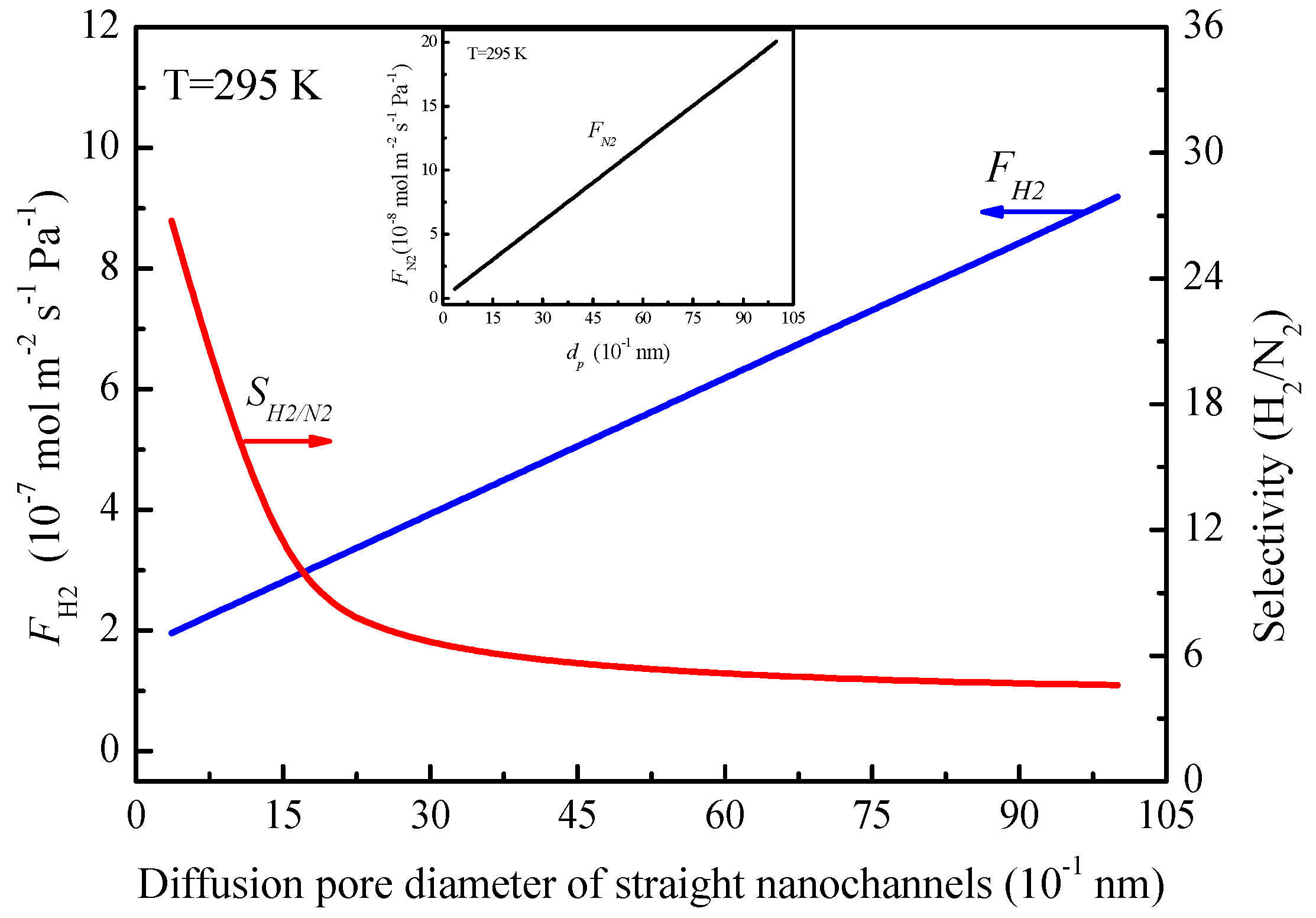
The change of the gas permeance and the transport fractions of Knudsen diffusion and molecular sieving with the pore diameter of the straight nanochannels can be calculated from Equations (7) and (12). According to the relationship between the gas permeance and the average pore diameter of straight nanochannels at 295 K as shown in
Figure 9, the hydrogen and nitrogen permeances increase with the average diffusion pore diameter of straight nanochannels in the MXene lamellar membrane. We can see the hydrogen permeance increased from 1.955 to 9.0 × 10
−7 mol m
−2s
−1Pa
−1 and nitrogen permeance 0.73 to 18.6 × 10
−8 mol m
−2s
−1Pa
−1 with the pore diameter of straight nanochannel alternation between 0.364 and 1.0 nm, respectively. The discrepancy between them becomes more pronounced with the increasing average pore diameter of straight nanochannels. This reflects that the larger nanochannel of structural defects will enhance Knudsen diffusion more significantly for permeance through the MXene lamellar membrane. Therefore, the selectivity of H
2/N
2 decreases from 26 to 4.87 (close to 3.74 of the Knudsen selectivity). This indicates that it is important to reduce the average pore diameter of straight nanochannels resulting from structural defects to ensure the good gas selectivity.
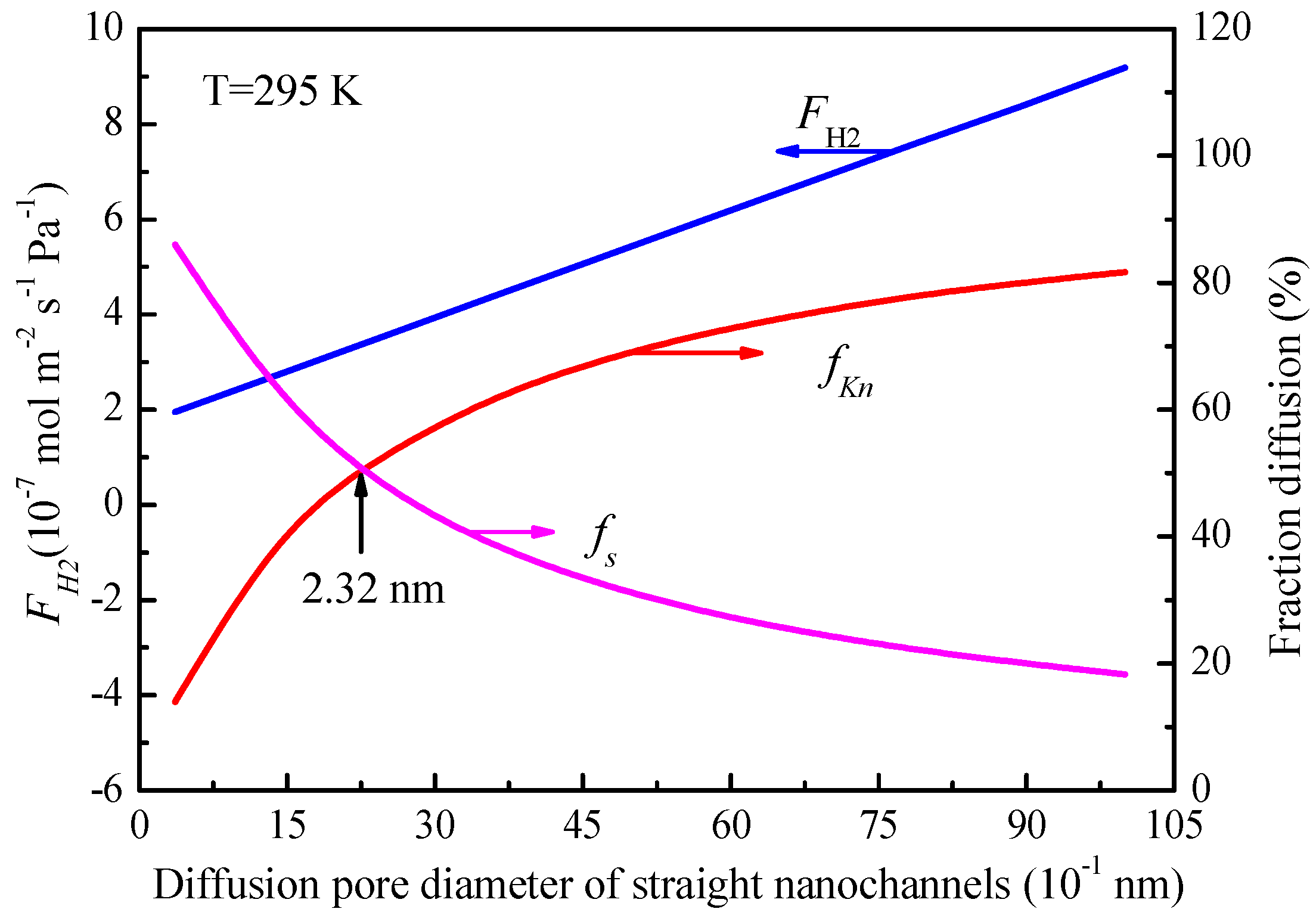
Figure 10 shows the fractions of Knudsen diffusion and molecular sieving contribution as a function of the average pore diameter of straight nanochannels at 295 K. As can be seen, the increase of the average pore diameter of straight nanochannels from 0.364 to 1.0 nm enlarges the fractions of Knudsen diffusion permeance from 14% to 82%, while the fractions of molecular sieving decreases from 86% to 18%. Moreover, the characteristic pore diameter (
dc) of 2.32 nm (23.2 Å) was also obtained from
Figure 10, at which the Knudsen diffusion and molecular sieving equally share the transport. in addition, increasing the average diffusion pore diameter of defects more than such characteristic value (
dc) will lead to the higher proportion of Knudsen diffusion than molecular sieving in the total permeance (
Figure 10).
4.6. The Effect of MXene Layer Thickness on the Gas Permeance and Fractional Diffusion of Knudsen Diffusion and Molecular Sieving
The dependence of the gas permeance and the fractions of Knudsen diffusion and molecular sieving on the effect of the thickness was determined by Equations (7) and (12), and
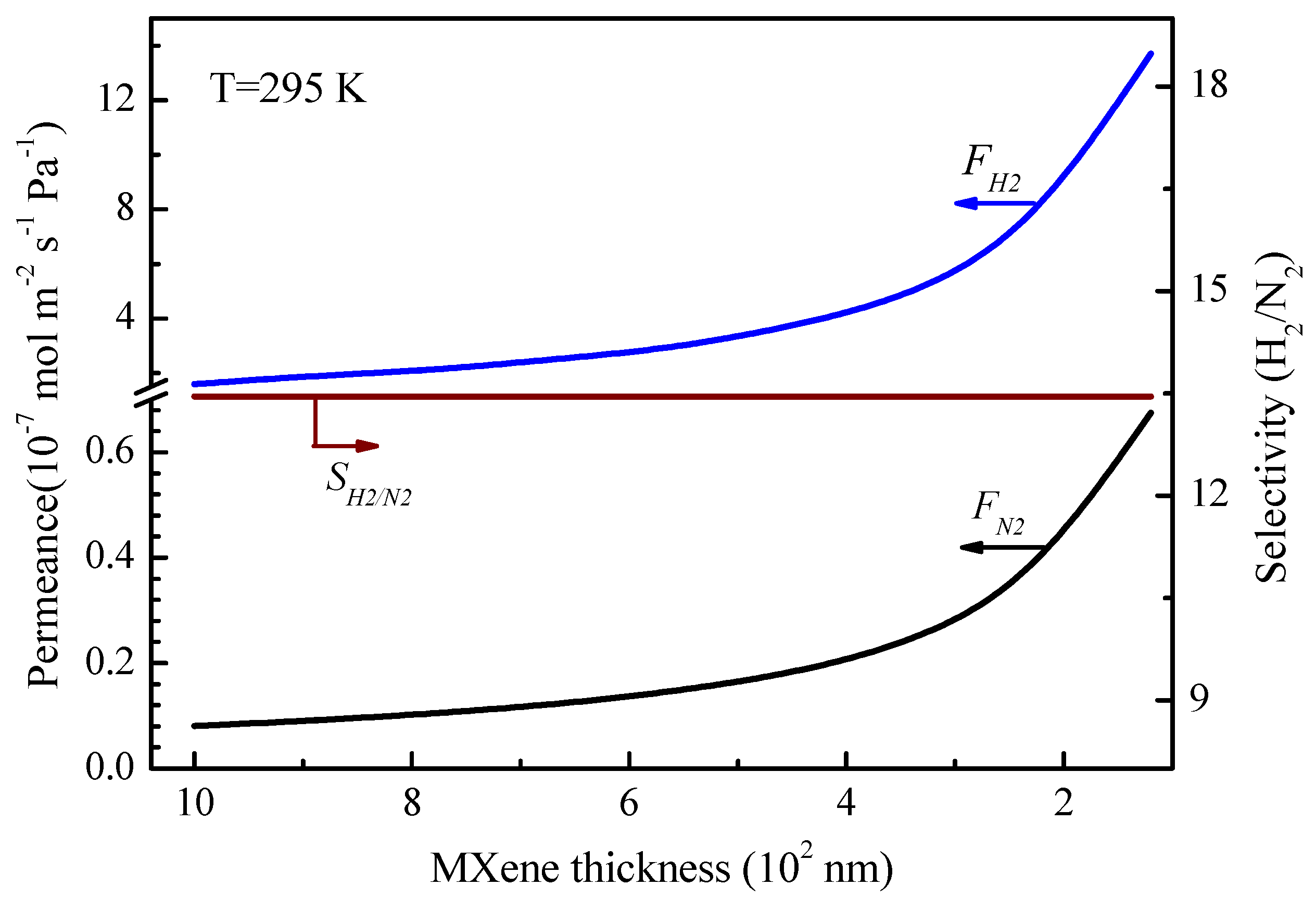
Figure 11 reveals the effect of the MXene membrane thickness on gas permeance at 295 K. From
Figure 11 we can see that the decrease of the thickness of the MXene layer leads to the increase for both hydrogen and nitrogen permeances. For example, the hydrogen and nitrogen permeances increase from 1.60 to 13.7 and 0.081 to 0.675 × 10
−7 mol m
−2s
−1Pa
−1, respectively, when the MXene thickness is reduced from 1000 to 20 nm. On the other hand, the H
2/N
2 selectivity maintains at 13.5. It indicates that the thinner MXene layer can lead to higher gas permeance for hydrogen or nitrogen (Equations (7) and (12)) but maintain the gas selectivity unaltered.
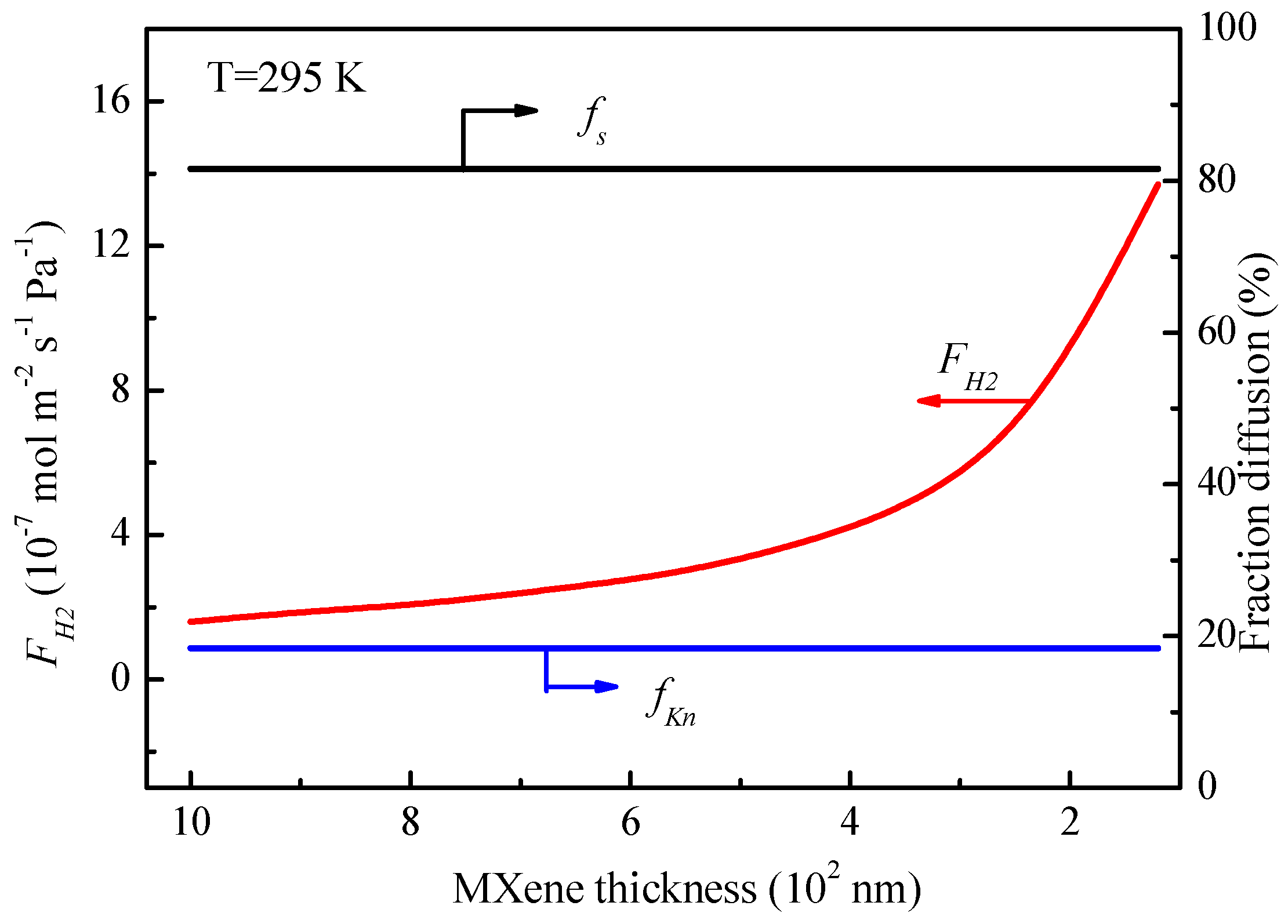
Figure 12 presents the transport fractions of Knudsen diffusion and molecular sieving to the total permeance as a function of the MXene membrane thickness (operated at 295 K). As can be seen, the decrease of the thickness of the MXene layer results in the substantial increase in the hydrogen permeance. However, the fractions of Knudsen diffusion and molecular sieving keep constant at around 18% and 82%, respectively. This can be explained from Equations (14) and (15), where the MXene membrane thickness does not affect the fractional diffusion to total transport from Knudsen diffusion and molecular sieving.
5. Conclusions
In conclusion, in order to determine the diffusion mechanism of gases in the MXene lamellar membrane, we evaluated the hydrogen and nitrogen permeation properties as a function of temperature using the prepared membrane. We proposed Knudsen diffusion and molecular sieving through the respective straight nanochannels that stemmed from structural defects and tortuous nanochannels formed by interlayer spacing. Furthermore, we performed linear regression on the experimental data to obtain the model parameters values for the MXene lamellar membrane, which were further applied to explain the Knudsen diffusion and molecular sieving mechanisms for hydrogen and nitrogen transport. Based on the modeling results, we simulated the effects of temperature, the pore size of the structural defects, and the thickness of the lamellar MXene membranes on hydrogen and nitrogen permeances. The relative contribution of Knudsen diffusion and molecular sieving to the total hydrogen permeance was also investigated. The model provides insights into the dominant diffusion at different operational condition and geometry variables. The results of theoretical and experimental study show that molecular sieving through tortuous nanochannels plays a dominant role in controlling the gas selectivity.