Building Block-Based Synthesis and Intensification of Work-Heat Exchanger Networks (WHENS)
Abstract
1. Introduction
2. A Building Block Representation of WHENS
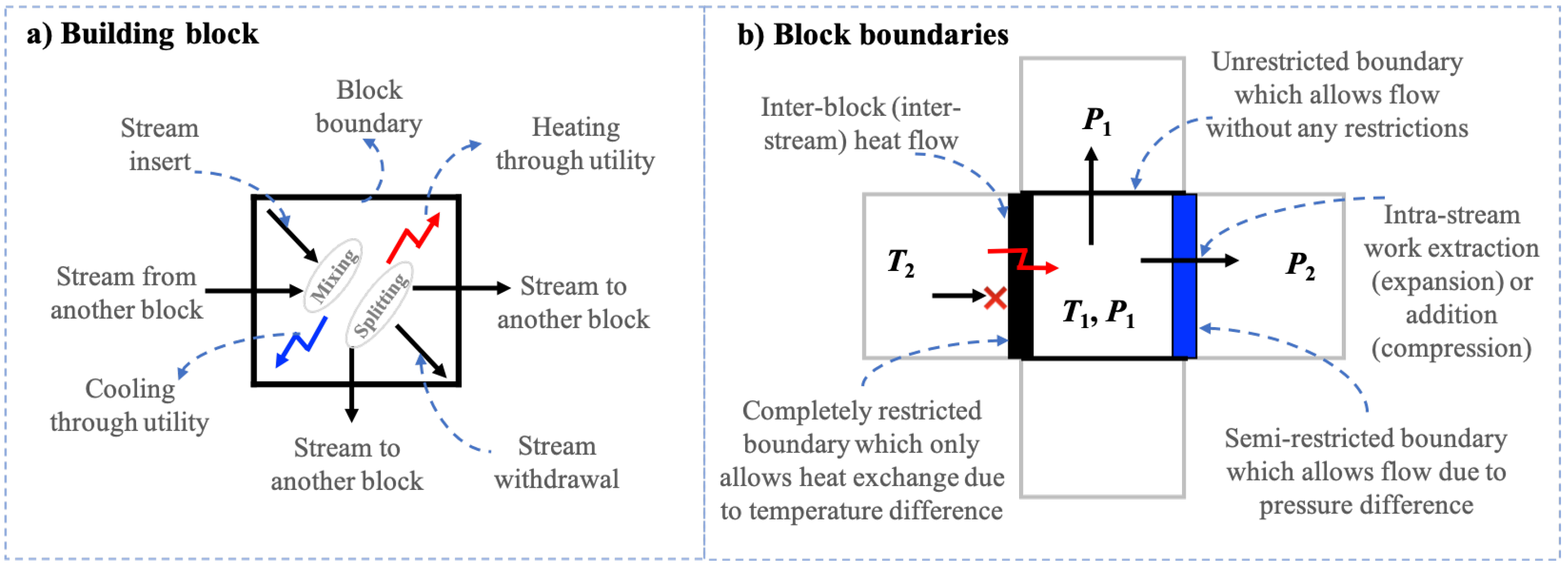
2.1. Elements of Building Block Representation
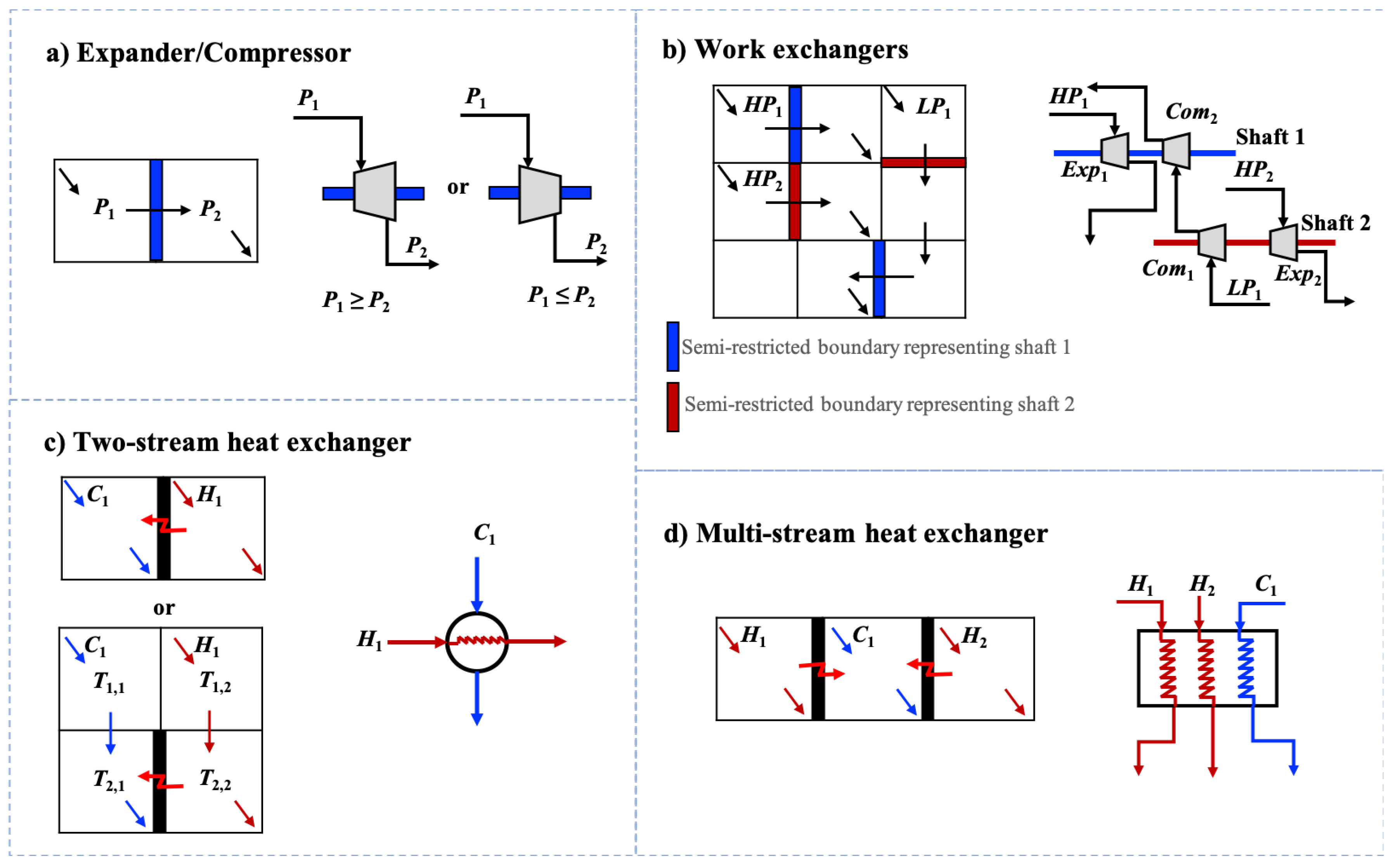
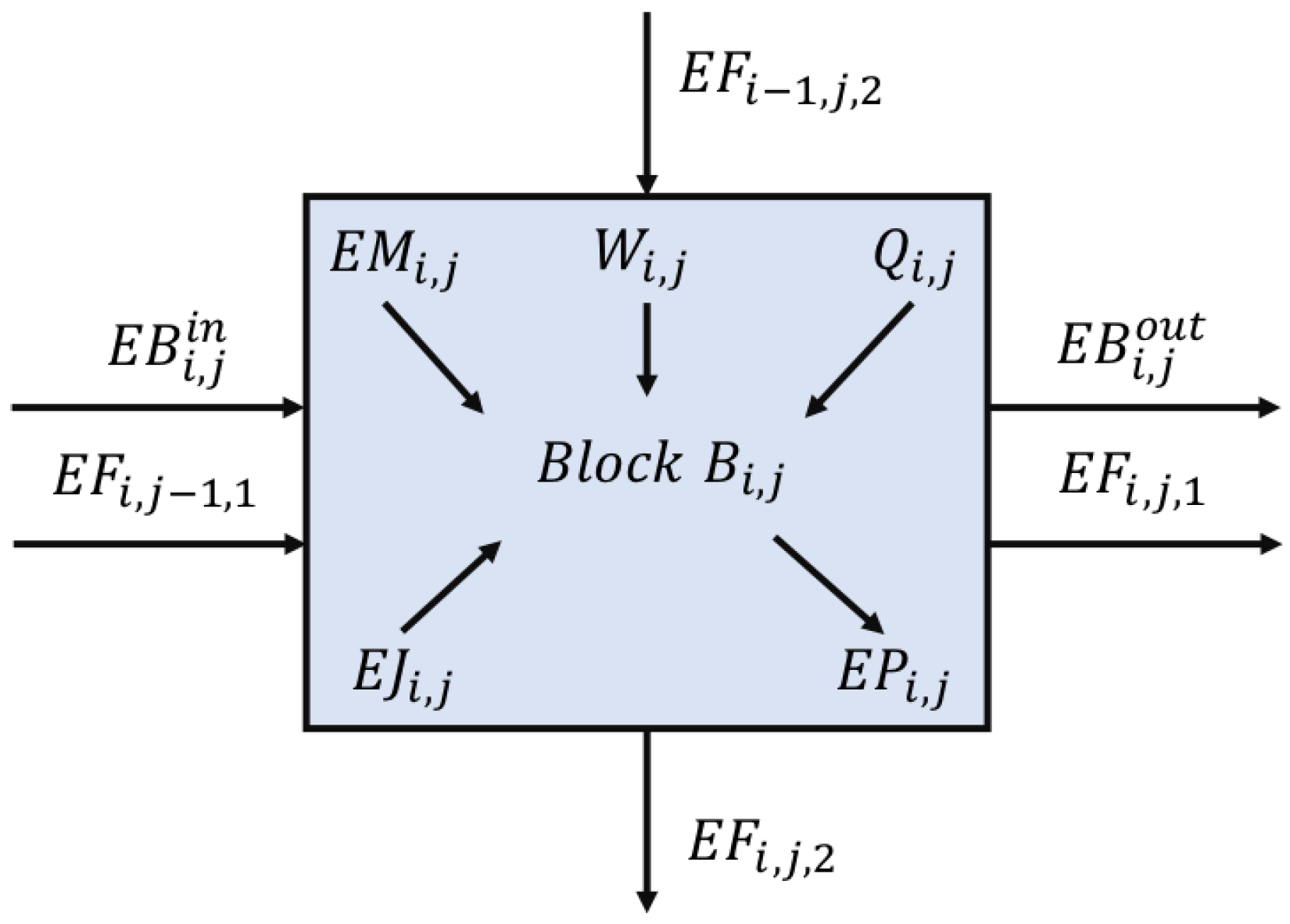
2.2. Equipment Representation
2.3. Flowsheet Representation
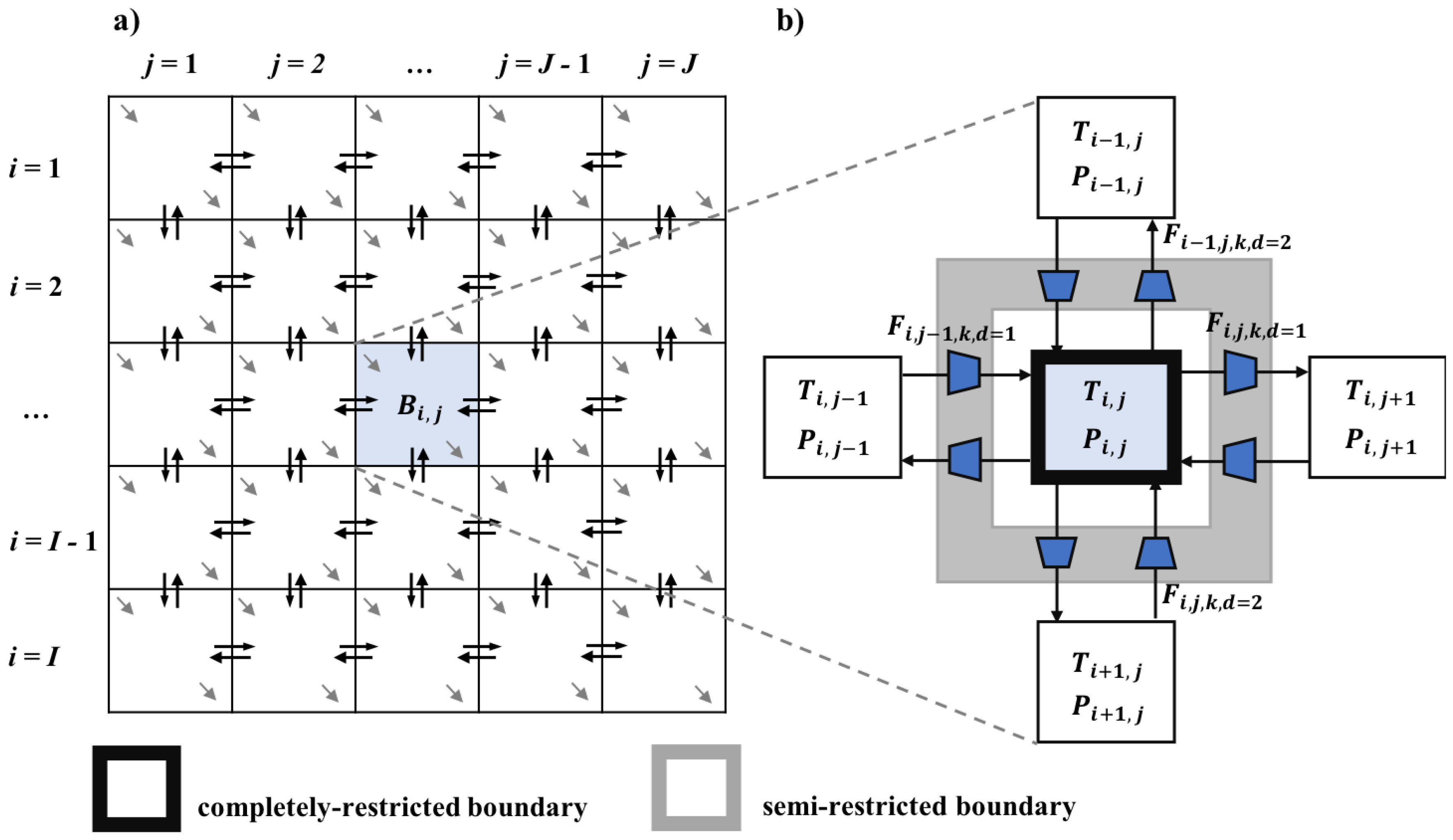
2.4. Block Superstructure for WHENS
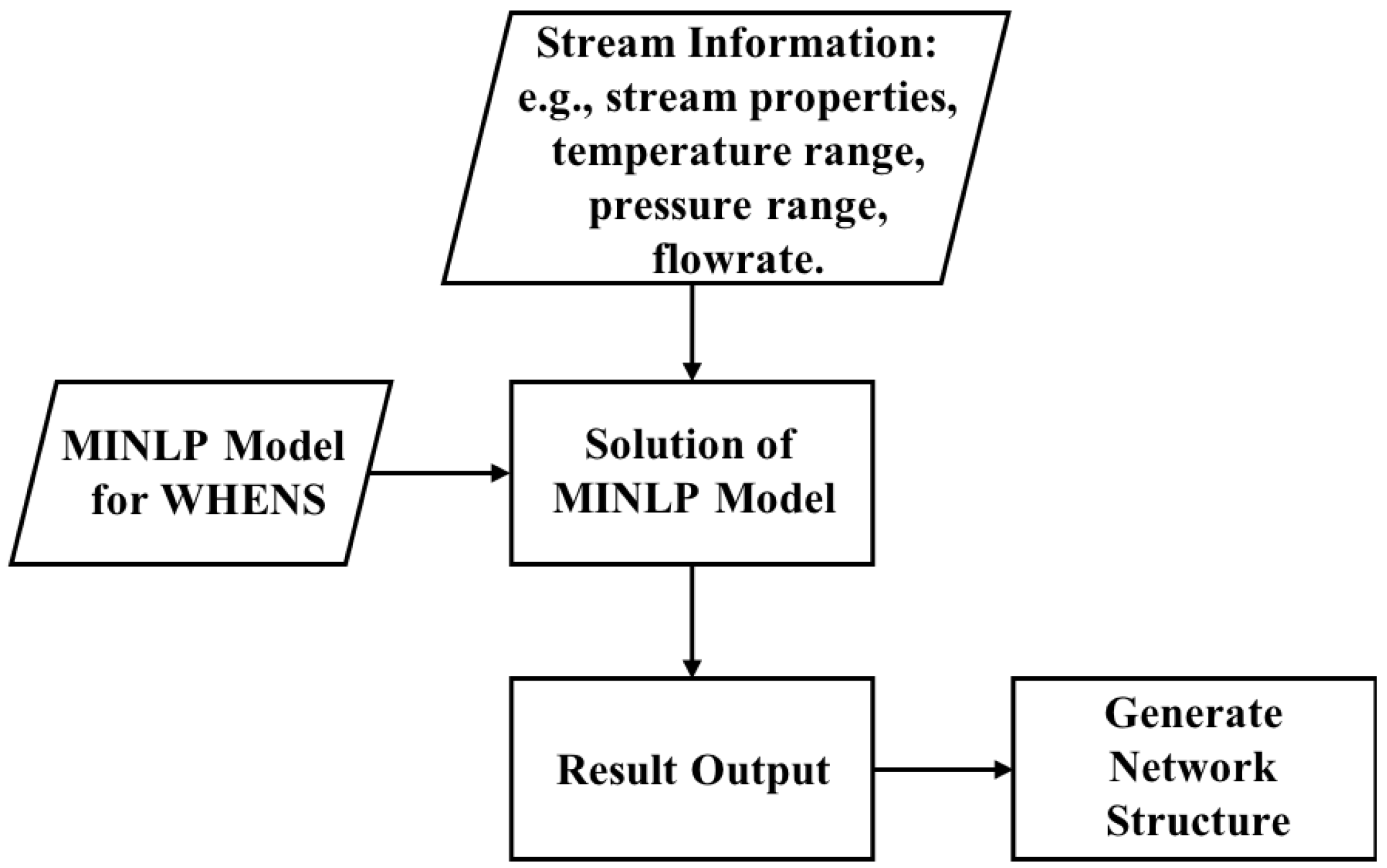
3. MINLP Model for WHENS
3.1. Block Material Balance
3.2. Flow Directions
3.3. Block Energy Balance
3.4. Product Stream Assignments and Logical Constraints
3.5. Boundary Assignment
3.6. Phase Relation and Stream Enthalpies
3.7. Heat Transfer Boundary Modeling
3.8. Work Calculation
3.9. Objective Function
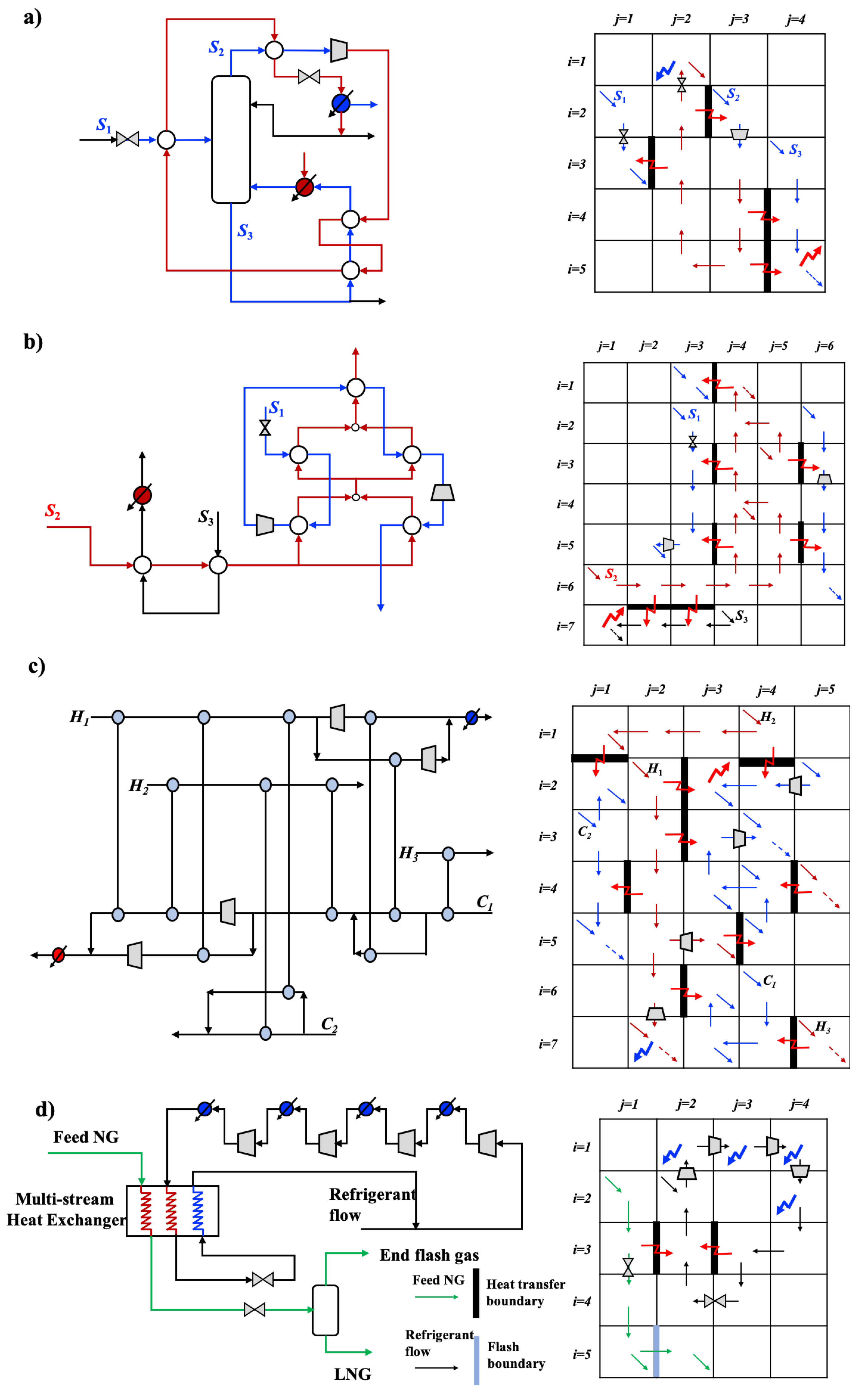
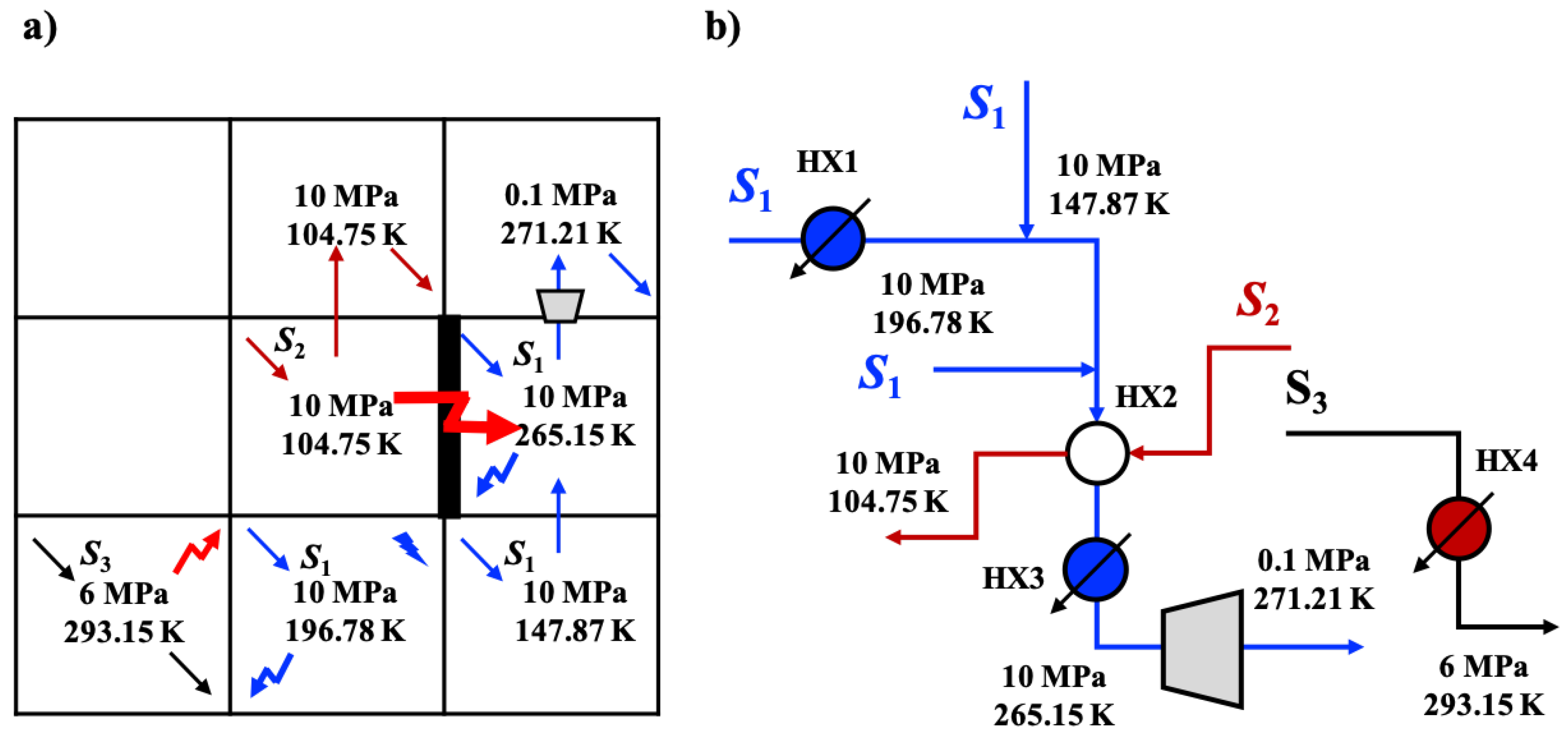
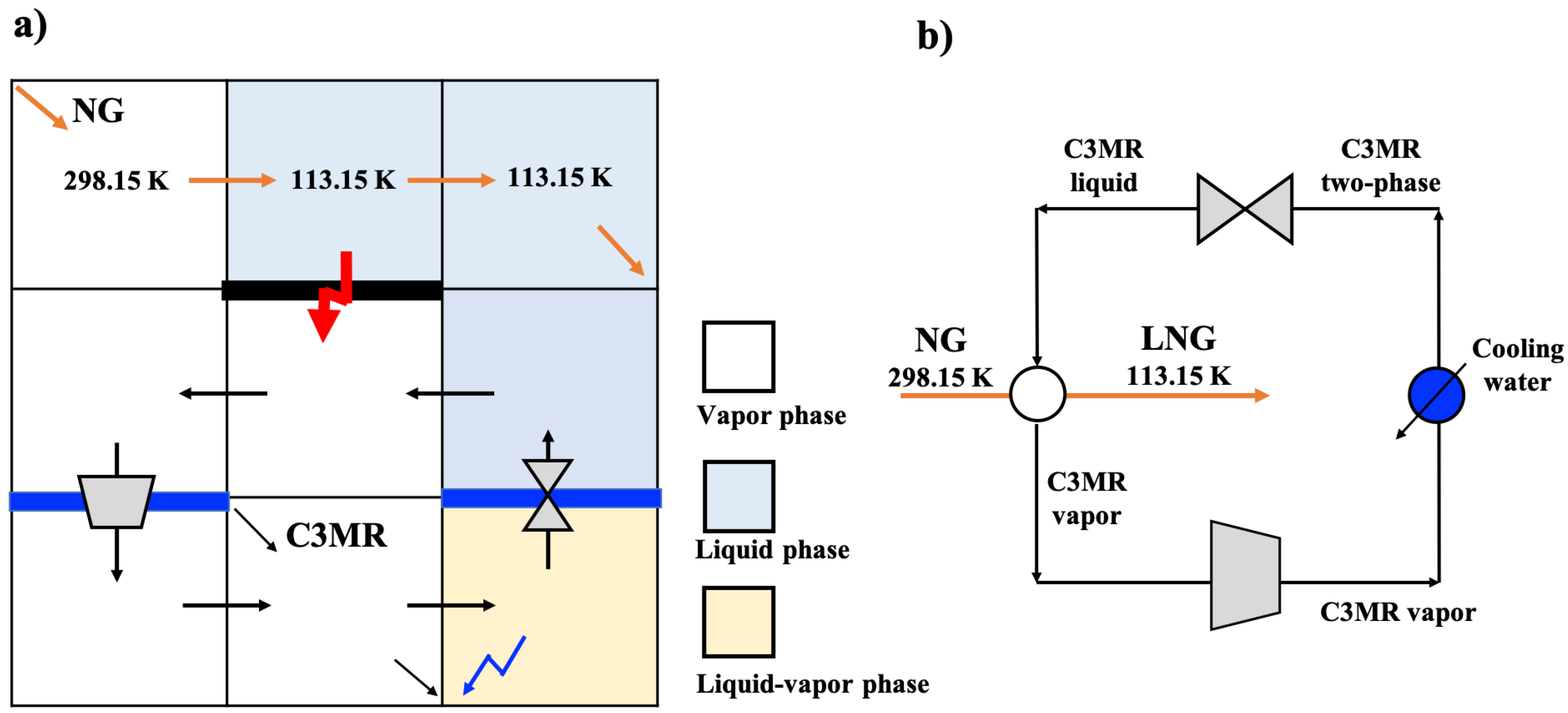
4. WHENS Case Study on Liquefied Natural Gas (LNG)-Based Cryogenic Energy Chain
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yu, H.; Fu, C.; Vikse, M.; Gundersen, T. Work and heat integration—A new field in process synthesis and PSE. AIChE J. 2018. [Google Scholar] [CrossRef]
- Fu, C.; Vikse, M.; Gundersen, T. Work and heat integration: An emerging research area. Energy 2018, 158, 796–806. [Google Scholar] [CrossRef]
- Huang, K.; Karimi, I. Work-heat exchanger network synthesis (WHENS). Energy 2016, 113, 1006–1017. [Google Scholar] [CrossRef]
- Subramanian, A.; Gundersen, T.; Adams, T.A., II. Modeling and simulation of energy systems: A Review. Processes 2018, 6, 238. [Google Scholar] [CrossRef]
- Furman, K.C.; Sahinidis, N.V. A critical review and annotated bibliography for heat exchanger network synthesis in the 20th century. Ind. Eng. Chem. Res. 2002, 41, 2335–2370. [Google Scholar] [CrossRef]
- Huang, Y.; Fan, L. Analysis of a work exchanger network. Ind. Eng. Chem. Res. 1996, 35, 3528–3538. [Google Scholar] [CrossRef]
- Razib, M.; Hasan, M.M.F.; Karimi, I.A. Preliminary synthesis of work exchange networks. Comput. Chem. Eng. 2012, 37, 262–277. [Google Scholar] [CrossRef]
- Liu, G.; Zhou, H.; Shen, R.; Feng, X. A graphical method for integrating work exchange network. Appl. Energy 2014, 114, 588–599. [Google Scholar] [CrossRef]
- Zhuang, Y.; Liu, L.; Zhang, L.; Du, J. Upgraded graphical method for the synthesis of direct work exchanger networks. Ind. Eng. Chem. Res. 2017, 56, 14304–14315. [Google Scholar] [CrossRef]
- Zhuang, Y.; Liu, L.; Du, J. Direct Work Exchange Networks Synthesis of Isothermal Process Based on Superstructure Method. Chem. Eng. Trans. 2017, 61, 133–138. [Google Scholar]
- Amini-Rankouhi, A.; Huang, Y. Prediction of maximum recoverable mechanical energy via work integration: A thermodynamic modeling and analysis approach. AIChE J. 2017, 63, 4814–4826. [Google Scholar] [CrossRef]
- Fu, C.; Gundersen, T. Heat and work integration: Fundamental insights and applications to carbon dioxide capture processes. Energy Convers. Manag. 2016, 121, 36–48. [Google Scholar] [CrossRef]
- Fu, C.; Gundersen, T. Correct integration of compressors and expanders in above ambient heat exchanger networks. Energy 2016, 116, 1282–1293. [Google Scholar] [CrossRef]
- Fu, C.; Gundersen, T. Integrating compressors into heat exchanger networks above ambient temperature. AIChE J. 2015, 61, 3770–3785. [Google Scholar] [CrossRef]
- Fu, C.; Gundersen, T. Integrating expanders into heat exchanger networks above ambient temperature. AIChE J. 2015, 61, 3404–3422. [Google Scholar] [CrossRef]
- Fu, C.; Gundersen, T. Sub-ambient heat exchanger network design including compressors. Chem. Eng. Sci. 2015, 137, 631–645. [Google Scholar] [CrossRef]
- Aspelund, A.; Berstad, D.O.; Gundersen, T. An extended pinch analysis and design procedure utilizing pressure based exergy for subambient cooling. Appl. Therm. Eng. 2007, 27, 2633–2649. [Google Scholar] [CrossRef]
- Gundersen, T.; Berstad, D.O.; Aspelund, A. Extending pinch analysis and process integration into pressure and fluid phase considerations. Chem. Eng. Trans. 2009, 18, 33–38. [Google Scholar]
- Kansha, Y.; Tsuru, N.; Sato, K.; Fushimi, C.; Tsutsumi, A. Self-heat recuperation technology for energy saving in chemical processes. Ind. Eng. Chem. Res. 2009, 48, 7682–7686. [Google Scholar] [CrossRef]
- Tsutsumi, A.; Kansha, Y. Thermodynamic mechanism of self-heat recuperative and self-heat recovery heat circulation system for a continuous heating and cooling gas cycle process. Chem. Eng. Trans. 2017, 61, 1759–1764. [Google Scholar]
- Dong, R.; Yu, Y.; Zhang, Z. Simultaneous optimization of integrated heat, mass and pressure exchange network using exergoeconomic method. Appl. Energy 2014, 136, 1098–1109. [Google Scholar] [CrossRef]
- Onishi, V.C.; Ravagnani, M.A.; Caballero, J.A. Simultaneous synthesis of work exchange networks with heat integration. Chem. Eng. Sci. 2014, 112, 87–107. [Google Scholar] [CrossRef]
- Vikse, M.; Fu, C.; Barton, P.I.; Gundersen, T. Towards the use of mathematical optimization for work and heat exchange networks. Chem. Eng. Trans. 2017, 61, 1351–1356. [Google Scholar]
- Nair, S.K.; Nagesh Rao, H.; Karimi, I.A. Framework for work-heat exchange network synthesis (WHENS). AIChE J. 2018, 61, 871–876. [Google Scholar] [CrossRef]
- Floudas, C.A.; Ciric, A.R.; Grossmann, I.E. Automatic synthesis of optimum heat exchanger network configurations. AIChE J. 1986, 32, 276–290. [Google Scholar] [CrossRef]
- Yeomans, H.; Grossmann, I.E. A systematic modeling framework of superstructure optimization in process synthesis. Comput. Chem. Eng. 1999, 23, 709–731. [Google Scholar] [CrossRef]
- Chen, Q.; Grossmann, I. Recent developments and challenges in optimization-based process synthesis. Annu. Rev. Chem. Biomol. Eng. 2017, 8, 249–283. [Google Scholar] [CrossRef] [PubMed]
- Demirel, S.E.; Li, J.; Hasan, M.M.F. Systematic process intensification. Curr. Opin. Chem. Eng. 2019, in press. [Google Scholar]
- Wechsung, A.; Aspelund, A.; Gundersen, T.; Barton, P.I. Synthesis of heat exchanger networks at subambient conditions with compression and expansion of process streams. AIChE J. 2011, 57, 2090–2108. [Google Scholar] [CrossRef]
- Uv, P.M. Optimal Design of Heat Exchanger Networks with Pressure Changes. Master’s Thesis, NTNU, Trondheim, Norway, 2016. [Google Scholar]
- Stankiewicz, A.I.; Moulijn, J.A. Process intensification: Transforming chemical engineering. Chem. Eng. Prog. 2000, 96, 22–34. [Google Scholar]
- Reay, D.; Ramshaw, C.; Harvey, A. Process Intensification: Engineering for Efficiency, Sustainability and Flexibility; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Tian, Y.; Demirel, S.E.; Hasan, M.M.F.; Pistikopoulos, E.N. An Overview of Process Systems Engineering Approaches for Process Intensification: State of the Art. Chem. Eng. Process.-Process Intensif. 2018, 133, 160–210. [Google Scholar] [CrossRef]
- Demirel, S.E.; Li, J.; Hasan, M.M.F. A General Framework for Process Synthesis, Integration and Intensification. Comput. Aided Chem. Eng. 2018, 44, 445–450. [Google Scholar]
- Hasan, M.M.F.; Karimi, I.A.; Alfadala, H.E.; Grootjans, H. Operational modeling of multistream heat exchangers with phase changes. AIChE J. 2009, 55, 150–171. [Google Scholar] [CrossRef]
- Nagesh Rao, H.; Karimi, I.A. A superstructure-based model for multistream heat exchanger design within flow sheet optimization. AIChE J. 2017, 63, 3764–3777. [Google Scholar] [CrossRef]
- Demirel, S.E.; Li, J.; Hasan, M.M.F. Systematic process intensification using building blocks. Comput. Chem. Eng. 2017, 105, 2–38. [Google Scholar] [CrossRef]
- Li, J.; Demirel, S.E.; Hasan, M.M.F. Process synthesis using block superstructure with automated flowsheet generation and optimization. AIChE J. 2018, 64, 3082–3100. [Google Scholar] [CrossRef]
- Li, J.; Demirel, S.E.; Hasan, M.M.F. Process Integration Using Block Superstructure. Ind. Eng. Chem. Res. 2018, 57, 4377–4398. [Google Scholar] [CrossRef]
- Li, J.; Demirel, S.E.; Hasan, M.M.F. Fuel Gas Network Synthesis Using Block Superstructure. Processes 2018, 6, 23. [Google Scholar] [CrossRef]
- Onishi, V.C.; Ravagnani, M.A.; Caballero, J.A. Simultaneous synthesis of heat exchanger networks with pressure recovery: optimal integration between heat and work. AIChE J. 2014, 60, 893–908. [Google Scholar] [CrossRef]
- Fu, C.; Gundersen, T. Sub-ambient heat exchanger network design including expanders. Chem. Eng. Sci. 2015, 138, 712–729. [Google Scholar] [CrossRef]
- Onishi, V.C.; Ravagnani, M.A.; Jiménez, L.; Caballero, J.A. Multi-objective synthesis of work and heat exchange networks: Optimal balance between economic and environmental performance. Energy Convers. Manag. 2017, 140, 192–202. [Google Scholar] [CrossRef]
- Zhuang, Y.; Liu, L.; Liu, Q.; Du, J. Step-wise synthesis of work exchange networks involving heat integration based on the transshipment model. Chin. J. Chem. Eng. 2017, 25, 1052–1060. [Google Scholar] [CrossRef]
- Qadeer, K.; Qyyum, M.A.; Lee, M. Krill-herd-based investigation for energy saving opportunities in offshore LNG processes. Ind. Eng. Chem. Res. 2018, 57, 14162–14172. [Google Scholar] [CrossRef]
- Yee, T.F.; Grossmann, I.E. Simultaneous optimization models for heat integration—II. Heat exchanger network synthesis. Comput. Chem. Eng. 1990, 14, 1165–1184. [Google Scholar] [CrossRef]
- Lim, W.; Choi, K.; Moon, I. Current status and perspectives of liquefied natural gas (LNG) plant design. Ind. Eng. Chem. Res. 2013, 52, 3065–3088. [Google Scholar] [CrossRef]
- Vikse, M.; Watson, H.; Gundersen, T.; Barton, P. Simulation of Dual Mixed Refrigerant Natural Gas Liquefaction Processes Using a Nonsmooth Framework. Processes 2018, 6, 193. [Google Scholar] [CrossRef]
- Kazda, K.; Li, X. Approximating nonlinear relationships for optimal operation of natural gas transport networks. Processes 2018, 6, 198. [Google Scholar] [CrossRef]
- Misener, R.; Floudas, C.A. ANTIGONE: Algorithms for continuous/integer global optimization of nonlinear equations. J. Glob. Optim. 2014, 59, 503–526. [Google Scholar] [CrossRef]
- Achterberg, T. SCIP: Solving constraint integer programs. Math. Program, Comput, 2009, 1, 1–41. [Google Scholar] [CrossRef]
| Reference | Approach | Application/Case Studies |
|---|---|---|
| Wechsung, Aspelund, Gundersen, Barton (2011) [29] | Combination of pinch analysis, exergy analysis, and optimization to find heat exchanger network (HEN) with minimal irreversibility by varying pressure levels of process streams | An offshore natural gas liquefaction process |
| Razib, Hasan, Karimi (2012) [7] | First formalization of an optimization-based systematic work exchange network (WEN) synthesis problem | Integration among high-pressure and low-pressure streams |
| Dong, Yu, Zhang (2014) [21] | Superstructure optimization for heat, mass and pressure exchange networks with exergoeconomic analysis | Wastewater distribution network in a petroleum refining process |
| Onishi, Ravagnani, Caballero (2014a) [41] | Superstructure optimization for HEN design with pressure recovery | Cryogenic process design |
| Onishi, Ravagnani, Caballero (2014b) [22] | MINLP-based WHENS using a multi-stage superstructure for optimal pressure recovery of process gaseous streams | Integration among high-pressure and low-pressure streams |
| Fu and Gundersen (2015a,b,c,d) [14,15,16,42] | Graphical methodology for HEN design including compressors or expanders to minimize exergy consumption above or below ambient temperature | Integration of process streams with supply and target states |
| Huang and Karimi (2016) [3] | MINLP-based approach to synthesize WHENS for optimized selection of end-heaters and end-coolers to meet the desired temperature targets | Integration among high-pressure and low-pressure streams and a transport chain for stranded natural gas |
| Fu, Gundersen (2016) [13] | Correct integration of both compressors and expanders in HEN to minimize exergy consumption | Integration of process streams with the same supply and target temperatures |
| Fu, Gundersen (2016c) [12] | Graphical methodology using thermodynamic insights for WHENS | CO capture processes |
| Onishi, Ravagnani, Caballero (2017) [43] | Multi-objective optimization of WHENS using a multi-stage superstructure | Integration among process streams based on economic and environmental criteria |
| Zhuang, Liu, Liu, Du (2017) [44] | Synthesis of direct work exchange network (WEN) in adiabatic process involving heat integration based on transshipment model | Integration of high-pressure and low-pressure streams in a chemical plant |
| Nair, Rao, Karimi (2018) [24] | MINLP-based general WHENS framework considering stream temperature, pressure and/or phase changes without a classification of stream identity | C3 splitting and offshore liquefied natural gas (LNG) processes |
| Specification/Parameter | HU | CU | ||||
|---|---|---|---|---|---|---|
| Feed pressure, (MPa) | 10 | 10 | 6 | - | - | - |
| Feed temperature, (K) | 103.45 | 319.80 (298.15) | 221.12 | - | 383.15 | 93.15 |
| Target pressure, (MPa) | 0.1 | 10 | 6 | - | - | - |
| Target pressure range, (K) | - | 104.75 (113.15) | 293.15 | - | 383.15 | 93.15 |
| Flowrate, (kg/s) | 1.2 | 1 | 2.46 | - | - | - |
| Molecular weight, (kg/kmol) | 28 | 19 | 44 | 23.82 | 28 | 18 |
| Stream | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Nitrogen | 10.284 | 93.947 | 10.284 | 93.948 | 2.495 | −0.57 | −625.05 | 1.15 | −2.38 | −342.2 |
| Natural gas | 0 | 197.35 | 0 | 265.15 | 3.51 | 0 | 0 | 3.46 | 0 | 123.77 |
| Carbon dioxide | - | - | - | - | 2.318 | 0 | 0 | - | - | - |
| Capital Cost (K $) | Operating Cost | ||||
|---|---|---|---|---|---|
| Compressor | 184.12 | 2.4 | 2.988 | 2.5 | - |
| Expander | 29.20 | 0.4872 | 1 | 2.5 | - |
| Motor | −1.1 | 2.1 | 0.6 | 4 | 455.04 ($/(KW·a)) |
| Generator | −1.1 | 2.1 | 0.6 | 4 | 455.04 ($/(KW·a)) |
| Heat exchanger | 27.05 | 0.5027 | 0.8003 | 3.5 | 337 ($/(KW·a)) |
| HU | - | - | - | - | 337 ($/(KW·a)) |
| CU | - | - | - | - | 1000 ($/(KW·a)) |
| , , K, mK/KW, mK/KW | |||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Demirel, S.E.; Hasan, M.M.F. Building Block-Based Synthesis and Intensification of Work-Heat Exchanger Networks (WHENS). Processes 2019, 7, 23. https://doi.org/10.3390/pr7010023
Li J, Demirel SE, Hasan MMF. Building Block-Based Synthesis and Intensification of Work-Heat Exchanger Networks (WHENS). Processes. 2019; 7(1):23. https://doi.org/10.3390/pr7010023
Chicago/Turabian StyleLi, Jianping, Salih Emre Demirel, and M. M. Faruque Hasan. 2019. "Building Block-Based Synthesis and Intensification of Work-Heat Exchanger Networks (WHENS)" Processes 7, no. 1: 23. https://doi.org/10.3390/pr7010023
APA StyleLi, J., Demirel, S. E., & Hasan, M. M. F. (2019). Building Block-Based Synthesis and Intensification of Work-Heat Exchanger Networks (WHENS). Processes, 7(1), 23. https://doi.org/10.3390/pr7010023






