Model Development and Validation of Fluid Bed Wet Granulation with Dry Binder Addition Using a Population Balance Model Methodology
Abstract
1. Introduction and Objectives
Objectives
2. Materials and Experimental Methods
2.1. Materials
2.2. Batch Design
2.3. Fluid Bed Granulation
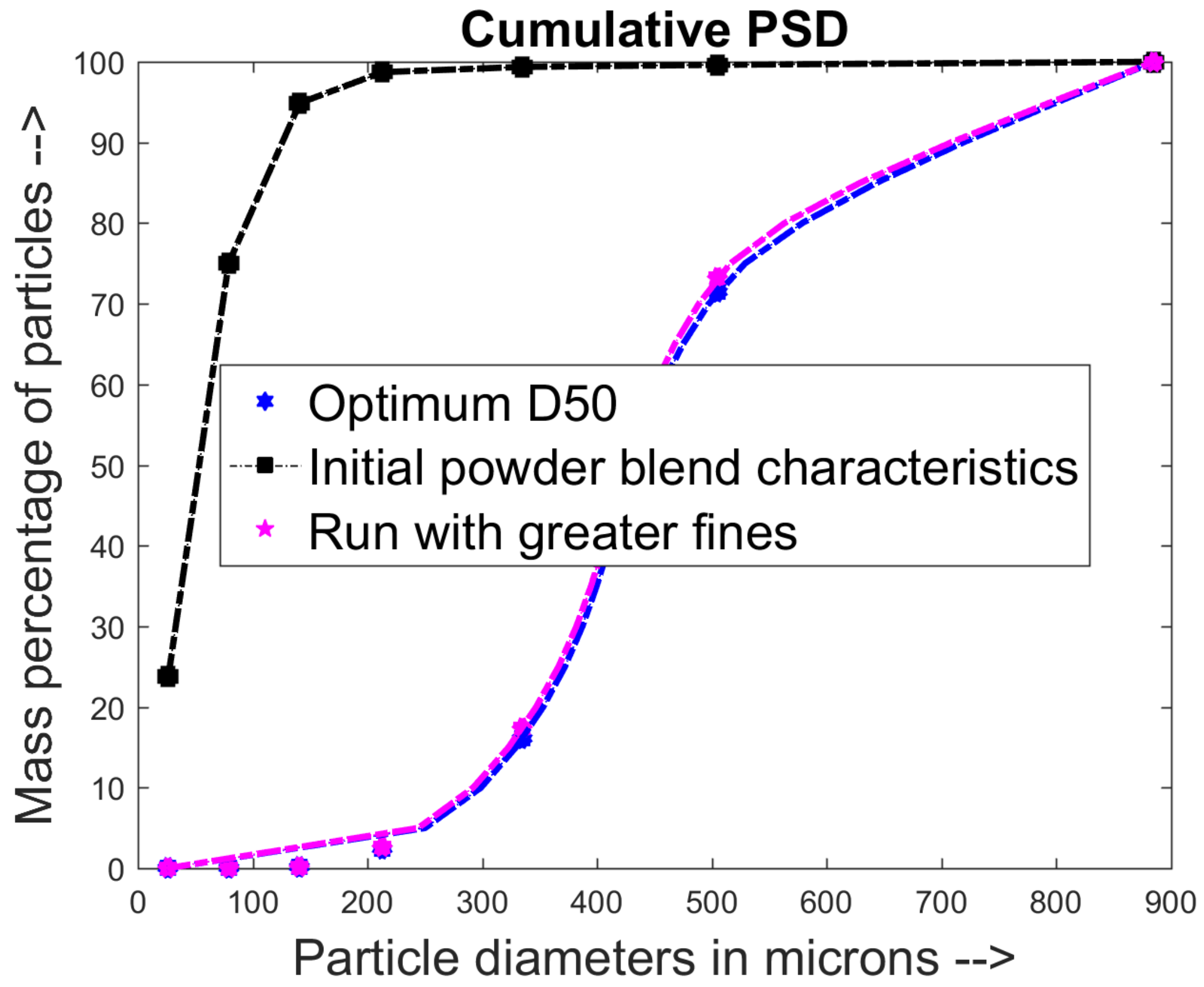
2.4. Particle Size Distribution
3. Mathematical Model Development
3.1. Particle Grid Configuration
3.2. Particle Wetness Classification
3.3. PBM Configuration
3.4. Aggregation Kernel Development
3.5. Liquid Balance of the Particle Bed
3.6. Integration of Heat Balance and Liquid Evaporation Due to the Heating of Particle Bed
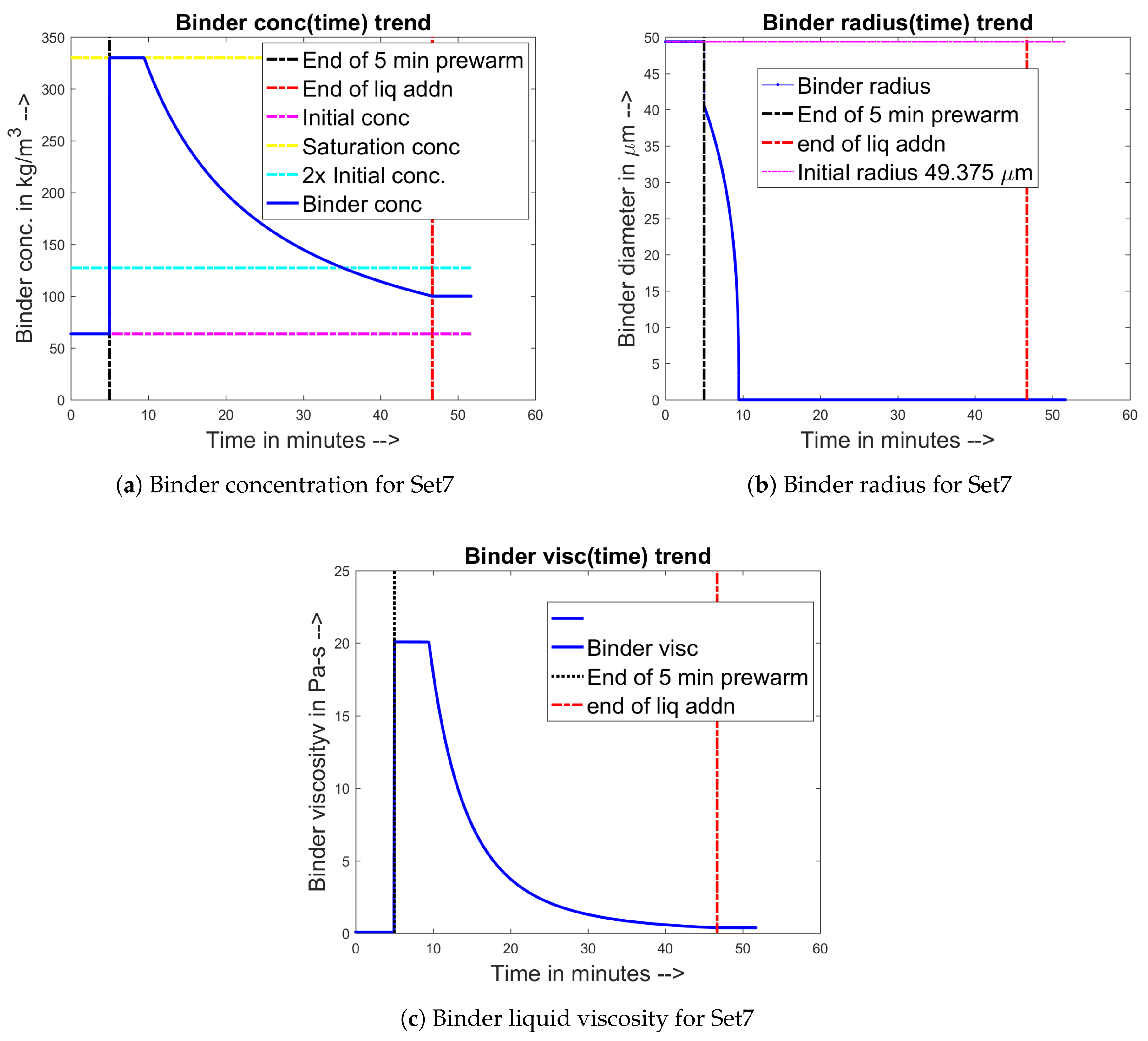
3.7. Binder Dissolution Module
3.8. Numerical Techniques
4. Results and Discussion
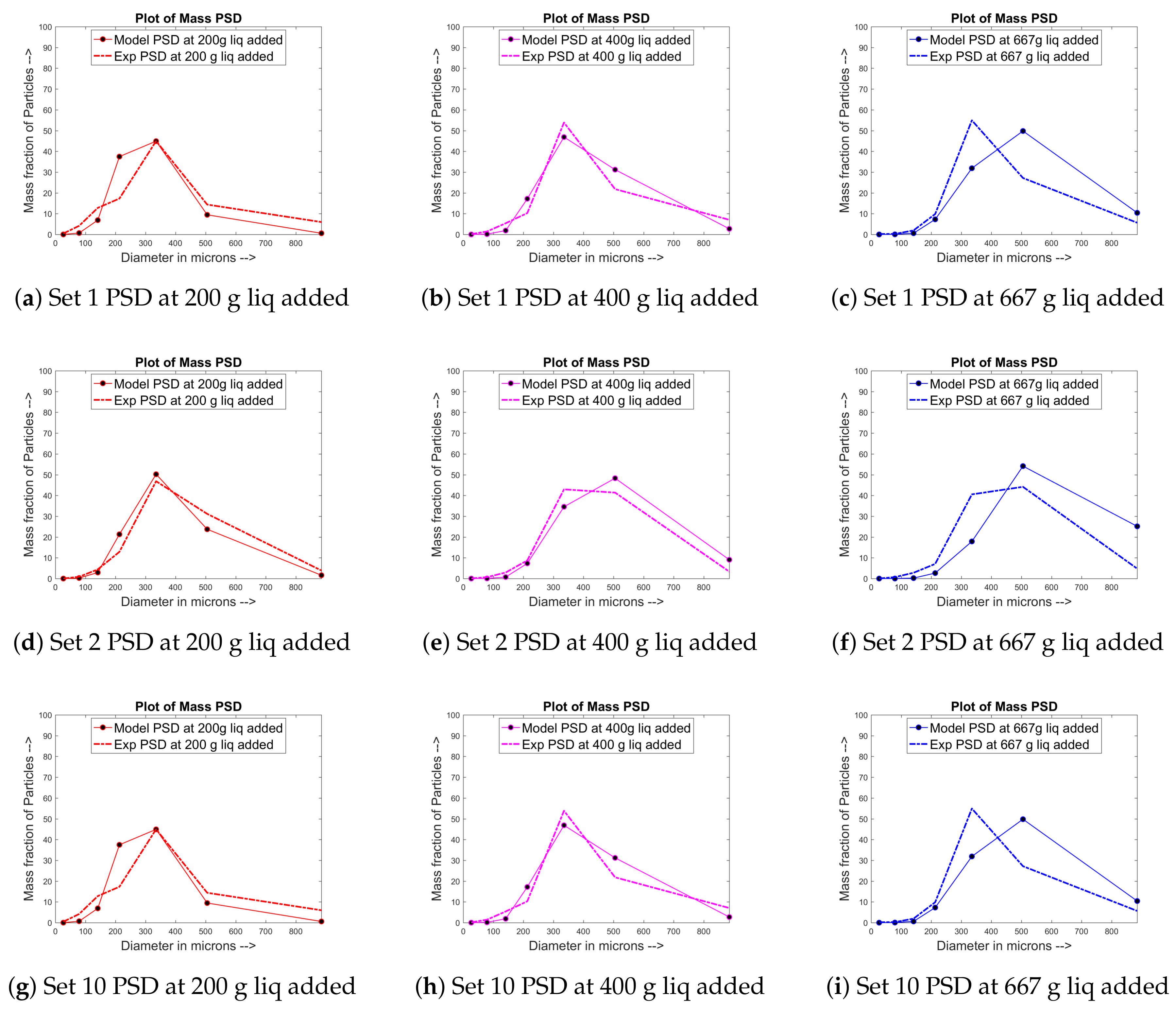
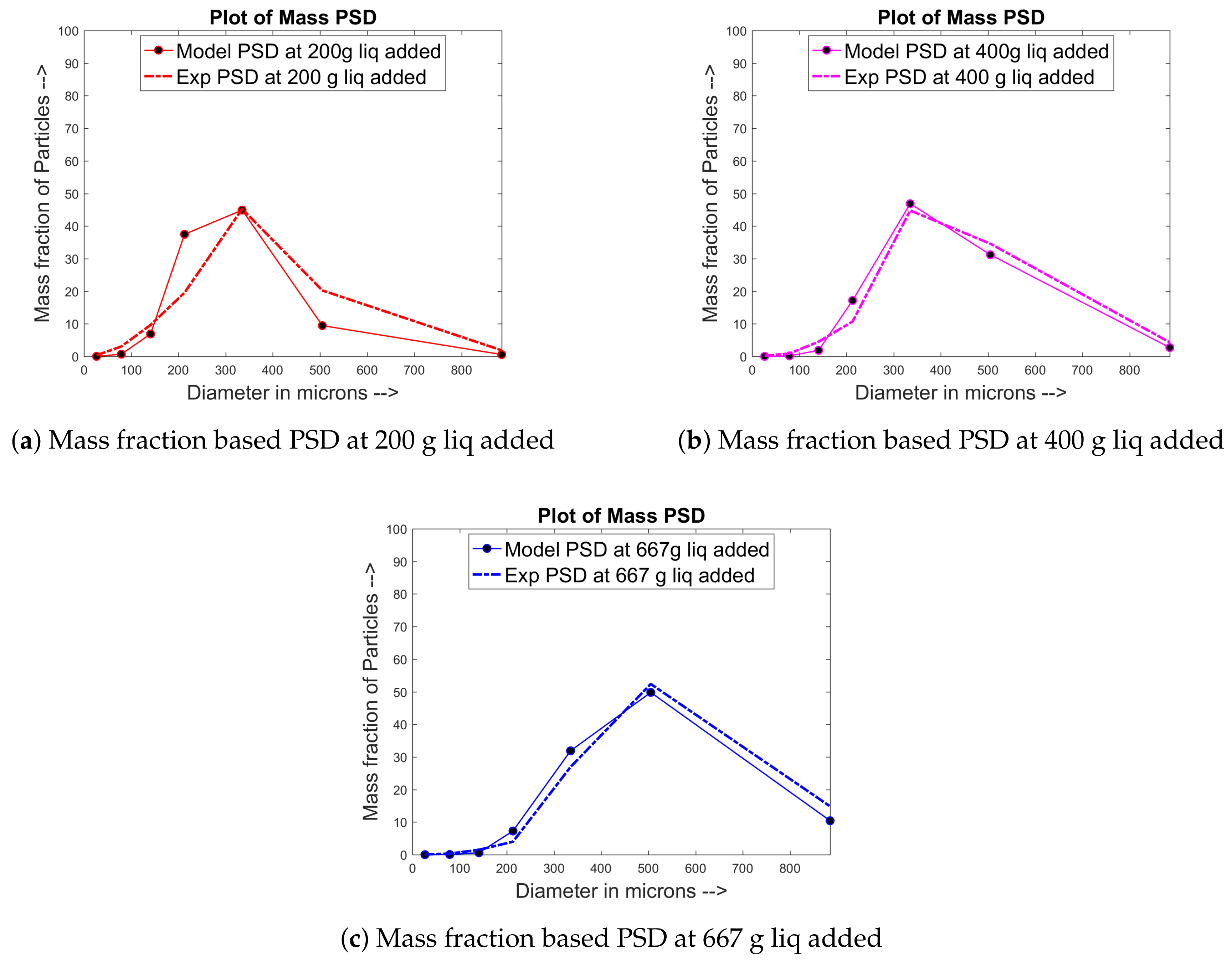
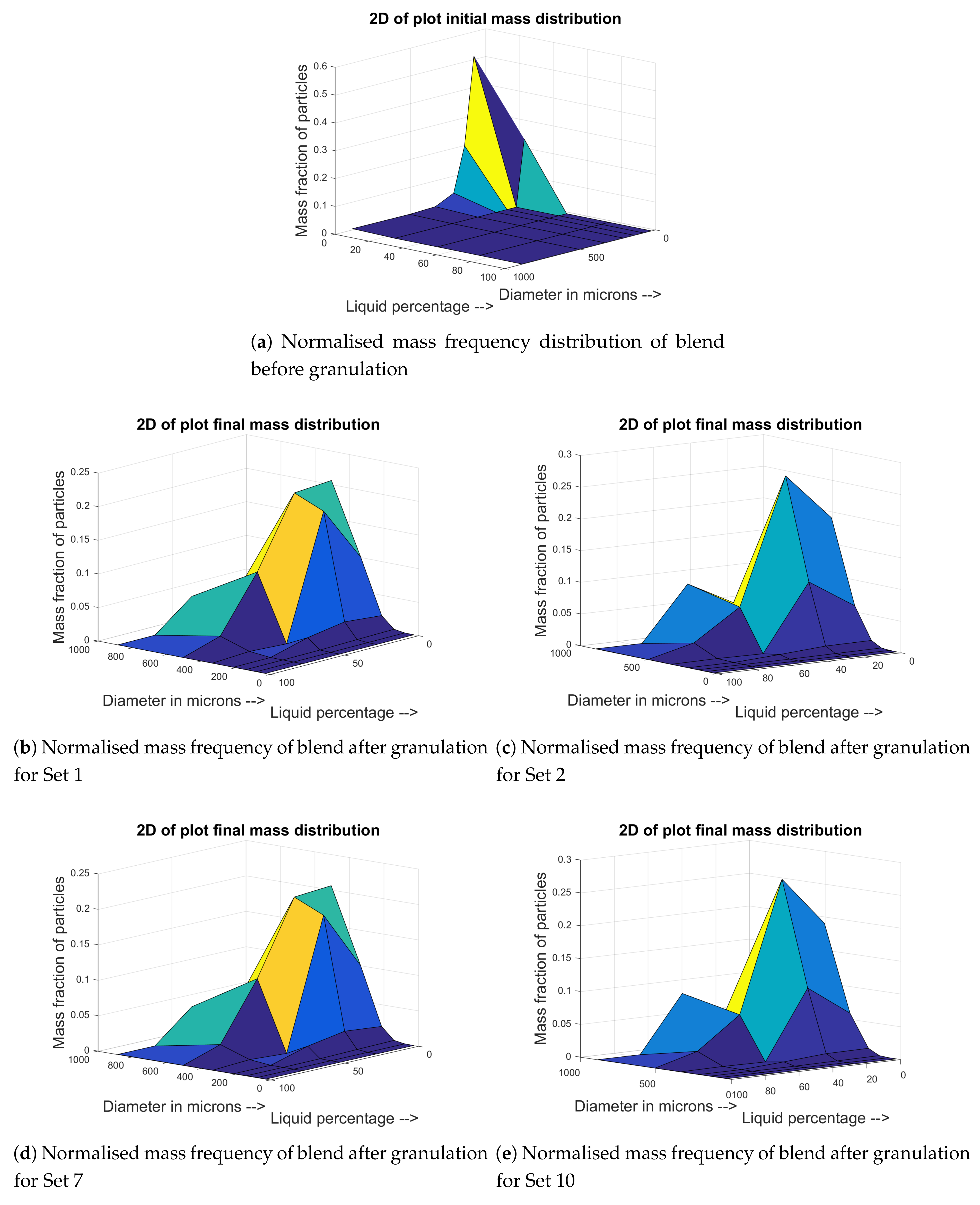
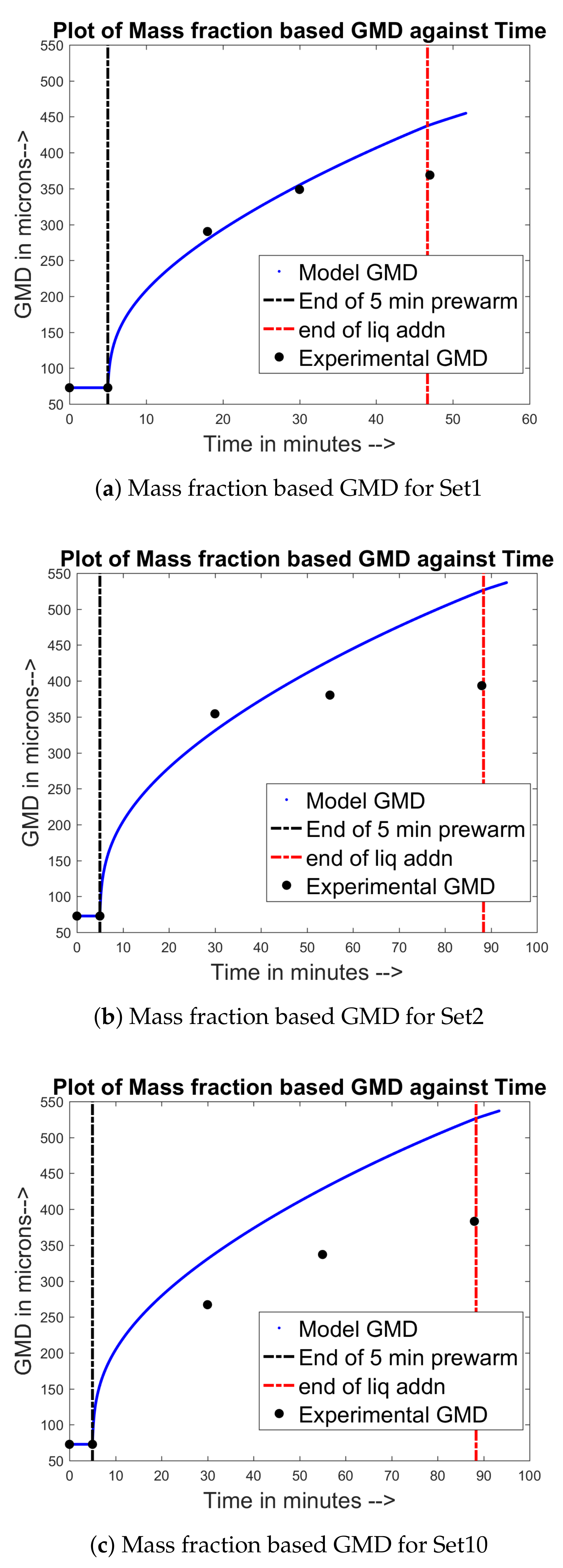
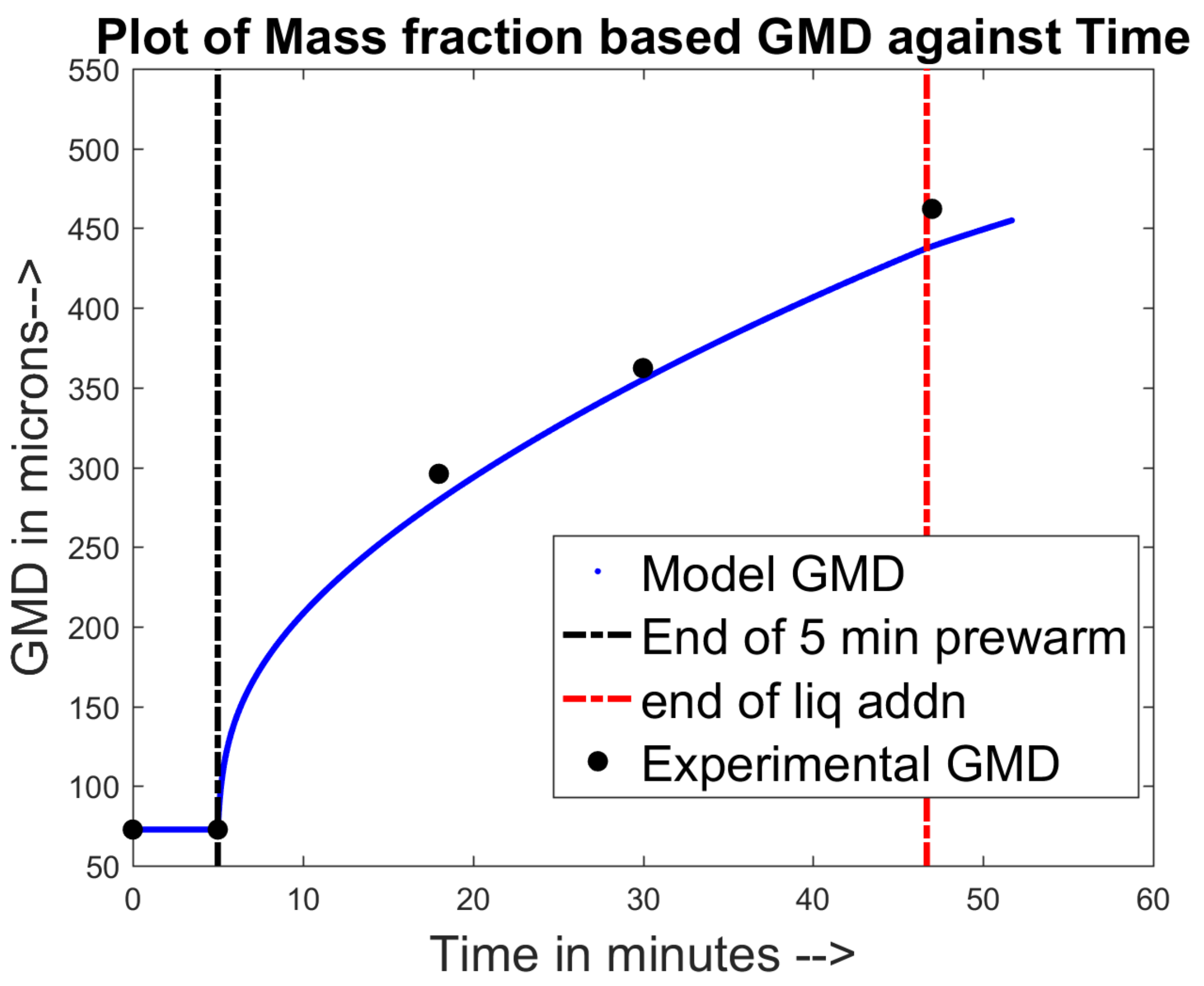
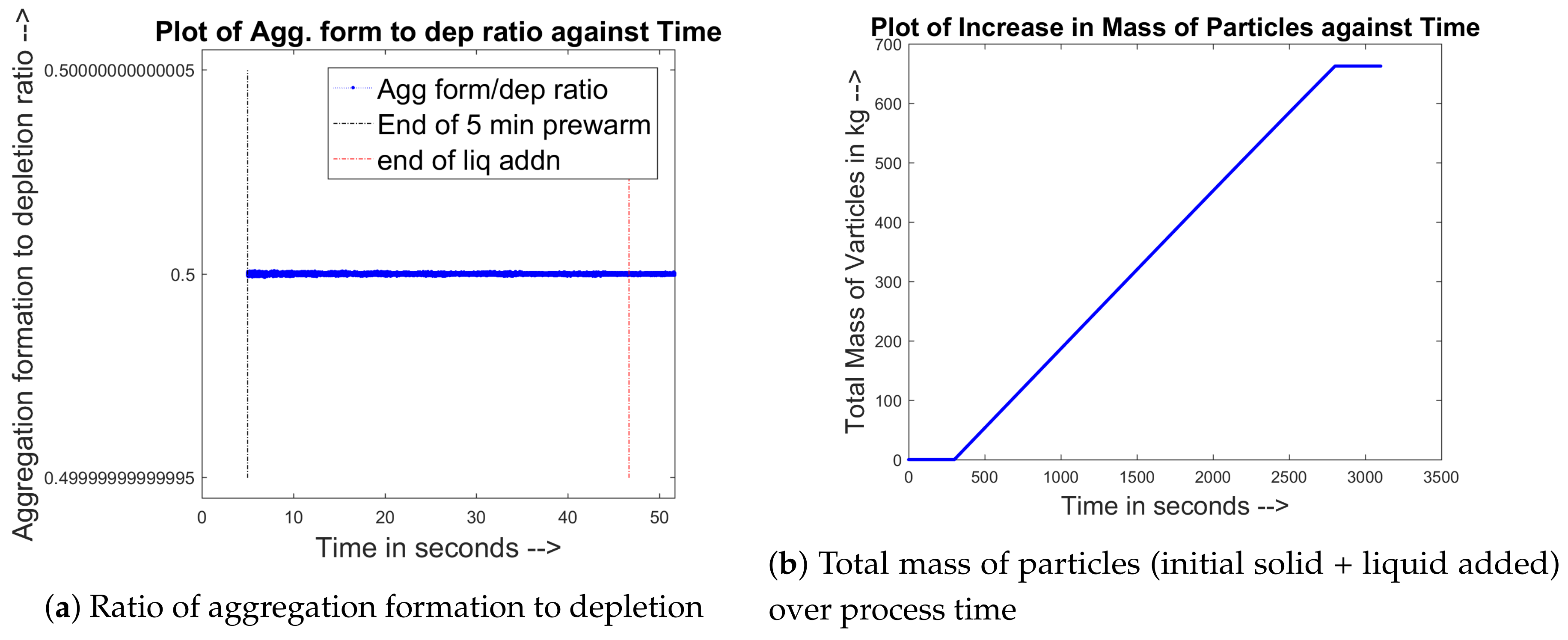
4.1. Training and Validation of the Model to Experimental Data
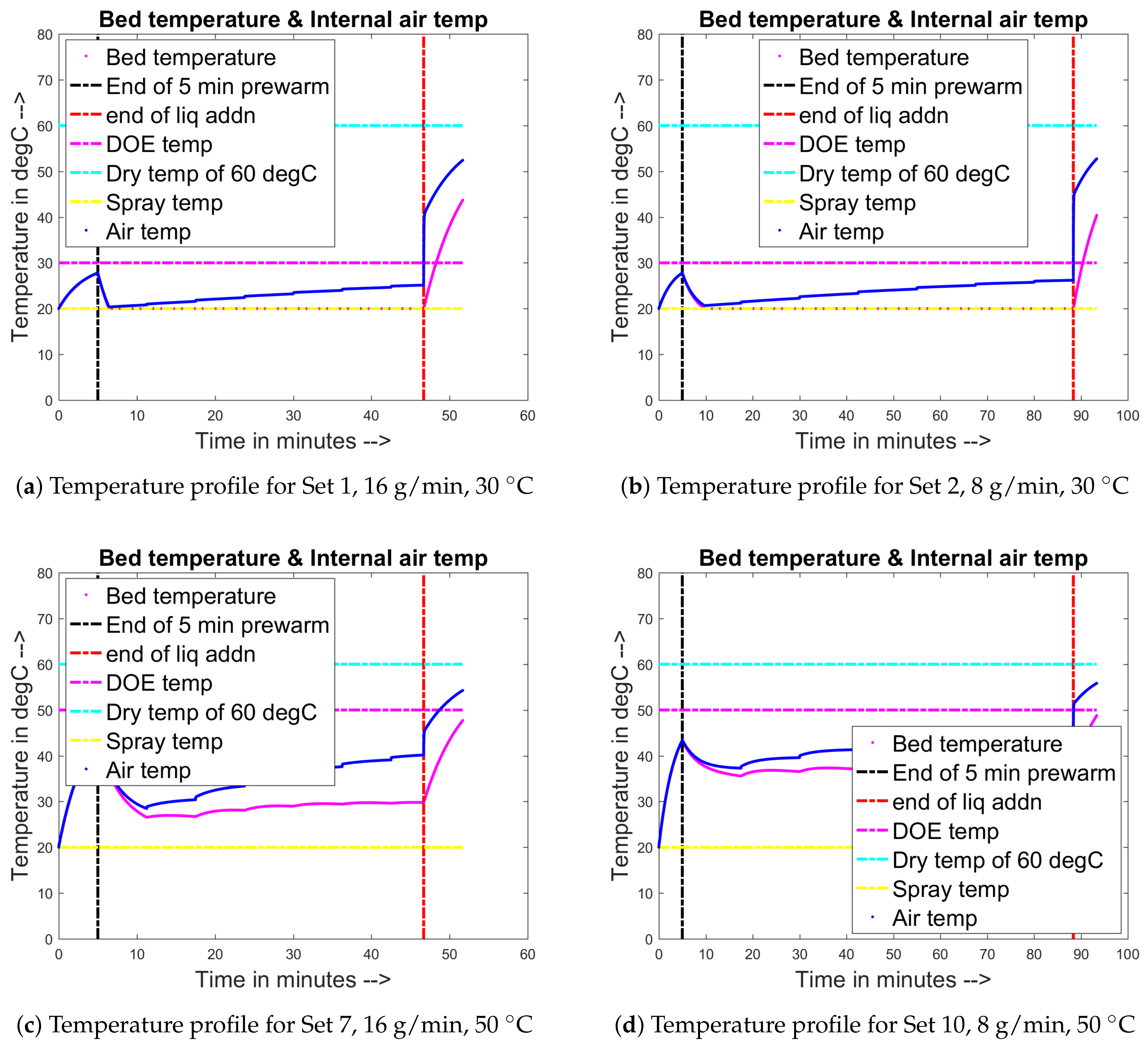
4.2. Prediction of Other Data for the Experimental Sets
4.3. Prediction of Regimes That Lead to Good Granulation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Boerefijn, R.; Hounslow, M. Studies of fluid bed granulation in an industrial r&d context. Chem. Eng. Sci. 2005, 60, 3879–3890. [Google Scholar]
- Haapaniemi, H. Development and Validation of Near Infrared Method and Manufacture of Tablet Calibration Set by Fluidized Bed Granulation. Master’s Thesis, Aalto University, Espoo, Finland, October 2017. Available online: https://aaltodoc.aalto.fi/handle/123456789/28499 (accessed on 22 August 2018).
- Abouzaid, A.S.; Salem, M.Y.; Elzanfaly, E.S.; el Gindy, A.E.; Hoag, S.; Ibrahim, A. Screening the fluid bed granulation process variables and moisture content determination of pharmaceutical granules by nir spectroscopy. Eur. J. Chem. 2017, 8, 265–272. [Google Scholar] [CrossRef]
- Fries, L.; Antonyuk, S.; Heinrich, S.; Palzer, S. DEM-CFD modeling of a fluidized bed spray granulator. Chem. Eng. Sci. 2011, 66, 2340–2355. [Google Scholar] [CrossRef]
- Lourenco, V.; Lochmann, D.; Reich, G.; Menezes, J.C.; Herdling, T.; Schewitz, J. A quality by design study applied to an industrial pharmaceutical fluid bed granulation. Eur. J. Pharm. Biopham. 2012, 81, 438–447. [Google Scholar] [CrossRef] [PubMed]
- Sen, M.; Barrasso, D.; Singh, R.; Ramachandran, R. A multi-scale hybrid cfd-dem-pbm description of a fluid–bed granulation process. Processes 2014, 2, 89–111. [Google Scholar] [CrossRef]
- Rajniak, P.; Stepanek, F.; Dhanasekharan, K.; Fan, R.; Mancinelli, C.; Chern, R. A combined experimental and computational study of wet granulation in a wurster fluid bed granulator. Powder Technol. 2009, 189, 190–201. [Google Scholar] [CrossRef]
- Drumm, C.; Attarakih, M.M.; Bart, H.-J. Coupling of CFD with DPBM for an RDC extractor. Chem. Eng. Sci. 2009, 64, 721–732. [Google Scholar] [CrossRef]
- Yan, W.; Luo, Z.-H.; Guo, A.-Y. Coupling of CFD with PBM for a pilot-plant tubular loop polymerization reactor. Chem. Eng. Sci. 2011, 66, 5148–5163. [Google Scholar] [CrossRef]
- Tan, H.; Goldschmidt, M.; Boerefijn, R.; Hounslow, M.; Salman, A.; Kuipers, J. Building population balance model for fluidized bed melt granulation: Lessons from kinetic theory of granular flow. Powder Technol. 2004, 142, 103–109. [Google Scholar] [CrossRef]
- Yuu, S.; Umekage, T.; Johno, Y. Numerical simulation of air and particle motions in bubbling fluidized bed of small particles. Powder Technol. 2000, 110, 158–168. [Google Scholar] [CrossRef]
- Bokkers, G.; Annaland, M.V.; Kuipers, J. Mixing and segregation in a bidisperse gas–solid fluidised bed: A numerical and experimental study. Powder Technol. 2004, 140, 176–186. [Google Scholar] [CrossRef]
- Fries, L.; Antonyuk, S.; Heinrich, S.; Dopfer, D.; Palzer, S. Collision dynamics in fluidised bed granulators: A DEM-CFD study. Chem. Eng. Sci. 2013, 86, 108–123. [Google Scholar] [CrossRef]
- Dosta, M.; Antonyuk, S.; Heinrich, S. Multiscale simulation of the fluidized bed granulation process. Chem. Eng. Technol. 2012, 35, 1373–1380. [Google Scholar] [CrossRef]
- Dosta, M.; Antonyuk, S.; Heinrich, S. Multiscale simulation of agglomerate breakage in fluidized beds. Ind. Eng. Chem. Res. 2013, 52, 11275–11281. [Google Scholar] [CrossRef]
- Tamrakar, A.; Devarampally, D.R.; Ramachandran, R. Advanced multiphase hybrid model development of fluidized bed wet granulation processes. Comput. Aided Chem. Eng. 2018, 41, 159–187. [Google Scholar]
- Pandey, P.; Bharadwaj, R. Predictive Modeling of Pharmaceutical Unit Operations; Woodhead Publishing: Sawston, UK, 2016. [Google Scholar]
- Barrasso, D.; Walia, S.; Ramachandran, R. Multi-component population balance modeling of continuous granulation processes: A parametric study and comparison with experimental trends. Powder Technol. 2013, 241, 85–97. [Google Scholar] [CrossRef]
- Ramachandran, R.; Immanuel, C.D.; Štěpánek, F.; Litster, J.D.; Doyle, F.J., III. A mechanistic model for breakage in population balances of granulation: Theoretical kernel development and experimental validation. Chem. Eng. Res. Des. 2009, 87, 598–614. [Google Scholar] [CrossRef]
- Heinrich, S.; Peglow, M.; Ihlow, M.; Henneberg, M.; Mörl, L. Analysis of the start-up process in continuous fluidized bed spray granulation by population balance modelling. Chem. Eng. Sci. 2002, 57, 4369–4390. [Google Scholar] [CrossRef]
- Tan, H.; Salman, A.; Hounslow, M. Kinetics of fluidized bed melt granulation–ii: Modelling the net rate of growth. Chem. Eng. Sci. 2006, 61, 3930–3941. [Google Scholar] [CrossRef]
- Vreman, A.; van Lare, C.; Hounslow, M. A basic population balance model for fluid bed spray granulation. Chem. Eng. Sci. 2009, 64, 4389–4398. [Google Scholar] [CrossRef]
- Cryer, S.A. Modeling agglomeration processes in fluid–bed granulation. AIChE J. 1999, 45, 2069–2078. [Google Scholar] [CrossRef]
- Chaudhury, A.; Niziolek, A.; Ramachandran, R. Multi-dimensional mechanistic modeling of fluid bed granulation processes: An integrated approach. Adv. Powder Technol. 2013, 24, 113–131. [Google Scholar] [CrossRef]
- Dosta, M.; Heinrich, S.; Werther, J. Fluidized bed spray granulation: Analysis of the system behaviour by means of dynamic flowsheet simulation. Powder Technol. 2010, 204, 71–82. [Google Scholar] [CrossRef]
- Börner, M.; Peglow, M.; Tsotsas, E. Derivation of parameters for a two compartment population balance model of wurster fluidised bed granulation. Powder Technol. 2013, 238, 122–131. [Google Scholar] [CrossRef]
- Liu, H.; Li, M. Two-compartmental population balance modeling of a pulsed spray fluidized bed granulation based on computational fluid dynamics (CFD) analysis. Int. J. Pharm. 2014, 475, 256–269. [Google Scholar] [CrossRef] [PubMed]
- Pandey, P.; Levins, C.; Pafiakis, S.; Zacour, B.; Bindra, D.; Trinh, J.; Buckley, D.; Gour, S.; Sharif, S.; Stamato, H. Enhancing tablet disintegration characteristics of a highly water-soluble high-drug-loading formulation by granulation process. Pharm. Dev. Technol. 2016, 23, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Chaturbedi, A.; Bandi, C.; Reddy, D.; Pandey, P.; Narang, A.; Bindra, D.; Tao, L.; Zhao, J.; Li, J.; Hussain, M.; et al. Compartment based population balance model development of a high shear wet granulation process via dry and wet binder addition. Chem. Eng. Res. Des. 2017, 123, 187–200. [Google Scholar] [CrossRef]
- Ennis, B.J.; Tardos, G.; Pfeffer, R. A microlevel-based characterization of granulation phenomena. Powder Technol. 1991, 65, 257–272. [Google Scholar] [CrossRef]
- Hu, X.; Cunningham, J.; Winstead, D. Understanding and predicting bed humidity in fluidized bed granulation. J. Pharm. Sci. 2008, 97, 1564–1577. [Google Scholar] [CrossRef] [PubMed]
- Stakic, M.; Stefanovic, P.; Cvetinovic, D.; Skobalj, P. Convective drying of particulate solids–packed vs. fluid bed operation. Int. J. Heat Mass Transf. 2013, 59, 66–74. [Google Scholar] [CrossRef]
- Fries, L.; Dosta, M.; Antonyuk, S.; Heinrich, S.; Palzer, S. Moisture distribution in fluidized beds with liquid injection. Chem. Eng. Technol. 2011, 34, 1076–1084. [Google Scholar] [CrossRef]
- Wang, J.; Flanagan, D.R. General solution for diffusion-controlled dissolution of spherical particles. 1. Theory. J. Pharm. Sci. 1999, 88, 731–738. [Google Scholar] [CrossRef] [PubMed]
- Chaudhury, A.; Kapadia, A.; Prakash, A.V.; Barrasso, D.; Ramachandran, R. An extended cell-average technique for a multi-dimensional population balance of granulation describing aggregation and breakage. Adv. Powder Technol. 2013, 24, 962–971. [Google Scholar] [CrossRef]
| Formulation | 5% SSG | 7.5% SSG | 10% SSG |
|---|---|---|---|
| Ingredient | % w/w | % w/w | % w/w |
| Intra-granular | |||
| Lamivudine (API) | 70.00 | 70.00 | 70.00 |
| MCC (Excipient) | 20.25 | 17.75 | 15.25 |
| SSG (super-disintegrant) | 2.50 | 3.75 | 5.00 |
| HPC (binder-dry) | 2.00 | 2.00 | 2.00 |
| HPC (binder-soln) | 2.00 | 2.00 | 2.00 |
| Extra-granular | |||
| SSG (super-disintegrant) | 2.50 | 3.75 | 5.00 |
| Mg Stearate (glidant) | 0.75 | 0.75 | 0.75 |
| Total | 100 | 100 | 100 |
| Formulation | 5% SSG | 7.5% SSG | 10% SSG | |||
|---|---|---|---|---|---|---|
| Ingredient | % w/w | % w/w | % w/w | |||
| Dry blend | All HPC bound | Dry blend | All HPC bound | Dry blend | All HPC bound | |
| Lamivudine | 73.88 | 72.35 | 74.87 | 73.30 | 75.88 | 74.27 |
| MCC | 21.37 | 20.93 | 18.98 | 18.59 | 16.53 | 16.18 |
| SSG | 2.64 | 2.58 | 4.01 | 3.93 | 5.42 | 5.31 |
| HPC | 2.11 | 4.13 | 2.14 | 4.19 | 2.17 | 4.24 |
| Total | 100 | 100 | 100 | 100 | 100 | 100 |
| Batch # | Atomization Air Pressure (Bar) | Disintegrant Amount % w/w | Inlet Air Temp. (°C) | Binder Spray Rate (g/min) |
|---|---|---|---|---|
| 1 | 1 | 10 | 30 | 16 |
| 2 | 1 | 5 | 30 | 8 |
| 3 | 2.5 | 7.5 | 40 | 12 |
| 4 | 4 | 5 | 50 | 8 |
| 5 | 4 | 10 | 50 | 16 |
| 6 | 4 | 5 | 30 | 16 |
| 7 | 1 | 5 | 50 | 16 |
| 8 | 2.5 | 7.5 | 40 | 12 |
| 9 | 4 | 10 | 30 | 8 |
| 10 | 1 | 10 | 50 | 8 |
| Varied Parameter | Parameter Values |
|---|---|
| Ratio of total liquid added to initial solid bed mass | 0.1334, 0.2001, 0.2668, 0.3335, 0.4002, 0.4669 and 0.5336 |
| Total SSG amt in formulation | 5%, 7.5% and 10% |
| Inlet air temperature during liquid addition | 30 °C, 40 °C and 50 °C |
| Liquid spray rate | 8 g/min, 12 g/min and 16 g/min |
| Symbol | Meaning | Parameter Value |
|---|---|---|
| Contact Angle | 42.7 ° | |
| Aggregation kernel constant | 6.87 Number·s | |
| Coefficient of restitution | 0.326 | |
| Heat Capacity of air | 1006 Jkg·K | |
| Heat Capacity of liquid water | 4187 Jkg·K | |
| Heat Capacity of water vapor | 1996 Jkg·K | |
| Heat Capacity of solids | 1000 Jkg·K | |
| Latent heat of evaporation for water | 2.27×10 J·kg | |
| Diffusivity of HPC | 8.3×10 m·s | |
| Density of HPC | 500 kg·m | |
| Saturated concentration of HPC | 330 kg·m | |
| Initial radius of HPC binder particles | 49.375 m | |
| Moisture content of inlet air | w.r.t. dry air |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muddu, S.V.; Tamrakar, A.; Pandey, P.; Ramachandran, R. Model Development and Validation of Fluid Bed Wet Granulation with Dry Binder Addition Using a Population Balance Model Methodology. Processes 2018, 6, 154. https://doi.org/10.3390/pr6090154
Muddu SV, Tamrakar A, Pandey P, Ramachandran R. Model Development and Validation of Fluid Bed Wet Granulation with Dry Binder Addition Using a Population Balance Model Methodology. Processes. 2018; 6(9):154. https://doi.org/10.3390/pr6090154
Chicago/Turabian StyleMuddu, Shashank Venkat, Ashutosh Tamrakar, Preetanshu Pandey, and Rohit Ramachandran. 2018. "Model Development and Validation of Fluid Bed Wet Granulation with Dry Binder Addition Using a Population Balance Model Methodology" Processes 6, no. 9: 154. https://doi.org/10.3390/pr6090154
APA StyleMuddu, S. V., Tamrakar, A., Pandey, P., & Ramachandran, R. (2018). Model Development and Validation of Fluid Bed Wet Granulation with Dry Binder Addition Using a Population Balance Model Methodology. Processes, 6(9), 154. https://doi.org/10.3390/pr6090154




