Abstract
This paper introduces GEKKO as an optimization suite for Python. GEKKO specializes in dynamic optimization problems for mixed-integer, nonlinear, and differential algebraic equations (DAE) problems. By blending the approaches of typical algebraic modeling languages (AML) and optimal control packages, GEKKO greatly facilitates the development and application of tools such as nonlinear model predicative control (NMPC), real-time optimization (RTO), moving horizon estimation (MHE), and dynamic simulation. GEKKO is an object-oriented Python library that offers model construction, analysis tools, and visualization of simulation and optimization. In a single package, GEKKO provides model reduction, an object-oriented library for data reconciliation/model predictive control, and integrated problem construction/solution/visualization. This paper introduces the GEKKO Optimization Suite, presents GEKKO’s approach and unique place among AMLs and optimal control packages, and cites several examples of problems that are enabled by the GEKKO library.
1. Introduction
Computational power has increased dramatically in recent decades. In addition, there are new architectures for specialized tasks and distributed computing for parallelization. Computational power and architectures have expanded the capabilities of technology to new levels of automation and intelligence with rapidly expanding artificial intelligence capabilities and computer-assisted decision processing. These advancements in technology have been accompanied by a growth in the types of mathematical problems that applications solve. Lately, machine learning (ML) has become the must-have technology across all industries, largely inspired by the recent public successes of new artificial neural network (ANN) applications. Another valuable area that is useful in a variety of applications is dynamic optimization. Applications include chemical production planning [1], energy storage systems [2,3], polymer grade transitions [4], integrated scheduling and control for chemical manufacturing [5,6], cryogenic air separation [7], and dynamic process model parameter estimation in the chemical industry [8]. With a broad and expanding pool of applications using dynamic optimization, the need for a simple and flexible interface to pose problems is increasingly valuable. GEKKO is not only an algebraic modeling language (AML) for posing optimization problems in simple object-oriented equation-based models to interface with powerful built-in optimization solvers but is also a package with the built-in ability to run model predictive control, dynamic parameter estimation, real-time optimization, and parameter update for dynamic models on real-time applications. The purpose of this article is to introduce the unique capabilities in GEKKO and to place this development in context of other packages.
2. Role of a Modeling Language
Algebraic modeling languages (AML) facilitate the interface between advanced solvers and human users. High-end, off-the-shelf gradient-based solvers require extensive information about the problem, including variable bounds, constraint functions and bounds, objective functions, and first and second derivatives of the functions, all in consistent array format. AMLs simplify the process by allowing the model to be written in a simple, intuitive format. The modeling language accepts a model (constraints) and objective to optimize. The AML handles bindings to the solver binary, maintains the required formatting of the solvers, and exposes the necessary functions. The necessary function calls include constraint residuals, objective function values, and derivatives. Most modern modeling languages leverage automatic differentiation (AD) [9] to facilitate exact gradients without explicit derivative definition by the user.
In general, an AML is designed to solve a problem in the form of Equation (1).
The objective function in Equation (1) is minimized by adjusting the state variables x and inputs u. The inputs u may include variables such as measured disturbances, unmeasured disturbances, control actions, feed-forward values, and parameters that are determined by the solver to minimize the objective function J. The state variables x may be solved with differential or algebraic equations. Equations include equality constraints (f) and inequality constraints (g).
3. Dynamic Optimization
Dynamic optimization is a unique subset of optimization algorithms that pertain to systems with time-based differential equations. Dynamic optimization problems extend algebraic problems of the form in Equation (1) to include the possible addition of the differentials in the objective function and constraints, as shown in Equation (2).
Differential algebraic equation (DAE) systems are solved by discretizing the differential equations to a system of algebraic equations to achieve a numerical solution. Some modeling languages are capable of natively handling DAEs by providing built-in discretization schemes. The DAEs are typically solved numerically and there are a number of available discretization approaches. Historically, these problems were first solved with a direct shooting method [10]. Direct shooting methods are still used and are best suited for stable systems with few degrees of freedom. Direct shooting methods eventually led to the development of multiple shooting, which provided benefits such as parallelization and stability [11]. For very large problems with multiples degrees of freedom, “direct transcription” (also known as “orthogonal collocation on finite elements”) is the state-of-the-art method [12]. Some fields have developed other unique approaches, such as pseudospectral optimal control methods [13].
Dynamic optimization problems introduce an additional set of challenges. Many of these challenges are consistent with those of other forms of ordinary differential equation (ODE) and partial differential equation (PDE) systems; only some challenges are unique to discretization in time. These challenges include handling stiff systems, unstable systems, numerical versus analytical solution mismatch, scaling issues (the problems get large very quickly with increased discretization), the number and location in the horizon of discretization points, and the optimal horizon length. Some of these challenges, such as handling stiff systems, can be addressed with the appropriate discretization scheme. Other challenges, such as the necessary precision of the solution and the location of discretizations of state variables, are better handled by a knowledgeable practitioner to avoid excessive computation.
Popular practical implementations of dynamic optimization include model predictive control (MPC) [14] (along with its nonlinear variation NMPC [15] and the economic objective alternative EMPC [16]), moving horizon estimation (MHE) [17] and dynamic real-time optimization (DRTO) [18]. Each of these problems is a special case of Equation (2) with a specific objective function. For example, in MPC, the objective is to minimize the difference between the controlled variable set point and model predictions, as shown in Equation (3).
where x is a state variable and is the desired set point or target condition for that state. The objective is typically a 1-norm, 2-norm, or squared error. EMPC modifies MPC by maximizing profit rather than minimizing error to a set point, but uses the same dynamic process model, as shown in Equation (4).
MHE adjusts model parameters to minimize the difference between measured variable values () and model predictions (x), as shown in Equation (5).
4. Previous Work
There are many software packages and modeling languages currently available for optimization and optimal control. This section, while not a comprehensive comparison, attempts to summarize some of the distinguishing features of each package.
Pyomo [19] is a Python package for modeling and optimization. It supports automatic differentiation and discretization of DAE systems using orthogonal collocation or finite-differencing. The resulting nonlinear programming (NLP) problem can be solved using any of several dozen AMPL Solver Library (ASL) supported solvers.
JuMP [20] is a modeling language for optimization in the Julia language. It supports solution of linear, nonlinear, and mixed-integer problems through a variety of solvers. Automatic differentiation is supplied, but, as of writing, JuMP does not include built-in support for differential equations.
Casadi [21] is a framework that provides a symbolic modeling language and efficient automatic differentiation. It is not a dynamic optimization package itself, but it does provides building blocks for solving dynamic optimization problems and interfacing with various solvers. Interfaces are available in MATLAB, Python, and C++.
GAMS [22] is a package for large-scale linear and nonlinear modeling and optimization with a large and established user base. It connects to a variety of commercial and open-source solvers, and programming interfaces are available for it in Excel, MATLAB, and R. Automatic differentiation is available.
AMPL [23] is a modeling system that integrates a modeling language, a command language, and a scripting language. It incorporates a large and extensible solver library, as well as fast automatic differentiation. AMPL is not designed to handle differential equations. Interfaces are available in C++, C#, Java, MATLAB, and Python.
The gPROMS package [24] is an advanced process modeling and flow-sheet environment with optimization capabilities. An extensive materials property library is included. Dynamic optimization is implemented through single and multiple shooting methods. The software is used through a proprietary interface designed primarily for the process industries.
JModelica [25] is an open-source modeling and optimization package based on the Modelica modeling language. The platform brings together a number of open-source packages, providing ODE integration through Sundials, automatic differentiation through Casadi, and NLP solutions through IPOPT. Dynamic systems are discretized using both local and pseudospectral collocation methods. The platform is accessed through a Python interface.
ACADO [26] is a self-contained toolbox for optimal control. It provides a symbolic modeling language, automatic differentiation, and optimization of differential equations through multiple shooting using the built in QP solver. Automatic C++ code generation is available for online predictive control applications, though support is limited to small to medium-sized problems. Interfaces are available in MATLAB and C++.
DIDO [27] is an object-oriented MATLAB toolbox for dynamic optimization and optimal control. Models are formulated in MATLAB using DIDO expressions, and differential equations are handled using a pseudospectral collocation approach. At this time, automatic differentiation is not supported.
GPOPS II [28] is a MATLAB-based optimal control package. Dynamic models are discretized using hp-adaptive collocation, and automatic differentiation is supported using the ADiGator package. Solution of the resulting NLP problem is performed using either the IPOPT or SNOPT solvers.
PROPT [29] is an optimal control package built on top of the TOMLAB MATLAB optimization environment. Differential equations are discretized using Gauss and Chebyshev collocation, and solutions of the resulting NLP are found using the SNOPT solver. Derivatives are provided through source transformation using TOMLAB’s symbolic differentiation capabilities. Automatic scaling and integer states are also supported. Access is provided through a MATLAB interface.
PSOPT [30] is an open-source C++ package for optimal control. Dynamic systems are discretized using both local and global pseudospectral collocation methods. Automatic differentiation is available by means of the ADOL-C library. Solution of NLPs is performed using either IPOPT or SNOPT.
In addition to those listed above, many other software libraries are available for modeling and optimization, including AIMMS [31], CVX [32], CVXOPT [33], YALMIP [34], PuLP [35], POAMS, OpenOpt, NLPy, and PyIpopt.
5. GEKKO Overview
GEKKO fills the role of a typical AML, but extends its capabilities to specialize in dynamic optimization applications. As an AML, GEKKO provides a user-friendly, object-oriented Python interface to develop models and optimization solutions. Python is a free and open-source language that is flexible, popular, and powerful. IEEE Spectrum ranked Python the #1 programming language in 2017. Being a Python package allows GEKKO to easily interact with other popular scientific and numerical packages. Further, this enables GEKKO to connect to any real system that can be accessed through Python.
Since Python is designed for readability and ease rather than speed, the Python GEKKO model is converted to a low-level representation in the Fortran back-end for speed in function calls. Automatic differentiation provides the necessary gradients, accurate to machine precision, without extra work from the user. GEKKO then interacts with the built-in open-source, commercial, and custom large-scale solvers for linear, quadratic, nonlinear, and mixed integer programming (LP, QP, NLP, MILP, and MINLP) in the back-end. Optimization results are loaded back to Python for easy access and further analysis or manipulation.
Other modeling and optimization platforms focus on ultimate flexibility. While GEKKO is capable of flexibility, it is best suited for large-scale systems of differential and algebraic equations with continuous or mixed integer variables for dynamic optimization applications. GEKKO has a graphical user interface (GUI) and several built-in objects that support rapid prototyping and deployment of advanced control applications for estimation and control. It is a full-featured platform with a core that has been successfully deployed on many industrial applications.
As a Dynamic Optimization package, GEKKO accommodates DAE systems with built-in discretization schemes and facilitates popular applications with built-in modes of operation and tuning parameters. For differential and algebraic equation systems, both simultaneous and sequential methods are built in to GEKKO. Modes of operation include data reconciliation, real-time optimization, dynamic simulation, moving horizon estimation, and nonlinear predictive control. The back-end compiles the model to an efficient low-level format and performs model reduction based on analysis of the sparsity structure (incidence of variables in equations or objective function) of the model.
Sequential methods separate the problem in Equation (2) into the standard algebraic optimization routine Equation (1) and a separate differential equation solver, where each problem is solved sequentially. This method is popular in fields where the solution of differential equations is extremely difficult. By separating the problems, the simulator can be fine-tuned, or wrapped in a “black box”. Since the sequential approach is less reliable in unstable or ill-conditioned problems, it is often adapted to a “multiple-shooting” approach to improve performance. One benefit of the sequential approach is a guaranteed feasible solution of the differential equations, even if the optimizer fails to find an optimum. Since GEKKO does not allow connecting to black box simulators or the multiple-shooting approach, this feasibility of differential equation simulations is the main benefit of sequential approaches.
The simultaneous approach, or direct transcription, minimizes the objective function and resolves all constraints (including the discretized differential equations) simultaneously. Thus, if the solver terminates without reaching optimality, it is likely that the equations are not satisfied and the dynamics of the infeasible solution are incorrect—yielding a worthless rather than just suboptimal solution. However, since simultaneous approaches do not waste time accurately simulating dynamics that are thrown away in intermediary iterations, this approach tends to be faster for large problems with many degrees of freedom [36]. A common discretization scheme for this approach, which GEKKO uses, is orthogonal collocation on finite elements. Orthogonal collocation represents the state and control variables with polynomials inside each finite element. This is a form of implicit Runga–Kutta methods, and thus it inherits the benefits associated with these methods, such as stability. Simultaneous methods require efficient large-scale NLP solvers and accurate problem information, such as exact second derivatives, to perform well. GEKKO is designed to provide such information and take advantage of the simultaneous approach’s benefits in sparsity and decomposition opportunities. Therefore, the simultaneous approach is usually recommended in GEKKO.
GEKKO is an open-source Python library with an MIT license. The back-end Fortran routines are not open-source, but are free to use for academic and commercial applications. It was developed by the PRISM Lab at Brigham Young University and is in version 0.1 at the time of writing. Documentation on the GEKKO Python syntax is available in the online documentation, currently hosted on Read the Docs. The remainder of this text explores the paradigm of GEKKO and presents a few example problems, rather than explaining syntax.
5.1. Novel Aspects
GEKKO combines the model development, solution, and graphical interface for problems described by Equation (2). In this environment, differential equations with time derivatives are automatically discretized and transformed to algebraic form (see Equation (6)) for solution by large-scale and sparse solvers.
where n is the number of time points in the discretized time horizon, is the combined state vector, and the collocation equations are added to relate differential terms to the state values. The collocation equations and derivation are detailed in [37]. GEKKO provides the following to an NLP solver in sparse form:
- Variables with initial values and bounds
- Evaluation of equation residuals and objective function
- Jacobian (first derivatives) with gradients of the equations and objective function
- Hessian of the Lagrangian (second derivatives) with second derivatives of the equations and objective
- Sparsity structure of first and second derivatives
Once the solution is complete, the results are loaded back into Python variables. GEKKO has several modes of operation. The two main categories are steady-state solutions and dynamic solutions. Both sequential and simultaneous modes are available for dynamic solutions. The core of all modes is the nonlinear model, which does not change between selection of the different modes. Each mode interacts with the nonlinear model to receive or provide information, depending on whether there is a request for simulation, estimation, or control. Thus, once a GEKKO model is created, it can be implemented in model parameter update (MPU), real-time optimization (RTO) [38], moving horizon estimation (MHE), model predictive control (MPC), or steady-state or dynamic simulation modes by setting a single option. The nine modes of operation are listed in Table 1.

Table 1.
Modes of operation.
There are several modeling language and analysis capabilities enabled with GEKKO. Some of the most substantial advancements are automatic (structural analysis) or manual (user specified) model reduction, and object support for a suite of commonly used modeling or optimization constructs. The object support, in particular, allows the GEKKO modeling language to facilitate new application areas as model libraries are developed.
5.2. Built-In Solvers
GEKKO has multiple high-end solvers pre-compiled and bundled with the executable program instead of split out as a separate programs. The bundling allows out-of-the-box optimization, without the need of compiling and linking solvers by the user. The integration provides efficient communication between the solver and model that GEKKO creates as a human readable text file. The model text file is then compiled to efficient byte code for tight integration between the solver and the model. Interaction between the equation compiler and solver is used to monitor and modify the equations for initialization [39], model reduction, and decomposition strategies. The efficient compiled byte-code model includes forward-mode automatic differentiation (AD) for sparse first and second derivatives of the objective function and equations.
The popular open-source interior-point solver IPOPT [40] is the default solver. The custom interior-point solver BPOPT and the MINLP active-set solver APOPT [41] are also included. Additional solvers such as MINOS and SNOPT [42] are also integrated, but are only available with the associated requisite licensing.
6. GEKKO Framework
Each GEKKO model is an object. Multiple models can be built and optimized within the same Python script by creating multiple instances of the GEKKO model class. Each variable type is also an object with property and tuning attributes. Model constraints are defined with Python variables and Python equation syntax.
GEKKO has eight types of variables, four of which have extra properties. Constants, Parameters, Variables, and Intermediates are the base types. Constants and Parameters are fixed by the user, while Variables are calculated by the solver and Intermediates are updated with every iteration by the modeling language. Fixed Variables (FV), Manipulated Variables (MV), State Variables (SV), and Controlled Variables (CV) expand Parameters and Variables with extra attributes and features to facilitate dynamic optimization problem formulation and robustness for real-time application use. All variable declarations return references to a new object.
6.1. User-Defined Models
This section introduces the standard aspects of AMLs within the GEKKO paradigm. Optimization problems are created as collections of variables, equations, and objectives.
6.1.1. Variable Types
The basic set of variable types includes Constants, Parameters, and Variables. Constants exist for programing style and consistency. There is no functional difference between using a GEKKO Constant, a Python variable, or a floating point number in equations. Parameters serve as constant values, but unlike Constants, they can be (and usually are) arrays. Variables are calculated by the solver to meet constraints and minimize the objective. Variables can be constrained to strict boundaries or required to be integer values. Restricting Variables to integer form then requires the use of a specialized solver (such as APOPT) that iterates with a branch-and-bound method to find a solution.
6.1.2. Equations
Equations are all solved together implicitly by the built-in optimizer. In dynamic modes, equations are discretized across the whole time horizon, and all time points are solved simultaneously. Common unary operators are available with their respective automatic differentiation routines such as absolute value, exponentiation, logarithms, square root, trigonometric functions, hyperbolic functions, and error functions. The GEKKO operands are used in model construction instead of Python Math or NumPy functions. The GEKKO operands are required so that first and second derivatives are calculated with automatic differentiation.
A differential term is expressed in an equation with , where x is a Variable. Differential terms can be on either the right or the left side of the equations, with equality or inequality constraints, and in objective functions. Some software packages require index-1 or index-0 differential and algebraic equation form for solution. There is no DAE index limit in GEKKO or need for consistent initial conditions. Built-in discretization is only available in one dimension (time). Discretization of the the differential equations is set by the user using the GEKKO model attribute . The time attribute is set as an array which defines the boundaries of the finite elements in the orthogonal collocation scheme. The number of nodes used to calculate the internal polynomial of each finite element is set with a global option. However, these internal nodes only serve to increase solution accuracy since only the values at the boundary time points are returned to the user.
Partial differential equations (PDEs) are allowed within the GEKKO environment through manual discretization in space with vectorized notation. For example, Listing 1 shows the numerical solution to the wave equation shown in Equation (7) through manual discretization in space and built-in discretization in time. The simulation results are shown in Figure 1.
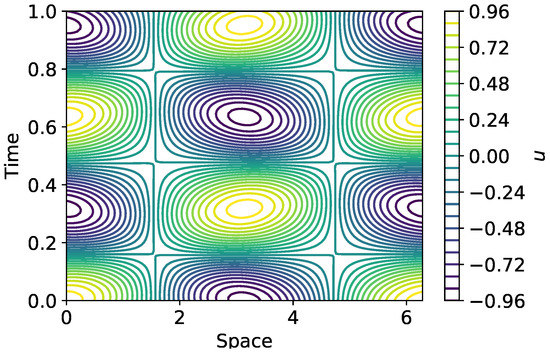
Figure 1.
Results of wave equation PDE simulation.
| Listing 1. PDE Example GEKKO Code with Manual Discretization in Space. |
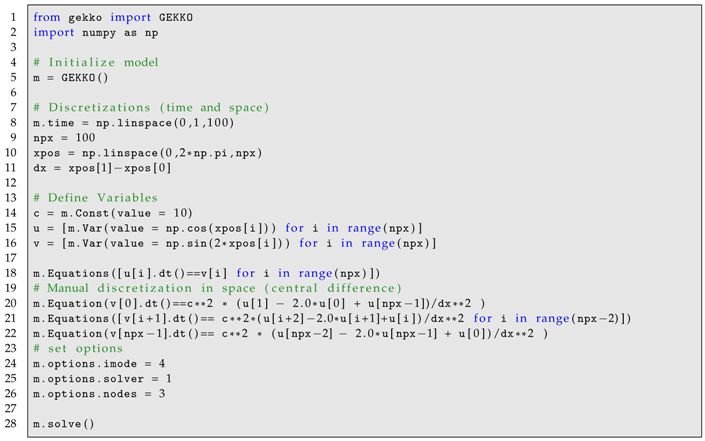 |
6.1.3. Objectives
All types of GEKKO quantities may be included in the objective function expression, including Constants, Parameters, Variables, Intermediates, FVs, MVs, SVs, and CVs. In some modes, GEKKO models automatically build objectives. MVs and CVs also contain objective function contributions that are added or removed with configuration options. For example, in MPC mode, a CV with a set point automatically receives an objective that minimizes error between model prediction and the set point trajectory of a given norm. There may be multiple objective function expressions within a single GEKKO model. This is often required to express multiple competing objectives in an estimation or control problem. Although there are multiple objective expressions, all objectives terms are summed into a single optimization expression to produce an optimal solution.
6.2. Special Variable Types
GEKKO features special variable types that facilitate the tuning of common industrial dynamic optimization problems with numerically robust options that are efficient and easily accessible. These special variable types are designed to improve model efficiency and simplify configuration for common problem scenarios.
6.2.1. Intermediates
Most modeling languages only include standard variables and constraints, where all algebraic constraints and their associated variables are solved implicitly through iterations of the optimizer. GEKKO has a new class of variables termed Intermediates. Intermediates, and their associated equations, are similar to variables except that they are defined and solved explicitly and successively substituted at every solver function call. Intermediate values, first derivatives, and second derivatives are substituted into other successive Intermediates or into the implicit equations. This is done outside of the solver in order to reduce the number of algebraic variables while maintaining the readability of the model. The intermediate equation must be an explicit equality. Each intermediate equation is solved in order of declaration. All variable values used in the explicit equation come from either the previous iteration or as an Intermediate declared previously.
In very large-scale problems, removing a portion of variables from the matrix math of implicit solutions can reduce matrix size, keeping problems within the efficient bounds of hardware limitations. This is especially the case with simultaneous dynamic optimization methods, where a set of model equations are multiplied over all of the collocation nodes. For each variable reduced in the base model, that variable is also eliminated from every collocation node. Intermediates are formulated to be highly memory-efficient during function calls in the back-end with the use of sparse model reduction. Intermediate variables essentially blend the benefits of sequential solver approaches into simultaneous methods.
6.2.2. Fixed Variable
Fixed Variables (FV) inherit Parameters, but potentially add a degree of freedom and are always fixed throughout the horizon (i.e., they are not discretized in dynamic modes). Estimated parameters, measured disturbances, unmeasured disturbances, and feed-forward variables are all examples of what would typically fit into the FV classification.
6.2.3. Manipulated Variable
Manipulated Variables (MV) inherit FVs but are discretized throughout the horizon and have time-dependent attributes. In addition to absolute bounds, relative bounds such as movement (), upper movement (), and lower movement () guide the selection by the optimizer. Hard constraints on movement of the value are sometimes replaced with a move suppression factor () to penalize movement of the MV. The move suppression factor is a soft constraint because it discourages movement with use of an objective function factor. is a penalty to minimize u (or maximize u with a negative sign). The MV object is given in Equation (8) for an -norm objective. The MV internal nodes for each horizon step are also calculated with supplementary equations based on whether it is a first-order or zero-order hold.
where n is the number of nodes in each time interval, is the change of u, is the negative change, is the positive change and is the slope. The MV object equations and objective are different for a squared error formulation as shown in Equation (9). The additional linear inequality constraints for and are not needed and the penalty on is squared as a move suppression factor that is compatible in a trade-off with the squared controlled variable objective.
Consistent with the vocabulary of the process control community, MVs are intended to be the variables that are directly manipulated by controllers. The practical implementations are often simplified, implemented by a distributed control system (DCS) and communicated to lower-level controllers (such as proportional-integral-derivative controllers [PIDs]). Thus, the internal nodes of MVs are calculated to reflect their eventual implementation. Rather than enabling each internal node of an MV as a degree of freedom, if there are internal points () then there is an option () that controls whether the internal nodes are equal to the starting value as a zero-order hold () or as a first-order linear interpolation between the beginning and end values of that interval (). The zero-order hold is common in discrete control where the MVs only change at specified time intervals. A linear interpolation is desirable to avoid sudden increments in MV values or when it is desirable to have a continuous profile. This helps match model predictions with actual implementation. For additional accuracy or less-frequent MV changes, the MV_STEP_HOR option can keep an MV fixed for a given number of consecutive finite elements. There are several other options that configure the behavior of the MV. The MV is either determined by the user with or the optimizer at the step end points with .
6.2.4. State Variable
State Variables (SV) inherit Variables with a couple of extra attributes that control bounds and measurements.
6.2.5. Controlled Variable
Controlled Variables (CV) inherit SVs but potentially add an objective. The CV object depends on the current mode of operation. In estimation problems, the CV object is constructed to reconcile measured and model-predicted values for steady-state or dynamic data. In control modes, the CV provides a setpoint that the optimizer will try to match with the model prediction values. CV model predictions are determined by equations, not as user inputs or solver degrees of freedom.
The CV object is given in Equation (10) for an -norm objective for estimation. In this case, parameter values (p) such as FVs or MVs with are adjusted to minimize the difference between model and measured values with weight . The states as well as the parameters are simultaneously adjusted by the solver to minimize the objective and satisfy the equations. There is a deadband with width around the measured values to avoid fitting noise and discourage unnecessary parameter movement. Unnecessary parameter movement is also avoided by penalizing with weight the change away from prior model predictions.
where is the feedback status that is 0 when the measurement is not used and 1 when the measurement reconciliation is included in the overall objective (intermediate values between 0 and 1 are allowed to weight the impact of measurements). A measurement may be discarded for a variety of reasons, including gross error detection and user specified filtering. For measurements from real systems, it is critical that bad measurements are blocked from influencing the solution. If bad measurements do enter, the -norm solution has been shown to be less sensitive to outliers, noise, and drift [43].
The CV object is different for a squared-error formulation, as shown in Equation (11). The desired norm is easily selected through a model option.
Important CV options are for estimation and for control. These options determine whether the CV objective terms contribute to the overall objective (1) or not (0).
In MPC, the CVs have several options for the adjusting the performance such as speed of reaching a new set point, following a predetermined trajectory, maximization, minimization, or staying within a specified deadband. The CV equations and variables are configured for fast solution by gradient-based solvers, as shown in Equations (12)–(14). In these equations, and are the upper and lower reference trajectories, respectively. The and are the weighting factors on upper or lower errors and is a factor that either minimizes (−) or maximizes (+) within the set point deadband between the set point range and .
An alternative to Equation (12b–e) is to pose the reference trajectories as inequality constraints and the error expressions as equality constraints, as shown in Equation (13). This is available in GEKKO to best handle systems with dead-time in the model without overly aggressive MV moves to meet a first-order trajectory.
While the -norm objective is default for control, there is also a squared error formulation, as shown in Equation (14). The squared error introduces additional quadratic terms but also eliminates the need for slack variables and as the objective is guided along a single trajectory () to a set point () with priority weight ().
It is important to avoid certain optimization formulations to preserve continuous first and second derivatives. GEKKO includes both MV and CV tuning with a wide range of options that are commonly used in advanced control packages. There are also novel options that improve controller and estimator responses for multi-objective optimization. One of these novel options is the ability to specify a tier for MVs and CVs. The tier option is a multi-level optimization where different combinations of MVs and CVs are progressively turned on. Once a certain level of MV is optimized, it is turned off and fixed at the optimized values while the next rounds of MVs are optimized. This is particularly useful to decouple the multivariate problem where only certain MVs should be used to optimize certain CVs although there is a mathematical relationship between the decoupled variables. Both MV and CV tuning can be employed to “tune” an application. A common trade-off for control is the speed of CV response to set point changes versus excessive MV movement. GEKKO offers a full suite of tuning options that are built into the CV object for control and estimation.
6.3. Extensions
Two additional extensions in GEKKO modeling are the use of Connections to link variables and object types (such as process flow streams). As an object-oriented modeling environment, there is a library of pre-built objects that individually consist of variables, equations, objective functions, or are collections of other objects.
6.3.1. Connections
All GEKKO variables (with the exception of FVs) and equations are discretized uniformly across the model time horizon. This approach simplifies the standard formulation of popular dynamic optimization problems. To add flexibility to this approach, GEKKO Connections allow custom relationships between variables across time points and internal nodes. Connections are processed after the parameters and variables are parsed but before the initialization of the values. Connections are the merging of two variables or connecting specific nodes of a discretized variable or setting just one unique point fixed to a given value.
6.3.2. Pre-Built Model Objects
The GEKKO modeling language encourages a disciplined approach to optimization. Part of this disciplined approach is to pose well-formed optimization problems that have continuous first and second derivatives for large-scale gradient-based solvers. An example is the use of the absolute value function, which has a discontinuous derivative at . GEKKO features a number of unique model objects that cannot be easily implemented through continuous equation restrictions. By implementing these models in the Fortran back-end, the unique gradients can be hard-coded for efficiency. The objects include an absolute value formulation, cubic splines, and discrete-time state space models.
Cubic splines are appropriate in cases where data points are available without a clear or simple mathematical relationship. When a high-fidelity simulator is too complex to be integrated into the model directly, a set of points from the simulator can act as an approximation of the simulator’s relationships. When the user provides a set of input and output values, the GEKKO back-end builds a cubic spline interpolation function. Subsequent evaluation of the output variable in the equations triggers a back-end routine to identify the associated cubic function and evaluate its value, first derivatives, and second derivatives. The cubic spline results in smooth, continuous functions suitable for gradient-based optimization.
6.4. Model Reduction, Sensitivity and Stability
Model reduction condenses the state vector x into a minimal realization that is required to solve the dynamic optimization problem. There are two primary methods of model reduction that are included with GEKKO, namely model construction (manual) and structural analysis (automatic). Manual model reduction uses Intermediate variable types, which reduce the size and complexity of the iterative solve through explicit solution and efficient memory management. Automatic model reduction, on the other hand, is a pre-solve strategy that analyzes the problem structure to explicitly solve simple equations. The equations are eliminated by direct substitution to condense the overall problem size. Two examples of equation eliminations are expressions such as and . Both equations can be eliminated by fixing the values and . The pre-solve analysis also identifies infeasible constraints such as if y were defined with an upper bound of 3. The equation is identified as violating a constraint before handing the problem to an NLP solver. Automatic model reduction is controlled with the option , which is zero by default. If is set to a non-zero integer value, it scans the model that many times to find linear equations and variables that can be eliminated.
Sensitivity analysis is performed in one of two ways. The first method is to specify an option in GEKKO () to generate a local sensitivity at the solution. This is performed by inverting the sparse Jacobian at the solution [44]. The second method is to perform a finite difference evaluation of the solution after the initial optimization problem is complete. This involves resolving the optimization problem multiple times and calculating the resultant change in output with small perturbations in the inputs. For dynamic problems, the automatic time-shift is turned off for sensitivity calculation to prevent advancement of the initial conditions when the problem is solved repeatedly.
Stability analysis is a well-known method for linear dynamic systems. A linear version of the GEKKO model is available from the sparse Jacobian that is available when . A linear dynamic model is placed into a continuous, sparse state space form, as shown in Equation (15).
If the model can be placed in this form, the open-loop stability of the model is determined by the sign of the eigenvalues of matrix A. Stability analysis can also be performed with the use of a step response for nonlinear systems or with Lyapunov stability criteria that can be implemented as GEKKO Equations.
6.5. Online Application Options
GEKKO has additional options that are tailored to online control and estimation applications. These include , , and . The attribute facilitates loading in new measurements in the appropriate place in the time horizon, based on the application type.
Gross error detection is critical for automation solutions that use data from physical sensors. Sensors produce data that may be corrupted during collection or transmission, which can lead to drift, noise, or outliers. For FV, MV, SV, and CV classifications, measured values are validated with absolute validity limits and rate-of-change validity limits. If a validity limit is exceeded, there are several configurable options such as “hold at the last good measured value” and “limit the rate of change toward the potentially bad measured value”. Many industrial control systems also send a measurement status () that can signal when a measured value is bad. Bad measurements are ignored in GEKKO and either the last measured value is used or else no measurement is used and the application reverts to a model predicted value.
The value of is updated from and the unbiased model prediction (). The is added to each point in the horizon, and the controller objective function drives the biased model () to the requested set point range. This is shown in Equation (16).
The parameter shifts all values through time with each subsequent resolve. This provides both accurate initial conditions for differential equations and efficient initialization of all variables (including values of derivatives and internal nodes) through the horizon by leaning on previous solutions.
6.6. Limitations
The main limitation of GEKKO is the requirement of fitting the problem within the modeling language framework. Most notably, user-defined functions in external libraries or other such connections to “black boxes” are not currently enabled. Logical conditions and discontinuous functions are not allowed but can be reformulated with binary variables or Mathematical Programming with Complementarity Constraints (MPCCs) [45] so they can be used in GEKKO. IF-THEN statements are purposely not allowed in GEKKO to prevent discontinuities. Set-based operations such as unions, exclusive OR, and others are also not supported. Regarding differential equations, only one discretization scheme is available and it only applies in one dimension (). Further discretizations must be performed by the user.
The back-end Fortran routines are only compiled for Windows and Linux at this time. The routines come bundled with the package for these operating systems to enable local solutions. MacOS and ARM processors must use the remote solve options to offload their problems to the main server.
Finally, it must be remembered that the actual optimization occurs in the bundled solvers. While these solvers are state-of-the-art, they are not infallible. GEKKO back-end adjustments, such as scaling, assist the solver, but it falls to the user to pose feasible problems and formulate them to promote convergence. Knowledge of the solver algorithms allows users to pose better problems and get better results.
7. Graphical User Interface
AML development history has moved from low-level models or text-based models to high-level implementations (e.g., Pyomo, JuMP, and Casadi) to facilitate rapid development. The next phase of accelerating the development process involves visual representation of the results. This is especially important in online control and estimation applications so the operator can easily visualize and track the application’s progress and intentions. In some modeling languages, simply loading the optimization results into a scripting language for further processing and analysis can be difficult. GEKKO includes a built-in graphical interface to facilitate visualizing results.
The GEKKO GUI uses Vue.js and Plotly to display optimization results quickly and easily. It also tracks past results for MHE and MPC problems, allowing time-dependent solutions to be displayed locally and in real-time as the iterative solution progresses. The GUI itself is implemented through a Python webserver that retrieves and stores optimization results and a Vue.js client that queries the Python webserver over HTTP. Polling between the client and webserver allows for live updating and seamless communication between the client and the webserver. The GUI allows plots to be created and deleted on demand, supporting individual visualization for variables on different scales. Model- and variable-specific details are displayed in tables to the left of the plots (see Figure 2).
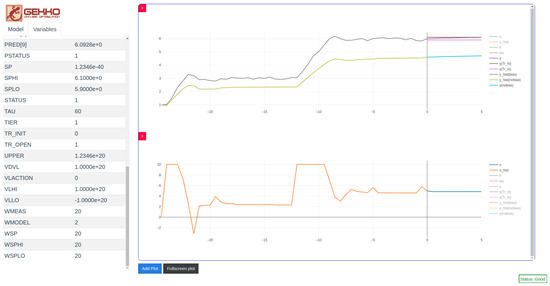
Figure 2.
Sample GEKKO GUI screen for rapidly visualizing solutions.
8. Examples
This section presents a set of example GEKKO models in complete Python syntax to demonstrate the syntax and available features. Solutions of each problem are also presented. Additional example problems are shown in the back matter, with an example of an artificial neural network in Appendix A and several dynamic optimization benchmark problems shown in Appendix B. Since the GEKKO Fortran backend is the successor to APMonitor [37], the many applications of APMonitor are also possible within this framework, including recent applications in combined scheduling and control [46], industrial dynamic estimation [43], drilling automation [47,48], combined design and control [49], hybrid energy storage [50], batch distillation [51], systems biology [44], carbon capture [52], flexible printed circuit boards [53], and steam distillation of essential oils [54].
8.1. Nonlinear Programming Optimization
First, problem 71 from the well-known Hock Schitkowski Benchmark set is included to facilitate syntax comparison with other AMLs. The Python code for this problem using the GEKKO optimization suite is shown in Listing 2.
| Listing 2. HS71 Example GEKKO Code. | |
 |
The output of this code is = 1.0, = 4.743, = 3.82115, and = 1.379408. This is the optimal solution that is also confirmed by other solver solutions.
8.2. Closed-Loop Model Predictive Control
The following example demonstrates GEKKO’s online MPC capabilities, including measurements, timeshifting, and MPC tuning. The MPC model is a generic first-order dynamic system, as shown in Equation (17). There exists plant–model mismatch (different parameters from the “process_simulator” function) and noisy measurements to more closely resemble a real system. The code is shown in Listing 3 and the results are shown in Figure 3, including the CV measurements and set points and the implemented MV moves.
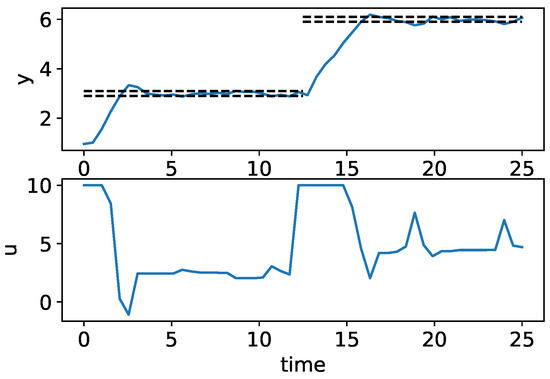
Figure 3.
Results of an online MPC example.
| Listing 3. Closed-Loop MPC GEKKO Code. |
 |
8.3. Combined Scheduling and Control
The final example demonstrates an approach to combining the scheduling and control optimization of a continuous, multi-product chemical reactor. Details regarding the model and objectives of this problem are available in [46]. This problem demonstrates GEKKO’s ability to efficiently solve large-scale problems, the ease of using the built-in discretization for differential equations, the applicability of special variables and their built-in tuning to various problems, and the flexibility provided by connections and custom objective functions. The code is shown in Listing 4 and the optimized horizons of the process concentrations and temperatures are shown in Figure 4.
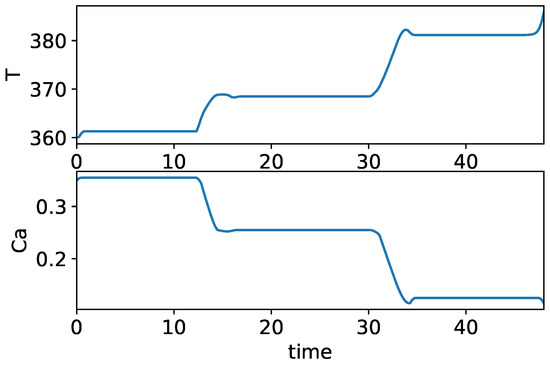
Figure 4.
Combined scheduling and control problem results.
| Listing 4. Combined Scheduling and Control Example GEKKO Code. |
  |
9. Conclusions
GEKKO is presented as a fully-featured AML in Python for LP, QP, NLP, MILP, and MINLP applications. Features such as AD and automatic ODE discretization using orthogonal collocation on finite elements and bundled large-scale solvers make GEKKO efficient for large problems. Further, GEKKO’s specialization in dynamic optimization problems is explored. Special variable types, built-in tuning, pre-built objects, result visualization, and model-reduction techniques are addressed to highlight the unique strengths of GEKKO. A few examples are presented in Python GEKKO syntax for comparison to other packages and to demonstrate the simplicity of GEKKO, the flexibility of GEKKO-created models, and the ease of accessing the built-in special variables types and tuning options.
Author Contributions
L.D.R.B. developed the Python code; D.C.H. developed the GUI; J.D.H. developed the Fortran backend; and R.A.M. provided assistance in all roles. All authors contributed in writing the paper.
Funding
This research was funded by National Science Foundation grant number 1547110.
Acknowledgments
Contributions made by Damon Peterson and Nathaniel Gates are gratefully acknowledged.
Conflicts of Interest
The authors are the principle developers of GEKKO, an open-source Python package. The Fortran backend belongs to Advanced Process Solutions, LLC which is associated with J.D.H. The founding sponsors had no role in the development of GEKKO; in the writing of the manuscript, and in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| AML | Algebraic Modeling Language |
| DAE | Differential and Algebraic Equations |
| NMPC | Nonlinear Model Predictive Control |
| RTO | Real-Time Optimization |
| MHE | Moving Horizon Estimation |
| ML | Machine Learning |
| ANN | Artificial Neural Networks |
| AD | Automatic (or Algorithmic) Differentiation |
| ODE | Ordinary Differential Equations |
| PDE | Partial Differential Equations |
| MPC | Model Predictive Control |
| EMPC | Economic Model Predictive Control |
| DRTO | Dynamic Real-Time Optimization |
| ASL | AMPL Solver Library |
| LP | Linear Programming |
| QP | Quadratic Programming |
| NLP | Non-Linear Programming |
| MILP | Mixed-Integer Linear Programming |
| MINLP | Mixed-Integer Non-Linear Programming |
| MPU | Model Parameter Update |
| FV | Fixed Variable |
| MV | Manipulated Variable |
| SV | State Variable |
| CV | Controlled Variable |
| DCS | Distributed Control System |
| GUI | Graphical User Interface |
| MPCC | Mathematical Programming with Complementarity Constraints |
Appendix A. Machine Learning with Artificial Neural Network
Machine learning has several areas of application, including regression and classification. This example problem is a simple case study that demonstrates GEKKO’s ability to create an artificial neural network, solved with a gradient based optimizer (IPOPT). In this case, the function is used to generate 20 equally spaced sample points between 0 and . These data are used to train the neural network with one input, a linear layer with two nodes, a nonlinear layer of three nodes with hyperbolic tangent activation functions, a linear layer with two nodes, and one output node. An overview of the neural network is shown in Figure A1, with a sample GEKKO implementation in Listing A1 and results in Figure A2.
| Listing A1. ANN Sample GEKKO Code. |
  |
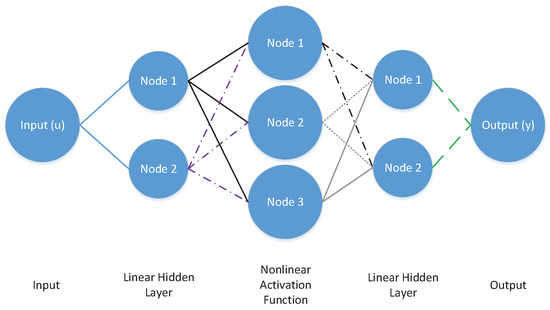
Figure A1.
Neural network structure.
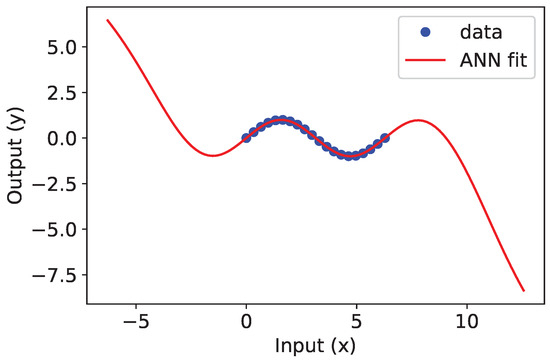
Figure A2.
Artificial neural network approximates function.
Appendix B. Dynamic Optimization Example Problems
The following three problems are examples of GEKKO used in solving classic dynamic optimization problems that are frequently used as benchmarks. The first example problem is a basic problem with a single differential equation, integral objective function, and specified initial condition, as shown in Listing A2. The second example problem is an example of a dynamic optimization problem that uses an economic objective function, similar to EMPC but without the iterative refinement as time progresses, as shown in Listing A3. The third example is a dynamic optimization problem that minimizes final time with fixed endpoint conditions, as shown in Listing A4.
| Listing A2. Luus Problem: Integral Objective. | |
| Original Form Equivalent Form for GEKKO | 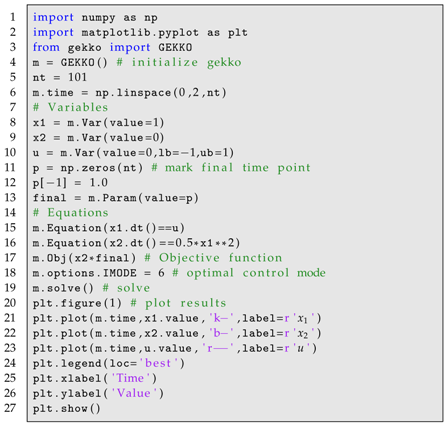 |
| LISTING A3. Commercial Fishing Dynamic Optimization. | |
| Original Form Equivalent Form for GEKKO | 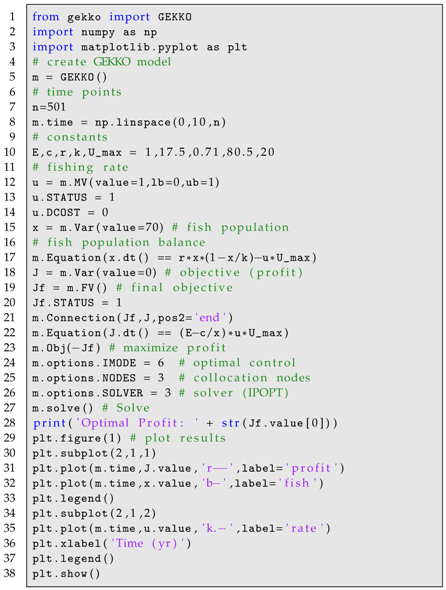 |
| Listing A4. Jennings Problem: Minimize Final Time. | |
| Original Form Equivalent Form for GEKKO |  |
References
- Nyström, R.H.; Franke, R.; Harjunkoski, I.; Kroll, A. Production campaign planning including grade transition sequencing and dynamic optimization. Comput. Chem. Eng. 2005, 29, 2163–2179. [Google Scholar] [CrossRef]
- Touretzky, C.R.; Baldea, M. Integrating scheduling and control for economic MPC of buildings with energy storage. J. Process Control 2014, 24, 1292–1300. [Google Scholar] [CrossRef]
- Powell, K.M.; Cole, W.J.; Ekarika, U.F.; Edgar, T.F. Dynamic optimization of a campus cooling system with thermal storage. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 4077–4082. [Google Scholar]
- Pontes, K.V.; Wolf, I.J.; Embiruçu, M.; Marquardt, W. Dynamic Real-Time Optimization of Industrial Polymerization Processes with Fast Dynamics. Ind. Eng. Chem. Res. 2015, 54, 11881–11893. [Google Scholar] [CrossRef]
- Zhuge, J.; Ierapetritou, M.G. Integration of Scheduling and Control with Closed Loop Implementation. Ind. Eng. Chem. Res. 2012, 51, 8550–8565. [Google Scholar] [CrossRef]
- Beal, L.D.; Park, J.; Petersen, D.; Warnick, S.; Hedengren, J.D. Combined model predictive control and scheduling with dominant time constant compensation. Comput. Chem. Eng. 2017, 104, 271–282. [Google Scholar] [CrossRef]
- Huang, R.; Zavala, V.M.; Biegler, L.T. Advanced step nonlinear model predictive control for air separation units. J. Process Control 2009, 19, 678–685. [Google Scholar] [CrossRef]
- Zavala, V.M.; Biegler, L.T. Optimization-based strategies for the operation of low-density polyethylene tubular reactors: Moving horizon estimation. Comput. Chem. Eng. 2009, 33, 379–390. [Google Scholar] [CrossRef]
- Rall, L.B. Automatic Differentiation: Techniques and Applications; Lecture Notes in Computer Science; Springer: Berlin, Germany, 1981; Volume 120. [Google Scholar]
- Cervantes, A.; Biegler, L.T. Optimization Strategies for Dynamic Systems. In Encyclopedia of Optimization; Floudas, C., Pardalos, P., Eds.; Kluwer Academic Publishers: Plymouth, MA, USA, 1999. [Google Scholar]
- Bock, H.; Plitt, K. A Multiple Shooting Algorithm for Direct Solution of Optimal Control Problems*. In Proceedings of the 9th IFAC World Congress: A Bridge Between Control Science and Technology, Budapest, Hungary, 2–6 July 1984; Volume 17, pp. 1603–1608. [Google Scholar]
- Biegler, L.T. Nonlinear Programming: Concepts, Algorithms, and Applications to Chemical Processes; Siam: Philadelphia, PA, USA, 2010. [Google Scholar]
- Ross, I.M.; Karpenko, M. A review of pseudospectral optimal control: From theory to flight. Ann. Rev. Control 2012, 36, 182–197. [Google Scholar] [CrossRef]
- Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Findeisen, R.; Allgöwer, F.; Biegler, L. Assessment and Future Directions of Nonlinear Model Predictive Control; Springer: Berlin, Germany, 2007; Volume 358, p. 642. [Google Scholar]
- Ellis, M.; Durand, H.; Christofides, P.D. A tutorial review of economic model predictive control methods. J. Proc. Control 2014, 24, 1156–1178. [Google Scholar] [CrossRef]
- Ji, L.; Rawlings, J.B. Application of MHE to large-scale nonlinear processes with delayed lab measurements. Comput. Chem. Eng. 2015, 80, 63–72. [Google Scholar] [CrossRef]
- Würth, L.; Rawlings, J.B.; Marquardt, W. Economic dynamic real-time optimization and nonlinear model predictive control on infinite horizons. Symp. Adv. Control 2009, 42, 219–224. [Google Scholar] [CrossRef]
- Hart, W.E.; Laird, C.; Watson, J.P.; Woodruff, D.L. Pyomo–Optimization Modeling in Python; Springer International Publishing: Cham, Switerland, 2012; Volume 67. [Google Scholar]
- Dunning, I.; Huchette, J.; Lubin, M. JuMP: A modeling language for mathematical optimization. SIAM Rev. 2017, 59, 295–320. [Google Scholar] [CrossRef]
- Andersson, J.; Åkesson, J.; Diehl, M. CasADi: A symbolic package for automatic differentiation and optimal control. In Recent Advances in Algorithmic Differentiation; Springer: Berlin, Germany, 2012; pp. 297–307. [Google Scholar]
- Bisschop, J.; Meeraus, A. On the development of a general algebraic modeling system in a strategic planning environment. In Applications; Springer: Berlin, Germany, 1982; pp. 1–29. [Google Scholar]
- Fourer, R.; Gay, D.; Kernighan, B. AMPL; A Modeling Language for Mathematical Programming; Boyd & Fraser Pub. Co.: Danvers, MA, USA, 1993. [Google Scholar]
- Barton, P.I.; Pantelides, C. gPROMS-A combined discrete/continuous modelling environment for chemical processing systems. Simul. Ser. 1993, 25, 25–25. [Google Scholar]
- Åkesson, J.; Årzén, K.E.; Gäfvert, M.; Bergdahl, T.; Tummescheit, H. Modeling and optimization with Optimica and JModelica. org—Languages and tools for solving large-scale dynamic optimization problems. Comput. Chem. Eng. 2010, 34, 1737–1749. [Google Scholar] [CrossRef]
- Houska, B.; Ferreau, H.J.; Diehl, M. ACADO toolkit—An open-source framework for automatic control and dynamic optimization. Opt. Control Appl. Meth. 2011, 32, 298–312. [Google Scholar] [CrossRef]
- Ross, I.M. User’s Manual for DIDO: A MATLAB Application Package for Solving Optimal Control Problems; Tomlab Optimization: Vasteras, Sweden, 2004; p. 65. [Google Scholar]
- Patterson, M.A.; Rao, A.V. GPOPS-II: A MATLAB software for solving multiple-phase optimal control problems using hp-adaptive Gaussian quadrature collocation methods and sparse nonlinear programming. ACM Trans. Math. Softw. 2014, 41. [Google Scholar] [CrossRef]
- Rutquist, P.E.; Edvall, M.M. Propt-Matlab Optimal Control Software; Tomlab Optimization Inc.: Pullman, WA, USA, 2010; p. 260. [Google Scholar]
- Becerra, V.M. Solving complex optimal control problems at no cost with PSOPT. In Proceedings of the 2010 IEEE International Symposium on Computer-Aided Control System Design (CACSD), Yokohama, Japan, 8–10 September 2010; pp. 1391–1396. [Google Scholar]
- Bisschop, J. AIMMS—Optimization Modeling; Paragon Decision Technology: Kirkland, WA, USA, 2006. [Google Scholar]
- Grant, M.; Boyd, S. Graph implementations for nonsmooth convex programs. In Recent Advances in Learning and Control; Blondel, V., Boyd, S., Kimura, H., Eds.; Lecture Notes in Control and Information Sciences; Springer: Berlin, Germany, 2008; pp. 95–110. [Google Scholar]
- Andersen, M.; Dahl, J.; Liu, Z.; Vandenberghe, L. Interior-point methods for large-scale cone programming. Optim. Mach. Learn. 2011, 5583, 55–83. [Google Scholar]
- Löfberg, J. YALMIP: A Toolbox for Modeling and Optimization in MATLAB. In Proceedings of the CACSD Conference, Taipei, Taiwan, 2–4 September 2004. [Google Scholar]
- Mitchell, S.; Consulting, S.M.; Dunning, I. PuLP: A Linear Programming Toolkit for Python; The University of Auckland: Auckland, New Zealand, 2011. [Google Scholar]
- Biegler, L.T. An overview of simultaneous strategies for dynamic optimization. Chem. Eng. Proc. Proc. Intensif. 2007, 46, 1043–1053. [Google Scholar] [CrossRef]
- Hedengren, J.D.; Shishavan, R.A.; Powell, K.M.; Edgar, T.F. Nonlinear modeling, estimation and predictive control in APMonitor. Comput. Chem. Eng. 2014, 70, 133–148. [Google Scholar] [CrossRef]
- De Souza, G.; Odloak, D.; Zanin, A.C. Real time optimization (RTO) with model predictive control (MPC). Comput. Chem. Eng. 2010, 34, 1999–2006. [Google Scholar] [CrossRef]
- Safdarnejad, S.M.; Hedengren, J.D.; Lewis, N.R.; Haseltine, E.L. Initialization strategies for optimization of dynamic systems. Comput. Chem. Eng. 2015, 78, 39–50. [Google Scholar] [CrossRef]
- Waechter, A.; Biegler, L.T. On the Implementation of a Primal-Dual Interior Point Filter Line Search Algorithm for Large-Scale Nonlinear Programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Hedengren, J.; Mojica, J.; Cole, W.; Edgar, T. APOPT: MINLP Solver for Differential and Algebraic Systems with Benchmark Testing. In Proceedings of the INFORMS National Meeting, Phoenix, AZ, USA, 14–17 October 2012. [Google Scholar]
- Gill, P.E.; Murray, W.; Saunders, M.A. SNOPT: An SQP algorithm for large-scale constrained optimization. SIAM Rev. 2005, 47, 99–131. [Google Scholar] [CrossRef]
- Hedengren, J.D.; Eaton, A.N. Overview of Estimation Methods for Industrial Dynamic Systems. Optim. Eng. 2017, 18, 155–178. [Google Scholar] [CrossRef]
- Lewis, N.R.; Hedengren, J.D.; Haseltine, E.L. Hybrid Dynamic Optimization Methods for Systems Biology with Efficient Sensitivities. Processes 2015, 3, 701–729. [Google Scholar] [CrossRef]
- Powell, K.M.; Eaton, A.N.; Hedengren, J.D.; Edgar, T.F. A Continuous Formulation for Logical Decisions in Differential Algebraic Systems using Mathematical Programs with Complementarity Constraints. Processes 2016, 4, 7. [Google Scholar] [CrossRef]
- Beal, L.D.; Petersen, D.; Grimsman, D.; Warnick, S.; Hedengren, J.D. Integrated scheduling and control in discrete-time with dynamic parameters and constraints. Comput. Chem. Eng. 2018, 115, 361–376. [Google Scholar] [CrossRef]
- Eaton, A.N.; Beal, L.D.; Thorpe, S.D.; Hubbell, C.B.; Hedengren, J.D.; Nybø, R.; Aghito, M. Real time model identification using multi-fidelity models in managed pressure drilling. Comput. Chem. Eng. 2017, 97, 76–84. [Google Scholar] [CrossRef]
- Park, J.; Webber, T.; Shishavan, R.A.; Hedengren, J.D.; others. Improved Bottomhole Pressure Control with Wired Drillpipe and Physics-Based Models. In Proceedings of the SPE/IADC Drilling Conference and Exhibition, Society of Petroleum Engineers, The Hague, The Netherlands, 14–16 March 2017. [Google Scholar]
- Mojica, J.L.; Petersen, D.; Hansen, B.; Powell, K.M.; Hedengren, J.D. Optimal combined long-term facility design and short-term operational strategy for CHP capacity investments. Energy 2017, 118, 97–115. [Google Scholar] [CrossRef]
- Safdarnejad, S.M.; Hedengren, J.D.; Baxter, L.L. Dynamic optimization of a hybrid system of energy-storing cryogenic carbon capture and a baseline power generation unit. Appl. Energy 2016, 172, 66–79. [Google Scholar] [CrossRef]
- Safdarnejad, S.M.; Gallacher, J.R.; Hedengren, J.D. Dynamic parameter estimation and optimization for batch distillation. Comput. Chem. Eng. 2016, 86, 18–32. [Google Scholar] [CrossRef]
- Safdarnejad, S.M.; Hedengren, J.D.; Baxter, L.L. Plant-level dynamic optimization of Cryogenic Carbon Capture with conventional and renewable power sources. Appl. Energy 2015, 149, 354–366. [Google Scholar] [CrossRef]
- DeFigueiredo, B.; Zimmerman, T.; Russell, B.; Howell, L.L. Regional Stiffness Reduction Using Lamina Emergent Torsional Joints for Flexible Printed Circuit Board Design. J. Electron. Packag. 2018. [Google Scholar] [CrossRef]
- Valderrama, F.; Ruiz, F. An optimal control approach to steam distillation of essential oils from aromatic plants. Comput. Chem. Eng. 2018, 117, 25–31. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).