Modeling the Dynamics of Human Liver Failure Post Liver Resection
Abstract
1. Introduction
2. Materials and Methods
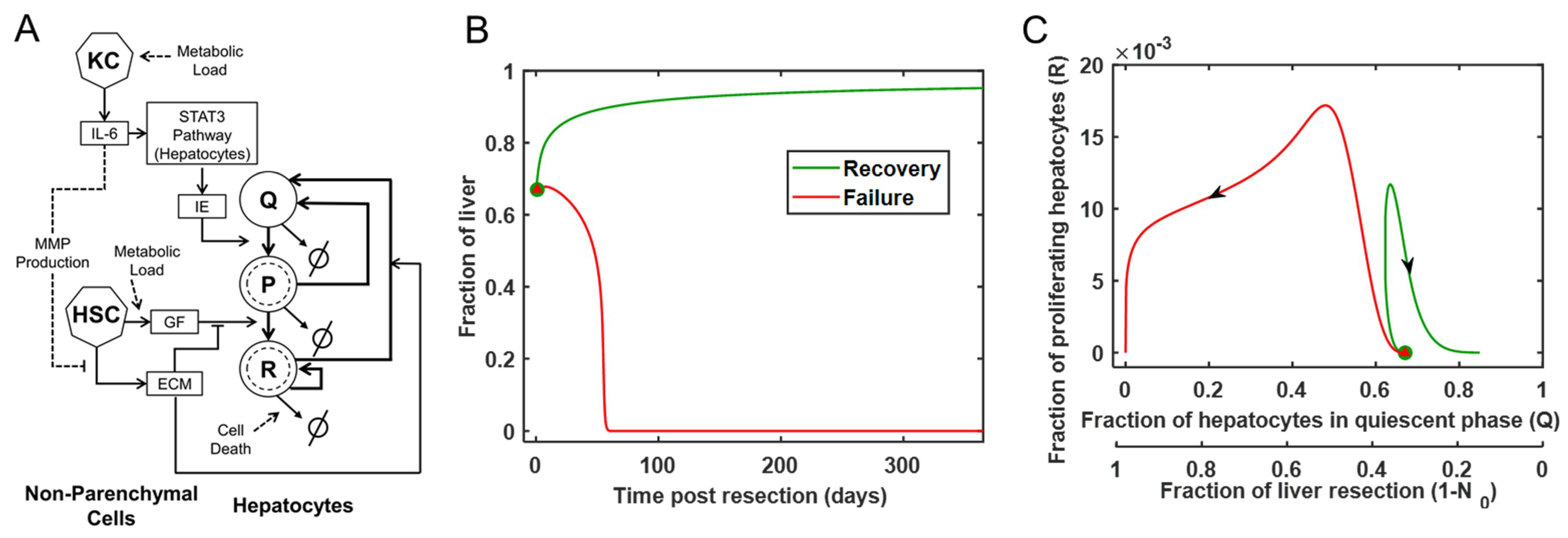
2.1. Mathematical Model
2.2. Defining Virtual Patient Cohort
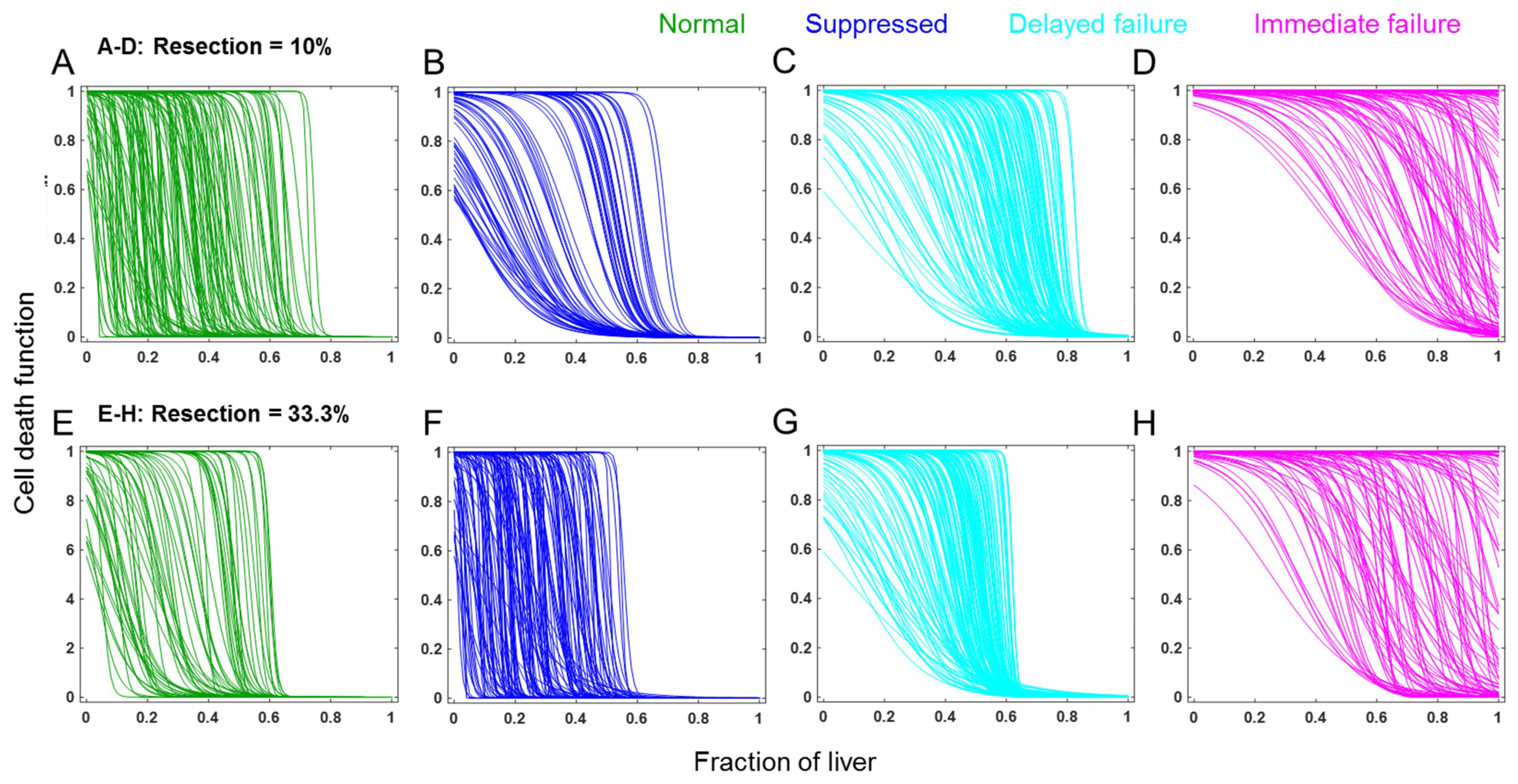
2.3 Identification of Distinct Response Modes
2.4 Parameter Optimization
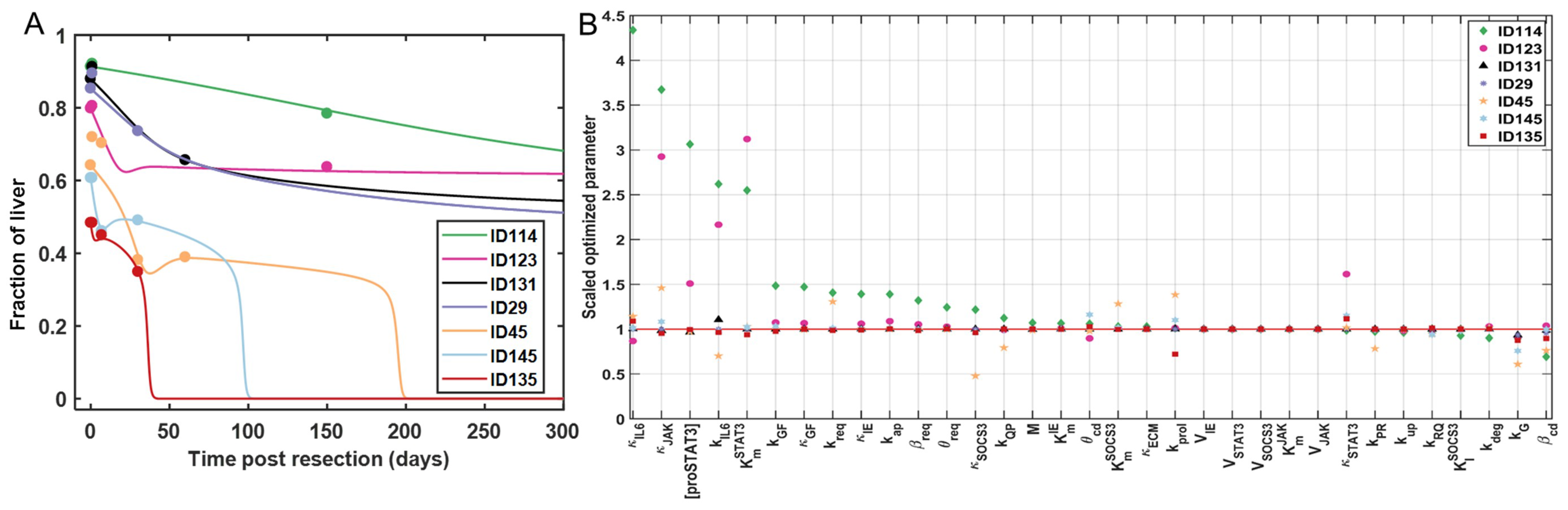
2.5 Clinical Dataset
2.6 Model Repeatability and Reproducibility
3. Results
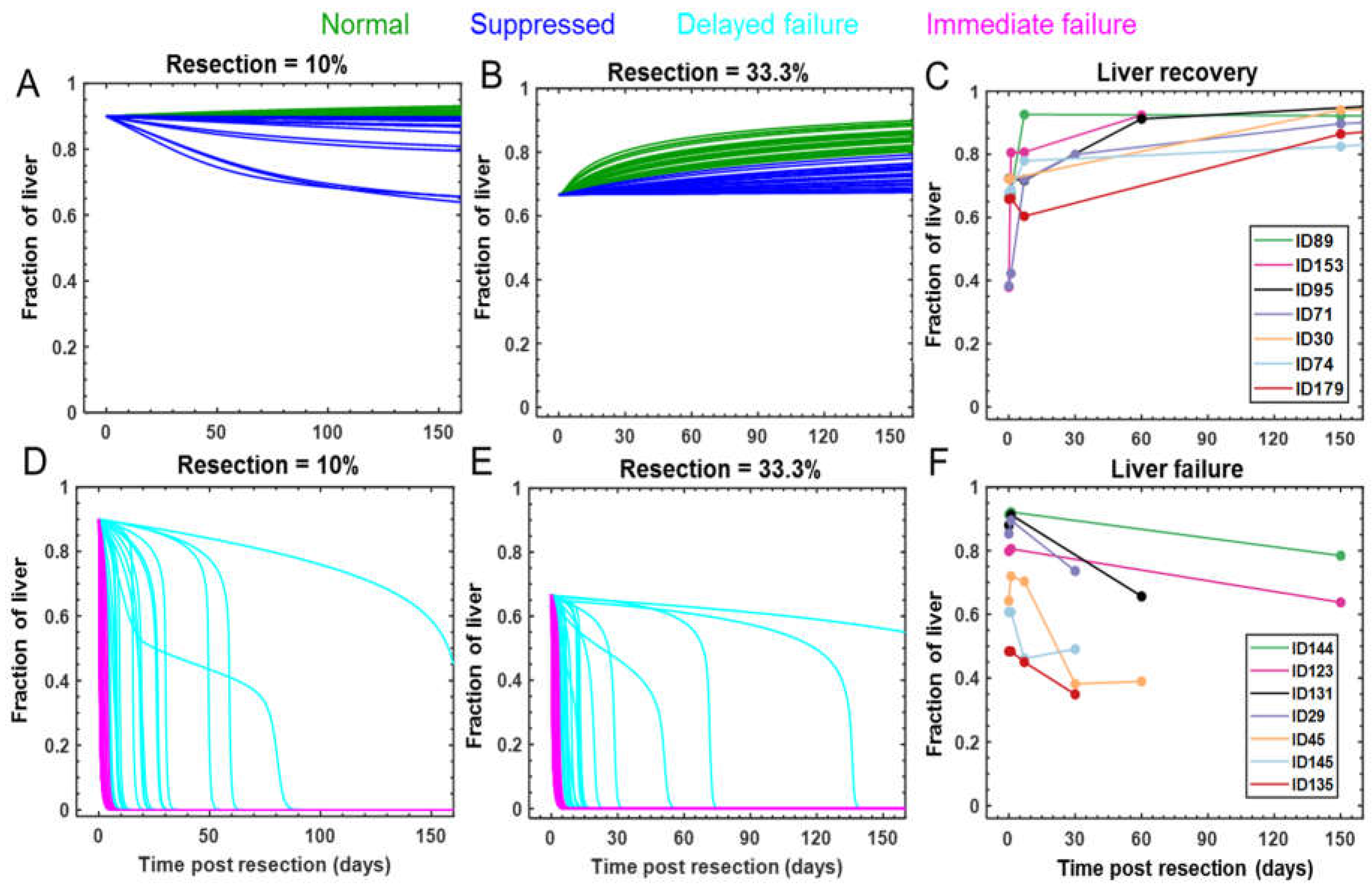
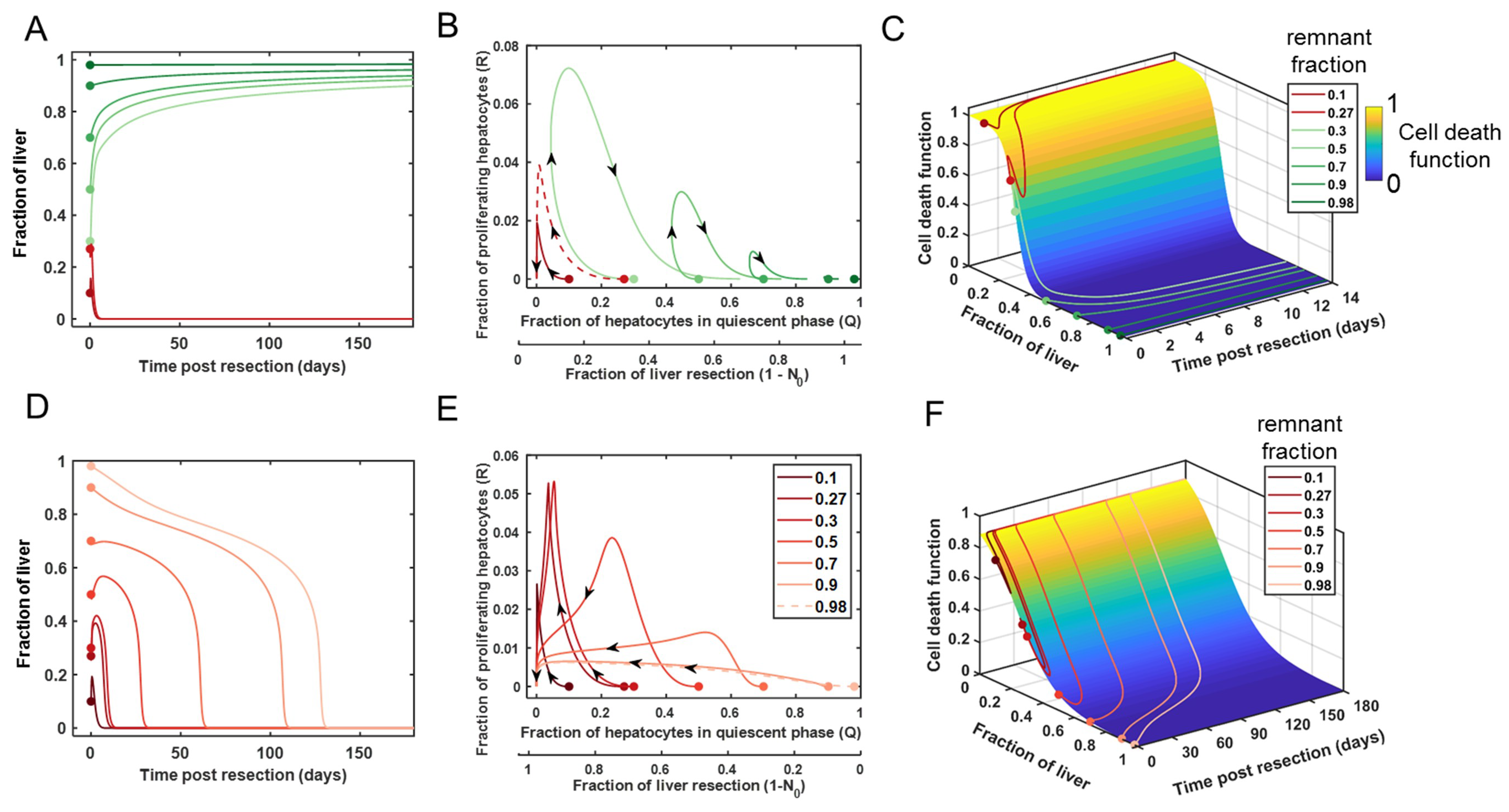
3.1. Modeling the Range of Response to Liver Resection in a Virtual Patient Cohort
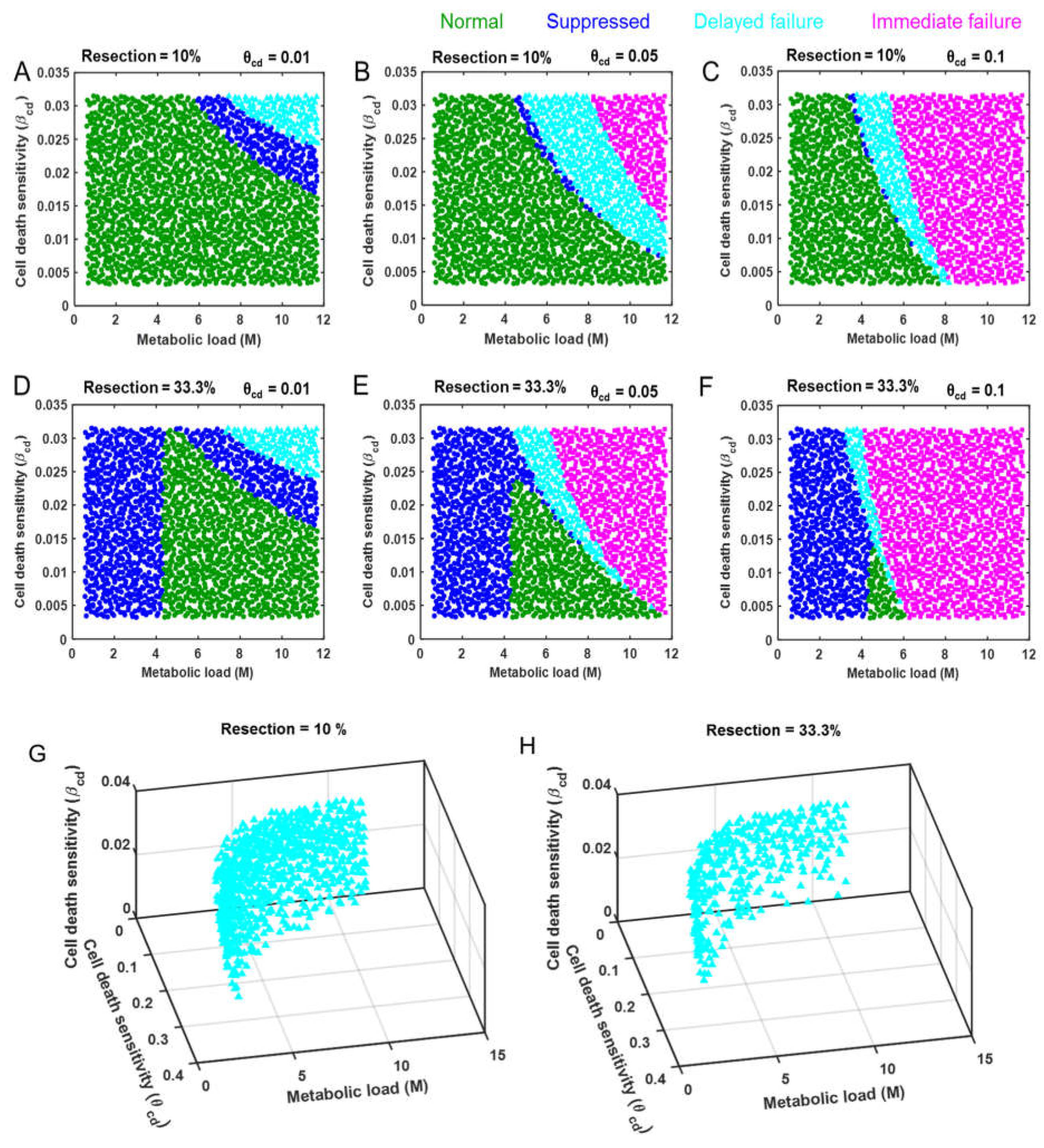
3.2. Cell Death as a Function of the Controlling Parameters in Different Classes of Patients
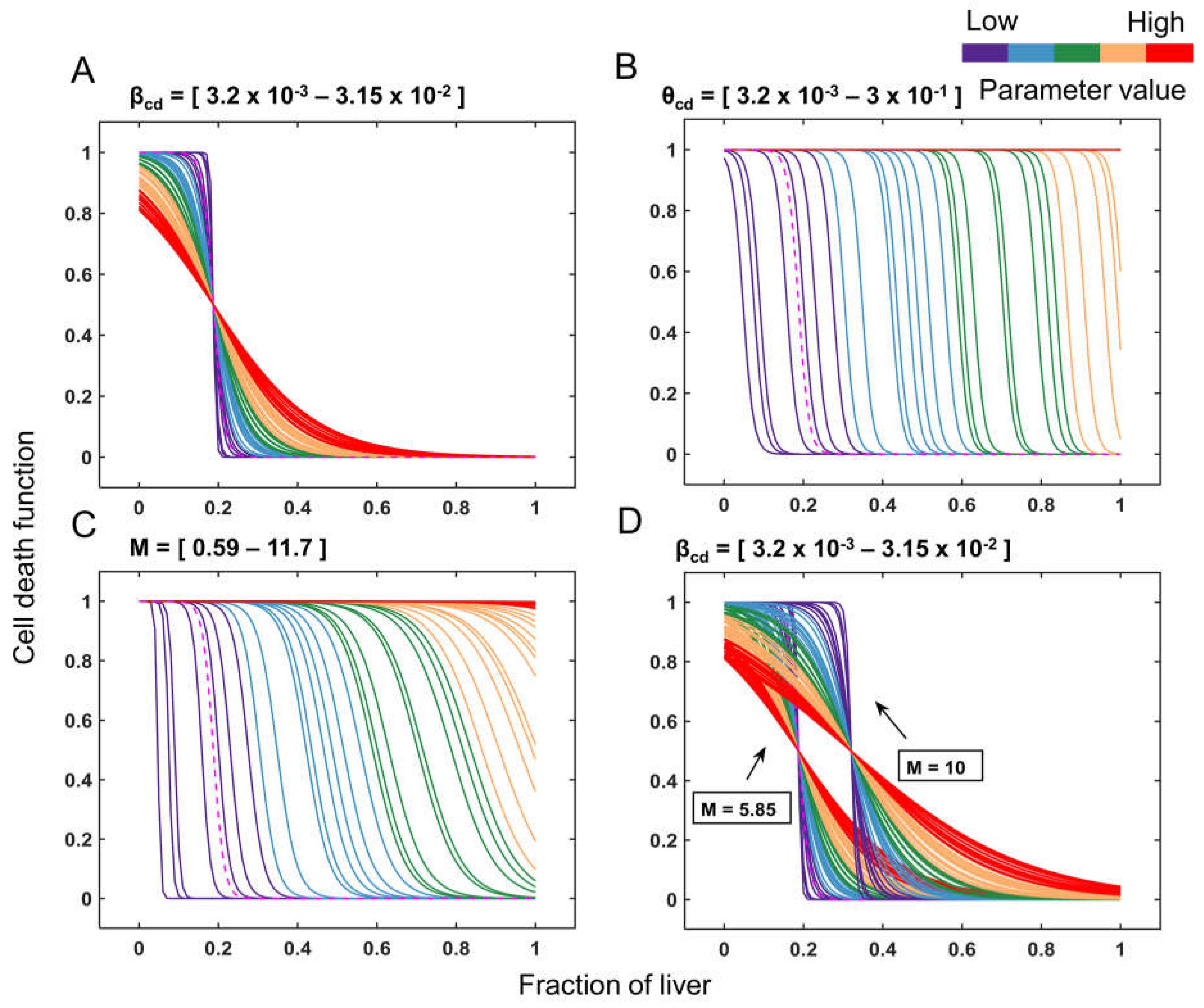
3.3. Comparison of Cell Death between Recovery versus Failure Scenarios for Varying Level of Resection
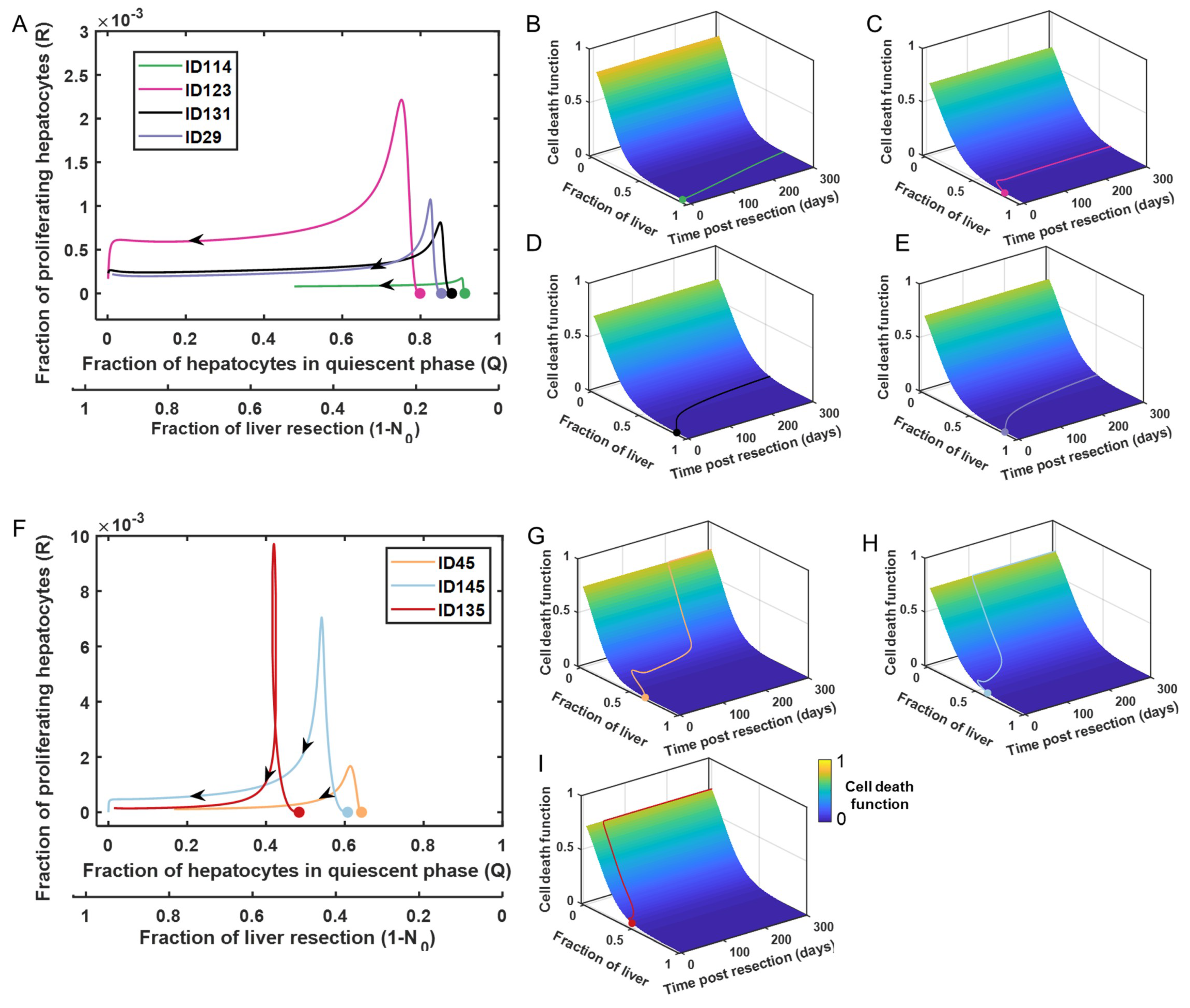
3.4. Tuning the Model for Different Liver Failure Patients
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Parameter | Range | Description |
|---|---|---|
| M | 1.00411–100.41126 | Mechanical stress or increased nutrient and detoxification demand |
| kIL6 | 0.15–15 | Rate of production of IL6 from non-parenchymal cells |
| κIL6 | 0.09–9 | Rate of IL6 degradation |
| VJAK | 2000–200,000 | Maximum rate of activation of JAK |
| 1000–100,000 | Concentration of JAK, when the rate of activation of JAK is half of the maximum rate | |
| κJAK | 0.04–4 | Rate of degradation of JAK |
| [proSTAT3] | 0.01–20 | Relative concentration of monomeric STAT3 |
| VST3 | 75–7500 | Maximum rate of STAT3 phosphorylation |
| 0.04–40 | Michaelis-Menten concentration of proSTAT3 | |
| κST3 | 0.05–1 | Rate of dephosphorylation of proSTAT3 |
| VSOCS3 | 14,000–34,000 | Maximum rate of SOCS3 activation |
| 0.0004–0.001 | Concentration of SOCS3, when it’s rate of activation is half the maximum rate | |
| κSOCS3 | 0.1–0.7 | Rate of degradation of SOCS3 |
| 0.005–0.025 | SOCS3 inhibition constant on STAT3 | |
| VIE | 150–350 | Maximum rate of activation of IE gene |
| 15–21 | Concentration of IE gene, when it’s rate of activation is half the maximum rate | |
| κIE | 3–7 | Rate of degradation of IE gene |
| kdeg | 5–9 | Rate of degradation of ECM by MMPs |
| κECM | 30–36 | Rate of degradation of ECM |
| kGF | 0.05–0.2 | Rate of production of growth factor from non-parenchymal cells |
| κGF | 0.1–0.35 | Rate of degradation of growth factor |
| kup | 0.04–0.08 | Rate of binding of growth factor to ECM |
| kQP | 0.005–0.009 | Rate of hepatocytes transition from quiescence to primed state |
| kPR | 0.003–0.006 | Rate of hepatocytes transition from primed to replicating state |
| kRQ | 0.04–0.065 | Rate of hepatocytes transition from replicating to quiescence state |
| kprol | 0.01–0.03 | Rate of proliferation of hepatocytes |
| kreq | 0.05–0.15 | Rate of requiescence of primed hepatocytes |
| θreq | 6–10 | Requiescence parameter in the sigmoidal function (σreq) defining the threshold of requiescence |
| βreq | 2–4 | Requiescence parameter in the sigmoidal function (σreq) defining the threshold of requiescence |
| kcd | 0.05–0.15 | Cell death rate of damaged hepatocytes |
| θcd | 0.00110–0.11050 | Cell death sensitivity parameter of the sigmoidal function (σcd) |
| βcd | 0.00260–0.26046 | Cell death sensitivity parameter of the sigmoidal function (σcd) defining the cell death threshold |
| kG | 0.0003–0.0007 | Rate of growth of relative cell mass |
| Parameter | Nominal Value | Patient Identification Number | ||||||
|---|---|---|---|---|---|---|---|---|
| ID114 | ID123 | ID131 | ID29 | ID45 | ID145 | ID135 | ||
| M | 10.041128 | 10.7480 | 10.0211 | 10.0173 | 10.0396 | 9.9112 | 10.0552 | 10.0425 |
| kIL6 | 1.5 | 3.9280 | 3.2484 | 1.6583 | 1.5000 | 1.0530 | 1.4620 | 1.4464 |
| κIL6 | 0.9 | 3.9040 | 0.7807 | 0.9043 | 0.9000 | 1.0276 | 0.9117 | 0.9800 |
| VJAK | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 | 20,000 |
| 10,000 | 10,000 | 10,000 | 10,000 | 10,000 | 10,000 | 10,000 | 10,000 | |
| κJAK | 0.4 | 1.4695 | 1.1701 | 0.3941 | 0.4000 | 0.5844 | 0.4330 | 0.3804 |
| [proSTAT3] | 2 | 6.1276 | 3.0179 | 1.9367 | 1.9736 | 1.9422 | 1.9866 | 1.9897 |
| VST3 | 750 | 750.0337 | 750.0022 | 750.0003 | 750.0001 | 750.0006 | 750.0000 | 749.9999 |
| 0.4 | 1.0194 | 1.2485 | 0.4001 | 0.4000 | 0.4115 | 0.4096 | 0.3752 | |
| κST3 | 0.1 | 0.0987 | 0.1614 | 0.1000 | 0.1000 | 0.1017 | 0.1152 | 0.1116 |
| VSOCS3 | 24000 | 24000 | 24000 | 24000 | 24000 | 24000 | 24000 | 24000 |
| 0.0007 | 0.0007 | 0.0007 | 0.0007 | 0.0007 | 0.0009 | 0.0007 | 0.0007 | |
| κSOCS3 | 0.4 | 0.4871 | 0.3970 | 0.4000 | 0.4000 | 0.1913 | 0.3855 | 0.3847 |
| 0.015 | 0.0139 | 0.0149 | 0.0150 | 0.0150 | 0.0150 | 0.0147 | 0.0150 | |
| VIE | 250 | 250.12 | 250.01 | 250.00 | 249.99 | 249.99 | 249.99 | 249.99 |
| 18 | 19.1762 | 18.1366 | 18.0041 | 18.0055 | 18.0474 | 18.0014 | 17.9778 | |
| κIE | 5 | 6.9573 | 5.3009 | 5.0022 | 4.9925 | 4.9951 | 5.0061 | 4.9493 |
| kdeg | 7 | 6.3119 | 7.2057 | 7.0017 | 6.9977 | 7.1109 | 6.9982 | 7.0171 |
| κECM | 33 | 33.9672 | 33.0645 | 32.9999 | 33.0004 | 32.9871 | 33.0004 | 32.9939 |
| kGF | 0.113 | 0.1677 | 0.1214 | 0.1130 | 0.1130 | 0.1128 | 0.1166 | 0.1103 |
| κGF | 0.23 | 0.3384 | 0.2453 | 0.2300 | 0.2300 | 0.2291 | 0.2298 | 0.2302 |
| kup | 0.06 | 0.0577 | 0.0590 | 0.0600 | 0.0600 | 0.0598 | 0.0600 | 0.0600 |
| kQP | 0.007 | 0.0079 | 0.0069 | 0.0070 | 0.0070 | 0.0056 | 0.0070 | 0.0070 |
| kPR | 0.0044 | 0.0043 | 0.0044 | 0.0044 | 0.0044 | 0.0034 | 0.0044 | 0.0044 |
| kRQ | 0.054 | 0.0517 | 0.0536 | 0.0540 | 0.0540 | 0.0509 | 0.0507 | 0.0547 |
| kprol | 0.02 | 0.0202 | 0.0202 | 0.0200 | 0.0200 | 0.0277 | 0.0220 | 0.0144 |
| kreq | 0.1 | 0.1407 | 0.0999 | 0.1000 | 0.1000 | 0.1308 | 0.1013 | 0.0987 |
| θreq | 8 | 9.9514 | 8.2151 | 7.9998 | 7.9994 | 7.9845 | 8.0009 | 8.0182 |
| βreq | 3 | 3.9615 | 3.1587 | 3.0021 | 3.0000 | 2.9657 | 2.9990 | 2.9563 |
| kcd | 0.1 | 0.1390 | 0.1089 | 0.1000 | 0.1000 | 0.1001 | 0.1006 | 0.1003 |
| θcd | 0.011050 | 0.0117 | 0.0099 | 0.0111 | 0.0111 | 0.0108 | 0.0128 | 0.0114 |
| βcd | 0.026046 | 0.0180 | 0.0270 | 0.0257 | 0.0249 | 0.0198 | 0.0260 | 0.0234 |
| kG | 0.000657 | 0.000588 | 0.000601 | 0.000613 | 0.000614 | 0.000400 | 0.000497 | 0.000574 |
References
- Fausto, N.; Campbell, J.S. The role of hepatocytes and oval cells in liver regeneration and repopulation. Mech. Dev. 2003, 120, 117–130. [Google Scholar] [CrossRef]
- Taub, R. Liver regeneration: From myth to mechanism. Nat. Rev. Mol. Cell Biol. 2004, 5, 836–847. [Google Scholar] [CrossRef] [PubMed]
- Michalopoulos, G.K. Hepatostat: Liver regeneration and normal liver tissue maintenance. Hepatology 2017, 65, 1384–1392. [Google Scholar] [CrossRef] [PubMed]
- Lorenzo, C.S.F.; Limm, W.M.L.; Lurie, F.; Wong, L.L. Factors affecting outcome in liver resection. HPB 2005, 7, 226–230. [Google Scholar] [CrossRef] [PubMed]
- Dimick, J.B. Hepatic Resection in the United States. Arch. Surg. 2003, 138, 185. [Google Scholar] [CrossRef] [PubMed]
- Guglielmi, A.; Ruzzenente, A.; Conci, S.; Valdegamberi, A.; Iacono, C. How much remnant is enough in liver resection? Dig. Surg. 2012, 29, 6–17. [Google Scholar] [CrossRef] [PubMed]
- Garcea, G.; Maddern, G.J. Liver failure after major hepatic resection. J. Hepatobiliary Pancreat. Surg. 2009, 16, 145–155. [Google Scholar] [CrossRef] [PubMed]
- Mann, D.V.; Lam, W.W.M.; Hjelm, N.M.; So, N.M.C.; Yeung, D.K.W.; Metreweli, C.; Lau, W.Y. Human liver regeneration: Hepatic energy economy is less efficient when the organ is diseased. Hepatology 2001, 34, 557–565. [Google Scholar] [CrossRef] [PubMed]
- Van Den Broek, M.A.J.; Olde Damink, S.W.M.; Dejong, C.H.C.; Lang, H.; Malagó, M.; Jalan, R.; Saner, F.H. Liver failure after partial hepatic resection: Definition, pathophysiology, risk factors and treatment. Liver Int. 2008, 28, 767–780. [Google Scholar] [CrossRef] [PubMed]
- Cook, D.; Ogunnaike, B.A.; Vadigepalli, R. Systems analysis of non-parenchymal cell modulation of liver repair across multiple regeneration modes. BMC Syst. Biol. 2015, 9, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, K.N.; Ishii, M.; Inoue, Y.; Hirokawa, F.; MacArthur, B.D.; Nakamura, A.; Haeno, H.; Uchiyama, K. Prediction of postoperative liver regeneration from clinical information using a data-led mathematical model. Sci. Rep. 2016, 6, 34214. [Google Scholar] [CrossRef] [PubMed]
- An, G.; Mi, Q.; Dutta-moscato, J.; Vodovotz, Y. Agent-based models in translational systems biology. Syst. Biol. Med. 2009, 1, 159–171. [Google Scholar] [CrossRef] [PubMed]
- An, G.; Mi, Q.; Dutta-moscato, J.; Vodovotz, Y. Mathematical models of the acute inflammatory response. Curr. Opin. Crit. Care 2004, 10, 383–390. [Google Scholar]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Miller, G.M.; Ogunnaike, B.A.; Schwaber, J.S.; Vadigepalli, R. Robust dynamic balance of AP-1 transcription factors in a neuronal gene regulatory network. BMC Syst. Biol. 2010, 4, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Howsmon, D.P.; Hahn, J. Regularization techniques to overcome over-parameterization of complex biochemical reaction networks. IEEE Life Sci. Lett. 2017, 3, 31–34. [Google Scholar] [CrossRef]
- Marongiu, F.; Marongiu, M.; Contini, A.; Serra, M.; Cadoni, E.; Murgia, R.; Laconi, E. Hyperplasia vs hypertrophy in tissue regeneration after extensive liver resection. World J. Gastroenterol. 2017, 23, 1764–1770. [Google Scholar] [CrossRef] [PubMed]
- Le Novère, N.; Hucka, M.; Mi, H.; Moodie, S.; Schreiber, F.; Sorokin, A.; Demir, E.; Wegner, K.; Aladjem, M.I.; Wimalaratne, S.M.; et al. The Systems Biology Graphical Notation. Nat. Biotechnol. 2009, 27, 735–742. [Google Scholar] [CrossRef] [PubMed]
- Strogatz, S.H. Nonlinear Dynamics and Chaos with Applications to Physics, Biology, Chemistry and Engineering, 1st ed.; Westview Press: Boulder, CO, USA, 2000. [Google Scholar]
- Wiggins, S. Introduction to Applied Nonlinear Dynamical Systems and Chaos, 2nd ed.; Springer: Berlin, Germany, 2006; ISBN 0387217495. [Google Scholar]
- Takeda, K.; Togo, S.; Kunihiro, O.; Fujii, Y.; Kurosawa, H.; Tanaka, K.; Endo, I.; Takimoto, A.; Sekido, H.; Hara, M.; et al. Clinicohistological features of liver failure after excessive hepatectomy. Hepatogastroenterology 2002, 49, 354–358. [Google Scholar] [PubMed]
- Nagasue, N.; Yukaya, H.; Ogawa, Y.; Kohno, H.; Nakamura, T. Human liver regeneration after major hepatic resection. A study of normal liver and livers with chronic hepatitis and cirrhosis. Ann. Surg. 1987, 206, 30–39. [Google Scholar] [CrossRef] [PubMed]
- Tanoue, S.; Uto, H.; Kumamoto, R.; Arima, S.; Hashimoto, S.; Nasu, Y.; Takami, Y.; Moriuchi, A.; Sakiyama, T.; Oketani, M.; et al. Liver regeneration after partial hepatectomy in rat is more impaired in a steatotic liver induced by dietary fructose compared to dietary fat. Biochem. Biophys. Res. Commun. 2011, 407, 163–168. [Google Scholar] [CrossRef] [PubMed]
- Meier, M.; Andersen, K.J.; Knudsen, A.R.; Nyengaard, J.R.; Hamilton-Dutoit, S.; Mortensen, F.V. Liver regeneration is dependent on the extent of hepatectomy. J. Surg. Res. 2016, 205, 76–84. [Google Scholar] [CrossRef] [PubMed]
- Van Poll, D.; Parekkadan, B.; Cho, C.H.; Berthiaume, F.; Nahmias, Y.; Tilles, A.W.; Yarmush, M.L. Mesenchymal stem cell-derived molecules directly modulate hepatocellular death and regeneration in vitro and in vivo. Hepatology 2008, 47, 1634–1643. [Google Scholar] [CrossRef] [PubMed]
- Kroemer, G.; Reed, J.C. Mitochondrial control of cell death. Nat. Med. 2000, 6, 513–519. [Google Scholar] [CrossRef] [PubMed]
- Lemasters, J.J.; Nieminen, A.L.; Qian, T.; Trost, L.C.; Elmore, S.P.; Nishimura, Y.; Crowe, R.A.; Cascio, W.E.; Bradham, C.A.; Brenner, D.A.; et al. The mitochondrial permeability transition in cell death: a common mechanism in necrosis, apoptosis and autophagy. Biochim. Biophys. Acta 1998, 1366, 177–196. [Google Scholar] [CrossRef]
- Lafaro, K.; Buettner, S.; Maqsood, H.; Wagner, D.; Bagante, F.; Spolverato, G.; Xu, L.; Kamel, I.; Pawlik, T.M. Defining Post Hepatectomy Liver Insufficiency: Where do We stand? J. Gastrointest. Surg. 2015, 19, 2079–2092. [Google Scholar] [CrossRef] [PubMed]
- Furchtgott, L.A.; Chow, C.C.; Periwal, V. A model of liver regeneration. Biophys. J. 2009, 96, 3926–3935. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Rudnick, D.A. Elucidating the metabolic regulation of liver regeneration. Am. J. Pathol. 2014, 184, 309–321. [Google Scholar] [CrossRef] [PubMed]
- Schenk, A.; Ghallab, A.; Hofmann, U.; Hassan, R.; Schwarz, M.; Schuppert, A.; Schwen, L.O.; Braeuning, A.; Teutonico, D.; Hengstler, J.G.; et al. Physiologically-based modelling in mice suggests an aggravated loss of clearance capacity after toxic liver damage. Sci. Rep. 2017, 7, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Gille, C.; Bölling, C.; Hoppe, A.; Bulik, S.; Hoffmann, S.; Hübner, K.; Karlstädt, A.; Ganeshan, R.; König, M.; Rother, K.; et al. HepatoNet1: A comprehensive metabolic reconstruction of the human hepatocyte for the analysis of liver physiology. Mol. Syst. Biol. 2010, 6. [Google Scholar] [CrossRef] [PubMed]
- Wright, G.; Noiret, L.; Olde Damink, S.W.M.; Jalan, R. Interorgan ammonia metabolism in liver failure: The basis of current and future therapies. Liver Int. 2011, 31, 163–175. [Google Scholar] [CrossRef] [PubMed]
- Cook, D.; Vadigepalli, R. Computational Modeling as an Approach to Study the Cellular and Molecular Regulatory Networks Driving Liver Regeneration. In Liver Regeneration Basic Mechanisms, Relevant Models and Clinical Applications; Academic Press: Boston, MA, USA, 2015; pp. 185–198. ISBN 9780124201286. [Google Scholar]
- Michalopoulos, G.K. Liver regeneration after partial hepatectomy: Critical analysis of mechanistic dilemmas. Am. J. Pathol. 2010, 176, 2–13. [Google Scholar] [CrossRef] [PubMed]
- Stutchfiel, B.M.; Forbes, S.J.; Wigmore, S.J. Prospects for Stem Cell Transplantation in the Treatment of Hepatic Disease. Liver Transplant. 2010, 16, 827–836. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verma, B.K.; Subramaniam, P.; Vadigepalli, R. Modeling the Dynamics of Human Liver Failure Post Liver Resection. Processes 2018, 6, 115. https://doi.org/10.3390/pr6080115
Verma BK, Subramaniam P, Vadigepalli R. Modeling the Dynamics of Human Liver Failure Post Liver Resection. Processes. 2018; 6(8):115. https://doi.org/10.3390/pr6080115
Chicago/Turabian StyleVerma, Babita K., Pushpavanam Subramaniam, and Rajanikanth Vadigepalli. 2018. "Modeling the Dynamics of Human Liver Failure Post Liver Resection" Processes 6, no. 8: 115. https://doi.org/10.3390/pr6080115
APA StyleVerma, B. K., Subramaniam, P., & Vadigepalli, R. (2018). Modeling the Dynamics of Human Liver Failure Post Liver Resection. Processes, 6(8), 115. https://doi.org/10.3390/pr6080115






