Modeling and Optimal Design of Absorbent Enhanced Ammonia Synthesis
Abstract
1. Introduction
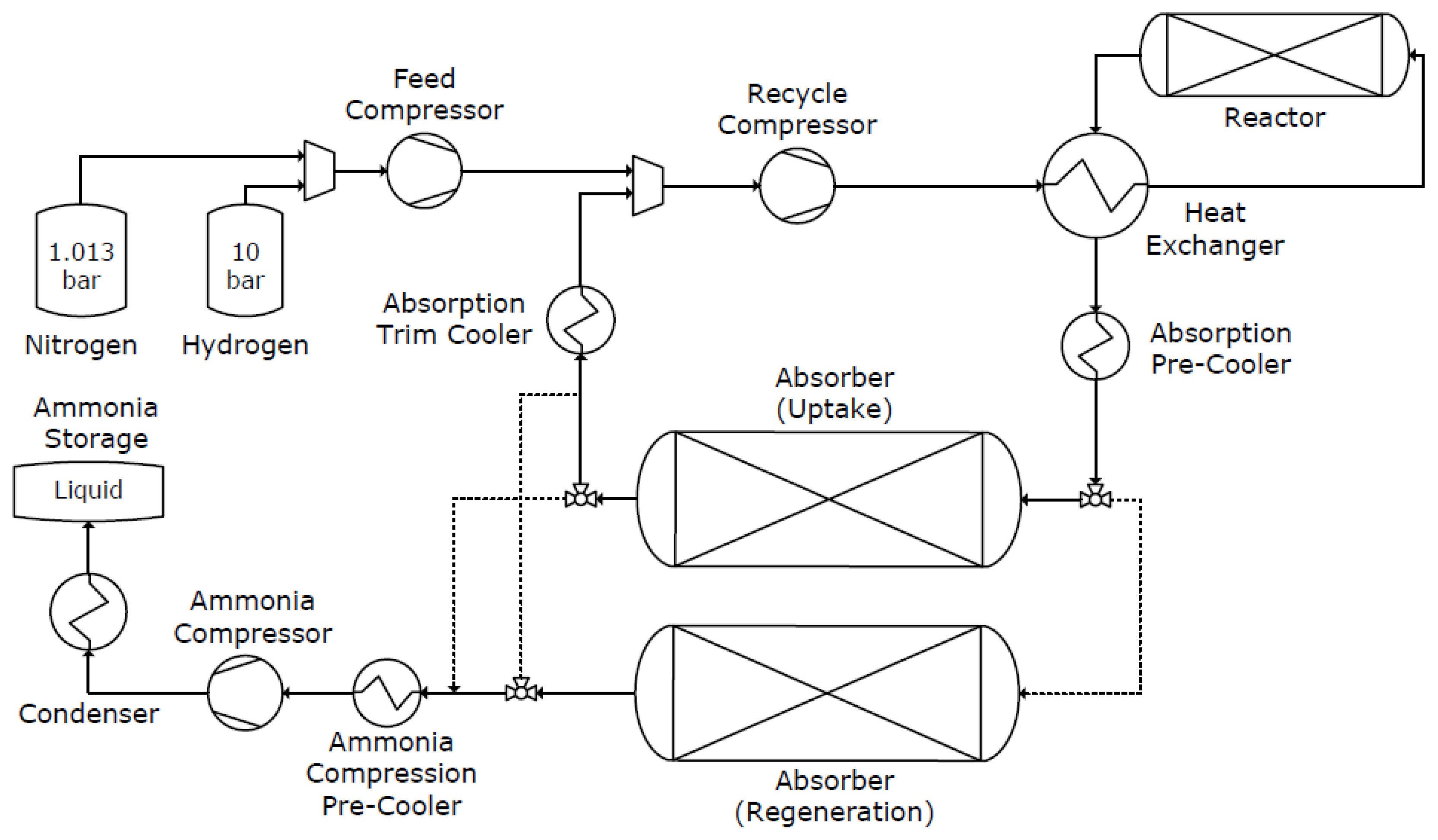
2. Process Description
3. Mathematical Model
3.1. Reactor
3.2. Absorber
3.3. Compressor
3.4. Heat Exchanger
3.5. Cooler with External Heat Removal
4. Design Optimization Formulation
4.1. Objective Function
4.1.1. Capital Costs
4.1.2. Operating Costs
4.2. Decision Variables
4.3. Constraints
4.4. Problem Summary and Computation
5. Results
5.1. Analysis of Optimal Design
5.2. Analysis of Energy Consumption
6. Discussion
Supplementary Materials
Supplementary File 1Author Contributions
Funding
Conflicts of Interest
References
- FAO. World Fertilizer Trends and Outlook to 2018; Annual Report 14; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2015; ISBN 978-92-5-108692-6. [Google Scholar]
- Smil, V. Enriching the Earth: Fritz Haber, Carl Bosch, and the Transformation of World Food Production; MIT Press: Massachusetts, MA, USA, 2004. [Google Scholar]
- Swaminathan, B.; Sukalac, K. Technology transfer and mitigation of climate change: The fertilizer industry perspective. In Proceedings of the IPCC Expert Meeting on Industrial Technology Development, Transfer and Diffusion, Tokyo, Japan, 21–23 September 2004. [Google Scholar]
- Rees, N.V.; Compton, R.G. Carbon-free energy: A review of ammonia-and hydrazine-based electrochemical fuel cells. Energy Environ. Sci. 2011, 4, 1255–1260. [Google Scholar] [CrossRef]
- Wang, G.; Mitsos, A.; Marquardt, W. Conceptual design of ammonia-based energy storage system: System design and time-invariant performance. AIChE J. 2017, 63, 1620–1637. [Google Scholar] [CrossRef]
- Reese, M.; Marquart, C.; Malmali, M.; Wagner, K.; Buchanan, E.; McCormick, A.; Cussler, E.L. Performance of a small-scale Haber process. Ind. Eng. Chem. Res. 2016, 55, 3742–3750. [Google Scholar] [CrossRef]
- Morgan, E.; Manwell, J.; McGowan, J. Wind-powered ammonia fuel production for remote islands: A case study. Renew. Energy 2014, 72, 51–61. [Google Scholar] [CrossRef]
- Morgan, E.R.; Manwell, J.F.; McGowan, J.G. Sustainable ammonia production from US offshore wind farms: A techno-economic review. ACS Sustain. Chem. Eng. 2017, 5, 9554–9567. [Google Scholar] [CrossRef]
- Bañares-Alcántara, R.; Dericks, G.; Fiaschetti, M.; Grünewald, P.; Lopez, J.M.; Tsang, E.; Yang, A.; Ye, L.; Zhao, S. Analysis of Islanded Ammonia-Based Energy Storage Systems; University of Oxford: Oxford, UK, 2015. [Google Scholar]
- Allman, A.; Daoutidis, P.; Tiffany, D.; Kelley, S. A framework for ammonia supply chain optimization incorporating conventional and renewable generation. AIChE J. 2017, 63, 4390–4402. [Google Scholar] [CrossRef]
- Wagner, K.; Malmali, M.; Smith, C.; McCormick, A.; Cussler, E.; Zhu, M.; Seaton, N.C. Column absorption for reproducible cyclic separation in small scale ammonia synthesis. AIChE J. 2017, 63, 3058–3068. [Google Scholar] [CrossRef]
- Malmali, M.; Le, G.; Hendrickson, J.; Prince, J.; McCormick, A.V.; Cussler, E.L. Better Absorbents for Ammonia Separation. ACS Sustain. Chem. Eng. 2018, 6, 6536–6546. [Google Scholar] [CrossRef]
- Malmali, M.; Wei, Y.; McCormick, A.; Cussler, E.L. Ammonia synthesis at reduced pressure via reactive separation. Ind. Eng. Chem. Res. 2016, 55, 8922–8932. [Google Scholar] [CrossRef]
- gPROMS ModelBuilder, version 5.1.1; Software for Advanced Process Modelling Platform; Process Systems Enterprise: London, UK, 2018.
- Multiflash, version 6.1; Software for PVT Modelling and Flow Assurance; KBC: Surrey, UK, 2017.
- Huber, M. (Ed.) NIST Thermophysical Properties of Hydrocarbon Mixtures Database (SUPERTRAPP); version 3.2; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2007.
- Nielsen, A.; Kjaer, J.; Hansen, B. Rate equation and mechanism of ammonia synthesis at industrial conditions. J. Catal. 1964, 3, 68–79. [Google Scholar] [CrossRef]
- Liu, H. Ammonia Synthesis Catalysts: Innovation and Practice, 1st ed.; World Scientific: Singapore; Chemical Industry Press: Beijing, China, 2013. [Google Scholar]
- Dyson, D.; Simon, J. Kinetic expression with diffusion correction for ammonia synthesis on industrial catalyst. Ind. Eng. Chem. Fundam. 1968, 7, 605–610. [Google Scholar] [CrossRef]
- Wakao, N.; Funazkri, T. Effect of fluid dispersion coefficients on particle-to-fluid mass transfer coefficients in packed beds: Correlation of Sherwood numbers. Chem. Eng. Sci. 1978, 33, 1375–1384. [Google Scholar] [CrossRef]
- Specchia, V.; Baldi, G.; Sicardi, S. Heat transfer in packed bed reactors with one phase flow. Chem. Eng. Commun. 1980, 4, 361–380. [Google Scholar] [CrossRef]
- Shafeeyan, M.S.; Daud, W.M.A.W.; Shamiri, A. A review of mathematical modeling of fixed-bed columns for carbon dioxide adsorption. Chem. Eng. Res. Des. 2014, 92, 961–988. [Google Scholar] [CrossRef]
- Smith, C.; Malmali, M.M.; Liu, C.Y.; McCormick, A.; Cussler, E.L. Rates of Ammonia Absorption and Desorption in Calcium Chloride. ACS Sustain. Chem. 2018. submitted. [Google Scholar]
- Mofidi, S.A.H.; Udell, K.S. Study of heat and mass transfer in mgcl2/nh3 thermochemical batteries. J. Energy Resour. Technol. 2017, 139, 032005. [Google Scholar] [CrossRef]
- Sørensen, R.Z.; Hummelshøj, J.S.; Klerke, A.; Reves, J.B.; Vegge, T.; Nørskov, J.K.; Christensen, C.H. Indirect, reversible high-density hydrogen storage in compact metal ammine salts. J. Am. Chem. Soc. 2008, 130, 8660–8668. [Google Scholar] [CrossRef] [PubMed]
- Jinasena, A.; Lie, B.; Glemmestad, B. Dynamic Model of an Ammonia Synthesis Reactor Based on Open Information. In Proceedings of the 9th EUROSIM Congress on Modelling and Simulation, Oulu, Finland, 12–16 September 2016; pp. 943–948. [Google Scholar]
- Woods, D.R. Rules of Thumb in Engineering Practice, 1st ed.; Wiley-VCH: Weinheim, Germany, 2007. [Google Scholar]
- Chemical Engineering. Chemical Engineering Economic Indicators; Technical Report for Chemical Engineering; Chemical Engineering: Rockville, MD, USA, 2016. [Google Scholar]
- Committee of Stainless Steel Producers. Stainless Steel in Ammonia Production; Technical Report; American Iron and Steel Institute: Washington, DC, USA, 1978. [Google Scholar]
- Indicative Chemical Prices A-Z; 2006 Price for Magnesium Chloride; Independent Chemical Information Service: Sutton, UK, 2008.
- 717177 ALDRICH Silica Gel; 2018 Price for Technical Grade, Pore Size 60 A, 70-230 mesh, 63-200 μm Silica Gel; Millapore Sigma: Darmstadt, Germany, 2018.
- Towler, G.; Sinnott, R.K. Chemical Engineering Design: Principles, Practice and Economics of Plant and Process Design, 2nd ed.; Elsevier: New York, NY, USA, 2012. [Google Scholar]
- Ilas, A.; Ralon, P.; Rodriguez, A.; Taylor, M. Renewable Power Generation Costs in 2017; International Renewable Energy Agency: Masdar City, UAE, 2018. [Google Scholar]
- Lee, D.; Hochgreb, S. Hydrogen autoignition at pressures above the second explosion limit (0.6–4.0 MPa). Intern. J. Chem. Kinet. 1998, 30, 385–406. [Google Scholar] [CrossRef]
- Tiffany, D.; Reese, M.; Marquart, C. Economic Evaluation of Deploying Small to Moderate Scale Ammonia Production Plants in Minnesota Using Wind and Grid-Based Electrical Energy Sources; Technical Report; Minnesota Corn Research and Promotion Council: Shakopee, MN, USA, 2015. [Google Scholar]
| Parameter | Symbol | Specification |
|---|---|---|
| Bed Void Fraction | 0.4 | |
| Catalyst Density, kg/m | 3000 | |
| Catalyst Particle Diameter, m | 2 × 10 |
| Parameter | Value |
|---|---|
| , mol/(m s atm) | 1.096 × 10 |
| , J/mol | 46,737 |
| , atm | 2.94 × 10 |
| , J/mol | 100,628 |
| 1.564 | |
| 0.64 | |
| −2.691122 | |
| , 1/K | −5.519265 × 10 |
| , 1/K | 1.848863 × 10 |
| , K | 2001.6 |
| 2.6899 |
| Parameter | |||||
|---|---|---|---|---|---|
| Value | 0.03582 | 8.366 | 35.94 | 7.705 | 36.11 |
| Parameter | Symbol | Specification |
|---|---|---|
| Bed Void Fraction | 0.32 | |
| Absorbent Void Fraction | 0.60 | |
| Total Void Fraction | 0.728 | |
| Absorbent Density, kg/m | 2507 | |
| Absorbent Particle Diameter, m | 2 × 10 | |
| Absorbent Heat Capacity , kJ/(kg K) | 1.21 |
| Parameter | Value |
|---|---|
| , mol/(kg bar s) | 0.4668 |
| K, bar | 5 × 10 |
| , mol/(kg bar s) | 7.002 × 10 |
| Parameter | Value |
|---|---|
| , bar | 1 |
| , J/mol | −87,000 |
| , K | 648.05 |
| Parameter | Symbol | Specification |
|---|---|---|
| Overall Heat Transfer Coefficient, kW/(m K) | U | 0.03 |
| Cooling Water Inlet Temperature, C | 20 | |
| Cooling Water Outlet Temperature, C | 40 | |
| Cooling Water Heat Capacity, kJ/(kg K) | 4.16 |
| Unit | Basis | ||||
|---|---|---|---|---|---|
| Reactor | Volume, m | 66,800 | 268,000 | 20 | 0.52 |
| Absorber | Area of Tubes, m | 66,800 | 1,039,000 | 100 | 0.68 |
| Compressor | Rated Power, kW | 7400 | 7,690,000 | 1000 | 0.9 |
| Heat Exchanger | Area, m | 28,600 | 208,000 | 100 | 0.71 |
| Pump | Rated Power | 7400 | 15,000 | 23 | 0.29 |
| Scale, kgNH/h | 100 | 500 | 1000 | 5000 | 10,000 |
|---|---|---|---|---|---|
| Net Present Cost, MM$ | 3.2 | 11.2 | 20.2 | 85.8 | 164.3 |
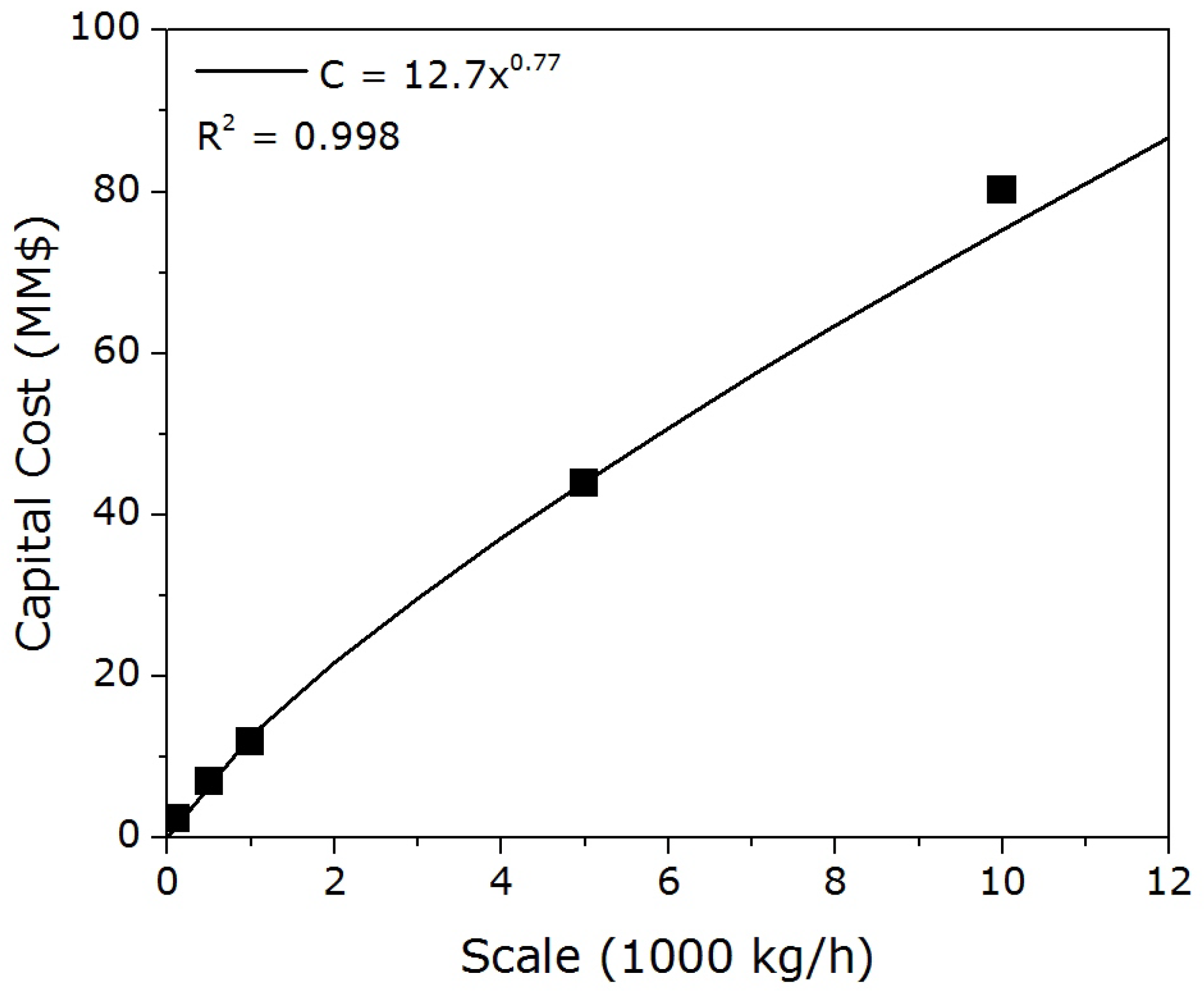
| Capital Cost, MM$ | 2.3 | 7.0 | 11.8 | 43.9 | 80.2 |
| Specific Energy Consumption, kWh/kgNH | 3.12 | 3.07 | 3.06 | 3.07 | 3.08 |
| Scale, kgNH/h | 100 | 500 | 1000 | 5000 | 10,000 |
|---|---|---|---|---|---|
| Recycle Ratio | 12.5 | 12.7 | 12.7 | 12.8 | 12.8 |
| Reaction-Absorption Pressure, bar | 20.3 | 20.3 | 20.3 | 20.3 | 20.3 |
| Reactor Temperature, C | 370 | 370 | 370 | 370 | 370 |
| Reactor Length, m | 1.48 | 2.68 | 3.52 | 7.68 | 10.68 |
| Reactor Diameter, m | 0.74 | 1.33 | 1.76 | 3.84 | 5.34 |
| Heat Exchanger Area, m | 247 | 1250 | 2520 | 12,700 | 30,200 |
| Absorber Temperature, C | 167 | 174 | 176 | 178 | 176 |
| Number of Absorber Tubes | 4 | 29 | 68 | 512 | 1183 |
| Absorber Tube Length, m | 1.14 | 1.00 | 0.96 | 0.84 | 0.80 |
| Absorber Tube Diameter, m | 0.57 | 0.50 | 0.48 | 0.42 | 0.40 |
| Trim Cooler Temperature, C | 141 | 142 | 142 | 141 | 97 |
| Desorption Pressure, bar | 13.4 | 13.4 | 13.4 | 13.4 | 13.4 |
| Desorption Temperature, C | 500 | 500 | 500 | 500 | 500 |
| Ammonia Compressor Precooler Temperature, C | 57 | 50 | 48 | 43 | 42 |
| Ammonia Storage Pressure, bar | 23.4 | 21.2 | 20.5 | 19.1 | 18.6 |
| Ammonia Storage Temperature, C | 56 | 52 | 50 | 48 | 47 |
| Scale, kgNH/h | 100 | 500 | 1000 | 5000 | 10,000 |
|---|---|---|---|---|---|
| Reactor Volume, m | 0.64 | 3.72 | 8.58 | 88.6 | 239 |
| Distance from Equilibrium, % | 0.07 | 0.04 | 0.02 | 0.001 | 0.0001 |
| Reactor Pressure Drop, bar | 0.04 | 0.14 | 0.24 | 0.57 | 0.85 |
| Total Pressure Drop, bar | 1.23 | 1.11 | 1.12 | 1.28 | 1.50 |
| Operation | Value |
|---|---|
| Compression | 0.16 |
| Pumping cooling water | 0.02 |
| Desorption | 0.82 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palys, M.J.; McCormick, A.; Cussler, E.L.; Daoutidis, P. Modeling and Optimal Design of Absorbent Enhanced Ammonia Synthesis. Processes 2018, 6, 91. https://doi.org/10.3390/pr6070091
Palys MJ, McCormick A, Cussler EL, Daoutidis P. Modeling and Optimal Design of Absorbent Enhanced Ammonia Synthesis. Processes. 2018; 6(7):91. https://doi.org/10.3390/pr6070091
Chicago/Turabian StylePalys, Matthew J., Alon McCormick, E. L. Cussler, and Prodromos Daoutidis. 2018. "Modeling and Optimal Design of Absorbent Enhanced Ammonia Synthesis" Processes 6, no. 7: 91. https://doi.org/10.3390/pr6070091
APA StylePalys, M. J., McCormick, A., Cussler, E. L., & Daoutidis, P. (2018). Modeling and Optimal Design of Absorbent Enhanced Ammonia Synthesis. Processes, 6(7), 91. https://doi.org/10.3390/pr6070091





