Critical Hydraulic Gradient of Internal Erosion at the Soil–Structure Interface
Abstract
1. Introduction
2. Soil–Structure-Interface Internal Erosion Tests
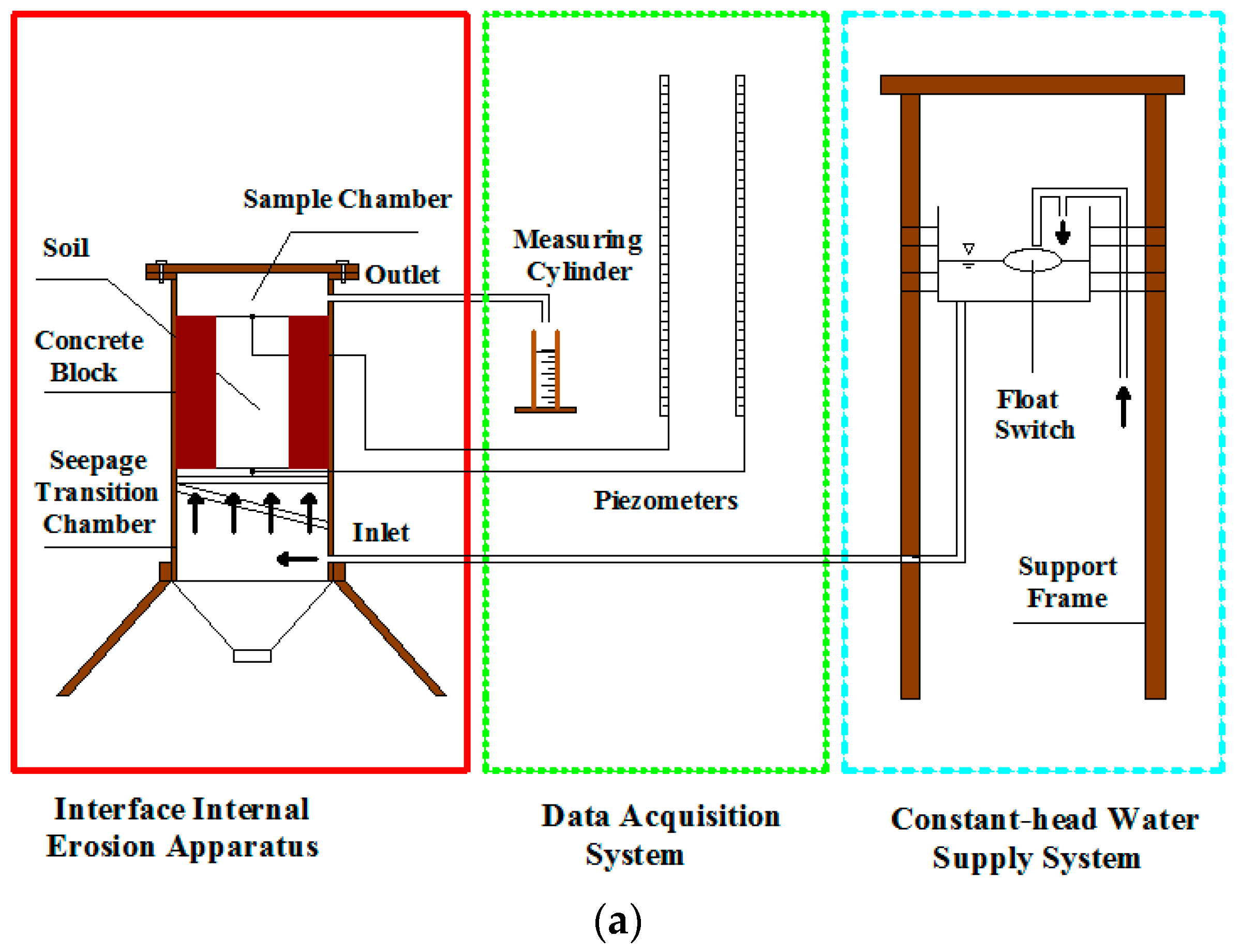
2.1. Soil–Structure Interface Seepage Failure Apparatus
2.2. Testing Materials
2.3. Soil Sample Preparation
2.4. Testing Program
2.5. Testing Schemes
3. Testing Results
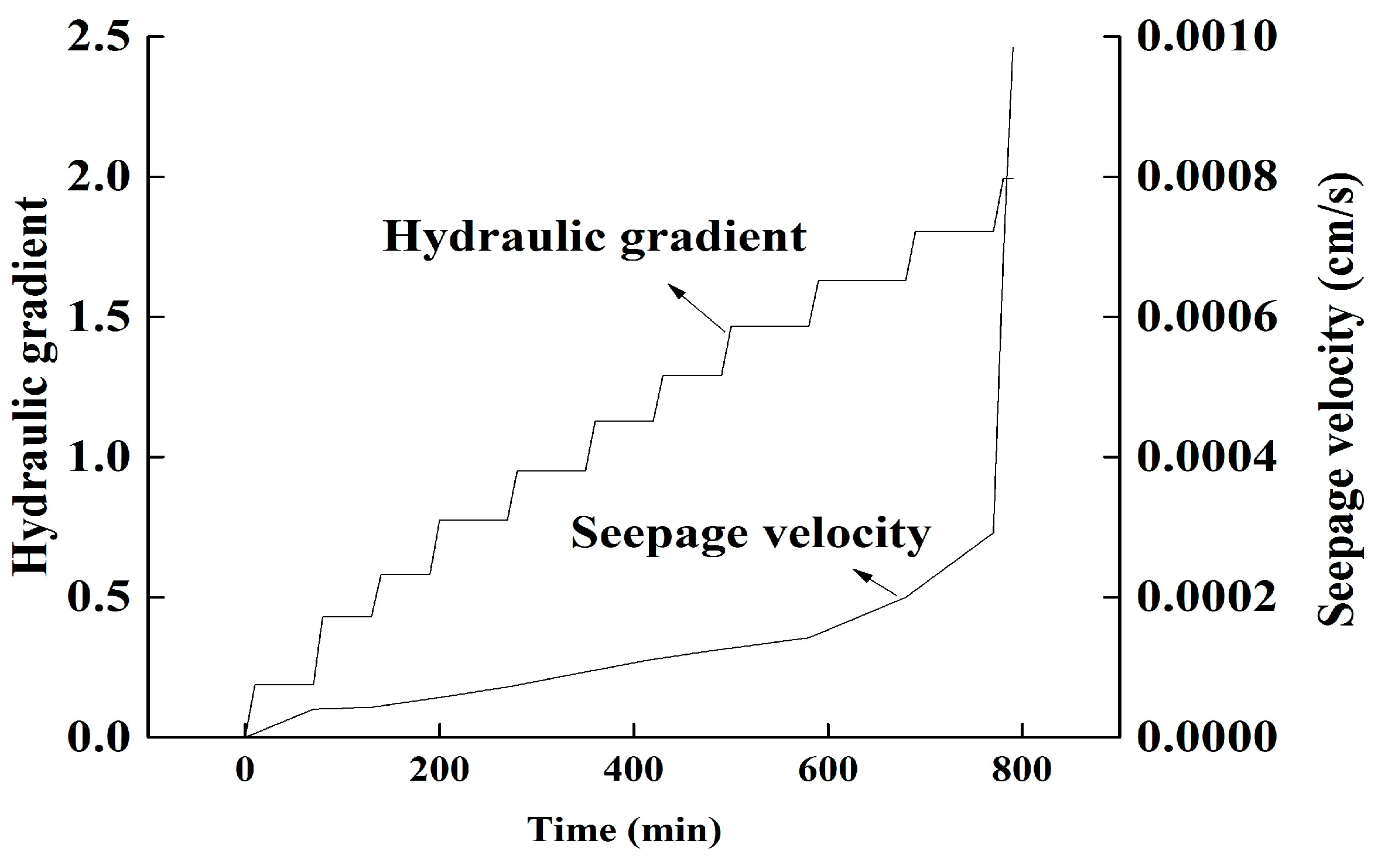
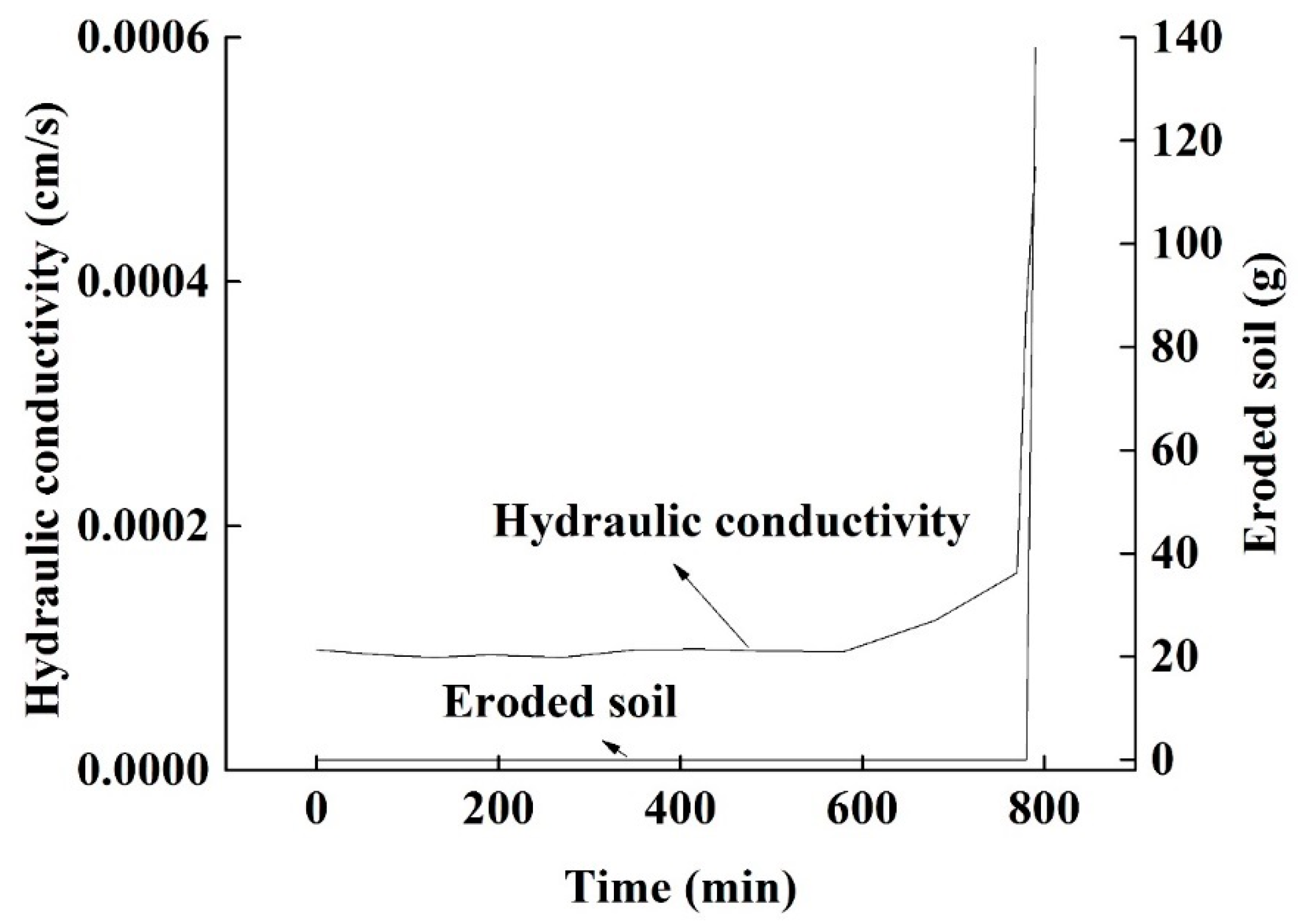
3.1. Observed Test Phenomena
3.2. Mechanism of Interface Internal Erosion
3.3. Orthogonal Test Results
3.3.1. Error Analysis
3.3.2. Range Analysis
3.3.3. Variance Analysis
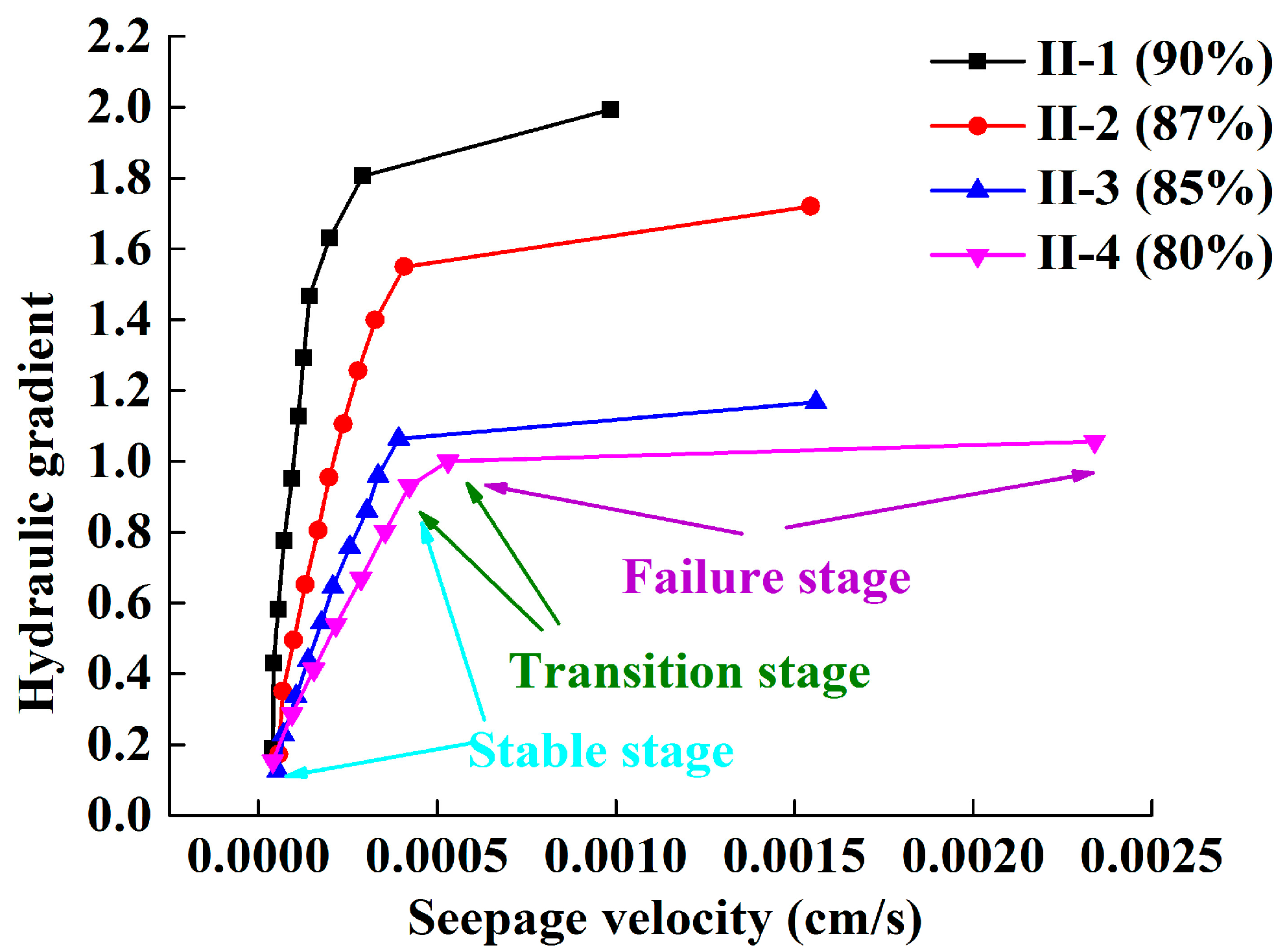
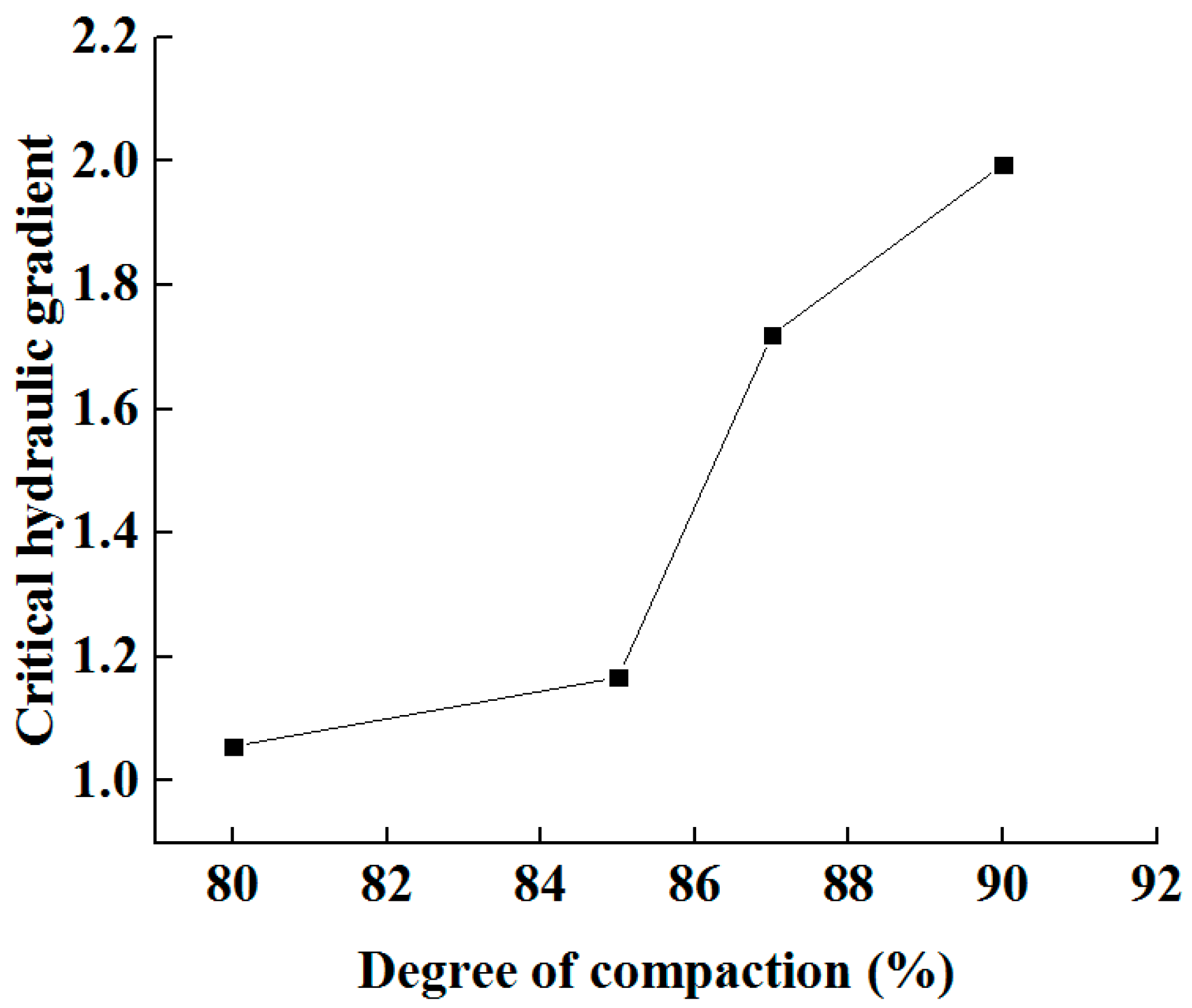
3.4. Effect of Degree of Compaction
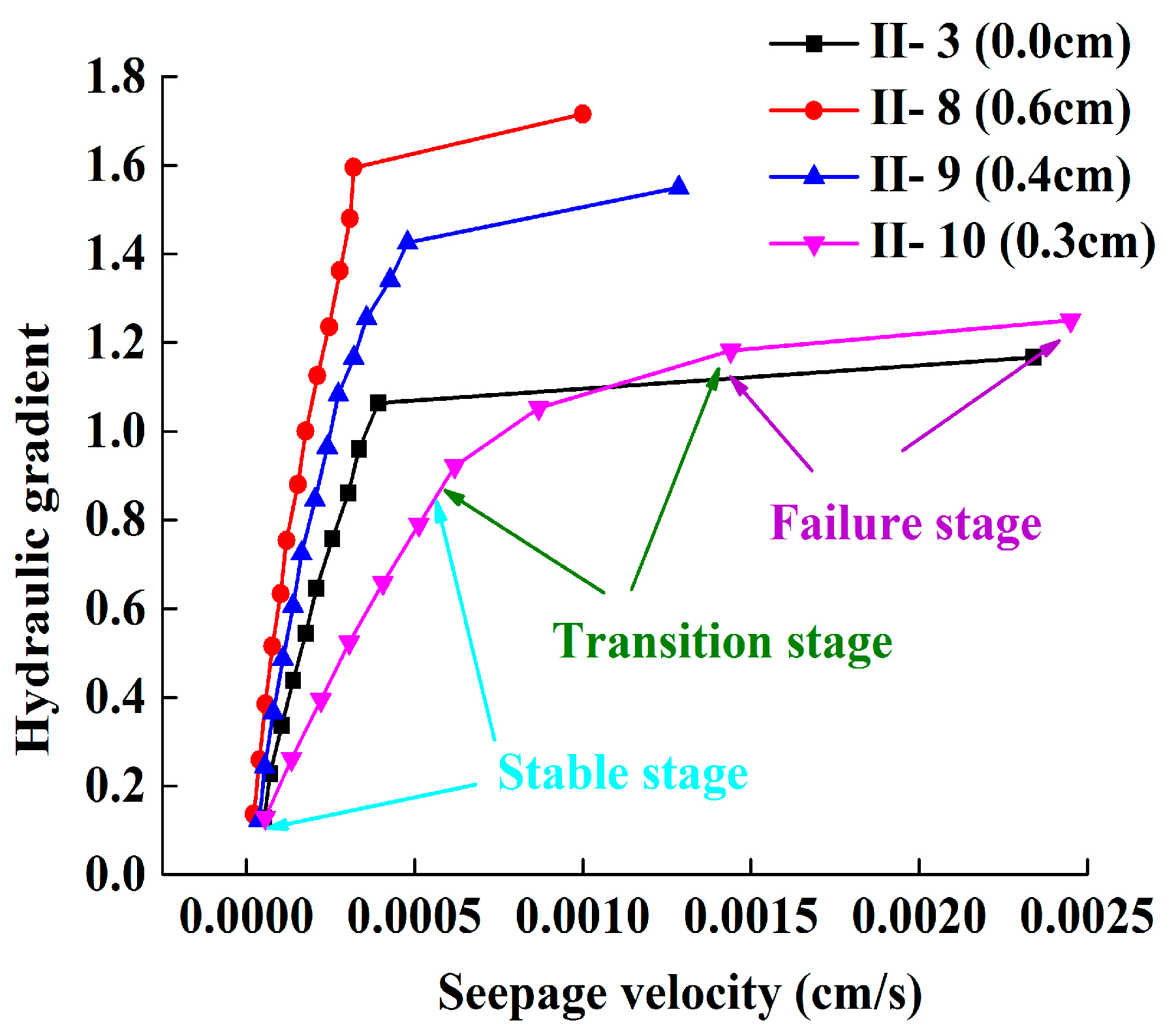
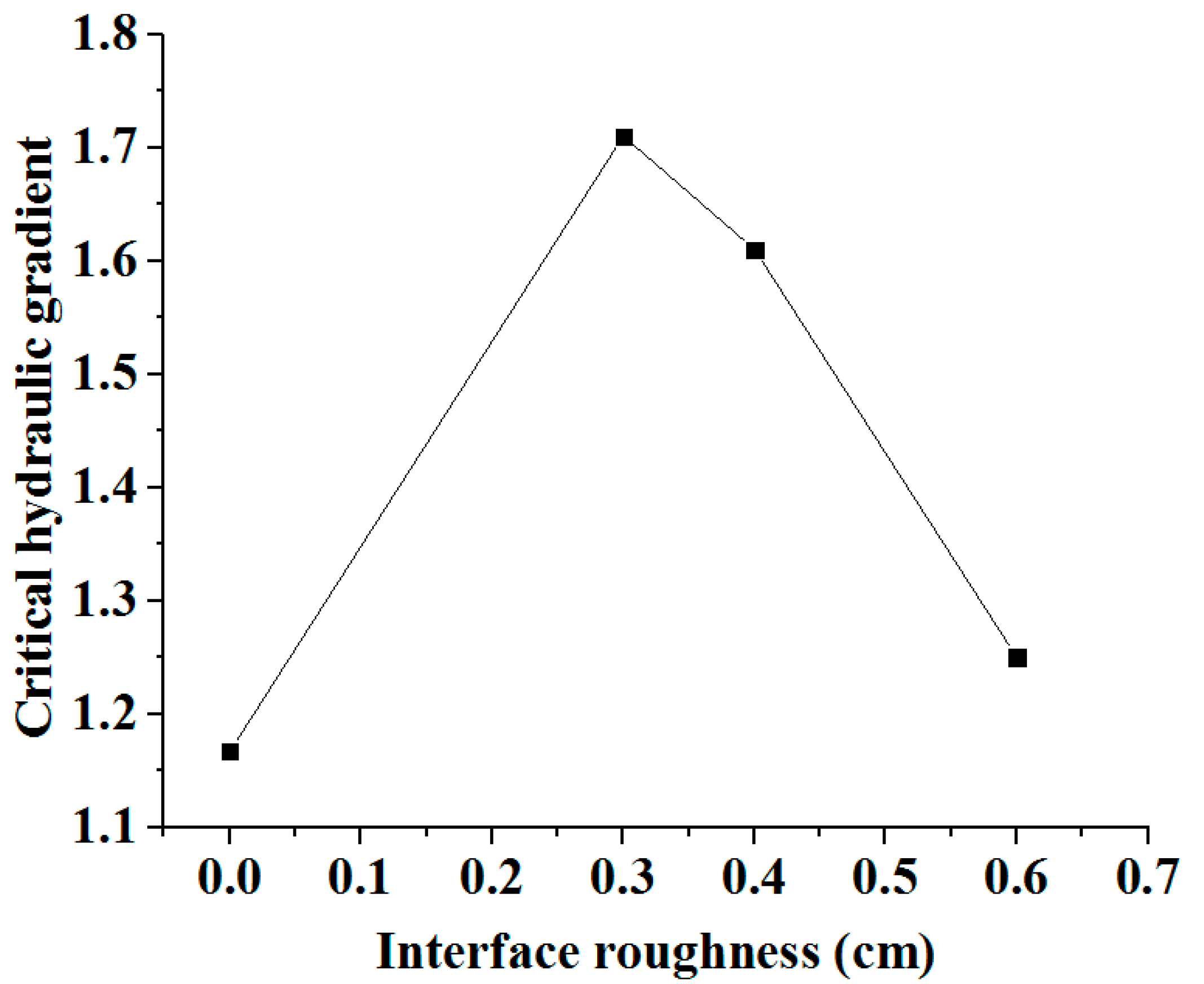
3.5. Effect of Interface Roughness
3.6. Effect of Clay Content
4. Discussion of Critical Hydraulic Gradient
5. Conclusions
- (1)
- The impact order of the three factors on the critical hydraulic gradient of interface internal erosion is: degree of compaction > roughness > clay content.
- (2)
- The critical hydraulic gradient increases as the levels of degree of compaction and clay content increase. This effect is found to be more obvious in the higher range of the degree of soil compaction and clay content. However, there exists an optimum interface roughness where the highest anti seepage strength can be obtained against interface internal erosion. This optimum roughness is found to be approximately 0.3 mm for the investigated cases.
- (3)
- The evolution of the interface internal erosion develops from inside to outside along the interface, and the soil particles on the interface flow as a whole.
- (4)
- The critical hydraulic gradient of interface internal erosion is related to the shear strength of the interface and the severity and porosity of the soil. The degree of compaction and clay content of soil affect the impermeability of the soil–structure-interface internal erosion through changing the porosity and severity of soil. The interface roughness mainly affects the shear strength of the soil–structure interface.
Author Contributions
Funding
Conflicts of Interest
References
- Sato, M.; Kuwano, R. Suffusion and clogging by one-dimensional seepage tests on cohesive soil. Soils Found. 2015, 55, 1427–1440. [Google Scholar] [CrossRef]
- Horikoshi, K.; Takahashi, A. Suffusion-induced change in spatial distribution of fine fractions in embankment subjected to seepage flow. Soils Found. 2015, 55, 1293–1304. [Google Scholar] [CrossRef]
- Poesen, J.; Luna, E.D.; Franca, A.; Nachtergaele, J.; Govers, G. Concentrated flow erosion rates as affected by rock fragment cover and initial soil moisture content. Catena 1999, 36, 315–329. [Google Scholar] [CrossRef]
- Marot, D.; Bendahmane, F.; Rosquoet, F.; Alexis, A. Internal flow effects on isotropic confined sand-clay mixtures. J. Soil Contam. 2009, 18, 294–306. [Google Scholar] [CrossRef]
- Mercier, F.; Bonelli, S.; Golay, F.; Anselmet, F.; Philippe, P.; Borghi, R. Numerical modelling of concentrated leak erosion during hole erosion tests. Acta Geotech. 2015, 10, 1–14. [Google Scholar] [CrossRef]
- Beek, V.M.V.; Sellmeijer, J.B.; Barends, F.B.J.; Bezuijen, A. Initiation of backward erosion piping in uniform sands. Géotechnique 2014, 64, 927–941. [Google Scholar] [CrossRef]
- Bendahmane, F.; Marot, D.; Alexis, A. Experimental parametric study of suffusion and backward erosion. J. Geotech. Geoenviron. Eng. 2008, 134, 57–67. [Google Scholar] [CrossRef]
- Richards, K.S.; Reddy, K.R. Experimental investigation of initiation of backward erosion piping in soils. Géotechnique 2012, 62, 933–942. [Google Scholar] [CrossRef]
- Germer, L.H. Physical processes in contact erosion. J. Appl. Phys. 1958, 29, 1067–1082. [Google Scholar] [CrossRef]
- Ke, L.; Takahashi, A. Experimental investigations on suffusion characteristics and its mechanical consequences on saturated cohesionless soil. Soils Found. 2014, 54, 713–730. [Google Scholar] [CrossRef]
- Yacine, S.; Didier, M.; Luc, S.; Alain, A. Suffusion tests on cohesionless granular matter. Eur. J. Environ. Civ. Eng. 2011, 15, 799–817. [Google Scholar] [CrossRef]
- Luo, Y.L.; Zhan, M.L.; Sheng, J.C.; Qiang, W. Hydro-mechanical coupling mechanism on joint of clay core-wall and concrete cut-off wall. J. Cent. South. Univ. 2013, 20, 2578–2585. [Google Scholar] [CrossRef]
- Kaoser, S.; Barrington, S.; Elektorowicz, M.; Ayadat, T. The influence of hydraulic gradient and rate of erosion on hydraulic conductivity of sand-bentonite mixtures. Soil Sediment Contam. An Int. J. 2006, 15, 481–496. [Google Scholar] [CrossRef]
- Armando, B.; Scheffler, M.L. Numerical analysis of the teton dam failure flood. J. Hydraul. Res. 1982, 20, 317–328. [Google Scholar] [CrossRef]
- Muhunthan, B.; Pillai, S. Teton dam, USA: Uncovering the crucial aspect of its failure. Civ. Eng. 2008, 161, 35–40. [Google Scholar] [CrossRef]
- Boulon, M.; Nova, R. Modelling of soil–structure interface behaviour a comparison between elastoplastic and rate type laws. Comput. Geotech. 1990, 9, 21–46. [Google Scholar] [CrossRef]
- Shahrour, I.; Rezaie, F. An elastoplastic constitutive relation for the soil–structure interface under cyclic loading. Comput. Geotech. 1997, 21, 21–39. [Google Scholar] [CrossRef]
- Hu, L.; Pu, J. Testing and modeling of soil–structure interface. J. Geotech. Geoenviron. Eng. 2004, 130, 851–860. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, J.M. Large-scale apparatus for monotonic and cyclic soil–structure interface test. ASTM Geotech. Test. J. 2006, 29, 401–408. [Google Scholar] [CrossRef]
- Ferdos, F.; Wörman, A.; Ekström, I. Hydraulic conductivity of coarse rockfill used in hydraulic structures. Transp. Porous Media 2015, 108, 1–25. [Google Scholar] [CrossRef]
- Kim, H.; Park, J.; Shin, J. Flow behaviour and piping potential at the soil–structure interface. Géotechnique 2018, 1–6. [Google Scholar] [CrossRef]
- Luo, Y.L.; Wu, Q.; Zhan, M.L.; Sheng, J.C. Study of critical piping hydraulic gradient of suspended cut-off wall and sand gravel foundation under different stress states. Rock Soil Mech. 2012, 36, 73–78. [Google Scholar] [CrossRef]
- Maeda, K.; Sakai, H.; Sakai, M. Development of seepage failure analysis method of ground with smoothed particle hydrodynamics. Struct. Eng. 2006, 23, 307–319. [Google Scholar] [CrossRef]
- Maeda, K.; Sakai, H. Seepage failure and erosion of ground with air bubble dynamics. Geotech. Spec. Publ. 2010, 204, 261–266. [Google Scholar] [CrossRef]
- Liu, R.; Li, B.; Jiang, Y. Critical hydraulic gradient for nonlinear flow through rock fracture networks: The roles of aperture, surface roughness, and number of intersections. Adv. Water Resour. 2016, 88, 53–65. [Google Scholar] [CrossRef]
- Liu, R.; Jiang, Y.; Li, B.; Wang, X. A fractal model for characterizing fluid flow in fractured rock masses based on randomly distributed rock fracture networks. Comput. Geotech. 2015, 65, 45–55. [Google Scholar] [CrossRef]
- Ervin, M.C.; Benson, N.D.; Morgan, J.R.; Pavlovic, N. Melbourne’s southbank interchange: A permanent excavation in compressible clay. Can. Geotech. J. 2004, 41, 861–876. [Google Scholar] [CrossRef]
- Wang, B.T.; Chen, X.A. Research on effect of suspended cut-off wall with simulation test. Chin. J. Rock Mech. Eng. 2008, 27, 2766–2771. [Google Scholar]
- Shao, S.J.; Yang, C.M. Research on the impermeability design method of the slurry protection diaphragm wall in the coarse-grained soil foundation. J. Hydraul. Eng. 2015, 46, 46–53. [Google Scholar]
- Barrospérsio, L.A.; Santospetrucio, J. Coefficients of active earth pressure with seepage effect. Can. Geotech. J. 2012, 49, 651–658. [Google Scholar] [CrossRef]
- Wang, S.; Chen, J.S.; Luo, Y.L.; Sheng, J.C. Experiments on internal erosion in sandy gravel foundations containing a suspended cut-off wall under complex stress states. Nat. Hazards 2014, 74, 1163–1178. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, H.; Liu, M.; Chen, Y. Seismic passive earth pressure with seepage for cohesionless soil. Mar. Georesour. Geotechnol. 2012, 30, 86–101. [Google Scholar] [CrossRef]

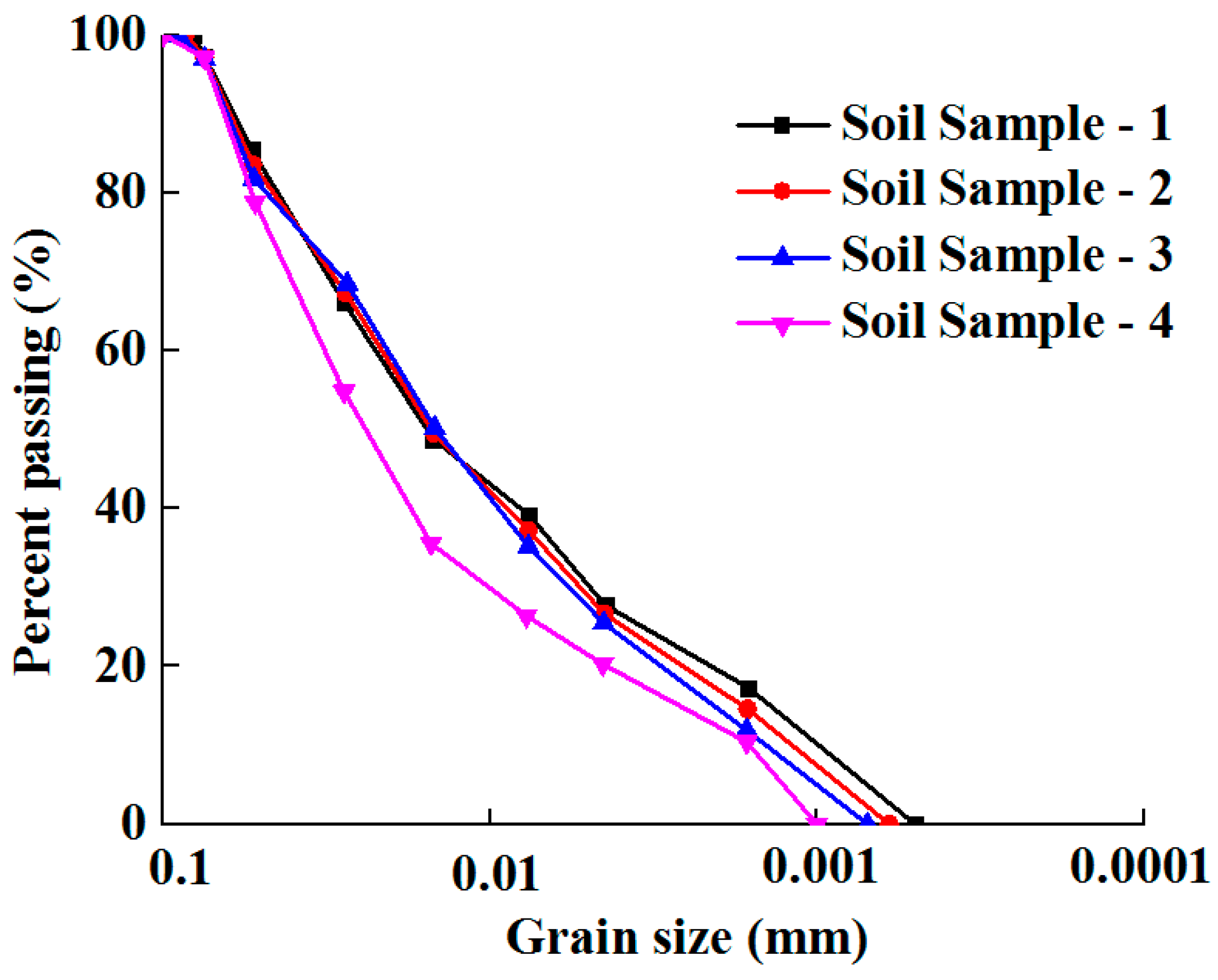





| Material Properties | Soil Sample-1 | Soil Sample-2 | Soil Sample-3 | Soil Sample-4 |
|---|---|---|---|---|
| Clay content (<0.005 mm) (%) | 29.8 | 27.9 | 26.8 | 21.8 |
| Liquid limit (%) | 33.78 | 33.51 | 33.07 | 31.84 |
| Plastic limit (%) | 18.90 | 18.42 | 18.36 | 17.14 |
| Specific gravity | 2.74 | 2.74 | 2.74 | 2.74 |
| Optimal water content (%) | 20.3 | 18.7 | 18.3 | 18.1 |
| Maximum dry density (g/cm3) | 1.660 | 1.672 | 1.678 | 1.683 |
| Factor Level | A Degree of Compaction (%) | B Clay Content (%) | C Roughness (cm) |
|---|---|---|---|
| 1 | 80 | 21.8 | 0 |
| 2 | 85 | 26.8 | 0.3 |
| 3 | 90 | 29.8 | 0.6 |
| Factor Test Number | A Degree of Compaction (%) | B Clay Content (%) | C Roughness (cm) |
|---|---|---|---|
| I-1 | 80 | 21.8 | 0.6 |
| I-2 | 80 | 26.8 | 0.3 |
| I-3 | 80 | 29.8 | 0 |
| I-4 | 85 | 21.8 | 0.3 |
| I-5 | 85 | 26.8 | 0 |
| I-6 | 85 | 29.8 | 0.6 |
| I-7 | 90 | 21.8 | 0 |
| I-8 | 90 | 26.8 | 0.6 |
| I-9 | 90 | 29.8 | 0.3 |
| Test Number | Degree of Compaction (%) | Clay Content (%) | Roughness (cm) |
|---|---|---|---|
| II-1 | 90 | 29.8 | 0 |
| II-2 | 87 | 29.8 | 0 |
| II-3 | 85 | 29.8 | 0 |
| II-4 | 80 | 29.8 | 0 |
| II-5 | 85 | 27.9 | 0 |
| II-6 | 85 | 26.8 | 0 |
| II-7 | 85 | 21.8 | 0 |
| II-8 | 85 | 29.8 | 0.6 |
| II-9 | 85 | 29.8 | 0.4 |
| II-10 | 85 | 29.8 | 0.3 |
| A Degree of Compaction (%) | B Clay Content (%) | C Roughness (cm) | E Empty Column | Critical Hydraulic Gradient | |
|---|---|---|---|---|---|
| I-1 | 1(80) | 1(21.8) | 3(0.6) | 1 | 0.98 |
| I-2 | 1(80) | 2(26.8) | 2(0.3) | 2 | 1.24 |
| I-3 | 1(80) | 3(29.8) | 1(0) | 3 | 1.06 |
| I-4 | 2(85) | 1(21.8) | 2(0.3) | 3 | 1.40 |
| I-5 | 2(85) | 2(26.8) | 1(0) | 1 | 1.00 |
| I-6 | 2(85) | 3(29.8) | 3(0.6) | 2 | 1.31 |
| I-7 | 3(90) | 1(21.8) | 1(0) | 2 | 1.81 |
| I-8 | 3(90) | 2(26.8) | 3(0.6) | 3 | 1.79 |
| I-9 | 3(90) | 3(29.8) | 2(0.3) | 1 | 2.74 |
| SSj | 1.83 | 0.23 | 0.45 | 0.04 |
| A Degree of Compaction (%) | B Clay Content (%) | C Roughness (cm) | |
|---|---|---|---|
| K1 | 1.09 | 1.40 | 1.36 |
| K2 | 1.24 | 1.34 | 1.79 |
| K3 | 2.11 | 1.70 | 1.29 |
| Range Ri | 1.02 | 0.36 | 0.5 |
| A Degree of Compaction (%) | B Fine Content (%) | C Roughness (cm) | E Empty Column | |
|---|---|---|---|---|
| K1j2 | 3.28 | 4.19 | 4.08 | 4.72 |
| K2j2 | 3.71 | 4.03 | 5.38 | 4.36 |
| K3j2 | 6.34 | 5.11 | 3.87 | 4.25 |
| Free degree | 2 | 2 | 2 | 2 |
| SS | 1.83 | 0.23 | 0.45 | 0.04 |
| MS | 0.92 | 0.12 | 0.23 | 0.02 |
| F | 42 | 6 | 11.50 | |
| F0.01(2,2) | 99 | 99 | 99 | |
| F0.025(2,2) | 39 | 39 | 39 | |
| F0.05(2,2) | 19 | 19 | 19 | |
| F0.10(2,2) | 9 | 9 | 9 | |
| F0.25(2,2) | 3 | 3 | 3 | |
| Significance level | ** (Greatly significant) | - (Relevant) | * (Significant) |
| Symbol | Definition |
|---|---|
| dh | the hydraulic head differentials between the two ends of the control body |
| dp | the water pressure differentials between the two ends of the control body |
| n | the porosity of soil |
| A | cross-sectional area of soil |
| dz | the height of control body |
| γω | unit weight of water |
| fz | the volume force acting on the soil particles’ unit volume |
| τ | the shear stress between soil and concrete |
| da | the thickness of control body |
| Gs | specific gravity of soil particles |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Q.; Liu, J.; Han, B.; Li, H.; Li, Y.; Li, X. Critical Hydraulic Gradient of Internal Erosion at the Soil–Structure Interface. Processes 2018, 6, 92. https://doi.org/10.3390/pr6070092
Xie Q, Liu J, Han B, Li H, Li Y, Li X. Critical Hydraulic Gradient of Internal Erosion at the Soil–Structure Interface. Processes. 2018; 6(7):92. https://doi.org/10.3390/pr6070092
Chicago/Turabian StyleXie, Quanyi, Jian Liu, Bo Han, Hongtao Li, Yuying Li, and Xuanzheng Li. 2018. "Critical Hydraulic Gradient of Internal Erosion at the Soil–Structure Interface" Processes 6, no. 7: 92. https://doi.org/10.3390/pr6070092
APA StyleXie, Q., Liu, J., Han, B., Li, H., Li, Y., & Li, X. (2018). Critical Hydraulic Gradient of Internal Erosion at the Soil–Structure Interface. Processes, 6(7), 92. https://doi.org/10.3390/pr6070092





