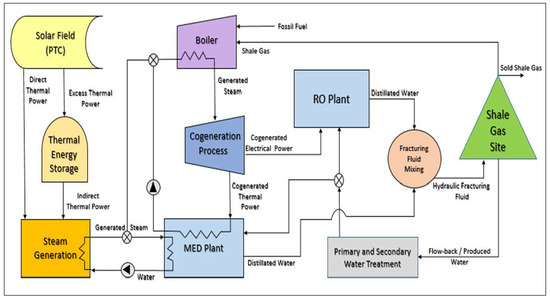
An Integrated Approach to Water-Energy Nexus in Shale-Gas Production
Abstract
:1. Introduction
2. Problem Statement
- Flowrate and characteristics of produced and flared shale gas.
- Demand for fresh water (flowrate and quality).
- Flowrate and characteristics of flowback and produced wastewater.
- Treats the wastewater for on-site recycling/reuse.
- Uses solar energy and fossil fuels to provide the needed electric and thermal power needs.
- Satisfies technical, economic and environmental requirements.
- Flowrate and composition of shale gas (sold and flared).
- Flowrate and purity needs for fresh water.
- Total volumetric flow of wastewater (flow-back and produced water) of shale gas play.
- Flowrate of flared gases that may be used in the cogeneration process.
- Electric energy requirement for RO and MED (kWhe/m3).
- Thermal energy requirement for MED (kWht/m3).
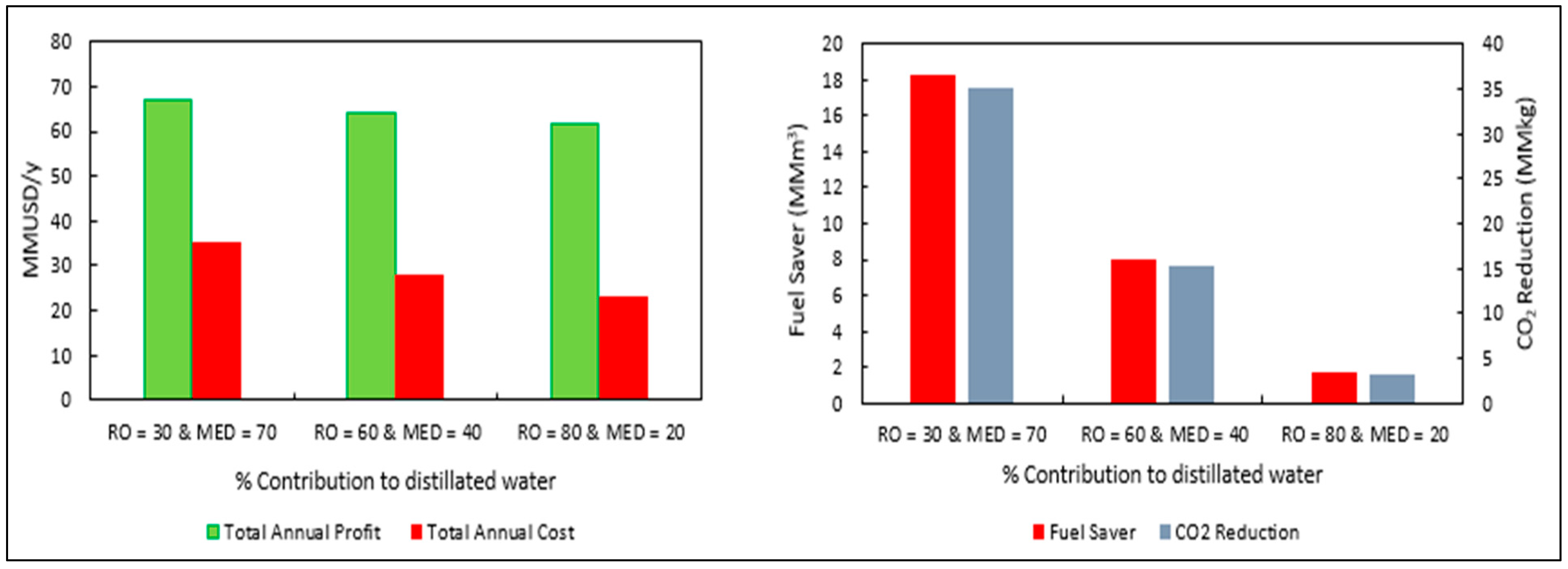
- What is the maximum annual profit of the whole system for producing desalinated water and electricity for the various percentage contributions of RO and MED in the total desalinated water production?
- What is the minimum total annual cost of the entire system?
- What is the economic feasibility of the system?
- What is the optimal mix of solar energy, thermal storage and fossil fuel for the MED plant and the entire system?
- What is the optimal design and integration of the system?
- What are the optimal values of the design and operating variables of the system (e.g., minimum area of a solar collector, maximum capacity of a thermal storage system, etc.)?
- What is the feasible range of the percentage contribution of RO and MED in the total desalinated water production?
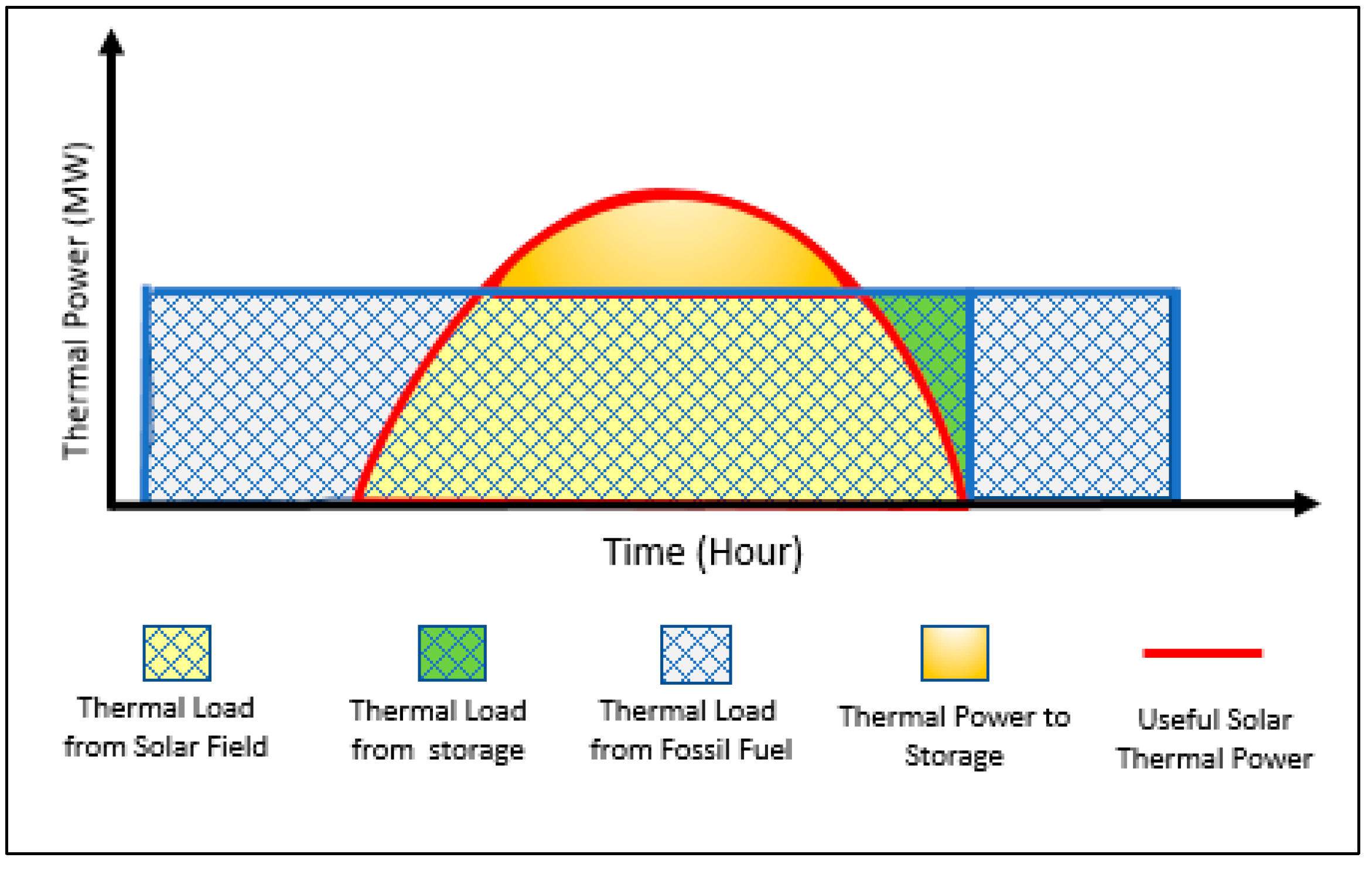
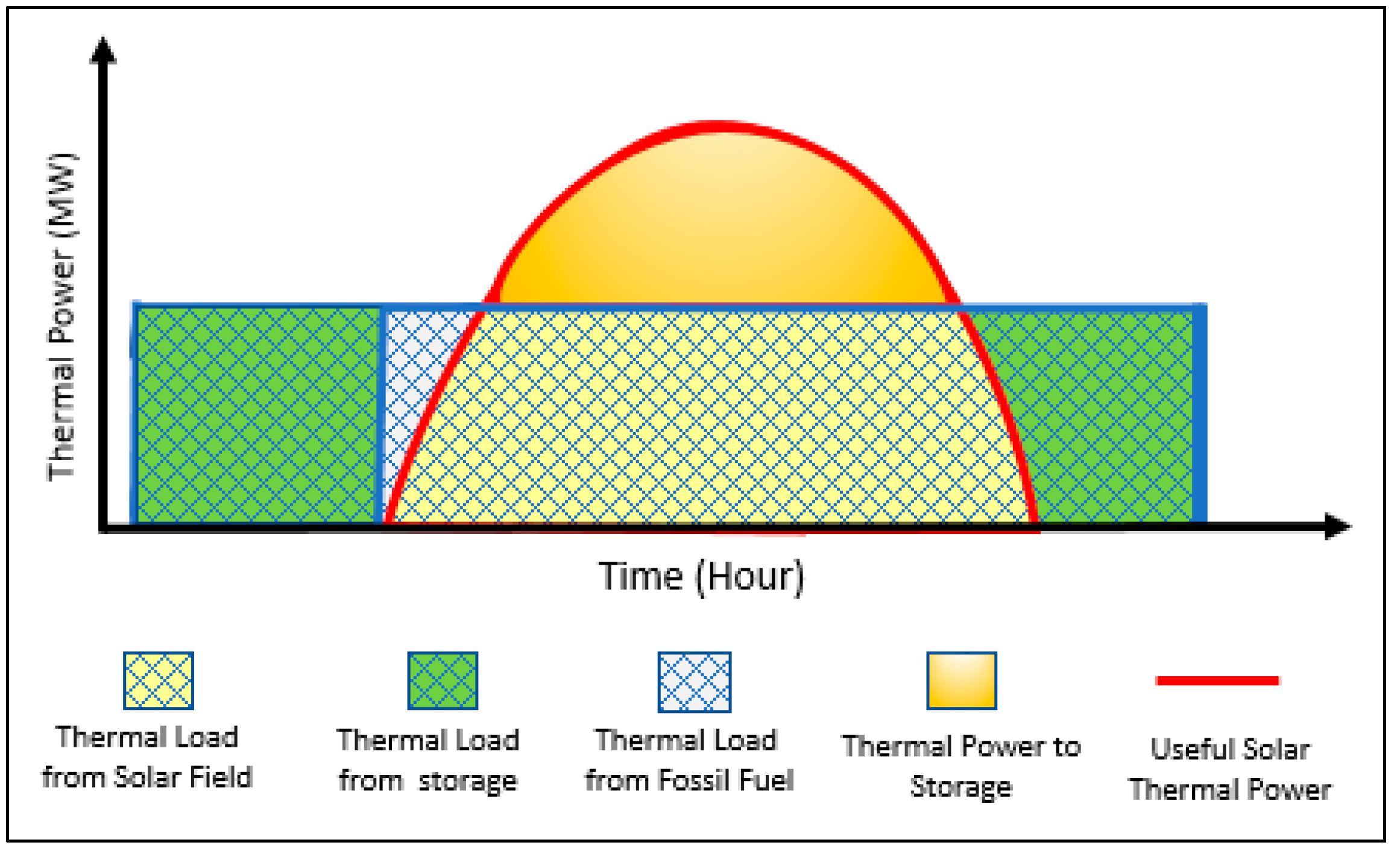
- To achieve a steady supply of thermal power to the whole system, solar energy (as direct solar thermal power), fossil fuel (shale gas, flared gas) and thermal energy storage (as indirect solar thermal power) are used.
- Solar energy is used as a source of heat to provide thermal power directly to the MED plant exclusively (to be more economically feasible), while the surplus thermal power is stored.
- A two-stage turbine is used to enhance the cogeneration process efficiency.
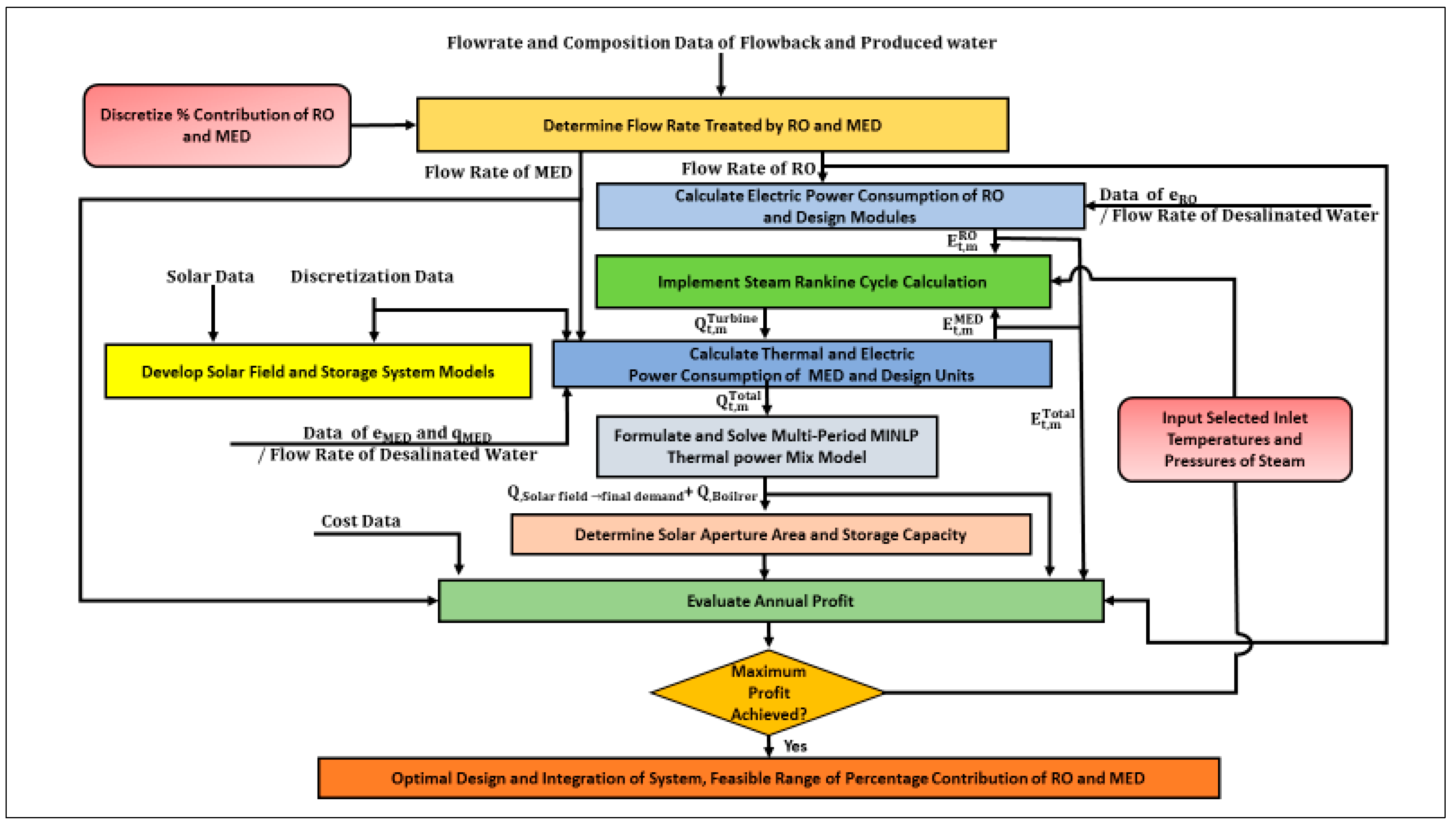
3. Approach
4. Modeling the Building Blocks
5. Optimization Formulation
6. Case Study
7. Flowback/Produced Water of Shale Gas Play
8. Solar Energy
9. Flared Gas
10. Total Cost
11. Results and Discussion
12. Conclusions
Author Contributions
Conflicts of Interest
Nomenclature
| , , , | Correlation constants |
| a, b and c | Coefficients for the LS-3 collector |
| Annualized fixed capital cost of the multi-effect desalination | |
| Annualized fixed capital cost of the reverse osmosis | |
| Annualized fixed capital cost of the solar collector | |
| Annualized fixed capital cost of the cogeneration system | |
| Effective surface area of the solar collector | |
| Solar field aperture area | |
| Total annual fixed cost | |
| Total annual operating cost | |
| A and B | Parameters that depend on the type of the turbine |
| Barrel | |
| Value of avoided cost of discharging wastewater | |
| Value of fossil fuel | |
| Disposal cost per volume unit | |
| Fuel cost per thermal power unit | |
| Fresh water cost per volume unit | |
| Operation and maintenance cost per thermal power unit | |
| Primary and secondary treatment cost per volume unit | |
| Solar field cost per area unit | |
| Steam generator system cost per thermal power unit | |
| Thermal storage system cost per thermal power unit | |
| Transportation cost per volume unit | |
| Specific heat of the molten salt | |
| Specific heat of oil | |
| Outer diameter of the receiver pipe | |
| Design variable of the turbine | |
| Direct normal irradiance | |
| Electric energy requirements of MED | |
| Electric energy requirements of RO | |
| Turbine shaft power output | |
| Electric energy provided by the cogeneration turbine | |
| Cubic feet | |
| Focal length of the collectors | |
| Fixed capital cost of a boiler | |
| Fixed capital cost of the primary and secondary treatment | |
| Total fixed capital cost of the solar field | |
| Fixed capital cost estimation of the steam generator system | |
| Fixed capital cost of the turbine | |
| Fixed capital cost of the thermal storage system | |
| Total fixed capital cost | |
| Soiling factor (mirror cleanliness) | |
| Flowback and produced water | |
| Volumetric flow rate of fossil fuel | |
| Volumetric flow rate of desalinated water from MED | |
| Volumetric flow rate of desalinated water from RO | |
| Actual outlet enthalpy of the turbine | |
| Inlet enthalpy of the steam | |
| Outlet isentropic enthalpy | |
| Sum of heat collection element | |
| Incidence angle modifier | |
| Length of a single collector assembly | |
| Length of spacing between troughs | |
| Inlet turbine steam flowrate | |
| Maximum mass flowrate of the turbine | |
| Mass flow rate of molten salt | |
| Mass flowrate of oil | |
| Multi-effect distillation plant | |
| Mixed integer nonlinear program | |
| Million | |
| Factor to account for the operation pressure of the boiler | |
| Factor accounting for the superheat temperature of the boiler | |
| Service life of the property in years | |
| National Solar Radiation Data Base | |
| Operation and maintenance cost | |
| Optical end loss | |
| Cost of fuel | |
| Operation variable of the turbine | |
| Annualized operational expenditure of MED | |
| Annualized operational expenditure of RO | |
| Annualized operational expenditure of the solar collector | |
| Annualized operational expenditure of the thermal storage system | |
| Annualized operational expenditure of the cogeneration system | |
| Gauge pressure of the boiler | |
| Parabolic trough collector | |
| Thermal energy requirements of MED | |
| Thermal power output of the boiler rate | |
| Thermal power that loss from the headers (pipes) | |
| Thermal power that loss from the expansion tank (vessel) | |
| Net thermal power inside the tank | |
| Inlet thermal power | |
| Amount of thermal power that produced by the boiler | |
| Accumulated thermal power in the tank from preceding iterations | |
| Total thermal power that loss from a collector to ambient | |
| Thermal power that transferred from a collector to a fluid | |
| Thermal power that absorbed by the receiver tube of a collector loop | |
| Outlet thermal power | |
| Useful thermal power that produced by the solar field | |
| Solar thermal power that produced by the solar field | |
| Thermal power loss | |
| Direct thermal power from the solar thermal collector | |
| Direct thermal power from the combustion of fossil fuels | |
| Inlet thermal power of the thermal storage system | |
| Indirect thermal from solar energy through the thermal storage system | |
| Thermal power captured by the solar collector | |
| Loss thermal power of the thermal storage system | |
| Thermal power stored in the thermal storage system | |
| Total thermal power needs for water treatment | |
| Thermal power from steam leaving the cogeneration turbine | |
| Thermal power stored from previous iterations | |
| Row shadow loss | |
| Reverse osmosis plant | |
| Return on investment | |
| Number of storage capacity hours | |
| Cold tank temperature | |
| Hot tank temperature | |
| Superheat temperature | |
| Ambient air temperature | |
| Temperature at the inlet of the turbine | |
| Temperature of the molten salt | |
| Mean receiver pipe temperature | |
| Saturation temperature at the inlet of a turbine | |
| Overall heat transfer coefficient of the receiver pipe | |
| Width of the collector aperture | |
| Volumetric flow rate of discharging wastewater | |
| Watt |
Subscript and Superscript Symbols
| ac | Actual |
| acc | Accumulated |
| amb | Ambient |
| B | Boiler |
| c | Collector aperture |
| Cogen | Cogeneration process |
| CT | Cold tank |
| DS | Disposal |
| EL | End loss |
| f | Factor |
| F | Fuel |
| FW | Freshwater |
| g | Gauge |
| HT | Hot tank |
| is | Isentropic |
| LFP | Loss from pipes |
| LFV | Loss from vessel |
| m | Time period (month) |
| MED | Multi-effect distillation plant |
| ms | Molten salt |
| OM | Operation and maintenance |
| P | Pressure |
| PST | Primary and secondary treatment |
| rec | Receiver |
| RO | Reverse osmosis plant |
| sat | Saturation |
| SC | Solar collector |
| SCA | Single collector assembly |
| SF | Solar field |
| SG | Steam generator |
| SH | Superheat |
| SL | Shadow loss |
| t | Time period (h) |
| T | Turbine |
| TES | Thermal energy storage |
| TR | Transportation |
| w | wastewater |
Greek Symbols
| Efficiency of the boiler | |
| Isentropic efficiency of the steam turbine | |
| Annual operation time | |
| Vector set of the turbine | |
| Value of produced water from MED | |
| Value of produced water from RO | |
| For every month (operational period) | |
| For every hour (sub- period) | |
| Isentropic enthalpy change | |
| ηopt | Peak optical efficiency of a collector |
| Solar incidence angle | |
| Solar zenith angle | |
| γ | Intercept factor |
| δ | Declination |
| ΔT | Difference between inlet and outlet of the oil |
| ρ | Reflectivity |
| τ | Glass transmissivity |
| ω | Hour angle |
| Absorptivity of the receiver pipe |
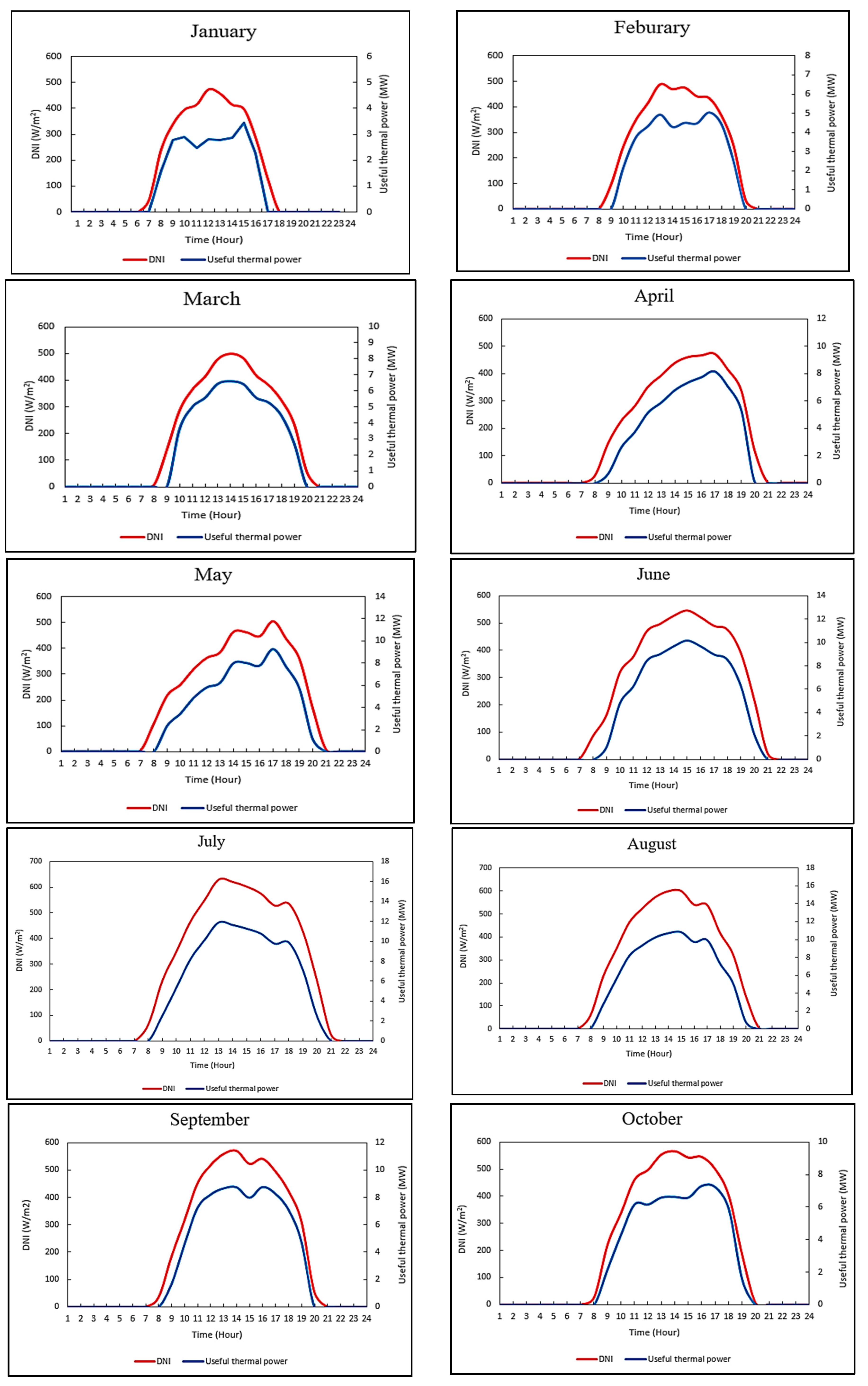
Appendix A. Solar Data for the Case Study
- Average hourly dry bulb temperature ()
- Average hourly wet bulb temperature ()
- Average hourly direct solar irradiance ()
- Average hourly solar incidence angle (degree).
| Month | January | February | March | April | May | June | July | August | September | October | November | December | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hour | |||||||||||||
| 0.5 | 7.1 | 8.1 | 13.4 | 17.3 | 20.9 | 23.6 | 13.4 | 25.1 | 24.1 | 18.9 | 13.1 | 8.2 | |
| 1.5 | 6.6 | 7.71 | 13.0 | 16.9 | 20.4 | 23.3 | 13.0 | 24.5 | 23.6 | 18.2 | 12.6 | 7.7 | |
| 2.5 | 6.1 | 7.24 | 12.6 | 16.4 | 19.9 | 23.1 | 12.6 | 24.0 | 23.2 | 17.4 | 12.3 | 7.36 | |
| 3.5 | 6.0 | 6.98 | 12.3 | 16.2 | 19.6 | 23.0 | 12.3 | 23.6 | 22.9 | 17.1 | 11.6 | 7.11 | |
| 4.5 | 5.9 | 6.74 | 12.0 | 16.0 | 19.3 | 22.8 | 12.0 | 23.2 | 22.6 | 16.8 | 11.4 | 7.13 | |
| 5.5 | 5.9 | 6.49 | 11.7 | 15.8 | 19.0 | 22.8 | 11.7 | 22.8 | 22.4 | 16.5 | 11.3 | 6.96 | |
| 6.5 | 5.5 | 7.37 | 12.6 | 16.8 | 20.1 | 23.3 | 12.6 | 24.2 | 22.4 | 17.9 | 10.9 | 7.03 | |
| 7.5 | 5.4 | 8.28 | 13.5 | 17.8 | 21.2 | 24.6 | 13.5 | 25.6 | 23.7 | 19.3 | 11.8 | 7.21 | |
| 8.5 | 7.7 | 9.20 | 14.5 | 18.8 | 22.3 | 26.0 | 14.5 | 27.0 | 25.6 | 20.6 | 14.0 | 9.10 | |
| 9.5 | 10 | 11.1 | 16.2 | 20.1 | 23.4 | 27.3 | 16.2 | 28.5 | 27.0 | 22.1 | 16.3 | 11.0 | |
| 10.5 | 12 | 13.0 | 17.9 | 21.4 | 24.5 | 28.4 | 17.9 | 30.1 | 28.2 | 23.6 | 18.0 | 12.8 | |
| 11.5 | 13 | 14.9 | 19.6 | 22.7 | 25.6 | 29.4 | 19.6 | 31.6 | 29.4 | 25.2 | 19.3 | 14.1 | |
| 12.5 | 14 | 15.7 | 20.5 | 23.5 | 26.2 | 30.4 | 20.5 | 32.4 | 30.3 | 25.8 | 20.3 | 15.1 | |
| 13.5 | 15 | 16.6 | 21.4 | 24.4 | 26.8 | 31.3 | 21.4 | 33.3 | 30.7 | 26.5 | 21.1 | 16.0 | |
| 14.5 | 15 | 17.5 | 22.3 | 25.2 | 27.5 | 31.4 | 22.3 | 34.1 | 31.0 | 27.2 | 21.3 | 16.4 | |
| 15.5 | 16 | 17.0 | 21.7 | 24.8 | 27.4 | 31.7 | 21.7 | 33.5 | 31.2 | 26.5 | 21.2 | 16.5 | |
| 16.5 | 15 | 16.5 | 21.2 | 24.4 | 27.4 | 31.2 | 21.2 | 32.9 | 31.0 | 25.8 | 20.5 | 16.0 | |
| 17.5 | 13 | 16.1 | 20.7 | 23.9 | 27.3 | 30.4 | 20.7 | 32.3 | 30.2 | 25.1 | 19.0 | 14.4 | |
| 18.5 | 12 | 14.6 | 19.1 | 22.5 | 26.1 | 29.0 | 19.1 | 30.9 | 28.8 | 24.0 | 17.3 | 12.7 | |
| 19.5 | 10.9 | 13.21 | 17.5 | 21.2 | 24.95 | 27.64 | 17.5 | 29.53 | 27.76 | 22.88 | 15.84 | 11.2 | |
| 20.5 | 9.73 | 11.77 | 16.0 | 19.8 | 23.7 | 26.47 | 16.0 | 28.10 | 26.68 | 21.75 | 14.63 | 10.3 | |
| 21.5 | 8.63 | 10.79 | 15.3 | 19.2 | 23.0 | 25.44 | 15.3 | 27.30 | 25.93 | 21.00 | 13.95 | 9.77 | |
| 22.5 | 7.91 | 9.825 | 14.5 | 18.5 | 22.3 | 24.75 | 14.5 | 26.46 | 25.36 | 20.25 | 13.45 | 9.55 | |
| 23.5 | 7.56 | 8.846 | 13.8 | 17.7 | 21.5 | 24.0 | 13.8 | 25.6 | 24.7 | 19.6 | 13.30 | 9.31 | |
| Month | January | February | March | April | May | June | July | August | September | October | November | December | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hour | |||||||||||||
| 0.5 | 5.7 | 6.3 | 9.85 | 15.3 | 18.5 | 21.6 | 22.9 | 22.0 | 21.5 | 16.3 | 11.4 | 6.41 | |
| 1.5 | 5.4 | 6.0 | 9.69 | 15.1 | 18.3 | 21.5 | 22.8 | 22.0 | 21.3 | 15.9 | 11.1 | 6.03 | |
| 2.5 | 4.9 | 5.7 | 9.52 | 14.9 | 18.0 | 21.4 | 22.7 | 21.9 | 21.2 | 15.4 | 10.8 | 5.75 | |
| 3.5 | 4.9 | 5.5 | 9.43 | 14.7 | 17.8 | 21.4 | 22.7 | 21.8 | 21.0 | 15.1 | 10.2 | 5.55 | |
| 4.5 | 4.8 | 5.3 | 9.35 | 14.6 | 17.6 | 21.4 | 22.6 | 21.6 | 20.9 | 14.9 | 10.1 | 5.56 | |
| 5.5 | 4.8 | 5.0 | 9.21 | 14.5 | 17.4 | 21.4 | 22.6 | 21.4 | 20.8 | 14.6 | 10.0 | 5.40 | |
| 6.5 | 4.5 | 5.7 | 9.64 | 15.1 | 18.1 | 21.7 | 22.9 | 22.0 | 20.8 | 15.6 | 9.78 | 5.44 | |
| 7.5 | 4.3 | 6.3 | 10.0 | 15.7 | 18.8 | 22.2 | 23.3 | 22.6 | 21.4 | 16.4 | 10.3 | 5.60 | |
| 8.5 | 6.1 | 7.0 | 10.4 | 16.3 | 19.4 | 22.6 | 23.4 | 23.1 | 22.0 | 17.2 | 11.6 | 6.99 | |
| 9.5 | 7.5 | 8.0 | 11.3 | 17.0 | 19.8 | 22.7 | 23.6 | 23.4 | 22.2 | 17.8 | 12.7 | 8.08 | |
| 10.5 | 8.4 | 8.9 | 12.0 | 17.6 | 20.1 | 22.8 | 23.6 | 23.4 | 22.2 | 18.3 | 13.3 | 8.90 | |
| 11.5 | 9.1 | 9.6 | 12.5 | 18.1 | 20.4 | 23.0 | 23.5 | 23.3 | 22.1 | 18.7 | 13.8 | 9.42 | |
| 12.5 | 9.5 | 10 | 12.7 | 18.4 | 20.7 | 23.0 | 23.5 | 23.3 | 22.3 | 18.8 | 14.0 | 9.82 | |
| 13.5 | 10 | 10 | 12.9 | 18.6 | 21.0 | 23.2 | 23.5 | 23.2 | 22.2 | 18.9 | 14.2 | 10.1 | |
| 14.5 | 10 | 10 | 13.0 | 18.8 | 21.2 | 22.9 | 23.5 | 23.0 | 22.1 | 19.0 | 14.1 | 10.3 | |
| 15.5 | 10 | 10 | 12.8 | 18.5 | 21.1 | 22.9 | 23.4 | 22.8 | 22.0 | 18.7 | 14.1 | 10.2 | |
| 16.5 | 9.8 | 10 | 12.5 | 18.3 | 20.9 | 22.8 | 23.3 | 22.6 | 22.0 | 18.5 | 13.8 | 10.0 | |
| 17.5 | 9.2 | 9.8 | 12.2 | 18.1 | 20.7 | 22.7 | 23.3 | 22.3 | 22.0 | 18.2 | 13.3 | 9.39 | |
| 18.5 | 8.6 | 9.4 | 11.9 | 17.6 | 20.5 | 22.4 | 23.4 | 22.4 | 21.8 | 18.0 | 12.7 | 8.72 | |
| 19.5 | 8.0 | 8.9 | 11.4 | 17.1 | 20.2 | 22.3 | 23.4 | 22.4 | 21.8 | 17.7 | 12.2 | 8.13 | |
| 20.5 | 7.4 | 8.3 | 10.8 | 16.5 | 19.8 | 22.1 | 23.2 | 22.1 | 21.6 | 17.3 | 11.7 | 7.78 | |
| 21.5 | 6.9 | 7.9 | 10.6 | 16.3 | 19.5 | 22.0 | 23.2 | 22.2 | 21.6 | 17.1 | 11.4 | 7.50 | |
| 22.5 | 6.4 | 7.4 | 10.3 | 16.0 | 19.2 | 21.9 | 23.1 | 22.1 | 21.6 | 16.9 | 11.3 | 7.37 | |
| 23.5 | 6.1 | 6.8 | 9.91 | 15.5 | 18.7 | 21.7 | 22.9 | 21.9 | 21.6 | 16.7 | 11.4 | 7.30 | |
| Month | January | February | March | April | May | June | July | August | September | October | November | December | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hour | |||||||||||||
| 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 2.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 3.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 5.5 | 0 | 0 | 0 | 0 | 5.1 | 3.8 | 1 | 0.0 | 0 | 0 | 0 | 0 | |
| 6.5 | 0 | 0 | 9.6 | 26 | 109 | 86 | 65 | 57 | 34 | 26 | 1.8 | 0 | |
| 7.5 | 48 | 95 | 140 | 145 | 216 | 164 | 236 | 229 | 184 | 221 | 171 | 49 | |
| 8.5 | 240 | 244 | 287 | 228 | 258 | 319 | 350 | 347 | 315 | 337 | 328 | 199 | |
| 9.5 | 339 | 346 | 365 | 281 | 318 | 377 | 467 | 463 | 450 | 460 | 388 | 272 | |
| 10.5 | 396 | 413 | 413 | 352 | 362 | 470 | 550 | 524 | 516 | 497 | 462 | 359 | |
| 11.5 | 415 | 487 | 478 | 394 | 383 | 496 | 630 | 573 | 557 | 553 | 545 | 389 | |
| 12.5 | 473 | 468 | 498 | 439 | 462 | 526 | 621 | 599 | 569 | 566 | 544 | 459 | |
| 13.5 | 457 | 474 | 481 | 461 | 460 | 545 | 603 | 600 | 521 | 542 | 504 | 489 | |
| 14.5 | 415 | 440 | 417 | 467 | 445 | 520 | 576 | 540 | 540 | 544 | 481 | 499 | |
| 15.5 | 397 | 433 | 380 | 473 | 503 | 489 | 529 | 539 | 493 | 498 | 437 | 440 | |
| 16.5 | 283 | 365 | 323 | 414 | 434 | 475 | 536 | 417 | 422 | 401 | 361 | 323 | |
| 17.5 | 128 | 246 | 234 | 338 | 356 | 389 | 427 | 323 | 311 | 181 | 93 | 80 | |
| 18.5 | 0.4 | 32 | 54 | 119 | 166 | 217 | 234 | 140 | 53 | 3.6 | 0 | 0 | |
| 19.5 | 0 | 0 | 0 | 0.1 | 7.2 | 21 | 24 | 4.3 | 0 | 0 | 0 | 0 | |
| 20.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 21.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 22.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 23.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Month | January | February | March | April | May | June | July | August | September | October | November | December | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hour | |||||||||||||
| 0.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 2.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 3.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 4.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 5.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 6.5 | 0 | 0 | 0 | 6.04 | 16.1 | 20.2 | 19.2 | 11.1 | 0 | 0 | 0 | 0 | |
| 7.5 | 0 | 4.33 | 7.10 | 2.51 | 9.26 | 13.4 | 12.3 | 5.49 | 4.95 | 16.1 | 23.4 | 0 | |
| 8.5 | 30.6 | 23.6 | 14.3 | 4.99 | 2.85 | 6.99 | 5.77 | 2.49 | 11.8 | 23.4 | 31.8 | 34.4 | |
| 9.5 | 37.8 | 30.5 | 20.7 | 10.9 | 2.76 | 1.52 | 1.14 | 7.13 | 18.0 | 29.8 | 38.5 | 41.4 | |
| 10.5 | 43.8 | 36.3 | 26.1 | 15.6 | 7.01 | 2.69 | 4.28 | 11.8 | 22.9 | 35.0 | 44.0 | 47.1 | |
| 11.5 | 48.2 | 40.6 | 30.0 | 18.7 | 9.73 | 5.40 | 7.20 | 14.9 | 26.3 | 38.4 | 47.6 | 51.1 | |
| 12.5 | 50.2 | 42.7 | 31.8 | 20.0 | 10.7 | 6.44 | 8.40 | 16.2 | 27.5 | 39.3 | 48.5 | 52.6 | |
| 13.5 | 49.5 | 42.1 | 31.0 | 19.0 | 9.79 | 5.70 | 7.78 | 15.3 | 26.2 | 37.5 | 46.5 | 51.1 | |
| 14.5 | 46.1 | 39.0 | 27.8 | 16.0 | 7.06 | 3.20 | 5.40 | 12.7 | 22.8 | 33.4 | 42.2 | 47.2 | |
| 15.5 | 40.7 | 34.0 | 22.9 | 11.5 | 2.79 | 0.83 | 1.58 | 8.49 | 17.8 | 27.8 | 36.2 | 41.4 | |
| 16.5 | 34.0 | 27.7 | 16.9 | 5.74 | 2.83 | 6.15 | 3.82 | 3.07 | 11.7 | 21.1 | 29.2 | 34.4 | |
| 17.5 | 21.1 | 20.4 | 9.96 | 2.65 | 9.23 | 12.4 | 10.1 | 3.61 | 4.78 | 11.5 | 0 | 0 | |
| 18.5 | 0 | 0 | 0.17 | 8.06 | 16.1 | 19.2 | 16.9 | 10.5 | 0.99 | 0 | 0 | 0 | |
| 19.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 20.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 21.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 22.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 23.5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
References
- Zhang, C.; El-Halwagi, M.M. Estimate the Capital Cost of Shale-Gas Monetization Projects. Chem. Eng. Prog. 2017, 113, 28–32. [Google Scholar]
- Al-Douri, A.; Sengupta, D.; El-Halwagi, M.M. Shale Gas Monetization—A Review of Downstream Processing to Chemicals and Fuels. J. Nat. Gas Sci. Eng. 2017, 45, 436–455. [Google Scholar]
- Ortiz-Espinoza, P.A.; Jiménez-Gutiérreza, A.; Nourledin, M.; El-Halwagi, M.M. Design, Simulation and Techno-Economic Analysis of Two Processes for the Conversion of Shale Gas to Ethylene. Comp. Chem. Eng. 2017, 107, 237–246. [Google Scholar] [CrossRef]
- Pérez-Uresti, S.I.; Adrián-Mendiola, J.M.; El-Halwagi, M.M.; Jiménez-Gutiérrez, A. Techno-Economic Assessment of Benzene Production from Shale Gas. Processes 2017, 5, 33. [Google Scholar] [CrossRef]
- Jasper, S.; El-Halwagi, M.M. A Techno-Economic Comparison of Two Methanol-to-Propylene Processes. Processes 2015, 3, 684–698. [Google Scholar] [CrossRef]
- Julián-Durán, L.; Ortiz-Espinoza, A.P.; El-Halwagi, M.M.; Jiménez-Gutiérrez, A. Techno-economic assessment and environmental impact of shale gas alternatives to methanol. ACS Sustain. Chem. Eng. 2014, 2, 2338–2344. [Google Scholar] [CrossRef]
- Salkuyeh, Y.K.; Adams, T.A., II. A novel polygeneration process to co-produce ethylene and electricity from shale gas with zero CO2 emissions via methane oxidative coupling. Energy Convers. Manag. 2015, 92, 406–420. [Google Scholar] [CrossRef]
- Ehlinger, M.V.; Gabriel, K.J.; Noureldin, M.M.B.; El-Halwagi, M.M. Process Design and Integration of Shale Gas to Methanol. ACS Sustain. Chem. Eng. 2014, 2, 30–37. [Google Scholar] [CrossRef]
- Salkuyeh, Y.K.; Adams, T.A., II. Shale gas for the petrochemical industry: Incorporation of novel technologies. In Computer Aided Chemical Engineering; Elsevier: New York, NY, USA, 2014; Volume 34, pp. 603–608. [Google Scholar]
- Hasaneen, R.; El-Halwagi, M.M. Integrated Process and Microeconomic Analyses to Enable Effective Environmental Policy for Shale Gas in the United States. Clean Technol. Environ. Policy 2017, 19, 1775–1789. [Google Scholar] [CrossRef]
- Arredondo-Ramírez, K.; Ponce-Ortega, J.M.; El-Halwagi, M.M. Optimal Planning and Infrastructure Development of Shale Gas. Energy Convers. Manag. 2016, 119, 91–100. [Google Scholar] [CrossRef]
- Gao, J.; You, F. Optimal design and operations of supply chain networks for water management in shale gas production: MILFP model and algorithms for the water-energy nexus. AIChE J. 2015, 61, 1184–1208. [Google Scholar] [CrossRef]
- Carrero-Parreño, A.; Onishi, V.C.; Salcedo-Díaz, R.; Ruiz-Femenia, R.; Fraga, E.S.; Caballero, J.A.; Reyes-Labarta, J.A. Optimal Pretreatment System of Flowback Water from Shale Gas Production. Ind. Eng. Chem. Res. 2017, 56, 4386–4398. [Google Scholar] [CrossRef]
- Yang, L.; Grossmann, I.E.; Manno, J. Optimization models for shale gas water management. AIChE J. 2014, 60, 3490–3501. [Google Scholar] [CrossRef]
- Nicot, J.-P.; Scanlon, B.R. Water Use for Shale-Gas Production in Texas. U.S. Environ. Sci. Technol. 2012, 46, 3580–3586. [Google Scholar] [CrossRef] [PubMed]
- Elsayed, A.N.; Barrufet, M.A.; Eljack, F.T.; El-Halwagi, M.M. Optimal Design of Thermal Membrane Distillation Systems for the Treatment of Shale Gas Flowback Water. Int. J. Membr. Sci. Technol. 2015, 2, 1–9. [Google Scholar]
- Boschee, P. Produced and Flowback Water Recycling and Reuse: Economics, Limitations, and Technology. Oil Gas Facil. 2014, 3, 16–21. [Google Scholar] [CrossRef]
- Lira-Barragán, L.; Ponce-Ortega, J.M.; Guillén-Gosálbez, G.; El-Halwagi, M.M. Optimal Water Management under Uncertainty for Shale Gas Production. Ind. Eng. Chem. Res. 2016, 55, 1322–1335. [Google Scholar] [CrossRef]
- Chen, H.; Carter, K.E. Water usage for natural gas production through hydraulic fracturing in the United States from 2008 to 2014. J. Environ. Manag. 2016, 170, 152–159. [Google Scholar] [CrossRef] [PubMed]
- Shaffer, D.L.; Chavez, L.H.A.; Ben-Sasson, M.; Castrillón, S.R.; Yip, N.Y.; Elimelech, M. Desalination and reuse of high-salinity shale gas produced water: Drivers, technologies, and future directions. Environ. Sci. Technol. 2013, 47, 9569–9583. [Google Scholar] [CrossRef] [PubMed]
- Lokare, O.R.; Tavakkoli, S.; Rodriguez, G.; Khanna, V.; Vidic, R.D. Integrating membrane distillation with waste heat from natural gas compressor stations for produced water treatment in Pennsylvania. Desalination 2017, 413, 144–153. [Google Scholar] [CrossRef]
- Tavakkoli, S.; Lokare, O.R.; Vidic, R.D.; Khanna, V. A techno-economic assessment of membrane distillation for treatment of Marcellus shale produced water. Desalination 2017, 416, 24–34. [Google Scholar] [CrossRef]
- Bamufleh, H.; Abdelhady, F.; Baaqeel, H.M.; El-Halwagi, M.M. Optimization of Multi-Effect Distillation with Brine Treatment via Membrane Distillation and Process Heat Integration. Desalination 2017, 408, 110–118. [Google Scholar] [CrossRef]
- Gabriel, K.; El-Halwagi, M.M.; Linke, P. Optimization Across Water-Energy Nexus for Integrating Heat, Power, and Water for Industrial Processes Coupled with Hybrid Thermal-Membrane Desalination. Ind. Eng. Chem. Res. 2016, 55, 3442–3466. [Google Scholar] [CrossRef]
- Elsayed, A.N.; Barrufet, M.A.; El-Halwagi, M.M. An Integrated Approach for Incorporating Thermal Membrane Distillation in Treating Water in Heavy Oil Recovery using SAGD. J. Unconv. Oil Gas Resour. 2015, 12, 6–14. [Google Scholar] [CrossRef]
- González-Bravo, R.; Nápoles-Rivera, F.; Ponce-Ortega, J.M.; Nyapathi, M.; Elsayed, N.A.; El-Halwagi, M.M. Synthesis of Optimal Thermal Membrane Distillation Networks. AIChE J. 2015, 61, 448–463. [Google Scholar] [CrossRef]
- González-Bravo, R.; Elsayed, N.A.; Ponce-Ortega, J.M.; Nápoles-Rivera, F.; Serna-González, M.; El-Halwagi, M.M. Optimal Design of Thermal Membrane Distillation Systems with Heat Integration with Process Plants. Appl. Therm. Eng. 2014, 75, 154–166. [Google Scholar] [CrossRef]
- Elsayed, A.N.; Barrufet, M.A.; El-Halwagi, M.M. Integration of Thermal Membrane Distillation Networks with Processing Facilities. Ind. Eng. Chem. Res. 2014, 53, 5284–5298. [Google Scholar] [CrossRef]
- Tovar-Facio, J.; Eljack, F.; Ponce-Ortega, J.M.; El-Halwagi, M.M. Optimal Design of Multiplant Cogeneration Systems with Uncertain Flaring and Venting. ACS Sustain. Chem. Eng. 2016, 5, 675–688. [Google Scholar] [CrossRef]
- Pham, V.; Laird, C.; El-Halwagi, M.M. Convex Hull Discretization Approach to the Global Optimization of Pooling Problems. Ind. Eng. Chem. Res. 2009, 48, 1973–1979. [Google Scholar] [CrossRef]
- Gabriel, F.; El-Halwagi, M.M. Simultaneous Synthesis of Waste Interception and Material Reuse Networks: Problem Reformulation for Global Optimization. Environ. Prog. 2005, 24, 171–180. [Google Scholar] [CrossRef]
- El-Halwagi, M.M. Sustainable Design through Process Integration: Fundamentals and Applications to Industrial Pollution Prevention, Resource Conservation, and Profitability Enhancement, 2nd ed.; IChemE/Elsevier: New York, NY, USA, 2017. [Google Scholar]
- Khor, S.C.; Foo, D.C.Y.; El-Halwagi, M.M.; Tan, R.R.; Shah, N. A Superstructure Optimization Approach for Membrane Separation-Based Water Regeneration Network Synthesis with Detailed Nonlinear Mechanistic Reverse Osmosis Model. Ind. Eng. Chem. Res. 2011, 50, 13444–13456. [Google Scholar] [CrossRef]
- Alnouri, S.; Linke, P.; El-Halwagi, M.M. Synthesis of Industrial Park Water Reuse Networks Considering Treatment Systems and Merged Connectivity Options. Comp. Chem. Eng. 2016, 91, 289–306. [Google Scholar] [CrossRef]
- El-Halwagi, M.A.; Manousiouthakis, V.; El-Halwagi, M.M. Analysis and Simulation of Hollwo Fiber Reverse Osmosis Modules. Sep. Sci. Technol. 1996, 31, 2505–2529. [Google Scholar] [CrossRef]
- El-Halwagi, M.M. Synthesis of Optimal Reverse-Osmosis Networks for Waste Reduction. AIChE J. 1992, 38, 1185–1198. [Google Scholar] [CrossRef]
- Goswami, D.Y.; Kreith, F. Energy Conversion; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Mittelman, G.; Epstein, M. A novel power block for CSP systems. Sol. Energy 2010, 84, 1761–1771. [Google Scholar] [CrossRef]
- Eck, M.; Hirsch, T.; Feldhoff, J.F.; Kretschmann, D.; Dersch, J.; Morales, A.G.; Gonzalez-Martinez, L.; Bachelier, C.; Platzer, W.; Riffelmann, K.-J. Guidelines for CSP yield analysis–optical losses of line focusing systems; definitions, sensitivity analysis and modeling approaches. Energy Procedia 2014, 49, 1318–1327. [Google Scholar] [CrossRef]
- Channiwala, S.; Ekbote, A. A generalized model to estimate field size for solar-only parabolic trough plant. In Proceedings of the 3rd Southern African Solar Energy Conference, Skukuza, South Africa, 11–13 May 2015. [Google Scholar]
- Lovegrove, K.; Stein, W. Concentrating Solar Power Technology: Principles, Developments and Applications; Elsevier: New York, NY, USA, 2012. [Google Scholar]
- Quaschning, V.; Kistner, R.; Ortmanns, W. Influence of direct normal irradiance variation on the optimal parabolic trough field size: A problem solved with technical and economical simulations. J. Sol. Energy Eng. 2002, 124, 160–164. [Google Scholar] [CrossRef]
- Herrmann, U.; Kearney, D.W. Survey of thermal energy storage for parabolic trough power plants. J. Sol. Energy Eng. 2002, 124, 145–152. [Google Scholar] [CrossRef]
- Al-Azri, N.; Al-Thubaiti, M.; El-Halwagi, M.M. An Algorithmic Approach to the Optimization of Process Cogeneration. J. Clean Technol. Environ. Policy 2009, 11, 329–338. [Google Scholar] [CrossRef]
- Mavromatis, S.; Kokossis, A. Conceptual optimisation of utility networks for operational variations—I. Targets and level optimisation. Chem. Eng. Sci. 1998, 53, 1585–1608. [Google Scholar] [CrossRef]
- Bamufleh, S.H.; Ponce-Ortega, J.M.; El-Halwagi, M.M. Multi-objective optimization of process cogeneration systems with economic, environmental, and social tradeoffs. Clean Technol. Environ. Policy 2013, 15, 185–197. [Google Scholar] [CrossRef]
- El-Halwagi, M.M. A Return on Investment Metric for Incorporating Sustainability in Process Integration and Improvement Projects. Clean Technol. Environ. Policy 2017, 19, 611–617. [Google Scholar] [CrossRef]
- Guillen-Cuevas, K.; Ortiz-Espinoza, A.P.; Ozinan, E.; Jiménez-Gutiérrez, A.; Kazantzis, N.K.; El-Halwagi, M.M. Incorporation of Safety and Sustainability in Conceptual Design via A Return on Investment Metric. ACS Sustain. Chem. Eng. 2018, 6, 1411–1416. [Google Scholar] [CrossRef]
- Kondash, J.A.; Albright, E.; Vengosh, A. Quantity of flowback and produced waters from unconventional oil and gas exploration. Sci. Total Environ. 2017, 574, 314–321. [Google Scholar] [CrossRef] [PubMed]
- Atilhan, S.; Linke, P.; Abdel-Wahab, A.; El-Halwagi, M.M. A Systems Integration Approach to the Design of Regional Water Desalination and Supply Networks. Int. J. Process Syst. Eng. 2011, 1, 125–135. [Google Scholar] [CrossRef]
- Ghaffour, N.; Missimer, T.M.; Amy, G.L. Technical review and evaluation of the economics of water desalination: Current and future challenges for better water supply sustainability. Desalination 2013, 309, 197–207. [Google Scholar] [CrossRef]
- Mezher, T.; Fath, H.; Abbas, Z.; Khaled, A. Techno-economic assessment and environmental impacts of desalination technologies. Desalination 2011, 266, 263–273. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory. Assessment of Parabolic Trough and Power Tower Solar Technology Cost and Performance Forecasts; DIANE Publishing: Collingdale, PA, USA, 2003. [Google Scholar]
- Price, H. A parabolic trough solar power plant simulation model. In Proceedings of the ASME International Solar Energy Conference, Kohala Coast, HI, USA, 15–18 March 2003. [Google Scholar]
- Horwitt, D.; Sumi, L. Up in Flames: US Shale Oil Boom Comes at Expense of Wasted Natural Gas, Increased CO2; Earthworks: Washington, DC, USA, 2014. [Google Scholar]
- RPSEA. Advanced Treatment of Shale Gas Fracturing Water to Produce Re-Use or Discharge Quality Water. 2015. Retrieved November, 2017. Available online: https://www.rpsea.org/node/222 (accessed on 18 Novemeber 2017).
- Giuliano, S.; Buck, R.; Eguiguren, S. Analysis of solar-thermal power plants with thermal energy storage and solar-hybrid operation strategy. J. Sol. Energy Eng. 2011, 133, 031007. [Google Scholar] [CrossRef]
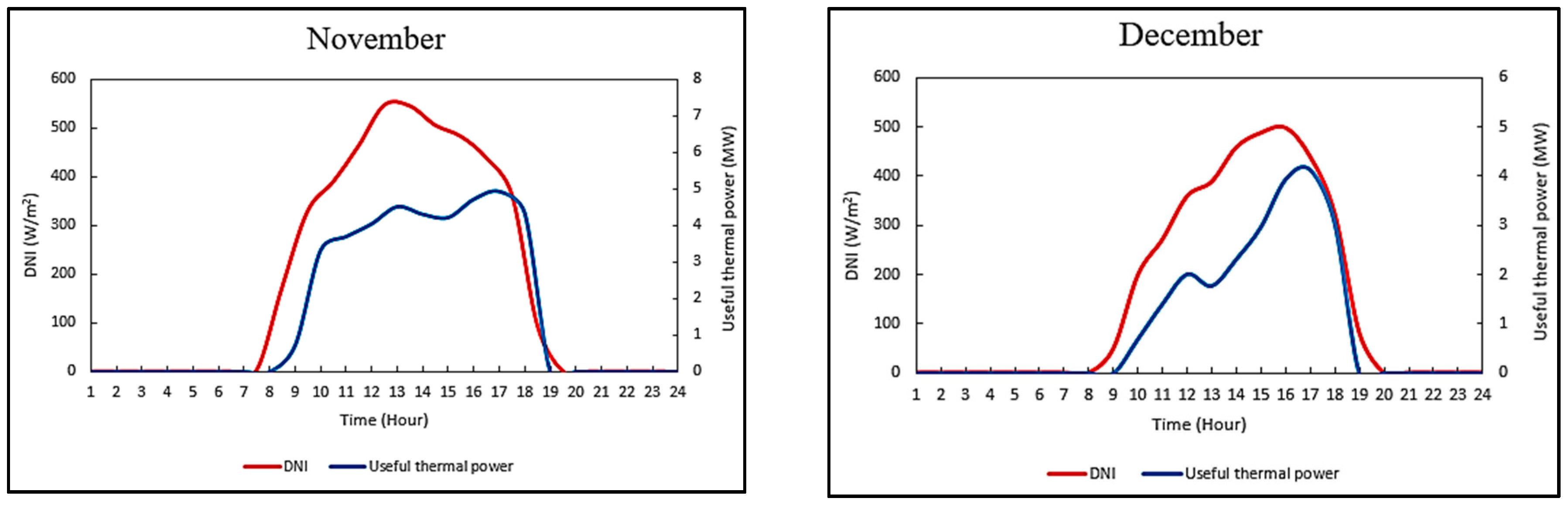
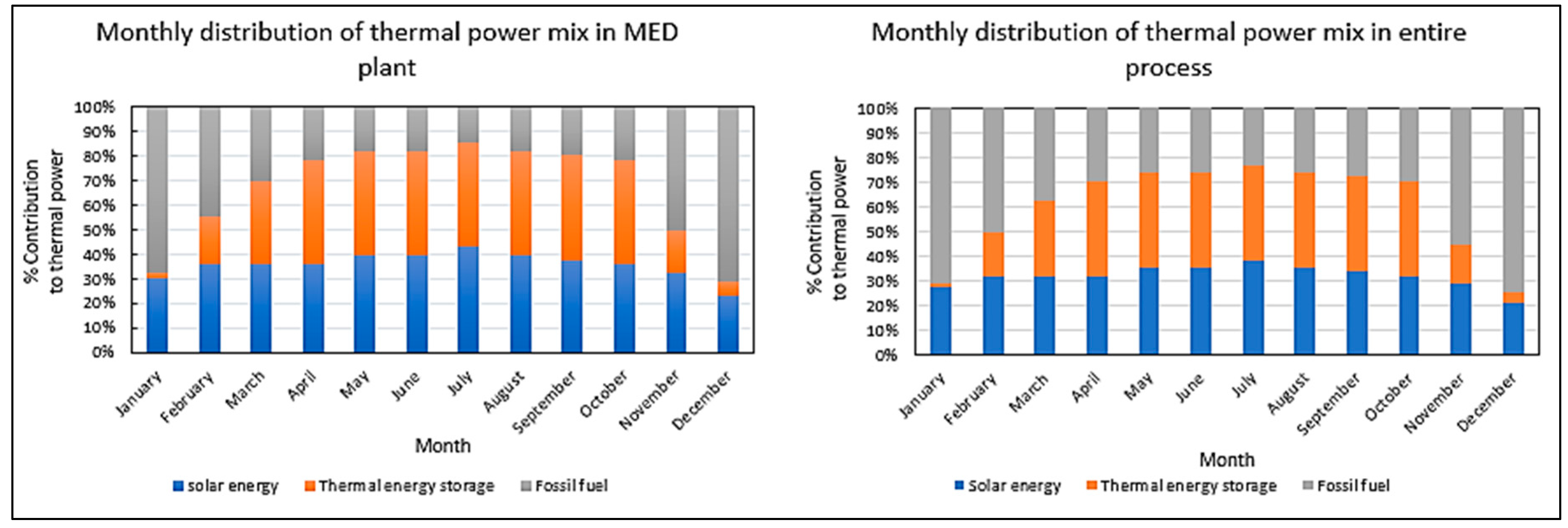
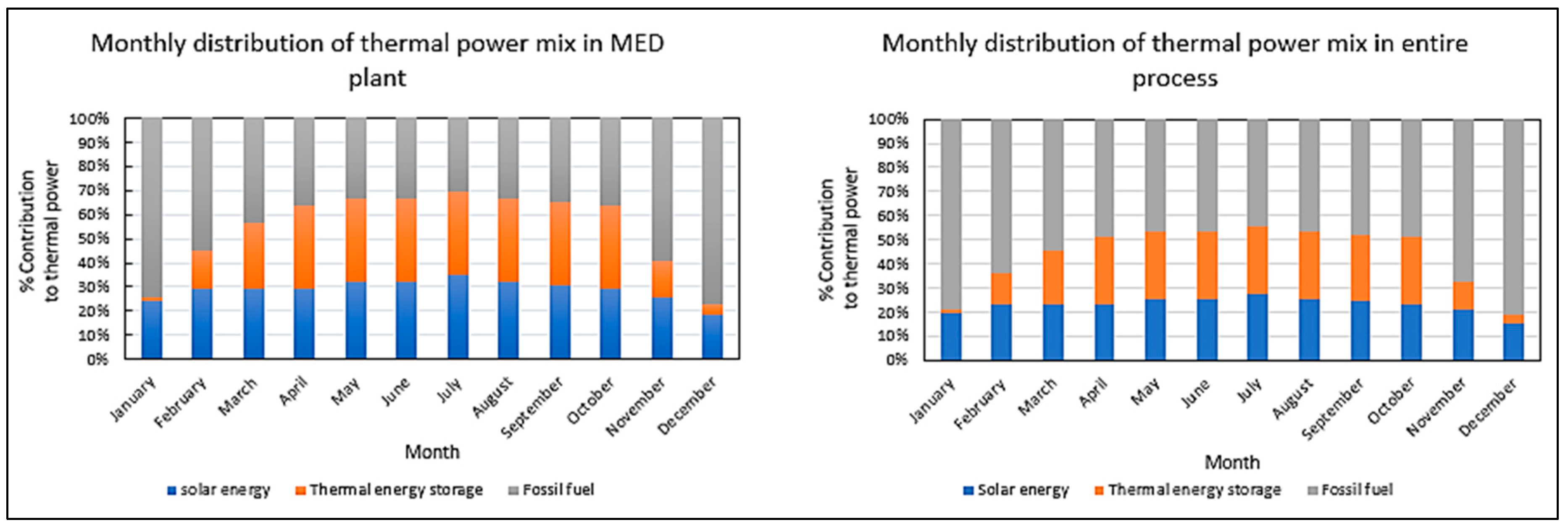
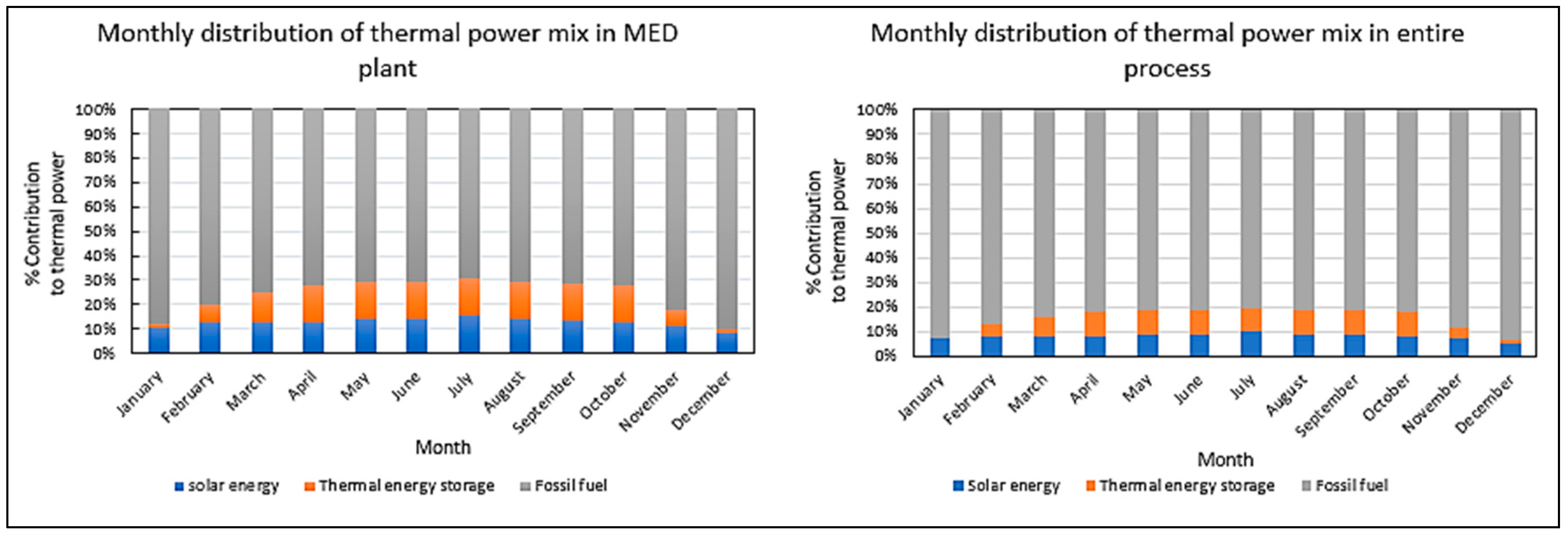
| Technology | Thermal Energy Consumption (kWht/m3 Desalinated Water) | Electric Energy Consumption (kWhe/m3 Desalinated Water) | Annualized Fixed Cost (AFC) ($/year) | Operating Cost ($/m3 seawater) | Water Recovery (m3 Desalinated Water/m3 Feed Seawater) | Value of Desalinated Water ($/m3 Desalinated Water) | Outlet Salt Content (ppm) |
|---|---|---|---|---|---|---|---|
| RO | - | 4 | 0.18 | 0.55 | 0.88 | 200 | |
| MED | 65 | 2 | 0.24 | 0.65 | 0.82 | 80 |
| Item | Receivers | Mirrors | Concentrator Structure | Concentrator Erection | Drive | Piping |
| Cost $/m2 | 43 | 40 | 47 | 14 | 13 | 10 |
| Item | Electronic and Control | Header Piping | Civil Works | Spares, HTF, Freight | Contingency | Structures and Improvement |
| Cost $/m2 | 14 | 7 | 18 | 17 | 11 | 7 |
| Type | ($/barrel) |
|---|---|
| Fresh water | 0.24 |
| Disposal (deep well + landfill) | 0.05 |
| Primary and secondary treatment | 0.34 |
| Transportation | 0.89 |
| Percentage Contribution * (%) | Percentage Contribution ** (%) | Total Annual Cost (MM $/year) | Annual Net (After Tax) Profit (MM $/year) | ROI (%) | Payback Period (year) |
|---|---|---|---|---|---|
| 0.0 | 35.3 | 50.4 | 14.9 | 5.9 | |
| 50 | 35.1 | 50.6 | 14.96 | 5.6 | |
| 100 | 34.8 | 50.8 | 15 | 5.5 | |
| 0.0 | 28.1 | 48.8 | 17.2 | 4.9 | |
| 50 | 27.8 | 49 | 17 | 4.8 | |
| 100 | 27.5 | 49.2 | 17.3 | 4.8 | |
| 0.0 | 23.5 | 47.7 | 19.1 | 4.4 | |
| 50 | 23.2 | 47.9 | 19.2 | 4.3 | |
| 100 | 22.8 | 48.1 | 19.3 | 4.3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Aboosi, F.Y.; El-Halwagi, M.M. An Integrated Approach to Water-Energy Nexus in Shale-Gas Production. Processes 2018, 6, 52. https://doi.org/10.3390/pr6050052
Al-Aboosi FY, El-Halwagi MM. An Integrated Approach to Water-Energy Nexus in Shale-Gas Production. Processes. 2018; 6(5):52. https://doi.org/10.3390/pr6050052
Chicago/Turabian StyleAl-Aboosi, Fadhil Y., and Mahmoud M. El-Halwagi. 2018. "An Integrated Approach to Water-Energy Nexus in Shale-Gas Production" Processes 6, no. 5: 52. https://doi.org/10.3390/pr6050052
APA StyleAl-Aboosi, F. Y., & El-Halwagi, M. M. (2018). An Integrated Approach to Water-Energy Nexus in Shale-Gas Production. Processes, 6(5), 52. https://doi.org/10.3390/pr6050052