The Impact of Global Sensitivities and Design Measures in Model-Based Optimal Experimental Design
Abstract
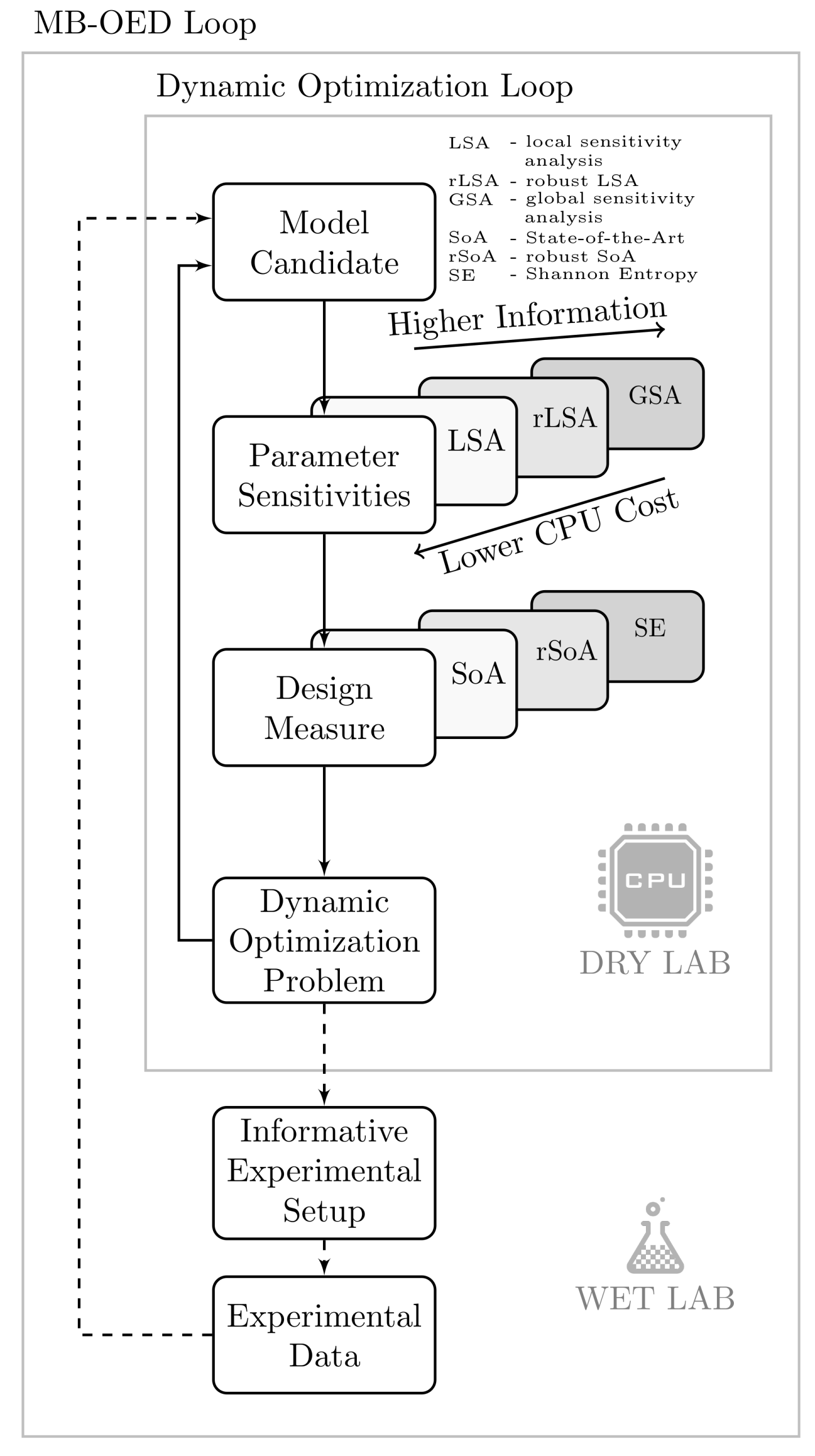
1. Introduction
2. Sensitivity Measures
2.1. Local Parameter Sensitivities
2.2. Robustification: Multi-Point Averaging Approach
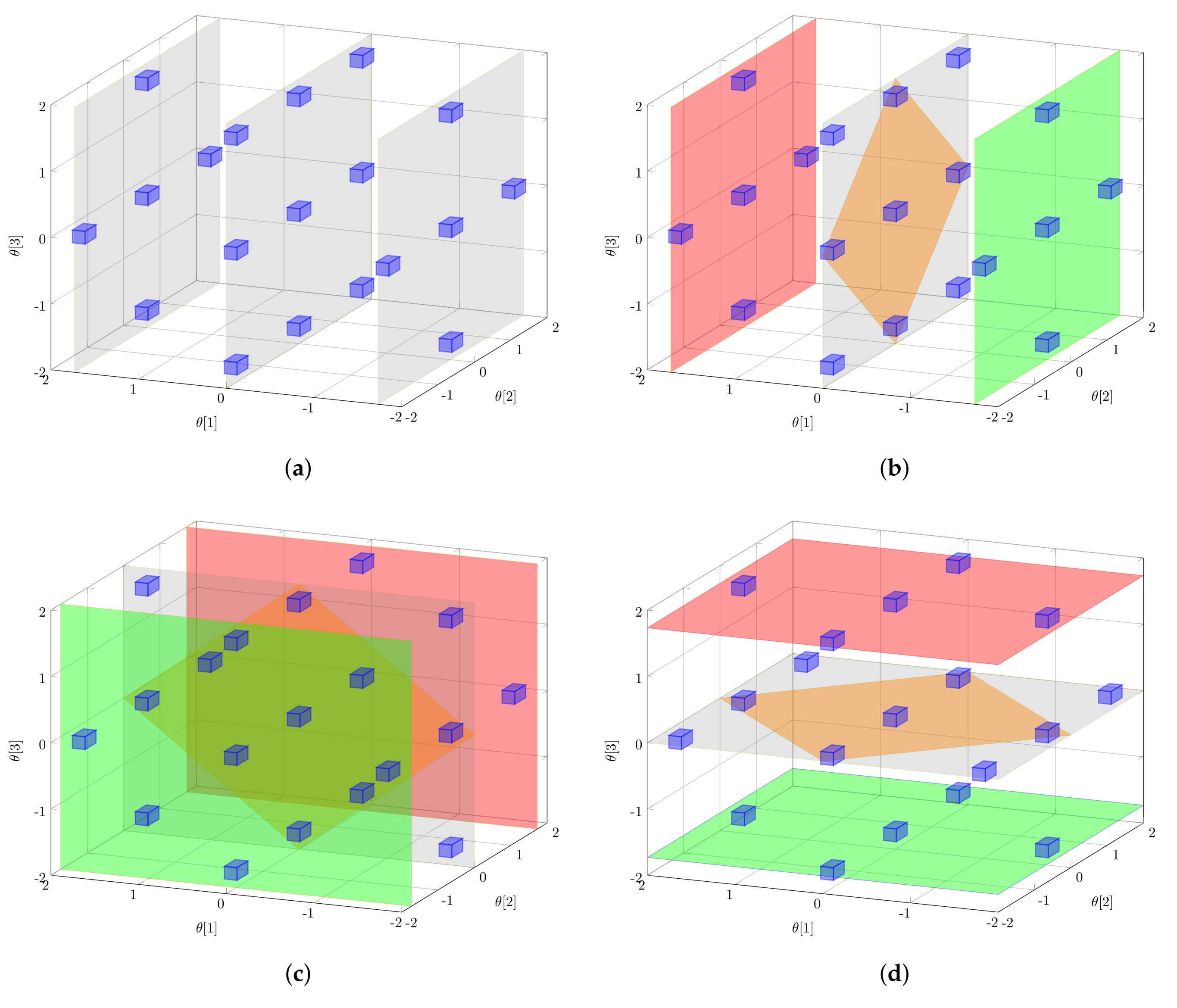
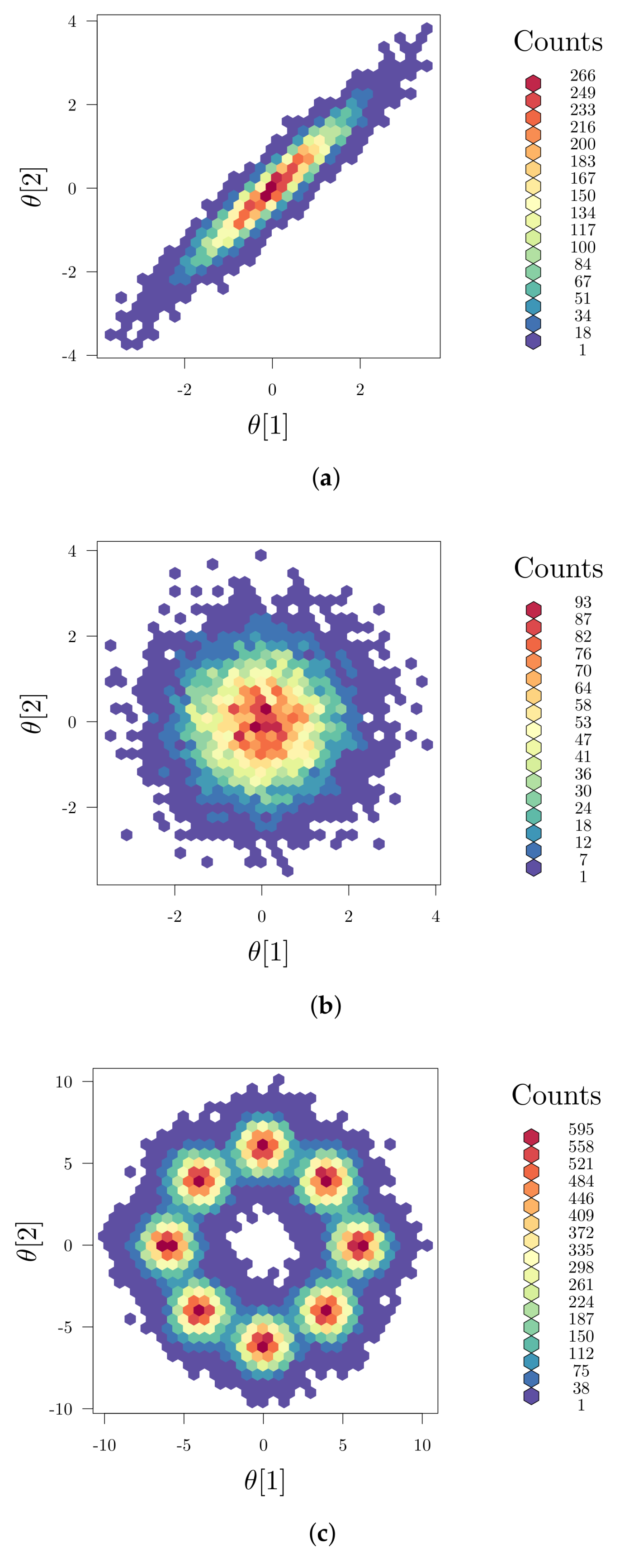
2.3. Global Parameter Sensitivities
2.4. Implementation Aspects
3. Optimal Design Measures
3.1. Local Design Measures
3.2. Global Design Measures
4. Case Studies
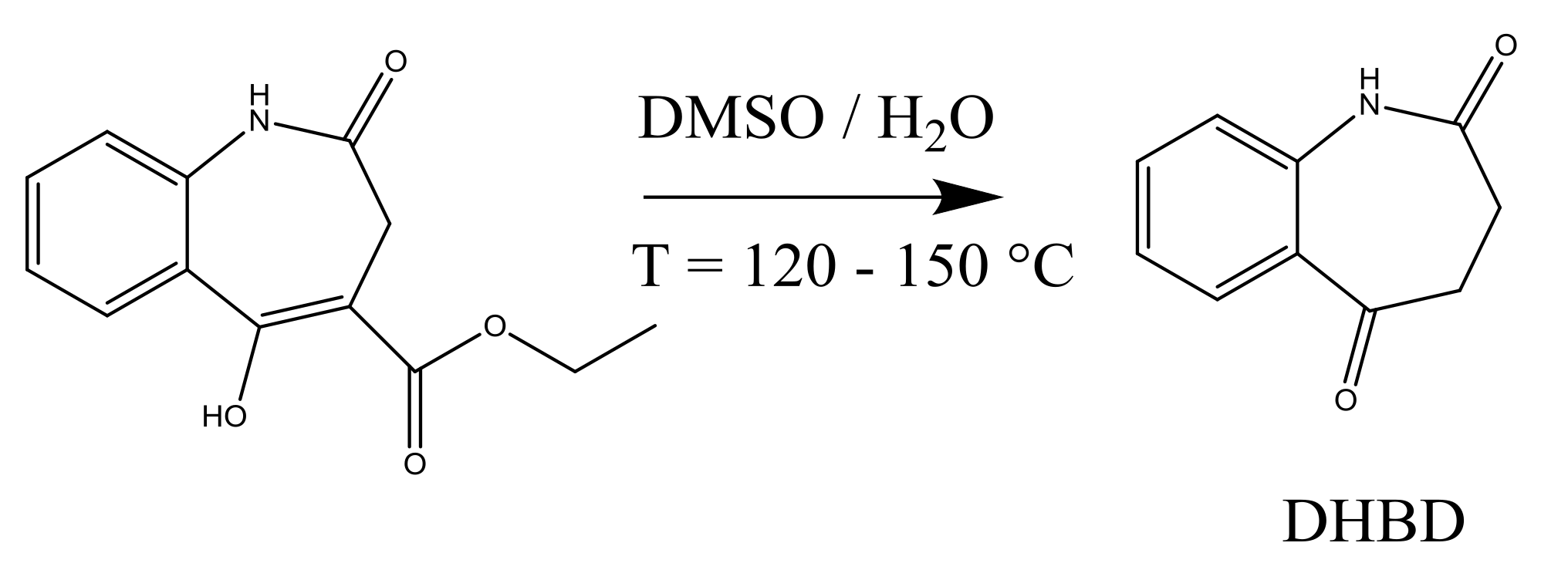
4.1. Synthesis of an API–Scaffold (DHBD)
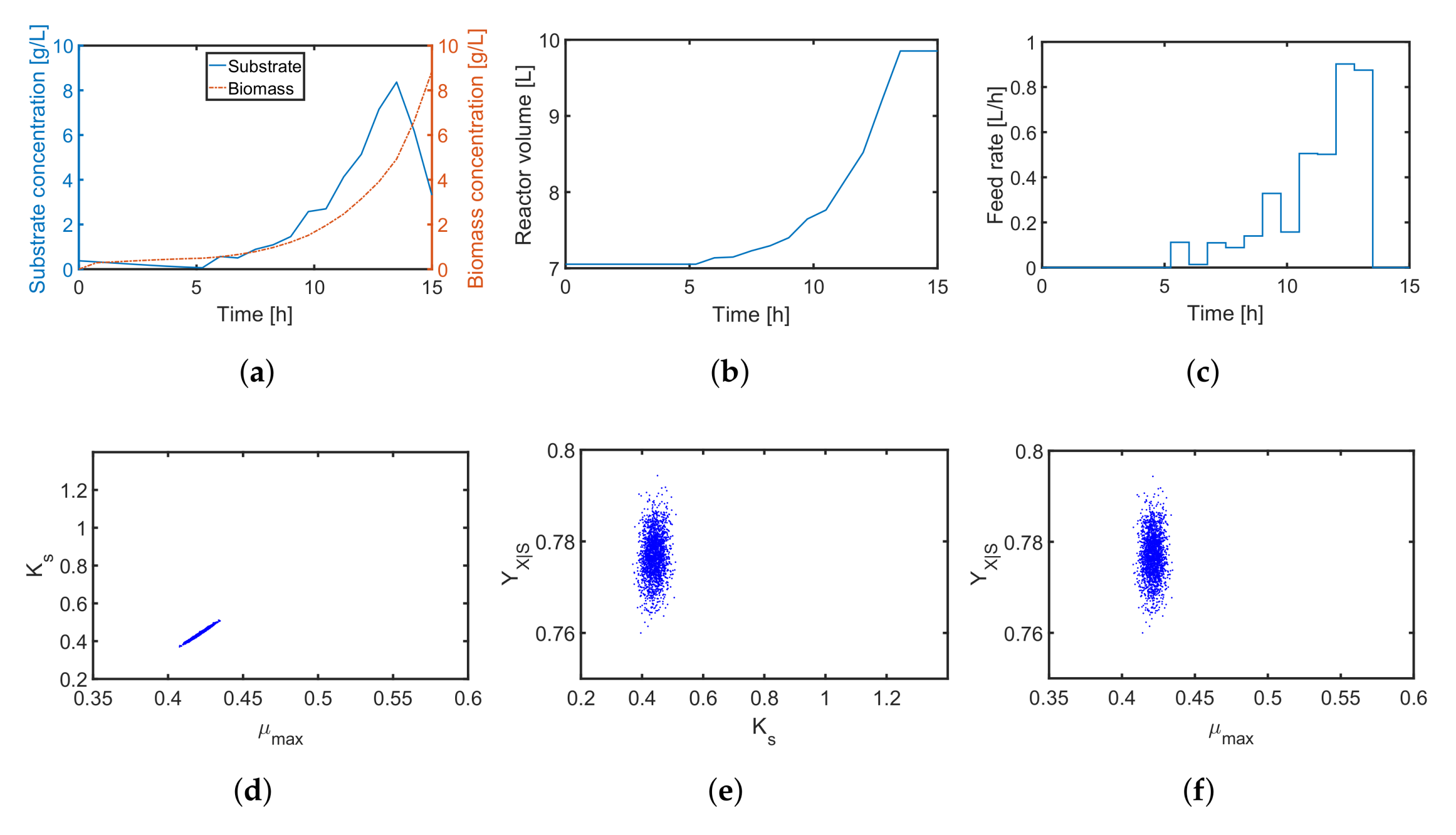
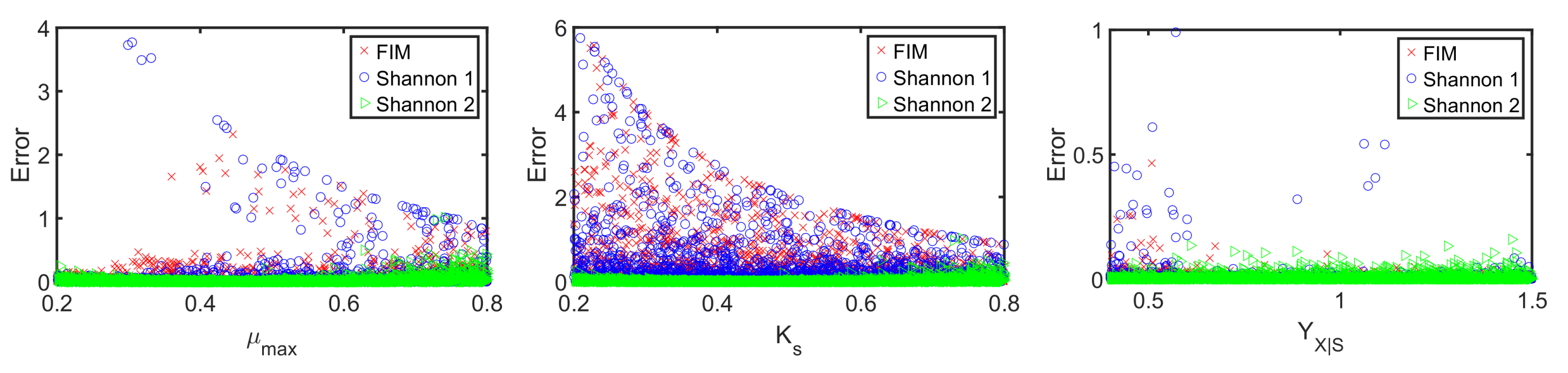
4.2. A Fed-Batch Bioreactor
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Franz, A.; Song, H.S.; Ramkrishna, D.; Kienle, A. Experimental and theoretical analysis of poly(β-hydroxybutyrate) formation and consumption in Ralstonia eutropha. Biochem. Eng. J. 2011, 55, 49–58. [Google Scholar] [CrossRef]
- Grimard, J.; Dewasme, L.; Wouwer, A.V. A review of dynamic models of hot-melt extrusion. Processes 2016, 4, 19. [Google Scholar] [CrossRef]
- Bück, A.; Neugebauer, C.; Meyer, K.; Palis, S.; Diez, E.; Kienle, A.; Heinrich, S.; Tsotsas, E. Influence of operation parameters on process stability in continuous fluidised bed layering with external product classification. Powder Technol. 2016, 300, 37–45. [Google Scholar] [CrossRef]
- Logist, F.; Erdeghem, P.V.; Smets, I.Y.; Impe, J.F.V. Multiple-objective optimisation of a jacketed tubular reactor. In Proceedings of the 2007 European Control Conference (ECC), Kos, Greece, 2–5 July 2007; pp. 963–970. [Google Scholar]
- Kunde, C.; Michaels, D.; Micovic, J.; Lutze, P.; Górak, A.; Kienle, A. Deterministic global optimization in conceptual process design of distillation and melt crystallization. Chem. Eng. Process. Process Intensif. 2016, 99, 132–142. [Google Scholar] [CrossRef]
- Kaiser, N.M.; Flassig, R.J.; Sundmacher, K. Probabilistic reactor design in the framework of elementary process functions. Comput. Chem. Eng. 2016, 94, 45–59. [Google Scholar] [CrossRef]
- Föste, H.; Schöler, M.; Majschak, J.P.; Augustin, W.; Scholl, S. Modeling and validation of the mechanism of pulsed flow cleaning. Heat Transf. Eng. 2013, 34, 753–760. [Google Scholar] [CrossRef]
- Schenkendorf, R. Supporting the shift towards continuous pharmaceutical manufacturing by condition monitoring. In Proceedings of the 2016 IEEE 3rd Conference on Control and Fault-Tolerant Systems (SysTol), Barcelona, Spain, 7–9 September 2016. [Google Scholar]
- Jelemensk, M.; Klauo, M.; Paulen, R.; Lauwers, J.; Logist, F.; Impe, J.V.; Fikar, M. Time-optimal control and parameter estimation of diafiltration processes in the presence of membrane fouling. IFAC-PapersOnLine 2016, 49, 242–247. [Google Scholar] [CrossRef]
- Rogers, A.J.; Inamdar, C.; Ierapetritou, M.G. An integrated approach to simulation of pharmaceutical processes for solid drug manufacture. Ind. Eng. Chem. Res. 2014, 53, 5128–5147. [Google Scholar] [CrossRef]
- Rantanen, J.; Khinast, J. The future of pharmaceutical manufacturing sciences. J. Pharm. Sci. 2015, 104, 3612–3638. [Google Scholar] [CrossRef] [PubMed]
- Ljung, L. System Identification: Theory for the User; Prentice-Hall: Upper Saddle River, NJ, USA, 1987. [Google Scholar]
- Balsa-Canto, E.; Alonso, A.A.; Banga, J.R. An iterative identification procedure for dynamic modeling of biochemical networks. BMC Syst. Biol. 2010, 4, 11. [Google Scholar] [CrossRef] [PubMed]
- Walter, E.E.; Pronzato, L. Identification of Parametric Models from Experimental Data; Springer: New York, NY, USA, 1997; p. 413. [Google Scholar]
- Rodríguez-Aragón, L.J.; López-Fidalgo, J. Optimal designs for the Arrhenius equation. Chemom. Intell. Lab. Syst. 2005, 77, 131–138. [Google Scholar] [CrossRef]
- Schenkendorf, R.; Kremling, A.; Mangold, M. Optimal experimental design with the sigma point method. IET Syst. Biol. 2009, 3, 10–23. [Google Scholar] [CrossRef] [PubMed]
- Galvanin, F.; Marchesini, R.; Barolo, M.; Bezzo, F.; Fidaleo, M. Optimal design of experiments for parameter identification in electrodialysis models. Chem. Eng. Res. Des. 2016, 105, 107–119. [Google Scholar] [CrossRef]
- Kiefer, J. Optimum experimental designs. J. R. Stat. Soc. Ser. B 1959, 21, 272–319. [Google Scholar]
- Martínez, E.C.; Cristaldi, M.D.; Grau, R.J. Design of Dynamic Experiments in Modeling for Optimization of Batch Processes. Ind. Eng. Chem. Res. 2009, 48, 3453–3465. [Google Scholar] [CrossRef]
- Sinkoe, A.; Hahn, J. Optimal experimental design for parameter estimation of an IL-6 signaling model. Processes 2017, 5, 49. [Google Scholar] [CrossRef]
- Manesso, E.; Sridharan, S.; Gunawan, R. Multi-objective optimization of experiments using curvature and Fisher information matrix. Processes 2017, 5, 63. [Google Scholar] [CrossRef]
- Chaloner, K.; Verdinelli, I. Bayesian experimental design: A review. Stat. Sci. 1995, 10, 273–304. [Google Scholar] [CrossRef]
- Gotwalt, C.M.; Jones, B.A.; Steinberg, D.M. Fast computation of designs robust to parameter uncertainty for nonlinear settings. Technometrics 2009, 51, 88–95. [Google Scholar] [CrossRef]
- Overstall, A.M.; Woods, D.C. Bayesian design of experiments using approximate coordinate exchange. Technometrics 2017, 59, 458–470. [Google Scholar] [CrossRef]
- Chu, Y.; Hahn, J. Necessary condition for applying experimental design criteria to global sensitivity analysis results. Comput. Chem. Eng. 2013, 48, 280–292. [Google Scholar] [CrossRef]
- Rodriguez-Fernandez, M.; Kucherenko, S.; Pantelides, C.; Shah, N. Optimal experimental design based on global sensitivity analysis. Comput. Aided Chem. Eng. 2007, 24, 63–68. [Google Scholar]
- Bockstal, P.J.V.; Mortier, S.; Corver, J.; Nopens, I.; Gernaey, K.V.; Beer, T.D. Global sensitivity analysis as good modelling practices tool for the identification of the most influential process parameters of the primary drying step during freeze-drying. Eur. J. Pharm. Biopharm. 2018, 123, 108–116. [Google Scholar] [CrossRef] [PubMed]
- Scire, J., Jr.; Dryer, F.; Yetter, R. Comparison of global and local sensitivity techniques for rate constants determined using complex reaction mechanisms. Int. J. Chem. Kinet. 2001, 33, 784–802. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Tarantola, S.; Campolongo, F. Sensititivity analysis for chemical Models. Chem. Rev. 2005, 105, 2811–2828. [Google Scholar] [CrossRef] [PubMed]
- Saltelli, A.; Aleksankina, K.; Becker, W.; Fennell, P.; Ferretti, F.; Holst, N.; Sushan, L.; Wu, Q. Why so many published sensitivity analyses are false. A systematic review of sensitivity analysis practices. arXiv, 2017; arXiv:1711.11359. [Google Scholar]
- Rao, M.M.; Swift, R.J. Probability Theory with Applications; Springer: New York, NY, USA, 2006. [Google Scholar]
- Turanyi, T. Sensitivity Analysis of Complex Kinetic Systems. Tools and Applications. J. Math. Chem. 1990, 5, 203–248. [Google Scholar] [CrossRef]
- Bauer, I.; Bock, H.G.; Körkel, S.; Schlöder, J.P. Numerical methods for optimum experimental design in DAE systems. J. Comput. Appl. Math. 2010, 120, 1–25. [Google Scholar] [CrossRef]
- Ten Broeke, G.; van Voorn, G.; Kooi, B.; Molenaar, J. Detecting tipping points in ecological models with sensitivity analysis. Math. Model. Nat. Phenom. 2016, 11, 47–72. [Google Scholar] [CrossRef]
- Kucherenko, S.; Rodriguez-Fernandez, M.; Pantelides, C.; Shah, N. Monte Carlo evaluation of derivative-based global sensitivity measures. Reliab. Eng. Syst. Saf. 2009, 94, 1135–1148. [Google Scholar] [CrossRef]
- Rakovec, O.; Hill, M.C.; Clark, M.P.; Weerts, A.H.; Teuling, A.J.; Uijlenhoet, R. Distributed evaluation of local sensitivity analysis (DELSA), with application to hydrologic models. Water Resour. Res. 2014, 50, 409–426. [Google Scholar] [CrossRef]
- Zádor, J.; Zsély, I.; Turányi, T. Local and global uncertainty analysis of complex chemical kinetic systems. Reliab. Eng. Syst. Saf. 2006, 91, 1232–1240. [Google Scholar] [CrossRef]
- Iooss, B.; Lemaître, P. A review on global sensitivity analysis methods. arXiv, 2014; arXiv:1404.2405. [Google Scholar]
- Sobol, I. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Buzzard, G.T. Global sensitivity analysis using sparse grid interpolation and polynomial chaos. Reliab. Eng. Syst. Saf. 2012, 107, 82–89. [Google Scholar] [CrossRef]
- Caflisch, R.E. Monte Carlo and quasi-Monte Carlo methods. Acta Numer. 1998, 7, 1–49. [Google Scholar] [CrossRef]
- Sudret, B. Uncertainty Propagation and Sensitivity Analysis in Mechanical Models Contributions to Structural Reliability and Stochastic Spectral Methods; Habilitation a diriger des recherches; Université Blaise Pascal: Clermont-Ferrand, France, 2007. [Google Scholar]
- Tyler, G.W. Numerical integration of functions of several variables. Can. J. Math. 1953, 5, 393–412. [Google Scholar] [CrossRef]
- Lerner, U.N. Hybrid Bayesian Networks for Reasoning about Complex Systems. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2002. [Google Scholar]
- Evans, D.H. An application of numerical integration techniques to statistical tolerancing. Technometrics 1967, 9, 441–456. [Google Scholar] [CrossRef]
- Joshi, M.; Seidel-Morgenstern, A.; Kremling, A. Exploiting the bootstrap method for quantifying parameter confidence intervals in dynamical systems. Metab. Eng. 2006, 8, 447–455. [Google Scholar] [CrossRef] [PubMed]
- Heine, T.; Kawohl, M.; King, R. Derivative-free optimal experimental design. Chem. Eng. Sci. 2008, 63, 4873–4880. [Google Scholar] [CrossRef]
- Schenkendorf, R.; Mangold, M. Qualitative and quantitative optimal experimental design for parameter identification of a MAP kinase model. IFAC Proc. Vol. 2011, 44, 11666–11671. [Google Scholar] [CrossRef]
- Schenkendorf, R.; Mangold, M. Online model selection approach based on unscented Kalman filtering. J. Process Control 2013, 23, 44–57. [Google Scholar] [CrossRef]
- Franceschini, G.; Macchietto, S. Novel anticorrelation criteria for design of experiments: Algorithm and application. AIChE J. 2008, 54, 3221–3238. [Google Scholar] [CrossRef]
- Ohs, R.; Wendlandt, J.; Spiess, A.C. How graphical analysis helps interpreting optimal experimental designs for nonlinear enzyme kinetic models. AIChE J. 2017, 63, 4870–4880. [Google Scholar] [CrossRef]
- Embrechts, P.; Mcneil, A.; Straumann, D. Correlation and dependence in risk management: Properties and pitfalls. In RISK Management: Value at Risk and Beyond; Cambridge University Press: Cambridge, UK, 2002; pp. 176–223. [Google Scholar]
- Kucerová, A.; Sỳkora, J.; Janouchová, E.; Jarušková, D.; Chleboun, J. Acceleration of robust experiment design using Sobol indices and polynomial chaos expansion. In Proceedings of the 7th International Workshop on Reliable Engineering Computing (REC), Bochum, Germany, 15–17 June 2016; pp. 411–426. [Google Scholar]
- Lindley, D.V. On a measure of the information provided by an experiment. Ann. Math. Stat. 1956, 27, 986–1005. [Google Scholar] [CrossRef]
- Becker, A.; Kohfeld, S.; Lader, A.; Preu, L.; Pies, T.; Wieking, K.; Ferandin, Y.; Knockaert, M.; Meijer, L.; Kunick, C. Development of 5-benzylpaullones and paullone-9-carboxylic acid alkyl esters as selective inhibitors of mitochondrial malate dehydrogenase (mMDH). Eur. J. Med. Chem. 2010, 45, 335–342. [Google Scholar] [CrossRef] [PubMed]
- Egert-Schmidt, A.M.; Dreher, J.; Dunkel, U.; Kohfeld, S.; Preu, L.; Weber, H.; Ehlert, J.E.; Mutschler, B.; Totzke, F.; Schc̎htele, C.; et al. Identification of 2-Anilino-9-methoxy-5,7-dihydro- 6H-pyrimido[5,4-d][1]benzazepin-6-ones as Dual PLK1/VEGF-R2 Kinase Inhibitor Chemotypes by Structure-Based Lead Generation. J. Med. Chem. 2010, 53, 2433–2442. [Google Scholar] [CrossRef] [PubMed]
- Falke, H.; Chaikuad, A.; Becker, A.; Loaëc, N.; Lozach, O.; Jhaisha, S.A.; Becker, W.; Jones, P.G.; Preu, L.; Baumann, K.; et al. 10-Iodo-11H-indolo[3,2-c]quinoline-6-carboxylic Acids Are Selective Inhibitors of DYRK1A. J. Med. Chem. 2015, 58, 3131–3143. [Google Scholar] [CrossRef] [PubMed]
- Kunick, C. Fused azepinones with antitumor activity. Curr. Pharm. Des. 1999, 5, 181–194. [Google Scholar] [PubMed]
- Tolle, N.; Kunick, C. Paullones as Inhibitors of Protein Kinases. Curr. Top. Med. Chem. 2011, 11, 1320–1332. [Google Scholar] [CrossRef] [PubMed]
- Kunick, C.; Bleeker, C.; Prühs, C.; Totzke, F.; Schächtele, C.; Kubbutat, M.H.; Link, A. Matrix compare analysis discriminates subtle structural differences in a family of novel antiproliferative agents, diaryl-3-hydroxy-2,3,3a,10a-tetrahydrobenzo[b]cycylopenta[e]azepine-4,10(1H,5H)-diones. Bioorg. Med. Chem. Lett. 2006, 16, 2148–2153. [Google Scholar] [CrossRef] [PubMed]
- Rehbein, M.C.; Husmann, S.; Lechner, C.; Kunick, C.; Scholl, S. Fast and calibration free determination of first order reaction kinetics in API synthesis using in situ ATR-FTIR. Eur. J. Pharm. Biopharm. 2017, in press. [Google Scholar]
- Varga, L.; Szabó, B.; Zsély, I.G.; Zempléni, A.; Turányi, T. Numerical investigation of the uncertainty of Arrhenius parameters. J. Math. Chem. 2011, 49, 1798–1809. [Google Scholar] [CrossRef]
- Nagy, T.; Turányi, T. Uncertainty of Arrhenius parameters. Int. J. Chem. Kinet. 2011, 43, 359–378. [Google Scholar] [CrossRef]
- Schwaab, M.; Lemos, L.P.; Pinto, J.C. Optimum reference temperature for reparameterization of the Arrhenius equation. Part 1: Problems involving one kinetic constant. Chem. Eng. Sci. 2007, 63, 2750–2764. [Google Scholar] [CrossRef]
- Biegler, L.; Grossmann, I.; Westerberg, A. Systematic Methods for Chemical Process Design; Prentice Hall: Old Tappan, NJ, USA, 1997. [Google Scholar]
- Cappuyns, A.M.; Bernaerts, K.; Smets, I.Y.; Ona, O.; Prinsen, E.; Vanderleyden, J.; Van Impe, J.F. Optimal fed batch experiment design for estimation of monod kinetics of Azospirillum brasilense: From theory to practice. Biotechnol. Prog. 2007, 23, 1074–1081. [Google Scholar] [CrossRef] [PubMed]
- Telen, D.; Vercammen, D.; Logist, F.; Van Impe, J. Robustifying optimal experiment design for nonlinear, dynamic (bio)chemical systems. Comput. Chem. Eng. 2014, 71, 415–425. [Google Scholar] [CrossRef]
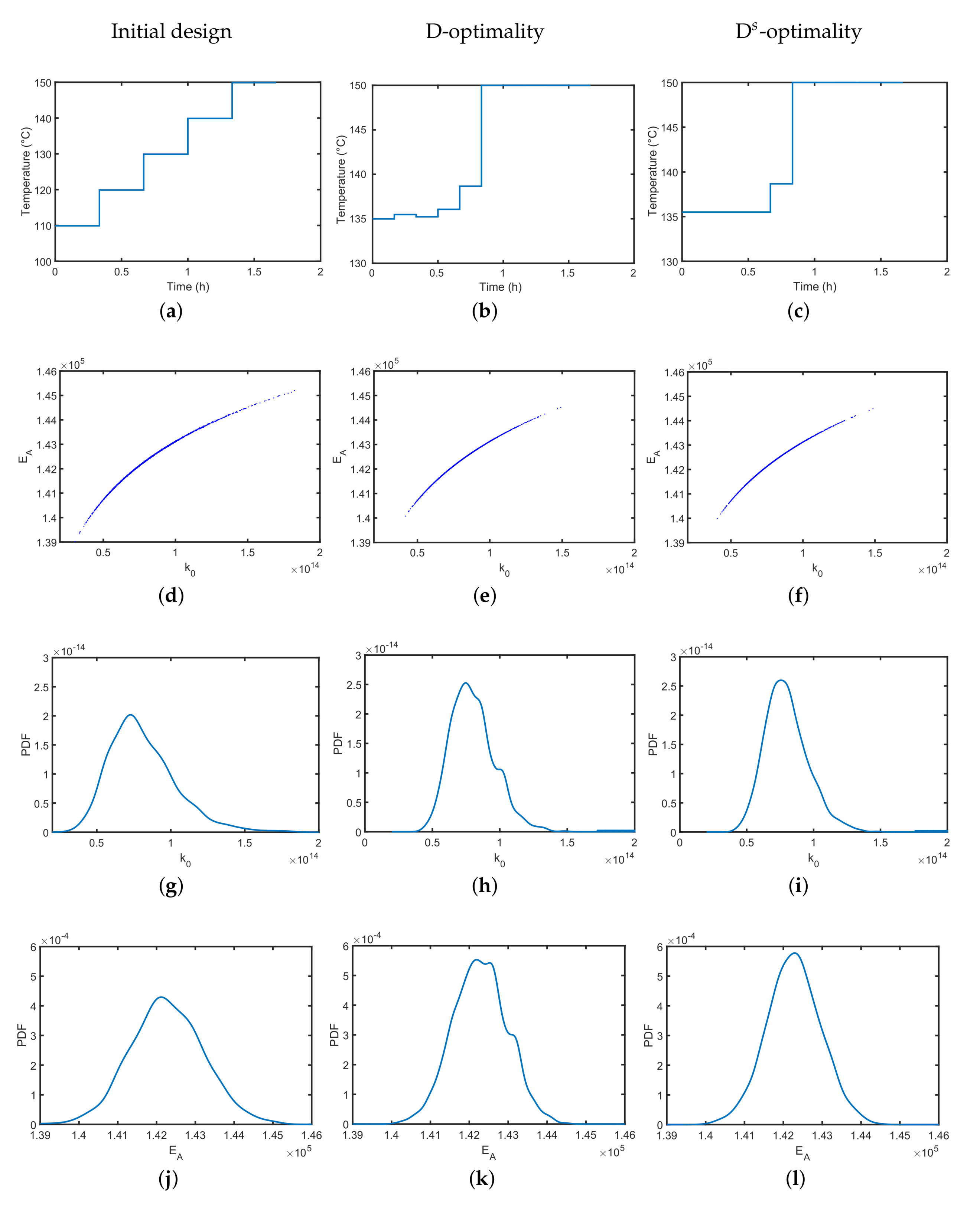
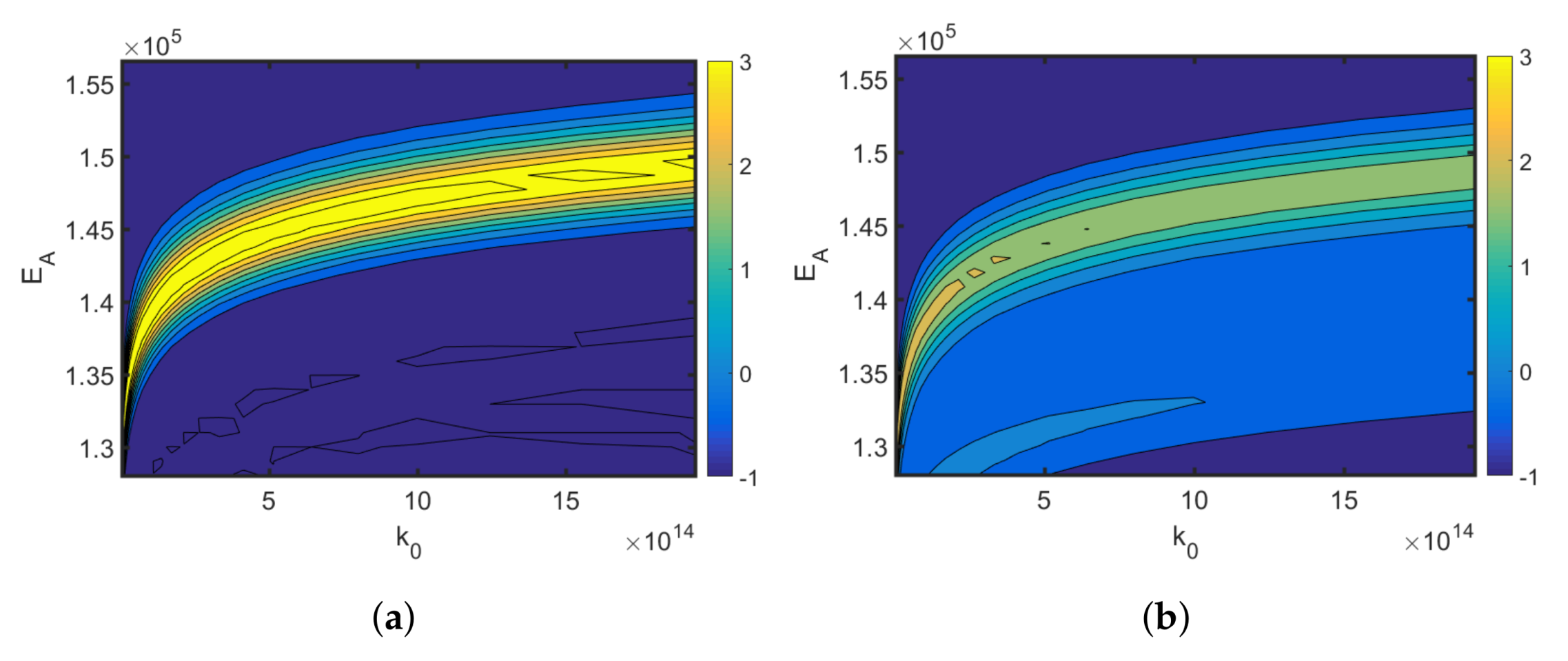

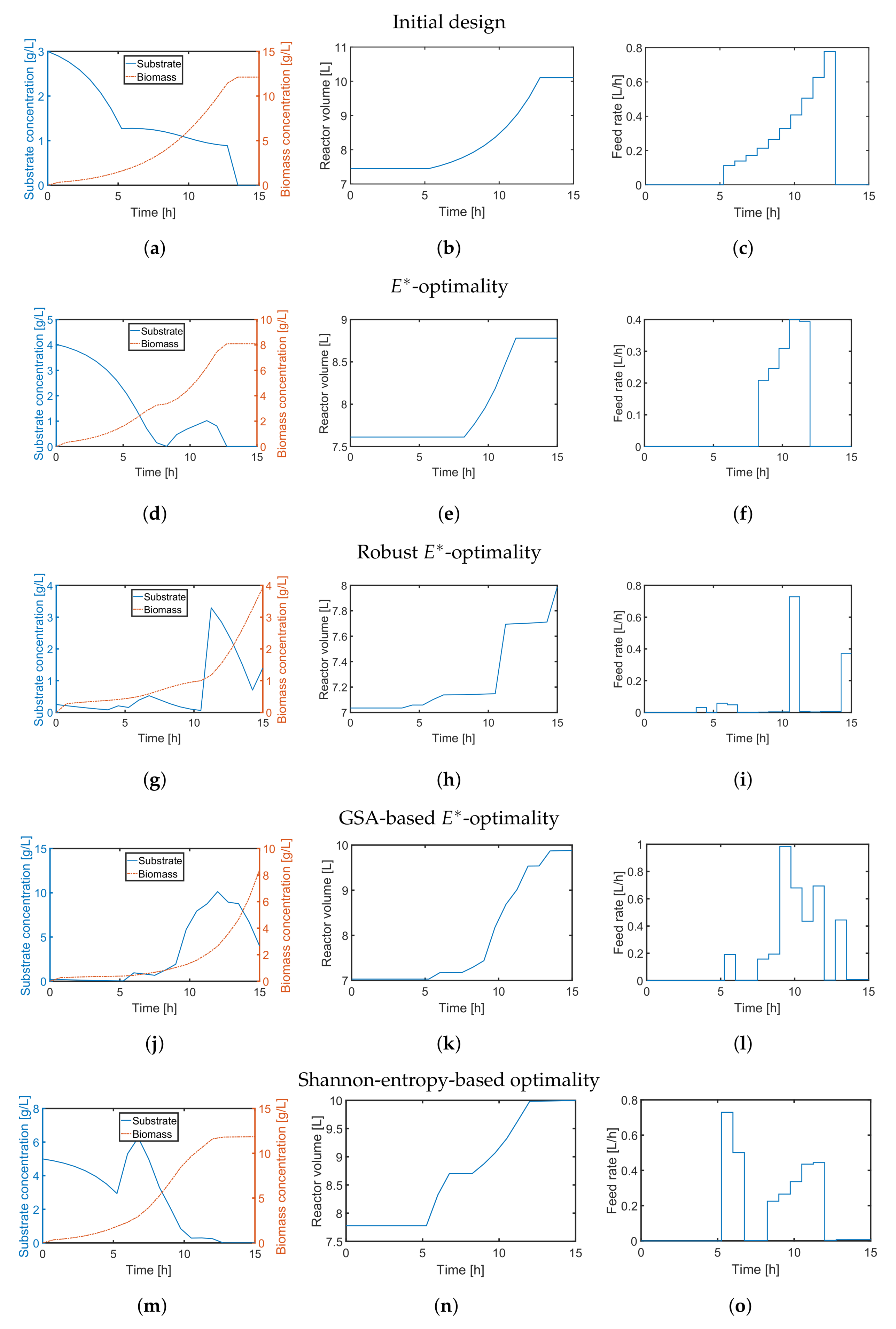
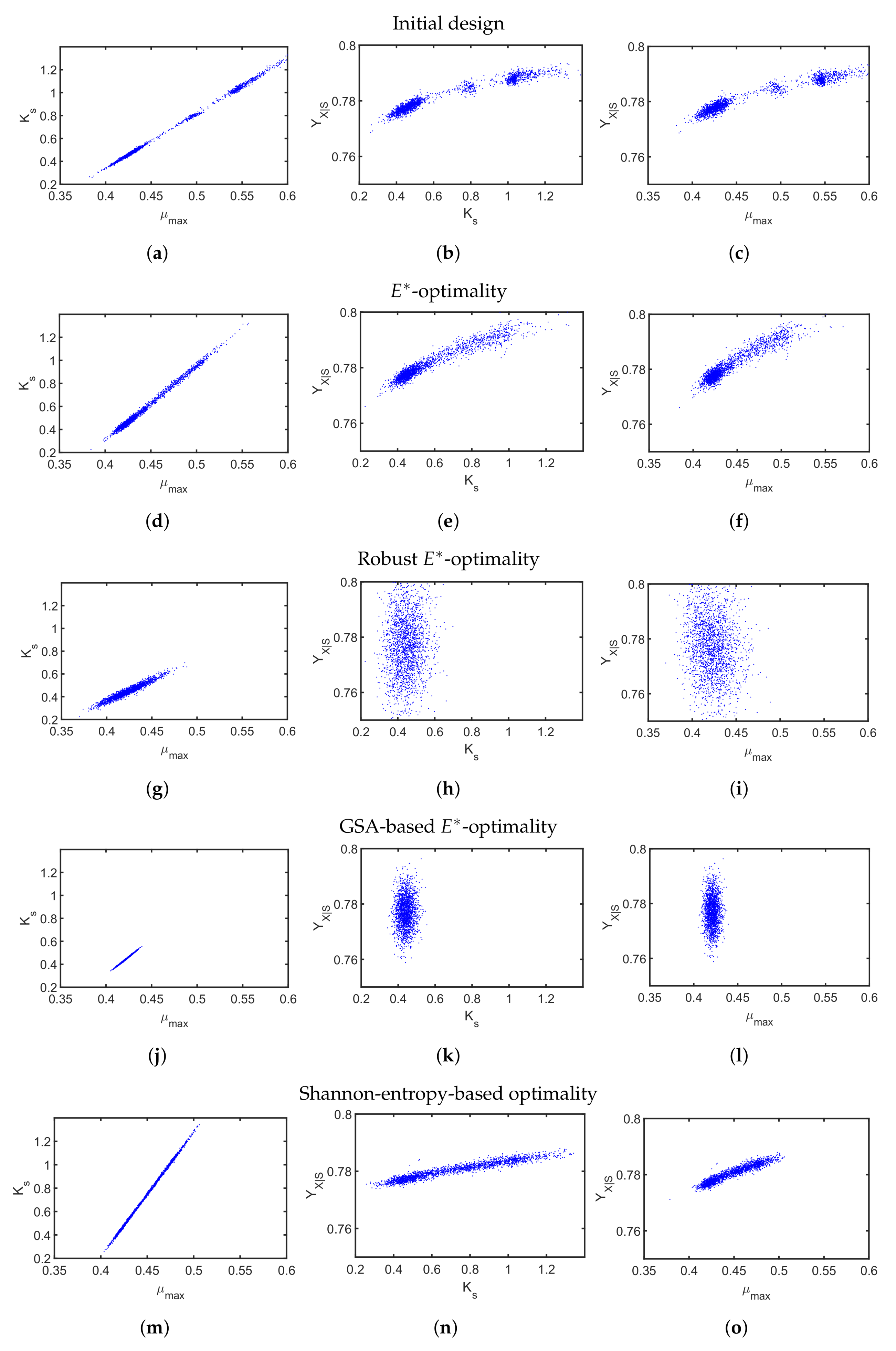
| Distribution | ||||
|---|---|---|---|---|
| 1 | 1 | 3 | 1 | |
| 1 | 1/3 | 3/5 | 1/9 | |
| 1 | 1/6 | 1/15 | 1/36 |
| Distribution | ||||
|---|---|---|---|---|
| Local Design Measures | Cost Functions |
|---|---|
| —optimal design | |
| —optimal design | |
| —optimal design |
| GSA-Based Design Measures | Cost Functions |
|---|---|
| —optimal design | |
| —optimal design | |
| —optimal design |
| Global Design Measures | Cost Function |
|---|---|
| (1) Shannon entropy (entire time horizon) | |
| (2) Shannon entropy (at single time point, ) | |
| (3) Parameter dependency | |
| (4) Overall output uncertainty |
| Symbol | Parameter | Unit | Nominal Value |
|---|---|---|---|
| initial concentration of biomass | 0.25 | ||
| initial concentration of substrate | 3 | ||
| initial volume of the liquid phase | 7 | ||
| substrate concentration in the feed | 50 | ||
| U | volumetric feed rate | 0–1 | |
| maximum specific growth rate | 0.421 | ||
| half velocity constant | 0.439 | ||
| yield coefficient of biomass over substrate | - | 0.777 | |
| m | maintenance factor | 0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schenkendorf, R.; Xie, X.; Rehbein, M.; Scholl, S.; Krewer, U. The Impact of Global Sensitivities and Design Measures in Model-Based Optimal Experimental Design. Processes 2018, 6, 27. https://doi.org/10.3390/pr6040027
Schenkendorf R, Xie X, Rehbein M, Scholl S, Krewer U. The Impact of Global Sensitivities and Design Measures in Model-Based Optimal Experimental Design. Processes. 2018; 6(4):27. https://doi.org/10.3390/pr6040027
Chicago/Turabian StyleSchenkendorf, René, Xiangzhong Xie, Moritz Rehbein, Stephan Scholl, and Ulrike Krewer. 2018. "The Impact of Global Sensitivities and Design Measures in Model-Based Optimal Experimental Design" Processes 6, no. 4: 27. https://doi.org/10.3390/pr6040027
APA StyleSchenkendorf, R., Xie, X., Rehbein, M., Scholl, S., & Krewer, U. (2018). The Impact of Global Sensitivities and Design Measures in Model-Based Optimal Experimental Design. Processes, 6(4), 27. https://doi.org/10.3390/pr6040027






