1. Introduction
Over 40% of the operating cost of a petrochemical plant is attributed to energy consumption [
1]. Energy is needed for raw material preprocessing (preheating, purification), separation of products from intermediates or impurities (product refining), and material transportation. There are multiple energy sources that can be exploited in a refinery, such as liquefied petroleum gas, fuel gas, off-gas, etc. [
2,
3]. These energy sources either come from external process raw materials and purchased fuels or from internal process products, and byproducts. Depending on where these fuel sources originate from, they can be classified as fuel from feed (FFF, e.g., natural gas) or fuel from product (FFP, e.g., products, byproducts) [
4]. In 2016, external fuels supplied to refinery industry in the United States mainly consisted of natural gas (31%), electricity (5%), purchased steam and coal (1%) [
5]. About 63% of the energy consumed by the refining industry comes from byproducts of the refining process for heat and power. These energy sources can be converted to each other. For example, fuel gas, produced internally from the distillation columns, crackers and reformers [
6], can be converted to steam, electricity or heat. Fuel gas accounts for 46% of all energy sources for the refining industry in the United States [
5,
7,
8,
9]. Fuel gas is often composed of hydrocarbons (methane, ethane, propane and butane), hydrogen, and carbon monoxide, which have large heating values [
10]. In most cases, these fuels are flared to the atmosphere, leading to detrimental effects on the environment and loss of heating values [
11,
12].
Due to the importance of fuel gas and the environment concern of fuel gas emission, many efforts have been made on improving the equipment efficiency [
13] or exploiting new energy sources to decrease fuel gas generation and pollution emission [
14]. Although these works give insights and directions on improving design of equipment and operating conditions, a generic and systematic strategy for elucidating the effective utilization of fuel gas is crucial. For example, in a typical fuel gas system, multiple fuel gas sources with different qualities are available for various equipment (sinks). As a result, effective and systematic management of fuel gas flow among fuel gas sources and fuel gas sinks can provide economic benefits for process design by fully utilizing the heating value embedded in the fuel gas [
15,
16].
Optimization-based methods enable the user to address fuel gas network (FGN) synthesis problems, which are aimed at redistributing the fuel gas at the system level [
1,
4,
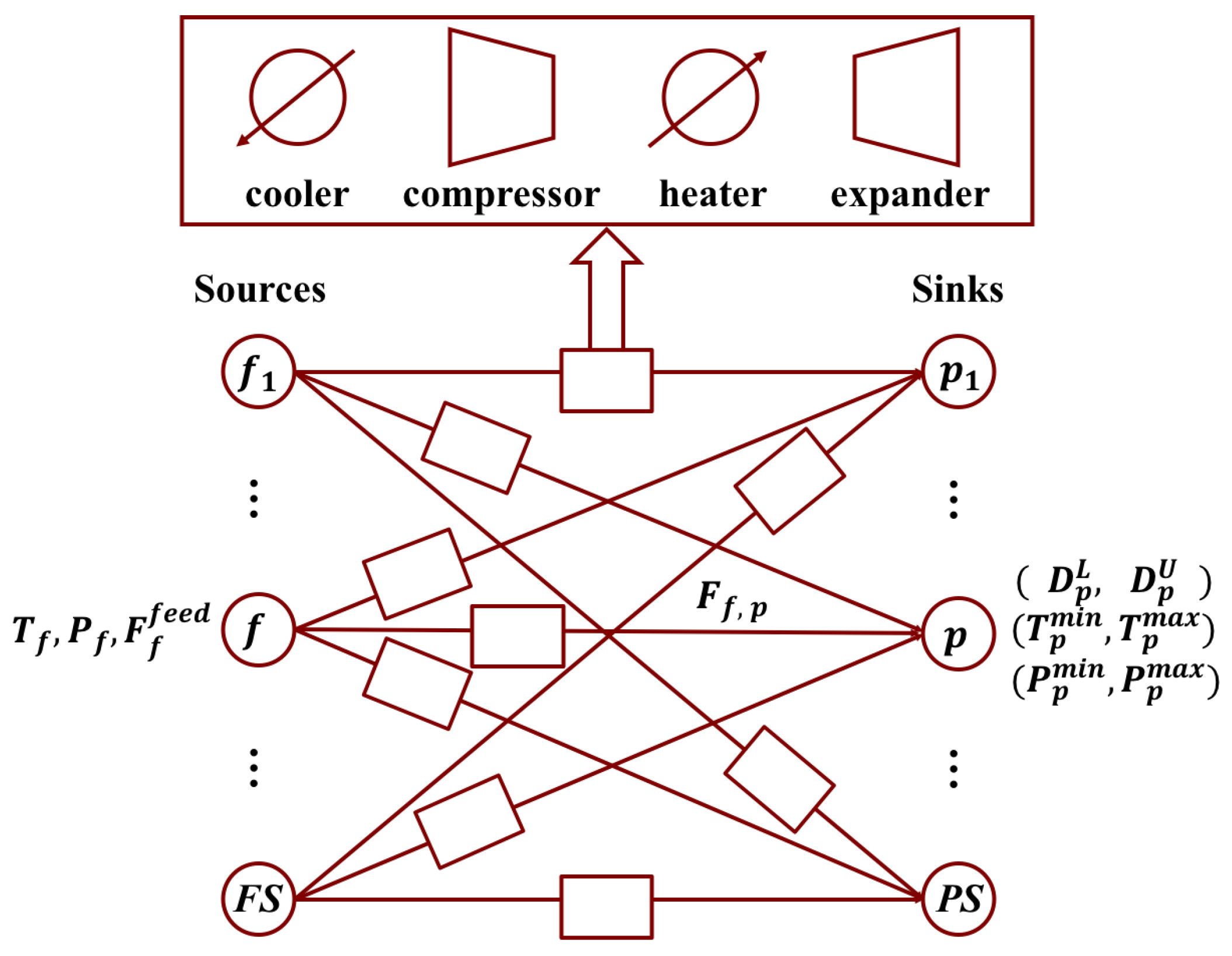
17]. To this end, Hasan et al. formalized the FGN synthesis problem as a nonlinear programming problem (NLP) considering the integration of fuel gases appropriately though auxiliary equipment (valves, pipelines, compressors, heaters/coolers, etc.) to achieve best utilization of them [
4]. They posed the FGN problem as a special class of pooling problem which leads a superstructure involving many practical features such as nonisobaric and nonisothermal operation, nonisothermal mixing, nonlinear fuel-quality specifications, and emission standards. Here the superstructure is defined as a superset of postulated process alternatives [
18]. The proposed FGN superstructure in the work of Hasan et al. (shown in
Figure 1) includes a set of fuel gas sources with temperature specification
, pressure specification
and feed availability specification
for each source
f, and a set of fuel gas sinks with demand range
,
, temperature range
, and pressure range
for each sink stream
p. To achieve the sink requirements, the intermediate operations such as cooling, compression, heating and expansion are considered in addition to mixing and splitting. Jagannath et al. [
17] extended this work to include the multi-period FGN operation. This FGN design makes dynamic plant operation more robust and helps to reduce capital costs. Nassim et al. [
1,
19] modified the FGN model introduced by Hasan et al. [
4] to include more constraints on addressing environmental issues and developed a novel methodology for grass-root and retrofit design of FGNs.
The first step for many optimization-based methods is the construction of a superstructure. Hence the appropriate selection of superstructure representation method is critical. There are many representations such as state-task-network [
20,
21], state-equipment-network [
21], P-graph [
22,
23], state-space [
24,
25] , HEN and MEN building blocks [
26,
27], phenomena building blocks [
28,
29,
30], process-group contribution method [
31], and unit-port-conditioning-stream (UPCS) approach [
32,
33]. We recently proposed a new superstructure representation method using building blocks for systematic process intensification [
34,
35,
36]. The block superstructure has been constructed based on the dissection of various unit operations into fundamental building blocks. Later on, the proposed block-based approach is applied to address process synthesis problems [
37].
In this work, we address the optimal synthesis of fuel gas networks using a block superstructure, originally proposed in our previous work for process synthesis and intensification [
34,
35,
36,
37]. Since the fuel gas network by its definition is a special class of pooling problem, our block representation method can be extended to general pooling problems as well. In this representation, each block allows multiple fuel gas inlet flows and single product outlet flow (unique composition for different product streams). The blocks with external feeds and external products serve as sources and sinks for fuel gas respectively. The material and energy flow among different blocks are achieved via jump flow streams connecting all nonadjacent blocks with each other and direct connecting streams connecting only adjacent blocks. The involvement of jump flows avoids the utilization of unnecessary intermediate blocks for inter-block connections. Each stream connecting two adjacent blocks are placed with compressors/expanders to adjust the pressure for achieving the sink requirements. Options for supplying extra hot/cold utility are provided to each block for allowing nonisothermal operation. When there is no direct connecting stream, the block boundary between adjacent blocks is regarded as completely restricted boundary. These blocks are collected in a two-dimensional grid to form a superstructure of blocks. We formulate the fuel gas synthesis problem as a mixed-integer nonlinear optimization (MINLP) problem. The model constraints involve mass and energy balance, flow directions, work calculation and logic constraints. The nonlinear terms of the proposed model arise from splitting, energy balances and work-related calculations.
The remaining of the article is structured as follows. First, we elaborate the representation of fuel gas network using block-based approach. Next, we present the MINLP formulation for fuel gas network synthesis problem. Finally, we demonstrate the applicability of our approach with one case study on FGN synthesis in an LNG plant.
2. Block-Based Representation of Fuel Gas Network
In this section, we describe how the classic fuel gas network superstructure such as the one proposed by Hasan et al. [
4] can be represented using block-based approach [
34,
37] as a generic tool for designing fuel gas utilization system. First, we illustrate the classic FGN superstructure and analyze the operation involved in synthesizing a FGN. Next, we construct a block superstructure that can also include the same features. We provide block superstructures for fuel gas network with or without intermediate pools which bring additional mixing operations for more economic benefits.
In a classic FGN superstructure (Hasan et al. [
4]), shown in
Figure 1, there are
number of fuel gas sources and
number of fuel gas sinks. The source stream
f has the temperature as
and the pressure as
. The sink stream
p is obtained with temperature range as
, pressure range as
and demand range as
. Each stream
connecting a source
f and a sink
p passes through two utility exchangers (heater and/or cooler) and one mover (compressor or expander). The sources completely or partially come from different fuel gas sources and are mixed at different fuel gas sinks with different temperature, pressure and quality requirements. The operations in a FGN problem typically include mixing, cooling, heating, pressurizing and depressurizing.
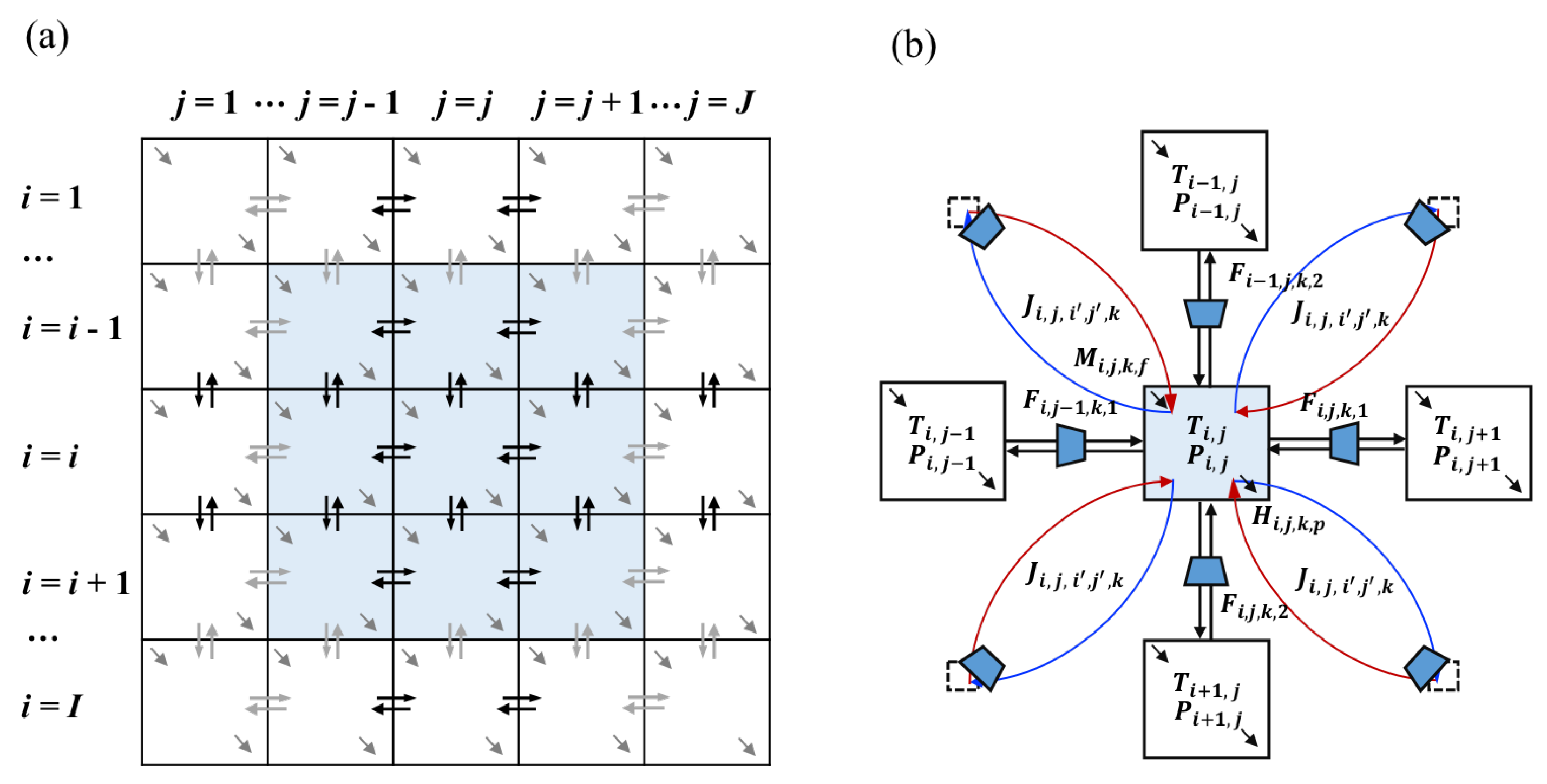
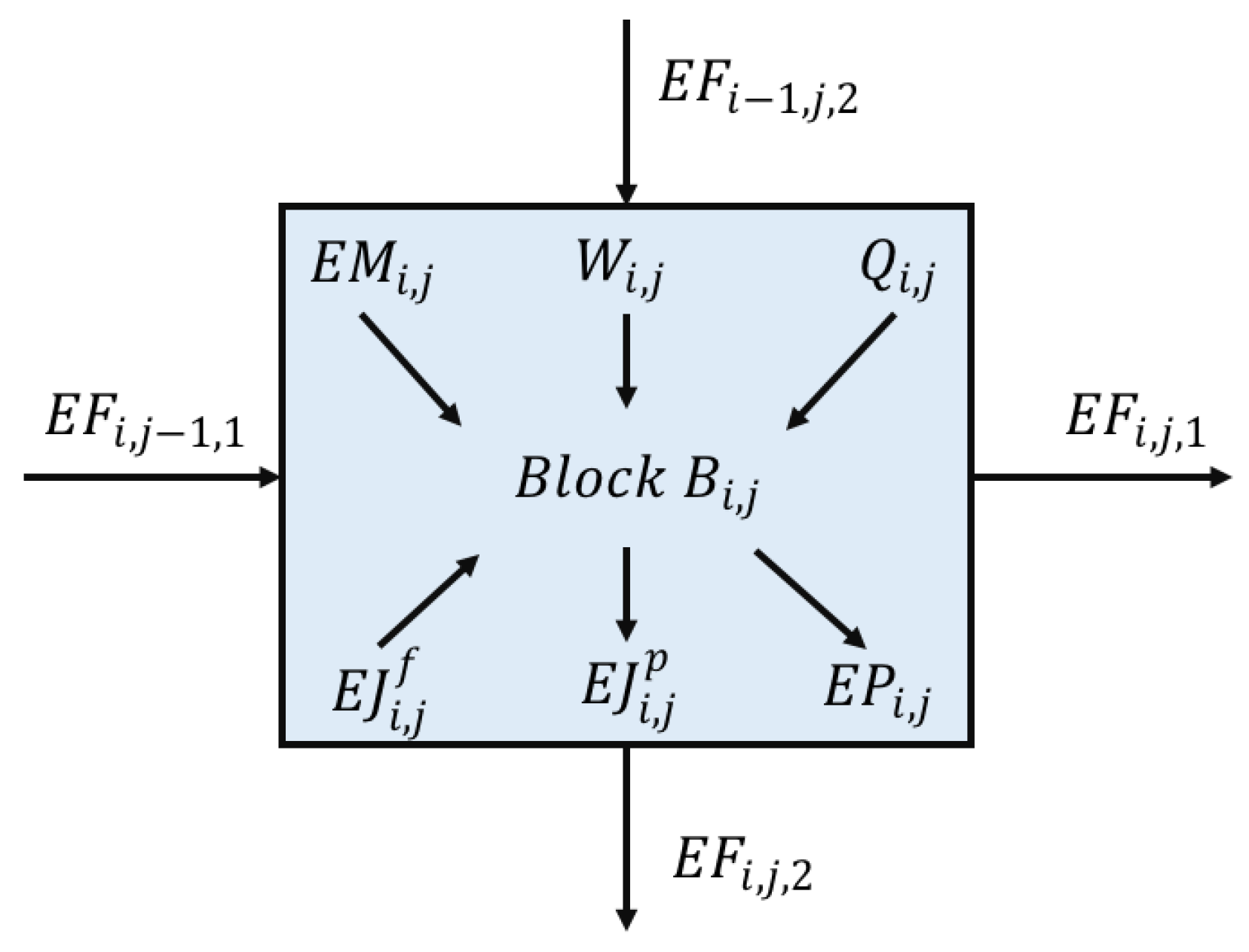
Most FGN synthesis problems involve multiple sources and multiple sinks. In addition, there are similar equipment assignment that are assigned between sources and sinks. This allows us to develop a general block representation for FGN synthesis as shown in
Figure 2. It involves
I number of rows and
J number of columns, where each row or column is a collection of blocks. Let
represent the block at row
i and column
j. Each block allows multiple external feed streams
to enter block
. The available amount of feed
f can be partially or completely fed into a block
with
fraction of available amount
. Similarly, product stream
p can be withdrawn from each block with the component flowrate of
.
As shown in
Figure 2b, the mass and energy transfer within the block superstructure is achieved through the direct connecting streams between adjacent blocks and jump connecting streams among all nonadjacent blocks. Direct connecting streams are achieved via inter-block flow
, which is the flowrate of component
k between block
and
when the flow alignment
(the connecting flow between adjacent blocks is in horizontal direction) or the flowrate of component
k between block
and
when the flow alignment
(the connecting flow between adjacent blocks is in vertical direction) . These direct connecting streams can be either positive when the flow is from block
to
for
(from block
to
for
) or negative when the flow is from block
to
for
(from block
to
for
). Also, these direct connecting stream flow across the block boundary between adjacent blocks. When there is no direct connecting stream (
), the block boundary between
and
(
d = 1) or between
and
(
d = 2) is identified as completely restricted boundary. The jump connecting streams are depicted by
, which is the flowrate of component
k from block
to
, where
and
designate the row number and column number of a different block. Because of this unidirectional feature,
is a jump flow withdrawn from
and supplied to
.
With these direct and jump connecting streams, blocks with multiple inlets and multiple outlets can serve as stream mixers and splitters, respectively. Source block is identified when multiple external feed streams enter into a block and get mixed, while blocks with external product stream are sinks. Note that splitting of the source streams is not regarded as a splitting operation because it can be achieved through the splitting fraction of source stream f into block and thus can be regarded as supplies of multiple source streams with the same specification.
The operation equipment (heaters/coolers, compressors/expanders) is embedded in the block superstructure through auxiliary units. To represent the pressurizing/depressurizing operation, both direct connecting streams and jump connecting streams are assigned with compressor or expander (only one of them would be selected). Each stream leaving block has a pressure designated as , which is also the inlet pressure for the compressors or expanders on these streams. The inlet temperature for these compressors/expanders arranged at outlet streams ( and ) of is the block temperature , which is also the common temperature of outlet streams from . The heating and cooling operations are achieved through the heat duty and cold duty , which are obtained from the energy balance around block .
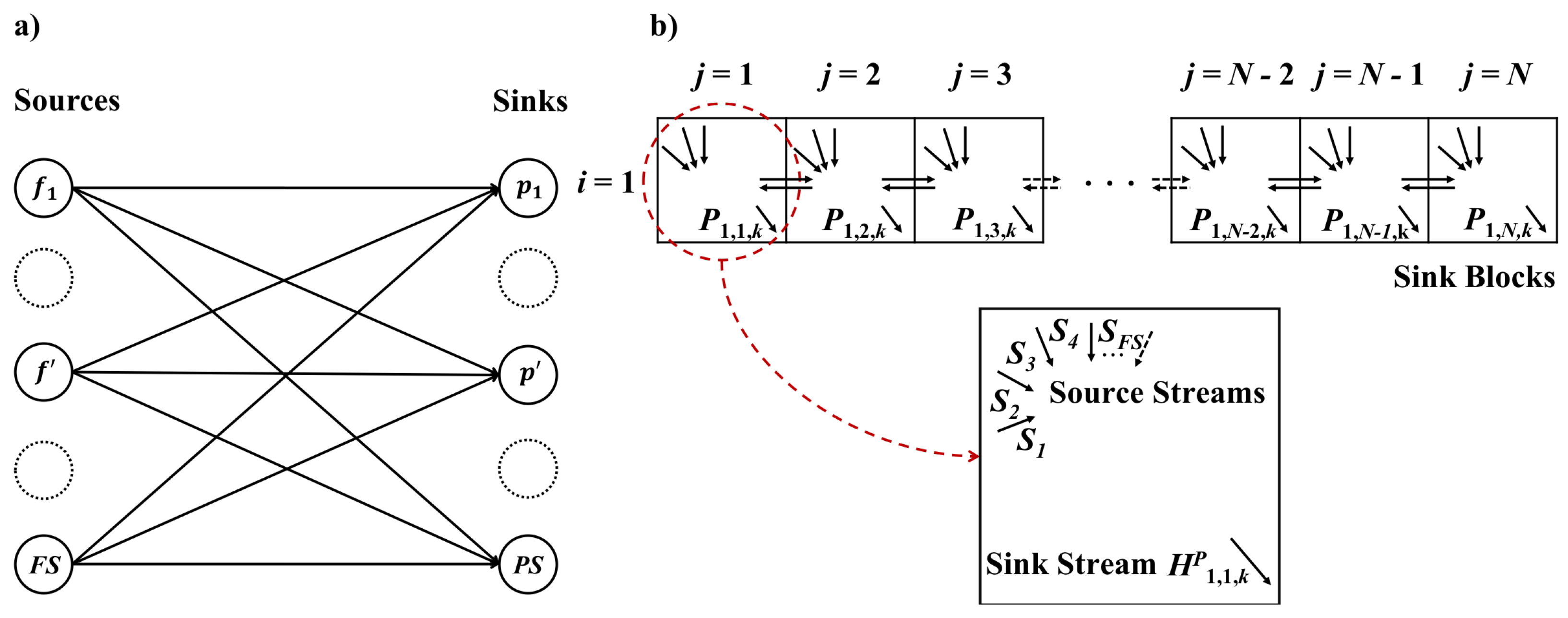
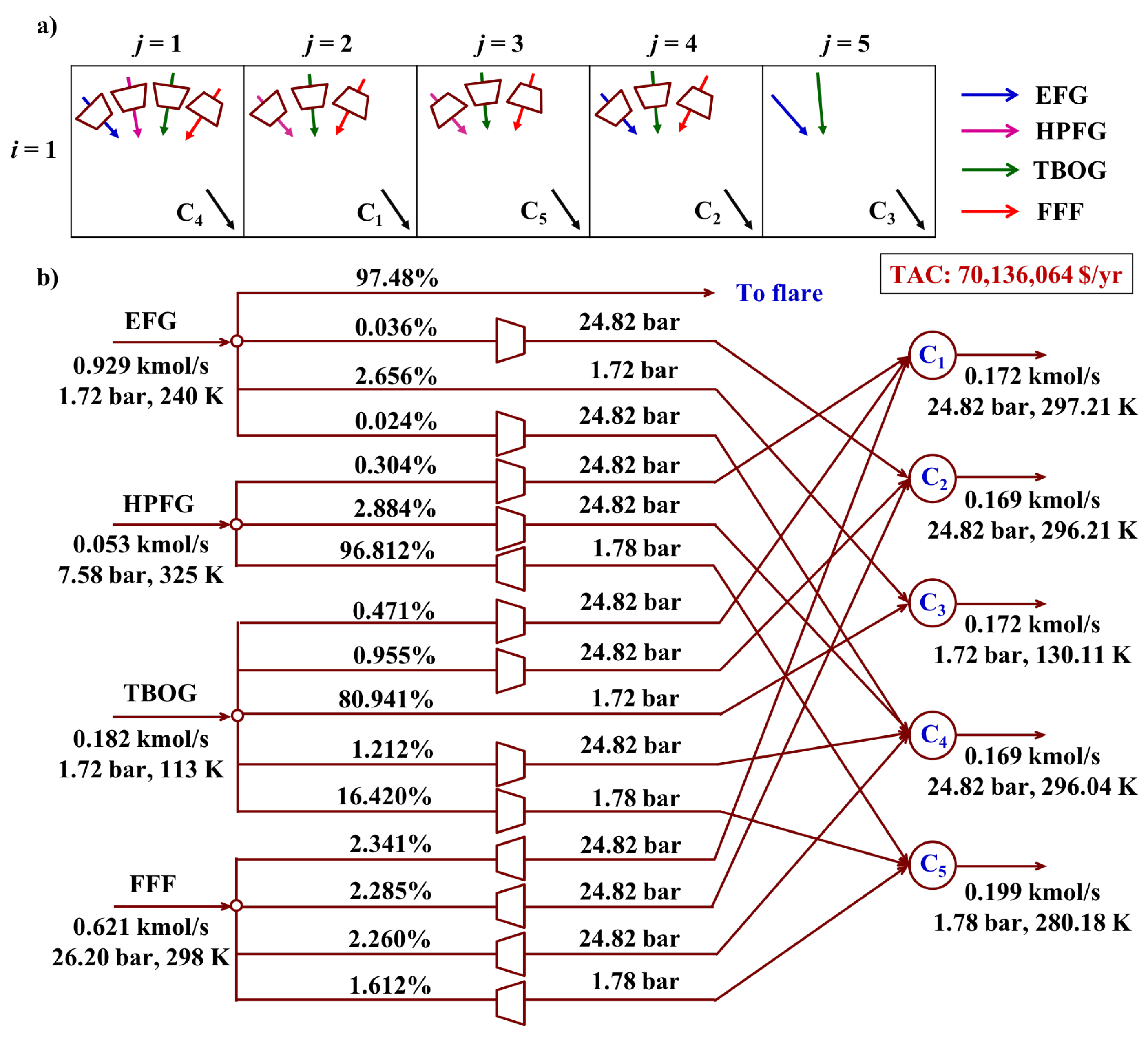
The general block superstructure for FGN synthesis problem developed in
Figure 2 can be reduced to block superstructure with smaller size if the number of intermediate pools is known beforehand. As an illustrative example, we first consider the case without intermediate pools. Knowing certain number of sources and sinks together with their specification and requirement, the classic superstructure is built by connecting each source and sink and shown in
Figure 3a. Here all stream heaters/coolers and expanders/compressors are ignored for representation simplicity. As is shown in
Figure 3b, we use a 1×
N block superstructure to incorporate the classic superstructure. In this case, the column number is directly equal to number of sinks (
). Since there are no intermediate pools, row number
. Each block serves as sink block, from which product streams are withdrawn. Meanwhile, each block could also function as feed block, where multiple types of source streams are fed. Specifically, taking the first sink block
as an example, there could be at most
number of source streams entering this block. The activation of connectivity between sources and sinks could be reflected by the feed fraction
of different sources
f. If the feed fraction
of source stream at the sink block
is zero, then there is no connectivity between the source
f and the sink
p in block
; source-sink connectivity exists as long as the feed fraction of source stream
is nonzero. Besides, the horizontal connecting streams between adjacent blocks in
Figure 3b are also allowed. This additional feature physically indicates the material flowing between two fuel gas sinks.
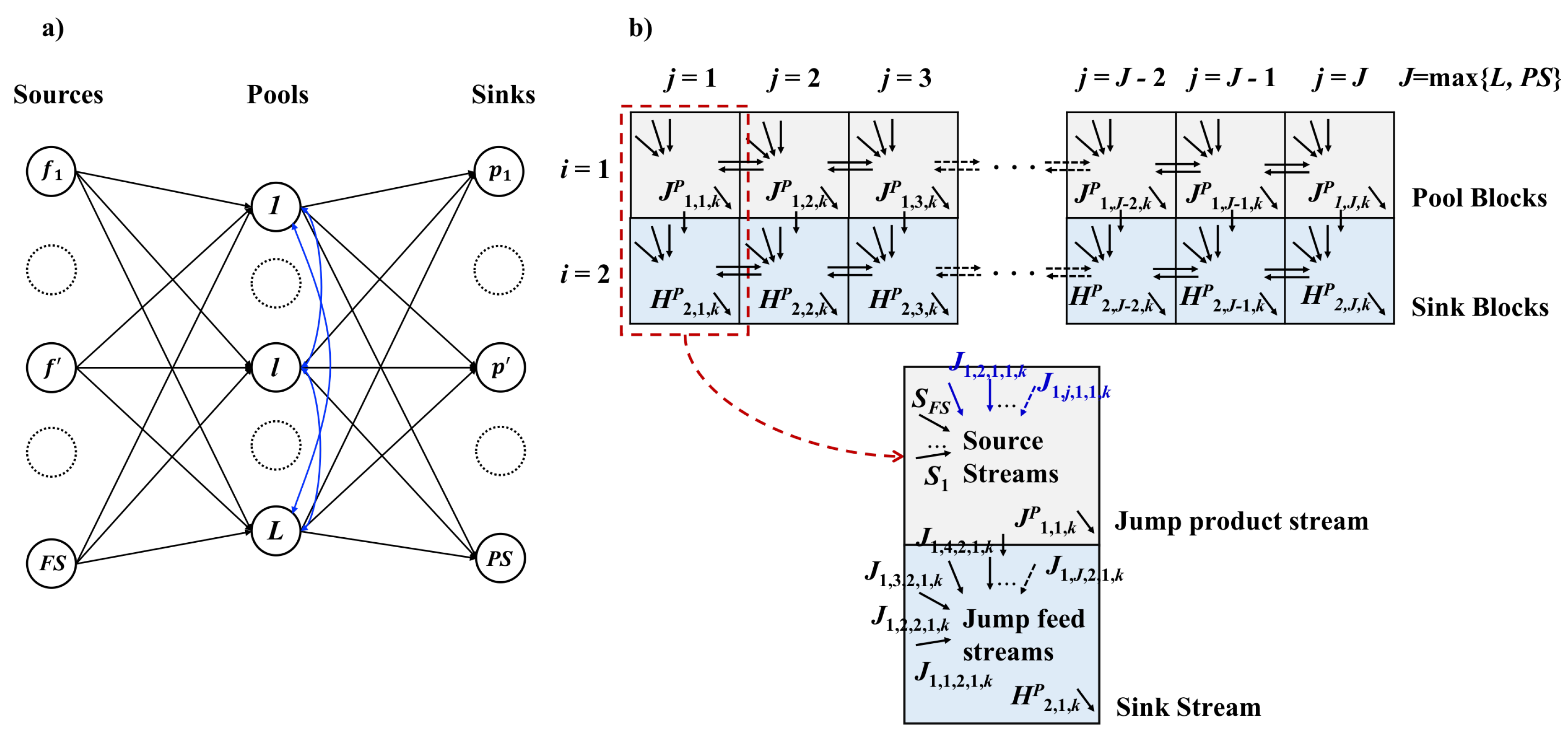
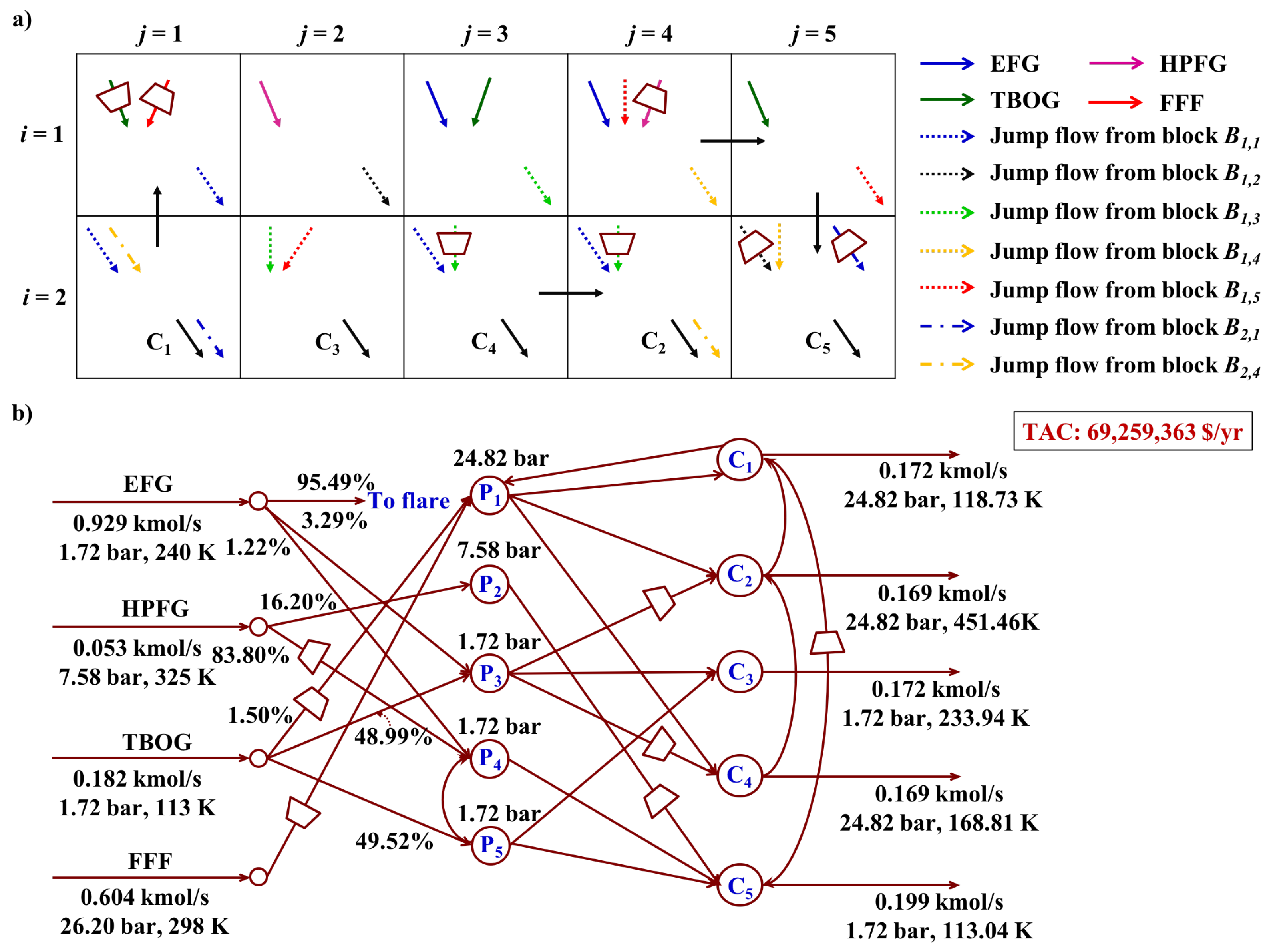
As for the more general case of the fuel gas network superstructure, between the sources and sinks layer, there can be another layer consisting of
L number of intermediate pools, as is shown in
Figure 4. Source streams first come into the intermediate pools, where certain operations such as mixing, purifying are executed according to different sink requirements. The outlet streams coming from the intermediate pools are further directed to the sinks or to the other different pools (shown as the blue line in
Figure 4a). One way to incorporate the general superstructure is to utilize a block superstructure with larger size so that pools (involving mixing and splitting operations) can be included into the system. With this new feature of intermediate pools, the updated block superstructure is shown in
Figure 4b. The first row consists of
L number of pool blocks (grey blocks) and the second row consists of
number of sink blocks (blue blocks). In this case, the number of columns can be taken as
. The existence of intermediate pools make the row number as
, one row to accommodate pools and another row for sinks. The distribution of source streams into each pool blocks is achieved through splitting operation of source streams. In the first row, the jump flows are withdrawn from each block as outlet streams of intermediate pools. Specifically, taking the first column of block superstructure in
Figure 4b as an example, the jump flow
(the summation of all the jump connecting streams to other blocks from block
) is withdrawn and directed to other blocks as inlet flows. The inlet jump flows,
, from nonadjacent blocks
(
) are mixed in the second row at sink block
and then taken as the final product
(the overall component flowrate for all product stream
p).
As is discussed above, the block superstructure can be converted from the classic superstructure of fuel gas network. When there is no prior information provided on flow connectivity among sources, pools and sinks, the block superstructure can be constructed by simply setting the row number I and column number J (i.e., {L,}), which then involves as many process alternatives as possible. The benefit for block representation method is on its generic feature that each block follows the same pattern with multiple inlet streams and outlet streams. Based on the representation method, we now develop the MINLP formulation for the FGN synthesis problem.
3. FGN Synthesis Problem Statement
This section gives the formal problem description for FGN synthesis problem using block superstructure. The sets given for this problem are the set of components, the set of fuel gas sources with component specification , a set of fuel gas sinks with the material demand range as [, ], energy demand range as [, ], purity range as [, ] for species k as well as ranges for other specifications [, ]. The objective is to synthesize a fuel gas network that systematically utilizes the arrangement of fuel gas resources and minimizes the total annual cost. The set designates the flow alignment. The flow alignment when the stream is flowing in the horizontal direction, i.e., from block to ; when the stream is flowing in the vertical direction, i.e., from block to . The temperature range and flowrate range for all connecting flows including direct connecting flow and jump connecting flow are set as [, ] and [, ] respectively.
We consider the assumptions for this work as constant properties (heat capacity, lower heating value, etc.), continuous steady-state operation, ideal gas condition, adiabatic expansion/compression, and ideal mixing. With this, we now describe the MINLP model for fuel gas network synthesis based on block superstructure.
4. MINLP Model Formulation for Block-Based Fuel Gas Network Synthesis
The main constraints for the MINLP model involve block material balance, flow directions, block energy balance, work calculation and task assignment/logic constraints. The objective of the FGN synthesis is to minimize the total annual cost.
4.1. Block Material Balance
The general material balance for each block
considers the material flows of component
k including horizontal inlet flow
, the horizontal outlet flow
, vertical inlet flow
, vertical outlet flow
, external feed stream
, external product stream
, jump flow into the block
, and jump flow from the block
. Specifically, the material balance relation is presented as follows.
The last four terms in the above relation are obtained though the following constraints.
All variables including , , and are obtained by summing multiple inlet streams or outlet streams within single block . The positive continuous variable indicates the amount of component flowrate k into block carried by feed stream f. The amount of component k taken from block through product stream p is designated by positive continuous variable . The material flowrate for component k from block to is . The index and indicate row position and column position of a block that is different from . The subset designates the connection between block and block . It should be noted that for jump connecting flow , and so as to avoid remixing in block . The stream connectivities at the outer boundary of block superstructure are set as to ensure that the interaction between the superstructure and the environment is only achieved through external feeds and products.
The flowrate
for each feed
f into block
is completely or partially from the overall available amount
. The distribution of feed stream
f is achieved by the feed fraction
in block
. Hence
can be determined as follows:
Typically, headers receiving fuel gas have purity requirement for inlet streams to ensure the required operating conditions of the corresponding equipment. This is achieved through the following inequality constraints:
Here, the purity range for component k in product stream p is given by . The set relates the key component k with product stream p with purity specifications. The product stream p have no purity restrictions when it does not appear in set .
On top of purity requirement of key component
k in product stream
p, possible requirement on ratio of different component
k in product stream
p is also considered.
where
is the minimum product ratio requirement between component
and component
for product
p.
We also impose the demand constraint for product
p supplied to different headers:
Here, and are minimum and maximum allowed amount for product stream p respectively. Hence if there is no specification existing for , or both, we set and .
Besides, energy demands
for each product stream
p should be satisfied based on the following constraint:
where
refers to lower heating value for each component
k, which measures energy content per unit mass or volume of pure combustible component.
Furthermore, each product stream should have acceptable limits on other certain specifications including lower heating value (
), reverse specific gravity (
), etc. Assuming that all the considered specifications are linearly related with mixture compositions, the following constraint is supplied below for each product stream
p [
4].
Here the parameter
denote the value of specification
s for component
k, and
is the acceptable range of specification
s for product stream
p. Note that the quality specification
is component flowrate-based instead of total flowrate-based, which is considered in the work of Hasan et al. [
4].
To obtain the total flowrate for all streams associated with the block
, we sum all components in each stream. Specifically, we obtain the total flowrate
,
,
,
, and
from the component flowrate for
,
,
,
, and
through the following relations.
With the total flowrate information, we model the splitting operation for achieving identical composition for all outlet streams as follows:
Here the positive continuous variable refers to the block composition of component k. This block composition refers to the composition of component k in all the outlet streams from block .
4.2. Flow Directions
The direct connectivity
among adjacent blocks is a bidirectional flow with its positive component
and negative component
. Only one of them is active when the connecting flow
is chosen to be nonzero. The selection of flow direction is a decision variable, which is achieved through the following binary variable:
As a result, the flow direction determination is achieved though the following constraints:
4.3. Block Energy Balance
The enthalpy terms for block energy balance includes inlet and outlet inter-block stream enthalpy, feed enthalpy, product enthalpy, external heating/cooling, work energy associated with expansion/compression. Then the steady-state energy balance for block
is formulated as follows:
where,
represents the stream enthalpy carried by the material flow
in flow direction
d,
is the overall enthalpy brought into block
along with external feed streams ,
is overall enthalpy taken away by external product streams,
is overall enthalpy carried into block
through jump flows,
is overall enthalpy taken out from block
through jump flows,
represents amount of heat added into or removed from the block
,
indicates the amount of work energy added into or withdrawn from block
. These energy flow variables are shown in
Figure 5.
The stream enthalpy is determined as follows with the information provided on flowrate, component heat capacities and the block temperature. Depending on the flow direction, in flow alignment
, the inlet temperature for block
is either
from block
to
or
from block
to
; in flow alignment
, the inlet temperature for block
is either
from block
to
or
from block
to
.
where
is the heat capacity of component
k.
The enthalpy amount brought into or withdrawn from block
through jump flows are determined as follows:
It should be noted that the inlet temperature of jump flow is always the temperature of the source block,
. Likewise, the feed enthalpy and product enthalpy are determined with the following constraints:
The amount of hot/cold utility consumed in block
can be evaluated through the amount of heat introduced into (
) or withdrawn from (
) block
.
The work energy can be also determined by the amount of work added into or taken out of block
, which are denoted as
for compression and
for expansion respectively. The calculation of
and
is explained later in this
Section 4.6.
Finally, to prevent condensation in the FGN and ensure sufficient superheating, the following constraints are supplied for product stream
p in block
[
4].
where parameter
is moisture dew-point temperature and parameter
is the hydrocarbon dew-point temperature for the product
p.
4.4. Product Stream Assignments and Logical Constraints
We define binary variables for each product stream
p at block
to determine whether they are active in
or not:
The identification of block as product block is achieved through the following logical relation, which involves product binary variable:
For each block, there are at most one type of product stream present in block
. The logic proposition is illustrated as follows:
Each product stream
p appears in the block superstructure for at least once so as to ensure the supply of fuel gas header.
The temperature range for block with product stream
p is from
to
.
Likewise, the pressure range for product block is
to
.
4.5. Boundary Assignment
The boundary type between adjacent blocks can be either completely restricted or not. If there is no direct connecting stream between adjacent blocks, then the inter-block boundary is identified as completely restricted boundary. The decision of boundary type is achieved through the following binary variable
.
According to the definition of completely restricted boundary, the following constraints are supplied to relate flowrate
with boundary type.
4.6. Work Calculation
The work term
consists of compression work term
and expansion work term
. Both
and
consist of work components for direct connecting streams (
and
for compression and expansion work of positive component,
and
for compression and expansion work of negative component), feed streams (
and
for compression and expansion work respectively), and jump connecting streams (
and
for compression and expansion work respectively). Accordingly,
We define the positive variable
to designate the pressure ratio between the block
and
for flow alignment
or between the block
and
for flow alignment
. In horizontal direction, the pressure ratio is determined as follows:
Similarly, in vertical direction, the pressure ratio is determined as follows:
For feed stream
f, the pressure ratio is taken as the ratio between block pressure
and parameter
for feed pressure .
From these pressure ratio definitions, we calculate the isentropic work on direct connecting streams, feed streams and jump connecting streams. In the horizontal direction, the inlet isentropic work is determined as follows:
Here
is the gas constant and
is the adiabatic compression coefficient for process streams.
is taken as heat capacity ratio.
is the adiabatic compression efficiency. Similarly, the isentropic work for a vertical entering stream is calculated as follows:
The work terms related to feed streams and jump connecting streams are calculated in a similar way:
Here is the adiabatic compression coefficient for source stream f.
4.7. Objective Function
We consider the components of economic objective in the work of Hasan et al. [
4] and derive the objective function for the FGN synthesis as follows.
This objective function aims at minimizing total annual cost (). Here parameter is the unit cost of different source streams, is the unit cost of treatment cost for unused source streams, is the unit profit from excess energy in product stream p. Besides, the parameter denotes the unit transportation cost for source stream f. Parameters , , and denote the unit cost of heaters, coolers, expansion operations and compression operations, respectively. The first term in the objective function consists of source stream purchase cost and disposal cost. The second term corresponds to the profit gained from the released excess amount of energy in product stream p. The third term indicates the transporting cost of source streams. The last four terms refer to overall cost (both capital cost and operating cost) for heaters, coolers, expansion operations and compression operations.
This completes the MINLP model for block-based FGN synthesis. It should be noted that commercial solvers can handle the proposed FGN design problems with small number of sinks or pools. However, when a large-scale problem is considered, further simplification can be made by fixing the streams associated with unused blocks to zero when the number of pools and sinks do not match each other. This fixing ensures that the number of blocks in the first row is only equal to the number of pools assigned in the system and the number of blocks in the second row is equal to the number of sinks.