Estimation of Pore Size Distribution of Amorphous Silica-Based Membrane by the Activation Energies of Gas Permeation
Abstract
1. Introduction
2. Theory of Mass Transfer Through Membrane
2.1. Activated Transport
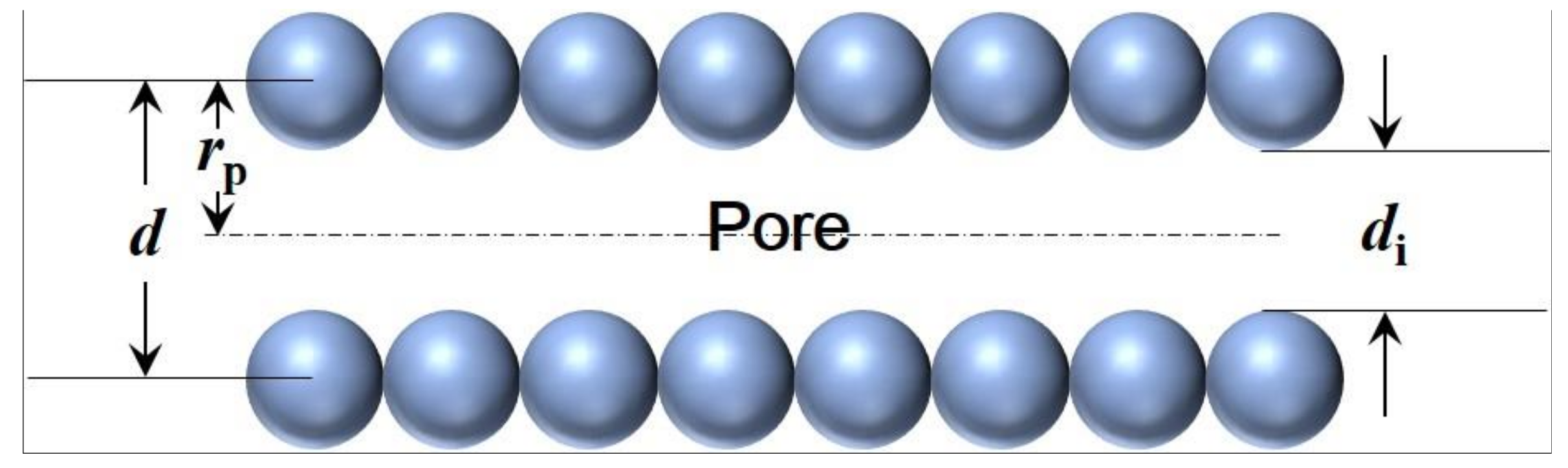
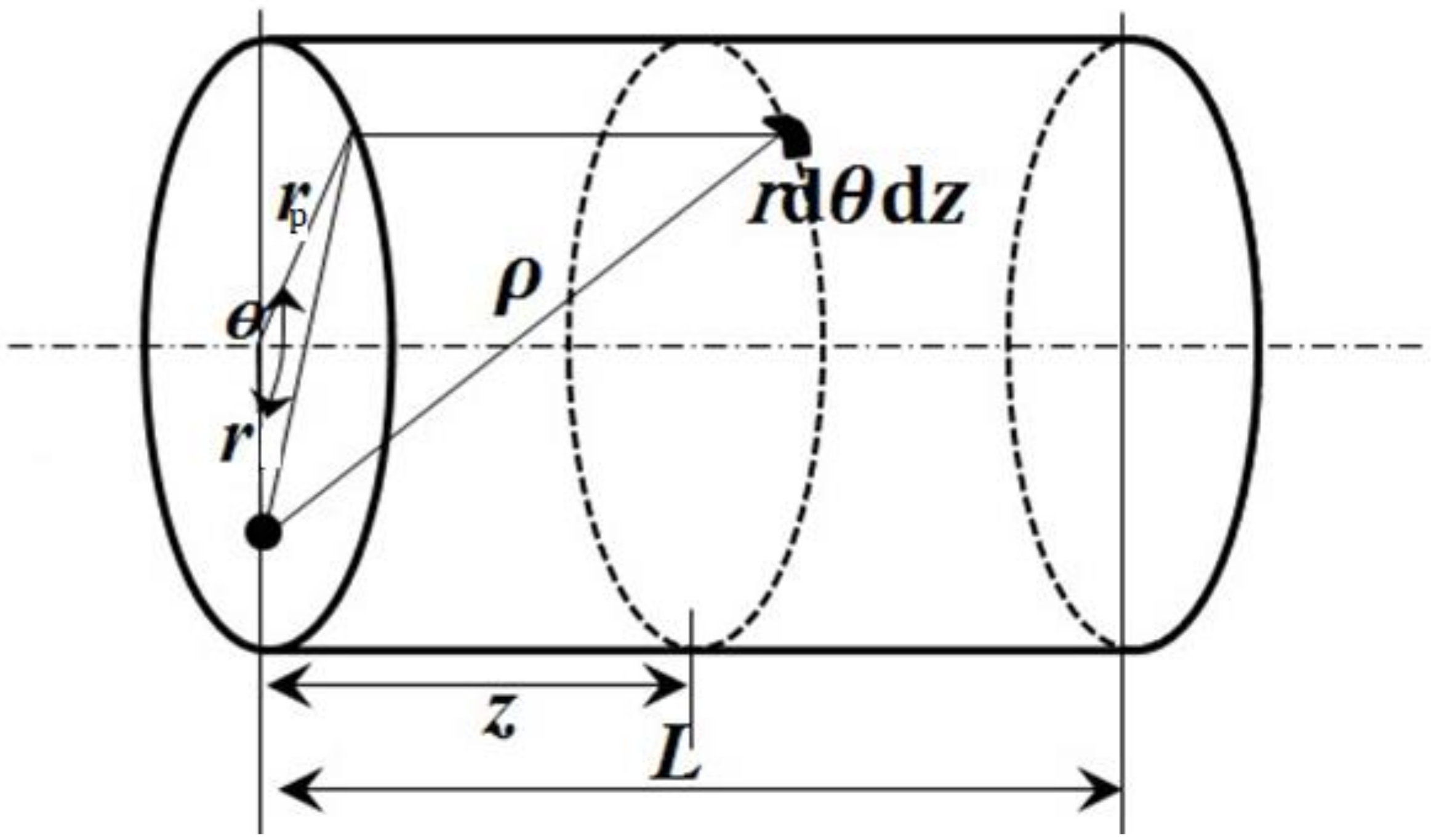
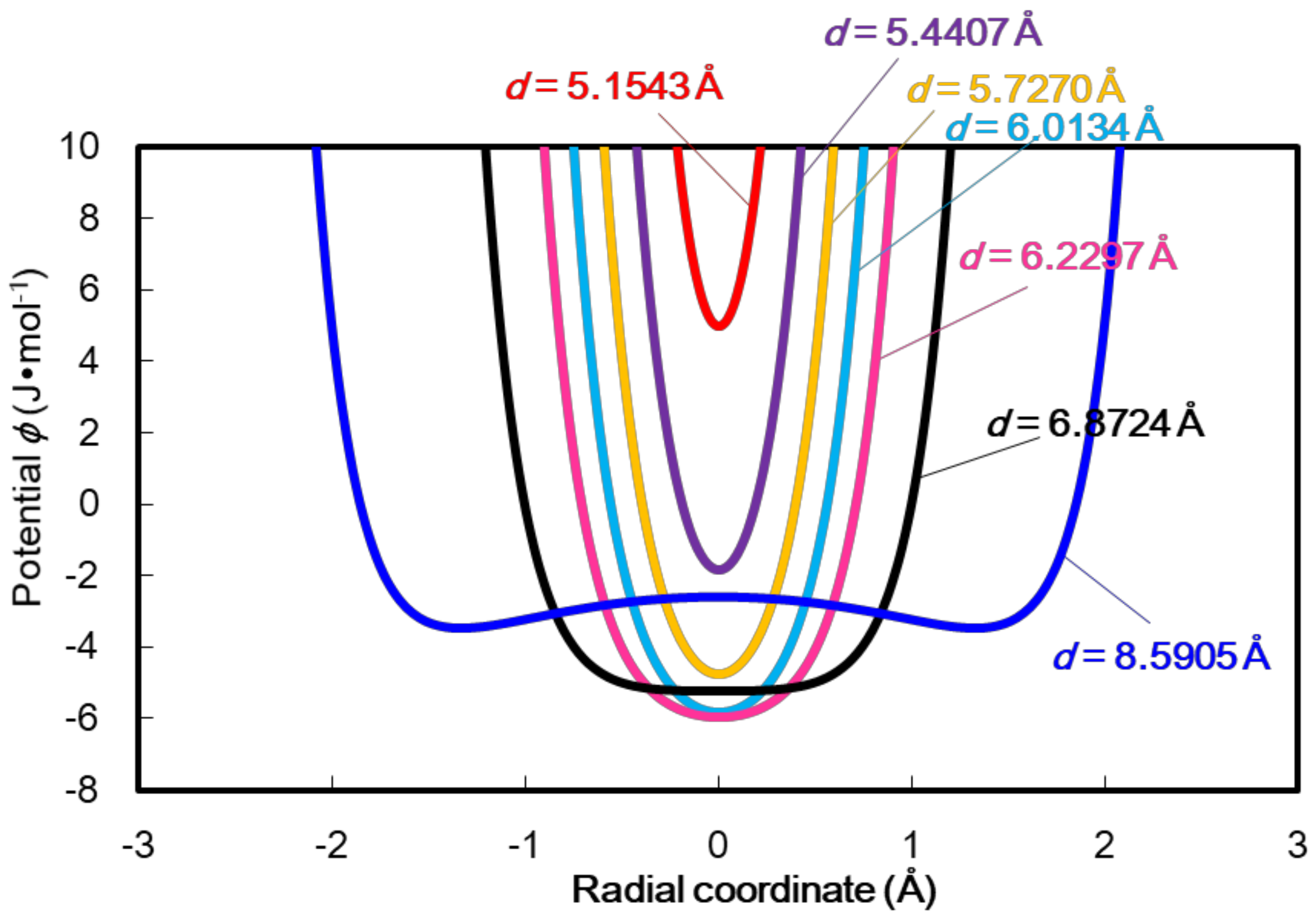
2.2. Potential in Cylindrical Pores
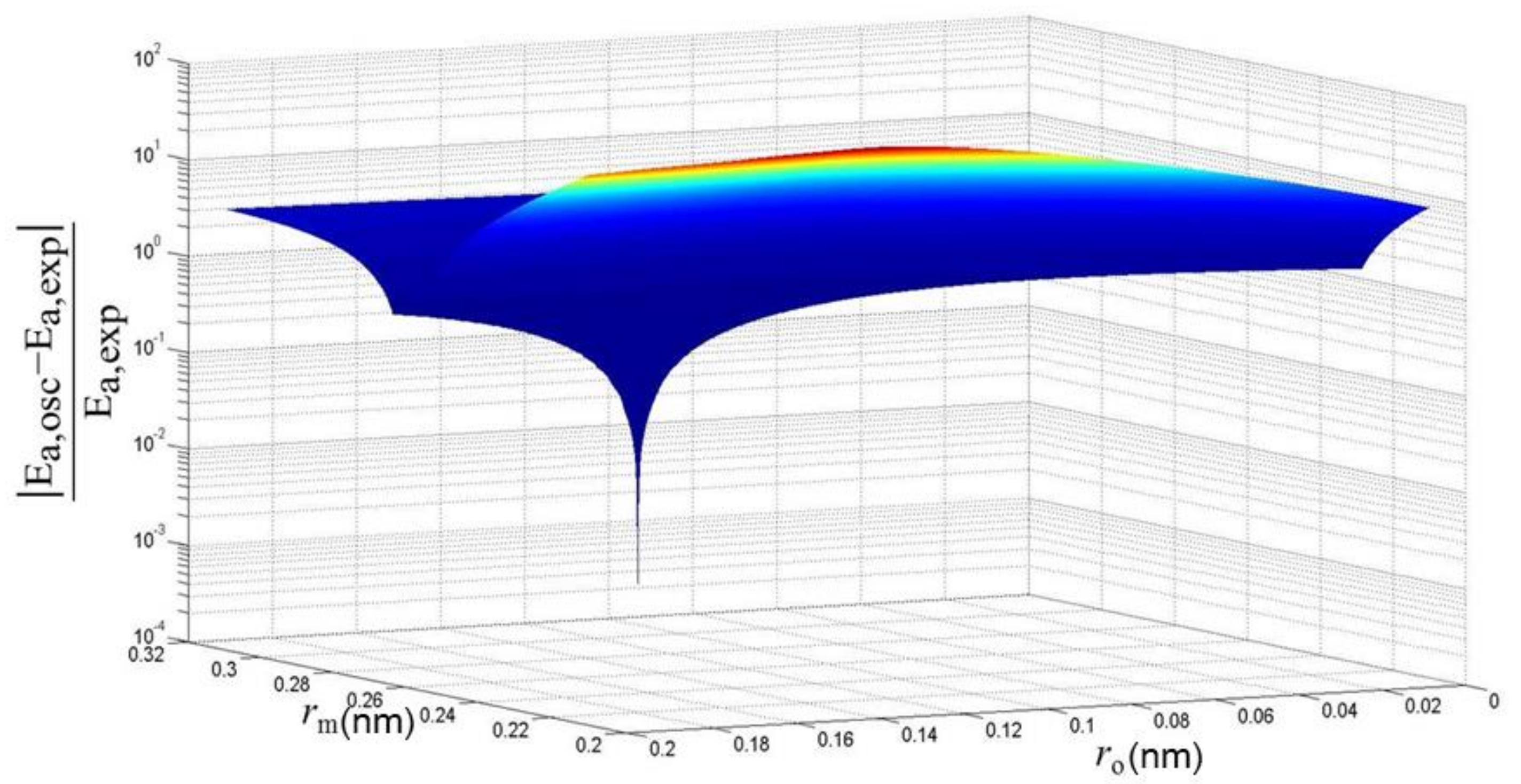
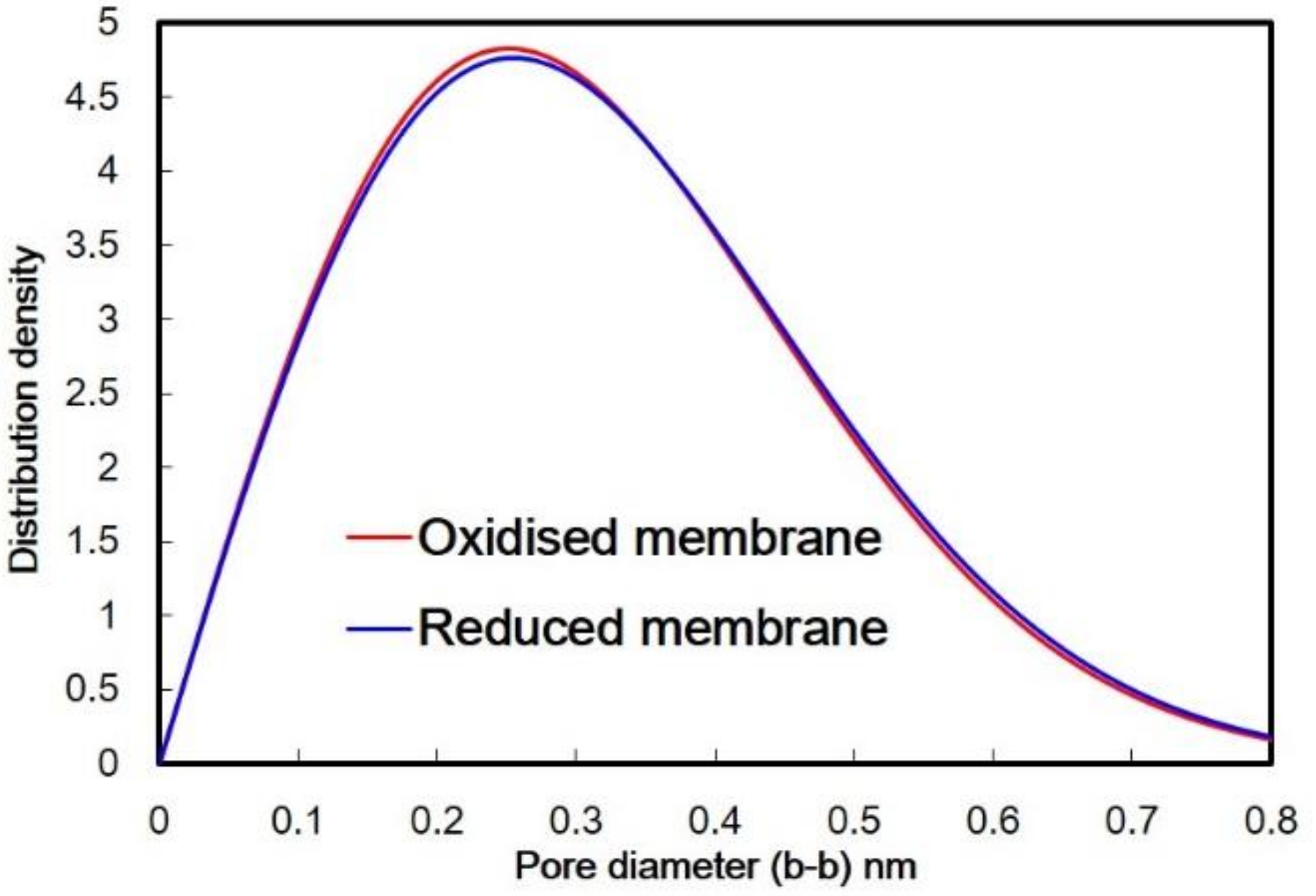
2.3. Pore Size Distribution (PSD) Estimation of A Membrane
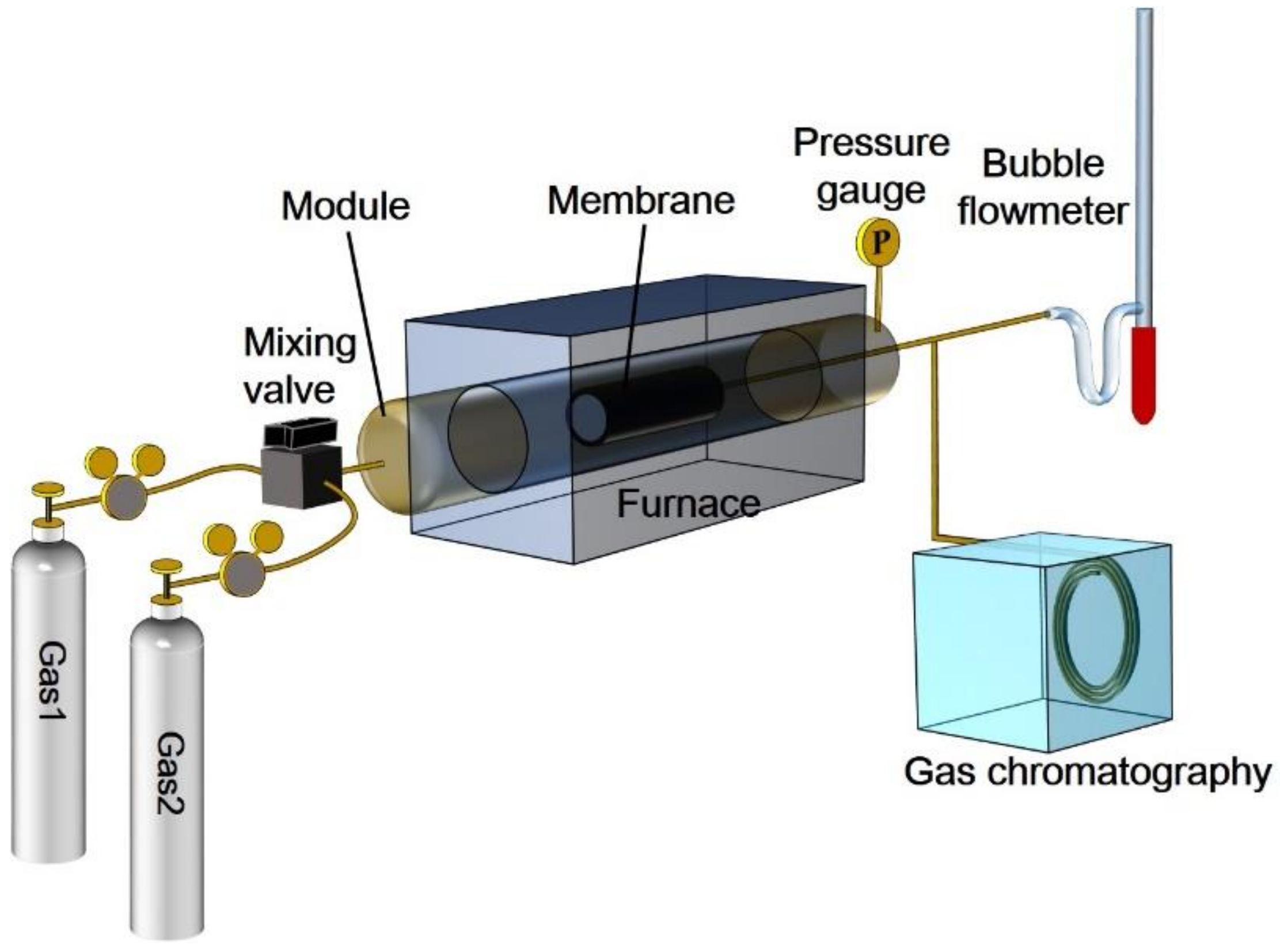
3. Experiment
3.1. Sol-Gel Preparation and Membrane Coating
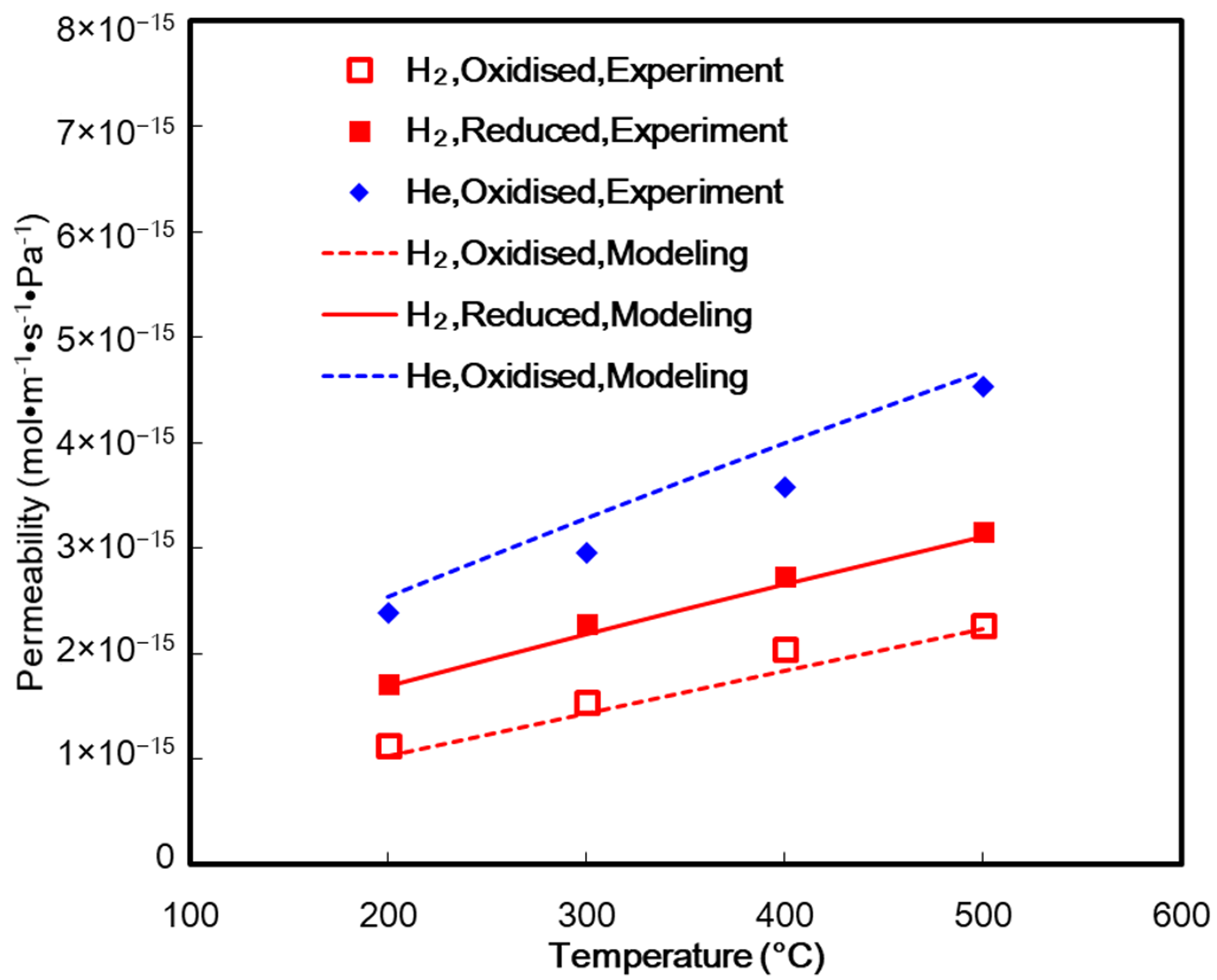
3.2. Gas Separation Measurement
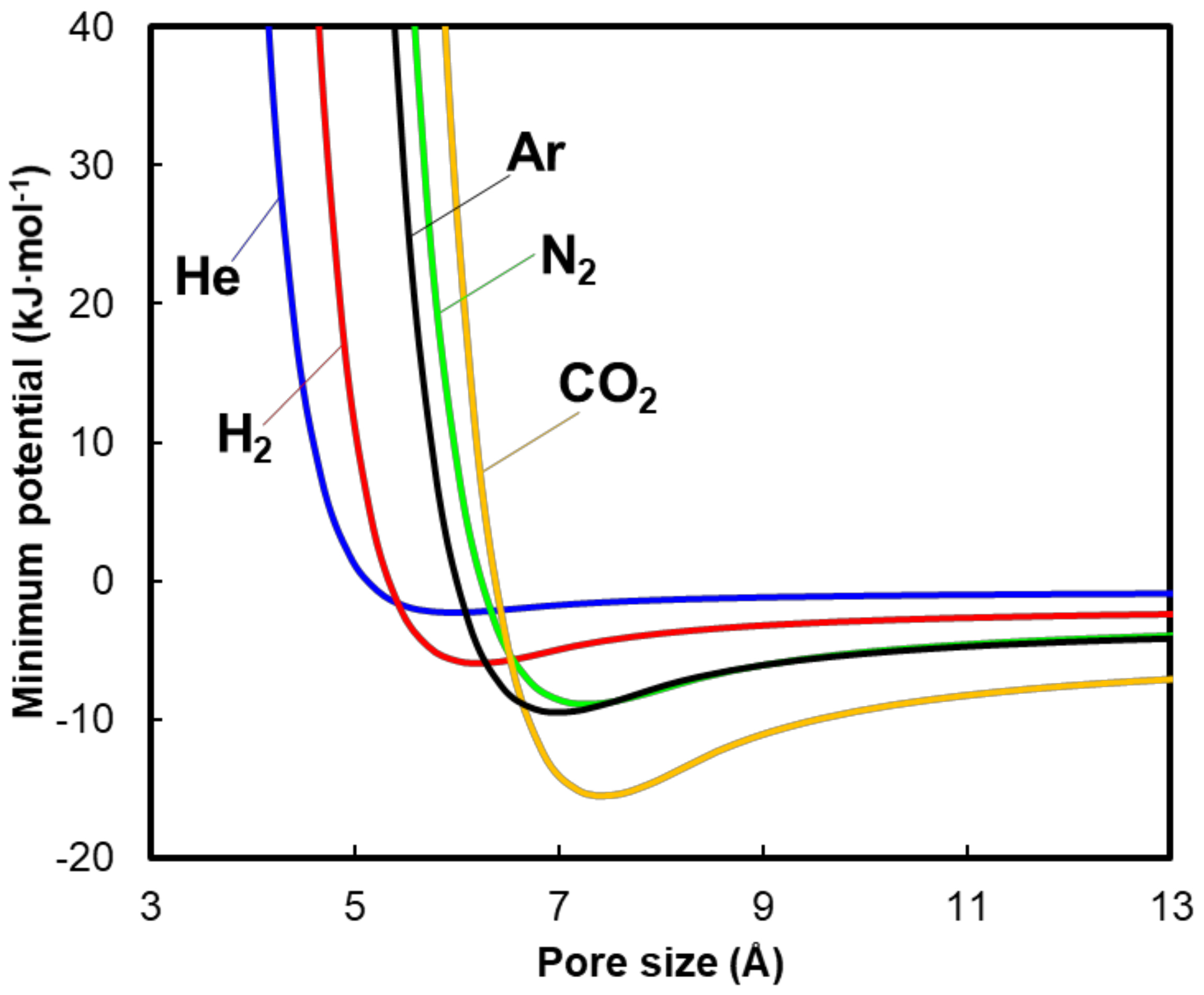
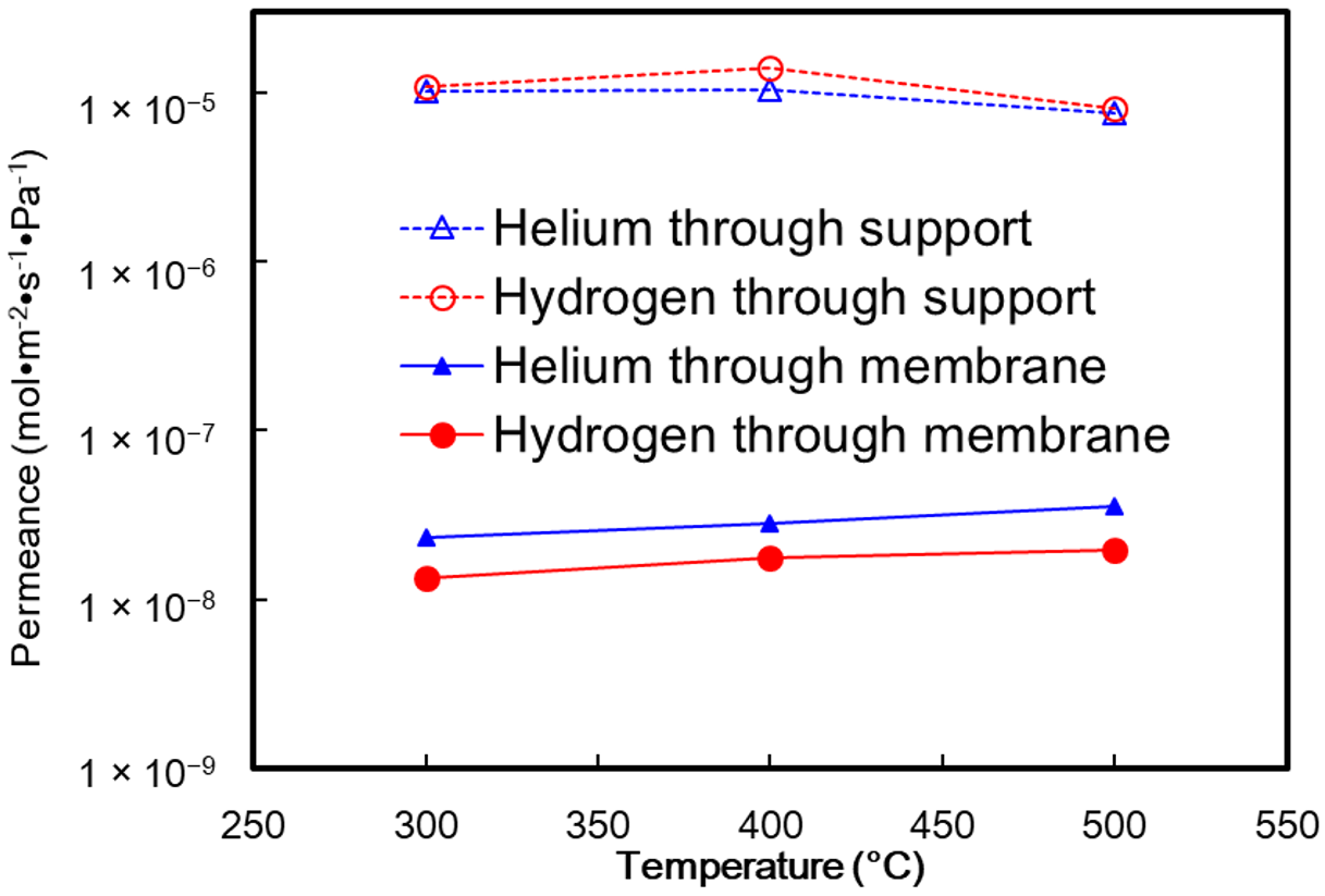
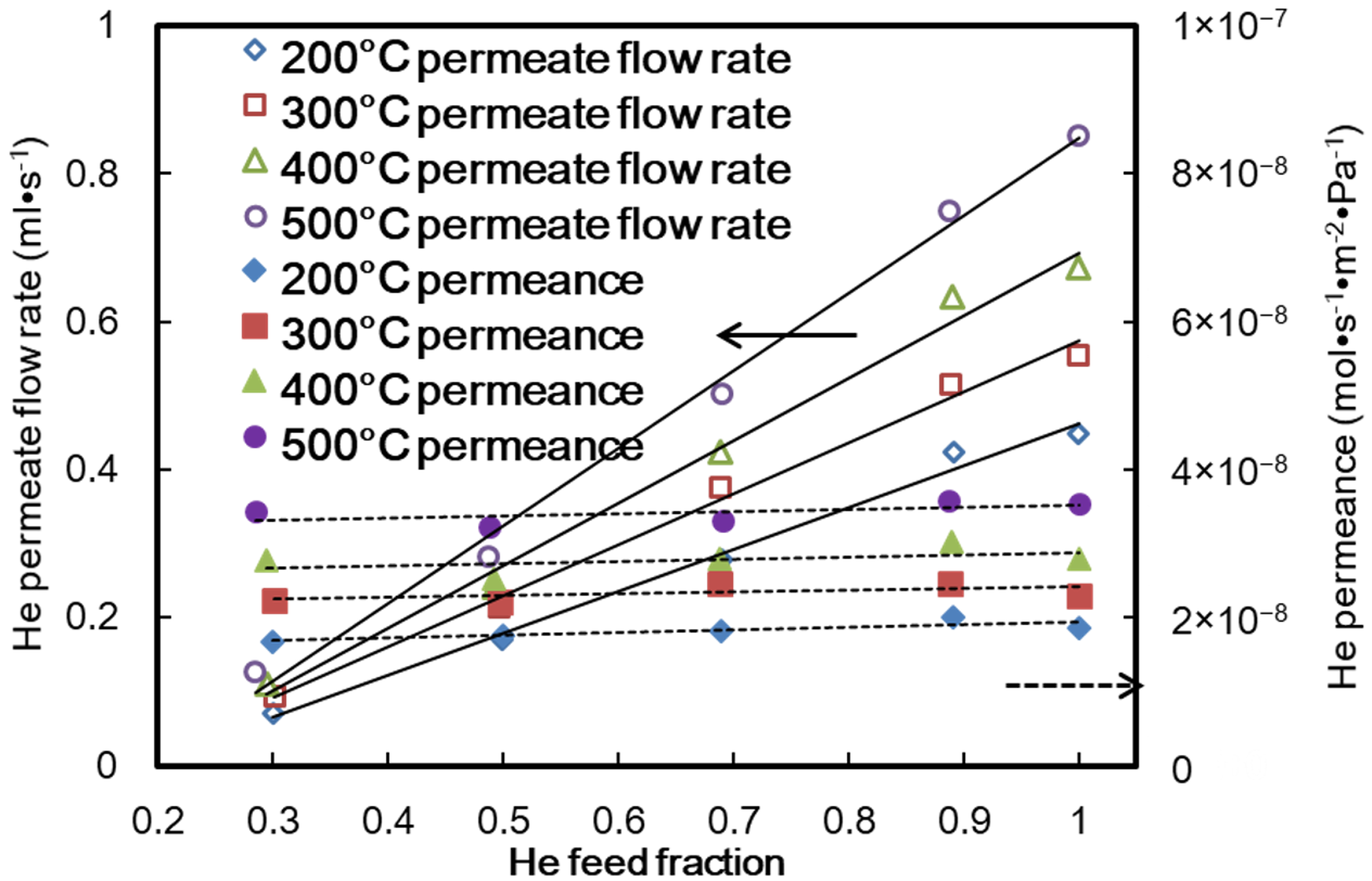
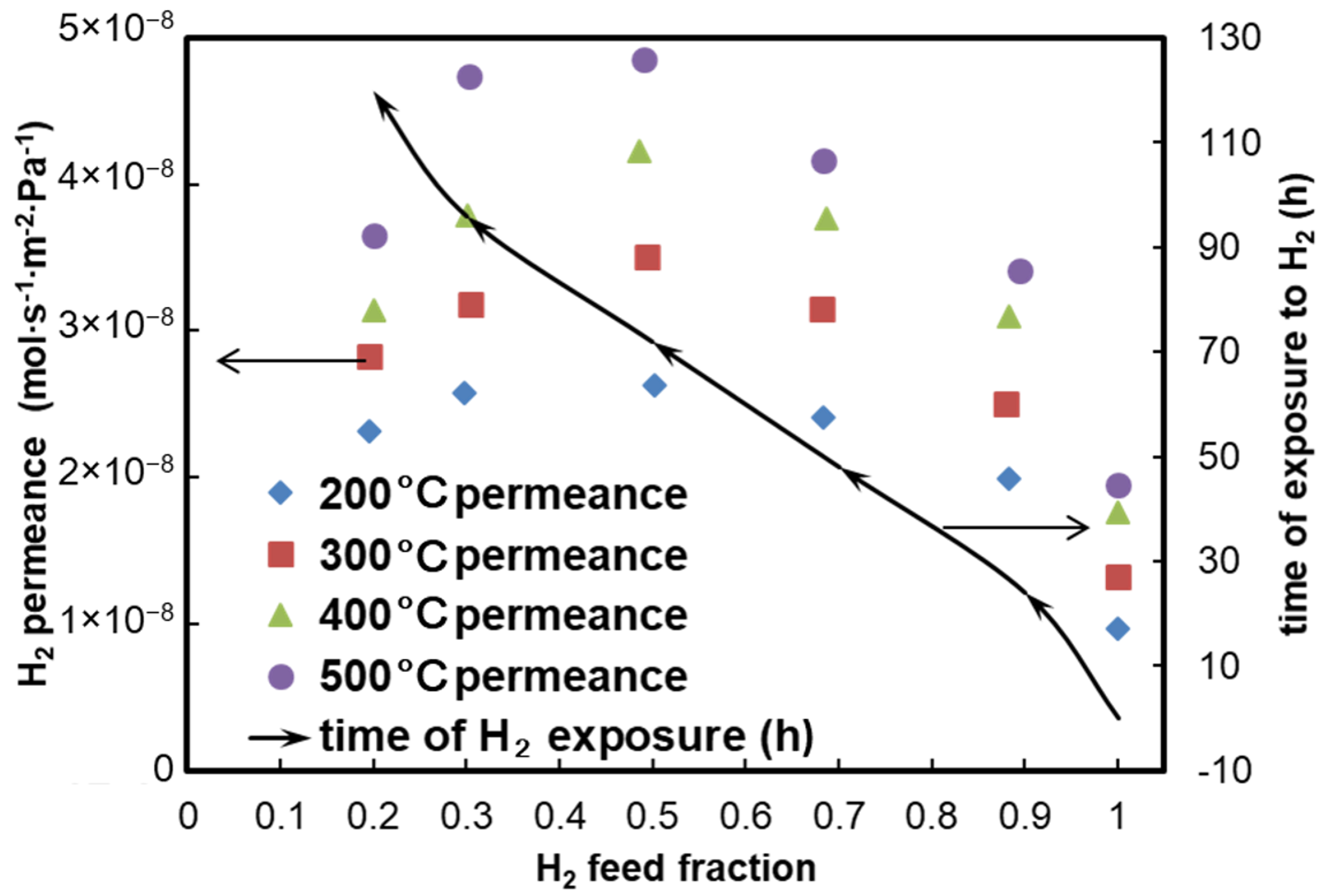
4. Results and Discussion
5. Conclusion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ji, G.; Wang, G.; Hooman, K.; Bhatia, S.; Diniz da Costa, J.C. Scale-Up Design Analysis and Modelling of Cobalt Oxide Silica Membrane Module for Hydrogen Processing. Processes 2013, 1, 49–66. [Google Scholar] [CrossRef]
- Ji, G.; George, A.; Skoulou, V.; Reed, G.; Millan, M.; Hooman, K.; Bhatia, S.K.; Diniz da Costa, J.C. Investigation and simulation of the transport of gas containing mercury in microporous silica membranes. Chem. Eng. Sci. 2018, 190, 286–296. [Google Scholar] [CrossRef]
- Smart, S.; Lin, C.X.C.; Ding, L.; Thambimuthu, K.; Diniz da Costa, J.C. Ceramic membranes for gas processing in coal gasification. Energy Environ. Sci. 2010, 3, 268–278. [Google Scholar] [CrossRef]
- Ji, G.; Yao, J.G.; Clough, P.T.; Diniz da Costa, J.C.; Anthony, E.J.; Fennell, P.S.; Wang, W.; Zhao, M. Enhanced hydrogen production from thermochemical processes. Energy Environ. Sci. 2018, 11, 2647–2672. [Google Scholar] [CrossRef]
- De Vos, R.M.; Verweij, H. High-Selectivity, High-Flux Silica Membranes for Gas Separation. Science 1998, 279, 1710–1711. [Google Scholar] [CrossRef] [PubMed]
- Raman, N.K.; Brinker, C.J. Organic “template” approach to molecular sieving silica membranes. J. Membr. Sci. 1995, 105, 273–279. [Google Scholar] [CrossRef]
- Kusakabe, K.; Sakamoto, S.; Saie, T.; Morooka, S. Pore structure of silica membranes formed by a sol–gel technique using tetraethoxysilane and alkyltriethoxysilanes. Sep. Purif. Technol. 1999, 16, 139–146. [Google Scholar] [CrossRef]
- Kanezashi, M.; Fujita, T.; Asaeda, M. Nickel-Doped Silica Membranes for Separation of Helium from Organic Gas Mixtures. Sep. Sci. Technol. 2005, 40, 225–238. [Google Scholar] [CrossRef]
- Kanezashi, M.; Asaeda, M. Hydrogen permeation characteristics and stability of Ni-doped silica membranes in steam at high temperature. J. Membr. Sci. 2006, 271, 86–93. [Google Scholar] [CrossRef]
- Battersby, S.; Duke, M.C.; Liu, S.; Rudolph, V.; Diniz da Costa, J.C. Metal doped silica membrane reactor: Operational effects of reaction and permeation for the water gas shift reaction. J. Membr. Sci. 2008, 316, 46–52. [Google Scholar] [CrossRef]
- Uhlmann, D.; Liu, S.; Ladewig, B.P.; Diniz da Costa, J.C. Cobalt-doped silica membranes for gas separation. J. Membr. Sci. 2009, 326, 316–321. [Google Scholar] [CrossRef]
- Uhlmann, D.; Smart, S.; Diniz da Costa, J.C. High temperature steam investigation of cobalt oxide silica membranes for gas separation. Sep. Purif. Technol. 2010, 76, 171–178. [Google Scholar] [CrossRef]
- Uhlmann, D.; Smart, S.; Diniz da Costa, J.C. H2S stability and separation performance of cobalt oxide silica membranes. J. Membr. Sci. 2011, 380, 48–54. [Google Scholar] [CrossRef]
- Liu, L.; Wang, D.K.; Martens, D.L.; Smart, S.; Diniz da Costa, J.C. Influence of sol–gel conditioning on the cobalt phase and the hydrothermal stability of cobalt oxide silica membranes. J. Membr. Sci. 2015, 475, 425–432. [Google Scholar] [CrossRef]
- Boffa, V.; Blank, D.H.A.; Ten Elshof, J.E. Hydrothermal stability of microporous silica and niobia–silica membranes. J. Membr. Sci. 2008, 319, 256–263. [Google Scholar] [CrossRef]
- Kanezashi, M.; Fuchigami, D.; Yoshioka, T.; Tsuru, T. Control of Pd dispersion in sol–gel-derived amorphous silica membranes for hydrogen separation at high temperatures. J. Membr. Sci. 2013, 439, 78–86. [Google Scholar] [CrossRef]
- Yoshida, K.; Hirano, Y.; Fujii, H.; Tsuru, T.; Asaeda, M. Hydrothermal Stability and Performance of Silica-Zirconia Membranes for Hydrogen Separation in Hydrothermal Conditions. J. Chem. Eng. Jpn. 2001, 34, 523–530. [Google Scholar] [CrossRef]
- Gu, Y.; Oyama, S.T. Permeation properties and hydrothermal stability of silica–titania membranes supported on porous alumina substrates. J. Membr. Sci. 2009, 345, 267–275. [Google Scholar] [CrossRef]
- Fotou, G.P.; Lin, Y.S.; Pratsinis, S.E. Hydrothermal stability of pure and modified microporous silica membranes. J. Mater. Sci. 1995, 30, 2803–2808. [Google Scholar] [CrossRef]
- Darmawan, A.; Motuzas, J.; Smart, S.; Julbe, A.; Diniz da Costa, J.C. Binary iron cobalt oxide silica membrane for gas separation. J. Membr. Sci. 2015, 474, 32–38. [Google Scholar] [CrossRef]
- Darmawan, A.; Motuzas, J.; Smart, S.; Julbe, A.; Diniz da Costa, J.C. Temperature dependent transition point of purity versus flux for gas separation in Fe/Co-silica membranes. Sep. Purif. Technol. 2015, 151, 284–291. [Google Scholar] [CrossRef]
- Ballinger, B.; Motuzas, J.; Smart, S.; Diniz da Costa, J.C. Palladium cobalt binary doping of molecular sieving silica membranes. J. Membr. Sci. 2014, 451, 185–191. [Google Scholar] [CrossRef]
- Ballinger, B.; Motuzas, J.; Miller, C.R.; Smart, S.; Diniz da Costa, J.C. Nanoscale assembly of lanthanum silica with dense and porous interfacial structures. Sci. Rep. 2015, 5, 8210. [Google Scholar] [CrossRef] [PubMed]
- Battersby, S.; Tasaki, T.; Smart, S.; Ladewig, B.; Liu, S.; Duke, M.C.; Rudolph, V.; Diniz da Costa, J.C. Performance of cobalt silica membranes in gas mixture separation. J. Membr. Sci. 2009, 329, 91–98. [Google Scholar] [CrossRef]
- Meixner, D.L.; Dyer, P.N. Characterization of the transport properties of microporous inorganic membranes. J. Membr. Sci. 1998, 140, 81–95. [Google Scholar] [CrossRef]
- Duke, M.C.; Pas, S.J.; Hill, A.J.; Lin, Y.S.; Diniz da Costa, J.C. Exposing the Molecular Sieving Architecture of Amorphous Silica Using Positron Annihilation Spectroscopy. Adv. Funct. Mater. 2008, 18, 3818–3826. [Google Scholar] [CrossRef]
- Diniz da Costa, J.C.; Lu, G.Q.; Rudolph, V.; Lin, Y.S. Novel molecular sieve silica (MSS) membranes: Characterisation and permeation of single-step and two-step sol–gel membranes. J. Membr. Sci. 2002, 198, 9–21. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.; Diniz da Costa, J.C. Hydrogen gas mixture separation by CVD silica membrane. J. Membr. Sci. 2008, 323, 144–147. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.; Yoshino, Y.; Nomura, M.; Nair, B.N.; Nakao, S.-I. A hybrid processing method for high performance hydrogen-selective silica membranes. J. Membr. Sci. 2007, 297, 5–9. [Google Scholar] [CrossRef]
- Zivkovic, T. Thin Supported Silica Membranes; The University Twente: Enschede, The Netherlands, 2007. [Google Scholar]
- Ha, H.Y.; Nam, S.W.; Lee, W.K. Chemical vapor deposition of hydrogen-permselective silica films on porous glass supports from tetraethylorthosilicate. J. Membr. Sci. 1993, 85, 279–290. [Google Scholar]
- Ghasemzadeh, K.; Aghaeinejad-Meybodi, A.; Vaezi, M.J.; Gholizadeh, A.; Abdi, M.A.; Babaluo, A.A.; Haghighi, M.; Basile, A. Hydrogen production via silica membrane reactor during the methanol steam reforming process: Experimental study. RSC Adv. 2015, 5, 95823–95832. [Google Scholar] [CrossRef]
- Kanezashi, M.; Sasaki, T.; Tawarayama, H.; Nagasawa, H.; Yoshioka, T.; Ito, K.; Tsuru, T. Experimental and Theoretical Study on Small Gas Permeation Properties through Amorphous Silica Membranes Fabricated at Different Temperatures. J. Phys. Chem. C 2014, 118, 20323–20331. [Google Scholar] [CrossRef]
- Kanezashi, M.; Sasaki, T.; Tawarayama, H.; Yoshioka, T.; Tsuru, T. Hydrogen Permeation Properties and Hydrothermal Stability of Sol–Gel-Derived Amorphous Silica Membranes Fabricated at High Temperatures. J. Am. Ceram. Soc. 2013, 96, 2950–2957. [Google Scholar] [CrossRef]
- Yoshioka, T.; Nakanishi, E.; Tsuru, T.; Asaeda, M. Experimental studies of gas permeation through microporous silica membranes. AlChE J. 2001, 47, 2052–2063. [Google Scholar] [CrossRef]
- De Vos, R.M.; Maier, W.F.; Verweij, H. Hydrophobic silica membranes for gas separation. J. Membr. Sci. 1999, 158, 277–288. [Google Scholar] [CrossRef]
- Krishna, R.; Baur, R. Modelling issues in zeolite based separation processes. Sep. Purif. Technol. 2003, 33, 213–254. [Google Scholar] [CrossRef]
- Van den Bergh, J.; Ban, S.; Vlugt, T.J.H.; Kapteijn, F. Modeling the Loading Dependency of Diffusion in Zeolites: The Relevant Site Model Extended to Mixtures in DDR-Type Zeolite. J. Phys. Chem. C 2009, 113, 21856–21865. [Google Scholar] [CrossRef]
- Ji, G.; Wang, G.; Hooman, K.; Bhatia, S.; Diniz da Costa, J.C. Simulation of binary gas separation through multi-tube molecular sieving membranes at high temperatures. Chem. Eng. J. 2013, 218, 394–404. [Google Scholar] [CrossRef]
- Burggraaf, A.J. Single gas permeation of thin zeolite (MFI) membranes: Theory and analysis of experimental observations. J. Membr. Sci. 1999, 155, 45–65. [Google Scholar] [CrossRef]
- Krishna, R. A unified approach to the modelling of intraparticle diffusion in adsorption processes. Gas Sep. Purif. 1993, 7, 91–104. [Google Scholar] [CrossRef]
- Krishna, R.; Van Baten, J.M. A simplified procedure for estimation of mixture permeances from unary permeation data. J. Membr. Sci. 2011, 367, 204–210. [Google Scholar] [CrossRef]
- Thornton, A.W.; Hilder, T.; Hill, A.J.; Hill, J.M. Predicting gas diffusion regime within pores of different size, shape and composition. J. Membr. Sci. 2009, 336, 101–108. [Google Scholar] [CrossRef]
- Bonilla, M.R.; Bhatia, S.K. The low-density diffusion coefficient of soft-sphere fluids in nanopores: Accurate correlations from exact theory and criteria for applicability of the Knudsen model. J. Membr. Sci. 2011, 382, 339–349. [Google Scholar] [CrossRef]
- Bhatia, S.K. Tractable molecular theory of transport of Lennard-Jones fluids in nanopores. J. Chem. Phys. 2004, 120, 4472–4485. [Google Scholar] [CrossRef] [PubMed]
- Tomozawa, M. Chapter 3—Amorphous silica. In Silicon-Based Material and Devices; Nalwa, H.S., Ed.; Academic Press: Burlington, NJ, USA, 2001; pp. 127–154. [Google Scholar]
- Lang, N.R.; Münster, S.; Metzner, C.; Krauss, P.; Schürmann, S.; Lange, J.; Aifantis, K.E.; Friedrich, O.; Fabry, B. Estimating the 3D Pore Size Distribution of Biopolymer Networks from Directionally Biased Data. Biophys. J. 2013, 105, 1967–1975. [Google Scholar] [CrossRef] [PubMed]
- Metzner, C.; Krauss, P.; Fabry, B. Poresizes in random line networks. arXiv 2011, arXiv:1110.1803v1. [Google Scholar]
- Phirani, J.; Pitchumani, R.; Mohanty, K.K. Transport Properties of Hydrate Bearing Formations from Pore-Scale Modeling. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 4–7 October 2009. [Google Scholar]
- Panfilov, M.; Panfilova, I.; Stepanyants, Y. Mechanisms of Particle Transport Acceleration in Porous Media. Transp. Porous Media 2008, 74, 49–71. [Google Scholar] [CrossRef]
- Park, C.-Y.; Ihm, S.-K. New hypotheses for Mercury porosimetry with percolation approach. AlChE J. 1990, 36, 1641–1648. [Google Scholar] [CrossRef]
- Mishra, B.K.; Sharma, M.M. Measurement of pore size distributions from capillary pressure curves. AlChE J. 1988, 34, 684–687. [Google Scholar] [CrossRef]
- Bhatia, S.K. Modeling Pure Gas Permeation in Nanoporous Materials and Membranes. Langmuir 2010, 26, 8373–8385. [Google Scholar] [CrossRef] [PubMed]
- Jepps, O.G.; Bhatia, S.K.; Searles, D.J. Wall Mediated Transport in Confined Spaces: Exact Theory for Low Density. Phys. Rev. Lett. 2003, 91, 126102. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Seaton, N.A. Prediction of the effective diffusivity in pore networks close to a percolation threshold. AlChE J. 1992, 38, 1816–1824. [Google Scholar] [CrossRef]
- Burganos, V.N.; Sotirchos, S.V. Diffusion in pore networks: Effective medium theory and smooth field approximation. AlChE J. 1987, 33, 1678–1689. [Google Scholar] [CrossRef]
- Kirkpatrick, S. Percolation and Conduction. Rev. Mod. Phys. 1973, 45, 574–588. [Google Scholar] [CrossRef]
- Landauer, R. The Electrical Resistance of Binary Metallic Mixtures. J. Appl. Phys. 1952, 23, 779–784. [Google Scholar] [CrossRef]
- Bhatia, S.K. Directional autocorrelation and the diffusional tortuosity of capillary porous media. J. Catal. 1985, 93, 192–196. [Google Scholar] [CrossRef]
- Bhatia, S.K. Stochastic theory of transport in inhomogeneous media. Chem. Eng. Sci. 1986, 41, 1311–1324. [Google Scholar] [CrossRef]
- Ji, G.; Smart, S.; Bhatia, S.K.; Diniz da Costa, J.C. Improved pore connectivity by the reduction of cobalt oxide silica membranes. Sep. Purif. Technol. 2015, 154, 338–344. [Google Scholar] [CrossRef]
- Bakker, W.J.W.; Kapteijn, F.; Poppe, J.; Moulijn, J.A. Permeation characteristics of a metal-supported silicalite-1 zeolite membrane. J. Membr. Sci. 1996, 117, 57–78. [Google Scholar] [CrossRef]
- Kapteijn, F.; Bakker, W.J.W.; Van de Graaf, J.; Zheng, G.; Poppe, J.; Moulijn, J.A. Permeation and separation behaviour of a silicalite-1 membrane. Catal. Today 1995, 25, 213–218. [Google Scholar] [CrossRef]
- Smart, S.; Vente, J.F.; Diniz da Costa, J.C. High temperature H2/CO2 separation using cobalt oxide silica membranes. Int. J. Hydrog. Energy 2012, 37, 12700–12707. [Google Scholar] [CrossRef]
- Bhatia, S.K.; Nicholson, D. Some pitfalls in the use of the Knudsen equation in modelling diffusion in nanoporous materials. Chem. Eng. Sci. 2011, 66, 284–293. [Google Scholar] [CrossRef]
- Gao, X.; Diniz da Costa, J.C.; Bhatia, S.K. Adsorption and transport of gases in a supported microporous silica membrane. J. Membr. Sci. 2014, 460, 46–61. [Google Scholar] [CrossRef]
- Yacou, C.; Smart, S.; Diniz da Costa, J.C. Long term performance cobalt oxide silica membrane module for high temperature H2 separation. Energy. Environ. Sci. 2012, 5, 5820–5832. [Google Scholar] [CrossRef]
- Ji, G.; Wang, G.; Hooman, K.; Bhatia, S.; Diniz da Costa, J.C. The fluid dynamic effect on the driving force for a cobalt oxide silica membrane module at high temperatures. Chem. Eng. Sci. 2014, 111, 142–152. [Google Scholar] [CrossRef]
- Miller, C.R.; Wang, D.K.; Smart, S.; Diniz da Costa, J.C. Reversible Redox Effect on Gas Permeation of Cobalt Doped Ethoxy Polysiloxane (ES40) Membranes. Sci. Rep. 2013, 3, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.; Wei, J. Diffusion mechanism of hydrocarbons in zeolites—I. Theory. Chem. Eng. Sci. 1992, 47, 1123–1141. [Google Scholar] [CrossRef]
- Xiao, J.; Wei, J. Diffusion mechanism of hydrocarbons in zeolites—II. Analysis of experimental observations. Chem. Eng. Sci. 1992, 47, 1143–1159. [Google Scholar] [CrossRef]
- Hacarlioglu, P.; Lee, D.; Gibbs, G.V.; Oyama, S.T. Activation energies for permeation of He and H2 through silica membranes: An ab initio calculation study. J. Membr. Sci. 2008, 313, 277–283. [Google Scholar] [CrossRef]
| Apparent Activation Energy (kJ·mol−1) | Reference | ||||
|---|---|---|---|---|---|
| H2 | He | CO2 | N2 | Ar | |
| 16.4~17.1 | 16.2~17.1 | - | - | - | [27] |
| 2.2 | 2.8 | −9.8 | −5.4 | - | [28] |
| 15.4~19.4 | - | - | 8.5~11.9 | - | [29] |
| 12.8 | 20.7 | −20 | - | - | [24] |
| - | 9.5 | - | −5.0 | - | [11] |
| - | 13.6 | - | - | - | [30] |
| 6 | - | - | - | - | [31] |
| 4.91 | 4.70 | −2.91 | −1.41 | - | [14] |
| 10.1 | - | −3.1 | - | −1.9 | [32] |
| 14.1 | 7.7 | - | 12.3 | - | [33] |
| ~9 | 7.2 | - | - | - | [34] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, G.; Gao, X.; Smart, S.; Bhatia, S.K.; Wang, G.; Hooman, K.; Diniz da Costa, J.C. Estimation of Pore Size Distribution of Amorphous Silica-Based Membrane by the Activation Energies of Gas Permeation. Processes 2018, 6, 239. https://doi.org/10.3390/pr6120239
Ji G, Gao X, Smart S, Bhatia SK, Wang G, Hooman K, Diniz da Costa JC. Estimation of Pore Size Distribution of Amorphous Silica-Based Membrane by the Activation Energies of Gas Permeation. Processes. 2018; 6(12):239. https://doi.org/10.3390/pr6120239
Chicago/Turabian StyleJi, Guozhao, Xuechao Gao, Simon Smart, Suresh K. Bhatia, Geoff Wang, Kamel Hooman, and João C. Diniz da Costa. 2018. "Estimation of Pore Size Distribution of Amorphous Silica-Based Membrane by the Activation Energies of Gas Permeation" Processes 6, no. 12: 239. https://doi.org/10.3390/pr6120239
APA StyleJi, G., Gao, X., Smart, S., Bhatia, S. K., Wang, G., Hooman, K., & Diniz da Costa, J. C. (2018). Estimation of Pore Size Distribution of Amorphous Silica-Based Membrane by the Activation Energies of Gas Permeation. Processes, 6(12), 239. https://doi.org/10.3390/pr6120239










