Abstract
Energy is a key driver of the modern economy, therefore modeling and simulation of energy systems has received significant research attention. We review the major developments in this area and propose two ways to categorize the diverse contributions. The first categorization is according to the modeling approach, namely into computational, mathematical, and physical models. With this categorization, we highlight certain novel hybrid approaches that combine aspects of the different groups proposed. The second categorization is according to field namely Process Systems Engineering (PSE) and Energy Economics (EE). We use the following criteria to illustrate the differences: the nature of variables, theoretical underpinnings, level of technological aggregation, spatial and temporal scales, and model purposes. Traditionally, the Process Systems Engineering approach models the technological characteristics of the energy system endogenously. However, the energy system is situated in a broader economic context that includes several stakeholders both within the energy sector and in other economic sectors. Complex relationships and feedback effects exist between these stakeholders, which may have a significant impact on strategic, tactical, and operational decision-making. Leveraging the expertise built in the Energy Economics field on modeling these complexities may be valuable to process systems engineers. With this categorization, we present the interactions between the two fields, and make the case for combining the two approaches. We point out three application areas: (1) optimal design and operation of flexible processes using demand and price forecasts, (2) sustainability analysis and process design using hybrid methods, and (3) accounting for the feedback effects of breakthrough technologies. These three examples highlight the value of combining Process Systems Engineering and Energy Economics models to get a holistic picture of the energy system in a wider economic and policy context.
1. Introduction
Energy is one primary driver of the modern economy that involves several stakeholders such as energy production and distribution firms, energy investors, end users, as well as government regulators. Population growth and improving standards of living, especially in developing countries, are expected to significantly increase energy consumption. The IEA predicts an increase in total primary energy demand (TPED) from 13.8 billion tonnes of oil equivalent (toe) in 2016 to 19.3 billion toe under its “current policies” scenario in 2040 [1]. Alternatively, in the “sustainable development” scenario where policies are enacted in order to achieve the objectives of the COP 21 Paris agreement (2015) together with universal access to energy services and a large reduction in energy-related pollution, TPED grows to 14.1 billion toe in 2040. In this period, CO2 emissions would increase from 32.1 billion tonnes to 42.7 billion tonnes under the current policies scenario or would have to decrease to 18.3 billion tonnes in the sustainable development scenario. Transitioning to a sustainable energy future through the accelerated adoption of clean energy technologies and energy efficiency practices requires the engagement of various decision makers from the scientific, financial, industrial, and public-policy communities with an interdisciplinary approach that combines engineering, economics, and environmental perspectives [2].
An energy system is defined by the Intergovernmental Panel on Climate Change (IPCC) in its fifth Assessment Report as a “system [that] comprises all components related to the production, conversion, delivery, and use of energy” [3]. Figure 1 shows the different components of an energy system. First, primary energy stored in natural resources (such as fossil fuels, uranium, renewable resources) is harvested and transported to the conversion site(s) in which a wide range of processes (such as combustion, refining, bioconversion, etc.) may take place to transform energy to more usable forms such as electricity and liquid fuels. This conversion process may integrate with local utilities such as the water distribution network. The usable energy is then transported and distributed through a potentially large number of infrastructure components to the final user. Final energy demand can be disaggregated into homogeneous categories of users such as transportation, residential, industrial, and commercial users. However, the energy production, conversion, transportation, and distribution steps combined typically also consume the largest amount of energy as a result of generally low efficiencies [4].
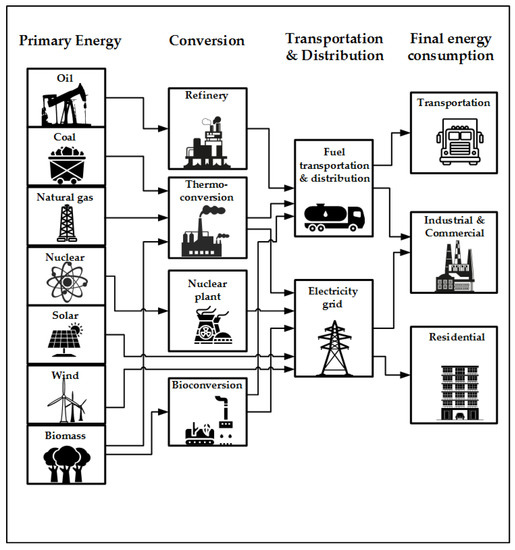
Figure 1.
Energy system showing the flow of energy from primary energy supply to final energy consumption.
Trade between suppliers and consumers occurs in energy markets with the primary energy price depending on a large number of factors such as supply and demand quantities, geopolitics and international trade policies, interaction with other economic sectors, technological changes, and even natural disasters. Figure 2 presents a comparison of the normalized prices (in $/GJ) of natural gas, oil, and coal fuels in the United States in order to illustrate the complex interdependencies between the energy sector and other sectors. For example, historically speaking, gas and oil have followed approximately the same price trends when expressed on a normalized per-energy basis up until the shale gas boom, which caused an unprecedented and sustained decoupling of oil and gas prices that has persisted for the past decade. Other recognizable events within the past generation include the gulf war of 1990, and the energy crisis and subsequent Great Recession during 2008–2009 that had major impacts on prices, although often temporary. Coal, on the other hand, has followed a relatively stable and consistent trend independent of world events, and has consistently been the lowest cost form of energy. However, it is possible that if gas continues its steady decline further below what are now the lowest prices in a generation, gas could even overtake coal as the cheapest form of energy within about 6–10 years at current rates.
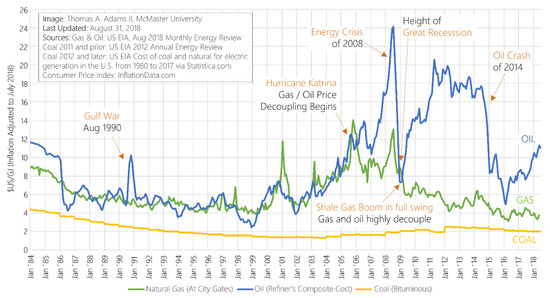
Figure 2.
The variation of the normalized prices of natural gas, oil, and coal fuels with a variety of factors such as supply and demand quantities, geopolitics and international trade policies, interaction with other economic sectors, technological changes, and even natural disasters. Coal, gas, and oil prices were collected from various publications from the US Energy Information Administration (see inset) depending on fuel type and year (See inset). Note that a small change in the standard indexing procedure for coal explains a slight jump in coal price at the beginning of 2012. Gas prices are for natural gas located at the city gates (i.e., prior to “last mile” transportation). Oil prices are the refiner’s composite cost of oil, which includes transportation and storage of oil, factoring in both domestic and imported crudes. Coal prices are free-on-board prices and do not include shipping or insurance. Prices are normalized by the consumer price index and converted to an energy basis using the following assumed energy densities: 32 GJ per tonne of coal (using medium-volatility bituminous), 6.118 GJ per barrel of oil, and 1037 BTU per standard ft3 of natural gas.
The need to understand and predict the functioning and performance of individual components of the energy system or the overall system behavior motivates the development of models. Several modeling approaches have been proposed in the literature for different purposes. In Section 2, we propose a classification of these approaches into computational, mathematical, and physical models, and outline the capabilities of the different formalisms in describing different phenomena. With this categorization, we highlight novel hybrid approaches that combine aspects of the different groups proposed. Simulation, on the other hand, involves solving the set of equations of mathematical models in order to determine the unknown variables so as to obtain key insights into the system’s behavior. The value of simulation lies in exploring the system’s behavior under a range of operational domains which may be expensive or even infeasible to do with the real-world system. Commonly, a further optimization step may be added in order to determine the conditions of optimal system performance with respect to a particular objective which may be economical, environmental, social, or a combination of the three [5].
Energy systems are studied by researchers in two different fields: Process Systems Engineering (PSE) and Energy Economics (EE). Figure 3 and Table 1 illustrate the division using different criteria such as the nature of variables, theoretical underpinnings, level of technological aggregation, spatial and temporal scales, and model purpose. Energy system models in PSE are typically at the unit operation, processing plant, or supply chain scale. Each of these scales represents a level of aggregation of technologies: Different unit operations are aggregated to give an overall conversion process at the plant scale and the conversion process together with the feedstock supply and product distribution network are aggregated at the supply chain scale. The purpose of modeling energy systems in PSE is to obtain insight into their technological performance for optimal decision making at the design, operations, and control level. Thus, the technological characteristics of the system components are modeled endogenously (i.e., are dependent on other variables or parameters in the model). The economic, environmental, or social parameters may be modeled exogenously (i.e., are independent of other variables or parameters in the model) depending on the optimization objective. Classically, modeling and simulation in PSE has been used for strategic, tactical, and operational decision-making at low levels of technological aggregation as illustrated in Figure 3 and detailed in Table 1. Energy economics approaches, on the other hand, use models with a high level of aggregation of technologies: All technologies comprising the entire energy sector at a regional, national or global scale may be studied (e.g., in bottom-up models) or even other sectors of the economy such as manufacturing, mining, construction, etc. (e.g., in top-down models). EE models are based on economic theory such as the laws of supply, demand and market equilibrium. Thus, the economic characteristics of the system components are modeled endogenously while technological, environmental, or social parameters may be modeled exogenously. The classic purpose of modeling energy systems in EE is to aid in making strategic decisions at regional, national, or global scales. EE models typically work with long-term time scales for a couple of reasons: first, the capital intensiveness, long gestation periods, and long payback periods motivate long term thinking; second, addressing sustainability issues requires planning of energy transformation pathways that may take decades to mature [6]. However, the advent of intermittent-supply renewable technologies and deregulation of the electricity market have led to the recent use of EE models for operational decision making as well. Application areas include determining the optimal operation of energy management systems and modeling electricity markets. To improve firm competitiveness, these EE models include several features such as seasonal demand variability, weather prediction, price spikes, etc. Reviews of electricity market modeling are given in [7,8].
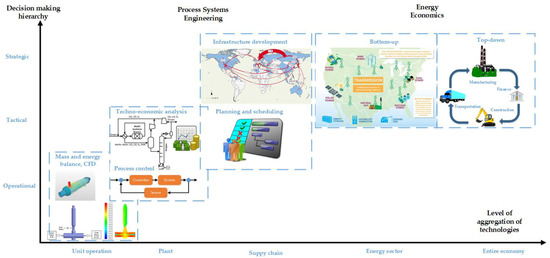
Figure 3.
Classification of energy system models according to discipline and level of technological aggregation. Computational Fluid Dynamics (CFD) Gasifier model reprinted from [11] with permission from Elsevier, Process flow diagram reprinted from [12] with permission of Adams, Thato, Le Feuvre and Swartz Copyright (2018), global supply chain reprinted from [13] with permission from Elsevier.

Table 1.
Classification of energy system models according to field.
To further explain the differences between PSE and EE models, we distinguish between a national energy supply chain PSE model (e.g., the biomass-to-bioenergy supply chain published by Elia et al. [9]) and an EE model for a national energy system (e.g., reviewed in [10]): While these two models are at the same scale, the PSE model contains information about the spatial (geographical) distribution of the different supply chain components while the EE model only abstracts their economic characteristics. In addition, while the PSE model only includes the biomass-to-bioenergy supply chain, the EE model would usually include all possible energy sources of the nation. Finally, the purpose of the two models may be different: EE models are typically used for strategic decision making by national planners and public policy officials, PSE supply chain models may be used for strategic, tactical, and operational decision-making typically by energy supply firms or enterprises.
Modeling and simulation of energy systems has received significant research interest from the PSE and EE communities. The methodology for this review paper began with a search using Engineering Village for journal papers published between 2015 and 2019 that contained the terms “energy system(s)” and “model” or “simulation” in the subject, title, or abstract which resulted in 5071 records, with the majority belonging to the EE field. In addition, we noticed that a large number of relevant papers from the PSE community were not included in this search because these used more plant-specific terms such as coal fired power plant, LNG processes, polygeneration system, etc. Considering this enormous body of literature, the scope of this paper is necessarily broad; we scrutinized for relevance according to the following criteria:
- Emphasis on critical review papers of the different sub-fields within EE and PSE. These are denoted using blue in Table 1.
- Emphasis on the most impactful papers (measured by number of citations) or seminal works that presented novel approaches. These are denoted using red in Table 1.
- Emphasis on the modeling approach used rather than the application area.
- Emphasis on open access models or modeling tools to reflect the open source ethos of the Processes journal. These are denoted using black in Table 1.
Considering the scope and audience of the Processes journal, we provide a detailed treatment of the PSE approach to energy system modeling and simulation, while we only provide a fundamental treatment of EE approaches. We discuss emerging trends in the PSE field, such as multi-scale systems engineering and sustainable process engineering, in detail. On the other hand, a discussion of the state-of-the-art in EE is outside the scope of this paper.
Previous reviews have primarily been from the EE field: Ringkjøb et al. presented a recent review of currently available modeling tools for energy systems containing significant renewable energy sources [146]. They provide an overview of the features and properties of the different tools, such as model purpose, approach, methodology, temporal resolution, modeling horizon, and geographical coverage, with the purpose of aiding modelers to choose the right tool. Lopion et al. presented a recent review of current challenges and trends in modeling national energy systems for the purpose of supporting governmental decision-making [10]. They provide a review of the different modeling tools used, the methodologies used, analytic approach, and the temporal and spatial resolutions. Hall and Buckley conducted a systematic review of energy systems modeling tools in the UK and found that certain modeling tools were preferred by academic and policy users [147]. They provide a review of the different purposes, model structure, geographical coverage, sectoral coverage, and temporal scale of prevalent UK energy systems models. Van Beeck proposed several ways of categorizing EE models of energy systems e.g., according to purpose, model structure and assumptions, analytical approach, underlying methodology, geographical coverage, and time horizon [148]. Jebaraj and Iniyan provided a review of different EE models used for a variety of purposes e.g., planning and emissions reductions, supply-demand forecasting, incorporating renewable energy sources, etc. [149]. Connolly et al. presented a review of computer tools used for integrating renewable energy sources into EE models, with the aim of helping future decision makers pick the right modeling tool [81]. They provide an analysis of the properties of 37 modeling tools with regards to criteria such as availability, tool capabilities, geographical coverage, and future time frame of uncertainty scenarios. Pfenninger et al. reviewed models used for national and international policy making and point out existing challenges in developing high spatial and temporal resolution models, handling uncertainty and complexity issues and incorporating human behavior and social risks [94]. Bhattacharyya and Timilsina provided a review of energy system models and illustrate the challenges for their use by energy, environment, and climate policy decision makers in developing countries [100]. Herbst et al. provided an introduction and overview of EE models and point out the strengths of bottom-up and top-down models as well as their weaknesses to motivate the development of linked models [150]. Nakata reviewed various EE models applied at local, national, and global scales and points out the issues arising from their incorrect application [151]. In another work, Nakata et al. reviewed EE models used for transforming to a low-carbon society and illustrate the need to consider a trans-disciplinary approach incorporating social, economic, and environmental considerations [79]. Weijermars et al. provided a review of models used to determine the optimal energy mix in order to mitigate climate change [77]. They provide a description of several modeling approaches such as forecasting and back-casting, and scenario and systems analysis, and point out the value of using integrated approaches.
In the PSE community, review papers have focused on individual feedstocks and their value chains such as: biomass [152,153], renewable sources [154,155], or hybrid feedstocks [156]. Other reviews have focussed on analysis along different scales such as district energy systems [157] and urban energy systems [158]. Zeng et al. provide a review of research done on modeling and optimization of energy systems for planning and emissions reduction purposes. Some reviewed papers use a PSE approach while the majority use an EE approach. Emphasis is on different optimization problem formulations that take parametric uncertainty into account: fuzzy, stochastic, and interval programming [159]. Liu et al. present an overview of different formulations of the optimal design and operation problem for a number of applications such as polygeneration energy systems, hydrogen infrastructure planning, commercial building systems as well as biofuels and biorefineries [160]. Adams provides a perspective on the opportunities for the design of new efficient energy systems. In particular, opportunities to integrate unrelated processes in order to exploit certain synergies, as well as the potentials to exploit waste feedstocks such as petroleum coke and flare gas, are highlighted [161]. Recently, Martin and Adams presented a perspective on near-term opportunities in PSE including the use of big data approaches, integrating process design, control and scheduling, and supply chain management [162]. In addition, they highlighted the potential for exploitation of new energy sources, production of new products for energy storage as well as the need for sustainable process design. Finally, Gani et al. provide an encyclopedic account of modeling and simulation approaches in PSE [19]. They provide a detailed description of the approach to modeling, the different model types and their properties and utility in representing various physical phenomena, different numerical methods and process simulation techniques. In addition, they present a review of general-purpose process simulation software with a discussion of their specific capabilities, strengths and weaknesses. To the authors’ knowledge, this review paper is the first to present the key contributions from both the PSE and EE fields to energy system modeling and simulation. The original contributions of this paper are as follows:
- First, we propose a categorization according to modeling approach namely into computational, mathematical, and physical approaches. With this categorization, we highlight certain novel hybrid approaches that combine aspects of the different groups proposed.
- Second, we propose a categorization according to field namely Process Systems Engineering (PSE) and Energy Economics (EE). We use the following criteria to illustrate the difference: the nature of variables, theoretical underpinnings, level of technological aggregation, spatial and temporal scales, and model purpose. With this categorization, we present the interaction between the PSE and EE fields and make the case for combining these two complementary approaches to get a more holistic picture of energy systems.
The remaining sections are organized as follows: Section 2 presents the categorization according to the modeling approach, Section 3 provides an overview of the PSE approach including a discussion of emerging trends, while Section 4 provides a basic overview of the EE approach, Section 5 makes the case for combining the PSE and EE approaches, and Section 6 presents our conclusions.
2. Categorization According to Modeling Approach
In this section, we present an overview of the different classes of energy system models. The categorization is made according to the modeling approach rather than the system boundary. Figure 4 illustrates the division into three classes: computational, mathematical, and physical models. The dichotomy between computational and mathematical models is explained by Fisher and Henzinger: computational models are a sequence of instructions that can be executed by a computer, yet mathematical models are a series of equations that denote relationships between different meaningful variables and parameters [163]. The development of mathematical models preceded the use of computers. However, approximations to mathematical models are usually developed using numerical techniques, which can then be solved (or simulated) using a computer. A variety of specialized numerical algorithms (e.g., Newton’s method, Secant method, etc. for root-finding) are available to solve the numerical approximation with different levels of accuracy and speed of convergence. In contrast, computational models are in the form of a single algorithm, which is immediately implementable by the computer. Thus, Fisher and Henzinger propose using the term “execution” for computational models in contrast to “simulation” for mathematical models implemented numerically on a computer. In physical models, on the other hand, the phenomena of the real-world system actually occur albeit at a smaller scale or with less complexity. For example, a physical model of a solid oxide fuel cell system has been built at the US Department of Energy National Energy Technology Laboratory for hardware simulation purposes as described by Tucker et al. [164,165].
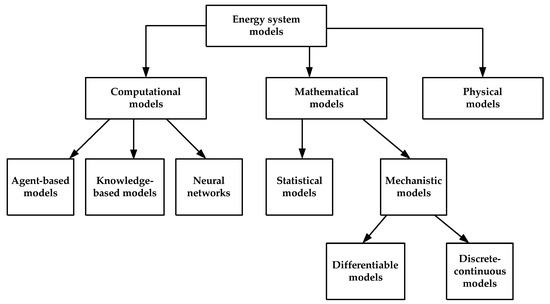
Figure 4.
Classification of energy system models according to modeling approach.
A large class of computational models, termed expert or intelligent systems, are programmed to imitate intelligent behavior. A general review of expert systems is provided by Liao [166], while a review of specific applications in process engineering is provided by Stephanopoulos and Han [167]. Expert systems include agent-based, neural networks, knowledge-based, fuzzy models, etc. Agent-based models are typically used to mimic the human element of energy systems. They consist of a number of autonomous, self-interested entities represented in computer code, which act according to certain rules. Thus, agent-based models are used to model supply chain entities [56,168], electricity markets [169], or technological change [170,171,172]. The interaction between multiple agents is simulated in order to determine the overall system behavior, which may highlight certain non-intuitive aspects not predictable by first-principles modeling [173]. Knowledge-based systems consist of a knowledge base of domain-specific expertise, an inference engine that deduces new knowledge based on certain rules, and a user interface [174]. PROSYN is an example of a commercially available knowledge-based system that contains a database of specialist information and heuristics to aid in conceptual process design [175]. Unlike knowledge-based systems, neural networks are generic and do not have explicit rules but instead consist of a collection of nodes that processes input and output information. Neural networks are trained by adjusting the weights of the connections between nodes. Neural networks have had wide application in energy systems, for instance, in modeling biomass gasifiers [176] and control systems [177], as described in the book by Baughman and Liu [178].
Mathematical models can be classified into statistical (empirical or black-box) and mechanistic (theoretical, first-principles or white box) models. Statistical methods use techniques such as regression and optimization [179], kriging [180], self-optimizing control [181], and neural networks to derive a set of simple mathematical relations from input and output data [182]. Mechanistic models, on the other hand, employ fundamental discipline-specific theories such as fluid mechanics, thermodynamics, economics, mass and energy balances, etc. that provide the model structure and generate equations to describe the phenomena of the real-world system. There are several ways of categorizing mathematical models, for instance, into discrete and continuous models according to the nature of the variables, into steady state and dynamic models according to whether the variables vary with time, or into deterministic or stochastic models according to the uncertainty of parameters. The division of mechanistic models into differentiable and discrete-continuous models is proposed by Watson [183]. Modeling different phenomena with differentiable equations requires different mathematical formalisms: steady state phenomena with no spatial variation are modeled by algebraic equations, dynamic phenomena, or steady state phenomena with spatial variation in one dimension are modeled by ordinary differential equations, and finally dynamic phenomena with spatially distributed phenomena are modeled by partial differential equations. A detailed description of the different formalisms for representing various physical phenomena is provided by Gani et al. [19]. While differentiable models are sufficient for modeling continuous phenomena, several energy system components also exhibit discrete phenomena such as thermodynamic phase changes, flow reversals, and changes in flow regimes such as from laminar to turbulent flow, etc. [22]. In addition, external actions on the system such as through the use of digital controllers, plant start-up and shut-down in batch processes, or mode changes in semicontinuous processes result in discrete behavior. Mathematical formalisms for modeling discrete-continuous phenomena include hybrid automata [184], disjunctive models [185], hybrid Petri nets [186], etc. as detailed in a review by Barton and Lee [23].
With this categorization, we note that several emerging approaches in energy systems modeling combine elements from two or more of the categories proposed in Figure 4. For instance, recent developments in non-smooth modeling by Barton and coworkers bridge the gap between differentiable and discrete-continuous models. Local sensitivity information for non-smooth models is obtained by calculating generalized derivatives automatically as explained in [187]. This approach has been applied to develop compact models for multi-stream heat exchangers [188], which have been incorporated into flowsheets of natural gas liquefaction [26] such as the simple mixed refrigerant [189,190] and dual mixed refrigerant processes [191,192].
Another emerging approach is hybrid modeling that combines aspects of mechanistic and statistical models, i.e., physical insights and constraints obtained from first principles are incorporated synergistically to adjust the statistical model. Significant advances have been made by Cozad et al. who developed the ALAMO framework to develop surrogate models by constrained regression such that first principles limitations such as. mass and energy balances, physical limitations, variable bounds, etc. are obeyed [179]. Similarly, Straus and Skogestad propose an approach that introduces auxiliary variables, such as the extent of reaction or the separation coefficient, in order to reduces the dimension of the surrogate model and satisfy mass balance constraints [193,194]. In addition, a hybrid approach of first principles and neural networks for modeling chemical processes has been developed by Psichogios and Ungar [27], and Thompson and Kramer [28], with Guo et al. [195] applying this approach to model biomass gasification processes. Finally, certain aspects of the model, such as demand and supply forecasting in EE models, may rely on statistical data with the other part based on economic theory.
3. The PSE Approach to Energy System Modeling and Simulation
Traditionally, PSE has focused on modeling chemical conversion systems at the processing plant scale. Any system can be modeled as a collection of sub-systems with interconnections depicting different types of flows to give a complex network [25]. The input to the system denotes the influence of factors outside the system (i.e., in the surroundings) and the output denotes the influence of the system on the surroundings. In a processing plant, the sub-systems are unit operations and the interconnections are mass, energy, or information flows between processing units. Modeling unit operations requires knowledge of the fundamentally occurring phenomena taking places such as thermodynamic processes, transport phenomena (mass transfer, fluid dynamics and heat transfer), and chemical reaction kinetics [196]. The mathematical formulation that incorporates all these phenomena and connects the molecular and continuum descriptions of matter is the differential balance equation (consisting of hold-up, transport and source terms) as developed by Bird, Stewart, and Lightfoot [24] that gave rise to the dominant BSL modeling paradigm of chemical engineering science [197]. Unit operation models are usually used together with simulation and optimization for a variety of purposes such as reaction path synthesis, design of the entire process flowsheet or subsections such as the reactor networks, heat exchanger networks, recycle systems, or separation networks [123]. If the purpose is operation or control modeling, transient effects and dynamic simulation is necessary. An alternative is to use empirical models, which rely on input and output experimental data for a wide range of the process operational domain, as discussed in Section 2. As a result of the chemical engineering science base, PSE models of energy systems typically focus on describing the technological characteristics of the components—economic, environmental, and social characteristics are passed on to the model as exogenous variables. For instance, at the process scale, the operating conditions (e.g., stream flow rates, temperatures, pressures) are modeled explicitly but parameters such as fuel prices and availability, product prices, and environmental impacts are considered exogenously. An encyclopedic account of the steps involved in model development in PSE is given by Gani et al. [19], while Marquardt provides a survey and tutorial of modeling procedures [20].
The scope of PSE has been expanded by Grossmann and Westerberg to encompass all approaches for improved decision making in the creation and operation of the chemical supply chain [198]. This necessitates analysis of energy systems over a range of scales from the unit operation to the supply chain scale (as shown in Figure 3), thus motivating the trend towards multi-scale systems engineering, which we describe in Section 3.1. The scope of PSE has been expanded in both directions to finer and coarser scales. Traditionally, in order to reduce the computational cost of model solution, lumped parameter models are used together with a number of assumptions (such as equilibrium, plug flow, perfect or ideal mixing, ignoring dispersion and other transport phenomena) in order to reduce complexity. The need for higher fidelity models that incorporate these effects has motivated modeling at finer scales [111]. On the other hand, there is significant economic potential in coordinating logistics with production planning thus it is necessary to include the supply chain level in decision-making [198,199]. Another emerging trend is the inclusion of sustainability factors quantified by the triple bottom line of economics, environment, and social criteria as described in Section 3.2 [121].
3.1. Multi-Scale Systems Engineering
Multi-scale systems engineering is a new paradigm in engineering science with the key idea of linking a network of models across different spatial and temporal scales such that information computed in one model can be used in another. The most common goal is to develop a high-fidelity model that accurately captures the overall system behavior at a large (coarse) scale by utilizing information provided by higher resolution models at smaller (finer) scales [197]. This approach is termed ‘upscaling’ because of the flow of information from smaller to larger scales with a corresponding reduction in degrees of freedom. However, the relatively under-examined ‘down-scaling’ approach, in which a desired outcome is determined at a larger scale and passed down to smaller scale models in order to determine a feasible technological path, may also be relevant. Multi-scale systems engineering has been aided by recent advances in computational capability, including progress in parallel computing, as well as by improvements in experimental techniques particularly at finer scales [200].
Floudas et al. present an outlook of the opportunities to apply multi-scale systems engineering at various time and length scales in order to address pressing energy and environmental challenges, such as generation of affordable energy in an environmentally sustainable way and ensuring future energy security [109]. A number of important design and operational problems in the energy systems engineering necessitate multi-scale modeling with upscaling or downscaling approaches. We present two applications next.
3.1.1. Designing Novel Conversion Processes for Heterogeneous Feedstocks
Unlocking the potential of the large amounts of lignocellulosic biomass available in agricultural, industrial, and forestry residues has enormous economic and environmental value [201]. However, biomass feedstocks have a variable and complex structure, thus accurate modeling of novel biomass conversion processes is challenging. Mettler et al. note that this problem is particularly severe for lignocellulosic biomass unlike other feedstocks like petroleum, natural gas, or coal: lignocellulosic biomass possesses a multiscale structure spanning eleven orders of magnitude over which different degradation phenomena can occur [202]. Thus, developing high fidelity thermoconversion process models (e.g., pyrolysis, combustion, gasification, liquefaction, and hydrogenation [152]) requires a deeper understanding of the underlying reaction mechanisms and transport phenomena. Similarly, multi-scale analysis, beginning at the molecular scale, has the potential to develop novel biochemical conversion pathways through systems and synthetic biology approaches. For example, Kumar et al. suggest that recombinant DNA technology, metabolic engineering, and genomics approaches have great potential to advance processes for bioconversion of cellulose to useful products [203]. Lee et al. suggest that such approaches of manipulating microbial activity may be used to efficiently produce drop in biofuels that are similar to existing petroleum-based fuels—an advance that would save significant capital by reusing existing transportation infrastructure [204].
Accurate modeling of the multi-scale phenomena occurring within the biomass conversion unit operation is particularly relevant because all further downstream cleaning and processing units utilize product stream information such as composition and flow rate. In addition, the conversion unit is typically a significant heat source or sink, thus optimal design of the heat exchanger network and utility system requires an accurate conversion model. Thus, the overall process economics may strongly depend on using a rigorous and more realistic model for the conversion process. An example of applying the multi-scale systems engineering approach to design novel biomass conversion processes is given in a series of papers by Baliban et al. In [205], Baliban et al. developed a novel stoichiometry-based mathematical model for the biomass gasifier in order to evaluate syngas compositions. The model consisted of several unknown parameters that were tuned to experimental data by non-linear parameter estimation. This reactor level model was dynamically linked to lumped parameter Aspen Plus models of the rest of the biomass-based conversion process. At the process plant level, Baliban et al. then used the gasifier model developed in [205], as part of the process flowsheet [113]. Several alternative biomass conversion flowsheets were modeled to generate a superstructure which could be used to determine the optimal process design. Finally, the heat, power, and water networks were integrated with the rest of the process resulting in an economical and environmentally optimal plant design [114].
Similarly for municipal solid waste (MSW), Onel et al. developed a generic model for a gasifier with an optimization based monomer model for the pyrolysis zone, and a detailed thermodynamic model for the oxidation and reduction zones [206]. Unknown parameters were fixed by non-linear parameter estimation using experimental data. In the following paper, Niziolek et al. used the MSW gasifier model as part of a superstructure for optimal synthesis of a MSW to liquid fuel conversion process [115].
Thermo-conversion of coal has received considerable attention from PSE researchers with models made with the aid of commercial software such as Aspen Plus [207,208,209] and multi-scale models. Coal gasification and combustion are complex processes: Singh et al. note that several spatially distributed phenomena occur between the gases and solid coal particles such as multiphase fluid flow, heterogeneous and homogeneous reactions, as well as heat and mass transfer [210]. In addition, key characteristics such as the flame shape, flow recirculation, and thus the flow field variables (gas composition, temperature, pressure and velocity) are dependent on the reactor geometry [211]. Computational fluid dynamics (CFD) tools have the potential to be used to develop more accurate models that offer insight into the inner workings of the combustor or gasifier unit operation and to predict the syngas product composition [210,211,212,213]. These models can be integrated with the rest of the process flowsheet for more rigorous simulation and optimization. For example, Shi et al. developed a computational fluid dynamics model of a two-stage, oxygen blown, entrained flow, coal slurry gasifier that predicted syngas compositions similar to restricted equilibrium reactor models tuned with experimental data [214]. Lang et al. developed a reduced order model of this detailed CFD model and converted it to an Aspen Plus module which was simulated as part of an integrated gasification combined cycle (IGCC) process [11]. Optimization of the process showed an increase in power output of 5–7% compared with conventional simplified unit operation models—a result that illustrates the value of the multi-scale systems engineering approach. Considering that gasification and combustion unit operations centerpieces of several processes, Zitney [118] and Biegler and Lang [215] note the potential of application of high-fidelity models to other coal based energy systems such as the oxy-fuel combustion of pulverized coal for carbon capture [216], integrated gasification fuel cell systems [217], and polygeneration plants [218,219].
The approach discussed so far is termed the “upscaling” approach in that there is an upward flow of information from detailed finer resolution models to coarser models. Multi-scale system engineering using a “downscaling” approach to design novel energy systems may also have significant value, but has received less research attention. A series of papers by Adams and colleagues illustrates the potential of the downscaling approach. First, Adams and Barton propose a novel scheme in which a coal gasifier is heat integrated with a natural gas reformer to produce syngas streams with different H2/CO ratios [220]. Blending these streams gives the correct ratios for downstream polygeneration of electricity, methanol, and liquid fuels, thereby eliminating the inefficient water gas shift reaction. However, the actual technology required to achieve the heat integration was purely theoretical, and a plant-level techno-economic analysis was performed on the assumption that such a technology could be created. The results of a techno-economic analysis performed at the plant scale suggested that the proposed polygeneration process is economically viable and more robust to market uncertainties, thus motivating further study of the design details of the heat integration scheme. Next, Ghouse and Adams developed a multi-scale two-dimensional dynamic heterogeneous model of the natural gas steam reforming reactor that accounted for both intra-particle and inter-phase mass transfer limitations [116]. This model illustrated the feasibility of the heat integration concept proposed in [220] where the endothermic natural gas reforming reaction takes place in the tube side of the radiant syngas cooling section of the entrained-flow coal gasifier. The model was used to aid in the design of the device [221] such that it would be able to meet the process requirements of the previous work [220]. The model was then used to design control schemes to respond to syngas composition requirements for downstream synthesis processes [117,222].
3.1.2. Modeling and Optimal Design of Supply Chains for Distributed Energy Sources
A typical energy supply chain consists of three sections: feedstock harvesting and transportation, conversion plant, and product distribution to end user. Analysis at the supply chain scale is essential for distributed energy sources because logistical costs are significant and thus a key determining factor of the economic viability of the overall process. There are several papers that provide an overview of the challenges and opportunities in supply chain modeling and optimization including the works of Garcia and You [34], Papageorgiou [36], Shah [35], Barbosa-Povoa [37], Nikolopoulou and Ierapetritou [38], and Lainez and Puigjaner [39]. More focused review on biomass-to-bioenergy supply chains are given by Sharma et al. [223], Yue et al. [224] and Hosseini and Shah [112], on waste biomass-to-energy by Iakovou et al. [225] and on shale gas supply chains by Cafaro and Grossmann [226]. These works highlight the complexity involved in modeling and optimal design of supply chains for distributed energy sources: Several constraints, such as the variable availability, composition, and geographical distribution of feedstock sources, feedstock degradation, the need for storage, logistical costs, conversion plant capacities, product demand locations and specifications need to be taken into account. Furthermore, supply chain components may be spread across large distances and thus require analysis at several different spatial scales: community energy systems and district heating, cooling, and power systems [227] require detailed modeling at the regional level, while various fuels and chemicals are produced at production plants worldwide and exchanged in international markets thus requiring modeling at the global level. Thus, moving up on the level of technological aggregation from unit operations to supply chains necessitates accounting for a large number of externalities.
Supply chain related decision-making spans all three temporal scales: strategic (long-term or over multiple years), tactical (medium term or over multiple months), and operational (short term or day-to-day) [225]. Strategic decisions include: determining how to make the optimal investments in supply and product distribution infrastructure, choosing the right conversion technology, choosing the right site location and capacity, choosing the types of transportation, and addressing sustainability issues over the plant lifetime. Tactical decisions deal with optimization of production planning and scheduling [46,47], e.g., determining the right time to run batch processes, managing the transportation fleet and inventory levels, etc. Operational decisions at the supply chain scale are made several times each day, such as determining production operating conditions, detailed logistical issues, and response to weather disruptions. In addition to this complexity, supply chains also face significant uncertainties such as supply disruption, transportation failures, feedstock and product price changes, emissions policies etc. [34]. Thus, supply chain optimization involves determining the feedstock types and quantities, transportation types and routes, conversion plant types and capacities, and final product distribution options that minimize the overall system cost under these uncertainties.
Considering the high logistical costs associated with distributed energy sources, supply chain modeling and optimization may be an important determining factor in overall project viability. For example, Iakovou et al. suggest that logistical costs are a crucial bottleneck limiting biomass utilization [225]. Papageorgiou highlights the opportunity supply chain optimization offers for huge economic savings in the process industry [36]—an observation corroborated by Min and Zhou who suggest that many firms have realized the value of planning, controlling and designing the entire supply chain rather than focusing on separate functions [40]. Example of multi-scale modeling that includes analysis at the supply chain level is the work of Elia et al. [9] who used the conversion process models of [113] as technology options to optimize the nationwide energy supply chain network and Niziolek et al. who developed a supply chain model for a municipal solid waste (MSW) to liquid fuel process [41]. The newly emerging field of enterprise-wide optimization is a further step that expands the scope of PSE past supply chain management to aid in making decisions in firm R&D efforts, corporate finance and management, demand modeling, etc. [228,229].
Several enabling technologies have facilitated multi-scale systems engineering. Work done by Zitney and co-workers at the US Department of Energy National Energy Technology Laboratories led to the development of the Advanced Process Engineering Co-Simulator (APECS) software framework that co-simulates unit operations modeled using CFD together with lumped parameter models for the rest of the process [118]. In this way, one can integrate CFD unit operation models developed with software such as FLUENT into a process flowsheet developed with software such as Aspen Plus or HYSYS. In subsequent work, Lang et al. developed reduced order models from the CFD models that were then used for simulation at the plant process scale, with the aim of reducing computational costs [119,120]. Finally, Biegler and Lang propose a framework to develop reduced order models that when used in a multi-scale model for optimization, guarantee convergence to the same solution as using the full model [111]. At the supply chain level, Lam et al. propose model reduction techniques such as eliminating unnecessary variables and constraints, and merging certain nodes, that lowered computational time by several orders of magnitude [230].
3.2. Modeling Sustainability Criteria
Sustainability is the concept of “meeting the needs of the present without compromising the ability of future generations to meet their own needs” [231]. Sustainability criteria can be divided into three dimensions: Economic, Environmental, and Social, together termed the “triple bottom line” of sustainability, as discussed in the next sub-sections [121,124,232]. The modeling of sustainability criteria for decision-making in PSE is a relatively recent trend—the vast majority of previous research efforts have focused on modeling the techno-economic performance of energy systems [5,133]. Bakshi and Fiksel suggest that the inclusion of sustainability objectives in a firm’s decision-making strategy represents a shift in thinking: environmental and social aspects may not necessarily be conflicting with economic objectives but instead represent a business opportunity to increase shareholder profits [121,124]. Environmentally-friendly energy projects that also present economic opportunities include: exploitation of waste feedstocks [233,234] such as petcoke [30] or coke oven and blast furnace gas from steel making [235,236], improving energy efficiency through process integration [237], for instance by work and heat integration [238], freshwater use minimization [239,240], etc. In addition, adopting a proactive approach to including sustainability considerations voluntarily may have pragmatic value in preventing crippling regulations and political backlash [121].
Incorporating sustainability considerations is important in every stage of the energy system project including through further retrofit projects. However, Cano-Ruiz and McRae point out that it is particularly valuable in the early design stage [123]. This is because regarding sustainability concerns as a design objective rather than a constraint on operations can motivate the search for novel processes with improved economic and environmental performance [134]. Several metrics have been proposed to incorporate the three sustainability criteria into process design decision-making, for instance, GREENSCOPE [241], and the indicators of Azapagic and Perdan [242]. An important challenge in sustainable process design is to quantify an objective function that includes metrics measuring all three of the competing economic, environmental, and social criteria. It may not be possible or even desirable to reduce all the metrics that measure different factors with different units into a single score. Several approaches have been proposed including assigning a dollar value to environmental and social criteria, instituting a carbon tax that in order to link economic and environmental criteria for a social good, and multi-objective optimization [243]. Bakshi presents a review of current approaches to sustainable process design as well as future research challenges [122]. Requirements for a process to claim to be sustainable are proposed: the overall demand for raw materials from the ecosystem and the release of emissions should not exceed nature’s regenerative capacity. In other work, Bakshi and Fiksel provide a perspective on why expertise built in the PSE community, for instance in mathematical programming techniques, is uniquely useful to addressing challenges in developing sustainable energy systems [121]. Grossmann and Guillén-Gosálbez present a review of the application of mathematical programming techniques to aid in sustainable process decision-making [5]. Hugo and Pistikopoulos present an optimization framework for inclusion of sustainability criteria in supply chain network design and planning [134].
3.2.1. Economic Criteria
Economic criteria are used to ensure the long-term profitability of firms taking part in the energy system project. Techno-economic modeling involves determining the economic performance of the designed process. In PSE, the technological characteristics of the process (e.g., pressure, temperature, flowrate, equipment size, etc.) are modeled endogenously while the economic characteristics (e.g., raw material and product prices, equipment transportation costs, etc.) are specified exogenously.
Modeling the economic characteristics can be divided into two activities: determining the capital and operational costs of the project (economic input) and determining the revenue from sales (economic output). Methods for economic analysis are detailed in widely used PSE textbooks such as [14,244,245,246]. Project capital costs includes several components such as land, offsite infrastructure, equipment costs, etc. For a given process flowsheet, accurate equipment costs can be determined by obtaining quotes from vendors. However, vendor quotes may not be available at the preliminary process design stage, thus estimates based on historical (base) costs are used together with certain empirically evaluated indices (e.g., CEPCI, Marshall and Swift equipment cost index) in order to account for the change in costs with time. The variation of capital cost with process capacity is determined either from actual vendor quotes or with smooth-curve generalizations based on historical data together with economy of scale indices. Cost parameters are available in literature references such as [247,248] for several pieces of equipment. Alternatively, commercial software such as Aspen Capital Cost Estimator, that contains a large database of cost quotes and scaling factor indices, may be incorporated directly into process flowsheet simulations as explained in [249]. Project operational costs include several expenses such as utilities, raw materials, labor, maintenance, etc. Raw material prices can be determined from published estimates such as [250]. Utility costs depend on the process flowsheet e.g., the heat exchanger network design. Utility costs are commonly estimated by using assumed constant cost rates per unit of energy delivered or unit of service. These constant rates can be estimated based on current market energy prices, as described in [244]. At the supply chain scale, costing can be done by determining the costs of the transportation and distribution system and adding these to the process costs.
Revenue from sales is determined from product flow rates and published product price data. Both project expenditures and revenues are accounted for in cash flow analysis, which involves determining the project’s overall economic performance. Methods used are categorized into non-discounted and discounted methods: Non-discounted methods do not consider the time value of money and are used for short-cut analysis of a project’s feasibility compared to competing projects by calculating metrics such as the return on investment or the payback time, while discounted methods are typically used for more detailed analysis and consider the time value of money with metrics such as net present value (NPV), breakeven time of a project, or annualized rate of return [14]. Pintarič and Kravanja provide a review of the different economic metrics such as total annual cost, profit, payback time, equivalent annual cost, net present value, and the internal rate of return that could be used as objective functions for optimal process design and conclude that net present value (or net present worth) with a discount rate equal to the minimum acceptable rate of return is the most suitable [125]. They mention that qualitative profitability measures, such as the internal rate of return and the payback time, favor cheaper projects with small cash flows and high profitability, while other quantitative measures, such as total annual cost or profit, favor solutions with higher cash flows but low profitability. They conclude that compromise measures, such as the NPV, the equivalent annual cost, and the modified profit account for both criteria resulting in a solution with relatively large cash flows and a promising internal rate of return.
One pertinent issue in techno-economic modeling is accounting for uncertainty. This uncertainty can arise either from components within the process plant boundary (e.g., uncertainties in kinetics or transfer coefficients of equipment, product yields, reservoir sizes, etc.) or from externalities (e.g., in product demands, market prices, emissions policies, etc.). It is essential to account for uncertainty because the optimal solution found using the nominal model may no longer be optimal or even feasible when applied in practice. One approach to account for uncertainty is to perform a sensitivity analysis to determine the impact on the process performance as a result of changes in the uncertain parameters. Another widely used approach is design under uncertainty that incorporates uncertain parameters directly into the design formulation. The main mathematical programming techniques for optimization of problems with parametric uncertainty include: stochastic programming [251], robust optimization [252], chance-constrained programming [253], and dynamic programming [254]. To address uncertainty, processes are designed to be flexible in that they are able to maintain feasible operation over a wide range of realizations of uncertainty. Flexible design strategies have been applied to several processes including distillation columns [12], air separation units [255], polygeneration systems [73], and supply chain networks [256], with details given in a review by Grossmann et al. [257]. In other work, Grossmann et al. also provide a review on the use of mathematical programming techniques for optimal process design under uncertainty [21].
3.2.2. Environmental Criteria
Modeling the effect of energy systems on the surrounding ecosystem requires accounting for two factors: The environmental impacts as a result of emission of pollutants and greenhouse gases, and the primary resources used by the system [121]. All the different components of the energy system from primary energy harvesting to final energy consumption contribute to these two environmental effects. Thus, analysis with a system boundary that is broader than the traditional PSE processing plant boundary is necessary to include all such systemic effects.
Life Cycle Assessment (LCA) is a commonly used framework used to systematically account for the environmental impacts and resource use of the different stages of the energy system [126,127,128,129,132,258]. The purpose of modeling with a comprehensive life cycle perspective is to maintain accounting consistency in the decision-making process by preventing burden shifting between different life cycle stages. In other words, one should ensure that efforts to lower environmental impacts or resource use in one lifecycle stage are not overwhelmed by unaccounted increased effects at another stage. Thus, it is essential to account for both the direct effects from within the processing plant and the indirect effects from relevant activities outside the processing plant.
Figure 5 illustrates the complexity involved in performing LCA to account for all systemic effects. For a given energy product (such as electricity or fuel), there are direct emissions associated with the processing plant as well as inflows of primary resources. However, each component of this processing plant requires certain inputs, usually from other economic sectors such as mining, manufacturing, logistics, etc. For instance, the processing equipment is supplied by manufacturers, the feedstock is supplied by primary energy harvesting firms (such as coal mining) and requires transportation to the processing plant, etc. Furthermore, each component of the upstream supply chain (Tier 1) requires its own supply chain (Tier 2), and so on to higher tiers. Figure 5 also illustrates the circular interactions between components of different tiers of the supply chain, which results in additional complexity. Each of these supply chain tiers is associated with environmental impacts that need to be proportionally included to the plant level impacts. Similarly, resource utilization in higher order supply chains need to be accounted for. Adding effects from higher supply chain tiers to the LCA model corresponds to expanding the system boundary until eventually all the inputs and outputs correspond to elementary flows, which are defined as material or energy flows drawn from the environment without previous human transformation, or released into the environment without subsequent human transformation [135]. Thus, LCA requires analysis at a high level of technological aggregation in order to account for the complex interdependencies between multiple supply chain tiers. These interdependencies may give rise to non-intuitive effects as illustrated by Nease and Adams, who performed a detailed cradle-to-grave life cycle analysis of a natural gas combined cycle plant with carbon capture [137]. They found that capturing 90% of the CO2 only reduced lifecycle GHG emissions by approximately 65%, but simultaneously increases the environmental damage from nearly every other category by 10–25%. This result showed the importance of accounting for all global effects using cradle-to-grave LCA with a comprehensive system boundary.
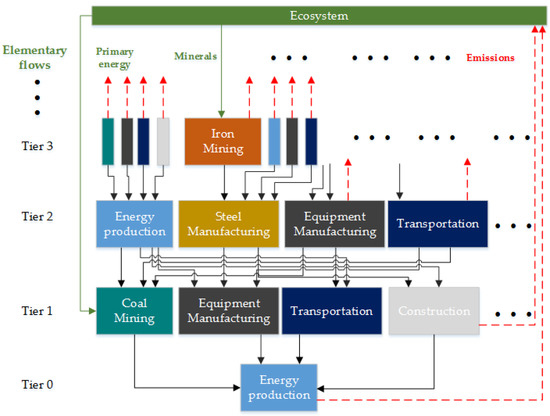
Figure 5.
The multi-tiered supply chain associated with energy production.
In order to provide a common basis for LCA modeling, the ISO framework was developed [259]. The motivation was to ensure comparability and consistency in assumptions, data, and methodologies as well as to provide transparency and thus more credibility to resulting decisions. The LCA framework consists of four steps [130]. The first is goal and scope definition which involves specifying the system boundary, the system’s inputs and outputs, and the purpose of the analysis. The second step is inventory analysis, which involves obtaining data on the mass and energy flows across the system boundary. For a given energy system, it is desirable to use specific local data corresponding to the modeled system components. However, data is often unavailable, especially for higher order supply chains. In these cases, the inventory can still be collected from simplified aggregate data obtained from the weighted-average of the different supply chain alternatives in the corresponding sector. The third step is impact assessment which involves determining the potential detrimental environmental effects such as global warming potential, terrestrial acidification, freshwater eutrophication, ozone depletion, nitrification, resource depletion, etc. [138]. Each assessment requires an impact assessment method, e.g., ReCiPe [260], TRACI [261], eco99 [262], etc. The final step is interpretation which involves using the results of impact assessment to answer the questions set out in the LCA scope including where to focus redesign efforts, or which new design or policy decisions to make [130].
Software such as SimaPro and OpenLCA [143] can help determine inventories and impacts. Inventory data for generic process steps common in many supply chains (such as transportation, energy distribution, bulk chemicals and materials production) are often available through databases such as The LCA Commons hosted by the National Agricultural Library at the US Department of Agriculture [263] and Ecoinvent [264]. Further details of the LCA methodology are presented in a review by Finnveden et al. [129]. In addition, a collection of guidelines, inventory and impact assessment data, and a registry of LCA software tools is available at the European LCA knowledge base [139].
In PSE, the purpose of LCA modeling is to make nuanced decisions that compare different process and technological options. Thus, the process LCA approach is used in contrast with input-output LCA of EE, which is explained in Section 4. Process LCA maps onto the process flow diagram model and requires specific data on the inputs, outputs and environmental impacts of each unit operation or process section. As far as possible, localized (often proprietary) data is used. Averaged data obtained at the sector level of aggregation is only used where localized data is unavailable or if the impact on the analysis is negligible. For this reason, process LCA models typically have a high level of granularity and are suited for detailed decision-making. The environmental impacts of components of progressively higher tiers of the supply chain are manually added until particular cut-off criteria are reached. The cut-off criteria quantify a threshold (e.g., <1–5% of total impacts) beyond which deletion of certain supply chain components is allowed. However, Suh et al. suggest that it may be difficult to choose the appropriate system boundary. They mention that deciding which components to exclude from the analysis may be challenging to do for the general case because the negligibility of their impacts cannot be guaranteed [135]. Furthermore, it may be time consuming and expensive to include all the complex upstream impacts suggested in Figure 5, especially with regards to higher tier supply chain components. This motivates the use of hybrid LCA methods as discussed in Section 5.2.
3.2.3. Social Criteria
Social criteria involve the cultural and personal connection to the technology and the way it impacts society (such as convenience, politics, personal values and beliefs, human behavior, and emotional factors). Thus, social criteria metrics measure the well-being and quality of life of the local communities served by the energy system. Several factors are included such as health and safety, access to education, access to energy services, employment situation, social equity, tolerance and diversity, etc. A list of social metrics for sustainability is provided by the Institute of Chemical Engineers [265]. However, the social dimension of the triple bottom line has been studied the least in the context of PSE as a result of being harder to quantify and outside the training and traditions of most systems engineers. As a result, the intersection between PSE and the social sciences in this way is not well studied today. A notable exception to this trend is the work of Othman et al. who include models of social criteria, such as safety considerations (operational safety, safe start-up and shut-down) and societal impacts of project (technology transfer, employment, effect on other industries, and regulations), in the process design stage [133]. A review of methodologies for social life cycle assessment is provided by Jørgensen et al. [266].
4. The EE Approach to Energy System Modeling and Simulation
The field of energy economics deals with the optimal allocation of scarce energy resources to satisfy consumer demand. It received increasing recognition as a distinct branch of economics during the energy crisis of the 1970’s which highlighted the central role of energy to economic development [6,99]. The scope has since widened to range from studies on the economic performance of a regional or national energy sector through to modeling of trade in international energy markets and finally to analysis on a global scale of the long-term implications of public policies, such as the emissions reduction goals agreed to at the Conference of Parties (COP) 21 in Paris [267]. The distinguishing feature of EE models is that the principles of economics are used as the underlying theoretical basis: consumer theory, producer theory and market equilibrium [268]. Consumer theory explains that rational consumers spend their income to choose certain goods that will maximize their “utility” i.e., provide the most satisfaction. Thus, the quantity of certain goods demanded (including electricity and fuels) can be determined by drawing relations to factors such as income levels, prices, emissions-related tax credit policies, etc. Producer theory, on the other hand, explains that supply firms will produce the optimal quantity of products that maximizes profitability. Market equilibrium resolves these two conflicting optimization problems by introducing the notion of “equilibrium price” at which the quantity of goods supplied equals the quantity demanded, i.e., the market clears.
Thus, in EE, economic characteristics (such as energy prices, demand quantities, supply capacities for each technological option, etc.) of the energy system are modeled endogenously together with their relationship to non-energy related variables such as income, population growth, growth of other industries, etc. A comprehensive treatment of the EE approach to energy systems modeling is presented in the book by Bhattacharyya [6]. To explain the EE approach to energy systems, we first present an overview of energy demand and supply forecasting models, followed by the bottom-up and finally top-down EE energy system models.
4.1. Demand and Supply Forecasting Models
Demand forecasting models use consumer theory and statistical data to predict the quantity of energy products demanded. Bhattacharyya and Timilsina [99] as well as Suganthi and Samuel [97] provide comparative reviews of various approaches to energy demand forecasting. Commonly, two approaches may be used: econometric approaches and end-use accounting [99]. The econometric approach uses statistical analysis of historical data to derive the relationship between the energy quantity demanded and several other driving variables such as GDP, average income, energy price, technology characteristics, macroeconomic influences, etc. Using estimates of the change in the driving variables (once again attained from historical data), the energy demand can be forecasted using the derived relationship [102]. The end-use accounting approach, on the other hand, divides the energy demand into a number of homogeneous categories such as transportation, residential, industrial, or commercial, after which historical data on energy demands and primary drivers in each of these categories is used to predict category-wise energy demand [99]. The difference between these two approaches is that the end-use approach forecasts demand with a higher level of granularity. Thus, the end-use approach has more explaining power than econometric approaches but is more data intensive and may not include all inter-sector interactions. In practice, a hybrid of both these approaches that includes complicated relationships between various factors is used, for example by the US Department of Energy to prepare the Annual Energy Outlook [269].
Supply forecasting models vary depending on the primary energy source under consideration. For renewable energy sources like wind and solar energy, meteorological models (e.g., [104,270]) may be required to model the day-to-day variability. Detailed sourcing models may be used to predict biomass availability [271,272]. Supply from non-renewable reserves can be forecasted using exponential decay production models together with fossil-fuel exploration data or by analyzing firm investment trends [6]. The IEA uses a data intensive forecasting approach that includes information about fossil fuel field developments worldwide to prepare the World Energy Outlook [6]. Energy supply forecasting can be also be done by using an econometric approach in a similar way to demand forecasting.
4.2. Bottom-Up Models
Bottom-up models are characterized by their high level of technological detail and are used to study the entire energy sector on the regional, national, or global scale. We explain the bottom-up approach with a schematic of a model used at the national scale shown in Figure 6 [273]. The inputs to the model are shown with inward pointing arrows: the bottom-up model requires modules that forecast the national energy demand (for instance, by using the end-use accounting approach) and primary energy supply both from imports and national energy resources. In addition, the bottom-up model connects to an extensive database containing the economic characteristics (such as the conversion process investment and operating costs, maintenance costs, logistical costs, processing plant capacities, etc.) of a wide range of technological components that may be involved in the national energy system. For the national energy system shown in Figure 6, the technological components considered in the bottom-up model comprising both the conversion processes (coal processing, refineries, power plants, CHP plants) and corresponding distribution processes (gas networks, transportation, district heat networks) are shown in red. Primary energy both from domestic sources and imports are shown in blue. The final user categories are shown in orange (industry, commercial and tertiary, households, and transportation) and the services provided by energy are shown in green (process energy, heating area, etc.).
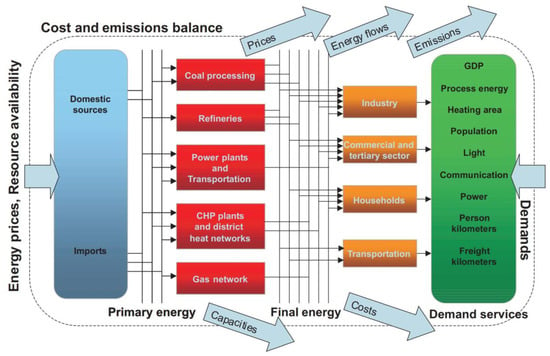
Figure 6.
A schematic of a bottom-up model used at the national scale. The inward pointing arrows indicate the inputs to the model while the outward pointing arrows show the outputs. Reprinted by permission from Springer: Operations Research Proceedings [273] Copyright (2001).
Bottom-up models are typically used together with multi-period optimization schemes to aid in strategic planning and policymaking. The optimization problem is defined as follows:
- Given a set of end users and forecasts for their demand over a certain (usually long term) time horizon, a set of candidate primary energy sources, and a set of corresponding conversion and distribution technologies; determine the optimal energy system configuration that minimizes overall costs (or maximizes overall efficiency) such that energy demand is satisfied by supply in each time period.
Typically, time horizons in the order of a few decades are used. In this period, both existing technological components as well as future technologies available through investments are included. The temporal resolution of the model should be sufficient to capture daily energy demand variations as well as seasonal variations. Thus, bottom-up models divide the time horizon into a number of time slices (such as summer day, summer night, winter day, winter night) and at each time slice the quantity of energy demanded should be equal to the quantity supplied. Thus, the key principle of bottom-up models is the market clearing condition together with energy balance satisfied by each technological component. The solution to the multi-period optimization problem highlights the national energy system configuration with the optimal primal energy mix, and optimal choice of present and future conversion and distribution technologies. In addition, the model can be augmented to include sustainability criteria, for instance by quantifying the emissions associated with each technological option [91]. Including an emissions penalty to the objective function (as shown in [91]) gives a solution representing the long-term energy system configuration that optimizes the trade-offs between economics and environmental factors.
The advantages of bottom-up models arise as a result of the high level of technological detail considered. First, new breakthrough technologies can be included into existing models and their impact and market penetration studied [274]. Thus, bottom-up models provide a plausible roadmap for adoption of new technologies, which can be used to inform policymaking decisions. In addition, bottom-up models have a lot of explaining power and can be used to understand why a certain outcome arises. However, the large amount of data required together with the high computational costs are drawbacks to bottom-up energy models. In addition, the mechanistic nature of bottom-up approaches suggests a disadvantage that factors which cannot be easily described or predicted (such as human agency) are not included.
The most widely used bottom-up models are the MARKAL (MARket ALlocation) family of models [274] developed by the International Energy Agency’s Energy Technology Systems Analysis Program (IEA-ETSAP), and the MESSAGE (Model for Energy Supply Strategy Alternatives and their General Environmental Impacts) family of models [275,276] developed by the International Atomic Energy Agency (IAEA) and the International Institute for Applied Systems Analysis (IIASA) [147]. MARKAL type models have been used in more than 250 institutions in 70 countries for various purposes including economic analysis of climate policies, studies on the potential of hydrogen fuel cells, nuclear power, etc. [277]. The MESSAGE family of models has been augmented with several other modules (such as a macro-economic module that predicts the interaction with other economic sectors, a climate module, an air pollution module, an agriculture and forestry module to predict land-use changes, etc.) to give the IIASA Integrated Assessment framework [278,279]. Such an Integrated Assessment Model (IAM) is a suite of tools that bring together knowledge and data from a variety of disciplines such as climate change modeling, energy economics, social studies, forestry and agriculture, etc. to aid in decision support in public policy making [280,281,282,283]. In order to keep the IAM computationally tractable, a very high level of technological aggregation is used typically at the national or global scale. Considering that energy models have profound public policy implications, several open source models have been developed. Efforts have included the launch of the open energy modeling initiative [90], and the recent OSeMOSYS framework [91,92] which has been extended for a global system boundary [93]. The open energy modeling initiative has a list of the different bottom-up modeling tools available. Open energy system models have the additional advantage of providing transparency when used to make public policies [95,284].
4.3. Top-Down Models
The top-down approach, on the other hand, models all the sectors within the entire economy. Energy is an input to virtually every other sector of the economy, thus top-down energy system models aim to capture the intersectoral connections and feedback that would not be predicted from a bottom-up analysis. For example, growth in industrial sectors (e.g., in the steel industry) may correspond to increased energy demand and higher energy prices. However, any productivity increases in the industrial sector may also spill over to reduce energy generation costs and energy prices. Thus, modeling the interaction between the energy sector and other economic sectors has value in highlighting the often counter-intuitive impact on the overall aggregated economy of specific decisions made in the energy sector and vice versa. Modeling such interconnections is particularly relevant for energy systems because of the strong impact of energy on other sectors. Furthermore, energy system decision-making is closely connected with sustainability considerations which necessitates analysis with broader system boundaries and a higher level of technological aggregation as discussed in Section 3.2. These factors make top-down models suitable tools to aid in general policy making such as tax, energy subsidy, or climate change policy at regional, national, or global scales. Advantages of top-down models include the ability to consistently take into account the entire economy, while their disadvantages include generalized results without much explaining power, inadequate accounting of technological progress, and insufficient detail at smaller scales as a result of using highly aggregated empirical data [285]. Details on the top-down modeling approach are presented in a review by Dannenberg et al. [286]. Top-down models can be divided into input-output models and equilibrium models as discussed next.
4.3.1. Input-Output (IO) Models
Input-output models were introduced by the Nobel laureate Vasily Leontief, and IO analysis is one of the most widely used methods in economics [287]. For instance, IO methods are used by the US department of commerce for planning at local, regional, and national scale as well as by the UN for planning on a global scale [287]. IO models are used to represent the fact that for an economic sector to make a unit of output, certain inputs from other economic sectors are required, in addition to inputs from non-sectoral actors such as labor. By analyzing these input-output connections between different economic sectors, the complex relationships between sectors can be studied. We illustrate how to build an input-output model using a toy example of an economy consisting of only sectors aggregated from the multi-tiered supply chain presented in Figure 5: energy production, mining (coal, iron, etc.), manufacturing, transportation, and construction. The input-output model consists of a system of linear equations describing the flows of products from each economic sector (acting as a producer) to itself and other economic sectors (acting as consumers), as well as to final non-sectoral demand. These flows can be represented in input-output tables as shown in Table 2. The intersectoral flows are shown in the shaded grey section of the table, in either monetary or physical units. Let the indices and denote row (producer) and column (consumer) sectors respectively, then the intersectoral flow of an output from producer sector to consumer sector is . Thus, the rows of the table show the distribution of a sector’s output to inputs of other sectors or to satisfy the final demand, while the columns describe the various inputs required by a particular sector to produce its outputs. Therefore, for a given sector the corresponding column represents all its expenses while the row represents all its revenues assuming the table is constructed in monetary units. The final demand for the output of sector , , includes demand from households, government, and foreign trade, i.e., from non-sectoral actors. This final demand is not modeled endogenously in IO analysis; instead, final demand data from other sources is used to specify this column. The value added accounts for inputs to the different sectors that do not arise from other economic sectors, such as labor, government services, etc. A country’s gross domestic product (GDP) can be calculated as a sum of the value-added row or equivalently as the sum of the final demand column. The total output from a given sector is given by the row sum, i.e., a sector’s total output consists of the portion that is an input to other sectors and the portion that is used to satisfy final demand. For a single sector i, the input-output model equation can thus be written:

Table 2.
Input-output table showing the intersectoral transactions, value-added and the final demand.
For all sectors, the input-output model can be written in matrix form. Let vector X denote the total output from the different economic sectors, i.e., the components of X are equal to the row sums, and let the vector F denote final demands. For each column sector, the intersectoral flows are normalized by that sector’s total output to give the “direct requirements matrix” A with elements aij, as shown in Table 2. Thus, the linear equations representing the input-output model can be rewritten as:
The key value of IO models is that they automatically account for all the complex interdependencies between various sectors suggested in Figure 5. Thus, the direct requirements matrix, A, can be used to explicitly derive the inputs and outputs of all the components of the multi-tiered supply chain [127]. The inputs and outputs of the first-tier supply chain are related by the equation , and of the second-tier supply chain by the equation and so on to higher tiers. Thus, Equation (1) can be written as [127]:
The infinite geometric series can be replaced by the matrix inverse thus the IO model is re-written:
The matrix is called the total requirements matrix or the Leontief inverse matrix.
Data on intersectoral interactions, the value added, and final demands is routinely collected in several countries; in the US data on 79 sectors is made available by the Bureau of economic analysis [288]. A comprehensive treatment of IO modeling is presented in the book by Miller and Blair [287]. Miller and Blair also outline application areas of IO in aiding energy related strategic decision-making. For instance, they highlight the work of Bullard and Herendeen who studied the potential impact of a tax on energy use in the system and showed that the tax would be distributed such that the prices of energy-intensive process products are substantially increased [289]. In addition, Miller and Blair point out the work of Just in 1974 who studied the potential impacts of the then new energy technologies of coal gasification or combined gas-and-steam-cycle electric power generation on the US economy [290]. A final more recent application of IO modeling is to aid in sustainability analysis using the IO LCA approach discussed next.
4.3.2. Input-Output LCA Models
IO LCA models extend economic IO models to account for direct, indirect, and total environmental effects of the various sectors. Thus, IO LCA models exploit the key advantage of IO models in that they inherently account for all environmental impacts associated with the multi-tiered supply chain. Thus, IO LCA models work with a system boundary that includes the entire economy of interconnected industrial sectors to give a comprehensive top-down view of environmental impacts [291]. Herein lies the key advantage of IO LCA models: the challenge faced by the process LCA approach in determining the appropriate system boundary is removed. Equation (4) can be modified to give:
E is the vector of economy-wide environmental impacts and R is the environmental burden matrix, which gives the impacts of a sector per unit output of the corresponding sector. Thus, E gives the total impacts over all economic sectors associated with satisfying the overall demand F [140].
IO LCA models operate at a high level of technological aggregation. Averaged data obtained at the sectoral level of aggregation is typically used to determine the environmental impacts. While this fact enables relatively quick and cheap assessment with publicly available data, it also implies that IO LCA models are usually not nuanced enough for detailed decision-making on choosing the optimal process or technological options. This is the major disadvantage of IO LCA models that motivated the development of hybrid LCA models as explained in Section 5.2. Further details on IO LCA models are provided in a review paper and book by Hendrickson et al. [292,293]. Software for IO LCA analysis is available from the Green design institute of Carnegie Mellon University [144] (free for non-commercial use) and the EPA (open source) [145].
4.3.3. Equilibrium Modeling
Equilibrium models use the notion of an equilibrium price to resolve the two conflicting optimization problems of consumers (who maximize utility) and producers (who maximize profitability). At this equilibrium price, the quantity of goods supplied by producers equals the quantity demanded, and it is not possible to change this quantity without a decrease in producer profitability or consumer utility. Thus, equilibrium models explicitly model product prices and final demand quantities unlike IO models. The purpose of equilibrium modeling is to determine the influence of changes such as new government policies, trade agreements, technological breakthroughs, or shocks such as natural disasters, which would result in a new equilibrium [269]. Equilibrium models are classified into either general equilibrium or partial equilibrium models: General equilibrium models include all sectors of the economy while partial equilibrium models only include the subset of sectors with significant interactions. A prominent example of an equilibrium model is the National Energy Modeling System (NEMS) developed by the U.S. Energy Information Administration to generate the Annual Energy Outlook [294]. The general structure of NEMS is documented in [294] while the mathematical structure and numerical convergence issues are described by Gabriel et al. [89].
5. Combining PSE and EE Approaches
In this section, we make the case for leveraging the features of both PSE and EE models to aid in optimal decision-making. Thus, we present the value of analysis of energy systems using models with different system boundaries, levels of technological aggregation, underlying theoretical frameworks, and purposes. Three opportunities are identified as explained next.
5.1. Optimal Design and Operation of Flexible Processes Using Demand and Price Forecasts
The idea behind this application is to use demand forecasts for a certain future time period obtained through techniques such as end-use accounting and econometrics, as discussed in Section 4.1, to determine the optimal design and operation of processing plants that maximizes profit over that time period. Thus, a demand forecasting model operating at a high level of technological aggregation in order to account for a number of external factors is used to influence plant level design and operation decisions. Such an approach is valuable for decision-making in processes that involve inputs and products with highly variable demand in the short-term (e.g., electricity) or medium to long-term (e.g., chemicals and fuels).
This approach is followed by Mitra et al. who propose a multi-period optimization framework to determine investment decisions (both for the initial design and for yearly retrofits) as well as operational decisions suitable for power-intensive processes such as air separation units, cement production, and steel and aluminum production [295]. For the case study of air separation units, a demand forecasting model over a 10-year horizon is developed for both electricity and the liquid oxygen and nitrogen products. The electricity demand forecasting model is developed using historical data from PJM Interconnection [296] together with EIA long-term price forecasts [297] with an hourly temporal resolution, while the product demand forecasting model is based on historical data assuming an annual growth rate. In order to account for uncertainty, stochastic demand models were used in addition to deterministic demand models, and the corresponding investment and operational decisions were determined. The results illustrated the value of initial design flexibility as well as the value of flexibility due to retrofitting (e.g., adding a new liquefaction train or a new storage tank) with both stochastic and deterministic demand forecasting models. Since the optimal investment and operational decisions as well as the net profitability depend strongly on the actual demand, there is significant value in developing accurate forecasting models that account for a wide range of external factors. Rolfsman also utilizes this idea of using forecasts to determine the optimal investment and operational decisions. In [298], a regression model that includes factors such as the outdoor temperature is used to forecast the electricity spot price with a temporal resolution of 3 h in the city of Linkoping, Sweden. This price information is used to make investment decisions on the optimal capacity of energy storage over a period of 1 year. In other work, Rolfsman also builds a model with regression analysis to determine Linkoping’s district heating demand profile with a temporal resolution of 3 h and uses it to determine the optimal investment over a 20-year period both in combined heat and power plants as well as demand-side measures such as wall insulation or triple glazing windows [298]. It is also suggested that detailed MARKAL-based models could be used to forecast the district heating demand. The results suggested that the quality of the forecasting model had a significant impact on economic performance thus motivating research to develop accurate models with higher temporal resolutions.
Accurate demand forecasting models may be relevant in plant scale operational decision-making as well. For instance, Nease and Adams used demand predictions from the Independent Electricity System Operator of Ontario (IESO) [299] to schedule the electricity supply of a solid-oxide fuel cell plant with compressed air energy storage using a rolling horizon optimization (RHO) framework with a forecast period of 24 h and resolution of 1 h [300]. The results showed that, over a time period of 1 week, the mismatch between electricity supply and demand (measured by the sum-of-squared errors) decreases by 68% when RHO is implemented. Uncertainties in the forecasted demand, however, reduced this improvement.
5.2. Sustainability Analysis and Process Design Using Hybrid Methods
Hybrid LCA models enable more accurate determination of environmental impacts by leveraging the key advantages of process and IO LCA models: they combine the specificity and process-level detail of process LCA models with the comprehensive assessment capability of IO LCA models. Hendrickson et al. provide a comparison of the IO LCA method and the process LCA method [301]. An overview of challenges that may arise in selecting the system boundary of LCA models is provided by Suh et al. [135], while Lenzen presents a more detailed analysis with several case studies of environmental impacts of a range of sectors such as agriculture, energy, transportation, finance, etc. [136]. The percentage errors associated with performing process LCA (with a system boundary containing the 1st, 2nd, and 3rd tiers of the supply chain) and IO LCA analysis are compared in an Australian context for a wide range of products. The results showed the errors of process LCA were smallest for energy-intensive processes, especially with a 3rd tier supply chain boundary, but were still significant. For instance, the errors of process LCA with a 1st, 2nd, and 3rd tier system boundary respectively compared to IO LCA for electricity production were 6%, 4%, and 2% vs. 7%. Similarly, the errors for basic chemical production were 29%, 16%, and 9% vs. 32% [136]. However, the errors for gas production and distribution were 27%, 20%, and 14% vs. 7%. These results illustrate the strengths and weaknesses of the two LCA approaches depending on the product type and motivate hybrid approaches.
Commonly used hybrid LCA models include tiered and IO-based models. Tiered models use the process LCA approach to determine the direct impacts of the main process facility and certain key upstream components, and use the IO approach for the indirect impacts of the remaining upstream processes. Thus, localized data is used for specific process equipment or process sections while aggregated data is used for upstream impacts, with special attention given to avoid double counting. IO-based models disaggregate the sectors of IO models into more homogenous categories that can be mapped onto particular processes. For example, the electricity production sector can be disaggregated into generation, transmission, and distribution categories [302]. In this way, emissions data of a representative plant can be used for the disaggregated categories. Further details on hybrid LCA methods to account for environmental impacts are presented in the book by Hendrickson et al. [293].
In addition to accounting for the broader environmental impacts of the system, the depletion of natural resources can also be accounted for by hybrid methods. Cornelissen and Hirs point out the weakness of conventional LCA analysis in quantifying the depletion of natural resources and propose combining LCA with thermodynamics-based methods [142]. Ukidwe et al. [131] present an overview and Rocco [132] provides a taxonomy of thermodynamics-based resource accounting methods, including those that quantify mass flow (such as Material Flow Analysis [303]), energy flow (such as Net Energy Analysis [304]), and exergy flows. In particular, exergy is valuable in providing a fair basis to measure the quality and value of an array of different material and energy resource streams [305]. Traditionally, exergy-based methods were used primarily in PSE for energy system analysis and optimization at plant scale as detailed in the books by Kotas [306] and Szargut et al. [307]. A historical account of the use of the concept of exergy is provided in the critical review (with more than 2600 references) by Sciubba and Wall [308].
However, exergy analysis at the plant level of technological aggregation only accounts for the direct resource utilization; several approaches have been proposed to expand the spatial and temporal boundaries of the model to account for the indirect resource depletion in the multi-tiered supply chain. These approaches fall within the broad field termed thermo-economics (in the US) or exergo-economics (in Europe), as reviewed in [132,308]. Two notable early (and ultimately equivalent) approaches were calculating the Cumulative Exergy Consumption (CEC) and the Exergy Cost. The CEC approach, developed by Szargut and Morris, is based on dividing the production chain from natural resources to final products into a series of industrial processes each of which contributes a certain proportion of its exergy input to the final product with the rest being destroyed [309]. Exergy Cost Theory (ECT), developed by Valero and coworkers, generates a function that relates the exergy in the final products to input exergy in resources, depending on the production chain configuration [310,311,312]. However, these two approaches may not account for all the complex effects of the different components in the multi-tiered supply chain: for instance, they may not account for goods and services that are not amenable to an exergy-based characterization, or for the different lifecycle stages of the energy system [132].
In order to address these challenges, the combination of exergy-based methods with LCA techniques was proposed to give the Exergy Life Cycle Assessment (ELCA) framework [132,142,313]. In this framework, first the Exergy Cost approach is applied at the level of the energy conversion system in order to generate a set of proposals to improve the design by minimizing the exergy cost of the products. Keshavarzian et al. provide a review of practical approaches to apply ECT to energy conversion systems [314]. Second, the impacts of these proposals on the broader system are verified by using ELCA to ensure a reduction in primary resource utilization in the different lifecycle stages. Rocco illustrates this framework with an example of a Waste-to-Energy plant situated in the Italian economic context [132]. First, ECT is applied to the plant and several process improvement proposals were highlighted focusing on redesign of the grate furnace, steam turbine, super heater, and preheater components. Next, the ELCA method is applied using the IO-based hybrid LCA approach, considering both the construction and operation phases, in order to account for the complex interaction of the energy system and other sectors of the Italian economy. The process improvement proposals made in the first phase were then independently verified based on the ELCA results. This two-step methodology was applied iteratively. The final result suggested a 4.5% reduction in both direct and primary exergy costs of the electricity generation implying that reducing conversion process inefficiencies had a ripple effect in lowering primary resource consumption. Other approaches to combine exergy-based methods with IO-based hybrid LCA methods were proposed by Hau and Bakshi [315] and Ukidwe et al. [131]. It is also worth noting other thermo-economic approaches that use the mathematical structure of IO analysis for design and analysis at the conversion plant level [314,316,317]
Hanes and Bakshi point out that although most research efforts have used hybrid approaches for process analysis, there may also be significant value in their use for sustainable process design [140,141]. With this motivation, they developed the “process to planet” (P2P) framework which includes sub-models that operate at different levels of technological aggregation: overall economy scale sub-models are combined with value chain scale and unit operation scale sub-models. As a result of its multi-scale nature, the P2P framework can be used for a variety of purposes including process design and supply chain network planning. Furthermore, the framework offers a way of evaluating the impact of decisions made at the overall economy scale of aggregation (such as the institution of a carbon tax) on detailed decisions made on the processing plant scale. The influence of public policies on process design decisions may be significant as illustrated by Adams and Barton, who analyzed the potential impacts of the American Clean Energy and Security (ACES) Act of 2009 (which was not passed) on the choice of power production technologies [318]. The ACES Act proposed using a cap-and-trade scheme to provide economic incentives for lowering emissions, and had a complex system of quotas, credits, and taxes. Adams and Barton calculated the change in the levelized cost of electricity (LCOE) of different power plant configurations with different generation technologies (such as gas turbines, solid oxide fuel cells, and combined cycles), different feedstocks (natural gas or coal), and different implementations of carbon capture and sequestration (CCS) technologies, with the lifetime average price of carbon credits. They found that pulverized coal without CCS was no longer the cheapest above a carbon credit price of $15/tonne, after which coal or natural gas-based processes with solid oxide fuel cells would become the most profitable. Hanes and Bakshi applied the P2P framework to aid in the sustainable design of a corn to ethanol plant. They compared the potential lifetime emissions with a plant designed with the state-of-the-art approach that only includes process and value chain emissions but not overall economy scale emissions [141]. They found that the P2P approach lowered overall emissions by 17%; the state-of-the-art approach had lower process and value chain emissions but neglected significant overall economy scale emissions. Other work on using hybrid approaches for sustainable process design was done by Yue et al. who combined a hybrid LCA approach with a multi-objective optimization framework [319]. They applied this framework to design a biomass to ethanol supply chain in the UK and found that indirect emissions were significant (up to 58.4%).
5.3. Accounting for Feedback Effects of Breakthrough Technologies
Innovation that leads to possible breakthrough energy technologies (for instance, in rechargeable batteries for energy storage, fuel or solar cells, carbon capture and sequestration or utilization (CCSU), novel catalysts for conversion processes, production of novel energy carriers such as hydrogen or ammonia, etc.) typically occurs at low levels of technological aggregation and relies on progress in basic science research [320]. Thereafter, the technological and economic feasibility of the innovation is analyzed usually at the unit operation or plant scale. Thus, a techno-economic model is built that studies the innovation in the context of several externalities such as market conditions, emissions policies, etc. resulting in information on its investment costs, operating costs, capacities, availability factors, fixed maintenance costs, etc. Such techno-economic analyses are typically used to influence decisions made at plant scale, such as whether to invest in the innovation. However, breakthrough technologies can have significant effects at higher levels of technological aggregation, for instance if public policy decisions are made to promote the use of the innovation. For this reason, developing approaches to transfer information about breakthrough technologies from smaller scales to the overall economy scale for strategic planning purposes is valuable. Similarly, it is valuable to analyze the feedback effects of these breakthroughs. In this way, the long-term trajectory of the use of the innovation can be mapped. Approaches suggested so far have linked PSE models to both bottom-up and top-down EE models as we explain next.
Bolat and Thiel present an approach to build a new technological module (for a hydrogen supply chain, in this case) for use in bottom-up models [321,322]. They surveyed different hydrogen production technologies and abstracted information from techno-economic models to develop a hydrogen production module compatible with the MARKAL family of bottom-up models. Such a model can be used to evaluate the feasibility of the hydrogen supply chain in the context of other technologies in the energy system. For instance, Sgobbi et al. used a MARKAL-type model with this hydrogen module to evaluate the potential for hydrogen in a future European energy system [323]. They concluded that hydrogen could become a viable option in 2030, and supply 5–6% of the final energy consumption in the transport and industrial sector in 2050 if certain emissions policies are enacted.
In addition to influencing favorable policies, a second key feedback effect is technological learning: this is the fact that the cost of a technological component falls with increasing total installed capacity. This cost reduction can be due to increased expertise, lower risk and uncertainty, improved manufacturing capacities, economies of scale, etc. Based on historical data, a technological learning curve can be derived which predicts the reduction in the cost of that technological component with increasing installed capacity. Quantifying the technological learning curve is done at a high level of aggregation since the overall global installed capacity is relevant. Details on estimating the learning curve and its incorporation into energy system models are presented in a review by Kahouli-Brahmi [324]. Models incorporating technological learning can be used to analyze the long-term prospects of certain technological options. Rubin et al. provide a comprehensive list of learning rates of a range of electricity supply technologies, including nuclear, fossil fuel, and renewable options [325]. M. van den Broek et al. used energy system models with technological learning to project the future (2040) LCOE of natural gas combined cycle power plants with CCS (71 €2012/MWh), concentrated solar power (68 €2012/MWh), offshore wind (82 €2012/MWh), and photovoltaic systems (104 €2012/MWh) [326]. In other work, M. van den Broek et al. evaluated the potential for technological learning and suggested that IGCC plants with CCS have the largest potential for reduced costs by 2050 because an expected 3100 GW of combined cycle capacity would have been installed [327]. They also highlight the role emissions policies that motivate the wider installation of clean technologies could play in lowering mitigation costs due to technological learning. The value of modeling technological learning is also highlighted by Creutzig et al. who suggest that ignoring learning effects has led to underestimating the potential of solar PV [328]. They calculate a range of LCOE values in 2050 from 0.02 to 0.06 $/kWh. Huang et al. use a MARKAL type model to study the influence of technological learning on the future use of low carbon power generation technologies [329]. They conclude that the introduction of endogenous technological learning could increase global installed capacity of wind power, solar PV, coal CCS, and natural gas CCS by 970, 312, 221, and 150 GW, respectively, by 2050.
Despite the potentially significant effect of the cost reductions on plant scale decisions, the inclusion of technological learning in optimization frameworks for process design remains an underexplored research area. In the vast majority of PSE studies covered in this review, techno-economic analyses of energy systems typically use an “Nth plant” approach to estimating technology costs. This means that the cost estimates assume that the technology is sufficiently “mature” such that enough prior attempts at constructing the technology have been made to get over the learning curve. A good example of this in energy systems is the IGCC process, in which Nth plant studies typically predict that capital costs are on the order of $1 bln [318] for the >500 MW scale. However, the two most recent (and only) IGCC plants constructed at the >500 MW scale in the US were made in Edwardsport, Indiana and in Kemper County, Mississippi, which had capital costs of about $3.4 bln [330] and $7.1 bln [331], respectively. In the latter case, operators gave up on the gasification portion and operated the downstream portion of the process solely on natural gas. Thus, the learning curve is a key barrier to adoption that should be considered in energy systems design directly.
To maximize the learning effects, Reiner highlighted the value of coordinated decision-making between energy firms on the design and development of new industrial projects [332]. For the particular case of lowering mitigation costs associated with CCSU technologies, Reiner proposed coordination to enable the global deployment of a portfolio of CCSU projects to facilitate learning by replication and learning by project diversity. Firms participating in this coordinated effort would make certain design decisions at the plant scale (for instance, choosing certain CCSU options from those reviewed by Adams et al. [333]) that maximize overall technological learning at the global scale over a future time period.
Feedback effects of breakthrough technologies can also involve other sectors of the economy, which motivates analysis using top-down models. For example, developments in biomass-to-biofuel processes and their wider adoption could have significant impacts on the wood market, which may need to be accounted for in making plant scale design decisions [334]. Voll et al. combined a preliminary model of a wood to 2-methyltetrahydrofuran process with a simple partial equilibrium model of the German wood market used to predict future wood prices [334]. The results showed that depending on the size of the biofuel plant, the price of wood could increase by up to a factor of 30, presenting significant changes to the plant’s NPV. Such results present the value of analysis over different levels of technological aggregation in order to account for the influence of externalities on plant scale decisions. In other words, it may be important to account for the impact of the implementation of the technology on the market price, rather than just the impact of the market price on the choice or design of the technology.
6. Concluding Remarks
The sustainable generation of energy is a key challenge involving several stakeholders including government regulators, energy production and distribution firms, intermediate suppliers, and final consumers. In view of the primary importance of energy to the modern economy, energy systems have been studied by researchers in both the Process Systems Engineering (PSE) and Energy Economics (EE) fields using modeling and simulation approaches with different nature of variables, theoretical underpinnings, level of technological aggregation, spatial and temporal scales, and model purpose. In addition, several modeling approaches have been proposed which can be categorized into computational, mathematical, and physical models. Although computational and hybrid modeling approaches are increasingly relevant, the majority of PSE models have a mechanistic mathematical structure and draw from theories in chemical engineering science. Thus, the PSE approach models the technological characteristics of energy systems endogenously. Traditionally, PSE tools have been used to aid in the design, operation, and control at the processing plant level. However, the processing plant is situated in a broader economic context that includes several actors, such as competing energy firms, research and technology developers, final consumers with evolving needs, and regulatory agencies. These externalities manifest as energy price and demand uncertainties, changes in emissions policies, and breakthroughs in competing technologies, which may have significant impacts on plant level decisions and profitability. For this reason, leveraging the expertise developed in the EE field on modeling these complexities that arise at higher levels of technological aggregation may be valuable to PSE engineers. Thus, this paper aims to build a bridge between these two communities in order to get a holistic picture of the long-term performance of the energy system in a wider economic and policy context. We point out three specific application areas in which combining the PSE and EE approaches is valuable: (1) optimal design and operation of flexible processes using demand and price forecasts, (2) sustainability analysis and process design using hybrid methods, and (3) accounting for the feedback effects of breakthrough technologies. With these examples, we submit that approaches linking the PSE and EE fields warrant more research attention.
Author Contributions
Conceptualization, A.S.R.S. and T.A.A.II; writing—original draft preparation, A.S.R.S.; writing—review and editing, T.A.A.II and T.G.; supervision, T.A.A.II and T.G.; project administration, T.G.; funding acquisition, T.G.
Funding
The first author gratefully acknowledges the financial support of the Ph.D. scholarship from NTNU’s Department of Energy and Process Engineering.
Acknowledgments
We thank Rahul Anantharaman of SINTEF Energy Research for his helpful insights.
Conflicts of Interest
The authors declare no conflict of interest.
References
- International Energy Agency. World Energy Outlook; International Energy Agency: Paris, France, 2017. [Google Scholar]
- Chu, S.; Majumdar, A. Opportunities and challenges for a sustainable energy future. Nature 2012, 488, 294–303. [Google Scholar] [CrossRef] [PubMed]
- Allwood, J.M.; Bosetti, V.; Dubash, N.K.; Gómez-Echeverri, L.; von Stechow, C. Glossary. In Climate Change 2014: Mitigation of Climate Change; Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Farahani, E., Kadner, S., Seyboth, K., Adler, A., Baum, I., Brunner, S., Eickemeier, P., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Bruckner, T.; Bashmakov, I.A.; Mulugetta, Y.; Chum, H.; Navarro, A.D.; Edmonds, J.; Faaij, A.; Fungtammasan, B.; Garg, A.; Hertwich, E.; et al. Energy Systems. In Climate Change 2014: Mitigation of Climate Change; Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Farahani, E., Kadner, S., Seyboth, K., Adler, A., Baum, I., Brunner, S., Eickemeier, P., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Grossmann, I.E.; Guillén-Gosálbez, G. Scope for the application of mathematical programming techniques in the synthesis and planning of sustainable processes. Comput. Chem. Eng. 2010, 34, 1365–1376. [Google Scholar] [CrossRef]
- Bhattacharyya, S.C. Energy Economics: Concepts, Issues, Markets and Governance; Springer: London, UK, 2011; ISBN 978-0-85729-267-4. [Google Scholar]
- Foley, A.M.; Gallachóir, B.Ó.; Hur, J.; Baldick, R.; McKeogh, E.J. A strategic review of electricity systems models. Energy 2010, 35, 4522–4530. [Google Scholar] [CrossRef]
- Ventosa, M.; Baíllo, Á.; Ramos, A.; Rivier, M. Electricity market modeling trends. Energy Policy 2005, 33, 897–913. [Google Scholar] [CrossRef]
- Elia, J.A.; Baliban, R.C.; Floudas, C.A. Nationwide energy supply chain analysis for hybrid feedstock processes with significant CO2 emissions reduction. AIChE J. 2012, 58, 2142–2154. [Google Scholar] [CrossRef]
- Lopion, P.; Markewitz, P.; Robinius, M.; Stolten, D. A review of current challenges and trends in energy systems modeling. Renew. Sustain. Energy Rev. 2018, 96, 156–166. [Google Scholar] [CrossRef]
- Lang, Y.; Zitney, S.E.; Biegler, L.T. Optimization of IGCC processes with reduced order CFD models. Comput. Chem. Eng. 2011, 35, 1705–1717. [Google Scholar] [CrossRef]
- Adams, T.A., II; Thatho, T.; Feuvre Le, M.C.; Swartz, C.L.E. The Optimal Design of a Distillation System for the Flexible Polygeneration of Dimethyl Ether and Methanol under Uncertainty. Front. Energy Res. 2018, 6, 41. [Google Scholar] [CrossRef]
- Chen, G.Q.; Wu, X.F. Energy overview for globalized world economy: Source, supply chain and sink. Renew. Sustain. Energy Rev. 2017, 69, 735–749. [Google Scholar] [CrossRef]
- Biegler, L.T.; Grossmann, I.E.; Westerberg, A.W. Systematic Methods for Chemical Process Design; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1997; ISBN 0-13-492422-3. Available online: https://www.osti.gov/biblio/293030-systematic-methods-chemical-process-design (accessed on 12 October 2018).
- Smith, R. Chemical Process: Design and Integration; John Wiley & Sons: Hoboken, NJ, USA, 2016; ISBN 9781118699096. [Google Scholar]
- Cameron, I.T.; Gani, R. Product and Process Modelling: A Case Study Approach; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Nishida, N.; Stephanopoulos, G.; Westerberg, A.W. A review of process synthesis. AIChE J. 1981, 27, 321–351. [Google Scholar] [CrossRef]
- Grossmann, I.E. Mixed-integer programming approach for the synthesis of integrated process flowsheets. Comput. Chem. Eng. 1985, 9, 463–482. [Google Scholar] [CrossRef]
- Gani, R.; Cameron, I.; Lucia, A.; Sin, G.; Georgiadis, M. Process Systems Engineering, 2. Modeling and Simulation. In Ullmann’s Encyclopedia of Industrial Chemistry; American Cancer Society: Atlanta, GA, USA, 2012; ISBN 978-3-527-30673-2. [Google Scholar]
- Marquardt, W. Trends in computer-aided process modeling. Comput. Chem. Eng. 1996, 20, 591–609. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Apap, R.M.; Calfa, B.A.; García-Herreros, P.; Zhang, Q. Recent advances in mathematical programming techniques for the optimization of process systems under uncertainty. Comput. Chem. Eng. 2016, 91, 3–14. [Google Scholar] [CrossRef]
- Barton, P.I.; Pantelides, C.C. Modeling of combined discrete/continuous processes. AIChE J. 1994, 40, 966–979. [Google Scholar] [CrossRef]
- Barton, P.I.; Lee, C.K. Modeling, simulation, sensitivity analysis, and optimization of hybrid systems. ACM Trans. Model. Comput. Simul. 2002, 12, 256–289. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport phenomena. Appl. Mech. Rev. 2002, 55, R1–R4. [Google Scholar] [CrossRef]
- Marquardt, W. Towards a Process Modeling Methodolgy. In Methods of Model Based Process Control; Springer: Dordrecht, The Netherlands, 1995; pp. 3–40. [Google Scholar]
- Watson, H.A.; Vikse, M.; Gundersen, T.; Barton, P.I. Reliable Flash Calculations: Part 2. Process flowsheeting with nonsmooth models and generalized derivatives. Ind. Eng. Chem. Res. 2017, 56, 14848–14864. [Google Scholar] [CrossRef]
- Psichogios, D.C.; Ungar, L.H. A hybrid neural network-first principles approach to process modeling. AIChE J. 1992, 38, 1499–1511. [Google Scholar] [CrossRef]
- Thompson, M.L.; Kramer, M.A. Modeling chemical processes using prior knowledge and neural networks. AIChE J. 1994, 40, 1328–1340. [Google Scholar] [CrossRef]
- Hoseinzade, L.; Adams, T.A., II. Modeling and simulation of an integrated steam reforming and nuclear heat system. Int. J. Hydrogen Energy 2017, 42, 25048–25062. [Google Scholar] [CrossRef]
- Okeke, I.J.; Adams, T.A., II. Combining petroleum coke and natural gas for efficient liquid fuels production. Energy 2018, 163, 426–442. [Google Scholar] [CrossRef]
- Miller, D.C.; Agarwal, D.; Bhattacharyya, D.; Boverhof, J.; Chen, Y.; Eslick, J.; Leek, J.; Ma, J.; Mahapatra, P.; Ng, B.; et al. Innovative computational tools and models for the design, optimization and control of carbon capture processes. In Process Systems and Materials for CO2 Capture: Modelling, Design, Control and Integration; Papadopoulos, A.I., Seferlis, P., Eds.; John Wiley & Sons Ltd.: Chichester, UK, 2017; pp. 311–342. Available online: https://github.com/CCSI-Toolset/ (accessed on 12 October 2018).
- Yu, M.; Miller, D.C.; Biegler, L.T. Dynamic Reduced Order Models for Simulating Bubbling Fluidized Bed Adsorbers. Ind. Eng. Chem. Res. 2015, 54, 6959–6974. [Google Scholar] [CrossRef]
- Modekurti, S.; Bhattacharyya, D.; Zitney, S.E. Dynamic modeling and control studies of a two-stage bubbling fluidized bed adsorber-reactor for solid–sorbent CO2 capture. Ind. Eng. Chem. Res. 2013, 52, 10250–10260. [Google Scholar] [CrossRef]
- Garcia, D.J.; You, F. Supply chain design and optimization: Challenges and opportunities. Comput. Chem. Eng. 2015, 81, 153–170. [Google Scholar] [CrossRef]
- Shah, N. Process industry supply chains: Advances and challenges. Comput. Chem. Eng. 2005, 29, 1225–1235. [Google Scholar] [CrossRef]
- Papageorgiou, L.G. Supply chain optimisation for the process industries: Advances and opportunities. Comput. Chem. Eng. 2009, 33, 1931–1938. [Google Scholar] [CrossRef]
- Barbosa-Póvoa, A.P. Progresses and challenges in process industry supply chains optimization. Curr. Opin. Chem. Eng. 2012, 1, 446–452. [Google Scholar] [CrossRef]
- Nikolopoulou, A.; Ierapetritou, M.G. Optimal design of sustainable chemical processes and supply chains: A review. Comput. Chem. Eng. 2012, 44, 94–103. [Google Scholar] [CrossRef]
- Laínez, J.M.; Puigjaner, L. Prospective and perspective review in integrated supply chain modelling for the chemical process industry. Curr. Opin. Chem. Eng. 2012, 1, 430–445. [Google Scholar] [CrossRef]
- Min, H.; Zhou, G. Supply chain modeling: Past, present and future. Comput. Ind. Eng. 2002, 43, 231–249. [Google Scholar] [CrossRef]
- Niziolek, A.M.; Onel, O.; Tian, Y.; Floudas, C.A.; Pistikopoulos, E.N. Municipal solid waste to liquid transportation fuels—Part III: An optimization-based nationwide supply chain management framework. Comput. Chem. Eng. 2017, in press. [Google Scholar] [CrossRef]
- You, F.; Grossmann, I.E. Design of responsive supply chains under demand uncertainty. Comput. Chem. Eng. 2008, 32, 3090–3111. [Google Scholar] [CrossRef]
- You, F.; Grossmann, I.E. Mixed-integer nonlinear programming models and algorithms for large-scale supply chain design with stochastic inventory management. Ind. Eng. Chem. Res. 2008, 47, 7802–7817. [Google Scholar] [CrossRef]
- You, F.; Tao, L.; Graziano, D.J.; Snyder, S.W. Optimal design of sustainable cellulosic biofuel supply chains: Multiobjective optimization coupled with life cycle assessment and input–output analysis. AIChE J. 2012, 58, 1157–1180. [Google Scholar] [CrossRef]
- Liu, S.; Papageorgiou, L.G. Multiobjective optimisation of production, distribution and capacity planning of global supply chains in the process industry. Omega 2013, 41, 369–382. [Google Scholar] [CrossRef]
- Verderame, P.M.; Elia, J.A.; Li, J.; Floudas, C.A. Planning and Scheduling under Uncertainty: A Review Across Multiple Sectors. Ind. Eng. Chem. Res. 2010, 49, 3993–4017. [Google Scholar] [CrossRef]
- Maravelias, C.T.; Sung, C. Integration of production planning and scheduling: Overview, challenges and opportunities. Comput. Chem. Eng. 2009, 33, 1919–1930. [Google Scholar] [CrossRef]
- Floudas, C.A.; Lin, X. Continuous-time versus discrete-time approaches for scheduling of chemical processes: A review. Comput. Chem. Eng. 2004, 28, 2109–2129. [Google Scholar] [CrossRef]
- Li, Z.; Ierapetritou, M. Process scheduling under uncertainty: Review and challenges. Comput. Chem. Eng. 2008, 32, 715–727. [Google Scholar] [CrossRef]
- Méndez, C.A.; Cerdá, J.; Grossmann, I.E.; Harjunkoski, I.; Fahl, M. State-of-the-art review of optimization methods for short-term scheduling of batch processes. Comput. Chem. Eng. 2006, 30, 913–946. [Google Scholar] [CrossRef]
- Kallrath, J. Planning and scheduling in the process industry. OR Spectr. 2002, 24, 219–250. [Google Scholar] [CrossRef]
- Reklaitis, G.V. Overview of scheduling and planning of batch process operations. In Batch Processing Systems Engineering; Springer: Berlin/Heidelberg, Germany, 1996; pp. 660–705. [Google Scholar]
- Mitra, S.; Grossmann, I.E.; Pinto, J.M.; Arora, N. Optimal production planning under time-sensitive electricity prices for continuous power-intensive processes. Comput. Chem. Eng. 2012, 38, 171–184. [Google Scholar] [CrossRef]
- Mitra, S.; Sun, L.; Grossmann, I.E. Optimal scheduling of industrial combined heat and power plants under time-sensitive electricity prices. Energy 2013, 54, 194–211. [Google Scholar] [CrossRef]
- Birewar, D.B.; Grossmann, I.E. Simultaneous production planning and scheduling in multiproduct batch plants. Ind. Eng. Chem. Res. 1990, 29, 570–580. [Google Scholar] [CrossRef]
- Julka, N.; Srinivasan, R.; Karimi, I. Agent-based supply chain management—1: Framework. Comput. Chem. Eng. 2002, 26, 1755–1769. [Google Scholar] [CrossRef]
- Karimi, I.A.; McDonald, C.M. Planning and Scheduling of Parallel Semicontinuous Processes. 2. Short-Term Scheduling. Ind. Eng. Chem. Res. 1997, 36, 2701–2714. [Google Scholar] [CrossRef]
- McDonald, C.M.; Karimi, I.A. Planning and Scheduling of Parallel Semicontinuous Processes. 1. Production Planning. Ind. Eng. Chem. Res. 1997, 36, 2691–2700. [Google Scholar] [CrossRef]
- Morari, M.; Zafiriou, E. Robust process control. Chem. Eng. Res. Des. 1987, 65, 462–479. [Google Scholar]
- Luyben, W.L. Process Modeling, Simulation and Control for Chemical Engineers, 2nd ed.; McGraw-Hill: New York, NY, USA, 1989; ISBN 978-0-07-039159-8. [Google Scholar]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design; Wiley: New York, NY, USA, 2007; Volume 2, pp. 359–368. [Google Scholar]
- Hussain, M.A. Review of the applications of neural networks in chemical process control—Simulation and online implementation. Artif. Intell. Eng. 1999, 13, 55–68. [Google Scholar] [CrossRef]
- Bequette, B.W. Nonlinear control of chemical processes: A review. Ind. Eng. Chem. Res. 1991, 30, 1391–1413. [Google Scholar] [CrossRef]
- Downs, J.J.; Vogel, E.F. A plant-wide industrial process control problem. Comput. Chem. Eng. 1993, 17, 245–255. [Google Scholar] [CrossRef]
- Skogestad, S. Plantwide control: The search for the self-optimizing control structure. J. Process Control 2000, 10, 487–507. [Google Scholar] [CrossRef]
- Skogestad, S. Control structure design for complete chemical plants. Comput. Chem. Eng. 2004, 28, 219–234. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Halemane, K.P.; Swaney, R.E. Optimization strategies for flexible chemical processes. Comput. Chem. Eng. 1983, 7, 439–462. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Morari, M. Operability, Resiliency, and Flexibility: Process Design Objectives for a Changing World. 1983. Available online: https://pdfs.semanticscholar.org/2b7c/85a9ff57ba9322910fc00128bca66ba0b544.pdf (accessed on 13 November 2018).
- Halemane, K.P.; Grossmann, I.E. Optimal process design under uncertainty. AIChE J. 1983, 29, 425–433. [Google Scholar] [CrossRef]
- Gonzalez-Salazar, M.A.; Kirsten, T.; Prchlik, L. Review of the operational flexibility and emissions of gas-and coal-fired power plants in a future with growing renewables. Renew. Sustain. Energy Rev. 2018, 82, 1497–1513. [Google Scholar] [CrossRef]
- Meerman, J.C.; Ramírez, A.; Turkenburg, W.C.; Faaij, A.P.C. Performance of simulated flexible integrated gasification polygeneration facilities. Part A: A technical-energetic assessment. Renew. Sustain. Energy Rev. 2011, 15, 2563–2587. [Google Scholar] [CrossRef]
- Liu, P.; Pistikopoulos, E.N.; Li, Z. A multi-objective optimization approach to polygeneration energy systems design. AIChE J. 2010, 56, 1218–1234. [Google Scholar] [CrossRef]
- Chen, Y.; Adams, T.A., II; Barton, P.I. Optimal Design and Operation of Flexible Energy Polygeneration Systems. Ind. Eng. Chem. Res. 2011, 50, 4553–4566. [Google Scholar] [CrossRef]
- Swaney, R.E.; Grossmann, I.E. An index for operational flexibility in chemical process design. Part I: Formulation and theory. AIChE J. 1985, 31, 621–630. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Floudas, C.A. Active constraint strategy for flexibility analysis in chemical processes. Comput. Chem. Eng. 1987, 11, 675–693. [Google Scholar] [CrossRef]
- Yunt, M.; Chachuat, B.; Mitsos, A.; Barton, P.I. Designing man-portable power generation systems for varying power demand. AIChE J. 2008, 54, 1254–1269. [Google Scholar] [CrossRef]
- Weijermars, R.; Taylor, P.; Bahn, O.; Das, S.R.; Wei, Y.-M. Review of models and actors in energy mix optimization-can leader visions and decisions align with optimum model strategies for our future energy systems? Energy Strateg. Rev. 2012, 1, 5–18. [Google Scholar] [CrossRef]
- Strantzali, E.; Aravossis, K. Decision making in renewable energy investments: A review. Renew. Sustain. Energy Rev. 2016, 55, 885–898. [Google Scholar] [CrossRef]
- Nakata, T.; Silva, D.; Rodionov, M. Application of energy system models for designing a low-carbon society. Prog. Energy Combust. Sci. 2011, 37, 462–502. [Google Scholar] [CrossRef]
- Pohekar, S.D.; Ramachandran, M. Application of multi-criteria decision making to sustainable energy planning—A review. Renew. Sustain. Energy Rev. 2004, 8, 365–381. [Google Scholar] [CrossRef]
- Connolly, D.; Lund, H.; Mathiesen, B.V.; Leahy, M. A review of computer tools for analysing the integration of renewable energy into various energy systems. Appl. Energy 2010, 87, 1059–1082. [Google Scholar] [CrossRef]
- Hafez, O.; Bhattacharya, K. Optimal planning and design of a renewable energy based supply system for microgrids. Renew. Energy 2012, 45, 7–15. [Google Scholar] [CrossRef]
- Manne, A.; Mendelsohn, R.; Richels, R. MERGE: A model for evaluating regional and global effects of GHG reduction policies. Energy Policy 1995, 23, 17–34. [Google Scholar] [CrossRef]
- Hennicke, P. Scenarios for a robust policy mix: The final report of the German study commission on sustainable energy supply. Energy Policy 2004, 32, 1673–1678. [Google Scholar] [CrossRef]
- Kydes, A.S. The Brookhaven Energy System Optimization Model: Its Variants and Uses. In Energy Policy Modeling: United States and Canadian Experiences; Springer: Dordrecht, The Netherlands, 1980; pp. 110–136. [Google Scholar]
- Naill, R.F. A system dynamics model for national energy policy planning. Syst. Dyn. Rev. 1992, 8, 1–19. [Google Scholar] [CrossRef]
- Jacobsson, S.; Lauber, V. The politics and policy of energy system transformation—Explaining the German diffusion of renewable energy technology. Energy Policy 2006, 34, 256–276. [Google Scholar] [CrossRef]
- Lund, H.; Mathiesen, B.V. Energy system analysis of 100% renewable energy systems—The case of Denmark in years 2030 and 2050. Energy 2009, 34, 524–531. [Google Scholar] [CrossRef]
- Gabriel, S.A.; Kydes, A.S.; Whitman, P. The National Energy Modeling System: A Large-Scale Energy-Economic Equilibrium Model. Oper. Res. 2001, 49, 14–25. [Google Scholar] [CrossRef]
- Available online: https://openmod-initiative.org/ (accessed on 12 October 2018).
- Howells, M.; Rogner, H.; Strachan, N.; Heaps, C.; Huntington, H.; Kypreos, S.; Hughes, A.; Silveira, S.; DeCarolis, J.; Bazillian, M. OSeMOSYS: The open source energy modeling system: An introduction to its ethos, structure and development. Energy Policy 2011, 39, 5850–5870. [Google Scholar] [CrossRef]
- Howells, M.; Welsch, M. OSeMOSYS-The Open Source Energy Modelling System; International Energy Workshop: Stockholm, Sweden, 2010. [Google Scholar]
- Löffler, K.; Hainsch, K.; Burandt, T.; Oei, P.-Y.; Kemfert, C.; von Hirschhausen, C. Designing a Model for the Global Energy System—GENeSYS-MOD: An Application of the Open-Source Energy Modeling System (OSeMOSYS). Energies 2017, 10, 1468. [Google Scholar] [CrossRef]
- Pfenninger, S.; Hawkes, A.; Keirstead, J. Energy systems modeling for twenty-first century energy challenges. Renew. Sustain. Energy Rev. 2014, 33, 74–86. [Google Scholar] [CrossRef]
- Pfenninger, S.; Hirth, L.; Schlecht, I.; Schmid, E.; Wiese, F.; Brown, T.; Davis, C.; Gidden, M.; Heinrichs, H.; Heuberger, C.; et al. Opening the black box of energy modelling: Strategies and lessons learned. Energy Strateg. Rev. 2018, 19, 63–71. [Google Scholar] [CrossRef]
- Kannan, R.; Strachan, N. Modelling the UK residential energy sector under long-term decarbonisation scenarios: Comparison between energy systems and sectoral modelling approaches. Appl. Energy 2009, 86, 416–428. [Google Scholar] [CrossRef]
- Suganthi, L.; Samuel, A.A. Energy models for demand forecasting—A review. Renew. Sustain. Energy Rev. 2012, 16, 1223–1240. [Google Scholar] [CrossRef]
- Torriti, J. A review of time use models of residential electricity demand. Renew. Sustain. Energy Rev. 2014, 37, 265–272. [Google Scholar] [CrossRef]
- Bhattacharyya, S.C.; Timilsina, G.R. Energy Demand Models for Policy Formulation: A Comparative Study of Energy Demand Models; Policy Research Working Papers; The World Bank: Washington, DC, USA, 2009. [Google Scholar]
- Bhattacharyya, S.C.; Timilsina, G.R. A review of energy system models. Int. J. Energy Sect. Manag. 2010, 4, 494–518. [Google Scholar] [CrossRef]
- Craig, P.P.; Gadgil, A.; Koomey, J.G. What Can History Teach us? A Retrospective Examination of Long-Term Energy Forecasts for the United States. Annu. Rev. Energy Environ. 2002, 27, 83–118. [Google Scholar] [CrossRef]
- Werbos, P.J. 2.1. Econometric techniques: Theory versus practice. Energy 1990, 15, 213–236. [Google Scholar] [CrossRef]
- Huang, Y.; Bor, Y.J.; Peng, C.Y. The long-term forecast of Taiwan’s energy supply and demand: LEAP model application. Energy Policy 2011, 39, 6790–6803. [Google Scholar] [CrossRef]
- Ulbricht, R.; Fischer, U.; Lehner, W.; Donker, H. First steps towards a systematical optimized strategy for solar energy supply forecasting. In Proceedings of the European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases (ECMLPKDD 2013), Prague, Czech Republic, 23–27 September 2013; Volume 2327. [Google Scholar]
- Ekonomou, L. Greek long-term energy consumption prediction using artificial neural networks. Energy 2010, 35, 512–517. [Google Scholar] [CrossRef]
- Kankal, M.; Akpınar, A.; Kömürcü, M.İ.; Özşahin, T.Ş. Modeling and forecasting of Turkey’s energy consumption using socio-economic and demographic variables. Appl. Energy 2011, 88, 1927–1939. [Google Scholar] [CrossRef]
- Kandananond, K. Forecasting electricity demand in Thailand with an artificial neural network approach. Energies 2011, 4, 1246–1257. [Google Scholar] [CrossRef]
- Hamzaçebi, C. Forecasting of Turkey’s net electricity energy consumption on sectoral bases. Energy Policy 2007, 35, 2009–2016. [Google Scholar] [CrossRef]
- Floudas, C.A.; Niziolek, A.M.; Onel, O.; Matthews, L.R. Multi-scale systems engineering for energy and the environment: Challenges and opportunities. AIChE J. 2016, 62, 602–623. [Google Scholar] [CrossRef]
- Hasan, M.F. Multi-scale Process Systems Engineering for Carbon Capture, Utilization, and Storage: A Review. In Process Systems and Materials for CO2 Capture: Modelling, Design, Control and Integration; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Biegler, L.T.; Lang, Y.; Lin, W. Multi-scale optimization for process systems engineering. Comput. Chem. Eng. 2014, 60, 17–30. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Shah, N. Multi-scale process and supply chain modelling: From lignocellulosic feedstock to process and products. Interface Focus 2011. [Google Scholar] [CrossRef] [PubMed]
- Baliban, R.C.; Elia, J.A.; Floudas, C.A. Optimization framework for the simultaneous process synthesis, heat and power integration of a thermochemical hybrid biomass, coal, and natural gas facility. Comput. Chem. Eng. 2011, 35, 1647–1690. [Google Scholar] [CrossRef]
- Baliban, R.C.; Elia, J.A.; Floudas, C.A. Simultaneous process synthesis, heat, power, and water integration of thermochemical hybrid biomass, coal, and natural gas facilities. Comput. Chem. Eng. 2012, 37, 297–327. [Google Scholar] [CrossRef]
- Niziolek, A.M.; Onel, O.; Hasan, M.M.F.; Floudas, C.A. Municipal solid waste to liquid transportation fuels—Part II: Process synthesis and global optimization strategies. Comput. Chem. Eng. 2015, 74, 184–203. [Google Scholar] [CrossRef]
- Ghouse, J.H.; Adams, T.A., II. A multi-scale dynamic two-dimensional heterogeneous model for catalytic steam methane reforming reactors. Int. J. Hydrogen Energy 2013, 38, 9984–9999. [Google Scholar] [CrossRef]
- Seepersad, D.; Ghouse, J.H.; Adams, T.A., II. Dynamic simulation and control of an integrated gasifier/reformer system. Part I: Agile case design and control. Chem. Eng. Res. Des. 2015, 100, 481–496. [Google Scholar] [CrossRef]
- Zitney, S.E. Process/equipment co-simulation for design and analysis of advanced energy systems. Comput. Chem. Eng. 2010, 34, 1532–1542. [Google Scholar] [CrossRef]
- Lang, Y.; Malacina, A.; Biegler, L.T.; Munteanu, S.; Madsen, J.I.; Zitney, S.E. Reduced order model based on principal component analysis for process simulation and optimization. Energy Fuels 2009, 23, 1695–1706. [Google Scholar] [CrossRef]
- Lang, Y.-D.; Biegler, L.T.; Munteanu, S.; Madsen, J.I.; Zitney, S.E. Advanced Process Engineering Co-Simulation Using CFD-Based Reduced Order Models; National Energy Technology Laboratory (NETL): Pittsburgh, PA, USA; Morgantown, WV, USA; Albany, OR, USA, 2007.
- Bakshi, B.R.; Fiksel, J. The quest for sustainability: Challenges for process systems engineering. AIChE J. 2003, 49, 1350–1358. [Google Scholar] [CrossRef]
- Bakshi, B.R. Methods and tools for sustainable process design. Curr. Opin. Chem. Eng. 2014, 6, 69–74. [Google Scholar] [CrossRef]
- Cano-Ruiz, J.A.; McRae, G.J. Environmentally Conscious Chemical Process Design. Annu. Rev. Energy Environ. 1998, 23, 499–536. [Google Scholar] [CrossRef]
- Fiksel, J. Designing Resilient, Sustainable Systems. Environ. Sci. Technol. 2003, 37, 5330–5339. [Google Scholar] [CrossRef] [PubMed]
- Pintarič, Z.N.; Kravanja, Z. Selection of the Economic Objective Function for the Optimization of Process Flow Sheets. Ind. Eng. Chem. Res. 2006, 45, 4222–4232. [Google Scholar] [CrossRef]
- Guinée, J.B. Handbook on life cycle assessment operational guide to the ISO standards. Int. J. Life Cycle Assess. 2002, 7, 311. [Google Scholar] [CrossRef]
- Matthews, H.S.; Hendrickson, C.T.; Matthews, D.H. Life Cycle Assessment: Quantitative Approaches for Decisions that Matter. 2015. Available online: http://www.lcatextbook.com (accessed on 12 October 2018).
- Curran, M.A. Environmental life-cycle assessment. Int. J. Life Cycle Assess. 1996, 1, 179. [Google Scholar] [CrossRef]
- Finnveden, G.; Hauschild, M.Z.; Ekvall, T.; Guinée, J.; Heijungs, R.; Hellweg, S.; Koehler, A.; Pennington, D.; Suh, S. Recent developments in Life Cycle Assessment. J. Environ. Manag. 2009, 91, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Klöpffer, W.; Grahl, B. Life Cycle Assessment (LCA): A Guide to Best Practice; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Ukidwe, N.U.; Hau, J.L.; Bakshi, B.R. Thermodynamic Input-Output Analysis of Economic and Ecological Systems. In Handbook of Input-Output Economics in Industrial Ecology; Suh, S., Ed.; Eco-Efficiency in Industry and Science; Springer: Dordrecht, The Netherlands, 2009; pp. 459–490. ISBN 978-1-4020-5737-3. [Google Scholar]
- Rocco, M.V. Primary Exergy Cost of Goods and Services; Springer Briefs in Applied Sciences and Technology; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-43655-5. [Google Scholar]
- Othman, M.R.; Repke, J.-U.; Wozny, G.; Huang, Y. A Modular Approach to Sustainability Assessment and Decision Support in Chemical Process Design. Ind. Eng. Chem. Res. 2010, 49, 7870–7881. [Google Scholar] [CrossRef]
- Hugo, A.; Pistikopoulos, E.N. Environmentally conscious long-range planning and design of supply chain networks. J. Clean. Prod. 2005, 13, 1471–1491. [Google Scholar] [CrossRef]
- Suh, S.; Lenzen, M.; Treloar, G.J.; Hondo, H.; Horvath, A.; Huppes, G.; Jolliet, O.; Klann, U.; Krewitt, W.; Moriguchi, Y.; et al. System Boundary Selection in Life-Cycle Inventories Using Hybrid Approaches. Environ. Sci. Technol. 2004, 38, 657–664. [Google Scholar] [CrossRef] [PubMed]
- Lenzen, M. Errors in Conventional and Input-Output—Based Life—Cycle Inventories. J. Ind. Ecol. 2000, 4, 127–148. [Google Scholar] [CrossRef]
- Nease, J.; Adams, T.A., II. Life cycle analyses of bulk-scale solid oxide fuel cell power plants and comparisons to the natural gas combined cycle. Can. J. Chem. Eng. 2015, 93, 1349–1363. [Google Scholar] [CrossRef]
- Singh, B.; Strømman, A.H.; Hertwich, E.G. Comparative life cycle environmental assessment of CCS technologies. Int. J. Greenh. Gas Control 2011, 5, 911–921. [Google Scholar] [CrossRef]
- Available online: http://eplca.jrc.ec.europa.eu/ (accessed on 12 October 2018).
- Hanes, R.J.; Bakshi, B.R. Process to planet: A multiscale modeling framework toward sustainable engineering. AIChE J. 2015, 61, 3332–3352. [Google Scholar] [CrossRef]
- Hanes, R.J.; Bakshi, B.R. Sustainable process design by the process to planet framework. AIChE J. 2015, 61, 3320–3331. [Google Scholar] [CrossRef]
- Cornelissen, R.L.; Hirs, G.G. The value of the exergetic life cycle assessment besides the LCA. Energy Convers. Manag. 2002, 43, 1417–1424. [Google Scholar] [CrossRef]
- Available online: http://www.openlca.org/ (accessed on 13 November 2018).
- Carnegie Mellon University, Green Design Institute. Economic Input-Output Life Cycle Assessment (EIO-LCA) Model; Carnegie Mellon University: Pittsburgh, PA, USA, 2003. [Google Scholar]
- Yang, Y.; Ingwersen, W.W.; Hawkins, T.R.; Srocka, M.; Meyer, D.E. USEEIO: A new and transparent United States environmentally-extended input-output model. J. Clean. Prod. 2017, 158, 308–318. [Google Scholar] [CrossRef] [PubMed]
- Ringkjøb, H.-K.; Haugan, P.M.; Solbrekke, I.M. A review of modelling tools for energy and electricity systems with large shares of variable renewables. Renew. Sustain. Energy Rev. 2018, 96, 440–459. [Google Scholar] [CrossRef]
- Hall, L.M.H.; Buckley, A.R. A review of energy systems models in the UK: Prevalent usage and categorisation. Appl. Energy 2016, 169, 607–628. [Google Scholar] [CrossRef]
- Van Beeck, N. Classification of Energy Models; Tilburg University: Tilburg, The Netherlands, 2000. [Google Scholar]
- Jebaraj, S.; Iniyan, S. A review of energy models. Renew. Sustain. Energy Rev. 2006, 10, 281–311. [Google Scholar] [CrossRef]
- Herbst, A.; Toro, F.; Reitze, F.; Jochem, E. Introduction to Energy Systems Modelling. Swiss J. Econ. Stat. 2012, 148, 111–135. [Google Scholar] [CrossRef]
- Nakata, T. Energy-economic models and the environment. Prog. Energy Combust. Sci. 2004, 30, 417–475. [Google Scholar] [CrossRef]
- Goyal, H.B.; Seal, D.; Saxena, R.C. Bio-fuels from thermochemical conversion of renewable resources: A review. Renew. Sustain. Energy Rev. 2008, 12, 504–517. [Google Scholar] [CrossRef]
- Zaimes, G.G.; Vora, N.; Chopra, S.S.; Landis, A.E.; Khanna, V. Design of Sustainable Biofuel Processes and Supply Chains: Challenges and Opportunities. Processes 2015, 3, 634–663. [Google Scholar] [CrossRef]
- Deshmukh, M.K.; Deshmukh, S.S. Modeling of hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2008, 12, 235–249. [Google Scholar] [CrossRef]
- Shivarama Krishna, K.; Sathish Kumar, K. A review on hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2015, 52, 907–916. [Google Scholar] [CrossRef]
- Floudas, C.A.; Elia, J.A.; Baliban, R.C. Hybrid and single feedstock energy processes for liquid transportation fuels: A critical review. Comput. Chem. Eng. 2012, 41, 24–51. [Google Scholar] [CrossRef]
- Allegrini, J.; Orehounig, K.; Mavromatidis, G.; Ruesch, F.; Dorer, V.; Evins, R. A review of modelling approaches and tools for the simulation of district-scale energy systems. Renew. Sustain. Energy Rev. 2015, 52, 1391–1404. [Google Scholar] [CrossRef]
- Keirstead, J.; Jennings, M.; Sivakumar, A. A review of urban energy system models: Approaches, challenges and opportunities. Renew. Sustain. Energy Rev. 2012, 16, 3847–3866. [Google Scholar] [CrossRef]
- Zeng, Y.; Cai, Y.; Huang, G.; Dai, J. A Review on Optimization Modeling of Energy Systems Planning and GHG Emission Mitigation under Uncertainty. Energies 2011, 4, 1624–1656. [Google Scholar] [CrossRef]
- Liu, P.; Georgiadis, M.C.; Pistikopoulos, E.N. Advances in Energy Systems Engineering. Ind. Eng. Chem. Res. 2011, 50, 4915–4926. [Google Scholar] [CrossRef]
- Adams, T.A., II. Future opportunities and challenges in the design of new energy conversion systems. Comput. Chem. Eng. 2015, 81, 94–103. [Google Scholar] [CrossRef]
- Martín, M.; Adams, T.A., II. Future directions in process and product synthesis and design. Comput. Aided Chem. Eng. 2018, 44, 1–10. [Google Scholar]
- Fisher, J.; Henzinger, T.A. Executable cell biology. Nat. Biotechnol. 2007, 25, 1239–1249. [Google Scholar] [CrossRef] [PubMed]
- Tucker, D.; Shelton, M.; Manivannan, A. The Role of Solid Oxide Fuel Cells in Advanced Hybrid Power Systems of the Future. Electrochem. Soc. Interface 2009, 18, 45. [Google Scholar]
- Tucker, D.; Liese, E.; VanOsdol, J.; Lawson, L.; Gemmen, R.S. Fuel Cell Gas Turbine Hybrid Simulation Facility Design. In ASME 2002 International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2002; pp. 183–190. [Google Scholar] [CrossRef]
- Liao, S.H. Expert system methodologies and applications—A decade review from 1995 to 2004. Expert Syst. Appl. 2005, 28, 93–103. [Google Scholar] [CrossRef]
- Stephanopoulos, G.; Han, C. Intelligent systems in process engineering: A review. Comput. Chem. Eng. 1996, 20, 743–791. [Google Scholar] [CrossRef]
- Mele, F.D.; Guillén, G.; Espuña, A.; Puigjaner, L. An agent-based approach for supply chain retrofitting under uncertainty. Comput. Chem. Eng. 2007, 31, 722–735. [Google Scholar] [CrossRef]
- Weidlich, A.; Veit, D. A critical survey of agent-based wholesale electricity market models. Energy Econ. 2008, 30, 1728–1759. [Google Scholar] [CrossRef]
- Ma, T.; Nakamori, Y. Agent-based modeling on technological innovation as an evolutionary process. Eur. J. Oper. Res. 2005, 166, 741–755. [Google Scholar] [CrossRef]
- Ma, T.; Nakamori, Y. Modeling technological change in energy systems–from optimization to agent-based modeling. Energy 2009, 34, 873–879. [Google Scholar] [CrossRef]
- Ma, T.; Grubler, A.; Nakamori, Y. Modeling technology adoptions for sustainable development under increasing returns, uncertainty, and heterogeneous agents. Eur. J. Oper. Res. 2009, 195, 296–306. [Google Scholar] [CrossRef]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. USA 2002, 99, 7280–7287. [Google Scholar] [CrossRef] [PubMed]
- Dhaliwal, J.S.; Benbasat, I. The use and effects of knowledge-based system explanations: Theoretical foundations and a framework for empirical evaluation. Inf. Syst. Res. 1996, 7, 342–362. [Google Scholar] [CrossRef]
- Available online: https://www.process-design-center.com/prosyn.html (accessed on 12 October 2018).
- Puig-Arnavat, M.; Hernández, J.A.; Bruno, J.C.; Coronas, A. Artificial neural network models for biomass gasification in fluidized bed gasifiers. Biomass Bioenergy 2013, 49, 279–289. [Google Scholar] [CrossRef]
- Hunt, K.J.; Sbarbaro, D.; Żbikowski, R.; Gawthrop, P.J. Neural networks for control systems—A survey. Automatica 1992, 28, 1083–1112. [Google Scholar] [CrossRef]
- Baughman, D.R.; Liu, Y.A. Neural Networks in Bioprocessing and Chemical Engineering; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Cozad, A.; Sahinidis, N.V.; Miller, D.C. A combined first-principles and data-driven approach to model building. Comput. Chem. Eng. 2015, 73, 116–127. [Google Scholar] [CrossRef]
- Lophaven, S.N.; Nielsen, H.B.; Søndergaard, J. DACE: A Matlab Kriging Toolbox; Technical Report; Technical University of Denmark: Lyngby, Denmark, 2002. [Google Scholar]
- Straus, J.; Skogestad, S. Surrogate model generation using self-optimizing variables. Comput. Chem. Eng. 2018, in press. [Google Scholar] [CrossRef]
- Forrester, A.; Keane, A. Engineering Design via Surrogate Modelling: A Practical Guide; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Watson, H.A.J. Robust Simulation and Optimization Methods for Natural Gas Liquefaction Processes. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2018. [Google Scholar]
- Henzinger, T.A. The theory of hybrid automata. In Verification of Digital and Hybrid Systems; Springer: Berlin, Germany, 2000; pp. 265–292. [Google Scholar]
- Oldenburg, J.; Marquardt, W. Disjunctive modeling for optimal control of hybrid systems. Comput. Chem. Eng. 2008, 32, 2346–2364. [Google Scholar] [CrossRef]
- David, R.; Alla, H. On hybrid Petri nets. Discret. Event Dyn. Syst. 2001, 11, 9–40. [Google Scholar] [CrossRef]
- Barton, P.I.; Khan, K.A.; Stechlinski, P.; Watson, H.A. Computationally relevant generalized derivatives: Theory, evaluation and applications. Optim. Methods Softw. 2017, 1–43. [Google Scholar] [CrossRef]
- Watson, H.A.; Khan, K.A.; Barton, P.I. Multistream heat exchanger modeling and design. AIChE J. 2015, 61, 3390–3403. [Google Scholar] [CrossRef]
- Watson, H.A.; Vikse, M.; Gundersen, T.; Barton, P.I. Optimization of single mixed-refrigerant natural gas liquefaction processes described by nondifferentiable models. Energy 2018, 150, 860–876. [Google Scholar] [CrossRef]
- Vikse, M.; Watson, H.A.; Gundersen, T.; Barton, P.I. Versatile Simulation Method for Complex Single Mixed Refrigerant Natural Gas Liquefaction Processes. Ind. Eng. Chem. Res. 2017, 57, 5881–5894. [Google Scholar] [CrossRef]
- Vikse, M.; Watson, H.A.; Barton, P.I.; Gundersen, T. Simulation of a Dual Mixed Refrigerant LNG Process using a Nonsmooth Framework. Comput. Aided Chem. Eng. 2018, 44, 391–396. [Google Scholar]
- Vikse, M.; Watson, H.A.; Gundersen, T.; Barton, P.I. Simulation of Dual Mixed Refrigerant Natural Gas Liquefaction Processes using a Nonsmooth Framework. Processes 2018, 6, 193. [Google Scholar] [CrossRef]
- Straus, J.; Skogestad, S. Variable reduction for surrogate modelling. In Proceedings of the Foundations of Computer-Aided Process Operations, Tucson, AZ, USA, 8–12 January 2017. [Google Scholar]
- Straus, J.; Skogestad, S. Use of Latent Variables to Reduce the Dimension of Surrogate Models. Comput. Aided Chem. Eng. 2017, 40, 445–450. [Google Scholar]
- Guo, B.; Li, D.; Cheng, C.; Lü, Z.; Shen, Y. Simulation of biomass gasification with a hybrid neural network model. Bioresour. Technol. 2001, 76, 77–83. [Google Scholar] [CrossRef]
- Takamatsu, T. The nature and role of process systems engineering. Comput. Chem. Eng. 1983, 7, 203–218. [Google Scholar] [CrossRef]
- Vlachos, D.G. A Review of Multiscale Analysis: Examples from Systems Biology, Materials Engineering, and Other Fluid–Surface Interacting Systems. In Advances in Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2005; Volume 30, pp. 1–61. ISBN 978-0-12-008530-9. [Google Scholar]
- Grossmann, I.E.; Westerberg, A.W. Research challenges in process systems engineering. AIChE J. 2000, 46, 1700–1703. [Google Scholar] [CrossRef]
- Grossmann, I.E. Challenges in the new millennium: Product discovery and design, enterprise and supply chain optimization, global life cycle assessment. Comput. Chem. Eng. 2004, 29, 29–39. [Google Scholar] [CrossRef]
- Horstemeyer, M.F. Multiscale Modeling: A Review. In Practical Aspects of Computational Chemistry; Springer: Dordrecht, The Netherlands, 2009; pp. 87–135. ISBN 978-90-481-2686-6. [Google Scholar]
- French, C.E. Synthetic biology and biomass conversion: A match made in heaven? J. R. Soc. Interface 2009, 6, S547–S558. [Google Scholar] [CrossRef] [PubMed]
- Mettler, M.S.; Vlachos, D.G.; Dauenhauer, P.J. Top ten fundamental challenges of biomass pyrolysis for biofuels. Energy Environ. Sci. 2012, 5, 7797–7809. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, S.; Singh, O.V. Bioconversion of lignocellulosic biomass: Biochemical and molecular perspectives. J. Ind. Microbiol. Biotechnol. 2008, 35, 377–391. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.K.; Chou, H.; Ham, T.S.; Lee, T.S.; Keasling, J.D. Metabolic engineering of microorganisms for biofuels production: From bugs to synthetic biology to fuels. Curr. Opin. Biotechnol. 2008, 19, 556–563. [Google Scholar] [CrossRef] [PubMed]
- Baliban, R.C.; Elia, J.A.; Floudas, C.A. Toward Novel Hybrid Biomass, Coal, and Natural Gas Processes for Satisfying Current Transportation Fuel Demands, 1: Process Alternatives, Gasification Modeling, Process Simulation, and Economic Analysis. Ind. Eng. Chem. Res. 2010, 49, 7343–7370. [Google Scholar] [CrossRef]
- Onel, O.; Niziolek, A.M.; Hasan, M.M.F.; Floudas, C.A. Municipal solid waste to liquid transportation fuels—Part I: Mathematical modeling of a municipal solid waste gasifier. Comput. Chem. Eng. 2014, 71, 636–647. [Google Scholar] [CrossRef]
- Field, R.P.; Brasington, R. Baseline flowsheet model for IGCC with carbon capture. Ind. Eng. Chem. Res. 2011, 50, 11306–11312. [Google Scholar] [CrossRef]
- Adams, T.A., II; Barton, P.I. High-efficiency power production from coal with carbon capture. AIChE J. 2010, 56, 3120–3136. [Google Scholar] [CrossRef]
- Kunze, C.; Spliethoff, H. Modelling, comparison and operation experiences of entrained flow gasifier. Energy Convers. Manag. 2011, 52, 2135–2141. [Google Scholar] [CrossRef]
- Singh, R.I.; Brink, A.; Hupa, M. CFD modeling to study fluidized bed combustion and gasification. Appl. Therm. Eng. 2013, 52, 585–614. [Google Scholar] [CrossRef]
- Zitney, S.E.; Syamlal, M. Integrated Process Simulation and CFD for Improved Process Engineering. Comput. Aided Chem. Eng. 2002, 10, 397–402. [Google Scholar]
- Baruah, D.; Baruah, D.C. Modeling of biomass gasification: A review. Renew. Sustain. Energy Rev. 2014, 39, 806–815. [Google Scholar] [CrossRef]
- Sloan, D.A.P.; Fiveland, W.A.P.; Zitney, S.E.; Osawe, M. Plant design: Integrating Plant and Equipment Models. Power Mag. 2007, 151, 8. [Google Scholar]
- Shi, S.-P.; Zitney, S.E.; Shahnam, M.; Syamlal, M.; Rogers, W.A. Modelling coal gasification with CFD and discrete phase method. J. Energy Inst. 2006, 79, 217–221. [Google Scholar] [CrossRef]
- Biegler, L.T.; Lang, Y. Multi-scale optimization for advanced energy processes. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2012; Volume 31, pp. 51–60. [Google Scholar]
- Chen, L.; Yong, S.Z.; Ghoniem, A.F. Oxy-fuel combustion of pulverized coal: Characterization, fundamentals, stabilization and CFD modeling. Prog. Energy Combust. Sci. 2012, 38, 156–214. [Google Scholar] [CrossRef]
- Adams, T.A., II; Barton, P.I. Combining coal gasification, natural gas reforming, and solid oxide fuel cells for efficient polygeneration with CO2 capture and sequestration. Fuel Process. Technol. 2011, 92, 2105–2115. [Google Scholar] [CrossRef]
- Adams, T.A., II; Ghouse, J.H. Polygeneration of fuels and chemicals. Curr. Opin. Chem. Eng. 2015, 10, 87–93. [Google Scholar] [CrossRef]
- Jana, K.; Ray, A.; Majoumerd, M.M.; Assadi, M.; De, S. Polygeneration as a future sustainable energy solution—A comprehensive review. Appl. Energy 2017, 202, 88–111. [Google Scholar] [CrossRef]
- Adams, T.A., II; Barton, P.I. Combining coal gasification and natural gas reforming for efficient polygeneration. Fuel Process. Technol. 2011, 92, 639–655. [Google Scholar] [CrossRef]
- Ghouse, J.H.; Seepersad, D.; Adams, T.A., II. Modelling, simulation and design of an integrated radiant syngas cooler and steam methane reformer for use with coal gasification. Fuel Process. Technol. 2015, 138, 378–389. [Google Scholar] [CrossRef]
- Seepersad, D.; Ghouse, J.H.; Adams, T.A., II. Dynamic simulation and control of an integrated gasifier/reformer system. Part II: Discrete and model predictive control. Chem. Eng. Res. Des. 2015, 100, 497–508. [Google Scholar] [CrossRef]
- Sharma, B.; Ingalls, R.G.; Jones, C.L.; Khanchi, A. Biomass supply chain design and analysis: Basis, overview, modeling, challenges, and future. Renew. Sustain. Energy Rev. 2013, 24, 608–627. [Google Scholar] [CrossRef]
- Yue, D.; You, F.; Snyder, S.W. Biomass-to-bioenergy and biofuel supply chain optimization: Overview, key issues and challenges. Comput. Chem. Eng. 2014, 66, 36–56. [Google Scholar] [CrossRef]
- Iakovou, E.; Karagiannidis, A.; Vlachos, D.; Toka, A.; Malamakis, A. Waste biomass-to-energy supply chain management: A critical synthesis. Waste Manag. 2010, 30, 1860–1870. [Google Scholar] [CrossRef] [PubMed]
- Cafaro, D.C.; Grossmann, I.E. Strategic planning, design, and development of the shale gas supply chain network. AIChE J. 2014, 60, 2122–2142. [Google Scholar] [CrossRef]
- Rezaie, B.; Rosen, M.A. District heating and cooling: Review of technology and potential enhancements. Appl. Energy 2012, 93, 2–10. [Google Scholar] [CrossRef]
- Varma, V.A.; Reklaitis, G.V.; Blau, G.E.; Pekny, J.F. Enterprise-wide modeling & optimization—An overview of emerging research challenges and opportunities. Comput. Chem. Eng. 2007, 31, 692–711. [Google Scholar] [CrossRef]
- Zhang, Q.; Grossmann, I.E. Enterprise-wide optimization for industrial demand side management: Fundamentals, advances, and perspectives. Chem. Eng. Res. Des. 2016, 116, 114–131. [Google Scholar] [CrossRef]
- Lam, H.L.; Klemeš, J.J.; Kravanja, Z. Model-size reduction techniques for large-scale biomass production and supply networks. Energy 2011, 36, 4599–4608. [Google Scholar] [CrossRef]
- Our Common Future, Chapter 2: Towards Sustainable Development-A/42/427 Annex, Chapter 2-UN Documents: Gathering a Body of Global Agreements. Available online: http://www.un-documents.net/ocf-02.htm (accessed on 9 September 2018).
- Elkington, J. Cannibals with Forks: The Triple Bottom Line of 21st Century Business; John Wiley and Sons: Hoboken, NJ, USA, 1999; ISBN 1841120847. [Google Scholar]
- Belgiorno, V.; De Feo, G.; Della Rocca, C.; Napoli, R.M.A. Energy from gasification of solid wastes. Waste Manag. 2003, 23, 1–15. [Google Scholar] [CrossRef]
- Psomopoulos, C.S.; Bourka, A.; Themelis, N.J. Waste-to-energy: A review of the status and benefits in USA. Waste Manag. 2009, 29, 1718–1724. [Google Scholar] [CrossRef] [PubMed]
- Ghanbari, H.; Pettersson, F.; Saxén, H. Sustainable development of primary steelmaking under novel blast furnace operation and injection of different reducing agents. Chem. Eng. Sci. 2015, 129, 208–222. [Google Scholar] [CrossRef]
- Deng, L.; Adams, T.A., II. Optimization of coke oven gas desulfurization and combined cycle power plant electricity generation. Ind. Eng. Chem. Res. 2018, in press. [Google Scholar] [CrossRef]
- Klemes, J.J. Handbook of Process Integration (PI): Minimisation of Energy and Water Use, Waste and Emissions; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Fu, C.; Vikse, M.; Gundersen, T. Work and Heat Integration: An emerging research area. Energy 2018, 158, 796–806. [Google Scholar] [CrossRef]
- Karuppiah, R.; Grossmann, I.E. Global optimization for the synthesis of integrated water systems in chemical processes. Comput. Chem. Eng. 2006, 30, 650–673. [Google Scholar] [CrossRef]
- Wang, Y.P.; Smith, R. Wastewater minimisation. Chem. Eng. Sci. 1994, 49, 981–1006. [Google Scholar] [CrossRef]
- Smith, R.L.; Ruiz-Mercado, G.J.; Gonzalez, M.A. Using GREENSCOPE indicators for sustainable computer-aided process evaluation and design. Comput. Chem. Eng. 2015, 81, 272–277. [Google Scholar] [CrossRef]
- Azapagic, A.; Perdan, S. Indicators of Sustainable Development for Industry. Process Saf. Environ. Prot. 2000, 78, 243–261. [Google Scholar] [CrossRef]
- Bamufleh, H.S.; Ponce-Ortega, J.M.; El-Halwagi, M.M. Multi-objective optimization of process cogeneration systems with economic, environmental, and social tradeoffs. Clean Technol. Environ. Policy 2013, 15, 185–197. [Google Scholar] [CrossRef]
- Sinnott, R.K.; Towler, G. Chemical Engineering Design: SI Edition; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Seider, W.D.; Seader, J.D.; Lewin, D.R. Product and Process Design Principles: Synthesis, Analysis and Evaluation; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Turton, R.; Bailie, R.C.; Whiting, W.B.; Shaeiwitz, J.A. Analysis, Synthesis and Design of Chemical Processes; Pearson Education: London, UK, 2008. [Google Scholar]
- Larson, E.D.; Jin, H.; Celik, F.E. Large-scale gasification-based coproduction of fuels and electricity from switchgrass. Biofuels Bioprod. Biorefin. 2009, 3, 174–194. [Google Scholar] [CrossRef]
- Hamelinck, C.; Faaij, A.; Denuil, H.; Boerrigter, H. Production of FT transportation fuels from biomass; technical options, process analysis and optimisation, and development potential. Energy 2004, 29, 1743–1771. [Google Scholar] [CrossRef]
- Adams, T.A., II. Learn Aspen Plus in 24 Hours; McGraw-Hill Education: New York, NY, USA, 2018; ISBN 978-1-260-11645-8. [Google Scholar]
- ICIS Pricing. Chemical Industry Trends. Available online: https://www.icis.com (accessed on 10 September 2018).
- Birge, J.R.; Louveaux, F. Introduction to Stochastic Programming; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Ben-Tal, A.; Nemirovski, A. Robust optimization–methodology and applications. Math. Program. 2002, 92, 453–480. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W. Chance-constrained programming. Manag. Sci. 1959, 6, 73–79. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Sirdeshpande, A.R.; Ierapetritou, M.G.; Andrecovich, M.J.; Naumovitz, J.P. Process synthesis optimization and flexibility evaluation of air separation cycles. AIChE J. 2005, 51, 1190–1200. [Google Scholar] [CrossRef]
- Wang, H.; Mastragostino, R.; Swartz, C.L. Flexibility analysis of process supply chain networks. Comput. Chem. Eng. 2016, 84, 409–421. [Google Scholar] [CrossRef]
- Grossmann, I.E.; Calfa, B.A.; Garcia-Herreros, P. Evolution of concepts and models for quantifying resiliency and flexibility of chemical processes. Comput. Chem. Eng. 2014, 70, 22–34. [Google Scholar] [CrossRef]
- Horne, R.; Grant, T.; Verghese, K. Life Cycle Assessment: Principles, Practice and Prospects; Csiro Publishing: Clayton, Australia, 2009. [Google Scholar]
- International Organization for Standardization. Environmental Management: Life Cycle Assessment; Principles and Framework; ISO: Geneva, Switzerland, 2006. [Google Scholar]
- Huijbregts, M.A.J.; Steinmann, Z.J.N.; Elshout, P.M.F.; Stam, G.; Verones, F.; Vieira, M.D.M.; Hollander, A.; Zijp, M.; van Zelm, R. ReCiPe 2016: A Harmonized Life Cycle Impact Assessment Method at Midpoint and Endpoint Level. Report I: Characterization; RIVM Report 2016-0104; National Institute for Public Health and the Environment: Bilthofen, The Netherlands, 2016. [Google Scholar]
- Bare, J.C. TRACI: The tool for the reduction and assessment of chemical and other environmental impacts. J. Ind. Ecol. 2002, 6, 49–78. [Google Scholar] [CrossRef]
- Eco-Indicator 99 Methodology Report; Pre Consultants B.V.: Amersfoort, The Netherlands, 22 June 2011.
- Available online: https://uslci.lcacommons.gov/ (accessed on 12 October 2018).
- Available online: https://www.ecoinvent.org/ (accessed on 12 October 2018).
- Azapagic, A.; Howard, A.; Parfitt, A.; Tallis, B.; Duff, C.; Hadfield, C.; Pritchard, C.; Gillett, J.; Hackitt, J.; Seaman, M.; et al. The Sustainability Metrics. Available online: http: //nbis.org/nbisresources/metrics/triple_bottom_line_indicators_process_industries.pdf (accessed on 12 October 2018).
- Jørgensen, A.; Le Bocq, A.; Nazarkina, L.; Hauschild, M. Methodologies for social life cycle assessment. Int. J. Life Cycle Assess. 2008, 13, 96. [Google Scholar] [CrossRef]
- Kober, T.; Panos, E.; Volkart, K. Energy system challenges of deep global CO2 emissions reduction under the World Energy Council’s scenario framework. In Limiting Global Warming to Well Below 2 °C: Energy System Modelling and Policy Development; Springer: Berlin, Germany, 2018; pp. 17–31. [Google Scholar]
- Perloff, J.M. Microeconomics; Pearson Addison Wesley: Boston, MA, USA, 2004. [Google Scholar]
- EIA-The National Energy Modeling System: An Overview. 2009. Available online: https://www.eia.gov/outlooks/aeo/nems/overview/index.html (accessed on 12 October 2018).
- Monteiro, C.; Bessa, R.; Miranda, V.; Botterud, A.; Wang, J.; Conzelmann, G. INESC Porto Wind Power Forecasting: State-of-the-Art 2009; Argonne National Lab.: Lemont, IL, USA, 2009. [Google Scholar]
- E3Mlab of ICCS/NTUA. The PRIMES Model. Available online: https://ec.europa.eu/energy/sites/ener/files/documents/sec_2011_1569_2_prime_model_0.pdf (accessed on 12 October 2018).
- Berndes, G.; Hoogwijk, M.; Van den Broek, R. The contribution of biomass in the future global energy supply: A review of 17 studies. Biomass Bioenergy 2003, 25, 1–28. [Google Scholar] [CrossRef]
- Remme, U.; Goldstein, G.A.; Schellmann, U.; Schlenzig, C. MESAP/TIMES—Advanced Decision Support for Energy and Environmental Planning. In Operations Research Proceedings 2001; Chamoni, P., Leisten, R., Martin, A., Minnemann, J., Stadtler, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Loulou, R.; Goldstein, G.; Noble, K. Documentation for the MARKAL Family of Models. Energy Technol. Syst. Anal. Program. 2004, 65–73. Available online: http://iea-etsap.org/MrklDoc-I_StdMARKAL.pdf (accessed on 12 October 2018).
- Schrattenholzer, L. The Energy Supply Model MESSAGE; International Institute for Applied Systems Analysis: Laxenburg, Austria, 1981; Available online: http://pure.iiasa.ac.at/id/eprint/1542/ (accessed on 12 October 2018).
- Krey, V.; Havlik, P.; Fricko, O.; Zilliacus, J.; Gidden, M.; Strubegger, M.; Kartasasmita, I.; Ermolieva, T.; Forsell, N.; Gusti, M. Message-Globiom 1.0 Documentation; International Institute for Applied Systems Analysis: Laxenburg, Austria, 2016; Available online: http://data.ene.iiasa.ac.at/message-globiom (accessed on 12 October 2018).
- Energy PLAN. MARKAL/TIMES. Available online: https://www.energyplan.eu/othertools/national/markaltimes/ (accessed on 12 October 2018).
- Available online: http://www.iiasa.ac.at/web/home/research/researchPrograms/Energy/IAMF.en.html (accessed on 13 November 2018).
- Huppmann, D.; Gidden, M.; Fricko, O.; Kolp, P.; Orthofer, C.; Pimmer, M.; Vinca, A.; Mastrucci, A.; Riahi, K.; Krey, V. The MESSAGEix Integrated Assessment Model and the ix modeling platform (ixmp). Environ. Model. Softw. 2018. Available online: http://pure.iiasa.ac.at/15157 (accessed on 12 October 2018).
- Dowlatabadi, H. Integrated assessment models of climate change: An incomplete overview. Energy Policy 1995, 23, 289–296. [Google Scholar] [CrossRef]
- Parker, P.; Letcher, R.; Jakeman, A.; Beck, M.B.; Harris, G.; Argent, R.M.; Hare, M.; Pahl-Wostl, C.; Voinov, A.; Janssen, M. Progress in integrated assessment and modelling1. Environ. Model. Softw. 2002, 17, 209–217. [Google Scholar] [CrossRef]
- Stanton, E.A.; Ackerman, F.; Kartha, S. Inside the integrated assessment models: Four issues in climate economics. Clim. Dev. 2009, 1, 166–184. [Google Scholar] [CrossRef]
- Rotmans, J. Methods for IA: The challenges and opportunities ahead. Environ. Model. Assess. 1998, 3, 155–179. [Google Scholar] [CrossRef]
- Pfenninger, S. Energy scientists must show their workings. Nat. News 2017, 542, 393. [Google Scholar] [CrossRef] [PubMed]
- Herbst, M.A.; Toro, F.A.; Reitze, F.; Eberhard, J. Bridging Macroeconomic and Bottom up Energy Models-the Case of Efficiency in Industry. Available online: https://www.eceee.org (accessed on 12 October 2018).
- Dannenberg, A.; Mennel, T.; Moslener, U. What does Europe pay for clean energy?—Review of macroeconomic simulation studies. Energy Policy 2008, 36, 1318–1330. [Google Scholar] [CrossRef]
- Miller, R.E.; Blair, P.D. Input-Output Analysis: Foundations and Extensions, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- US Bureau of Economic Analysis. Input-Output Accounts Data. Available online: https://www.bea.gov/industry/input-output-accounts-data (accessed on 12 October 2018).
- Bullard, C.W.; Herendeen, R.A. Energy impact of consumption decisions. Proc. IEEE 1975, 63, 484–493. [Google Scholar] [CrossRef]
- Just, J.E. Impacts of new energy technology using generalized input-output analysis. Comput. Oper. Res. 1974, 1, 97–109. [Google Scholar] [CrossRef]
- Matthews, H.S.; Small, M.J. Extending the boundaries of life-cycle assessment through environmental economic input-output models. J. Ind. Ecol. 2000, 4, 7–10. [Google Scholar] [CrossRef]
- Hendrickson, C.; Horvath, A.; Joshi, S.; Lave, L. Peer reviewed: Economic input–output models for environmental life-cycle assessment. Environ. Sci. Technol. 1998, 32, 184A–191A. [Google Scholar] [CrossRef]
- Hendrickson, C.T.; Lave, L.B.; Matthews, H.S. Environmental Life Cycle Assessment of Goods and Services: An Input-Output Approach; Resources for the Future: Washington, DC, USA, 2006. [Google Scholar]
- U.S. Energy Information Administration (EIA). Annual Energy Outlook 2016. Available online: https://www.eia.gov/outlooks/archive/aeo16/appendixe.php (accessed on 8 October 2018).
- Mitra, S.; Pinto, J.M.; Grossmann, I.E. Optimal multi-scale capacity planning for power-intensive continuous processes under time-sensitive electricity prices and demand uncertainty. Part I: Modeling. Comput. Chem. Eng. 2014, 65, 89–101. [Google Scholar] [CrossRef]
- PJM Interconnection, 2011. Daily Day-Ahead Locational Marginal Pricing. Available online: http://www.pjm.com (accessed on 12 October 2018).
- U.S. Energy Information Administration (EIA). Electric Power Annual 2016. Available online: https://www.eia.gov/electricity/annual/ (accessed on 12 October 2018).
- Rolfsman, B. Combined heat-and-power plants and district heating in a deregulated electricity market. Appl. Energy 2004, 78, 37–52. [Google Scholar] [CrossRef]
- Independent Electricity System Operator. Ontario Demand and Market Prices. 2012. Available online: http://www.ieso.ca/imoweb/siteShared/demandprice.asp?sid=ic (accessed on 12 October 2018).
- Nease, J.; Adams, T.A., II. Application of rolling horizon optimization to an integrated solid-oxide fuel cell and compressed air energy storage plant for zero-emissions peaking power under uncertainty. Comput. Chem. Eng. 2014, 68, 203–219. [Google Scholar] [CrossRef]
- Hendrickson, C.T.; Horvath, A.; Joshi, S.; Klausner, M.; Lave, L.B.; McMichael, F.C. Comparing two life cycle assessment approaches: A process model vs. economic input-output-based assessment. In Proceedings of the 1997 IEEE International Symposium on Electronics and the Environment. ISEE-1997, San Francisco, CA, USA, 5–7 May 1997; pp. 176–181. [Google Scholar]
- Joshi, S. Product environmental life-cycle assessment using input-output techniques. J. Ind. Ecol. 1999, 3, 95–120. [Google Scholar] [CrossRef]
- Adriaanse, A.; Bringezu, S.; Hammond, A.; Moriguchi, Y.; Rodenburg, E.; Rogich, D.; Schütz, H. Resource Flows: The Material Basis of Industrial Economies; World Resources Institute: Washington, DC, USA, 1997. [Google Scholar]
- Spreng, D.T. Net-Energy Analysis and the Energy Requirements of Energy Systems; Praeger: Westport, CT, USA, 1988. [Google Scholar]
- Ukidwe, N.U.; Bakshi, B.R. Thermodynamic Accounting of Ecosystem Contribution to Economic Sectors with Application to 1992 U.S. Economy. Environ. Sci. Technol. 2004, 38, 4810–4827. [Google Scholar] [CrossRef] [PubMed]
- Kotas, T.J. The Exergy Method of Thermal Plant Analysis; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Szargut, J.; Morris, D.R.; Steward, F.R. Exergy Analysis of Thermal, Chemical, and Metallurgical Processes; Springer: Berlin, Germany, 1987. [Google Scholar]
- Sciubba, E.; Wall, G. A brief commented history of exergy from the beginnings to 2004. Int. J. Thermodyn. 2007, 10, 1–26. [Google Scholar]
- Szargut, J.; Morris, D.R. Cumulative exergy consumption and cumulative degree of perfection of chemical processes. Int. J. Energy Res. 1987, 11, 245–261. [Google Scholar] [CrossRef]
- Lozano, M.A.; Valero, A. Theory of the exergetic cost. Energy 1993, 18, 939–960. [Google Scholar] [CrossRef]
- Valero, A.; Lozano, M.A.; Serra, L.; Torres, C. Application of the exergetic cost theory to the CGAM problem. Energy 1994, 19, 365–381. [Google Scholar] [CrossRef]
- Valero, A.; Serra, L.; Uche, J. Fundamentals of exergy cost accounting and thermoeconomics. Part I: Theory. Energy Resour. Technol. 2006, 128, 1–8. [Google Scholar] [CrossRef]
- Ayres, R.U.; Ayres, L.W.; Martinás, K. Exergy, waste accounting, and life-cycle analysis. Energy 1998, 23, 355–363. [Google Scholar] [CrossRef]
- Keshavarzian, S.; Rocco, M.V.; Gardumi, F.; Colombo, E. Practical approaches for applying thermoeconomic analysis to energy conversion systems: Benchmarking and comparative application. Energy Convers. Manag. 2017, 150, 532–544. [Google Scholar] [CrossRef]
- Hau, J.L.; Bakshi, B.R. Expanding Exergy Analysis to Account for Ecosystem Products and Services. Environ. Sci. Technol. 2004, 38, 3768–3777. [Google Scholar] [CrossRef] [PubMed]
- Keshavarzian, S.; Gardumi, F.; Rocco, M.V.; Colombo, E. Off-Design Modeling of Natural Gas Combined Cycle Power Plants: An Order Reduction by Means of Thermoeconomic Input–Output Analysis. Entropy 2016, 18, 71. [Google Scholar] [CrossRef]
- Keshavarzian, S.; Rocco, M.V.; Colombo, E. Thermoeconomic diagnosis and malfunction decomposition: Methodology improvement of the Thermoeconomic Input-Output Analysis (TIOA). Energy Convers. Manag. 2018, 157, 644–655. [Google Scholar] [CrossRef]
- Adams, T.A., II; Barton, P.I. High-efficiency power production from natural gas with carbon capture. J. Power Sources 2010, 195, 1971–1983. [Google Scholar] [CrossRef]
- Yue, D.; Pandya, S.; You, F. Integrating Hybrid Life Cycle Assessment with Multiobjective Optimization: A Modeling Framework. Environ. Sci. Technol. 2016, 50, 1501–1509. [Google Scholar] [CrossRef] [PubMed]
- Dresselhaus, M.S.; Thomas, I.L. Alternative energy technologies. Nature 2001, 414, 332–337. [Google Scholar] [CrossRef] [PubMed]
- Bolat, P.; Thiel, C. Hydrogen supply chain architecture for bottom-up energy systems models. Part 1: Developing pathways. Int. J. Hydrogen Energy 2014, 39, 8881–8897. [Google Scholar] [CrossRef]
- Bolat, P.; Thiel, C. Hydrogen supply chain architecture for bottom-up energy systems models. Part 2: Techno-economic inputs for hydrogen production pathways. Int. J. Hydrogen Energy 2014, 39, 8898–8925. [Google Scholar] [CrossRef]
- Sgobbi, A.; Nijs, W.; De Miglio, R.; Chiodi, A.; Gargiulo, M.; Thiel, C. How far away is hydrogen? Its role in the medium and long-term decarbonisation of the European energy system. Int. J. Hydrogen Energy 2016, 41, 19–35. [Google Scholar] [CrossRef]
- Kahouli-Brahmi, S. Technological learning in energy–environment–economy modelling: A survey. Energy Policy 2008, 36, 138–162. [Google Scholar] [CrossRef]
- Rubin, E.S.; Azevedo, I.M.L.; Jaramillo, P.; Yeh, S. A review of learning rates for electricity supply technologies. Energy Policy 2015, 86, 198–218. [Google Scholar] [CrossRef]
- Van den Broek, M.; Berghout, N.; Rubin, E.S. The potential of renewables versus natural gas with CO2 capture and storage for power generation under CO2 constraints. Renew. Sustain. Energy Rev. 2015, 49, 1296–1322. [Google Scholar] [CrossRef]
- Van den Broek, M.; Hoefnagels, R.; Rubin, E.; Turkenburg, W.; Faaij, A. Effects of technological learning on future cost and performance of power plants with CO2 capture. Prog. Energy Combust. Sci. 2009, 35, 457–480. [Google Scholar] [CrossRef]
- Creutzig, F.; Agoston, P.; Goldschmidt, J.C.; Luderer, G.; Nemet, G.; Pietzcker, R.C. The underestimated potential of solar energy to mitigate climate change. Nat. Energy 2017, 2, 17140. [Google Scholar] [CrossRef]
- Huang, W.; Chen, W.; Anandarajah, G. The role of technology diffusion in a decarbonizing world to limit global warming to well below 2 °C: An assessment with application of Global TIMES model. Appl. Energy 2017, 208, 291–301. [Google Scholar] [CrossRef]
- Patel, S. Duke Hit Hard by Exorbitant O&M Costs at Edwardsport IGCC Facility. Power Magzine. 27 September 2018. Available online: https://www.powermag.com/duke-hit-hard-by-exorbitant-om-costs-at-edwardsport-igcc-facility/?pagenum=3 (accessed on 12 October 2018).
- Wagman, D. Three Factors that Doomed kemper County IGCC. IEEE Spectrum. 30 June 2017. Available online: https://spectrum.ieee.org/energywise/energy/fossil-fuels/the-three-factors-that-doomed-kemper-county-igcc (accessed on 12 October 2018).
- Reiner, D.M. Learning through a portfolio of carbon capture and storage demonstration projects. Nat. Energy 2016, 1, 15011. [Google Scholar] [CrossRef]
- Adams, T.A., II; Hoseinzade, L.; Madabhushi, P.B.; Okeke, I.J. Comparison of CO2 Capture Approaches for Fossil-Based Power Generation: Review and Meta-Study. Processes 2017, 5, 44. [Google Scholar] [CrossRef]
- Voll, A.; Sorda, G.; Optehostert, F.; Madlener, R.; Marquardt, W. Integration of market dynamics into the design of biofuel processes. Comput. Aided Chem. Eng. 2012, 31, 850–854. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).