Eden Model Simulation of Re-Epithelialization and Angiogenesis of an Epidermal Wound

Abstract

Among the vital processes of cutaneous wound healing are epithelialization and angiogenesis. The former leads to the successful closure of the wound while the latter ensures that nutrients are delivered to the wound region during and after healing is completed. These processes are regulated by various cytokines and growth factors that subtend their proliferation and migration into the wound region until full healing is attained. Wound epithelialization can be enhanced by the administration of epidermal stem cells (ESC) or impaired by the presence of an infection. This paper uses the Eden model of a growing cluster to independently simulate the processes of epithelialization and angiogenesis in a cutaneous wound for different geometries. Further, simulations illustrating bacterial infection are provided. Our simulation results demonstrate contraction and closure for any wound geometry due to a collective migration of epidermal cells from the wound edge in fractal form and the diffusion of capillary sprouts with the laying down of capillary blocks behind moving tips into the wound area.

1. Introduction

Many different biological interactions involving various cells and chemicals are responsible for the healing of skin wounds. The healing process occurs in three phases, namely the inflammation phase, the proliferation phase, and the maturation phase [1,2]. The first phase of wound healing prepares the wound bed for the growth of new tissue. It begins with blood coagulation, yielding a temporary closure in the form of a blood clot. Here, immune cells such as neutrophils and monocytes are recruited into the wound region to keep it clean from dead tissues and any pathogens [3,4]. The second phase constitutes replacement of lost tissue to fill and cover the entire wound space. This is achieved by the secretion of growth factors that promote the recruitment and proliferation of vascular endothelial cells and epidermal cells. In the final phase, the newly constructed epidermis and the dermis are gradually strengthened, enabling the replaced skin at the wound site to resume its normal function. Though the above phases are distinct, they do overlap.

A skin wound can only be considered healed when there is successful wound closure, that is, full re-epithelialization. Epithelialization is an important component of wound healing and it depends on keratinocytes which are the major cellular component of the epidermis. The keratinocytes are responsible for restoring the epidermis after injury, and when activated by multiple stimuli, including epidermal growth factor (EGF), they begin to differentiate. Epithelialization occurs through migration and proliferation. When stimulated, keratinocytes at the wound edge loosen their adhesion to each other and to the basal layer of the epidermis. The free keratinocytes start migrating into the wound area. The keratinocytes behind the migrating front proliferate so there are enough cells available to cover the wound [5,6]. The epithelialization process is impaired in all types of chronic wounds irrespective of the underlying course [7].

An injury of the skin is associated with the disruption of blood vessels. The repair of damaged vasculature ensures the supply of nutrients from the bloodstream to support the increased local cell activity necessary for healing to occur and be maintained. The process by which new blood capillaries grow into a wound space after injury is known as angiogenesis and it is an important part of the proliferative phase of healing. The healing of a cutaneous wound cannot occur without angiogenesis. In order to repair the vasculature, secreted stimuli, including vascular endothelial growth factor (VEGF), trigger the endothelial cells (ECs) of blood vessels near the wound edge to migrate and proliferate into the wound region. New vasculature is formed as capillary sprouts within the wound merge, forming closed loops [8,9].

Migration and proliferation of keratinocytes and ECs leads to wound contraction and eventual closure when other required processes are progressing normally. Any interruption to epithelialization and angiogenesis such as an infection or other underlying physiological problem renders the wound as chronic. Experimental studies, including computational simulations, do provide more understanding of the wound healing process and can be used to enhance treatment planning for skin wounds in a clinical setting. Models for cluster aggregation have been considered for a variety of natural phenomena. Among the earliest is the Eden model [10,11,12], which was initially formulated to simulate tumor formation and has been used to describe different biological growth processes [13,14,15]. Variants of the Eden model have been used to study wound healing [16,17]. A modified version of the Eden model, an inverted approach in which clusters shrink, is used to model epidermal wound healing in Savakis and Maggelakis [16], with focus on re-epithelialization. A variant of diffusion limited aggregation (DLA) that produces more realistic results compare to the Eden variant is also provided. In Callaghan et al. [17], a discrete stochastic model of wound healing, which when extended to 2 dimensions, becomes an Eden model is considered. The model focuses on the propagation of front epidermal cells into the wound space.

Other approaches have also been used to model wound healing such as agent based techniques [18,19,20,21]; conservation models in which species mass or momentum is conserved, mechanical models when chemical gradients are neglected, and mechanochemical models that incorporate chemical stimuli (see Jorgensen et al. [22] for a very comprehensive review and Valero et al. [23] detailing the challenges in modeling wound healing). While these methods have been successful in modeling certain aspects of wound healing, some do fall short in that even when formulated for higher dimensions, they only provide numerical computations for the 1-dimensional case. We remark here that 1-dimensional simulations of wound healing are often based on the simplified assumption of symmetry which indeed is usually for purposes of simplicity, analysis, computational expense, and reducing the number of parameters. In reality, even the most studied aspect of wound healing, which is epithelialization, has not been reproduced experimentally and there is no unified theoretical description of the processes involved [24]. Because wounds do not heal in a symmetric fashion but rather in a fractal-like manner, as some edges always heal faster than others, there is need for models that are a more biologically accurate representation of epithelialization and angiogenesis [25,26].

In this paper, we use the Eden model which is a very simple and basic aggregation method to address two different aspects of wound healing, namely, re-epithelialization, and angiogenesis. The Eden model is 2-dimensional, readily applicable to any geometry, and does not require symmetry or the need for the wound shape to be retained as healing progresses. We begin by considering a variant of the Eden model for epithelialization that adapts and improves on the shrinking cluster approach in [16], and that demonstrates wound contraction and closure. The procedure is augmented and used to study the pathologies of different types of bacterial infections and their effect on wound re-epithelialization. Next, we turn our attention to develop a variant of the Eden model that addresses the first of five open problems in wound healing angiogenesis listed in the recent paper by Flegg et al. [27]. The first open problem is listed as, “developing more accurate representations of the behaviors of capillary tip and vessel densities, in the contexts of anastomosis, budding and vessel remodeling/maturation” [27]. The problem stated here is that of creating a model that demonstrate in at least 2-dimensions the effective laying down of capillary blocks behind moving capillary sprouts and tips. We use the Eden model to address this process of angiogenesis, that recreates a damaged vasculature and further investigates it in the presence of a bacterial infection. The simplicity of implementation and computational efficiency of our Eden variants are attributed to the few parameters required by the procedures.

2. The Eden Model

The simplest version of the Eden model grows clusters beginning with a seed at a predetermined location on a two dimensional lattice by adding particles to its perimeter. The cluster is composed of occupied sites and growth sites that are connected. Any two sites are connected if they are immediate neighbors. The neighbors of an occupied site can be defined as, (i) the four growth sites bordering it up, down, left, and right (Figure 1a); or (ii) the eight growth sites bordering it with the diagonals included (Figure 1b); or (iii) using a prescribed angle (Figure 1c). Each growth site on the perimeter has an equal chance of being selected and added to the cluster.

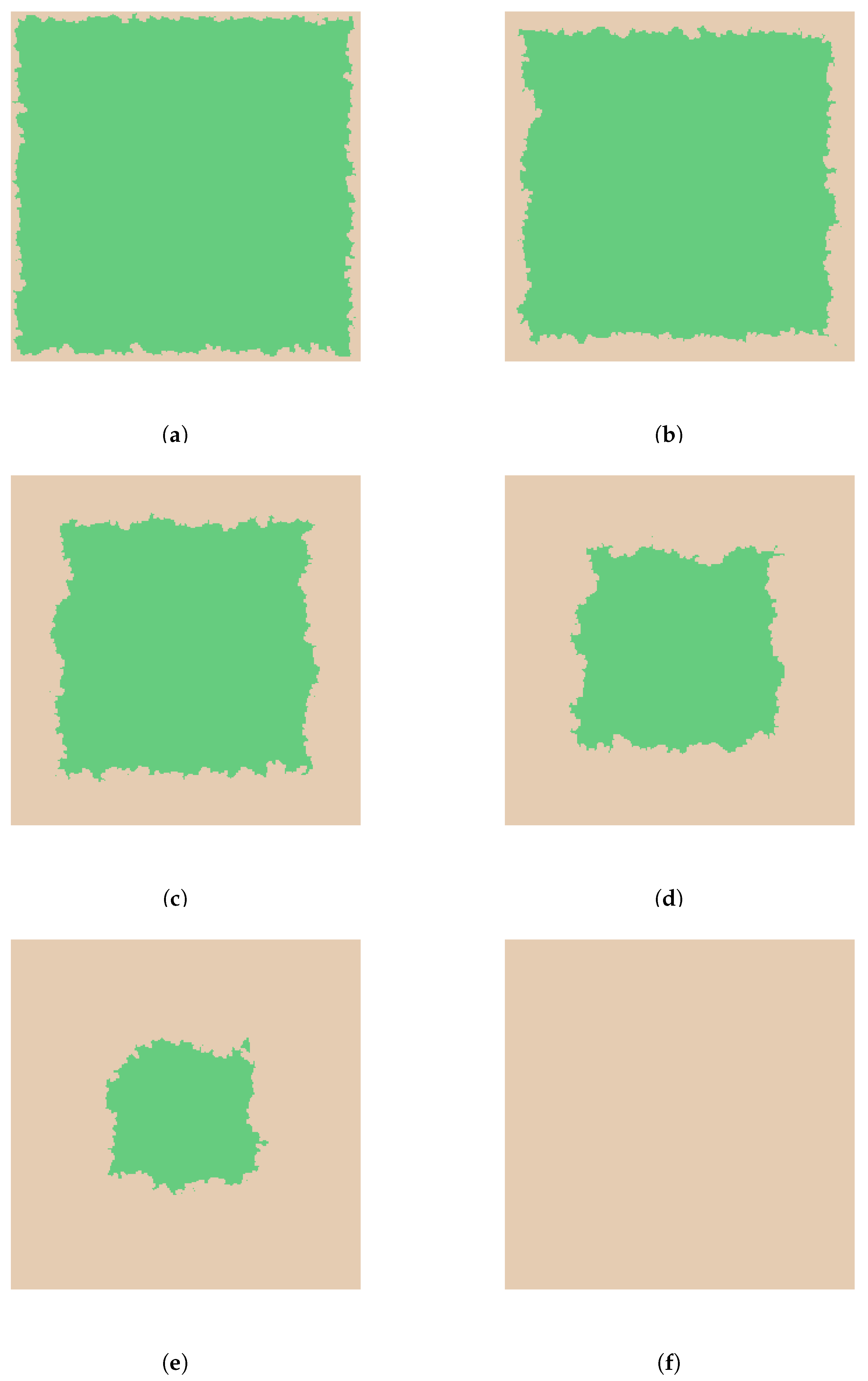
2.1. Epithelialization Algorithm:

The re-epithelialization process is described below and a pseudocode for a growing cluster is provided in Appendix A.

• The size of the simulation cell and the domain where growth occurs is defined for a given wound geometry. Each cell is represented by a grid point on the surface. A grid point can only be occupied by a single cell and is either seeded (occupied) or a growth site (empty).
• Since wounds heal by contraction, grid points on the wound border are delineated and initial seeds are placed along the wound edge. A cell, that is an occupied grid point, can only grow into an immediate neighboring vacant growth site.
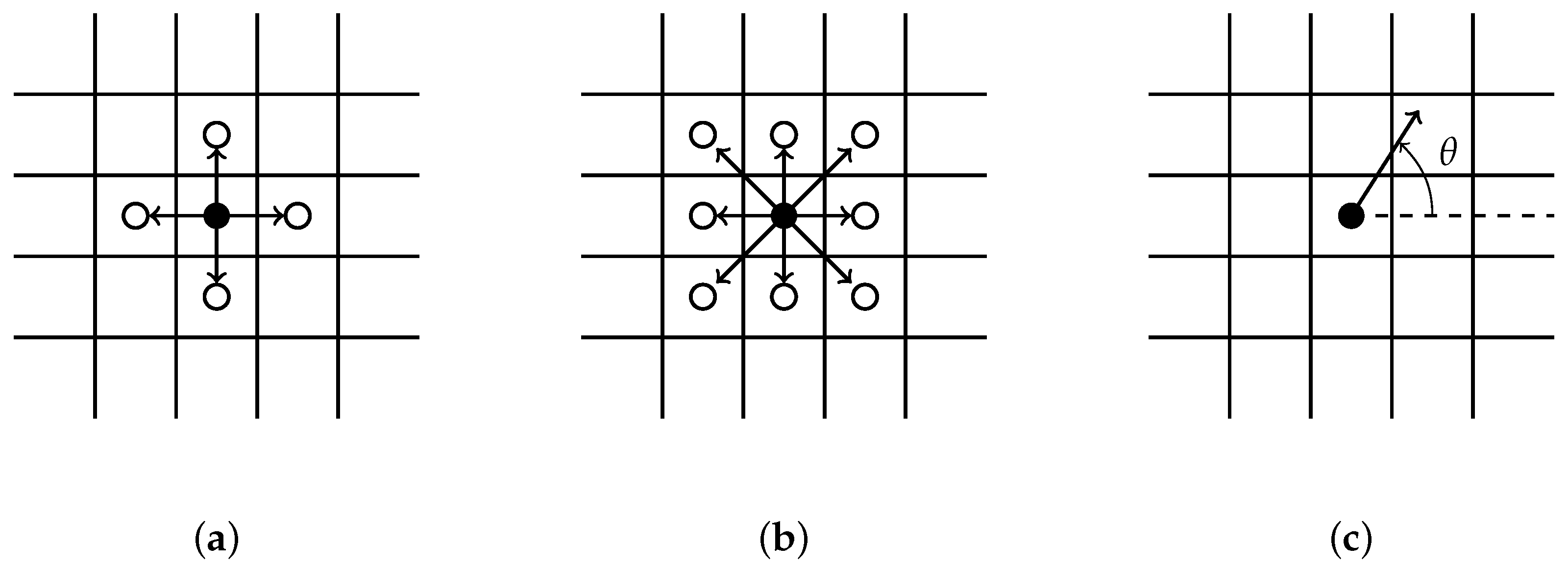
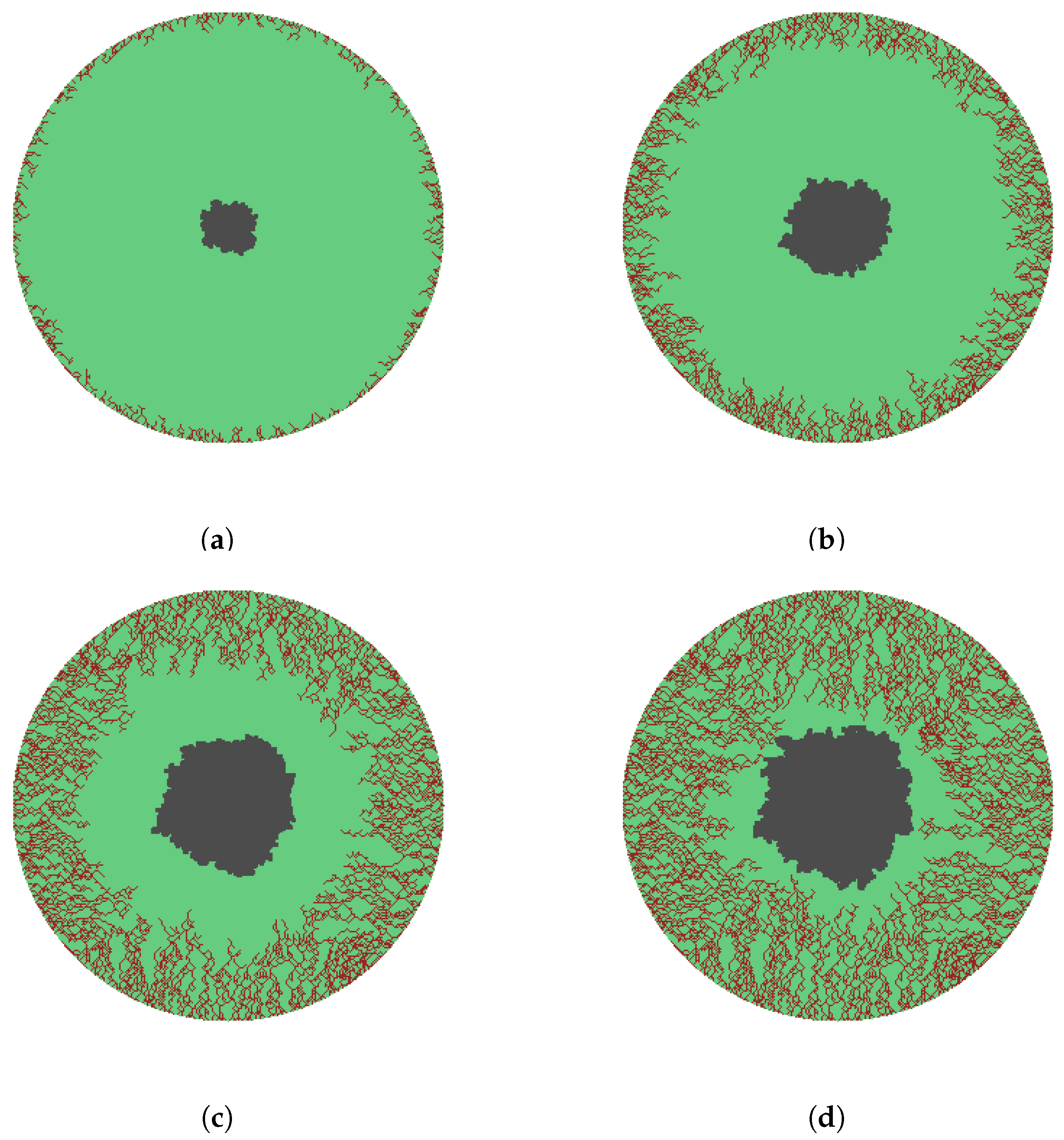
• All clusters originating along the wound edge grow simultaneously into wound space. An occupied grid point for each cluster grows by randomly selecting a growth site from its immediate neighbors. We implement a selection criterion that includes diagonal representation, illustrated by Figure 1b.
• A cell stops growing in a randomly chosen direction if there is no available immediate growth site. Growth terminates when all possible directions are exhausted. The growth process ends and wound considered re- epithelialized when the entire domain is covered.

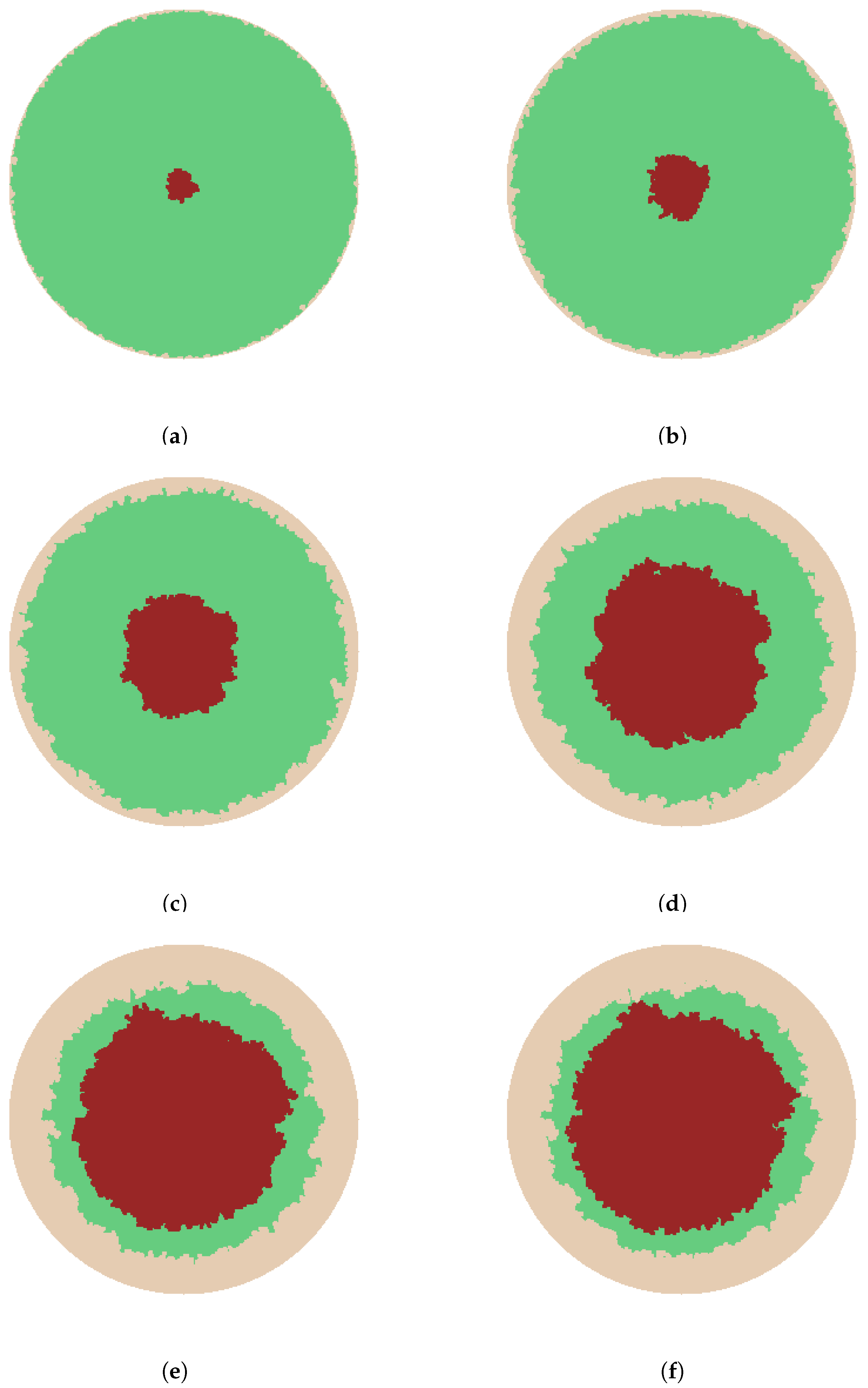
2.2. Angiogenesis Algorithm

The reconstruction of the vasculature is a diffusive process and is described below and a pseudocode for building the capillary network is provided in Appendix B.

• The size of the simulation cell and the domain where growth occurs is defined for a given wound geometry. The growth rate of sprouts per generation, that is the length (number of grid spaces) is specified. The branching and merging conditions are also specified.
• Initial seeds representing capillary sprouts are placed at prescribed points along the wound border. All sprouts originating along the wound edge grow simultaneously into wound space.
• Each sprout randomly selects a single direction for growth from possible growth sites. Two random growth directions are chosen when conditions for branching are satisfied. A backward growth direction is not allowed.
• The sprouts grow by diffusing into the wound space depending on the growth rate, the branching and merging strategies. The vascularization process is completed when sprouts reach the center of the wound.

Remark: The above algorithms are augmented to simulated bacterial infection of the wound. The bacteria seed can be placed anywhere within the wound space and allowed to grow as a cluster. For simplicity the bacteria is grown from the center of the wound for all the infection simulations reported in this work. The growth rate parameter for a given entity is defined as the number of grid points per step (or iteration). The branching criterion for capillary sprouts is given by the number of steps before branching. Capillary sprouts merge forming blocks when they come across each other.

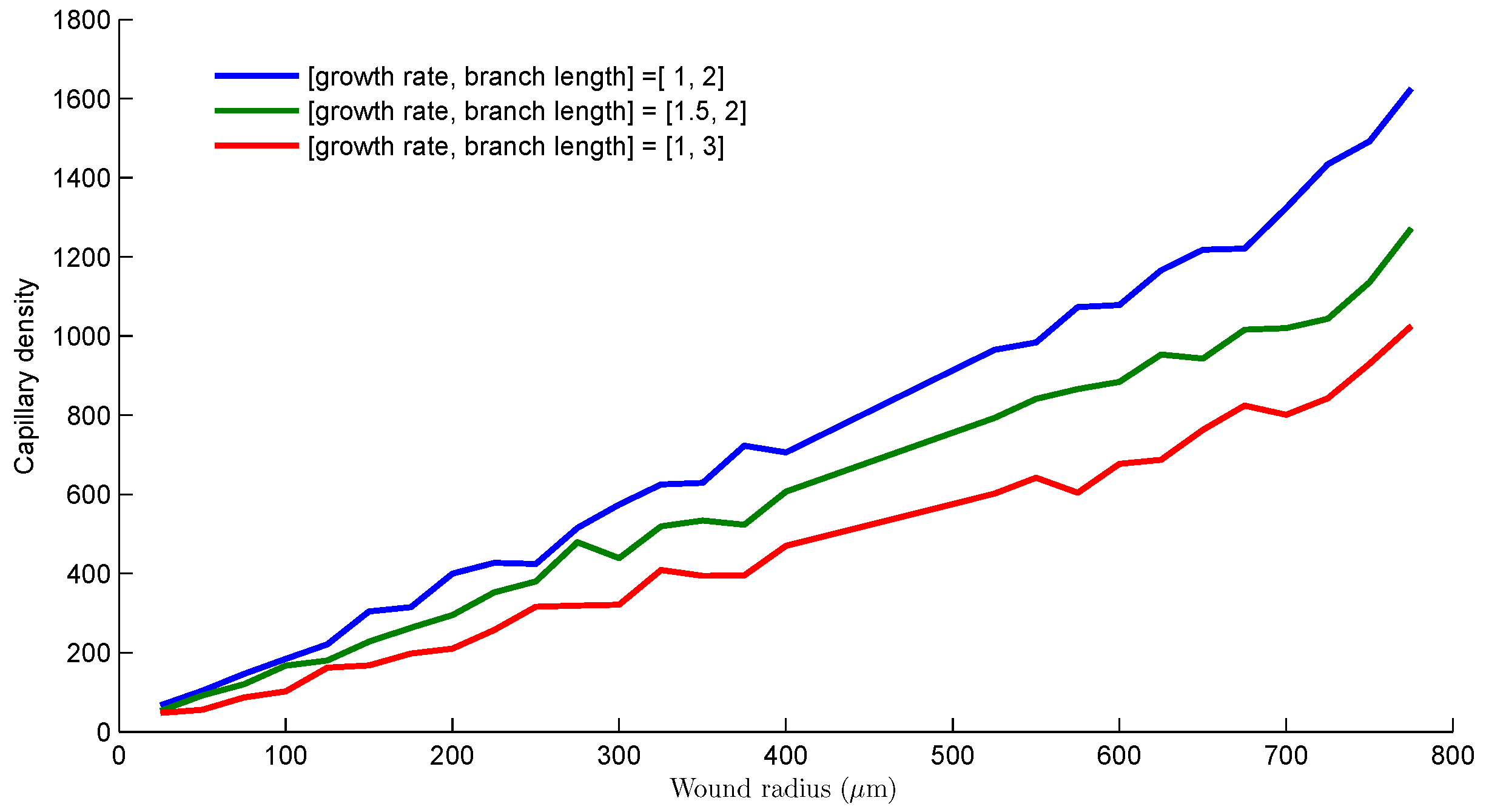
3. Results and Discussion

The healing of an epidermal wound occurs in a contraction manner leading to wound closure and the effectual restoration of skin function at the wound site. The variants of Eden model for cluster growth presented above are employed in this section to simulate the processes of epithelialization and angiogenesis. We present simulations for uninfected and infected wounds with circular and square geometries. All simulations are presented for 2-dimensional skin wounds. Unless otherwise started, the diameter of circular wounds reported below was set at $300\mathsf{\mu }$m and the edge of a square wound was also set at $300\mathsf{\mu }$m. Results for much larger dimensions are reported in this work. The model does not distinctively incorporate growth factors and therefore assumes that all processes required for epithelialization or angiogenesis are satisfied.

We begin by considering re-epithelialization for uninfected wounds. The simulations in Figure 2 and Figure 3 illustrate epithelialization for wounds with circular and square geometries respectively. For each geometry, seeds generated along the entire wound edge grow in cluster formation into the available wound space till it is completely filled. For both geometries, it is clearly observed that epithelialization originating from the wound’s edge propagates towards the wound center. Figure 2a–f and Figure 3a–f respectively show different stages during the contraction process, representing $10\%$, $25\%$, $50\%$, $70\%$, $85\%$, and $100\%$ re-epithelialization.

By taking each grid point to represent the diameter of a cell, the computed average radius of the unhealed wound space for the simulations in Figure 2a–f are respectively, 120 $\mathsf{\mu }$m, 110 $\mathsf{\mu }$m, 90 $\mathsf{\mu }$m, 67 $\mathsf{\mu }$m, 49 $\mathsf{\mu }$m, and 0 $\mathsf{\mu }$m, where 0 $\mathsf{\mu }$m implies total re-epithelialization of the wound. The computed average length of an edge for the simulations in Figure 3a–f are respectively, 285 $\mathsf{\mu }$m, 262 $\mathsf{\mu }$m, 219 $\mathsf{\mu }$m, 169 $\mathsf{\mu }$m, 120 $\mathsf{\mu }$m, and 0 $\mathsf{\mu }$m, where again 0 $\mathsf{\mu }$, indicates complete re-epithelialization.

Figure 2 shows that the wound with a circular geometry initially maintains its shape in the form of a fractal and eventually losing it as healing progresses. This is in agreement with experimental results and continuum models for circular wounds [28,29]. A more realistic collective migration of epidermal cells into the wound area compare to the continuum model in [30] for circular wounds is observed. The wound with a square geometry also retains its shape in the form of a fractal at the onset of epithelialization but quickly loses it. The strong deformity in the square wound shape as epithelialization evolves correlates with experimental observations that the areas of highest curvature, the corners in this case, are healed first [31] in epidermal wounds. While the wound geometries in both cases are symmetric, it can be closely observed that re-epithelialization does not occur equally from opposite edges of the wound. The Eden model captures very well the asymmetric manner of healing which is also an accurate biological representation of epithelialization.

It is not uncommon for wounds to be contaminated by microbes. In the absence of significant immune system response, the microbes can grow and colonize the wound, and depending on their virulence lead to an infection. Bacterial infections usually stall the healing rate of a wound. The next set of simulations presented in Figure 4 and Figure 5, predict the progression of wound infection by bacteria for circular and square wound geometries respectively. Epithelialization and bacteria growth are demonstrated.

Similar to the uninfected wounds, epithelialization starts from the initial wound edge and propagates toward the center of the wound for any geometry. In our simulations, the bacteria growth starts at the center of the wound. We remark here that, bacteria seed can be made to grow from any point within the wound space.

When compared to the initial wound size, re-epithelialization and bacteria burden at the different stages in Figure 4 are approximately (a) $3\%$ and $1\%$; (b) $6\%$ and $3\%$; (c) $15\%$ and $12\%$; (d) $29\%$ and $27\%$; (e) $39\%$ and $38\%$; and (f) $42\%$ and $40\%$. In a like manner, re-epithelialization and bacteria burden at the different stages in Figure 5 are approximately (a) $3\%$ and $1\%$; (b) $6\%$ and $3\%$; (c) $15\%$ and $12\%$; (d) $29\%$ and $27\%$; (e) $39\%$ and $38\%$; and (f) $42\%$ and $40\%$. The simulation of all growth processes stops immediately bacteria first come in contact with epithelialization. At this point we consider the healing process stalled and this is depicted in Figure 4f and Figure 5f for the circular and square wound respectively.

The algorithm provides the ability to alter the growth rates of different processes. The simulations in Figure 6 illustrate the stalling process of an infected wound for different bacteria growth rates. We consider cases in which the bacteria growth rate is half that of epithelialization Figure 6a, the same as that of epithelialization Figure 6b, one and half times that of epithelialization Figure 6c and twice that of epithelialization Figure 6d. The growth rate for epithelialization in these cases was set at two grid points per time step. It can be seen from

Table 1. Epithelialization and infection for stalled wounds.

Bacteria Growth Rate	Amount of Epithelialization	Amount of Bacteria
half that of epithelialization growth rate	53%	27%
equal to the epithelialization growth rate	42%	41%
one and half times epithelialization growth rate	34%	46%
twice that of epithelialization growth rate	30%	53%

that the smaller the bacteria growth rate, the more the amount of epithelialization before healing stalls, and the higher the bacteria growth rate, the lower the amount of epithelialization before stalling occurs. The amount of epithelialization and bacteria growths are approximately the same when the growth rates are equal. Although all the wounds in Figure 6 are chronic, the degree of severity which is associated with higher bacteria growth rates increases from Figure 6a through Figure 6d.

Bacterial contamination and colonization does not always lead to an infection and stalled healing. To simulate such a wound using our model, the epithelialization growth rate is made bigger than that of bacteria and a stopping criteria that requires full epithelialization of the wound space is prescribed. A higher weighted epithelialization rate enables wound space occupied by harmless bacteria to be replaced by epidermal cells during wound contraction. Further, to simulate wound infection that results in the degradation of epithelialization process, a higher weight is assigned to the bacteria growth rate, and a prescribed stopping criterion that permits the growing bacteria to occupy the original wound space.

Formation of new blood vessels is critical for normal skin wound healing. We next turn our attention to simulating angiogenesis for circular and square wound geometries. We recall here that the growth of blood vessels into the wound region begins when endothelial cells of blood vessels near the wound edge are triggered by growth factors such as VEGF. Capillary tips grow into the wound space producing sprouts that with due course merge to form capillary blocks. The reconstructed capillary network or vasculature is vital for supplying essential nutrients and oxygen to cells and tissues in the wound space.

The simulations in Figure 7 and Figure 8 show the evolution of capillary tips, capillary sprouts and capillary blocks for wounds circular and square geometries respectively. The capillary tips together with the sprouts were assigned a growth rate of two grid points which we call a step. The sprouts were allowed to branch out on attaining a length of two steps. The new vasculature is constructed with the growth direction of capillary tips randomly chosen and biased with orientation towards the center of the wound. Figure 7a–d and Figure 8a–d, representing $25\%$, $50\%$, $75\%$, and $100\%$ vascularization, respectively, depict the propagation of capillary tips, capillary sprouts, and capillary blocks at various stages of angiogenesis process. The wound space is completely vascularized in Figure 7d and Figure 8d.

We emphasize here that the majority of mathematical models of angiogenesis are 1-dimensional [27,32,33]. Even when formulated for higher dimensions, numerical computations are usually provided in 1-dimension [34,35,36]. Further, the simulations usually provide only counts for density of capillary tips or sprouts or blocks [27]. The 2-dimensional formulation presented in the current paper is novel in that it accomplishes the effective laying down of blood vessels behind moving capillary tips, leading to wound contraction and closure for any given geometry. A close visual examination of the 2-dimensional simulations of angiogenesis shown in Figure 8 are in close agreement with experimental results reported in Machado et al. [37] for square wounds. The results are also a more biological accurate representation of angiogenesis compared to simulations in [37]. The 2-dimensional simulations of angiogenesis shown in Figure 7 for circular wounds are more realistic compared to the attempt by Valero et al. [38] that describes capillary density in isolation.

The results in Figure 9 provides a measure for the capillary densities at different distances from the center of a wound with circular geometry. The capillary density was measured along the circumference of the circle for each radius. We investigate different growth strategies, that is, capillary growth steps and lengths before branching, by considering 3 cases. The first case has capillary growth rate of 1 step and branch length of 2 steps.

The second case has capillary growth rate of 1.5 steps and growth rate of 2 steps. Finally, the third case has capillary growth rate of 1 step and branch length of 3 steps. We simulate a circular wound of radius $800\mathsf{\mu }$m. For all cases, Figure 9 shows an almost linear relationship between capillary density and distance from the wound center. The capillary density decreases as the wound contracts. The first case produces the most capillary density while the third case consisting of 3 steps before branching yielded the least amount of capillaries as angiogenesis progresses from the wound edge towards the center. The performance of second case though having a higher growth rate is sandwiched between the others. A drop in the capillary density profiles when sprout growth step or branch length is increased suggest that the sooner capillary sprouts branch out, the richer the capillary network generated. This result provides an insight into the structure of vascular systems in general, asserting that a coarse vasculature is associated with long sprout strands while a dense vasculature is characterized by short sprout strands.

Finally, the results in Figure 10 and Figure 11 simulate angiogenesis in the presence of a bacteria infection. The bacteria cluster was also grown from the center of the wound. The amount of vascularization and bacteria burden with respect to the initial size at the different stages of the circular wound in Figure 10 are approximately (a) $11\%$ and $2\%$; (b) $31\%$ and $6\%$; (c) $59\%$ and $10\%$; and (d) $77\%$ and $13\%$. Similarly, amount of vascularization and bacteria burden at the different stages of the square wound in Figure 11 are approximately (a) $10\%$ and $1\%$; (b) $38\%$ and $4\%$; (c) $59\%$ and $8\%$; and (d) $78\%$ and $11\%$. The simulation of capillary and bacteria growths stops when bacteria comes in contact with capillary sprouts. We again consider the healing process stalled and this is depicted in Figure 10d and Figure 11d for the circular and square wound respectively.

4. Conclusions

In this paper, we developed variants of the Eden model of cluster aggregation for skin wounds, focusing on the processes of epithelialization and angiogenesis. The important stochastic growths exhibited by both epithelialization and angiogenesis are captured for circular and square wounds. The models’ simulations mimic the contraction and closure of skin wounds. The models can be easily extended to wounds of any geometry. For a normal wound, epithelialization is observed to migrate towards the wound center in the form of a fractal that resembles the original shape of the wound in the early stages of the healing process. Further, in the case of epithelialization, the model was augmented by introducing bacteria growth on the wound surface. The interaction of the bacteria which leads to delayed healing was observed to be mostly dependent on the virulence of the bacteria. Our 2-dimensional model for wound vascularization addresses an open problem in wound healing and therefore fills an acute gap that most existing models for angiogenesis have been unable to do. The model provides an essential framework for building blood vessels behind moving capillary tips for any wound geometry. Further, by observing that early branching leads to the production of a denser capillary network, our simulation for angiogenesis sheds more light into the structure of vascularized systems other than wounds. Simulations of the model also demonstrate that bacterial infection leads to a delay in the reconstruction of the vasculature.