Glycosylation Flux Analysis of Immunoglobulin G in Chinese Hamster Ovary Perfusion Cell Culture
Abstract
1. Introduction
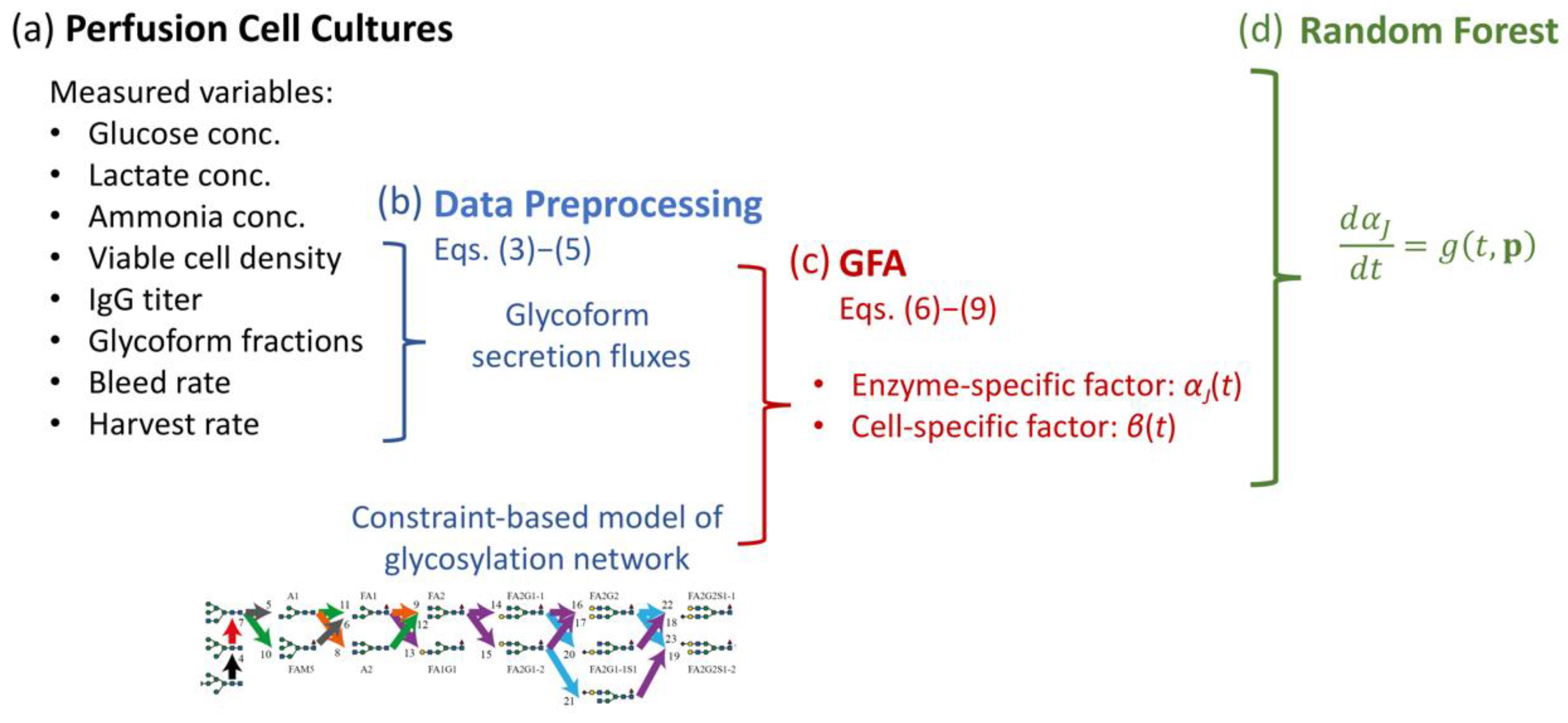
2. Materials and Methods
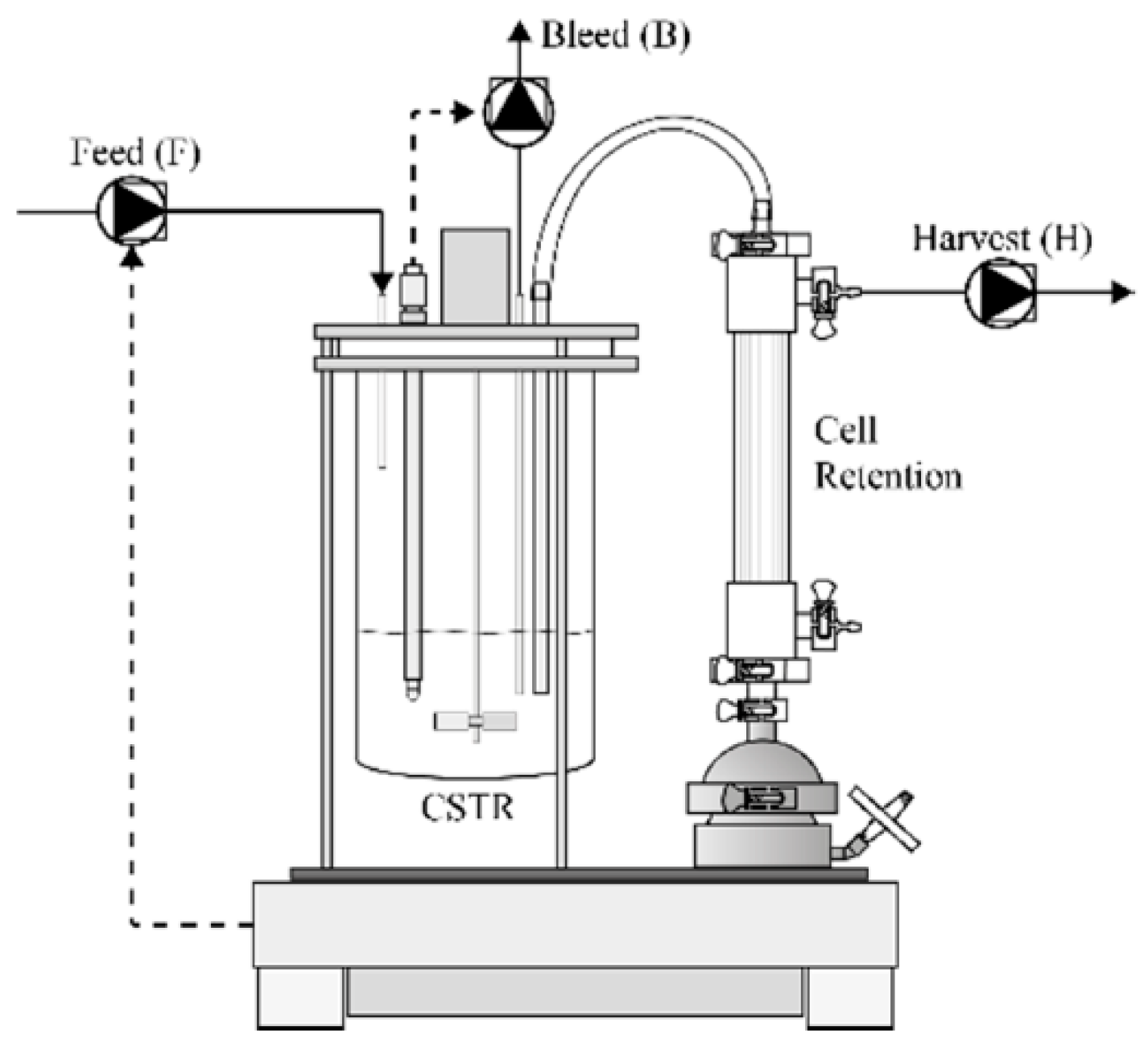
2.1. Continuous Perfusion Cell Cultures
2.2. Estimation of Secretion and Uptake Fluxes
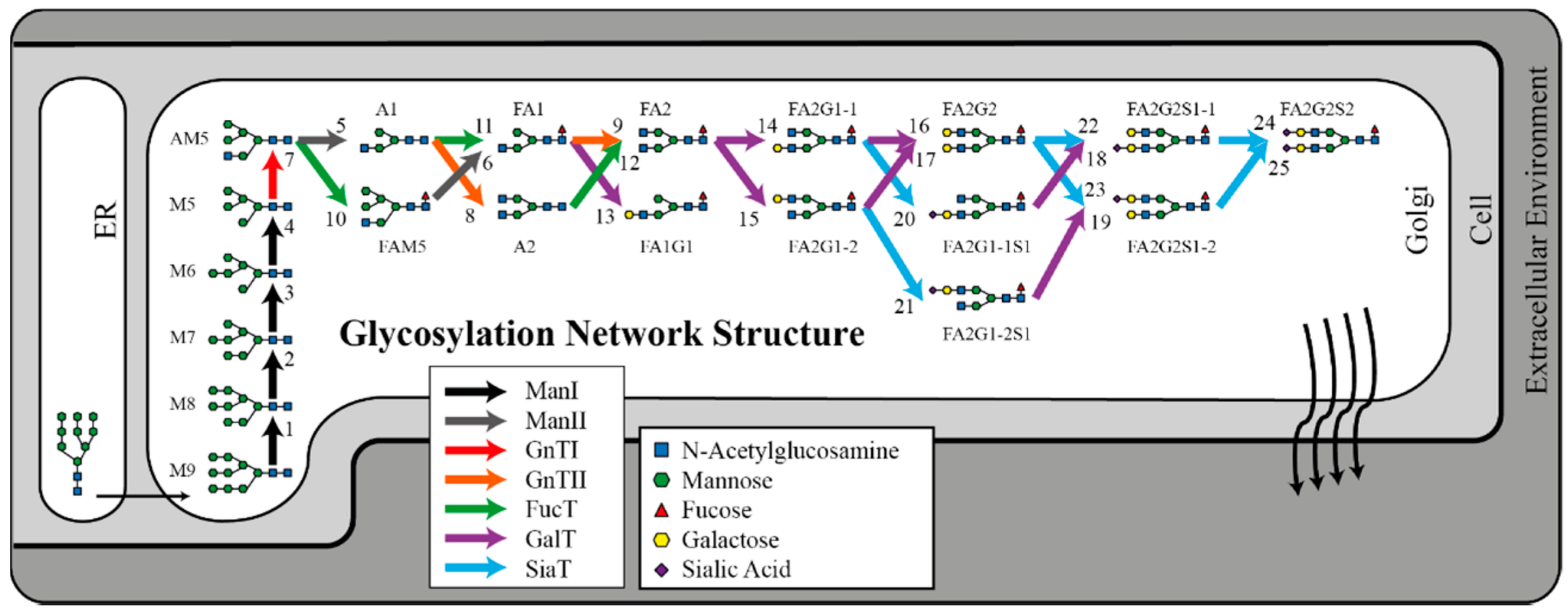
2.3. Glycosylation Flux Analysis
- (1)
- generate a uniformly distributed random vector of within a biologically feasible range (),
- (2)
- given from step (1), solve for or update using Equation (10),
- (3)
- given from step (2), solve for or update using Equation (11), and
- (4)
- repeat steps (2) and (3) until the change of as described in Equation (9) becomes smaller than a threshold (default 10−10).
2.4. Random Forest for Regression
3. Results
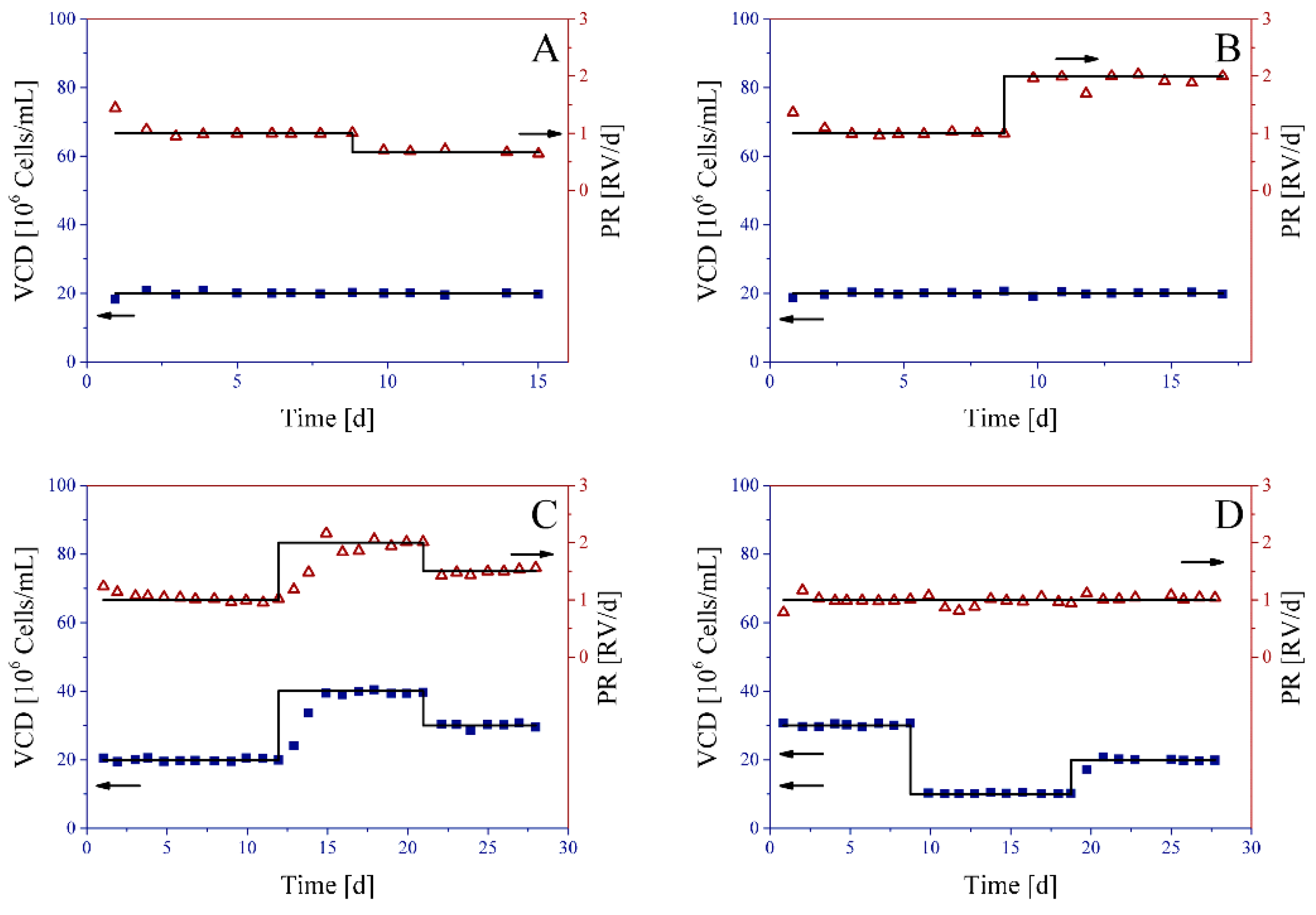
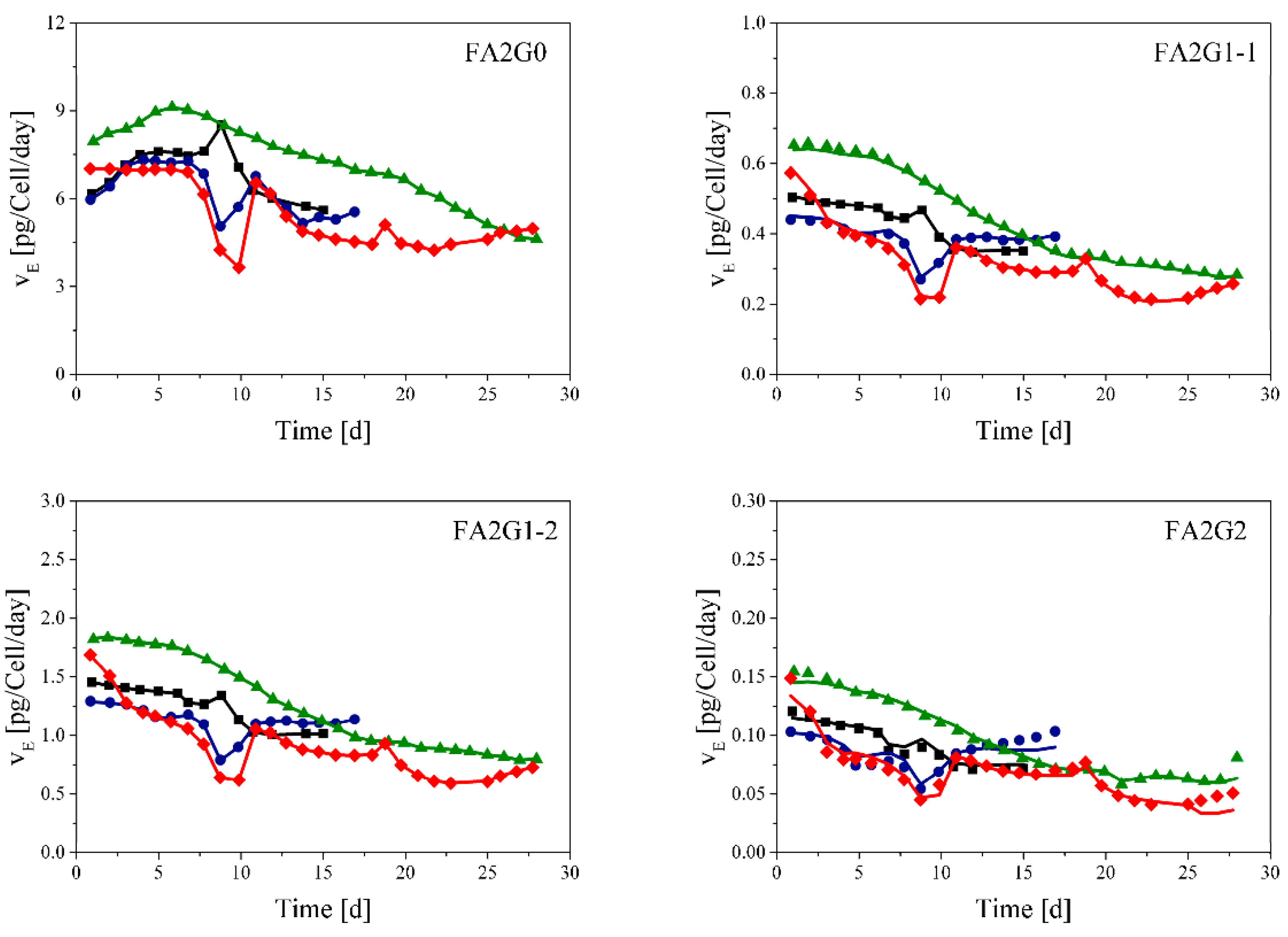
3.1. Perfusion Cell Culture Experiments
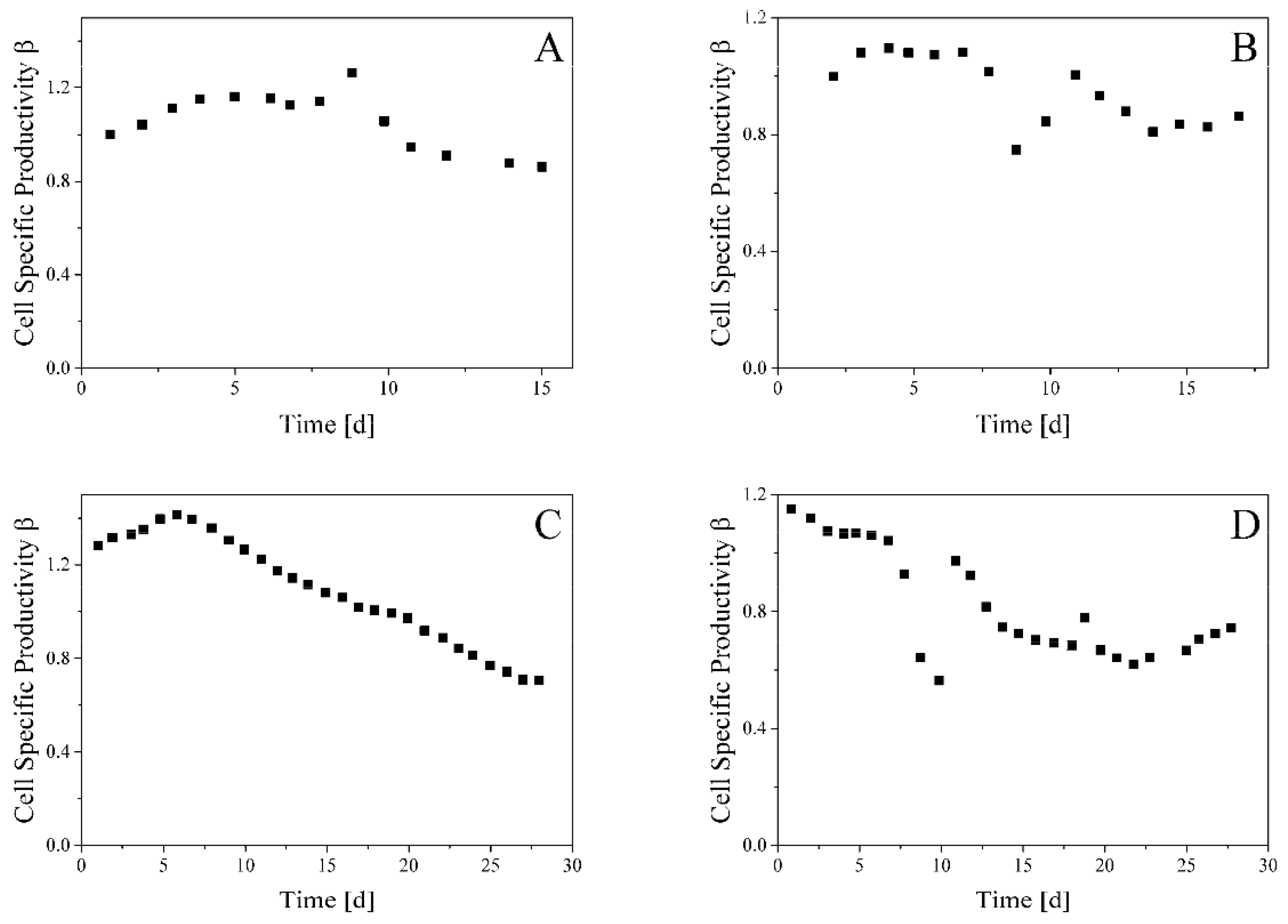
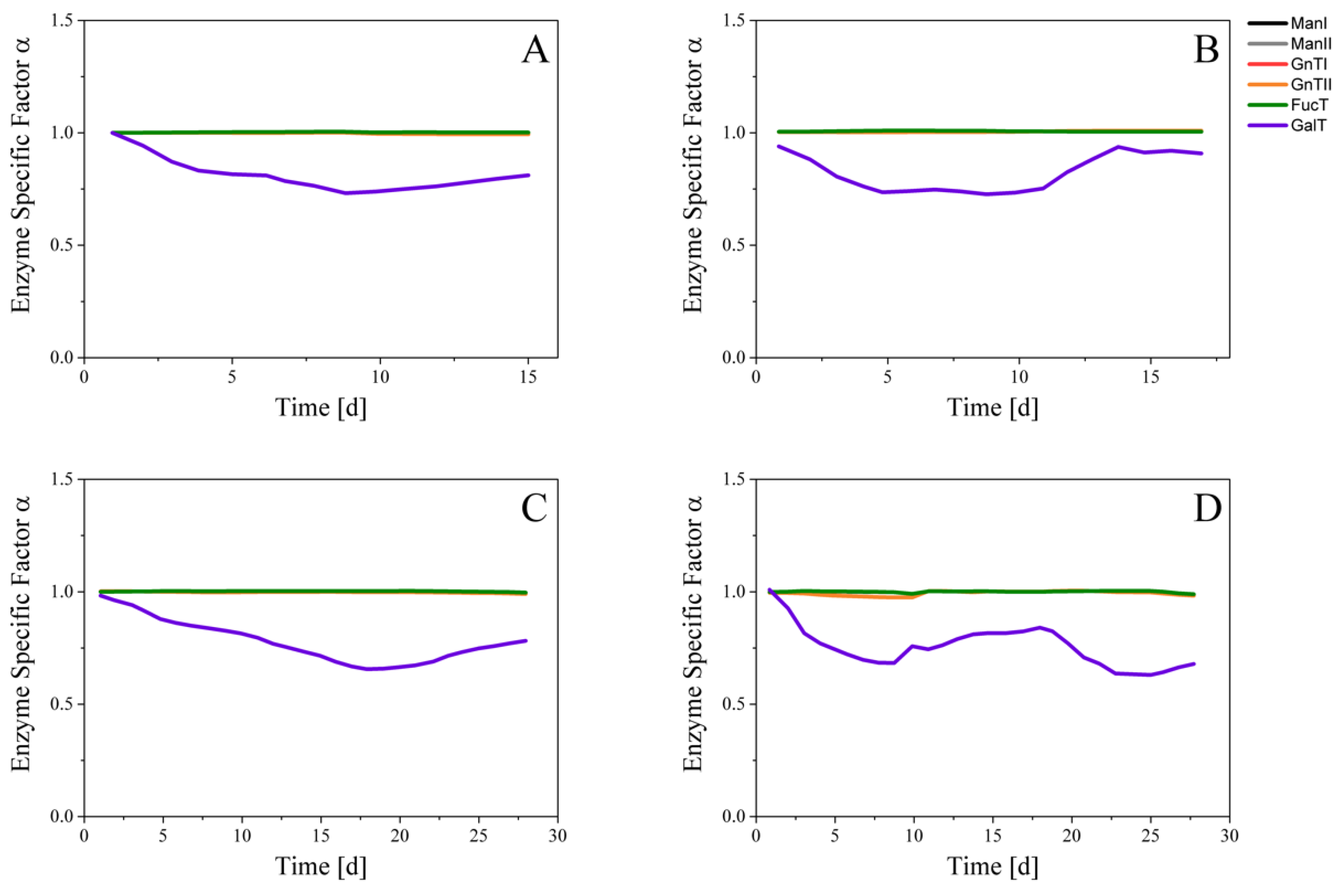
3.2. Glycosylation Flux Analysis
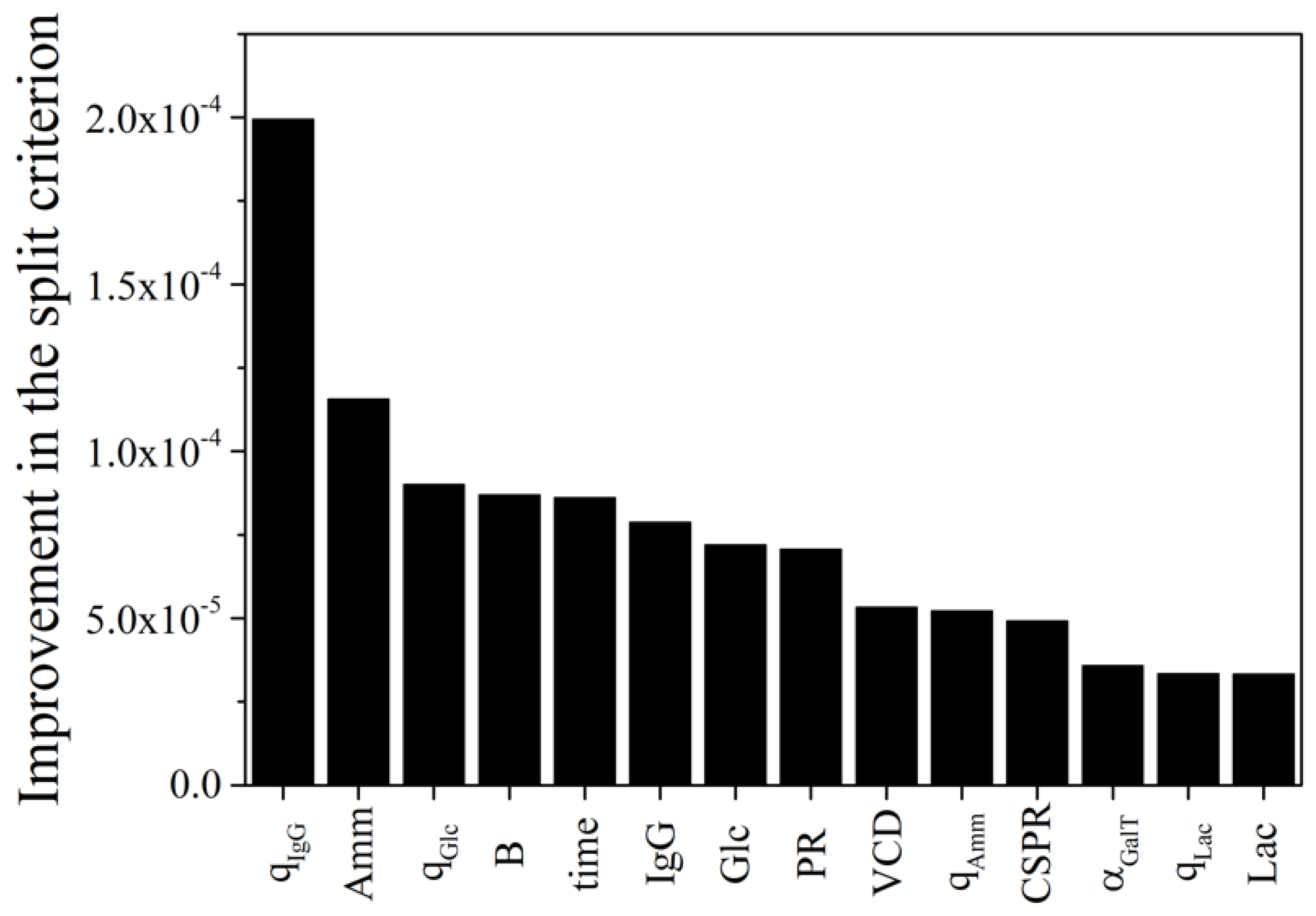
3.3. Effects of Process Parameters on Glycosylation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ecker, D.M.; Jones, S.D.; Levine, H.L. The therapeutic monoclonal antibody market. MAbs 2015, 7, 9–14. [Google Scholar] [CrossRef] [PubMed]
- Kelley, B. Industrialization of MAb production technology. MAbs 2009, 1, 443–452. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Vijayasankaran, N.; Shen, A.; Kiss, R.; Amanullah, A. Cell culture processes for monoclonal antibody production. MAbs 2010, 2, 466–479. [Google Scholar] [CrossRef] [PubMed]
- Rathore, A.S. Roadmap for implementation of quality by design (QbD) for biotechnology products. Trends Biotechnol. 2009, 27, 546–553. [Google Scholar] [CrossRef] [PubMed]
- Food and Drug Administration. FDA Guidance for Industry. PAT—A Framework for Innovative Pharmaceutical Development, Manufacturing, and Quality Assurance; Food and Drug Administration: Rockville, MD, USA, 2004.
- Reay, D.; Ramshaw, C.; Harvey, A. Process Intensification: Engineering for Efficiency, Sustainability and Flexibility, 2nd ed.; Elsevier: New York, NY, USA, 2013. [Google Scholar]
- Boedeker, B.G.D. Recombinant factor VIII (Kogenate®) for the treatment of Hemophilia A: The first and only world-wide licensed recombinant protein produced in high-throughput perfusion culture. In Modern Biopharmaceuticals; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2013; pp. 429–443. [Google Scholar]
- Clincke, M.F.; Molleryd, C.; Zhang, Y.; Lindskog, E.; Walsh, K.; Chotteau, V. Very high density of CHO cells in perfusion by ATF or TFF in WAVE bioreactorTM, Part I: Effect of the cell density on the process. Biotechnol. Prog. 2013, 29, 754–767. [Google Scholar] [CrossRef] [PubMed]
- Meuwly, F.; Weber, U.; Ziegler, T.; Gervais, A.; Mastrangeli, R.; Crisci, C.; Rossi, M.; Bernard, A.; von Stockar, U.; Kadouri, A. Conversion of a CHO cell culture process from perfusion to fed-batch technology without altering product quality. J. Biotechnol. 2006, 123, 106–116. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.-Y.; Kwon, Y.-B.; Cho, J.-M.; Park, K.-H.; Chang, S.-J.; Kim, D.-I. Effect of process change from perfusion to fed-batch on product comparability for biosimilar monoclonal antibody. Process Biochem. 2012, 47, 1411–1418. [Google Scholar] [CrossRef]
- Ryll, T.; Dutina, G.; Reyes, A.; Gunson, J.; Krummen, L.; Etcheverry, T. Performance of small-scale CHO perfusion cultures using an acoustic cell filtration device for cell retention: Characterization of separation efficiency and impact of perfusion on product quality. Biotechnol. Bioeng. 2000, 69, 440–449. [Google Scholar] [CrossRef]
- Lüllau, E.; Kanttinen, A.; Hassel, J.; Berg, M.; Haag-Alvarsson, A.; Cederbrant, K.; Greenberg, B.; Fenge, C.; Schweikart, F. Comparison of Batch and Perfusion Culture in Combination with Pilot-Scale Expanded Bed Purification for the Production of Soluble Recombinant β-Secretase. Biotechnol. Prog. 2003, 19, 37–44. [Google Scholar] [CrossRef] [PubMed]
- Lipscomb, M.L.; Palomares, L.A.; Hernández, V.; Ramírez, O.T.; Kompala, D.S. Effect of production method and gene amplification on the glycosylation pattern of a secreted reporter protein in CHO cells. Biotechnol. Prog. 2005, 21, 40–49. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, C.; Zheng, C.; Chen, Y.; Huang, Z.; Wang, Y.; Fu, Q.; Zeng, C.; Wu, T.; Yang, L.; Qi, N. Different fermentation processes produced variants of an anti-CD52 monoclonal antibody that have divergent in vitro and in vivo characteristics. Appl. Microbiol. Biotechnol. 2017, 101, 5997–6006. [Google Scholar] [CrossRef] [PubMed]
- Karst, D.J.; Steinebach, F.; Morbidelli, M. Continuous integrated manufacturing of therapeutic proteins. Curr. Opin. Biotechnol. 2018, 53, 76–84. [Google Scholar] [CrossRef] [PubMed]
- Berger, M.; Kaup, M.; Blanchard, V. Protein glycosylation and its impact on biotechnology. In Genomics and Systems Biology of Mammalian Cell Culture; Hu, W.S., Zeng, A.-P., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 165–185. [Google Scholar]
- Aebi, M. N-linked protein glycosylation in the ER. Biochim. Biophys. Acta-Mol. Cell Res. 2013, 1833, 2430–2437. [Google Scholar] [CrossRef] [PubMed]
- Solá, R.J.; Griebenow, K. Glycosylation of therapeutic proteins: An effective strategy to optimize efficacy. BioDrugs 2010, 24, 9–21. [Google Scholar] [CrossRef] [PubMed]
- Jefferis, R. Glycosylation as a strategy to improve antibody-based therapeutics. Nat. Rev. 2009, 8, 226–234. [Google Scholar] [CrossRef] [PubMed]
- Goh, J.S.Y.; Liu, Y.; Liu, H.; Chan, K.F.; Wan, C.; Teo, G.; Zhou, X.; Xie, F.; Zhang, P.; Zhang, Y.; et al. Highly sialylated recombinant human erythropoietin production in large-scale perfusion bioreactor utilizing CHO-gmt4 (JW152) with restored GnT I function. Biotechnol. J. 2014, 9, 100–109. [Google Scholar] [CrossRef] [PubMed]
- Harding, F.A.; Stickler, M.M.; Razo, J.; DuBridge, R.B. The immunogenicity of humanized and fully human antibodies: Residual immunogenicity resides in the CDR regions. MAbs 2010, 2, 256–265. [Google Scholar] [CrossRef] [PubMed]
- Matasci, M.; Hacker, D.L.; Baldi, L.; Wurm, F.M. Protein therapeutics Recombinant therapeutic protein production in cultivated mammalian cells: Current status and future prospects. Drug Discov. Today Technol. 2008, 5, 37–42. [Google Scholar] [CrossRef] [PubMed]
- Jayapal, K.P.; Wlaschin, K.F.; Hu, W.-S.; Yap, M.G.S. Recombinant protein therapeutics from CHO cells—20 years and counting. Chem. Eng. Prog. 2007, 103, 40–47. [Google Scholar]
- Wright, A.; Morrison, S.L. Effect of glycosylation on antibody function: Implications for genetic engineering. Trends Biotechnol. 1997, 15, 26–32. [Google Scholar] [CrossRef]
- Moremen, K.W.; Ramiah, A.; Stuart, M.; Steel, J.; Meng, L.; Forouhar, F.; Moniz, H.A.; Gahlay, G.; Gao, Z.; Chapla, D.; et al. Expression system for structural and functional studies of human glycosylation enzymes. Nat. Chem. Biol. 2017, 14, 156–162. [Google Scholar] [CrossRef] [PubMed]
- Radhakrishnan, D.; Robinson, A.S.; Ogunnaike, B.A. Controlling the glycosylation profile in mAbs using time-dependent media supplementation. Antibodies 2018, 7, 1. [Google Scholar] [CrossRef]
- Ivarsson, M.; Villiger, T.K.; Morbidelli, M.; Soos, M. Evaluating the impact of cell culture process parameters on monoclonal antibody N-glycosylation. J. Biotechnol. 2014, 188, 88–96. [Google Scholar] [CrossRef] [PubMed]
- Varki, A. Biological roles of oligosaccharides: All of the theories are correct. Glycobiology 1993, 3, 97–130. [Google Scholar] [CrossRef] [PubMed]
- Umaña, P.; Bailey, J.E. A Mathematical model of N-linked glycoform biosynthesis. Biotechnol. Bioeng. 1997, 55, 890–908. [Google Scholar] [CrossRef]
- Krambeck, F.J.; Bennun, S.V.; Narang, S.; Choi, S.; Yarema, K.J.; Betenbaugh, M.J. A mathematical model to derive N-glycan structures and cellular enzyme activities from mass spectrometric data. Glycobiology 2009, 19, 1163–1175. [Google Scholar] [CrossRef] [PubMed]
- Jimenez del Val, I.; Nagy, J.M.; Kontoravdi, C. A dynamic mathematical model for monoclonal antibody N-linked glycosylation and nucleotide sugar donor transport within a maturing Golgi apparatus. Biotechnol. Prog. 2011, 27, 1730–1743. [Google Scholar] [CrossRef] [PubMed]
- Jiménez del Val, I.; Constantinou, A.; Dell, A.; Haslam, S.; Polizzi, K.M.; Kontoravdi, C. A quantitative and mechanistic model for monoclonal antibody glycosylation as a function of nutrient availability during cell culture. BMC Proc. 2013, 7, O10. [Google Scholar] [CrossRef]
- Jedrzejewski, P.M.; Jiménez del Val, I.; Constantinou, A.; Dell, A.; Haslam, S.M.; Polizzi, K.M.; Kontoravdi, C. Towards controling the glycoform: A model framework linking extracellular metabolites to antibody glycosylation. Int. J. Mol. Sci. 2014, 15, 4492–4522. [Google Scholar] [CrossRef] [PubMed]
- Spahn, P.N.; Hansen, A.H.; Henning, G.; Arnsdorf, J.; Kildegaard, H.F.; Lewis, N.E.; Arnsdorf, J.; Kildegaard, H.F.; Lewis, N.E.; Markov, A. A markov chain model for N-linked protein glycosylation—Towards a low-parameter tool for model-driven. Metab. Eng. 2015, 33, 52–66. [Google Scholar] [CrossRef] [PubMed]
- Spahn, P.N.; Hansen, A.H.; Kol, S.; Voldborg, B.; Lewis, N.E. Predictive glycoengineering of biosimilars using a Markov chain glycosylation model. Biotechnol. J. 2017, 12, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Hutter, S.; Villiger, T.K.; Brühlmann, D.; Stettler, M.; Broly, H.; Soos, M.; Gunawan, R. Glycosylation flux analysis reveals dynamic changes of intracellular glycosylation flux distribution in Chinese hamster ovary fed-batch cultures. Metab. Eng. 2017, 43, 9–20. [Google Scholar] [CrossRef] [PubMed]
- Antoniewicz, M.R. Methods and advances in metabolic flux analysis: A mini-review. J. Ind. Microbiol. Biotechnol. 2015, 42, 317–325. [Google Scholar] [CrossRef] [PubMed]
- Wolf, M. Development and Optimization of Mammalian Cell Perfusion Cultures for Continuous Biomanufacturing. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2018. [Google Scholar]
- Karst, D.J.; Serra, E.; Villiger, T.K.; Soos, M.; Morbidelli, M. Characterization and comparison of ATF and TFF in stirred bioreactors for continuous mammalian cell culture processes. Biochem. Eng. J. 2016, 110, 17–26. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Villiger, T.K.; Scibona, E.; Stettler, M.; Broly, H.; Morbidelli, M.; Soos, M. Controlling the time evolution of mAb N-linkedglycosylation—Part II: Model-based predictions. Biotechnol. Prog. 2016, 32, 1135–1148. [Google Scholar] [CrossRef] [PubMed]
- Egea, J.A.; Henriques, D.; Cokelaer, T.; Villaverde, A.F.; MacNamara, A.; Danciu, D.-P.; Banga, J.R.; Saez-Rodriguez, J. MEIGO: An open-source software suite based on metaheuristics for global optimization in systems biology and bioinformatics. BMC Bioinform. 2014, 15, 136. [Google Scholar] [CrossRef] [PubMed]
- Del Val, I.J.; Polizzi, K.M.; Kontoravdi, C. A theoretical estimate for nucleotide sugar demand towards Chines Hamster Ovary cellular glycosylation. Sci. Rep. 2016, 6, 28547. [Google Scholar] [CrossRef] [PubMed]
- Gawlitzek, M.; Ryll, T.; Lofgren, J.; Sliwkowski, M.B. Ammonium alters N-glycan structures of recombinant TNFR-IgG: Degradative versus biosynthetic mechanisms. Biotechnol. Bioeng. 2000, 68, 637–646. [Google Scholar] [CrossRef]
- Walther, J.; Lu, J.; Hollenbach, M.; Yu, M.; Hwang, C.; McLarty, J.; Brower, K. Perfusion cell culture decreases process and product heterogeneity in a head-to-head comparison with fed-batch. Biotechnol. J. 2018, e1700733. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hutter, S.; Wolf, M.; Papili Gao, N.; Lepori, D.; Schweigler, T.; Morbidelli, M.; Gunawan, R. Glycosylation Flux Analysis of Immunoglobulin G in Chinese Hamster Ovary Perfusion Cell Culture. Processes 2018, 6, 176. https://doi.org/10.3390/pr6100176
Hutter S, Wolf M, Papili Gao N, Lepori D, Schweigler T, Morbidelli M, Gunawan R. Glycosylation Flux Analysis of Immunoglobulin G in Chinese Hamster Ovary Perfusion Cell Culture. Processes. 2018; 6(10):176. https://doi.org/10.3390/pr6100176
Chicago/Turabian StyleHutter, Sandro, Moritz Wolf, Nan Papili Gao, Dario Lepori, Thea Schweigler, Massimo Morbidelli, and Rudiyanto Gunawan. 2018. "Glycosylation Flux Analysis of Immunoglobulin G in Chinese Hamster Ovary Perfusion Cell Culture" Processes 6, no. 10: 176. https://doi.org/10.3390/pr6100176
APA StyleHutter, S., Wolf, M., Papili Gao, N., Lepori, D., Schweigler, T., Morbidelli, M., & Gunawan, R. (2018). Glycosylation Flux Analysis of Immunoglobulin G in Chinese Hamster Ovary Perfusion Cell Culture. Processes, 6(10), 176. https://doi.org/10.3390/pr6100176





