Abstract
The bottleneck in creating dynamic models of biological networks and processes often lies in estimating unknown kinetic model parameters from experimental data. In this regard, experimental conditions have a strong influence on parameter identifiability and should therefore be optimized to give the maximum information for parameter estimation. Existing model-based design of experiment (MBDOE) methods commonly rely on the Fisher information matrix (FIM) for defining a metric of data informativeness. When the model behavior is highly nonlinear, FIM-based criteria may lead to suboptimal designs, as the FIM only accounts for the linear variation in the model outputs with respect to the parameters. In this work, we developed a multi-objective optimization (MOO) MBDOE, for which the model nonlinearity was taken into consideration through the use of curvature. The proposed MOO MBDOE involved maximizing data informativeness using a FIM-based metric and at the same time minimizing the model curvature. We demonstrated the advantages of the MOO MBDOE over existing FIM-based and other curvature-based MBDOEs in an application to the kinetic modeling of fed-batch fermentation of baker’s yeast.
1. Introduction
Dynamic models of biological networks and processes are often created to gain a better understanding of the system behavior. The creation of dynamic biological models requires the values of kinetic parameters, many of which are system-specific and typically not known a priori. These parameters are commonly estimated by calibrating model simulations to the available experimental data. Such parameter fitting is known to be challenging, as there often exist multiple parameter combinations that fit the available data equally well; that is, the model parameters are not identifiable [1,2,3,4,5]. While there exist a number of reasons for such lack of parameter identifiability, experimental conditions have a strong influence on this issue and thus should be carefully designed. In addition, biological experiments and data collection are often costly and time-consuming, further motivating the need for well-planned experiments that would give the maximum information given finite resources.
Model-based design of experiments (MBDOEs) offer a means for integrating dynamic modeling with experimental efforts, as illustrated by the iterative procedure in Figure 1. The role of the model here is to capture the knowledge and information about the system up to a given iteration. By using MBDOEs, one could harness this knowledge to guide experiments in the next iteration. MBDOE techniques have been used extensively for chemical process modeling [6], and more recently, they have been applied to the modeling of cellular processes [7,8]. For the purpose of parameter estimation, experiments are generally designed to improve the precision of the estimated parameters. In this regard, the Fisher information matrix (FIM), whose inverse provides an estimate of the lower bound of parameter variance-covariance by the Cramér-Rao inequality [9], has been commonly used to define the objective function in the optimal experimental design (see [8] and references therein). Since the turn of the century, FIM-based MBDOE methods have had newfound applications in the emerging area of systems biology [10,11,12,13,14,15,16]. Besides FIM, Bayesian approaches have also been used for MBDOEs, where given the prior distribution of the model parameters, experiments are designed to minimize the posterior parameter variance [8]. Bayesian MBDOE strategies have been applied to the modeling of biological networks for reducing parametric uncertainty [17,18,19]. While our work is concerned with MBDOEs for the purpose of parameter estimation, MBDOE strategies have also been developed and applied for discriminating between biological model structures [20,21,22,23,24] and reducing cellular process output uncertainty [19,25,26].
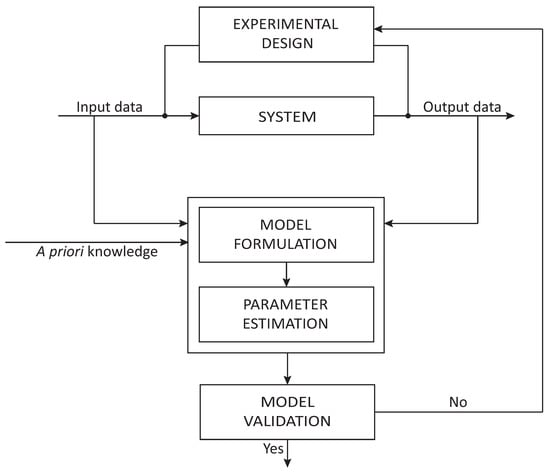
Figure 1.
Iterative model identification cycle. The model building process involves the following key steps: experimental design, model structure formulation, parameter estimation, and model validation.
In this work, we focused on FIM-based MBDOEs for parameter estimation. The FIM relies on a linear approximation of the model behavior as a function of the parameters. More precisely, the FIM is computed as a function of the first-order parametric sensitivity coefficients (Jacobian matrix) of model outputs. For systems with a high degree of nonlinearity, the optimal experimental design using the FIM may perform poorly [27]. For this reason, Bates and Watts proposed a MBDOE based on minimizing model curvature by using the second-order parametric sensitivities (Hessian matrix) [28]. Hamilton and Watts further introduced a design criterion, called Q-optimality, based on a quadratic approximation of the volume of the parameter confidence region [29]. More recently, Benabbas et al., proposed two curvature-based MBDOEs [30]. In one design, the authors used a minimization of the root mean square (RMS) of the Hessian matrix, while in another design, they employed a constrained optimization guaranteeing the RMS to be lower than a given level. While the second strategy using a curvature threshold was demonstrated to give more informative experiments, how to set the appropriate RMS threshold value in a particular application was not described.
Recently, Maheshwari et al. described a multi-objective optimization (MOO) formulation for optimizing the design of the experiment using a combination of FIM-based metric and parameter correlation [15]. Because parameter correlations could not account for model nonlinearity, the strategy has the same drawback as FIM-based methods when applied to nonlinear models. In this work, we proposed a MOO MBDOE method using a combination of a FIM criterion and model curvature. We demonstrated the advantages of the proposed MOO MBDOE over FIM-based and other curvature-based methods in an application to the kinetic modeling of the fed-batch fermentation of baker’s yeast [30,31].
2. Model-Based Optimal Design of Experiments
We assume that the experimental data are contaminated by additive random noise, as follows:
where and denote the mean of the measurement data and the random noise, respectively. When the total number of data points n is greater than the number of parameters p, spans a p-dimensional space , where
Here, denotes the state vector, denotes the parameter vector, denotes the input and denotes the vector of nonlinear model equations. The subspace is also called the expectation surface or the solution locus. For a dynamic system, the state is often described by a set of ordinary differential equations (ODEs):
The estimation of model parameters from a given set of data is typically formulated as a minimization of the weighted sum of squares of the difference between the model prediction and the measurement data . For example, the maximum likelihood estimator (MLE) of the model parameters for normally distributed data with known variance is given by the minimum of the following objective function:
When the model is a linear function of the parameters , , then the parameter estimates are given by . In this case, the MLE is the minimum variance unbiased estimator of , where the covariance matrix of the parameter estimates is given by . When the model is nonlinear (with respect to the parameters), the parameter estimates do not necessarily correspond to the minimum variance estimator. According to the Cramér-Rao inequality [9], the inverse of the FIM provides a lower bound for the covariance of the parameter estimates , that is
where is the first-order sensitivity matrix of with respect to the parameters .
On the basis of the Cramér-Rao inequality, the FIM has been commonly used as a criterion of data informativeness in MBDOEs. Many methods for MBDOEs, such as those listed in Table 1, are based on finding experimental conditions that optimize a FIM-based information metric. As shown in Equation (5), the FIM relies on a linearization of the model behavior with respect to the parameters. Essentially, the linearization replaces the expectation surface by its tangent plane at . The performance of the experimental design using a FIM-based criterion would therefore depend on whether (1) the model outputs vary proportionally with the parameter values (planar assumption), and (2) whether this proportionality is constant (uniform coordinate assumption) [32]. When the model is highly nonlinear with respect to the parameters, FIM-based MBDOEs may produce suboptimal designs [33,34]. A recent MOO MBDOE using a combination of a FIM criterion and parameter correlation has been shown to provide an improvement over FIM-based MBDOE methods [15]. However, this method also relies on the first-order parametric sensitivity matrix, and thus it could not account for model nonlinearity.

Table 1.
Model-based designs of experiments (MBDOEs) using the Fisher information matrix (FIM).
Curvature-based design of experiment methods such as the Q-optimality have been introduced to account for model nonlinearity by employing a second-order approximation of the model output. Here, the curvature of the expectation surface is captured using the second-order sensitivities of based on the Taylor series expansion:
where is the Hessian matrix. As mentioned in the Introduction, several curvature-based MBDOE methods are available, for example, by minimizing curvature or using a curvature threshold [30]. In this work, we employed a MOO approach based on curvatures for designing optimal experiments. The basic premise of our MBDOE is to select experimental conditions that maximize the informativeness of data and ensure that the model behaves relatively linearly with respect to the parameters. More specifically, our MBDOE uses two objective functions, the first of which involves the maximization of a FIM-based information metric, and the second of which involves the minimization of relative curvature measures [28]. The second objective function ensures that the FIM can provide a reliable measure of data informativeness.
2.1. Multi-Objective Design of Experiments Based on Curvatures
In this section, we derive the relative curvature measures by following the work of Bates and Watts [28]. We consider an arbitrary straight line in the parameter space passing through :
where is a non-zero vector. As the scalar parameter b varies, a curve is traced through the expectation surface, also referred to as the lifted line, according to
The tangent line of this curve at is given by
The set of all such tangent lines, that is, the column space of , describes the tangent (hyper)plane at .
Meanwhile, the curvature measures come from a quadratic approximation of . In this case, the acceleration of at b = 0 can be written as follows:
The acceleration vector can be subsequently decomposed into two components:
where at , is tangential to the tangent plane and is normal to the tangent plane. The tangential acceleration is also called the parameter-effect curvature [28] and provides a measure of nonlinearity along the parameter vector . The degree of the parameter-effect curvature can change upon reparameterization of the model. Meanwhile, the normal acceleration does not vary with model parameterization, and hence it is called the intrinsic curvature. Finally, the relative curvature measures in the direction of are given by [28,32]:
Below, we describe the decomposition of the Hessian into the tangential and the normal component. We consider the QR-factorization of the Jacobian , that is, . By rotating the parameter axes into , a new Jacobian matrix can be computed as , which comprises the first p column vectors of (i.e., ). The remaining column vectors of (i.e., ) are orthonormal to the tangent surface at . In the same manner, the Hessian matrix in the rotated axes can be written as , where and . The decomposition of the Hessian into the tangential and normal components is given by the following equation [28]:
The matrices and respectively correspond to the parameter-effect and intrinsic curvature components of the Hessian.
To normalize the relative curvatures in Equations (12) and (13), Bates and Watts [28] used the scaling factor , where and . Following the same procedure, we define the normalized relative curvatures as follows:
In addition, recasting in the rotated axes as , the tangent line will have a unit norm (i.e., ) when is a unit vector. The computation of and is thus simplified into
In the proposed experimental design, the maximum of these curvature measures are used, where
As mentioned above, in formulating the MOO for the design of experiments, two design criteria have been taken into account. The first is that the experiment should be designed to maximize the informativeness of the data for parameter estimation. In this case, we employ an information metric based on the FIM. Meanwhile, the second design criterion in the MOO aims to minimize both the parameter-effect and intrinsic curvatures. The MOO formulation offers certain advantages, for example, that there is no need to prioritize any one of the criteria beforehand. Instead, we generate the Pareto set or Pareto frontier representing the set of solutions for which we cannot improve the value of one objective function without negatively affecting the other(s) [35].
Considering the kinetic ODE model given in Equation (3), our multi-objective formulation using the D-optimal criterion is given by
subject to
where is the ith eigenvalue of the FIM (Equation (5)). The first objective function can be substituted with other FIM-based metrics (see Table 1). The parameter vector is either an initial guess of the parameter values or the parameter estimates from the current iteration of an iterative model identification procedure [6]. The decision variables may include the initial condition of the states , the sampling time points of measurements , and the dynamic input . In the case study below, we considered a control vector parametrization (CVP) of the input as illustrated in Figure 2.
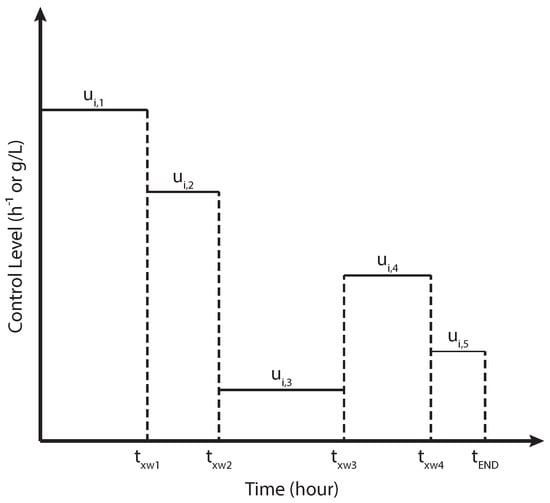
Figure 2.
Control vector parametrization of input profiles. In the baker yeast case study, we implemented piecewise constant input profiles with = [, , , , ] and four switching times: , , , and .
2.2. Numerical Implementation of the Curvature-Based MOO Design
As described in the previous section, the parameter-effect and intrinsic curvatures require the computation of the first- and second-order model sensitivities. For the ODE model in Equation (3), the first-order sensitivities can be calculated according to
The sensitivities in the above equation are normalized with respect to the parameter values. The last term on the right-hand side is the first-order sensitivities of the ODE model, which obey the following differential equation:
Here, we have assumed that is not part of the parameter estimation, but such an assumption can be easily relaxed. In the case study, the sensitivities were computed by solving the ODE in Equation (24) simultaneously to Equation (3), following a procedure known as the direct differential method [36]. Meanwhile, the Hessian matrix was approximated using a finite-difference method, as follows:
where is the jth elementary vector and uses 1% parameter perturbations (i.e., = 0.01). The second-order sensitivities above are also normalized with respect to the parameter values.
Meanwhile, the curvature measures and in Equations (19) and (20) were calculated from the Hessian matrix using the alternating least squares (ALS) method [37], an algorithm created to find the maximum singular value of a three-dimensional matrix. Based on the definitions in Equations (19) and (20), the maximum curvature measures can be determined by computing the maximum singular values of the matrices and , respectively. More specifically, we implemented the ALS method to solve for
where is either or . The ALS algorithm started with initial guess values of the vectors and and used the above equation to solve for one variable while fixing the other in an alternating manner. Zhang and Golub showed that the method linearly converges in a neighbourhood of the optimal solution [37].
In the case study, the MOO problem was solved using the non-dominated sorting genetic algorithm II (NSGAII) in MATLAB, producing a Pareto frontier in the space of the objective functions [38]. We employed a population size of 300 and set the number of generations to 50 times the number of parameters (i.e., 1450). We recasted a maximization of an objective function as the minimization of its negative counterpart. The optimal design was selected from the Pareto frontier by balancing the trade-offs among the objective functions. More specifically, we first normalized the objective functions such that their values on the Pareto frontier ranged between 0 and 1. Finally, we chose among the solutions on the Pareto frontier that which minimized the Euclidean distance of all (normalized) objective functions as the final design.
3. Results
3.1. MBDOEs of Baker Yeast Fermentation Model
We evaluated the performance of the proposed MBDOE in an application to a kinetic model of a fed-batch fermentation of baker’s yeast [30,31]. In addition to a D-optimal criterion, we also implemented A-optimal, E-optimal and modified E-optimal criteria (see Table 1) with our MOO MBDOE. We compared the performance of our method to other MBDOEs, including (a) FIM-based MBDOEs, that is, D-optimal, A-optimal, E-optimal and modified E-optimal designs; (b) a D-optimal design with a curvature threshold [30]; (c) a Q-optimal MBDOE [29]; and (d) a MOO MBDOE using parameter correlation [15]. In total, we applied and compared 14 MBDOE methods. For the optimizations in (a), (b) and (c), we employed the enhanced scatter search metaheuristic (eSSm) algorithm [39,40,41]. For the MOO in (d), we used the optimization algorithm and optimal Pareto point selection, as described in the previous section.
In the fed-batch fermenter model, cellular growth and product formation are captured by the biomass variable , which is assumed to rely on a single substrate variable . The fermenter operates at a constant temperature and the feed is free from product. The model equations are given by
where the input is the dilution factor (in the range of 0.05–0.20 h) and the input is the substrate concentration in the feed (in the range of 5–35 g/L). In the model, the biomass growth follows Monod-type kinetics. The parameters and are the Monod kinetic parameters, is the yield coefficient, and is the cell death rate constant.
In the MBDOE, the design variables consisted of the initial condition of the biomass in the range between 1 and 10 g/L, 10 measurement sampling times (), and the inputs and . The piecewise-constant dynamic inputs were each parametrized using the CVP, as shown in Figure 2. Thus, the MOO was performed with 29 design parameters (, 10 ’s, 10 ’s, and 8 ’s). The length of the time interval between two successive measurement sampling points was constrained to be between 1 and 20 h, while that between two input switching times was bounded between 2 and 20 h. The calculations of the Jacobian and Hessian matrices in MBDOEs were made using parameter values [15,42], which were different from the “true” parameter values used for noisy data generation in the next section. The reason for using a different parameter set in the MBDOE to the true values was to emulate the typical scenario in practice, for which one would start only with an estimate or guess of the model parameters. Figure 3 and Figure 4 show the optimal dynamic inputs and data sampling times resulting from all the MBDOE methods mentioned above (see also the Pareto frontiers in Figures S1 and S2 in the Supplementary Materials). Meanwhile, Table 2 gives the optimal initial biomass concentration .
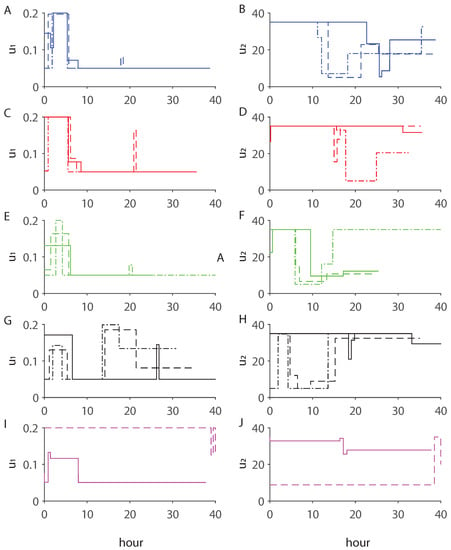
Figure 3.
Optimal dilution factor and feed substrate concentration. Optimal dilution factor ( in h, left panels) and feed substrate concentration ( in g/L, right panels). (A,B) D-optimal (blue). (C,D) A-optimal (red). (E,F) E-optimal (green). (G,H) modified E-optimal (black). In panels (A–H), the optimal and using Fisher information matrix (FIM)-based criteria are shown by solid line. Those using FIM-based criteria combined with curvatures are shown by dashed line, while those using FIM-based criteria combined with parameter correlation are drawn with dashed-dot line. (I–J) Threshold curvature (magenta, solid line), and Q-optimal design (magenta, dashed line).
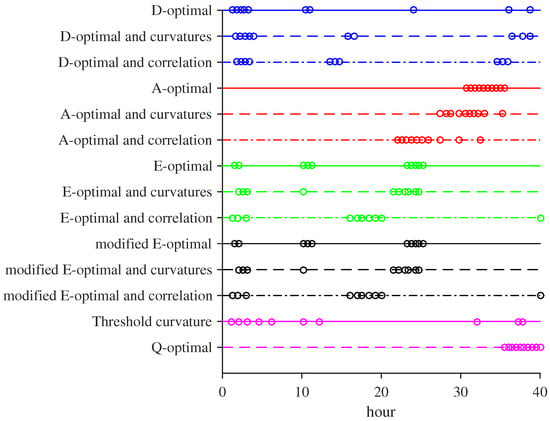
Figure 4.
Optimal sampling grid from model-based design of experiments (MBDOEs). Simple Fisher information matrix (FIM)-based criteria shown by continuous line, FIM-based criteria combined with curvatures by dashed line, and FIM-based criteria combined with parameter correlation by dashed-pointed line. Dots indicate the sampling times.

Table 2.
Optimal initial condition of biomass (g/L) from model-based design of experiments (MOO: multi-objective optimization).
3.2. Performance Evaluation
For each of the optimal experimental designs above, we generated in silico datasets by simulating the ODE model using the parameter values = [0.31, 0.18, 0.55, 0.05], as reported in previous publications [15,42]. We subsequently added independent and identically distributed (i.i.d.) Gaussian random white noise to the model simulations using a relative variance of 0.04 for both and [15,42]. For each in silico dataset, we then performed a parameter estimation using the resulting data ( and ) by maximum likelihood estimation, that is, by minimizing
We also employed the following constraints for in the optimization above:
and
Finding the globally optimal solution to the parameter estimation in Equation (4) is challenging. Here, we solved the constrained parameter optimization problem using the interior-point algorithm (implemented by the subroutine fmincon function in MATLAB) with the true parameter values as the initial guess. By employing the true values as the initial starting point of the optimization, we expected that the parameter accuracy would mainly be affected by the experimental design and not by the ability of the parameter optimization algorithm to find the globally optimal solution.
We repeated the in silico data generation and parameter estimation as described above 100 times, which resulted in a set of 100 parameter estimates. The performance of each MBDOE was assessed by the average accuracy of the parameter estimates, measured by the average of the normalized mean-square error (nMSE):
where
The variance of was computed using the set of 100 parameter estimates, while the bias was calculated as the difference between the average of and . Table 3 gives the average nMSE of the parameter estimates from each MBDOE under consideration.

Table 3.
Model-based design of experiment (MBDOE) performance on the fed-batch fermentation of baker’s yeast model. The overall parameter accuracy is represented by the average of the normalized mean-square error (nMSE). The reported parameter values and errors are the averages and standard deviations from 100 repeated runs of parameter estimation.
4. Discussion
As shown in Figure 3, the MBDOEs prescribed manipulating the input mostly at the beginning of the experiment and the input for the entire duration of the experiment. For the majority of the MBDOEs in this study, the optimal sampling times spread unevenly over the duration of the experiment (see Figure 4). A more detailed comparison between Figure 3 and Figure 4 showed that the optimal sampling points were typically placed before and after a change in the dynamic inputs and . The exception to this observation was for the optimal design using the A-optimal criterion, which gave the worst parameter accuracy among the MBDOEs considered.
The consideration of model curvature using the proposed MOO MBDOE generally led to improved parameter accuracy over using only model curvature (i.e., Q-optimal and threshold curvature) or using only FIM-based criteria. The lowest nMSE came from the MOO MBDOE design using the modified E-optimal with model curvature. In comparison to MOO MBDOE using parameter correlation, employing model curvature in the MOO framework gave better experimental designs with lower average nMSEs. Meanwhile, Q-optimality and curvature thresholding strategies provided better nMSEs than the majority of the FIM-based criteria, except the D-optimal design. Finally, the optimal experiments based on the A-optimal criterion, either alone or in MOO MBDOE, performed poorly. The poor performance of the A-optimal design has also been reported in a previous publication [15].
The obvious drawback of curvature-based MBDOEs in comparison to FIM-based strategies is the higher computational cost associated with computing the Hessian matrix. While the number of first-order sensitivities (Jacobian) increases linearly with the number of parameters p, the number of second-order sensitivities scales with . Fortunately, the calculation of the Hessian matrix can be easily parallelized and implemented using multiple computing cores. In practice, one often focuses on only a subset of the model parameters, and therefore the MBDOE is typically done for a handful of parameters.
We note that the MBDOE methods considered in this work consider only parametric uncertainty in the models and assume that uncertainty in model equations, that is, structural uncertainty, is not significant. For certain types of models, such as generalized mass action and S-system models [43,44], model structural uncertainty can be treated as parametric uncertainty, and therefore the MBDOE strategies developed here could be applied. As mentioned in the Introduction, MBDOE methods for discriminating between model structures have been developed, many of which are based on the Bayesian approach. Furthermore, in applications for which there exists intrinsic parametric variability, for example, batch-to-batch variability in cell culture fermentation processes, Bayesian MBDOE methods would be more suitable than FIM-based strategies, as Bayesian methods are able to incorporate the prior (intrinsic) distribution of the parameter values in the design. Nevertheless, as demonstrated in the case study, even when the MOO MBDOEs were performed using model parameters that were quite different from the true values, the resulting optimal designs led to precise and accurate parameter estimates. Meanwhile, biological systems, like other complex systems, have been argued to be sloppy. In the context of our work, sloppy systems lead to mathematical models whose FIMs have eigenvalues that are logarithmically spread evenly over large orders of magnitude [45]. In other words, the system behavior is sensitive to or is controlled by a small number of parameter combinations (along the FIM eigenvectors corresponding to large eigenvalues). At the same time, there exist many parameter combinations that can be varied without affecting the system behavior. Such sloppiness could arise in a system governed by processes that span large and evenly distributed length and/or time scales, such that there exists no clear separation between relevant and irrelevant mechanisms. A recent study demonstrated that in the case of sloppy systems, reducing the model parametric uncertainty by MBDOEs beyond a certain point might not necessarily translate to any improvement in model prediction accuracy [45]. However, it is possible to construct reduced-order models of sloppy systems, whose parameters correspond to the important parameter combinations [46,47]. Parameter estimation and MBDOE strategies can then be applied to these reduced models.
5. Conclusions
Existing MBDOE methods for parameter estimation mostly rely on the FIM to define information criteria. Because the FIM is based on first-order sensitivities with respect to the model parameters, the related MBDOEs may perform poorly for nonlinear models. Here, a new MBDOE using a MOO framework was presented, employing the maximization of a FIM-based information metric and the minimization of model curvatures. The application to a model of the fermentation of baker’s yeast demonstrated that accounting model nonlinearity through model curvatures in designing the experiment could lead to improved parameter accuracy over using only a FIM-based criterion. The proposed MOO MBDOE also outperformed other curvature-based designs, including the Q-optimality and curvature thresholding and another MOO MBDOE strategy using parameter correlation. The use of the MOO framework further gives flexibility to accommodate other criteria that may arise in a particular application, in the design of experiments.
Supplementary Materials
The following are available online at http://www.mdpi.com/2227-9717/5/4/63/s1. Figure S1: Pareto frontier of the MOO MBDOE using curvatures and a FIM-based criterion. Figure S2: Pareto frontier of the MOO MBDOE using correlation and a FIM-based criterion.
Acknowledgments
The authors would like to acknowledge funding from ETH Zurich and the Ministry of Education, Singapore.
Author Contributions
R.G. conceived and designed the study; E.M. and S.S. performed the design of the experiments and parameter estimations; E.M., S.S. and R.G. analyzed the data; E.M., S.S. and R.G. wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest. The funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| MBDOE | Model-based design of experiments |
| FIM | Fisher information matrix |
| MOO | Multi-objective optimization |
| RMS | Root mean square |
| ODE | Ordinary differential equation |
| MLE | Maximum likelihood estimator |
| CVP | Control vector parametrization |
| nMSE | Normalized mean-square error |
References
- Srinath, S.; Gunawan, R. Parameter identifiability of power-law biochemical system models. J. Biotechnol. 2010, 149, 132–140. [Google Scholar] [CrossRef] [PubMed]
- Jia, G.; Stephanopoulos, G.; Gunawan, R. Ensemble kinetic modeling of metabolic networks from dynamic metabolic profiles. Metabolites 2012, 2, 891–912. [Google Scholar] [CrossRef] [PubMed]
- Gábor, A.; Hangos, K.; Banga, J.; Szederkànyi, G. Reaction network realizations of rational biochemical systems and their structural properties. J. Math. Chem. 2015, 53, 1657–1686. [Google Scholar] [CrossRef]
- Liu, Y.; Manesso, E.; Gunawan, R. REDEMPTION: Reduced dimension ensemble modeling and parameter estimation. Bioinformatics 2015, 31, 3387–3389. [Google Scholar] [CrossRef] [PubMed]
- Villaverde, A.F.; Banga, J.R. Structural properties of dynamic systems biology models: Idenfiability, reachability and initial conditions. Processes 2017, 5, 29. [Google Scholar] [CrossRef]
- Franceschini, G.; Macchietto, S. Model-based design of experiments for parameter precision: State of the art. Chem. Eng. Sci. 2008, 63, 4846–4872. [Google Scholar] [CrossRef]
- Kreutz, C.; Timmer, J. Systems biology: Experimental design. FEBS J. 2009, 276, 923–942. [Google Scholar] [CrossRef] [PubMed]
- Chakrabarty, A.; Buzzard, G.T.; Rundell, A.E. Model-based design of experiments for cellular processes. WIREs Syst. Biol. Med. 2013, 5, 181–203. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Faller, D.; Klingmüller, U.; Timmer, J. Simulation methods for optimal experimental design in systems biology. Simulation 2003, 79, 717–725. [Google Scholar] [CrossRef]
- Gadkar, K.G.; Gunawan, R.; Doyle, F.J., III. Iterative approach to model identification of biological networks. BMC Bioinformatics 2005, 6, 155. [Google Scholar] [CrossRef] [PubMed]
- Balsa-Canto, E.; Alonso, A.A.; Banga, J.R. Computational procedures for optimal experimental design in biological systems. IET Syst. Biol. 2008, 2, 163–172. [Google Scholar] [CrossRef] [PubMed]
- Chung, M.; Haber, E. Experimental design for biological systems. SIAM J. Control Optim. 2012, 50, 471–489. [Google Scholar] [CrossRef]
- Transtrum, M.K.; Qiu, P. Optimal experiment selection for parameter estimation in biological differential equation models. BMC Bioinform. 2012, 13, 181. [Google Scholar] [CrossRef] [PubMed]
- Maheshwari, V.; Rangaiah, G.P.; Samavedham, L. A multi-objective framework for model based design of experiments to improve parameter precision and minimize parameter correlation. Ind. Eng. Chem. Res. 2013, 52, 8289–8304. [Google Scholar] [CrossRef]
- Sinkoe, A.; Hahn, J. Optimal experimental design for parameter estimation of an IL-6 signaling model. Processes 2017, 5, 49. [Google Scholar] [CrossRef]
- Vanlier, J.; Tiemann, C.A.; Hilbers, P.A.J.; van Riel, N.A.W. A Bayesian approach to targeted experiment design. Bioinformatics 2012, 28, 1136–1142. [Google Scholar] [CrossRef] [PubMed]
- Weber, P.; Kramer, A.; Dingler, C.; Radde, N. Trajectory-oriented Bayesian experiment design versus Fisher A-optimal design: An in-depth comparison study. Bioinformatics 2012, 28, i535–i541. [Google Scholar] [CrossRef] [PubMed]
- Liepe, J.; Filippi, S.; Komorowski, M.; Stumpf, M.P.H. Maximizing the information content of experiments in systems biology. PLoS Comput. Biol. 2013, 9, e1002888. [Google Scholar] [CrossRef] [PubMed]
- Apgar, J.F.; Toettcher, J.E.; Endy, D.; White, F.M.; Tidor, B. Stimulus design for model selection and validation in cell signaling. PLoS Comput. Biol. 2008, 4, e30. [Google Scholar] [CrossRef] [PubMed]
- Daunizeau, J.; Preuschoff, K.; Friston, K.; Stephan, K. Optimizing experimental design for comparing models of brain function. PLoS Comput. Biol. 2011, 7, e1002280. [Google Scholar] [CrossRef] [PubMed]
- Flassig, R.J.; Sundmacher, K. Optimal design of stimulus experiments for robust discrimination of biochemical reaction networks. Bioinformatics 2012, 28, 3089–3096. [Google Scholar] [CrossRef] [PubMed]
- Busetto, A.G.; Hauser, A.; Krummenacher, G.; Sunnaker, M.; Dimopoulos, S.; Ong, C.S.; Stelling, J.; Buhmann, J.M. Near-optimal experimental design for model selection in systems biology. Bioinformatics 2013, 29, 2625–2632. [Google Scholar] [CrossRef] [PubMed]
- Silk, D.; Kirk, P.D.W.; Barnes, C.P.; Toni, T.; Stumpf, M.P.H. Model selection in systems biology depends on experimental design. PLoS Comput. Biol. 2014, 10, e1003650. [Google Scholar] [CrossRef] [PubMed]
- Bazil, J.N.; Buzzard, G.T.; Rundell, A.E. A global parallel model based design of experiments method to minimize model output uncertainty. Bull. Math. Biol. 2012, 74, 688–716. [Google Scholar] [CrossRef] [PubMed]
- Mdluli, T.; Buzzard, G.T.; Rundell, A.E. Efficient optimization of stimuli for model-based design of experiments to resolve dynamical uncertainty. PLoS Comput. Biol. 2015, 11, e1004488. [Google Scholar] [CrossRef] [PubMed]
- Cochran, W.G. Experiments for Nonlinear Functions. J. Am. Stat. Assoc. 1973, 68, 771–781. [Google Scholar] [CrossRef]
- Bates, D.M.; Watts, D.G. Relative Curvature Measures of Nonlinearity. J. R. Stat. Soc. Ser. B 1980, 42, 1–25. [Google Scholar]
- Hamilton, D.C.; Watts, D.G. A quadratic design criterion for precise estimation in nonlinear regression models. Technometrics 1985, 27, 241–250. [Google Scholar] [CrossRef]
- Benabbas, L.; Asprey, S.P.; Macchietto, S. Curvature-based methods for designing optimally informative experiments in multiresponse nonlinear dynamic situations. Ind. Eng. Chem. Res. 2005, 44, 7120–7131. [Google Scholar] [CrossRef]
- Asprey, S.P.; Macchietto, S. Statistical tools for optimal dynamic model building. Comput. Chem. Eng. 2000, 24, 1261–1267. [Google Scholar] [CrossRef]
- Seber, G.A.F.; Wild, C.J. Nonlinear Regression; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Merlé, Y.; Tod, M. Impact of pharmacokinetic-pharmacodynamic model linearization on the accuracy of population information matrix and optimal design. J. Pharmacokinet. Pharmacodyn. 2001, 28, 363–388. [Google Scholar] [CrossRef] [PubMed]
- Bogacka, B.; Wright, F. Comparison of two design optimality criteria applied to a nonlinear model. J. Biopharm. Stat. 2004, 14, 909–930. [Google Scholar] [CrossRef] [PubMed]
- Rangaiah, G.P. Multi-Objective Optimization: Techniques and Applications in Chemical Engineering; World Scientific: Singapore, 2008; Volume 1. [Google Scholar]
- Varma, A.; Morbidelli, M.; Wu, H. Parametric Sensitivity in Chemical Systems; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Zhang, T.; Golub, G.H. Rank-One Approximation to High Order Tensors. SIAM J. Matrix Anal. Appl. 2001, 23, 534–550. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Egea, J.A.; Martí, R.; Banga, J.R. An evolutionary method for complex-process optimization. Comput. Oper. Res. 2010, 37, 315–324. [Google Scholar] [CrossRef]
- Egea, J.A.; Rodriguez-Fernandez, M.; Banga, J.R.; Martí, R. Scatter search for chemical and bioprocess optimization. J. Glob. Optim. 2007, 37, 481–503. [Google Scholar] [CrossRef]
- Rodriguez-Fernandez, M.; Egea, J.A.; Banga, J.R. Novel metaheuristic for parameter estimation in nonlinear dynamic biological systems. BMC Bioinform. 2006, 7, 483. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Edgar, T.F. PCA combined model-based design of experiments (DOE) criteria for differential and algebraic system parameter estimation. Ind. Eng. Chem. Res. 2008, 47, 7772–7783. [Google Scholar] [CrossRef]
- Chou, I.C.; Voit, E. Recent developments in parameter estimation and structure identification of biochemical and genomic systems. Math. Biosci. 2009, 219, 57–83. [Google Scholar] [CrossRef] [PubMed]
- Voit, E. Biochemical systems theory: A review. ISRN Biomath. 2013, 2013, 897658. [Google Scholar] [CrossRef]
- White, A.; Tolman, M.; Thames, H.D.; Withers, H.R.; Mason, K.A.; Transtrum, M.K. The limitations of model-based experimental design and parameter estimation in sloppy systems. PLoS Comput. Biol. 2016, 12, e1005227. [Google Scholar] [CrossRef] [PubMed]
- Transturm, M.K.; Qiu, P. Model reduction by manifold boundaries. Phys. Rev. Lett. 2014, 113, 098701. [Google Scholar] [CrossRef] [PubMed]
- Transturm, M.K.; Qiu, P. Bridging mechanistic and phenomenological models of complex biological systems. PLoS Comput. Biol. 2016, 12, e1004915. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).