Abstract
Water-soluble polymers with high molecular weights are known to decrease the frictional drag in turbulent flow very effectively at concentrations of tens or hundreds of ppm. This drag reduction efficiency of water-soluble polymers is well known to be closely associated with the flow conditions and rheological, physical, and/or chemical characteristics of the polymers added. Among the many promising polymers introduced in the past several decades, this review focuses on recent progress in the drag reduction capability of various water-soluble macromolecules in turbulent flow including both synthetic and natural polymers such as poly(ethylene oxide), poly(acrylic acid), polyacrylamide, poly(N-vinyl formamide), gums, and DNA. The polymeric species, experimental parameters, and numerical analysis of these water-soluble polymers in turbulent drag reduction are highlighted, along with several existing and potential applications. The proposed drag reduction mechanisms are also discussed based on recent experimental and numerical researches. This article will be helpful to the readers to understand better the complex behaviors of a turbulent flow with various water-soluble polymeric additives regarding experimental conditions, drag reduction mechanisms, and related applications.
Keywords:
drag reduction; aqueous polymer; turbulent flow; poly(ethylene oxide); polyacrylamide; gum 1. Introduction
A liquid flow passing through pipelines generally experiences chaotic changes in the flow velocity and pressure in the process of overcoming frictional losses. These changes depend on the fluid characteristics such as the velocity, viscosity, and density and on the flow geometry, including the pipe diameter and length. This flow regime with a sufficiently high Reynolds number is commonly called turbulent flow [1] and is characterized by a less orderly flow phase in which the eddy currents of the fluid elements can result in chaotic lateral mixing [2]. For turbulent flow in pipelines, as well as in open and external flow, the friction can be reduced by introducing a minor quantity of a flexible, linear polymer with a high molecular weight into the flow [3]. This behavior is termed the polymer-induced turbulent drag reduction (DR) effect [4,5] which is an active friction reduction mechanism compared to the prevailing passive friction reduction. Thus, DR techniques have been applied in various industrial and engineering arenas, such as oil pipelines, open channels, marine applications, agricultural field irrigation, fire hoses, and biomedical systems [6,7,8].
In general, different types of additives, including solid particles, surfactants, and polymers have been used to induce the turbulent DR phenomenon. Several surfactants have been applied as drag-reducing agents because of their self-assembly characteristics and ability to form thread-like micelles in fluids [9,10,11]. Self-assembly of surfactants is a physicochemical process; the self-assembly properties depend on the surfactant type, concentration, and temperature, etc. Because of these characteristics, surfactant molecules can be rapidly recombined under high shear, allowing the surfactants to resist mechanical degradation and become more stable in the flow, leading to highly efficient DR [12,13,14]. Nonetheless, one of the disadvantages of using surfactants is that, compared to water-soluble polymeric drag reducers, a rather high concentration is required to initiate the DR. Thus, high-molecular-weight polymers are considered as more efficient drag reducing agents when dissolved in a suitable solvent system of either aqueous or non-aqueous media [15,16]. Due to the particular viscoelastic properties, polymeric additives strongly influence the turbulent flow characteristics, even when used in small quantities. High levels of DR can be obtained when polymers are added to the turbulent flow [17]. It is also possible to customize polymers to harness the specific characteristics of different polymers. The selection of polymeric additives for a potential application is related to the unique properties of the polymer, including the polymer structure, molecular weight, and fluid characteristics [18]. The energy loss caused by the turbulent flow increases operating costs; thus, the DR capability of polymeric additives has been widely studied based on the recognized economical benefits.
When a polymer is dissolved in a suitable solvent, its DR effect can be maximized under the right conditions. Although several water-soluble polymers successfully reduced the drag in the turbulent flow of aqueous systems, oil-soluble polymers such as polyisobutylene and polystyrene are known to demonstrate high DR efficiency when dissolved in organic solvents or oils [19]. Therefore, these polymers are very important in engineering areas, including crude oil pipeline transport.
Over several decades, many kinds of natural and synthetic polymers have been discussed in isolation as promising turbulent DR additives, whereas there are few general discussions and summaries covering polymer combinations. In addition, the role of DNA on turbulent DR is also focused. In this short review, we focus on the recent progress in research on the DR of water-soluble polymers in turbulent flow, with special emphasis on the polymer species, experimental parameters, and applications, along with the fundamental characteristics of these polymers. Synthetic and natural water-soluble drag reducing polymers for various potential agricultural and industrial applications, including field irrigation, slurry transport, fracking, enhanced oil recovery, and biomedical applications [20,21], are covered.
2. Mechanism of Turbulent Drag Reduction with Polymers
Based on the extensive industrial and engineering applications of DR, this phenomenon has been the topic of numerous theoretical and experimental studies for more than sixty years [22,23,24]. However, the DR mechanism still requires further investigation. Herein, we summarize the qualitative explanations of polymer-induced DR. Some mechanisms focusing on viscoelasticity, vortex stretching, non-isotropic properties, molecular stretching of polymers, and laminarization of turbulent flow will be mainly discussed along with the behaviors of polymeric additives in a turbulent flow such as polymer extension, extensional viscosity of polymers, mechanical degradation, and polymer relaxation.
Astarita [25] proposed a general explanation of the DR phenomenon based on the viscoelasticity of the turbulent DR solution, suggesting that the energy dissipation in a turbulent flow can be used to explain the DR phenomenon by investigation of the energy dissipation of viscoelastic liquids.
On the other hand, Gadd [26] suggested that the DR phenomenon induced by the addition of miniscule amounts of polymers (as little as tens of ppm) to the turbulent flow might be related to the anomalous performance of the fluid particles during rapid deformation. In this scenario, vortex stretching arises near the wall, and extensive elongation of the polymeric molecules may take place, causing large elongational forces in the direction of the streamlines. Finally, this system resists the vortex stretching, resulting in the DR. The fluid with added polymer molecules has a longer relaxation time, and large polymeric chains with a longer relaxation time would likely induce large eddies with a lower stretching rate, leading to the rapid decay of the eddies.
For the mechanism of non-isotropic properties, it is known that polymeric chains will migrate in the solution influenced by the shear flow, hence the structure and the viscosity of solution will be changed. Since the shear rate is directionally dependant, the structure and the viscosity of the solution will be directionally dependant, in other words is non-isotropic. These non-isotropic properties were considered to be sources of turbulent structure changes and the DR phenomenon [27].
Molecular stretching of the polymers was also assumed to be responsible for the DR. According to this assumption, the macromolecules added to the turbulent solution increase the resistance to extensional flow, which is associated with shear hardening behavior, impeding turbulent bursts near the wall. Tulin [28] concluded that an increase in the laminar sub-layer thickness caused greater turbulence dissipation, accounting for the DR. Furthermore, Lumley [29] proposed a mechanism for the DR phenomenon based on polymeric chain extension, in which extension of the molecules absorbs the energy from the turbulent eddies, giving rise to the DR. Min et al. [30] proposed that polymer additives store the elastic energy from the flow very near the wall as shown in Figure 1, in which when the relaxation time is long enough, this high elastic energy is transported to and dissipated into the buffer by near-wall vortical motion, resulting in significant drag reduction.
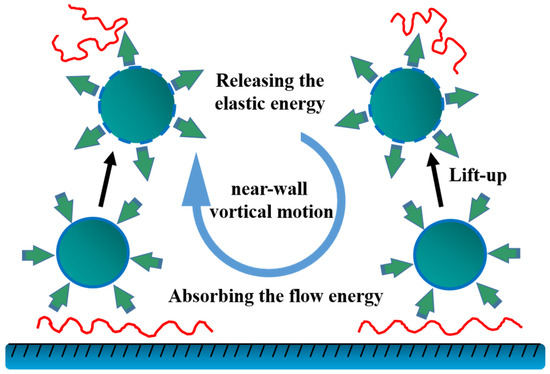
Figure 1.
Schematic representation of polymer-induced turbulent drag reduction (DR) mechanism.
The idea of an extended laminar flow was also considered as an important mechanism for the generation of DR. The component of flow not in the main flow direction is futile to the main flow, which induces wasteful energy dissipation via turbulent eddies and leads to the increased frictional drag [31]. In other words, the laminarization of turbulent flow will reduce the dissipation of fluid energy, therefore contributing to the DR. The most low energy consumption of viscous fluid would occur in the corresponding laminar flow under no matter how big the Reynolds number is, in which the frictional drag becomes the minimum value, just enough to overcome the viscous friction. Hence, the maximum effect of DR can be obtained while the fluctuating velocity components in turbulent flow are completely suppressed. Meanwhile, the heat transfer in this laminar condition would be the physical minimum for a given flow rate. The DR effect range of polymeric additives is between the asymptotic polymer solution and turbulent Newtonian fluid [31].
On the other hand, many studies of the polymeric behavior in turbulent flow have been carried out. Armstrong and Jhon [32] explained the polymer conformation by empolying the bead-spring model by using the connector potential, in which the polymer was considered as a chain of idential beads linked together by arbitrary spring potential. They then established the self-consistent process based on the relationship between the friction factor and molecular dissipation. It was proposed that the effect of the stochastic velocity field on the molecule can be explained as a “renormalization” of the connector potential, where the dumbbell probability density was derived for an arbitrary connector potential. It was determined that for a Hookean potential, at some value of the turbulent strength, the probability density would have an infinite second moment. It was found that the renormalization of the connector potential between the beads will reduce the connector force, which makes the bead extend; that is to say, the polymer molecule expands in the turbulent flow.
Regarding the effect of the extensional viscosity on the DR, the two-dimensional grid turbulent flow produced from a vertically flowing soap film was evaluated by introducing polyethylene oxide (PEO) using several extensional rates [33]. The mechanisms of energy transfer were found to be different in the normal and stream-wise directions. The critical polymer concentration for producing DR in a two-dimensional turbulent flow varied with the elongational rate. When the elongational rate was higher, the DR was efficient from a lower polymer concentration.
Moreover, compared to other drag reducing additives such as surfactants and particles, polymers under a turbulent flow face the issue of severe mechanical degradation. Brostow [34] reported that the energy supplied to a polymeric molecule in a turbulent flow leads to two processes, i.e., mechanical degradation and polymer relaxation. They proposed a model of the polymeric chain conformations based on statistical mechanics, and the effects on the DR efficiency and mechanical degradation of the polymer chains in a turbulent flow were established by considering the relationship between the extent of mechanical degradation of the polymer chains and the flow time. Recently, Pereira and Soares [35] further showed that the DR increased with time to reach a maximum, before decreasing due to chain degradation. They also presented the relative DR quantity, defined as the ratio of the current DR to the maximum DR obtained before degradation. They then suggested another decay function based on the relative drag reduction as a function of the molecular weight, polymer concentration, temperature, and Reynolds number.
In order to study the mechanism of DR by polymeric additives, some modern experimental and simulation techniques, such as direct numerical simulation, laser Doppler velocimetry, and particle image velocimetry, have been widely used for various measurements of the turbulence statistics. Den Toonder et al. [36] investigated the roles of stress anisotropy and elasticity by means of direct numerical simulation and laser Doppler velocimetry. They proposed that when polymers are extended, viscous anisotropic effects cause a change in the turbulence structure, and the entropy change results in drag reduction. White et al. [37] studied the turbulence structure in a drag-reduced flat-plate boundary layer flow by means of particle image velocimetry, providing information for further understanding the interaction between the polymer and the near-wall vortex. In addition, various research groups [38,39,40,41,42] performed a series of studies on the turbulent flow with polymer addition and clarified the velocity profile using particle image velocimetry and laser Doppler velocimetry.
Concurrently, the finite elastic non-linear extensibility-Peterlin (FENE-P) model as a kind of polymer model has been often adopted for DR studies. The FENE-P model is obtained by a pre-averaging approximation applied to a suspension of non interacting finitely extensible non-linear elastic (FENE) dumbbells, which accounts for the finite extensibility of the molecule [43]. Li et al. [44] carried out the direct numerical simulation of the forced homogeneous isotropic turbulence with/without polymer additives. They adopted the FENE-P model as the conformation tensor equation for the viscoelastic polymer solution.
Furthermore, Eshrati et al. [45] investigated the turbulent DR phenomenon in many oil-water flow systems with dissolved polymers. They used fuzzy logic [46] to study the DR phenomenon of water-soluble polymers in multiphase in-pipeline flow, and proposed that compared with the traditional logics, fuzzy logic is more useful for linking the multiple inputs to produce a single output. They also investigated the connection between DR and many parameters such as the polymer molecular weight, polymer concentration, charge density, mixture velocity, and oil fraction to estimate how fuzzy logic performs in prediction of the DR. The results showed that the effectiveness of the drag reducer increases with an increase in the velocity of the mixture; the polymer molecular weight and the increase in the oil fraction and the polymer charge density also affect the maximum drag reduction. From these results, a fuzzy logic model was developed to predict the DR, and the prediction was also verified through various results obtained with many polymers. Furthermore, dimensional analysis was carried out to find the best equation fitting the results. The result showed that a quadratic form was the most appropriate.
The two-dimensional (2-D) flows have also been adopted for DR studies [47,48,49]. Unlike the three-dimensional (3-D) flow, the flow velocity at each point in the 2-D flow is parallel to a fixed plane. Hidema et al. [50] pointed out that in the 3-D flow, it is difficult to avoid the effects of shear stress and to extract the extensional stress completely. In order to study the relationship between the extensional viscosity of polymers and turbulent DR, they used flowing soap films to generate 2-D turbulent flow to eliminate shear stress.
Therefore, it is highly possible that more than one kind of mechanism can lead to the DR phenomenon. Extensive research has led to the development of many proposed prediction models, but the accuracy of the mechanism of these predictions is still an open question; the above discussion is an attempt to provide a possible mechanism. In order to more accurately explain the mechanism of DR, further research is required.
3. Synthetic Water-Soluble Polymers
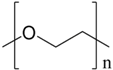
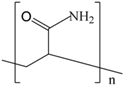
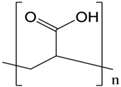
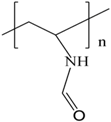
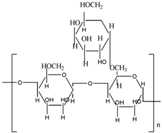
Synthetic water-soluble polymers usually have repeating units that can be synthesized by controlling the chemical structure, molecular weight, and number of functional groups on the polymeric backbone. These synthetic polymers, which possess a linear flexible chain and high molecular weight, have been extensively studied as drag reducing agents over the years. However, the drawbacks of chemical and mechanical degradation must be overcome. Table 1 summarizes the structures of four major synthetic water-soluble polymers that are used in DR research and are discussed in this review in detail.

Table 1.
Structures of synthetic water-soluble polymers: Poly (ethylene oxide), Polyacrylamide, Poly (acrylic acid) and Poly(N-vinyl formamide).
3.1. Poly(ethylene oxide)
Drag-reducing polymers generally have linear flexible chain structures with a very high average molecular weight. PEO, a polymer with ethylene oxide as the repeating unit, has been extensively adopted as an effective drag reducer in aqueous systems.
Virk et al. [51] studied the effects of solutions of five homologous PEOs with different molecular weights in distilled water on DR in a turbulent flow. They found that the strength of the DR produced by the homologous PEOs in a pipe flow is a universal function of the molecular weight, polymer concentration, and flow rate. The maximum DR efficiency was possibly limited by an asymptotic value that is independent of the pipe diameter and polymeric species. This experiment also presented the intrinsic concentration, (where [R] is the DR value of an initial increment of the polymeric chain), and demonstrated that the DR efficiency increased with a decrease in the diameter of the pipe and increasing polymer concentration [52].
Based on Virk’s drag reduction equation, Little [53] presented a simplified equation from experimental analysis:
where C is the concentration of the additive and DRmax is the maximum DR value. From the concentration-dependence of the DR, the intrinsic concentration [C] was found to be very useful for normalization of the DR values of different-molecular-weight components of a homologous series of polymers [54]. The relationship between the DR and the polymer properties, such as the molecular weight and concentration, was represented as Equation (2).
Similarly, Choi et al. [55] investigated the effect of the concentration of dilute solutions of water-soluble PEO on turbulent DR in a rotating disk flow system. The results demonstrated that the DR efficiency of PEO increased with increasing concentration of PEO, to reach a critical concentration at which the DR was maximal. The DR efficiency then declined with a further increase in the polymer concentration. Figure 2 illustrates the dependence of the DR efficiency of PEO with different viscosity-average molecular weight (Mv) as a function of the additive concentration. The optimum critical polymer concentration decreased with an increase in the polymer viscosity-average molecular weight. On the other hand, the appearance of a maximum was reported to be due to the DR characteristics of the polymeric solute and the increased solution viscosity, wherein both become important at higher polymer concentration.
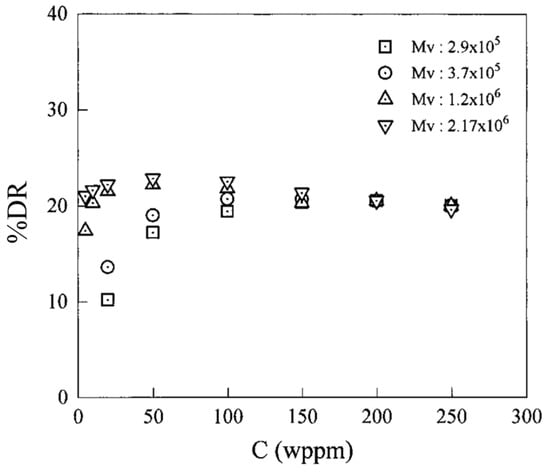
Figure 2.
Drag reduction of PEO versus the concentration of polymers of various molecular weights at 2800 rpm, reprinted with permission from [55]. Copyright American Chemical Society, 1996.
Kim et al. [56] applied PEO as a potential drag reducer in seawater piping in an ocean thermal energy conversion (OTEC) process, and investigated the drag reducing characteristics and mechanical degradation of PEO with different molecular weights and concentrations. Figure 3 presents the stability and mechanical degradation of PEO with a weight-average molecular weight (Mw) of 5.0 × 106 g/mol in a turbulent flow. The drag reduction was initially time-dependent and then remained at the limiting value due to degradation of the polymer chains. With the degradation of the polymer chains, the drag reduction ability decreased significantly. The temperature-dependent DR efficiency was also investigated. As presented in Figure 4, although the initial percentage DR was the highest at a room temperature, the DR declined most rapidly at this temperature. A higher DR efficiency was obtained at a lower temperature than at a higher temperature over time. The mechanical degradation of PEO molecules in seawater was compared with that in the PEO-deionized water system, as shown in Figure 5. Equation (3) was used to plot the degradation behavior:
where DR(t) and DR0 are the percentage drag reduction at time t and at the beginning of flow, respectively. The term h indicates the degradation velocity and W indicates the shear stability. The results showed that PEO polymer chains in the deionized-water system undergo more degradation in the original state than in seawater; however, the shear stability in the aqueous system was higher than that in seawater. Based on this study, it was proved that the DR effect induced by PEO could be exploited in the OTEC system to reduce the pumping energy cost. Choi et al. [57] also investigated the drag reduction efficiency of PEO in synthetic seawater and found that a maximum DR of 30% was obtained near 50 wppm concentration for higher-molecular-weight PEO. They confirmed that the behavior of PEO in seawater was similar to that in the deionized-water system, which could be a possible indicator of the commercial viability of PEO.
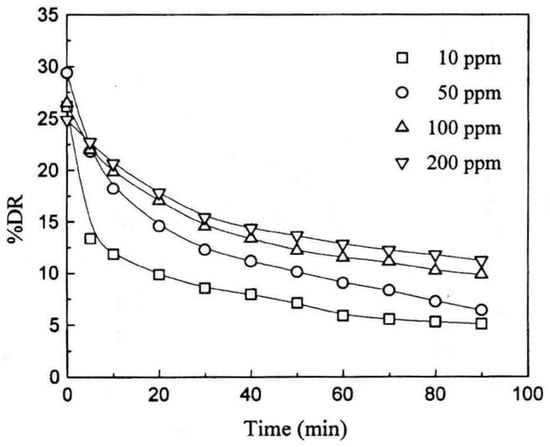
Figure 3.
Percent drag reduction of PEO (Mw = 5 × 106) as function of time for various polymer concentrations, reprinted with permission from [56]. Copyright The Society of Chemical Engineers, Japan, 1999.
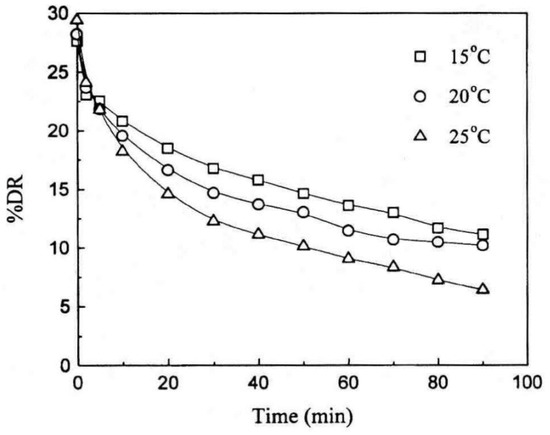
Figure 4.
Percent drag reduction of PEO (Mw = 5 × 106) as function of time for three different temperatures, reprinted with permission from [56]. Copyright The Society of Chemical Engineers, Japan, 1999.
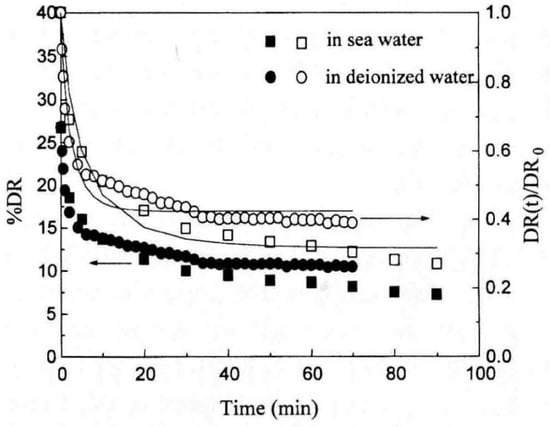
Figure 5.
Comparison of drag reduction (solid symbol) and degradation process (open symbol) of 50 ppm PEO (Mw = 4 × 106) in seawater and deionized water at same Reynolds number. Symbols represent experimental results (square for PEO in seawater and circle for PEO in deionized water); lines are obtained from equation [3], reprinted with permission from [56]. Copyright The Society of Chemical Engineers, Japan, 1999.
Recently, Lim et al. [58] used aqueous PEO solutions to explore the relationship between the drag reduction efficiency and the polymer molecular conformation. Note that the chain conformation may be affected by the solvent quality of the polymer solution. The specific temperature where the solvent is exactly poor enough to cancel the effect of excluded volume expansion of the dissolved polymeric chain is called the theta temperature (Tθ). Thus, they measured the drag reduction efficiency of PEO aqueous solutions at various increments from Tθ, and found that the drag reduction properties were sensitive to the conformation of the polymers, even at very low concentrations. In addition, they carried out temperature quenching experiments and proposed that the faster decrease in the drag reduction efficiency for polymers closer to Tθ is not due to mechanical molecular degradation, but rather, to shrinkage of the PEO molecules.
3.2. Polyacrylamide
Polyacrylamide (PAAM), a synthetic macromolecule formed from acrylamide subunits, has been extensively studied as the most commonly used drag reducing agent. One of the extensive usages of PAAM is in the flocculation of solid particles dispersed in a medium, with potential applications in water treatment and the papermaking process. Another common use is in the oil and gas industries. Enhanced oil recovery is an important example of PAAM application. A highly viscous aqueous solution can be obtained even with a low PAAM concentration. This technique could also be used to address (water) flooding problems.
The DR efficiency of PAAM has been more widely examined than that of other drag reducing polymeric agents. Sung et al. [59] investigated the DR efficiency of PAAM in a rotating disk flow system by comparison with that of PEO. The effect of temperature on the DR was evaluated at a polymer concentration of 50 wppm for both PAAM and PEO, as shown in Figure 6. The results showed that mechanical degradation of the PEO chains increased with temperature, whereas PAAM remained mechanically stable even at high temperature. Therefore, PEO was more susceptible to thermal and mechanical degradation, whereas PAAM exhibited relatively high shear resistance. Therefore, PAAM is prospectively an excellent DR additive for high-temperature and long-period transportation applications.
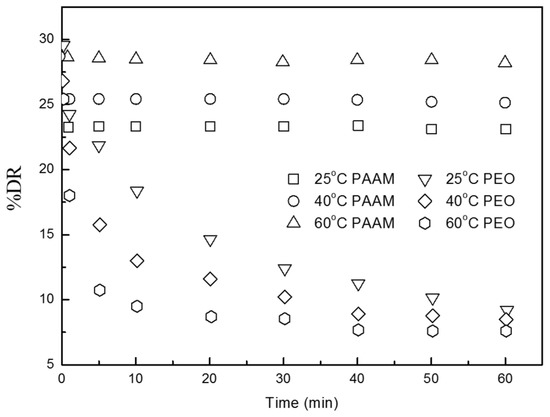
Figure 6.
DR of both PAAM and PEO (50 wppm) at three different temperatures, reprinted with permission from [59]. Copyright Marcel Dekker, Inc., Japan, 2004.
Sandoval et al. [60] also compared the degradation phenomenon for three different aqueous solutions of PEO, PAAM, and xanthan gum (XG) using a pipe flow device. PEO and PAAM have flexible chains, whereas the chain structure of XG is rigid. Figure 7 presents a comparison of the DR efficiency of the flexible polymers versus the rigid polymer. PAAM was found to be as effective as PEO, whereas the DR efficiency of the PAAM solution declined to a lesser extent than that of the PEO solution, which suggested that polymeric chain scission was more significant for PEO. Moreover, the drag reduction achieved with rigid chain XG fell abruptly in the first step and remained constant, which is different from the cases with PEO and PAAM. Similarly, Pereira et al. [61] compared the drag reduction efficiency of PEO, PAAM, and XG over time by using a rotating cylindrical double-gap device. They also found that there was no decrease in the drag reduction at a high PAAM concentration, which suggested that the PAAM chain is mechanically stronger than that of PEO.
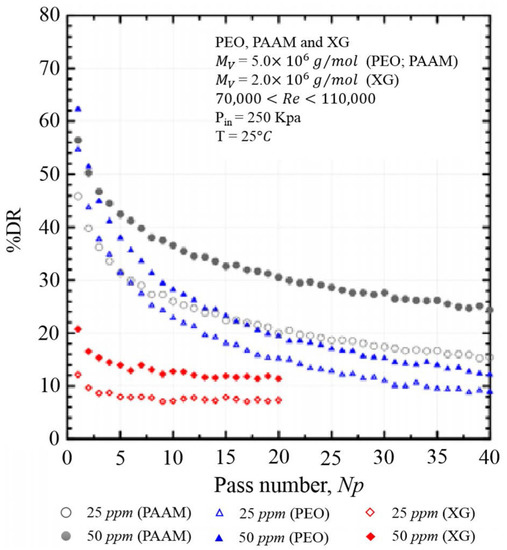
Figure 7.
Comparison of DR between flexible polymers (PEO and PAM) and rigid polymer, XG, reprinted with permission from [60]. Copyright Engenharia Térmica (Thermal Engineering), 2015.
On the other hand, Lim et al. [62] examined the turbulent DR of λ-DNA and compared it to that of PAAM in continuous and stepwise mode using an in-house designed rotating disk apparatus. Figure 8 confirmed that the mechanical degradation behavior of linear flexible PAAM was very different from that of λ-DNA due to differences in the molecular weight, polydispersity, and flexibility. Although PAAM produced a much higher initial DR value, this drag reduction effect decreased to zero in 5 min.
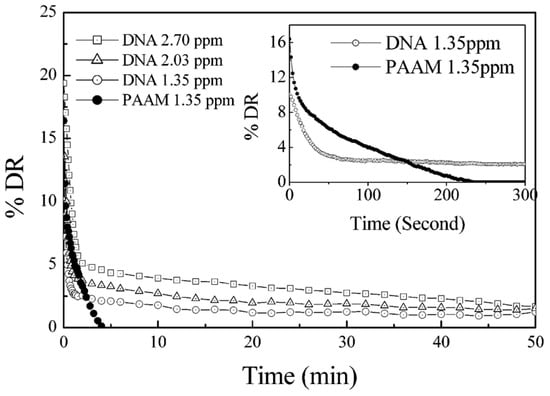
Figure 8.
Comparison of λ-DNA percent DR (1.35, 2.03 and 2.70 wppm) with PAAM (Mw = 18 × 106 g/mol) on long-term scale at 1980 rpm and 25 °C. The inset represents the initial changes in the drag reducing efficiency for λ-DNA and PAAM at 1.35 wppm, reprinted with permission from [62]. Copyright American Chemical Society, 2015.
Zhang et al. [63] experimentally investigated heat transfer and frictional DR in the two-phase flow of air-water with and without PAAM additives in a horizontal circular tube. They showed that with the addition of PAAM, the heat transfer coefficients were reduced from 36.8% to 70.3%, and the pressure drop was reduced from 31.9% to 54.7% compared to those without the PAAM additive.
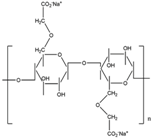
3.3. Poly(acrylic acid)
Poly(acrylic acid) (PAA) is another high-molecular-weight water-soluble polymer of acrylic acid, possessing a carboxyl group in each monomeric unit of the main chain. This polymer has a highly negative charge density in aqueous medium due to dissociation of the acid groups. Therefore, PAA is one of the most extensively used aqueous anionic polyelectrolytes, and its degree of ionization is dependent on the pH of the solution [64,65]. At a low pH, PAA is known to adopt a more compact conformation and can associate with various non-ionic polymers to form hydrogen-bonded inter-polymeric complexes due to the absence of negative charges in the backbone of PAA. In aqueous solutions, PAA can also form poly-complexes with oppositely charged polymers and surfactants.
Based on this interesting property of the ionic polymer PAA, Kim et al. [66] used a polymer–surfactant (SDS) complex system as a drag reducer and investigated the effects of the surfactant and pH on the DR efficiency of PAA in an external flow using a rotating disk system. A schematic diagram of the conformational changes in the molecular structure of PAA at various pH values is shown in Figure 9. As the pH increased, the PAA underwent a conformational transition from the compact helical structure to the highly extended rigid rod form, and its shear viscosity increased. Figure 10 illustrates the effect of pH on the turbulent DR efficiency of PAA at different pH values. The DR efficiency at pH 4 was found to be smaller than that at higher pH, indicating that the turbulent DR efficiency of the polymers in water is directly related to their chain conformations. They suggested that the extended conformation of PAA is more beneficial for drag reduction in a turbulent flow, compared with the compact helical form. Furthermore, as the SDS concentration (M = mol/L) increased, the drag reduction efficacy of PAA increased, as shown in Figure 11. This can be explained by the formation of an association complex between the polymer chains and surfactant, which enhanced the bonding force of the polymer molecules, resulting in extension of the polymer chains, especially at low pH. Figure 12 illustrates the conformational variation of the PAA molecule with addition of the surfactant SDS.
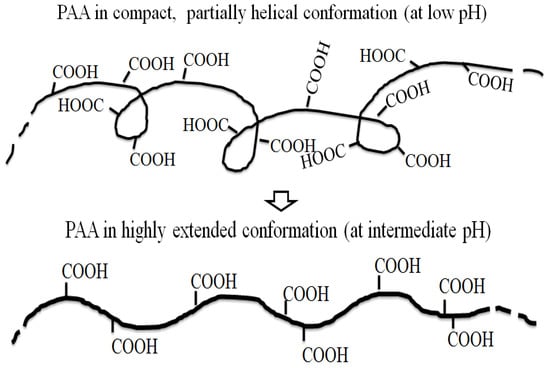
Figure 9.
A schematic representation of the conformational variation in the PAA molecular at different pH levels, reprinted with permission from [66]. Copyright Elsevier, 2011.
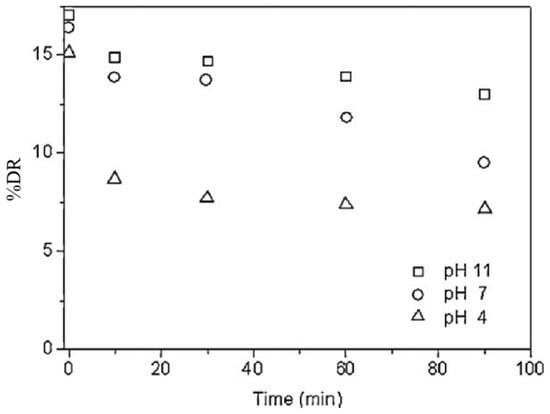
Figure 10.
Effect of pH of PAA597 solution (100 ppm) on DR, reprinted with permission from [66]. Copyright Elsevier, 2011.
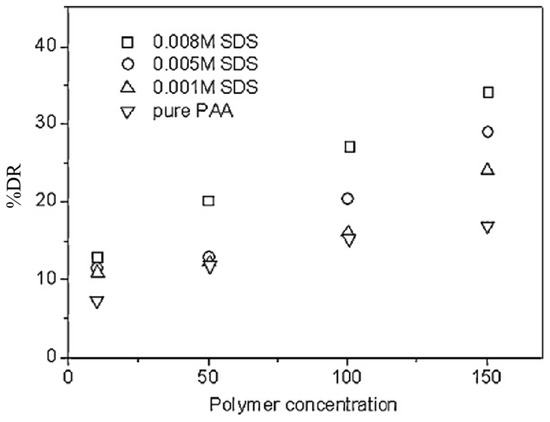
Figure 11.
Effect of SDS concentrations as a function of polymer concentrations (pH 4), reprinted with permission from [66]. Copyright Elsevier, 2011.
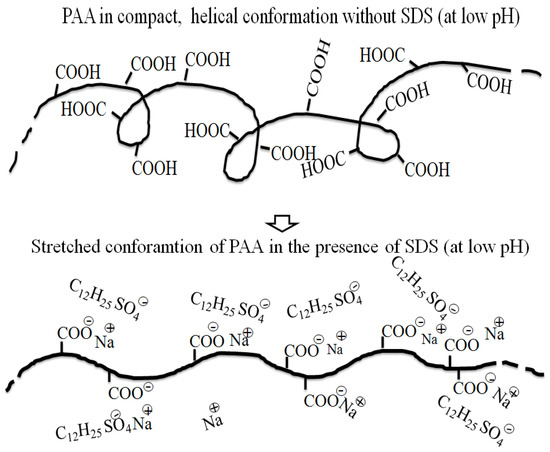
Figure 12.
The variation in PAA conformation by adding surfactant SDS, reprinted with permission from [66]. Copyright Elsevier, 2011.
Kim et al. [67] studied the conformational changes of the PAA chains under high shear flow, and found a severe decrease in the turbulent DR (%DR) with increasing rotational speed of the disk and time. They also confirmed that these changes in the drag reduction are sensitive to external parameters such as the pH, polymer concentration, and PAA molecular weight. Such DR changes were explained as a direct consequence of inter-chain association via hydrogen bonding.
Recently, Zhang et al. [68,69] studied the turbulent DR efficiency of aqueous poly(acrylamide-co-acrylic acid) copolymers with various molecular parameters in a rotating disk flow system, and found a maximum DR of 45% at 50 wppm concentration. The influence of temperature on the drag reduction efficacy is presented in Figure 13. As the temperature increased, the initial drag reduction efficacy increased; however, the persistent drag reduction activity decreased over the course of the examination. This was attributed to the fact that the thermal motion of the molecules increased with increasing temperature under turbulent flow conditions, resulting in weakness of the solvated flow regions.
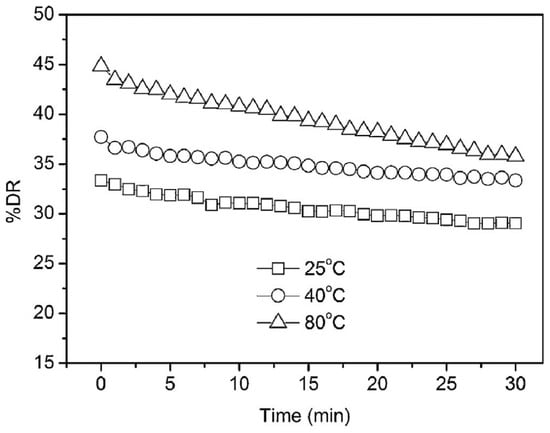
Figure 13.
%DR versus time of copolymer solution (Mw = 1.5 × 107 g/mole) for different temperatures (25 °C, 40 °C and 80 °C) at 1980 rpm, reprinted with permission from [68]. Copyright Springer-Verlag, 2011.
In addition, Cole et al. [70] synthesized 4-arm star PAA for use as a new water-soluble drag reducing agent by applying a Cu(0)-mediated polymerization technique. The results confirmed that 4-arm star PAA was effective as a drag reducing agent, with a drag reduction of 24.3%. Moreover, 4-arm star PAA showed superior mechanical stability compared with the commercial product Praestol, PEO, and linear PAA.
3.4. Poly(N-vinyl formamide)
With continued improvement of the methods for synthesis and purification of the hydrophilic cationic N-vinyl formamide monomer, water-soluble poly(N-vinyl formamide) (PNVF) and its copolymers have been adopted in industrial and biomedical applications. Due to the very high molecular weight and the structural similarity to PAAM, PNVF has been studied as a potential candidate as an effective drag reducing agent [71]. Furthermore, PNVF has been introduced as a replacement for acrylamide polymers for industrial application. The potential uses of PNVF and its hydrolyzed products have been demonstrated in the areas of papermaking, water treatment, coatings, rheology modifiers, and in the oil field industry [72].
Based on its very low toxicity and good solubility in water, Marhefka et al. [73] investigated the drag reduction efficacy, viscoelasticity, and mechanical degradation behavior of PNVF in a turbulent pipe flow, specifically for biomedical applications. They found that PNVF with a high molecular weight demonstrated DR characteristics, and its mechanical chain degradation was much lower than that of PEO. Besides this, in vivo analysis of PNVF suggested that it can be adopted as a drag reducing agent for clinical use. On the other hand, Mishra et al. [74] synthesized an aqueous graft copolymer of κ-carrageenan-g-N-vinyl formamide and studied its swelling behavior, metal ion sorption, flocculation, and anti-biodegradation characteristics. The results showed that this grafted polymer exhibits better water swelling behavior and resistance to biodegradation. Efficient flocculation capability could also be obtained, which may enable its application in the treatment of coal wastewater.
3.5. Water-Soluble Copolymer
Water-soluble copolymers are one of the fastest growing materials in industrial products. Due to their interesting characteristics that differ from those of homopolymers, water-soluble copolymers can be widely used in water treatment, coatings, personal care formulations, and commercial drag reducing agents.
McCormick and co-workers [75] extensively studied water-soluble copolymers. They synthesized four series of water-soluble acrylamide copolymers and investigated their corresponding DR effectiveness using a modified rotating disk in tube flow. The synthetic copolymers, including polyacrylamide-co-sodium acrylate (PAAM-co-NaA), polyacrylamide-co-(sodium2-(acrylamido)-2-methylpropanesulfonate) (PAAM-co-NaAMPS), polyacrylamide-co-(sodium3-(acrylamido)-3-methylbutanoate) (PAAM-co-NaAMB), and polyacrylamide-co-diacetone acrylamide (PAAM-co-DAAM), exhibited differences in terms of the hydrophobicity, charge density, and the degree of inter-molecular or intra-molecular association. The researchers presented a simple way of examining the DR effectiveness based on the DR efficacy as a function of the hydrodynamic volume of the polymer ([η]C), and demonstrated the dependence of the DR performance on the polymeric structure. They found that the incorporation of low quantities of charged co-monomers afforded copolymers with a high intrinsic viscosity and a high molecular weight with the greatest DR, even better than that of PEO or PAAM.
Moreover, Mumick et al. [76] synthesized a series of aqueous polyampholytes (containing both negative and positive charges in the same polymeric chain) based on acrylamide (AM), sodium 2-acrylamido-2-methylpropanesulfonate (NaAMPS), (2-acrylamido-2-methylpropyl)trimethylammonium chloride (AMPTAC), sodium 3-acrylamido-3-methylbutanoate (NaAMB), and 3-((2-acrylamido-2-methylpropyl)dimethylammonio)-1-propanesulfonate (AMPDAPS) and studied their chain confirmation and solvation in a turbulent flow. They reported that all of these macromolecules showed higher DR effectiveness and intrinsic viscosity with an increase in the ionic strength of the solvent. Among these synthesized copolymers, the betaine species exhibited the best DR characteristics, whereas the polyampholyte with a high charge density exhibited the lowest efficiency. Figure 14 illustrates the drag reduction characteristics of DAPS-10 (copolymers of AAM and AMPDAPS).
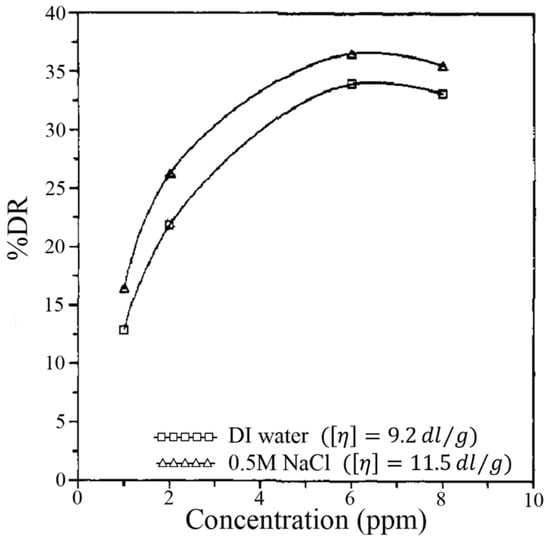
Figure 14.
Percent DR versus concentration for DAPS-10 in deionized water and 0.5 M NaCl at wall shear stress TW = 1122 dyn/cm2 in the rotating-disk rheometer, reprinted with permission from [76]. Copyright American Chemical Society, 1994.
Recently, Brun et al. [77] investigated the DR and mechanical stability of poly(AAm-co-NaAMPS) solutions under shear in a turbulent pipe flow, and found that the NaAMPS portion in the main backbone of the drag reducer enhances the DR efficiency of PAAM. They also suggested that the presence of NaAMPS in the copolymer does not significantly influence the mechanical degradation of the polymeric chains. The lowest fanning friction factor value of poly(AAm-co-NaAMPS) was achieved with 15% NaAMPS, whereas the highest measured drag reduction of 75% was obtained for the 100 ppm solution. Further, the PAAM-PEO copolymer was also highly efficient for decreasing the pressure drop of the pipe flows. A DR efficiency of 33% was achieved with PAAM-PEO in water [78]. Reis et al. [79] carried out an experiment using PAAM-g-poly(propylene oxide) (PAAM-g-PPO) as a water-soluble drag reducer. The grafted amphiphilic copolymer PAAM-g-PPO produced a better DR effect than pure PAAM based on different parameters, including the average molecular weight, molecular chain length, intrinsic viscosity, and polymer size distribution. The amphiphilic graft copolymer was found to be more resistant to shear degradation and fluid recirculation than pure PAAM. Other derivatives, including copolymers of N-alkyl- and N-arylalkylacrylamides with AM [80], (acrylamido tert-butyl sulfonic acid)-acrylamide copolymer [81], polyacrylamide-grafted chitosan [82], and guar-g-polyacrylamide [83], etc., are also being studied as drag reducing agents.
4. Natural Water-Soluble Polymers
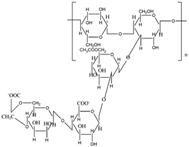
Polysaccharides, as an important class of natural polymers, have been studied as promising drag reducing agents due to their unique molecular structure, safety, shear-stability, low cost, biodegradability, and reproducibility (Table 2). They can be used to circumvent the safety and environmental influence issues associated with artificial polymers. However, their biodegradability may reduce their efficiency period and shelf life. To control this characteristic, many attempts (such as grafting, derivatization, and cross-linking) have been made to improve their properties to fit various applications, including polymer-induced DR.

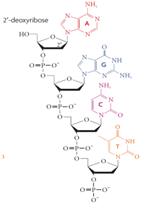
Table 2.
Structures of natural water-soluble polymer: Guar Gum, Xanthan Gum, Carboxymethyl cellulose and DNA, reprinted with permission from [97]. Copyright Nature Publishing Group, 2007.
4.1. Guar Gum
Guar gum (GG), which belongs to the hydrocolloid polysaccharide family, consists of mannose and galactose sugars, and is generally obtained from the endosperm of Cyamopsis tetragonolobus. It is mainly composed of the linear backbone chains of 1,4-linked β-d-mannopyranosyl units with short side-branches of 1,6-linked α-d-galactopyranosyl units. GG has been widely used in various industries, including food, hydraulic fracturing, suspending agents, agriculture, bioremediation, cosmetics, and pharmaceuticals.
Kim et al. [84] examined the DR behavior of GG with three different-molecular-weight fractions in water using a rotating disk apparatus. Because natural GG has a single average molecular weight, three different molecular weights of GGV, GG30 and GG60 were obtained by ultrasonic degradation for 0, 30 and 60 min, respectively. They tested the drag reduction efficacies of GG, and observed that GG is an effective aqueous drag reducing agent, and is more stable towards mechanical chain degradation than synthetic aqueous drag reducing agents like PEO. Figure 15 shows the results of mechanical degradation of these GG samples with the three molecular weights over 10 h at 1800 rpm. All of the GG solutions gave rise to a certain percentage drag reduction of between 62% and 80% of the initial DR efficiency.
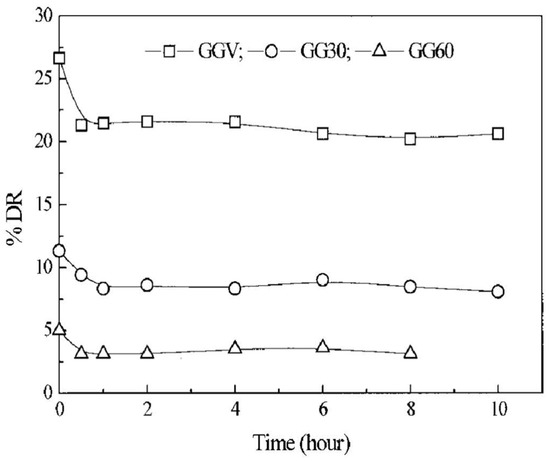
Figure 15.
%DR versus time for a 100 wppm GG solution, reprinted with permission from [84]. Copyright John Wiley and Sons, 2002.
Chemical modification of GG has also been studied by many researchers as a method to overcome its inherent deficiencies, such as its facile biodegradability. Singh et al. [85] compared the DR efficiencies of pristine GG, purified GG, and grafted GG in water, as shown in Figure 16. They found that the grafted GG copolymer combined the robustness of GG and the efficiency of the synthetic PAAM polymer, resulting in enhanced drag reduction efficiency. Moreover, Deshmukh et al. [86] studied the grafting of polyacrylamide onto GG, and compared the graft polymer with commercial GG and purified GG. They found that the grafted GG and purified GG exhibited good biodegradation resistance and enhanced drag reduction efficiencies.
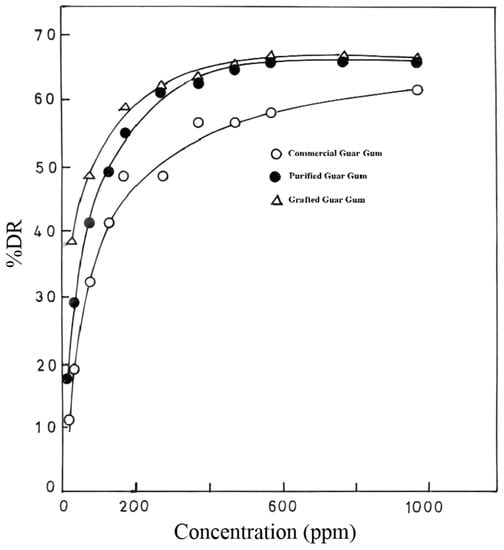
Figure 16.
DR characteristics of commercial guar gum, purified guar gum, and grafted guar gum, reprinted with permission from [85]. Copyright De Gruyter, 2009.
Behari et al. [87] prepared copolymers in which methacrylamide was grafted onto GG using a redox pair comprising potassium chromate/malonic acid and investigated the reaction conditions that could produce less of the homopolymer and generate more of the graft copolymer. They observed that the extent of grafting increased with an increase in the concentration of hydrogen ions or chromate ions. Furthermore, the grafting ratio and drag reduction efficiency increased with an increase in the malonic acid concentration from 3.5 × 10−3 to 10 × 10−3 mol∙dm−3.
4.2. Xanthan Gum
Xanthan gum (XG) is an acidic polymer that is secreted by Xanthomonas campestris bacterium. Its main structure consists of one d-glucopyranosyluronic unit, two d-glucopyranosyl units, and two d-mannopyranosyl units. Due to its ability for rheological control in aqueous systems, XG has been widely used in industries. In the case of agricultural applications, XG has been used to enhance the fluidity of fungicides and insecticides [88]. Moreover, XG can produce a high shear viscosity polymer solution at low concentrations or under shear forces, which makes it effective as a thickener and stabilizer in the food and petroleum industries, such as in cosmetics, toothpastes, oil drilling fluids, enhanced oil recovery, and pipeline cleaning [89].
The drag reduction capability of XG continues to be widely researched. Sohn et al. [90] evaluated the effect of various molecular parameters on the DR of XG, including the molecular weight, polymer concentration, temperature, solution ionic strength, and rotational speed of the disk. The results showed that the DR efficiency of XG is closely associated with various molecular parameters. Its higher shear-stability in both water and salt solutions compared to other flexible polymers was documented.
Hong et al. [91] studied the DR efficiency induced by different concentrations of XG in aqueous KCl solutions in a closed chamber using a rotating disc, and found that the mechanical degradation as a function of time decreased with increased KCl concentration. The anionic charges on XG allow interaction with the added salt ions to induce a conformational change of XG in solution, resulting in changes in the shear viscosity. The DR efficiency of XG as a function of the concentration in the initial period and after 40 min is illustrated in Figure 17. The DR increased with higher XG concentrations, and the DR efficiency of XG/KCl declined with increasing KCl concentration. This is because the polymeric chain conformation of XG tends to be more rigid, leading to lower sensitivity to the high shear conditions.
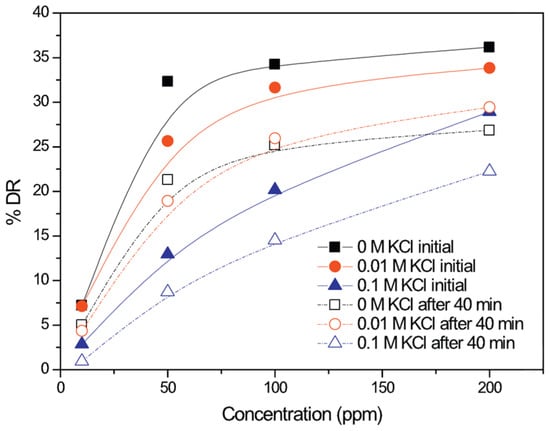
Figure 17.
Concentration dependence of %DR with XG, reprinted with permission from [91]. Copyright Elsevier, 2015.
Recently, Andrade et al. [92] analyzed the drag reduction efficiency of PEO, PAAM, and XG by dissolving these three polymers in deionized water with and without synthetic sea salt. The effect of the salt concentration on the DR over time was studied by using a double-gap Couette-type rheometer device. In the presence of salt, the maximum DR efficiency was reduced for both the PEO and XG macromolecular solutions over time; however, the DR of the PAAM solutions did not change significantly. The time-dependent DR profiles, DR(t), for XG in de-ionized water and synthetic saline solution are illustrated in Figure 18. The dramatic decrease in the efficiency is associated with the structural transition from helical to coiled with addition of the salt. For the 50 ppm solution, the maximum drag reduction decreased from 0.195 to 0.04.
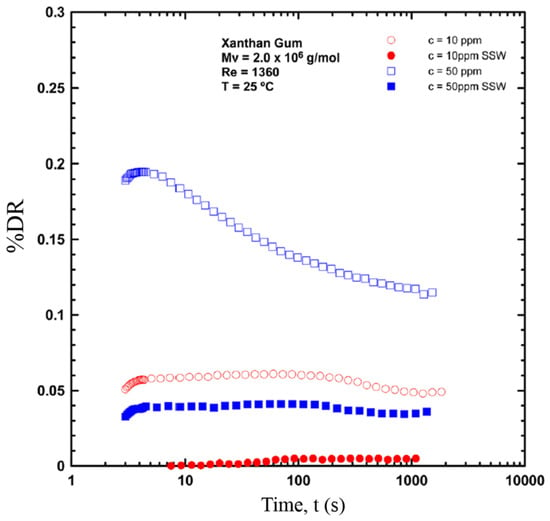
Figure 18.
DR(t) for a range of concentrations of XG in synthetic seawater and deionized water reprinted with permission from [92]. Copyright American Society of Mechanical Engineers (ASME), 2016.
4.3. Carboxymethyl Cellulose
Cellulose, the most common biopolymer, is mainly found in the cell wall of plants. Cellulose possesses interesting properties such as a high mechanical strength and good thermal stability; however, the principal disadvantage is its insolubility in both aqueous and organic solvents, which limits its use in industry. Thus, chemical modification of the hydroxyl groups of cellulose may be used to confer greater solubility [93]. Carboxymethyl cellulose (CMC), which is a cellulose derivative possessing hydroxyl groups bound to carboxymethyl groups, shows good solubility in aqueous solvents. CMC is an important industrial polymer that is used in a number of applications such as DR, flocculation, detergents, foods, and oil-well drilling technology [94,95].
Deshmukh and co-workers [96] published a method of synthesizing CMC-based graft copolymers by grafting acrylamide chains onto the CMC backbone, and measured their DR efficacy, shear stability and biodegradability. The copolymers (CAm1, CAm2, CAm3 and CAm4) were synthesized with the same amount of CMC (1 g) and acrylamide (0.14 mol) with gradually increasing concentrations of ceric-ions (0.05, 0.10, 0.20, 0.30 mol). The increased ceric-ion concentrations resulted in an increase in the number of grafts, but led to shorter chains. The presence of the grafted polyacrylamide chains led to enhanced DR efficacy and good mechanical shear stability, and these factors were also found to be dependent on the number and length of the grafts. Figure 19 illustrates the drag reduction efficacies of unmodified CMC and its copolymers. As the polymer concentration increased, the drag reduction efficacies changed in two different ways. All of the graft copolymers were more effective than unmodified CMC, and a maximum DR of about 68% was obtained with a concentration of CAm1 of 75 ppm. These graft copolymer solutions exhibited significantly reduced biodegradability.
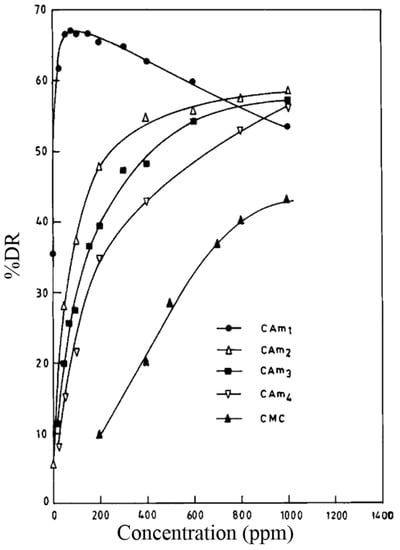
Figure 19.
Drag reduction vs. polymer concentration for CMC and its graft copolymers, reprinted with permission from [96]. Copyright John Wiley and Sons, 1991.
Similarly, Biswal and Singh [94] synthesized six different CMC-g-PAAM copolymers with variation of the amount of monomer and catalyst, and found that these grafted copolymers exhibited significant flocculation and viscosifying characteristics.
4.4. DNA
DNA, a long polymer made from repeating nucleotide units, carries the genetic instructions for all living organisms and many viruses. Most DNA molecules are composed of two biopolymer strands that are coiled around each other by hydrogen bonds to form a double helix. The DNA structure is dynamic along the length and can be coiled into tight loops or other shapes [97].
It is well known that configurational changes of DNA can be induced by changing the pH and temperature. The DNA molecules can change from their double-stranded state to two single-strands under certain temperature or pH conditions. Based on the above property, Choi et al. [98] employed λ-DNA as a drag reducing agent to probe the mechanism of drag reduction and mechanical molecular degradation. They reported that λ-DNA is considered to be a better polymeric DR additive than the high-molecular-weight linear long-chain PEO. Figure 20 illustrates the DR efficiency of λ-DNA in comparison with that of PEO. The λ-DNA exhibited a high and stable percentage DR over time at a concentration of only 2.7 wppm. This DR behavior over a sufficiently long time is considered to be the main distinction compared with other high-molecular-weight, linear, flexible macromolecules. The mechanical degradation test showed that λ-DNA was always divided exactly into half, after which there was no further degradation. These results suggested that the mechanism of mechanical shear degradation of λ-DNA is quite different from that of traditional linear flexible macromolecules. Similarly, Lim et al. [99] compared the drag reduction efficiency of calf thymus DNA (CT-DNA) with that of λ-DNA, and found that CT-DNA has no drag reduction efficiency due to its rapid degradation.
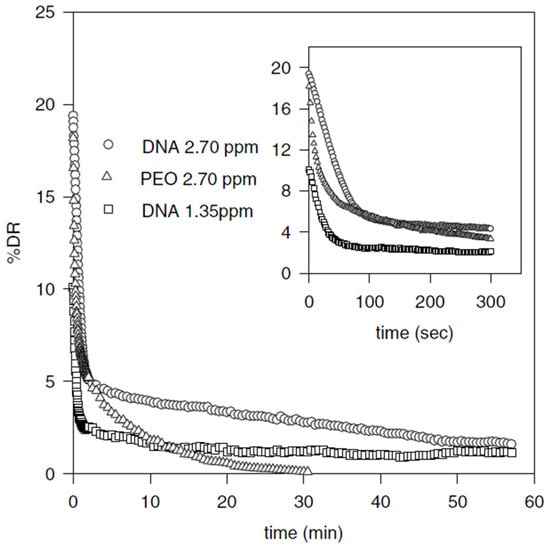
Figure 20.
Time dependence of drag-reduction percentage for 1.35 and 2.70 wppm λ-DNA in buffer solution compared with PEO (Mw = 5 × 106) at 1980 rpm (Re = 1.2 × 106). Inset shows the same data at early times, reprinted with permission from [98]. Copyright American Physical Society, 2002.
Subsequently, Lim et al. [100] examined the coil-globule transition of monodisperse λ-DNA in an external flow of turbulence, thereby studying the effects of structure on drag reduction. They added spermidine (SPD) as an electrostatic condensing agent to generate the negatively charged λ-DNA in the turbulent flow, and compared its drag reducing phenomena with that of simple λ-DNA. As shown in Figure 21, in the absence of SPD, a relatively high drag reduction efficiency was achieved and was maintained with low mechanical shear degradation of λ-DNA for 1 h in the turbulent flow. In contrast, an abrupt decrease in the drag reduction efficiency was observed after SPD injection. This can be explained as follows: during the short period when the concentration of SD is sufficiently high, the original coil form of λ-DNA is changed into the globular state, which hardly produces any DR. Furthermore, they indicated that despite the different flow conditions, all λ-DNA molecules had the same half-dimension, indicating that discrete variation of the DNA conformation can significantly alter the flow characteristics.
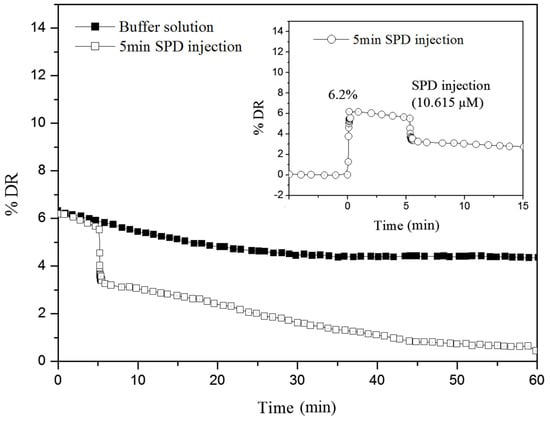
Figure 21.
The percent DR vs. time for 1.35 wppm λ -DNA in buffer solution at 1157 rpm (NRe = 5.9 × 105) and 25 °C with and without (SPD). The inset shows the magnification of initial change of DR by SPD injection, reprinted with permission from [100]. Copyright John Wiley and Sons, 2005.
Recently, Ueberschar et al. [101] compared the fluid friction of single micrometer-sized blank and DNA-grafted PS microspheres under shear flow, and found that a thick DNA brush layer grafted onto PS microspheres reduced the frictional drag significantly, especially in dilute λ-DNA solution. This effect was more pronounced depending on the average molecular weight of the grafted DNA macromolecules, and was predicted to find use in chip devices or biomedical engineering.
5. Applications of Polymer-Induced Drag Reduction
With the recognition of polymers as prospective turbulent drag reducers, many possible applications were put forward, including in the fields of crude oil transportation through a pipeline, sewage, floodwater disposal, biomedical areas, oil well, heating circuits, and so on. In this section, we review a few of these applications, and hope that the principles used in these fields can be applied to other areas.
Drag reduction is considered to be a very important application prospect in the crude oil industry. The introduction of drag reducing polymeric additives in the long-distance crude oil pipeline has attracted huge attention. Evans [102] reported improved mechanical shear stability in non-aqueous systems using a tri-n-butylstannyl fluoride drag reducer. Belokin et al. [103] demonstrated that certain soluble high-molecular organosilicone polymers, such as poly(dimethyl siltrimethylene) and poly(dimethyl silmethylene), are very effective for reduction of turbulent frictional resistance in kerosene, and there are many ongoing studies [104,105,106]. In addition, a number of other applications of drag in oilfields have been studied, including enhanced oil recovery (EOR) applications [107,108] and hydraulic fracturing [77,109].
Another major application of polymer-induced DR in sewers has also aroused the interest of researchers. Forester et al. [110] analyzed the effect of a polymeric additive on DR in a pipe flow (where the pipe diameter was 254 mm), and suggested the potential application of drag reduction to sewer systems. Experimental evidence suggested that the discharge capacities of sewers can be increased significantly by appropriate polymer dosing. Detailed studies of this application have been published by Sellin et al. [111] for a number of sewer situations. The cost estimates, pollution, and toxicity problem are also discussed in their study.
Many tests have confirmed that a soluble polymer coating can be used to reduce the friction of ship models. Thurston and Jones [112] reported reduction of friction drag by application of soluble coatings to underwater vessels. Tests were performed in both fresh water and saline water, although the coating location was confined to the stagnation point of the nose. The DR achieved in the model was 33% in fresh water and 30% in seawater. Choi et al. [113] evaluated the effect of compliant coating on the turbulent boundary layer thickness in an aqueous channel flow, and observed significant turbulent DR, induced by the compliant coatings. Their investigation indicated that in order to build up the compliant coating for turbulent skin-frictional DR, the proper combination of material characteristics was necessary.
The use of biocompatible polymeric DR additives in biomedical areas has also been extensively studied [114], and blood-soluble drag reducing polymers have been demonstrated to influence the hydrodynamics in the blood flow of animals when injected intravenously at very low polymer concentration. Many experiments with intravenous drag reduction polymers showed positive hemorheological effects in several animal systems [115,116,117]. These studies indicate that the use of drag reducing polymers in blood has great potential for improving blood flow, and thus affords the possibility for prevention or treatment of circulatory system diseases.
As is well known, polymer induced drag reduction has a wide range of applications in many fields, which provides high impetus for continued study of the drag reduction phenomenon, and we believe that there are yet unearthed application prospects.
6. Conclusions
This article summarizes the recent research on typical synthetic and natural water-soluble polymers and their application as promising drag reducing agents, along with the research achievements in terms of the drag reduction capability. A selective overview of the proposed mechanisms of the polymer-induced turbulent DR and the current state of the experimental and simulation techniques are discussed, focusing on the drag reducing capability and complexity of water-soluble polymers in aqueous flows. The DR efficiency of water-soluble polymers could be dramatically altered by slight changes in experimental factors, including temperature, Reynolds number, pH values, pipe diameter, etc. or in molecular parameters including the molecular weight, polydispersity, intrinsic viscosity, concentration, etc. Therefore, the introduction of relative drag reduction capability for different polymers could be an alternative way covering specific molecular parameters and experimental conditions.
Regarding the importance of polymer structure and chemical composition to the DR, comparison of the DR efficiency of flexible and rigid polymers demonstrates the importance of molecular conformation. Among various polymeric drag reducing agents, synthetic water-soluble polymers can be fabricated with control of the molecular weight, structure, molecular weight distribution, and the characteristics of the ionic groups. Natural water-soluble polymers are inexpensive, biodegradable, fairly shear stable, and can be easily obtained from agricultural resources. However, the biodegradability of natural water-soluble polymers limits their application. It is evident that both synthetic polymers and natural polymers have their own optimum drag reduction conditions, which are closely associated with the rheological, physical, and/or chemical characteristics. Therefore, future work could be extended to improve the drag reduction efficiency of water-soluble polymers by combining the best characteristics of various polymers, e.g., by grafting synthetic polymers onto the backbone of natural polymers. It is believed that these new water-soluble polymers will exhibit more excellent drag reduction capability, thereby expanding the range of applications.
Acknowledgments
This research was financially supported by Inha University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- White, C.M.; Mungal, M.G. Mechanics and prediction of turbulent drag reduction with polymer additives. Annu. Rev. Fluid Mech. 2008, 40, 235–256. [Google Scholar] [CrossRef]
- Ranade, V.V.; Mashelkar, R.A. Turbulent mixing in dilute polymer-solutions. Chem. Eng. Sci. 1993, 48, 1619–1628. [Google Scholar] [CrossRef]
- Abubakar, A.; Al-Wahaibi, T.; Al-Wahaibi, Y.; Al-Hashmi, A.R.; Al-Ajmi, A. Roles of drag reducing polymers in single- and multi-phase flows. Chem. Eng. Res. Des. 2014, 92, 2153–2181. [Google Scholar] [CrossRef]
- Toms, B.A. Some observations on the flow of linear polymer solutions through straight tubes at large Reynolds numbers. Proc. First Int. Congr. Rheol. 1948, 2, 135–141. [Google Scholar]
- Manzhai, V.N.; Nasibullina, Y.R.; Kuchevskaya, A.S.; Filimoshkin, A.G. Physico-chemical concept of drag reduction nature in dilute polymer solutions (the Toms effect). Chem. Eng. Process. 2014, 80, 38–42. [Google Scholar] [CrossRef]
- Brostow, W. Drag reduction in flow: Review of applications, mechanism and prediction. J. Ind. Eng. Chem. 2008, 14, 409–416. [Google Scholar] [CrossRef]
- Greene, H.L.; Mostardi, R.F.; Nokes, R.F. Effects of drag reducing polymers on initiation of atherosclerosis. Polym. Eng. Sci. 1980, 20, 499–504. [Google Scholar] [CrossRef]
- Usui, H.; Li, L.; Suzuki, H. Rheology and pipeline transportation of dense fly ash-water slurry. Korea-Aust. Rheol. J. 2001, 13, 47–54. [Google Scholar]
- Zhang, Y.; Schmidt, J.; Talmon, Y.; Zakin, J.L. Co-solvent effects on drag reduction, rheological properties and micelle microstructures of cationic surfactants. J. Colloid Interface Sci. 2005, 286, 696–709. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.J.; Kawaguchi, Y.; Li, F.C.; Yu, B.; Zakin, J.L.; Hart, D.J.; Zhang, Y. Drag-reducing and heat transfer characteristics of a novel zwitterionic surfactant solution. Int. J. Heat Mass Tranf. 2009, 52, 3547–3554. [Google Scholar] [CrossRef]
- Li, F.C.; Wang, D.Z.; Kawaguchi, Y.; Hishida, K. Simultaneous measurements of velocity and temperature fluctuations in thermal boundary layer in a drag-reducing surfactant solution flow. Exp. Fluids 2004, 36, 131–140. [Google Scholar] [CrossRef]
- Mizunuma, H.; Kobayashi, T.; Tominaga, S. Drag reduction and heat transfer in surfactant solutions with excess counterion. J. Non-Newton. Fluid 2010, 165, 292–298. [Google Scholar] [CrossRef]
- Brunchi, C.E.; Morariu, S.; Bercea, M. Intrinsic viscosity and conformational parameters of xanthan inaqueous solutions: Salt addition effect. Colloid Surf. B 2014, 122, 512–519. [Google Scholar] [CrossRef] [PubMed]
- Qi, Y.; Kawaguchi, Y.; Lin, Z.; Ewing, M.; Christensen, R.N.; Zakin, J.L. Enhanced heat transfer of drag reducing surfactant solutions with fluted tube-in-tube heat exchanger. Int. J. Heat Mass Tranf. 2001, 44, 1495–1505. [Google Scholar] [CrossRef]
- Fu, Z.; Otsuki, T.; Motozawa, M.; Kurosawa, T.; Yu, B.; Kawaguchi, Y. Experimental investigation of polymer diffusion in the drag-reduced turbulent channel flow of inhomogeneous solution. Int. J. Heat Mass Transf. 2014, 77, 860–873. [Google Scholar] [CrossRef]
- Yang, J.W.; Park, H.; Chun, H.H.; Ceccio, S.L.; Perlin, M.; Lee, I. Development and performance at high Reynolds number of a skin-friction reducing marine paint using polymer additives. Ocean Eng. 2014, 84, 183–193. [Google Scholar] [CrossRef]
- Sadicoff, B.L.; Brandão, E.M.; Lucas, E.F. Rheological Behaviour of Poly (Acrylamide-G-Propylene Oxide) Solutions: Effect of Hydrophobic Content, Temperature and Salt Addition. Int. J. Polym. Mater. 2000, 47, 399–406. [Google Scholar] [CrossRef]
- Bhambri, P.; Narain, R.; Fleck, B.A. Thermo-responsive polymers for drag reduction in turbulent Taylor–Couette flow. J. Appl. Polym. Sci. 2016, 133, 44191. [Google Scholar] [CrossRef]
- Patterson, G.K.; Zakin, J.L.; Rodriguez, J.M. Drag Reduction-Polymer Solutions, Soap Solutions and Solid Particle Suspensions in Pipe Flow. Ind. Eng. Chem. 1969, 61, 22–30. [Google Scholar] [CrossRef]
- Wu, X.; Wang, D.; Gao, Y.; Zhao, S.S.; Zheng, W.L. Mechanism analysis on powerful chip and drag reduction of the polymer drilling fluid. Procedia Eng. 2014, 73, 41–47. [Google Scholar]
- Chagas, B.S., Jr.; Machado, D.L.P.; Haag, R.B.; Sousa, C.R.D.; Lucas, E.F. Evaluation of hydrophobically associated polyacrylamide-containing aqueous fluids and their potential use in petroleum recovery. J. Polym. Sci. Part A Polym. Chem. 2004, 91, 3686–3692. [Google Scholar] [CrossRef]
- Eshrati, M.; Al-Hashmi, A.R.; Al-Wahaibi, T.; Al-Wahaibi, Y.; Al-Ajmi, A.; Abubakar, A. Drag reduction using high molecular weight polyacrylamides during multiphase flow of oil and water: A parametric study. J. Petrol. Sci. Eng. 2015, 135, 403–409. [Google Scholar] [CrossRef]
- Yusuf, N.; Al-Wahaibi, T.; Al-Wahaibi, Y.; Al-Ajmi, A.; Al-Hashmi, A.R.; Olawale, A.S.; Mohammed, I.A. Experimental study on the effect of drag reducing polymer on flow patterns and drag reduction in a horizontal oil-water flow. Int. J. Heat Fluid Flow 2012, 37, 74–80. [Google Scholar] [CrossRef]
- Abubakar, A.; Al-Wahaibi, Y.; Al-Hashmi, A.R.; Al-Wahaibi, Y.; Al-Ajmi, A.; Eshrati, M. Empirical correlation for predicting pressure gradients of oil-water flow with drag-reducing polymer. Exp. Therm. Fluid Sci. 2016, 79, 275–282. [Google Scholar] [CrossRef]
- Astarita, G. Possible interpretation of mechanism of drag reduction in viscoelastic liquids. Ind. Eng. Chem. Fundam. 1965, 4, 354–356. [Google Scholar] [CrossRef]
- Gadd, G.E. Reduction of turbulent drag in liquids. Nature 1971, 230, 29–31. [Google Scholar] [CrossRef]
- Shenoy, A.V. A review on drag reduction with special reference to micellar systems. Colloid Polym. Sci. 1984, 262, 319–337. [Google Scholar] [CrossRef]
- Tulin, M.P.B. Hydrodynamic aspects of macromolecular solutions. In Proceedings of the 6th Symposium on Naval Hydrodynamics, Washington, DC, USA, 28 September–4 October 1966; pp. 3–18. [Google Scholar]
- Lumley, J.L. Drag reduction in turbulent flow by polymer additives. J. Polym. Sci. Macromol. Rev. 1973, 7, 263–290. [Google Scholar] [CrossRef]
- Min, T.; Yoo, J.Y.; Choi, H.; Joseph, D.D. Drag reduction by polymer additives in a turbulent channel flow. J. Fluid Mech. 2003, 486, 213–238. [Google Scholar] [CrossRef]
- Kostic, M. The ultimate asymptotes and possible causes of friction drag and heat transfer reduction phenomena. J. Energy Heat Mass Transf. 1994, 16, 1–14. [Google Scholar]
- Armstrong, R.; Jhon, M.S. Turbulence induced change in the conformation of polymer molecules. J. Chem. Phys. 1983, 79, 3143–3147. [Google Scholar] [CrossRef]
- Hidema, R.; Suzuki, H.; Hisamatsu, S.; Komoda, Y.; Furukawa, H. Effects of the extensional rate on two-dimensional turbulence of semi-dilute polymer solution flows. Rheol. Acta 2013, 52, 949–961. [Google Scholar] [CrossRef]
- Brostow, W. Drag reduction and mechanical degradation in polymer solutions in flow. Polymer 1983, 24, 631–638. [Google Scholar] [CrossRef]
- Pereira, A.S.; Soares, E.J. Polymer degradation of dilute solutions in turbulent drag reducing flows in a cylindrical double gap rheometer device. J. Non-Newton. Fluid Mech. 2012, 179–180, 9–22. [Google Scholar] [CrossRef]
- Den Toonder, J.M.J.; Hulsem, M.A.; Kuiken, G.D.C.; Nieuwstadt, F.M. Drag reduction by polymer additives in a turbulent pipe flow: numerical and laboratory experiments. J. Fluid Mech. 1997, 337, 193–231. [Google Scholar] [CrossRef]
- White, C.M.; Somandepalli, V.S.R.; Mungal, M.G. The turbulence structure of drag-reduced boundary layer flow. Exp. Fluids 2004, 36, 62–69. [Google Scholar] [CrossRef]
- Zadrazil, I.; Bismarck, A.; Hewitt, G.F.; Markides, C.N. Shear layers in the turbulent pipe flow of drag reducing polymer solutions. Chem. Eng. Sci. 2012, 72, 142–154. [Google Scholar] [CrossRef]
- Cai, W.H.; Li, F.C.; Zhang, H.N.; Li, X.B.; Yu, B.; Wei, J.J.; Kawaguchi, Y.; Hishida, K. Study on the characteristics of turbulent drag-reducing channel flow by particle image velocimetry combining with proper orthogonal decomposition analysis. Phys. Fluids 2009, 21, 115103. [Google Scholar] [CrossRef]
- Warholic, M.D.; Massah, H.; Hanratty, T.J. Influence of drag-reducing polymers on turbulence: effects of Reynolds number, concentration and mixing. Exp. Fluids 1999, 27, 461–472. [Google Scholar] [CrossRef]
- Itoh, M.; Tamano, S.; Yokota, K.; Ninagawa, M. Velocity measurement in turbulent boundary layer of drag-reducing surfactant solution. Phys. Fluids 2005, 17, 075107. [Google Scholar] [CrossRef]
- Wei, T.; Willmarth, W.W. Modifying turbulent structure with drag-reducing polymer additives in turbulent channel flows. J. Fluid Mech. 1992, 245, 619–641. [Google Scholar] [CrossRef]
- Wedgewood, L.E.; Ostrov, D.N.; Bird, B.R. A finitely extensible beadspring chain model for dilute polymer solutions. J. Non-Newton. Fluid Mech. 1991, 40, 119–139. [Google Scholar] [CrossRef]
- Li, F.C.; Cai, W.H.; Zhang, H.N.; Wang, Y. Inuence of polymer additives on turbulent energy cascading in forced homogeneous isotropic turbulence studied by direct numerical simulations. Chin. Phys. B 2012, 21, 114701. [Google Scholar] [CrossRef]
- Eshrati, M.; Al-Hashmi, A.R.; Ranjbaran, M.; Al-Wahaibi, T.; Al-Wahaibi, Y.; Al-Ajmi, A.; Abubakar, A. Prediction of water-soluble polymer drag reduction performance in multiphase flow using fuzzy logic technique. Int. J. Adv. Chem. Environ. Eng. Biol. Sci. 2016, 3, 1507–1515. [Google Scholar]
- Zadeh, L.A. Similarity relations and fuzzy orderings. Inform. Sci. 1971, 3, 177–200. [Google Scholar] [CrossRef]
- Amrouchene, Y.; Kellay, H. Polymer in 2D turbulence: Suppression of large scale fluctuation. Phys. Rev. Lett. 2002, 89, 088302. [Google Scholar] [CrossRef] [PubMed]
- Jun, Y.; Zhang, J.; Wu, X.L. Polymer effect on small and large scale two-dimensional turbulece. Phys. Rev. Lett. 2006, 96, 024502. [Google Scholar] [CrossRef] [PubMed]
- Kraichnan, R.H. Inertial ranges in Two-dimensional turbulence. Phys. Fluids 1967, 10, 1417–1423. [Google Scholar] [CrossRef]
- Hidema, R.; Suzuki, H.; Hisamatsu, S.; Komoda, Y. Characteristic scales of two-dimensional turbulence in polymer solutions. AIChE J. 2014, 60, 1854–1862. [Google Scholar] [CrossRef]
- Virk, P.S.; Merrill, E.W.; Mickley, H.S.; Smith, K.A. The Toms phenomenon: Turbulent pipe flow of dilute polymer solutions. J. Fluid Mech. 1967, 30, 305–328. [Google Scholar] [CrossRef]
- Little, R.C.; Patterson, R.L.; Ting, R.Y. Characterization of the Drag Reducing Properties of Poly(ethylene oxide) and Poly(acrylamide) Solutions in External Flows. J. Chem. Eng. Data 1976, 21, 281–283. [Google Scholar] [CrossRef]
- Little, R.C. Drag reduction in capillary tubes as a function of polymer concentration and molecular weight. J. Colloid Interface Sci. 1971, 37, 811–818. [Google Scholar] [CrossRef]
- Little, R.C. Flow Properties of Polyox Solutions. Ind. Eng. Chem. Fund. 1969, 8, 557–559. [Google Scholar] [CrossRef]
- Choi, H.J.; Jhon, M.S. Polymer induced Turbulent Drag Reduction. Ind. Eng. Chem. Res. 1996, 35, 2993–2998. [Google Scholar] [CrossRef]
- Kim, C.A.; Sung, J.H.; Choi, H.J.; Kim, C.B.; Chun, W.; Jhon, M.S. Drag Reduction and Mechanical Degradation of Poly(ethylene oxide) in Seawater. J. Chem. Eng. Jpn. 1999, 32, 803–811. [Google Scholar] [CrossRef]
- Choi, H.J.; Kim, C.A.; Sung, J.H.; Kim, C.B.; Chun, W.; Jhon, M.S. Universal drag reduction characteristics of saline water-soluble poly(ethylene oxide) in a rotating disk apparatus. Colloid Polym. Sci. 2000, 278, 701–705. [Google Scholar] [CrossRef]
- Lim, S.T.; Hong, C.H.; Choi, H.J.; Lai, P.Y.; Chan, C.K. Polymer turbulent drag reduction near the theta point. Eur. Phys. Lett. 2007, 80, 58003. [Google Scholar] [CrossRef]
- Sung, J.H.; Kim, C.A.; Choi, H.J.; Hur, B.K.; Kim, J.G.; Jhon, M.S. Turbulent drag reduction efficiency and mechanical degradation of poly(acrylamide). J. Macromol. Sci. Phys. 2004, B43, 507–518. [Google Scholar] [CrossRef]
- Sandoval, G.A.B.; Trevelin, R.; Soares, E.J.; Silveira, L.; Thomaz, F.; Pereira, A.S. Polymer degradation in turbulent drag reducing flows in pipes. Therm. Eng. 2015, 14, 03–06. [Google Scholar]
- Pereira, A.S.; Andrade, R.M.; Soares, E.J. Drag reduction induced by flexible and rigid molecules in a turbulent flow into a rotating cylindrical double gap device: Comparison between Poly(ethylene oxide), Polyacrylamide, and Xanthan Gum. J. Non-Newton. Fluid 2013, 202, 72–87. [Google Scholar] [CrossRef]
- Lim, S.T.; Choi, H.J. λ-DNA induced turbulent drag reduction and its characteristics. Macromolecules 2003, 36, 5348–5354. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, L.; Cheng, L.; Guo, Q.; Zhang, N. Experimental study on heat transfer and pressure drop characteristics of air–water two-phase flow with the effect of polyacrylamide additive in a horizontal circular tube. Int. J. Heat Mass Tranf. 2013, 58, 427–440. [Google Scholar] [CrossRef]
- Terao, K. Poly(acrylic acid) (PAA). In Encyclopedia of Polymeric Nanomaterials; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–6. [Google Scholar]
- Montante, G.; Laurenzi, F.; Paglianti, A.; Magelli, F. A study on some effects of a drag-reducing agent on the performance of a stirred vessel. Chem. Eng. Des. Des. 2011, 89, 2262–2267. [Google Scholar] [CrossRef]
- Kim, J.T.; Kim, C.A.; Zhang, K.; Jang, C.H.; Choi, H.J. Effect of polymer–surfactant interaction on its turbulent drag reduction. Colloid Surf. A 2011, 391, 125–129. [Google Scholar] [CrossRef]
- Kim, O.K.; Choi, L.S.; Long, T.; McGrath, K.; Armistead, J.P.; Yoon, T.H. Unusual complexation behavior of poly(acry1ic acid) induced by shear. Macromolecules 1993, 26, 379–384. [Google Scholar] [CrossRef]
- Zhang, K.; Choi, H.J.; Jang, C.H. Turbulent drag reduction characteristics of poly(acrylamide-co-acrylic acid) in a rotating disk apparatus. Colloid Polym. Sci. 2011, 289, 821–1827. [Google Scholar] [CrossRef]
- Zhang, K.; Lim, G.H.; Choi, H.J. Mechanical degradation of water-soluble acrylamide copolymer under a turbulent flow: Effect of molecular weight and temperature. J. Ind. Eng. Chem. 2016, 33, 156–161. [Google Scholar] [CrossRef]
- Cole, D.P.; Khosravi, E.; Musa, O.M. Efficient water-Soluble drag reducing star polymers with improved mechanical stability. J. Polym. Sci. Polym. Chem. 2016, 54, 335–344. [Google Scholar] [CrossRef]
- Pinschmidt, R.K.; Renz, W.L.; Carroll, W.E.; Yocoub, K.; Drescher, J.; Nordquist, A.F.; Chen, N. N-Vinylformamide—Building Block for Novel Polymer Structures. J. Macromol. Sci. Pure Appl. Chem. 1997, A34, 1885–1905. [Google Scholar] [CrossRef]
- Gu, L.; Zhu, S.; Hrymak, A.N.; Pelton, R.H. Kinetics and modeling of free radical polymerization of N-vinylformamide. Polymer 2001, 42, 3077–3086. [Google Scholar] [CrossRef]
- Marhefka, J.N.; Marascalco, P.J.; Chapman, T.M.; Russell, A.J.; Kameneva, M.V. Poly(N-vinylformamide)—A drag-reducing polymer for biomedical applications. Biomacromolecules 2006, 2, 1597–1603. [Google Scholar] [CrossRef] [PubMed]
- Mishra, M.M.; Yadav, M.; Sand, A.; Tripathy, J.; Behari, K. Water soluble graft copolymer (κ-carrageenan-g-N-vinyl formamide): Preparation characterization and application. Carbohydr. Polym. 2010, 80, 235–241. [Google Scholar] [CrossRef]
- Mccormick, C.L.; Hester, R.D.; Morgan, S.E.; Safieddine, A.M. Water-Soluble Copolymers. 30. Effects of Molecular Structure on Drag Reduction Efficiency. Macromolecules 1990, 23, 2124–2131. [Google Scholar] [CrossRef]
- Mumick, P.S.; Welch, P.M.; Salazar, L.C.; Mccormick, C.L. Water-Soluble Copolymers. 56. Structure and Solvation Effects of Polyampholytes in Drag Reduction. Macromolecules 1994, 27, 323–331. [Google Scholar] [CrossRef]
- Brun, N.L.; Zadrazil, I.; Norman, L.; Bismarck, A.; Markides, C.N. On the drag reduction effect and shear stability of improved acrylamide copolymers for enhanced hydraulic fracturing. Chem. Eng. Sci. 2016, 146, 135–143. [Google Scholar] [CrossRef]
- Lumley, J.L. Drag reduction by additives. Ann. Rev. Fluid Mech. 1969, 1, 367–384. [Google Scholar] [CrossRef]
- Reis, L.G.; Oliveira, I.P.; Pires, R.V.; Lucas, E.F. Influence of structure and composition of poly(acrylamide-g-propylene oxide) copolymers on drag reduction of aqueous dispersions. Colloid Surf. A 2016, 502, 121–129. [Google Scholar] [CrossRef]
- Camail, M.; Margaillan, A.; Martin, I. Copolymers of N-alkyl- and N-arylalkylacrylamides with acrylamide: influence of hydrophobic structure on associative properties. Part I: viscometric behaviour in dilute solution and drag reduction performance. Polym. Int. 2009, 58, 149–154. [Google Scholar] [CrossRef]
- Al-Hashmi, A.; Al-Maamari, R.; Al-Shabibi, I.; Mansoor, A.; Al-Sharji, H.; Zaitoun, A. Mechanical stability of high-Molecular-weight polyacrylamides and an (acrylamido tert-butyl sulfonic acid)-acrylamide copolymer used in enhanced oil recovery. J. Appl. Polym. Sci. 2014, 131, 40921. [Google Scholar] [CrossRef]
- Akbar Ali, S.K.; Singh, R.P. An investigation of the flocculation characteristics of polyacrylamide-grafted chitosan. J. Appl. Polym. Sci. 2009, 114, 2410–2414. [Google Scholar]
- Singha, V.; Tiwaria, A.; Tripathia, D.N.; Sanghib, R. Microwave assisted synthesis of Guar-g-polyacrylamide. Carbohydr. Polym. 2004, 58, 1–6. [Google Scholar] [CrossRef]
- Kim, C.A.; Lim, S.T.; Choi, H.J.; Sohn, J.I.; Jhon, M.S. Characterization of drag reducing guar gum in a rotating disk flow. J. Appl. Polym. Sci. 2002, 83, 2938–3944. [Google Scholar] [CrossRef]
- Singh, R.P.; Pal, S.; Krishnamoorthy, S.; Adhikary, P.; Ali, S.A. High-technology materials based on modified polysaccharides. Pure Appl. Chem. 2009, 81, 525–547. [Google Scholar] [CrossRef]
- Deshmukh, S.R.; Chaturvedi, P.N.; Singh, R.P. The turbulent drag reduction by graft copolymers of guargum and polyacrylamide. J. Appl. Polym. Sci. 1985, 30, 4013–4018. [Google Scholar] [CrossRef]
- Behari, K.; Kumar, R.; Tripathi, M.; Pandey, P.K. Graft Copolymerization of Methacrylamide onto guar Gum using a potassium chromate/malonic acid redox pair. Macromol. Chem. Phys. 2001, 202, 1873–1877. [Google Scholar] [CrossRef]
- Bewersdorff, H.W.; Singh, R.P. Rheological and drag reduction characteristics of xanthan gum solutions. Rheol. Acta 1988, 27, 617–627. [Google Scholar] [CrossRef]
- Katzbauer, B. Properties and applications of xanthan gum. Polym. Degrad. Stabil. 1998, 59, 81–84. [Google Scholar] [CrossRef]
- Sohn, J.I.; Kim, C.A.; Choi, H.J.; Jhon, M.S. Drag-reduction effectiveness of xanthan gum in a rotating disk apparatus. Carbohydr. Polym. 2001, 45, 61–68. [Google Scholar] [CrossRef]
- Hong, C.H.; Choi, H.J.; Zhang, K.; Renou, F.; Grisel, M. Effect of salt on turbulent drag reduction of xanthan gum. Carbohydr. Polym. 2015, 121, 342–347. [Google Scholar] [CrossRef] [PubMed]
- Andrade, R.M.; Pereira, A.S.; Soares, E.J. Drag reduction in synthetic seawater by flexible and rigid polymer addition into a rotating cylindrical double gap device. J. Fluid Eng. 2016, 138, 021101. [Google Scholar] [CrossRef]
- Pushpamalar, V.; Langford, S.J.; Ahmad, M.; Lim, Y.Y. Optimization of reaction conditions for preparing carboxymethyl cellulose from sago waste. Carbohydr. Polym. 2006, 64, 312–318. [Google Scholar] [CrossRef]
- Biswal, D.R.; Singh, R.P. Characterisation of carboxymethyl cellulose and polyacrylamide graft copolymer. Carbohydr. Polym. 2004, 57, 379–387. [Google Scholar] [CrossRef]
- Abdulbari, H.A.; Shabirin, A.; Abdurrahman, H.N. Bio-polymers for improving liquid flow in pipelines—A review and future work opportunities. J. Ind. Eng. Chem. 2014, 20, 1157–1170. [Google Scholar] [CrossRef]
- Deshmukh, S.R.; Sudhakar, K.; Singh, R.P. Drag-reduction efficiency, shear stability, and biodegradation resistance of carboxymethyl cellulose-based and starch-based graft copolymers. J. Appl. Polym. Sci. 1991, 43, 1091–1101. [Google Scholar] [CrossRef]
- Rana, T.M. Illuminating the silence: Understanding the structure and function of small RNAs. Nat. Rev. Mol. Cell Biol. 2007, 8, 23–36. [Google Scholar] [CrossRef] [PubMed]
- Choi, H.J.; Lim, S.T.; Lai, P.Y.; Chan, C.K. Turbulent drag reduction and degradation of DNA. Phys. Rev. Lett. 2002, 89, 088302. [Google Scholar] [CrossRef] [PubMed]
- Lim, S.T.; Park, S.J.; Chan, C.K.; Choi, H.J. Turbulent drag reduction characteristics induced by calf-thymus DNA. Physica A 2005, 350, 84–88. [Google Scholar] [CrossRef]
- Lim, S.T.; Choi, H.J.; Chan, C.K. Effect of turbulent flow on coil-globule transition of lambda-DNA. Macromol. Rapid. Commun. 2005, 26, 1237–1240. [Google Scholar] [CrossRef]
- Ueberschär, O.; Wagner, C.; Stangner, T.; Kühne, K.; Gutsche, C.; Kremer, F. Drag reduction by DNA-grafting for single microspheres in a dilute lambda-DNA solution. Polymer 2011, 52, 4021–4032. [Google Scholar] [CrossRef]
- Evans, A.P. A new drag-reducing polymer with improved Shear Stability for nonaqueous systems. J. Appl. Polym. Sci. 1974, 18, 1919–1925. [Google Scholar] [CrossRef]
- Belokon, V.S.; Bespalova, N.B.; Vdovin, V.M.; Vlasov, S.A.; Kalashnikov, V.N.; Ushakov, N.V. Reduction of the hydrodynamic friction of hydrocarbons by means of small additions of certain organosilicon polymers. J. Eng. Phys. Thermophys. 1979, 36, 1–3. [Google Scholar] [CrossRef]
- Rodrigues, R.K.; Folsta, M.G.; Martins, A.L.; Sabadini, E. Tailoring of wormlike micelles as hydrodynamic drag reducers for gravel-pack in oil field operations. J. Petrol. Sci. Eng. 2016, 146, 142–148. [Google Scholar] [CrossRef]
- Mortazavi, S.M.M. Correlation of polymerization conditions with drag reduction efficiency of poly(1-hexene) in oil pipelines. Iran. Polym. J. 2016, 25, 731–737. [Google Scholar] [CrossRef]
- Wang, Z.H.; Yu, X.Y.; Li, J.X.; Wang, J.G.; Zhang, L. The use of biobased surfactant obtained by enzymatic syntheses for wax deposition inhibition and drag reduction in crude Oil Pipelines. Catalysts 2016, 6, 61. [Google Scholar] [CrossRef]
- Taylor, K.C.; Nasr-El-Din, H.A. Water-soluble hydrophobically associating polymers for improved oil recovery: A literature review. J. Petrol. Sci. Eng. 1998, 19, 265–280. [Google Scholar] [CrossRef]
- Wever, D.A.Z.; Picchioni, F.; Broekhuis, A.A. Polymers for enhanced oil recovery: A paradigm for structure–property relationship in aqueous solution. Prog. Polym. Sci. 2011, 36, 1558–1628. [Google Scholar] [CrossRef]
- Wang, L.; Wang, D.; Shen, Y.; Lai, X.; Guo, X. Study on properties of hydrophobic associating polymer as drag reduction agent for fracturing fluid. J. Polym. Res. 2016, 23. [Google Scholar] [CrossRef]
- Forester, R.H.; Larson, R.E.; Hayden, J.W.; Wetzel, J.M. Effects of polymer addition on friction in a 10-inch diameter pipe. J. Hydronaut. 1969, 3, 59–62. [Google Scholar] [CrossRef]
- Sellin, R.H.J. Increasing sewer capacity by polymer dosing. Proc. Inst. Civ. Eng. 1977, 63, 49–67. [Google Scholar] [CrossRef]
- Thurston, S.; Jones, R.D. Experimental model studies of non-newtonian soluble coatings for drag reduction. AIAA 1964. [Google Scholar] [CrossRef]
- Choi, K.S.; Yang, X.; Clayton, B.R.; Glover, E.J.; Altar, M.; Semenov, B.N.; Kulik, V.M. Turbulent drag reduction using compliant surfaces. Proc. Math. Phys. Eng. Sci. 1997, 453, 2229–2240. [Google Scholar] [CrossRef]
- Greene, H.L.; Nokes, R.F.; Thomas, L.C. Biomedical implications of drag reducing agents. Biorheology 1971, 7, 221–223. [Google Scholar] [PubMed]
- Polimeni, P.L.; Coleman, P. Enhancement of aortic blood flow with a linear anionic macropolymer of extraordinary molecular length. J. Mol. Cell. Cardiol. 1985, 17, 721–724. [Google Scholar] [CrossRef]
- Sawchuk, A.P.; Unthank, J.L.; Dalsing, M.C. Drag reducing polymers may decrease atherosclerosis by increasing shear in areas normally exposed to low shear stress. J. Vasc. Surg. 1999, 30, 761–764. [Google Scholar] [CrossRef]
- Kameneva, M.V.; Wu, Z.J.; Uraysh, A.; Repko, B.; Litwak, K.N.; Billiar, T.R.; Fink, M.P.; Simmons, R.L.; Griffith, B.P.; Borovetz, H. Blood soluble drag-reducing polymers prevent lethality from hemorrhagic shock in acute animal experiments. Biorheology 2004, 41, 53–64. [Google Scholar] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).