Modeling and Optimization of High-Performance Polymer Membrane Reactor Systems for Water–Gas Shift Reaction Applications
Abstract
:1. Introduction and Prior Work
2. Systems Analysis—Process Modeling, Simulation and Optimization Approach
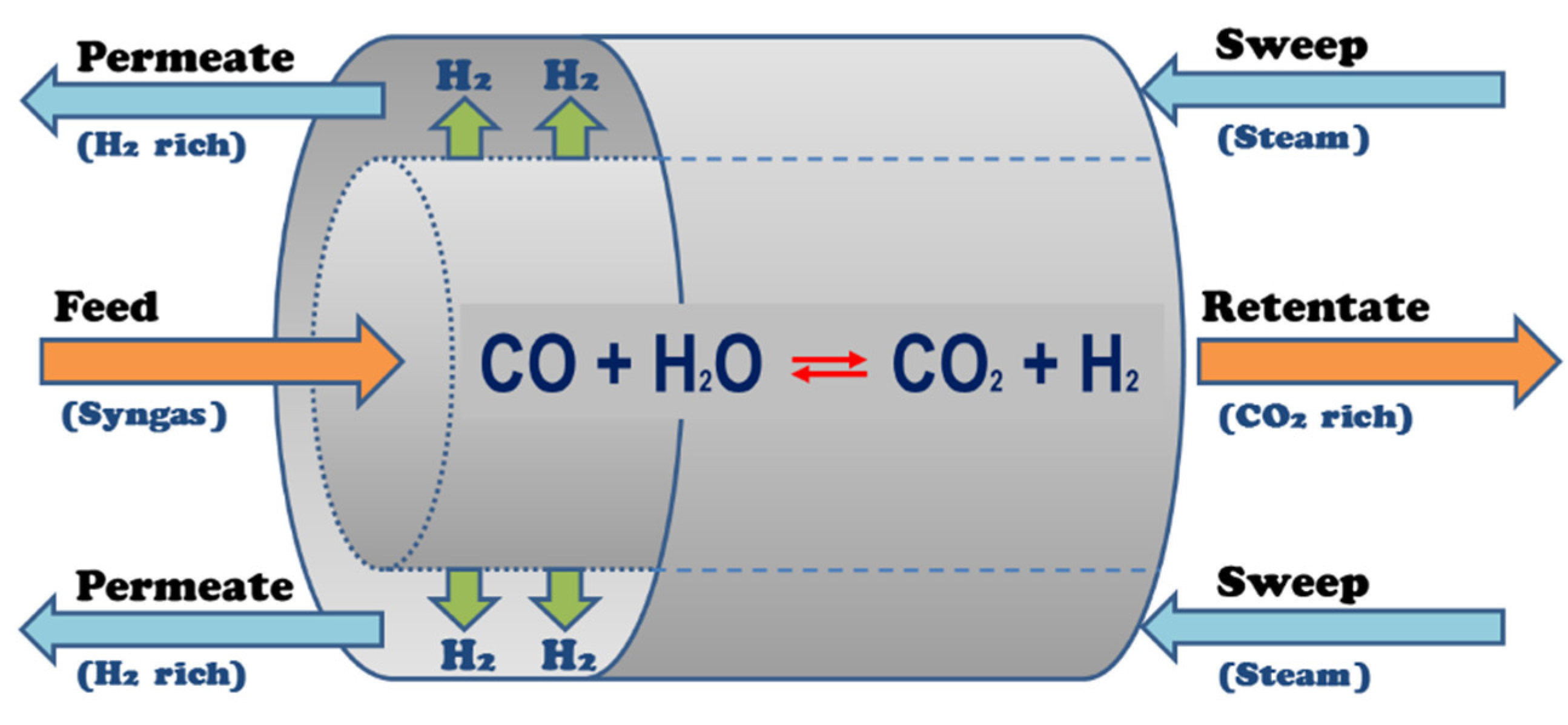
2.1. Membrane Modeling
- QH2 = 250 GPU
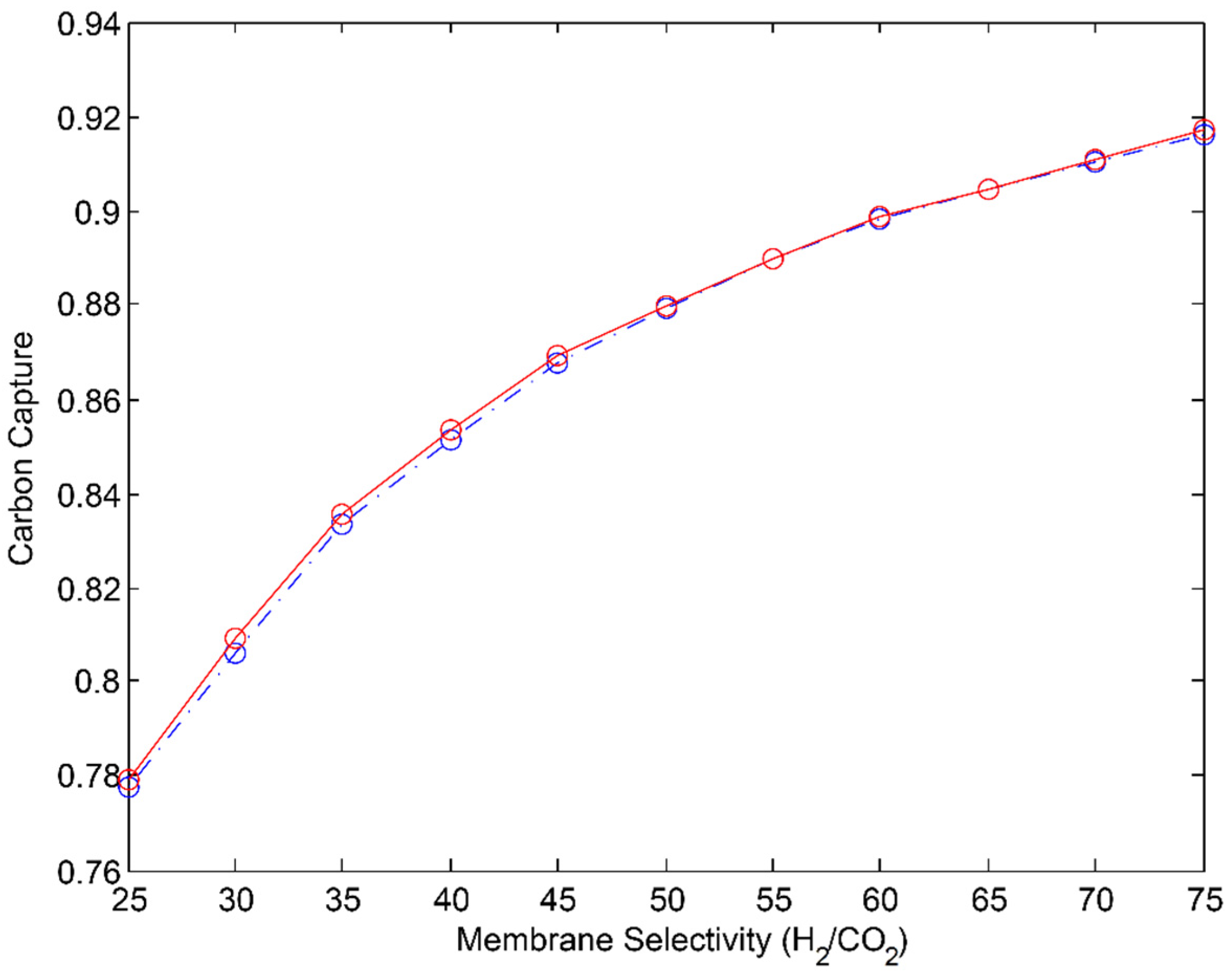
- αH2/CO2 = 20–28
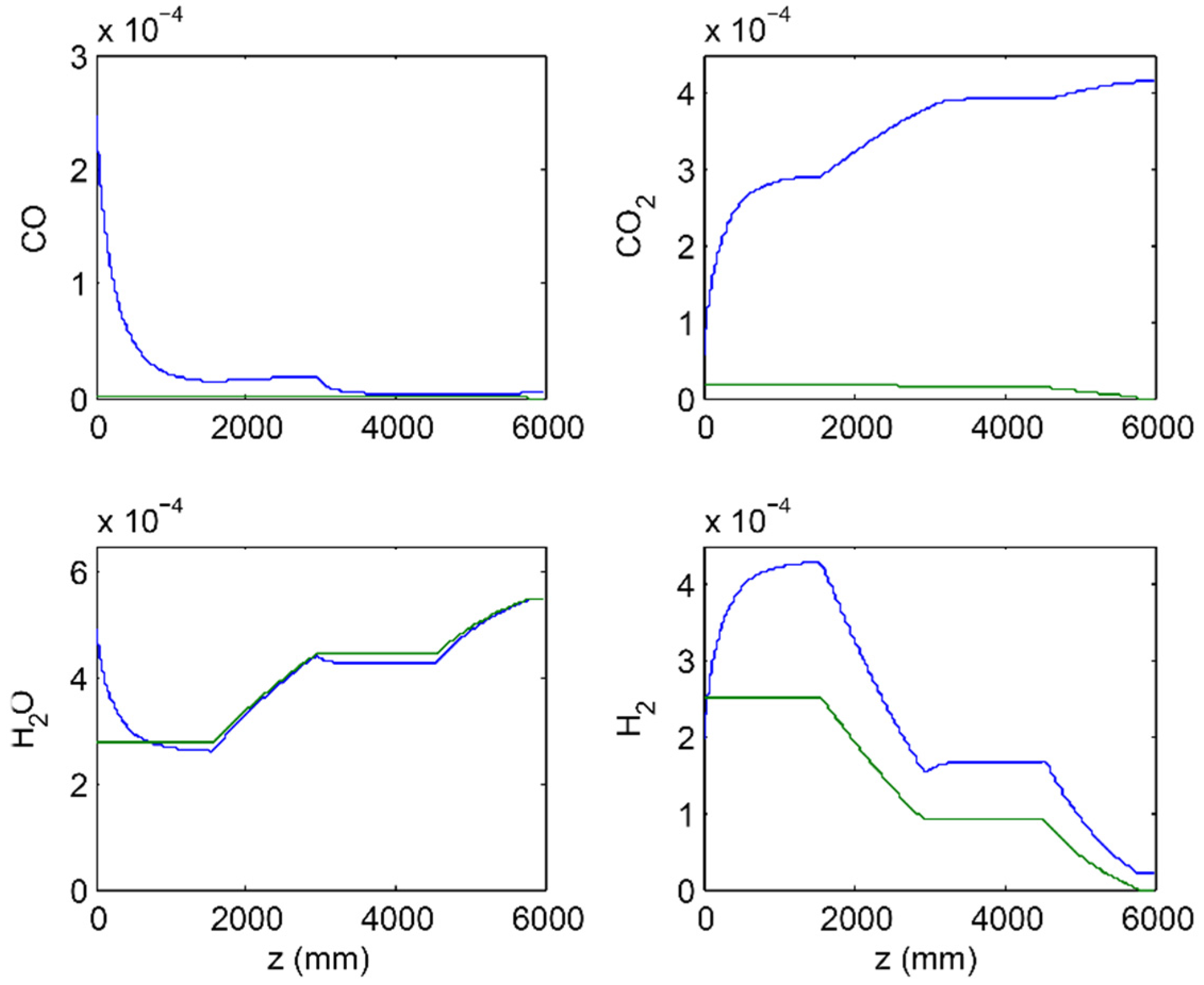
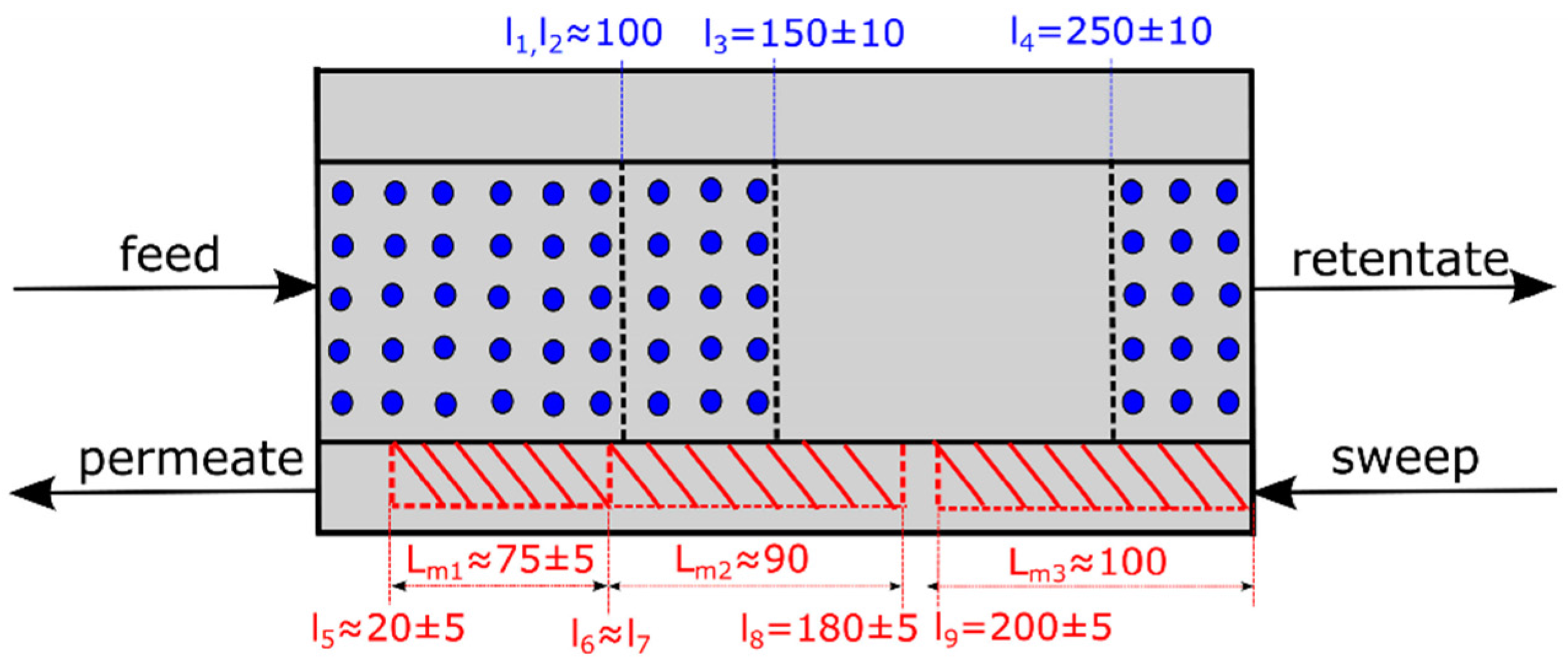
2.2. Simulation Set Up
- CO conversion (XCO)
- H2 recovery (RH2)
- CO2 Capture (CCO2)
- CO2 + H2O purity in the retentate
- H2 mole fraction in the retentate
- H2 purity in the permeate
2.3. Optimization Problem Formulations
3. Systems Analysis Results
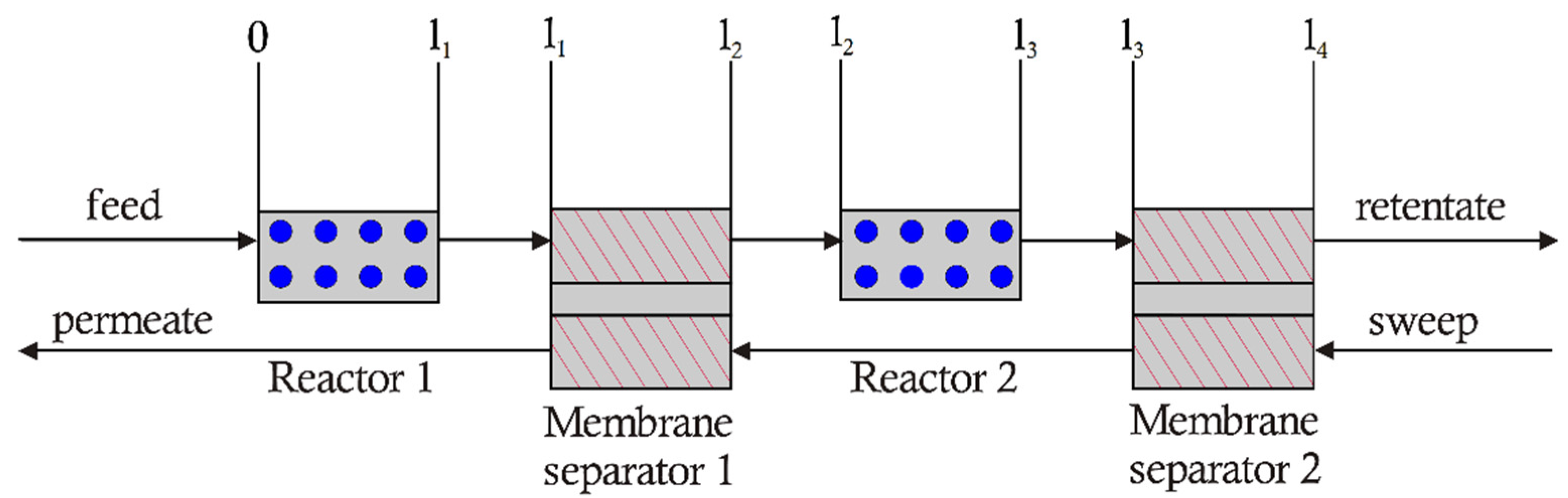
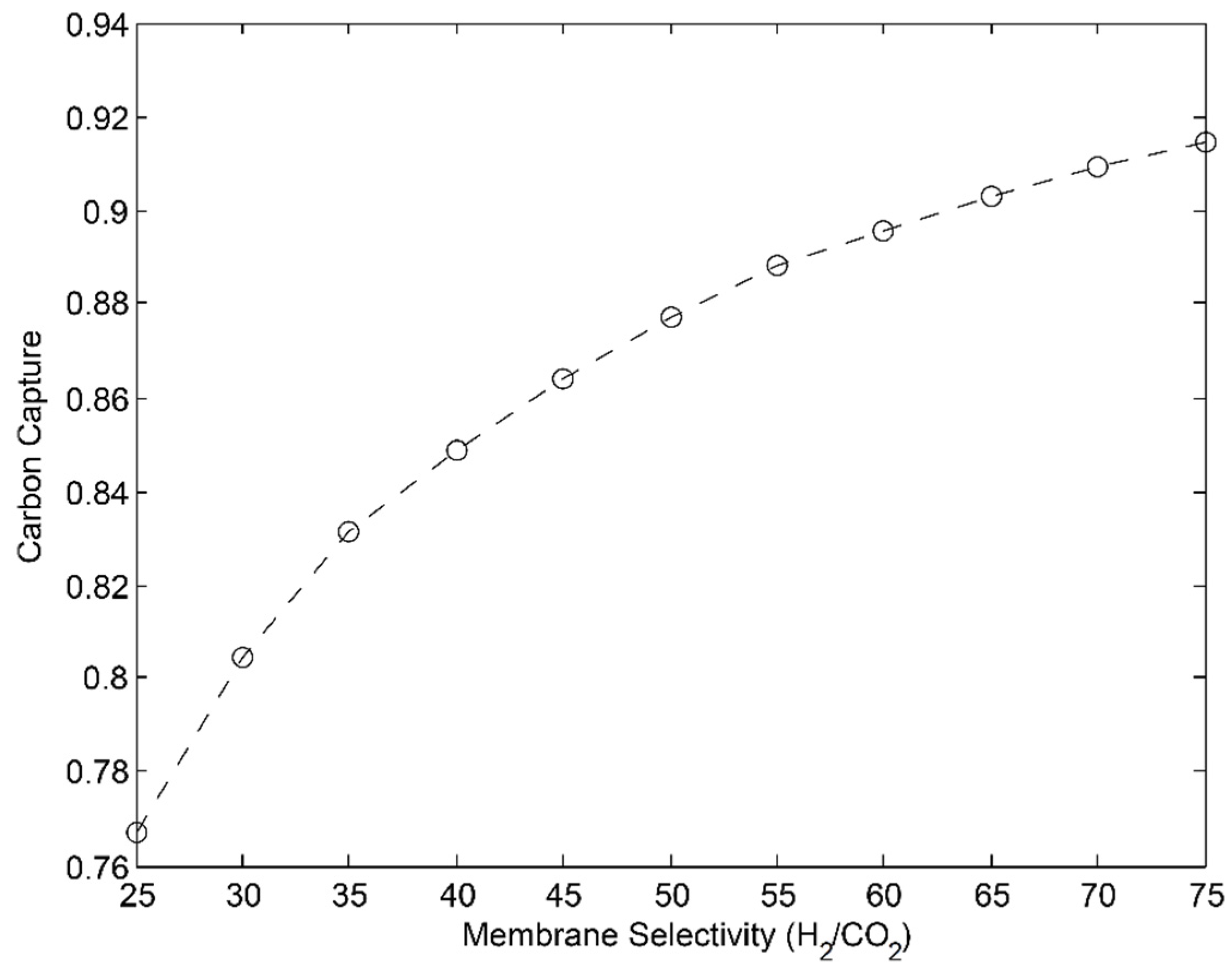
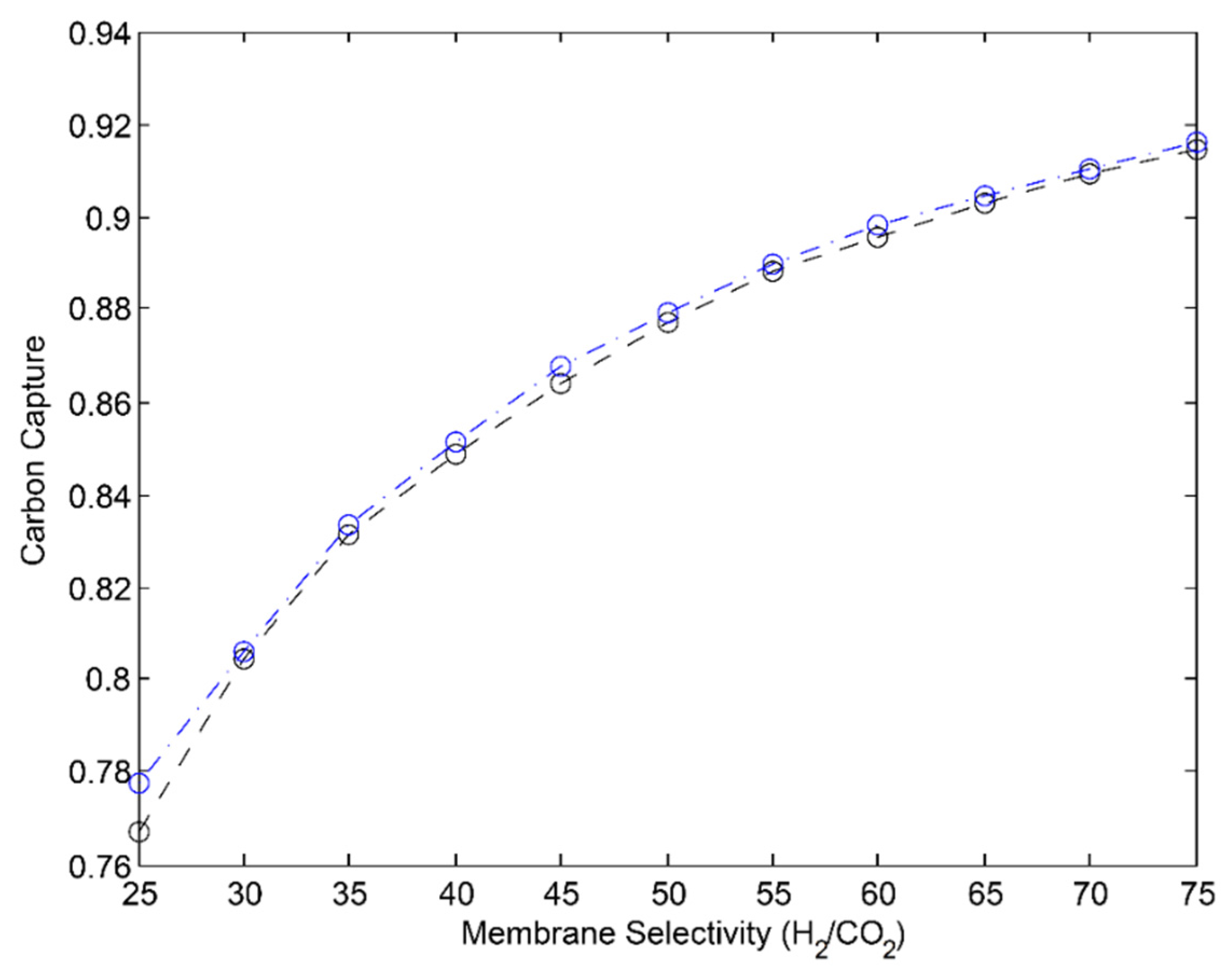
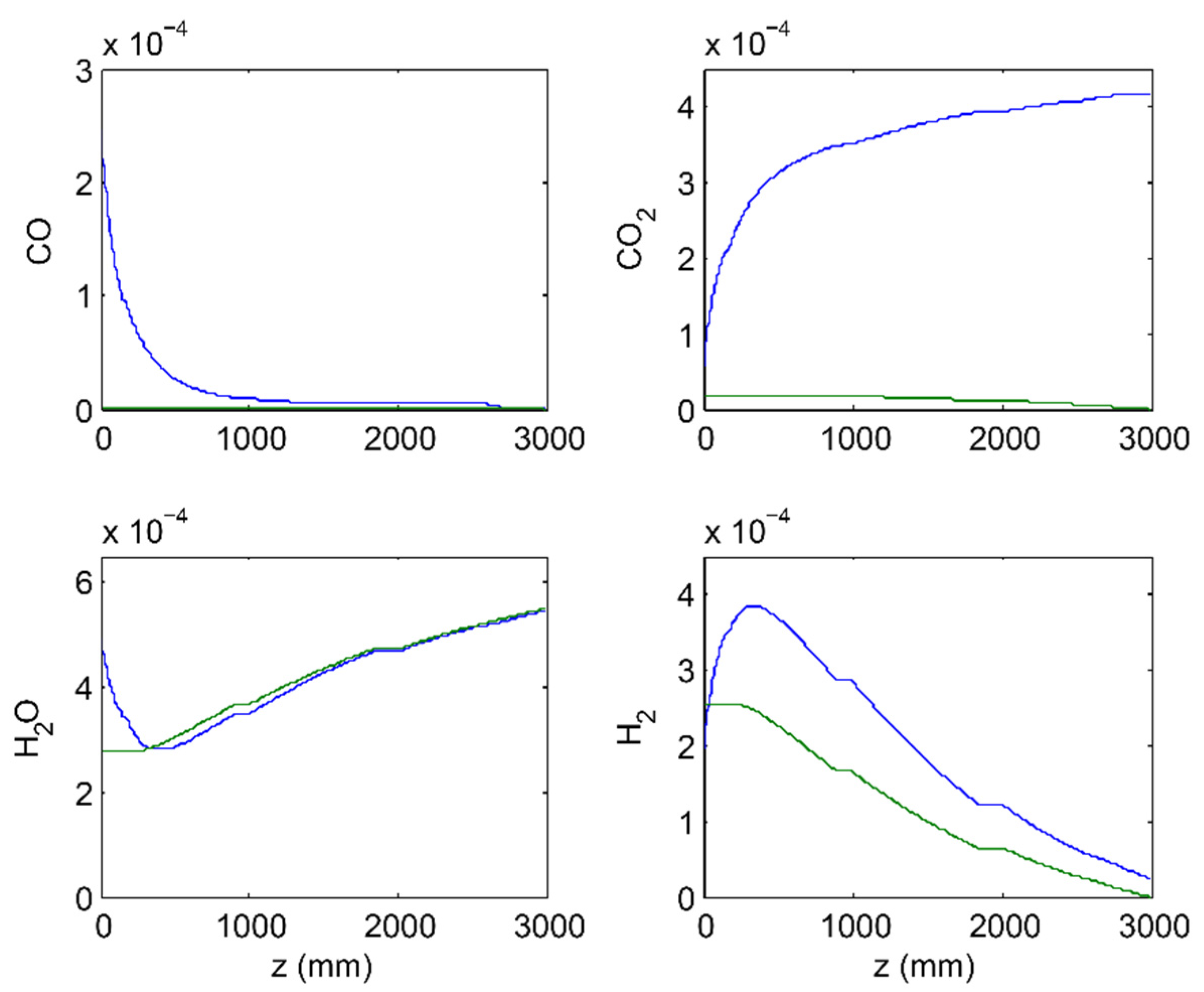
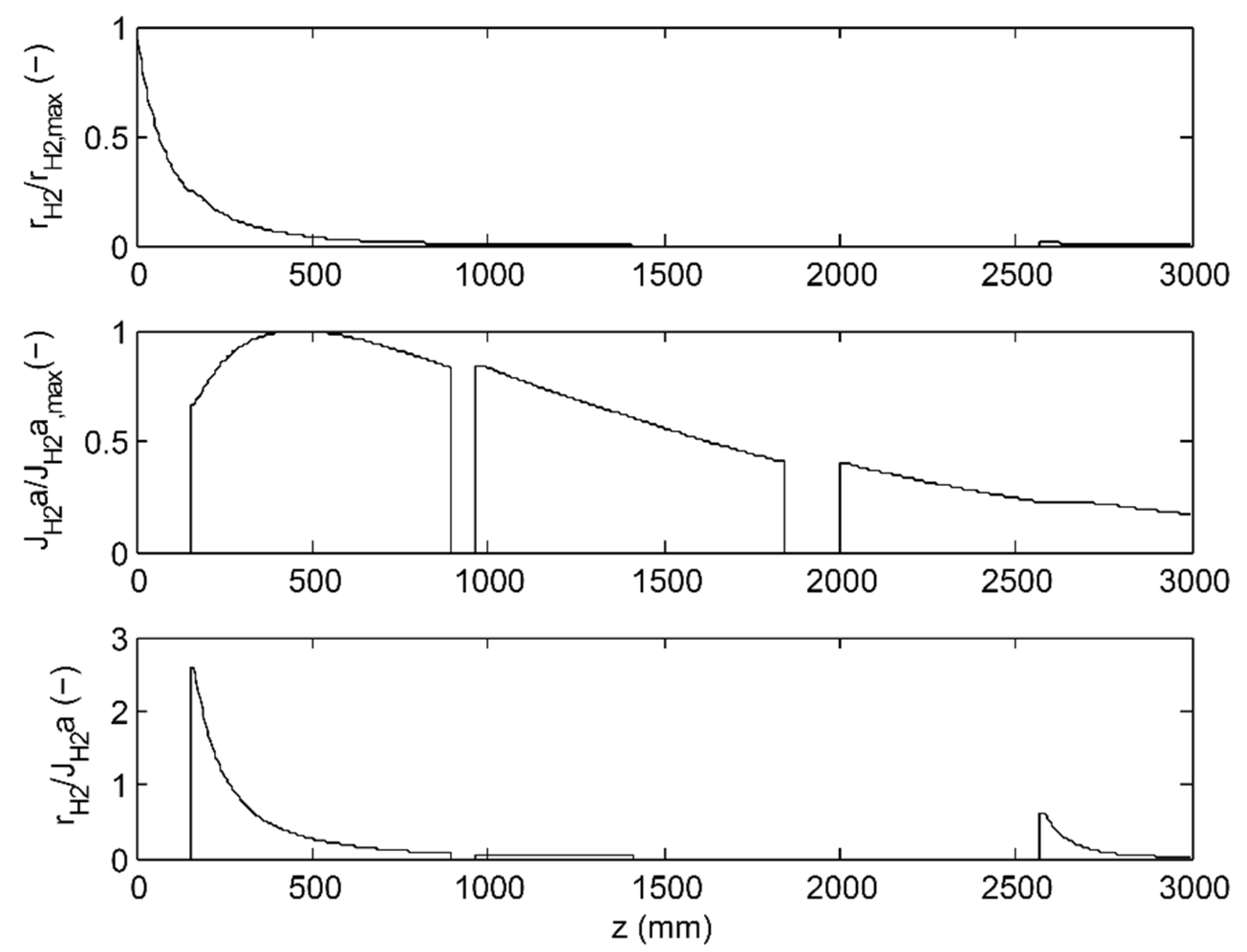
3.1. 2-Stage Permeative Stage Membrane Reactor Performance, Optimization
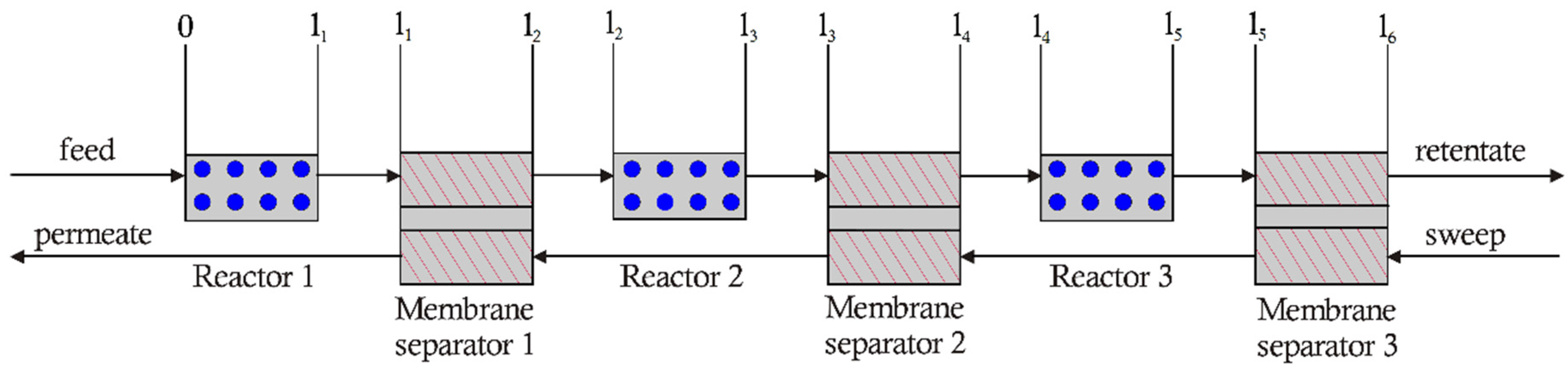
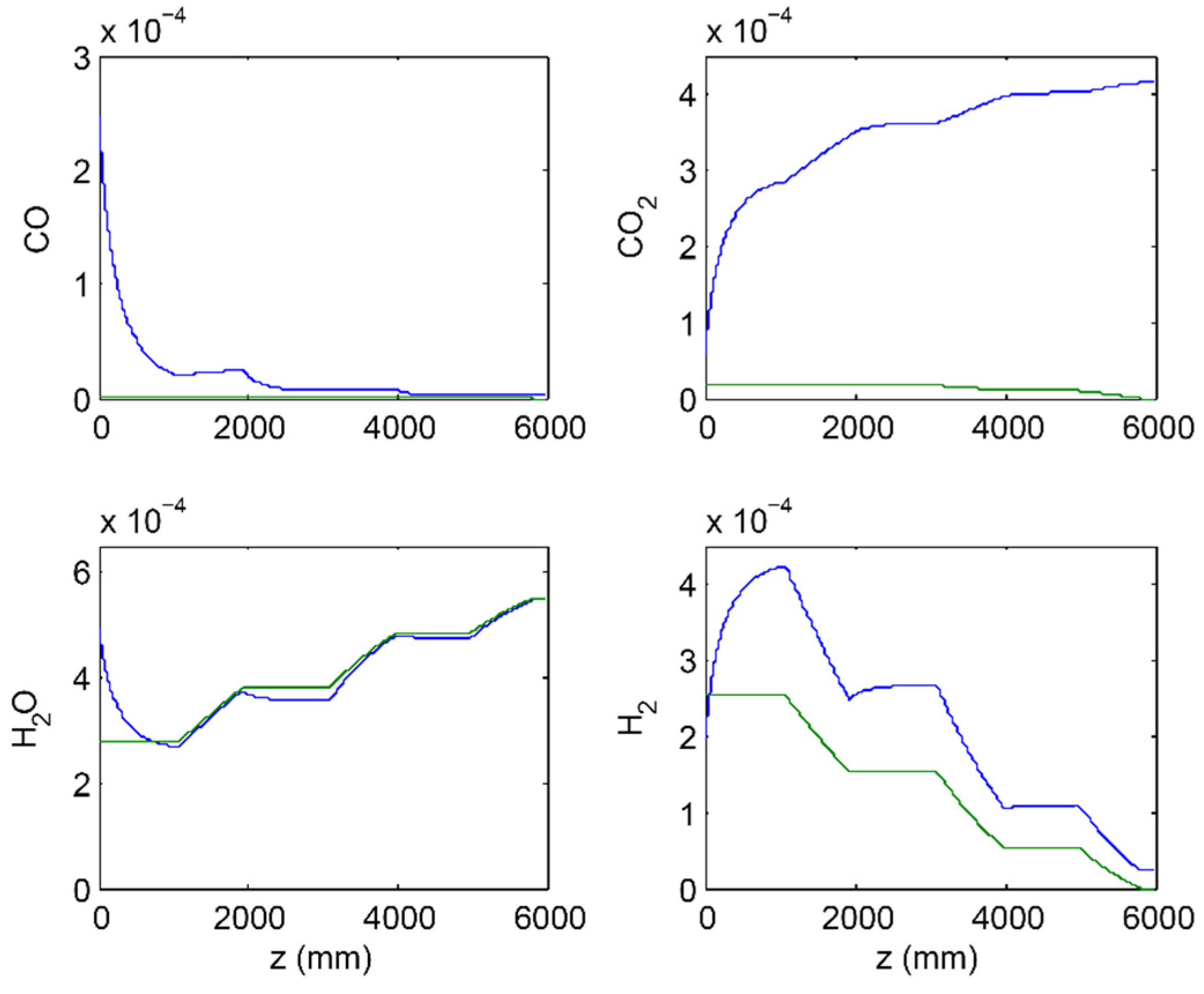
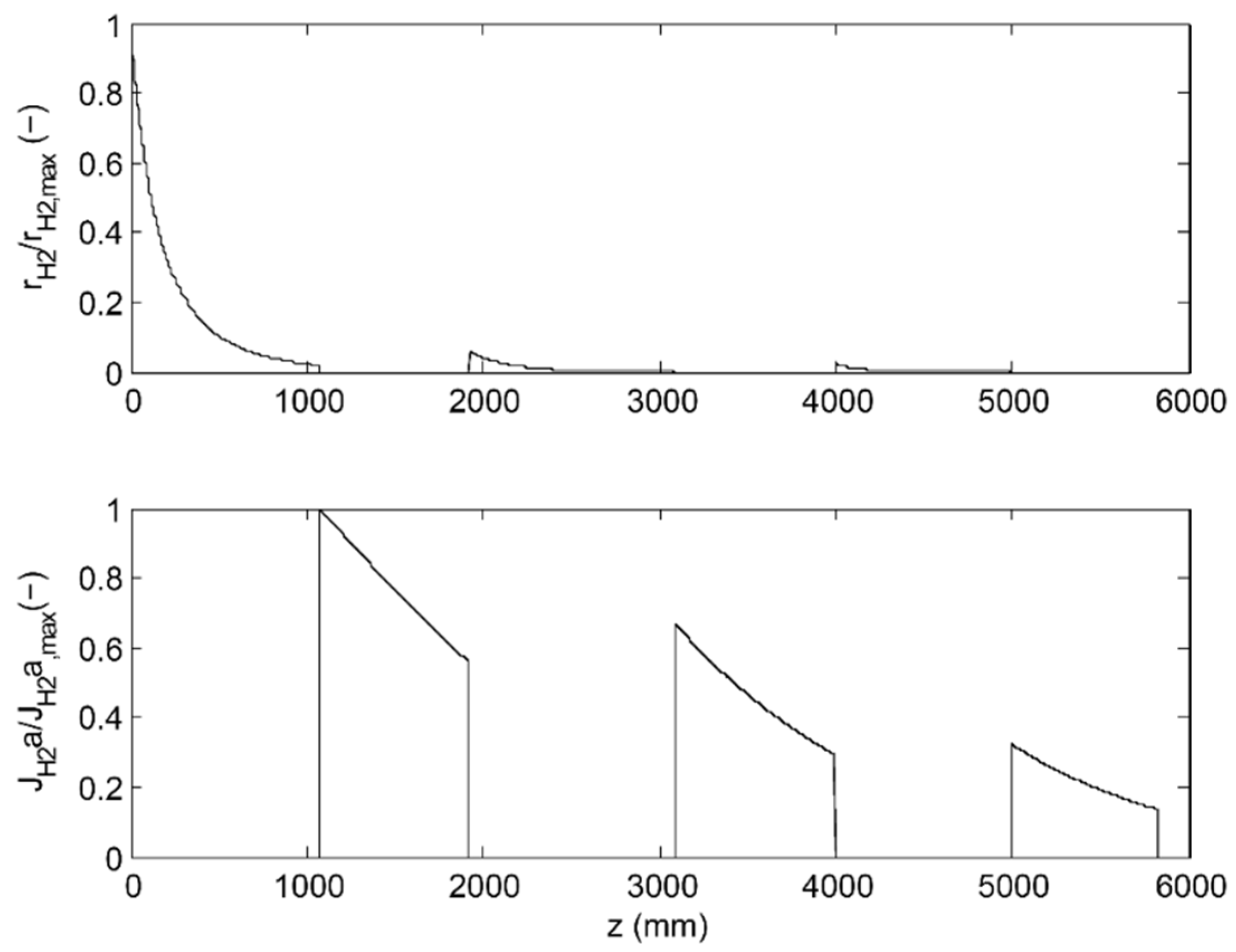
3.2. 3-Stage Permeative Stage Membrane Reactor Performance, Optimization
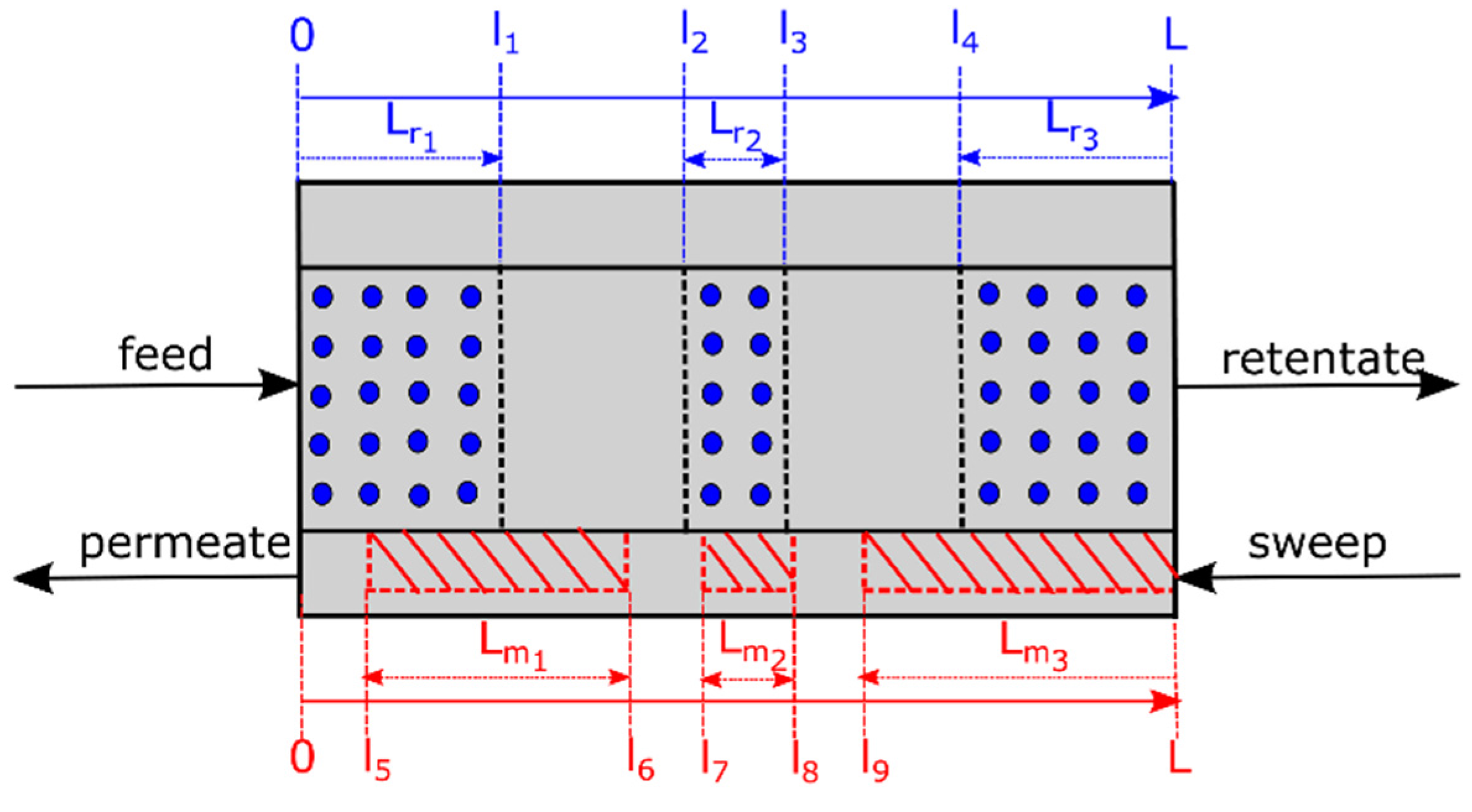
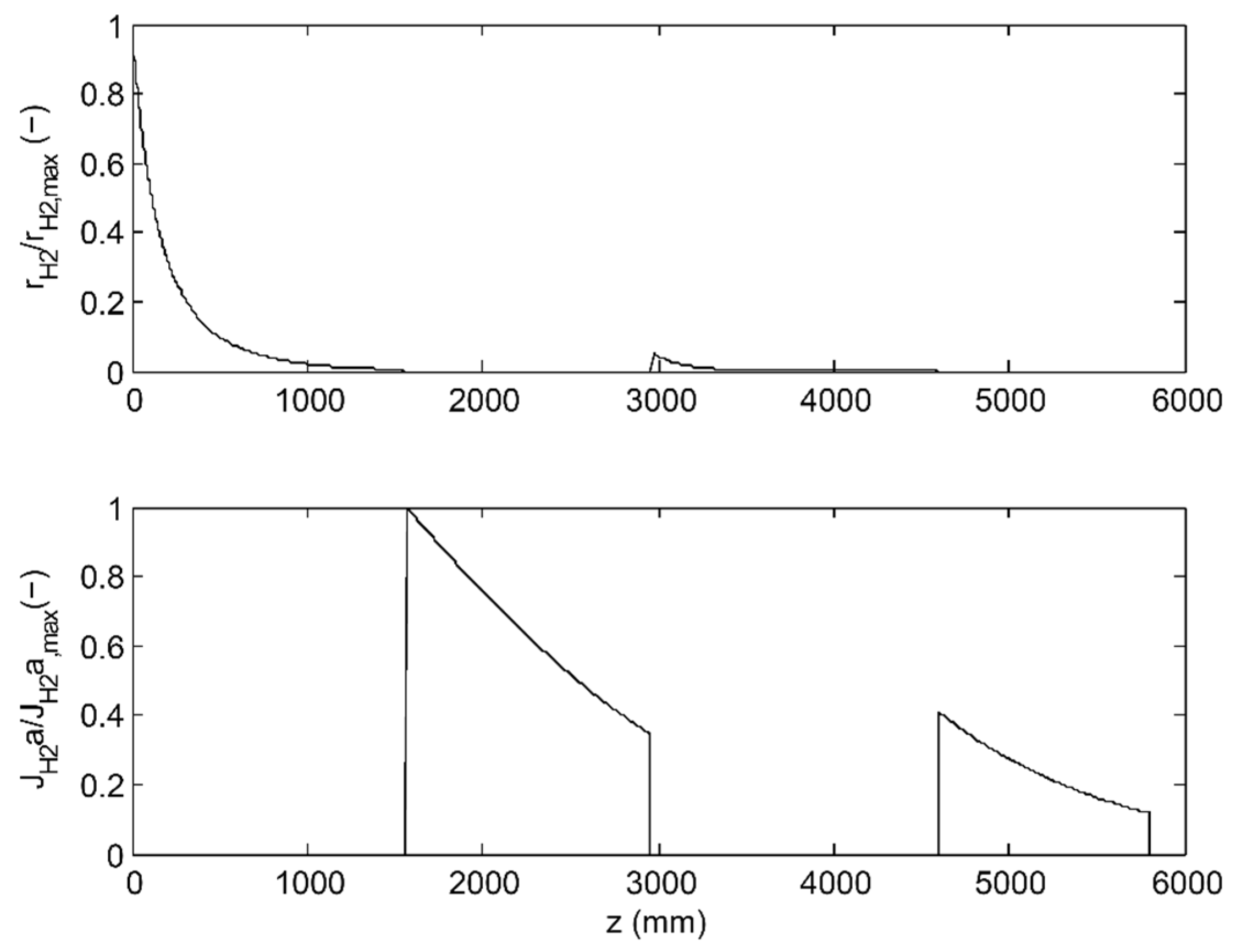
3.3. Membrane Reactor Performance, Optimization
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Marbán, G.; Valdés-Solís, T. Towards the hydrogen economy? Int. J. Hydrogen Energy 2007, 32, 1625–1637. [Google Scholar] [CrossRef]
- Lima, F.V.; Daoutidis, P.; Tsapatsis, M.; Marano, J.J. Modeling and optimization of membrane reactors for carbon capture in integrated gasification combined cycle units. Ind. Eng. Chem. Res. 2012, 51, 5480–5489. [Google Scholar] [CrossRef]
- Woods, M.C.; Capicotto, P.J.; Haslbeck, J.L.; Kuehn, N.J.; Matuszewski, M.; Pinkerton, L.L.; Rutkowski, M.D.; Schoff, R.L.; Vaysman, V. Cost and Performance Baseline for Fossil Energy Plants. Volume 1: Bituminous Coal and Natural Gas to Electricity; Final Report, Technical Report Revision 1, DOE/NETL-2007/1281; U.S. Department of Energy: Washington, DC, USA, 2007.
- Lima, F.V.; Daoutidis, P.; Tsapatsis, M. Modeling, optimization, and cost analysis of an IGCC plant with a membrane reactor for carbon capture. AIChE J. 2016. [Google Scholar] [CrossRef]
- Berchtold, K.A.; Singh, R.P.; Young, J.S.; Dudeck, K.W. Polybenzimidazole composite membranes for high temperature synthesis gas separations. J. Membr. Sci. 2012, 415–416, 265–270. [Google Scholar] [CrossRef]
- Singh, R.P.; Berchtold, K.A. Chapter 6—H2 Selective Membranes for Precombustion Carbon Capture. In Novel Materials for Carbon Dioxide Mitigation Technology; Morreale, F.S., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; pp. 177–206. [Google Scholar]
- Li, X.; Singh, R.P.; Dudeck, K.W.; Berchtold, K.A.; Benicewicz, B.C. Influence of polybenzimidazole main chain structure on H2/CO2 separation at elevated temperatures. J. Membr. Sci. 2014, 461, 59–68. [Google Scholar] [CrossRef]
- Zou, J.; Ho, W.S.W. Hydrogen purification for fuel cells by carbon dioxide removal membrane followed by water gas shift reaction. J. Chem. Eng. Japan 2007, 40, 1011–1020. [Google Scholar] [CrossRef]
- Huang, J.; El-Azzami, L.; Ho, W.S.W. Modeling of CO2-selective water-gas-shift membrane reactor for fuel cell. J. Membr. Sci. 2005, 261, 67–75. [Google Scholar] [CrossRef]
- Singh, R.P.; Dahe, G.J.; Dudeck, K.W.; Welch, C.F.; Berchtold, K.A. High temperature polybenzimidazole hollow fiber membranes for hydrogen separation and carbon dioxide capture from synthesis gas. Energy Procedia 2014, 63, 153–159. [Google Scholar] [CrossRef]
- Merkel, T.C.; Zhou, M.; Baker, R.W. Carbon dioxide capture with membranes at an IGCC power plant. J. Membr. Sci. 2012, 389, 441–450. [Google Scholar] [CrossRef]
- Caravella, A.; di Maio, F.P.; di Renzo, A. Optimization of membrane area and catalyst distribution in a permeative-stage membrane reactor for methane steam reforming. J. Membr. Sci. 2008, 321, 209–221. [Google Scholar] [CrossRef]
- Caravella, A.; di Maio, F.P.; di Renzo, A. Computation study of staged membrane reactor configurations for methane steam reforming. I. Optimization of stage lengths. AIChE J. 2010, 56, 248–258. [Google Scholar] [CrossRef]
- Caravella, A.; di Maio, F.P.; di Renzo, A. Computation study of staged membrane reactor configurations for methane steam reforming. II. Effect of number of stages and catalyst amount. AIChE J. 2010, 56, 259–267. [Google Scholar] [CrossRef]
- Adrover, M.E.; López, E.; Borio, D.O.; Pedernera, M.N. Theoretical study of a membrane reactor for the water gas shift reaction under nonisothermal conditions. AIChE J. 2009, 55, 3206–3213. [Google Scholar] [CrossRef]
- Choi, Y.; Stenger, H.G. Water gas shift reaction kinetics and reactor modeling for fuel cell grade hydrogen. J. Power Sources 2003, 124, 432–439. [Google Scholar] [CrossRef]
- Kärger, J.; Ruthven, D.M. Diffusion in Zeolites and Other Microporous Solids; Wiley-Interscience: New York, NY, USA, 1992. [Google Scholar]
- Ghosal, K.; Freeman, B.D. Gas separation using polymer membranes: An overview. Polym. Adv. Technol. 1994, 5, 673–697. [Google Scholar] [CrossRef]
- Baker, R.W. Membrane Technology and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2012; p. 152. [Google Scholar]
- Vora, S.; Brickett, L. DOE/NETL Advanced Carbon Dioxide Capture R & D Program: Technology Update; U.S. Department of Energy/National Energy Technology Laboratory: Washington, DC, USA, 2013.
- Marano, J.J. Integration of H2 Separation Membranes with CO2 Capture and Compression; Report to DoE, Contract No. DE-AC2605NT41816, DOE/NETL-401/113009; U.S. Department of Energy/National Energy Technology Laboratory: Washington, DC, USA, 2009.
| Component | Syngas Feed | Steam Sweep |
|---|---|---|
| H2 | 0.1933 | 0 |
| CO2 | 0.0568 | 0 |
| H2O | 0.4886 | 1 |
| CO | 0.2443 | 0 |
| N2 | 0.017 | 0 |
| Parameter | Value (%) | Target (%) |
|---|---|---|
| 98.95 | 98 | |
| 98.60 | 95 | |
| 74.71 | 90 | |
| 95.98 | 95 | |
| 41.71 | 44 | |
| 0.77 | ≤4 |
| Parameter | Value (%) | Target (%) |
|---|---|---|
| 99.44 | 98 | |
| 98.82 | 95 | |
| 74.73 | 90 | |
| 96.17 | 95 | |
| 41.82 | 44 | |
| 0.71 | ≤4 |
| Parameter | Value (%) | Target (%) |
|---|---|---|
| 99.36 | 98 | |
| 98.38 | 95 | |
| 75.77 | 90 | |
| 96.05 | 95 | |
| 42.05 | 44 | |
| 1.01 | ≤4 |
| Reactor Configuration | XCO (%) | RH2 (%) |
|---|---|---|
| 2-stage PSMR | 98.68 | 96.17 |
| 3-stage PSMR | 99.16 | 96.07 |
| MR | 99.62 | 96.21 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radcliffe, A.J.; Singh, R.P.; Berchtold, K.A.; Lima, F.V. Modeling and Optimization of High-Performance Polymer Membrane Reactor Systems for Water–Gas Shift Reaction Applications. Processes 2016, 4, 8. https://doi.org/10.3390/pr4020008
Radcliffe AJ, Singh RP, Berchtold KA, Lima FV. Modeling and Optimization of High-Performance Polymer Membrane Reactor Systems for Water–Gas Shift Reaction Applications. Processes. 2016; 4(2):8. https://doi.org/10.3390/pr4020008
Chicago/Turabian StyleRadcliffe, Andrew J., Rajinder P. Singh, Kathryn A. Berchtold, and Fernando V. Lima. 2016. "Modeling and Optimization of High-Performance Polymer Membrane Reactor Systems for Water–Gas Shift Reaction Applications" Processes 4, no. 2: 8. https://doi.org/10.3390/pr4020008
APA StyleRadcliffe, A. J., Singh, R. P., Berchtold, K. A., & Lima, F. V. (2016). Modeling and Optimization of High-Performance Polymer Membrane Reactor Systems for Water–Gas Shift Reaction Applications. Processes, 4(2), 8. https://doi.org/10.3390/pr4020008






