A Review of Dynamic Models of Hot-Melt Extrusion
Abstract
:1. Introduction
2. A Simple Case Study
3. The Earlier Models: Static Maps
- Plug flow reactors characterized by a uniform residence time distribution for all particles.
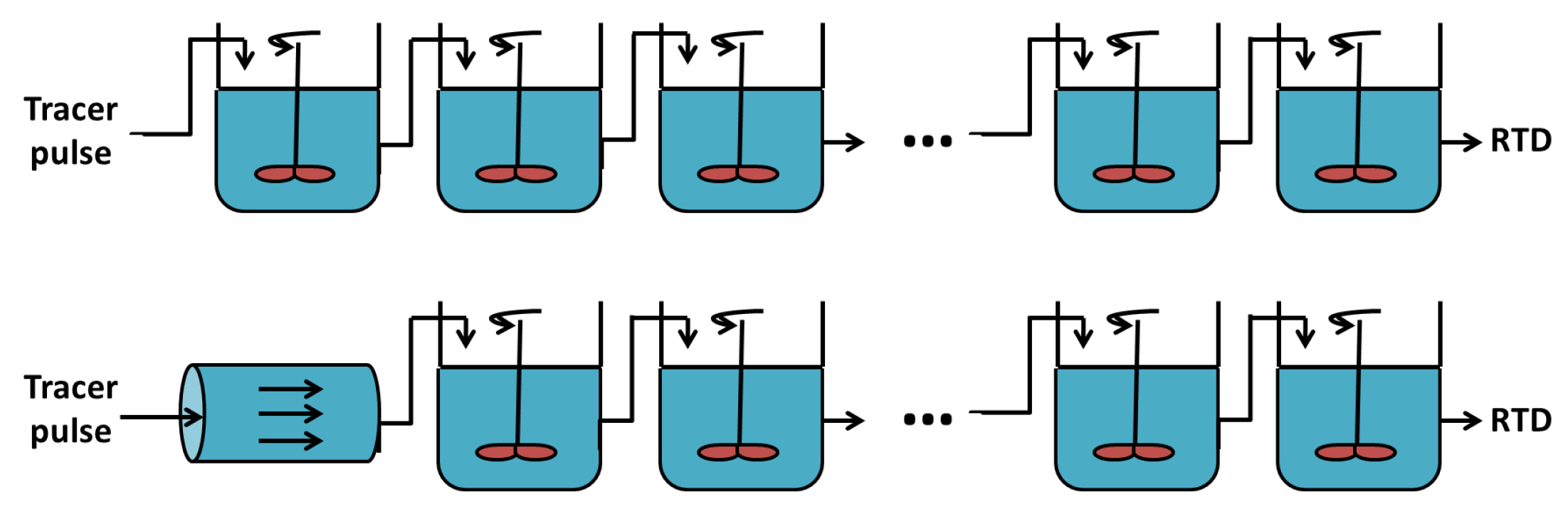
- Continuous stirred-tank reactors (CSTRs) assuming the non-uniformity of the residence time, but a uniform composition of the flow.
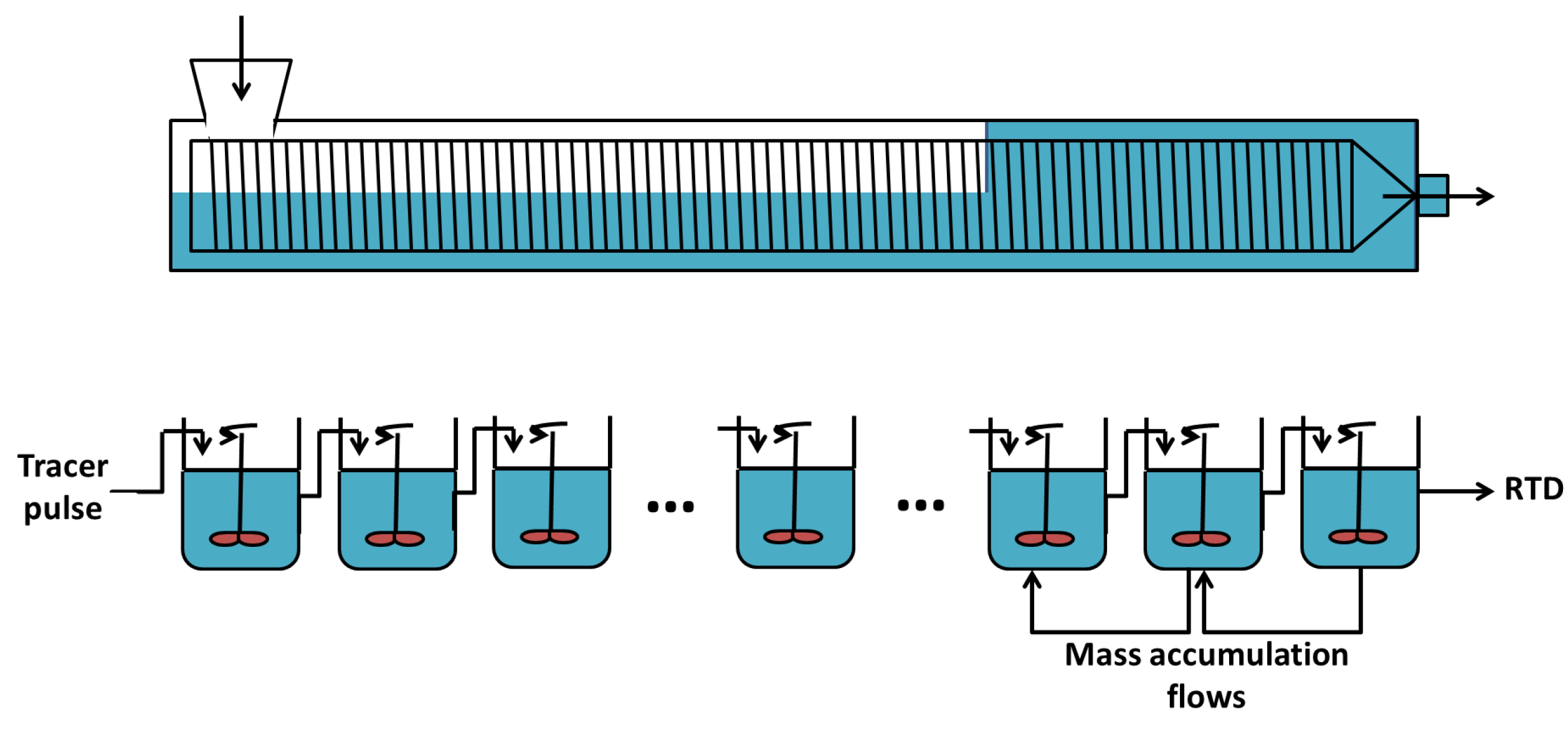
- The work in [49] models the RTD of wheat flour particles using five volume elements of different sizes, each sub-divided in a series of CSTRs with identical volumes. In order to represent the tail in the RTD, three reactors with backward flows are included so as to explain material accumulation at the die (see Figure 6).
- The work in [50] uses a combination of a plug flow reactor with a cascade of CSTRs with the same volume and a backward flow (see Figure 7). The plug flow reactor represents the feeding zone and is characterized by a delay . The cascade of CSTRs models the completely filled part inducing a reflux and characterized by two parameters: the number of reactors n and the ratio between the forward and backward flows .
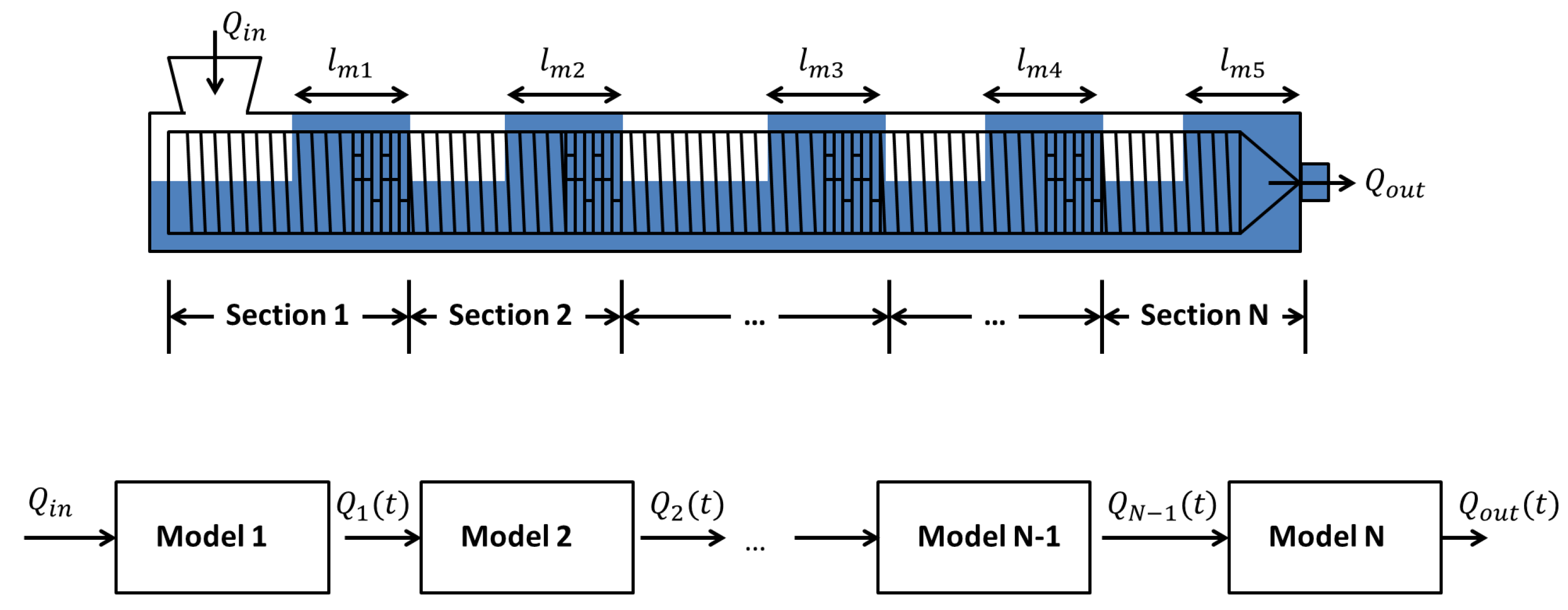
4. Reactors-In-Series Approach
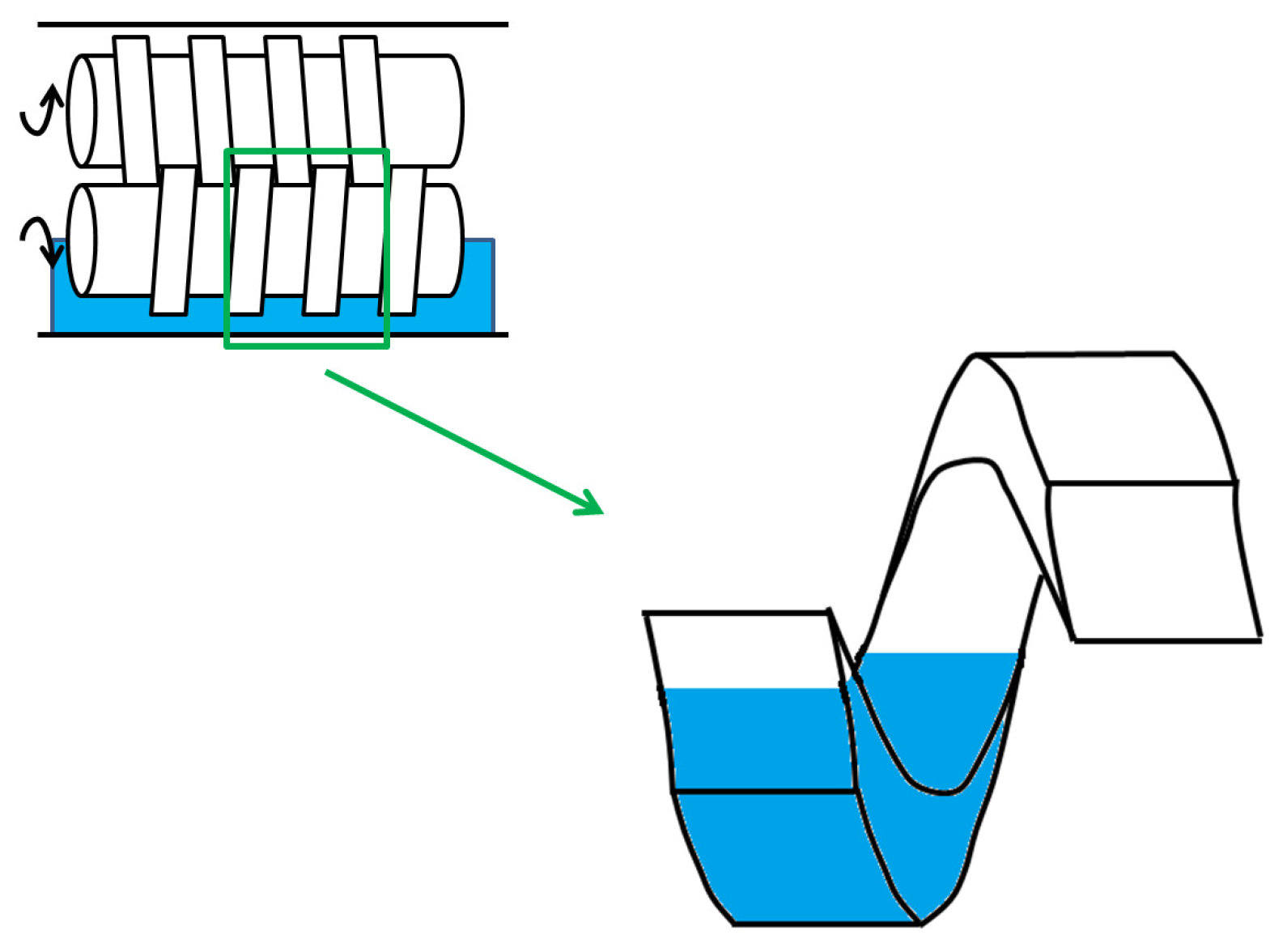
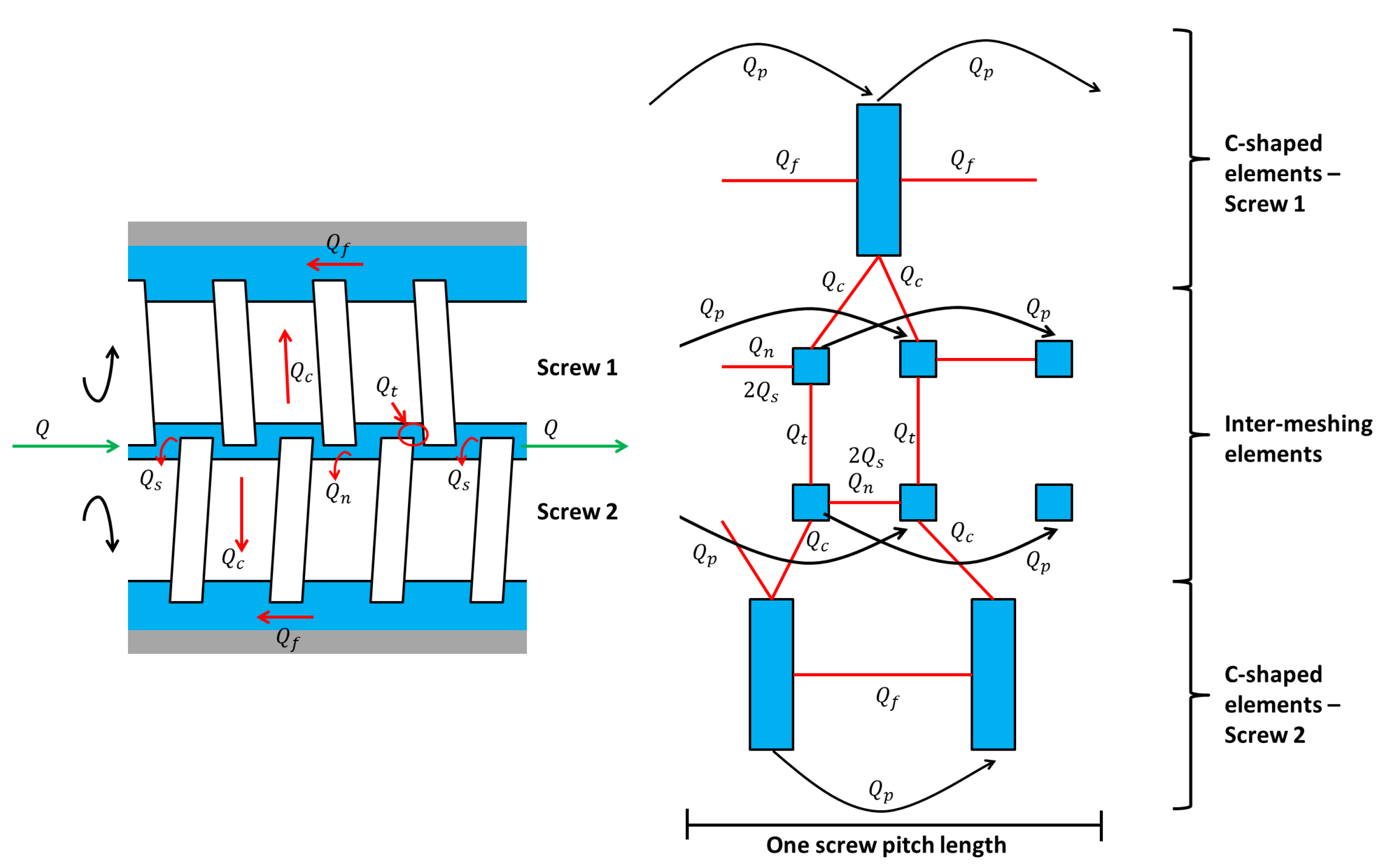
- Models with Predetermined Screw DiscretizationIn [56,57], the filling ratio, monomer concentration, temperatures and RTD are determined for a counter-rotating twin screw extruder using a subdivision of the screws in C-chambers (see Figure 10) where mass and energy balances are expressed using continuum mechanics. If the system includes a high inter-meshing area between the screws, other volume elements may be added to model the specific flows in this zone (see [52]).An extrusion device presents a varying filling level, a function of the local screw geometry. It is generally considered that an extruder comprises two different zones, which can be partially or completely filled, inducing specific mass balance expressions. Indeed, mass flow networks are different in each zone. In partially-filled zones, only a pumping flow , due to the screw rotation, transports the material along the section. In completely filled zones, the presence of a pressure gradient creates leakage flows, and the resulting mass flow network is modeled by parallel C-chambers, in which the leakage locations are divided into five groups [59] (see Figure 11):
- −
- the flight gap (with flow ) between the barrel and the screw flight;
- −
- the tetrahedron gap () between the flight walls;
- −
- the calender gap () between the flight of one screw and the bottom of the other screw channel;
- −
- the side gap () between the flanks of the two screws flight;
- −
- the channel gap () down-channel flow in the screw channel.
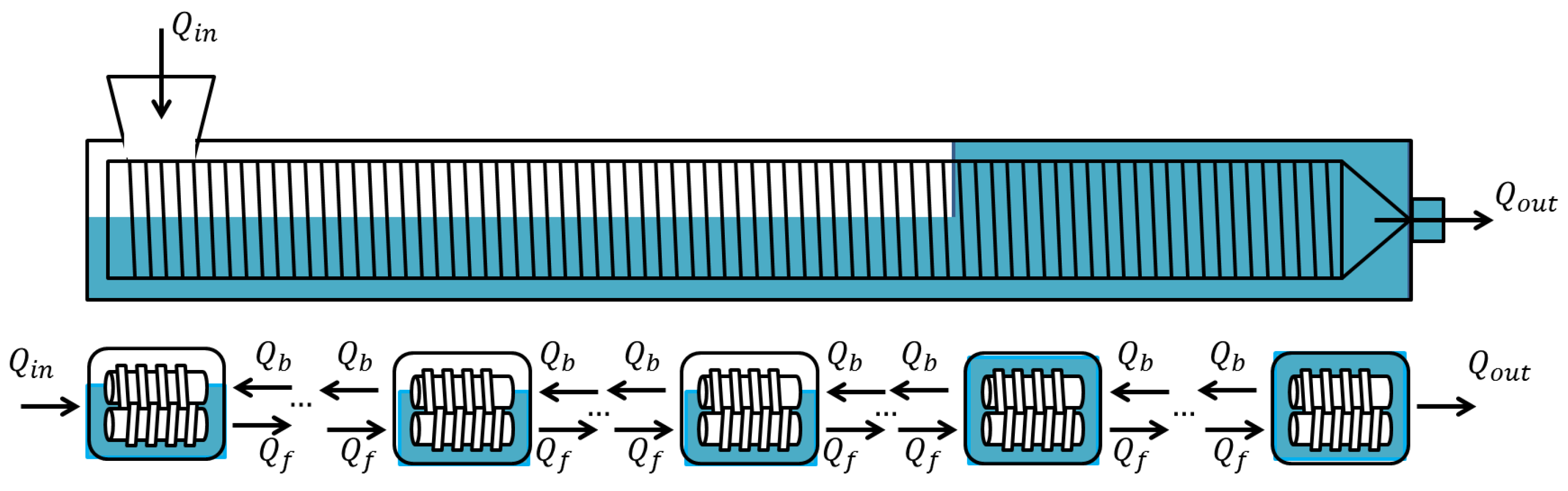
- Models with Adjustable DiscretizationIn [35,53], the different screw sections can be discretized using an adjustable number of CSTRs (see Figure 12). Material can flow in the forward direction, with flow due to the screw rotation, and in the backward direction, with flow due to the pressure difference between two reactors, as shown in Figure 12 and Table 3 [60].Based on the filling ratio, the pressure in each reactor can be computed using a simple algebraic method. Two different situations may happen: in partially-filled reactors (), the pressure P matches the atmospheric pressure , and in the completely filled reactors (), the pressure is above the atmospheric pressure; and flow continuity is verified. The problem can therefore be expressed as a system of linear algebraic equations , where is the pressure vector and A a tridiagonal matrix.
5. Distributed Parameter Models
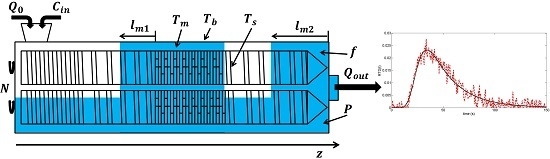
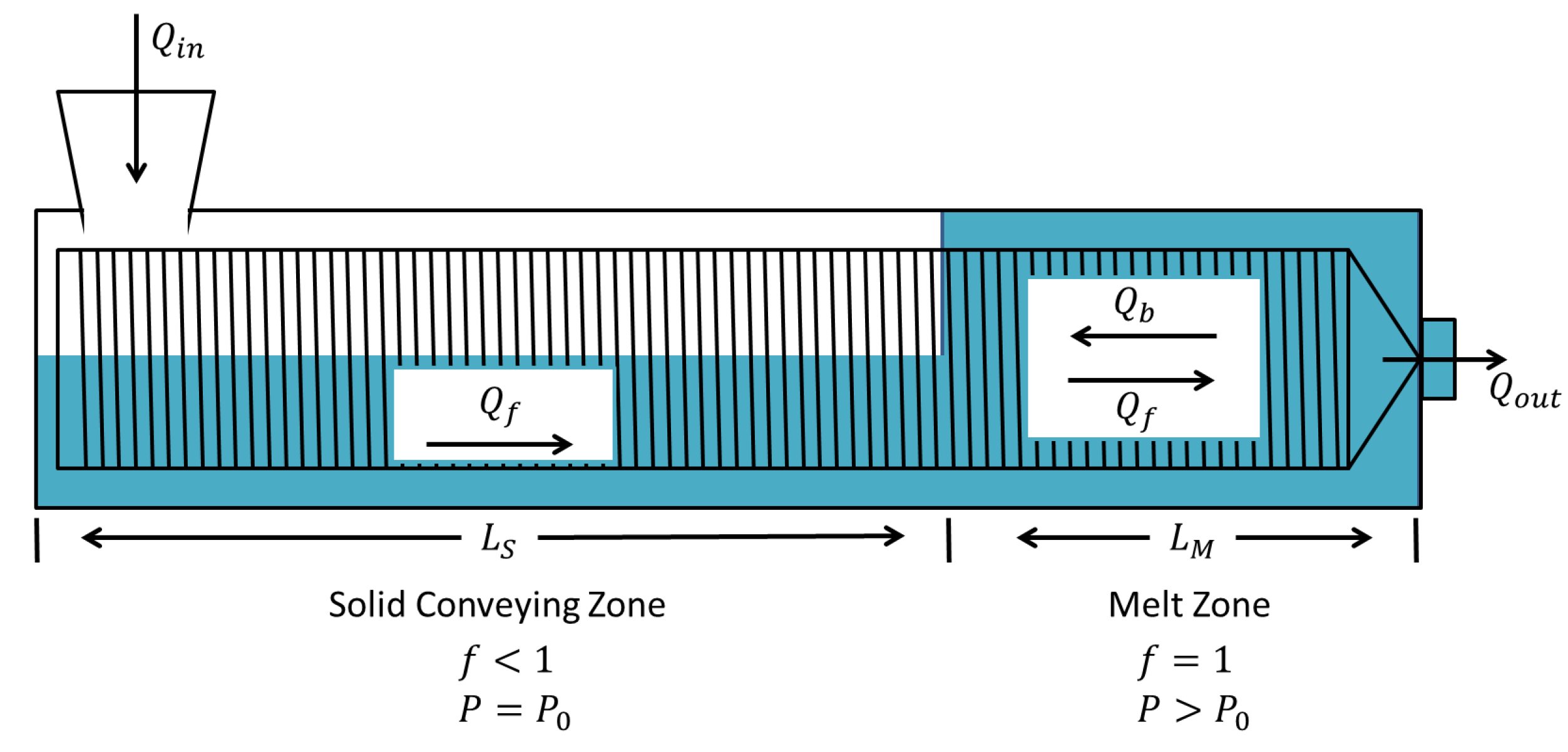
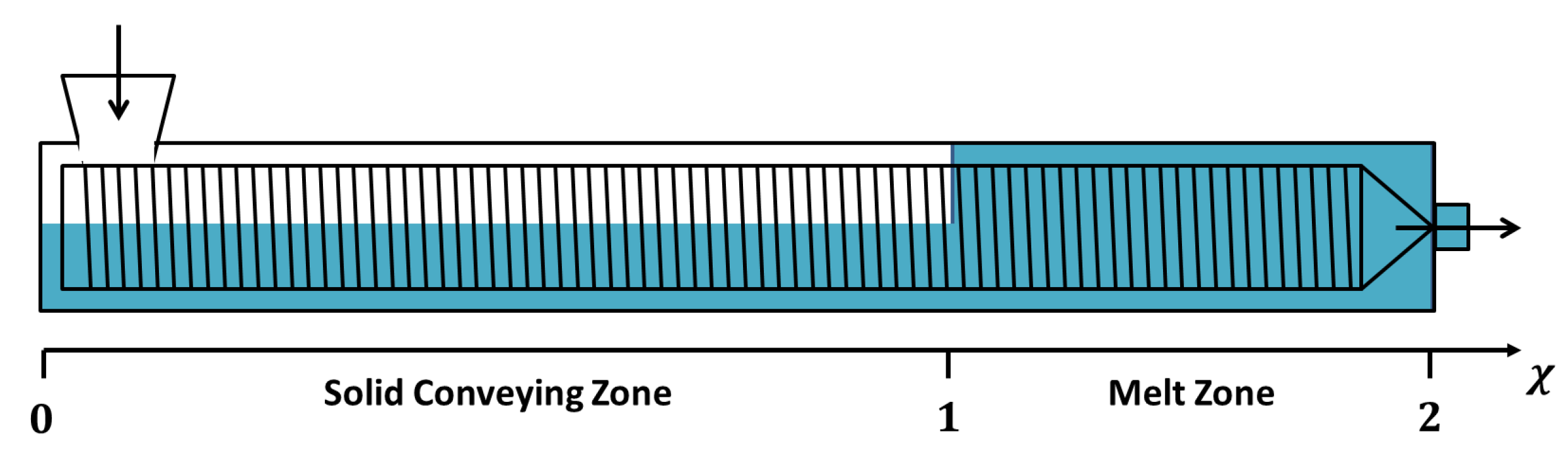
- Solid conveying zone:This zone is characterized by a varying filling ratio . Material accumulates or flows along this zone during the transient period. Mass and energy balances are therefore expressed by the following equations:
- −
- Mass balance:where ξ and N are respectively the screw pitch and rotation speed.
- −
- Energy balance:where T is the material temperature, ϕ the viscous energy dissipation factor, a geometric parameter characterizing the viscous energy dissipation [104], the viscosity, ρ the density, V the shear volume, the specific heat capacity, the convective heat transfer coefficient, the equivalent circumference of the twin screw and the barrel temperature.
- Melt zone:Unlike the solid conveying zone, the forward flow is considered as constant since the density itself is constant and the zone completely filled. In the following equations, the backward flow is associated with the pressure flow between two parallel plates assuming that the screw gaps are much smaller than the screw diameter. The net flow rate at any location in the melt zone equals the output flow at the die, . The mass and energy balance equations are:
- −
- Mass balance:where B is a constant governing the leakage back flow and P the pressure.Determination of this pressure is possible using the following equation:
- −
- Energy balance:where is a geometric parameter characterizing the viscous energy dissipation [104] and η is the viscosity. U is the convective heat transfer coefficient.
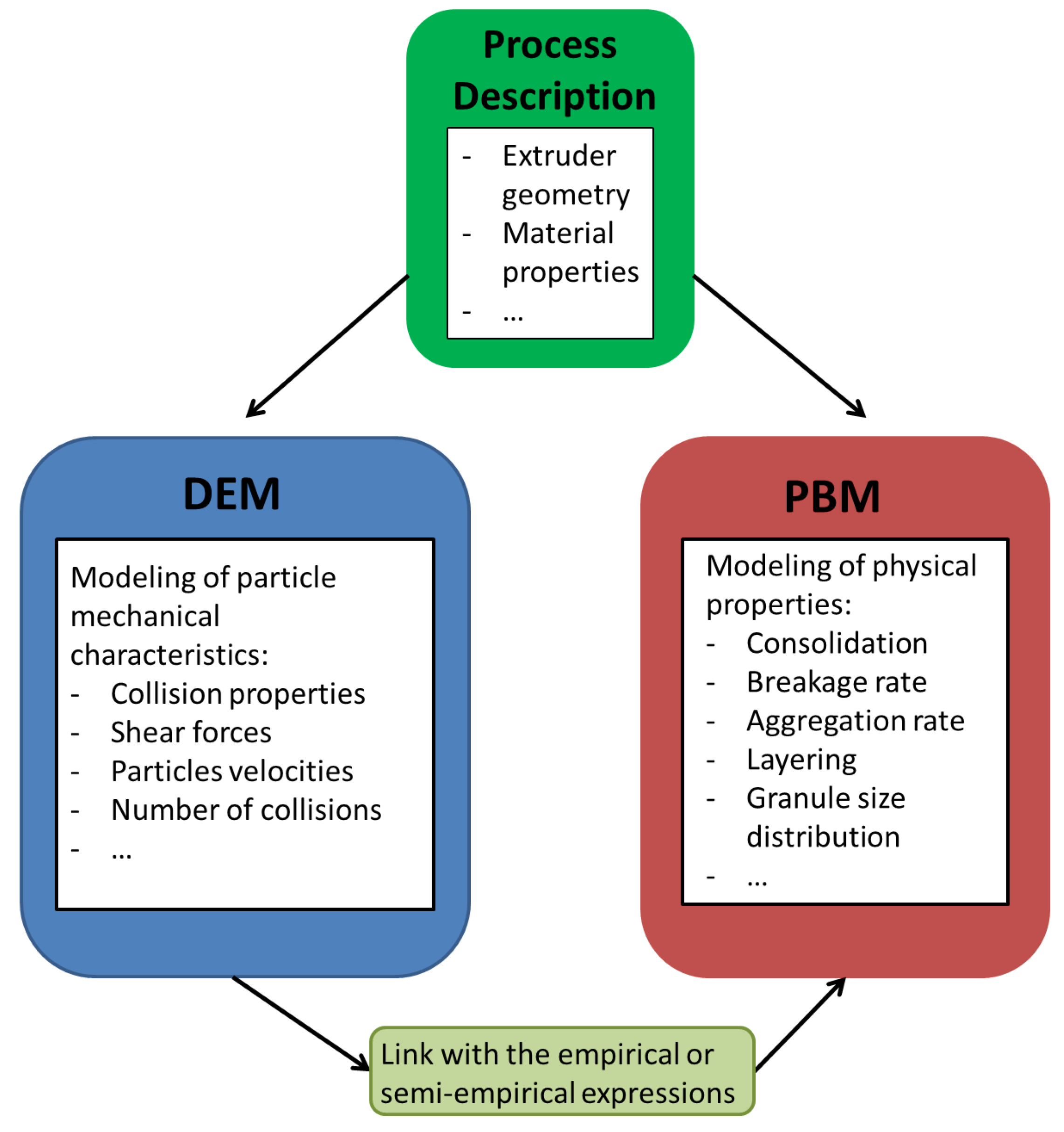
6. Population Balance Modeling and Discrete Element Modeling
7. Data-Driven Models
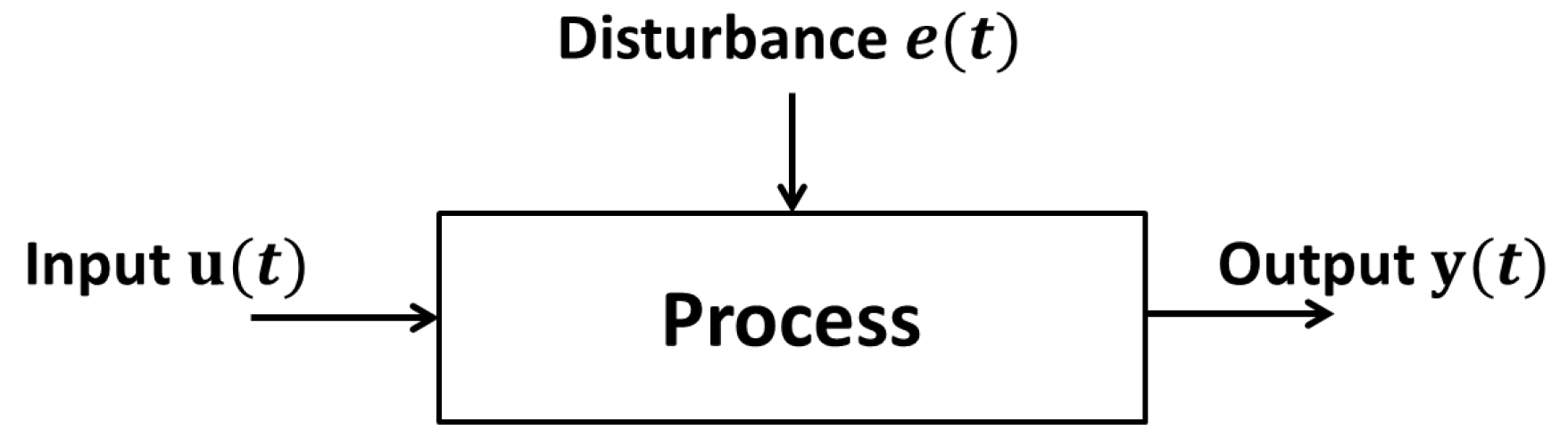
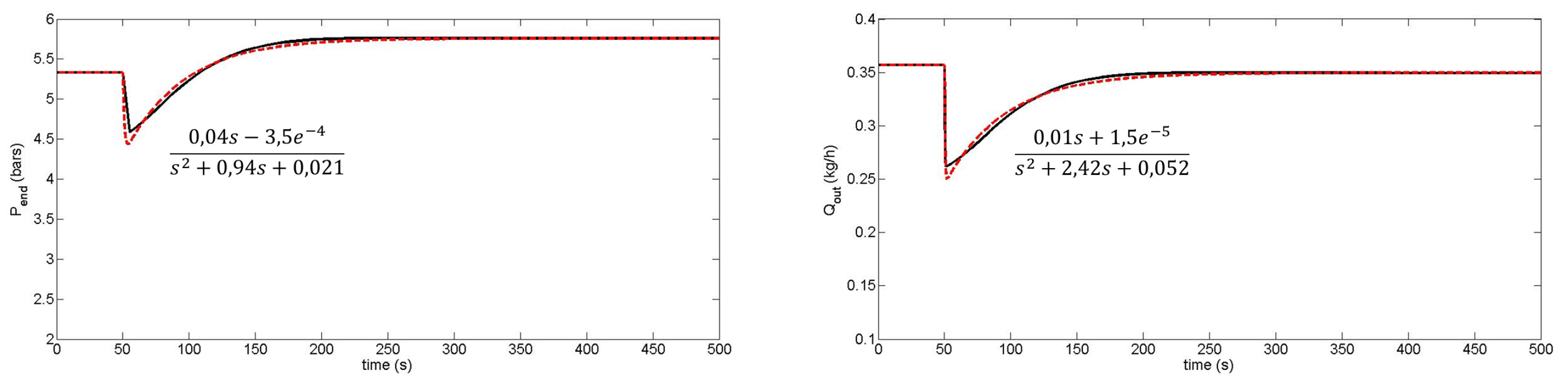
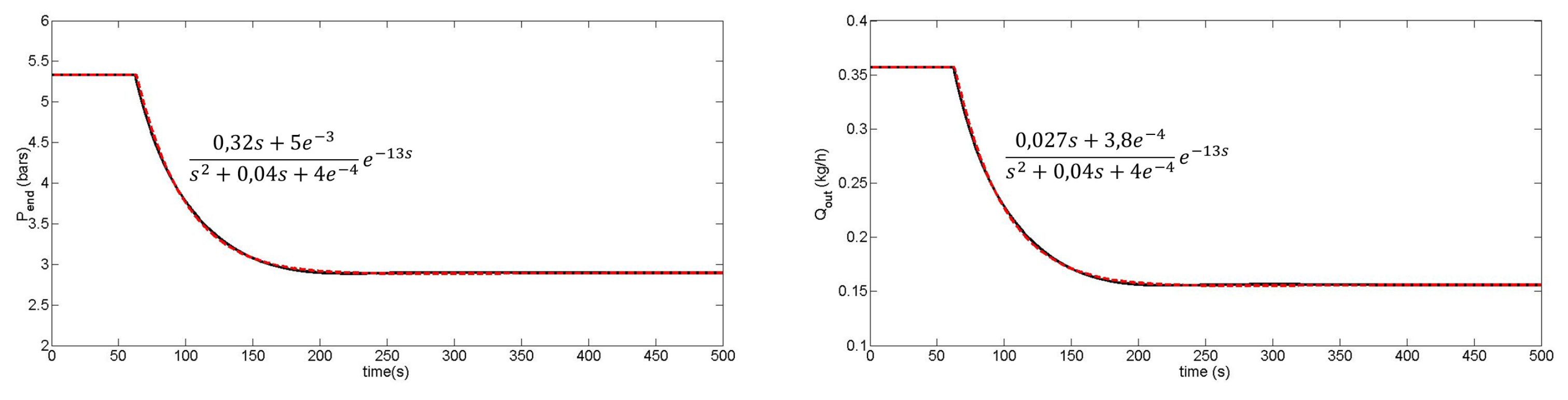
- Transfer function models:The input-output behavior of the process around a specific operating point can be described by a transfer function of the form:where and are the Laplace transforms of and , while is defined by a set of parameters () with .There exist many techniques to build transfer function models based on output responses to input solicitations, and some of them are summarized in [140]. Examples of single-screw extruder modeling can also be found in [141,142,143] and serve the development of more specific techniques related to twin-screw configurations, as in [19,20,144,145].Common features of these works include:
- −
- parameter identification based on input step changes;
- −
- first- or second-order transfer functions;
- −
- inclusion of time delays in some input-output relations (feed flow/die pressure, moisture content/die material temperature, etc).
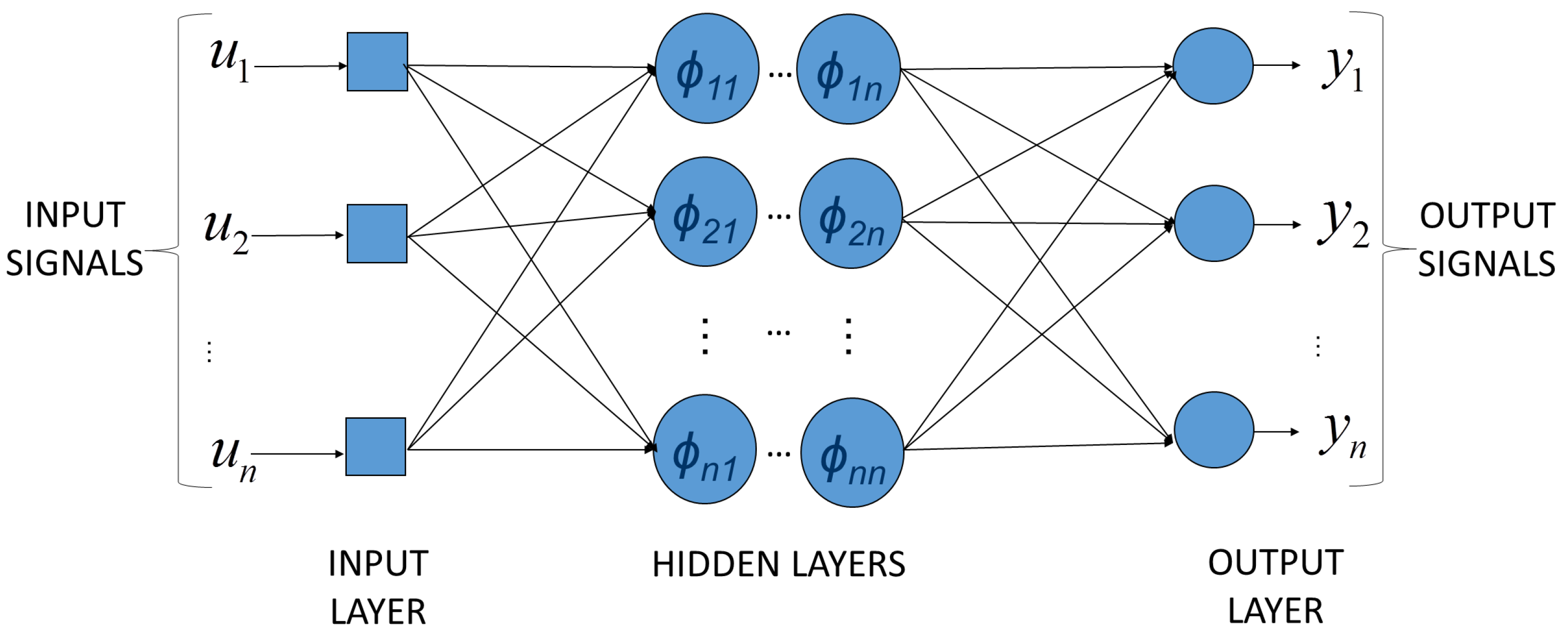
In [146], a comparative study of different parameter identification methods is achieved. Different algorithms are analyzed in the context of cooking extrusion. The couple “screw rotation speed/motor load” supports relay feedback as a well-performing online method, while batch output error parameters provide an accurate modeling across a large range of operating points.The main advantages of transfer function models are their simplicity and the availability of a broad array of well-established control techniques, including PID control. However, transfer function models assume that the process behavior is linear in a limited range of operation. If several distinct operating points have to be considered, different transfer functions will usually have to be identified for each of them. In this latter case, gain-scheduling or adaptive controllers will be required. - Neural networks (NN):Standard feedforward NNs basically define a nonlinear static map between a selected number of inputs (u) and outputs (y):where i represents a discrete element of sample set I.One of the most common NN architectures in system modeling is the perceptron [147] consisting of an on/off static function (called the activation function or decision function) delivering a binary output (e.g., zero or one). The sum of a weighted input linear combination is compared to a threshold separating the activation and inactivation zones as in:Perceptron networks may be built using multiple layer structures where all of the neuron outputs depend only on the inputs from the previous layer and do not interact with the same-layer neurons. These structures are called multilayer perceptrons (MLP; [148,149]; Figure 25). The nonlinearity used in the corresponding activation function is continuous (for instance, sigmoid or Gaussian functions). A significant advantage of multilayer NN models is their ability to exploit information contained in every available measurement from nonlinear processes, while, however, the main detrimental consequences are the huge required amount of data to reach acceptable training performances (i.e., the ability to reproduce correctly the outputs) and the fast increasing number of parameters following the addition of layers.The first and the last layers, respectively called the input and output (visible) layers, are distinguished from the intermediate ones, also called the hidden layers. Many other neural network structures, static or dynamic (i.e., using temporally-shifted inputs and outputs), exist, such as the radial basis function network, which, for instance, has proved quite useful in modeling bioprocesses [150] or perceptron-based structures applied to pattern recognition [151,152]. These structures generally differ from each other by the activation principle and the training rules.Steady progress in computational technology allows neural networks to be implemented on-line on many experimental plants [153,154]. SISO (single input single output) or MIMO (multi inputs multi outputs) NNs can be used to describe input-output relationships [155,156,157]. In [158], a relation between classical input variables (screw speed, feed flow rate, feed moisture, moisture content, die diameter and temperature) and outlet physical and chemical product properties (radial expansion, density, bulk density, water adsorption and solubility indexes) is established. The selected black-box model is a static three-layered feed-forward network with logistic activation functions trained by a backpropagation algorithm [148]. Results show that the method is performing well in reproducing specific material properties and could aim at obtaining generalized models predicting required input parameters to get the desired product properties.
8. Conclusion
- explicit solutions of the mass balance equations, i.e., functions of time describing the residence time distribution;
- systems of differential equations, resulting from mass and energy balances expressed around a representation of the systems in the form of continuous-stirred reactors in series;
- systems of partial differential equations resulting from mass and energy (possibly momentum) balances in a distributed parameter representation of the system;
- PBM-DEM methods, including material properties in differential equation systems describing each particle characteristic evolutions using Newton’s second law of motion and the angular momentum
- black-box representations of the system, e.g., transfer functions or neural networks linking input and output operational variables, inferred from experimental data and using little or no a priori physical knowledge of the system.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gerrens, H. Handbuch der Technischen Polymerchemie. Von A. Echte. VCH Verlagsgesellschaft mbH, Weinheim 1993. 721 S., 398 Abb. und 57 Tab., geb., DM 276,–. Chem. Ing. Technik 1994, 66, 239. [Google Scholar] [CrossRef]
- Dover, H.W. Apparatus for Insulating or Covering Strands and Forming Same into Cables. U.S. Patent 699,459, 6 May 1902. [Google Scholar]
- DiNunzio, J.C.; Brough, C.; Hughey, J.R.; Miller, D.A.; Williams, R.O.; McGinity, J.W. Fusion production of solid dispersions containing a heat-sensitive active ingredient by hot melt extrusion and Kinetisol® dispersing. Eur. J. Pharm. Biopharm. 2010, 74, 340–351. [Google Scholar] [CrossRef] [PubMed]
- Crowley, M.M.; Zhang, F.; Repka, M.A.; Thumma, S.; Upadhye, S.B.; Kumar Battu, S.; McGinity, J.W.; Martin, C. Pharmaceutical applications of hot-melt extrusion: Part I. Drug Dev. Ind. Pharm. 2007, 33, 909–926. [Google Scholar] [CrossRef] [PubMed]
- Repka, M.A.; Battu, S.K.; Upadhye, S.B.; Thumma, S.; Crowley, M.M.; Zhang, F.; Martin, C.; McGinity, J.W. Pharmaceutical applications of hot-melt extrusion: Part II. Drug Dev. Ind. Pharm. 2007, 33, 1043–1057. [Google Scholar] [CrossRef] [PubMed]
- Hughey, J.R.; Keen, J.M.; Miller, D.A.; Kolter, K.; Langley, N.; McGinity, J.W. The use of inorganic salts to improve the dissolution characteristics of tablets containing Soluplus®-based solid dispersions. Eur. J. Pharm. Sci. 2013, 48, 758–766. [Google Scholar] [CrossRef] [PubMed]
- Thiry, J.; Krier, F.; Evrard, B. A review of pharmaceutical extrusion: Critical process parameters and scaling-up. Int. J. Pharm. 2015, 479, 227–240. [Google Scholar] [CrossRef] [PubMed]
- Harper, J.M.; Clark, J.P. Food extrusion. Crit. Rev. Food Sci. Nutr. 1979, 11, 155–215. [Google Scholar] [CrossRef]
- Van Zuilichem, D. Extrusion Cooking, Craft or Science? Ph.D. Thesis, Wageningen Agricultural University, Wageningen, 29 January 1992. [Google Scholar]
- Singh, S.; Gamlath, S.; Wakeling, L. Nutritional aspects of food extrusion: A review. Int. J. Food Sci. Technol. 2007, 42, 916–929. [Google Scholar] [CrossRef]
- Johnson, W.; Kudō, H. The Mechanics of Metal Extrusion; Manchester University Press: Manchester, England, 1962. [Google Scholar]
- Lee, E.; Mallett, R.; Yang, W.H. Stress and deformation analysis of the metal extrusion process. Computer Methods Appl. Mech. Eng. 1977, 10, 339–353. [Google Scholar] [CrossRef]
- Erisken, C.; Kalyon, D.M.; Wang, H. A hybrid twin screw extrusion/electrospinning method to process nanoparticle-incorporated electrospun nanofibres. Nanotechnology 2008, 19. [Google Scholar] [CrossRef] [PubMed]
- Ergun, A.; Yu, X.; Valdevit, A.; Ritter, A.; Kalyon, D.M. In vitro analysis and mechanical properties of twin screw extruded single-layered and coextruded multilayered poly (caprolactone) scaffolds seeded with human fetal osteoblasts for bone tissue engineering. J. Biomed. Mater. Res. Part A 2011, 99, 354–366. [Google Scholar] [CrossRef] [PubMed]
- Kalyon, D.; Yu, X.; Wang, H.; Valdevit, A.; Ritter, A. Twin Screw Extrusion Based Technologies Offer Novelty, Versatility, Reproducibility and Industrial Scalability for Fabrication of Tissue Engineering Scaffolds. J. Tissue Sci. Eng. 2013, 4. [Google Scholar] [CrossRef]
- Aktas, S.; Gevgilili, H.; Kucuk, I.; Sunol, A.; Kalyon, D.M. Extrusion of poly (ether imide) foams using pressurized CO2: Effects of imposition of supercritical conditions and nanosilica modifiers. Polym. Eng. Sci. 2014, 54, 2064–2074. [Google Scholar] [CrossRef]
- Saha, P.K. Aluminum Extrusion Technology; Asm International: Novelty, OH, USA, 2000. [Google Scholar]
- Hudson, R. Developments in the European Extrusion Industry; Rapra Technology Limited: Shrewsbury, England, 1995. [Google Scholar]
- Moreira, R.G.; Srivastava, A.K.; Gerrish, J.B. Feedforward control model for a twin-screw food extruder. Food Control 1990, 1, 179–184. [Google Scholar] [CrossRef]
- Singh, B.; Mulvaney, S.J. Modeling and process control of twin-screw cooking food extruders. J. Food Eng. 1994, 23, 403–428. [Google Scholar] [CrossRef]
- Schlosburg, J. Twin-Screw Food Extrusion: Control Case Study. Available online: http://homepages.rpi.edu/bequeb/URP/JoelS-presentation.pdf (accessed on 27 May 2016).
- Wang, L.; Smith, S.; Chessari, C. Continuous-time model predictive control of food extruder. Control Eng. Pract. 2008, 16, 1173–1183. [Google Scholar] [CrossRef]
- Trifkovic, M.; Sheikhzadeh, M.; Choo, K.; Rohani, S. Model predictive control of a twin-screw extruder for thermoplastic vulcanizate (TPV) applications. Comput. Chem. Eng. 2012, 36, 247–254. [Google Scholar] [CrossRef]
- Zhou, P.; Liu, H.; Tan, K.; Chen, C. Application and Research of Fuzzy Control Simulation in Twin Screw Extruder. Procedia Eng. 2012, 29, 542–546. [Google Scholar] [CrossRef]
- Kalyon, D.M.; Gotsis, A.D.; Yilmazer, U.; Gogos, C.G.; Sangani, H.; Aral, B.; Tsenoglou, C. Development of experimental techniques and simulation methods to analyze mixing in co-rotating twin screw extrusion. Adv. Polym. Technol. 1988, 8, 337–353. [Google Scholar] [CrossRef]
- Yilmazer, U.; Gogos, C.G.; Kalyon, D.M. Mat formation and unstable flows of highly filled suspensions in capillaries and continuous processors. Polym. Compos. 1989, 10, 242–248. [Google Scholar] [CrossRef]
- Kalyon, D.M.; Sangani, H.N. An experimental study of distributive mixing in fully intermeshing, co-rotating twin screw extruders. Polym. Eng. Sci. 1989, 29, 1018–1026. [Google Scholar] [CrossRef]
- Kalyon, D.; Jacob, C.; Yaras, P. An experimental study of the degree of fill and melt densification in fully-intermeshing, co-rotating twin screw extruders. Plast. Rubber Compos. Process. Appl. 1991, 16, 193–200. [Google Scholar]
- Kalyon, D.M.; Yazici, R.; Jacob, C.; Aral, B.; Sinton, S.W. Effects of air entrainment on the rheology of concentrated suspensions during continuous processing. Polym. Eng. Sci. 1991, 31, 1386–1392. [Google Scholar] [CrossRef]
- Kalyon, D.M.; Birinci, E.; Yazici, R.; Karuv, B.; Walsh, S. Electrical properties of composites as affected by the degree of mixedness of the conductive filler in the polymer matrix. Polym. Eng. Sci. 2002, 42, 1609–1617. [Google Scholar] [CrossRef]
- Lu, G.; Kalyon, D.M.; Yilgör, I.; Yilgör, E. Rheology and extrusion of medical-grade thermoplastic polyurethane. Polym. Eng. Sci. 2003, 43, 1863–1877. [Google Scholar] [CrossRef]
- Erol, M.; Kalyon, D. Assessment of the degree of mixedness of filled polymers: Effects of processing histories in batch mixer and co-rotating and counter-rotating twin screw extruders. Int. Polym. Proc. 2005, 20, 228–237. [Google Scholar] [CrossRef]
- Kalyon, D.M.; Dalwadi, D.; Erol, M.; Birinci, E.; Tsenoglu, C. Rheological behavior of concentrated suspensions as affected by the dynamics of the mixing process. Rheol. Acta 2006, 45, 641–658. [Google Scholar] [CrossRef]
- Kalyon, D.M.; Gevgilili, H.; Kowalczyk, J.E.; Prickett, S.E.; Murphy, C.M. Use of adjustable-gap on-line and off-line slit rheometers for the characterization of the wall slip and shear viscosity behavior of energetic formulations. J. Energetic Mater. 2006, 24, 175–193. [Google Scholar] [CrossRef]
- Choulak, S.; Couenne, F.; Le Gorrec, Y.; Jallut, C.; Cassagnau, P.; Michel, A. Generic dynamic model for simulation and control of reactive extrusion. Ind. Eng. Chem. Res. 2004, 43, 7373–7382. [Google Scholar] [CrossRef]
- Carneiro, O.S.; Covas, J.A.; Vergnes, B. Experimental and theoretical study of twin-screw extrusion of polypropylene. J. Appl. Polym. Sci. 2000, 78, 1419–1430. [Google Scholar] [CrossRef]
- Khalifeh, A.; Clermont, J.R. Numerical simulations of non-isothermal three-dimensional flows in an extruder by a finite-volume method. J. Non-Newton. Fluid Mech. 2005, 126, 7–22. [Google Scholar] [CrossRef]
- Kulshreshtha, M.; Zaror, C. An unsteady state model for twin screw extruders. Food Bioprod. Proc. Trans. Inst. Chem. Eng. Part C 1992, 70, 21–28. [Google Scholar]
- Kumar, A.; Ganjyal, G.M.; Jones, D.D.; Hanna, M.A. Digital image processing for measurement of residence time distribution in a laboratory extruder. J. Food Eng. 2006, 75, 237–244. [Google Scholar] [CrossRef]
- Altomare, R.E.; Ghossi, P. An analysis of residence time distribution patterns in a twin screw cooking extruder. Biotechnol. Prog. 1986, 2, 157–163. [Google Scholar] [CrossRef] [PubMed]
- Mange, C.; Boissonnat, P.; Gelus, M. Distribution of residence times and comparison of three twin-screw extruders of different size. In Extrusion Technology for the Food Industry; O’Connor, C., Ed.; Elsevier Applied Sciences: London, England, 1987; pp. 117–131. [Google Scholar]
- Danckwerts, P. Continuous flow systems: Distribution of residence times. Chem. Eng. Sci. 1953, 2, 1–13. [Google Scholar] [CrossRef]
- Brenner, H. The diffusion model of longitudinal mixing in beds of finite length. Numerical values. Chem. Eng. Sci. 1962, 17, 229–243. [Google Scholar] [CrossRef]
- Levenspiel, O. Chemical reaction engineering. Ind. Eng. Chem. Res. 1999, 38, 4140–4143. [Google Scholar] [CrossRef]
- Kumar, A.; Vercruysse, J.; Vanhoorne, V.; Toiviainen, M.; Panouillot, P.E.; Juuti, M.; Vervaet, C.; Remon, J.P.; Gernaey, K.V.; De Beer, T.; et al. Conceptual framework for model-based analysis of residence time distribution in twin-screw granulation. Eur. J. Pharm. Sci. 2015, 71, 25–34. [Google Scholar] [CrossRef] [PubMed]
- Ziegler, G.R.; Aguilar, C.A. Residence time distribution in a co-rotating, twin-screw continuous mixer by the step change method. J. Food Eng. 2003, 59, 161–167. [Google Scholar] [CrossRef]
- Poulesquen, A.; Vergnes, B. A study of residence time distribution in co-rotating twin-screw extruders. Part I: Theoretical modeling. Polym. Eng. Sci. 2003, 43, 1841–1848. [Google Scholar] [CrossRef]
- Poulesquen, A.; Vergnes, B.; Cassagnau, P.; Michel, A.; Carneiro, O.S.; Covas, J.A. A study of residence time distribution in co-rotating twin-screw extruders. Part II: Experimental validation. Polym. Eng. Sci. 2003, 43, 1849–1862. [Google Scholar] [CrossRef]
- De Ruyck, H. Modelling of the residence time distribution in a twin screw extruder. J. Food Eng. 1997, 32, 375–390. [Google Scholar] [CrossRef]
- Puaux, J.; Bozga, G.; Ainser, A. Residence time distribution in a corotating twin-screw extruder. Chem. Eng. Sci. 2000, 55, 1641–1651. [Google Scholar] [CrossRef]
- Kumar, A.; Ganjyal, G.M.; Jones, D.D.; Hanna, M.A. Modeling residence time distribution in a twin-screw extruder as a series of ideal steady-state flow reactors. J. Food Eng. 2008, 84, 441–448. [Google Scholar] [CrossRef]
- Elsey, J.R. Dynamic Modelling, Measurement and Control of Co-rotating Twin-Screw Extruders. Ph.D. Thesis, University of Sydney, Sydney, Australia, 25 August 2002. [Google Scholar]
- Choulak, S.E. Modélisation et Commande d’un Procédé D’extrusion Réactive. Ph.D. Thesis, Université Claude Bernard-Lyon I, Lyon, France, 2004. [Google Scholar]
- De Ville d’Avray, M.A.; Isambert, A.; Brochot, S. Development of a global mathematical model for reactive extrusion processes in corotating twin-screw extruders. Comput. Aided Chem. Eng. 2010, 28, 769–774. [Google Scholar]
- Eitzlmayr, A.; Koscher, G.; Reynolds, G.; Huang, Z.; Booth, J.; Shering, P.; Khinast, J. Mechanistic modeling of modular co-rotating twin-screw extruders. Int. J. Pharm. 2014, 474, 157–176. [Google Scholar] [CrossRef] [PubMed]
- Ganzeveld, K.; Capel, J.; Van Der Wal, D.; Janssen, L. The modelling of counter-rotating twin screw extruders as reactors for single-component reactions. Chem. Eng. Sci. 1994, 49, 1639–1649. [Google Scholar] [CrossRef]
- De Graaf, R.; Rohde, M.; Janssen, L. A novel model predicting the residence-time distribution during reactive extrusion. Chem. Eng. Sci. 1997, 52, 4345–4356. [Google Scholar] [CrossRef]
- Goma-Bilongo, T.; Couenne, F.; Jallut, C.; Le Gorrec, Y.; Di Martino, A. Dynamic Modeling of the Reactive Twin-Screw Corotating Extrusion Process: Experimental Validation by Using Inlet Glass Fibers Injection Response and Application to Polymers Degassing. Ind. Eng. Chem. Res. 2012, 51, 11381–11388. [Google Scholar] [CrossRef]
- Janssen, L. Twin Screw Extrusion; Elsevier Scientific Publishing Company: Amsterdam, Netherlands, 1978. [Google Scholar]
- Booy, M. Isothermal flow of viscous liquids in corotating twin screw devices. Polym. Eng. Sci. 1980, 20, 1220–1228. [Google Scholar] [CrossRef]
- Goffart, D.; Van der Wal, D.; Klomp, E.; Hoogstraten, H.; Janssen, L.; Breysse, L.; Trolez, Y. Three-dimensional flow modeling of a self-wiping corotating twin-screw extruder. Part I: The transporting section. Polym. Eng. Sci. 1996, 36, 901–911. [Google Scholar] [CrossRef]
- Van Der Wal, D.; Goffart, D.; Klomp, E.; Hoogstraten, H.; Janssen, L. Three-dimensional flow modeling of a self-wiping corotating twin-screw extruder. Part II: The kneading section. Polym. Eng. Sci. 1996, 36, 912–924. [Google Scholar] [CrossRef]
- Cheng, H.; Manas-Zloczower, I. Distributive mixing in conveying elements of a ZSK-53 co-rotating twin screw extruder. Polym. Eng. Sci. 1998, 38, 926–935. [Google Scholar] [CrossRef]
- Ishikawa, T.; Kihara, S.i.; Funatsu, K. 3-D non-isothermal flow field analysis and mixing performance evaluation of kneading blocks in a co-rotating twin srew extruder. Polym. Eng. Sci. 2001, 41, 840–849. [Google Scholar] [CrossRef]
- Potente, H.; Többen, W.H. Improved Design of Shearing Sections with New Calculation Models Based on 3D Finite-Element Simulations. Macromol. Mater. Eng. 2002, 287, 808–814. [Google Scholar] [CrossRef]
- Bertrand, F.; Thibault, F.; Delamare, L.; Tanguy, P.A. Adaptive finite element simulations of fluid flow in twin-screw extruders. Comput. Chem. Eng. 2003, 27, 491–500. [Google Scholar] [CrossRef]
- Ficarella, A.; Milanese, M.; Laforgia, D. Numerical study of the extrusion process in cereals production: Part I. Fluid-dynamic analysis of the extrusion system. J. Food Eng. 2006, 73, 103–111. [Google Scholar] [CrossRef]
- Malik, M.; Kalyon, D. 3d finite element simulation of processing of generalized newtonian fluids in counter-rotating and tangential tse and die combination. Int. Polym. Proc. 2005, 20, 398–409. [Google Scholar] [CrossRef]
- Kalyon, D.; Malik, M. An integrated approach for numerical analysis of coupled flow and heat transfer in co-rotating twin screw extruders. Int. Polym. Proc. 2007, 22, 293–302. [Google Scholar] [CrossRef]
- Barrera, M.; Vega, J.; Martínez-Salazar, J. Three-dimensional modelling of flow curves in co-rotating twin-screw extruder elements. J. Mater. Proc. Technol. 2008, 197, 221–224. [Google Scholar] [CrossRef]
- Rodríguez, E.O. Numerical Simulations of Reactive Extrusion in Twin Screw Extruders. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 18 January 2009. [Google Scholar]
- Sarhangi Fard, A.; Hulsen, M.A.; Meijer, H.E.; Famili, N.M.; Anderson, P.D. Tools to Simulate Distributive Mixing in Twin-Screw Extruders. Macromol. Theory Simul. 2012, 21, 217–240. [Google Scholar] [CrossRef]
- Fard, A.S.; Anderson, P.D. Simulation of distributive mixing inside mixing elements of co-rotating twin-screw extruders. Comput. Fluids 2013, 87, 79–91. [Google Scholar] [CrossRef]
- Hétu, J.F.; Ilinca, F. Immersed boundary finite elements for 3D flow simulations in twin-screw extruders. Comput. Fluids 2013, 87, 2–11. [Google Scholar] [CrossRef]
- Rathod, M.L.; Kokini, J.L. Effect of mixer geometry and operating conditions on mixing efficiency of a non-Newtonian fluid in a twin screw mixer. J. Food Eng. 2013, 118, 256–265. [Google Scholar] [CrossRef]
- Djoudi, H.; Gelin, J.; Barrière, T. Simulation numérique par éléments finis de l écoulement dans un mélangeur bi-vis et l interaction mélange-mélangeur. 11e Colloque National en Calcul des Structures. 2013. Available online: http://csma2013.csma.fr/resumes/rN47U19K8.pdf (accessed on 27 May 2016).
- Carneiro, O.; Nóbrega, J.; Pinho, F.; Oliveira, P. Computer aided rheological design of extrusion dies for profiles. J. Mater. Proc. Technol. 2001, 114, 75–86. [Google Scholar] [CrossRef]
- Lin, Z.; Juchen, X.; Xinyun, W.; Guoan, H. Optimization of die profile for improving die life in the hot extrusion process. J. Mater. Proc. Technol. 2003, 142, 659–664. [Google Scholar] [CrossRef]
- Patil, P.D.; Feng, J.J.; Hatzikiriakos, S.G. Constitutive modeling and flow simulation of polytetrafluoroethylene (PTFE) paste extrusion. J. Non-Newton. Fluid Mech. 2006, 139, 44–53. [Google Scholar] [CrossRef]
- Mitsoulis, E.; Hatzikiriakos, S.G. Steady flow simulations of compressible PTFE paste extrusion under severe wall slip. J. Non-Newton. Fluid Mech. 2009, 157, 26–33. [Google Scholar] [CrossRef]
- Radl, S.; Tritthart, T.; Khinast, J.G. A novel design for hot-melt extrusion pelletizers. Chem. Eng. Sci. 2010, 65, 1976–1988. [Google Scholar] [CrossRef]
- Ardakani, H.A.; Mitsoulis, E.; Hatzikiriakos, S.G. Thixotropic flow of toothpaste through extrusion dies. J. Non-Newton. Fluid Mech. 2011, 166, 1262–1271. [Google Scholar] [CrossRef]
- Lawal, A.; Railkar, S.; Kalyon, D.M. Mathematical modeling of three-dimensional die flows of viscoplastic fluids with wall slip. J. Reinf. Plast. Compos. 2000, 19, 1483–1492. [Google Scholar] [CrossRef]
- Kalyon, D.M.; Gevgilili, H. Wall slip and extrudate distortion of three polymer melts. J. Rheol. (1978-present) 2003, 47, 683–699. [Google Scholar] [CrossRef]
- Kalyon, D.M. Apparent slip and viscoplasticity of concentrated suspensions. J. Rheol. (1978-present) 2005, 49, 621–640. [Google Scholar] [CrossRef]
- Birinci, E.; Kalyon, D.M. Development of extrudate distortions in poly (dimethyl siloxane) and its suspensions with rigid particles. J. Rheol. (1978-present) 2006, 50, 313–326. [Google Scholar] [CrossRef]
- Kalyon, D.M. An analytical model for steady coextrusion of viscoplastic fluids in thin slit dies with wall slip. Polym. Eng. Sci. 2010, 50, 652–664. [Google Scholar] [CrossRef]
- Tang, H.; Kalyon, D.M. Unsteady circular tube flow of compressible polymeric liquids subject to pressure-dependent wall slip. J. Rheol. (1978-present) 2008, 52, 507–525. [Google Scholar] [CrossRef]
- Tang, H.; Kalyon, D.M. Time-dependent tube flow of compressible suspensions subject to pressure dependent wall slip: Ramifications on development of flow instabilities. J. Rheol. (1978-present) 2008, 52, 1069–1090. [Google Scholar] [CrossRef]
- Lawal, A.; Kalyon, D.M.; Ji, Z. Computational study of chaotic mixing in co-rotating two-tipped kneading paddles: Two-dimensional approach. Polym. Eng. Sci. 1993, 33, 140–148. [Google Scholar] [CrossRef]
- Lawal, A.; Kalyon, D.M. Mechanisms of mixing in single and co-rotating twin screw extruders. Polym. Eng. Sci. 1995, 35, 1325–1338. [Google Scholar] [CrossRef]
- Lawal, A.; Kalyon, D. Three Dimensional Analysis of Co-rotating Twin Screw Extrusion Using Tools of Dynamics. In Technical Papers of the Annual Technical Conference-Society of Plastics Engineers Incorporated; Society of plastics engineers Inc.: Bethel, AK, USA, 1993; p. 3397. [Google Scholar]
- Zhu, L.; Narh, K.A.; Hyun, K.S. Evaluation of numerical simulation methods in reactive extrusion. Adv. Polym. Technol. 2005, 24, 183–193. [Google Scholar] [CrossRef]
- Werner, H.P. Das Betriebsverhalten der zweiwelligen Knetscheiben-Schneckenpresse vom Typ ZSK bei der Verarbeitung von hochviskosen Flüssigkeiten: Ein Beitrag zur Theorie und Praxis der ZSK. Ph.D. Thesis, Technische Universität München, Munich, Germany, 1976. [Google Scholar]
- Yacu, W. Modeling a twin screw co-rotating extruder. J. Food Process Eng. 1985, 8, 1–21. [Google Scholar] [CrossRef]
- Meijer, H.; Elemans, P. The modeling of continuous mixers. Part I: The corotating twin-screw extruder. Polym. Eng. Sci. 1988, 28, 275–290. [Google Scholar] [CrossRef]
- Tayeb, J.; Vergnes, B.; Valle, G.D. Theoretical computation of the isothermal flow through the reverse screw element of a twin screw extrusion cooker. J. Food Sci. 1988, 53, 616–625. [Google Scholar] [CrossRef]
- Tayeb, J.; Vergnes, B.; Valle, G.D. A basic model for a twin-screw extruder. J. Food Sci. 1989, 54, 1047–1056. [Google Scholar] [CrossRef]
- Della Valle, G.; Barres, C.; Plewa, J.; Tayeb, J.; Vergnes, B. Computer simulation of starchy products’ transformation by twin-screw extrusion. J. Food Eng. 1993, 19, 1–31. [Google Scholar] [CrossRef]
- White, J.L.; Chen, Z. Simulation of non-isothermal flow in modular co-rotating twin screw extrusion. Polym. Eng. Sci. 1994, 34, 229–237. [Google Scholar] [CrossRef]
- Michaeli, W.; Grefenstein, A. An analytical model of the conveying behaviour of closely intermeshing co-rotating twin screw extruders. Int. Polym. Process. 1996, 11, 121–128. [Google Scholar] [CrossRef]
- Vergnes, B.; Valle, G.D.; Delamare, L. A global computer software for polymer flows in corotating twin screw extruders. Polym. Eng. Sci. 1998, 38, 1781–1792. [Google Scholar] [CrossRef]
- Kulshreshtha, M.; Jukes, D.; Zaror, C. Generalized steady state model for twin screw extruders. Food Bioprod. Process. 1991, 69, 189–199. [Google Scholar]
- Martelli, F.G. Twin-Screw Extruders: A Basic Understanding; Van Nostrand Reinhold Company: New York, NY, USA, 1983. [Google Scholar]
- Li, C.H. Modelling extrusion cooking. Math. Comput. Model. 2001, 33, 553–563. [Google Scholar] [CrossRef]
- Diagne, M.; Dos Santos Martins, V.; Couenne, F.; Maschke, B.; Jallut, C. Modélisation d’un procédé d’extrusion par deux systèmes d’équations d’évolution couplés par une interface mobile. J. Eur. des Syst. Autom. 2011, 45, 665–691. [Google Scholar]
- Vande Wouwer, A.; Saucez, P.; Vilas, C. Simulation of Ode/Pde Models with MATLAB®, OCTAVE and SCILAB: Scientific and Engineering Applications; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Ramkrishna, D. Population Balances: Theory and Applications to Particulate Systems in Engineering; Academic Press: London, UK, 2000. [Google Scholar]
- Iveson, S.; Litster, J.; Ennis, B. Fundamental studies of granule consolidation Part 1: Effects of binder content and binder viscosity. Powder Technol. 1996, 88, 15–20. [Google Scholar] [CrossRef]
- Hounslow, M.; Pearson, J.; Instone, T. Tracer studies of high-shear granulation: II. Population balance modeling. AIChE J. 2001, 47, 1984–1999. [Google Scholar] [CrossRef]
- Darelius, A.; Brage, H.; Rasmuson, A.; Björn, I.N.; Folestad, S. A volume-based multi-dimensional population balance approach for modelling high shear granulation. Chem. Eng. Sci. 2006, 61, 2482–2493. [Google Scholar] [CrossRef]
- Poon, J.M.H.; Ramachandran, R.; Sanders, C.F.; Glaser, T.; Immanuel, C.D.; Doyle, F.J., III; Litster, J.D.; Stepanek, F.; Wang, F.Y.; Cameron, I.T. Experimental validation studies on a multi-dimensional and multi-scale population balance model of batch granulation. Chem. Eng. Sci. 2009, 64, 775–786. [Google Scholar] [CrossRef]
- Gerstlauer, A.; Motz, S.; Mitrović, A.; Gilles, E.D. Development, analysis and validation of population models for continuous and batch crystallizers. Chem. Eng. Sci. 2002, 57, 4311–4327. [Google Scholar] [CrossRef]
- Sen, M.; Ramachandran, R. A multi-dimensional population balance model approach to continuous powder mixing processes. Adv. Powder Technol. 2013, 24, 51–59. [Google Scholar] [CrossRef]
- Bilgili, E.; Scarlett, B. Population balance modeling of non-linear effects in milling processes. Powder Technol. 2005, 153, 59–71. [Google Scholar] [CrossRef]
- Verkoeijen, D.; Pouw, G.A.; Meesters, G.M.; Scarlett, B. Population balances for particulate processes—A volume approach. Chem. Eng. Sci. 2002, 57, 2287–2303. [Google Scholar] [CrossRef]
- Cameron, I.; Wang, F.; Immanuel, C.; Stepanek, F. Process systems modelling and applications in granulation: A review. Chem. Eng. Sci. 2005, 60, 3723–3750. [Google Scholar] [CrossRef]
- Sen, M. Multiscale Modeling and Validation of Particulate Processes. Ph.D. Thesis, Rutgers University-Graduate School-New Brunswick, New Brunswick, NJ, USA, May 2015. [Google Scholar]
- Kumar, A. Experimental and model-based analysis of twin-screw wet granulation in pharmaceutical processes. Ph.D. Thesis, Ghent University, Ghent, Belgium, 14 October 2015. [Google Scholar]
- Barrasso, D.; Walia, S.; Ramachandran, R. Multi-component population balance modeling of continuous granulation processes: A parametric study and comparison with experimental trends. Powder Technol. 2013, 241, 85–97. [Google Scholar] [CrossRef]
- Barrasso, D.; Eppinger, T.; Pereira, F.E.; Aglave, R.; Debus, K.; Bermingham, S.K.; Ramachandran, R. A multi-scale, mechanistic model of a wet granulation process using a novel bi-directional PBM–DEM coupling algorithm. Chem. Eng. Sci. 2015, 123, 500–513. [Google Scholar] [CrossRef]
- Gantt, J.A.; Gatzke, E.P. High-shear granulation modeling using a discrete element simulation approach. Powder Technol. 2005, 156, 195–212. [Google Scholar] [CrossRef]
- Zhu, H.; Zhou, Z.; Yang, R.; Yu, A. Discrete particle simulation of particulate systems: A review of major applications and findings. Chem. Eng. Sci. 2008, 63, 5728–5770. [Google Scholar] [CrossRef]
- Ketterhagen, W.R.; am Ende, M.T.; Hancock, B.C. Process modeling in the pharmaceutical industry using the discrete element method. J. Pharm. Sci. 2009, 98, 442–470. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Yang, R.; Yu, A. DEM study of the transverse mixing of wet particles in rotating drums. Chem. Eng. Sci. 2013, 86, 99–107. [Google Scholar] [CrossRef]
- Herrmann, H.; Luding, S. Modeling granular media on the computer. Contin. Mech. Thermodyn. 1998, 10, 189–231. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Moysey, P.; Thompson, M. Modelling the solids inflow and solids conveying of single-screw extruders using the discrete element method. Powder Technol. 2005, 153, 95–107. [Google Scholar] [CrossRef]
- Yang, R.; Zou, R.; Yu, A. Microdynamic analysis of particle flow in a horizontal rotating drum. Powder Technol. 2003, 130, 138–146. [Google Scholar] [CrossRef]
- Hassanpour, A.; Tan, H.; Bayly, A.; Gopalkrishnan, P.; Ng, B.; Ghadiri, M. Analysis of particle motion in a paddle mixer using Discrete Element Method (DEM). Powder Technol. 2011, 206, 189–194. [Google Scholar] [CrossRef]
- Wang, M.; Yang, R.; Yu, A. DEM investigation of energy distribution and particle breakage in tumbling ball mills. Powder Technol. 2012, 223, 83–91. [Google Scholar] [CrossRef]
- Kumar, A.; Gernaey, K.V.; De Beer, T.; Nopens, I. Model-based analysis of high shear wet granulation from batch to continuous processes in pharmaceutical production–a critical review. Eur. J. Pharm. Biopharm. 2013, 85, 814–832. [Google Scholar] [CrossRef] [PubMed]
- Barrasso, D. Multi-scale modeling of wet granulation processes. Ph.D. Thesis, Rutgers University-Graduate School-New Brunswick, New Brunswick, NJ, USA, October 2015. [Google Scholar]
- Kumar, A.; Vercruysse, J.; Mortier, S.T.; Vervaet, C.; Remon, J.P.; Gernaey, K.V.; De Beer, T.; Nopens, I. Model-based analysis of a twin-screw wet granulation system for continuous solid dosage manufacturing. Comput. Chem. Eng. 2016, 89, 62–70. [Google Scholar] [CrossRef]
- Kulju, T.; Paavola, M.; Spittka, H.; Keiski, R.L.; Juuso, E.; Leiviskä, K.; Muurinen, E. Modeling continuous high-shear wet granulation with DEM-PB. Chem. Eng. Sci. 2016, 142, 190–200. [Google Scholar] [CrossRef]
- Ramachandran, R. Integrated PBM-DEM Model Of A Continuous Granulation Process; Department of Chemical and Biochemical Engineering Rutgers University: Piscataway, NJ, USA, 2016. Available online: http://www.star-global-conference.com/sites/default/files/publicpdfpresentation/SGC2016RutgersUniversityRohitRamachandran.pdf (accessed on 27 May 2016).
- Rajniak, P.; Stepanek, F.; Dhanasekharan, K.; Fan, R.; Mancinelli, C.; Chern, R. A combined experimental and computational study of wet granulation in a Wurster fluid bed granulator. Powder Technol. 2009, 189, 190–201. [Google Scholar] [CrossRef]
- Fries, L.; Antonyuk, S.; Heinrich, S.; Palzer, S. DEM–CFD modeling of a fluidized bed spray granulator. Chem. Eng. Sci. 2011, 66, 2340–2355. [Google Scholar] [CrossRef]
- Sen, M.; Barrasso, D.; Singh, R.; Ramachandran, R. A multi-scale hybrid CFD-DEM-PBM description of a fluid-bed granulation process. Processes 2014, 2, 89–111. [Google Scholar] [CrossRef]
- Seborg, D.E.; Mellichamp, D.A.; Edgar, T.F.; Doyle, F.J., III. Process Dynamics and Control; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Hassan, G.; Parnaby, J. Model reference optimal steady-state adaptive computer control of plastics extrusion processes. Polym. Eng. Sci. 1981, 21, 276–284. [Google Scholar] [CrossRef]
- Costin, M.; Taylor, P.; Wright, J. On the dynamics and control of a plasticating extruder. Polym. Eng. Sci. 1982, 22, 1095–1106. [Google Scholar] [CrossRef]
- Chan, D.; Nelson, R.; Lee, L.J. Dynamic behavior of a single screw plasticating extruder part II: Dynamic modeling. Polym. Eng. Sci. 1986, 26, 152–161. [Google Scholar] [CrossRef]
- Lu, Q.; Mulvaney, S.; Hsieh, F.; Huff, H. Model and strategies for computer control of a twin-screw extruder. Food Control 1993, 4, 25–33. [Google Scholar] [CrossRef]
- Cayot, N.; Bounie, D.; Baussart, H. Dynamic modelling for a twin screw food extruder: Analysis of the dynamic behaviour through process variables. J. Food Eng. 1995, 25, 245–260. [Google Scholar] [CrossRef]
- Haley, T.A.; Mulvaney, S.J. On-line system identification and control design of an extrusion cooking process: Part I. System identification. Food Control 2000, 11, 103–120. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed]
- Werbos, P. Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. Ph.D. Thesis, Harvard University, Cambridge, MA, USA, 1974. [Google Scholar]
- Minsky, M.; Papert, S. Perceptrons: An Introduction to Computational Geometry, expanded ed.; MIT Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Vande Wouwer, A.; Renotte, C.; Bogaerts, P. Biological reaction modeling using radial basis function networks. Comput. Chem. Eng. 2004, 28, 2157–2164. [Google Scholar] [CrossRef]
- Morgan, N.; Bourlard, H. Neural networks for statistical recognition of continuous speech. Proc. IEEE 1995, 83, 742–772. [Google Scholar] [CrossRef]
- Gosselin, B. Multilayer perceptrons combination applied to handwritten character recognition. Neural Proc. Lett. 1996, 3, 3–10. [Google Scholar] [CrossRef]
- Willis, M.J.; Montague, G.A.; Di Massimo, C.; Tham, M.T.; Morris, A. Artificial neural networks in process estimation and control. Automatica 1992, 28, 1181–1187. [Google Scholar] [CrossRef]
- Chiu, S. Developing commercial applications of intelligent control. Control Syst. IEEE 1997, 17, 94–100. [Google Scholar] [CrossRef]
- Linko, P.; Uemura, K.; Zhu, Y.; Ferikainen, T. Application of neural network models in fuzzy extrusion control. Food Bioprod. Proc. Trans. Inst. Chem. Eng. Part C 1992, 70, 131–137. [Google Scholar]
- Eerikäinen, T.; Zhu, Y.H.; Linko, P. Neural networks in extrusion process identification and control. Food Control 1994, 5, 111–119. [Google Scholar] [CrossRef]
- Popescu, O.; Popescu, D.C.; Wilder, J.; Karwe, M.V. A new approach to modeling and control of a food extrusion process using artificial neural network and an expert system. J. Food Process Eng. 2001, 24, 17–36. [Google Scholar] [CrossRef]
- Ganjyal, G.; Hanna, M.; Jones, D. Modeling Selected Properties of Extruded Waxy Maize Cross-Linked Starches with Neural Networks. J. Food Sci. 2003, 68, 1384–1388. [Google Scholar] [CrossRef]
- Kim, E.K.; White, J.L. Isothermal transient startup of a starved flow modular co-rotating twin screw extruder. Polym. Eng. Sci. 2000, 40, 543–553. [Google Scholar] [CrossRef]



| Screw Geometry | Parameters | Values |
|---|---|---|
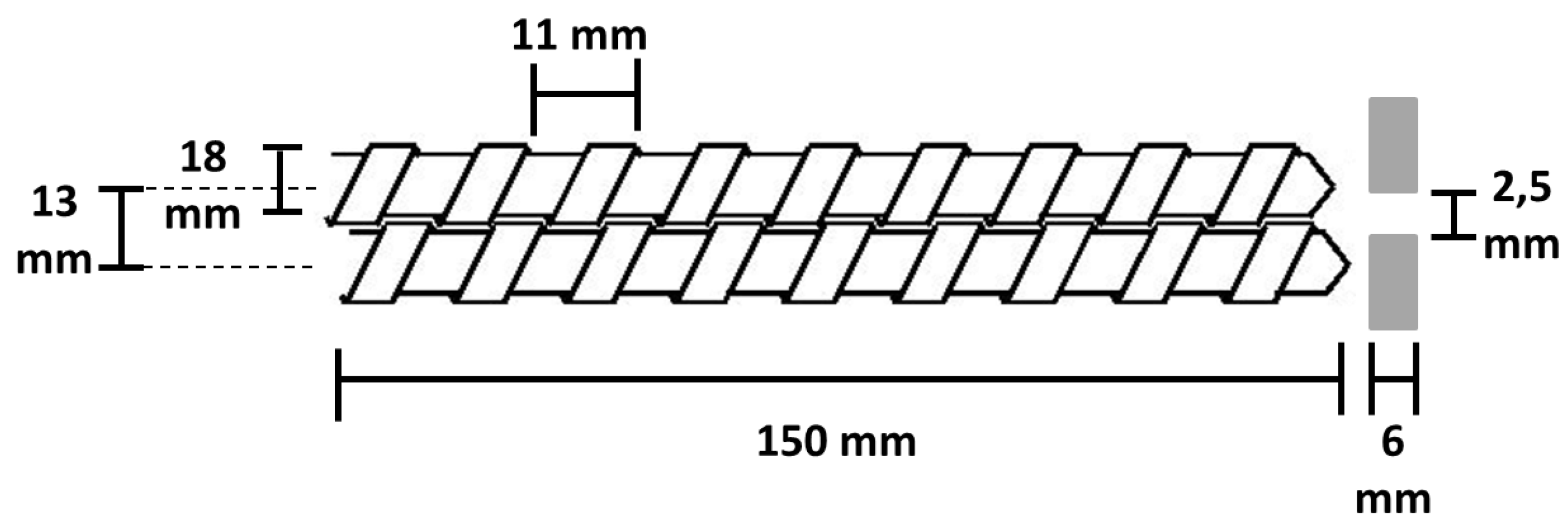
| Screw exterior diameter: | 18 mm | |
| Spacing screw: | 13 mm | |
| Screw pitch: ξ | 11 mm | |
| Screw threads number | 1 | |
| Total length: L | 150 mm | |
| Die geometry | Parameters | Values |
| Die diameter | 2.5 mm | |
| Die length | 6 mm | |
| Thermal properties | Parameters | Values |
| Specific heat capacity: | 5000 J/(kg K) | |
| Thermal conductivity: | 0.016 W/(m K) | |
| Material/barrel heat exchange coefficient: U | 1200 W/(m K) | |
| Barrel temperature: | 140 °C | |
| Material property | Parameter | Value |
| Density: ρ | 550 kg/m | |
| Yasuda-Carreau equations | Parameters | Values |
| b | 0.022 | |
| λ | 0.12 | |
| a | 10 | |
| 0.251 |
| Parameters | Values |
|---|---|
| n | 4 |
| 5.62 | |
| d | 0.063 |
| Reactor i | ||
|---|---|---|
| Direct pitch | if or : | |
| Reverse pitch | if or : | |
| if or : | ||
| Die |
| Parameters | Values |
|---|---|
| n | 13 |
| 0.6 | |
| 0.16 |
| Parameters | Values | Absolute Confidence Intervals at 95 % |
|---|---|---|
| V | m | ± m |
| B | m | ± m |
| D | m/s | ± m/s |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grimard, J.; Dewasme, L.; Vande Wouwer, A. A Review of Dynamic Models of Hot-Melt Extrusion. Processes 2016, 4, 19. https://doi.org/10.3390/pr4020019
Grimard J, Dewasme L, Vande Wouwer A. A Review of Dynamic Models of Hot-Melt Extrusion. Processes. 2016; 4(2):19. https://doi.org/10.3390/pr4020019
Chicago/Turabian StyleGrimard, Jonathan, Laurent Dewasme, and Alain Vande Wouwer. 2016. "A Review of Dynamic Models of Hot-Melt Extrusion" Processes 4, no. 2: 19. https://doi.org/10.3390/pr4020019
APA StyleGrimard, J., Dewasme, L., & Vande Wouwer, A. (2016). A Review of Dynamic Models of Hot-Melt Extrusion. Processes, 4(2), 19. https://doi.org/10.3390/pr4020019