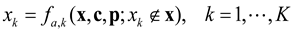Mathematical Modeling of Microbial Community Dynamics: A Methodological Review
Abstract
:1. Introduction
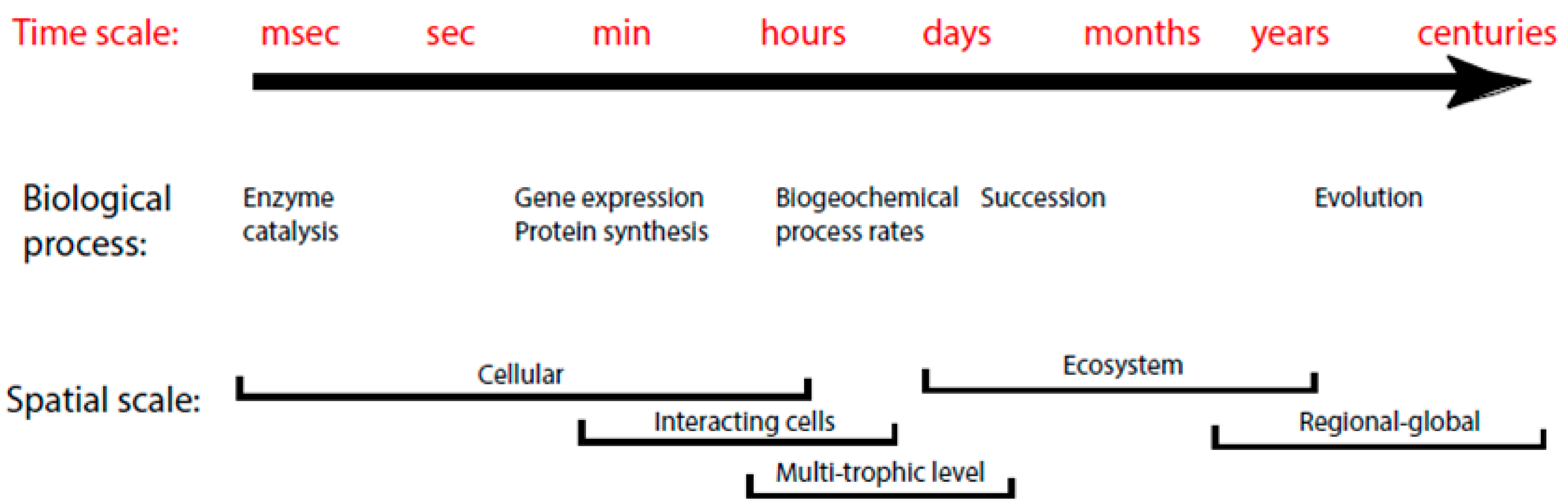
2. Background Information
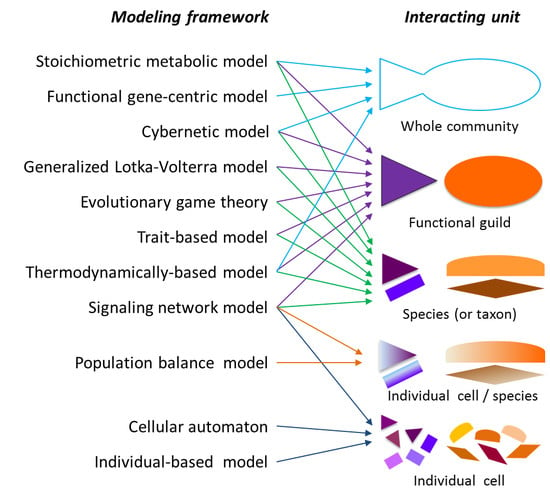
2.1. Modeling Units and Model Classification

2.2. Mathematical Notations
- c = [c1, c2,…,cI]: The vector of concentration of J extracellular metabolites (such as substrates and produced metabolites) in environment
- rk = [r1,k, r2,k,…,rJk,k]: The vector of Jk fluxes (or reaction rates) for species k
- Sk: (I΄k × Jk) Stoichiometric matrix of species k
- x = [x1, x1,…,xK]: The vector of relative abundance or biomass concentration of K species
- I = [1,2, …,I]: Indices of I metabolites in environment
- I΄k = [1,2, …,I΄k] Indices of I΄k intracellular metabolites for species k
- Jk = [1,2, …,Jk] Indices of Jk fluxes for species k
- K = [1,2, …,K]: Indices of K species
- Yi,k: The yield of metabolite i for species k
- Yx,k: The biomass yield of species k
- µk: The growth rate of species k
3. Supra-Organismal Approaches
3.1. Stoichiometric Model-Based Analysis

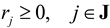 (by splitting reversible reactions into irreversible pairs). Together, the mass balances given in Equation (1) along with appropriate flux bounds are called stoichiometric models. Metabolic network models are often represented in a standard format called the Systems Biology Markup Language (SBML).
(by splitting reversible reactions into irreversible pairs). Together, the mass balances given in Equation (1) along with appropriate flux bounds are called stoichiometric models. Metabolic network models are often represented in a standard format called the Systems Biology Markup Language (SBML).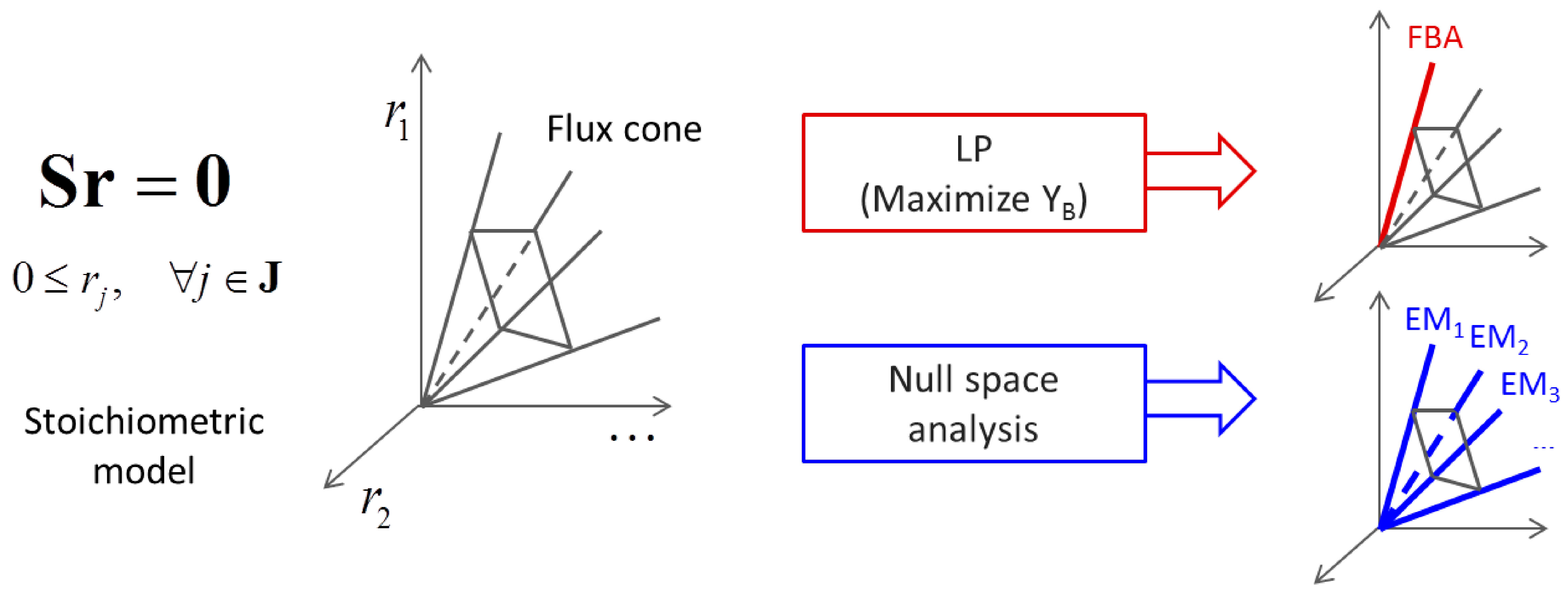
3.2. Metabolic Function-Based Dynamic Modeling
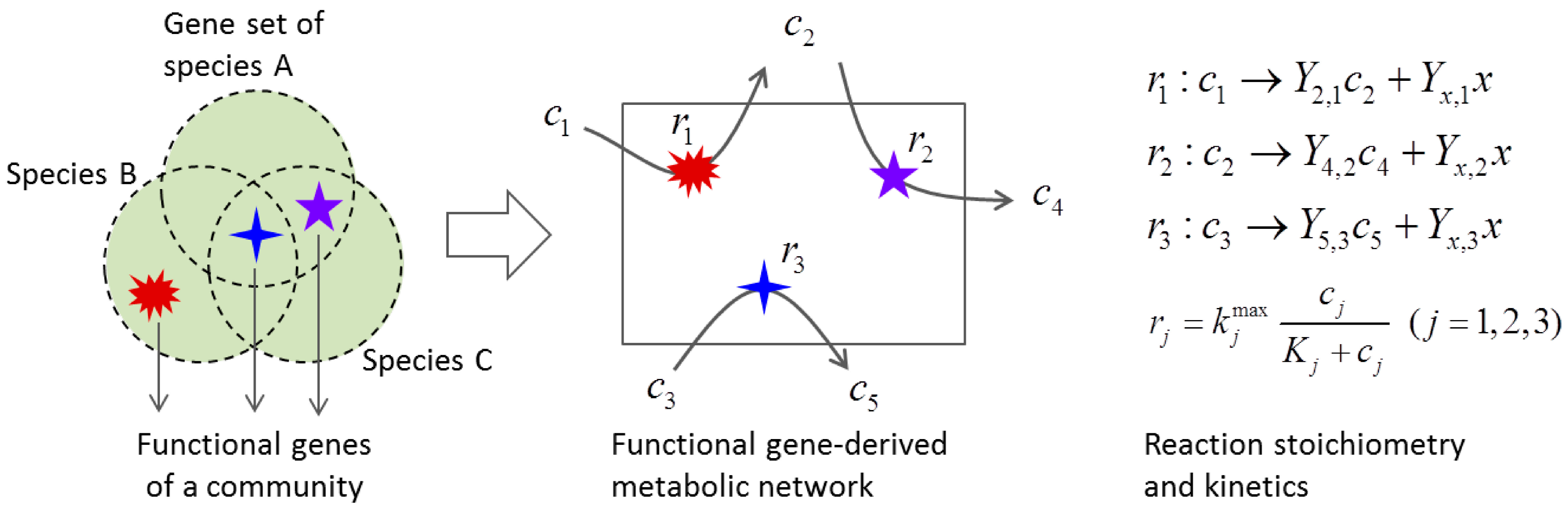

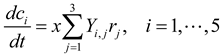


4. Population-Based Models
4.1. Inference of Microbial Interactions
| Relation | Examples | ||
|---|---|---|---|
| Bidirectional | Mutualism or synergism | ⊕⊕ | Biofilm formation to confer antibiotic resistance to the community members [52,53] |
| Syntropy (or cross-feeding): Hydrogen transfer between sulfate reducers and methanogens [54] | |||
| Competition | ⊖⊖ | Species with similar niches: Paramecium aurelia and Paramecium caudatum [55] | |
| Antagonism | ⊕⊖ | Predation: Ciliates feeding on bacteria [50] | |
| Parasitism: Bacteria and bacteriophages [50] | |||
| Unidirectional | Commensalism | ⊕⊙ | Acetobacter oxydans oxidizing mannitol to produce fructose, which is used by other species such as Saccharomyces carlsbergensis that can metabolize fructose, but cannot mannitol (http://www.eoearth.org/view/article/171918/) |
| Mycobacterium vaccae metabolizing cyclohexane to cyclohexanol, which is subsequently used by Pseudomonas species (http://www.eoearth.org/view/article/171918/) | |||
| Amensalism | ⊖⊙ | Lactobacilli producing acids that lower the pH of the surrounding environment [50] | |
| The bread mold Penicillium secreting penicillin that kills bacteria [56] | |||
| Non-directional | Neutralism | ⊙⊙ | Growth of yogurt starter strains of Streptococcus and Lactobacillus in a chemostat [51]: The populations of these strains do not change much regardless of whether cultured separately or together |
4.1.1. Network Inference
4.1.2. Stoichiometric Modeling of Multiple Species
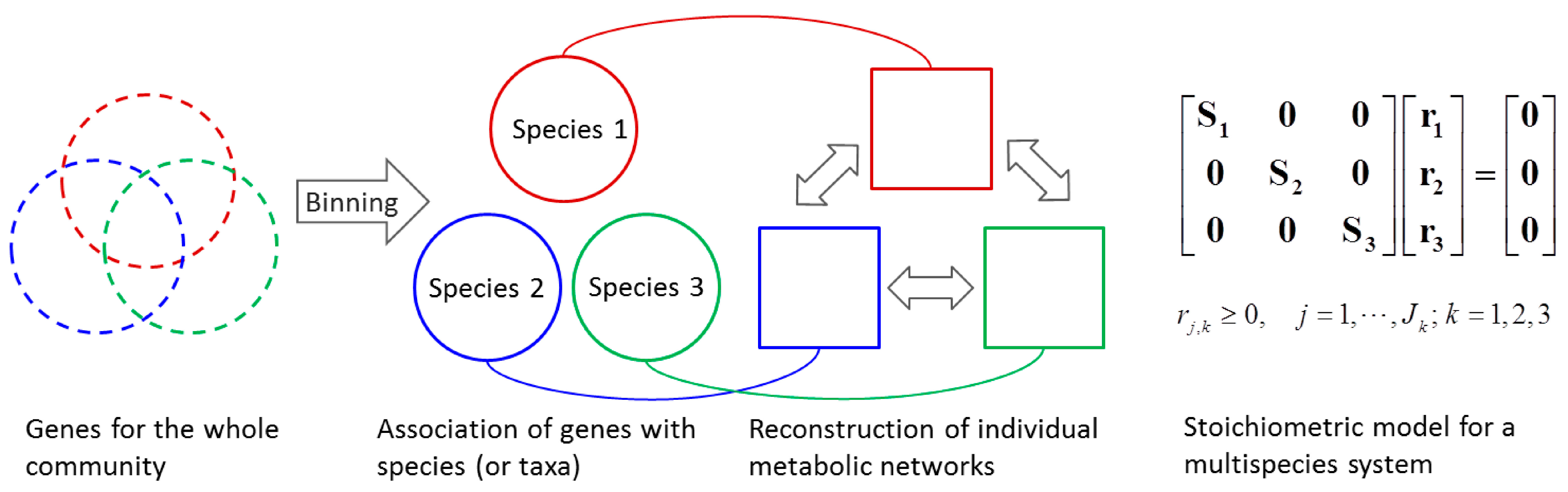
4.2. Nonlinear Regression Models
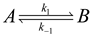
4.3. Thermodynamically-Based Models

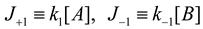
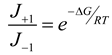
4.4. Trait-Based Modeling
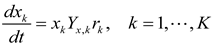
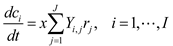
4.5. Lotka-Volterra Model
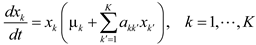
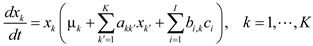
4.6. Evolutionary Game Theory

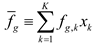

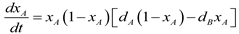
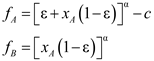
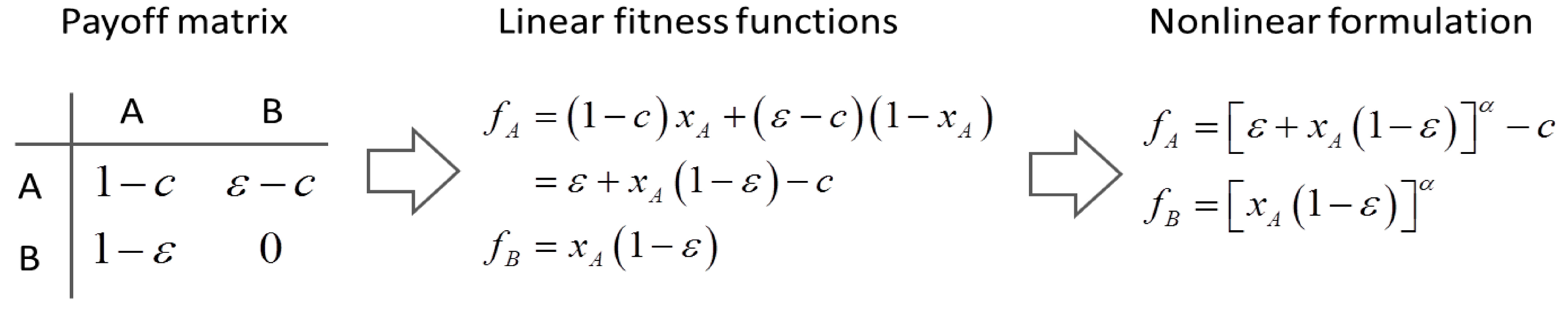
5. Tools for Simulating Heterogeneity
5.1. Simulation of Spatial Heterogeneity Using Population-Based Models

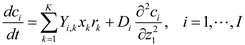
5.2. Individual-Based Modeling
5.3. Population Balance Modeling

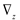 and
and 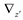 denote partial divergence operators. In general, the above equation is solved by coupling to the conservation equation of environmental variables as shown in Equation (22). In conditions where cells are uniformly distributed in space and characterized only by an internal state z΄, the PBM reduces to
denote partial divergence operators. In general, the above equation is solved by coupling to the conservation equation of environmental variables as shown in Equation (22). In conditions where cells are uniformly distributed in space and characterized only by an internal state z΄, the PBM reduces to

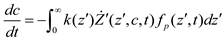
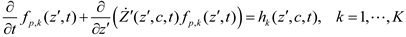
6. Integrative Modeling Strategies
6.1. Information Feedback
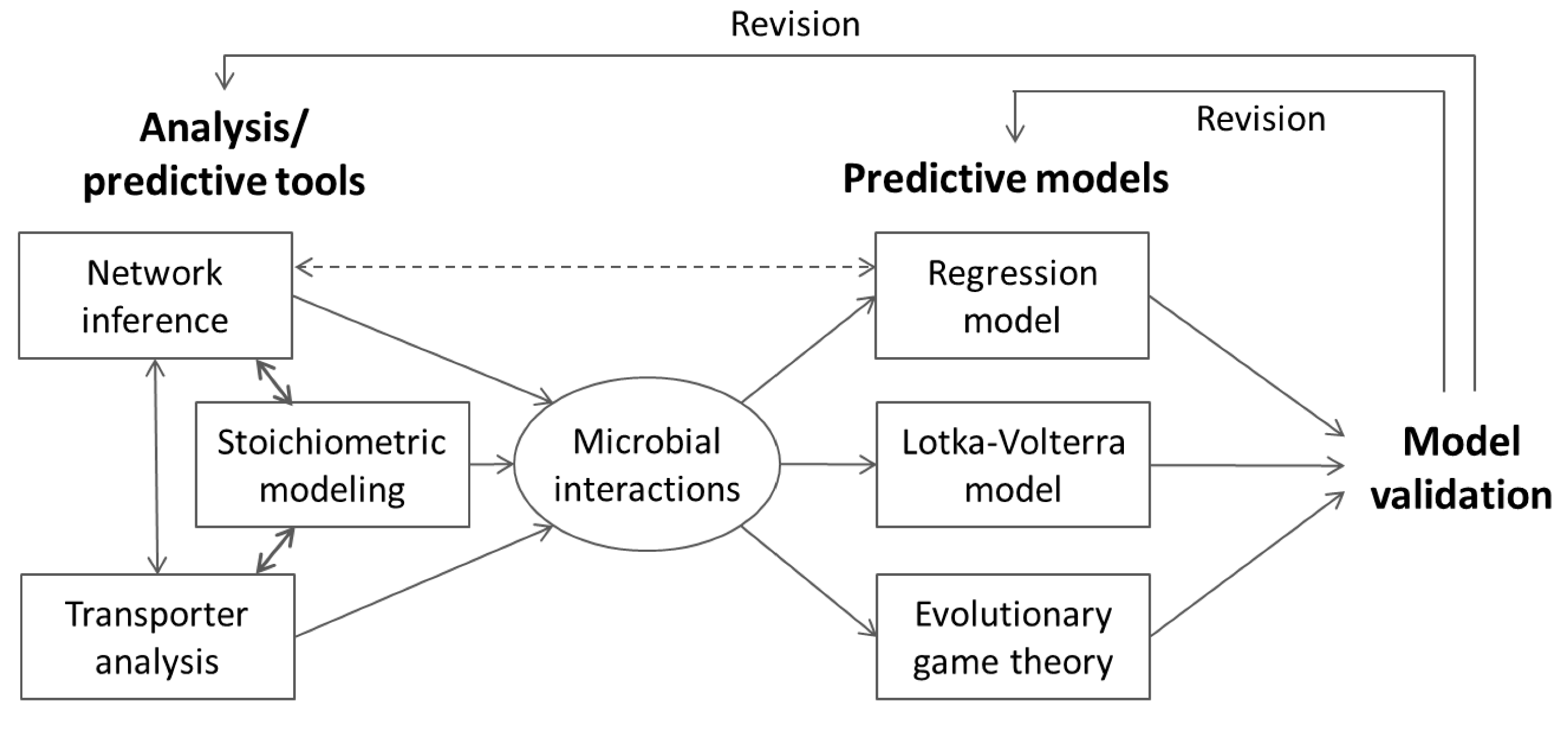
6.2. Indirect Coupling
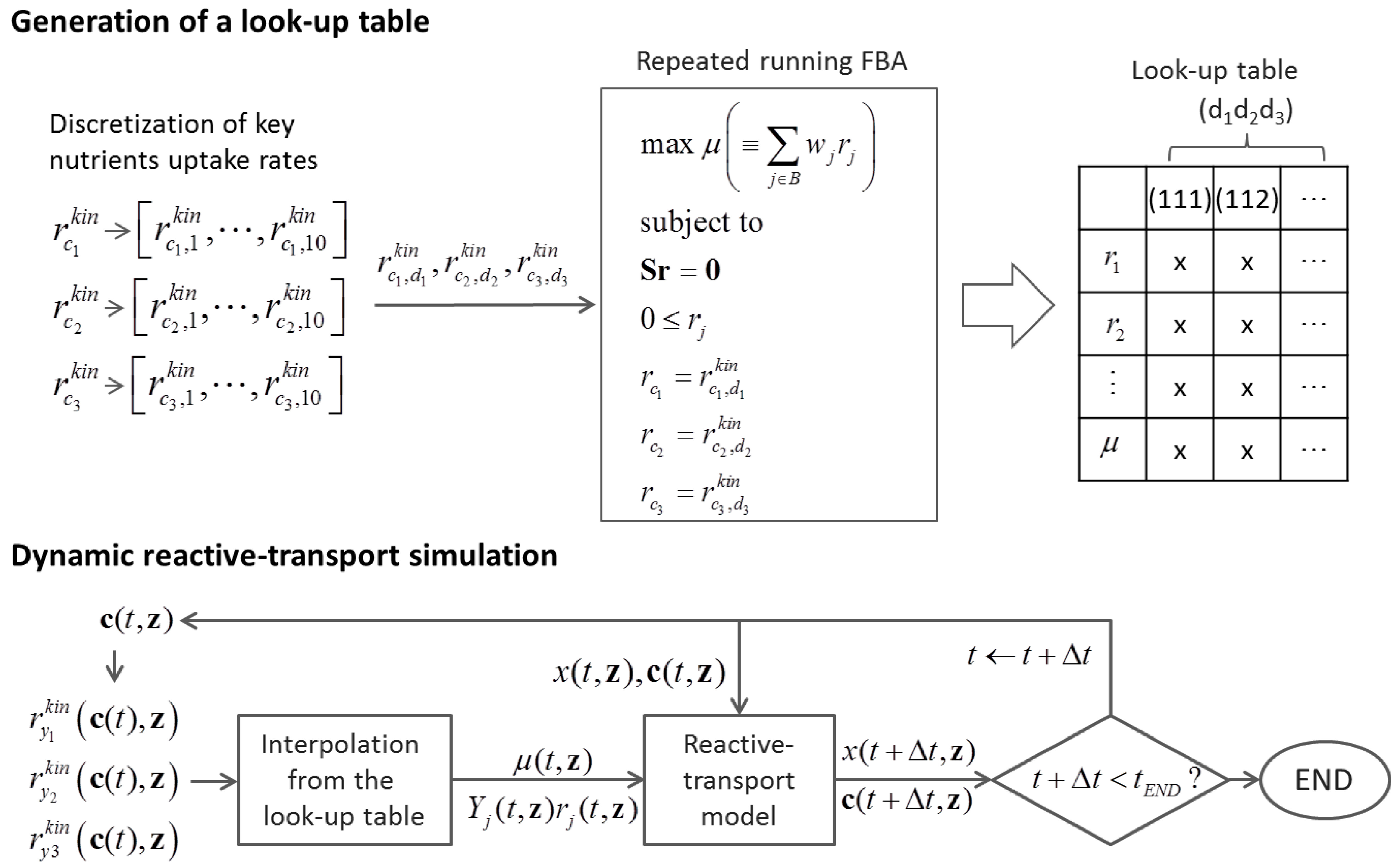
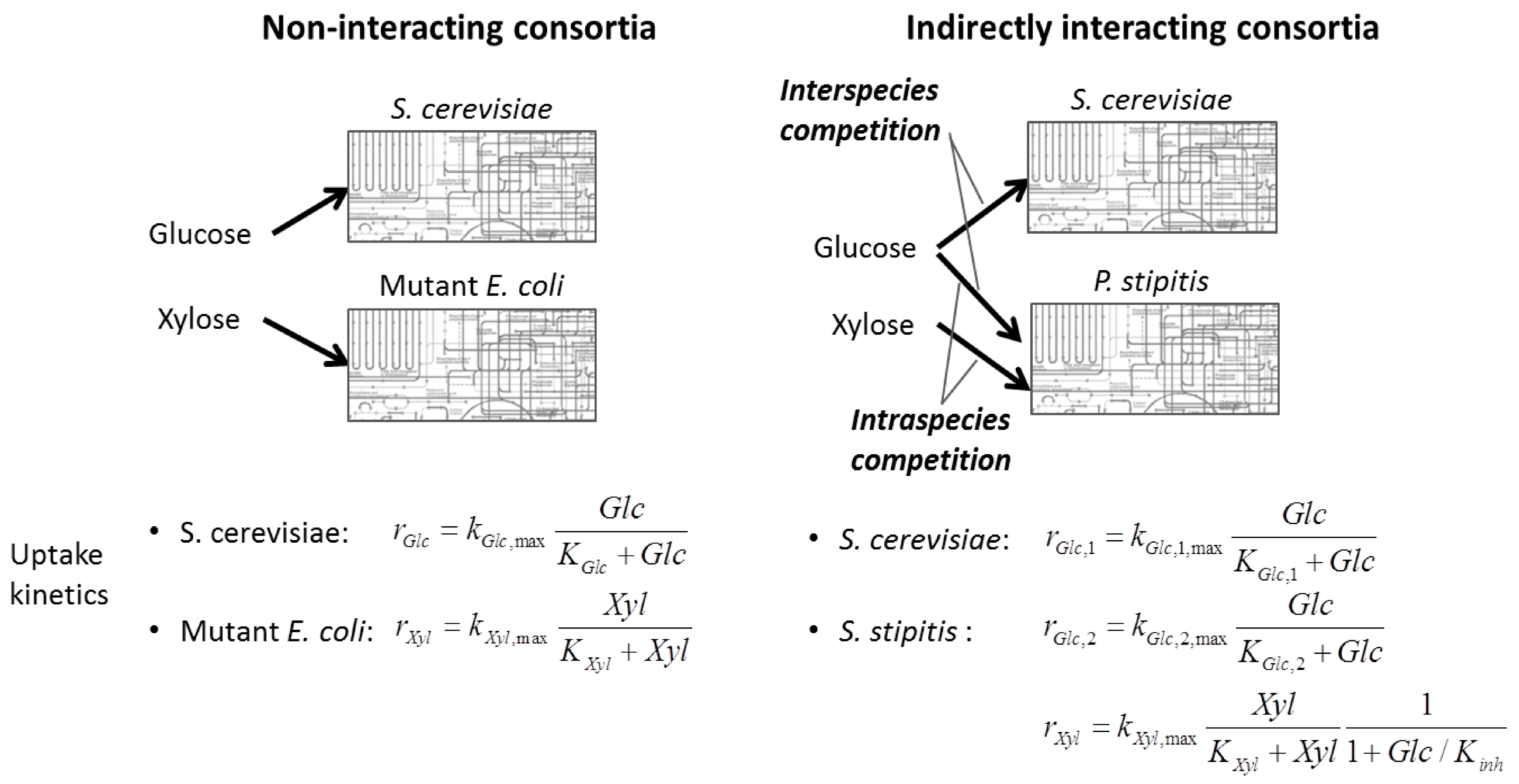
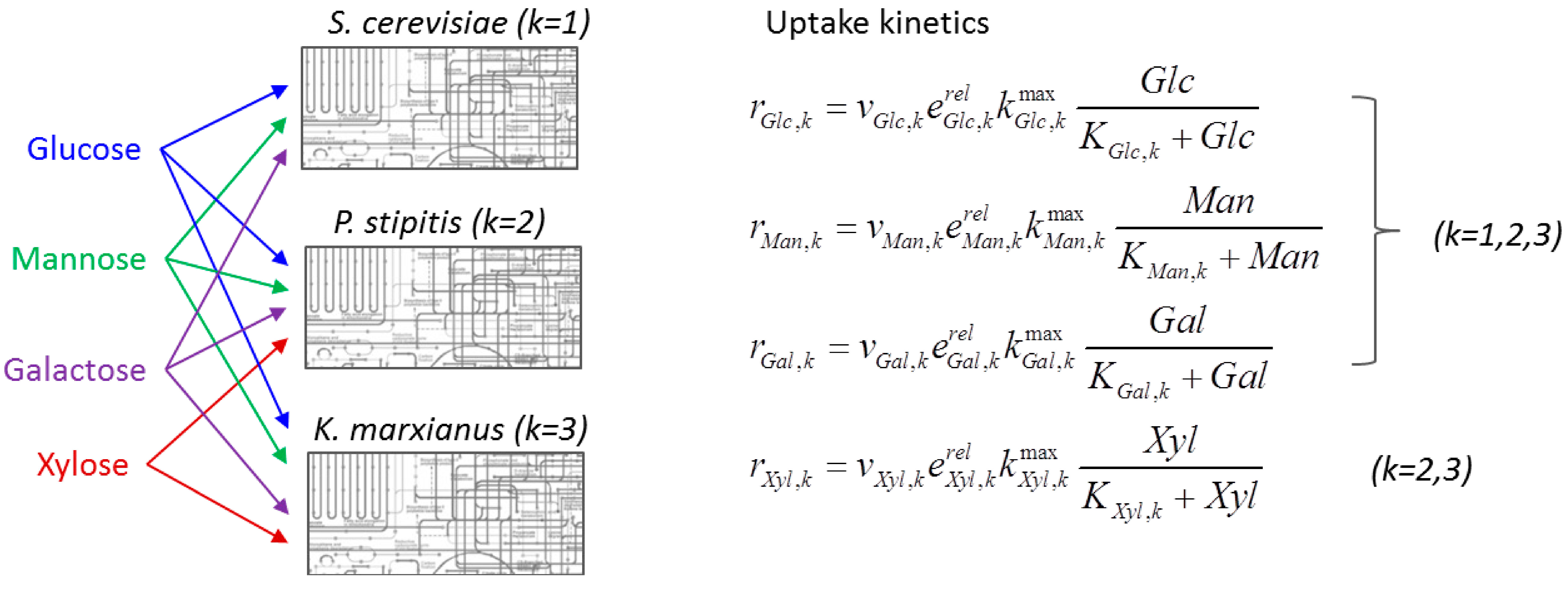
6.3. Direct Coupling

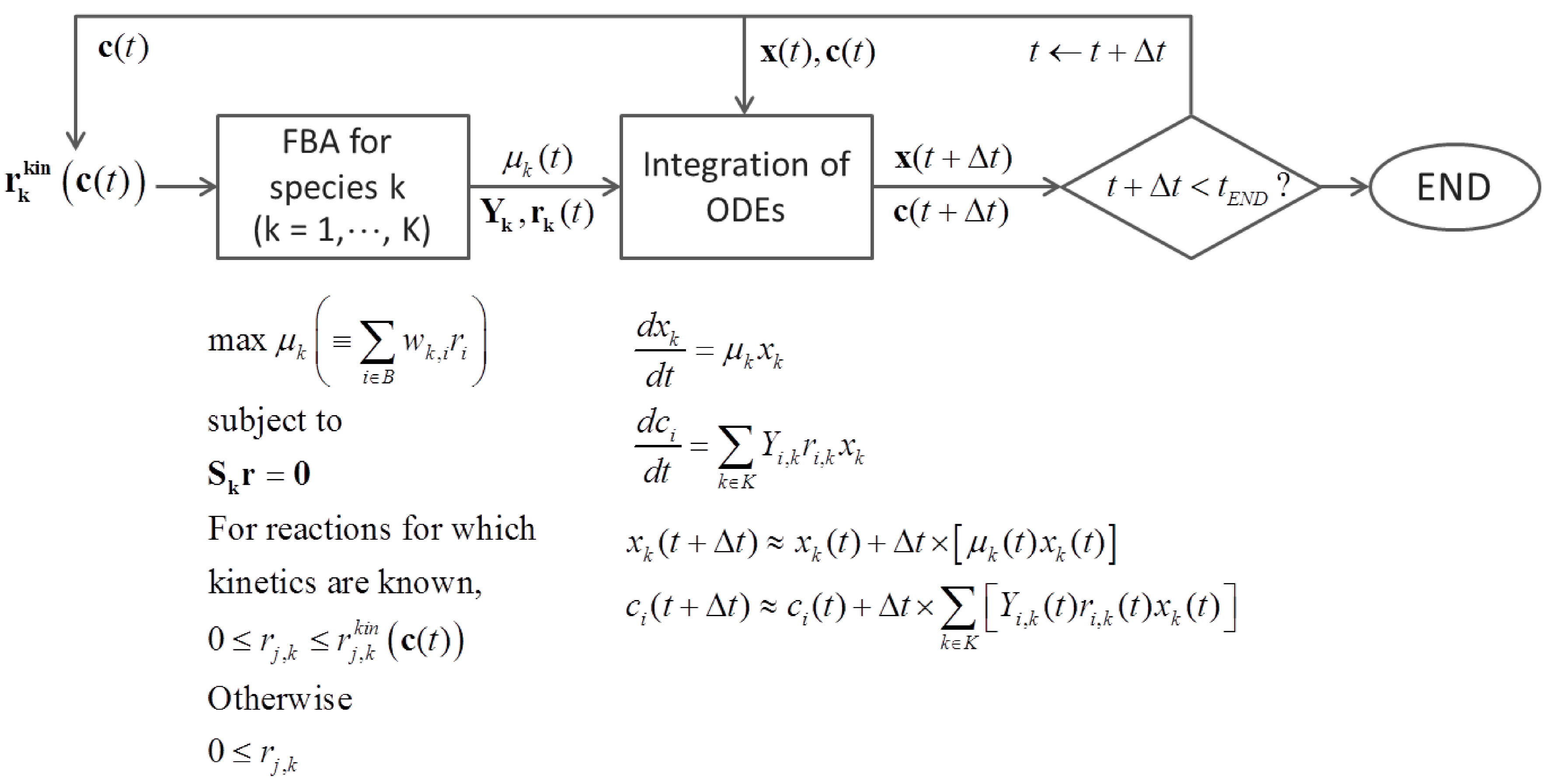
7. Summary and Recommendations
| Approach | Data for Parameter Identification | Inputs for Simulation | Outputs from Simulation | Remarks |
|---|---|---|---|---|
| Flux balance analysis (FBA) ([64]) | N/A (FBA has no parameters to tune) | x_spe and rin_tot in a certain condition | r_spe in the given condition |
|
| Elementary mode (EM) analysis ([41]) | N/A (no parameters to tune) | Information on x_spe and rin_tot in a certain condition | r_spe in the given condition |
|
| Gene-centric approach ([42]) | e_tot(t,z), x_tot(t,z), and c(t,z) upon (designed) perturbations | e_tot(0,z), x_tot(0,z), c(0,z) ( i.e., initial distributions) | e_tot(t,z), x_tot(t,z), c(t,z), r_tot(t,z) in any new conditions |
|
| Nonlinear regression ([75]) | x_spe and c across conditions/times/locations | c at a specific condition/ time/location | x_spe in the given condition/time/location |
|
| Trait-based model ([99]) | x_spe(t) and c(t) upon (designed) perturbations | x_spe(0) and c(0) ( i.e., initial conditions) | x_spe(t) and c(t) |
|
| Generalized Lotka-Volterra (gLV) model ([103]) | x_spe(t) and c(t) (to model the growth rate as a function of c(t)) | x_spe(0) and c(0) | x_spe(t) |
|
| Evolutionary game theory ([27]) | Understanding or knowledge on the interspecies relationship | x_spe(0) and assumed parameter values | x_spe(t) |
|
| Thermodynamically-based model ([77]) | Information on chemical potentials (or reaction rate values) | x_spe(0) and c(0) | x_spe(∞) and c(∞) ( i.e., values after sufficiently enough time) |
|
| Population balance model (PBM) ([120]) | x_spe(t), c(t), and information on population heterogeneity | x_spe(0), c(0), and initial population heterogeneity | x_spe(t), c(t), and population heterogeneity (evolving with time) |
|
| Individual-based model (IbM) ([113]) | x_cell(t,z) and c(t,z) | x_cell(0,z) and c(0,z) | x_cell(t,z) and c(t,z) |
|
| Dynamic FBA (dFBA) ([125]) | x_spe(t) and c(t) | x_spe(0) and c(0) | x_spe(t), r_spe(t), and c(t) |
|
| Cybernetic model ([129]) | x_spe(t) and c(t) | x_spe(0) and c(0) | x_spe(t), r_spe(t), e_spe, and c(t) |
|
| Dynamic multispecies metabolic modeling (DyMMM) ([132]) | x_spe(t) and c(t) | x_spe(0) and c(0) | x_spe(t), r_spe(t), and c(t) |
|
| Dynamic OptCom (d-OptCom) ([73]) | x_spe(t) and c(t) | x_spe(0) and c(0) | x_spe(t), r_spe(t), and c(t) |
|
| Indirect coupling FBA with transport ([122]) | x_spe(t,z) and c(t,z) | x_spe(0,z) and c(0,z) | x_spe(t,z), r_spe(t,z) and c(t,z) |
|
8. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Whitman, W.B.; Coleman, D.C.; Wiebe, W.J. Prokaryotes: The unseen majority. Proc. Natl. Acad. Sci. USA 1998, 95, 6578–6583. [Google Scholar]
- Microbiology by numbers. Nat. Rev. Microbiol. 2011, 9, 628. [CrossRef]
- Fukuda, S.; Ohno, H. Gut microbiome and metabolic diseases. Semin. Immunopathol. 2014, 36, 103–114. [Google Scholar]
- Heintz, C.; Mair, W. You are what you host: Microbiome modulation of the aging process. Cell 2014, 156, 408–411. [Google Scholar] [CrossRef]
- Moloney, R.D.; Desbonnet, L.; Clarke, G.; Dinan, T.G.; Cryan, J.F. The microbiome: Stress, health and disease. Mamm. Genome 2014, 25, 49–74. [Google Scholar] [CrossRef]
- Maukonen, J.; Saarela, M. Microbial communities in industrial environment. Curr. Opin. Microbiol. 2009, 12, 238–243. [Google Scholar] [CrossRef]
- Konopka, A. What is microbial community ecology? ISME J. 2009, 3, 1223–1230. [Google Scholar] [CrossRef]
- Bond, P.L.; Smriga, S.P.; Banfield, J.F. Phylogeny of microorganisms populating a thick, subaerial, predominantly lithotrophic biofilm at an extreme acid mine drainage site. Appl. Environ. Microbiol 2000, 66, 3842–3849. [Google Scholar] [CrossRef]
- Caporaso, J.G.; Lauber, C.L.; Costello, E.K.; Berg-Lyons, D.; Gonzalez, A.; Stombaugh, J.; Knights, D.; Gajer, P.; Ravel, J.; Fierer, N.; et al. Moving pictures of the human microbiome. Genome Biol. 2011, 12. [Google Scholar] [CrossRef]
- Wagg, C.; Bender, S.F.; Widmer, F.; van der Heijden, M.G.A. Soil biodiversity and soil community composition determine ecosystem multifunctionality. Proc. Natl. Acad. Sci. USA 2014, 111, 5266–5270. [Google Scholar] [CrossRef]
- Fierer, N.; Lennon, J.T. The generation and maintenance of diversity in microbial communities. Am. J. Bot. 2011, 98, 439–448. [Google Scholar] [CrossRef]
- Zengler, K.; Palsson, B.O. A road map for the development of community systems (cosy) biology. Nat. Rev. Microbiol. 2012, 10, 366–372. [Google Scholar]
- Haruta, S.; Yoshida, T.; Aoi, Y.; Kaneko, K.; Futamata, H. Challenges for complex microbial ecosystems: Combination of experimental approaches with mathematical modeling. Microbes Environ. 2013, 28, 285–294. [Google Scholar] [CrossRef]
- Mee, M.T.; Wang, H.H. Engineering ecosystems and synthetic ecologies. Mol. Biosyst. 2012, 8, 2470–2483. [Google Scholar] [CrossRef]
- Larsen, P.; Hamada, Y.; Gilbert, J. Modeling microbial communities: Current, developing, and future technologies for predicting microbial community interaction. J. Biotechnol. 2012, 160, 17–24. [Google Scholar] [CrossRef]
- Larsen, P.E.; Gibbons, S.M.; Gilbert, J.A. Modeling microbial community structure and functional diversity across time and space. FEMS Microbiol. Lett. 2012, 332, 91–98. [Google Scholar] [CrossRef]
- Kissling, W.D.; Dormann, C.F.; Groeneveld, J.; Hickler, T.; Kuhn, I.; McInerny, G.J.; Montoya, J.M.; Romermann, C.; Schiffers, K.; Schurr, F.M.; et al. Towards novel approaches to modelling biotic interactions in multispecies assemblages at large spatial extents. J. Biogeogr. 2012, 39, 2163–2178. [Google Scholar]
- Roling, W.F.M.; van Bodegom, P.M. Toward quantitative understanding on microbial community structure and functioning: A modeling-centered approach using degradation of marine oil spills as example. Front. Microbiol. 2014, 5. [Google Scholar] [CrossRef]
- Stegen, J.C.; Lin, X.J.; Konopka, A.E.; Fredrickson, J.K. Stochastic and deterministic assembly processes in subsurface microbial communities. ISME J. 2012, 6, 1653–1664. [Google Scholar] [CrossRef]
- Klapper, I.; Dockery, J. Mathematical description of microbial biofilms. SIAM Rev. 2010, 52, 221–265. [Google Scholar] [CrossRef]
- Tringe, S.G.; von Mering, C.; Kobayashi, A.; Salamov, A.A.; Chen, K.; Chang, H.W.; Podar, M.; Short, J.M.; Mathur, E.J.; Detter, J.C.; et al. Comparative metagenomics of microbial communities. Science 2005, 308, 554–557. [Google Scholar]
- Lidstrom, M.E.; Konopka, M.C. The role of physiological heterogeneity in microbial population behavior. Nat. Chem. Biol. 2010, 6, 705–712. [Google Scholar] [CrossRef]
- Majed, N.; Chernenko, T.; Diem, M.; Gu, A.Z. Identification of functionally relevant populations in enhanced biological phosphorus removal processes based on intracellular polymers profiles and insights into the metabolic diversity and heterogeneity. Environ. Sci. Technol. 2012, 46, 5010–5017. [Google Scholar] [CrossRef]
- Ramkrishna, D.; Mahoney, A.W. Population balance modeling. Promise for the future. Chem. Eng. Sci. 2002, 57, 595–606. [Google Scholar] [CrossRef]
- Hellweger, F.L.; Bucci, V. A bunch of tiny individuals-individual-based modeling for microbes. Ecol. Model. 2009, 220, 8–22. [Google Scholar] [CrossRef]
- Scheffer, M.; Baveco, J.M.; Deangelis, D.L.; Rose, K.A.; Vannes, E.H. Super-individuals a simple solution for modeling large populations on an individual basis. Ecol. Model. 1995, 80, 161–170. [Google Scholar] [CrossRef]
- Gore, J.; Youk, H.; van Oudenaarden, A. Snowdrift game dynamics and facultative cheating in yeast. Nature 2009, 459, 253–256. [Google Scholar] [CrossRef]
- Borenstein, E. Computational systems biology and in silico modeling of the human microbiome. Brief. Bioinform. 2012, 13, 769–780. [Google Scholar] [CrossRef]
- Orth, J.D.; Thiele, I.; Palsson, B.O. What is flux balance analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar]
- Trinh, C.T.; Wlaschin, A.; Srienc, F. Elementary mode analysis: A useful metabolic pathway analysis tool for characterizing cellular metabolism. Appl. Microbiol. Biotechnol 2009, 81, 813–826. [Google Scholar] [CrossRef]
- Song, H.-S.; DeVilbiss, F.; Ramkrishna, D. Modeling metabolic systems: The need for dynamics. Curr. Opin. Chem. Eng. 2013, 2, 373–382. [Google Scholar] [CrossRef]
- Yoo, S.J.; Kim, J.H.; Lee, J.M. Dynamic modelling of mixotrophic microalgal photobioreactor systems with time-varying yield coefficient for the lipid consumption. Biores. Technol. 2014, 162, 228–235. [Google Scholar] [CrossRef]
- Urbanczik, R.; Wagner, C. An improved algorithm for stoichiometric network analysis: Theory and applications. Bioinformatics 2005, 21, 1203–1210. [Google Scholar] [CrossRef]
- De Figueiredo, L.F.; Podhorski, A.; Rubio, A.; Kaleta, C.; Beasley, J.E.; Schuster, S.; Planes, F.J. Computing the shortest elementary flux modes in genome-scale metabolic networks. Bioinformatics 2009, 25, 3158–3165. [Google Scholar]
- Terzer, M.; Stelling, J. Large-scale computation of elementary flux modes with bit pattern trees. Bioinformatics 2008, 24, 2229–2235. [Google Scholar] [CrossRef]
- Terzer, M.; Stelling, J. Parallel extreme ray and pathway computation. Lect. Notes Comput. Sci. 2010, 6068, 300–309. [Google Scholar]
- Song, H.S.; Ramkrishna, D. Reduction of a set of elementary modes using yield analysis. Biotechnol. Bioeng. 2009, 102, 554–568. [Google Scholar] [CrossRef]
- Chan, S.H.J.; Ji, P. Decomposing flux distributions into elementary flux modes in genome-scale metabolic networks. Bioinformatics 2011, 27, 2256–2262. [Google Scholar] [CrossRef]
- Ballerstein, K.; von Kamp, A.; Klamt, S.; Haus, U.U. Minimal cut sets in a metabolic network are elementary modes in a dual network. Bioinformatics 2012, 28, 381–387. [Google Scholar] [CrossRef]
- Greenblum, S.; Turnbaugh, P.J.; Borenstein, E. Metagenomic systems biology of the human gut microbiome reveals topological shifts associated with obesity and inflammatory bowel disease. Proc. Natl. Acad. Sci. USA 2012, 109, 594–599. [Google Scholar]
- Taffs, R.; Aston, J.E.; Brileya, K.; Jay, Z.; Klatt, C.G.; McGlynn, S.; Mallette, N.; Montross, S.; Gerlach, R.; Inskeep, W.P.; et al. In silico approaches to study mass and energy flows in microbial consortia: A syntrophic case study. BMC Syst. Biol. 2009, 3. [Google Scholar] [CrossRef]
- Reed, D.C.; Algar, C.K.; Huber, J.A.; Dick, G.J. Gene-centric approach to integrating environmental genomics and biogeochemical models. Proc. Natl. Acad. Sci. USA 2014, 111, 1879–1884. [Google Scholar] [CrossRef]
- Ramkrishna, D.; Song, H.S. Dynamic models of metabolism: Review of the cybernetic approach. AIChE J. 2012, 58, 986–997. [Google Scholar] [CrossRef]
- Kim, J.I.; Song, H.S.; Sunkara, S.R.; Lali, A.; Ramkrishna, D. Exacting predictions by cybernetic model confirmed experimentally: Steady state multiplicity in the chemostat. Biotechnol. Prog. 2012, 28, 1160–1166. [Google Scholar]
- Song, H.S.; Ramkrishna, D. Prediction of metabolic function from limited data: Lumped hybrid cybernetic modeling (l-hcm). Biotechnol. Bioeng. 2010, 106, 271–284. [Google Scholar]
- Song, H.S.; Ramkrishna, D. Cybernetic models based on lumped elementary modes accurately predict strain-specific metabolic function. Biotechnol. Bioeng. 2011, 108, 127–140. [Google Scholar] [CrossRef]
- Song, H.S.; Ramkrishna, D. Prediction of dynamic behavior of mutant strains from limited wild-type data. Metab. Eng. 2012, 14, 69–80. [Google Scholar] [CrossRef]
- Song, H.S.; Ramkrishna, D.; Pinchuk, G.E.; Beliaev, A.S.; Konopka, A.E.; Fredrickson, J.K. Dynamic modeling of aerobic growth of shewanella oneidensis. Predicting triauxic growth, flux distributions, and energy requirement for growth. Metab. Eng. 2013, 15, 25–33. [Google Scholar]
- Young, J.D.; Henne, K.L.; Morgan, J.A.; Konopka, A.E.; Ramkrishna, D. Integrating cybernetic modeling with pathway analysis provides a dynamic, systems-level description of metabolic control. Biotechnol. Bioeng. 2008, 100, 542–559. [Google Scholar] [CrossRef]
- Faust, K.; Raes, J. Microbial interactions: From networks to models. Nat. Rev. Microbiol. 2012, 10, 538–550. [Google Scholar] [CrossRef]
- Shuler, M.L.; Kargi, F. Bioprocess Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Burmolle, M.; Webb, J.S.; Rao, D.; Hansen, L.H.; Sorensen, S.J.; Kjelleberg, S. Enhanced biofilm formation and increased resistance to antimicrobial agents and bacterial invasion are caused by synergistic interactions in multispecies biofilms. Appl. Environ. Microb. 2006, 72, 3916–3923. [Google Scholar] [CrossRef]
- Rodriguez-Martinez, J.M.; Pascual, A. Antimicrobial resistance in bacterial biofilms. Rev. Med. Microbiol. 2006, 17, 65–75. [Google Scholar] [CrossRef]
- Pak, K.R.; Bartha, R. Mercury methylation by interspecies hydrogen and acetate transfer between sulfidogens and methanogens. Appl. Environ. Microb. 1998, 64, 1987–1990. [Google Scholar]
- Gause, G.F. Experimental studies on the struggle for existence i mixed population of two species of yeast. J. Exp. Biol. 1932, 9, 389–402. [Google Scholar]
- Moon, D.C.; Moon, J.; Keagy, A. Direct and indirect interactions. Available online: http://www.nature.com/scitable/knowledge/library/direct-and-indirect-interactions-15650000 (accessed on 11 October 2014).
- Berry, D.; Widder, S. Deciphering microbial interactions and detecting keystone species with co-occurrence networks. Front. Microbiol. 2014, 5. [Google Scholar] [CrossRef]
- Wooley, J.C.; Godzik, A.; Friedberg, I. A primer on metagenomics. PLOS Comput. Biol. 2010, 6. [Google Scholar] [CrossRef]
- Mande, S.S.; Mohammed, M.H.; Ghosh, T.S. Classification of metagenomic sequences: Methods and challenges. Brief. Bioinform. 2012, 13, 669–681. [Google Scholar] [CrossRef]
- Fuhrman, J.A. Microbial community structure and its functional implications. Nature 2009, 459, 193–199. [Google Scholar] [CrossRef]
- Barabasi, A.L. Scale-free networks: A decade and beyond. Science 2009, 325, 412–413. [Google Scholar] [CrossRef]
- Barabasi, A.L.; Bonabeau, E. Scale-free networks. Sci. Am. 2003, 288, 60–69. [Google Scholar] [CrossRef]
- Albert, R.; Jeong, H.; Barabasi, A.L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef]
- Stolyar, S.; van Dien, S.; Hillesland, K.L.; Pinel, N.; Lie, T.J.; Leigh, J.A.; Stahl, D.A. Metabolic modeling of a mutualistic microbial community. Mol. Syst. Biol. 2007, 3, 92. [Google Scholar] [CrossRef]
- Freilich, S.; Zarecki, R.; Eilam, O.; Segal, E.S.; Henry, C.S.; Kupiec, M.; Gophna, U.; Sharan, R.; Ruppin, E. Competitive and cooperative metabolic interactions in bacterial communities. Nat. Commun. 2011, 2. [Google Scholar] [CrossRef]
- Klitgord, N.; Segre, D. Environments that induce synthetic microbial ecosystems. PLOS Comput. Biol. 2010, 6. [Google Scholar] [CrossRef]
- Wintermute, E.H.; Silver, P.A. Emergent cooperation in microbial metabolism. Mol. Syst. Biol. 2010, 6. [Google Scholar] [CrossRef]
- Segre, D.; Vitkup, D.; Church, G.M. Analysis of optimality in natural and perturbed metabolic networks. Proc. Natl. Acad. Sci. USA 2002, 99, 15112–15117. [Google Scholar] [CrossRef]
- Bordbar, A.; Feist, A.M.; Usaite-Black, R.; Woodcock, J.; Palsson, B.O.; Famili, I. A multi-tissue type genome-scale metabolic network for analysis of whole-body systems physiology. BMC Syst. Biol. 2011, 5. [Google Scholar] [CrossRef]
- Lewis, N.E.; Schramm, G.; Bordbar, A.; Schellenberger, J.; Andersen, M.P.; Cheng, J.K.; Patel, N.; Yee, A.; Lewis, R.A.; Eils, R.; et al. Large-scale in silico modeling of metabolic interactions between cell types in the human brain. Nat. Biotechnol. 2010, 28, U1279–U1291. [Google Scholar]
- Khandelwal, R.A.; Olivier, B.G.; Roling, W.F.M.; Teusink, B.; Bruggeman, F.J. Community flux balance analysis for microbial consortia at balanced growth. PLOS ONE 2013, 8. [Google Scholar] [CrossRef]
- Zomorrodi, A.R.; Maranas, C.D. Optcom: A multi-level optimization framework for the metabolic modeling and analysis of microbial communities. PLOS Comput. Biol. 2012, 8. [Google Scholar] [CrossRef]
- Zomorrodi, A.R.; Islam, M.M.; Maranas, C.D. D-optcom: Dynamic multi-level and multi-objective metabolic modeling of microbial communities. ACS Synth. Biol. 2014, 3, 247–257. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R. Species distribution models: Ecological explanation and prediction across space and time. Annu. Rev. Ecol. Evol. Syst. 2009, 40, 677–697. [Google Scholar]
- Larsen, P.E.; Field, D.; Gilbert, J.A. Predicting bacterial community assemblages using an artificial neural network approach. Nat. Methods 2012, 9, 621–625. [Google Scholar] [CrossRef]
- Schmidt, M.; Lipson, H. Distilling free-form natural laws from experimental data. Science 2009, 324, 81–85. [Google Scholar] [CrossRef]
- Istok, J.D.; Park, M.; Michalsen, M.; Spain, A.M.; Krumholz, L.R.; Liu, C.; McKinley, J.; Long, P.; Roden, E.; Peacock, A.D.; et al. A thermodynamically-based model for predicting microbial growth and community composition coupled to system geochemistry: Application to uranium bioreduction. J. Contam. Hydrol. 2010, 112, 1–14. [Google Scholar]
- Larowe, D.E.; Dale, A.W.; Regnier, P. A thermodynamic analysis of the anaerobic oxidation of methane in marine sediments. Geobiology 2008, 6, 436–449. [Google Scholar] [CrossRef]
- Rodriguez, J.; Kleerebezem, R.; Lema, J.M.; van Loosdrecht, M.C.M. Modeling product formation in anaerobic mixed culture fermentations. Biotechnol. Bioeng. 2006, 93, 592–606. [Google Scholar] [CrossRef]
- Beard, D.A.; Qian, H. Relationship between thermodynamic driving force and one-way fluxes in reversible processes. PLOS ONE 2007, 2, e144. [Google Scholar] [CrossRef]
- Noor, E.; Bar-Even, A.; Flamholz, A.; Reznik, E.; Liebermeister, W.; Milo, R. Pathway thermodynamics highlights kinetic obstacles in central metabolism. PLOS Comput. Biol. 2014, 10, e1003483. [Google Scholar] [CrossRef]
- Zhu, Y.; Song, J.; Xu, Z.; Sun, J.; Zhang, Y.; Li, Y.; Ma, Y. Development of thermodynamic optimum searching (tos) to improve the prediction accuracy of flux balance analysis. Biotechnol. Bioeng. 2013, 110, 914–923. [Google Scholar] [CrossRef]
- Meysman, F.J.; Bruers, S. Ecosystem functioning and maximum entropy production: A quantitative test of hypotheses. Philos. Trans. R. Soc. B 2010, 365, 1405–1416. [Google Scholar]
- Schrödinger, E. What is Life? The Physical Aspect of the Living Cell, 1st ed.; Cambridge University Press: New York, NY, USA, 1944. [Google Scholar]
- Prigogine, I. Time, structure, and fluctuations. Science 1978, 201, 777–785. [Google Scholar] [CrossRef]
- Morowitz, H.J. Energy Flow in Biology: Biological Organization as a Problem in Thermal Physics; Ox Bow Press: Woodbridge, NJ, USA, 1979. [Google Scholar]
- Dewar, R.C. Maximum entropy production and plant optimization theories. Philos. Trans. R. Soc. B 2010, 365, 1429–1435. [Google Scholar] [CrossRef]
- Dewar, R.C.; Juretic, D.; Zupanovic, P. The functional design of the rotary enzyme atp synthase is consistent with maximum entropy production. Chem. Phys. Lett. 2006, 430, 177–182. [Google Scholar] [CrossRef]
- Unrean, P.; Srienc, F. Metabolic networks evolve towards states of maximum entropy production. Metab. Eng. 2011, 13, 666–673. [Google Scholar] [CrossRef]
- Cannon, W.R. Simulating metabolism with statistical thermodynamics. PLOS ONE 2014, 9, e103582. [Google Scholar] [CrossRef]
- Schmiedl, T.; Seifert, U. Stochastic thermodynamics of chemical reaction networks. J. Chem. Phys. 2007, 126. [Google Scholar] [CrossRef]
- Gillespie, D.T. Stochastic simulation of chemical kinetics. Annu. Rev. Phys. Chem. 2007, 58, 35–55. [Google Scholar] [CrossRef]
- Boon, E.; Meehan, C.J.; Whidden, C.; Wong, D.H.J.; Langille, M.G.I.; Beiko, R.G. Interactions in the microbiome: Communities of organisms and communities of genes. FEMS Microbiol. Rev. 2014, 38, 90–118. [Google Scholar] [CrossRef]
- Webb, C.T.; Hoeting, J.A.; Ames, G.M.; Pyne, M.I.; Poff, N.L. A structured and dynamic framework to advance traits-based theory and prediction in ecology. Ecol. Lett. 2010, 13, 267–283. [Google Scholar] [CrossRef]
- Laughlin, D.C.; Laughlin, D.E. Advances in modeling trait-based plant community assembly. Trends Plant Sci. 2013, 18, 584–593. [Google Scholar] [CrossRef]
- Shipley, B.; Vile, D.; Garnier, E. From plant traits to plant communities: A statistical mechanistic approach to biodiversity. Science 2006, 314, 812–814. [Google Scholar] [CrossRef]
- Shipley, B.; Paine, C.E.T.; Baraloto, C. Quantifying the importance of local niche-based and stochastic processes to tropical tree community assembly. Ecology 2012, 93, 760–769. [Google Scholar] [CrossRef]
- Laughlin, D.C.; Joshi, C.; van Bodegom, P.M.; Bastow, Z.A.; Fule, P.Z. A predictive model of community assembly that incorporates intraspecific trait variation. Ecol. Lett. 2012, 15, 1291–1299. [Google Scholar] [CrossRef]
- Jin, Q.S.; Roden, E.E. Microbial physiology-based model of ethanol metabolism in subsurface sediments. J. Contam. Hydrol. 2011, 125, 1–12. [Google Scholar] [CrossRef]
- Bouskill, N.J.; Tang, J.; Riley, W.J.; Brodie, E.L. Trait-based representation of biological nitr fication: Model development testing, and predicted community composition. Front. Microbiol. 2012, 3. [Google Scholar] [CrossRef]
- Edelstein-Keshet, L. Mathematical Models in Biology; Siam: Philadelphia, PA, USA, 1987; Volume 46. [Google Scholar]
- Fisher, C.K.; Mehta, P. Identifying keystone species in the human gut microbiome from metagenomic timeseries using sparse linear regression. Available online: http://arxiv.org/pdf/1402.0511v1.pdf (accessed on 11 October 2014).
- Stein, R.R.; Bucci, V.; Toussaint, N.C.; Buffie, C.G.; Ratsch, G.; Pamer, E.G.; Sander, C.; Xavier, J.B. Ecological modeling from time-series inference: Insight into dynamics and stability of intestinal microbiota. PLOS Comput. Biol. 2013, 9. [Google Scholar] [CrossRef]
- Mounier, J.; Monnet, C.; Vallaeys, T.; Arditi, R.; Sarthou, A.S.; Helias, A.; Irlinger, F. Microbial interactions within a cheese microbial community. Appl. Environ. Microb. 2008, 74, 172–181. [Google Scholar] [CrossRef]
- Nowak, M.A. Evolutionary Dynamics; Harvard University Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Nowak, M.A.; Sigmund, K. Evolutionary dynamics of biological games. Science 2004, 303, 793–799. [Google Scholar] [CrossRef]
- Frey, E. Evolutionary game theory: Theoretical concepts and applications to microbial communities. Phys. A 2010, 389, 4265–4298. [Google Scholar] [CrossRef]
- Minty, J.J.; Singer, M.E.; Scholz, S.A.; Bae, C.H.; Ahn, J.H.; Foster, C.E.; Liao, J.C.; Lin, X.N. Design and characterization of synthetic fungal-bacterial consortia for direct production of isobutanol from cellulosic biomass. Proc. Natl. Acad. Sci. USA 2013, 110, 14592–14597. [Google Scholar] [CrossRef]
- Sousa, M.D. Kinetics of distribution of thymus and marrow cells in peripheral lymphoid organs of mouse-ecotaxis. Clin. Exp. Immunol. 1971, 9, 371–380. [Google Scholar]
- Kleene, S.J.; Hobson, A.C.; Adler, J. Attractants and repellents influence methylation and demethylation of methyl-accepting chemotaxis proteins in an extract of escherichia-coli. Proc. Natl. Acad. Sci. USA 1979, 76, 6309–6313. [Google Scholar] [CrossRef]
- Tindall, M.J.; Maini, P.K.; Porter, S.L.; Armitage, J.P. Overview of mathematical approaches used to model bacterial chemotaxis ii: Bacterial populations. Bull. Math. Biol. 2008, 70, 1570–1607. [Google Scholar] [CrossRef]
- Ferrer, J.; Prats, C.; Lopez, D. Individual-based modelling: An essential tool for microbiology. J. Biol. Phys. 2008, 34, 19–37. [Google Scholar] [CrossRef]
- Resat, H.; Bailey, V.; McCue, L.A.; Konopka, A. Modeling microbial dynamics in heterogeneous environments: Growth on soil carbon sources. Microb. Ecol. 2012, 63, 883–897. [Google Scholar] [CrossRef]
- Tang, Y.N.; Valocchi, A.J. An improved cellular automaton method to model multispecies biofilms. Water Res. 2013, 47, 5729–5742. [Google Scholar] [CrossRef]
- Kang, S.; Kahan, S.; Momeni, B. Simulating microbial community patterning using biocellion. In Engineering and Analyzing Multicellular Systems; Springer: Berlin, Germany, 2014; pp. 233–253. [Google Scholar]
- Lardon, L.A.; Merkey, B.V.; Martins, S.; Dotsch, A.; Picioreanu, C.; Kreft, J.U.; Smets, B.F. Idynomics: Next-generation individual-based modelling of biofilms. Environ. Microbiol. 2011, 13, 2416–2434. [Google Scholar] [CrossRef]
- Kreft, J.U.; Booth, G.; Wimpenny, J.W.T. Bacsim, a simulator for individual-based modelling of bacterial colony growth. Microbiol.-UK 1998, 144, 3275–3287. [Google Scholar] [CrossRef]
- Ramkrishna, D. Population Balances: Theory and Applications to Particulate Systems in Engineering; Academic Press: Pittsburgh, PA, USA, 2000. [Google Scholar]
- Henson, M.A. Dynamic modeling of microbial cell populations. Curr. Opin. Biotechnol. 2003, 14, 460–467. [Google Scholar] [CrossRef]
- Shu, C.C.; Chatterjee, A.; Dunny, G.; Hu, W.S.; Ramkrishna, D. Bistability versus bimodal distributions in gene regulatory processes from population balance. PLOS Comput. Biol. 2011, 7. [Google Scholar] [CrossRef]
- Fernandes, R.L.; Nierychlo, M.; Lundin, L.; Pedersen, A.E.; Tellez, P.E.P.; Dutta, A.; Carlquist, M.; Bolic, A.; Schapper, D.; Brunetti, A.C.; et al. Experimental methods and modeling techniques for description of cell population heterogeneity. Biotechnol. Adv. 2011, 29, 575–599. [Google Scholar]
- Scheibe, T.D.; Mahadevan, R.; Fang, Y.L.; Garg, S.; Long, P.E.; Lovley, D.R. Coupling a genome-scale metabolic model with a reactive transport model to describe in situ uranium bioremediation. Microb. Biotechnol. 2009, 2, 274–286. [Google Scholar] [CrossRef]
- Mahadevan, R.; Edwards, J.S.; Doyle, F.J. Dynamic flux balance analysis of diauxic growth in escherichia coli. Biophys. J. 2002, 83, 1331–1340. [Google Scholar] [CrossRef]
- Hanly, T.J.; Henson, M.A. Dynamic flux balance modeling of microbial co-cultures for efficient batch fermentation of glucose and xylose mixtures. Biotechnol. Bioeng. 2011, 108, 376–385. [Google Scholar] [CrossRef]
- Hanly, T.J.; Henson, M.A. Dynamic metabolic modeling of a microaerobic yeast co-culture: Predicting and optimizing ethanol production from glucose/xylose mixtures. Biotechnol. Biofuels 2013, 6. [Google Scholar] [CrossRef]
- Tzamali, E.; Poirazi, P.; Tollis, I.G.; Reczko, M. A computational exploration of bacterial metabolic diversity identifying metabolic interactions and growth-efficient strain communities. BMC Syst. Biol. 2011, 5. [Google Scholar] [CrossRef]
- Kim, J.I.; Varner, J.D.; Ramkrishna, D. A hybrid model of anaerobic e. Coli gjt001: Combination of elementary flux modes and cybernetic variables. Biotechnol. Progr. 2008, 24, 993–1006. [Google Scholar]
- Song, H.S.; Morgan, J.A.; Ramkrishna, D. Systematic development of hybrid cybernetic models: Application to recombinant yeast co-consuming glucose and xylose. Biotechnol. Bioeng. 2009, 103, 984–1002. [Google Scholar] [CrossRef]
- Geng, J.; Song, H.S.; Yuan, J.Q.; Ramkrishna, D. On enhancing productivity of bioethanol with multiple species. Biotechnol. Bioeng. 2012, 109, 1508–1517. [Google Scholar] [CrossRef]
- Fang, Y.L.; Scheibe, T.D.; Mahadevan, R.; Garg, S.; Long, P.E.; Lovley, D.R. Direct coupling of a genome-scale microbial in silico model and a groundwater reactive transport model. J. Contam. Hydrol. 2011, 122, 96–103. [Google Scholar] [CrossRef]
- King, E.L.; Tuncay, K.; Ortoleva, P.; Meile, C. In silico geobacter sulfurreducens metabolism and its representation in reactive transport models. Appl. Environ. Microb. 2009, 75, 83–92. [Google Scholar] [CrossRef]
- Zhuang, K.; Izallalen, M.; Mouser, P.; Richter, H.; Risso, C.; Mahadevan, R.; Lovley, D.R. Genome-scale dynamic modeling of the competition between rhodoferax and geobacter in anoxic subsurface environments. ISME J. 2011, 5, 305–316. [Google Scholar] [CrossRef]
- Harcombe, W.R.; Riehl, W.J.; Dukovski, I.; Granger, B.R.; Betts, A.; Lang, A.H.; Bonilla, G.; Kar, A.; Leiby, N.; Mehta, P.; et al. Metabolic resource allocation in individual microbes determines ecosystem interactions and spatial dynamics. Cell Rep. 2014, 7, 1104–1115. [Google Scholar]
- Zhuang, K.; Ma, E.; Lovley, D.R.; Mahadevan, R. The design of long-term effective uranium bioremediation strategy using a community metabolic model. Biotechnol. Bioeng. 2012, 109, 2475–2483. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Proceedings of the 2nd International Symposium on Information Theory; Akadémiai Kiadó: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, H.-S.; Cannon, W.R.; Beliaev, A.S.; Konopka, A. Mathematical Modeling of Microbial Community Dynamics: A Methodological Review. Processes 2014, 2, 711-752. https://doi.org/10.3390/pr2040711
Song H-S, Cannon WR, Beliaev AS, Konopka A. Mathematical Modeling of Microbial Community Dynamics: A Methodological Review. Processes. 2014; 2(4):711-752. https://doi.org/10.3390/pr2040711
Chicago/Turabian StyleSong, Hyun-Seob, William R. Cannon, Alexander S. Beliaev, and Allan Konopka. 2014. "Mathematical Modeling of Microbial Community Dynamics: A Methodological Review" Processes 2, no. 4: 711-752. https://doi.org/10.3390/pr2040711
APA StyleSong, H.-S., Cannon, W. R., Beliaev, A. S., & Konopka, A. (2014). Mathematical Modeling of Microbial Community Dynamics: A Methodological Review. Processes, 2(4), 711-752. https://doi.org/10.3390/pr2040711