Application of Reactive Power Management from PV Plants into Distribution Networks: An Experimental Study and Advanced Optimization Algorithms

Abstract

This study aims to optimize the voltage profile of the grid by obtaining an optimum level of reactive power support from photovoltaic (PV) plants, thereby enhancing the efficiency of PV systems in power distribution networks and ensuring grid stability. Initially, voltage profiles in the sector, together with the structure and operating principles of PV plants, were considered in detail. Subsequently, the limits of reactive power support that can be provided by PV plants were determined. Then, the optimum levels of reactive power from the plants were determined using particle swarm optimization, genetic algorithm, Jaya algorithm, and firefly algorithm separately. The algorithms were tested through simulations conducted on a power distribution system operator in Türkiye. Additionally, a Modbus-based communication application was developed and tested, as a feasibility demonstration, to verify PV inverter accessibility and the capability of remotely writing reactive power reference setpoints. The quantitative optimization results reported in this manuscript are obtained from DIgSILENT PowerFactory simulations using the actual feeder model and time-series profiles. The results have revealed that PV plants can be effectively utilized as reactive power compensators to contribute to the operation of the grid under more ideal voltage profile conditions. In Türkiye, there is no regulatory or market mechanism to support reactive power provision from PV plants. Therefore, this study is novel in the Turkish market. The experimental results confirm that power generation from renewable energy can provide reactive support effectively when needed, which reveals that this approach is both technically feasible and practically relevant.

1. Introduction

The widespread use of photovoltaic (PV) plants is an important part of the sustainable transformation of the power generation industry. In regions with high potential for solar energy, PV plants can generate large amounts of power and diversify the energy supply. Moreover, the use of PV plants contributes to lowering energy costs and increasing energy security. With advances in technology and decreases in costs, the use of PV plants has been increasing. At the same time, the integration of PV plants into the electricity distribution grid represents a pioneering approach for modern electricity distribution system studies [1].

The voltage profile can vary along its distribution from power generation sources to consumption points. These changes occur depending on the distribution of sources and consumption points, the amount of load, the length, and the resistance of transmission lines. The voltage profile of the grid is a parameter that must be kept within the nominal voltage value and the specified tolerance range. A voltage drop or rise can lead to energy quality problems, equipment failures, and even grid collapse. Optimization of the voltage profile of the grid involves efforts to keep voltage levels within the desired range and ensure efficient energy flow. This optimization is one of the tasks of grid operators responsible for power transmission and distribution. It usually includes voltage regulation, voltage stabilization, and voltage drop compensation. Voltage regulation involves adjusting voltage levels to compensate for voltage drops in power transmission. This is usually accomplished using regulating devices or automatic voltage control systems [2].

In recent years, it has been found that PV plants can play a key role in the voltage profile optimization of the grid. PV inverters can actively take part in voltage regulation through reactive power support, and they significantly reduce voltage deviations in power distribution networks [3]. In addition to providing active power generation to the grid, PV plants can also provide reactive power support [4]. With the reactive power generation of PV plants, it may be possible to keep the grid voltage levels within the desired range and prevent voltage drops. Thus, grid stability can be increased, and energy efficiency can be achieved. Especially with the development of smart grids, PV plants are expected to play an active role in voltage profile optimization. Smart grids can use advanced control systems, which are effective in voltage profile optimization and can dynamically adjust the reactive power generation of PV plants according to the needs of the grid.

Grid voltage profile optimization is of great importance for the reliability, energy efficiency, and sustainability of power transmission and distribution systems. Optimization studies that are performed using methods such as voltage regulation, voltage balancing, and voltage drop compensation can be made even more effective thanks to the reactive power support of PV plants. This is an important step that supports the integration of renewable energy sources and the development of smart grids in the power industry.

In recent years, numerous studies have focused on the integration of PV power plants into power distribution networks. However, the majority of these studies are limited to fixed power factor control strategies, reactive power control relays, centralized control systems, or simulation-based analyses. In the existing literature, there is a notable lack of comprehensive studies that perform dynamic reactive power optimization for inverter-based PV systems based on operating conditions derived from time-series profiles, supported by actual distribution network data and validated through a Modbus-based feasibility demonstration for inverter communication. Furthermore, distributed control approaches that compare different optimization algorithms and integrate them with grid models to directly communicate with inverters are also scarce. The method proposed in this study aims to address this research gap by providing a novel contribution that combines algorithm-based reactive power optimization with practical implementation feasibility.

Recent studies on reactive power management in distribution networks, particularly those with high PV generation, have increasingly focused on improving voltage regulation, enhancing inverter coordination, and optimizing control strategies at the system level. For instance, Fan et al. [5] introduce a coordinated reactive power and voltage optimization approach based on filtered multiband decomposition (FMD). Initially, to manage the random variations in PV power, an enhanced FMD-based forecasting model is proposed. The model utilizes an adaptive finite impulse response (FIR) filter for signal decomposition and captures both periodic patterns and uncertainties through kurtosis-based feature extraction. Similarly, Daccò et al. [6] present a novel distributed voltage control approach that treats distributed energy resources (DERs), especially those using inverter technology, as independent controllers, which complies with the latest European technical regulations and grid requirements. Alwez et al. [7] propose an adaptive reactive power control method to address voltage rise in low-voltage networks with high PV penetration. Unlike traditional techniques, it dynamically adjusts reactive power using both voltage and active power data. Simulations show improved voltage regulation and reduced losses, despite slightly slower response times. Lee et al. [8] introduced a study related to an enhanced control and dispatch strategy for dynamic VAR compensators (DVCs) to improve voltage regulation in distribution systems with high renewable penetration. A multi-objective optimization framework is developed to determine optimal DVC placement and dispatch. Two supervisory controls adjust the Volt/VAR Curve (VV-C) dynamically. Simulations on an IEEE 123-bus system revealed a better voltage stability than the standard IEEE 1547-based VV-C. Rostami et al. [9] present a reactive power control method for low-voltage networks with high PV penetration, combining local and distributed cooperative control. A dynamic leader PV system at the critical bus coordinates voltage regulation using local and neighbor data. The method enhances voltage profiles under varying conditions, supports plug-and-play functionality, and remains effective despite communication delays or network reconfiguration, which has been validated by simulations. Zhang et al. [10] propose a reactive power compensation method using a static VAR generator (SVG) with variable droop control to stabilize PCC voltage in PV areas. An improved particle swarm optimization algorithm further enhances reactive power distribution, reducing network losses and improving voltage stability under high PV penetration. Unlike the studies in the literature, the proposed study contributes to the field by employing four distinct metaheuristic optimization algorithms: Particle Swarm Optimization (PSO), Genetic Algorithm (GA), Jaya Algorithm, and Firefly Algorithm. These algorithms are used to determine optimal reactive power setpoints for PV inverters. The proposed model is developed and tested on a real distribution feeder (Adiyaman TM City 1) operated by AKEDAS in Türkiye, using a simulation environment that reflects actual grid topology, operational limits, and regulatory constraints. This multi-layered framework, which incorporates algorithmic diversity, context-specific modeling, and national compliance, offers a robust, adaptable, and practically implementable solution for improving voltage stability and reactive power control in renewable-rich distribution systems.

This study contributes to the compensation studies required for voltage regulation of electricity distribution networks through PV inverters that are currently connected to the distribution company’s network. Optimization algorithms have been applied to improve the overall voltage profile of the grid, as well as the optimal level of reactive power support that can be obtained from the inverters of each PV power plant connected to the electricity distribution system. These algorithms are integrated with the DIgSILENT PowerFactory 2022 (DIgSILENT GmbH, Gomaringen, Germany) application used for grid modeling and analysis. In the algorithm, there is no restriction on the current active power generation of the power plant, and the reactive power limits, which can be provided by the inverters, are taken into consideration.

Traditional compensation approaches are generally configured with fixed values and therefore have limited flexibility in responding to voltage fluctuations. In contrast, the algorithms employed in this study (PSO, GA, Jaya, and Firefly) compute optimal reactive power setpoints considering inverter capability limits and feeder operating conditions derived from time-series profiles. The optimized setpoints are implemented and evaluated in the DIgSILENT PowerFactory simulation environment. In addition, a Modbus-based feasibility demonstration is included to verify inverter accessibility and the capability of remotely writing reactive power reference values. A closed-loop real-time implementation that integrates online measurements and automated setpoint updating is considered as future work. Conventional compensation control systems rely on individual devices or centralized controllers. In these systems, standalone capacitors or shunt reactors may be used, and centralized control can be achieved through a reactive power control relay. However, in the event of a malfunction in the compensation system, the overall system performance can be adversely affected. In contrast, the approach proposed in this study is based on a decentralized decision-making principle, allowing individual optimization at the inverter level, thereby enhancing system reliability. Each inverter can operate independently. Furthermore, each algorithm was tested under various conditions to evaluate the consistency and stability of the results. The low standard deviation values obtained clearly support the reliability of the proposed methods. In conclusion, the optimization-based approach offers faster response times, as well as more flexible and reliable voltage profile management compared to traditional fixed control structures. Several algorithms, such as PSO, GA, Jaya, and Firefly, have been applied to optimization problems in power systems. However, these algorithms were usually evaluated individually and under simulation-based conditions. Therefore, there is an uncertainty about their relative effectiveness in real grid conditions. As a result, this study tries to determine which optimization algorithm performs better in terms of reactive power management in a real distribution network with high PV penetration. In order to determine the method performing the best, a comparative evaluation was conducted by testing four widely used algorithms, which have been validated with actual grid data from Türkiye and supported by a Modbus-based feasibility demonstration on a real PV inverter to verify inverter communication and setpoint writing capability. This allowed us to go beyond theoretical results of a simulation and offered detailed information on the strengths and weaknesses of each method in a real-world operation.

PV plants in Türkiye have not yet been offered incentives to provide reactive power support to the distribution grid. Actually, they are not required to do so. Therefore, revealing this potential by using actual measurements through experimental validation is particularly significant. Our study reveals that renewable power generation can be practically used to improve voltage stability through reactive support. This aspect of renewable power generation has not been sufficiently examined by previous studies.

The other parts of this study have been organized as follows. In the next part, we present the model and optimization framework for reactive power management. Then, we report the results of the simulation, followed by a Modbus-based feasibility demonstration on a real PV inverter. Finally, we conclude the study by presenting key findings and proposals for future studies.

2. Materials and Methods

When determining the reactive power support limit of an inverter, the first consideration should be the available capacity of the inverter. This limit is commonly referred to as the inverter’s current limit. From the current limit perspective, Equations (1) and (2) are presented for the reactive power limits to be taken from the inverter.

$$P^2+Q^2=S^2$$

(1)

$$-\sqrt{S^2-P^2}\le Q\le \sqrt{S^2-P^2}$$

(2)

Equations (1) and (2) define a circle of radius S with its center at the origin. As can be seen from the equation and Figure 1, the total power of the inverter in PV systems is limited by the vector sum of the active and reactive powers. Therefore, when the active power generation of the PV system is at its maximum, its capacity to provide reactive power support is limited or completely disabled. However, when the active power generation decreases, there is room for more reactive power generation within the total power of the inverter, thus increasing the reactive power support limit [11].

Under stable operating conditions, the reactive power support available from the inverter of a PV plant must be within a voltage-dependent limit, which can be expressed by Equation (3) [12]

$$-\sqrt{{\displaystyle \frac{V_g\times V_t}{x_{eq}}}-P^2}-{\displaystyle \frac{V_g^2}{x\_eq}}\le Q\le \sqrt{{\displaystyle \frac{V_g\times V_t}{x_{eq}}}-P^2}-{\displaystyle \frac{V_g^2}{x\_eq}}$$

(3)

where V_g denotes the grid voltage to which the PV system is connected, V_t denotes the output voltage of the inverter, and x_eq denotes the equivalent impedance between the connection point of the PV system and the inverter. This equation is expressed in units of per-unit (p.u.) at the center point $(0.-{\displaystyle \frac{V_g^2}{x}})$ with radius $\sqrt{{\displaystyle \frac{V_g\times V_t}{x}}}$, which is a circle. This circle represents the area where the inverter can provide reactive power support considering both current and voltage limits.

Each inverter has allowable power factor limits inherent in its design. These limits vary depending on the technology used, but most inverters can operate between 0.8 capacitive and 0.8 inductive power factors. From the perspective of the power factor (pf) limit, Equation (4) shows the reactive power limits (p.u.) to be taken from the inverter.

$$-\sqrt{1-p{f}_{kap}^2}\le Q\le \sqrt{1-p{f}_{end}^2}$$

(4)

In Equation (4), $p{f}_{kap}^2$ and $p{f}_{end}^2$ represent the minimum power factor value of the PV inverter while operating in capacitive mode and inductive mode, respectively. In the light of these limits, the minimum and maximum reactive power values in p.u. that can be received from PV plants are given in Equations (5) and (6) [11]:

$$Q_{min}=max(-\sqrt{S^2-P^2}, -\sqrt{{\displaystyle \frac{V_g\times V_t}{x_{eq}}}-P^2}-{\displaystyle \frac{V_g^2}{x_{eq}}}, -\sqrt{1-p{f}_{kap}^2})$$

(5)

$$Q_{max}=min(\sqrt{S^2-P^2}, \sqrt{{\displaystyle \frac{V_g\times V_t}{x_{eq}}}-P^2}-{\displaystyle \frac{V_g^2}{x_{eq}}}, \sqrt{1-p{f}_{end}^2})$$

(6)

The objective Voltage Deviation Index (VDI) is defined as follows:

$$VDI = {\sum }_{i=0}^{N_b}|V_i - V_{ref}|$$

(7)

where N_b is the total number of buses, V_i is the voltage magnitude at bus i, and V_ref = 1.0 p.u. is the nominal reference voltage. In this study, all buses are equally weighted.

The optimization respects operational voltage limits (V_min ≤ V_i ≤ V_max), and inverter capability constraints based on rated apparent power ($P_k^2+Q_k^2\le S_{k, rated}^2$). Reactive power references are therefore always generated within allowable operating boundaries, and the proposed approach does not modify feeder protection schemes.

Particle swarm optimization (PSO) is a computational method that optimizes a problem by iteratively trying to improve a candidate solution according to a given quality measure [13]. It solves a problem by having a population of candidate solutions, called particles, and moving these particles through the search space according to a simple mathematical formula on the position and velocity of the particle. All particles try to move towards the best position for optimal fitness. Each particle in PSO updates its position to find the global optimum. The position update equation can also vary depending on the type of PSO. The position update of the original PSO is given in Equation (8).

$$V_i\left(t+1\right)=V_i\left(t\right)+C_1\times r_1\ast \left(Y_{best}-X_i\left(t\right)\right)+C_2\times r_2\times \left(K_{best}-X_i\left(t\right)\right)$$

$$X_i\left(t+1\right)=X_i\left(t\right)+V_i(t+1)$$

(8)

In Equation (8), V_i is the velocity of particle i, X_i is the position of particle i, t is the current iteration number, Y_best is the local best position of the particle, K_best is the global best position of the swarm up to the current iteration, r₁ and r₂ are random values between [0, 1] that are regenerated at each iteration, and C₁ and C₂ are the learning factors. In the original PSO, C₁ and C₂ are created as fixed values before the iteration and are not changed during the iteration, while in some variants of PSO, these values are updated throughout the iteration. Studies have found that learning factors C₁ = C₂ = 2 are ideal for a fast solution [14].

The Firefly Algorithm (FA) is inspired by the flashing behavior of fireflies. This behavior aims to optimize light communication within a swarm and increase efficiency. In FA, fireflies represent possible solutions, and their movements are guided by specific rules to improve their position in the solution space. Attractiveness refers to the interaction between fireflies. Brighter fireflies are more attractive, and attractiveness decreases with increasing distance. The fitness function evaluates the effectiveness of each solution [15].

The attractiveness function, which is one of the mathematical formulas of the Firefly Algorithm, is given in Equation (9).

$$\beta \left(r\right)={\beta }_0\times e^{-\gamma r^2}$$

(9)

In this equation, ${\beta }_0$ represents the attractiveness value when the distance is zero, γ is the ambient light absorption coefficient and r is the Euclidean distance between the fireflies. The position update formula is presented below in Equation (10).

$$x_i\left(t+1\right)={x_i\left(t\right)+\beta }_0\times e^{-\gamma r^2}\times \left(x_i-x_j\right)+\alpha {\epsilon }_i$$

(10)

where $x_i\left(t\right)$ is the position of the firefly i at time t, $x_j\left(t\right)$ is the position of the firefly j at time t, ${\beta }_0\times e^{-\gamma r^2}$ is the attraction due to firefly j, α is the randomness parameter, ${\epsilon }_i$ is a random number in the range [0, 1].

Figure 2 shows the proposed optimization workflow. The workflow includes: (i) environment configuration and connection to DIgSILENT PowerFactory, (ii) acquisition and processing of PV and network operating data, (iii) determination of inverter reactive power capability limits (Q_min–Q_max), (iv) execution of metaheuristic optimization algorithms (Firefly Algorithm, PSO, Jaya, and GA), (v) assignment of optimal reactive power setpoints to PV inverters and performance evaluation (voltage profile and feeder active power losses), and (vi) Modbus feasibility demonstration to validate inverter read/write communication for real-time applicability.

3. Results

Numerical and Experimental Results

In this study, a sample distribution network of AKEDAS, which provides electricity distribution services in Kahramanmaras and Adiyaman provinces in southern Turkey, is used for the analysis and simulations. The numerical analysis and optimization are performed in DIgSILENT PowerFactory using the actual distribution feeder model and PV inverter rated data and locations. The operating point analyzed in this manuscript corresponds to the PowerFactory study-time selection of Hour-of-Year 5051–5052 (i.e., 30 July 2021 11:00–12:00) based on the annual time-series profiles. This representative time window was selected to provide a consistent comparison of optimization algorithms under identical system conditions.

Table 1. Study time and validation setup.

Item	Value
Study time (PowerFactory)	30 July 2021 11:00–12:00
Hour-of-year index	5051–5052
Optimization environment	DIgSILENT PowerFactory
Time resolution	Hourly operating point
Field activity	Modbus feasibility demonstration only (inverter read/write access)

shows the details about the study time and the validation setup.

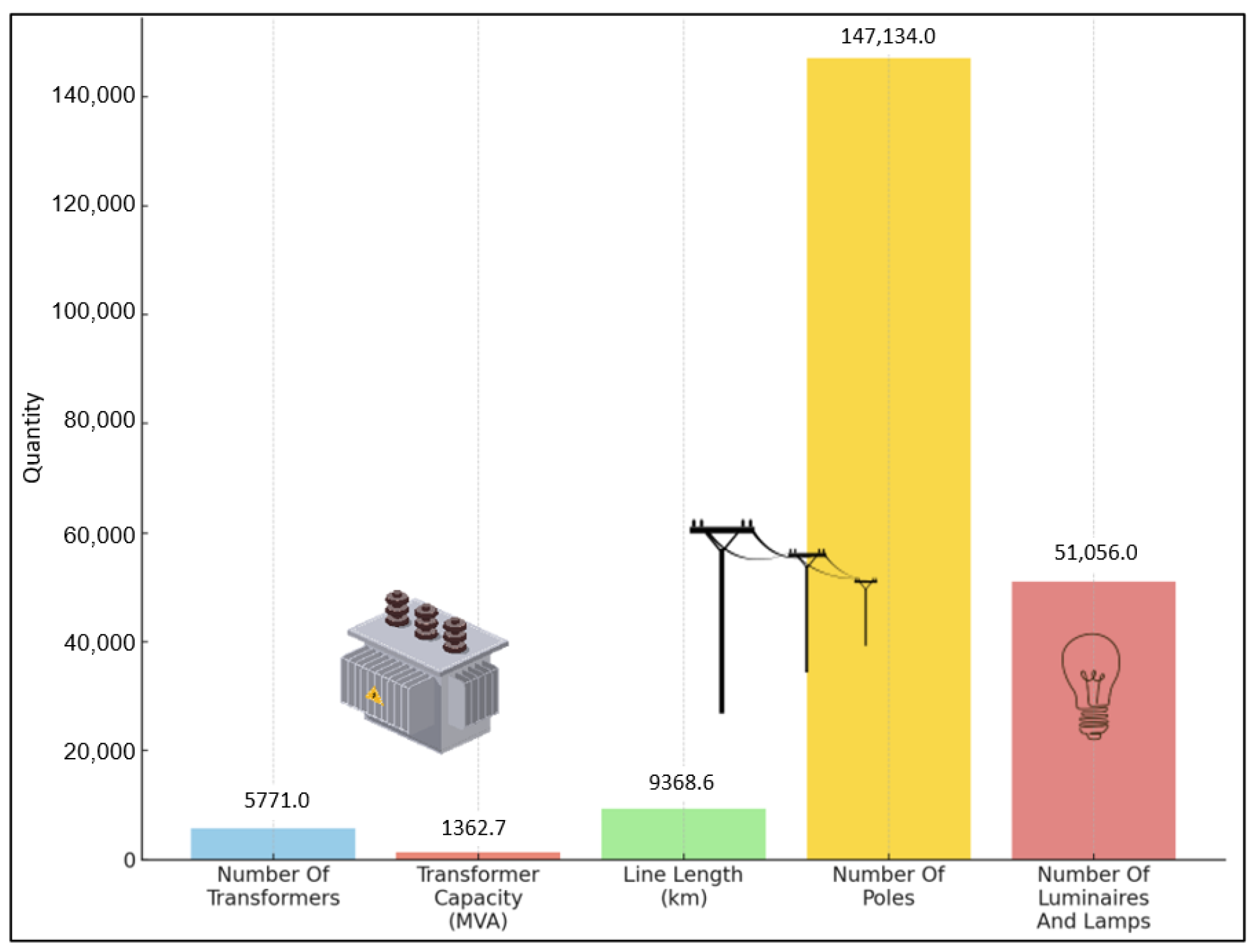
AKEDAS, which provides electricity distribution services to a population of 1,672,890 in Kahramanmaras and Adiyaman, operates in distribution region 20, which was privatized by Turkish Electricity Distribution Corporation. Figure 3 shows the amount of equipment in the electricity distribution network in the Adiyaman region as of 2023. As seen in this figure, there are 5771 transformers connected to AKEDAS in Adiyaman province, where the study was conducted, and their total installed power is 1362.7 MVA. The total line length is 9368.6 km. The total number of poles is 147,134, while the number of armatures and lamps is 51,056.

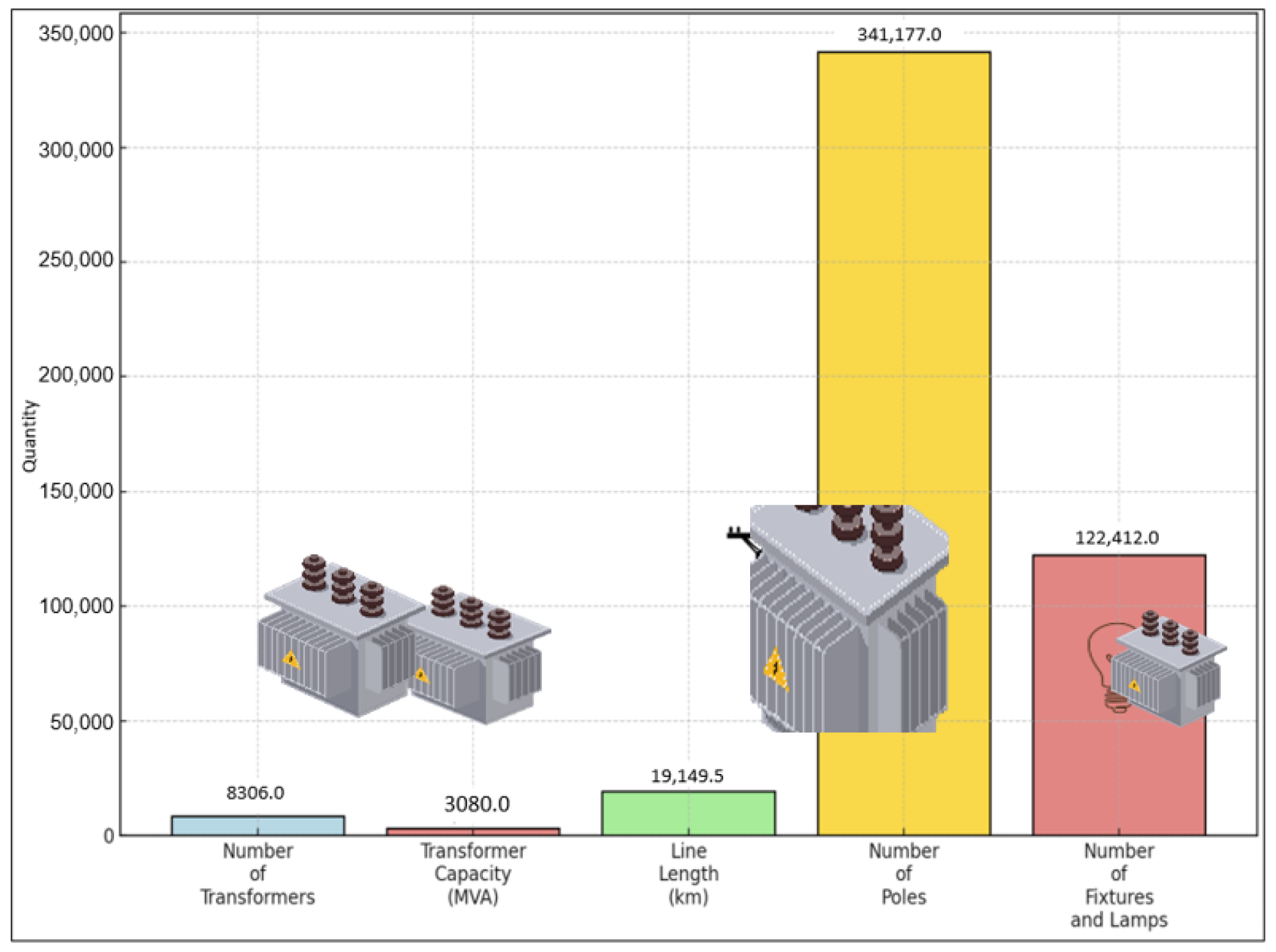
Figure 4 shows the network information and the amount of equipment within AKEDAS in Kahramanmaras. As can be seen in the figure, there are 8306 transformers connected to AKEDAS in Kahramanmaras. The total installed power of these transformers is 3080 MVA, and the total line length is 19,149.50 km. The total number of poles is 341,777, and the number of armatures and lamps is 122,412. In this study, samples taken from the Adiyaman TM1 city feeder were studied. There are 12 PV power plants with an installed capacity of 11.8 MW in this region.

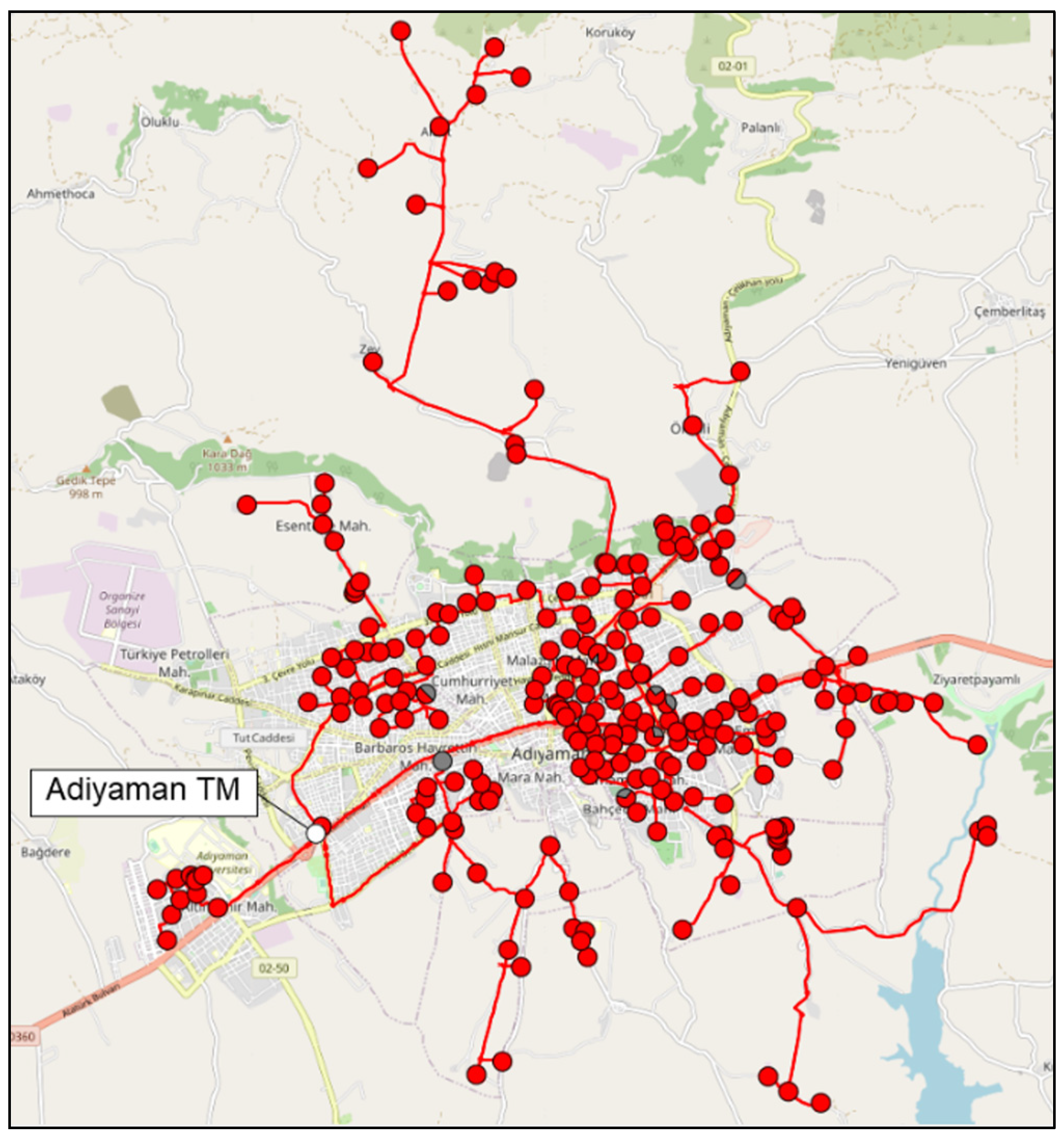
Figure 5 shows the image of Adiyaman TM1 city feeder taken from the geographical information system used in AKEDAS. A simulation study was carried out on the substation in the Adiyaman region and the City1 TM feeder connected to it. A grid connection model was created by integrating the data obtained from the geographical information system with DIgSILENT PowerFactory 2022 software (DIgSILENT GmbH, Gomaringen, Germany). Geographical information system data are processed and embedded in DIgSILENT software. In Figure 5, the red markers connected to this substation indicate the distribution transformer posts.

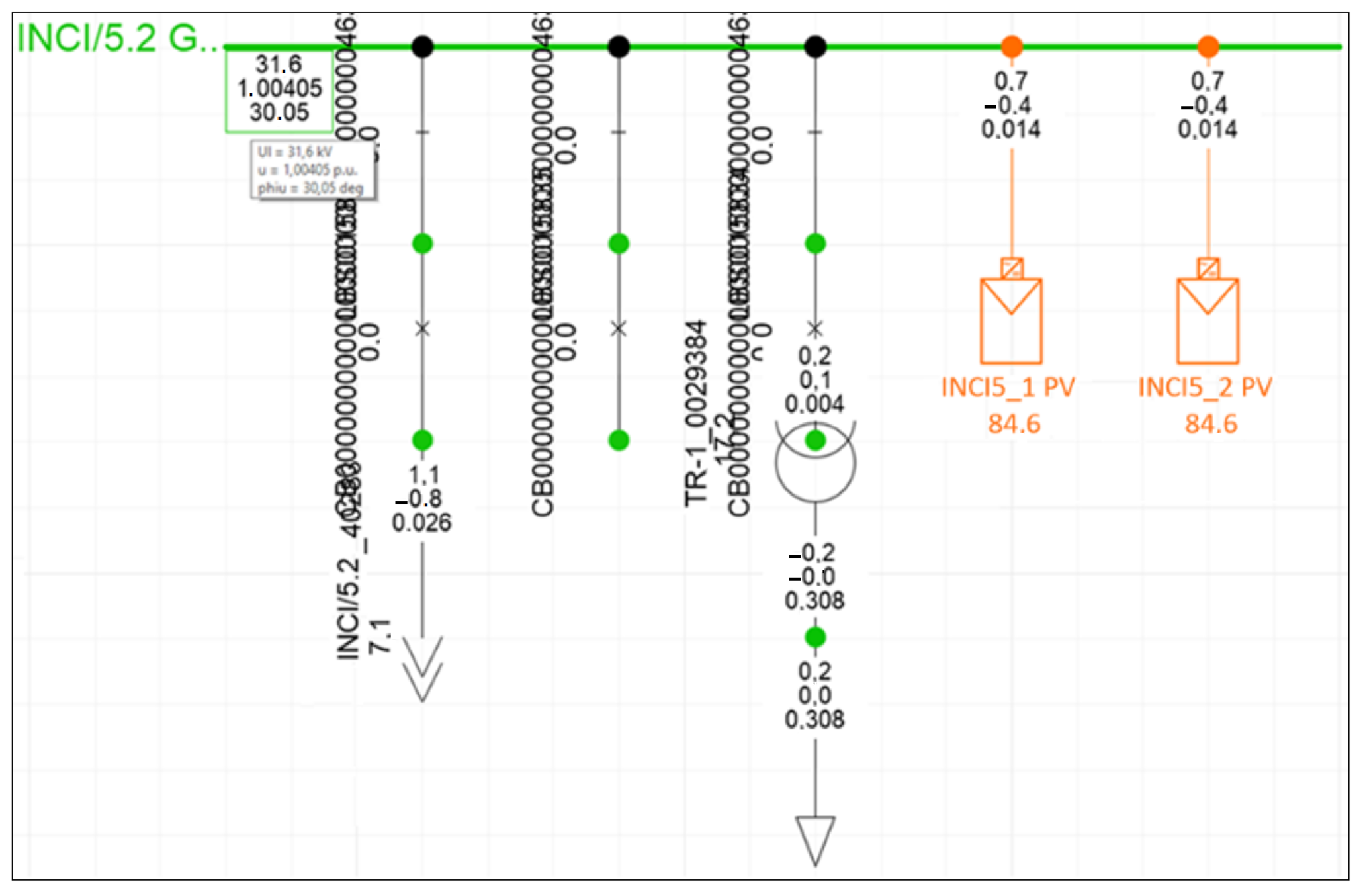
Each of the colors in the simulation has a meaning, and the meaning of these colors as voltage equivalent (as p.u) is seen on the DIgSILENT application. In 258 busbars, where load flow analysis was performed, voltage and angle details were obtained after the analysis. Regarding the simulation, a separate study was carried out for the busbar to which 2 PV power plants are connected. Here, voltage data was analyzed as 1.00405 p.u. and phase-angle information as 30.05 degrees. At the same time, while the active generation of the PV plants is 0.7 MW, the reactive energy support from these 2 plants is −0.4 MVAR. Since the voltage is high on the INCI5_2 PV plant line, the PV plant draws reactive energy from the line to reduce the voltage. Figure 6 shows the voltage and load information on a sample busbar. As seen in Figure 6, it is possible to access information such as Active Power, Reactive Power, etc., from the LOAD FLOW screen on DIgSILENT for INCI5_2 PV, one of the 2 PV plants taken as an example. The annual load profile of INCI5_2 PV on the DIgSILENT application is shown in Figure 7.

Table 2. List of PV Plants with optimum reactive power support.

PV Plant Name	Reactive Power	Active Power
	MVAr	MW
A.Kadireroglu	0.383051	0.73073
Famor	0.053758	0.73142
Gazi Kaya	0.125962	0.73073
Hasanbasri Kaya	−0.341544	0.73073
Inci5_1	−0.390523	0.67291
Inci5_2	−0.390523	0.67291
Nazan Bagci	0.109919	0.73073
Ormes 2	0.261024	0.70219
Ormes 3	−0.061656	0.73071
Ormes 4	0.319201	0.73072
Sinan Bagci	−0.146507	0.73073
Zeynaleroglu	0.393026	0.73073

includes the list of the 12 PV plants in the sample grid and their active and reactive power information.

Although DIgSILENT PowerFactory offers multiple tools and capabilities, it can be challenging to apply these tools effectively as network and scenario analyses become more complex. For example, it was not possible to run four different algorithms developed in this study on the data read from the network and apply the results back to the sample network directly through the software. To overcome this issue, the Python API (Python 3.13.9) provided by DIgSILENT PowerFactory is used. The main purpose of the API is to automate tasks that can be time-consuming and error-prone when implemented manually, making them easier and more reliable.

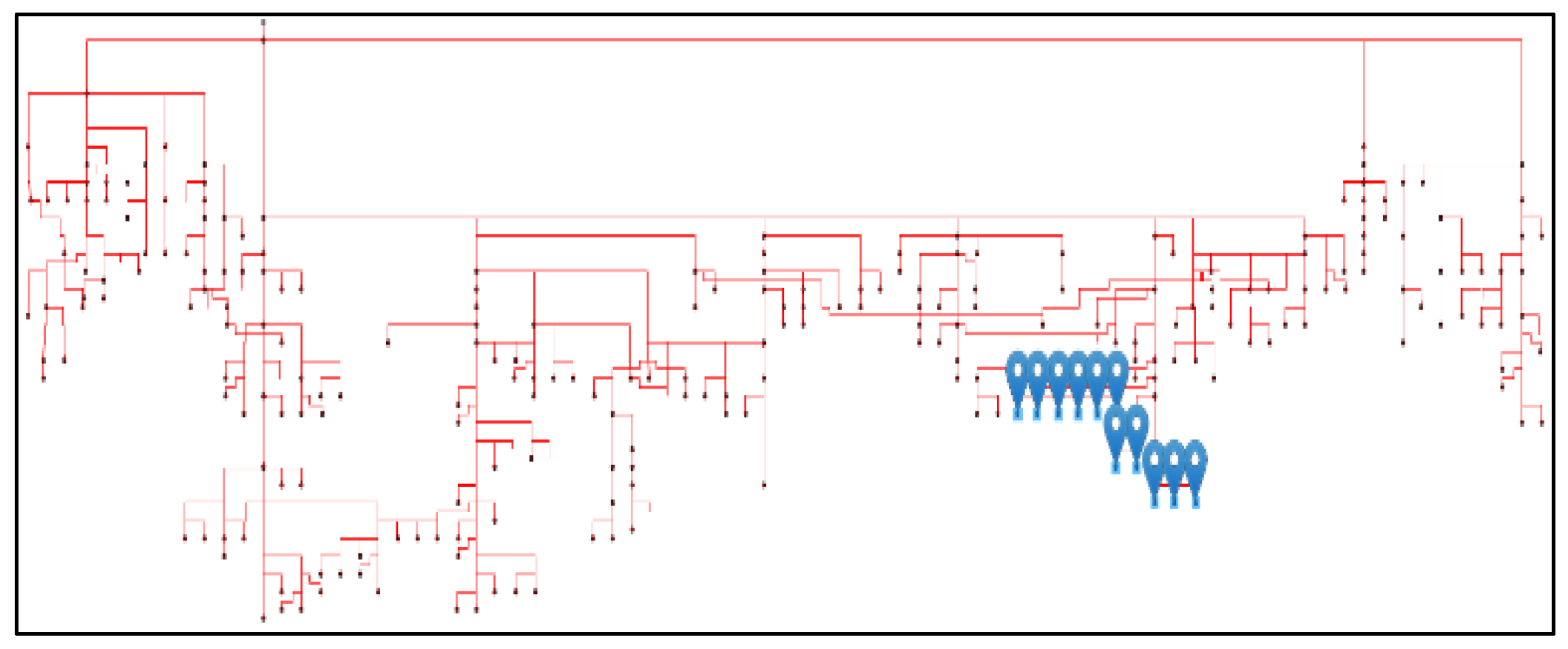
In this study, the analysis is performed on the Adiyaman TM-City 1 feeder of AKEDAS, the distribution system operator of Kahramanmaras and Adiyaman provinces in southern Turkey. There are 12 PV plants in the grid with a total installed capacity of 11.792 MW, and the geographical locations of the PV plants are marked on the DIgSILENT application in Figure 8. The model was built using real network data integrated with the Geographic Information System (GIS) to reflect actual grid conditions.

As part of the test infrastructure, a Python-based control application was developed to communicate directly with the PV inverters via the Modbus RTU protocol. This Modbus-based activity was conducted solely as a feasibility demonstration to verify inverter accessibility and the capability of remotely writing reactive power reference values. Importantly, the optimization algorithms were not executed in real time in the field; all optimization routines and the quantitative results reported in this manuscript were obtained using the DIgSILENT PowerFactory simulation environment based on the actual feeder model, inverter data, and time-series profiles.

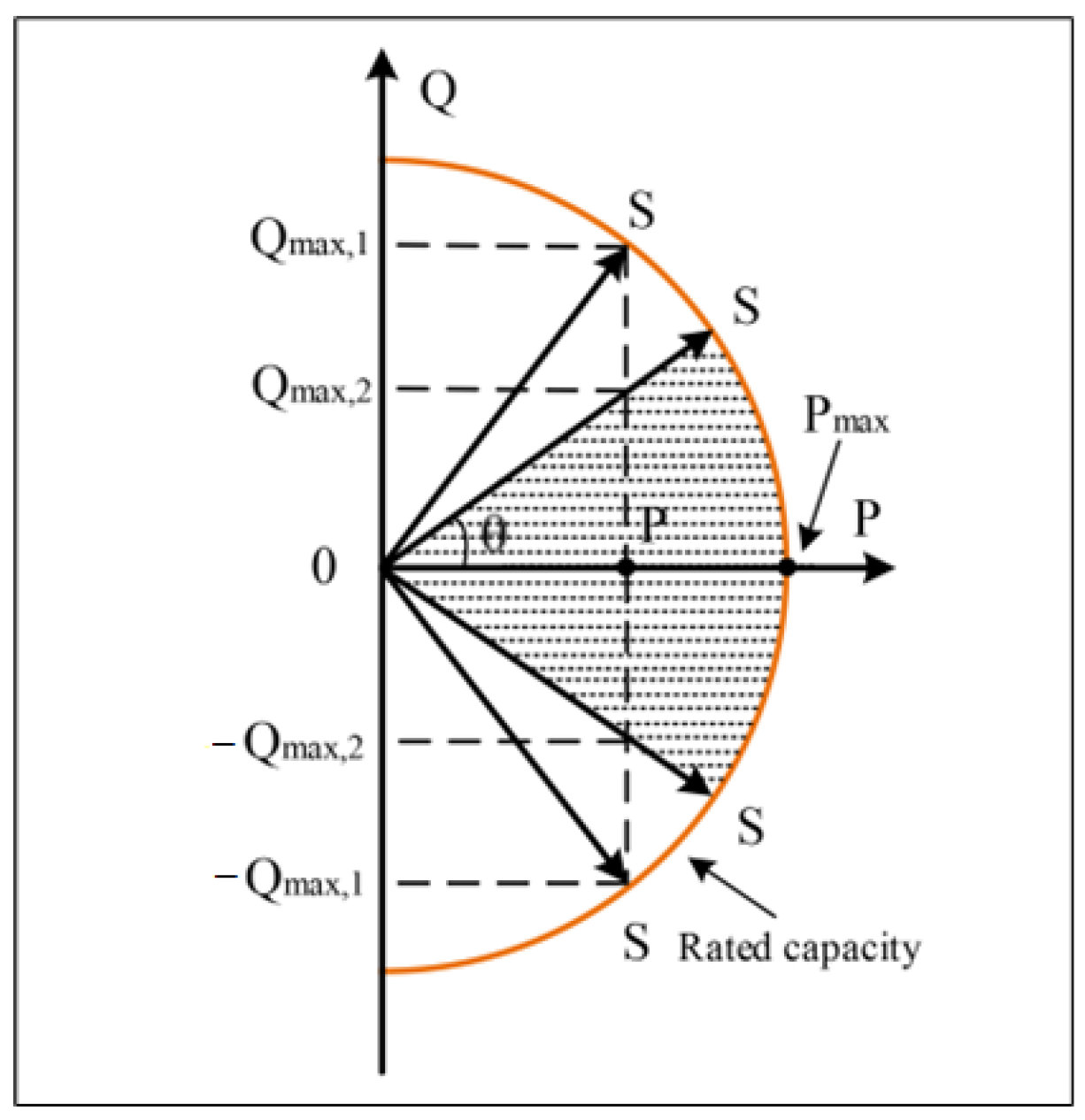
In terms of compliance and protection, the proposed reactive power control respects operational constraints consistent with Turkish distribution grid practice. Specifically, bus voltages are maintained within predefined limits (V_min ≤ V_i ≤ V_max), and inverter reactive power references are bounded by inverter capability curves based on rated apparent power (P_k² + Q_k² ≤ S_k,rated²). The proposed approach does not modify the feeder’s existing protection settings or current protection schemes; it only generates inverter reactive power reference values within allowable operating boundaries. In addition, the Modbus-based feasibility demonstration does not bypass inverter internal protection functions (e.g., over/under-voltage, overcurrent, and anti-islanding) and is only used to verify remote communication and setpoint writing capability.

In addition to voltage profile improvement, the impact of reactive power optimization on feeder active power losses was evaluated using DIgSILENT PowerFactory loss outputs. Reactive power support may redistribute power flows and may increase losses in certain feeder sections due to reactive circulation. Therefore, the main indicator reported in this study is the overall system-level total active power losses (LossP).

Table 3. Total system active power losses (LossP) at Hour-of-Year 5051–5052.

Case	Total LossP (MW)
Baseline (no Q support)	0.277566983952578
PSO (with Q support)	0.2775666
GA (with Q support)	0.2775659
Jaya (with Q support)	0.2750054
FA (with Q support)	0.2775398

presents the total LossP values for the baseline case and for each optimized solution at the analyzed operating point (Hour-of-Year 5051–5052).

As shown in Table 3, the Jaya-based solution achieves the highest reduction in system losses for the analyzed operating point, while the other methods yield losses comparable to the baseline.

It aims to improve the overall voltage profile of the grid with the optimal level of reactive power support from the inverters of each PV power plant connected to the distribution system. Therefore, four different Python-based algorithms are tested on the DIgSILENT PowerFactory application for grid modeling.

The algorithms are designed to optimize the reactive energy generation from the idle capacity of the inverters without limiting the current active power generation of the power plant. During the design, the current, voltage, and defined maximum power limits of the inverters were taken into account, and it was aimed to determine the optimum reactive power values within these limits. Thus, the available capacities of the inverters were effectively utilized, and grid voltage profiles were improved.

Within the scope of the study, each algorithm was run 100 times, and at the end of each run, the deviations of the voltage levels of the busbars in the grid from the ideal value of 1 p.u. were calculated. These deviations were summed, and the average of 100 different results was determined. Finally, the performance of each algorithm was evaluated based on these results.

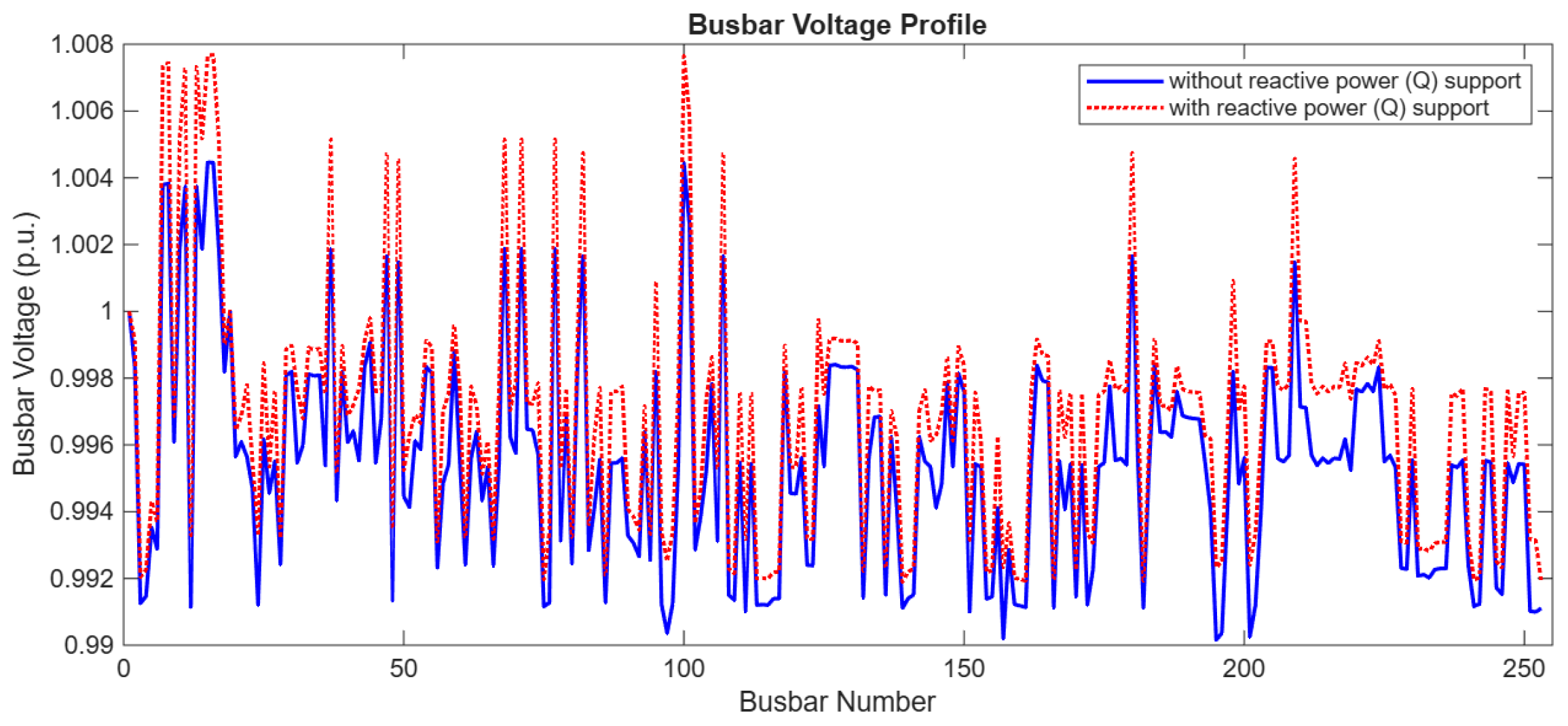
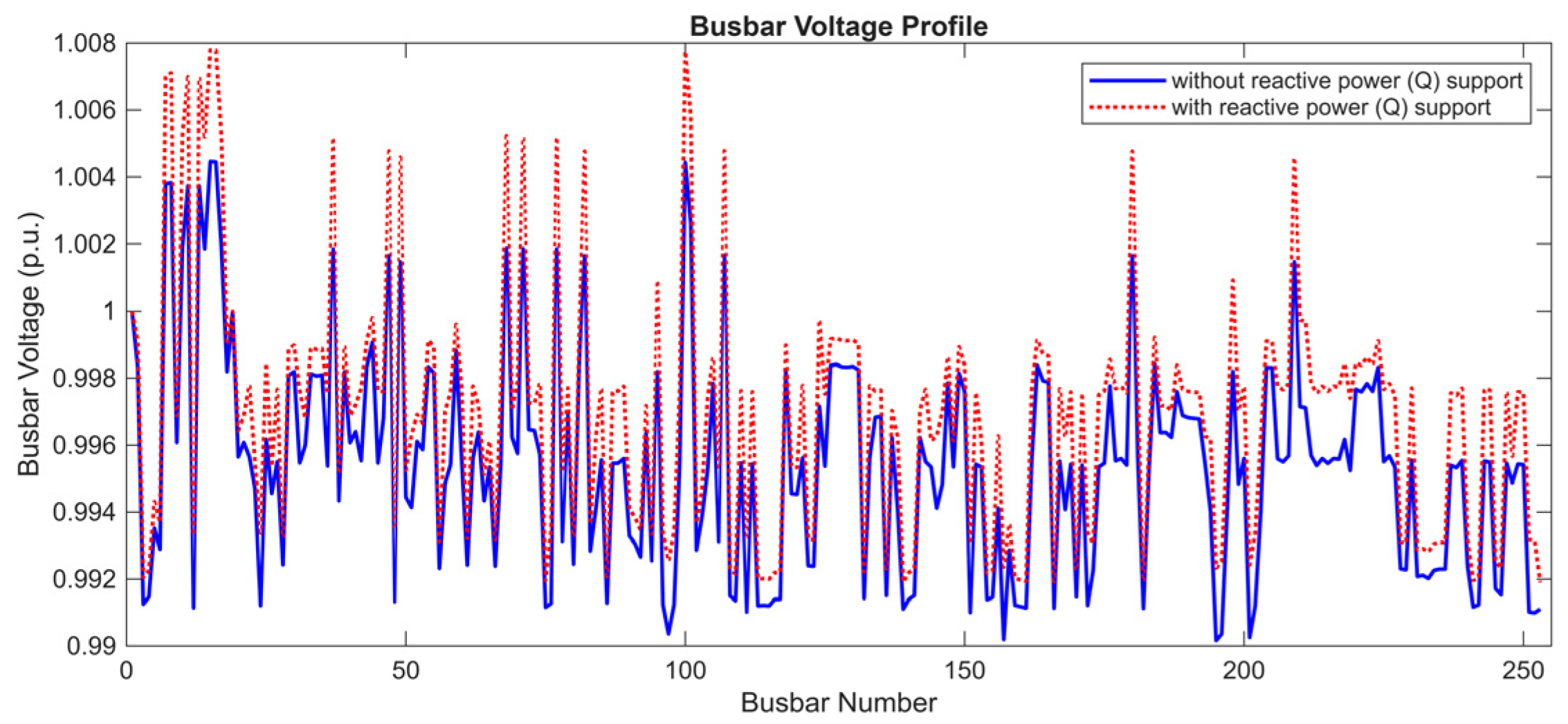
PSO is a population-based meta-heuristic algorithm inspired by collective behavior, such as a flock of birds or a school of fish. The graph of the result obtained with the developed Particle Swarm Optimization algorithm is given in Figure 9. It shows the changes in the grid voltage profile before and after the application of the PSO Algorithm. The horizontal axis represents the busbars in the grid. The vertical axis represents the deviation of the voltage level of each busbar from the ideal value of 1 p.u.

The blue color represents the voltage deviations before the application of the algorithm, while the red color shows the improved voltage levels after the application of the algorithm and the provision of reactive energy support. The red graph shows that the voltages are closer to the ideal level, indicating that the PSO Algorithm plays an effective role in reducing voltage deviations. The effect of the PSO algorithm on the grid voltage profile is summarized in

Table 4. Voltage deviation index improvement rate with the PSO algorithm.

Average	19.336%
Min	17.802%
Max	20.940%
Standard deviation	0.935%

, with the data obtained by running the algorithm for 100 iterations.

These results show that the PSO Algorithm is an effective method for optimizing grid voltage profiles. An average improvement rate of 19.336% demonstrates the overall performance of the algorithm, while the standard deviation value of 0.935% emphasizes the stability and consistency of the results. With its fast convergence and balanced exploration-exploitation structure, the PSO Algorithm proves to be a successful optimization tool for voltage control in distribution networks. Moreover,

Table 5. PV inverter operating points: reactive power injection/absorption (Q) with corresponding P and S values.

PV Plant Name	Q (kVAR)	P (kW)	S (kVA)	Installed Power (kW)
A.Kadir Eroglu	164.84	778.05	818.93	999
Famor	120.61	810.00	818.25	1020
Gazi Kaya	171.36	800.1	860.94	999
Hasan Basri Kaya	309.86	803.25	758.01	999
Inci5_1	−195.46	732.37	773.74	920
Inci5_2	188.52	749.7	878.58	920
Nazan Bagci	395.59	782.77	857.79	999
Ormes 2	329.32	789.07	909.18	960
Ormes 3	236.76	878.85	926.66	999
Ormes 4	−469.59	800.1	875.61	999
Sinan Bagci	344.41	803.25	790.74	999
Zeynal Eroglu	11.68	790.65	818.93	999

indicates the amounts of reactive energy supplied and withdrawn from the PV plants.

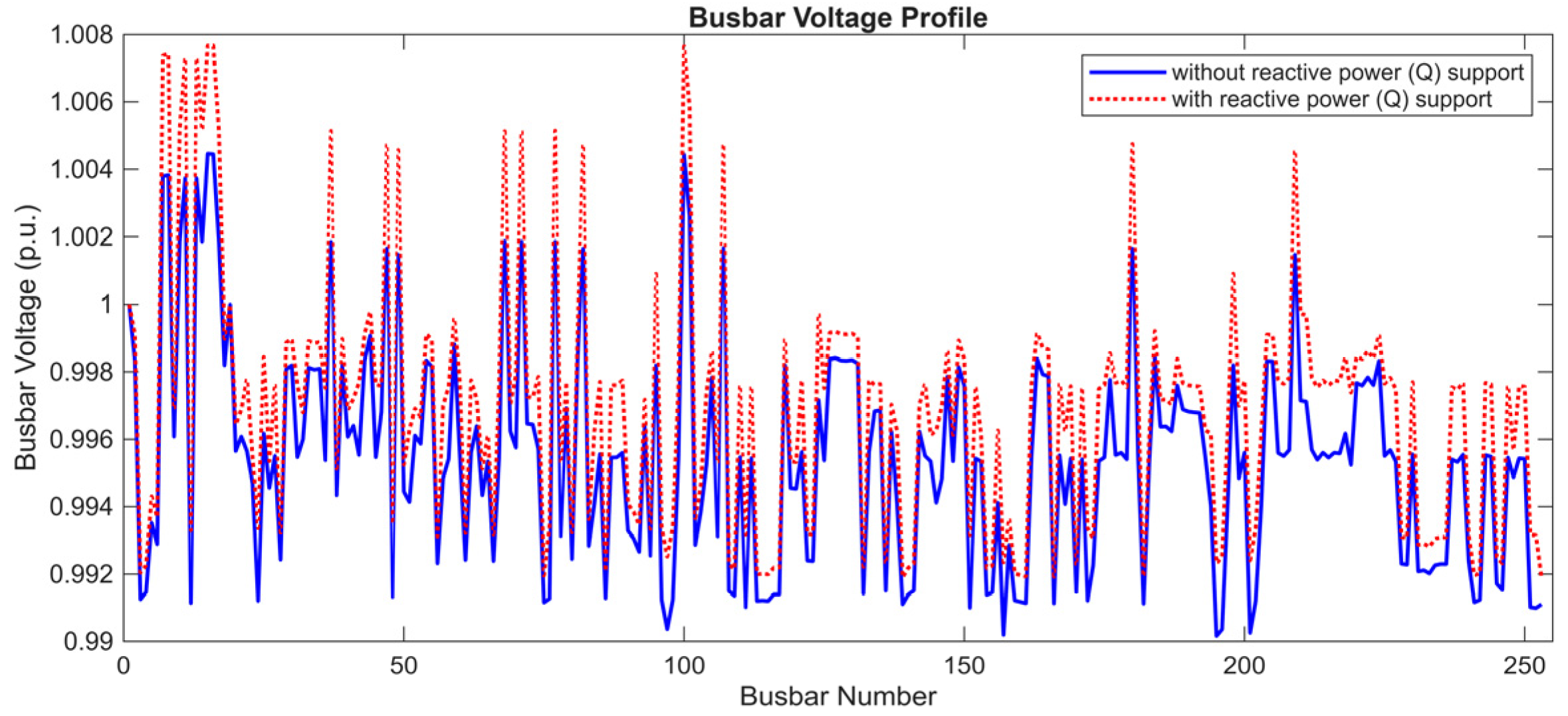
Genetic Algorithm (GA) is a powerful optimization technique inspired by the process of natural selection and evolution. Figure 10 shows the result obtained using the GA. Here, it shows the changes in the grid voltage profile before and after GA application. The horizontal axis represents the busbars in the grid. The vertical axis shows the deviation of the voltage level of each busbar from the ideal value of 1 p.u.

The blue graph represents the voltage deviations before the application of the algorithm while the red graph represents the improved voltage levels after running the algorithm, which provides reactive energy support. The red graph clearly shows that the voltages are closer to the ideal level (1 p.u.). This shows the effectiveness of GA in reducing voltage deviations. The performance of GA in improving the grid voltage profile is summarized in

Table 6. Voltage deviation index improvement rate with GA.

Average	19.177%
Min	17.628%
Max	20.787%
Standard deviation	0.961%

based on the data obtained by running the algorithm for 100 iterations.

These results show that GA is effective in optimizing grid voltage profiles. An average improvement rate of 19.177% demonstrates the overall performance of the algorithm, while the standard deviation value of 0.961% emphasizes the consistency and stability of the results. This improvement provided by the Genetic Algorithm proves that it is a viable method for voltage control in distribution networks.

Table 7. Exported-Extracted power values by the PV plants.

PV Plant Name	Q (kVAR)	P (kW)	S (kVA)	Installed Power (kW)
A.Kadir Eroglu	304.44	778.05	835.49	999
Famor	389.03	810	898.58	1020
Gazi Kaya	395.62	800.1	892.57	999
Hasan Basri Kaya	337.72	803.25	871.36	999
Inci5_1	95.79	732.37	738.61	920
Inci5_2	−488.79	749.7	894.97	920
Nazan Bagci	−243.24	782.77	819.70	999
Ormes 2	159.45	789.07	805.02	960
Ormes 3	276.98	878.85	921.46	999
Ormes 4	−31.31	800.1	800.71	999
Sinan Bagci	350.37	803.25	876.34	999
Zeynal Eroglu	52.74	790.65	792.41	999

shows the amounts of reactive energy supplied and withdrawn from PV plants.

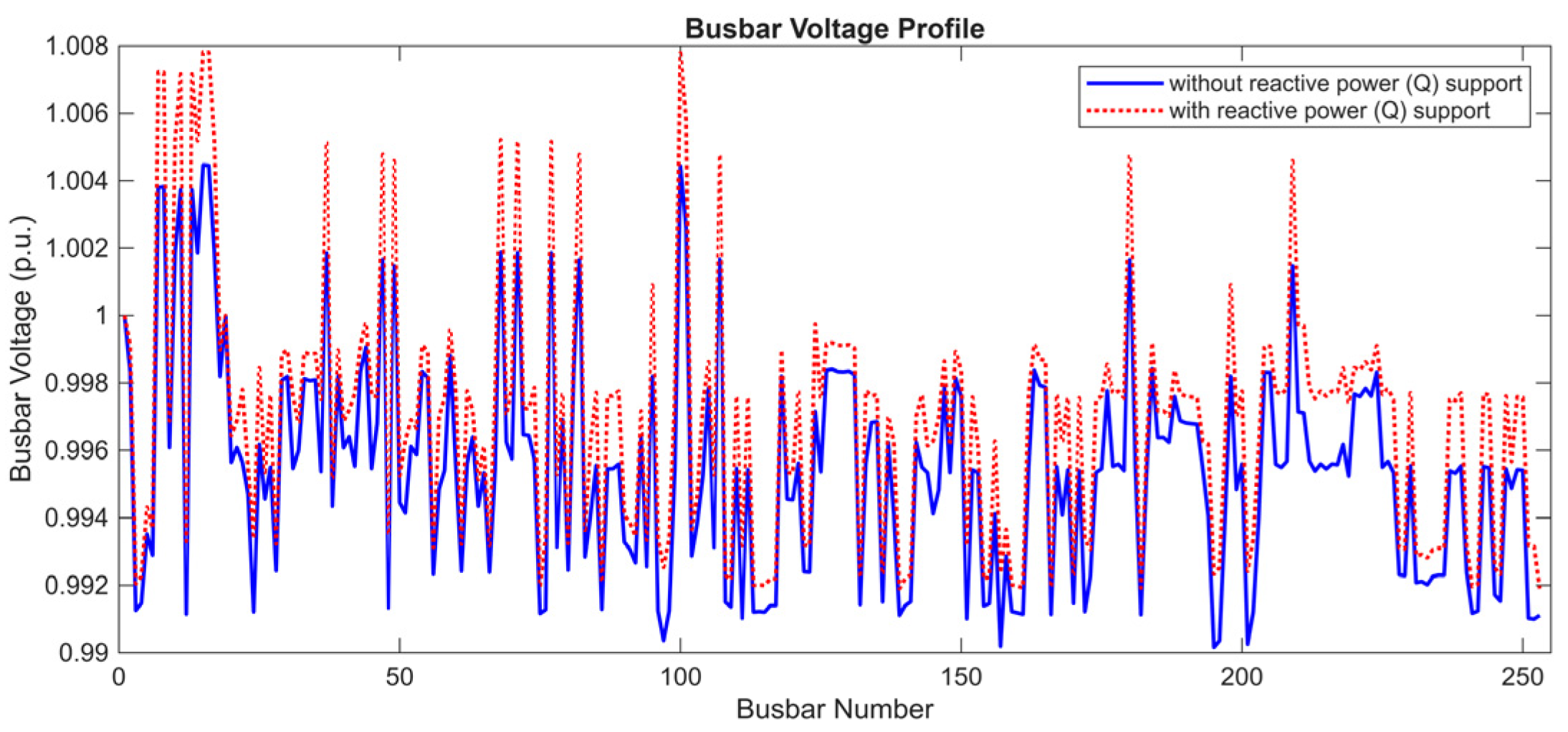
The Jaya algorithm aims to solve optimization problems by improving the quality of a population of potential solutions over iterations. It achieves this by iteratively updating the individuals in the population according to their performance. Figure 11 shows the results of the algorithm. The figure shows the improvement in the grid voltage profile before and after the implementation of the Jaya algorithm. The horizontal axis represents the busbars in the grid. The vertical axis represents the distance of the voltage level of each busbar from the ideal value of 1 p.u.

The red graph clearly shows that the voltages are closer to the ideal level (1 p.u.), which demonstrates the performance of the Jaya algorithm in reducing voltage deviations. The impact of the Jaya algorithm on the grid voltage profile is summarized in

Table 8. Voltage deviation index improvement rates with the Jaya algorithm.

Average	19.919%
Min	18.430%
Max	21.579%
Standard deviation	0.891%

according to the data obtained after running the algorithm for 100 iterations.

These results show that the Jaya algorithm optimizes the grid voltage profiles in an efficient and stable manner. The average improvement rate is about 20%, which indicates the strong performance of the algorithm. Moreover, the low standard deviation value (0.891%) emphasizes the stability and reproducibility of the results obtained. The amounts of reactive energy supplied by and withdrawn from the PV plants are given in

Table 9. Delivered–Drawn power values from the PV plants.

PV Plant Name	Q (kVAR)	P (kW)	S (kVA)	Installed Power (kW)
A.Kadir Eroglu	395.24	778.05	872.69	999
Famor	−600.00	810	1008.02	1020
Gazi Kaya	381.02	800.1	886.19	999
Hasan Basri Kaya	36.60	803.25	804.08	999
Inci5_1	309.39	732.37	795.05	920
Inci5_2	309.39	749.7	811.03	920
Nazan Bagci	395.20	782.77	876.88	999
Ormes 2	374.95	789.07	873.63	960
Ormes 3	51.61	878.85	880.36	999
Ormes 4	−218.50	800.1	829.4	999
Sinan Bagci	−8.70	803.25	803.3	999
Zeynal Eroglu	73.40	790.65	794.05	999

.

The result of the Firefly Algorithm (FA) is presented in Figure 12. The figure demonstrates the changes in the grid voltage profile before and after the implementation of the Firefly Algorithm. The horizontal axis represents the busbars in the grid. The vertical axis shows the deviation of the voltage level of each busbar from the ideal value of 1 p.u.

The blue graph represents the voltage deviations before running the algorithm, while the red graph represents the improved voltage levels after the application of the algorithm, which provides reactive energy support. The red graph shows that the voltages are closer to the ideal level, which reveals that the Firefly Algorithm is successful in reducing voltage deviations. The effect of the Firefly Algorithm on the grid voltage profile is summarized in

Table 10. Firefly voltage deviation index improvement rates.

Average	19.250%
Min	17.872%
Max	20.882%
Standard deviation	0.870%

based on the data obtained after running the algorithm for 100 iterations.

These results reveal that the Firefly Algorithm is effective in improving the grid voltage profile. An average improvement rate of 19.250% demonstrates the strong performance of the algorithm, while the low standard deviation value of 0.870% emphasizes the stability and consistency of the obtained results. This capability of the algorithm proves to be an effective tool for optimizing the voltage profile in distribution systems.

Table 11. Exported–Extracted power values by the PV plants.

PV Plant Name	Q (kVAR)	P (kW)	S (kVA)	Installed Power (kW)
A.Kadir Eroglu	304.44	810.00	865.32	999
Famor	389.03	778.05	869.89	1020
Gazi Kaya	395.62	800.1	892.57	999
Hasan Basri Kaya	337.72	803.25	871.36	999
Inci5_1	95.79	732.37	738.61	920
Inci5_2	−488.79	749.7	894.97	920
Nazan Bagci	−243.24	782.77	819.70	999
Ormes 2	159.45	789.07	805.02	960
Ormes 3	276.98	878.85	921.46	999
Ormes 4	−31.31	800.1	800.71	999
Sinan Bagci	350.37	803.25	876.34	999
Zeynal Eroglu	52.74	790.65	792.41	999

indicates the amounts of reactive energy supplied by and withdrawn from the PV plants.

In the study, it is observed that Jaya, PSO, GA, and FA are all capable of improving the grid voltage profile by providing optimal reactive power support. After optimization, it is clearly seen that the overall voltage profiles approach the ideal level of 1 p.u. However, there is a limited increase in the voltages on some busbars, mainly due to the relocation of the reactive power source. This causes the voltage to move slightly away from 1 p.u. in the centers connected to or near these PV plants, as the reactive power required by the feeder is taken from PV inverters rather than the substation. As a result, a slight increase in voltage is observed at these substations and feeders.

In the PSO algorithm, fixed learning coefficients (C₁ = C₂ = 2.0), which are widely recommended in the literature for fast convergence, were employed. The inertia weight was set to W_max = 0.9 and W_min = 0.4 to ensure a balance between exploration and exploitation. Simulations were conducted for a swarm size of 30 particles for 50 iterations. These parameters are based on proven configurations in previous studies and yielded stable and reliable results in our analysis.

For the Genetic Algorithm, the population size was set to 100, with a mating pool of 20 individuals and 80 offspring generated in each generation. The crossover rate was assigned randomly for each cycle, and the mutation rate was kept constant. This structure enabled the algorithm to maintain diversity while effectively steering the population toward the global optimum.

The Jaya algorithm is a parameter-free optimization method that eliminates the need for manual tuning and offers a simple implementation. The algorithm was run for a population size of 25 for 50 iterations. The simulation delivered consistent and effective results.

In the Firefly Algorithm, the attractiveness coefficient (β) was set to 1.0, the light absorption coefficient (γ) to 1.0, and the randomness parameter (α) to 0.5. The algorithm was executed for a population size of 40 for 100 iterations. These values were chosen to ensure both exploration capabilities and convergence performance under varying scenarios.

The parameter values, number of particles, and number of iterations used in the algorithms are given in

Table 12. Algorithm parameters and values.

Algorithm	Number of Iterations	Number of Particles	Parameters
PSO	50	30	W_max: 0.9, W_min: 0.4, C1: 2.0, C2: 2.0
GA	50	100	Matting Pool Size: 20, Offspring Size: 80, Crossover Rate: Randomly
JAYA	50	25	Parameter-free
FA	100	40	Alpha (Randomness): 0.5, Beta (Attractiveness): 1.0, Gamma (Light Absorption): 1.0

.

Since metaheuristic optimization methods may yield different solutions across independent executions, each algorithm was evaluated over 100 independent runs under identical parameter settings. The mean improvement, best/worst values, and standard deviation are reported in

Table 13. Statistical performance after 100 runs (VDI improvement).

Algorithm	Best (%)	Mean (%)	Std (%)	Worst (%)
PSO	20.940%	19.336%	0.935%	17.802%
GA	20.787%	19.177%	0.961%	17.628%
Jaya	21.579%	19.919%	0.891%	18.430%
FA	20.882%	19.250%	0.870%	17.872%

to quantify robustness and uncertainty.

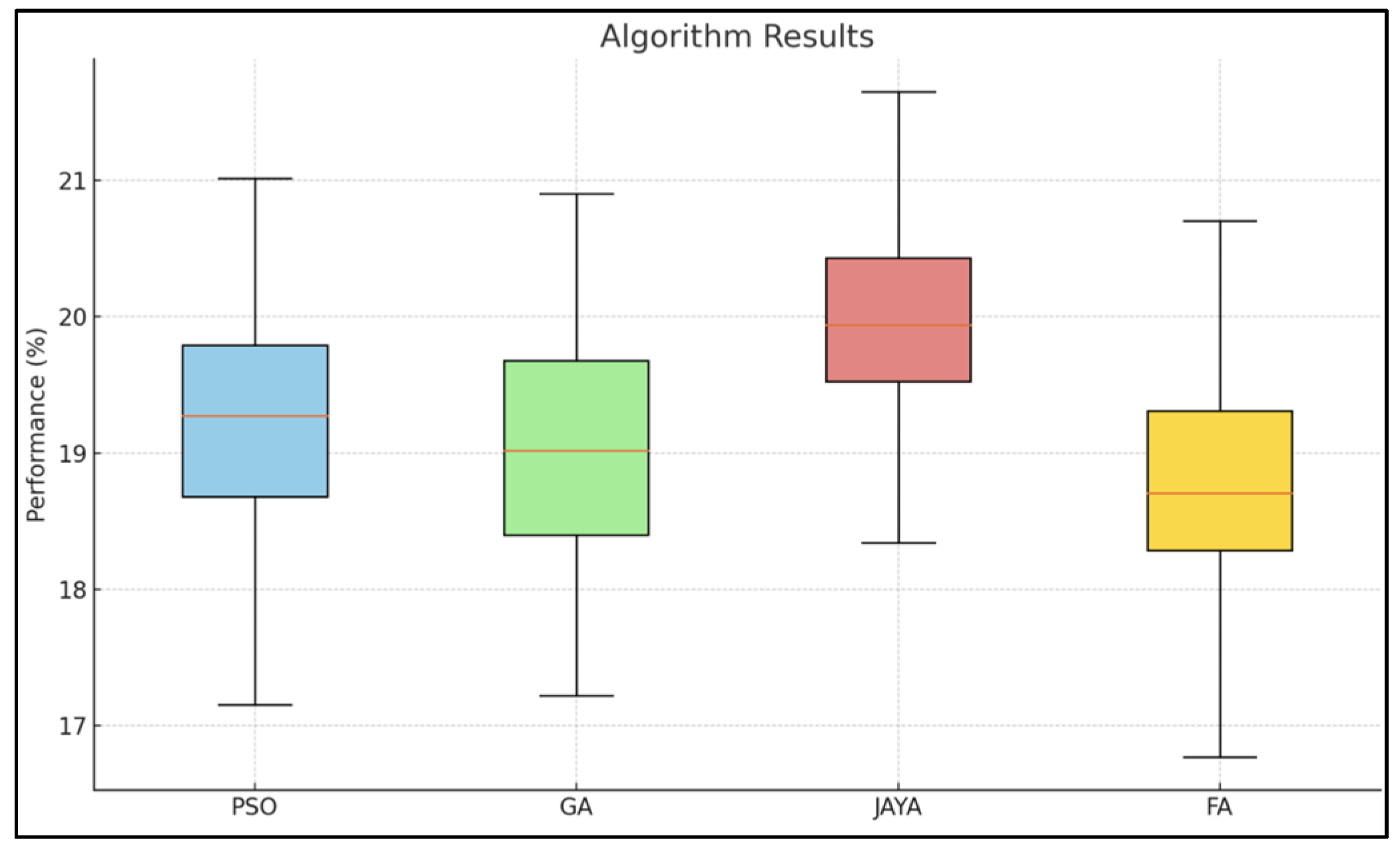
Figure 13 compares the performance of Jaya, PSO, GA, and FA in terms of improvement in the grid voltage profiles. In this figure, the Median is the line in the center of each box, and it represents the median value (midpoint) of the results of that algorithm; the Interquartile Range (IQR) covers the 25th and 75th percentiles of the results. This represents the middle 50% of the distribution of the data. Whisker (extensions) shows the lowest and highest values (with exceptions). X Sign represents the mean value.

It is observed that the Jaya algorithm achieved the best voltage improvement after optimization with 19.919%. The PSO algorithm also showed a similar performance with an improvement of 19.336%, while the FA and GA demonstrated slightly lower improvement rates despite yielding close results (FA = 19.25% and GA = 19.177%). It can be stated that the FA provided more stable and consistent results with the lowest standard deviation value (0.87%).

This evaluation clearly reveals that the Jaya algorithm exhibits superior performance and minimizes voltage deviations more effectively compared to the other algorithms. While the balanced structure of PSO presents a good alternative, the FA and GA contributed to overall stability but with a limited improvement. These results highlight the optimization capabilities of each algorithm from different perspectives.

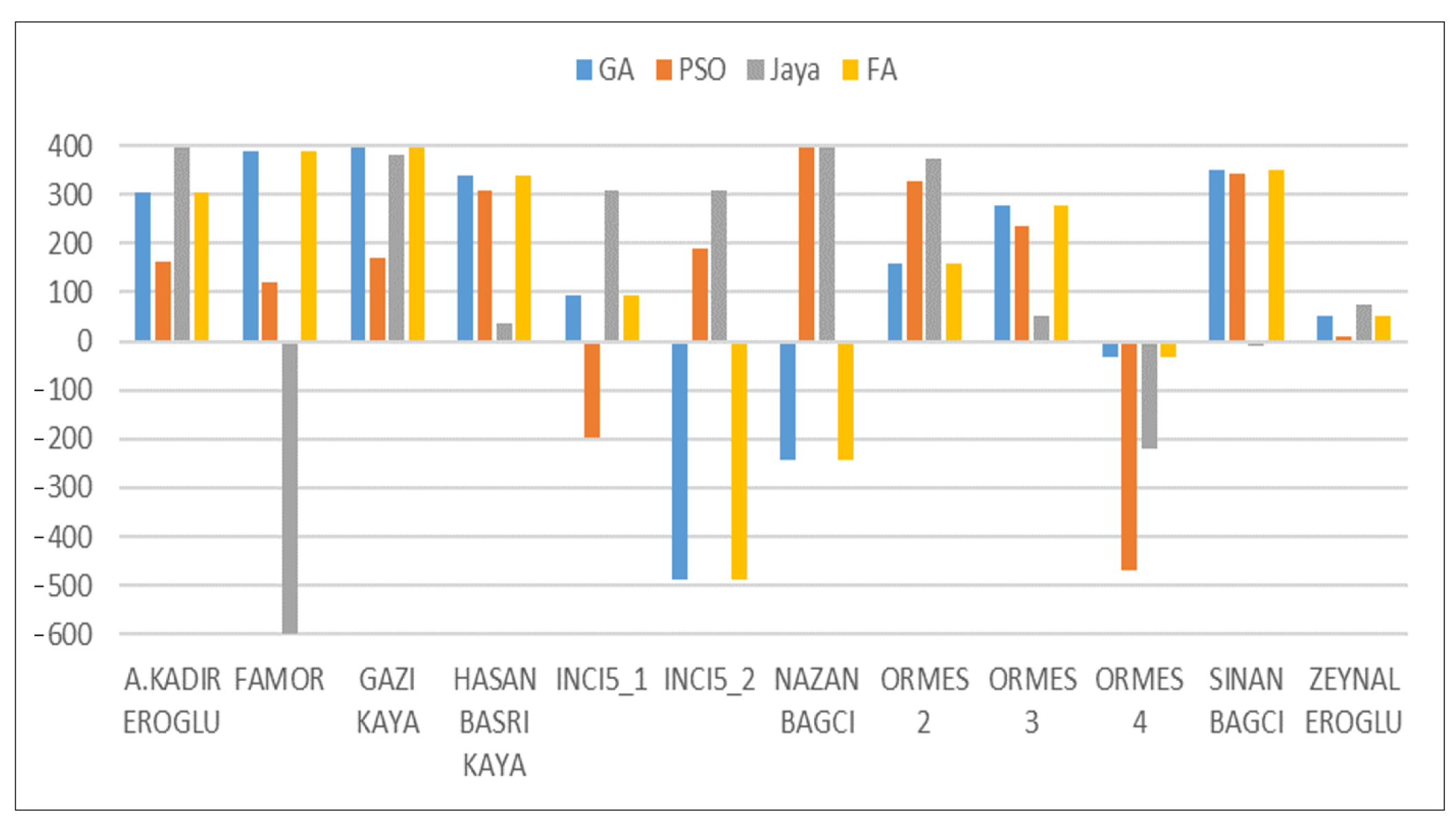
Figure 14 illustrates the reactive power support provided by each algorithm from the PV plants. Positive reactive power values indicate that a voltage drop occurred at the corresponding bus and that the PV plant is attempting to increase the voltage by generating reactive power. Negative reactive power values, on the other hand, indicate that the voltage at the bus is high and that the PV plant is trying to reduce the voltage by absorbing reactive power. Therefore, PV inverters can actively play a role in improving voltage profiles by managing reactive power during their interactions with the grid.

4. Discussion

In practical distribution networks, both solar energy generation and load demand exhibit high temporal variability. This affects the available reactive power capacity of PV inverters, which is inherently dependent on their instantaneous active power output. The optimization-based approach presented in this study is designed to handle such dynamic conditions effectively.

The optimization algorithms (PSO, GA, Jaya, and Firefly) dynamically compute reactive power setpoints for each inverter based on feeder operating conditions derived from the PowerFactory model and time-series profiles, while respecting inverter capability limits. As a result, the system can adapt to sudden changes in generation or demand without compromising the voltage profile optimization.

Additionally, a Modbus-based feasibility demonstration is included to confirm that inverter reactive power reference values can be communicated and written remotely. The implementation of a closed-loop real-time control framework that integrates online measurements and real-time optimization is considered as future work. This ensures that the optimization process remains responsive and stable, even under fluctuating solar generation or load patterns.

Therefore, the proposed method is highly suitable for deployment in modern, distributed power grids where the integration of renewable energy sources and demand-side variability requires fast, distributed, and adaptive control strategies.

In this study, the proposed algorithms were used to optimize reactive power injection under steady-state conditions with the goal of improving voltage profiles in the distribution network. However, the dynamic behavior of the system under low-voltage ride-through conditions, particularly during temporary voltage sag events, was not analyzed. Future research will focus on evaluating the performance of the proposed algorithms during LVRT scenarios and exploring their potential to enhance dynamic voltage stability by leveraging inverter-based reactive power support.

5. Conclusions

In this study, reactive power support from PV inverters was applied to a real distribution feeder with a capacity of 11.8 MW. An improvement by up to 19.9% was observed in the overall voltage deviation index. This indicates the effectiveness of the proposed framework at the system level. Moreover, local feeder analyses also revealed additional enhancements with a range between 0.87–0.96%. This confirms that the improvements are not observed only in the global indices but also at the feeder level. All four algorithms provided consistent performance, which suggests that metaheuristic-based optimization can reliably improve both local and global voltage profiles. These findings reveal that employing PV inverters as a source of reactive support in distribution networks is practical and feasible.

In future studies, the proposed framework will be extended to cover dynamic disturbance scenarios by employing additional performance indices such as feeder losses, computational efficiency, and inverter loading. Also, LSTM/deep learning methods can be integrated into PV power forecasting. In this way, performance data of the algorithms will be evaluated under closed-loop real-time operation conditions by integrating online measurements and automated setpoint updating in a more comprehensive way, rather than just using the global voltage deviation index.