Acoustic–Electric Conversion Characteristics of a Quadruple Parallel-Cavity Helmholtz Resonator-Based Triboelectric Nanogenerator (4C–HR TENG)

Abstract

This paper presents the design and fabrication of a triboelectric nanogenerator based on a Quadruple Parallel-cavity Helmholtz Resonator (4C–HR TENG) for the efficient harvesting of noise energy in marine engine room environments. The device utilizes sound waves to drive periodic contact and separation between polytetrafluoroethylene (PTFE) particles in the resonant cavity and the vibrating diaphragm as well as the upper electrode plate, thereby converting sound energy into mechanical energy and finally into electrical energy. The device consists of an acoustic waveguide with a length of 350 mm and both width and height of 60 mm, along with a Helmholtz Resonator with a diameter of 60 mm and a height of 40 mm. Experimental results indicate that under resonance conditions with a sound pressure level of 109.8 dB and a frequency of 110 Hz, the device demonstrates excellent output performance, achieving a peak output voltage of 250 V and a current of 4.85 μA. We analyzed and investigated the influence mechanism of key parameters (filling ratio, sound pressure level, the height between the electrode plates, and particle size) on the output performance. Through COMSOL Multiphysics simulation analysis, the sound pressure enhancement effect and the characteristic of concentrated diaphragm center displacement at the first-order resonance frequency were revealed, verifying the advantage of the four-cavity structure in terms of energy distribution uniformity. In practical applications, the minimum responsive sound pressure level corresponding to the operating frequency range of the 4C–HR TENG was determined. The output power reaches a maximum of 0.27 mW at a load resistance of 50 MΩ. At a sound pressure level of 115.1 dB, the device can charge a 1 μF capacitor to 4.73 V in just 32 s and simultaneously illuminate 180 LEDs in real-time, demonstrating its potential for environmental noise energy harvesting and micro-energy supply applications. This study provides new insights and experimental evidence for the efficient recovery of noise energy.

1. Introduction

With the rapid development of distributed sensing technology, a large number of sensing nodes have been deployed in fields such as environmental monitoring, industrial inspection, and smart homes [1,2,3,4]. Powering these vast numbers of miniaturized electronic devices has become a bottleneck constraining the development of sensors. Traditional chemical batteries face issues such as limited lifespan, the need for regular replacement, and potential environmental pollution, while wired power supply significantly restricts the flexibility and deployment scope of devices. Given this current situation, seeking and utilizing a clean and ubiquitous energy source provides a new direction for powering electronic devices [5,6].

Among common environmental energy sources, sound energy is widely present in human production and daily life, such as industrial noise, traffic noise, and noisy public spaces. While such sound energy is typically regarded as harmful noise to be eliminated, it inherently contains usable energy. If these waste sound energies can be efficiently captured and converted, they could not only power low-power electronic devices but also contribute to noise reduction and emission mitigation to a certain extent, offering positive implications. However, traditional electromagnetic induction-based sound energy harvesting devices generally exhibit low efficiency in converting sound waves, along with complex structures and high costs, which limit their large–scale application.

In recent years, first proposed by Wang et al. [7,8], the triboelectric nanogenerator (TENG) based on the principle of Maxwell’s displacement current has emerged as a novel energy harvesting technology, offering new perspectives for addressing micro–energy challenges [9]. TENG exhibits advantages such as a wide range of material choices, simple structure, low cost, and diverse energy conversion methods [10]. Its potential in harvesting mechanical energy, vibrational energy [11,12], wind energy, and wave energy has also been validated [13,14]. Its working principle primarily relies on the coupling effect of contact electrification and electrostatic induction, which effectively converts slight mechanical disturbances into electrical energy [15,16,17]. Currently, acoustic energy–driven TENGs based on structures such as thin–film vibration and cavity resonance demonstrate significant potential [5,18,19,20,21,22]. However, existing designs still face several challenges: the acoustic–to–electric conversion efficiency requires further enhancement [23,24,25,26]; the effective operating bandwidth of the device is relatively narrow, making it sensitive to sound frequency; the influence patterns of environmental acoustic parameters on output performance remain unclear, and systematic optimization studies are lacking [27,28,29,30].

To address the aforementioned issues, this paper designs and fabricates a triboelectric–acoustic energy hybrid harvesting device based on granular dielectric materials. This device converts the air vibrations caused by sound waves into mechanical vibrations through a diaphragm, which in turn drives specially designed granular media within the cavity to undergo collisions and friction, thereby achieving efficient conversion of sound energy into electrical energy. As shown in Figure 1a, noise energy is collected and utilized under ship cabin and traffic environmental conditions.

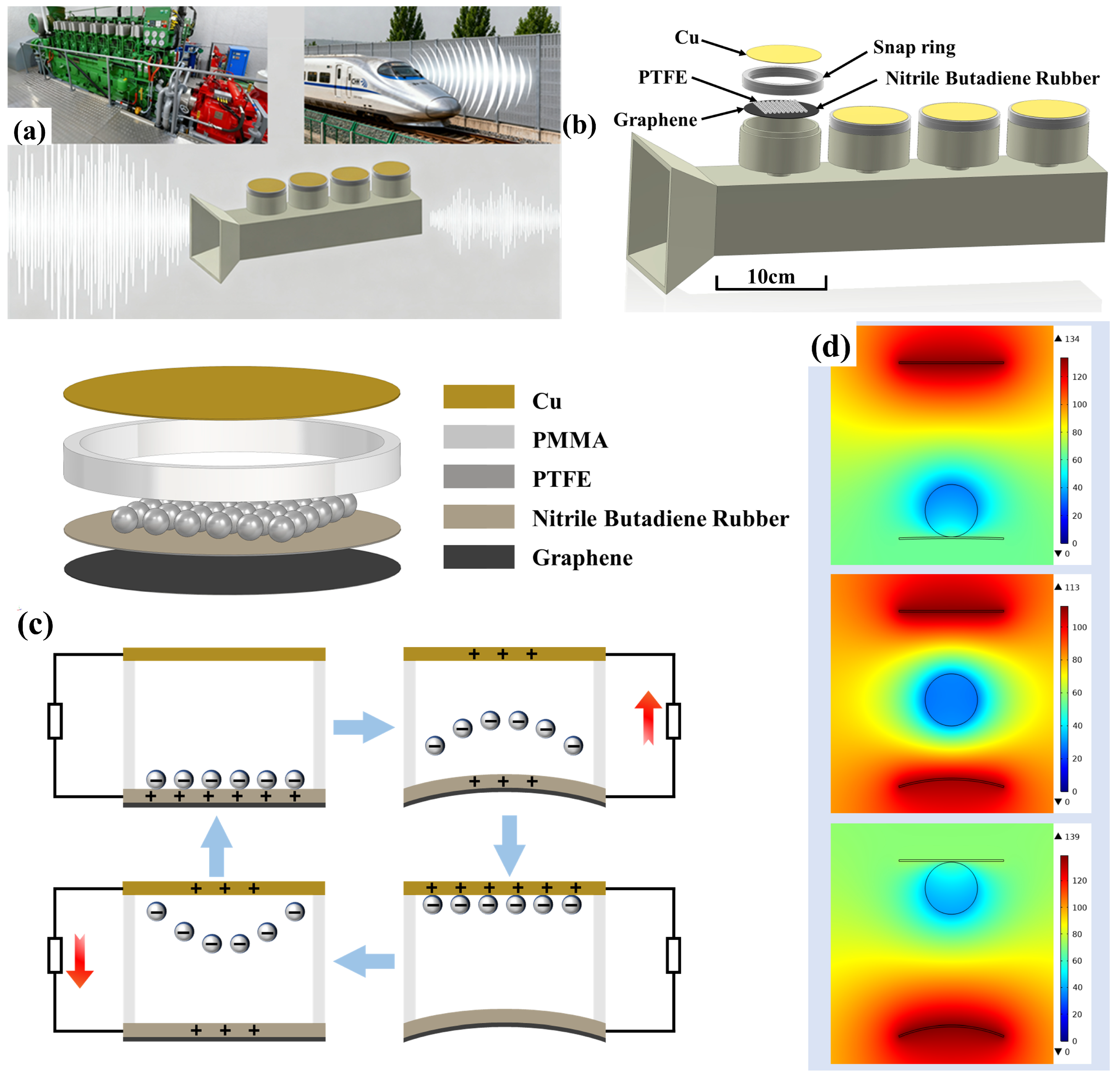
2. Working Principle and Simulation Analysis

2.1. Theoretical Analysis and Output Performance Simulation

As shown in Figure 1b, sound wave transmission induces periodic pressure changes within the Helmholtz resonant cavity, causing the diaphragm to vibrate and thereby driving the particles to oscillate vertically. Figure 1c illustrates the working principle of the 4C–HR TENG. As the particles come into contact with the diaphragm, electrons transfer from the surface of the diaphragm to the PTFE particles due to the stronger electron affinity of the PTFE material. At this moment, the diaphragm, serving as the lower electrode plate, and the surface of the PTFE particles carry equal amounts of positive charges and triboelectric negative charges, respectively. When the PTFE particles vibrate and move upward, the distance between the particles and the lower electrode plate increases, weakening the interaction between the negative charges on the particle surfaces and the lower electrode plate. As a result, the potential of the lower electrode plate becomes higher than that of the upper electrode plate, generating an instantaneous current from the lower electrode to the upper electrode. Positive charges are thus transferred from the lower electrode plate to the upper electrode plate through the external circuit. When the PTFE particles come into contact with the upper copper sheet, the charge transfer is completed. As the PTFE particles move away from the copper sheet and gradually approach the lower electrode plate, this reverse motion causes the triboelectric charges to transfer in the opposite direction through the external circuit. Similarly, an instantaneous current is generated in the external circuit, flowing from the upper electrode plate to the lower electrode plate. At this point, the triboelectric nanogenerator completes one full operating cycle. Subsequently, due to the continuous action of the sound waves, the diaphragm vibrates again, causing particle displacement and initiating another power generation cycle.

The electric field distribution diagram shown in Figure 1d can be obtained through simulation. It can be observed from the figure that the electric potential (open-circuit voltage) varies with the displacement of the particles. Charges are uniformly distributed on the inner surface of the particles, forming an electric field between the upper electrode plate, the lower electrode plate, and the interior of the particles. The magnitude of the transferred charge determines the strength of the electric field. Under a constant electric field strength, the electric potential is proportional to the separation distance between the triboelectric layers. Therefore, the electric potential also changes with particle displacement.

2.2. Model Analysis

Sound Pressure Level (SPL) is a physical quantity used in acoustics to measure the intensity or strength of a sound. It is a logarithmic scale that represents the ratio of the effective sound pressure to a reference sound pressure.

$$L_p=20{\log }_{10}\left({\displaystyle \frac{p_{\mathrm{rms}}}{p_{\mathrm{ref}}}}\right)\mathrm{dB}$$

(1)

where L_p is the sound pressure level, p_rms is the root–mean–square (effective) sound pressure, and p_ref is the reference sound pressure.

Sound waves enter through the opening of the sound waveguide. When the frequency of the sound source is below the cutoff frequency of the waveguide, only a single plane wave can propagate within the tube. The cut-off frequency corresponds to the lowest non-zero normal frequency. For a rectangular sound waveguide propagating waves along its length, the normal frequencies are given by:

$$f_{n_x{n}_y}={\displaystyle \frac{c_0}{2}}\sqrt{{\left({\displaystyle \frac{n_x}{l_x}}\right)}^2+{\left({\displaystyle \frac{n_y}{l_y}}\right)}^2}$$

(2)

In this equation: l_x represents the width of the waveguide, l_y represents the height of the waveguide, and c₀ is the speed of sound in air. Different normal waves will be obtained for different values of $\left(n_x,n_y\right)$. In this experiment, the sound waveguide is designed with identical height and width. Therefore, the (0,1) mode is selected as the subject of study. Given l_x = 0.06 m, l_y = 0.06 m, n_x = 0, n_y = 1, and c₀ = 343 m/s², substituting these values into the equation above yields f_c = 2858 Hz. Consequently, when the sound source frequency is below the cutoff frequency of 2858 Hz, the designed experimental setup will only propagate a single plane wave along the length direction of the waveguide.

In the sound waveguide, when the loudspeaker begins to operate and emits sound waves, these waves enter the waveguide and continue to propagate. Upon striking the baffle at the end of the waveguide, they are reflected back. The superposition of the incident and reflected waves forms a standing wave. Positions with maximum sound pressure amplitude are referred to as antinodes, while positions with zero sound pressure amplitude are called nodes. The sound pressure of the standing wave is expressed as:

$$p=2p_{re}\cos kx{e}^{j\omega t}+\left(p_{ia}-p_{ra}\right)e^{j\left(\omega t-kx\right)}$$

(3)

The energy of a standing wave does not propagate outside the waveguide but undergoes periodic conversion between antinodes and nodes. It can also form a stable planar standing wave within a specific frequency range. Essentially, a rectangular sound waveguide is a structure that confines the direction of sound wave propagation, enabling directional transmission of sound waves through its specific geometric configuration.

For the basic structure of the triboelectric nanogenerator part in the 4C–HR TENG device, let d₁ represent the diameter of the PTFE particles, x denote the displacement of the particles away from the lower electrode plate, and the distance between the electrode plates be g + d₁, where g is the air gap, which also represents the maximum distance the particles can travel. Charge transfer occurs when the particles contact the electrode plate. To simplify the analysis, the TENG device can be modeled as two dielectric parallel plates, each with an area S, a separation distance of d₁, and carrying an identical charge density of –σ. Due to charge conservation, the amount of positive charge on the upper and lower electrode plates should equal the total negative charge on the particles, which is 2σ.

Assume the charge on the upper electrode is Q₁ and that on the lower electrode is Q₂, then Q₂ = 2σ − Q₁. In this case, a uniform electric field perpendicular to the charged plane exists within the particles and the air gap, with the positive direction defined as pointing toward the upper electrode plate. According to Gauss’s theorem, the electric field strength in each part of the 4C–HR TENG can be expressed as follows:

Between the upper electrode plate and the upper surface of the particle:

$$E_1=-{\displaystyle \frac{{\sigma }_1}{{\epsilon }_0}}$$

(4)

where ${\sigma }_1={\displaystyle \frac{Q_1}{s}}$ is the surface charge density on the upper electrode plate, and ε₀ is the vacuum permittivity.

Inside the particles:

$$E_2={\displaystyle \frac{\sigma -{\sigma }_1}{{ϵ}_0{ϵ}_r}}$$

(5)

Between the lower electrode plate and the lower surface of the particles:

$$E3={\displaystyle \frac{{\sigma }_2}{{ϵ}_0}}={\displaystyle \frac{2\sigma -{\sigma }_1}{{ϵ}_0}}$$

(6)

where ε_r is the relative permittivity of the PTFE material. Based on the equations above, the potential difference between the upper and lower electrodes can be expressed as:

$$\begin{array}{cc}\hfill V& =-\left[{\displaystyle \frac{2\sigma -{\sigma }_1}{{ϵ}_0}}·x+{\displaystyle \frac{\sigma -{\sigma }_1}{{ϵ}_0}}·d_1+\left(-{\displaystyle \frac{{\sigma }_1}{{ϵ}_0}}\right)·(g-x)\right]\hfill \\ & ={\displaystyle \frac{1}{{ϵ}_0}}\left[{\sigma }_1(d_1+g)-\sigma (2x+d_1)\right]\hfill \end{array}$$

(7)

This expression for the potential difference indicates that V varies linearly with the particle displacement x and depends on the charge density σ₁ of the upper electrode plate. Under open-circuit conditions, σ₁ is constant, and thus V varies solely with x. However, under short-circuit or other circuit conditions, σ₁ may vary with x, requiring a solution that couples this equation with the circuit equations. This model provides the theoretical foundation for analyzing TENG performance.

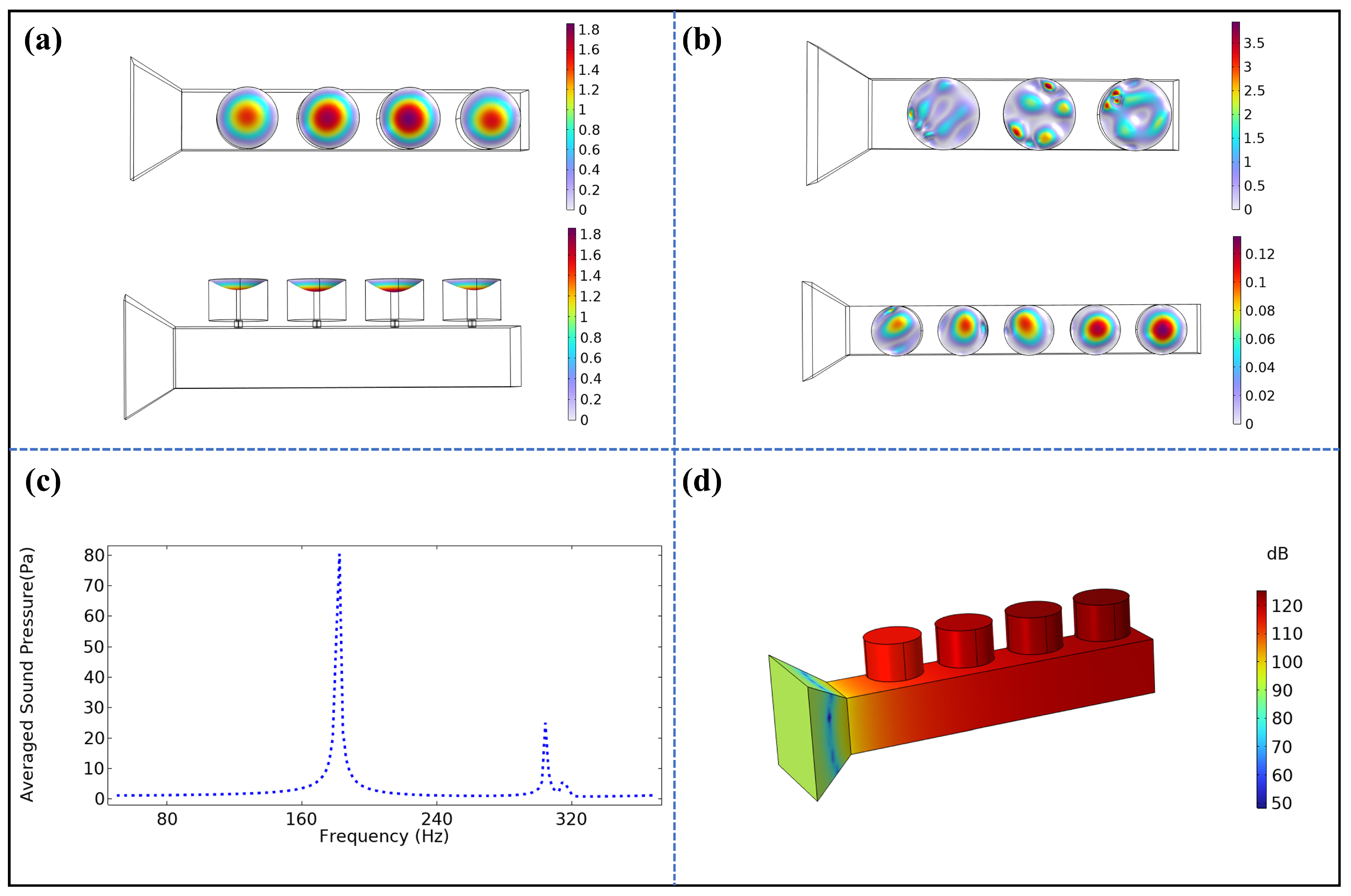
2.3. Simulation Analysis of Diaphragm Displacement Characteristics and Acoustic Performance

The Helmholtz Resonator, serving as a key structure for acoustic energy focusing and amplification, can enhance mechanical vibrations through resonance effects, thereby providing energy input for the 4C–HR TENG. In this paper, COMSOL Multiphysics 6.3 is employed to construct a three-dimensional model of the device, which includes a conical energy concentrator, an acoustic waveguide, and the Helmholtz Resonator.

The contour plot of the diaphragm cross-sectional displacement for the experimental setup is shown in Figure 2. For the device simulation, the sound source was defined as a pressure input in COMSOL. Specifically, the pressure at the input boundary was set as the function: 1 + linper(1) Pa, where the linper function represents a linear perturbation. For the 4C–HR TENG device, after sound wave incidence, the displacement amplitude is maximum at the central region of the diaphragm and gradually attenuates towards the edges. This distribution occurs because the central area, being free from structural constraints, responds more readily to sound pressure excitation; while the edges, subjected to the fixed constraints of the cavity boundary, have their displacement suppressed. This demonstrates the effect of sound wave energy concentrating towards the center of the diaphragm. The longitudinal cross-sectional displacement distribution exhibits a characteristic of being higher in the center and lower at the edges, with the maximum diaphragm displacement amplitude reaching approximately 1.8 mm. This confirms that when sound waves propagate within the waveguide, the energy can be uniformly distributed to each resonator.

Figure 2b presents the displacement simulation diagrams for the 3C–HR TENG device and the 5C–HR TENG device under the same acoustic source, at their first-order resonant frequencies of 220 Hz and 150 Hz, respectively. As can be observed from the figure, although the 3C–HR TENG device achieves the highest displacement amplitude, reaching 3.7 mm, its limited number of cavities results in significantly poor uniformity and stability, leading to an uneven distribution of energy. Figure 2b presents the displacement simulation diagrams for the 3C–HR TENG device and the 5C–HR TENG device under the same acoustic source, at their first-order resonant frequencies of 220 Hz and 150 Hz, respectively. It can be observed from the figure that although the 3C–HR TENG device achieves the highest displacement amplitude, reaching 3.7 mm, its limited number of resonant cavities results in significantly poor uniformity and stability, leading to an uneven energy distribution. In contrast, while the 5C–HR TENG device has a larger number of resonant cavities, its diaphragm displacement amplitude reaches only 0.13 mm, and the displacement distribution is relatively dispersed across the five cavities, with each cavity’s area of concentrated displacement being quite small. Consequently, it fails to effectively focus energy within specific regions, which negatively impacts the device’s operational efficiency and overall performance. Compared to the two structures mentioned above, the displacement distribution of the 4C–HR TENG exhibits superior uniformity and symmetry. The uniform displacement distribution effectively concentrates energy within the target region, resulting in a pronounced displacement focusing effect. This ensures the four-cavity structure plays a favorable role in energy transfer efficiency. Furthermore, it enhances the overall reliability and service life of the device while maintaining its performance. The simulations demonstrate that the four-cavity Helmholtz resonance structure can effectively capture sound wave energy and drive diaphragm vibration.

An acoustic–structure coupled multiphysics simulation environment was established to conduct the analysis. The variation curve of the Averaged sound pressure with frequency is shown in Figure 2c. The device exhibits a sound pressure peak of approximately 80 Pa at around 182 Hz, indicating that this frequency corresponds to the first-order resonance frequency of the device. At this first-order resonance frequency, the schematic diagram of the sound pressure level of the device is presented in Figure 2d. The occurrence of the first-order resonance frequency indicates that the incident sound wave frequency matches the natural frequency of the Helmholtz Resonator. This results in a sharp increase in sound pressure within the cavity, driving the diaphragm within the resonator into motion and thereby converting the acoustic mechanical energy into vibrational energy. A discrepancy exists between the experimentally measured resonance frequency of the device (110 Hz) and the simulation results for the empty cavity state (182 Hz). This discrepancy primarily stems from two factors: (1) The simulation model did not account for the mass of the PTFE particles, whereas in the experiments, the substantial number of particles filling the four resonant cavities significantly increased the equivalent damping of the vibration system. According to the resonance frequency formula for a mass-spring system: $f={\displaystyle \frac{1}{2\pi }}\sqrt{{\displaystyle \frac{k}{m}}}\sqrt{1-2{\zeta }^2}$ (where $\zeta$ is the damping ratio), an increase in mass will cause the resonance frequency to shift to lower frequencies. (2) During the fabrication and assembly of the device, inevitable dimensional tolerances and assembly stresses also affect the resonance frequency. Therefore, the experimental resonance frequency is lower than the simulation predicted value.

3. Results and Discussion

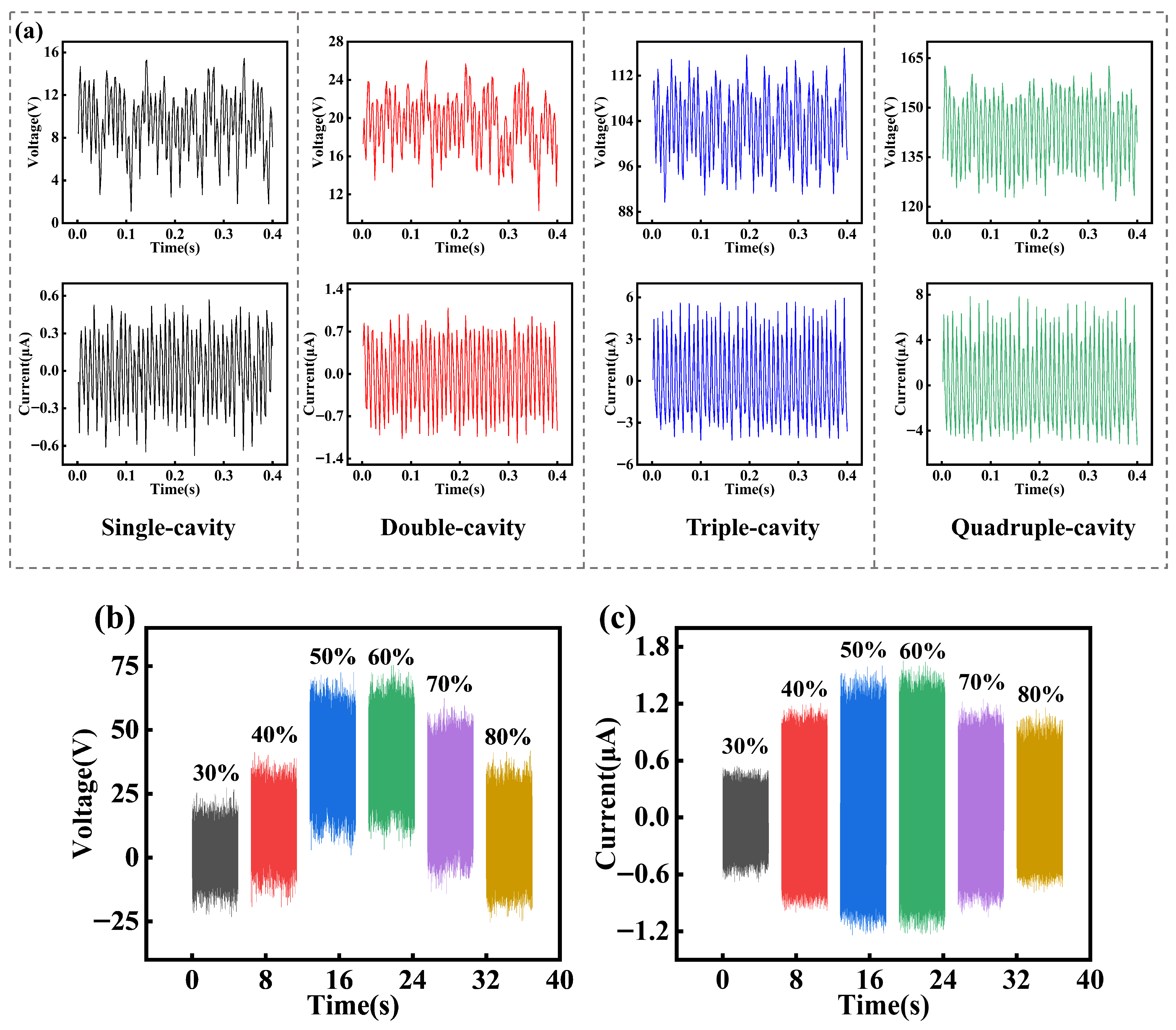
3.1. Influence of Filling Ratio

To investigate the impact of the number of resonant cavities and the filling ratio on the output performance of the 4C–HR TENG, the study separately considers varying the number of resonant cavities and the quantity of particles. As shown in Figure 3a, the number of device resonant cavities is modified, increasing successively from a single cavity to four cavities, while measuring the corresponding voltage and current output variation curves of the device. Under the conditions of a 50% filling ratio and a sound pressure level of 109.4 dB, tests were conducted on a single cavity (the first chamber), yielding a peak voltage of approximately 14 V and a peak current of 0.5 μA. As multiple cavities were connected in parallel, with each cavity set to a 50% filling ratio, the peak voltage reached 160 V and the peak current reached 6 μA in the four-cavity parallel configuration. As can be seen from the figure, the output performance improves with the increase in the number of parallel cavities due to the enlarged contact area between the particle medium and the electrode.

The effective area of the electrode is defined as [9]:

$$S_{pellets}=n\left(\pi r^2\right)N$$

(8)

where n is the number of particles in each cavity, r is the particle radius, and N is the number of cavities. According to the structure of the 4C–HR TENG device, the effective area corresponds to the bottom area of the Helmholtz Resonator cavity, which is 28.26 cm². Based on the number of particles and the bottom area of the cavity (S_hole), the filling ratio (F) of the device can be obtained. The filling ratio can be calculated using the following equation:

$$\mathrm{F} = {\mathrm{S}}_{\mathrm{pellets}}/{\mathrm{S}}_{\mathrm{hole}}$$

(9)

Under the conditions of 105.9 dB at 110 Hz, with an equal number of particles filled in each of the four cavities, the influence of the filling ratio of the Helmholtz resonance cavity (ranging from 30% to 80%) on the output voltage and current is shown in Figure 3b,c. At a 30% filling ratio, the voltage is 24.8 V and the current is 0.5 μA. The particle vibration is restricted, resulting in low output levels. When the filling ratio reaches 50% to 60%, the output voltage reaches its optimum range of 70.98–73.8 V, with a current of approximately 1.5 μA. At this point, the number of particles is well-matched to the structural space, achieving optimal coupling between vibration and friction, leading to high output levels. When the filling ratio increases to 70% and 80%, the output voltage drops to 58.7 V and 39.5 V, respectively, while the output currents are 1.1 μA and 0.9 μA. At these higher filling ratios, the increased number of particles intensifies the friction damping, leading to greater energy loss and consequently reduced output.

The effect of filling ratio on device output: At low filling ratios (<50%), excess particle motion space results in insufficient frictional contact. At the optimal filling ratio (50–60%), the vibration frequency and amplitude of the particles match the structural resonance, maximizing the triboelectric effect. However, at high filling ratios, particle collisions reduce the transmission of effective vibrational energy, leading to energy loss.

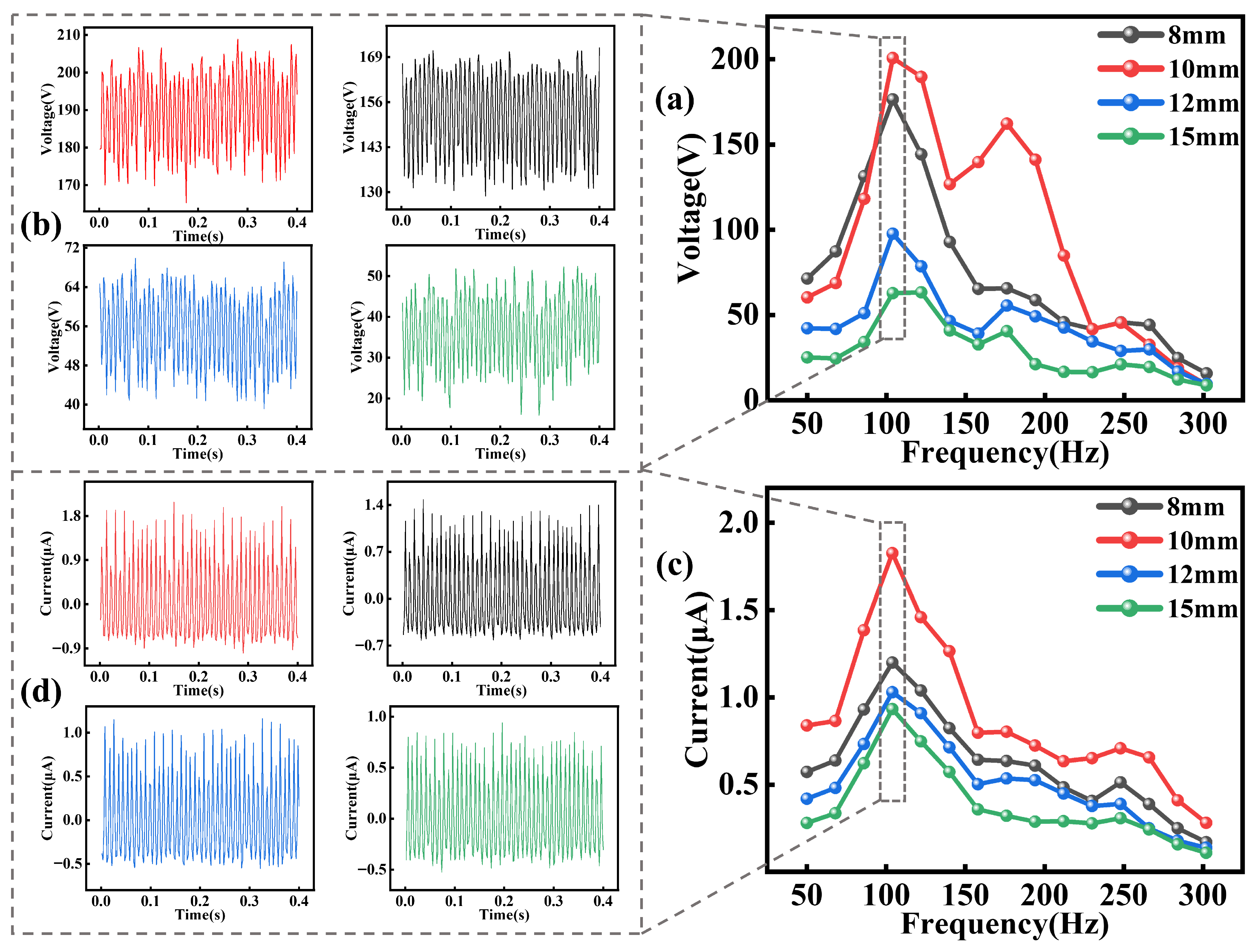
3.2. Height Between the Electrode Plates

By altering the height of the snap ring, the output performance of the device under different inter-electrode plate distances was investigated. As shown in Figure 4, the frequency response curves are compared for four different heights (8–15 mm), with a fixed quantity of 120 particles per cavity and a sound pressure level of 107.6 dB. Figure 4b,d present the voltage and current variations for these four different snap ring heights at the resonance frequency of 110 Hz.

As shown in Figure 4a,c, at a height of 8 mm within the operating frequency range, the peak voltage and current reach 176 V and 1.2 μA, respectively. This indicates that the excessively small gap between the electrode plates restricts the vibration space for the particles, leading to insufficient friction. At a height of 10 mm, the device achieves optimal output performance, characterized by a distinct frequency response. The voltage and current peaks reach 200 V and 1.8 μA, respectively. This specific spacing provides the particles with an appropriate degree of freedom for movement, allowing them to vibrate fully under acoustic wave excitation. Consequently, this enables a larger displacement in the contact-separation process, thereby enhancing charge transfer. Furthermore, at this gap, the coupling effect between particle vibration and triboelectrification is significantly improved. In the case of a 12 mm height, the peak voltage of the device drops to approximately 95 V, and the effective operating frequency range narrows. The increased distance between the electrode plates weakens the electric field coupling strength. At a height of 15 mm, the voltage fluctuations are significant, with a peak around 60 V, but the output decays rapidly and exhibits poor stability. This indicates that an excessively large gap disrupts the vibration–friction balance. The figure illustrates the differential impact of electrode plate height on the frequency–voltage characteristics.

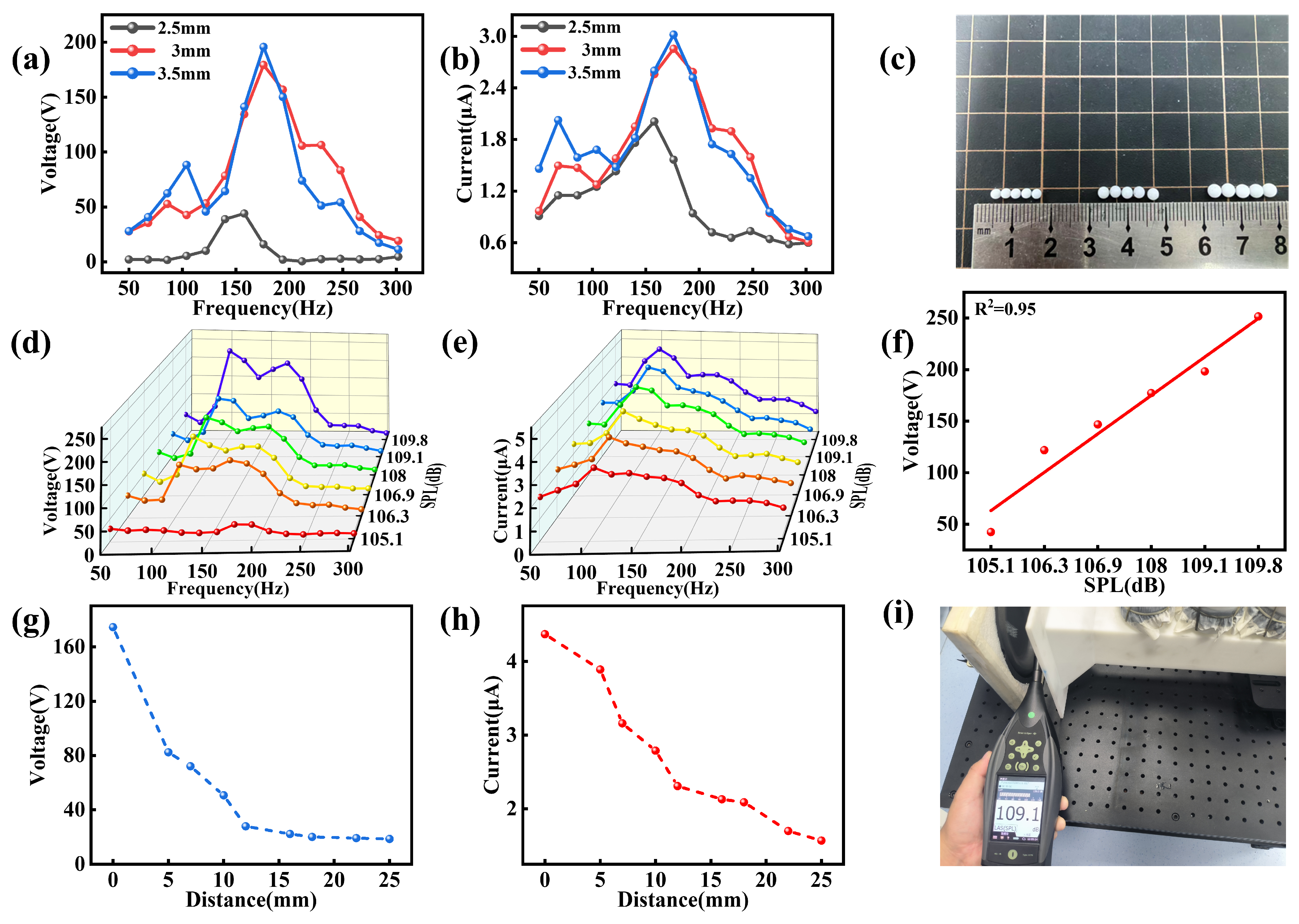
3.3. Influence of Particle Size on the Power Generation Characteristics of the 4C–HR TENG

To elucidate the impact of particle size on the 4C–HR TENG, this section investigates the variations in output current and voltage with different particle sizes. As shown in Figure 5a,b, tests were conducted under single-cavity (first chamber) conditions with a sound pressure level of 115.2 dB, an inter-electrode distance of 10 mm, and a filling ratio of 55%. PTFE particles with diameters of 2.5 mm, 3 mm, and 3.5 mm were used, and the output voltage and current were measured across the 50–300 Hz frequency range. Figure 5c shows photographs of the three particle sizes.

Figure 5a shows the variation of peak output voltage with frequency. Within the 50–140 Hz range, the output voltages for all three PTFE particle sizes were relatively low and increased slowly. As the frequency rose above 140 Hz, for the 3.5 mm particles, the voltage initially increased rapidly with frequency, reaching a maximum of 195.7 V at 182 Hz, and then decreased sharply with further frequency increase. The voltage for the 3 mm particles was slightly lower than that for the 3.5 mm particles, reaching a maximum of 179.3 V at 182 Hz, and declined more gradually afterwards compared to the 3.5 mm particles. The voltage for the 2.5 mm particles was the lowest, with its frequency response curve showing little fluctuation, a maximum voltage around 44 V, and a relatively gentle overall response. The current curves are shown in Figure 5b. The trend of the current variation curves generally follows that of the voltage curves. In the frequency range of 50–140 Hz, the currents generated by the three PTFE particle sizes are all at a low level. As the frequency increases, the 3.5 mm PTFE particles reach a maximum current of approximately 3.02 μA at 182 Hz, while the 3 mm particles achieve 2.8 μA and maintain a relatively stable output. The 2.5 mm particles reach their peak value of 1.56 μA at 164 Hz, after which the current drops rapidly.

Based on the experimental data, this study reveals that particle size affects the output by altering the vibration characteristics and contact conditions. The analysis indicates a non-monotonic dependence of output voltage on particle size, among which the 3 mm particles exhibit relatively superior comprehensive performance. The 3.5 mm particles have larger mass and volume, resulting in a larger contact area with the electrode plates. Under acoustic excitation, they are prone to resonate with the structure, achieving the maximum vibration amplitude near the matched frequency (around 182 Hz), which leads to a pronounced triboelectric effect and consequently higher peak voltage and current. However, at higher frequencies, they struggle to respond quickly to frequency changes, causing rapid attenuation in voltage and current. The 3 mm particles exhibit better vibration–friction synergy. Although their peak output voltage and current are slightly lower than those of the 3.5 mm particles, they offer a wider effective operating frequency band and maintain a good response between 150–300 Hz. Due to their smaller mass and volume, the 2.5 mm particles experience more dispersed vibrational energy and insufficient triboelectric contact, resulting in overall limited voltage output.

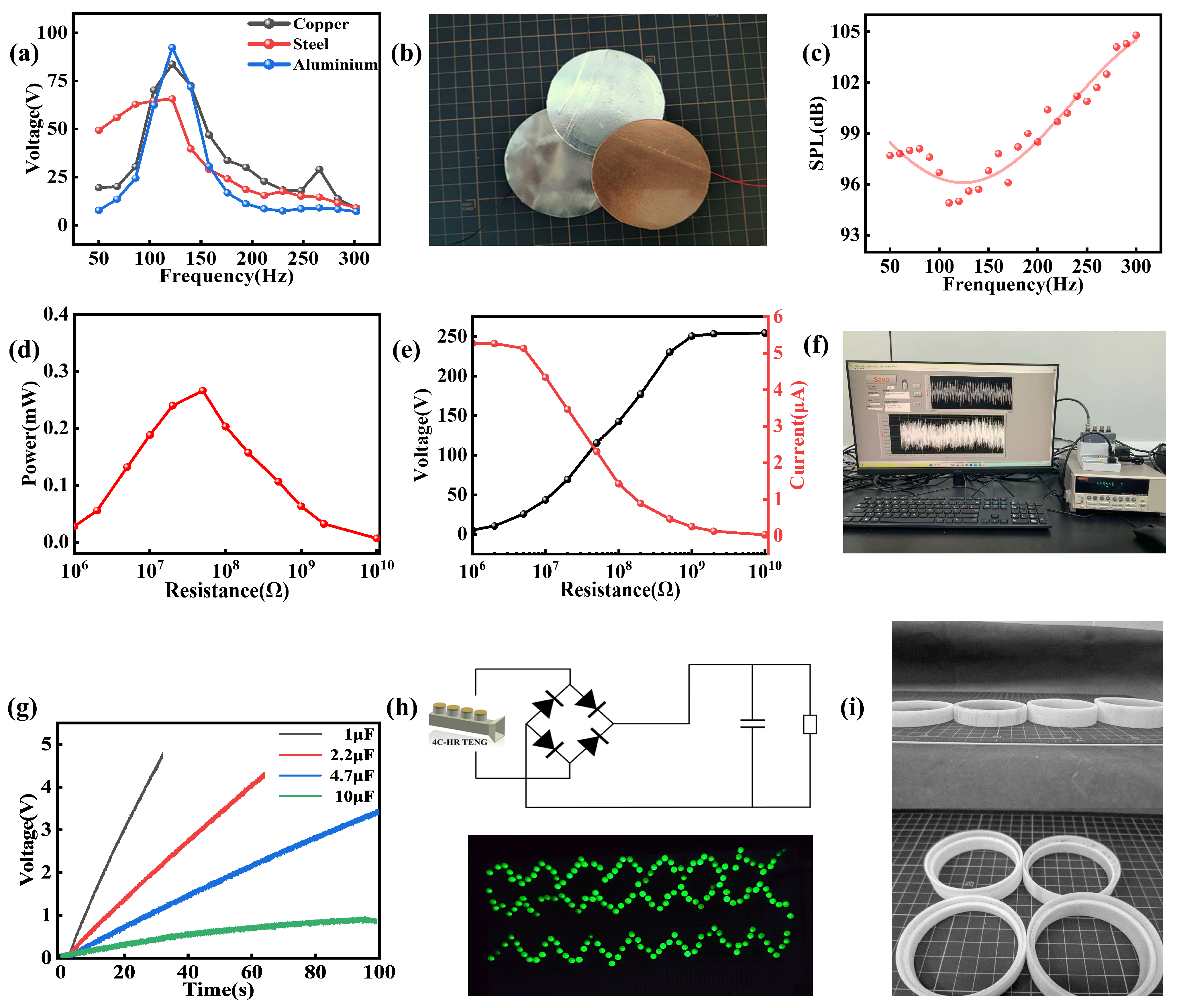
3.4. Acoustic Source Characteristics of 4C–HR TENG

Figure 5d,e illustrates the variation curves of the output voltage and current of the 4C–HR TENG device across the 50–300 Hz frequency range under different sound pressure levels (SPL). To investigate the electrical output characteristics of the 4C–HR TENG under acoustic excitation, the output voltage and current responses of the device were measured using a sound level meter. Measurements were taken across the 50–300 Hz frequency range at different SPL (105.1 dB to 109.8 dB) by controlling the SPL and frequency. At the same frequency, the output voltage shows a significant increasing trend as the SPL rises. At 110 Hz, when the SPL is increased from 105.1 dB to 109.8 dB, the peak output voltage rises from approximately 42 V to nearly 250 V. Figure 5d,e shows the output voltage and current curves of the 4C–HR TENG device across a 50–300 Hz frequency range under different sound pressure levels (SPL). To investigate the electrical output characteristics of the 4C–HR TENG under acoustic excitation, the output voltage and current responses of the device were measured using a sound level meter by controlling the SPL and frequency within the 50–300 Hz range at various SPL (105.1 dB to 109.8 dB). At a given frequency, the output voltage shows a significant upward trend as the SPL increases. Specifically, at 110 Hz, when the SPL rises from 105.1 dB to 109.8 dB, the peak output voltage increases from approximately 42 V to nearly 250 V.

Below 110 Hz, the system is not in resonance, and the diaphragm vibration strengthens with increasing frequency. Above 110 Hz, the acoustic wavelength shortens, the acoustic impedance of the resonator increases, and the damping effect on particle vibration intensifies, leading to voltage attenuation. This indicates that around 110 Hz is the optimal response range of the device to acoustic excitation. When the sound source frequency matches the device’s resonance frequency, the conversion efficiency from mechanical to electrical energy reaches its maximum, thereby producing the peak output voltage. Figure 5e presents the frequency–SPL response pattern of the output current, which is highly consistent with the voltage characteristics. At 110 Hz, the current increases with rising SPL, from 3.3 μA to 4.85 μA.

As shown in Figure 5f, with 3 mm particles and a filling ratio of 55%, the output voltage reaches 42 V when the SPL is fixed at 105.1 dB. As the SPL increases, the output voltage of the 4C–HR TENG is enhanced. When the SPL reaches 109.8 dB, the output voltage attains 250 V. The linear correlation coefficient between the output voltage and the SPL is 0.95, which directly verifies the positive correlation between the input sound energy intensity and the output electrical amplitude.

To further evaluate the impact of varying the distance from the sound source on the output of the 4C–HR TENG, the electrical output shown in Figure 5g,h was measured under conditions of 110 Hz and 109.1 dB. As the distance increased from 0 mm to 25 mm, a dramatic reduction in output performance is observed, with voltage plummeting by 89.3% (from 174.5 V to 18.6 V) and current declining by 64.1% (from 4.37 μA to 1.57 μA). The test results show that as the distance from the sound source increases from 0 mm to 25 mm, the device’s output voltage and current significantly decrease. This variation essentially stems from the attenuation of the received sound pressure at the inlet. The underlying reason lies in the fact that, in a spherical sound field, sound pressure is inversely proportional to the propagation distance. The increase in distance leads to a reduction in the sound pressure acting on the device inlet, thereby causing a decline in the electrical output.

The experimental results indicate that the electrical output characteristics of the 4C–HR TENG are closely related to parameters such as the frequency, SPL, and distance of the sound source. A resonance effect is observed at 110 Hz, and the output amplitude significantly increases with higher SPL. As the distance from the sound source increases, the excitation intensity weakens. At lower SPL, the driving force of the sound waves is insufficient, restricting particle vibration and resulting in a weak triboelectric effect. As the SPL increases, the acoustic excitation on the particles strengthens, leading to an increase in particle vibration amplitude, enhanced transfer of triboelectric charges, and improved energy transfer efficiency, which correlates positively with the voltage output. With the increase in SPL, both the voltage and current rise accordingly. This observed pattern provides experimental support for optimizing the device’s performance.

3.5. Material of the Upper Electrode Plate

To investigate the influence of electrode plate materials on the 4C–HR TENG, the effects of three different materials on the output voltage were compared. Figure 6b shows photographs of the three materials. From the voltage variation curve in Figure 6a, it can be observed that in the low–frequency range (50–100 Hz), the steel sheet exhibits a higher voltage output, starting at 49.32 V at 50 Hz and reaching approximately 64.64 V at 100 Hz. The voltage output of the aluminum sheet increases relatively slowly within this frequency range, rising from about 7.73 V to 62.41 V. The voltage output of the copper sheet also increases from 20 V to around 70 V.

When the frequency increases to 100–150 Hz, the voltage output of the aluminum sheet rises rapidly, reaching a peak of 92.22 V at 110 Hz, which is higher than that of the copper and steel sheets. The voltage output of the copper sheet is approximately 83.69 V at 110 Hz, while that of the steel sheet is about 65.62 V. In the 150–300 Hz frequency band, the voltage outputs of all three materials show a declining trend. The voltage drop of the aluminum sheet is the most pronounced, decreasing from a peak of 90 V to 7.11 V. The voltage output of the copper sheet declines more slowly compared to the other materials, reaching 8.93 V. The voltage output of the steel sheet decreases relatively steadily to 9.01 V. Overall, these results align with the triboelectric series of the materials regarding static charge generation. The aluminum sheet performs best within a narrower frequency range, the steel sheet responds well in the low–frequency band but has limited applicability and a smaller peak output. Although the peak output of the copper sheet is slightly lower than that of the aluminum sheet, it offers a broader response bandwidth and a slower decline, demonstrating more stable performance across the 100–300 Hz range and thus being more suitable for practical applications.

In summary, the material of the upper electrode plate significantly influences the output voltage of the triboelectric nanogenerator. Although the aluminum sheet exhibits the highest peak voltage near 110 Hz, its effective operating bandwidth is relatively narrow. While the copper sheet has a slightly lower peak voltage, it maintains stable output across a wide frequency range of 100–300 Hz, demonstrating superior environmental adaptability and thus being regarded as the optimal choice. This provides important guidance for optimizing the design of triboelectric nanogenerators and improving their energy harvesting efficiency. Future research can further explore the effects of factors such as material surface treatment and structural design on the performance of the 4C–HR TENG, aiming to achieve higher energy conversion efficiency.

3.6. Applications

Figure 6c illustrates the minimum sound pressure level (SPL) response characteristics of the 4C–HR TENG across frequencies, specifically showing the response threshold within the 50–300 Hz range. The measured data points are marked as red scatter plots, and the fitted curve reveals the response pattern. The results demonstrate that the acoustic response of the TENG exhibits a distinct ‘U-shaped’ distribution: in the 50–120 Hz interval, the SPL monotonically decreases with increasing frequency, reaching a minimum of 94.9 dB at 110–120 Hz. Beyond 120 Hz, the SPL increases nonlinearly with frequency, rising to 104.7 dB at 300 Hz, representing an increase of 9.8 dB.

Figure 6d,e shows the variation trends of the output power, output current, and output voltage of the 4C–HR TENG with respect to the load resistance. As can be seen from the figures, the voltage increases with rising resistance, from 5.2 V to 254 V. When matched with different external load resistances, the output power of the 4C–HR TENG first increases and then decreases with the load resistance, reaching a maximum of 0.27 mW at a matched load resistance of 50 MΩ.

As an acoustic energy harvesting device with excellent output performance, the 4C–HR TENG exhibits significant application potential. To demonstrate its capability under sound pressure excitation, we conducted an application validation at an SPL of 115.2 dB. As shown in Figure 6g, the charging characteristics and circuit diagrams for different capacitors (1 μF, 2.2 μF, 4.7 μF, and 10 μF) are presented. The AC output of the 4C–HR TENG is applied to both ends of the capacitor via a rectifier bridge, storing electrical energy in the capacitor. For the 1 μF capacitor, the charging rate is the fastest, reaching 4.73 V within 32 s. The 2.2 μF capacitor requires 60 s to charge, eventually stabilizing at 4.3 V. The 4.7 μF capacitor reaches about 3.3 V in 100 s. Smaller capacitors are suitable for rapid storage of instantaneous noise energy, while larger capacitors rely on sustained noise energy input for accumulation. Figure 6h shows the device powering 180 LEDs in real time, fully demonstrating its output capacity and reliability.

4. Experimental Section

4.1. Fabrication of the 4C–HR TENG

The 4C–HR TENG device comprises a sound energy harvesting unit and a sound–electricity conversion unit. The sound energy harvesting unit consists of a tapered concentrator and an acoustic waveguide. The sound–electricity conversion unit is composed of a Helmholtz Resonator and a triboelectric nanogenerator (TENG) utilizing PTFE particles as the working medium.

The Helmholtz Resonator features a neck diameter of 17 mm, a neck height of 7 mm, a cavity diameter of 60 mm, and a cavity height of 40 mm. The upper electrode is a 0.1 mm-thick copper sheet, while the lower electrode is a 0.1 mm-thick diaphragm (Nitrile Butadiene Rubber, NBR) coated with graphene, where the graphene serves as the conductive layer. The gap between the electrodes is defined by the height of the snap ring (8–15 mm). Under standard conditions, the cavity is filled with PTFE particles of 3 mm in diameter.

The tapered concentrator has a cone angle of 30° to enhance acoustic energy focusing. The acoustic waveguide, which connects the sound source to the resonant cavity, has a length of 350 mm and a cross-section of 60 mm × 60 mm. This configuration constitutes the sound energy harvester: the 4C–HR TENG.

4.2. Relevant Equipment for the Acoustic–Electric Conversion Experiment

As shown in Figure 7, in the acoustic energy harvesting experiment, signals of different frequencies are generated by a signal generator (Model: ATF20B), which are then transmitted via a power amplifier (SA–5016) to a loudspeaker. The loudspeaker emits sound waves into the 4C–HR TENG device, driving the particles within the four Helmholtz Resonators in the upper part of the device to generate electricity. The output voltage of the TENG device is measured using an electrometer (Keithley 6517B), while the sound pressure level is measured with a sound level meter (Model: B&K 2270). The electrometer transmits the acquired electrical signals to a computer through an NI data acquisition card, which are then analyzed and processed using LabVIEW 2024 Q1 software to obtain the output performance curves of the device under different parameters.

5. Conclusions

This paper successfully designed and fabricated a triboelectric nanogenerator based on a four-cavity parallel Helmholtz Resonator for efficiently harvesting acoustic energy from the environment, with a specific focus on low-frequency noise in scenarios such as ship engine rooms. Through systematic experimental investigation, theoretical analysis, and COMSOL Multiphysics simulation, the acoustic–electric conversion mechanism and output characteristics of the device were thoroughly explored, and its feasibility was verified. The study examined the output performance of the 4C–HR TENG device—composed of an acoustic waveguide with a length of 350 mm, width and height of 60 mm, and Helmholtz resonant cavities with a diameter of 60 mm and height of 40 mm—under different structural parameters. Under excitation at the resonance frequency of 110 Hz and a SPL of 109.8 dB, the device achieved a high open-circuit voltage of 250 V and a short-circuit current of 4.85 μA. The particle filling ratio exhibits an optimal range (50–60%). If too low, triboelectric contact is insufficient; if too high, energy dissipation increases due to intensified particle collisions. Particle size determines the balance between vibration characteristics and contact area, with the 3 mm particles exhibiting relatively good stability and output performance across a broad frequency range of 150–300 Hz. An electrode plate height of 10 mm enables optimal matching between particle vibration space and electric field distribution, resulting in peak voltage (200 V) and current (1.8 μA). Regarding electrode material selection, although the copper electrode has a slightly lower peak voltage than the aluminum electrode, it demonstrates stable response within a broad bandwidth of 100–300 Hz and offers better adaptability. The study also explored the relationship between external acoustic excitation and output performance. The device’s output peaks at the resonance frequency, and the output voltage is positively correlated with the SPL (with a linear correlation coefficient of 0.95). The fundamental mechanism underlying the influence of sound source distance on output performance was revealed: as the distance increases (from 0 mm to 25 mm), both the output voltage and current decrease significantly. This is because, for spherical sound waves, the sound pressure is inversely proportional to the propagation distance. Consequently, the actual sound pressure received at the device inlet attenuates, leading to a reduction in output performance. This finding provides crucial guidance for the practical deployment and scenario selection of the device.

Finally, the application validation demonstrated the minimum response SPL of the 4C–HR TENG within its operating frequency range and its maximum output power of 0.27 mW at a load resistance of 50 MΩ. This showcases the practical potential of the device. The 4C–HR TENG can charge a 1 μF capacitor to 4.73 V within 32 s and simultaneously illuminate 180 commercial LEDs, fully demonstrating its capability to power small electronic devices or sensor nodes.

In summary, this study successfully designed and developed a triboelectric nanogenerator based on a quadruple parallel-cavity Helmholtz Resonator (4C–HR TENG). Through experimental and simulation approaches, the decisive influence of key structural parameter optimization and acoustic field characteristics on the device’s output performance was elucidated. This research provides an effective solution for energy harvesting in typical low- to medium-frequency noise environments such as ship engine rooms and industrial equipment noise, demonstrating promising application prospects in areas such as self-powered sensing systems and condition monitoring. Future research may focus on the following directions: first, further broadening the operating frequency band of the device to enhance its adaptability to complex spectral noise; second, optimizing particle dielectric materials and surface properties to improve triboelectric charge density and energy conversion efficiency; and third, conducting performance validation under real-world noise conditions, examining the device’s dynamic response characteristics, long-term stability, and practical integration schemes under conditions such as rectangular pulses, impact noise, and broadband random noise.