Distributionally Robust Optimization for Integrated Energy System with Tiered Carbon Trading: Synergizing CCUS with Hydrogen Blending Combustion

Abstract

In this study, an Integrated Energy System (IES) with hydrogen refinement within a tiered carbon trading mechanism (TCTM) is presented to improve energy efficiency and support decarbonization. To address uncertainties in the IES, a distributionally robust optimization (DRO) approach, employing a fuzzy set framework with Kernel Density Estimation (KDE) to construct error distributions and specify output ranges for renewable energy (RE), is proposed. Latin hypercube sampling (LHS) and K-means clustering are, respectively, applied to generate original and representative scenarios. Subsequently, case studies are performed to evaluate advantages of the presented model. The results indicate that hydrogen refinement within the TCTM framework has substantial benefits for the IES. Specifically, the proposed scenario integrates hydrogen blending combustion (HBC) with synthetic methane, demonstrating significant economic and carbon benefits, with cost reductions of 7.3%, 7.1%, and 4.3% and carbon emission reductions of 6%, 3%, and 2.4% compared to scenarios with no hydrogen utilization, HBC only, and synthetic methane only, respectively. In contrast, to exclude carbon trading and include fixed-price trading, the TCTM achieves a 3.5% and 1.1% reduction in carbon emissions, respectively. Finally, a comprehensive sensitivity analysis is performed, examining factors such as the ratio of hydrogen blending, price, and growth rate of carbon trading.

1. Introduction

Amid the worldwide shift toward cleaner energy, the global energy system is undergoing a profound transformation. The conventional energy supply model, characterized by greenhouse gas emissions and resource depletion, can no longer support sustainable development. In response, the global power sector is shifting toward cleaner and more efficient modes of energy utilization [1]. Meanwhile, to fulfill its commitment to global carbon neutrality, China is accelerating the structural transformation of its energy supply, gradually shifting from traditional fossil energy to renewable energy. By 2050, it is expected that renewable energy will account for 60–70% of China’s total electricity supply [2]. However, traditional energy systems are often planned and operated independently, which limits their ability to fully exploit the complementary advantages of different energy forms, thereby restricting the efficiency of renewable energy utilization [3]. To overcome this issue, Integrated Energy System (IES) has emerged. Due to its ability to achieve synergies among different energy forms and significantly improve overall efficiency, it has become a mainstream solution for enhancing energy efficiency and driving renewable energy (RE) consumption [4].

The uncertainty of the power output of RE leads to difficulties in consumption, while also introducing inherent uncertainty, volatility, and intermittency into the scheduling of IES [5]. While distribution optimization may achieve lower costs, it also introduces informatic concerns during data interactions. It may not be sufficient to ensure system stability when the data flow between systems is vulnerable to leaks, hacking, or malware attacks [6]. Therefore, future work could also address issues related to information leakage or cyber attacks in the network. Compared to the latter, the former is the focus of this study, because ignoring uncertainty will undermine the reliability of optimization results [7]. Currently, stochastic robust optimization (RO) and programming (SP) are widely recognized methods for dealing with uncertainty [8,9], but SP places high demands on probability distributions, leading to significant errors when they are complex or difficult to describe precisely [9]. RO, on the other hand, is overly conservative and sensitive to parameters and the radius of uncertain sets [8]. To address the gap between SP and RO, distributionally robust optimization (DRO) has been introduced in recent research and has gained widespread attention [10,11]. Compared to SP and RO, DRO is particularly suitable when accurate probability distributions cannot be fully obtained or when the system’s actual uncertainty is complex [10]. DRO combines the robustness of RO with the flexibility of SP, providing a more flexible yet robust solution, particularly when dealing with uncertainties in systems such as photovoltaic and wind power systems, helping to optimize decisions and improve system stability [11].

However, the fuzzy sets used in DRO play a crucial role in computational accuracy and reliability. The fuzzy sets used in DRO primarily consist of distance-based and moment-based fuzzy sets [12]. Reference [13] formulates a multi-objective DRO-based planning framework for a hydrogen–cooling–heating–power system, accounting for variability in sources and loads, utilizing moment-based probability distributions to build fuzzy sets. Reference [14] introduces a two-stage DRO model to address economic dispatch problems, utilizing Wasserstein distances to extract fuzzy sets for wind turbine (WT) and photovoltaic (PV) probability distributions. While distance-based fuzzy sets make full use of valuable historical data, this model faces difficulties in model conversion, complex mathematical tools, and low solution efficiency [15], therefore a moment-based fuzzy set is worth exploring. For instance, Reference [16] adopts an innovative data-driven DRO method employing a novel approach to construct fuzzy sets, which utilizes non-parametric Kernel Density Estimation (KDE) to approximate the error probability distribution and establish the prediction intervals for the output of WT and PV based on a level of confidence.

In summary, traditional DRO-based IES models typically rely on parametric assumptions, such as moment-based sets or Wasserstein distances, which may fail to capture the non-Gaussian, multi-modal, and asymmetric nature of wind and solar uncertainty. In contrast, the KDE-based approach constructs data-driven fuzzy uncertainty sets that directly reflect the empirical distribution of renewable energy outputs, enhancing flexibility and accuracy without assuming a specific parametric form. The distributions derived from non-parametric KDE closely align with the actual distributions, enhancing the objectivity of the analysis and alleviating the inherent conservatism in fuzzy sets and optimization scheduling.

It is well known that hydrogen energy systems are usually integrated into the IES structure to stabilize the intermittent output of WT and PV systems. Reference [17] introduced an IES model incorporating hydrogen generators and storage modules to assess the impact of hydrogen storage on the operation of gas–electric Integrated Energy Systems. Reference [18] presented an integrated energy service station operating independently of the grid that combines solar photovoltaics, wind energy, and hydrogen storage to promote the advancement of new energy vehicles. Reference [19] proposed using hydrogen in IES for methanol production as a chemical feedstock for industrial parks, adding hydrogen fuel cells in IES for power generation to enhance system flexibility. Reference [20] suggested coupling thermal power plants with carbon capture, utilization, and storage (CCUS) technology to use hydrogen for methane production, thereby reducing fuel costs. In summary, hydrogen, as an efficient energy carrier that can flexibly circulate across various sectors such as electricity, gas, and heat, is a key hub for achieving multi-energy coupling and collaborative optimization in IES [21]. Currently, hydrogen utilization is categorized into three types of main directions: direct sale; co-firing; and the synthesis of hydrogen-based gases like methane, methanol, and ammonia [22]. Therefore, further discussions are needed on how to fully utilize hydrogen in a more economical and environmentally friendly manner.

Economic feasibility, flexibility, and carbon emission levels are the three primary factors that IES must consider [23]. As carbon markets expand, carbon is traded as a commodity through emission allowances [24], which means that the carbon trading market can further stimulate IES to promote low-carbon reforms [25]. Therefore, it is essential for IES to function within the regulations of the carbon trading market [26]. Compared to other trading mechanisms, the tiered carbon trading mechanism (TCTM) has advantages in controlling carbon emissions and its application [27]. Reference [28] introduces a strategy for a demand response aimed at industrial parks, incorporating the TCTM to minimize carbon emissions and operational costs. Reference [29] combines a carbon tax and the TCTM to limit the carbon emissions of an electric–thermal–hydrogen IES based on steel plants. Reference [30] presents a scheduling model for a park-level IES in the carbon market, incorporating multi-objective optimization and considering the impact of the TCTM on operational profit and carbon emissions. Reference [31] employed a two-stage optimization scheduling framework in a traditional coal-fired power plant combined with a power-to-gas system, incorporating tiered carbon trading with incentives and penalties for CO₂ emissions control. In light of these, studying the optimization of hydrogen-based IES with TCTM is of significant importance.

This paper proposes a novel model that integrates hydrogen blending combustion (HBC), CCUS, and the TCTM within the energy system, providing an effective solution to carbon emission reductions and energy system optimization. To highlight the novelty of this paper,

Table 1. A comparison of the proposed methodology with related studies.

References	Category	Technical Measure	TCTM Parameter Analysis	Uncertainty
				PV	WT	Method
[4,32]	Park-IES (kw)	CCS, P2G	×	×	×	×
[18]	Service station-IES (kw)	P2G	√	√	√	SP
[3]	Park-IES (kw)	P2G	×	√	√	SP
[33]	Power plant-IES (MW)	P2G, HBC	√	×	√	SP
[34]	Resident-IES (kw)	×	×	√	√	RO
[35]	Industrial park-IES (MW)	CCS, P2G	×	√	√	Two stage-RO
[10]	Park-IES (kw)	×	×	×	√	DRO
[5]	Park-IES (kw)	P2G, HBC	×	√	√	DRO
Proposed	Power plant-IES (MW)	CCS, P2G, HBC	√	√	√	DRO

Note: × indicates not adopt, √ indicates adopt.

presents a summary of the key methodological differences and contributions compared to the relevant studies.

To address these pressing challenges and further enhance system efficiency, this study reveals a novel model that combines hydrogen utilization with carbon trading mechanisms within a DRO framework. The major contributions are detailed below:

• To effectively handle the uncertainty of RE, a data-driven DRO approach is employed to maintain stability between economic performance and system robustness considering the WT and PV variability. A fuzzy set formulation based on KDE is proposed to handle this uncertainty.
• This paper introduces a model for the refined use of hydrogen generated by RE, encompassing blending combustion in CHP and gas synthesis using CCUS technology, as well as storage in tanks. This approach aims to improve the consumption rate of RE and enhance hydrogen utilization rates.
• A TCTM model is developed to further reduce CO₂ emissions. The effects of related TCTM parameters, including transaction benchmark prices and growth ratios when the carbon trading range is fixed, on overall costs, CO₂ emissions, and expenses of carbon trading expenses are thoroughly examined, offering guidance for selecting appropriate trading parameters.

This paper is organized as follows: Section 2 presents the composition and modeling of the IES. Section 3 develops the DRO model, while Section 4 analyzes the results of the case study. Section 5 provides a further discussion on system parameters and compares results across different scenarios. Finally, Section 6 concludes this paper and offers an outlook for future work.

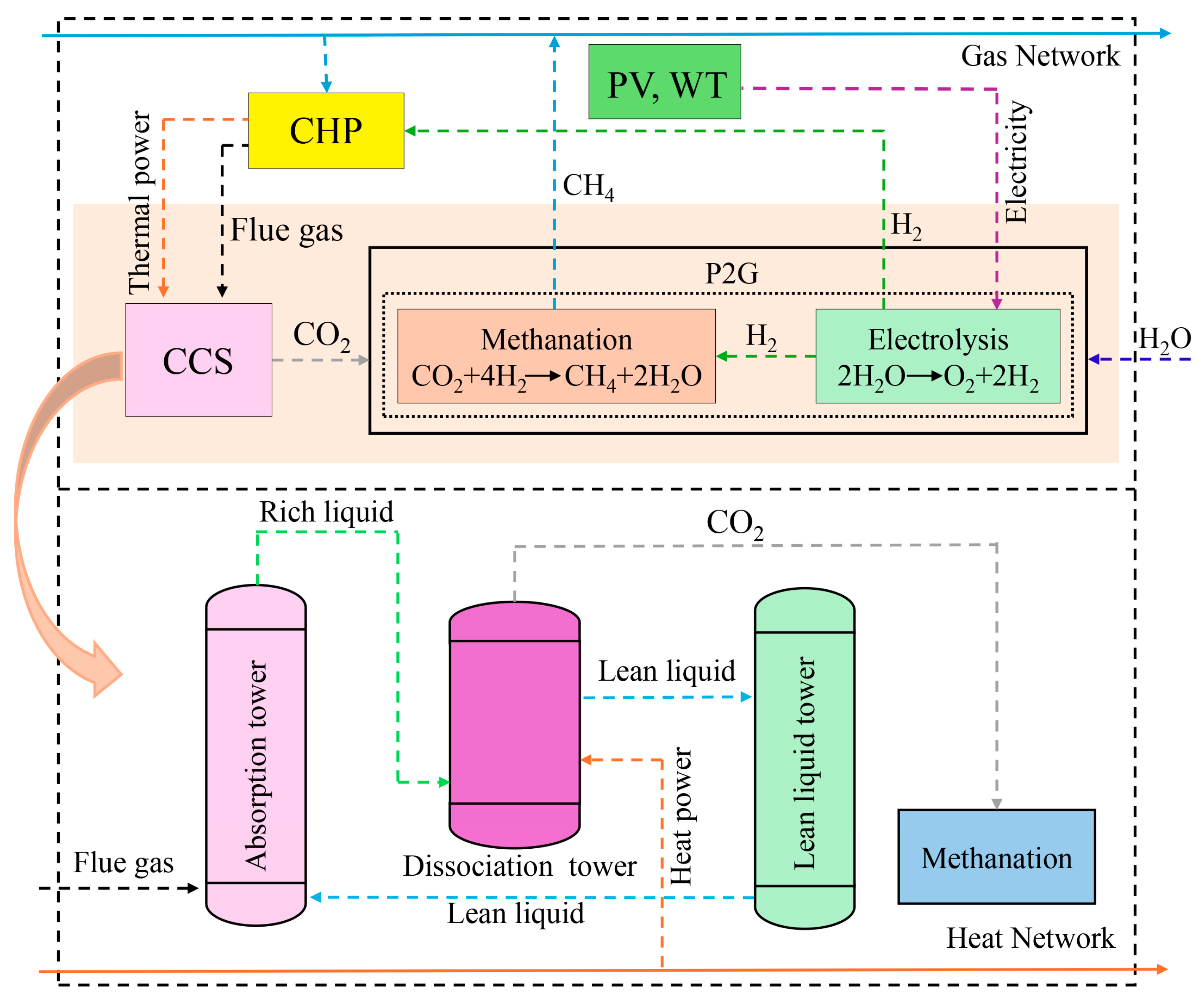
2. The Framework of the Proposed IES

Figure 1 illustrates the structure and energy flow relationship of the multi-energy complementary optimization system proposed in this study. The system is made up of the supply, demand, and conversion sides. The demand side mainly includes thermal and electrical loads. Excess electricity generated by RE can be converted into hydrogen through EL devices and stored in hydrogen storage devices. The waste heat boiler (WHB) serves as the primary heat supply to meet the thermal loads. Furthermore, the connection to higher-level power grid enables the system to achieve energy flexibly. Finally, this system operates within the carbon trading market framework.

The relationship between the CCUS and IES is illustrated in Figure 2. The captured CO₂ is supplied to the methanation reactor (MR). Meanwhile, the electrolysis (EL) system converts electricity into hydrogen via the water electrolysis method. Finally, the MR unit catalyzes the reaction between CO₂ and H₂ to produce synthetic CH₄ product.

2.1. Model of CHP with Flexible Hydrogen Blending Combustion and Thermoelectric Ratio

In traditional CHP models, the heat-to-power ratio is fixed, like backpressure CHP units where power and heating outputs are linearly linked and constrained by the heating load, limiting system flexibility. In contrast, the condensation CHP units allow real-time adjustments of the heat-to-power ratio by altering the condensation pressure and steam flow, thereby optimizing efficiency and flexibility. The output characteristics of a condensation CHP unit are shown in Figure 3. The change in the thermoelectric ratio is limited by the output of the GT and WHB, with their ramp-up rates constraining the change.

A variable heat-to-power ratio model allows for adjustments based on real-time conditions, further optimizing operational efficiency. To reduce the complexity of the model, we simplified the CHP modeling, focusing on the overall system performance rather than the detailed combustion dynamics. The CHP unit in this system consists of a GT and WHB. The model is as follows:

$$P_{\mathrm{CHP}}(t)=Q_{\mathrm{LHV},\mathrm{g}}{P}_{\mathrm{n}\mathrm{g}}(t)+Q_{\mathrm{LHV},\mathrm{h}}{P}_{{\mathrm{H}}_2}(t)$$

(1)

where $P_{\mathrm{CHP}}(t)$ indicates the power output from the CHP at time t; $Q_{\mathrm{LHV},\mathrm{g}}$ and $Q_{\mathrm{LHV},\mathrm{h}}$ are lower heating values of gas and hydrogen, respectively. $P_{\mathrm{ng}}(t)$ and $P_{{\mathrm{H}}_2}(t)$ are the gas and hydrogen input of the CHP at time t, respectively. $E_{\mathrm{GT}}(t)$ and $H_{\mathrm{WHB}}(t)$ are, respectively, the electricity and thermal energy output.

The following gas turbine model assumes constant efficiency despite hydrogen blending, with blending based on the volume. The turbine efficiency is minimally affected by hydrogen concentrations below typical operational limits, with a blending limit of 20% [36]. This simplification allows us to focus on the overall system performance without introducing unnecessary complexity.

$$\left\{\begin{array}{c}{E}_{\mathrm{GT}}(t)={\eta }_{\mathrm{GT}}{\psi }_{\mathrm{CHP}}(t)P_{\mathrm{CHP}}(t)\\ E_{\mathrm{GT}}^{min}\le E_{\mathrm{GT}}(t)\le E_{\mathrm{GT}}^{max}\\ \Delta E_{\mathrm{GT}}^{min}\le E_{\mathrm{GT}}(t+1)-E_{\mathrm{GT}}(t)\le \Delta E_{\mathrm{GT}}^{max}\end{array}\right.$$

(2)

where ${\eta }_{\mathrm{GT}}$ denotes the conversion efficiency of the GT, ${\psi }_{\mathrm{CHP}}(t)$ is the proportion of total energy utilized by the GT at time t, $P_{\mathrm{ng}}(t)$ and $P_{{\mathrm{H}}_2}(t)$ are, respectively, the gas and hydrogen input. $E_{\mathrm{GT}}^{max}$ and $E_{\mathrm{GT}}^{min}$ are the upper and lower constraints of the electricity output. $\Delta E_{\mathrm{GT}}^{max}$ and $\Delta E_{\mathrm{GT}}^{min}$ serve as the boundaries for the GT ramp constraints.

$$\left\{\begin{array}{c}{H}_{\mathrm{W}\mathrm{H}\mathrm{B}}(t)={\eta }_{\mathrm{WHB}}(1-{\psi }_{\mathrm{CHP}}(t))P_{\mathrm{CHP}}(t)\\ H_{\mathrm{WHB}}^{min}\le H_{\mathrm{W}\mathrm{H}\mathrm{B}}(t)\le H_{\mathrm{WHB}}^{max}\\ \Delta H_{\mathrm{WHB}}^{min}\le H_{\mathrm{W}\mathrm{H}\mathrm{B}}(t+1)-H_{\mathrm{W}\mathrm{H}\mathrm{B}}(t)\le \Delta H_{\mathrm{WHB}}^{max}\end{array}\right.$$

(3)

where ${\eta }_{\mathrm{WHB}}$ is the conversion efficiency of the thermal energy. $H_{\mathrm{WHB}}^{max}$ and $H_{\mathrm{WHB}}^{min}$ are the maximum and minimum constraints of the thermal power output. $\Delta H_{\mathrm{WHB}}^{max}$ and $\Delta H_{\mathrm{WHB}}^{min}$ are the upper and lower limits of WHB ramp constraints.

In addition, the 20% hydrogen blend limit is technically feasible, enhancing combustion efficiency and performance while mitigating safety risks such as backfires or pre-ignition. It also improves combustion stability, leading to more complete combustion and reduced CO and HC emissions and maintaining NO_x within controllable levels [37]. Therefore, the CHP unit should also meet the following constraints:

$$\left\{\begin{array}{c}{k}_{\mathrm{CHP}}(t)=H_{\mathrm{WHB}}\left(t\right)/E_{\mathrm{GT}}(t)={\displaystyle \frac{{\eta }_{\mathrm{WHB}}(1-{\psi }_{\mathrm{CHP}}(t))}{{\eta }_{\mathrm{GT}}{\psi }_{\mathrm{CHP}}(t)}}\\ \begin{array}{c}{k}_{\mathrm{CHP}}^{min}\le k_{\mathrm{CHP}}(t)\le k_{\mathrm{CHP}}^{max}\\ {\alpha }_{\mathrm{CHP},\mathrm{h}}(t)=P_{{\mathrm{H}}_2}(t)/(P_{\mathrm{ng}}(t)+P_{{\mathrm{H}}_2}(t))\\ 0\le {\alpha }_{\mathrm{CHP},\mathrm{h}}(t)\le 0.2\end{array}\end{array}\right.$$

(4)

where $k_{\mathrm{CHP}}(t)$ represents the thermoelectric ratio of the CHP at time t; $k_{\mathrm{CHP}}^{max}$ and $k_{\mathrm{CHP}}^{max}$ are, respectively, the maximum and minimum thermoelectric ratio. ${\alpha }_{\mathrm{CHP},\mathrm{h}}(t)$ is the hydrogen blend ratio of the CHP at time t.

2.2. Model of Electrolysis (EL)

As a crucial energy conversion device, the hydrogen product is produced through the electrolysis of the liquid water. The model of EL is as follows:

$$\left\{\begin{array}{c}{P}_{\mathrm{EL},\mathrm{h}}(t)=P_{\mathrm{EL},\mathrm{e}}(t){\eta }_{\mathrm{EL}}\\ \begin{array}{c}{P}_{\mathrm{EL},\mathrm{e}}^{min}\le P_{\mathrm{EL},\mathrm{e}}(t)\le P_{\mathrm{EL},\mathrm{e}}^{max}\\ \Delta P_{\mathrm{EL},\mathrm{e}}^{min}\le P_{\mathrm{EL},\mathrm{e}}(t+1)-P_{\mathrm{EL},\mathrm{e}}(t)\le \Delta P_{\mathrm{EL},\mathrm{e}}^{max}\end{array}\end{array}\right.$$

(5)

where $P_{\mathrm{EL},\mathrm{e}}(t)$ is the electricity input to the EL at time t, $P_{\mathrm{EL},\mathrm{h}}(t)$ is the hydrogen volume generated at time t, ${\eta }_{\mathrm{EL}}$ is the electricity-to-hydrogen conversion rate, $P_{\mathrm{EL},\mathrm{e}}^{max}$ and $P_{\mathrm{EL},\mathrm{e}}^{min}$ represent upper and lower bounds of the electrical energy input, respectively. $\Delta P_{\mathrm{EL},\mathrm{e}}^{max}$ and $\Delta P_{\mathrm{EL},\mathrm{e}}^{min}$ represent the maximum and minimum ramp rates of EL, respectively.

2.3. Model of Methanation Reaction (MR)

The MR can convert hydrogen and CO₂ into methane. Given that the system operates within the range where catalysts exhibit stable activity and a previous study [38] has shown that temperature and pressure variations within typical operational conditions have little impact on conversion efficiency, we assumed constant CO₂ conversion coefficients for simplicity and consistency across the model. The math model of the MR is as follows.

$$\left\{\begin{array}{c}\begin{array}{c}{P}_{\mathrm{MR},\mathrm{g}}(t)={\eta }_{\mathrm{MR}}{P}_{\mathrm{MR},\mathrm{h}}(t)\\ P_{\mathrm{MR},\mathrm{h}}^{min}\le P_{\mathrm{MR},\mathrm{h}}(t)\le P_{\mathrm{MR},\mathrm{h}}^{max}\end{array}\\ \Delta P_{\mathrm{MR},\mathrm{h}}^{min}\le P_{\mathrm{MR},\mathrm{h}}(t+1)-P_{\mathrm{MR},\mathrm{h}}(t)\le \Delta P_{\mathrm{MR},\mathrm{h}}^{max}\end{array}\right.$$

(6)

where $P_{\mathrm{MR},\mathrm{h}}(t)$ and $P_{\mathrm{MR},\mathrm{g}}(t)$ are the hydrogen input of the MR and the methanation output of the MR at time t, respectively. ${\eta }_{\mathrm{MR}}$ is the methanation efficiency of the MR; $P_{\mathrm{MR},\mathrm{h}}^{max}$ and $P_{\mathrm{MR},\mathrm{h}}^{min}$ represent the maximum and minimum limits of the hydrogen energy input, respectively; $\Delta P_{\mathrm{MR},\mathrm{h}}^{max}$ and $\Delta P_{\mathrm{MR},\mathrm{h}}^{min}$ represent the maximum and minimum ramp rates of the MR, respectively.

2.4. Model of Energy Storage

The storage devices described in this study include three categories, namely electric, hydrogen, and thermal energy storage devices. Due to the similarity of their mathematical models, this paper adopts a unified approach to model them. The energy storage model is presented as Equation (7).

$$\left\{\begin{array}{c}0\le P_{\mathrm{ES},\mathrm{d}}(t)\le B_{\mathrm{E}\mathrm{S},\mathrm{d}}(t)P_{\mathrm{ES}}^{max}\\ 0\le P_{\mathrm{ES},\mathrm{c}}(t)\le B_{\mathrm{E}\mathrm{S},\mathrm{c}}(t)P_{\mathrm{ES}}^{max}\\ P_{\mathrm{ES}}(t)={\eta }_{\mathrm{ES},\mathrm{c}}{P}_{\mathrm{ES},\mathrm{c}}(t)-{\eta }_{\mathrm{ES},\mathrm{d}}{P}_{\mathrm{ES},\mathrm{d}}(t)\\ Z\left(t\right)=Z(t-1)+P_{\mathrm{ES}}(t)/P_{\mathrm{ES},\mathrm{cap}}(t)\\ Z\left(1\right)=Z\left(T\right)\\ B_{\mathrm{E}\mathrm{S},\mathrm{d}}(t)+B_{\mathrm{E}\mathrm{S},\mathrm{c}}(t)=1\\ Z_{min}\le Z\left(t\right)\le Z_{max}\end{array}\right.$$

(7)

where $P_{\mathrm{ES},\mathrm{d}}(t)$ and $P_{\mathrm{ES},\mathrm{c}}(t)$ are the charging and discharging power of the energy storage device at time t, respectively. $P_{\mathrm{ES}}^{max}$ is the maximum charging and discharging power of the energy storage device, $B_{\mathrm{E}\mathrm{S},\mathrm{d}}(t)$ and $B_{\mathrm{E}\mathrm{S},\mathrm{c}}(t)$ are binary variables, representing the discharging and charging states, respectively. $B_{\mathrm{E}\mathrm{S},\mathrm{c}}(t)=1$ and $B_{\mathrm{E}\mathrm{S},\mathrm{d}}(t)=0$ represent the charging state of the storage device, $B_{\mathrm{E}\mathrm{S},\mathrm{c}}(t)=0$ and $B_{\mathrm{E}\mathrm{S},\mathrm{d}}(t)=1$ represent the discharging state of the storage device. $P_{\mathrm{ES}}(t)$ represents the power output of the energy storage device at time t. ${\eta }_{\mathrm{ES},\mathrm{c}}$ and ${\eta }_{\mathrm{ES},\mathrm{d}}$ are, respectively, the energy storage device efficiency of the charging and discharging. $\mathrm{Z}(t)$ is the capacity of the energy storage device, $P_{\mathrm{ES},\mathrm{cap}}(t)$ is the nominal capacity, $Z_{max}$ and $Z_{min}$ are the maximum and minimum capacity of the energy storage device, respectively.

2.5. Model of Carbon Capture and Storage (CCS)

This study uses a method of carbon capture after combustion; the lean solution in a tank absorbs CO₂, becoming a rich solution that is stored in another tank. The rich solution is then heated and pyrolyzed to release CO₂ and produce a lean solution, thereby achieving the recycling of carbon dioxide absorbents. The carbon capture model is expressed below:

$$\{\begin{array}{c}{V}_{\mathrm{ra}}(t)=V_{\mathrm{ra}}(t-1)+V_{\mathrm{ra},\mathrm{in}}(t)-V_{\mathrm{ra},\mathrm{out}}(t)\\ V_{\mathrm{ra},\mathrm{in}}^{\mathit{min}}\le V_{\mathrm{ra},\mathrm{in}}(t)\le V_{\mathrm{ra},\mathrm{in}}^{\mathit{max}}\\ \Delta V_{\mathrm{ra},\mathrm{in}}^{\mathit{min}}\le V_{\mathrm{ra}}(t+1)-V_{\mathrm{ra}}(t)\le \Delta V_{\mathrm{ra},\mathrm{in}}^{\mathit{max}}\\ V_{\mathrm{ls}}(t)=V_{\mathrm{ls}}(t-1)+V_{\mathrm{ls},\mathrm{in}}(t)-V_{\mathrm{ls},\mathrm{out}}(t)\\ V_{\mathrm{ls},\mathrm{out}}^{\mathit{min}}\le V_{\mathrm{ls}}(t)\le V_{\mathrm{ls},\mathrm{out}}^{\mathit{max}}\\ \Delta V_{\mathrm{ls},\mathrm{out}}^{\mathit{min}}\le V_{\mathrm{ls}}(t+1)-V_{\mathrm{ls}}(t)\le \Delta V_{\mathrm{ls},\mathrm{out}}^{\mathit{max}}\\ V_{\mathrm{ra},\mathrm{out}}(t)=V_{\mathrm{ls,in}}(t)\\ V_{\mathrm{ls},\mathrm{out}}(t)=V_{\mathrm{ra},\mathrm{in}}(t)\\ V_{\mathrm{ra}}(t)+V_{\mathrm{ls}}(t)=C\\ H_{\text{ra-ls}}(t)=a_{\mathrm{de}}{\rho }_{\mathrm{ra}}{V}_{\mathrm{ra},\mathrm{out}}(t)\end{array}$$

(8)

where $V_{\mathrm{ra}}(t)$ and $V_{\mathrm{ls}}(t)$ are the volume of the rich liquid tower and lean liquid at time t, respectively. $V_{\mathrm{ra},\mathrm{in}}^{min}$ and $V_{\mathrm{ra},\mathrm{in}}^{max}$ are, respectively, the minimum and maximum absorption of the lean liquid. $\Delta V_{\mathrm{ra},\mathrm{in}}^{min}$ and $\Delta V_{\mathrm{ra},\mathrm{in}}^{max}$ are the minimum and maximum of absorption rate of the lean solution. $V_{\mathrm{ls},\mathrm{out}}^{min}$ and $V_{\mathrm{ls},\mathrm{out}}^{max}$ are, respectively, the minimum and maximum pyrolysis volume of the rich liquid. $\Delta V_{\mathrm{ls},\mathrm{out}}^{min}$ and $\Delta V_{\mathrm{ls},\mathrm{out}}^{\max }$ are lower and upper limits of the pyrolysis rate for the rich solution. $V_{\mathrm{ra},\mathrm{in}}(t)$ and $V_{\mathrm{ra},\mathrm{out}}(t)$ represent rich liquid flows into and out of the rich liquid tower, respectively. $V_{\mathrm{ls},\mathrm{in}}(t)$ and $V_{\mathrm{ls},\mathrm{out}}(t)$ denote the lean liquid flow into and out of the lean liquid tower. C is a constant, representing the fixed total volume of the rich liquid and lean liquid stored in the storage device at time t. ${\rho }_{\mathrm{ra}}$ is the density of the rich liquid, $H_{\text{ra-ls}}(t)$ and $a_{\mathrm{de}}$ are total the thermal energy consumption of the rich liquid’s pyrolysis and the heat required for the pyrolysis of the rich liquid per unit mass.

According to the current research [39] on CO₂ Monoethanolamide (MEA) absorbent solutions, the lean liquid (30% MEA) can absorb 0.25~0.45 times its quantity of CO₂ per unit; thus, it is taken to be 0.35 in this study.

$$0.35({\rho }_{\mathrm{ra}}{V}_{\mathrm{ra},\mathrm{out}}(t)-{\rho }_{\mathrm{ls}}{V}_{\mathrm{ls},\mathrm{in}}(t))=M_{{\mathrm{CO}}_2}$$

(9)

Additionally, since this paper standardizes the units to MW, for a methanation reaction where CO₂ is converted into methane, approximately 0.207 tons of CO₂ are needed to promote the reaction when the process consumes 1 MW of energy.

$$M_{{\mathrm{CO}}_2}=0.207P_{\mathrm{MR},\mathrm{g}}(t)$$

(10)

Therefore, through Equations (9) and (10), the simplification is as follows:

$$({\rho }_{\mathrm{ra}}{V}_{\mathrm{ra},\mathrm{out}}(t)-{\rho }_{\mathrm{ls}}{V}_{\mathrm{ls},\mathrm{in}}(t))={\displaystyle \frac{0.207}{0.35}}{P}_{\mathrm{MR},\mathrm{g}}(t)=0.59P_{\mathrm{MR},\mathrm{g}}(t)$$

(11)

2.6. Power Balance Constraints

2.6.1. Electric Power Constraints

$$\left\{\begin{array}{c}{E}_{\mathrm{WT}}(t)+E_{\mathrm{PV}}(t)+P_{\mathrm{e},\mathrm{buy}}(t)+E_{\mathrm{G}\mathrm{T}}(t)+\\ P_{\mathrm{ES},\mathrm{e},\mathrm{dis}}(t)=E_{\mathrm{load}}(t)+P_{\mathrm{ES},\mathrm{e},\mathrm{cha}}(t)+P_{\mathrm{E}\mathrm{L},\mathrm{e}}(t)\\ 0\le P_{\mathrm{e},\mathrm{buy}}(t)\le P_{\mathrm{e},\mathrm{buy}}^{max}\end{array}\right.$$

(12)

where $E_{\mathrm{PV}}(t)$ and $E_{\mathrm{WT}}(t)$ denote the outputs of the PV and WT at time t, respectively. $P_{\mathrm{e},\mathrm{buy}}(t)$ is the external electricity purchase at time t, $P_{\mathrm{ES},\mathrm{e},\mathrm{dis}}(t)$ represents the discharge power of the electrical energy storage at time t, $P_{\mathrm{ES},\mathrm{e},\mathrm{cha}}(t)$ denotes the electric energy storage charging power at time t, and $E_{\mathrm{load}}(t)$ is the electric load. $P_{\mathrm{e},\mathrm{buy}}^{max}$ is the upper limit for external electricity procurement.

2.6.2. Thermal Power Constraints

$$H_{\mathrm{W}\mathrm{H}\mathrm{B}}(t)+P_{\mathrm{E}\mathrm{S},\mathrm{t},\mathrm{d}\mathrm{i}\mathrm{s}}(t)=H_{\mathrm{load}}(t)+P_{\mathrm{E}\mathrm{S},\mathrm{t},\mathrm{c}\mathrm{h}\mathrm{a}}(t)+H_{\text{ra-ls}}(t)$$

(13)

where $P_{\mathrm{ES},\mathrm{t},\mathrm{dis}}(t)$ represents the thermal power discharging from the thermal storage device at time t, $P_{\mathrm{ES},\mathrm{t},\mathrm{cha}}(t)$ denotes the thermal storage device charging power at time t, and $H_{\mathrm{load}}(t)$ is the thermal load.

2.6.3. Hydrogen and Natural Gas Constraints

$$P_{\mathrm{EL},\mathrm{h}}(t)+P_{\mathrm{ES},\mathrm{h},\mathrm{dis}}(t)=P_{\mathrm{M}\mathrm{R},\mathrm{h}}(t)+P_{{\mathrm{H}}_2}(t)+P_{\mathrm{ES},\mathrm{h},\mathrm{cha}}(t)$$

(14)

$$\left\{\begin{array}{c}{N}_{\mathrm{g},\mathrm{buy}}(t)+P_{\mathrm{MR},\mathrm{g}}(t)=P_{\mathrm{n}\mathrm{g}}(t)\\ 0\le N_{\mathrm{g},\mathrm{buy}}(t)\le N_{\mathrm{g},\mathrm{buy},max}\end{array}\right.$$

(15)

where $P_{\mathrm{ES},\mathrm{h},\mathrm{dis}}(t)$ and $P_{\mathrm{ES},\mathrm{h},\mathrm{cha}}(t)$ are, respectively, the hydrogen storage charge and discharge power at time t. $N_{\mathrm{g},\mathrm{buy}}(t)$ is the external natural gas procurement at time t. $N_{\mathrm{g},\mathrm{buy},max}$ is the maximum natural gas purchase limit.

2.7. Model of Carbon Trading

The carbon trading mechanism functions by assigning carbon emission allowances to regulated entities and allowing them to trade these allowances in a market-based environment to meet emission reduction targets [40]. If a producer’s actual emissions exceed the allocated quota, the producer is required to purchase additional allowances to comply with regulations [41]. The core concept of the carbon trading market is illustrated in Figure 4.

2.7.1. Model of Allocated Carbon Emission Quota in System

In the system, primary carbon emission sources include CHP and electricity purchased from the grid. Currently, the common carbon emission allocation method is the free allocation system; the model is as follows.

$$\left\{\begin{array}{c}{E}_{\mathrm{IES}}=E_{\mathrm{CHP}}+E_{\mathrm{e},\mathrm{buy}}\\ E_{\mathrm{e},\mathrm{buy}}+E_{\mathrm{CHP}}={\tau }_{\mathrm{buy}}{\displaystyle \sum _{t=1}^T{P}_{\mathrm{e},\mathrm{buy}}(t)}+{\tau }_{\mathrm{gas}}{\displaystyle \sum _{t=1}^T(E_{\mathrm{GT}}(t)+H_{\mathrm{WHB}}(t))}\end{array}\right.$$

(16)

where $E_{\mathrm{IES}}$ denotes the carbon emission quota of the IES, $E_{\mathrm{e},\mathrm{buy}}$ and $E_{\mathrm{CHP}}$ are, respectively, carbon emission quotas for externally purchased electricity and CHP, ${\tau }_{\mathrm{buy}}$ and ${\tau }_{\mathrm{gas}}$ are, respectively, the carbon emission allocated coefficient of purchased electricity and CHP, and $P_{\mathrm{e},\mathrm{buy}}(t)$ denotes the electricity purchased at time t.

2.7.2. Model of Actual Carbon Emission in System

Gas synthesis within MR and blending hydrogen in combustion can reduce carbon emissions. Therefore, the actual CO₂ emission model is as follows:

$$C_{\mathrm{IES}}=C_{\mathrm{e},\mathrm{buy}}+C_{\mathrm{CHP}}-C_{\mathrm{MR}}-C_{\mathrm{CHP},\mathrm{h}}$$

(17)

where $C_{\mathrm{IES}}$ is the carbon emissions from the IES in practice, $C_{\mathrm{e},\mathrm{buy}}$ and $C_{\mathrm{CHP}}$ are, respectively, carbon emissions from purchased external electricity and CHP, $C_{\mathrm{MR}}$ is the amount of carbon utilized by MR, and $C_{\mathrm{CHP},\mathrm{h}}$ is the reduction in carbon emissions due to hydrogen blending in CHP.

2.7.3. Model of Tiered Carbon Trading Mechanism

From Equations (14) and (15), the carbon emission quota and actual carbon emissions of the IES can be determined. Consequently, the carbon emissions eligible for participation in the carbon trading market can be calculated.

$$E_{\mathrm{IES},\mathrm{trade}}=E_{\mathrm{IES}}-C_{\mathrm{IES}}$$

(18)

where $E_{\mathrm{IES},\mathrm{trade}}$ refers to the volume of carbon transactions in IES.

The TCTM provides incentives for producers to adopt carbon reduction technologies, and the model is specified as follows.

$$T_{{\mathrm{CO}}_2}=\left\{\begin{array}{cc}\alpha E_{\mathrm{IES},\mathrm{trade}}& \hspace{1em}\hspace{1em}{E}_{\mathrm{IES},\mathrm{trade}}\le d\\ d\alpha +(1+\theta )\alpha (E_{\mathrm{IES},\mathrm{trade}}-d)& \hspace{1em}\hspace{1em}d\le E_{\mathrm{IES},\mathrm{trade}}<2d\\ d(2+\theta )\alpha +(1+2\theta )\alpha (E_{\mathrm{IES},\mathrm{trade}}-2d)& \hspace{1em}\hspace{1em}2d\le E_{\mathrm{IES},\mathrm{trade}}<3d\\ d(3+3\theta )\alpha +(1+3\theta )\alpha (E_{\mathrm{IES},\mathrm{trade}}-3d)& \hspace{1em}\hspace{1em}3d\le E_{\mathrm{IES},\mathrm{trade}}<4d\\ d(4+6\theta )\alpha +(1+4\theta )\alpha (E_{\mathrm{IES},\mathrm{trade}}-3d)& 4d\le E_{\mathrm{IES},\mathrm{trade}}\end{array}\right.$$

(19)

where $T_{{\mathrm{CO}}_2}$ is the tiered carbon trading cost; $\alpha$ denotes the base price for carbon trading; $d$ represents the carbon emission interval length; and $\theta$ denotes the increase rate of carbon trading prices.

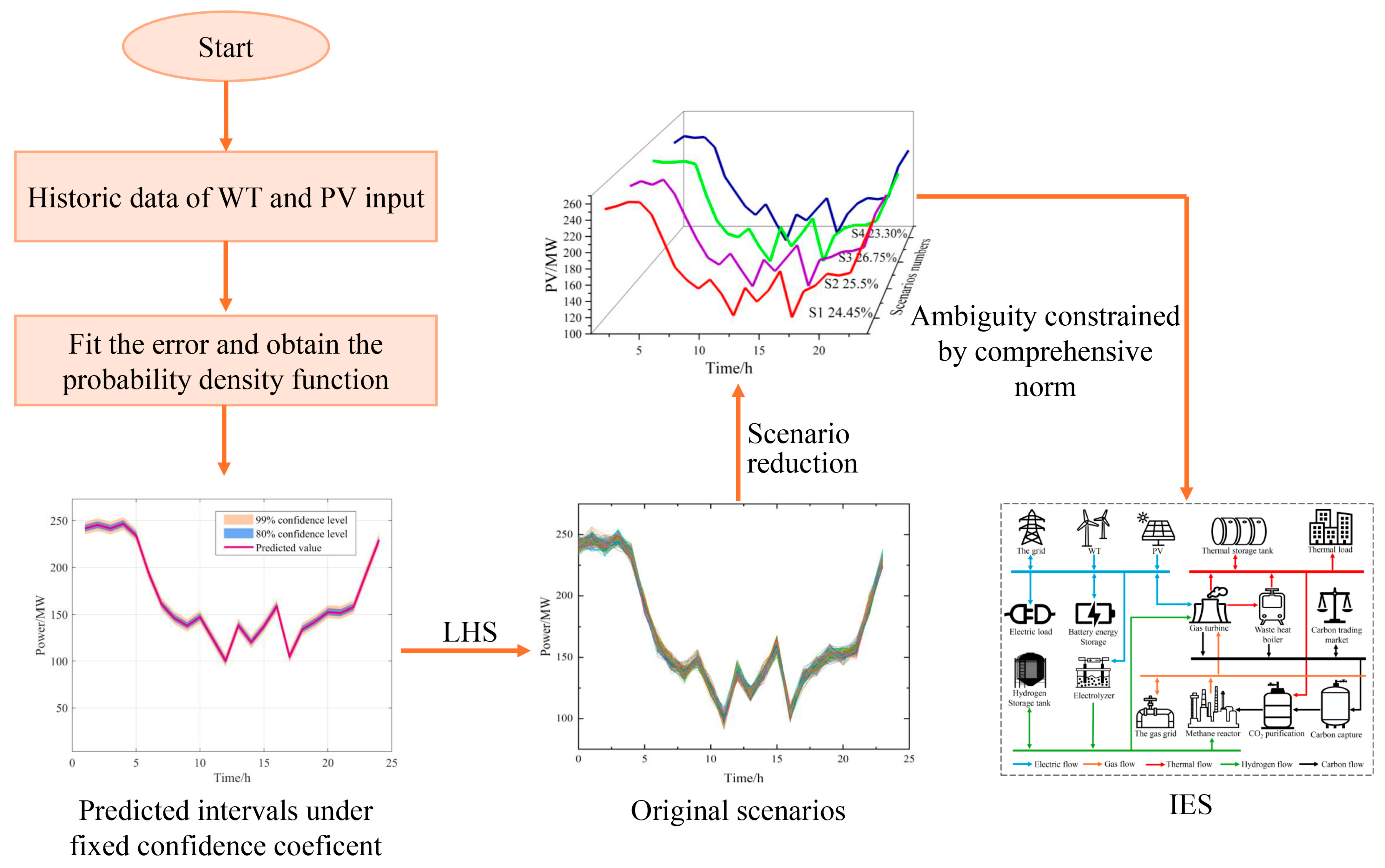
3. Model of DRO in IES

A DRO method is developed to calculate anticipated costs based on worst-case probability distributions of stochastic variables; the optimized objective function is as below.

$$F_{\mathrm{IES}}=\underset{P_m\in \xi }{max}\underset{y\in Y}{min}\left({\displaystyle \sum _{m=1}^{N_m}{P}_m(C_1+C_2+C_3+C_4)}\right)$$

(20)

where $N_m$ is the total number of scenario groups, $P_m$ is the odd of the scenario m happening, and $\xi$ is the fuzzy set of the comprehensive norm based on probability distributions. Y and y represent assembled and decision variables, respectively. $F_{\mathrm{IES}}$ is the optimization objective.

$$\left\{\begin{array}{c}{C}_1={\displaystyle \sum _{t=1}^N(E_{\mathrm{price}}(t)\ast P_{\mathrm{buy},\mathrm{e}}(t))+{\displaystyle \sum _{t=1}^N(G_{\mathrm{price}}(t)\ast P_{\mathrm{buy},\mathrm{g}}(t))}}\\ C_2={\displaystyle \sum _{t=1}^N{\displaystyle \sum _i({\phi }_i\ast P_i(t))+{\displaystyle \sum _{t=1}^T{\beta }_{\mathrm{BE},i}}(P_{\mathrm{ch},i}(t)+\left|P_{\mathrm{dis},i}(t)\right|)}}\\ +{\displaystyle \sum _{t=1}^T{\beta }_{\mathrm{ccs}}}(V_{\mathrm{ra},\mathrm{in}}(t)+V_{\mathrm{ra},\mathrm{out}}(t))\\ C_3=T_{{\mathrm{CO}}_2}\\ C_4=\delta *{\displaystyle \sum _{t=1}^N(P_{\mathrm{WT},\mathrm{f}}(t)-P_{\mathrm{WT},\mathrm{a}}(t))+\delta *{\displaystyle \sum _{t=1}^N(P_{\mathrm{PV},\mathrm{f}}(t)-P_{\mathrm{PV},\mathrm{a}}(t))}}\end{array}\right.$$

(21)

where $C_1$ represents the cost of the electricity and gas purchased; $C_2$ represents operational costs; $C_3$ denotes the cost of carbon trading; $C_4$ is the penalty cost of the RE curtailment; $E_{\mathrm{price}}(t)$ and $G_{\mathrm{price}}(t)$ are, respectively, the prices for purchasing power and gas; $P_{\mathrm{buy},\mathrm{e}}(t)$ and $P_{\mathrm{buy},\mathrm{g}}(t)$ are the purchased electricity and gas, respectively. a represents a type of equipment in the system; ${\phi }_i$ and $P_i(t)$ are the price of the O&M and power output of certain devices, excluding ES; ${\beta }_{\mathrm{BE},i}$ is the O&M cost price of energy storage devices; ${\beta }_{\mathrm{ccs}}$ is the O&M cost price of carbon capture and storage devices; $P_{\mathrm{WT},\mathrm{f}}(t)$ and $P_{\mathrm{WT},\mathrm{a}}(t)$ are, respectively, forecasted and actual power outputs of WT; $P_{\mathrm{PV},\mathrm{f}}(t)$ and $P_{\mathrm{PV},\mathrm{a}}(t)$ are, respectively, the forecasted and actual power outputs of PV; and $\delta$ is the RE curtailment penalty coefficient.

The most used clustering methods are K-means, Copula, and GAN. Copula captures nonlinear and complex dependencies, suitable for data with non-Gaussian distributions. GAN, based on adversarial deep learning, requires large datasets and significant computation. In contrast, K-means is a simple and efficient method, ideal for large-scale datasets, as it minimizes the squared distance between data points and cluster centers. Its speed and ease of implementation make it the chosen method for the scenario reduction in this study.

The proposed approach for constructing the fuzzy set is outlined in Figure 5. First, a non-parametric KDE is applied to fit historical forecast errors of RE, resulting in the error probability density function curve. Secondly, from this curve, the prediction interval at a given confidence level is derived, which reveals the potential fluctuations in the future power output. Thirdly, using the confidence interval and LHS, $N$ original scenarios are created. Finally, the scenario reduction method based on k-means is used to obtain $N_m$ typical scenarios along with the probability $P_0$. The process of transforming KDE-based forecast error distributions into the ambiguity set is as follows:

Step 1. Collect forecast error data: Calculate the error by comparing actual and predicted renewable energy outputs.

Step 2. Apply KDE: Use KDE to obtain a smoothed density function of probability for the forecast errors.

Step 3. Construct the uncertainty set: Transform the error distribution obtained from the KDE into an uncertainty set. The set is constructed by defining bounds on the forecast errors based on specific confidence levels, which represent the probability that the true distribution will lie within the uncertainty set.

Step 4. Define the boundaries of the uncertainty set: Set the boundaries of the forecast errors based on specified confidence levels.

Step 5. Integrate the uncertainty set into the optimization model: Incorporate the uncertainty set as a constraint in the optimization model to account for uncertainty.

The density function of the probability $f(e)$ of the prediction error e can be formulated as follows:

$$f(e)=1/N_{i}h{\displaystyle \sum _{m=1}^{N_i}g(e-e_m/h)}$$

(22)

where $N_i$ is the total sample number, $g(x)$ is the gaussian kernel adopted in this paper, $e_m$ denotes the error samples, and $h$ refers the bandwidth parameter.

For each power output range, the corresponding probability density of the forecast error is calculated according to Equation (20). The interval at a given confidence level can be derived by employing probability density curves of the output power and deterministic forecast.

The probability distribution based on N representative scenarios and their respective probabilities, p, is bound to deviate from the true distribution. Moreover, for renewable energy sources like wind and solar, this deviation involves both small-scale fluctuations and rare, large deviations caused by weather conditions, which can be handled by the 1-norm and ∞-norm, respectively. This combination ensures the robustness of the optimization process, as it minimizes large deviations while still allowing for the inherent variability in renewable energy generation. To mitigate this deviation, the probability distribution is confined to an ambiguity set constructed using a composite norm that integrates both the 1-norm and the ∞-norm:

$$\left\{\begin{array}{c}Pr\left\{\left.{‖p-p_0‖}_1\le {\theta }_1\right\}\right.\ge 1-2N\cdot exp(-2K{\theta }_1/N)\\ Pr\left\{\left.{‖p-p_0‖}_{\infty }\le {\theta }_{\infty }\right\}\right.\ge 1-2N\cdot exp(-2K{\theta }_{\infty })\end{array}\right.$$

(23)

where $Pr\left\{\right\}$ represents the probability measure, ${\theta }_{\infty }$ and ${\theta }_1$ represent allowable probability deviations under the ∞-norm and 1-norm constraints, respectively, $N$ denotes the total original scenario number, $p_0$ and $p$ are, respectively, the forecasted probability distribution and probability distribution within the fuzzy set.

For clarity, ${\alpha }_1$ and ${\alpha }_{\infty }$ are introduced to denote the confidence level imposed on given probability distributions. ${\alpha }_1$ represents the confidence in the uncertainty set, indicating the probability that the true distribution lies within the defined set. A higher α₁ corresponds to a greater level of assurance that the model will perform well under typical conditions. ${\alpha }_{\infty }$ represents the confidence in the worst-case scenario and is related to the tail of the uncertainty distribution. It accounts for rare, extreme events and ensures that the model remains robust even under the most adverse conditions. Consequently, the transformation is provided below:

$$\left\{\begin{array}{l}Pr\left\{\left.{‖p-p_0‖}_1\le {\theta }_1\right\}\right.\ge {\alpha }_1\\ Pr\left\{\left.{‖p-p_0‖}_{\infty }\le {\theta }_{\infty }\right\}\right.\ge {\alpha }_{\infty }\end{array}\right.$$

(24)

$$\left\{\begin{array}{l}{\theta }_1={\displaystyle \frac{N}{2K}}In(2N/1-{\alpha }_1)\\ {\theta }_{\infty }={\displaystyle \frac{1}{2K}}In(2N/1-{\alpha }_{\infty })\end{array}\right.$$

(25)

In summary, the ambiguity set formulated under the joint 1-norm and ∞-norm constraints is expressed as follows:

$$\left\{\left.p_n\left|\begin{array}{c}{p}_s\ge 0\\ {\displaystyle \sum _{s=1}^{N_s}{p}_s=1}\\ {\displaystyle \sum _{s=1}^{N_s}\left|p_s-p_{s0}\right|\le {\theta }_1}\\ \underset{1\le s\le N_s}{max}\left|p_s-p_{s0}\right|\le {\theta }_{\infty }\end{array}\right.\right\}\right.$$

(26)

where $p_s$ and $p_{s0}$ are the probability value and forecasted probability of scenario s, respectively.

Since Equation (24) involves absolute value constraints, it is linearized by introducing binary auxiliary variables, leading to the following conversion:

$$\left\{\begin{array}{c}{\displaystyle \sum _{s=1}^{N_s}\left|p_{s^{+}}-p_{s^{-}}\right|\le {\theta }_1}\\ p_{s^{+}}+p_{s^{-}}\le {\theta }_{\infty }\\ {\epsilon }_{s^{+}}+{\epsilon }_{s^{-}}\le 1\\ 0\le p_{s^{+}}\le {\epsilon }_{s^{+}}{\theta }_1\\ 0\le p_{s^{-}}\le {\epsilon }_{s^{-}}{\theta }_1\\ p_s=p_{s0}+p_{s^{+}}+p_{s^{-}}\end{array}\right.$$

(27)

where $p_{s^{+}}$ and $p_{s^{-}}$ represent the deviations above and below the expected probability distribution $p_s$ of scenarios s relative to $p_0$, respectively. ${\epsilon }_{s^{+}}$ and ${\epsilon }_{s^{-}}$ denote positive and negative variations for $p_s$, respectively.

4. Case Studies

The case study analyses are intended to assess the effectiveness and feasibility of the proposed IES model under the TCTM framework. To prove the feasibility and advantages of the presented system, several scenarios were established in this study, as shown in

Table 2. Coupled devices/systems under different scenarios.

Scenarios	CCUS	HBC	Fixed-Price Carbon Trading	TCTM
1	×	×	×	×
2	×	√	×	×
3	√	×	×	×
4	√	√	×	×
5	√	√	√	×
6	√	√	×	√

. Scenarios 1–4 explore the optimal approaches to hydrogen utilization. Scenario 1 is the basic scenario without hydrogen utilization, Scenario 2 only considers hydrogen blending combustion, Scenario 3 only considers CCUS, and Scenario 4 considers HBC and CCUS. Scenarios 4–6 explore the advantages of carbon trading—Scenario 4 does not use carbon trading as the basic scenario—and Scenarios 5 and 6 implement fixed-price trading and tiered carbon trading mechanisms, respectively.

4.1. Basic Data

In the case studies, the price of natural gas is fixed at 2.72 CNY/m³, while electricity is priced according to the time-of-use, as shown in

Table 3. Electricity price in different periods.

Category	Time/h	Unit Price CNY/MWh
Valley tariff	22:00–5:00	295
Parity tariff	6:00–7:00 12:00–17:00	550
Peak tariff	8:00–11:00 18:00–21:00	804
Valley tariff	22:00–5:00	295

[28]. The fundamental equipment parameters of the proposed IES are presented in

Table 4. Energy storage device parameters.

Device	Charge and Discharge Efficiency	Storage Capacity/ MW	Lower Bound of Storage State	Upper Bound of Storage State
EES	0.9	150	0.1	0.8
TES	0.9	150	0.1	0.9
HES	0.9	200	0.2	0.8
CCS	0.9	50 (tons)	0.2	0.8
EES	0.9	150	0.1	0.8

[16,19,29], energy storage equipment parameters as delineated in

Table 5. Basic equipment parameters.

Equipment	Parameters	Values
GT	$E_{\mathrm{GT}}^{min}$/MW	100
	$E_{\mathrm{GT}}^{min}$/MW	350
	${\eta }_{\mathrm{GT}}$	0.35
WHB	$H_{\mathrm{WHB}}^{min}$/MW	80
	$H_{\mathrm{WHB}}^{max}$/MW	300
	${\eta }_{\mathrm{WHB}}$	0.9
CHP	${\eta }_{\mathrm{CHP}}$	0.95
	${\alpha }_{CHP}(t)$	[0, 0.2]
	${\psi }_{CHP}(t)$	(0, 1)
	$k_{CHP}(t)$	[0.6, 3]
EL	$P_{EL,e}^{min}$/MW	0
	$P_{EL,e}^{min}$/MW	200
	${\eta }_{EL}$	0.88
MR	$P_{\mathrm{MR},\mathrm{h}}^{min}$/MW	0
	$P_{\mathrm{MR},\mathrm{h}}^{max}$/MW	150
	${\eta }_{MR}$	0.65

, and O&M parameters are listed in

Table 6. O&M cost parameters.

Equipment	O&M Values (CNY/MW)
GT	25
WHB	18
EES	20
TES	12
HES	35
CCS	40
EL	40
MR	55
PV/WT	350 (punishment for abandoning RE cost, CNY/MWh)

[24,29]. Furthermore, the carbon quota and actual emissions for external electricity procurement are 0.798 t/MWh and 1.08 t/MWh, respectively, while for natural gas, these values are 0.324 t/MWh and 0.385 t/MWh. The tiered carbon trading range is 150 t, with a base price of 150 CNY/t and a price growth rate of 25%. These values for the base price and growth rate are derived from the discussions in Section 5.4.

The RE curtailment penalty coefficient (δ) is estimated based on electricity prices to calculate the revenue loss from curtailment. In this study, the electricity price ranges from 295 CNY/MWh to 804 CNY/MWh, and the penalty cost is set at 350 CNY/MWh to reflect real-world conditions. The total cost of RE accommodation is 190 CNY/MWh (including the cost of MR, EL, etc.). Therefore, a penalty cost above 190 CNY/MWh effectively incentivizes methane conversion. Hence, the penalty cost is set at 350 CNY/MWh, promoting CO₂ reuse while reflecting practical considerations.

Additionally, this study focuses on CO₂ emissions and carbon trading impacts and, thus, does not consider NOx emissions, as modern CHP plants already achieve ultra-low NOx emissions, making it outside the scope of this study. Regarding combustion stability, it is assumed to remain within acceptable limits for typical hydrogen blending ratios (up to 20%), as moderate hydrogen blending has minimal effects on stability. Furthermore, the impact of hydrogen blending on maintenance costs is minimal at lower blending ratios (0–20%) since modern gas turbines are designed to handle various fuel mixtures, with higher blending ratios potentially increasing maintenance costs due to higher temperatures and reactivity.

The data in this paper are from solar and wind power plants, as well as a gas-fired cogeneration plant in North China. The predicted data for the WT and PV output, along with electricity and thermal loads, is shown in Figure 6. The model introduced is a mixed-integer linear programming framework. Therefore, optimal IES scheduling is developed using the YALMIP modeling technique on the MATLAB 2023a platform, with the Gourbi commercial solver employed to solve the model. Figure 7 illustrates the entire workflow of building and solving the IES scheduling model.

4.2. Fuzzy Sets of RE

In the IES, it is crucial to consider the randomness and interdependence of WT and PV outputs to guarantee the security and dependability of both scheduling and operations. Due to the larger variability and higher uncertainty of wind power, while the variability in solar power is smaller with weaker uncertainty, the bandwidth values are primarily influenced by the uncertainty in wind and solar generation. In this study, the bandwidth is optimized using leave-one-out cross-validation (LOO-CV). The optimal bandwidth may vary depending on the historical data, and in this study, the bandwidth for solar power is 0.8, while the bandwidth for wind power is 1.2. The forecasted interval curves for WT and PV at 80% and 99% confidence levels are illustrated in Figure 8. The interval size can be modified based on the confidence level. As the confidence level increases, the probability of the actual output being included within the prediction interval increases. Figure 9 displays the probability of four representative scenarios obtained through LHS and k-means clustering. Based on the forecast intervals of WT and PV, LHS is applied to generate 2000 original scenarios. Then, the k-means clustering method is applied to derive representative scenarios with their corresponding probability values.

4.3. Optimization Scheduling Results

As illustrated in Figure 10a, the electric load is mainly provided by WT, PV, and GT, supplemented by externally purchased electricity. To minimize costs, the RE output is prioritized for supply to the user, with any shortfall met by the GT unit and electricity support from the grid. Excess WT and PV output is converted by EL to generate hydrogen, enabling spatial and temporal electricity transfer. Additionally, EL operates primarily during WT peak periods, while the GT output is increased in high electricity price intervals to minimize electricity purchase costs. Given that the RE output is higher during periods of valley tariffs and the purchasing electricity from the grid is higher during peak periods of peak tariffs, the system opts to purchase electricity from the grid during periods of weak RE outputs and parity prices.

As shown in Figure 10b, the WHB provides the primary heat supply. The thermal energy storage system stores heat in low-load periods and releases it in peak-load periods. Liquid-rich pyrolysis occurs during times of high RE output, enabling the utilization of surplus hydrogen for CO₂ methanation.

As seen in Figure 10c, the output of EL is primarily concentrated between 23:00 and 08:00, especially from 23:00 to 07:00; excess hydrogen is even stored. This period coincides with the peak output of RE and the lower demand for electricity. Additionally, hydrogen stored in the storage device is mainly consumed for blending combustion between 14:00 and 16:00. Due to the limitations of hydrogen blend ratios and the higher costs associated with CCUS, only approximately 27.5% of the hydrogen is used for gas synthesis in MR, while about 72.5% is combusted in GT. Through the energy conversion and hydrogen utilization processes, refining the three-stage hydrogen utilization process, in contrast to a single-stage approach, can enhance the flexibility of the IES, while also reducing carbon emissions and cascading energy losses.

As illustrated in Figure 10d, the main source of natural gas consumed in the system is supplied by the upper natural gas network, with a small portion sourced from MR. Gas consumption is mainly determined by the output of the GT and WHB, which depends on the electric–thermal load. The gas produced by MR helps reduce gas procurement costs and carbon trading expenses to a certain extent.

As shown in Figure 11, the system, with a flexible thermoelectric and hydrogen blending ratio, optimizes the economic performance based on factors such as the load demand, renewable energy generation, electricity prices, and other variables. The hydrogen blending ratio increases in high RE output periods and decreases in low RE output periods. These strategies allow the system to optimize both operational costs and the integration of RE, ensuring a cost-effective and sustainable energy supply.

Figure 12 illustrates the dynamic relationships between different energy inputs and consumptions, which visualizes the electricity, thermal, gas, and hydrogen energy flows, including the conversion, storage, and usage across carriers.

5. Further Discussion and Analysis

5.1. Comparative Analysis of Hydrogen Utilizations

To confirm the effectiveness of the proposed IES model at reducing total costs and carbon emissions. Scenarios 1–4 explore different methods of hydrogen utilization.

Scenario 1, as the basic scenario, excludes the EL and MR device, which is vital in RE utilization and carbon reduction, consequently increasing carbon emissions and RE curtailment costs. Scenario 2 includes the EL and adopts HBC, which reduces the gas consumption to a certain extent. However, constrained by the upper limit of the hydrogen blend ratio, the full absorption of RE cannot be achieved. In Scenario 3, hydrogen is exclusively utilized for gas synthesis, a process that achieves complete RE absorption but incurs higher costs owing to the high expense and low hydrogen utilization efficiency associated with CCUS. Scenario 4 includes HBC and CCUS, which combined Scenarios 2 and 3, to explore the optimal route for hydrogen utilization. The generated hydrogen is prioritized for blending combustion, as the hydrogen that cannot be consumed by the hydrogen blending will be used for methane generation, achieving the optimal RE consumption rate and cost of the system. The results presented in Figure 12 and Figure 13 match the experimental results.

The costs of Scenarios 1–6 is shown in Figure 13, involving total costs, operation and maintenance (O&M) costs, natural gas procurement cost, electricity procurement costs, RE curtailment penalty costs, and so on. In comparison to other scenarios, Scenario 4 results in the lowest total costs, as it excludes carbon trading costs, while the accommodation ratio of RE reaches its peak at approximately 99.89%. This demonstrates that the refined utilization of hydrogen positively impacts the reduction in carbon emissions and enhances WT and PV utilization rates. Additionally, a comparative study of Scenario 1 and Scenario 2 reveals that integrating hydrogen utilization can significantly reduce RE penalty costs. However, the sole use of hydrogen blending does not fully utilize RE; when the hydrogen blending rate in Scenario 2 reaches its maximum, as shown in Figure 11, the capacity for RE utilization reaches a bottleneck. Comparing Scenario 2 with Scenario 3 reveals that syngas production via MR has a significant effect for reducing carbon emissions and increasing RE utilization rates. However, O&M costs in Scenario 3 are 29.42% and 16.05% higher than in Scenarios 2 and 4, respectively. The results from Scenario 4 demonstrate that when CCUS is combined with hydrogen blending, it achieves a near-complete utilization of RE while reducing system operating costs. Compared to the baseline scenario, the carbon emissions in Scenario 4 decrease by 5.7%, and the RE utilization rate increases from 79% to 99.89%.

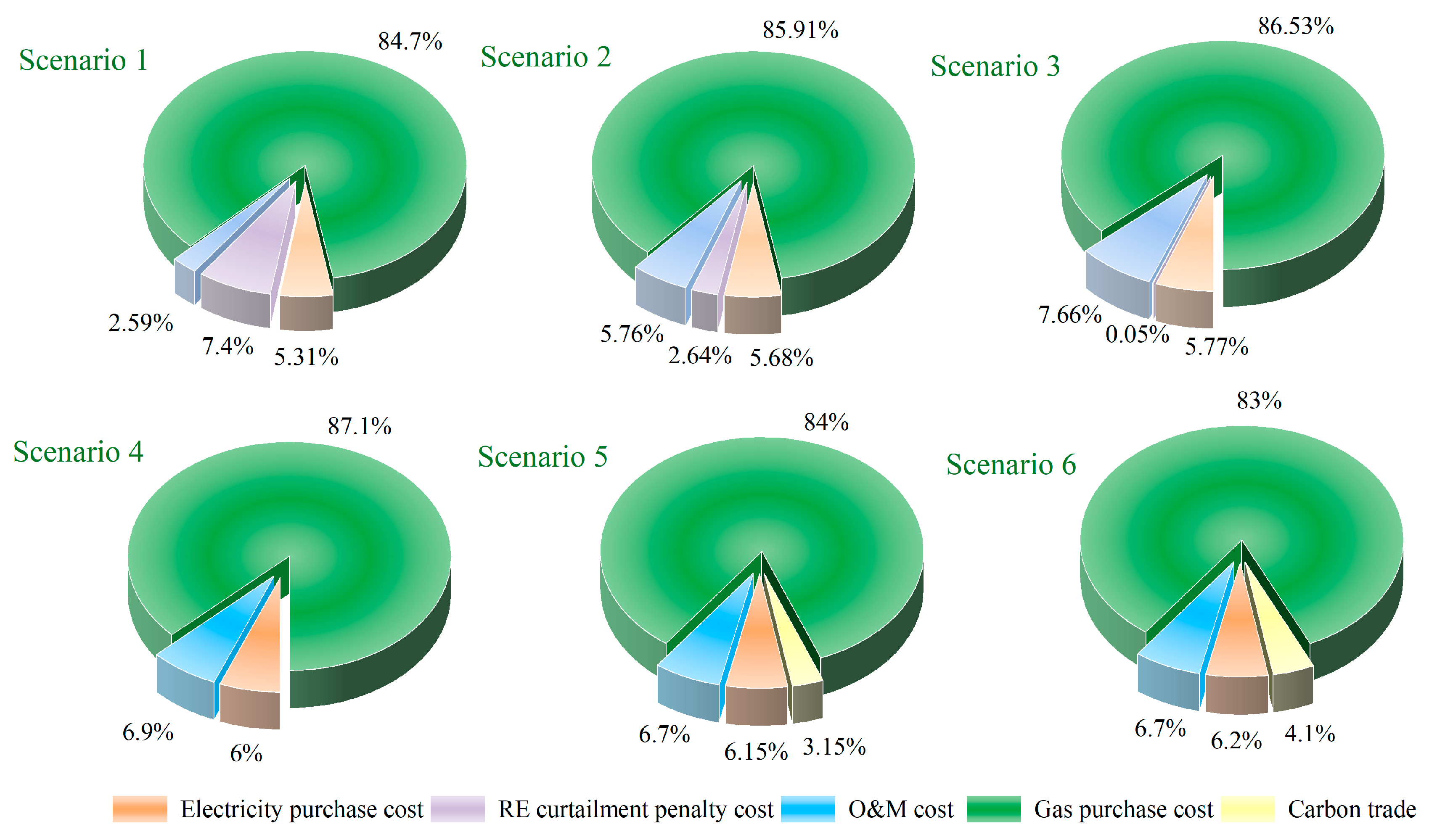
5.2. Comparative Discussion of Carbon Trading Mechanism

To highlight the advantages of the TCTM, Scenario 4, which excludes carbon trading, is compared with Scenarios 5 and 6, which implement fixed-price trading and tiered carbon trading mechanisms, respectively.

As illustrated in Figure 13 and Figure 14, it is essential for IES to operate within the carbon trading market, which can further decrease carbon emissions. As mentioned, Scenario 4 excludes the carbon trading cost, making it zero and resulting in the lowest total cost at this point. Additionally, compared to Scenario 4, the TCTM and fixed-price carbon trading can reduce carbon emissions by approximately 3.4% and 2.4%, respectively. Compared to the carbon trading mechanism with a fixed price, the TCTM shows better effectiveness at reducing carbon emissions.

5.3. Hydrogen Blending Combustion Rate of CHP Analysis

Figure 15 presents the results of experiments with different fixed and adjustable hydrogen blending ratios. When the HBC ratio of the CHP is fixed, the total cost of the IES initially decreases as the hydrogen blending ratio increases. This is due to the greater utilization of RE and a reduction in gas consumption. However, when the blending ratio reaches 12%, the total cost reaches its minimum, and after this point, the system’s total cost increases rapidly with the rise in the blending ratio. At this point, the electricity generated by the GT is required to produce hydrogen via EL during high electrical demand and low RE output periods, which is then fed into the GT for combustion to maintain the set hydrogen blending ratio. This not only significantly reduces the system’s energy efficiency but also increases the system’s gas purchase costs. In contrast, the adjustable hydrogen blending ratio can optimize the blending ratio based on the RE output and electric load characteristics, maximizing the system cost reduction. An adjustable hydrogen blending ratio reduces the total cost by CNY 14,063 relative to a fixed hydrogen blending ratio of 12%.

5.4. The Analysis of the Tiered Carbon Trading Mechanism Parameters

This study examines how the carbon base price and growth rate influence the system’s carbon emissions, as shown in Figure 16. The carbon trade base price has a more significant effect on carbon emissions than the rate of the price growth. As the base price increases, carbon emissions decrease more sharply than with the gradual decline observed with the growth rate of the carbon trading price. While both the carbon trading base price and its growth rate contribute to the reduction in carbon emissions through operational optimization, the reduction remains limited.

Furthermore, as the trading price and the increase rate of the TCTM rise, the rate of the reduction in carbon emissions gradually slows down. Carbon emissions reach their smallest threshold when the carbon trading base price is approximately CNY 120/t, CNY 150/t, CNY 225/t, and CNY 250/t, with corresponding growth rates of 65%, 30%, 20%, and 0%, respectively. To optimize the carbon mitigation potential of the proposed IES while maintaining economic efficiency, an optimal balance of the base price and growth rate is required—such as a benchmark price around CNY 150/t and an increasing rate around 25%, resulting in a lower total cost of CNY 3,854,222.94. Excessive rises in the carbon trading price and its rate of increase may not significantly reduce carbon emissions. Instead, they result in a substantial rise in costs. The experimental results presented here offer insights for the application of the TCTM and configuring its parameters.

5.5. Comparison of Methods for Handling Uncertainty

Table 7. A comparison of the outcomes from different methods.

Optimization Method	Total Costs/CNY	Amount of Carbon Emissions/Tons	Calculation Time/s
SP	3,846,410.53	4213.54	786
RO	3,931,307.64	4507.74	34
DRO	3,854,222.94	4227.67	55

shows a comparison between the total cost and carbon emissions of the IES under different uncertainty-based optimization approaches. Among them, SP exploits the probability distributions of uncertain variables to minimize expected costs, typically delivering stronger economic performances. However, representing uncertainty with large scenario sets inflates the model size and degrades computational efficiency. In contrast, RO disregards historical data and relies on an unrealistically wide fluctuation range to ensure the system performs effectively, even under the most extreme conditions. While this strategy enhances system robustness and computational efficiency, it does not guarantee economic efficiency. In summary, compared with conventional uncertainty treatments, the total cost and calculation time under DRO typically lie between that of SP and RO. The proposed DRO approach simultaneously accounts for economic efficiency, computational efficiency, and robustness, making it an ideal method for handling WT and PV uncertainties.

6. Conclusions and Outlook

This study proposes an optimal dispatch model for an IES based on a power plant, combining CCUS and HBC within a tiered carbon trading market. To address the uncertainty in RE outputs, a data-driven DRO method using KDE is applied. Numerical simulations confirm the effectiveness of the proposed model. The key conclusions are as follows:

• Dealing with the uncertainty of the RE output, SP minimizes the expected cost under probabilistic scenarios and is typically more economical, but its scalability deteriorates as the number of scenarios grows. RO enforces worst-case feasibility over a prescribed uncertainty set, enhancing robustness at the expense of a higher operating cost. In contrast, DRO yields total costs between SP and RO, while achieving a better balance of the economy and robustness, making it well suited to address WT/PV uncertainty.
• Due to the upper limit of the hydrogen blend rate—using HBC alone with an RE utilization rate of about 93%—using hydrogen for methanation alone further raises RE utilization but drives up O&M costs sharply. Combining HBC with CCUS delivers the best overall performance: it achieves near-complete RE utilization and the lowest total cost. The joint deployment of HBC and CCUS offers the most favorable cost–emissions trade-off for the IES.
• A comparison between the TCTM and other carbon trading mechanisms demonstrates the former’s superior operational performance. Specifically, the TCTM and fixed-price trading reduce the carbon emissions of the system by approximately 3.4% and 2.4%, respectively. Moreover, we examined the impact of the TCTM parameters, like the carbon trading price and increasing rate, on CO₂ emissions of the system. The suitable carbon trading parameters play a critical role in preventing a higher expenditure and weaker involvement of the carbon market.

In the future, the integration of increasing amounts of renewable energy into IESs will significantly raise system-level uncertainty. Artificial intelligence has great potential to enhance forecast accuracy, presenting a promising direction for future research. Moreover, this study primarily focuses on daily scenarios, with an insufficient analysis of optimal dispatches over long-term and multiple time scales. Therefore, further validation is needed to assess the reliability and economic viability of long-term operations.