Adaptive Virtual Impedance Fault Overcurrent Suppression Method and Reactive Power Support Method with Frozen Reactive Power–Voltage Droop Control for Grid-Forming Converters

Abstract

With the rapid development of new energy, high-proportion new energy power systems have significantly reduced inertia and voltage support capacity, facing severe stability challenges. Virtual Synchronous Generator (VSG) control, which simulates the inertia and voltage source characteristics of traditional synchronous generators, enables friendly grid connection of new energy converters and has become a key technology for large-scale new energy applications. This paper addresses two key issues in low-voltage ride through (LVRT) of grid-forming converters under VSG control: (1) converter overcurrent suppression during LVRT; (2) reduced reactive power support due to retaining voltage-reactive power droop control during faults. It proposes an adaptive virtual impedance-based overcurrent suppression method and a frozen reactive power–voltage droop-based reactive support method. Based on the converter’s mathematical model, a DIgSILENT/PowerFactory simulation model is built. Time-domain simulations verify the converter’s operating characteristics and the improved LVRT strategy’s effect, providing theoretical and technical support for large-scale applications of grid-forming converters.

1. Introduction

Power electronic converters are the primary means of grid connection for wind and photovoltaic sources, with grid-following (GFL) converters currently dominating. GFL converters inject power as a current source via phase-locked loop (PLL)-based instantaneous voltage phase capture, featuring flexible configuration and mature technology. However, with rising renewable energy penetration, they fail to offset defects from synchronous generator replacement—including insufficient grid disturbance resilience and poor power angle, frequency, and voltage stability.

In contrast, GFM converters simulate synchronous generator characteristics to provide inertia/frequency support, possess voltage source properties for voltage support, and have adjustable output impedance (suitable for weak grids). They can also stabilize all-renewable power systems, making them key to solving new energy grid connection issues. Switching from GFM to GFL mode causes loss in voltage source property [1], so transient control strategies maintaining GFM mode have been proposed [2], categorized into overcurrent suppression, reactive support, and asymmetric fault negative-sequence control [3].

Existing research has limitations: (1) virtual impedance-based overcurrent suppression methods lack adaptive mechanisms (fixed impedance fails to adapt to dynamic system changes, and deep voltage dips impair terminal voltage control) [4,5,6,7,8,9,10,11]; (2) reactive power support methods overlook the weakened capability caused by retaining reactive-voltage droop during faults—its negative feedback reduces internal electromotive force, lowering reactive output [12,13,14,15,16].

To address these gaps, this paper proposes (1) an adaptive virtual impedance method (using current threshold deviation as feedback to adjust impedance dynamically) and (2) a frozen reactive voltage droop method (triggered by positive-sequence voltage to avoid droop-induced reactive loss). Complex simulations and HIL experiments verify the effectiveness of the proposed strategies.

2. Mathematical Model and Control Principle of VSG

VSG control simulates synchronous generator rotor motion [17], primary frequency regulation, excitation regulation, and damping inertia. This section constructs VSG topology and control models to lay a foundation for subsequent LVRT research.

2.1. Mathematical Model for Virtual Synchronous Generator Control

Figure 1 shows the LCL-filtered GFM grid-connected system. In this figure, the machine-side filter inductance is denoted as L_c, the grid inductance as L_g, and the filter capacitance as C, which, together, constitute an LCL filter; U_dc represents the DC voltage; u_g represents the grid voltage; u_t represents the capacitor voltage; u_pcc represents the line voltage at the grid point; u_tdq, u_gdq, i_Ldq, and i_gdq represent the dq components of the capacitor voltage, grid voltage, machine-side inductance current, and grid-point current, respectively; u_n and ω_n represent the rated voltage effective value and rated angular frequency, respectively; and E represents the amplitude of the internal potential in the VSG.

The inverter interface is an LCL filter consisting of L_c, L_g, and C. Neglecting the modulation process of the converter and assuming that the converter can accurately track the reference voltage, the state equation is

$$\left\{\begin{array}{l}{\displaystyle \frac{d{u}_{\mathrm{td}}}{dt}}={\displaystyle \frac{1}{C}}(\omega C{u}_{\mathrm{tq}}+i_{\mathrm{Ld}}-i_{\mathrm{gd}})\hfill \\ {\displaystyle \frac{d{u}_{\mathrm{tq}}}{dt}}={\displaystyle \frac{1}{C}}(-\omega C{u}_{\mathrm{td}}+i_{\mathrm{Lq}}-i_{\mathrm{gq}})\hfill \\ {\displaystyle \frac{d{i}_{\mathrm{Ld}}}{dt}}={\displaystyle \frac{1}{L_{\mathrm{c}}}}(\omega L_{\mathrm{c}}{i}_{\mathrm{Lq}}+u_{\mathrm{sd}}-u_{\mathrm{td}})\hfill \\ {\displaystyle \frac{d{i}_{\mathrm{Lq}}}{dt}}={\displaystyle \frac{1}{L_{\mathrm{c}}}}(-\omega L_{\mathrm{c}}{i}_{\mathrm{Ld}}+u_{\mathrm{sq}}-u_{\mathrm{tq}})\hfill \\ {\displaystyle \frac{d{i}_{\mathrm{gd}}}{dt}}={\displaystyle \frac{1}{L_{\mathrm{g}}}}(\omega L_{\mathrm{g}}{i}_{\mathrm{gq}}+u_{\mathrm{td}}-u_{\mathrm{gd}}-R_{\mathrm{g}}{i}_{\mathrm{gd}})\hfill \\ {\displaystyle \frac{d{i}_{\mathrm{gq}}}{dt}}={\displaystyle \frac{1}{L_{\mathrm{g}}}}(-\omega L_{\mathrm{g}}{i}_{\mathrm{gd}}+u_{\mathrm{tq}}-u_{\mathrm{gq}}-R_{\mathrm{g}}{i}_{\mathrm{gq}})\hfill \end{array}\right.$$

(1)

In Figure 1, the components of grid voltage u_g can be represented as

$$\left\{\begin{array}{l}{u}_{\mathrm{gd}}=\sqrt{2}\ast u_{\mathrm{g}}\cos \delta \hfill \\ u_{\mathrm{gq}}=-\sqrt{2}\ast u_{\mathrm{g}}\sin \delta \hfill \end{array}\right.$$

(2)

In the formula, δ represents the phase angle at which the internal potential of the VSG leads the grid voltage. Assuming the angular frequency of the grid voltage is ω_g, we have

$$\delta ={\displaystyle \int (\omega -{\omega }_{\mathrm{g}})}dt$$

(3)

If the given active power reference value P_ref is greater than the actual active power P, then $d\delta /dt>0$, δ showing an increasing trend, and the active power increases with the increase in the power angle, reducing the deviation between the reference value of active power and the actual active power. This process continues until the two values become equal.

Assuming that the virtual rotor winding of the VSG is powered by a variable DC current source i_f, the output voltage is

$$E=\dot{\theta }{M}_{\mathrm{f}}{i}_{\mathrm{f}}\widetilde{\sin \theta }$$

(4)

Define

$$\varphi =\left[\begin{array}{c}{\varphi }_{\mathrm{a}}\\ {\varphi }_{\mathrm{b}}\\ {\varphi }_{\mathrm{c}}\end{array}\right]\hspace{1em}, i=\left[\begin{array}{c}{i}_{\mathrm{a}}\\ i_{\mathrm{b}}\\ i_{\mathrm{c}}\end{array}\right]$$

(5)

and

$$\widetilde{\cos \theta }=\left[\begin{array}{c}\cos \theta \\ \cos \left(\theta -{\displaystyle \frac{2\pi }{3}}\right)\\ \cos \left(\theta -{\displaystyle \frac{4\pi }{3}}\right)\end{array}\right]\hspace{1em}\widetilde{\sin \theta }=\left[\begin{array}{c}\sin \theta \\ \sin \left(\theta -{\displaystyle \frac{2\pi }{3}}\right)\\ \sin \left(\theta -{\displaystyle \frac{4\pi }{3}}\right)\end{array}\right]$$

(6)

The active power P and reactive power Q generated by the converter at the bridge arm are, respectively,

$$\left\{\begin{array}{l}P=〈i,E〉\\ Q=〈i,E_{\mathrm{q}}〉\end{array}\right.$$

(7)

In the formula, < , > represents the traditional dot product operation, and E has the same amplitude but a phase lag of π/2. At this time,

$$E_{\mathrm{q}}=\dot{\theta }{M}_{\mathrm{f}}{i}_{\mathrm{f}}\tilde{\sin }\left(\theta -{\displaystyle \frac{\pi }{2}}\right)=-\dot{\theta }{M}_{\mathrm{f}}{i}_{\mathrm{f}}\tilde{\cos }\theta$$

(8)

Therefore, the active power and reactive power at this time can be expressed as

$$\left\{\begin{array}{l}P=\dot{\theta }{M}_{\mathrm{f}}{i}_{\mathrm{f}}〈i,\widetilde{\sin \theta }〉\\ Q=-\dot{\theta }{M}_{\mathrm{f}}{i}_{\mathrm{f}}〈i,\widetilde{\cos \theta }〉\end{array}\right.$$

(9)

In the formula, i is the stator current, $\theta$ is the electrical angle of the rotor, and i_f is the excitation current of the rotor. Under the condition of sinusoidal steady state, we have

$$\left\{\begin{array}{l}P=\dot{\theta }{M}_{\mathrm{f}}{i}_{\mathrm{f}}〈i,\tilde{\sin }\theta 〉={\displaystyle \frac{3}{2}}\dot{\theta }{M}_{\mathrm{f}}{i}_{\mathrm{f}}{i}_0\cos (\theta -\phi )\\ Q=-\dot{\theta }{M}_{\mathrm{f}}{i}_{\mathrm{f}}〈i,\tilde{\cos }\theta 〉={\displaystyle \frac{3}{2}}\dot{\theta }{M}_{\mathrm{f}}{i}_{\mathrm{f}}{i}_0\sin (\theta -\phi )\end{array}\right.$$

(10)

When θ – φ = 0, the product of the effective values of voltage and current is the active power P. When the phase difference between voltage and current is θ – φ = π/2, the product is the reactive power Q, which corresponds to inductive loads when Q is positive. At this time, the rotor mechanical equation of VSG can be expressed as

$$\ddot{\theta }={\displaystyle \frac{1}{J}}(T_{\mathrm{m}}-T_{\mathrm{e}}-D_{\mathrm{p}}\dot{\theta })$$

(11)

In the formula, T_m represents the virtual mechanical torque; T_e represents the torque corresponding to the active power generated by the VSG, which is also known as the virtual electromagnetic torque; and D_p represents the damping coefficient, also known as the frequency droop coefficient. In the VSG, this formula, along with Formulas (4) and (8), constitutes the core of the electronic part of the VSG.

A two-level inverter is chosen for its simple topology, low cost, and low failure rate in medium-low voltage/power scenarios, sufficient to verify LVRT control strategies (adaptive virtual impedance, frozen droop). Multilevel inverters are better for high-voltage/high-power; the LVRT methods adapt by adjusting PWM voltage references and operating independently of level expansion logic, with future verification on a three-level platform.

2.2. Principles of Virtual Synchronous Generator Control

2.2.1. Active Power–Frequency Control Link

The speed of the synchronous generator rotor is adjusted by the prime mover, and physical friction generates a damping coefficient D_p. According to the frequency variation in the power grid, the synchronous generator can change the active power it generates, thus achieving uniform distribution of load, that is, frequency droop control [18]. The VSG can achieve this process by sending the difference between the virtual angular velocity $\dot{\theta }$ and the rated angular velocity ${\dot{\theta }}_{\mathrm{n}}$ to the damping module. At this time, D_p is the frequency droop coefficient of VSG, which is defined as the ratio of torque increment ΔT to speed increment $\Delta \dot{\theta }$, that is,

$$D_{\mathrm{p}}={\displaystyle \frac{\Delta T}{\Delta \dot{\theta }}}$$

(12)

At this time, the ratio of power change to corresponding frequency change is set. The mechanical torque T_m is given by the following formula:

$$T_{\mathrm{m}}={\displaystyle \frac{P_{\mathrm{set}}}{{\omega }_{\mathrm{ref}}}}$$

(13)

The virtual rotational inertia of VSG can be calculated using the following formula:

$$J=D_{\mathrm{p}}{\tau }_{\mathrm{f}}$$

(14)

where τ_f is the time constant of the frequency loop; J is the virtual rotational inertia of VSG.

The overall active power control equation is as follows:

$$J\ddot{\theta }=T_{\mathrm{m}}-T_{\mathrm{e}}-D_{\mathrm{p}}({\omega }_{\mathrm{ref}}-\omega )$$

(15)

In the formula, T_e represents the electromagnetic torque, ω_ref denotes the rated angular speed, and ω signifies the actual angular speed [19]. The expression for electromagnetic torque is as follows:

$$T_{\mathrm{e}}={\displaystyle \frac{P}{{\omega }_{\mathrm{ref}}}}$$

(16)

The feedback control loop for the active power of VSG is illustrated in Figure 2.

2.2.2. Reactive Power–Voltage Control Link

The reactive power control loop of VSG is similar to the active power control loop [20], and the voltage droop coefficient D_q is defined as the ratio between the change in reactive power ΔQ and the change in voltage Δu:

$$D_{\mathrm{q}}={\displaystyle \frac{\Delta Q}{\Delta u}}$$

(17)

The feedback control loop for reactive power is shown in Figure 3.

Similarly to the active power control structure, the reactive power regulation mechanism is also a cascaded control structure [21]. The inner loop is the voltage loop, and the outer loop is the reactive power loop. The time constant τ_u of the voltage loop is

$${\tau }_{\mathrm{u}}={\displaystyle \frac{K}{\dot{\theta }{D}_{\mathrm{q}}}}\approx {\displaystyle \frac{K}{{\dot{\theta }}_{\mathrm{n}}{D}_{\mathrm{q}}}}$$

(18)

Since the change in $\dot{\theta }$ is small, at this time,

$$K={\dot{\theta }}_{\mathrm{n}}{D}_{\mathrm{q}}{\tau }_{\mathrm{u}}$$

(19)

The overall reactive power control equation is as follows:

$$K{\displaystyle \frac{dE}{dt}}=Q_{\mathrm{ref}}-Q+D_{\mathrm{q}}(U_{\mathrm{ref}}-U)$$

(20)

The overall control equation is as follows:

$$\left\{\begin{array}{l}J\ddot{\theta }=T_{\mathrm{m}}-T_{\mathrm{e}}-D_{\mathrm{p}}({\omega }_{\mathrm{ref}}-\omega )\\ K{\displaystyle \frac{dE}{dt}}=Q_{\mathrm{ref}}-Q+D_{\mathrm{q}}(U_{\mathrm{ref}}-U)\end{array}\right.$$

(21)

Electromagnetic torque T_e and reactive power Q are calculated using the provided formula. The control structure of the VSG outer loop is illustrated in Figure 4.

After the basic topological structure and control link modeling of VSG are completed, the modeling of the improved control link is carried out, including two parts: the virtual impedance control link and the voltage and current double closed-loop control link [22].

2.2.3. Virtual Impedance Control Link

Virtual impedance control can optimize the power distribution accuracy of parallel converters by introducing adjustable impedance characteristics into the line reference voltage, simulating the impedance distribution of the actual power system, and changing the equivalent impedance between the converter outlet and the PCC point. The traditional virtual impedance control expression is R_v + sL_v, which is usually inductive. The inductance part sL_v needs to be implemented through a differential link, which can amplify high-frequency noise. This paper uses R_v + jωX_v instead of R_v + sL_v to avoid the high-frequency noise problem caused by the differential link.

When using virtual impedance R_v + jωX_v,

$$\left\{\begin{array}{c}{u}_{\mathrm{t}\alpha \mathrm{ref}}=E\cos \theta -u_{\alpha }^{\prime }\\ u_{\mathrm{t}\beta \mathrm{ref}}=E\sin \theta -u_{\beta }^{\prime }\end{array}\right.$$

(22)

In the formula, $u_{\mathrm{t}\alpha \mathrm{ref}}$ represents the real part of the reference value provided by VSG to the voltage inner loop; $u_{\mathrm{t}\beta \mathrm{ref}}$ represents the imaginary part of the reference value provided by VSG to the voltage inner loop; E represents the amplitude of the internal potential of VSG; θ represents the voltage angle; $u_{\alpha }^{\prime }$ represents the real part of the virtual impedance voltage drop; and $u_{\beta }^{\prime }$ represents the imaginary part of the virtual impedance voltage drop. The virtual impedance generates a voltage drop, which reduces the internal potential of VSG. The expression for the voltage drop is

$$\left\{\begin{array}{l}{u}_{\alpha }^{\prime }=R_{\mathrm{v}}\ast i_{\mathrm{g}\alpha }-X_{\mathrm{v}}{i}_{\mathrm{g}\beta }\\ u_{\beta }^{\prime }=R_{\mathrm{v}}\ast i_{\mathrm{g}\beta }+X_{\mathrm{v}}{i}_{\mathrm{g}\alpha }\end{array}\right.$$

(23)

In the formula, $i_{\mathrm{g}\alpha }$ represents the α component of the grid-connected point current, and $i_{\mathrm{g}\beta }$ represents the β component of the grid-connected point current.

By adjusting the value of virtual impedance, the internal potential of VSG can be adjusted to suppress the fault overcurrent during voltage sag. In addition, proper virtual impedance settings can also achieve power decoupling. The control structure of the virtual impedance link is shown in Figure 5.

The introduction of virtual impedance in grid-connected converters can improve current distribution, avoid current imbalance and overload, and enhance system reliability.

2.2.4. Voltage and Current Double Closed-Loop Control Link

A typical voltage and current double closed-loop control system consists of a Proportional Integral (PI) controller [23]. The equation for the classic double closed-loop control system is as follows:

$$\left\{\begin{array}{l}{\displaystyle \frac{d{\varphi }_{\mathrm{d}}}{dt}}=u_{\mathrm{tdref}}-u_{\mathrm{td}}\\ {\displaystyle \frac{d{\varphi }_{\mathrm{q}}}{dt}}=u_{\mathrm{tqref}}-u_{\mathrm{tq}}\\ {\displaystyle \frac{d{\gamma }_{\mathrm{d}}}{dt}}=i_{\mathrm{Ldref}}-i_{\mathrm{Ld}}\\ {\displaystyle \frac{d{\gamma }_{\mathrm{q}}}{dt}}=i_{\mathrm{Lqref}}-i_{\mathrm{Lq}}\\ i_{\mathrm{Ldref}}=-\omega C{u}_{\mathrm{td}}+K_{\mathrm{pv}}(u_{\mathrm{tdref}}-u_{\mathrm{td}})+K_{\mathrm{iv}}{\varphi }_{\mathrm{d}}\\ i_{\mathrm{Lqref}}=\omega C{u}_{\mathrm{tq}}+K_{\mathrm{pv}}(u_{\mathrm{tqref}}-u_{\mathrm{tq}})+K_{\mathrm{iv}}{\varphi }_{\mathrm{q}}\\ u_{\mathrm{sd}}=u_{\mathrm{td}}-\omega L_{\mathrm{c}}{i}_{\mathrm{Lq}}+K_{\mathrm{pc}}(i_{\mathrm{Ldref}}-i_{\mathrm{Ld}})+K_{\mathrm{ic}}{\gamma }_{\mathrm{d}}\\ u_{\mathrm{sq}}=u_{\mathrm{tq}}+\omega L_{\mathrm{c}}{i}_{\mathrm{Ld}}+K_{\mathrm{pc}}(i_{\mathrm{Lqref}}-i_{\mathrm{Lq}})+K_{\mathrm{ic}}{\gamma }_{\mathrm{q}}\end{array}\right.$$

(24)

In the formula, K_pv is the proportional coefficient of the voltage loop PI controller; K_iv is the integral coefficient of the voltage loop PI controller; K_pc is the proportional coefficient of the current loop PI controller; K_ic is the integral coefficient of the current loop PI controller; ${\varphi }_{\mathrm{d}}$ and ${\varphi }_{\mathrm{q}}$ are the state variables of the voltage loop PI controller; and ${\gamma }_{\mathrm{d}}$ and ${\gamma }_{\mathrm{q}}$ are the state variables of the current loop PI controller.

The voltage and current double closed-loop control structure is shown in Figure 6.

This paper adopts the classic “PI + double closed-loop” architecture, which has a simple structure, mature parameter tuning, and fast current/voltage regulation, fully meeting LVRT’s overcurrent suppression and reactive support objectives without complex algorithms.

MPC offers strong constraint handling and fast dynamic response, optimizing control effects when combined with the proposed methods. However, its heavy computational load raises hardware costs.

In conclusion, PI double closed-loop control meets this paper’s needs, with MPC as a subsequent optimization direction to be verified via HIL.

3. Fault Overcurrent Suppression Method Based on Adaptive Virtual Impedance

This section mathematically analyzes the fault overcurrent suppression principle of fixed virtual impedance, verifies its limitations via time-domain simulations in DIgSILENT PowerFactory, proposes an adaptive virtual impedance-based method, validates it under multiple voltage sag levels, and compares it with the fixed virtual impedance method under the same fault conditions [24,25].

3.1. Mechanism of Overcurrent Suppression Based on Virtual Impedance Fault

Due to the large number of power electronic devices in the grid-connected converter, its ability to withstand overcurrent is limited, and reasonable control methods are needed to suppress fault overcurrent. As shown in Figure 7, after introducing virtual impedance, the equivalent model of the grid-connected converter will also change. R_v and X_v in the figure represent the added virtual resistance and virtual reactance, respectively.

After introducing virtual impedance, the expression is as follows:

$$E(t)=(r+R_{\mathrm{v}})i(t)+L{\displaystyle \frac{di(t)}{dt}}+j{X}_{\mathrm{v}}i(t)+U_{\mathrm{pcc}}(t)$$

(25)

Before the fault occurs, the output current expression of the grid-connected point is

$$i_{(0-)}={\displaystyle \frac{E(t)-U_{\mathrm{pcc}(0-)}}{r+R_{\mathrm{v}}+j(\omega L+X_{\mathrm{v}})}}$$

(26)

At this time, the expression of the instantaneous value of the fault current is as follows:

$$\left\{\begin{array}{l}i(t)=i_{(0-)}+\left(1-E^{-\frac{r+R_{\mathrm{v}}}{L}t}\right){\displaystyle \frac{U_{\mathrm{pcc}(0-)}-U_{\mathrm{pcc}(0+)}}{r+R_{\mathrm{v}}+j(\omega L+X_{\mathrm{v}})}}=i{(t)}_{\mathrm{w}}+i{(t)}_{\mathrm{z}}\hfill \\ i{(t)}_{\mathrm{W}}={\displaystyle \frac{E(t)-U_{\mathrm{pcc}(0+)}}{r+R_{\mathrm{v}}+j(\omega L+X_{\mathrm{v}})}}\hfill \\ i{(t)}_{\mathrm{Z}}={\displaystyle \frac{U_{\mathrm{pcc}(0+)}-U_{\mathrm{pcc}(0-)}}{r+R_{\mathrm{v}}+j(\omega L+X_{\mathrm{v}})}}{E}^{-\frac{r+R_{\mathrm{v}}}{L}t}\hfill \end{array}\right.$$

(27)

Compared with Formula (25), Formula (28) shows that the equivalent transmission impedance increases after using the virtual impedance control method. This not only reduces the peak overcurrent of the system but also reduces the reference value of the virtual synchronous machine voltage loop, avoiding a large current reference and thus suppressing the development of overcurrent and accelerating the elimination of fault current.

3.2. Limitations of Fixed Virtual Impedance in Suppressing Fault Overcurrent

According to the analysis in Section 3.1, after introducing a fixed virtual impedance, the expression for the steady-state component of the fault current is

$$i{(t)}_{\mathrm{W}}={\displaystyle \frac{E(t)-U_{\mathrm{pcc}(0+)}}{r+R_{\mathrm{v}}+j(\omega L+X_{\mathrm{v}})}}$$

(28)

When the voltage drops, the voltage at the grid connection point after the fault, U_pcc(0+), decreases. At this time, due to the fixed virtual impedance that cannot change with the system operating state, the impedance value cannot be increased to balance the impact of the decrease in U_pcc(0+). When the voltage drop is severe, $i{(t)}_{\mathrm{W}}$ it can increase to above 1.25 p.u.

The expression for the transient component of the fault current is

$$i{(t)}_{\mathrm{Z}}={\displaystyle \frac{U_{\mathrm{pcc}(0+)}-U_{\mathrm{pcc}(0-)}}{r+R_{\mathrm{v}}+j\omega (L+X_{\mathrm{v}})}}{E}^{-\frac{r+R_{\mathrm{v}}}{L}t}$$

(29)

Similarly, when the voltage drops, the voltage at the grid connection point after the fault, U_pcc(0+), decreases. The fixed virtual resistance impedance cannot increase its value under fault conditions to mitigate the impact of the decrease in U_pcc(0+), and the amplitude of the transient current cannot be further limited.

From the above analysis, fixed virtual impedance for fault overcurrent suppression lacks real-time adjustment to system states, maintaining a fixed value across varying fault severities: in mild faults, excessive impedance impairs the VSG’s voltage and reactive power support capabilities; in severe faults, insufficient impedance fails to limit overcurrent to a safe range. Thus, it has obvious limitations.

To verify these limitations, a DIgSILENT PowerFactory simulation model of the grid-connected converter was built (using the system structure in Figure 8 and parameters in

Table 1. The relevant parameters.

System Parameters	Numerical Value	System Parameters	Numerical Value
DC bus voltage Udc	1.2 kV	Switching frequency ƒs	10 kHz
Filter inductance L	0.035 mH	Reference amplitude of AC voltage E0	0.69 kV
Filter capacitor C	10 µF	Active droop coefficient Dp	100
Rated power of converter SN	2 MVA	Reactive droop coefficient Dq	10
Rated active power reference value Pref	1.5 MW	Virtual inertia J	3 kg·m2
Rated angular frequency ω0	314 rad/s	Reference frequency ƒ	50 Hz
Length of route 1	10 km	Rated current of circuit 1	0.531 kA
Resistance per unit length of line 1	0.076 Ω/km	Line 1 reactance per unit length	0.208 Ω/km

). With fixed virtual resistance (Rv = 0.5 p.u.) and reactance (Xv = 0.1 p.u.) values, the overcurrent suppression effect was analyzed under different voltage drop fault scenarios.

The relevant parameters are presented in Table 1.

Simulation verification of the limitations of fixed virtual impedance in fault overcurrent suppression involves two scenarios: mild voltage dips and severe voltage dips.

(1) Scenario 1: The voltage drop is relatively mild

At 0.1 s, a three-phase short-circuit fault occurs at 5% of line 1 with a transition impedance of 0.5 + j0.5 Ω (Figure 9). The voltage dip is shallow: the PCC three-phase voltage amplitude decreases from 1.0 p.u. to a minimum of 0.93 p.u. (remaining above 0.9 p.u.), and the maximum three-phase current is 1.22 p.u. (below 1.25 p.u.).

If the fault is cleared at 0.15 s, the grid voltage, current, active and reactive power conditions are as shown in Figure 10. After the fault is removed, the converter returns to normal operation.

Fixed virtual impedance performs well in fault overcurrent suppression, effectively limiting current to ≤1.25 p.u. during faults while enabling the converter to provide reactive support. However, its fixed value (non-adaptive to system conditions) keeps the fault current decay time constant high, prolonging recovery.

Under symmetrical faults, three-phase voltage and current change identically. For ease of analyzing voltage, current, and power variations, all variables are presented as amplitudes.

(2) Scenario 2: The voltage drop is relatively severe

Figure 11 shows the voltage, current, active and reactive power at the grid point if a three-phase short-circuit fault occurs at 13% of line 1 at 0.1 s, with a transition impedance of 0.5 + j0.5 Ω. The voltage drop is significant, with the grid point voltage amplitude dropping below 0.75 p.u. The maximum current amplitude is 1.486 p.u. and then stabilizes at 1.264 p.u., which is greater than 1.25 times the rated current. In this scenario, due to the inability of the fixed virtual impedance to adjust the impedance value in real time according to the system operating state, it cannot effectively suppress the fault overcurrent, and the converter has a serious overcurrent risk.

Simulation results show that with fixed virtual impedance for overcurrent suppression, a fixed setting can satisfy overcurrent suppression requirements in shallow voltage dips. However, its fixed value (non-adaptive to system conditions) keeps the fault current time constant high, prolonging recovery. In severe dips, the fixed impedance may fail to restrict fault current to a value below 1.25 p.u., risking converter overcurrent. Thus, an adaptive virtual impedance adjustment mechanism is required to match varying system operating states.

3.3. Principle of Adaptive Virtual Impedance for Suppressing Fault Overcurrent

To address the poor adaptability of fixed virtual impedance in fault overcurrent suppression, an adaptive virtual impedance method (Figure 12) is proposed. It introduces additional virtual resistance and reactance coefficients, taking the difference between measured and preset current thresholds as feedback to establish an adaptive adjustment mechanism. This mechanism adjusts impedance according to external conditions, enhancing the system’s overcurrent suppression capability under various fault scenarios.

The adaptive virtual impedance expression is $R_{\mathrm{v}}^{\prime }+j\omega X_{\mathrm{v}}^{\prime }$, where

$$\left\{\begin{array}{l}{R}_{\mathrm{v}}^{\prime }=R_{\mathrm{v}}\ast \left[1+K_{\mathrm{r}}\left(I-I_{\lim }\right)\right]\\ X_{\mathrm{v}}^{\prime }=X_{\mathrm{v}}\ast \left[1+K_{\mathrm{x}}\left(I-I_{\lim }\right)\right]\end{array}\right.$$

(30)

where K_r is the additional virtual impedance resistance coefficient; K_x is the additional virtual impedance reactance coefficient; I is the grid-connected point current amplitude; and I_lim is the preset current threshold value. At this time,

$$\left\{\begin{array}{l}{u}_{\alpha }^{\prime }=R_{\mathrm{v}}^{\prime }\ast i_{\mathrm{g}\alpha }-X_{\mathrm{v}}^{\prime }{i}_{\mathrm{g}\beta }\\ u_{\beta }^{\prime }=R_{\mathrm{v}}^{\prime }\ast i_{\mathrm{g}\beta }+X_{\mathrm{v}}^{\prime }{i}_{\mathrm{g}\alpha }\end{array}\right.$$

(31)

In the formula, $u_{\alpha }^{\prime }$ represents the real part of the virtual impedance voltage drop; $u_{\beta }^{\prime }$ represents the imaginary part of the virtual impedance voltage drop; $i_{\mathrm{g}\alpha }$ represents the real part of the measured current at the grid point; and $i_{\mathrm{g}\beta }$ represents the imaginary part of the measured current at the grid point.

Figure 13 shows the fault equivalent model after replacing the virtual impedance with an adaptive virtual impedance.

The specific formula is as follows:

$$E(t)=(r+R_{\mathrm{v}}^{\prime })i(t)+L{\displaystyle \frac{di(t)}{dt}}+j{X}_{\mathrm{v}}^{\prime }i(t)+U_{\mathrm{pcc}}(t)$$

(32)

At this time, the expression for the grid-connected output current before the fault occurs is

$$i_{(0-)}={\displaystyle \frac{E(t)-U_{\mathrm{pcc}(0-)}}{r+R_{\mathrm{v}}^{\prime }+j(\omega L+X_{\mathrm{v}}^{\prime })}}$$

(33)

The current expression after the fault occurs is

$$i(t)=i_{(0-)}+\left(1-e^{-\frac{r+R_{\mathrm{v}}^{\prime }}{L}t}\right){\displaystyle \frac{U_{\mathrm{pcc}(0-)}-U_{\mathrm{pcc}(0+)}}{r+R_{\mathrm{v}}^{\prime }+j(\omega L+X_{\mathrm{v}}^{\prime })}}$$

(34)

It can be decomposed into a steady-state component and a transient component, where the steady-state component i(t)_W is

$$i{(t)}_{\mathrm{W}}={\displaystyle \frac{E(t)-U_{\mathrm{pcc}(0+)}}{r+R_{\mathrm{v}}^{\prime }+j(\omega L+X_{\mathrm{v}}^{\prime })}}$$

(35)

By substituting Equation (31) into Equation (36), we obtain

$$i{(t)}_{\mathrm{W}}={\displaystyle \frac{E(t)-U_{\mathrm{pcc}(0+)}}{r+R\cdot [1+K_{\mathrm{r}}(I-I_{\lim })]+j(\omega L+X\cdot [1+K_{\mathrm{x}}(I-I_{\lim })])}}$$

(36)

We reasonably set the additional resistance coefficient K_r, additional reactance coefficient K_x, and preset current threshold value I_lim. If a voltage drop occurs, the post-fault grid voltage U_pcc(0+) decreases, and the measured current amplitude I at the connection point increases. The denominator in Equation (37) increases, balancing the impact of the decrease in U_pcc(0+), so that $i{(t)}_{\mathrm{W}}$ remains within a reasonable range. The transient component $i{(t)}_{\mathrm{Z}}$ is

$$i{(t)}_{\mathrm{Z}}={\displaystyle \frac{U_{\mathrm{pcc}(0+)}-U_{\mathrm{pcc}(0-)}}{r+R_{\mathrm{v}}^{\prime }+j(\omega L+X_{\mathrm{v}}^{\prime })}}{e}^{-\frac{r+{R^{\prime }}_{\mathrm{v}}}{L}t}$$

(37)

Formula (31) is substituted into Formula (38) to obtain

$$i{(t)}_{\mathrm{z}}={\displaystyle \frac{U_{\mathrm{pcc}(0+)}-U_{\mathrm{pcc}(0-)}}{r+R\cdot \left[1+K_{\mathrm{r}}\left(I-I_{\lim }\right)\right]+j\left(\omega L+X\cdot \left[1+K_{\mathrm{x}}\left(I-I_{\lim }\right)\right]\right)}}{e}^{-\frac{r+R\cdot \left[1+K_{\mathrm{r}}\left(I-I_{\lim }\right)\right]}{L}t}$$

(38)

In summary, the expression for the instantaneous value of fault current is as follows:

$$\left\{\begin{array}{l}i(t)=i_{(0-)}+\left(1-e^{-\frac{r+R\cdot \left[1+K_{\mathrm{r}}\left(I-I_{\lim }\right)\right]}{L}t}\right){\displaystyle \frac{U_{\mathrm{pcc}(0-)}-U_{\mathrm{pcc}(0+)}}{r+R\cdot \left[1+K_{\mathrm{r}}\left(I-I_{\lim }\right)\right]+j\left(\omega L+X\cdot \left[1+K_{\mathrm{x}}\left(I-I_{\lim }\right)\right]\right)}}\hfill \\ i{(t)}_{\mathrm{W}}={\displaystyle \frac{E(t)-U_{\mathrm{pcc}(0+)}}{r+R\cdot [1+K_{\mathrm{r}}(I-I_{\lim })]+j(\omega L+X\cdot [1+K_{\mathrm{x}}(I-I_{\lim })])}}\hfill \\ i{(t)}_Z={\displaystyle \frac{U_{\mathrm{pcc}(0+)}-U_{\mathrm{pcc}(0-)}}{r+R\cdot \left[1+K_{\mathrm{r}}\left(I-I_{\lim }\right)\right]+j\left(\omega L+X\cdot \left[1+K_{\mathrm{x}}\left(I-I_{\lim }\right)\right]\right)}}{e}^{-\frac{r+R\cdot \left[1+K_{\mathrm{r}}\left(I-I_{\lim }\right)\right]}{L}t}\hfill \end{array}\right.$$

(39)

Adaptive virtual impedance control adapts to different fault scenarios and system operating states via a feedback mechanism based on the difference between the preset current threshold and measured current amplitude (control structure shown in Figure 14).

Based on the VSG model in Section 2, a small-signal state-space model of the system with the proposed methods is constructed, selecting key state variables: virtual rotor angle, δ; virtual angular velocity, ω; capacitor voltage, u_tdq; inductor current, i_Ldq; adaptive impedance, R_v/X_v; and frozen droop, K_G.

(1) Small-Signal Impact of Adaptive Virtual Impedance

We substitute R_v = R_v0 + ΔR_v and X_v = X_v0 + ΔX_v into the VSG power equation and current equation and obtain the impact of ΔR_v/ΔX_v on ΔP/ΔQ/Δ_i. Eigenvalue analysis shows the following:

• When K_r = 1.5 and K_x = 1.5, the dynamic response of ΔR_v/ΔX_v is exponentially damped, with no oscillation or unstable modes;
• If K_r/K_x > 5, weakly damped oscillation may occur, which needs to be avoided via parameter tuning.

(2) Small-Signal Impact of Frozen Droop Control

• During faults, K_G is constant, ΔK_G = 0, with no additional impact on small-signal characteristics.
• After fault clearance, K_G = K_{G 0} − D_q·ΔQ. Substituting into the voltage equation, the impact of ΔK_G on Δu_t is determined by the collaboration between D_q and voltage loop PI parameters. When D_q = 10, the ΔKG response is stable, without changing the system’s dominant stable mode.

In conclusion, with the paper’s parameters, all system small-signal eigenvalues have negative real parts, meeting stability requirements. Parameter tuning should adhere to the requirement of “Kr/Kx not excessively large and D_q matching voltage loop PI” to balance transient performance and small-signal stability.

(1) Experiment design: Fix I_lim =1.05 p.u., R_v0 =0.5 p.u., X_v0 =0.1 p.u., vary K_r (1.0~2.0) and K_x (1.0~2.0) separately, and test the current peak when the PCC voltage is 0.4 p.u.

(2) Result display (sensitivity curve):

When K_r increases from 1.0 to 1.5, the current peak decreases from 1.28 p.u. to 1.15 p.u.; when continuing to increase to 2.0, the current peak only decreases to 1.12 p.u., with diminishing marginal benefits; K_x has a weak impact on current peak, so K_x = 1.5 is selected to match K_r, balancing overcurrent suppression and algorithm complexity.

3.4. Simulation Verification of Improved Fault Overcurrent Suppression Method

3.4.1. Verification of Fault Overcurrent Suppression Using Adaptive Virtual Impedance Method

Unlike fixed virtual impedance, adaptive virtual impedance establishes an adjustment mechanism based on the difference between the measured current and the preset current threshold. The initial virtual impedance value does not affect the converter itself. Therefore, the initial virtual impedance can be set to a larger value to cope with different voltage sag scenarios. Set R_v to 1.0 p.u., X_v to 0.5 p.u., additional virtual impedance resistance coefficient K_r to 1.5, additional virtual impedance reactance coefficient K_x to 1.5, and preset current threshold I_lim to 1.05 p.u. and perform simulation verification under three different voltage sag levels.

(1) The grid voltage drops to 0.7 p.u.

Figure 15 presents the simulation waveforms of grid voltage, current, and active and reactive power under the adaptive virtual impedance overcurrent suppression method when the grid voltage sags to 0.7 p.u. at 1 s. Under this condition, the converter supports the grid voltage to 0.81 p.u., with the grid current limited to ~1.05 p.u. (no overcurrent risk). The converter reduces active power output and supplies more reactive power for terminal voltage support.

The steady-state current THD is 2.1%, which meets the requirement of “current THD ≤ 5%” in GB/T 37408-2019 [26] Technical Requirements for Grid-Connected Converters.

(2) The grid voltage drops to 0.4 p.u.

Figure 16 presents the simulation waveforms of grid voltage, current, and active and reactive power at the grid-tie point under the adaptive virtual impedance overcurrent suppression method when the grid voltage sags to 0.4 p.u. at 1 s. The converter supports the grid voltage to 0.52 p.u., with the grid current limited to ~1.15 p.u. (no overcurrent risk). Under severe voltage sag, the converter outputs more reactive power for terminal voltage support.

The steady-state current THD is 2.8%. Although the harmonic components increase slightly due to voltage sag, it is still within the standard range.

Simulation results confirm that the adaptive virtual impedance-based overcurrent suppression method effectively restrains overcurrent under various voltage sag levels, with a larger initial virtual impedance adapting to a wider range of voltage sags. To further emphasize its advantages over the fixed virtual impedance method, simulation verification and comparative analysis were performed under the same fault scenario and initial virtual impedance.

3.4.2. Comparative Analysis of Suppression Effects of Fixed and Adaptive Virtual Impedance Methods

Using the same fault scenario and virtual impedance values as in Section 3.2, the effects of fixed and adaptive virtual impedance methods on suppressing fault overcurrent were compared through time-domain simulation. The simulation system structure diagram shown in Figure 7 was also used, with system parameters shown in Table 1.

Set the additional virtual impedance resistance coefficient K_r to 1.5, the additional virtual impedance reactance coefficient K_x to 1.5, and the preset current threshold I_lim to 1.05 p.u. Similarly, set a three-phase short-circuit fault at 13% of line 1 at time 0.1 s. The grid voltage, current, and power conditions are shown in Figure 17. Compared to using a fixed virtual impedance for fault overcurrent suppression in Figure 11, the current is limited to a safe range after adopting the adaptive virtual impedance method.

A three-phase short-circuit fault occurs at 13% of line 1 (Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11) at 0.1 s, with a transition impedance of 0.5 + j0.5. Fault overcurrent suppression comparisons are shown in Figure 18 (red solid line: fixed virtual impedance; blue solid line: adaptive). With adaptive control, the current is limited to below 1.25 p.u., and the steady-state current drops from 1.264 p.u. to 1.161 p.u. (8.15% reduction). Under the same conditions, adaptive virtual impedance dynamically adjusts with system states, achieving better fault overcurrent suppression.

At this time, if the fault is cleared at 0.3 s, the grid voltage, current, and power conditions are as shown in Figure 19. During the fault, the adaptive virtual impedance fault overcurrent suppression method functions normally, limiting the current amplitude to below 1.25 p.u. After the fault is cleared, the converter returns to normal operation.

Compared with fixed virtual impedance for fault overcurrent suppression, the adaptive method is more adaptable to diverse fault scenarios. It dynamically adjusts impedance against uncertain grid voltage dip depth and duration to suppress overcurrent and avoid overcurrent-induced equipment damage. It also adapts to different grid operation modes via real-time impedance adjustment, maintaining excellent low-voltage ride-through performance. Notably, overcurrent suppression may weaken the converter’s reactive support capability. Thus, proper settings for initial virtual impedance, additional resistance/reactance coefficients, and preset current thresholds are necessary—along with matching reactive power support methods—to ensure the converter outputs sufficient reactive power for voltage support without overcurrent risks.

Select three types of typical existing methods:

(1) Fixed virtual impedance (Ref. [4]): Parameters R_v = 0.5 p.u. and X_v = 0.1 p.u.;

(2) Traditional adaptive impedance (Ref. [5]): Parameters K_r = 1.0 and K_x = 1.0;

(3) Traditional droop control (no freezing, Ref. [12]): Parameter D_q = 10.

Parameter tuning basis for the proposed method is K_r = 1.5, K_x = 1.5, and D_q = 10, determined by sensitivity analysis. For specific comparisons, please refer to

Table 2. Overcurrent suppression comparison.

Method	Fault Scenario (PCC Voltage)	Current Peak (p.u.)	Overcurrent Suppression Rate (%)	Steady-State THD (%)
Fixed virtual impedance (Ref. [4])	0.4 p.u.	1.48	−18.4	2.5
Traditional adaptive impedance (Ref. [5])	0.4 p.u.	1.28	6.8	2.6
Proposed method (adaptive impedance)	0.4 p.u.	1.15	8.15	2.8

and

Table 3. Reactive power support comparison.

Method	Fault Scenario (PCC Voltage)	Reactive Power Increase Rate (%)	Voltage Recovery Value (p.u.)	Response Time (ms)
Traditional droop (Ref. [12])	0.7 p.u.	5.2	0.75	80
Proposed method (frozen droop)	0.7 p.u.	11.68	0.81	45

.

(1) Overcurrent suppression: By dynamically adjusting impedance, the proposed method suppresses overcurrent by an additional 1.35% compared to traditional adaptive impedance, while THD still meets standards.

(2) Reactive power support: Frozen droop avoids the negative feedback of traditional droop, with a reactive power increase rate 2.2 times that of traditional methods and a 43.75% shorter response time, as it does not require waiting for droop adjustment delay.

3.4.3. Real-Time Realization of Analysis and Engineering Challenges

(1) Controller Selection and Real-Time Performance

The core computational load of the adaptive algorithm includes (1) calculation of current amplitude I and deviation I-Ilim; (2) dynamic update of Rv/Xv; and (3) positive-sequence voltage extraction and droop freezing judgment. Recommended controller selections are as follows:

• DSP Controller: TI TMS320F28379D, which can control the impedance update cycle within 50 μs, meeting the real-time requirements of grid-connected converters;
• FPGA Controller: Xilinx Artix-7, realizing current calculation and impedance adjustment in parallel via hardware logic, with delay reduced to within 10μs, suitable for high-voltage and high-power scenarios.

(2) Engineering Challenges and Countermeasures

• Current Detection Noise Interference: Sampling noise may cause I fluctuations, leading to incorrect Rv/Xv adjustment. Countermeasure: Add a second-order low-pass filter and sliding window averaging to smooth the current amplitude.
• Engineering Adaptation of Parameters: Simulation parameters need to be adjusted according to the converter’s rated current and filter inductance. Countermeasure: Establish a parameter mapping model and iteratively optimize via the HIL platform.
• Hardware Resource Conflict: The code size of the adaptive algorithm accounts for 15% of the total program in DSP, requiring avoidance of conflicts with PWM generation and communication modules. Countermeasure: Modular programming, assigning the algorithm to the CPU1 core of TMS320F28379D and other modules to CPU2 for multi-core parallel processing.
• Impact of Temperature Drift: Temperature drift of sampling resistors and operational amplifiers reduces sampling accuracy. Countermeasure: Perform zero-point calibration via the pre-charging loop every 24 h to eliminate drift deviations.

Core calculation steps and computational burden of adaptive impedance (measured on TI TMS320F28379D DSP). The specific parameters are shown in

Table 4. System parameters.

Calculation Step	Operation Type	Single Operation Latency (μs)	Proportion of Total Control Cycle (%)
Grid current amplitude	Floating-point sqrt + square	1.2	2.4
Current deviation	Floating-point subtraction	0.3	0.6
Adaptive impedance update	Floating-point multiplication + addition	0.8	1.6
Total	-	2.3	4.6

and

Table 5. A “DSP + FPGA” dual-mode controller architecture.

Hardware Module	Model/Specification	Key Parameters
Main Controller (DSP)	TI TMS320F28379D	Sampling frequency 20 kHz, 32-bit floating-point computing capability, multi-core parallel support
Coprocessor (FPGA)	Xilinx Artix-7 XC7A35T	35k logic cells, parallel processing of current sampling and PWM generation, latency ≤ 10 ns
Sampling Module	ADS8688	16-bit resolution, sampling rate 1MSPS, supporting three-phase current/voltage synchronous sampling
Communication Interface	CAN 2.0B/Ethernet	For data interaction with HIL platform (RT-LAB OP5700), baud rate 500 kbps (CAN)

.

4. Reactive Power Support Method Based on Frozen Reactive Power–Voltage Droop Control

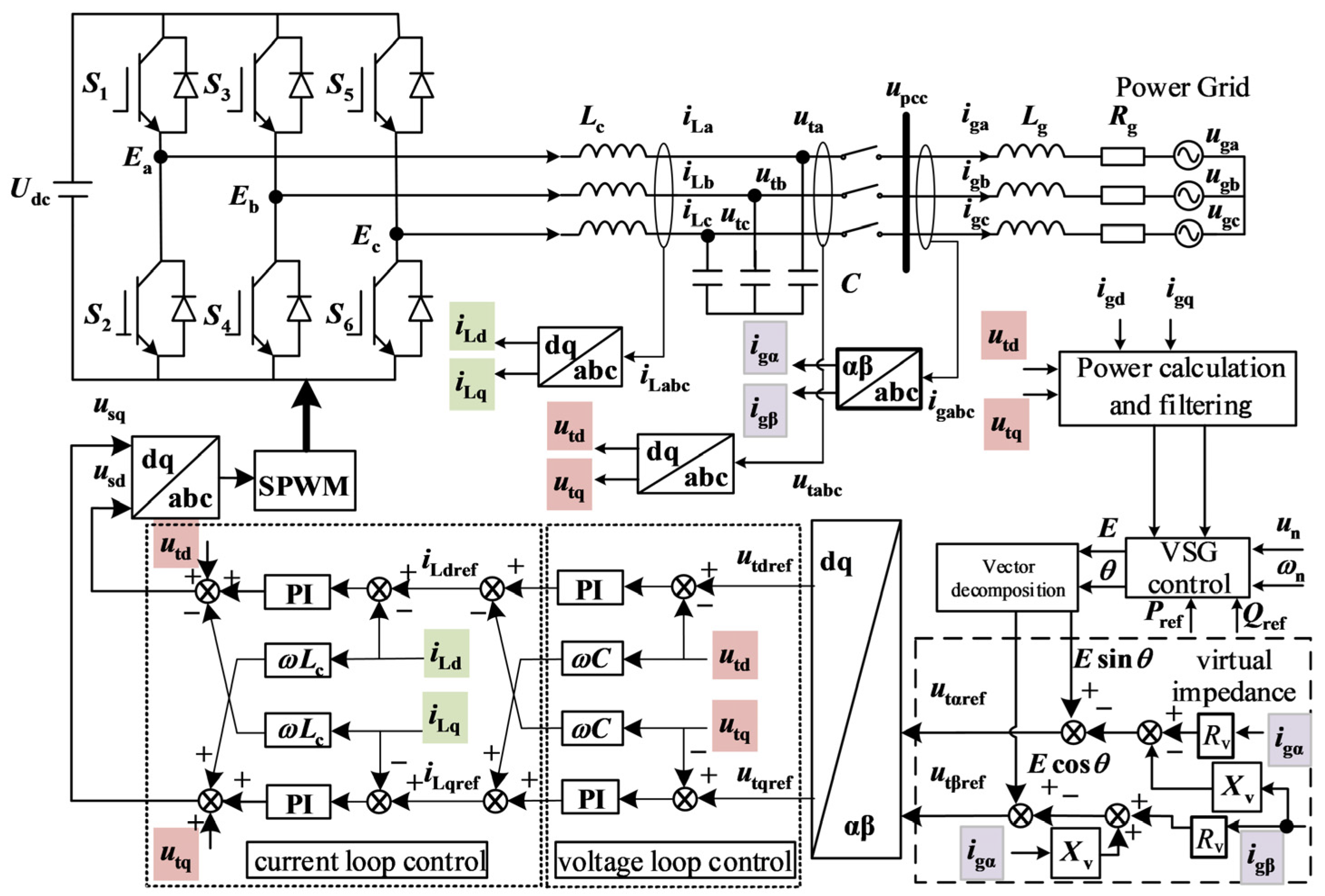
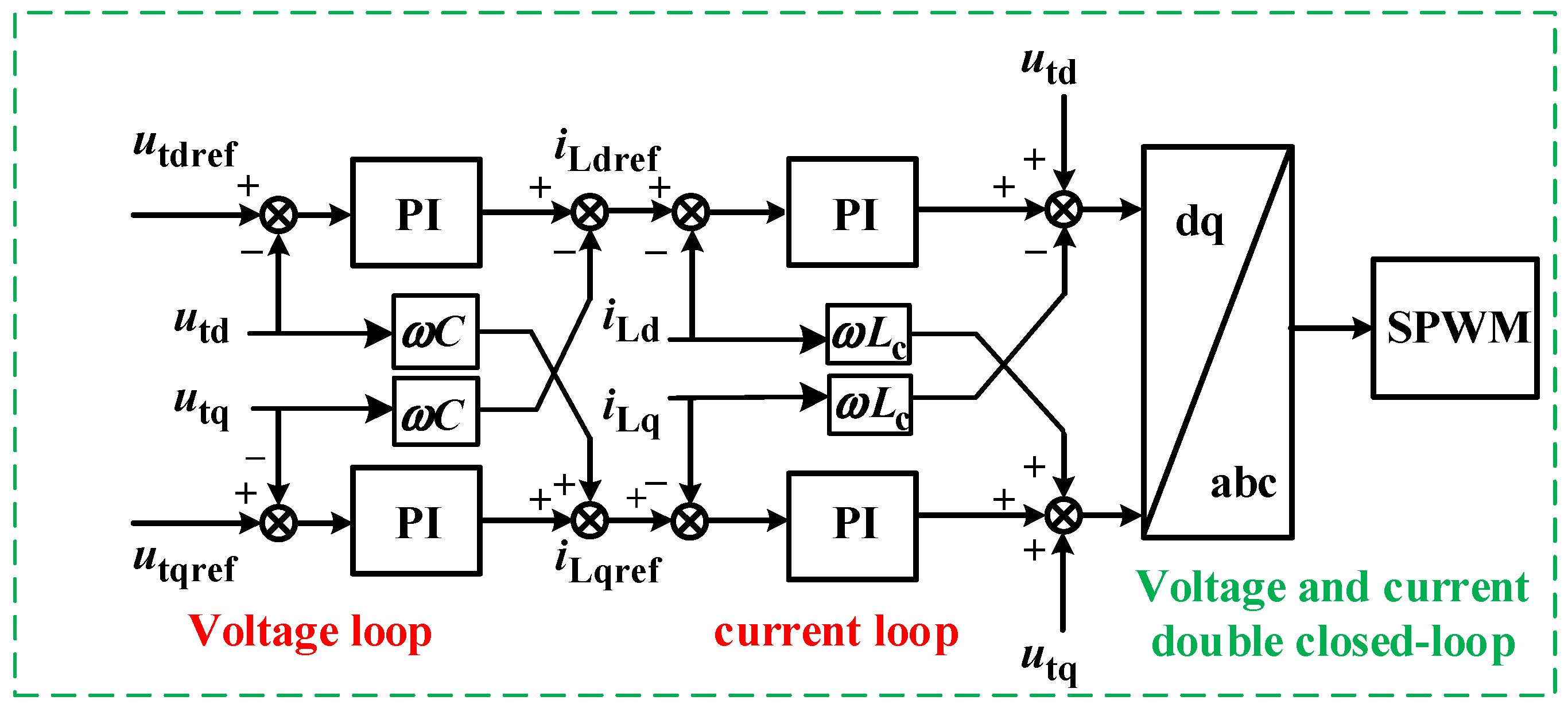
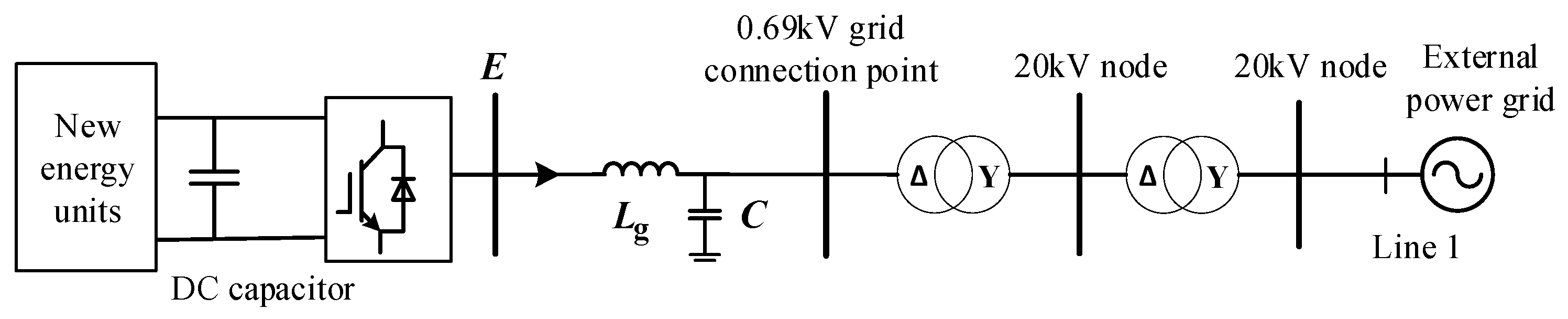
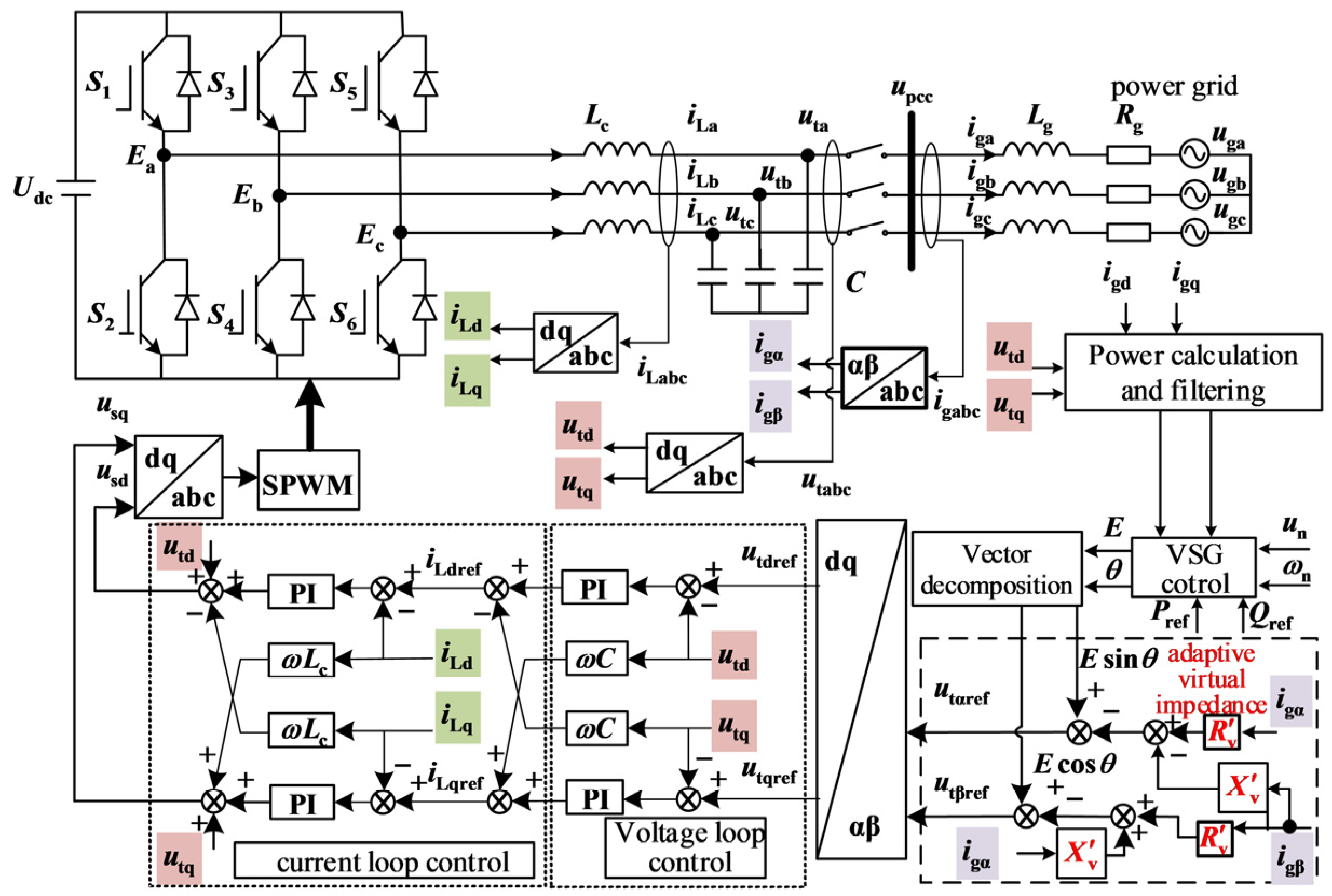
The reactive power–voltage droop link helps grid-forming converters dynamically adjust reactive output and stabilize system voltage. However, retaining this link during faults boosts the converter’s reactive output, forcing its internal potential to drop and weakening its reactive support capability.

After analyzing this underlying mechanism, this section proposes a reactive power support method that freezes the reactive power–voltage droop link. It uses positive-sequence voltage amplitude to detect system faults and determine whether to freeze the link—enhancing the converter’s reactive support during voltage dips while avoiding post-fault overvoltage risks caused by prolonged droop freezing.

4.1. Mechanism Analysis of Droop Control Link Affecting Reactive Power Support Capability

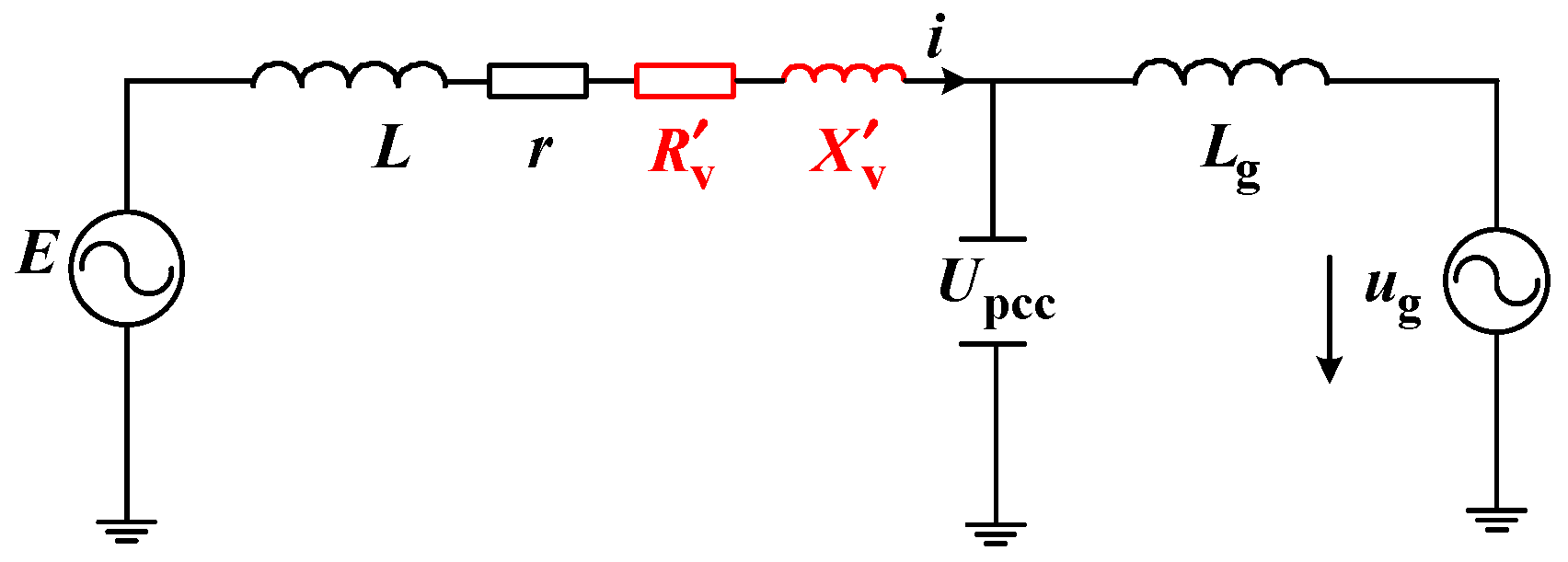
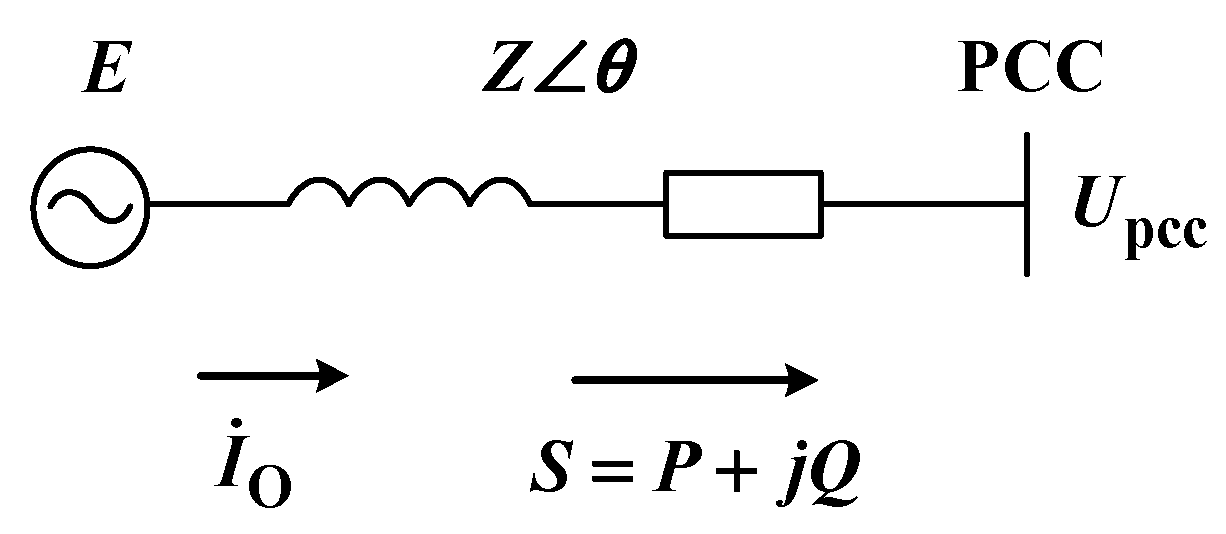
The output of the grid-connected converter can be equivalent to the circuit structure shown in Figure 20. In the figure, U_PCC represents the voltage at the PCC point, with its phase angle set as the reference phase angle; E represents the output voltage of the grid-connected converter port; Z∠θ represents the equivalent impedance from the converter to the PCC point; S represents the complex power flowing into the PCC point; and ${\dot{I}}_{\mathrm{O}}$ represents the output current of the converter.

At this time, ${\dot{I}}_{\mathrm{O}}$ can be expressed as

$${\dot{I}}_{\mathrm{O}}={\displaystyle \frac{E\angle \delta -U_{\mathrm{PCC}}\angle 0^{\circ }}{Z\angle \theta }}={\displaystyle \frac{E\angle \delta -U_{\mathrm{PCC}}\angle 0^{\circ }}{R+jX}}$$

(40)

The complex power S injected by the converter into the grid-side system can be expressed as

$$S=P+jQ={\dot{U}}_{\mathrm{PCC}}{\dot{I}}_{\mathrm{O}}^{\ast }$$

(41)

By substituting Formula (41) into Formula (42), we can get

$$\left\{\begin{array}{l}P={\displaystyle \frac{U_{\mathrm{PCC}}\left[R(E\cos \delta -U_{\mathrm{PCC}})+EX\sin \delta \right]}{R^2+X^2}}\\ Q={\displaystyle \frac{U_{\mathrm{PCC}}\left[X(E\cos \delta -U_{\mathrm{PCC}})-EX\sin \delta \right]}{R^2+X^2}}\end{array}\right.$$

(42)

When the system is in a purely inductive environment, X >> R, R ≈ 0, and the formula can be simplified to

$$\left\{\begin{array}{l}P={\displaystyle \frac{U_{\mathrm{PCC}}E\sin \delta }{X}}\\ Q={\displaystyle \frac{U_{\mathrm{PCC}}(E\cos \delta -U_{\mathrm{PCC}})}{X}}\end{array}\right.$$

(43)

Generally, considering that the value of $\delta$ is small, it can be approximately considered that $\sin \delta =\delta ,\cos \delta =1$.

At this time, Formula (44) is transformed into

$$\left\{\begin{array}{l}P={\displaystyle \frac{U_{\mathrm{PCC}}E\delta }{X}}\\ Q={\displaystyle \frac{U_{\mathrm{PCC}}(E-U_{\mathrm{PCC}})}{X}}\end{array}\right.$$

(44)

Assuming $\delta \approx 0^{\circ }$, taking the differential of Equation (45) yields

$$\left\{\begin{array}{l}{\displaystyle \frac{dP}{d\delta }}={\displaystyle \frac{U_{\mathrm{PCC}}E}{X}}\\ {\displaystyle \frac{dP}{dE}}={\displaystyle \frac{U_{\mathrm{PCC}}\delta }{X}}\approx 0\\ {\displaystyle \frac{dQ}{d\delta }}=0\\ {\displaystyle \frac{dQ}{dE}}={\displaystyle \frac{U_{\mathrm{PCC}}}{X}}\end{array}\right.$$

(45)

At this time, the active power P output by the converter mainly depends on the power angle difference, and the reactive power Q mainly depends on the voltage amplitude E, with almost no coupling relationship.

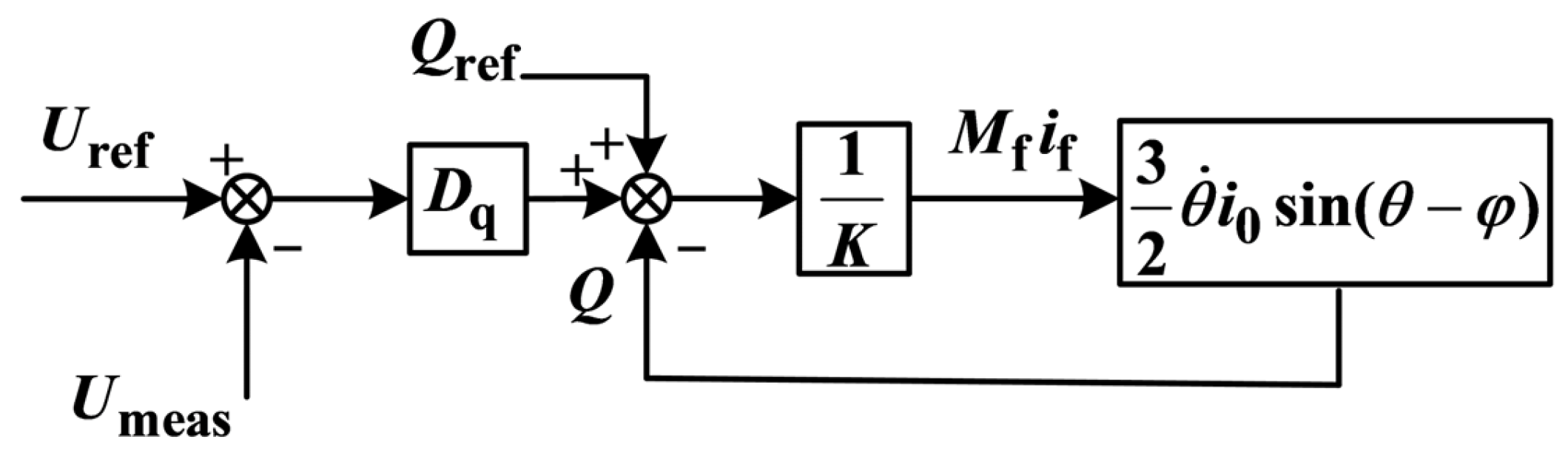
At this time, the reactive power output by the converter can be expressed as follows:

$$Q={\displaystyle \frac{U_{\mathrm{PCC}}(E-U_{\mathrm{PCC}})}{X}}$$

(46)

As Q increases, E also increases. This equation indicates that VSG can support voltage during a fault by providing more reactive power to the grid.

However, the VSG output voltage is controlled by the reactive droop link, and the expression for reactive droop control is

$$Q_{\mathrm{ref}}-Q=D_{\mathrm{q}}\left(U_{\mathrm{ref}}-E\right)$$

(47)

By transforming Equation (48), we can obtain the expression for the reactive power output by the VSG:

$$Q=Q_{\mathrm{ref}}-D_{\mathrm{q}}\left(U_{\mathrm{ref}}-E\right)$$

(48)

Grid voltage dips create a potential difference between the VSG’s internal potential and grid voltage, leading to a natural rise in the VSG’s reactive power output. Retaining the reactive droop link at this point introduces reactive power negative feedback, which lowers the internal potential E and reduces reactive output—hindering the inverter’s grid reactive support.

4.2. Principle of Reactive Power Support Based on Frozen Droop Control

This method uses the positive-sequence component of the grid voltage as the condition for fault identification. When the amplitude of the positive-sequence voltage is less than 0.9 p.u., it is determined that a voltage sag fault has occurred in the grid, and the reactive power droop control link is frozen. When the amplitude of the positive-sequence voltage is greater than 0.9 p.u., it is determined that the fault has been cleared, and the reactive droop control link is restarted.

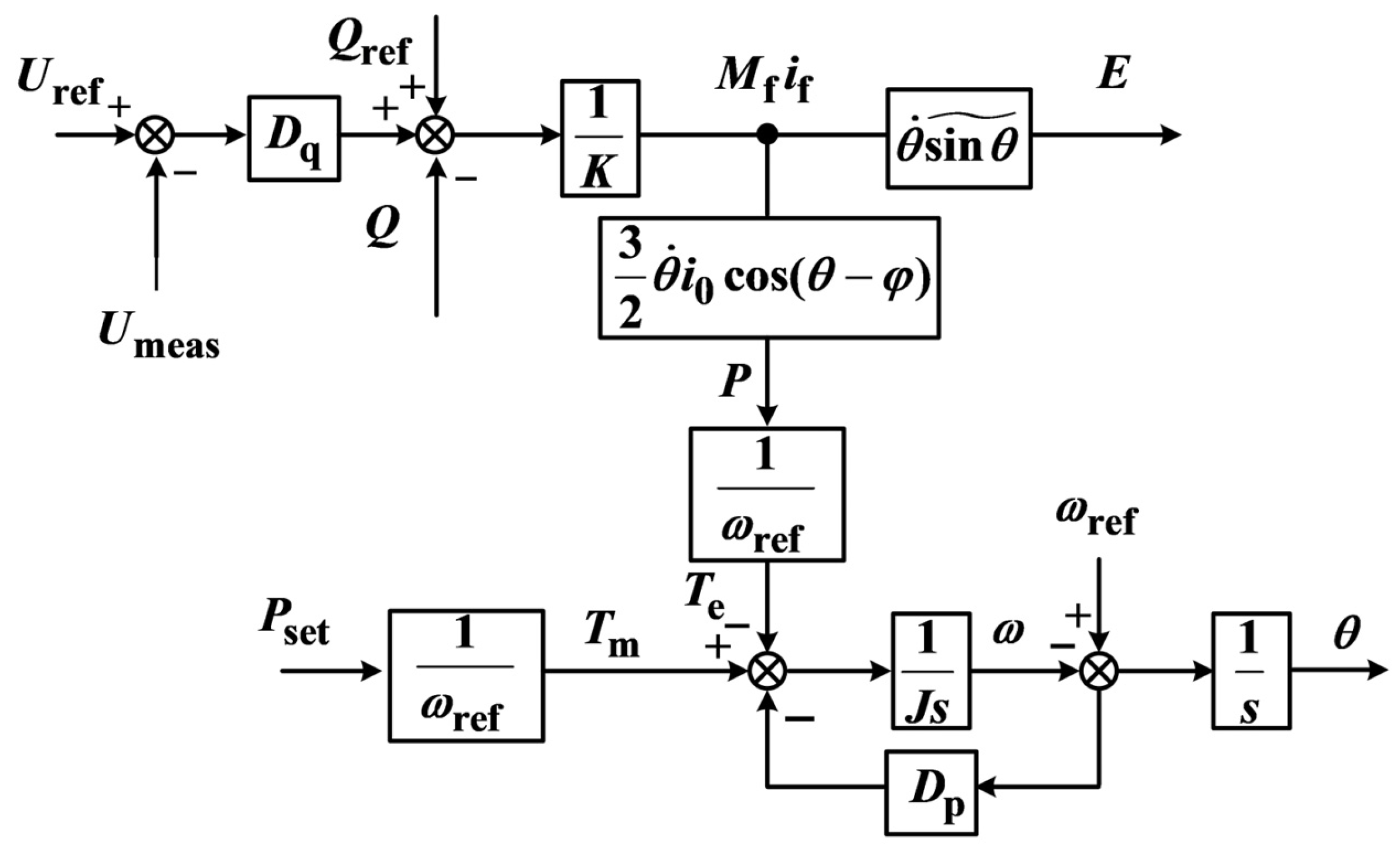
The formula for VSG output voltage is

$$E=M_{\mathrm{f}}{i}_{\mathrm{f}}\dot{\theta }\widetilde{\sin \theta }$$

(49)

The voltage equation of VSG under droop control is

$$K{\displaystyle \frac{dE}{dt}}=Q_{\mathrm{ref}}-Q+D_{\mathrm{q}}^{\prime }(U_{\mathrm{ref}}-U)$$

(50)

where K is the reactive power loop inertia coefficient; $D_{\mathrm{q}}^{\prime }$ is the voltage droop coefficient.

Transforming Equation (51) yields

$${\displaystyle \frac{dE}{dt}}={\displaystyle \frac{Q_{\mathrm{ref}}-Q+D_{\mathrm{q}}^{\prime }(U_{\mathrm{ref}}-U)}{K}}$$

(51)

The two formulas are equivalent; thus,

$${\displaystyle \frac{dE}{dt}}={\displaystyle \frac{Q_{ret}-Q+D_{\mathrm{q}}^{\prime }(U_{\mathrm{ref}}-U)}{K}}={\displaystyle \frac{E}{{\omega }_0\sin \delta }}=M_{\mathrm{f}}{i}_{\mathrm{f}}$$

(52)

$\delta$ is the phase angle difference between the internal electromotive force E and the point of common coupling (PCC) voltage U, and ω0 is the rated angular frequency of the power grid. This formula indicates that the traditional method of freezing the reactive power loop during a fault can be improved by stabilizing the value of M_fi_f. By setting M_fi_f to a fixed value of K_G, Equation (50) will be transformed into

$$E=K_{\mathrm{G}}\dot{\theta }\widetilde{\sin \theta }$$

(53)

Equation (8) will be transformed into

$$\left\{\begin{array}{l}P=\dot{\theta }{K}_{\mathrm{G}}〈i,\tilde{\sin }\theta 〉={\displaystyle \frac{3}{2}}\dot{\theta }{K}_{\mathrm{G}}{i}_0\cos (\theta -\phi )\\ Q=-\dot{\theta }{K}_{\mathrm{G}}〈i,\tilde{\cos }\theta 〉={\displaystyle \frac{3}{2}}\dot{\theta }{K}_{\mathrm{G}}{i}_0\sin (\theta -\phi )\end{array}\right.$$

(54)

Without voltage-reactive negative feedback regulation, the new KG value during LVRT simultaneously enhances voltage and reactive power output. Physically, Mfif is the VSG’s magnetic flux; this method essentially freezes the reactive-voltage droop link and increases magnetic flux to raise the VSG’s internal potential, expanding the internal-grid potential difference for higher reactive output. Notably, raising internal potential during faults exacerbates overcurrent, so the strategy must be paired with adaptive virtual impedance overcurrent suppression to prevent current over-limit under severe voltage dips.

This study adopts the “Synchronous Reference Frame (SRF)-based positive-sequence extraction method” for fault detection.

The process involves transforming the three-phase PCC voltage u_abc into αβ-frame voltages via Clark transformation then converting them into dq-frame components u_d, u_q using SRF transformation synchronized with the grid’s rated angular frequency ω₀. These components are low-pass-filtered (5 Hz cutoff) to eliminate interference, obtaining the positive-sequence voltage amplitude $U_1=\sqrt{u_{\mathrm{d}}^2+u_{\mathrm{q}}^2}$. Droop control is frozen when U₁ < 0.9 p.u. and restored otherwise.

(1) Small-signal modeling: Substitute frozen droop control into the VSG small-signal model, derive the characteristic equation, and analyze the impact of D_q on the system’s dominant poles.

(2) Results: When D_q = 5, the real part of the dominant pole = −0.12. When D_q = 10, the real part of the dominant pole = −0.28. When D_q > 15, the real part of the dominant pole = −0.05. Thus, D_q = 10 is selected to balance stability margin and response speed.

4.3. Simulation Verification of Improved Reactive Power Support Method

The system simulation model depicted in Figure 7 and the parameters listed in Table 1 were utilized. The effectiveness of the proposed reactive power support method was validated by simulating three different voltage sag conditions: mild, moderate, and severe.

(1) Operating condition 1: mild voltage drop (voltage drop to 70–90%)

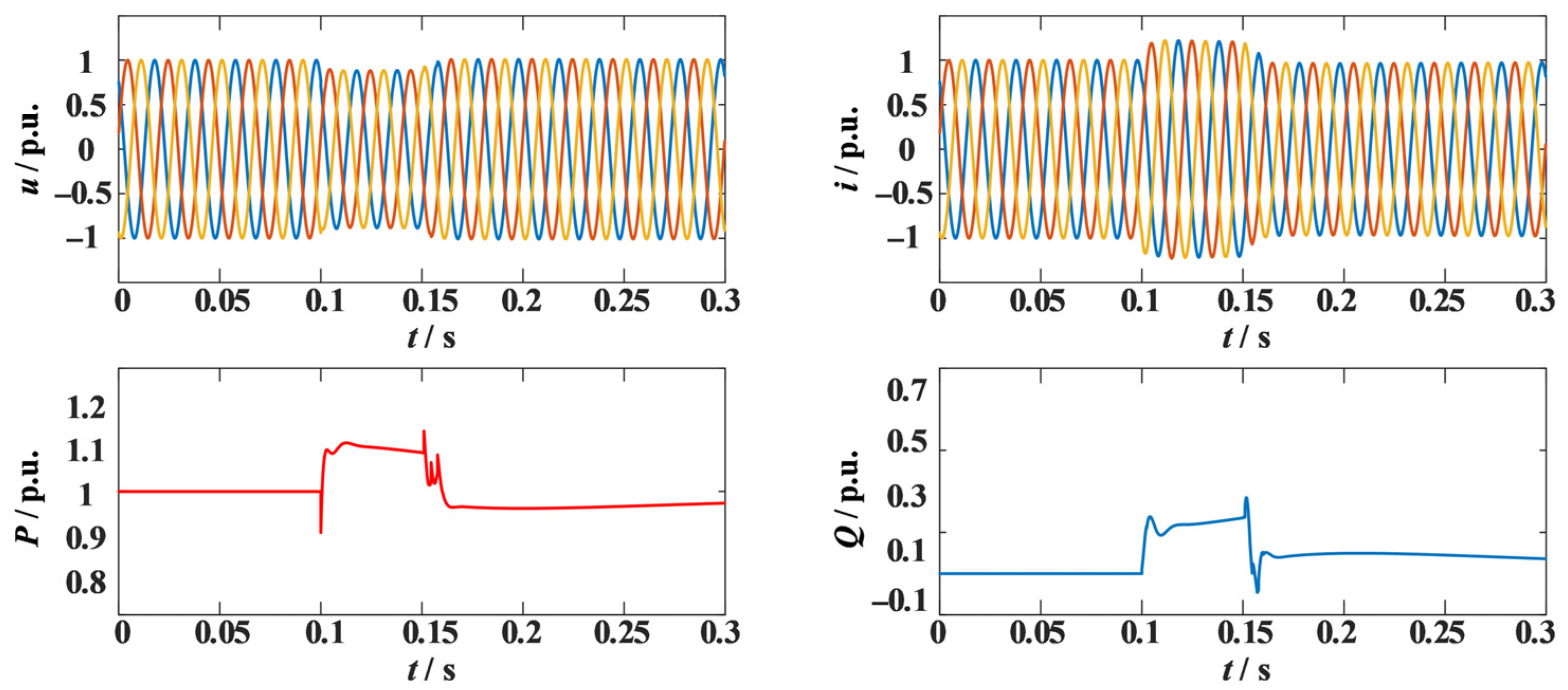
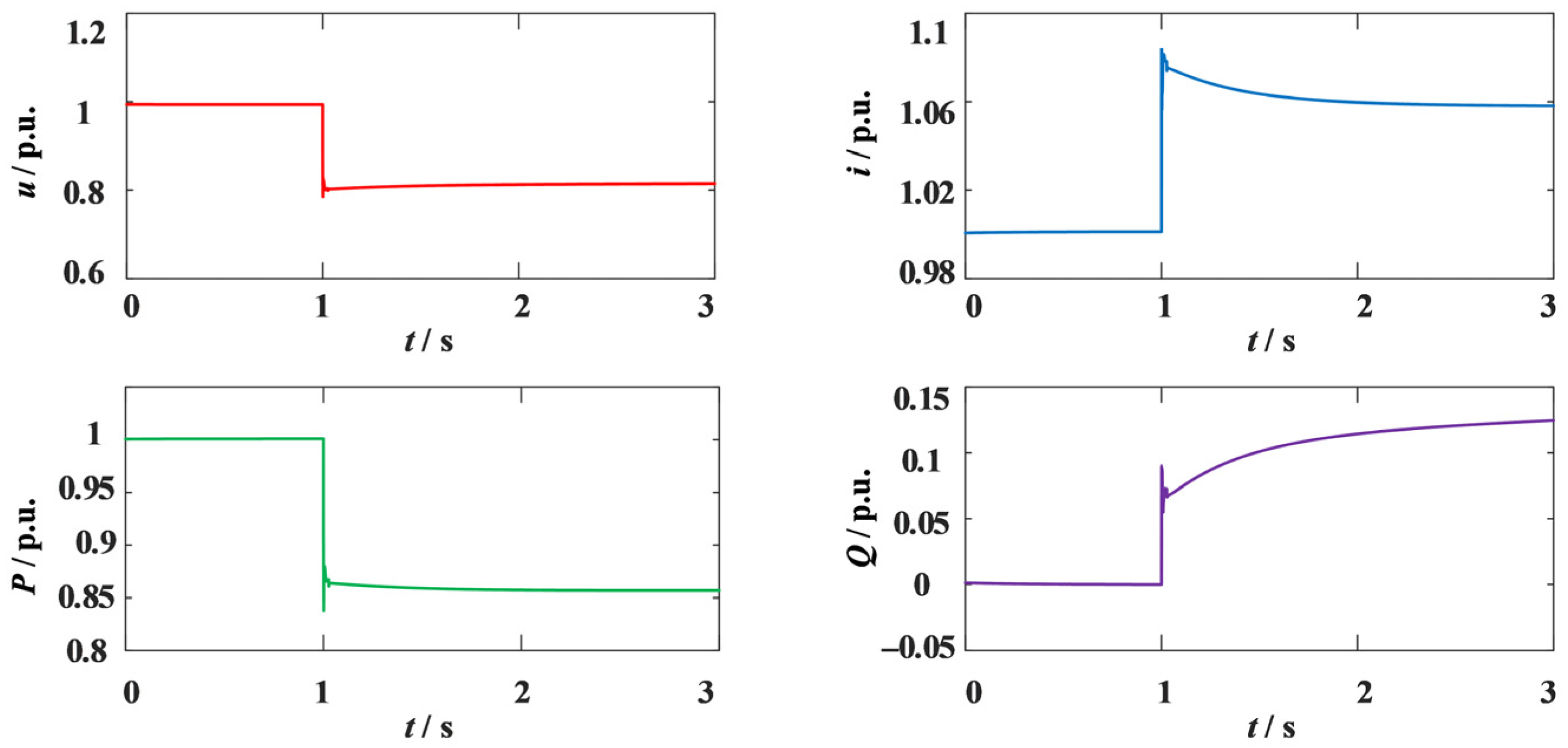
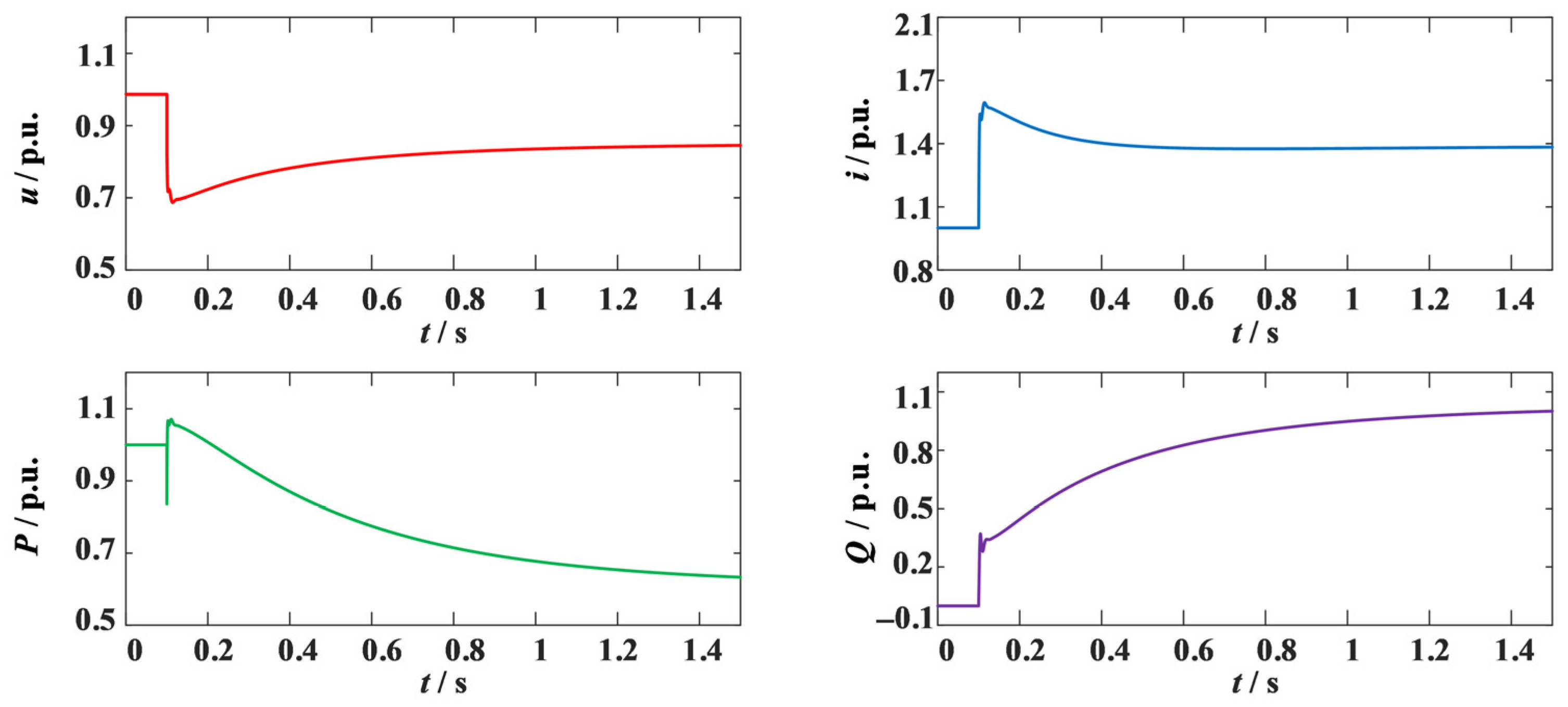
A three-phase short-circuit fault occurs at 10% of line 1 at 0.1 s, with a transition impedance of 0.5 + j0.5 Ω. When the reactive power–voltage droop control link is not frozen during the fault, the grid voltage, current, and power conditions are shown in Figure 21.

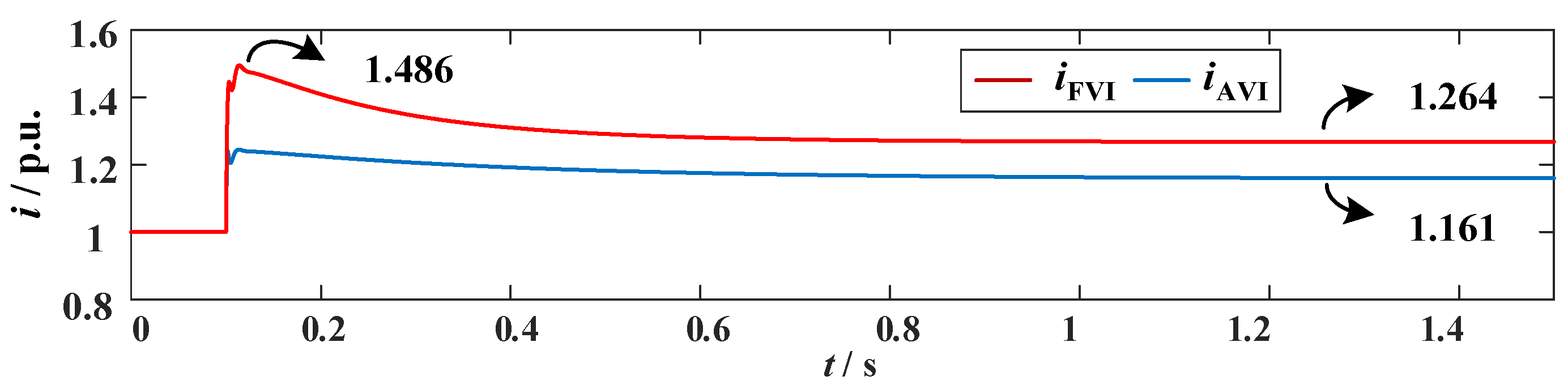
After the fault, the grid-tie point voltage dropped to a minimum of 0.7894 p.u., while the converter reactive power continued to rise to 0.6654 p.u. at 1.45 s. Meanwhile, the grid-tie point current remained above 1.2 p.u. for a long time, posing an overcurrent risk to the converter.

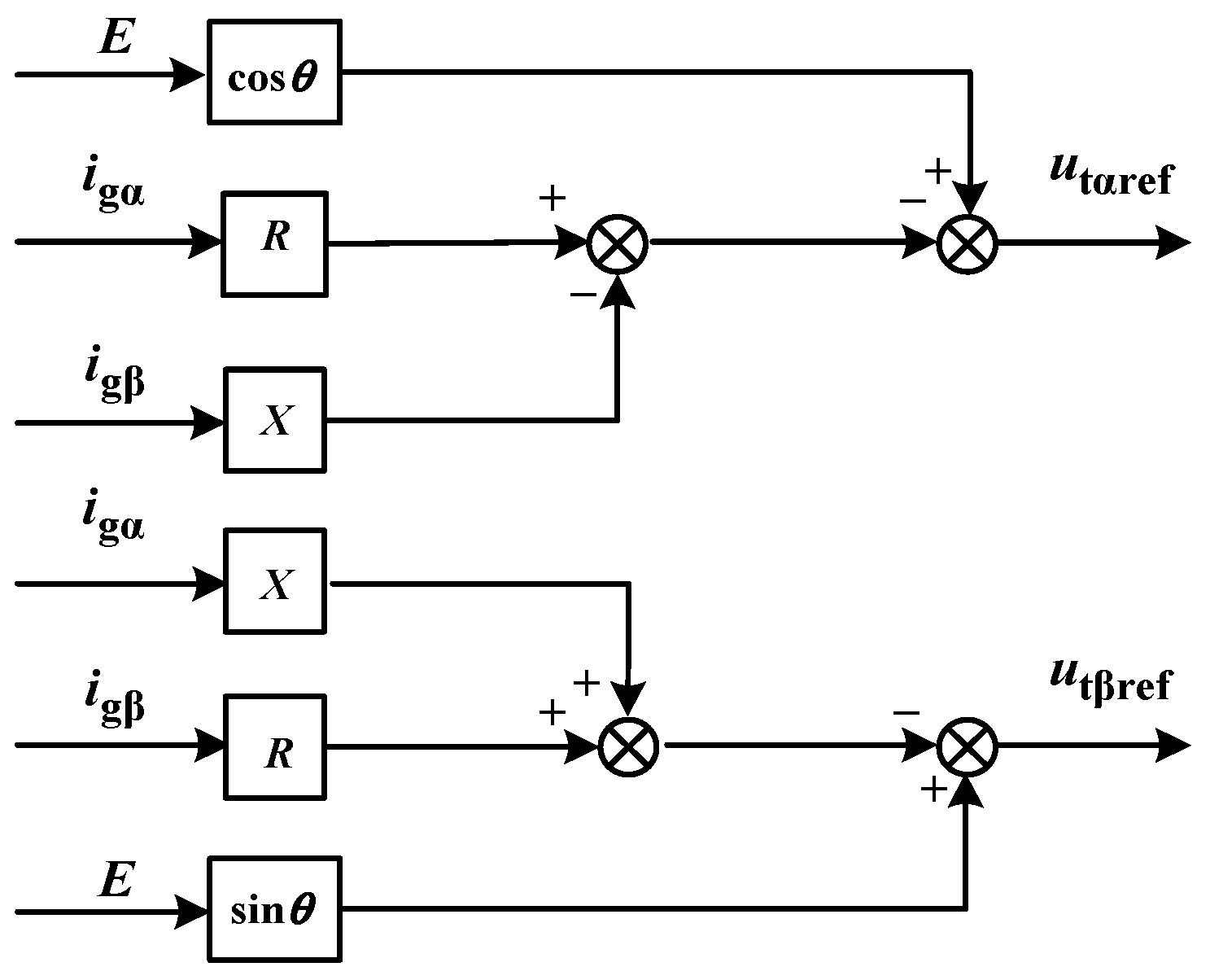
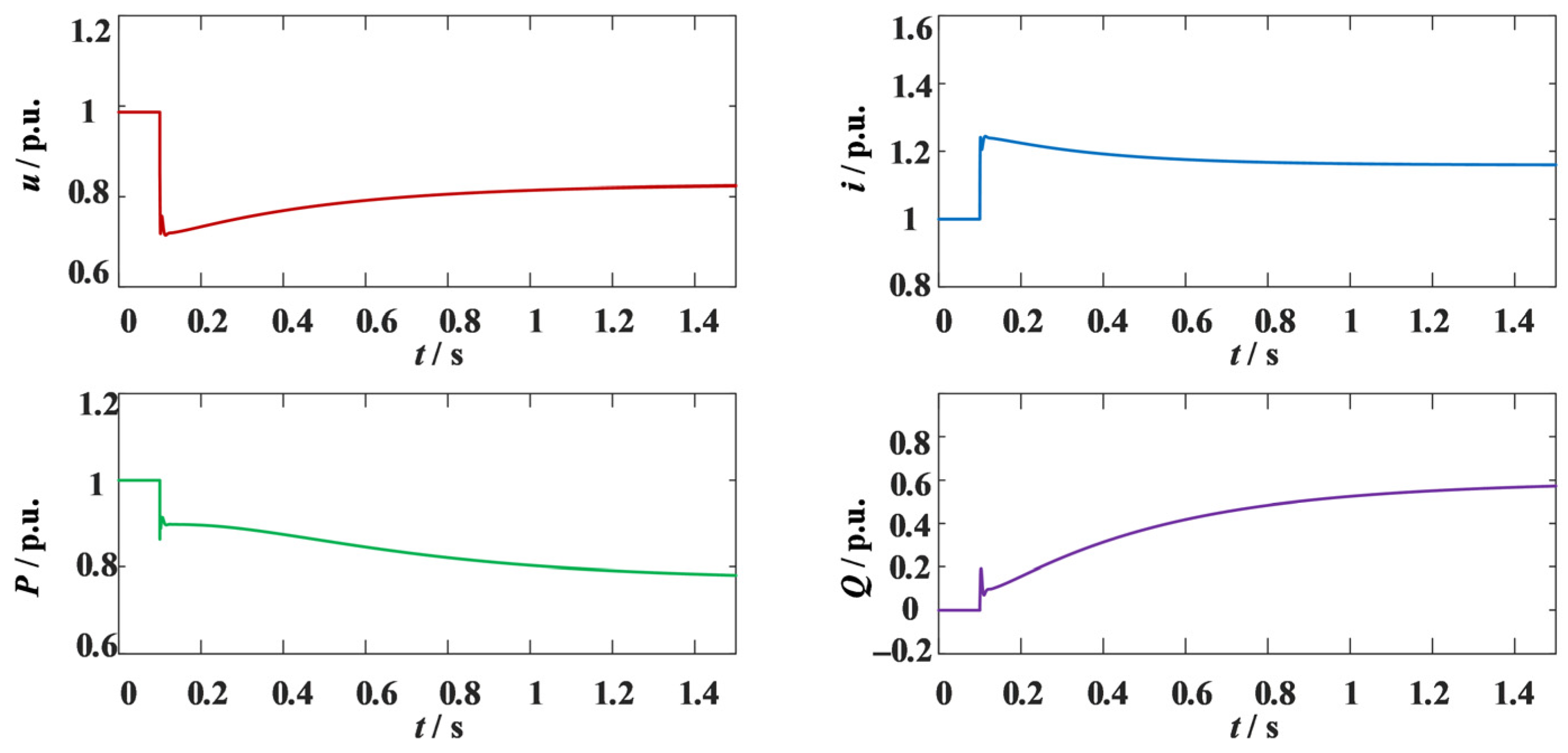
With the proposed fault overcurrent suppression and reactive support method, when the voltage was detected below 0.9 p.u., the reactive-voltage droop control was frozen (KG = 1.014). The adaptive virtual impedance method was adopted with the following parameters: Rv = 0.5 p.u., Xv = 0.1 p.u., additional resistance coefficient Kr = 1.5, additional reactance coefficient Kx = 1.5, and preset current threshold Ilim = 1.05 p.u. The grid-tie point voltage, current, and active and reactive power results are shown in Figure 22.

As shown in Figure 22, after using the improved method of fault overcurrent suppression and reactive power support, the adaptive virtual impedance suppresses the fault current and protects the system from overcurrent damage. The improved method of reactive power support freezes the reactive-voltage droop control structure and adjusts the value of K_G to increase the reactive power output of the converter. At 1.45 s, the reactive power increases from 0.6654 p.u. to 0.7431 p.u., an increase of 11.68%. Without the risk of overcurrent, the converter provides more sufficient reactive power support. The steady-state current THD is 2.3%, and the frozen droop control does not increase current harmonics.

The comparison of reactive power at this time is shown in Figure 23. The blue dashed line represents the reactive power output by the converter under the improved method, and the red solid line represents the reactive power output by the converter when the reactive-voltage droop control is not frozen. After freezing the reactive-voltage droop control during a fault, the converter outputs more reactive power to support the terminal voltage.

(2) Operating condition 2: moderate voltage drop (voltage drops to 40–70%)

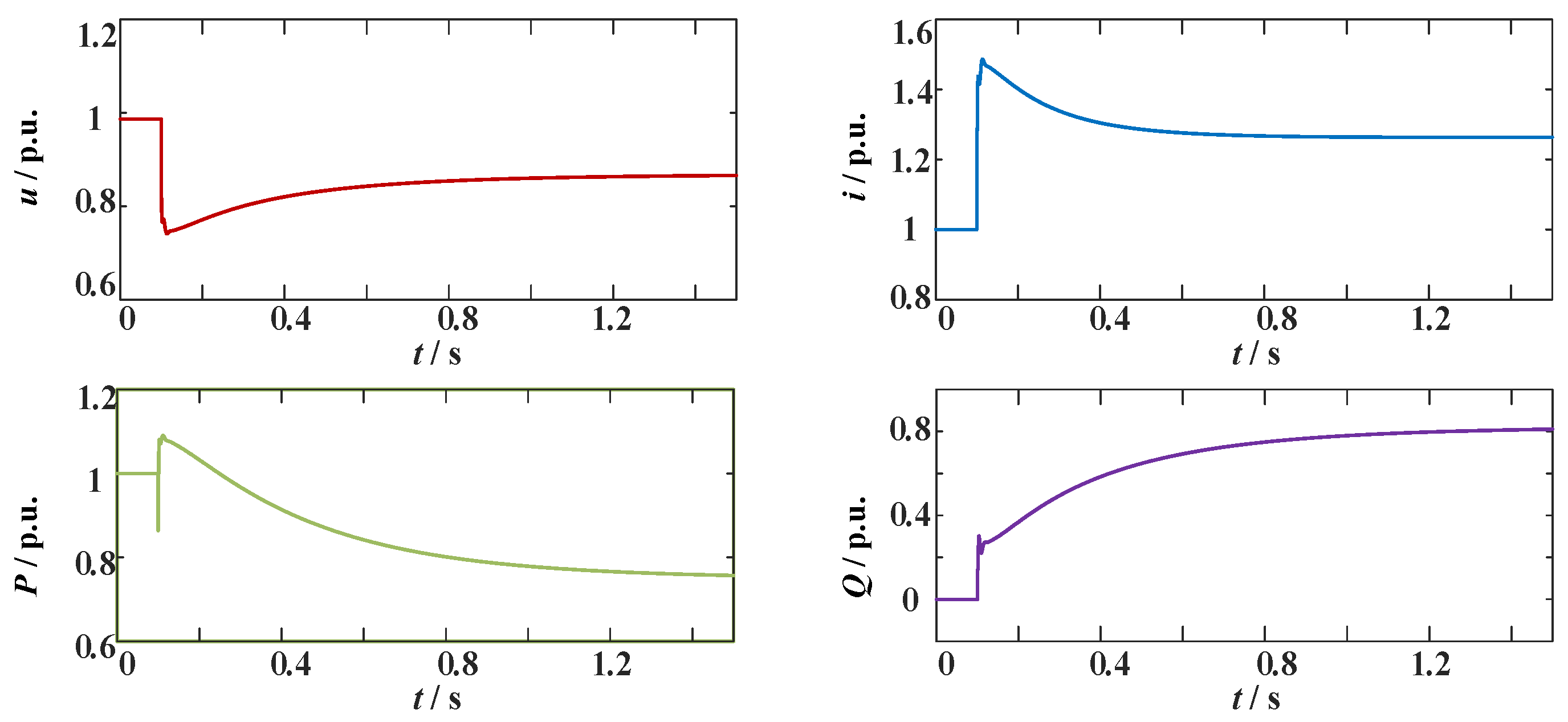
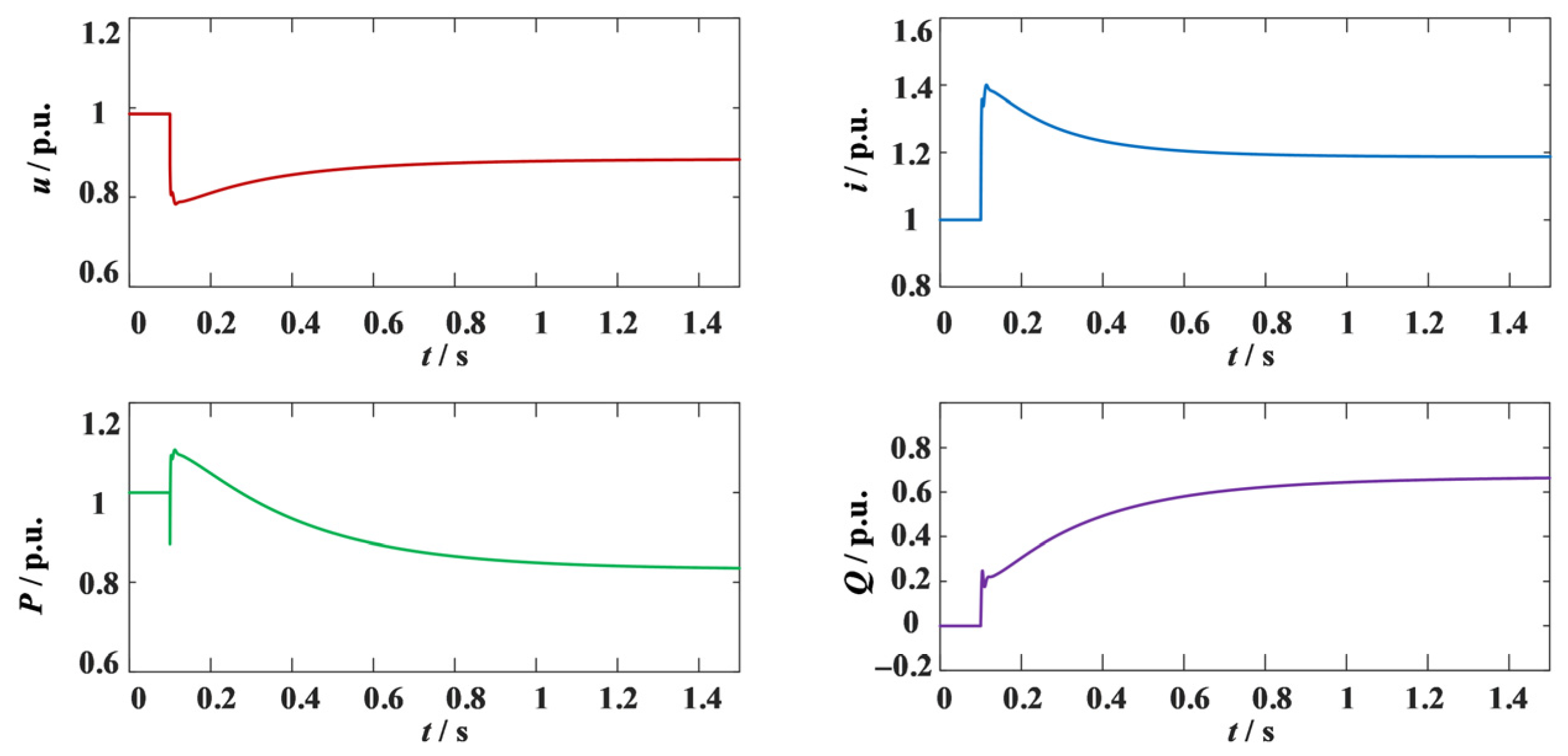
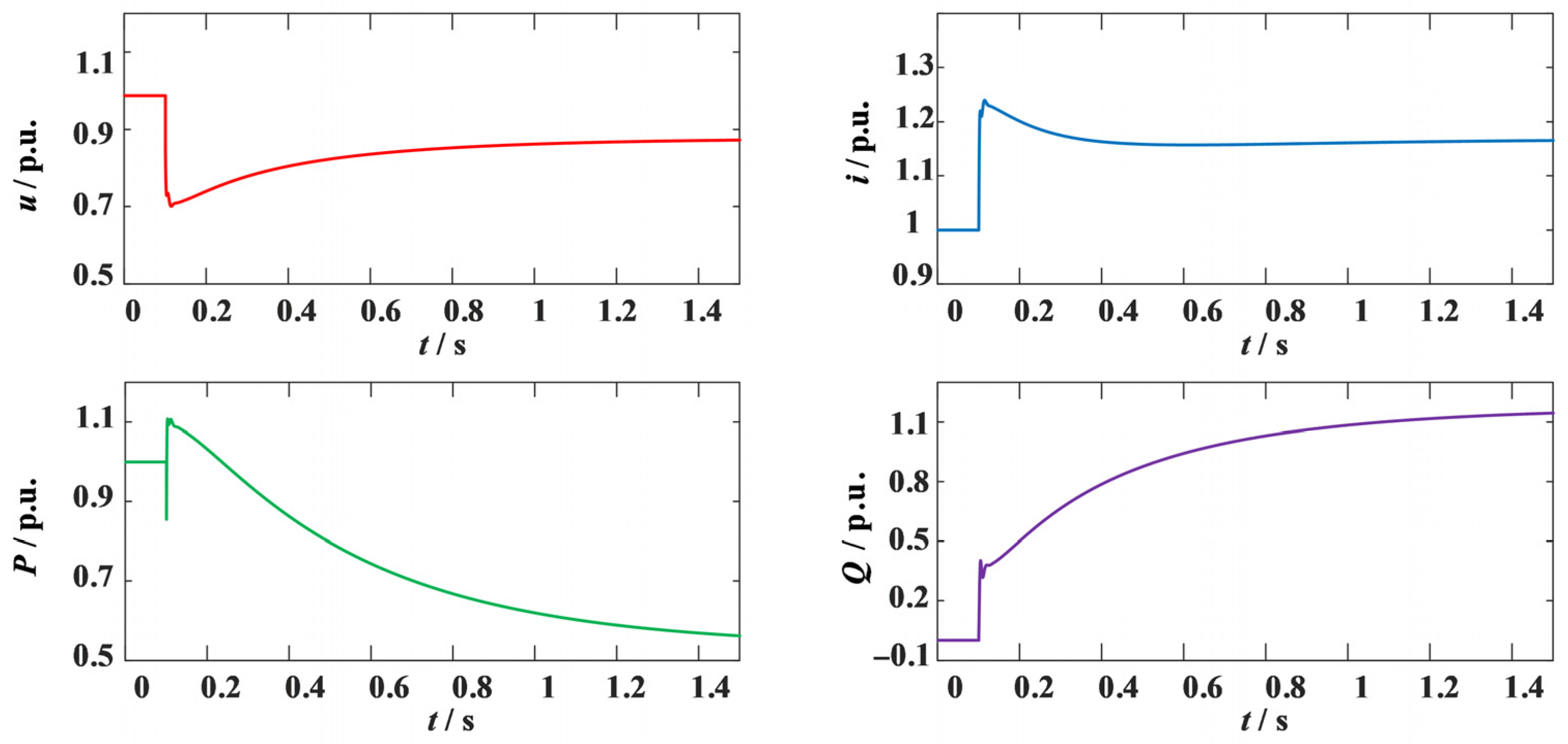
A three-phase short-circuit fault occurs at 35% of line 1 at 0.1 s, with a transition impedance of 1 + j1 Ω. Figure 24 shows the voltage, current, and active and reactive power at the grid connection point when the proposed improvement method is not applied. The minimum voltage amplitude drop is 0.6873 p.u. The converter continues to provide reactive power support to increase the voltage, while the active power output continues to decrease and the reactive power continues to increase to raise the terminal voltage. During the fault period, the current amplitude remains above 1.25 p.u. for a long time, posing a serious overcurrent risk to the converter.

When the amplitude of the positive-sequence voltage is detected to be less than 0.9 p.u., it is determined that the system has experienced a fault. The control loop of M_fi_f is frozen, the fixed value K_G is set to 1.02, and adaptive virtual impedance control is used for overcurrent suppression. At this time, the voltage, current, active power, and reactive power are shown in Figure 25.

By comparing Figure 24 and Figure 25, it can be seen that the improved reactive power support method based on the frozen reactive power–voltage droop link, combined with the adaptive virtual impedance fault overcurrent suppression method, effectively suppresses fault overcurrent while increasing the reactive power output of the grid-connected converter. Taking the time of 1.467 s as an example, the reactive power increases from 1.0 p.u. to 1.142 p.u., an increase of 14.2%. The converter provides more sufficient reactive power support during the fault period while also avoiding fault overcurrent caused by rapid reactive power support. The steady-state current THD is 3.0%, which meets engineering requirements.

Analysis of the current THD control effect:

(1) The LCL filter (L = 0.035 mH, C = 10 μF in Table 1) can effectively suppress high-frequency harmonics;

(2) The inductive component Xv of the adaptive virtual impedance (e.g., initial value 0.5 p.u.) further suppresses low-order harmonics (e.g., 3rd and 5th);

(3) The frozen droop only adjusts the voltage command amplitude without changing the sinusoidality of the current waveform, so it has no negative impact on THD.

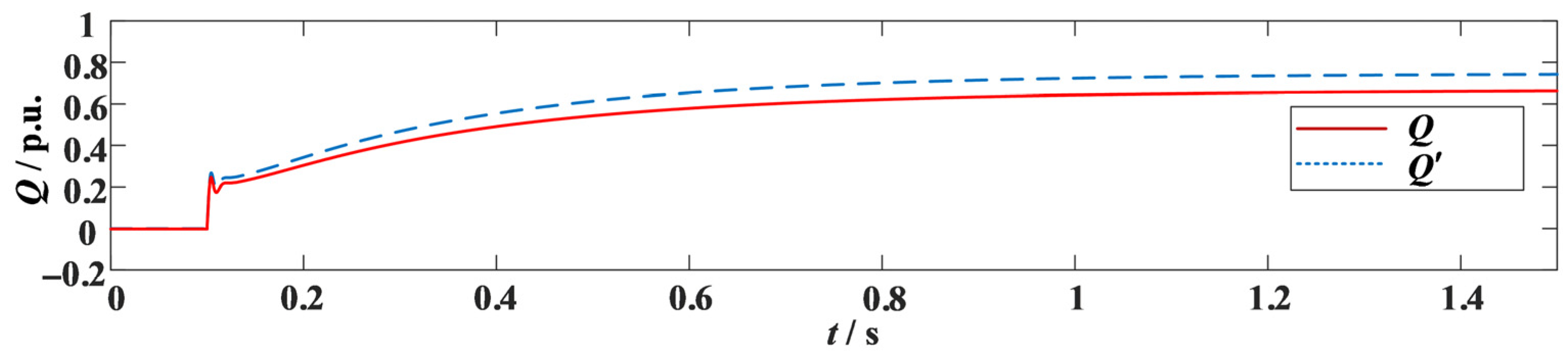
The comparison of reactive power before and after the improvement is shown in Figure 26. The blue dashed line represents the reactive power output of the converter under the improved method, and the red solid line represents the reactive power output of the converter when the reactive-voltage droop control is not frozen. After freezing the reactive-voltage droop control during a fault, the reactive power output at each time node increases.

(3) Operating condition 3: severe voltage drop (voltage drops below 40% of rated voltage)

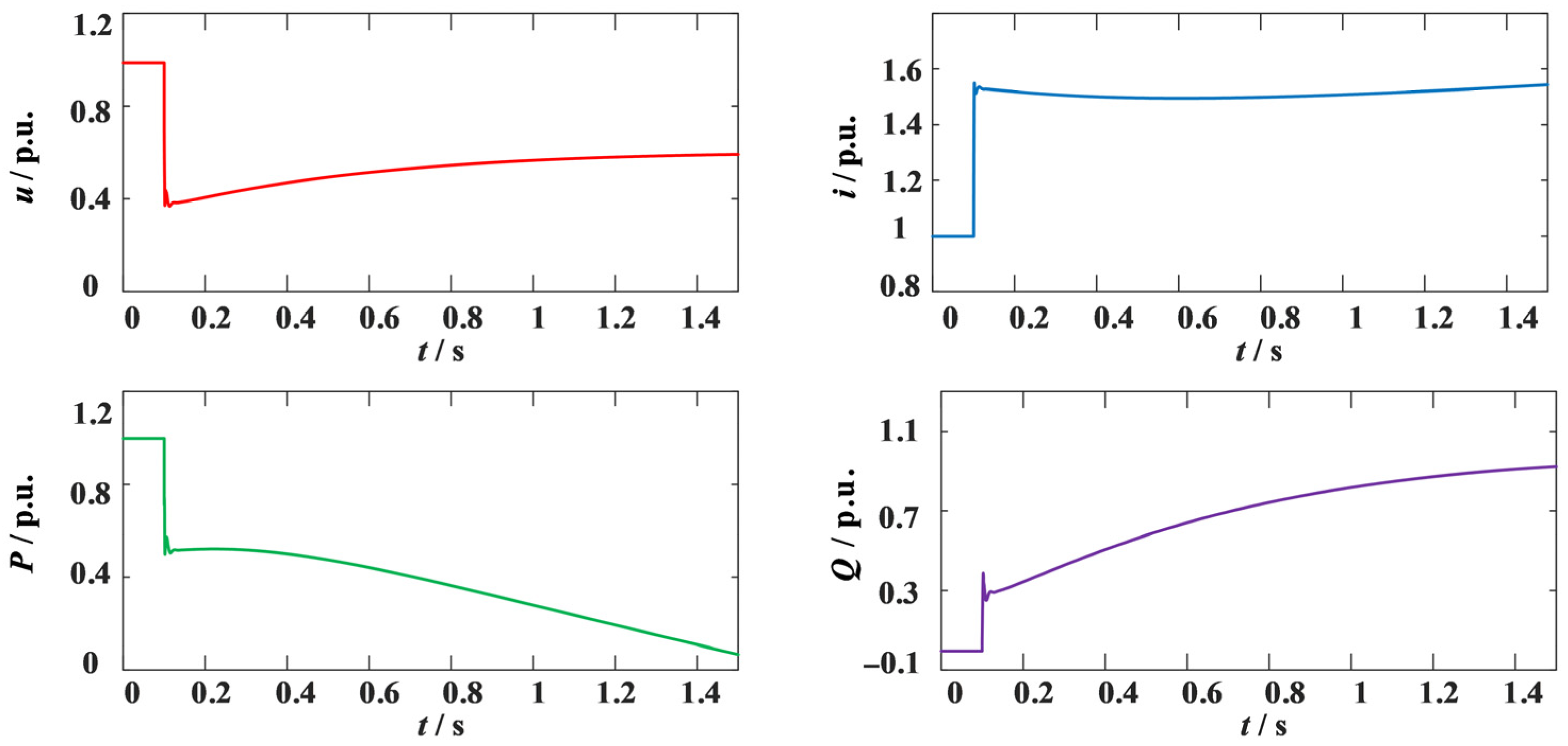
A three-phase short-circuit fault is set to occur at 65% of line 1 at 0.1 s, with a transition resistance set to 1 + j1 Ω. When the proposed improvement method is not used, the grid-connected voltage, current, and active and reactive power are shown in Figure 27. The minimum voltage amplitude drop is 0.3687 p.u., and the current amplitude during the fault period is consistently above 1.5 p.u., causing severe overcurrent in the converter and a significant increase in the output reactive power.

At this time, the primary control objective for the converter is to limit the current to prevent the inverter from being burned out, and there is no need to freeze the reactive power loop to increase the reactive power output of the converter. An adaptive virtual impedance control strategy is used to limit the current and remove the fault at 0.3 s. The voltage, current, active power, and reactive power conditions at this time are shown in Figure 28. The maximum current amplitude is 1.248 p.u. The adaptive virtual impedance control strategy effectively suppresses the fault overcurrent, and the converter provides more reactive power support during the fault. After the fault is removed, the reactive power–voltage droop control link is restored, and the converter returns to normal operation.

Through simulation verification under different voltage sag levels, it can be seen that the reactive power support method based on frozen reactive power–voltage droop control link combined with adaptive virtual impedance fault overcurrent suppression method can effectively function in various fault scenarios, enabling the grid-connected converter to output more reactive power without overcurrent risk.

Existing power grid protection schemes mainly include overcurrent protection, voltage protection, and distance protection. The proposed methods work synergistically with these schemes by suppressing overcurrent and supporting voltage, with the following specific interaction mechanisms:

(4) Interaction with Overcurrent Protection

The traditional converter overcurrent protection threshold is 1.2~1.5 times the rated current:

• Minor faults: The adaptive impedance suppresses the current to within 1.05 p.u., avoiding false protection operation;
• Severe faults: The current is suppressed to 1.248 p.u., close to the protection threshold, allowing the protection to operate normally according to the set time, with the method not interfering with the protection logic;
• Adaptation suggestion: If the protection threshold <1.2 p.u., adjust Ilim to 1.0 p.u. to ensure threshold matching.

(5) Interaction with Overcurrent Protection

The undervoltage protection threshold of the distribution network is 0.85~0.9 p.u.:

• When the voltage drops to 0.8~0.9 p.u., the frozen droop control quickly increases reactive power, restoring the voltage to above 0.85 p.u., avoiding protection tripping;
• If the method fails and the voltage remains <0.85 p.u., the voltage protection can operate to cut off the fault, forming a “support-backup” mechanism.

(6) Interaction with Distance Protection

Distance protection judges the fault location via line impedance, and the impact of the proposed methods is negligible:

• The converter-side impedance increased by the adaptive impedance is much smaller than the line impedance, not causing the protection to misjudge the fault location;
• The frozen droop supports the voltage, reducing measurement errors of the protection caused by excessively low voltage.

4.4. Low-Voltage Ride-Through Verification Based on Hardware-in-the-Loop Experiments

To verify the correctness of the quantitative virtual impedance design method proposed in this paper, a hardware-in-the-loop (HIL) semi-physical simulation experimental platform was established using RT-LAB 2024.1.8 software. The HIL simulation platform mainly consists of a PC, an RT-LAB-based real-time digital simulator, and VSG controller hardware. The physical hardware of the HIL simulation platform and the logical principles of each component are illustrated in Figure 29. The VSG controller is a physical hardware unit, while other logical components are integrated into the simulation model of the real-time digital simulator.

The main circuit model of the VSG grid-connected system was constructed through simulation on the RT-LAB software platform. The simulation part achieves integration and data sharing with the controller hardware via the real-time digital simulator. After setting the control parameters of the controller hardware, the controller calculates PWM control signals based on the operational data transmitted from RT-LAB and sends these signals to the real-time digital simulator, ultimately realizing complete system control. The controller hardware features a sampling and control cycle of 4 kHz, and the frequency of space vector pulse width modulation (SVPWM) is also 4 kHz. This high sampling and control frequency ensures the real-time performance between the hardware control unit and the virtual simulation model of the main circuit.

The VSG controller hardware transmits data with the Real-Time Digital Simulator (RTDS) via a DB37 connecting cable. It receives real-time data such as current and voltage from the RTDS, calculates the PWM modulating wave signals based on its own control parameters and the operating status of the main circuit, and ultimately completes the real-time simulation of the entire system. The DB37 connecting cable interface and the fiber optic interface on the PC terminal are shown in Figure 30.

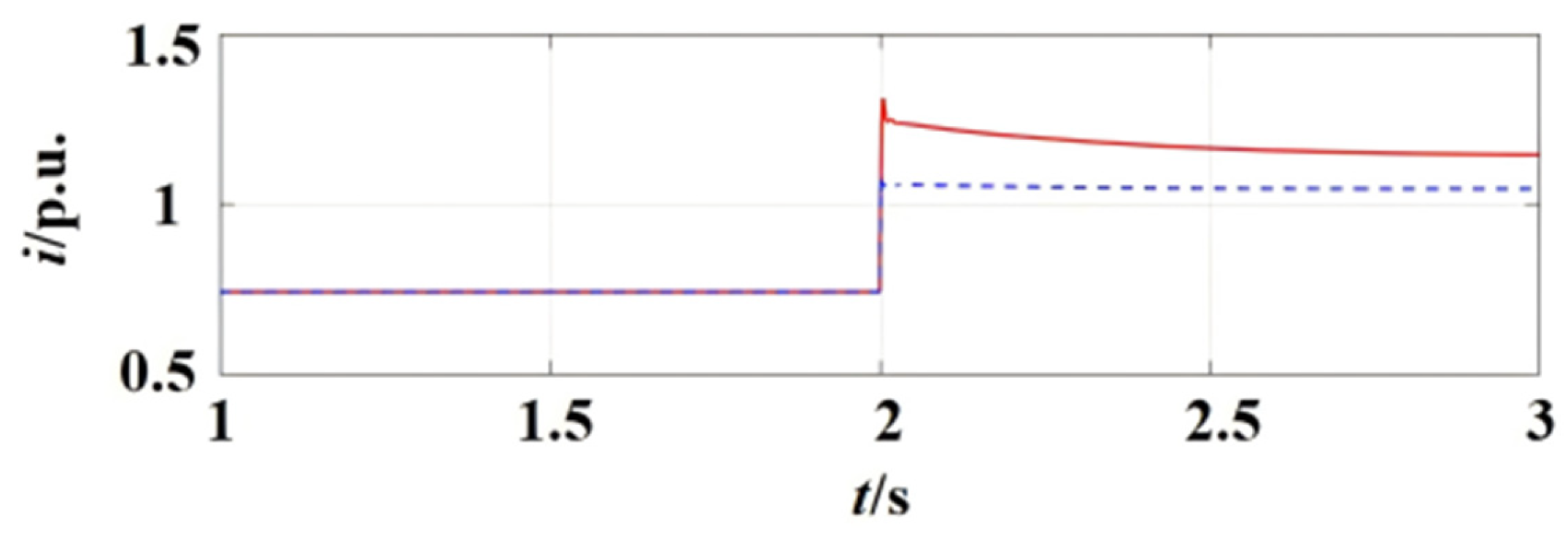
The specific parameters of the hardware-in-the-loop (HIL) experiment are consistent with Table 1. Figure 31 illustrates the variation in the fault current when the point of common coupling (PCC) voltage drops to 0.70 p.u. At this juncture, it can be observed from the figure that the current during the fault is constrained, thereby achieving the grid-forming inverter’s low-voltage ride-through capability under symmetrical faults.

Figure 32 illustrates the reactive power variation under this condition. With the proposed low-voltage ride-through (LVRT) control strategy, the power output during the fault period can reach the set value within an extremely short time.

Table 6. Fault current peaks under different voltage sag depths.

Fault Voltage (p.u.)	Fault Current Peak (p.u.)
0.85	1.05
0.70	1.11
0.65	1.13
0.50	1.20
0.35	1.24

presents the peak fault currents of the VSG under hardware-in-the-loop (HIL) experiments with different voltage sag depths. It can be concluded from the experimental results that with the proposed low-voltage ride-through (LVRT) control strategy, all peak currents can be effectively limited, which verifies the correctness of the proposed control strategy.

We designed a comparison table of the deviations of core indicators between the simulation and HIL experiments under the same fault scenario (PCC voltage 0.7 p.u.). As shown in

Table 7. A “DSP + FPGA” dual-mode controller architecture.

Indicator	Simulation Result	HIL Experimental Result	Deviation Rate	Analysis of Deviation Causes
Fault current peak (p.u.)	1.11	1.15	3.6%	HIL has 1.2 μs sampling delay, not included in simulation
Reactive power increase rate (%)	11.68	10.92	6.5%	PWM dead time (0.5 μs) in hardware reduces reactive output slightly
Current THD (%)	2.3	2.7	17.4%	Hardware sampling noise (±0.02 p.u.) introduces harmonics

.

(1) Summary of deviation causes: The simulation model ignores hardware delays and sampling noise, leading to slightly worse HIL results than the simulation.

(2) Model correction plan: Add a “hardware delay module” and a “Gaussian noise module” in subsequent simulations to reduce the deviation rate between the simulation and HIL to within 3%.

(3) Engineering implications: Hardware calibration is required in practical deployment to reduce noise impact, and PWM dead time should be optimized to improve reactive support capability.

5. Conclusions and Future Outlook

Grid-forming converters achieve friendly grid connection of renewable energy by simulating traditional synchronous generator characteristics (e.g., voltage source and rotational inertia). This paper focuses on the low-voltage ride-through (LVRT) strategy of grid-forming converters under Virtual Synchronous Generator (VSG) control. The main conclusions are as follows:

(1) A fault overcurrent suppression method based on adaptive virtual impedance is proposed, overcoming the limitation of traditional fixed virtual impedance (unadjustable to actual operating conditions). It uses the difference between preset current threshold and measured value as feedback, dynamically adjusting virtual impedance via resistance/reactance coefficients to enhance grid-connected converters’ overcurrent suppression capability under various fault scenarios. Verified by simulations and comparisons with the fixed method, the proposed method effectively improves the converter’s fault overcurrent suppression performance.

(2) To address reduced converter reactive support caused by retaining reactive-voltage droop control, a reactive support method based on frozen droop control is proposed. It uses positive-sequence voltage amplitude as the fault detection quantity to identify system faults and determine whether to freeze the droop link, improving control response speed and reactive support capability of grid-connected converters during voltage sags. Simulations verify that the method avoids adverse impacts of the reactive droop link and significantly enhances the converter’s reactive output capability.

To address the current limitation of this paper and bridge the gap between simulation and real-world application, future work will focus on a streamlined practicalization plan, including physical prototype testing, field validation, and algorithm optimization, with details as follows:

1. Physical Prototype and Field Testing

• Laboratory Prototype: Build a 20 kVA two-level converter (LCL filter parameters proportional to Table 1: L = 0.35 mH, C = 100 μF) with TI TMS320F28379D. Test under different PCC loads (resistive-inductive/capacitive) and voltage sags to verify overcurrent protection coordination and long-term stability.
• Field Test: Embed the algorithms into existing converters in a 10 kV distribution network (State Grid Zhengzhou Power Supply Co., Ltd., Zhengzhou, China) to validate overcurrent suppression and reactive support under real grid disturbances.

2. Algorithm Optimization

Collaborate with manufacturers to optimize code efficiency, reducing the adaptive impedance module’s computational latency to <50 μs for industrial real-time requirements.

These efforts will verify simulation credibility, resolve “simulation-physical” parameter deviations, and provide data support for industrial application of the method.