A Systematic Review of Numerical Modelling Approaches for Cryogenic Energy Storage Systems

Abstract

Cryogenic Energy Storage (CES) has emerged as a promising solution for large-scale and long-duration energy storage, offering high energy density, zero local emissions, and compatibility with intermittent renewable energy sources. This systematic review critically examines recent advances in the numerical modeling of CES systems, with the objective of identifying prevailing methodologies, emerging trends, and existing research gaps. The studies analyzed are classified into three main categories: global thermodynamic modeling, simulation of specific components, and transient dynamic modeling. The findings highlight the continued use of thermodynamic models due to their simplicity and computational efficiency, alongside a growing reliance on high-fidelity CFD and transient models for more realistic operational analyses. A clear trend is also observed toward hybrid approaches, which integrate deterministic modeling with machine learning techniques and response surface methodologies to enhance predictive accuracy and computational performance. Nevertheless, significant challenges persist, including the absence of multiscale integrative models, the scarcity of high-resolution experimental data under transient conditions, and the limited consideration of operational uncertainties and material degradation. It is concluded that the development of integrated numerical frameworks will be critical to advancing the technological maturity of CES systems and ensuring their robust deployment in real-world energy transition scenarios. Additionally, the review also discusses local thermal non-equilibrium (LTNE) conditions, the influence of geometric and operational parameters, and the role of multidimensional and multi-region modeling in predicting thermal and exergy performance of packed-bed TES within LAES cycles.

1. Introduction

Cryogenic Energy Storage (CES) has increasingly established itself as a technically robust and promising solution for large-scale and long-duration energy storage, offering high energy density, zero local emissions, and strong compatibility with intermittent renewable energy sources [1,2]. This systematic review provides a critical assessment of recent advances in the numerical modelling of CES systems, with the aim of identifying predominant methodologies, emerging trends, and the main research gaps that remain in the current state of the art. The studies examined are grouped into three major categories: global thermodynamic modelling [3,4,5], component-level simulations [6,7,8,9], and transient dynamic modelling [10,11,12]. The findings reveal that thermodynamic modelling continues to be widely employed due to its conceptual simplicity and computational efficiency, while a significant growth in the use of high-fidelity CFD-based and transient approaches is observed, enabling more realistic representation of operating conditions [13,14]. A clear trend is also identified toward the development of hybrid modelling strategies that combine deterministic methods with machine-learning techniques and response-surface methodologies to enhance predictive accuracy and reduce computational cost [15,16]. Despite these advances, several challenges persist, including the lack of multiscale integrative frameworks, the limited availability of high-resolution experimental data under transient conditions, and the insufficient consideration of operational uncertainties and material degradation phenomena [17,18,19]. It is concluded that the development of integrated numerical frameworks will be essential for advancing the technological maturity of CES systems and ensuring their reliable deployment within real-world energy-transition scenarios. Furthermore, this review examines the role of local thermal non-equilibrium (LTNE) conditions [20], the influence of geometric and operational parameters [21,22], and the importance of multidimensional and multi-region modelling in predicting the thermal and exergetic behaviour of packed-bed thermal energy storage units integrated into LAES cycles [23,24].

2. Fundamentals of Cryogenic Energy Storage

2.1. Thermodynamic Principles of Air Liquefaction

Cryogenic systems operate based on fundamental thermodynamic principles, employing refrigeration cycles such as the Claude, Kapitza, and Linde-Hampson cycles to achieve extremely low temperatures [1]. Cryogenic Energy Storage (CES) relies on the transformation of gases—predominantly atmospheric air—into a liquid state through sequential processes of compression, cooling, and expansion, governed by the principles of real-gas thermodynamics, including the Joule–Thomson effect, which induces a temperature drop during isothermal or isenthalpic expansion [2].

The efficiency of these processes depends on several factors, including the number of compression stages, the integration of interstage cooling, the performance of heat exchangers, thermal insulation, and the minimization of thermodynamic irreversibilities [5]. An accurate thermodynamic description of these phenomena is essential to predict the specific work requirement and optimize the overall energy consumption of the cycle [1].

Comparative studies of different liquefaction cycles indicate that the Claude and Kapitza cycles exhibit significantly higher efficiencies than the Linde-Hampson cycle [5,9]. This performance advantage is largely due to the use of more efficient bypass turbines, which provide the necessary cooling while generating work. According to Borri et al. [5], the Linde-Hampson system operates at higher pressures (24–26 MPa), resulting in substantially higher specific consumption (2.5–2.6 kWh/kg), whereas the Claude and Kapitza cycles exhibit lower specific consumption (0.72–0.73 kWh/kg and 0.71–0.72 kWh/kg, respectively) and considerably higher exergy efficiencies (12.16% and 12.1%, compared to 2.47% for the Linde cycle). Parametric analyses reported by Borri et al. [5] show that for a single-stage compression cycle, the Claude and Kapitza cycles achieve the lowest specific consumption (0.52 kWh/kg) at 1 MPa, while two-stage compression reduces consumption by approximately 20%. Furthermore, the third heat exchanger in the Claude cycle can be omitted, making the Kapitza cycle slightly more efficient. Although the Heylandt cycle demonstrates superior performance, its higher operating pressures require more expensive equipment, making the Claude and Kapitza cycles more practical in terms of cost and operational feasibility [1,3,9]. Consequently, the Claude cycle is the most widely employed system in practical applications due to its favorable balance between efficiency and operational viability.

The Claude liquefaction system, illustrated in Figure 1, comprises a high-pressure compressor, heat exchangers, an expansion turbine, and a Joule–Thomson valve, enabling efficient gas liquefaction at very low temperatures. Figure 2 depicts the corresponding thermodynamic cycle, highlighting the stages of compression, cooling, expansion, and refrigeration that define the process.

Figure 2 illustrates the thermodynamic behavior of the Claude liquefaction cycle on a temperature–entropy (T–s) diagram. The diagram highlights the main stages of the process, including compression, cooling in heat exchangers, adiabatic expansion through the turbine, and isenthalpic expansion via the Joule–Thomson valve. This representation provides a clear visualization of the energy transformations and entropy changes occurring throughout the cycle, which are essential for evaluating the system’s performance and efficiency.

2.2. Principles of Cryogenic Systems

The processing and storage of gases in a liquid state constitute fundamental stages of cryogenic systems [3,4,25]. This process involves essential operations, including gas compression, expansion, and refrigeration, ultimately leading to liquefaction [1]. Liquefied gases, such as air or hydrogen, are subsequently stored in thermally insulated tanks to preserve the critical temperatures required to maintain the liquid state and minimize energy losses [26].

These technologies are characterized by high energy density, providing significant potential for large-scale applications. Figure 3 illustrates the working principle of a cryogenic energy storage system, highlighting the key stages involved in the liquefaction and subsequent storage of gases.

Cryogenic Energy Storage (CES) systems, including Liquid Air Energy Storage (LAES), operate based on fundamental thermodynamic principles, notably the Joule–Thomson effect and the first and second laws of thermodynamics, which govern energy conversion and transfer [3,5,7,11]. The process involves compression, liquefaction, expansion, and refrigeration of gases, which are then stored in thermally insulated reservoirs to maintain critical temperatures and minimize energy losses [8,13,26,27,28]. These systems are characterized by high energy density, making them suitable for medium- to large-scale applications. Performance is assessed via round-trip efficiency (RTE), defined as the ratio of energy recovered to energy consumed. Conventional LAES systems exhibit 45–60% RTE, exceeding 70% when coupled with heat recovery and sensible thermal energy storage [3,5,7,11]. Hybrid solutions, including TES, cold storage, or direct integration with industrial low-grade heat, further enhance exergetic efficiency and reduce external energy dependence [12,13]. CES also benefits from abundant, non-toxic materials, modularity, and operational flexibility, supporting grid applications, peak load management, and renewable integration [1,6,7,8,14]. Thermal management relies on efficient TES units, particularly packed-bed TES (PB-TES), which provide necessary temperature gradients during charging and discharging, improving thermodynamic performance and exergetic efficiency [15,16].

2.3. Energy Efficiency in Cryogenic Systems

Energy efficiency is a key performance metric for evaluating cryogenic energy storage technologies, including LAES systems, CO₂ cryogenic systems, and hybrid configurations [27,28,29,30,31]. LAES systems exhibit efficiencies between 45% and 70%, largely depending on the recovery and utilization of residual heat and cold. Integration with complementary cryogenic cycles, such as Rankine cycles, can further increase efficiency up to approximately 75% by reducing exergy losses and optimizing thermal management [27,28,29,30]. Improvements in liquefaction (advanced precooling, regenerative heat exchangers, high-conductivity materials) and expansion (high-efficiency turbines, multi-stage cycles, thermal energy recovery) can enhance performance even further [13,29]. The efficiency of CO₂ cryogenic systems, typically 40–60%, is mainly governed by compression and liquefaction stages, operating pressure, thermal insulation quality, and exhaust gas temperature. Lower temperatures can enhance CO₂ capture but also increase energy consumption, negatively impacting both energy efficiency and exergy [31,32,33,34].

Hybrid systems combine cryogenic technologies with Rankine cycles, air separation units (ASUs), and LNG regasification processes, achieving efficiencies of 55–80%, depending on configuration [29,35,36,37]. Utilizing residual cold from LNG regasification and operational flexibility improves responsiveness to grid fluctuations [29,35]. However, integration complexity, the requirement for dynamic control, and material limitations at cryogenic temperatures can reduce efficiency and increase operational costs, particularly in large-scale applications [37,38].

3. Numerical Methods Applied to the Study of Cryogenics

Numerical modeling plays a fundamental role in the study and optimization of cryogenic energy storage systems, particularly Liquid Air Energy Storage (LAES) systems. These systems involve complex phenomena, including nonlinear thermodynamic processes, phase changes, heat transfer, and multiphase flows, which necessitate advanced computational methods for detailed performance analysis [17,18]. Thermodynamic modeling typically represents the various stages of the LAES cycle—compression, cooling, liquefaction, storage, and expansion—through energy and mass balances that incorporate the real fluid properties at low temperatures, enabling the calculation of critical parameters such as efficiency and losses [19,20].

Heat transfer is among the most critical aspects, as thermal losses in storage tanks and heat exchangers directly affect overall system efficiency. Simplified one-dimensional models are commonly employed for rapid simulations; however, increased computational capacity has enabled the use of three-dimensional simulations based on Computational Fluid Dynamics (CFD) [17,18,21]. CFD solves the Navier–Stokes equations to accurately characterize fluid flow, turbulence, and thermal exchange with high spatial and temporal resolution. Integrated thermodynamic simulations further allow the study of the dynamic behavior of the cycle, including load variations and realistic operating conditions. Software such as ANSYS Fluent R2 and CFX R2 are widely used for CFD analysis, COMSOL 6.1 Multiphysics facilitates Multiphysics modeling, and MATLAB/Simulink R2024a supports dynamic system modeling and control development. Tools like Engineering Equation Solver (EES) and Aspen Plus are also commonly applied for detailed thermodynamic calculations and industrial process simulations. Despite their increasing fidelity, most CFD and heat transfer studies rely on the assumption of local thermal equilibrium (LTE) between solid and fluid phases. This assumption can lead to inaccuracies under certain operating conditions, such as high heat transfer rates, large particle sizes, or steep temperature gradients. In these cases, local thermal non-equilibrium (LTNE) models become necessary to more realistically capture the distinct energy exchange dynamics, particularly in packed-bed thermal energy storage (PB-TES) integrated into LAES systems [22,23].

Despite these advances, significant challenges remain, including the complex characterization of the thermophysical properties of cryogenic fluids at low temperatures and the simulation of dynamic multiphase phenomena, which often require simplifications that may compromise accuracy. Balancing model detail with computational cost also poses challenges, especially for large-scale or real-time simulations. Experimental validation remains essential to ensure that models accurately reflect real system behavior under varying operating conditions. Thus, the combination of thermodynamic modeling, CFD, and dynamic simulations represents the state of the art in numerical studies of cryogenic energy storage, enabling significant progress in the design, control, and optimization of LAES systems. The ongoing development of these methodologies, supported by experimental data, is crucial to overcoming current limitations and facilitating the commercial deployment of these technologies [19,24,39,40].

4. Systematic Review of Numerical Studies on Cryogenic Energy Storage (CES)

This section presents a systematic and comprehensive review of the scientific literature addressing numerical studies in cryogenic energy storage (CES), with a particular emphasis on Liquid Air Energy Storage (LAES) systems. The objective is to critically examine the main numerical methodologies, recent advancements in modeling and simulation, and existing research gaps within this domain. The selection and analysis of studies were conducted according to the PRISMA (Preferred Reporting Items for Systematic Reviews and Meta-Analyses) methodology, ensuring transparency, reproducibility, and traceability throughout the review process.

4.1. Methodology for the Systematic Retrieval and Selection of Scientific Publications

The systematic review was conducted following PRISMA guidelines to provide a structured and reproducible approach to literature identification, screening, and selection. Bibliographic searches were performed in the Web of Science, Scopus, and ScienceDirect databases using keyword combinations relevant to CES and LAES, including “Liquid Air Energy Storage,” “CFD,” “numerical modeling,” “thermodynamic simulation,” “cryogenic storage,” and “energy storage system.”

The inclusion criteria encompassed articles published between 2010 and 2025, written in English, and demonstrating the application of numerical modeling techniques—such as computational fluid dynamics (CFD) and thermodynamic simulations—within cryogenic energy storage systems. Exclusion criteria comprised purely experimental studies, review articles lacking computational analysis, and works not directly related to CES.

The application of sequential filters yielded the following selection process: initially, 1683 publications were identified: 1677 were in English, 764 were restricted to the Energy subject area, 690 were peer-reviewed research articles, and 669 publications matched the temporal range 2015–2025. Title screening further reduced the set to 105 articles, and subsequent abstract evaluation led to a final curated sample of 55 articles considered suitable for detailed review. This data set forms a robust basis for evaluating methodologies, recent technological developments, and research gaps in numerical modeling for LAES systems.

Figure 4 presents the PRISMA flow diagram, illustrating the stages of identification, screening, eligibility assessment, and inclusion of studies. The diagram explicitly details the inclusion and exclusion criteria applied and the number of records removed at each stage, providing a clear and reproducible overview of the systematic review process.

4.2. Classification of Numerical Studies

This section presents a review of the main numerical studies conducted in the field of cryogenic energy storage (CES), organized according to the methodological approach employed and the scope of each investigation. The analysis focuses on the most relevant works, allowing the identification of prevailing trends, technological advancements, and gaps in the numerical modeling of CES systems. To structure the review, the studies have been grouped into five main categories: global thermodynamic modeling, simulations of specific components, transient dynamic modeling, modeling and Performance of PB-TES under LTNE Conditions, and multidimensional and multi-region approaches in LAES cycles. This methodological classification enables a systematic examination of the different strategies employed in literature, providing a comprehensive overview of the progress achieved, current limitations, and ongoing challenges in the development and optimization of cryogenic energy storage technologies.

4.2.1. Global Thermodynamic Modeling Studies

Global thermodynamic modeling represents a central approach in the investigation of Liquid Air Energy Storage (LAES) systems, focusing on the integrated simulation of system performance across its main operational stages—liquefaction, cryogenic storage, and expansion. These studies apply rigorous mass and energy balances, exergy analysis, and complete thermodynamic cycle modeling, enabling the evaluation of key performance indicators such as round-trip efficiency, energy density, and the exploitation of internal thermal gradients.

Manassaldi et al. [41] developed a deterministic optimization model for LAES, reporting a 63% increase in cycle efficiency and a 48% improvement in liquid air production. Remarkably, the model also enabled the elimination of one system component, simplifying the overall configuration while enhancing optimization and simulation capabilities. Earlier work by Hamdy et al. [42] demonstrated that advanced cryogenic storage configurations with exergy recovery during discharge could double liquid air production and significantly increase exergetic efficiency. Their results showed that direct expansion cycles with cold storage achieved a round-trip efficiency of 40%, while coupling with Organic Rankine Cycles boosted discharge power output by up to 25%.

Borri et al. [43] analyzed air liquefaction configurations for microgrid-scale LAES applications, comparing the Linde, Claude, and Kapitza cycles. Their findings indicated that the two-stage Kapitza cycle with a pressurized phase separator achieved the best performance, with specific energy consumption between 520 and 560 kWh/t. The study highlighted the critical role of heat exchangers in determining system efficiency, as well as the importance of heat and cold recovery for future improvements. Similarly, Qing et al. [44] conducted thermodynamic and exergy analyses of a four-stage compression–expansion LAES system, identifying optimal storage and discharge pressures of 15 MPa and 7.1 MPa, respectively, and emphasizing the influence of component adiabatic efficiencies on overall system performance.

Guizzi et al. [45] reinforced the relevance of integrating cold and heat storage in stand-alone LAES systems, showing efficiencies approaching 50% and identifying the cryoturbine’s isentropic efficiency as a critical factor, recommending a minimum threshold of 70%. Their study concluded that LAES represents a viable option for grid-scale energy storage due to its geographical independence, reliability, and low environmental impact. Expanding on this perspective, Yan et al. [46] proposed optimal operation strategies for multi-energy systems incorporating LAES. Using information gap decision theory and demand response programs, they demonstrated cost reductions of up to 6.82% and identified the substitution of grid electricity with natural gas during high-price periods as the most economical strategy.

More recently, Duan et al. [47] introduced a multi-objective optimization of a hybrid biomass–LNG–LAES system combined with two-stage Organic Rankine Cycles, employing adaptive genetic algorithms and neural networks to improve model convergence. Their results showed that a mixed combustion ratio, maximum pressure operation, and full utilization of compressed air minimized both exergy cost and carbon intensity. Complementarily, Manassaldi et al. [48] proposed a nonlinear optimization strategy for LAES systems, using derivative-based algorithms and dynamic link libraries for accurate property estimation. Their results yielded a 20% increase in efficiency and a 21% improvement in liquid air production, further demonstrating the potential of advanced optimization frameworks.

From a thermo-economic perspective, Liang et al. [49] applied the NSGA-II genetic algorithm for multi-objective optimization, identifying trade-offs among efficiency, capital cost, and exergy destruction. They recommended configurations with three-stage compressors and four-stage expanders for high-budget investments (>£48 million), which achieved efficiency improvements of 9–14% and reductions in exergy destruction of 16%. Ansarinasab et al. [50] proposed the integration of active magnetic refrigeration (AMR) precooling into conventional liquefaction cycles, reducing specific energy consumption by up to 11.2% and improving exergy efficiency, with the Kapitza-AMR configuration achieving the lowest levelized cost of product. Finally, Tan et al. [11] developed a steady-state LAES model combining the Linde process with an open Rankine cycle. Using genetic algorithm optimization, they achieved a round-trip efficiency of 53.33%, a liquefaction ratio of 86.96%, and a 10.02% reduction in compressor power consumption.

Overall, the reviewed studies demonstrate that global thermodynamic modeling and multi-objective optimization represent fundamental tools for advancing LAES technologies, enabling the evaluation of key performance indicators, the identification of irreversibility sources, and the proposal of design and operational improvements. Nevertheless, many models still rely on oversimplifications—such as steady-state assumptions and limited thermophysical correlations—that constrain their applicability under dynamic and industrial conditions. Moreover, the integration of more comprehensive environmental assessments, particularly life-cycle analyses, remains insufficiently addressed. Future progress in this field depends on the adoption of hybrid models that couple thermodynamic, exergy, and dynamic approaches, while explicitly accounting for operational uncertainties and environmental impacts. Such integration is essential to reliably support industrial-scale design and consolidate LAES as a scalable, sustainable, and adaptive solution for renewable energy storage.

Table 1. Comparative summary of global thermodynamic modeling studies in Liquid Air Energy Storage (LAES) systems.

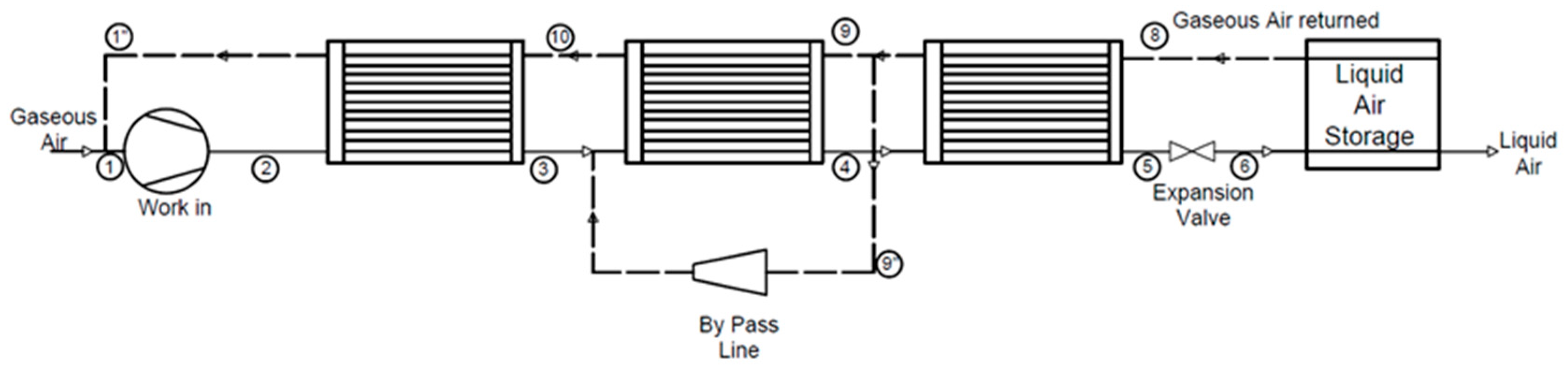
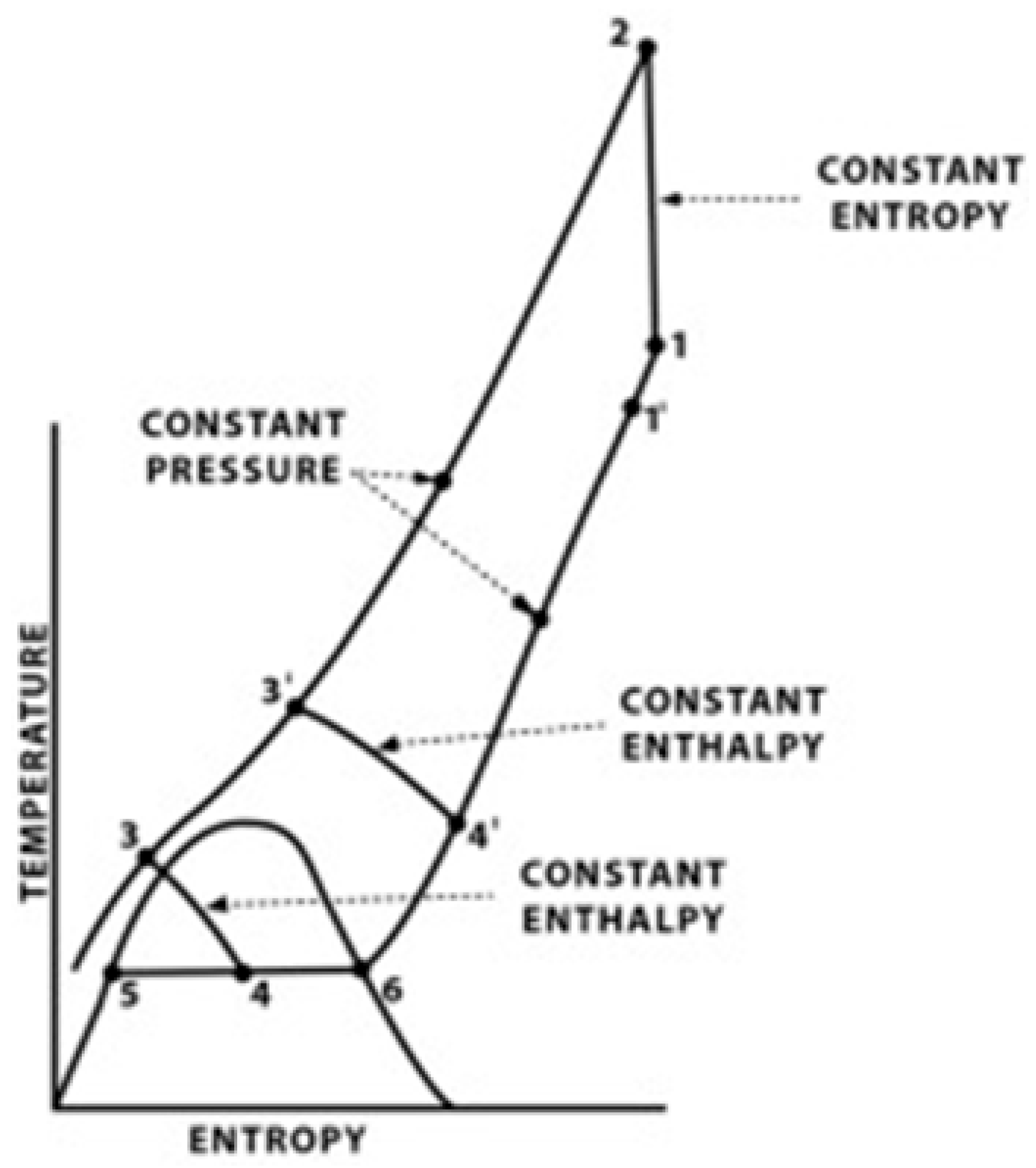
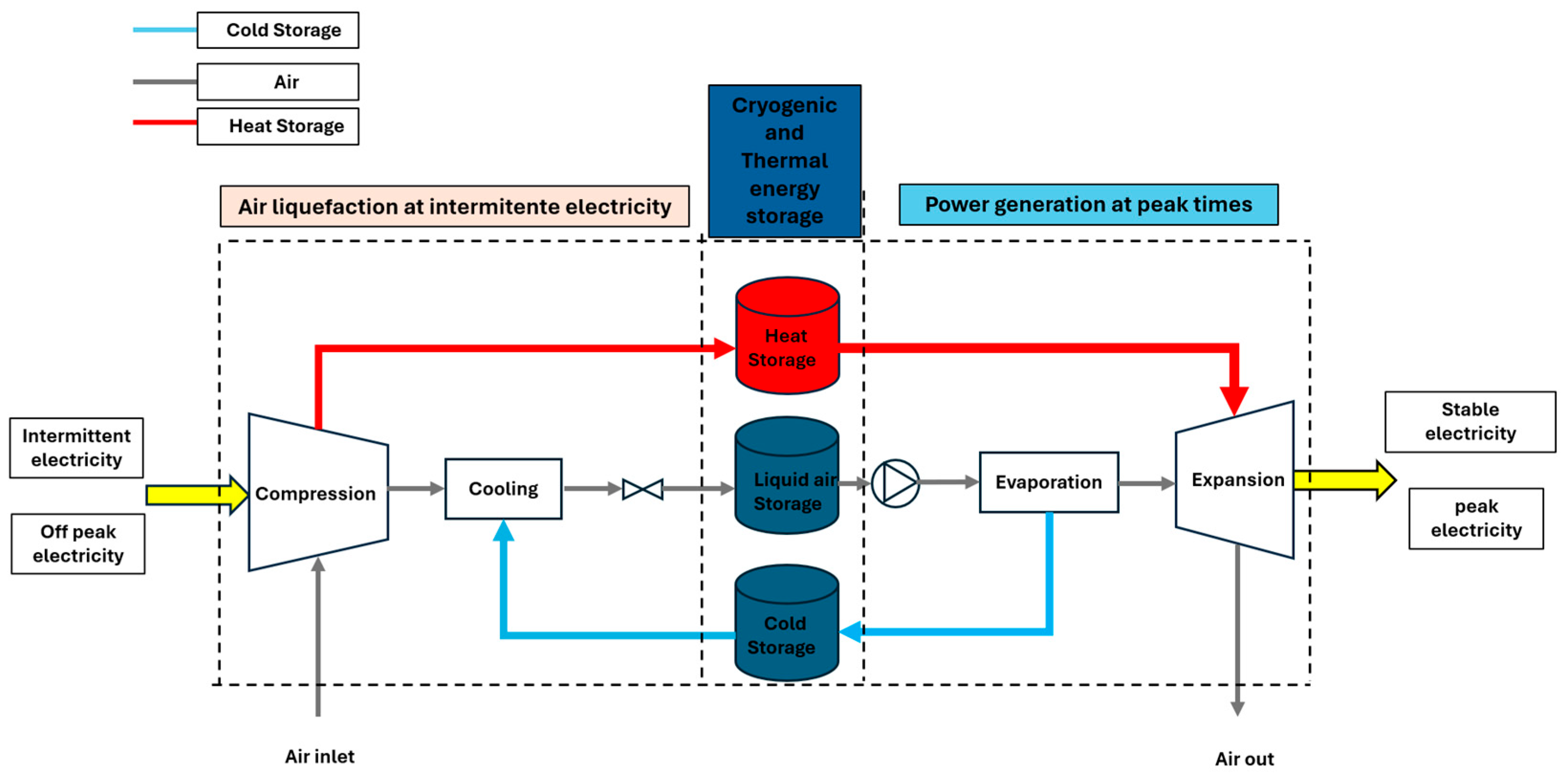
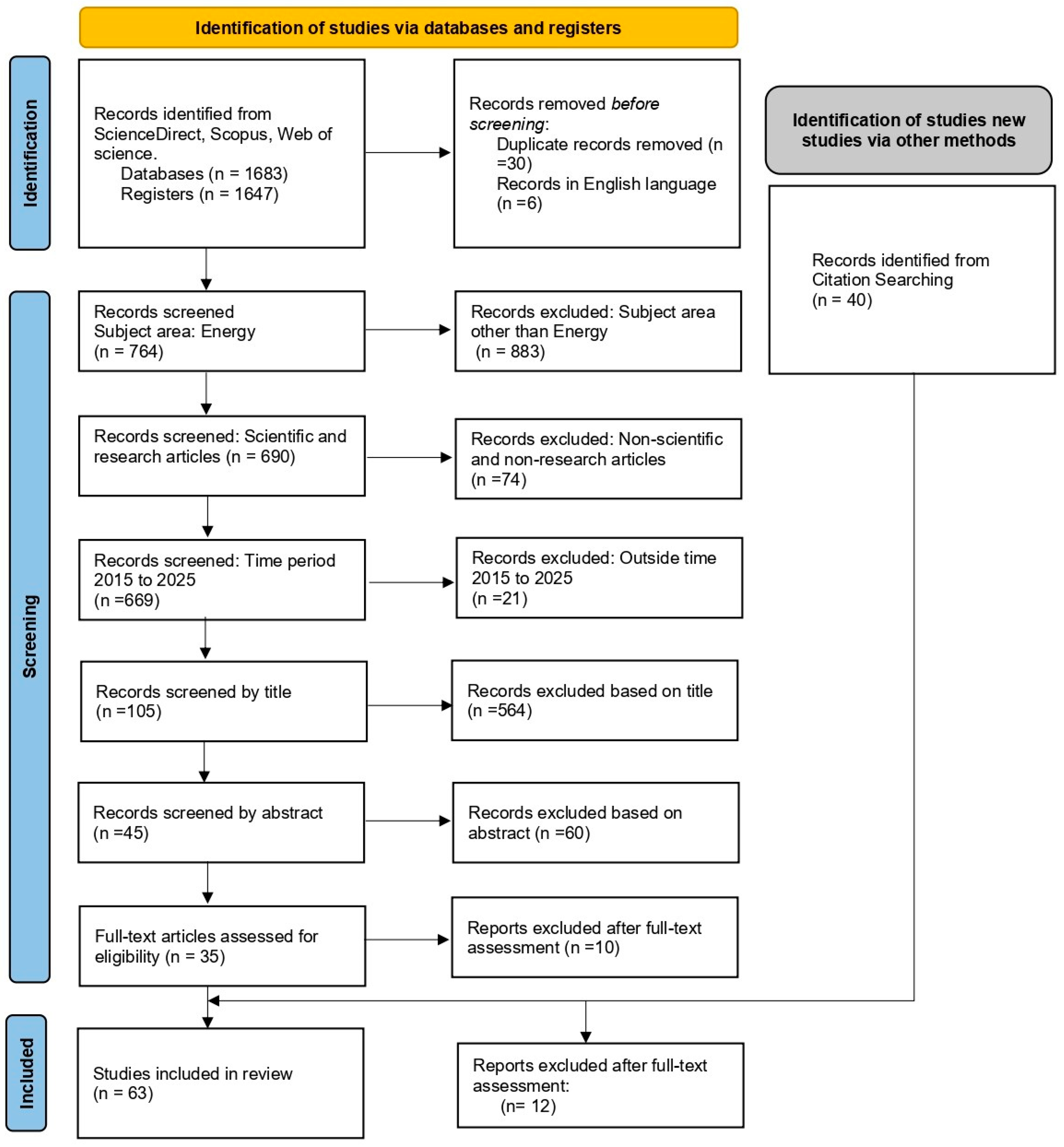
Study	Modeling Approach	System/Scale	Key Results/Performance Indicators	Remarks
Manassaldi et al. [41]	Deterministic optimization	LAES	+63% cycle efficiency; +48% liquid air production	Eliminated one component, simplifying system configuration
Hamdy et al. [42]	Thermodynamic modeling with exergy recovery	LAES with direct expansion & ORC	Round-trip efficiency (RTE) 40%; +25% discharge power	Significant increase in exergetic efficiency
Borri et al. [43]	Cycle comparison (Linde, Claude, Kapitza)	Microgrid-scale LAES	Specific energy consumption: 520–560 kWh/t	Two-stage Kapitza cycle with pressurized phase separator most efficient; highlights heat exchanger importance
Qing et al. [44]	Thermodynamic & exergy analysis	4-stage compression-expansion LAES	Optimal storage/discharge pressures: 15 MPa/7.1 MPa	Component adiabatic efficiencies strongly influence overall performance
Guizzi et al. [45]	Integration of cold and heat storage	Stand-alone LAES	Efficiency ≈ 50%	Cryoturbine isentropic efficiency critical (>70%)
Yan et al. [46]	Multi-energy operational strategies	LAES in hybrid systems	Cost reduction up to 6.82%	Substitution of grid electricity with natural gas most economical during high-price periods
Duan et al. [47]	Multi-objective optimization + genetic algorithms & neural networks	Hybrid biomass–LNG–LAES system	Minimized exergy cost and carbon intensity	Demonstrates effectiveness of hybrid optimization frameworks
Manassaldi et al. [48]	Nonlinear optimization	LAES	+20% efficiency; +21% liquid air production	Highlights potential of advanced optimization frameworks
Liang et al. [49]	NSGA-II multi-objective optimization	LAES (high-budget investment)	Efficiency +9–14%; exergy destruction −16%	Trade-offs between efficiency, capital cost, and exergy destruction
Ansarinasab et al. [50]	Integration of Active Magnetic Refrigeration (AMR)	LAES	Specific energy consumption reduced by up to 11.2%	Kapitza-AMR achieved lowest levelized cost of product
Tan et al. [11]	Steady-state modeling + genetic algorithm	LAES	RTE 53.33%; liquefaction ratio 86.96%; compressor power −10.02%	Demonstrates effective optimization under steady-state conditions

provides a comparative overview of the main global thermodynamic modeling studies on LAES systems, highlighting consistent improvements in efficiency, reductions in specific energy consumption, and enhanced operational performance. This consolidated evidence underscores the relevance of advanced optimization and thermal-integration approaches, reinforcing the trends and limitations discussed throughout this section.

4.2.2. Simulations of Specific Components

This category of studies focuses on the detailed analysis of critical components in cryogenic energy storage systems, with particular emphasis on storage tanks and heat exchangers. These components operate under complex conditions of heat transfer and fluid dynamics, being subject to phenomena such as thermal stratification, self-pressurization, and boil-off gas (BOG) generation. Thermal stratification arises from the formation of fluid layers with different temperatures and densities, induced either by non-uniform external heat fluxes or by internal processes such as partial evaporation of the cryogenic liquid. This heterogeneous distribution of thermophysical properties leads to the development of pressure gradients that compromise operational stability, increase BOG generation rates, and ultimately degrade overall system performance.

Zuo et al. [51] investigated the rollover phenomenon in cryogenic tanks using Schlieren visualization applied to stratified saline solutions as an experimental analogue. The rollover process was divided into four stages, with particular emphasis on the prolonged transition stage. Results demonstrated that higher heat flux accelerates interface collapse and intensifies mixing, while small density differences significantly increase susceptibility to rollover. These findings were correlated with analytical models, providing relevant contributions to improving both safety and efficiency in cryogenic storage. In an earlier study, Zuo et al. [52] examined the suppression of thermal stratification in liquid hydrogen tanks through the use of self-actuated rotating spray bars. Their results showed substantial improvements, including a 41.2% reduction in thermal non-uniformity, a 50% decrease in cooling time depending on subcooled fluid velocity, and a 76.5% reduction in system weight. These outcomes highlight the potential of active stratification control to optimize efficiency and minimize energy losses in cryogenic storage systems.

Sha et al. [53] analyzed interfacial instability and rollover patterns in stratified NaCl solutions, representative of multi-component systems. They identified distinct convective transport modes—“W-shaped,” “Y-shaped,” and hourglass patterns—depending on initial buoyancy ratios. Importantly, higher buoyancy ratios did not necessarily imply greater rollover risk in layered systems, such as liquefied natural gas tanks. Similarly, Kassemi et al. [54], using CFD with Sharp Interface and VOF methods, assessed the sensitivity of self-pressurization predictions to accommodation coefficients and turbulence treatments. Their results revealed that laminar models matched experimental data more closely, whereas conventional turbulence models underestimated vapor stratification and pressurization rates, underscoring the need for improved turbulence representation in CFD simulations.

Huerta et al. [55] further advanced CFD modeling in OpenFOAM to simulate both isobaric and non-isobaric cryogen evaporation in cylindrical tanks. Under isobaric conditions, they demonstrated that vertical stratification suppresses buoyancy-driven convection, with vapor flows predominantly ascending along tank walls and recirculating near the center. In non-isobaric regimes, validated against experimental LN₂ data, the simulations showed that most heat transfer occurs at the liquid–vapor interface, driving wall evaporation and creating gradients of temperature and pressure that inhibit local convection. Additionally, localized bottom heating was shown to promote liquid mixing, highlighting the critical role of boundary conditions in cryogenic tank design and operation.

Experimental studies further reinforce the importance of these phenomena. Heo et al. [56], investigating liquid air tanks in LAES systems, demonstrated that destratification times were 8–29% shorter compared with liquid nitrogen, but increased by a factor of 2.4 at elevated pressures. Contrary to conventional assumptions, the study showed that stratification can be strategically exploited to reduce BOG generation and improve system efficiency. Kang et al. [17] confirmed these insights, establishing a strong correlation between liquid fill level and stratification degree, with BOR values ranging from 0.05%/min to 0.34%/min, substantially lower than those predicted by homogeneous models. Complementary studies further expand this perspective. Liu et al. [18] demonstrated that tank rotation can extend the time to full stratification by up to an order of magnitude under microgravity conditions, while ullage pressure increased by 18.27% when evaporation was included, even with relatively small, evaporated masses. Joseph et al. [23] assessed the role of insulation thickness, showing that reduced insulation significantly increased heat ingress and pressurization while also emphasizing the strong influence of external factors, such as solar radiation and wind, on tank pressure evolution.

In summary, the available literature converges on the identification of critical thermal accumulation zones, accurate prediction of rollover conditions, and the development of strategies to mitigate stratification and self-pressurization. However, current approaches remain limited by steady-state assumptions, simplified thermophysical properties, and insufficient treatment of coupled transient phenomena and environmental effects. Future progress in this domain requires the development of hybrid, multiphysics, and experimentally validated models capable of capturing the complex interactions between thermal, fluid, and structural dynamics, thereby enabling the design of cryogenic energy storage systems that are more efficient, reliable, and industrially scalable.

Table 2. Experimental and numerical studies on cryogenic tanks and critical components in cryogenic energy storage systems.

Reference	Component/Focus	Methodology	Key Findings/Observations	Remarks
Zuo et al. [51]	Cryogenic tanks	Experimental (Schlieren visualization)	Identified four-stage rollover process; higher heat flux accelerates interface collapse; small density differences increase rollover susceptibility	Analytical correlations support safety and efficiency improvements
Zuo et al. [52]	Liquid hydrogen tanks	Experimental (self-actuated rotating spray bars)	Reduced thermal non-uniformity by 41.2%, decreased cooling time by 50% and system weight by 76.5%	Demonstrates potential of active stratification control
Sha et al. [53]	Stratified NaCl solutions	Experimental	Identified W-shaped, Y-shaped, and hourglass convection patterns; higher buoyancy ratios did not necessarily increase rollover risk	Relevant to multi-component cryogenic systems
Kassemi et al. [54]	Cryogenic tanks	CFD (Sharp Interface & VOF)	Laminar models matched experiments; conventional turbulence models underestimated stratification and pressurization	Highlights need for improved turbulence representation
Huerta et al. [55]	Cylindrical tanks	CFD (OpenFOAM)	Vertical stratification suppressed buoyancy-driven convection; non-isobaric regime showed interface-driven heat transfer; bottom heating enhanced mixing	Boundary conditions critically influence tank design
Heo et al. [56]	Liquid air tanks	Experimental	Destratification times 8–29% shorter than LN2; times increased by factor of 2.4 at higher pressures	Stratification can be exploited to reduce BOG and improve efficiency
Kang et al. [17]	Liquid air tanks	Experimental	Strong correlation between fill level and stratification; BOR 0.05–0.34%/min, lower than homogeneous models	Confirms strategic use of stratification
Liu et al. [18]	Microgravity tanks	Experimental/CFD	Tank rotation extended time to full stratification; ullage pressure increased by 18.27% with evaporation	Microgravity effects relevant for space storage
Joseph et al. [23]	Cryogenic tanks	Experimental	Reduced insulation increased heat ingress and pressurization; solar radiation and wind strongly affected pressure evolution	Highlights importance of external conditions

summarizes key experimental and numerical studies on cryogenic tanks, highlighting the dominant mechanisms driving stratification, self-pressurization, and rollover. The comparative results reinforce the trends and modelling limitations discussed in this section.

4.2.3. Transient Dynamic Modeling

Transient dynamic modeling plays a fundamental role in analyzing the non-steady-state behavior of Liquid Air Energy Storage (LAES) systems and related cryogenic technologies. By solving time-dependent mass and energy balance equations coupled with thermodynamic relations, such models provide a detailed description of the evolution of pressure, temperature, and mass flow within system components. This approach is indispensable for assessing operational stability, identifying transient effects—such as pressure surges, thermal inertia, stratification, and boil-off gas (BOG) generation—and optimizing control strategies for compressors, expanders, and heat exchangers under variable load conditions, start-up and shutdown sequences, and integration with intermittent renewable energy sources. Several studies have demonstrated the relevance of this approach. Dai et al. [57] developed a dynamic model for liquid CO₂ storage tanks, showing that two-phase operation significantly reduces pressure fluctuations but leads to a progressive decline in effective storage density (ESD). To mitigate this effect, the authors proposed a cooling strategy, though with distinct energy requirements for high- and low-pressure tanks. Zhou et al. [58,59] investigated solar-aided LAES (SALAES) systems, demonstrating that solar irradiance variability and molten salt depletion strongly affect cycle and exergy efficiencies. Their dynamic modeling of the discharging process proved crucial for mitigating fluctuations caused by solar variability and heat exchanger faults, enabling rapid system load adjustments.

From a thermodynamic and techno-economic perspective, Mousavi et al. [60] applied transient modeling to LAES systems employing phase change materials (PCMs) in packed beds. Their results revealed efficiency penalties of approximately 5.9% due to transient storage behavior, with a payback period of 6.2 years, suggesting that optimization should focus on PCM layering and melting temperatures. Complementarily, Guo et al. [61] showed that cold energy losses and interruptions between charging and discharging lead to an efficiency reduction of ~16.8%, highlighting the need to account for transient dynamics in packed-bed design.

The integration of LAES in hybrid and industrial contexts has also benefited from this approach. Liang et al. [62] demonstrated that LAES units effectively compensate for wind power fluctuations on time scales longer than 130 s, with LAES–battery hybrid systems proving both technically feasible and economically advantageous compared to battery-only configurations. Wang et al. [63] proposed a standalone LAES system employing pebble/rock-packed beds, showing that despite slightly lower efficiency than fluid-based systems, the configuration exhibits strong industrial applicability, achieving overall efficiencies above 80% in cogeneration mode.

At the component level, Cui et al. [64] developed a dynamic model for a 12.5 MW expansion unit, proposing a segmented start-up strategy that significantly reduced stabilization time and enabled frequency regulation within 20 s, while also identifying the negative impact of valve delays. Lu et al. [65] investigated the operational safety of a 500 kW expansion unit, concluding that rotor time constant and valve closing time are critical parameters for limiting maximum rotor speed and ensuring safe shutdown during fault conditions. In a pioneering contribution, Sciacovelli et al. [66] validated algebraic-differential models against experimental data from a pilot plant, demonstrating the importance of packed-bed design and thermal management in mitigating performance degradation caused by thermal front propagation during repetitive charge–discharge cycles.

In summary, the literature shows that transient dynamic modeling is indispensable for the accurate design, optimization, and safe operation of LAES systems, as it provides realistic predictions of system behavior under variable conditions and identifies key limitations associated with thermal losses, inertia, and transient effects. Despite significant progress, challenges remain in accurately representing the coupled thermal, fluid dynamic, and mechanical interactions and extrapolating model predictions to multi-cycle, real-world operations. Future developments should focus on hybrid, multiphysics, and experimentally validated models capable of capturing nonlinear effects and supporting real-time optimization for large-scale industrial implementation.

Table 3. Summary of transient and dynamic modeling studies on LAES and related cryogenic systems.

Study	System or Process Modelled	Methodology	Key Findings
Dai et al. [57]	Liquid CO2 storage tank	Dynamic modelling of two-phase operation	Reduced pressure fluctuations; decrease in effective storage density (ESD); cooling strategy proposed for mitigation.
Zhou et al. [58,59]	Solar-aided LAES (SALAES)	Dynamic modelling of discharge and solar variability	Solar fluctuations and molten salt depletion significantly affect cycle/exergy efficiency; dynamic modelling enables rapid load adjustment and fault mitigation.
Mousavi et al. [60]	LAES with PCM-packed beds	Transient thermo-economic modelling	~5.9% efficiency penalty due to transient PCM behaviour; payback period of 6.2 years; optimisation depends on PCM layering and melting temperature.
Guo et al. [61]	LAES cold-packed bed	Transient dynamic modelling	Cold energy losses and interruptions reduce efficiency by ~16.8%; highlights need for transient-aware packed-bed design.
Liang et al. [62]	LAES–battery hybrid system	Transient modelling under fluctuating wind input	LAES stabilises fluctuations > 130 s; hybrid configuration more economically viable than batteries alone.
Wang et al. [63]	Standalone LAES with pebble/rock beds	Dynamic modelling	Efficiency slightly lower than fluid-packed beds but industrially robust; cogeneration efficiency > 80%.
Cui et al. [64]	12.5 MW expansion unit	Dynamic simulation	Segmented start-up reduces stabilisation time; enables frequency regulation within 20 s; valve delays negatively affect performance.
Lu et al. [65]	500 kW expansion unit	Transient safety modelling	Rotor time constant and valve closing time are critical for limiting overspeed and ensuring safe shut-down.
Sciacovelli et al. [66]	Packed-bed LAES pilot plant	Validated algebraic-differential dynamic model	Thermal front propagation degrades performance; importance of thermal management and packed-bed design.

summarizes key transient modeling studies, underscoring the importance of time-dependent analysis for understanding fluctuations, efficiency losses, and control performance in LAES systems.

4.2.4. Modeling and Performance of PB-TES Under LTNE Conditions

The modeling of packed beds in thermal energy storage systems (Packed Bed Thermal Energy Storage—PB-TES) indicates that the assumption of Local Thermal Equilibrium (LTE) may be insufficient to accurately represent the thermodynamic and exergy performance, particularly under non-ideal operational conditions [67,68]. In LTE models, it is assumed that the solid and fluid phases share the same temperature at every point within the bed, which significantly simplifies the energy equations. However, in beds with larger particle diameters, low solid thermal conductivity, high fluid flow rates, or rapid charge/discharge cycles, significant temperature gradients arise between the phases, limiting the applicability of the LTE approach. The adoption of Local Thermal Non-Equilibrium (LTNE) models, which solve separate energy equations for the solid and fluid phases, allows these gradients to be captured, providing more realistic predictions of temperature distribution, thermal losses, and discharge profiles within the packed bed [69].

The performance of Packed Bed Thermal Energy Storage (PB-TES) systems is strongly influenced by both geometric and operational parameters. Among the geometric factors, particle diameter, bed porosity, and aspect ratio are particularly significant, as they directly affect the available surface area for heat transfer and the fluid flow paths, thereby influencing thermal gradients and local thermal non-equilibrium (LTNE) phenomena [70]. Smaller particles increase the solid–fluid interfacial area, promoting faster thermal equilibration and reducing thermocline degradation, but simultaneously result in higher pressure drops and increased pumping requirements. Conversely, larger particles or highly porous arrangements can amplify local thermal gradients, especially under high fluid flow rates or rapid charge/discharge cycles.

Operational parameters, including fluid flow rate, inlet temperature, cycle duration, and operational frequency, also play a critical role in PB-TES performance. Higher flow rates enhance convective heat transfer, mitigating thermal non-uniformities, but incur additional pressure losses and higher pumping energy consumption. Rapid cycling may prevent full thermal equilibration between phases, highlighting the necessity of LTNE modeling to accurately predict the system’s thermal and exergy performance.

Buonomo et al. [71] developed an LTNE model for porous fins with adiabatic tips, enabling the separate evaluation of solid–fluid temperature profiles and the Nusselt number. The study demonstrated that the LTE assumption tends to overestimate heat transfer, particularly for low Biot numbers, and provided criteria for fin optimization considering LTNE effects. Building on this approach, Zhang et al. [72] presented an LTNE model for CO₂ in enhanced geothermal systems, showing that LTNE significantly affects production temperature and thermal breakthrough time, with more pronounced effects at higher volumetric heat transfer coefficients. This study highlights the necessity of accounting for temperature differences between phases in porous media for accurate thermal performance predictions.

In the context of thermal energy storage in packed beds, Peng et al. [73] numerically analyzed PB-TES with PCM particles in Compressed Air Energy Storage (CAES) systems. The study revealed that higher porosity reduces thermal capacity and charging efficiency, whereas smaller particles enhance efficiency without significantly affecting total storage capacity. Furthermore, higher inlet pressures and packed beds containing multiple storage materials improved overall system performance. Finally, Tan et al. [20] developed a three-dimensional CFD model of solid cryogenic packed beds, assessing the effects of inlet temperature, packing material, and porosity. Results indicated that cold storage efficiency is relatively insensitive to porosity, although pressure drop increases significantly with decreasing porosity. Among the materials evaluated, basalt demonstrated the best performance, achieving 77.69% cold storage efficiency and 75.21% cold exergy efficiency.

Collectively, these studies underscore the importance of considering LTNE, as well as the influence of porosity, packing material, and particle diameter, in the optimization of packed beds for PB-TES systems, providing a solid foundation for the efficient design and operation of these energy storage technologies.

Table 4. Overview of numerical and CFD studies on packed bed thermal energy storage (PB-TES) systems.

Study	System or Process Modelled	Methodology	Key Findings
Buonomo et al. [71]	Porous fins with adiabatic tips	LTNE modelling of solid–fluid temperature profiles	LTE assumption overestimates heat transfer for low Biot numbers; LTNE approach allows optimization of fin design considering phase temperature differences.
Zhang et al. [72]	CO2 in enhanced geothermal systems	LTNE numerical modelling	LTNE significantly affects production temperature and thermal breakthrough time; higher volumetric heat transfer coefficients amplify LTNE effects; highlights importance of accounting for phase temperature differences.
Peng et al. [73]	PB-TES with PCM particles in CAES systems	Numerical analysis	Higher porosity reduces thermal capacity and charging efficiency; smaller particles improve efficiency without major effect on total storage capacity; multiple storage materials and higher inlet pressures enhance performance.
Tan et al. [20]	Solid cryogenic packed beds	3D CFD modelling	Cold storage efficiency relatively insensitive to porosity; pressure drop increases with decreasing porosity; basalt packing material achieves highest cold storage (77.69%) and cold exergy efficiency (75.21%).

presents LTNE-based studies on PB-TES, showing how particle size, porosity, and material affect thermal performance and emphasizing the importance of LTNE modeling for accurate phase temperature prediction and packed-bed optimization.

4.2.5. Multidimensional and Multi-Region Approaches in LAES

The modeling of packed beds in Liquid Air Energy Storage (LAES) systems has significantly evolved beyond traditional one-dimensional (1-D) formulations, which assume radial uniformity and simplify the analysis along the axial direction. While 1-D models are useful for preliminary assessments, they fail to capture radial temperature gradients, wall heat losses, and insulation effects, limiting the accuracy of thermodynamic performance and exergy efficiency evaluations. In this context, Huerta et al. [55] developed a transient 1-D model for the non-isobaric evaporation of cryogenic liquids in storage tanks, capable of predicting time-dependent liquid and vapor temperature profiles, tank pressure, liquid volume, and evaporation rates. Natural convection was simplified by volumetric heat sources, assuming instantaneous and uniform radial mixing, and the liquid-vapor interface was treated at the saturation temperature dependent on pressure. Comparison with CFD simulations demonstrated comparable accuracy, but with computation times reduced by more than three orders of magnitude, highlighting that calibrated 1-D transient models provide rapid and reliable predictions suitable for operational optimization and model-based control of cryogenic tanks.

The need to capture radial gradients and natural convection effects has led to the development of two-dimensional (2-D) models. Huerta et al. [74] proposed a 2-D CFD model for cylindrical cryogenic tanks with axial symmetry, combining a 1-D sub-model for the vapor phase and a 2-D representation of the liquid phase based on the Navier-Stokes equations and the Boussinesq approximation. The study showed that more than 96% of the heat entering through the vapor phase is transferred directly to the liquid-vapor interface, generating intense wall evaporation, while thermal stratification in the liquid layer dampens wall-induced natural convection. Bottom heating, however, efficiently circulates and heats the liquid bulk. Similarly, Wen et al. [75] developed a transient 2-D model for Packed Bed Cold Storage (PBCS) in LAES systems, incorporating fluid-solid temperature differences and demonstrating that superficial fluid velocity and the number of storage cycles strongly influence cyclic exergy efficiency, emphasizing the importance of detailed analysis of internal dynamics. Saleem et al. [76] applied a 2-D CFD approach to full-scale LNG storage tanks using an axisymmetric VOF model to track the liquid-vapor interface and the Lee model for phase change, demonstrating that surface evaporation dominates in well-insulated tanks, nucleate boiling occurs only under insufficient insulation, and small-scale experiments do not fully replicate the dynamic behavior of full-scale tanks.

Three-dimensional (3-D) modeling allows for the representation of complex interactions between fluid, walls, insulation, and phase change, capturing phenomena not addressed by 1-D or 2-D approaches. Ovidi et al. [77] developed a 3-D CFD model using the Volume-Of-Fluid (VOF) method to simulate vaporization and condensation in cryogenic tanks, with boundary conditions derived from a 1-D model for heat transfer through insulation. Applied to a 100 m³ industrial tank, the study analyzed the effects of fluid type, filling level, and insulation on thermal stratification and tank pressurization, providing performance indices and supporting integrated modeling and operational decision-making at a large scale. Complementarily, Wang et al. [78] investigated the thermodynamic behavior of liquid hydrogen tanks during successive space operations with variable gravity, including multicomponent effects and helium diffusion in the ullage, showing that acceleration changes affect liquid coverage and vapor condensation, and that detailed 3-D modeling is necessary to capture these complex phenomena accurately.

In summary, the evolution from 1-D to 3-D modeling demonstrates that while 1-D models offer computational efficiency for preliminary predictions and operational optimization, only 2-D and 3-D approaches can capture radial gradients, flow heterogeneities, thermal stratification, and detailed multiphase interactions. Multi-region models, treating fluid, solid beds, tank walls, and separate insulation, are essential for accurate exergy loss prediction and for optimizing the design and operation of cryogenic and LAES systems, providing a robust basis for large-scale implementation and performance improvement.

Table 5. Overview of System or Process Modelled.

Study	System or Process Modelled	Methodology	Key Findings
Huerta et al. [55]	Cryogenic liquid storage tanks	Transient 1-D model for non-isobaric evaporation	Predicts time-dependent liquid/vapor temperatures, tank pressure, liquid volume, and evaporation rates; simplifies natural convection; calibrated 1-D models achieve accuracy comparable to CFD with >1000× faster computation.
Huerta et al. [74]	Cylindrical cryogenic tanks	2-D CFD model with axial symmetry	>96% of heat through vapor phase transferred directly to liquid-vapor interface; wall-induced natural convection dampened by thermal stratification; bottom heating effectively circulates and warms liquid bulk.
Wen et al. [75]	Packed Bed Cold Storage (PBCS) in LAES	Transient 2-D model incorporating fluid-solid temperature differences	Superficial fluid velocity and number of storage cycles strongly affect cyclic exergy efficiency; emphasizes importance of detailed internal dynamics analysis.
Saleem et al. [76]	Full-scale LNG storage tanks	2-D axisymmetric CFD with VOF and Lee phase-change model	Surface evaporation dominates in well-insulated tanks; nucleate boiling occurs only with poor insulation; small-scale experiments cannot fully replicate full-scale dynamic behavior.
Ovidi et al. [77]	Industrial cryogenic tanks (100 m3)	3-D CFD with VOF, boundary conditions from 1-D insulation model	Captures vaporization and condensation; analyzes effects of fluid type, filling level, insulation on stratification and pressurization; supports large-scale operational decision-making.
Wang et al. [78]	Liquid hydrogen tanks under variable gravity	3-D CFD with multicomponent effects and helium diffusion	Acceleration changes affect liquid coverage and vapor condensation; detailed 3-D modelling necessary to capture complex multiphase and microgravity phenomena accurately.

highlights 1-D to 3-D modeling in LAES, showing that multidimensional approaches are necessary to capture stratification, radial gradients, and multiphase effects for accurate performance and design optimization.

5. Challenges, Limitations, and Emerging Trends in Cryogenic Energy Storage Modeling

Recent advances in the numerical modeling of Cryogenic Energy Storage (CES) systems demonstrate significant progress through the integration of hybrid approaches that combine deterministic optimization, surrogate modeling, and machine learning techniques [20,48]. These methodologies have enabled substantial reductions in computational cost while maintaining predictive accuracy, contributing to more effective system optimization. High-fidelity computational fluid dynamics (CFD) simulations and transient dynamic models have been increasingly validated against experimental data and sensitivity analyses, improving reliability under variable operational conditions [72].

5.1. System-Level Limitations

Despite these advancements, CES modeling faces critical challenges associated with the multiscale and multiphysics nature of these systems. Many global thermodynamic models rely on steady-state assumptions and idealized component behavior, which limit their capacity to capture transient phenomena such as start-up, shutdown, or fluctuations associated with intermittent renewable energy sources. One-dimensional and some two-dimensional models also fail to represent radial temperature gradients, wall heat losses, and multi-region interactions, which are essential for accurate exergy analyses and large-scale LAES system optimization. Operational variability introduces additional complexity. Transient studies have shown efficiency reductions of up to 16–20% due to load fluctuations, renewable generation variability, or component performance limitations [49,57,58,59]. Furthermore, lifecycle assessments and techno-economic analyses are often limited or omitted, constraining understanding of environmental impact, economic feasibility, and long-term operational reliability. Material degradation, insulation aging, and thermal cycling effects remain largely unaddressed, further restricting predictive capability for industrial applications.

5.2. Component-Level Limitations

At the component level, Packed Bed Thermal Energy Storage (PB-TES) systems and cryogenic tanks face significant challenges due to complex physical phenomena. PB-TES operating under Local Thermal Non-Equilibrium (LTNE) conditions exhibit substantial solid-fluid temperature gradients, thermal stratification, and pressure drops [67,68,69,70]. Simplified Local Thermal Equilibrium (LTE) assumptions tend to over-estimate heat transfer and exergy efficiency, underestimating irreversibilities and compromising accuracy in system-level performance predictions.

Cryogenic storage tanks are affected by multiphase phenomena, including boil-off gas (BOG) generation, self-pressurization, and rollover events [55,67,68,69,70,71,72,73,74,75]. Reliable mitigation strategies require detailed CFD simulations or hybrid approaches. The lack of high-resolution experimental data under transient conditions limits the calibration and validation of numerical models [51,52,56]. Moreover, degradation mechanisms, insulation aging, and dynamic operational uncertainties remain insufficiently explored, restricting predictive maintenance and robust industrial implementation.

5.3. Emerging Trends in CES Modeling

Emerging trends aim to address these limitations through the adoption of hybrid and Multiphysics modeling frameworks that integrate system-level thermodynamic models, transient dynamic simulations, and multidimensional CFD approaches [51,52,53,54,56]. Multidimensional modeling enables accurate prediction of radial temperature gradients, wall heat losses, thermal stratification, and exergy degradation, enhancing performance analysis and cycle optimization for large-scale LAES systems.

Machine learning, surrogate models, and digital twin architecture are increasingly being applied to enable real-time optimization, predictive maintenance, and operational control. Coupled with uncertainty quantification and advanced sensitivity analyses, these methods improve safety, efficiency, and economic viability in dynamic operational environments. Multi-objective optimization algorithms, such as genetic algorithms and NSGA-II, provide the capability to simultaneously optimize efficiency, exergy recovery, and costs, supporting robust operational strategies [13,49,50,57,58,59].

At the component level, geometric and material optimization of packed beds under LTNE conditions reduces thermal losses, improves exergy efficiency, and enhances overall system performance [66,67,68,71,72]. Integration of these approaches with high-fidelity experimental validation is essential to scale laboratory insights to industrial applications and consolidate operational and control strategies for CES systems.

Finally, the integration of CES with hybrid renewable energy systems, including solar, wind, and biomass, presents opportunities to stabilize energy supply, improve cycle efficiency, and reduce operational costs [50,60]. Standardized experimental protocols and high-fidelity measurement campaigns remain critical to validate numerical models, enabling reliable industrial implementation and the development of CES as a scalable and sustainable energy storage solution.

6. Conclusions

This systematic review of numerical studies on cryogenic energy storage (CES) systems highlights significant advances in modeling approaches, including global thermodynamic models, component-level simulations, transient dynamic analyses, LTNE modeling of packed beds, and multidimensional approaches for LAES systems. Global thermodynamic models and multi-objective optimization have provided essential insights into cycle efficiency, energy density, and operational trade-offs, emphasizing the importance of component efficiency and exergy management. Component-level studies, particularly on storage tanks and heat exchangers, have demonstrated the critical role of thermal stratification, self-pressurization, and boil-off gas (BOG) generation in operational performance and system safety. Transient dynamic modeling has been essential to capture time-dependent effects, efficiency losses, and performance variations that stationary models cannot represent. Furthermore, LTNE and multidimensional CFD approaches offer a more accurate representation of radial gradients, multiphase interactions, and complex thermo-fluid phenomena, which are crucial for large-scale industrial applications.

Despite these advances, several gaps persist that limit the predictive capabilities and practical applicability of existing numerical models. Many studies rely on oversimplified assumptions, including steady-state analysis or local thermal equilibrium, which do not reflect the real operating conditions of CES systems. The scarcity of high-resolution experimental data, particularly under transient conditions, hinders model calibration, validation, and generalization. Moreover, material degradation mechanisms, insulation aging, and long-term reliability remain largely unexplored, which are critical factors for ensuring safe and sustainable industrial operation. Integrated assessments of life cycle, techno-economic performance, and environmental impacts are still insufficient, limiting the development of economically viable and environmentally sustainable solutions.

Future research should focus on several key directions. The development of hybrid and multiphysics frameworks combining global thermodynamic models, high-fidelity CFD, and transient analyses is essential to capture nonlinear phenomena, multi-region interactions, and complex thermal gradients. Experimentally validated models, including high-fidelity measurements in packed beds and cryogenic tanks, will improve predictive reliability and reduce uncertainties associated with critical events such as rollover or self-pressurization. The integration of life-cycle assessment, techno-economic analysis, and environmental impact metrics into numerical studies will enable optimization not only in terms of efficiency and exergy but also sustainability and economic feasibility.

Future studies should also address material degradation, insulation aging, and repeated thermal cycling effects to predict system lifespan more accurately. The integration of CES with renewable energy sources and AI-assisted operational control, including real-time optimization and digital twin architectures, represents a promising path to maximize efficiency, stabilize energy supply, and enhance economic viability. Finally, the standardization of experimental protocols and high-fidelity measurements is essential for inter-study comparability, scaling laboratory results to industrial applications, and consolidating best practices in numerical modeling.

In conclusion, while the state-of-the-art demonstrates substantial progress in the numerical modeling of CES systems, critical gaps remain regarding model simplifications, lack of experimental data, insufficient consideration of environmental and material factors, and limited long-term reliability assessment. The development of hybrid frameworks, experimentally validated multiphysics models, advanced optimization techniques, and integrated life-cycle analyses will be fundamental to establishing cryogenic energy storage as a scalable, reliable, and sustainable solution for large-scale energy storage and renewable energy integration.