Reliability Study of Metal Bellows in Low-Temperature High-Pressure Liquid Carbon Dioxide Transportation Systems: Failure Mechanism Analysis
Abstract
1. Introduction
2. Failure Analysis and Testing of Metal Bellows
2.1. Selection of Experimental Materials
2.2. Macro Analysis
2.3. Local Analysis
2.4. Metallographic Analysis
2.4.1. Metallographic Analysis of Stainless Steel Wire
2.4.2. Metallographic Analysis of the Welded Area Cross-Section
2.5. EDS Composition Analysis
2.6. Scanning Electron Microscope Analysis of the Fracture Surface
2.6.1. Scanning Electron Microscope Analysis of the Weld Cross-Section
2.6.2. Analysis of the Fracture Morphology of the Woven Wire Mesh
2.6.3. Analysis of the Fracture Morphology of the Corrugated Tube [17]
2.6.4. SEM Analysis of the Fracture Surface at the Interface Between the Corrugated Tube and the Woven Wire Mesh
2.6.5. SEM Observation of the Transverse Section of the Broken Steel Wire
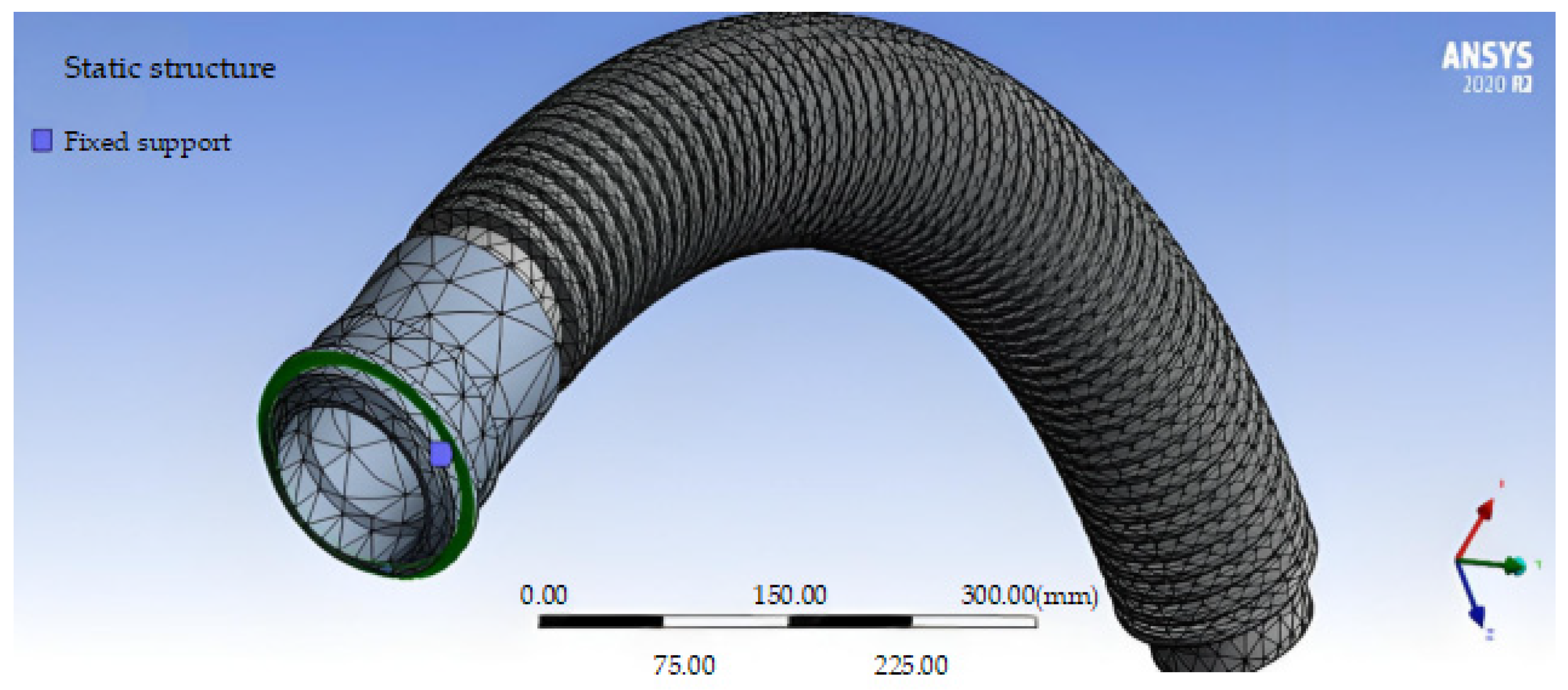
3. Establishment of the Finite Element Model of the Metal Corrugated Tube
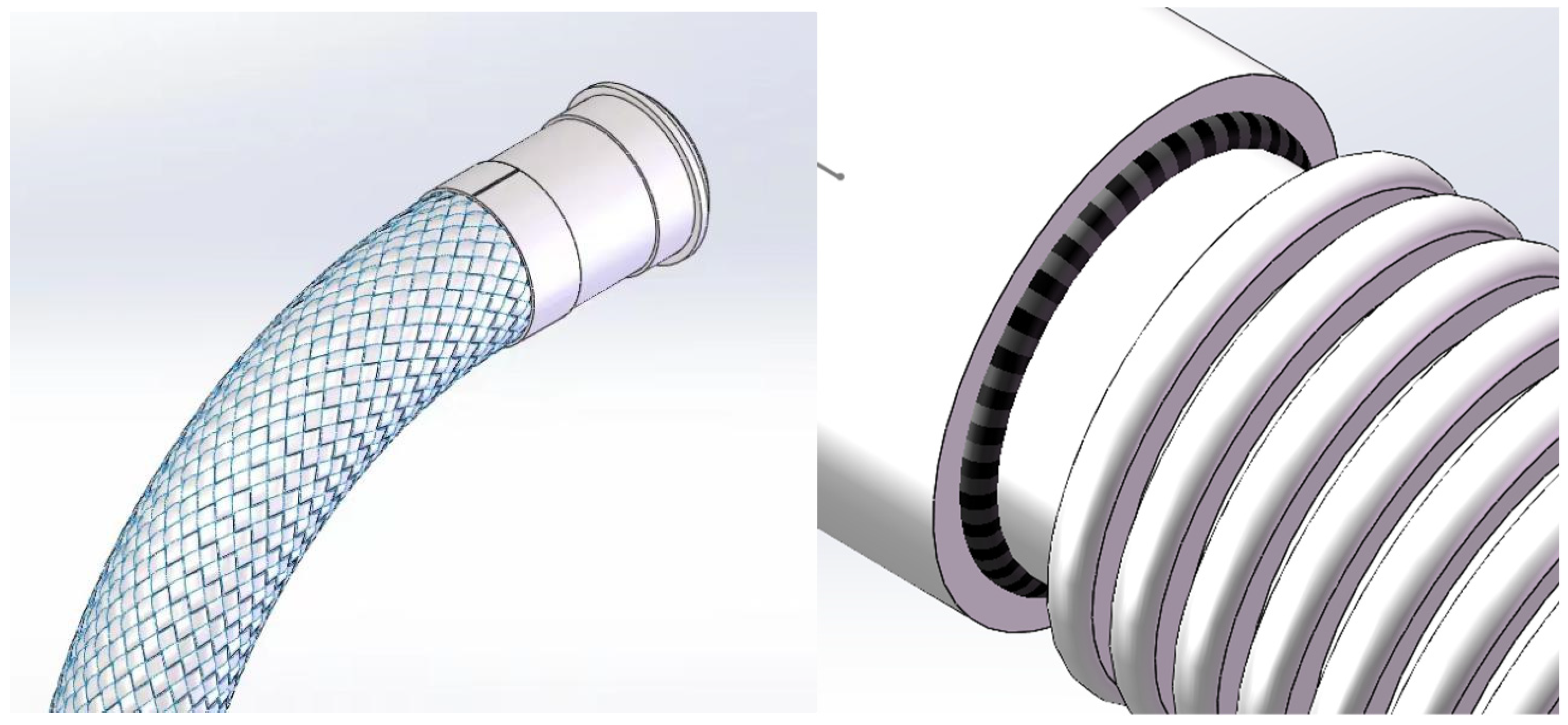
3.1. Establishment of the Corrugated Tube Model
3.2. Mathematical Models
3.3. Parameter Settings
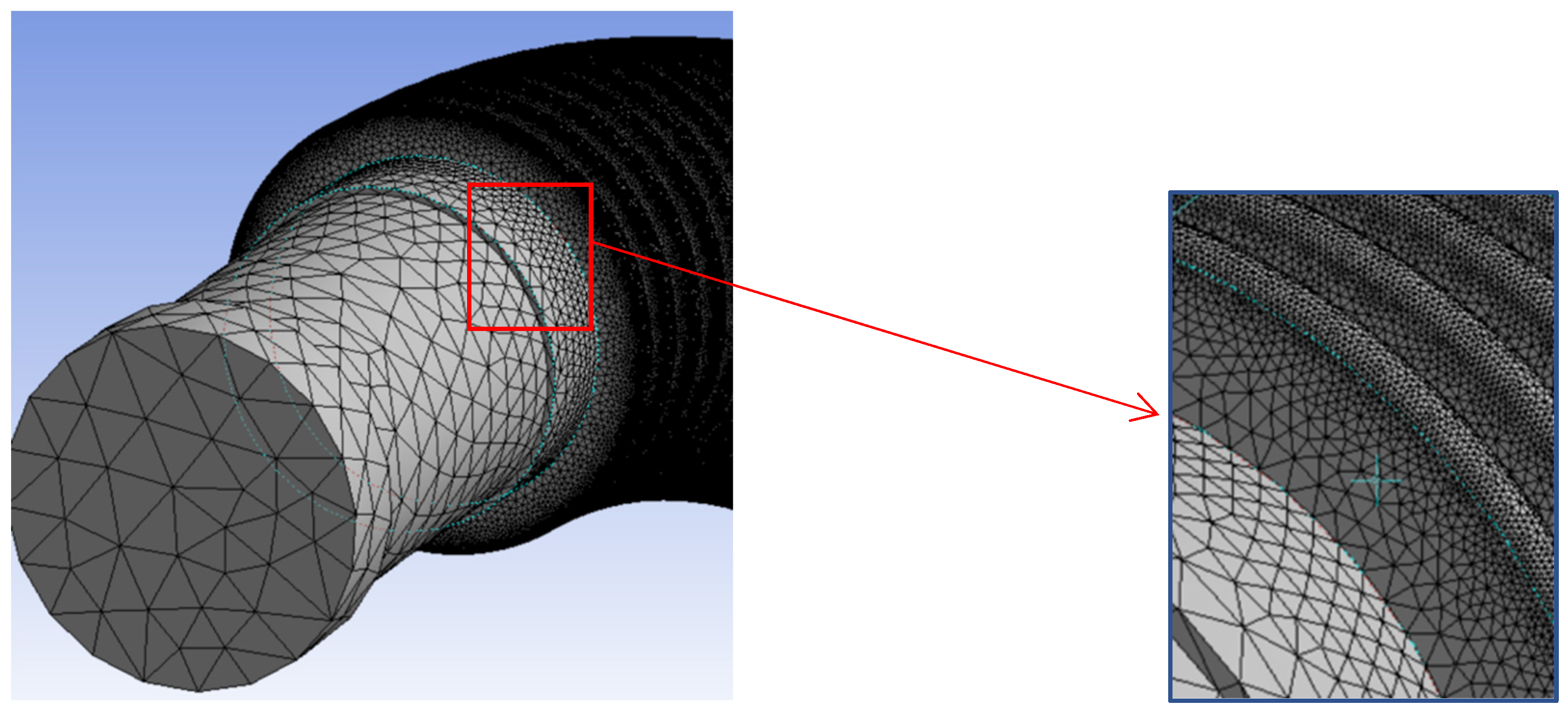
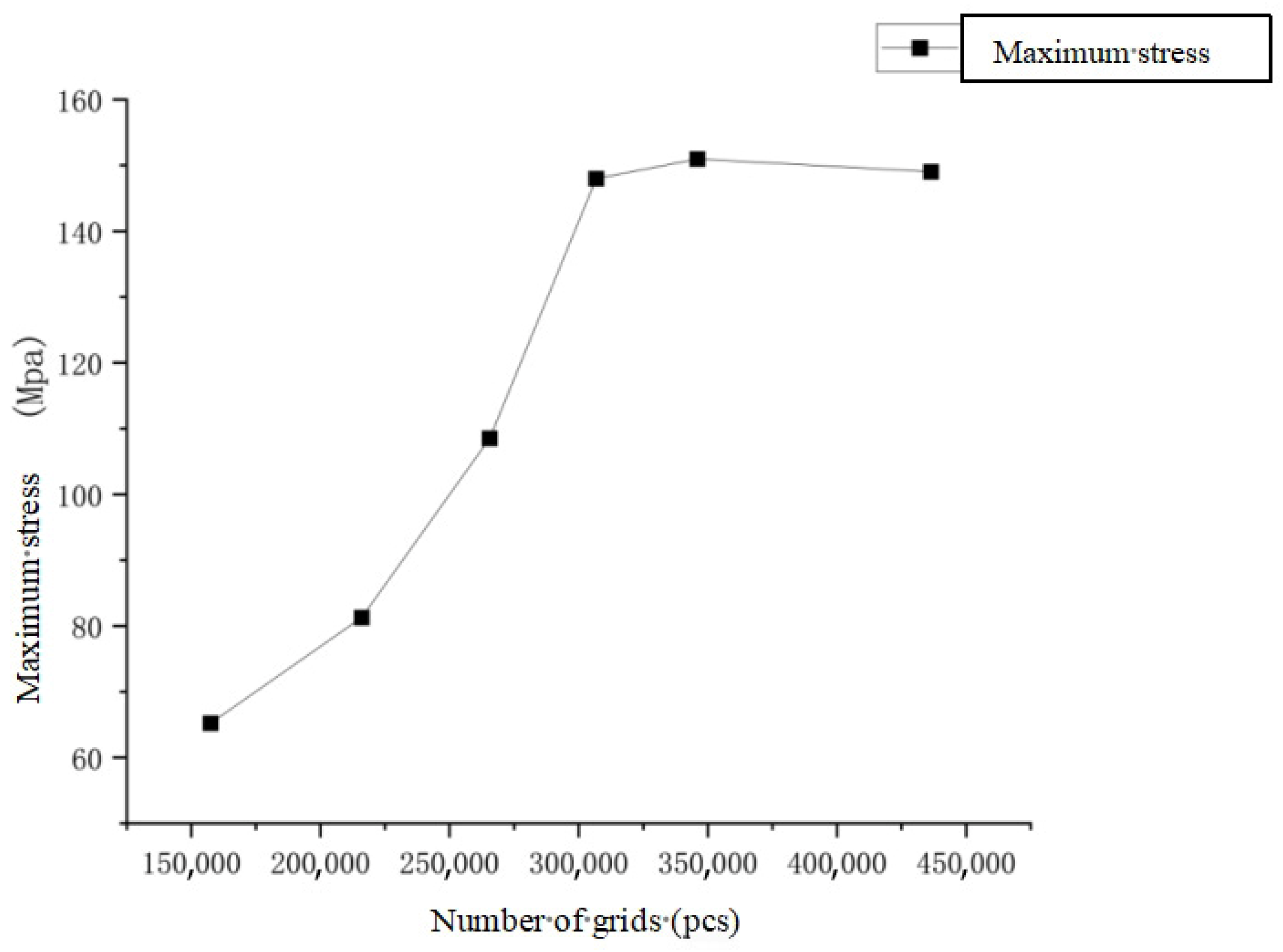
3.4. Mesh Generation
3.4.1. Fluid Domain Mesh Generation [34]
3.4.2. Solid Domain Mesh Partitioning
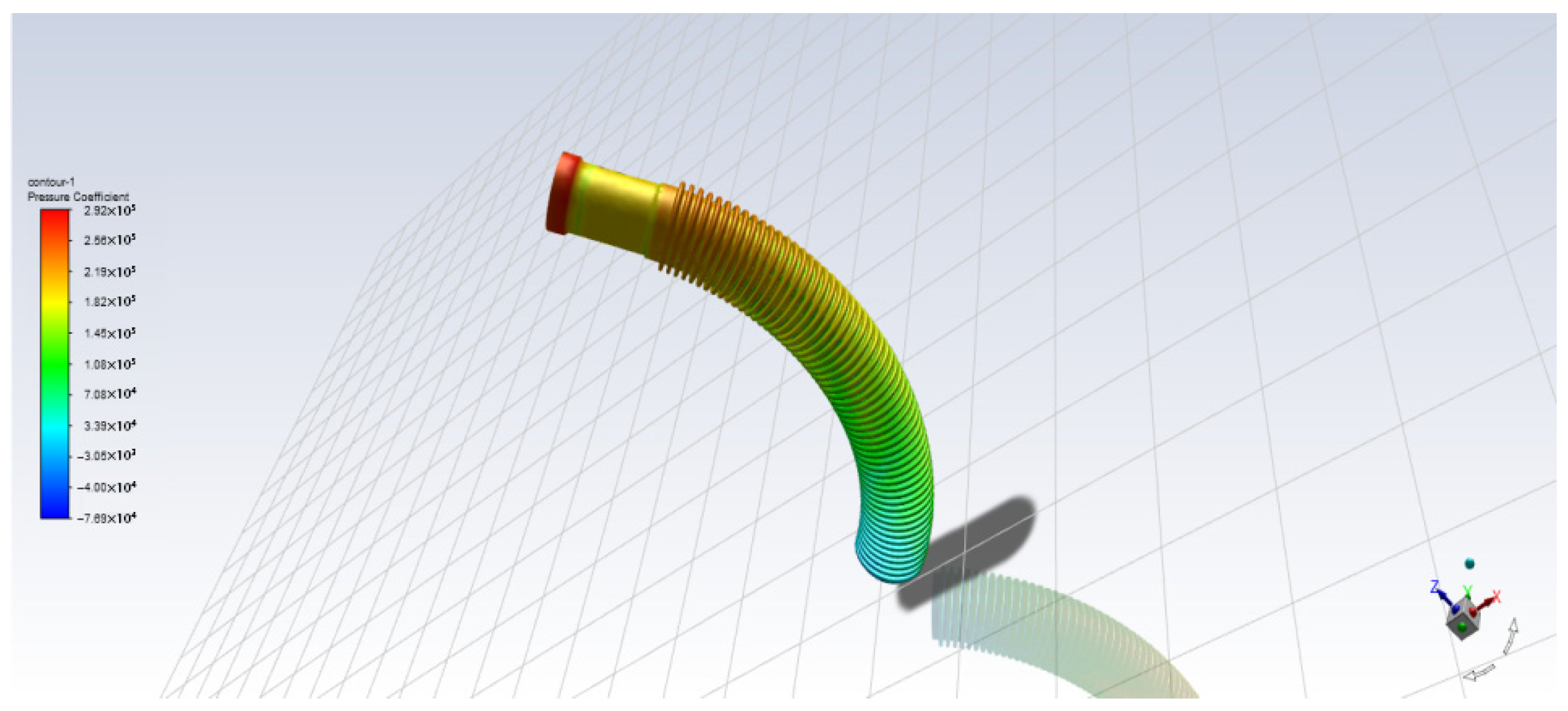
3.5. Model Validation
3.6. Finite Element Stress Analysis of Bellows Under Different Defects
3.7. Analysis of the Effects of Different Inlet Parameters on Defective Corrugated Pipes
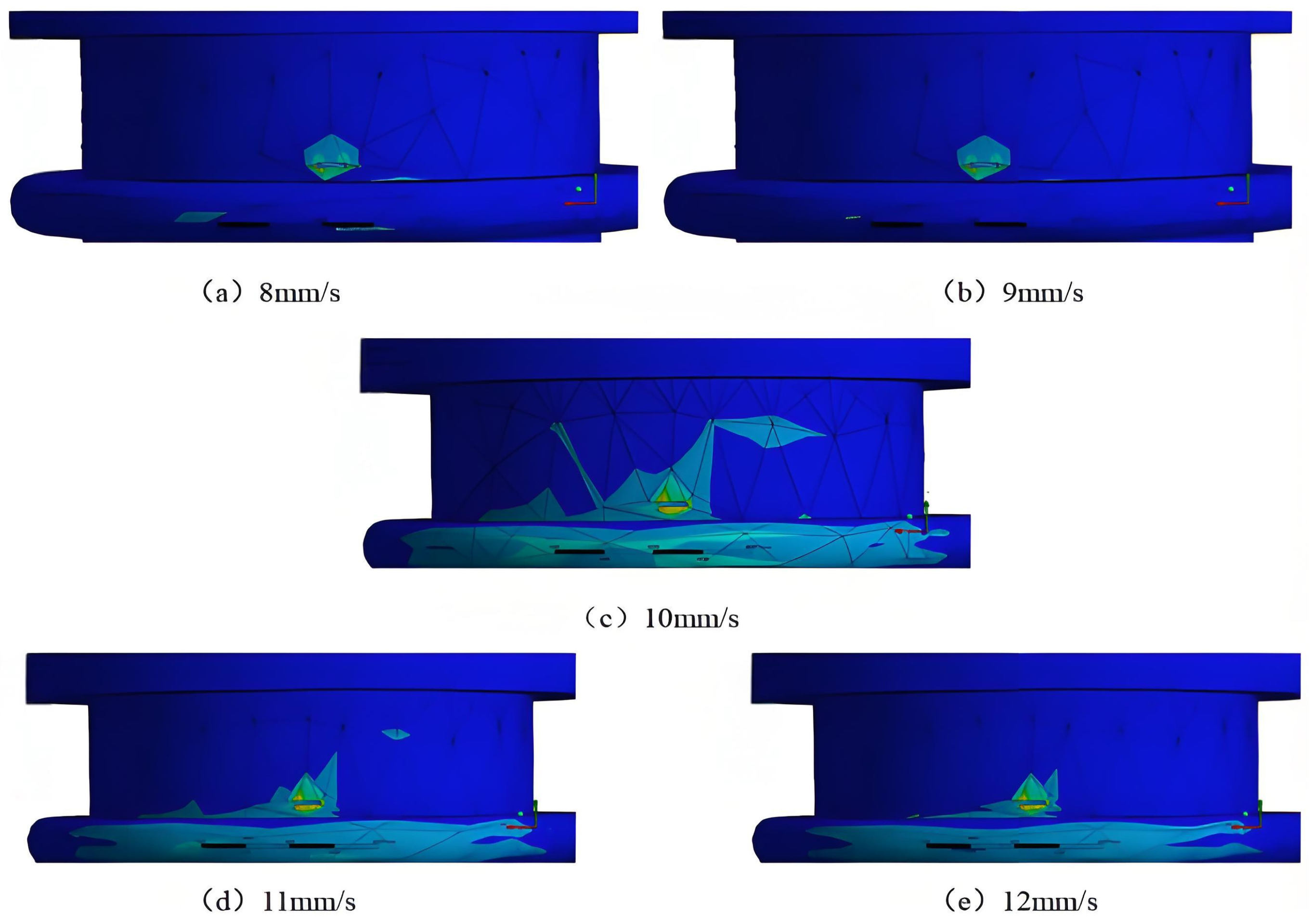
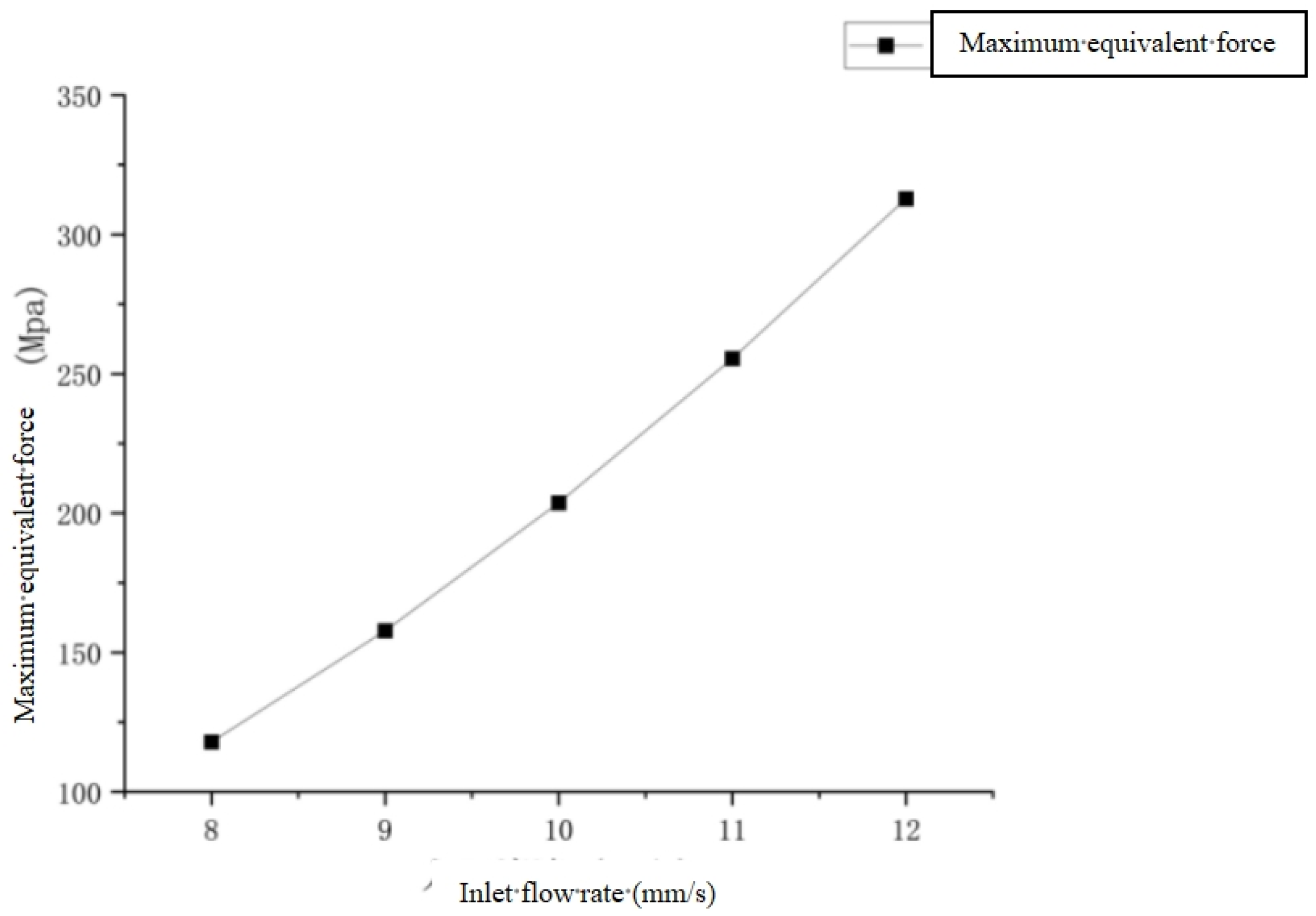
3.7.1. Analysis of the Effect of Inlet Flow Velocity on the Stress of Defect-Containing Bellows
3.7.2. Analysis of the Effect of Different Temperatures on the Stress Distribution of a Defective Corrugated Tube [38]
4. Conclusions
- (1)
- For the failure analysis of metal bellows, metallographic analysis, EDS component analysis, fracture scanning electron microscopy analysis, mechanical property detection, and other methods are used to experimentally detect and analyze the fracture, and the fracture cause of the metal bellows is mainly a crack of about 20 μm perpendicular to the surface of the bellows at the root of the bellows. Subsequently, the bellows are further bent, causing the crack direction to be tilted, resulting in the bellows being pulled. If the A side of the workpiece is impacted (the source of the outer impact mark is not clear), the crack and its propagation will be accelerated [39]. At the same time, due to the deformation of the workpiece, the outer braided steel wire is broken, and the wire in the first fracture area with the greatest tensile stress is broken first, and its fracture position is closest to the welding point. Even if the pressure of the internal solvent is not over-pressurized, it will lead to cracking of the outer surface of the inner bellows and then further bending, accelerating crack propagation and finally leading to the failure and fracture of the workpiece.
- (2)
- The finite element model of the metal bellows under normal conditions and the metal bellows model with welding cracks are established, respectively. The stress situation of the fluid medium was determined, and the stress distribution in the normal state and the presence of cracks was compared. The maximum stress of metal bellows under normal conditions is less than its own yield strength, and the material can work normally.
- (3)
- When the welding crack of the metal bellows is greater than 2 mm, the stress generated at the crack exceeds the yield strength of the material itself, and the stress concentration becomes more obvious with the increase in the crack. Yield deformation will occur in the work. Because the workpiece is perpendicular to the ground after connection, it will lead to large angle bending, and the stress diagram can show that there has been a stress concentration phenomenon at this position, which may cause structural instability during operation. The simulation results were consistent with the actual physical verification results, and it was finally determined that the accident was caused by welding defects. At the same time, it is proved that the establishment of a finite element simulation model can be used as one of the important auxiliary methods for bellows failure analysis.
- (4)
- The effects of different inlet flow velocities and temperatures on stress concentration under the same fracture conditions were analyzed. The results show that the stress will increase with the increase in flow velocity, and the stress at the crack will increase by about 30% for every 1 mm/s increase in the inlet flow velocity, but it will decrease with the increase in temperature. In actual working conditions, by appropriately reducing the flow rate and carefully increasing the temperature, the vibration state of the conveyor system can be improved to a certain extent, and the flow resistance can be reduced, thus having a positive impact on the stiffness and fatigue life of the system. Therefore, before practical application, systematic modeling, simulation, and experimental verification must be carried out, and it must be comprehensively compared and decided with other technical schemes (such as optimized support and material upgrading) under the framework of multi-objective optimization. At the same time, a sound monitoring and maintenance plan can ensure the safe, economical, and long-term operation of the conveyor system [40].
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Agraja, M.; Umamagesh, G.; Raji, S. Key parameters that affect the fatigue life of metal bellows-type expansion joint: Another look. Mater. Today Commun. 2024, 38, 108400. [Google Scholar] [CrossRef]
- Pagar, N.D.; Gawande, S.H. Parametric design analysis of meridional deflection stresses in metal expansion bellows using gray relational grade. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 256. [Google Scholar] [CrossRef]
- Fernand, B.; Maurice, B. Daniel Thomasset, Control of a planar fine positioner actuated by metal bellows. Automatica 1994, 30, 1677–1691. [Google Scholar] [CrossRef]
- Snedden, N.W. Analysis and design guidance for the lateral stiffness of bellows expansion joints. Thin-Walled Struct. 1985, 3, 145–162. [Google Scholar] [CrossRef]
- Yu, S.; Wan, Z.; Lin, J.; Zhou, Z.; Liu, Y. Effect of residual stress on the axial buckling behaviour of the hydraulic-formed bellows. Int. J. Press. Vessel. Pip. 2025, 215, 105468. [Google Scholar] [CrossRef]
- Hou, K.; Guo, J.; Liu, X.; Lv, K.; He, M. Dynamic characteristics and performance analysis of typical liquid carbon dioxide energy storage systems. Energy 2025, 336, 138463. [Google Scholar] [CrossRef]
- Kim, S.; Chang, S.; Jeon, B.; Ju, B. Limit state assessment for bending deformation of multi-ply bellows systems. J. Constr. Steel Res. 2023, 206, 107928. [Google Scholar] [CrossRef]
- Zheng, P.; Shi, P.; Yue, Y.; Hao, J.; Yang, J.; Li, X.; Zhang, Z. Numerical simulation and characteristic analysis of cold storage and release of a liquid carbon dioxide energy storage system. J. Energy Storage 2025, 132 Pt B, 117655. [Google Scholar] [CrossRef]
- Li, H.; Su, W.; Dai, H.; Lin, X.; Ding, R.; Wang, J.; Guan, S.; Zheng, Z.; Ye, Q. Thermo-economic analysis on the gas-liquid compressed carbon dioxide energy storage under different sliding pressure ranges of low-pressure gas storage. J. Energy Storage 2025, 134 Pt A, 118167. [Google Scholar] [CrossRef]
- Wang, M.; Yan, M.; Zhang, H.; Liu, Y.; Huang, H. A new dual strengthening strategy to improve the bending resistance of thin-walled bellows using prefabricated martensite and a gradient structure. Eng. Fract. Mech. 2025, 316, 110902. [Google Scholar] [CrossRef]
- Hao, Z.; Luo, J.; Chen, L.; Cai, Y.; Chen, Y.; Cheng, M. Failure mechanism of unequal parameters metal bellows under repeated bending process. Eng. Fail. Anal. 2021, 129, 105671. [Google Scholar] [CrossRef]
- Gan, C.; Chen, Y.; Wan, F.; Lu, X. Failure analysis and optimization design of metal hose under vibration loads. Eng. Fail. Anal. 2025, 179, 109818. [Google Scholar] [CrossRef]
- Xiang, X.; Lu, G.; Li, Z.; Lv, Y. Finite element analysis and experimental study on a bellows joint. Eng. Struct. 2017, 151, 584–598. [Google Scholar] [CrossRef]
- Tsuyoshi, F.; Nguyen, Q.; Manabe, K.; Osamu, S. Development of semi-dieless metal bellows forming process. J. Mater. Process. Technol. 2013, 213, 1406–1411. [Google Scholar] [CrossRef]
- Creep-fatigue testing of metal bellows in sodium: Balachander, K.; Rajan, K.K.; Ramalingam, P.; Vijayashree, M.; Gupta, S.K.; Chellapandi, P.; Chetal, S.C. and Kale, R.D. Transactions of the Indian Institute of Metals (1996) 49, 595–600. Int. J. Fatigue 1998, 20, 84. [CrossRef]
- Yuan, Z.; Huo, S.; Ren, J. Mathematical description and mechanical characteristics of reinforced S-shaped bellows. Int. J. Press. Vessel. Pip. 2019, 175, 103931. [Google Scholar] [CrossRef]
- Lee, S.W. Study on the forming parameters of the metal bellows. J. Mater. Process. Technol. 2002, 130–131, 47–53. [Google Scholar] [CrossRef]
- Prelle, C.; Jutard, A.; Betemps, M. Compliance adjustment of a metal bellows actuator by control law parameters. Mechatronics 2001, 11, 631–647. [Google Scholar] [CrossRef]
- Pierce, S.O.; Evans, J.L. Failure analysis of a metal bellows flexible hose subjected to multiple pressure cycles. Eng. Fail. Anal. 2012, 22, 11–20. [Google Scholar] [CrossRef]
- Aakash; Krovvid, S.C.S.P.K.; Khan, I.A.; Sapra, M.K.; Dureja, A.K. A finite element based parametric study to assess the suitability of factors used in EJMA for estimation of the meridional stresses in bellows. Mater. Today Proc. 2023, 90 Pt 1, 221–225. [Google Scholar] [CrossRef]
- Prithvirajan, R.; Sugavaneswaran, M.; Sathishkumar, N.; Arumaikkannu, G. Metal bellow hydroforming using additive manufactured die: A case study. Rapid Prototyp. J. 2019, 25, 765–774. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, Y.; Su, T.; Yuan, Q.; Song, Z.; Pang, H. Improved SWT model for predicting multiaxial fatigue life of bellows under combined movement load. Int. J. Press. Vessel. Pip. 2024, 208, 105146. [Google Scholar] [CrossRef]
- Faraji, G.; Mashhadi, M.M.; Norouzifard, V. Evaluation of effective parameters in metal bellows forming process. J. Mater. Process. Technol. 2009, 209, 3431–3437. [Google Scholar] [CrossRef]
- Mechanical seal assembly with metal bellows. Seal. Technol. 2004, 10, 11. [CrossRef]
- Bijayani, P.; Sujata, M.; Madan, M.; Bhaumik, S.K. Stress corrosion cracking in 316L stainless steel bellows of a pressure safety valve. Eng. Fail. Anal. 2014, 36, 379–389. [Google Scholar] [CrossRef]
- Lu, M.; Ge, j.; Xie, Y.; Gong, Z.; Liu, S.; Li, Z. Structural assumption on design of rounded rectangular bellows under pressure. Int. J. Press. Vessel. Pip. 2024, 210, 105256. [Google Scholar] [CrossRef]
- Ma, Y.; Li, P.; Su, T.; Yuan, Q.; Wang, J.; Xia, L. Fatigue life and experimental study of high-temperature bellows based on the improved Manson-Coffin equation. Int. J. Press. Vessel. Pip. 2024, 209, 105216. [Google Scholar] [CrossRef]
- Gao, Y.; Wei, Y.; Liu, X.; Jia, H.; Zhao, W. Stress interaction analysis and mitigation in multi-process bellows manufacturing using continuous finite element simulation. J. Mater. Process. Technol. 2025, 339, 118826. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, Y.; Zou, H.; Tao, S.; Zhang, Q.; Zhang, E. Experimental study: Correcting the calculation formula for a welded metal bellows’ effective diameter. Seal. Technol. 2016, 10, 7–12. [Google Scholar] [CrossRef]
- Guo, H.; Mao, C.; Ke, C.; Liu, W.; Luo, J. Failure analysis and structural optimization of unequal-parameter metal bellows in resistance to bending and torsional composite deformation. Eng. Fail. Anal. 2024, 166, 108844. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, A.; Wang, J.; Ling, C.; Gui, X. Study on the effect of solid solution treatment on the microstructure evolution and properties of 304 stainless steel bellows. Results Eng. 2025, 26, 104565. [Google Scholar] [CrossRef]
- Pavithra, E.; Senthil Kumar, V.S. Experimental Investigation and Numerical Analysis on Fatigue Life of Bellows. Mater. Today Proc. 2018, 5 Pt 3, 18848–18856. [Google Scholar] [CrossRef]
- Atkinson, S. Mechanical seal with metal bellows and Plan 66A solve process pump sealing problems. Seal. Technol. 2018, 2018, 5–6. [Google Scholar] [CrossRef]
- Hao, Z.; Luo, J.; Jin, Y.; Wei, W.; Liu, L. Failure analysis of corrugated metal hose under ultimate repeated bending process. Eng. Fail. Anal. 2020, 109, 104295. [Google Scholar] [CrossRef]
- Wankhede, S.D.; Gawande, S.H. Design and analysis aspect of metal expansion bellows: A review. Forces Mech. 2023, 13, 100244. [Google Scholar] [CrossRef]
- Lin, J.; Wang, X.; Lei, Y.; Ding, J.; Li, K.; Guo, F. Residual stress analysis and measurement in multi-layer bellows. J. Manuf. Process. 2021, 72, 179–194. [Google Scholar] [CrossRef]
- Guo, H.; Xuan, Y.; Qiao, W.; Liu, W.; Luo, J. Failure analysis and waveform structure optimization of bending and torsion composite deformation of metal bellows. Int. J. Press. Vessel. Pip. 2025, 214, 105445. [Google Scholar] [CrossRef]
- Ying, X.; Yan, J.; Zhang, K.; Zhou, B.; Yang, Z.; Geng, D.; Cao, H. Study on equivalent mechanical properties of U-shaped bellows based on novel implementation of asymptotic homogenization method. Mar. Struct. 2024, 96, 103622. [Google Scholar] [CrossRef]
- Metal bellows condition-monitoring system. Seal. Technol. 2016, 1, 14. [CrossRef]
- Wang, M.; Yan, M.; Liu, Z.; Liu, Y.; Huang, H. Enhancement of bending fracture resistance of thin-walled stainless steel bellows with minor deformation through a new gradient strengthening strategy. Eng. Fail. Anal. 2025, 174, 109538. [Google Scholar] [CrossRef]







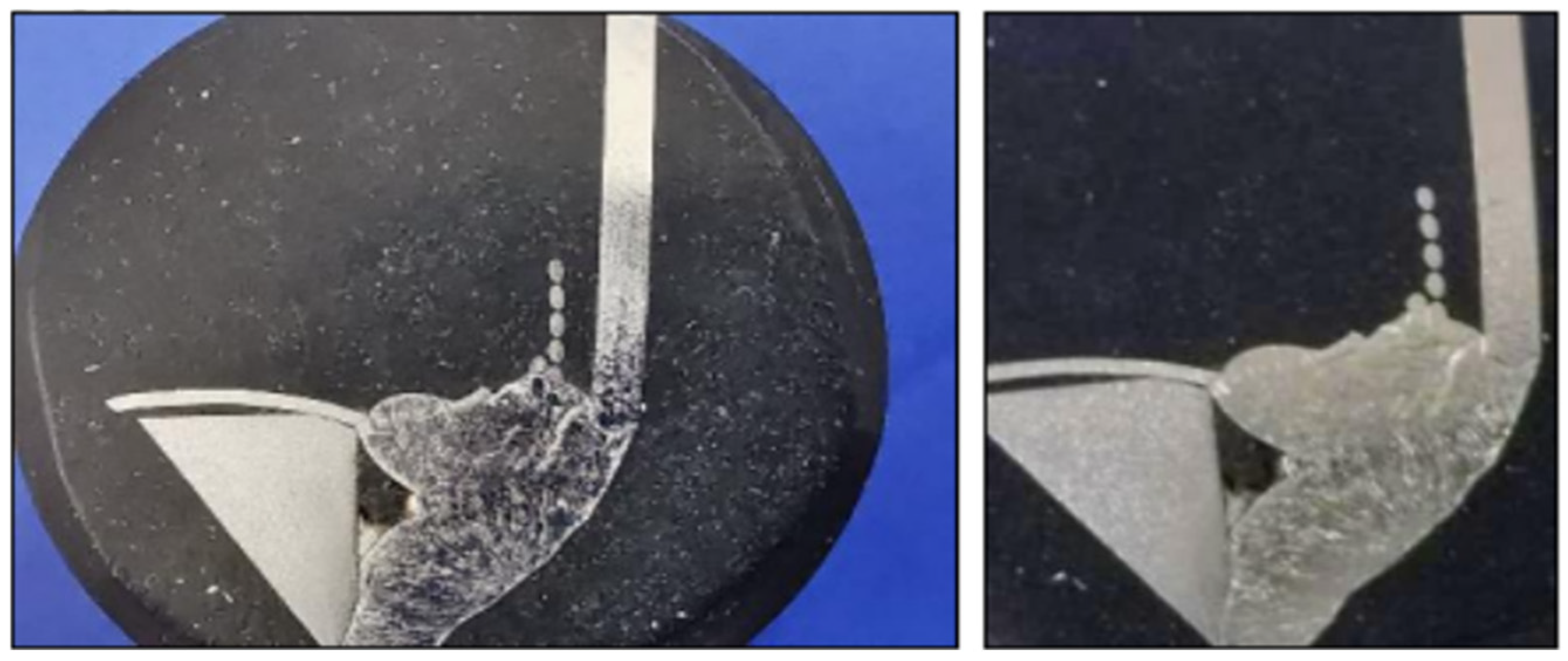

















| Spectrum wt.% | Cr | Mn | Fe | Ni | C | Corresponding Materials |
|---|---|---|---|---|---|---|
| Spectrum 1 | 18.55 | 1.67 | 70.15 | 9.62 | 0.05 | 304 stainless steel |
| Spectrum 2 | 18.37 | 1.75 | 71.08 | 8.80 | 0.04 | 304 stainless steel |
| Spectrum wt.% | Cr | Mn | Fe | Ni | C | Corresponding Materials |
|---|---|---|---|---|---|---|
| Spectrum 1 | 18.03 | 1.42 | 71.22 | 9.28 | 0.05 | 304 stainless steel |
| Spectrum 2 | - | 1.09 | 98.23 | 0.55 | 0.13 | carbon steel (Q355) |
| Spectrum 3 | 14.51 | 10.61 | 72.17 | 2.70 | --- | stainless steel welding rod composition |
| Spectrum wt.% | Cr | Mn | Fe | Ni | C | Corresponding Materials |
|---|---|---|---|---|---|---|
| Spectrum 1 | 18.17 | 1.50 | 71.44 | 8.85 | 0.04 | 304 stainless steel |
| Spectrum 2 | 14.32 | 10.97 | 72.00 | 2.71 | --- | stainless steel welding rod composition |
| Spectrum wt.% | Cr | Mn | Fe | Ni | C | Corresponding Materials |
|---|---|---|---|---|---|---|
| Spectrum 1 | 20.95 | 0.60 | 78.40 | 0.02 | 0.04 | 304 stainless steel |
| Total Length/mm | Outside Diameter/mm | Inner Diameter /mm | Wave Height /mm | Pitch/mm | The Walls Are Thick/mm |
|---|---|---|---|---|---|
| 700 | 120 | 100 | 10 | 12 | 2 |
| Relevant Parameters | Density (kg/m3) | Dynamic Viscosity (Mpa × S) | Thermal Conductivity (W/(m k)) | Specific Heat Capacity (J/(kg °C)) |
|---|---|---|---|---|
| Liquid CO2 | 983 | 0.12 | 0.14 | 2.5 |
| 304 stainless steel | 7930 | ---- | 16.2 | 0.5 |
| Temperature | Room Temperature (Approx. 20 °C) | Low Temperature (−10 °C) | Trends and Explanations |
|---|---|---|---|
| Material grade | 18Cr-8Ni | 18Cr-8Ni | unchanged |
| Density (kg/m3) | 7930 | 7930 | is largely unchanged |
| Elastic modulus (GPa) | 193 | Slightly elevated (approx. 1–3 GPa increase) | Slightly enlarged |
| Poisson’s ratio | Approx. 0.29 | Approx. 0.285 | Basically stable |
| yield strength (MPa) | 205 | Rise to 220–240 | Significantly increased |
| tensile strength (MPa) | 520 | 550–580 | Significantly increased |
| Elongation (%) | 40 | Slight decline (may drop to 38–39%) | Slightly lowered but still good |
| Calculation Conditions | Parameter |
|---|---|
| Medium | Liquid carbon dioxide |
| Turbulence model | standard k-ω |
| Entrance boundary conditions | Speed entry |
| Inlet pressure | 30 Mpa |
| Export boundary conditions | Pressure outlet |
| Algorithm | Phase-coupled SIMPLE |
| Temperature | −10 °C |
| Inlet displacement | 5 m3/min |
| Entrance speed | 10.6157 mm/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Gu, Y.; Wen, H.; Zhu, S.; Jiang, P. Reliability Study of Metal Bellows in Low-Temperature High-Pressure Liquid Carbon Dioxide Transportation Systems: Failure Mechanism Analysis. Processes 2025, 13, 2908. https://doi.org/10.3390/pr13092908
Liu C, Gu Y, Wen H, Zhu S, Jiang P. Reliability Study of Metal Bellows in Low-Temperature High-Pressure Liquid Carbon Dioxide Transportation Systems: Failure Mechanism Analysis. Processes. 2025; 13(9):2908. https://doi.org/10.3390/pr13092908
Chicago/Turabian StyleLiu, Chao, Yunlong Gu, Hua Wen, Shangwen Zhu, and Peng Jiang. 2025. "Reliability Study of Metal Bellows in Low-Temperature High-Pressure Liquid Carbon Dioxide Transportation Systems: Failure Mechanism Analysis" Processes 13, no. 9: 2908. https://doi.org/10.3390/pr13092908
APA StyleLiu, C., Gu, Y., Wen, H., Zhu, S., & Jiang, P. (2025). Reliability Study of Metal Bellows in Low-Temperature High-Pressure Liquid Carbon Dioxide Transportation Systems: Failure Mechanism Analysis. Processes, 13(9), 2908. https://doi.org/10.3390/pr13092908






