Use of Cedrela odorata L. as a Biomaterial for Dye Adsorption in Wastewater: Simulation and Machine Learning Approaches for Scale-Up Analysis
Abstract
1. Introduction
2. Materials and Methods
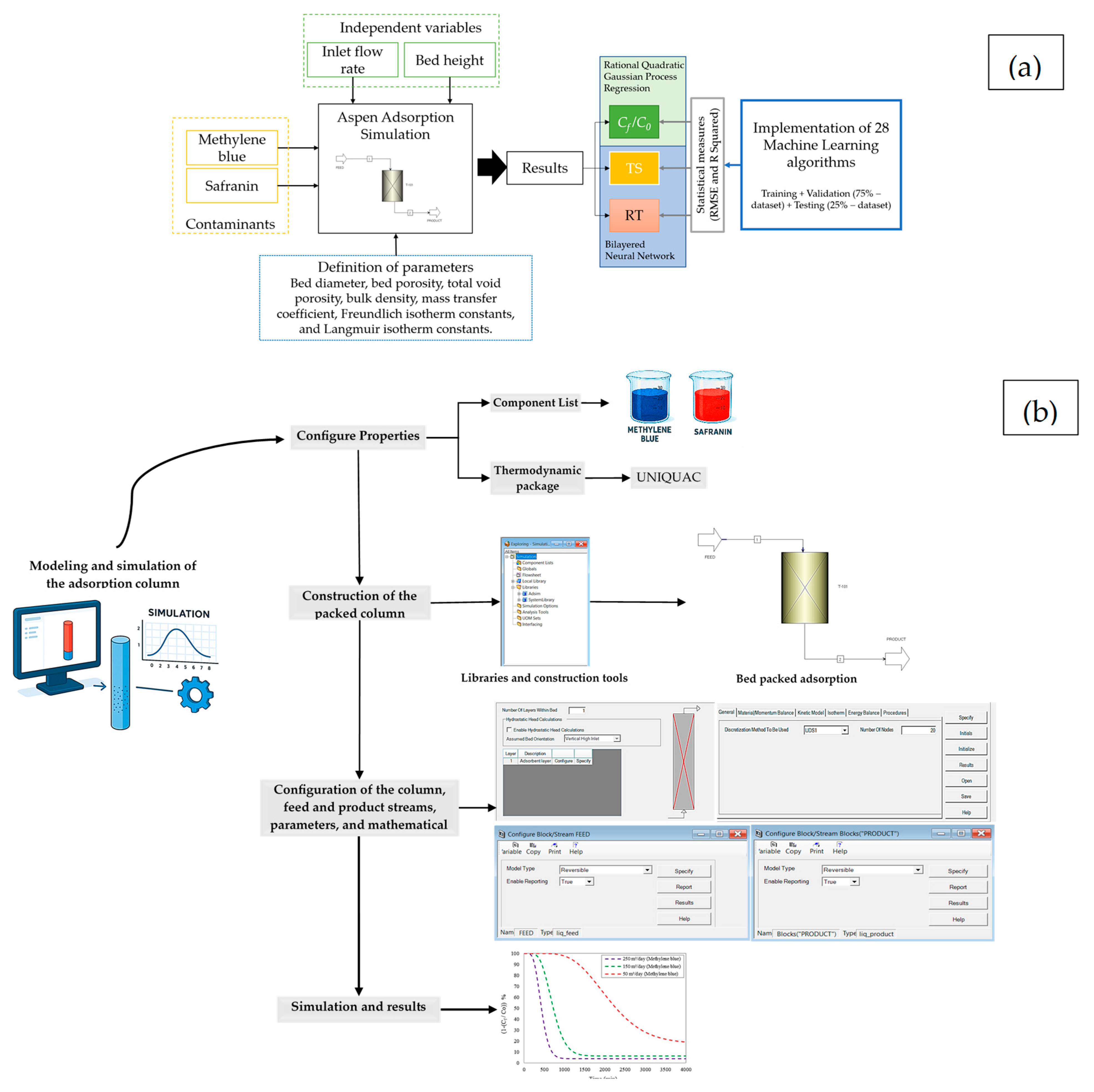
2.1. Adsorption Column Configuration
2.1.1. General Section
2.1.2. Mass/Momentum Balance Section
2.1.3. Kinetic Model Section
2.1.4. Isotherm Model Section
| Definition | Equation | Observation | Reference | |
| Langmuir isotherm model | : Adsorption capacity of the contaminant at equilibrium. : Maximum loading capacity of the adsorbent. Langmuir constant. : Equilibrium concentration of the contaminant in solution. | [22,23] | ||
| Freundlich isotherm model | : Adsorption capacity of the contaminant at equilibrium. : Freundlich constant. : Equilibrium concentration of the contaminant in solution. : Reflects the influence of the initial concentration on the adsorption capacity. | [24,25] | ||
| Langmuir–Freundlich isotherm model | Adsorption capacity of the contaminant at equilibrium. : Maximum adsorption capacity. Equilibrium concentration of the contaminant in solution. Affinity or adsorption energy constant. : Surface heterogeneity factor. | [26,27]. | ||
2.1.5. Energy Balance Section
2.2. Parameters Required for the Parametric Sensitivity Analysis
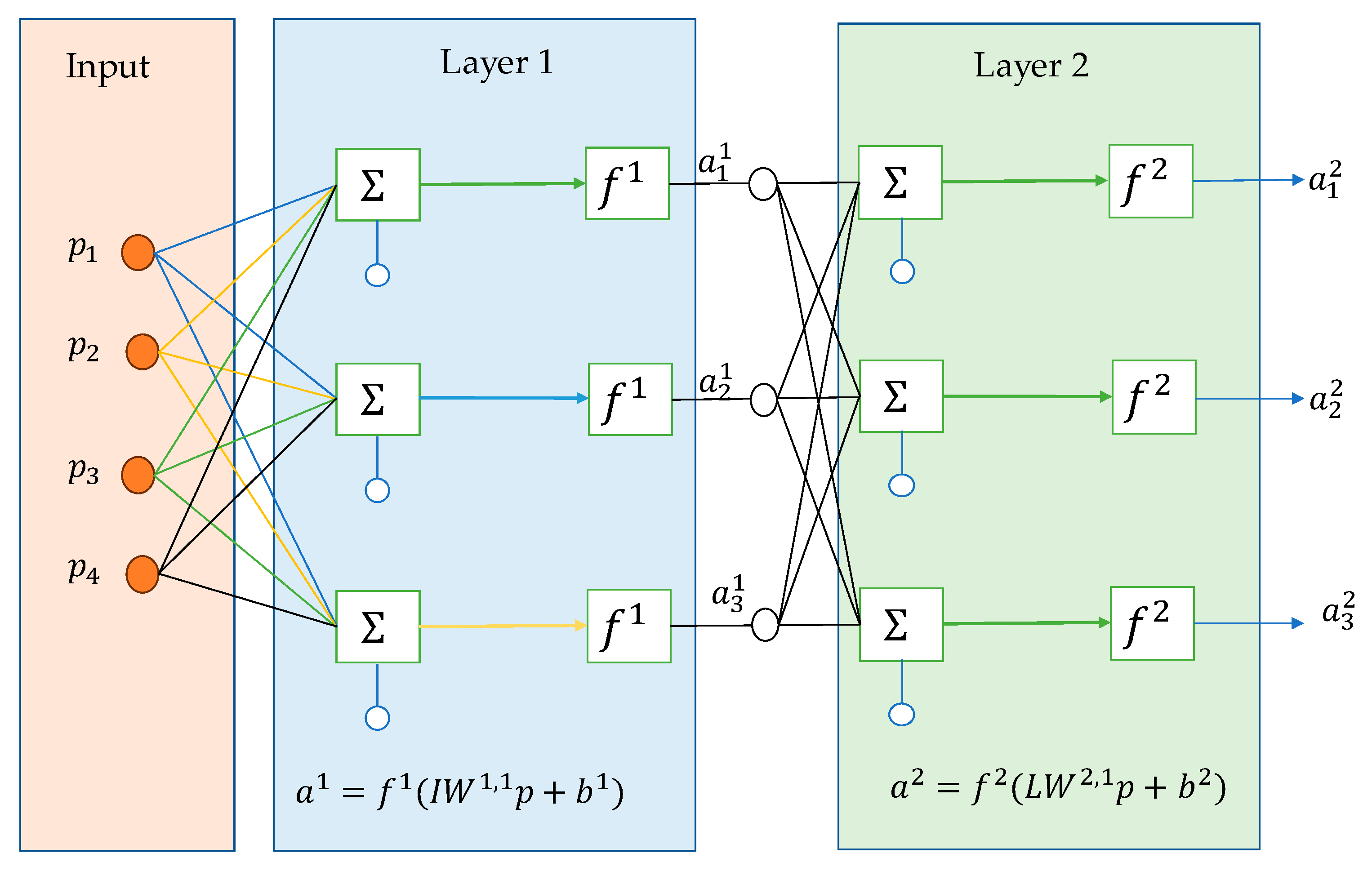
2.3. Machine Learning Techniques
3. Results and Discussion
3.1. Aspen Adsorption Simulation
3.2. Parametric Sensitivity Analysis
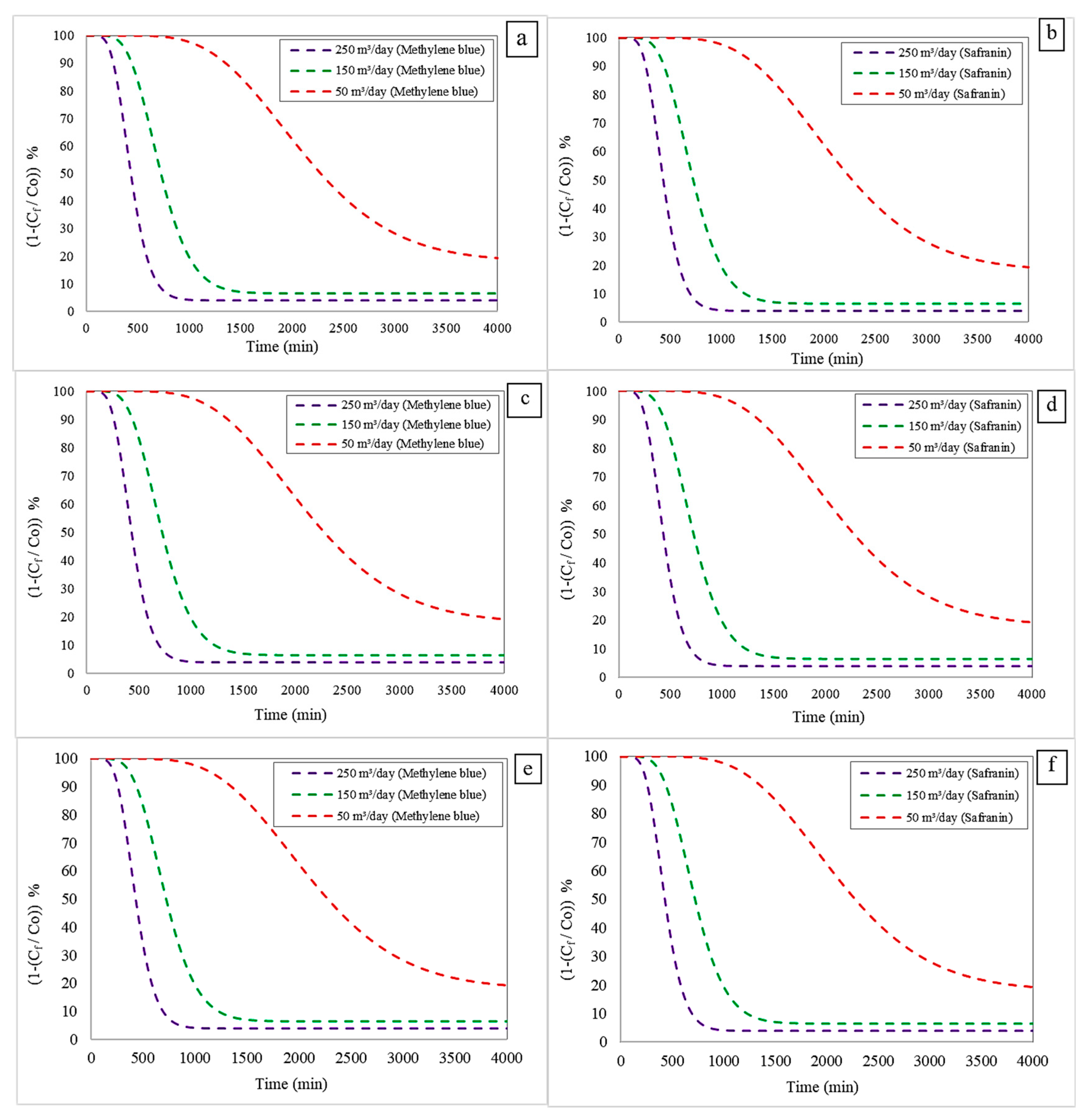
3.2.1. Effect of Varying the Inlet Flow Rate
- In the case of methylene blue, at 50 m3/day, the RT and ST were 241 min and 1430 min, respectively. When the flow rate was increased to 150 m3/day, these times decreased to 193 min and 1151 min. Further increasing the flow to 250 m3/day resulted in values of 141 min (RT) and 870 min (ST).
- A similar trend was observed for safranin, with times of 241 min and 1430 min at 50 m3/day, decreasing to 193 min and 1151 min at 150 m3/day, and finally reaching 142 min and 870 min at 250 m3/day.
- For methylene blue, the RT and ST at 50 m3/day were 246 min and 1439 min, respectively. These decreased to 195 min and 1158 min at 150 m3/day, and 142 min and 872 min at 250 m3/day.
- The same behaviour was observed for safranin, with times of 241 min and 1430 min at 50 m3/day, reducing to 193 min and 1151 min at 150 m3/day, and 142 min and 870 min at 250 m3/day.
- The results followed the same trend. For methylene blue, the RT and ST > were 241 min and 1430 min at 50 m3/day, decreasing to 193 min and 1151 min at 150 m3/day, and to 141 min and 870 min at 250 m3/day.
- Similarly, for safranin, the times were 241 min and 1430 min at 50 m3/day, 193 min and 1151 min at 150 m3/day, and 142 min and 872 min at 250 m3/day.
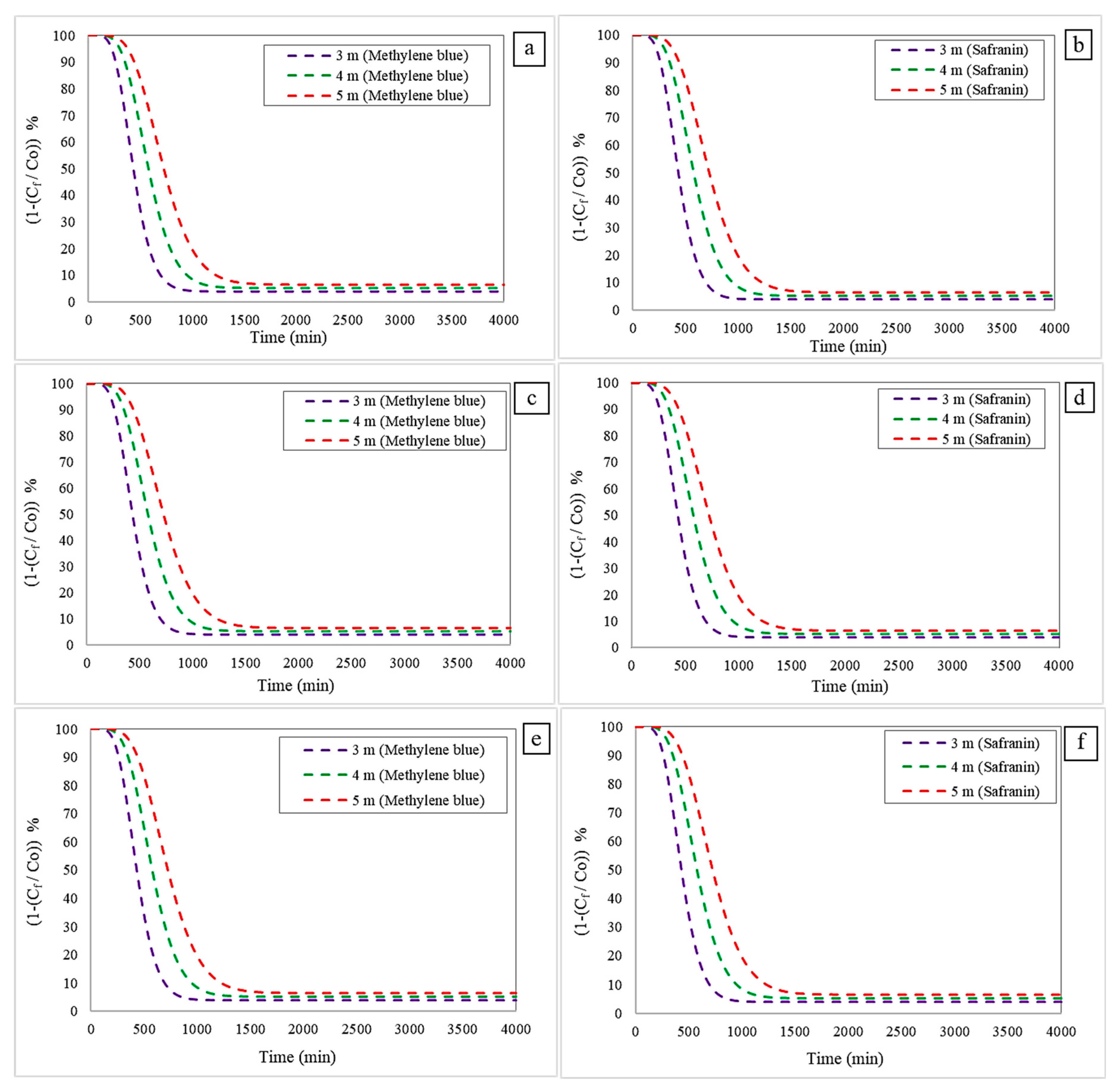
3.2.2. Effect of Changing the Column Height
- Freundlich–LDF model: For methylene blue removal, a bed height of 3 m resulted in RT and ST values of 145 min and 870 min, respectively. Increasing the height to 4 m extended these times to 244 min (RT) and 1430 min (ST). At 5 m, the values rose further to 760 min (RT) and 4183 min (ST). The same trend was observed for safranin removal: at 3 m, RT and ST were 142 min and 870 min; at 4 m, these increased to 244 min and 1430 min; and at 5 m, they reached 761 min and 4183 min, respectively.
- Langmuir–LDF model: A similar pattern was found. For methylene blue, a bed height of 3 m resulted in 142 min (RT) and 872 min (ST); increasing the height to 4 m led to 244 min and 1436 min, while at 5 m, the values were 760 min and 4215 min. For safranin, RT and ST at 3 m were 142 min and 870 min; at 4 m, they increased to 244 min and 1430 min; and at 5 m, to 761 min and 4183 min.
- Langmuir–Freundlich–LDF model: This model exhibited the same behaviour. For methylene blue, the RT and ST at 3 m were 141 min and 870 min, respectively. At 4 m, values rose to 244 min and 1430 min, and at 5 m, to 760 min and 4183 min. For safranin, at 3 m the times were 142 min (RT) and 872 min (ST); at 4 m, 244 min and 1430 min; and 5 m, 761 min and 4183 min.
3.3. Machine Learning Implementations
3.4. Comparison with Results from the Literature
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Output vector; | |
| Langmuir constant (L/mg), which indicates the affinity of the adsorbate for the adsorbent surface/bias vector; | |
| Equilibrium concentration of the contaminant in solution (mg/L); | |
| Contaminant concentration at the column outlet (mg/L); | |
| Inlet contaminant concentration (mg/L); | |
| ) | Indicates the adsorption process efficiency (−, %); |
| Latent variable; | |
| Matrix of basis functions; | |
| Affinity or adsorption energy constant [(L/mg)n]; | |
| Freundlich constant, which indicates the adsorption capacity ((mg/g) (mL/g)n); | |
| Location within the adsorption bed where the equation is being evaluated (-); | |
| Identity matrix (-); | |
| Input weight matrix (-); | |
| Layer weight matrix (-); | |
| Total number of observations (-); | |
| Surface heterogeneity factor (-); | |
| Reflects the influence of the initial concentration on the adsorption capacity; | |
| Mass transfer coefficient (1/s); | |
| Predicted value of a response (min, %); | |
| Input vector; | |
| Adsorption capacity of the contaminant at equilibrium (mg/g); | |
| Maximum loading capacity of the adsorbent (mg/g); | |
| True value of a response (min,%); | |
| Weight matrix (-); | |
| (mg/g); | |
| Amount that would be adsorbed if the system were in instantaneous equilibrium with the fluid phase (mg/g); | |
| Analysed predictor; | |
| Response variable (min, %); | |
| Distance between two nodes in the discretised bed (m); | |
| Previous node in the direction of flow (-); | |
| (mol/m3). | |
| Coefficient computed from the dataset (-); | |
| Error variance |
References
- Dwivedi, Y.D.; Manoj Kumar, P.; Gupta, A.; Ahalya, N.; Rana, D.; Sharma, M.; Surakasi, R. Experimental Study on the Treatment of Urban Garment Industry Wastewater to Mitigate Groundwater Contamination Using a Solar Evaporative Still. Urban Clim. 2023, 49, 101435. [Google Scholar] [CrossRef]
- Ravindiran, G.; Jeyaraju, R.M.; Nandipati, G.; Seerangagounder, S.; Al-Zaqri, N.; Boshaala, A.; Hayder, G. Prevention of Groundwater Contamination from the Pollutants Released from Dyeing Industries Using Biochar Produced from Palm Shell. Urban Clim. 2023, 49, 101515. [Google Scholar] [CrossRef]
- Negash, A.; Tibebe, D.; Mulugeta, M.; Kassa, Y. A Study of Basic and Reactive Dyes Removal from Synthetic and Industrial Wastewater by Electrocoagulation Process. S. Afr. J. Chem. Eng. 2023, 46, 122–131. [Google Scholar] [CrossRef]
- Al-Tohamy, R.; Ali, S.S.; Li, F.; Okasha, K.M.; Mahmoud, Y.A.G.; Elsamahy, T.; Jiao, H.; Fu, Y.; Sun, J. A Critical Review on the Treatment of Dye-Containing Wastewater: Ecotoxicological and Health Concerns of Textile Dyes and Possible Remediation Approaches for Environmental Safety. Ecotoxicol. Environ. Saf. 2022, 231, 113160. [Google Scholar] [CrossRef] [PubMed]
- Badawi, A.K.; Salama, R.S.; Mostafa, M.M.M. Natural-Based Coagulants/Flocculants as Sustainable Market-Valued Products for Industrial Wastewater Treatment: A Review of Recent Developments. RSC Adv. 2023, 13, 19335–19355. [Google Scholar] [CrossRef]
- Boinpally, S.; Kolla, A.; Kainthola, J.; Kodali, R.; Vemuri, J. A State-of-the-Art Review of the Electrocoagulation Technology for Wastewater Treatment. Water Cycle 2023, 4, 26–36. [Google Scholar] [CrossRef]
- Ravindiran, G.; Sundaram, H.; Rajendran, E.M.; Ramasamy, S.; Nabil, A.Z.; Ahmed, B. Removal of Azo Dyes from Synthetic Wastewater Using Biochar Derived from Sewage Sludge to Prevent Groundwater Contamination. Urban Clim. 2023, 49, 101502. [Google Scholar] [CrossRef]
- Sukmana, H.; Bellahsen, N.; Pantoja, F.; Hodur, C. Adsorption and Coagulation in Wastewater Treatment—Review. Prog. Agric. Eng. Sci. 2021, 17, 49–68. [Google Scholar] [CrossRef]
- Taiwo, A.F.; Chinyere, N.J. Sorption Characteristics for Multiple Adsorption of Heavy Metal Ions Using Activated Carbon from Nigerian Bamboo. J. Mater. Sci. Chem. Eng. 2016, 4, 39–48. [Google Scholar] [CrossRef]
- Homagai, P.L.; Poudel, R.; Poudel, S.; Bhattarai, A. Adsorption and Removal of Crystal Violet Dye from Aqueous Solution by Modified Rice Husk. Heliyon 2022, 8, e09261. [Google Scholar] [CrossRef]
- Salah Omer, A.; El Naeem, G.A.; Abd-Elhamid, A.I.; Farahat, O.O.M.; El-Bardan, A.A.; Soliman, H.M.A.; Nayl, A.A. Adsorption of Crystal Violet and Methylene Blue Dyes Using a Cellulose-Based Adsorbent from Sugercane Bagasse: Characterization, Kinetic and Isotherm Studies. J. Mater. Res. Technol. 2022, 19, 3241–3254. [Google Scholar] [CrossRef]
- Akter, M.; Rahman, F.B.A.; Abedin, M.Z.; Kabir, S.M.F. Adsorption Characteristics of Banana Peel in the Removal of Dyes from Textile Effluent. Textiles 2021, 1, 361–375. [Google Scholar] [CrossRef]
- Li, B.; Ma, R.; Jiang, J.; Guo, L.; Li, K. Deployment of interpretable machine learning in a water treatment device—feasibility exploration of performance enhancement. J. Water Process Eng. 2024, 58, 104781. [Google Scholar] [CrossRef]
- Rodríguez-Alonso, C.; Pena-Regueiro, I.; García, Ó. Digital Twin Platform for Water Treatment Plants Using Microservices Architecture. Sensors 2024, 24, 1568. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.J.; Li, H.; He, Z.; Tao, Y.; Wang, H.; Yang, M.; Savic, D.; Daigger, G.T.; Ren, N. Digital Twins for Wastewater Treatment: A Technical Review. Engineering 2024, 36, 21–35. [Google Scholar] [CrossRef]
- Pylianidis, C.; Snow, V.; Overweg, H.; Osinga, S.; Kean, J.; Athanasiadis, I.N. Simulation-assisted machine learning for operational digital twins. Environ. Model. Softw. 2022, 148, 105274. [Google Scholar] [CrossRef]
- Nieva, A.D.; Garcia, R.C.; Ped, R.M. Simulated Biosorption of Cr6+ Using Peels of Litchi chinensis sonn by Aspen Adsorption® V8.4. Int. J. Environ. Sci. Dev. 2019, 10, 331–337. [Google Scholar] [CrossRef]
- Durán-García, M.E.; Ruiz-Navas, R.A. Simulator of thermodynamic properties in the conversion of forest biomass of pine sawdust. Maderas Cienc. Tecnol. 2020, 22, 347–364. [Google Scholar] [CrossRef]
- Soriano, A.N.; Orfiana, O.N.; Pangon, M.B.J.; Nieva, A.D.; Adornado, A.P. Simulated Biosorption of Cd(II) and Cu(II) in Single and Binary Metal Systems by Water Hyacinth (Eichhornia crassipes) Using Aspen Adsorption®. ASEAN J. Chem. Eng. 2016, 16, 21–43. [Google Scholar] [CrossRef]
- Hameed, A.; Hameed, B.H.; Almomani, F.A.; Usman, M.; Ba-Abbad, M.M.; Khraisheh, M. Dynamic simulation of lead(II) metal adsorption from water on activated carbons in a packed-bed column. Biomass Convers. Biorefinery 2024, 14, 8283–8292. [Google Scholar] [CrossRef]
- Nikam, S.; Mandal, D.; Dabhade, P. LDF Based Parametric Optimization to Model Fluidized Bed Adsorption of Trichloroethylene on Activated Carbon Particles. Particuology 2022, 65, 72–92. [Google Scholar] [CrossRef]
- Ragadhita, R.; Bayu, A.; Nandiyanto, D. Curcumin Adsorption on Zinc Imidazole Framework-8 Particles: Isotherm Adsorption Using Langmuir, Freundlich, Temkin, And Dubinin-Radushkevich Models. J. Eng. Sci. Technol. 2022, 17, 1078–1089. [Google Scholar]
- Ezzati, R. Derivation of Pseudo-First-Order, Pseudo-Second-Order and Modified Pseudo-First-Order Rate Equations from Langmuir and Freundlich Isotherms for Adsorption. Chem. Eng. J. 2020, 392, 123705. [Google Scholar] [CrossRef]
- Stromer, B.S.; Woodbury, B.; Williams, C.F. Tylosin Sorption to Diatomaceous Earth Described by Langmuir Isotherm and Freundlich Isotherm Models. Chemosphere 2018, 193, 912–920. [Google Scholar] [CrossRef]
- Fouad, M.R. Physical Characteristics and Freundlich Model of Adsorption and Desorption Isotherm for Fipronil in Six Types of Egyptian Soil. Curr. Chem. Lett. 2023, 12, 207–216. [Google Scholar] [CrossRef]
- Jeppu, G.P.; Clement, T.P. A Modified Langmuir-Freundlich Isotherm Model for Simulating PH-Dependent Adsorption Effects. J. Contam. Hydrol. 2012, 129–130, 46–53. [Google Scholar] [CrossRef]
- Amrutha; Jeppu, G.; Girish, C.R.; Prabhu, B.; Mayer, K. Multi-Component Adsorption Isotherms: Review and Modeling Studies. Environ. Process. 2023, 10, 1–52. [Google Scholar] [CrossRef]
- De Araujo, C.M.B.; Ghislandi, M.G.; Rios, A.G.; da Costa, G.R.B.; do Nascimento, B.F.; Ferreira, A.F.P.; da Motta Sobrinho, M.A.; Rodrigues, A.E. Wastewater Treatment Using Recyclable Agar-Graphene Oxide Biocomposite Hydrogel in Batch and Fixed-Bed Adsorption Column: Bench Experiments and Modeling for the Selective Removal of Organics. Colloids Surf. A Physicochem. Eng. Asp. 2022, 639, 128357. [Google Scholar] [CrossRef]
- Dadebo, D.; Atukunda, A.; Ibrahim, M.G.; Nasr, M. Integrating Chemical Coagulation with Fixed-Bed Column Adsorption Using Rice Husk-Derived Biochar for Shipboard Bilgewater Treatment: Scale-up Design and Cost Estimation. Chem. Eng. J. Adv. 2023, 16, 100520. [Google Scholar] [CrossRef]
- Agarwal, A.; Upadhyay, U.; Sreedhar, I.; Anitha, K.L. Simulation Studies of Cu(II) Removal from Aqueous Solution Using Olive Stone. Clean. Mater. 2022, 5, 100128. [Google Scholar] [CrossRef]
- Villabona-Ortiz, Á.; Tejada-Tovar, C.; González-Delgado, Á. Parametric Evaluation of a Packed Adsorption Column to Remove Cr (VI) Using Langmuir and Freundlich with (LDF) and (QDF). Desalination Water Treat. 2025, 321, 101023. [Google Scholar] [CrossRef]
- Singh, V.; Nemalipuri, P.; Vitankar, V.; Das, H.C. Multifluid Computational Fluid Dynamics Simulation for Sawdust Gasification inside an Industrial Scale Fluidized Bed Gasifier. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Koua, B.K.; Koffi, P.M.E.; Gbaha, P. Evolution of Shrinkage, Real Density, Porosity, Heat and Mass Transfer Coefficients during Indirect Solar Drying of Cocoa Beans. J. Saudi Soc. Agric. Sci. 2019, 18, 72–82. [Google Scholar] [CrossRef]
- Babalola, J.O.; Koiki, B.A.; Eniayewu, Y.; Salimonu, A.; Olowoyo, J.O.; Oninla, V.O.; Alabi, H.A.; Ofomaja, A.E.; Omorogie, M.O. Adsorption Efficacy of Cedrela Odorata Seed Waste for Dyes: Non Linear Fractal Kinetics and Non Linear Equilibrium Studies. J. Environ. Chem. Eng. 2016, 4, 3527–3536. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar] [CrossRef]
- Demuth, H.; Beale, M.; Hagan, M. Neural Network Toolbox; For Use with MATLAB; MathWorks Inc.: Carlsbad, CA, USA, 2004; Volume 4. [Google Scholar]
- Zhang, Y.P.; Adi, V.S.K.; Huang, H.L.; Lin, H.P.; Huang, Z.H. Adsorption of Metal Ions with Biochars Derived from Biomass Wastes in a Fixed Column: Adsorption Isotherm and Process Simulation. J. Ind. Eng. Chem. 2019, 76, 240–244. [Google Scholar] [CrossRef]
- Rial, A.; Pimentel, C.H.; Gómez-Díaz, D.; Freire, M.S.; González-Álvarez, J. Evaluation of Almond Shell Activated Carbon for Dye (Methylene Blue and Malachite Green) Removal by Experimental and Simulation Studies. Materials 2024, 17, 6077. [Google Scholar] [CrossRef]
- Hoseini Dastgerdi, Z.; Meshkat, S.S.; Jalili, H. Investigation of an Adsorptive Indigo Carmine Dye Removal via Packed Bed Column: Experiments and Computational Fluid Dynamics Simulation. AUT J. Mech. Eng. 2020, 4, 315–330. [Google Scholar] [CrossRef]
- Baharlouei, A.; Jalilnejad, E.; Sirousazar, M. Fixed-bed column performance of methylene blue biosorption by Luffa cylindrica: Statistical and mathematical modeling. Chem. Eng. Commun. 2018, 205, 1537–1554. [Google Scholar] [CrossRef]
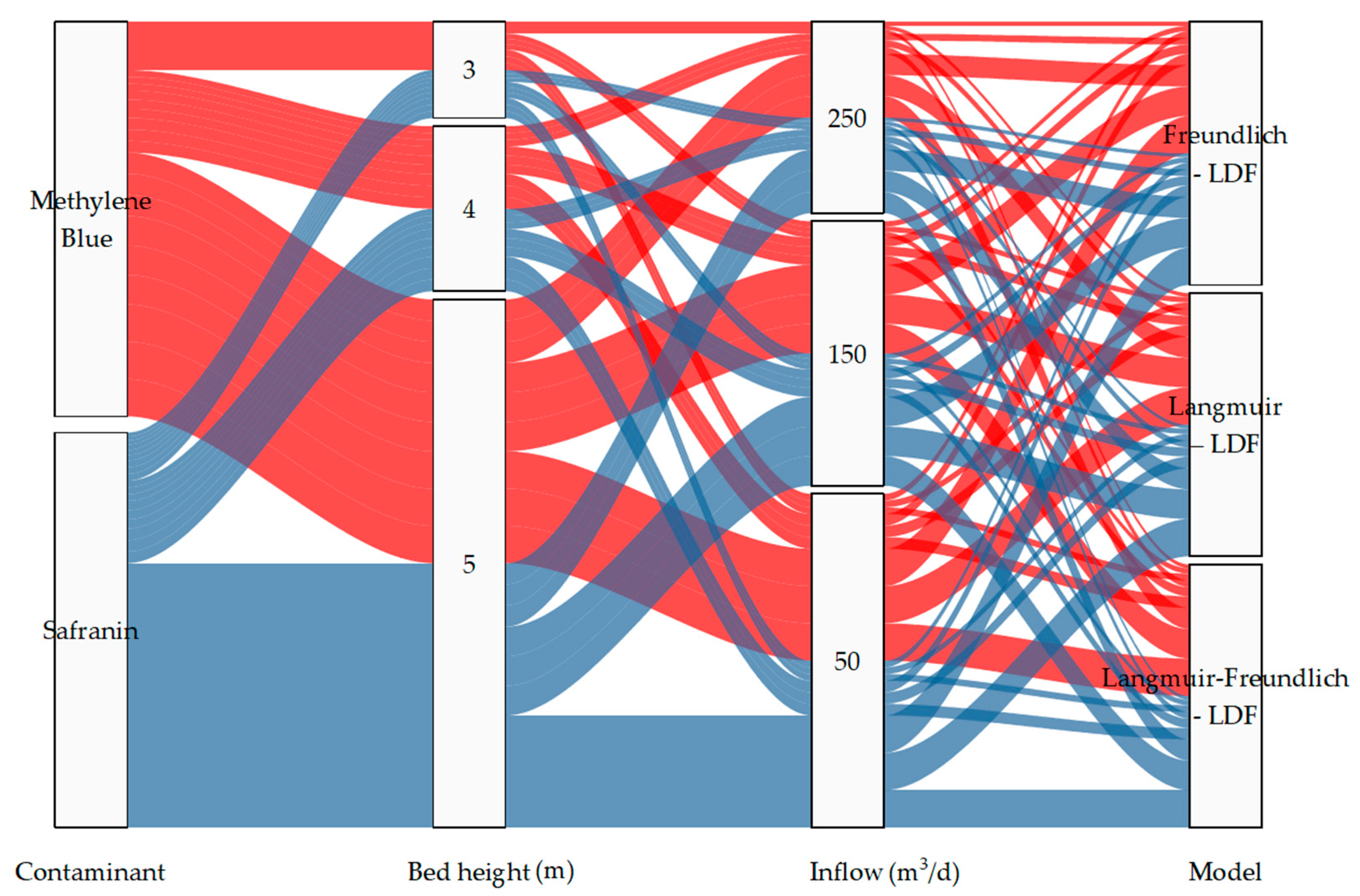

| Independent Variable | Unit | Range | Reference |
|---|---|---|---|
| Inlet flow rate | m3/day | 50, 150, 250 | [28] |
| Bed height | m | 3, 4, 5 | [29] |
| Parameter | Unit | Value | Reference |
|---|---|---|---|
| Bed diameter | m | 1 | [30] |
| Bed porosity | m3 void/m3 bed | 0.667 | [31] |
| Total void porosity | m3 void/m3 bed | 0.4 | [32] |
| Bulk density | kg/m3 | 1400 | [32] |
| Mass transfer coefficient | 1/s | 1.37 × 10−4 | [33] |
| Freundlich isotherm constants | |||
| ((mg/g) (mg/L)n) | 0.205 | [34] | |
| – | 0.058 | [34] | |
| Langmuir isotherm constants | |||
| L/mg | 0.958 | [34] | |
| mg/g | 0.262 | [34] | |
| Langmuir–Freundlich isotherm constants | |||
| KLangmuir | L/mg | 0.958 | [34] |
| KFreundlich | ((mg/g) (mg/L)n) | 0.205 | [34] |
| Model Type | Present |
|---|---|
| Tree | Fine (TF), Medium (TM), and Coarse (TC). |
| Linear regression | Linear (LRL), Interactions Linear (LRI), and Robust Linear (LRR). |
| Stepwise Linear Regression | Stepwise Linear (SLR). |
| Support Vector Machine (SVM) | Linear (SVML), Quadratic (SVMQ), Cubic (SVMC), Fine Gaussian (SVMF), Medium Coarse (SVMM), and Coarse Gaussian (SVMG). |
| Efficient Linear | Efficient Linear Least Squares (ELE) and Efficient Linear SVM (EEL). |
| Ensemble | Boosted (EBO) and Bagged (EBA) Trees. |
| Gaussian Process Regression | Squared Exponential (GPRS), Matern 5/2 (GPRM), Exponential (GPRE), and Rational Quadratic (GPRR). |
| Neural Network | Narrow (NNN), Medium (NNM), Wide (NNW), Bilayered (NNB), and Trilayered (NNT). |
| Kernel | SVM (KSVM) and Least Squares Regression (KLSR). |
| Response | Selected Model | R Squared | RMSE | Training Time (s) | ||
|---|---|---|---|---|---|---|
| Validation | Test | Validation | Test | |||
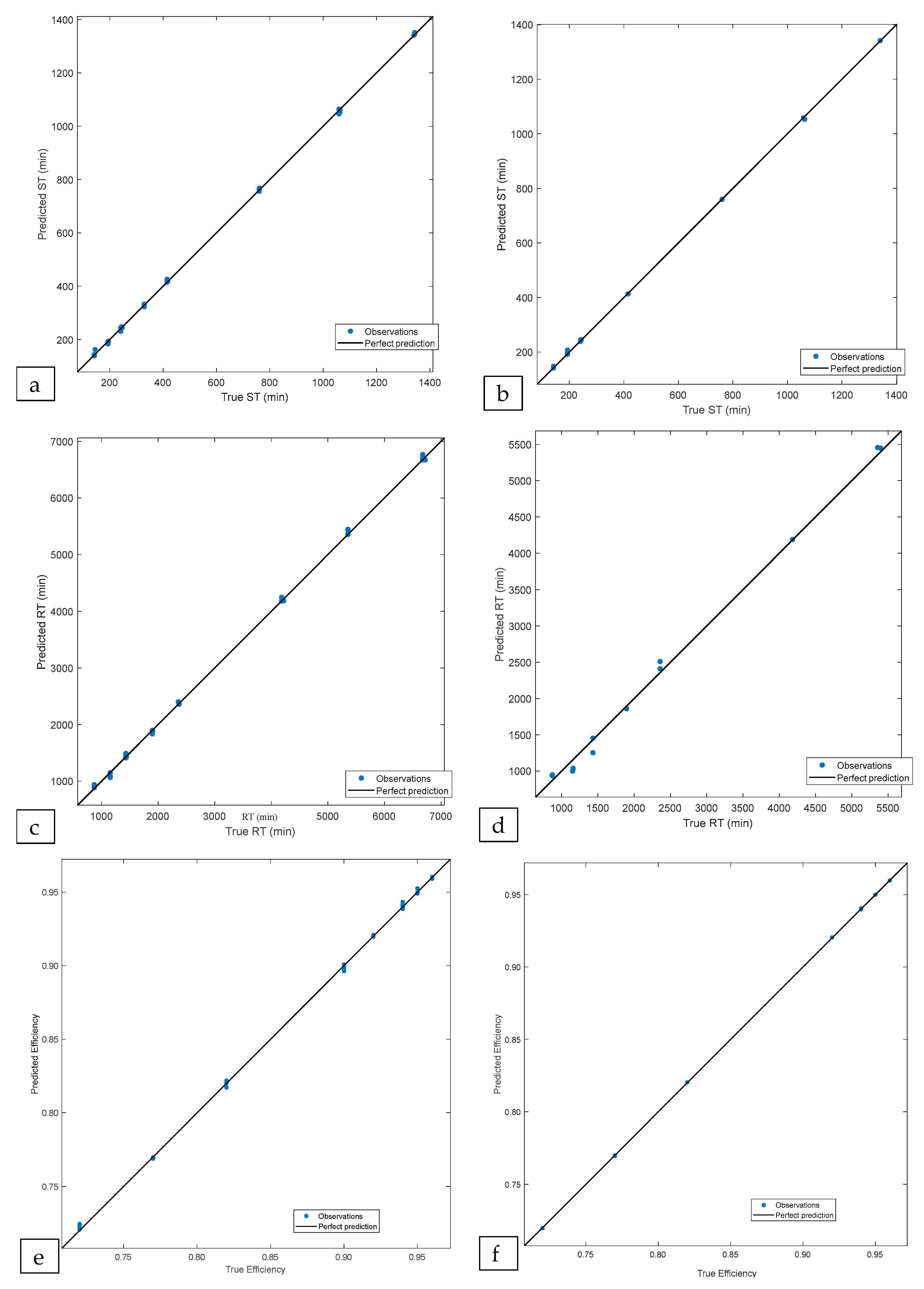
| ST (min) | NNB | 0.999 | 0.999 | 5.542 | 5.200 | 1.81 |
| RT (min) | NNB | 0.999 | 0.996 | 39.615 | 97.630 | 2.89 |
| (%) | GPRR | 0.999 | 0.999 | 0.0016 | 0.0003 | 3.64 |
| Parameter | Methylene Blue/ Malachite Green | Indigo Carmine | Methylene Blue | Methylene Blue/ Safranin |
|---|---|---|---|---|
| Adsorbent | Almond Shell | Graphene | NaOH-modified Luffa cylindrica | Cedar sawdust |
| Initial concentration (mg/L) | 200 | 10 | 39 | 2000 |
| Inlet flow rate (m3/day) | 1.44 × 10−5 | 1.44 × 10−2 | 1.44 × 10−3 | 250 |
| Bed height (m) | 0.024 | 0.28 | 0.2 | 3 |
| Rupture time (min) | 2620/3500 | 87 | 100 | 142/142 |
| Saturation time (min) | 2690/4000 | - | - | 870/872 |
| Capacity Adsorption (mg/g) | 341/364 | 349 | 46.6 | 0.262; 0.205 |
| Regenerative capacity | - | - | - | 3 |
| Reference | [38] | [39] | [40] | This research |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tejada-Tovar, C.; Villabona-Ortíz, Á.; Coronado-Hernández, O.E.; Pérez-Sánchez, M.; Hueto-Polo, M. Use of Cedrela odorata L. as a Biomaterial for Dye Adsorption in Wastewater: Simulation and Machine Learning Approaches for Scale-Up Analysis. Processes 2025, 13, 2907. https://doi.org/10.3390/pr13092907
Tejada-Tovar C, Villabona-Ortíz Á, Coronado-Hernández OE, Pérez-Sánchez M, Hueto-Polo M. Use of Cedrela odorata L. as a Biomaterial for Dye Adsorption in Wastewater: Simulation and Machine Learning Approaches for Scale-Up Analysis. Processes. 2025; 13(9):2907. https://doi.org/10.3390/pr13092907
Chicago/Turabian StyleTejada-Tovar, Candelaria, Ángel Villabona-Ortíz, Oscar E. Coronado-Hernández, Modesto Pérez-Sánchez, and María Hueto-Polo. 2025. "Use of Cedrela odorata L. as a Biomaterial for Dye Adsorption in Wastewater: Simulation and Machine Learning Approaches for Scale-Up Analysis" Processes 13, no. 9: 2907. https://doi.org/10.3390/pr13092907
APA StyleTejada-Tovar, C., Villabona-Ortíz, Á., Coronado-Hernández, O. E., Pérez-Sánchez, M., & Hueto-Polo, M. (2025). Use of Cedrela odorata L. as a Biomaterial for Dye Adsorption in Wastewater: Simulation and Machine Learning Approaches for Scale-Up Analysis. Processes, 13(9), 2907. https://doi.org/10.3390/pr13092907











