A Robust Planning Method for Multi-Village Coupled Rural Micro-Energy Grid Based on Information Gap Decision Theory
Abstract
1. Introduction
- All of the studies predominantly focus on meeting the energy demands of a single village. Although Refs. [16,20] optimize many energy equipment, these devices still belong to an RMEG composed of a single village. That is, both the energy production and consumption of each equipment are confined to a single and definite entity. In reality, significant differences exist in industrial structures and energy supply–demand relationships between neighboring villages, accompanied by strong complementary effects. Therefore, further research is warranted to leverage the respective resource characteristics of each village and establish a multi-village coupled RMEG (MV-RMEG). The challenge of developing a framework to integrate the energy facilities of multiple villages into a single system, while ensuring their operation during off-grid periods, needs to be addressed.
- Most studies adopt deterministic optimization strategies, ignoring the uncertainties during the operation of RMEG. Actually, the distributed generation (DG) output in RMEGs exhibits significant randomness. Neglecting the uncertainty issues degrades the optimality of the planning scheme [25]. The simulation results based on historical data and predicting values clearly cannot take into account the impact of these fluctuations. Ref. [23] considers meteorological data fluctuations in numerical simulations, but the proposed model still belongs to deterministic optimization. Although Refs. [19,22] handle the uncertainties leveraging the robust optimization, the feasibility of the planning scheme is poor due to the overly conservative nature of the method. Therefore, an effective approach is required to properly handle the uncertainties in the MV-RMEG planning process.
- A planning method for the MV-RMEG under the collaborative/autonomous operation framework is proposed. The planning scheme can achieve interconnection and mutual assistance among multiple villages during regular operation. Simultaneously, it ensures a reliable energy supply to critical loads during off-grid periods.
- The stochastic nature of DG output and load within the MV-RMEG is effectively addressed by applying the information gap decision theory (IGDT). The proposed method enables the artificial control of the robustness level of optimization results without relying on such prior information. This endows the planning scheme with enhanced robustness against operational uncertainties.
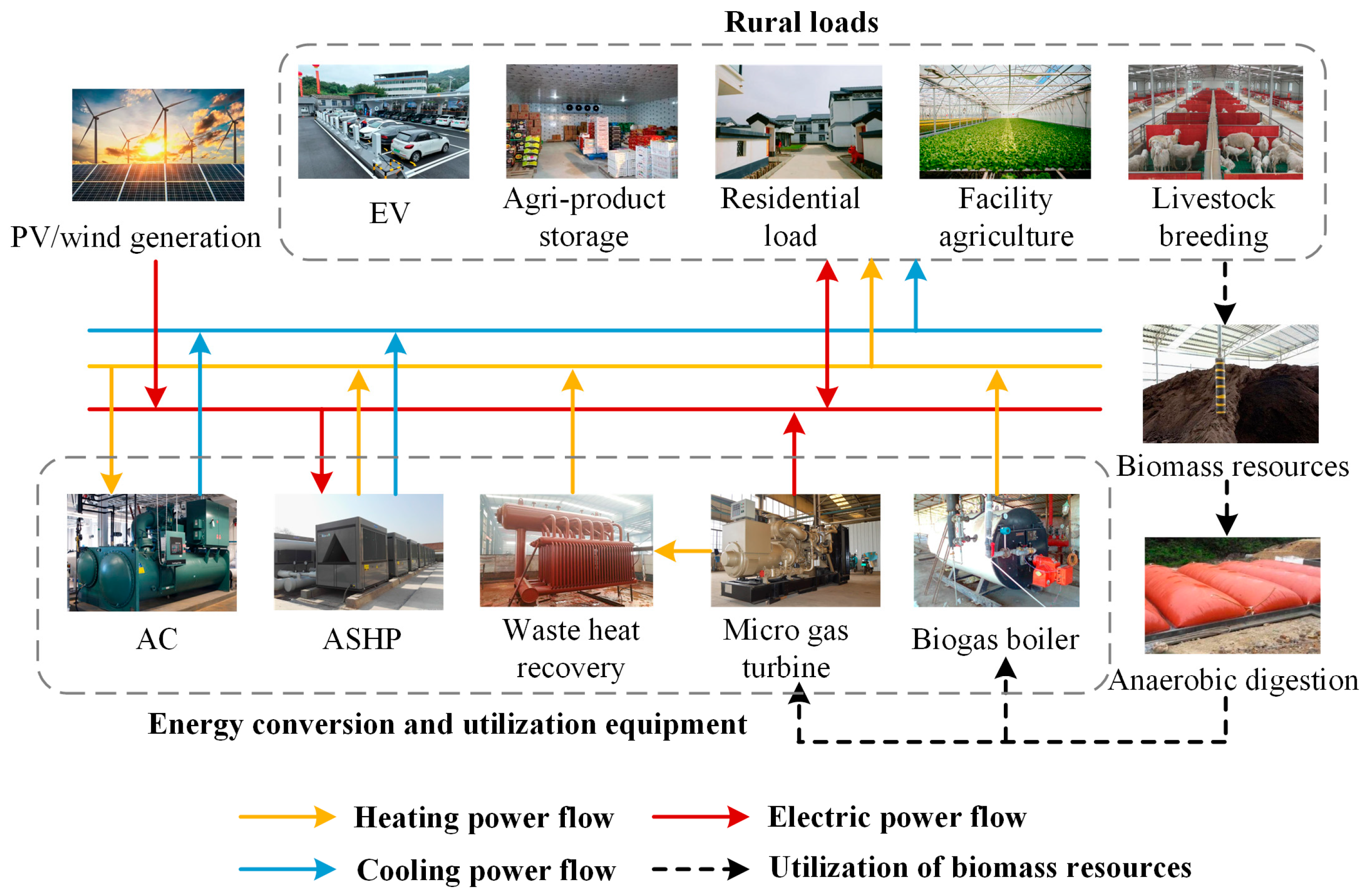
2. Modeling of MV-RMEG Components
2.1. DG Modeling
2.2. CHP Modeling
2.3. ASHP Modeling
2.4. AC Modeling
2.5. EV Modeling
2.6. Facility Agriculture and Livestock Farming Modeling
2.7. Network Modeling
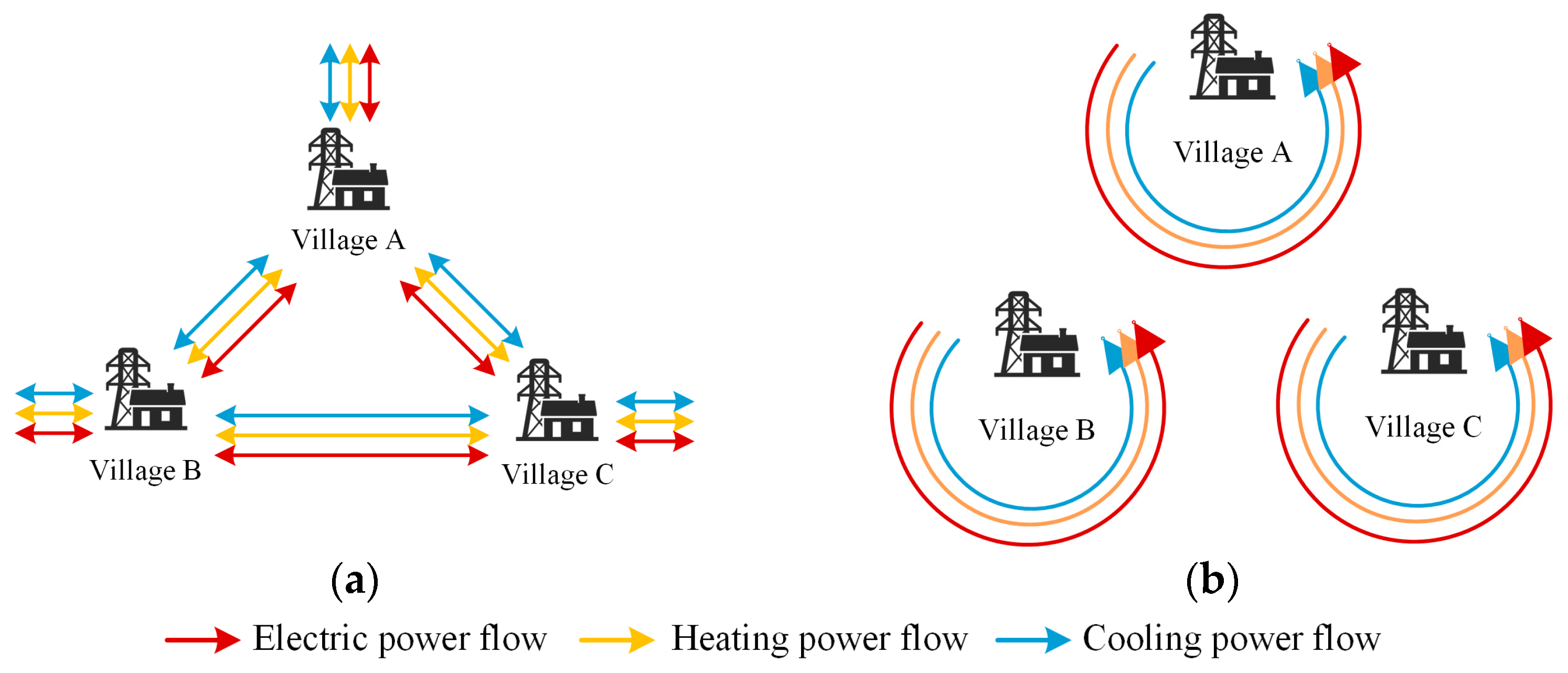
3. Planning Method for MV-RMEG Under Collaborative/Autonomous Operation Framework
3.1. Collaborative/Autonomous Framework for MV-RMEG
3.2. MV-RMEG Planning Model
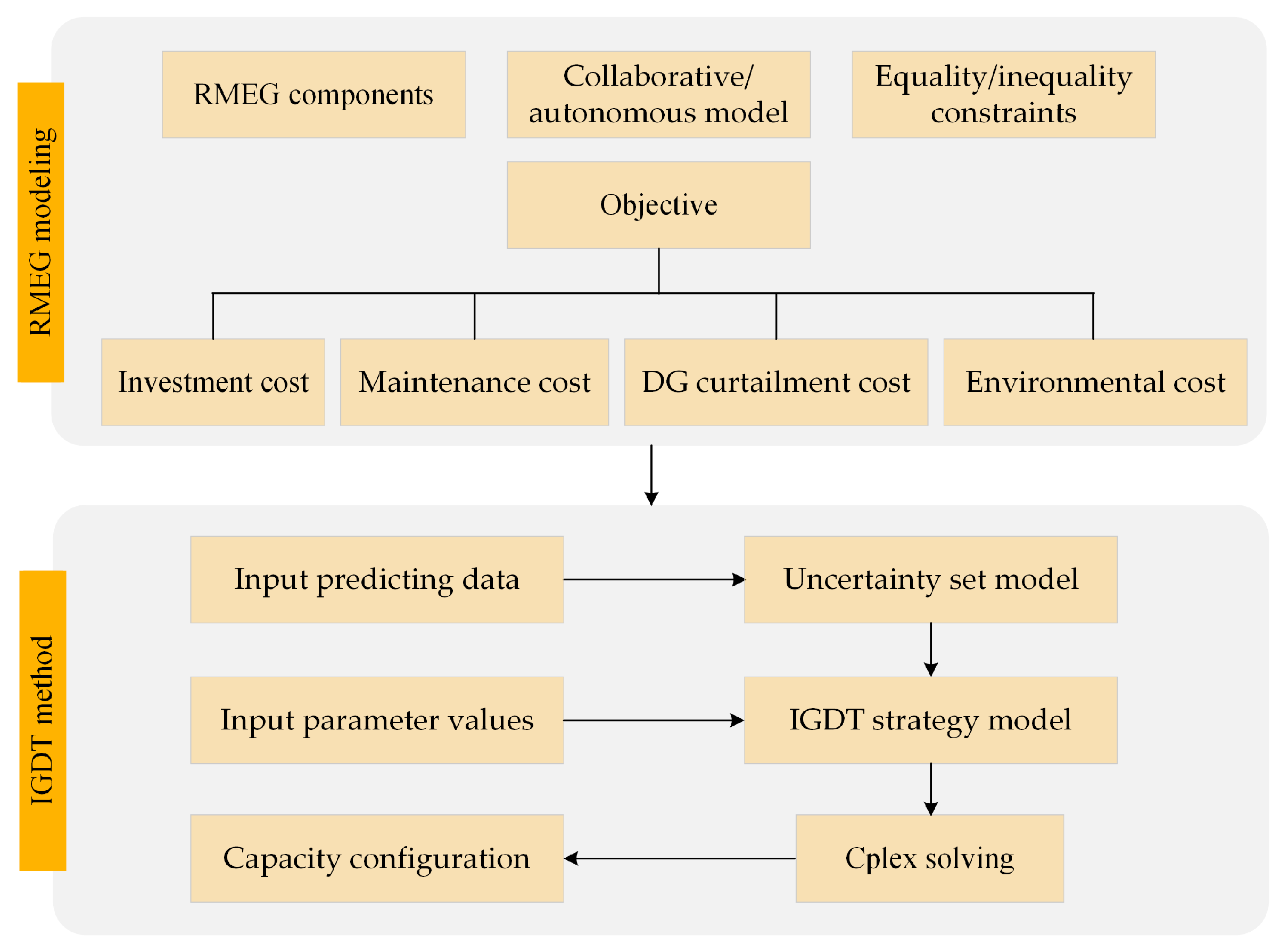
4. IGDT-Based Uncertainty Handling Method for MV-RMEG
4.1. IGDT Method
4.2. Solution Method
5. Case Studies
5.1. Parameter Settings
5.2. Planning Scheme and Result Analysis
5.3. Analysis of Collaborative/Autonomous Operation Framework
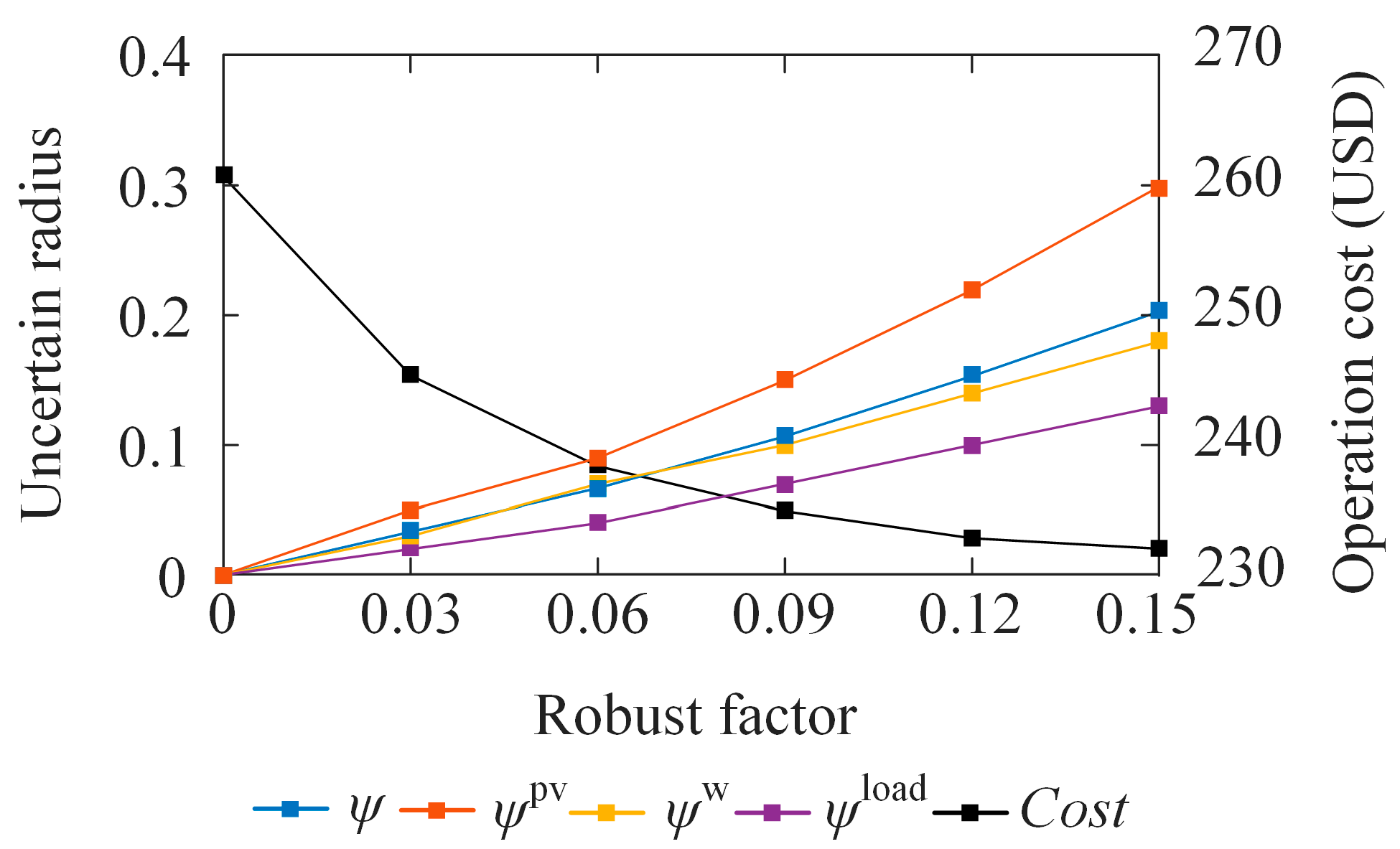
5.4. Analysis of the IGDT Planning Method
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RMEG | Rural micro-energy grid |
| MV-RMEG | Multi-village coupled rural micro-energy grid |
| DG | Distributed generation |
| IGDT | Information gap decision theory |
| EV | Electric vehicle |
| ASHP | Air-source heat pump |
| PV | Photovoltaic |
| WT | Wind turbine |
| AC | Absorption chiller |
| CHP | Combined heat and power |
References
- Wang, Q.; Xiao, Y.; Tan, H.; Mohamed, M.A. Day-Ahead Scheduling of Rural Integrated Energy Systems Based on Distributionally Robust Optimization Theory. Appl. Therm. Eng. 2024, 246, 123001. [Google Scholar] [CrossRef]
- National Energy Administration. Guiding Opinions on Promoting the Transformation and Development of Rural Energy to Support Rural Revitalization. Available online: https://www.gov.cn/zhengce/zhengceku/2022-01/07/content_5666809.htm (accessed on 31 July 2025).
- Wang, Y.; Jin, J.; Liu, H.; Zhang, Z.; Liu, S.; Ma, J.; Gong, C.; Zheng, Y.; Lin, Z.; Yang, L. The Optimal Emergency Demand Response (EDR) Mechanism for Rural Power Grid Considering Consumers’ Satisfaction. Energy Rep. 2021, 7, 118–125. [Google Scholar] [CrossRef]
- Chawda, G.S.; Shaik, A.G. Power Quality Improvement in Rural Grid Using Adaptive Control Algorithm to Enhance Wind Energy Penetration Levels. IEEE Trans. Smart Grid 2023, 14, 2075–2084. [Google Scholar] [CrossRef]
- Yang, S.; Fang, J.; Zhang, Z.; Lv, S.; Lin, H.; Ju, L. Two-Stage Coordinated Optimal Dispatching Model and Benefit Allocation Strategy for Rural New Energy Microgrid. Energy 2024, 292, 130274. [Google Scholar] [CrossRef]
- Li, P.; Zhao, M.; Zhang, H.; Zhang, O.; Li, N.; Yue, X.; Tan, Z. An Operational Optimization Model for Micro Energy Grids in Photovoltaic-Storage Agricultural Greenhouses Based on Operation Mode Selection. Processes 2025, 13, 1622. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, L.; Ma, Y.; Han, X.; Xing, J.; Miao, W.; Wang, H. Study on Operation Optimization of Decentralized Integrated Energy System in Northern Rural Areas Based on Multi-Objective. Energy Rep. 2022, 8, 3063–3084. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, X.; Liu, Y.; Liu, J.; Hu, W.; Yang, N.; Jawad, S.; Wei, Z. Operational Optimization of a Rural Multi-Energy System Supported by a Joint Biomass-Solid-Waste-Energy Conversion System and Supply Chain. Energy 2024, 312, 133528. [Google Scholar] [CrossRef]
- Ju, L.; Lv, S.; Zhang, Z.; Li, G.; Gan, W.; Fang, J. Data-Driven Two-Stage Robust Optimization Dispatching Model and Benefit Allocation Strategy for a Novel Virtual Power Plant Considering Carbon-Green Certificate Equivalence Conversion Mechanism. Appl. Energy 2024, 362, 122974. [Google Scholar] [CrossRef]
- Li, W.; Zou, Y.; Yang, H.; Fu, X.; Xiang, S.; Li, Z. Two-Stage Stochastic Energy Scheduling for Multi-Energy Rural Microgrids With Irrigation Systems and Biomass Fermentation. IEEE Trans. Smart Grid 2025, 16, 1075–1087. [Google Scholar] [CrossRef]
- Han, F.; Zhao, Y.; Zeng, J.; Zhang, S.; Wu, T. Uncertain Parameters Adjustable Two-Stage Robust Optimization of a Rural Housing Integrated Energy System Considering Biomass on-Site Utilization. Energy 2024, 296, 131106. [Google Scholar] [CrossRef]
- Wu, S.; Wang, Y.; Liu, L.; Yang, Z.; Cao, Q.; He, H.; Cao, Y. Two-Stage Distributionally Robust Optimal Operation of Rural Virtual Power Plants Considering Multi Correlated Uncertainties. Int. J. Electr. Power Energy Syst. 2024, 161, 110173. [Google Scholar] [CrossRef]
- Ugwoke, B.; Sulemanu, S.; Corgnati, S.P.; Leone, P.; Pearce, J.M. Demonstration of the Integrated Rural Energy Planning Framework for Sustainable Energy Development in Low-Income Countries: Case Studies of Rural Communities in Nigeria. Renew. Sustain. Energy Rev. 2021, 144, 110983. [Google Scholar] [CrossRef]
- Liu, W.; Gao, X.; Liu, C.; Shi, Q. Reliability-Constrained Bi-Level Collaborative Planning of Distribution Network and Micro-Energy Grid. Int. J. Electr. Power Energy Syst. 2023, 152, 109199. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, L.; Wang, Y.; Zhang, Y.; Zhang, S.; Liu, Z.; Xing, J.; Liu, X. Bi-Level Programming Optimization Method of Rural Integrated Energy System Based on Coupling Coordination Degree of Energy Equipment. Energy 2024, 298, 131289. [Google Scholar] [CrossRef]
- Kumar, R.; Channi, H.K. A PV-Biomass off-Grid Hybrid Renewable Energy System (HRES) for Rural Electrification: Design, Optimization and Techno-Economic-Environmental Analysis. J. Clean. Prod. 2022, 349, 131347. [Google Scholar] [CrossRef]
- Chen, M.; Wei, J.; Yang, X.; Fu, Q.; Wang, Q.; Qiao, S. Multi-Objective Optimization of Multi-Energy Complementary Systems Integrated Biomass-Solar-Wind Energy Utilization in Rural Areas. Energy Convers. Manag. 2025, 323, 119241. [Google Scholar] [CrossRef]
- Abazari, A.; Soleymani, M.M.; Kamwa, I.; Babaei, M.; Ghafouri, M.; Muyeen, S.M.; Foley, A.M. A Reliable and Cost-Effective Planning Framework of Rural Area Hybrid System Considering Intelligent Weather Forecasting. Energy Rep. 2021, 7, 5647–5666. [Google Scholar] [CrossRef]
- Li, X.; Zhang, L.; Wang, R.; Sun, B.; Xie, W. Two-Stage Robust Optimization Model for Capacity Configuration of Biogas-Solar-Wind Integrated Energy System. IEEE Trans. Ind. Appl. 2023, 59, 662–675. [Google Scholar] [CrossRef]
- Li, S.; Zhang, L.; Wang, X.; Zhu, C. A Decision-Making and Planning Optimization Framework for Multi-Regional Rural Hybrid Renewable Energy System. Energy Convers. Manag. 2022, 273, 116402. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, A.; Gu, H.; Wang, X.; Xie, D.; Gu, C. Planning of the Multi-Energy Circular System Coupled with Waste Processing Base: A Case from China. Energies 2019, 12, 3910. [Google Scholar] [CrossRef]
- Ju, L.; Lu, X.; Yang, S.; Li, G.; Fan, W.; Pan, Y.; Qiao, H. A Multi-Time Scale Dispatching Optimal Model for Rural Biomass Waste Energy Conversion System-Based Micro-Energy Grid Considering Multi-Energy Demand Response. Appl. Energy 2022, 327, 120155. [Google Scholar] [CrossRef]
- Fu, X.; Wei, Z.; Sun, H.; Zhang, Y. Agri-Energy-Environment Synergy-Based Distributed Energy Planning in Rural Areas. IEEE Trans. Smart Grid 2024, 15, 3722–3738. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, X.; Xu, L.; Liu, Y.; Liu, J.; Hu, W.; Yang, N.; Jawad, S.; Luo, Y. Multi-Timescale Collaborative Operation of Renewable Energy-Based Power System and Agri-Product Supply Chain Considering Dynamic Energy Consumption-Based Crop Growth. Appl. Energy 2025, 377, 124359. [Google Scholar] [CrossRef]
- Jiang, M.; Xu, Y.; Zhang, D.; Liu, Y.; Du, Q.; Gao, X.; Qi, S.; Zou, H. Research on an Active Distribution Network Planning Strategy Considering Diversified Flexible Resource Allocation. Processes 2025, 13, 2254. [Google Scholar] [CrossRef]
- Liang, H.; Yu, L.; Yan, L.; Han, J. Design of Micro-Grid with Biogas Power Generation. In Proceedings of the International Conference on Renewable Power Generation (RPG 2015), Beijing, China, 17–18 October 2015; Institution of Engineering and Technology: Hong Kong, China, 2015; p. 5. [Google Scholar]
- Wang, R.; Wang, J. Multi-Objective Collaborative Optimization of System Configurations and Energy Scheduling of Integrated Energy System with Electricity-Fuel-Heat Storage Systems. J. Energy Storage 2025, 132, 117846. [Google Scholar] [CrossRef]
- Sun, L.; Hu, Z.; Mae, M.; Imaizumi, T. A Predictive COP Model for Air Source Heat Pumps under Extreme Heat Conditions Using No Experimental Data. Energy Build. 2025, 339, 115749. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, X.; Wu, D.; Jin, G.; Fan, G.; Guo, J.; Xu, H. Multi-Time-Scale Optimization Method Based on an Integrated Cooperative Cooling, Heating, and Electricity Storage Supply System. J. Energy Storage 2025, 122, 116592. [Google Scholar] [CrossRef]
- Habash, R.; Gediz ilis, G.; Ünal, Ş.; Saha, B.B. Enhancing COP of Electric Vehicle Cooling Systems Using Adsorption Heat Pumps. Therm. Sci. Eng. Prog. 2025, 64, 103788. [Google Scholar] [CrossRef]
- Chen, X.; Leung, K.C. Non-Cooperative and Cooperative Optimization of Scheduling with Vehicle-to-Grid Regulation Services. IEEE Trans. Veh. Technol. 2020, 69, 114–130. [Google Scholar] [CrossRef]
- Wu, C.; Gao, S.; Liu, Y.; Song, T.E.; Han, H. A Model Predictive Control Approach in Microgrid Considering Multi-Uncertainty of Electric Vehicles. Renew. Energy 2021, 163, 1385–1396. [Google Scholar] [CrossRef]
- Topa, A.O.; Gil, J.D.; Álvarez, J.D.; Torres, J.L. A Hybrid-MPC Based Energy Management System with Time Series Constraints for a Bioclimatic Building. Energy 2024, 287, 129652. [Google Scholar] [CrossRef]
- Li, M.; Liu, Q.; Zhao, G.; Zhou, B.; Xia, H.; Zang, T. Rural Integrated Energy System Planning Considering Multi-Industry Synergy. Zhongguo Dianli/Electr. Power 2022, 55, 14–22. [Google Scholar] [CrossRef]
- Van Phu, P.; Huy, T.H.B.; Park, S.; Kim, D. An IGDT Approach for the Multi-Objective Framework of Integrated Energy Hub with Renewable Energy Sources, Hybrid Energy Storage Systems, and Biomass-to-Hydrogen Technology. J. Energy Storage 2024, 89, 111488. [Google Scholar] [CrossRef]
- Cao, X.; Wang, J.; Zeng, B. A Chance Constrained Information-Gap Decision Model for Multi-Period Microgrid Planning. IEEE Trans. Power Syst. 2018, 33, 2684–2695. [Google Scholar] [CrossRef]
- Liao, S.; Liu, H.; Liu, B.; Zhao, H.; Wang, M. An Information Gap Decision Theory-Based Decision-Making Model for Complementary Operation of Hydro-Wind-Solar System Considering Wind and Solar Output Uncertainties. J. Clean. Prod. 2022, 348, 131382. [Google Scholar] [CrossRef]
- NASA. NASA Power. Available online: https://power.larc.nasa.gov/data-access-viewer/ (accessed on 31 July 2025).
- China EV100 Research on the Development of Electric Vehicles in China’s Rural Areas. Available online: http://www.nrdc.cn/Public/uploads/2020-07-17/5f1125d5ac64d.pdf (accessed on 31 July 2025).





| Reference | RMEG Area | Optimization Approach |
|---|---|---|
| Ref. [16] | Single-village | Deterministic optimization with historical data |
| Ref. [17] | Single-village | Deterministic optimization with historical data |
| Ref. [18] | Single-village | Deterministic optimization with predicting data based on fuzzy c-means clustering technique |
| Ref. [19] | Single-village | Two-stage robust optimization |
| Ref. [20] | Single-village | Deterministic optimization with historical data |
| Ref. [21] | Single-village | Deterministic optimization with historical data |
| Ref. [22] | Single-village | Two-stage robust optimization |
| Ref. [23] | Single-village | Deterministic optimization with historical data |
| Ref. [24] | Single-village | Deterministic optimization with historical data |
| Equipment | Village A | Village B | Village C |
|---|---|---|---|
| PV | √ | ||
| WT | √ | ||
| Micro gas turbine | √ | ||
| Biogas boiler | √ | ||
| AC | √ | ||
| ASHP | √ | √ | |
| Charging piles | √ |
| Parameters | Pigs | Cattle | Poultry |
|---|---|---|---|
| Breeding scale (animal) | 10,000 | 3000 | 30,000 |
| Daily manure excretion (kg/animal) | 2 | 20 | 0.1 |
| Gas production rate (m3/t) | 361 | 77 | 54 |
| CH4 emission (kg/animal·day) | 1.4 × 10−2 | 2.28 × 10−2 | 5.48 × 10−5 |
| N2O emission (kg/animal·day) | 4.93 × 10−4 | 5.67 × 10−3 | 2.74 × 10−5 |
| Parameters | Unit | Value |
|---|---|---|
| Pw,rate | kW | 100 |
| Ppv,rate | kW | 0.3 |
| ηmt,e/hl/bb | 0.35/0.5/0.9 | |
| ηwhr,r/whr,h | 0.6/0.8 | |
| ηch/dis | 0.9/0.9 | |
| μarr/dep | 8/18 | |
| σarr/dep | 1/1 | |
| Eev | kWh | 57.6 |
| kW | 20/20 | |
| ypla | year | 10 |
| π | 0.1 | |
| λpv/w/load | 0.33 |
| Equipment | Capacity (kW) |
|---|---|
| PV | 1560 |
| WT | 6500 |
| Charging piles | 1280 |
| Micro gas turbine | 2430 |
| Biogas boiler | 4150 |
| ASHP in Village A | 1530 |
| ASHP in Village C | 270 |
| AC | 470 |
| Equipment | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 |
|---|---|---|---|---|---|
| Annualized investment cost (103 USD) | 908.29 | 962.20 | 1145.79 | 1236.95 | 1281.3 |
| Maintenance cost (103 USD) | 27.76 | 21.36 | 27.94 | 27.52 | 27.91 |
| DG curtailment cost (103 USD) | 7.58 | 7.54 | 13.90 | 13.69 | 0 |
| Power purchasing cost (103 USD) | 680.04 | 701.22 | 0.01 | 2.62 | 1.88 |
| Environmental cost (103 USD) | −60.33 | −59.80 | −63.55 | −63.38 | −64.17 |
| Load shedding rate during off-grid (%) | 31.23 | 10.73 | 34.56 | 3.96 | 3.43 |
| λpv | λw | λload | Annualized Investment Cost of PV (103 USD) | Annualized Investment Cost of WT (103 USD) | PV Curtailment Cost (103 USD) | WT Curtailment Cost (103 USD) |
|---|---|---|---|---|---|---|
| 0.33 | 0.33 | 0.33 | 131.85 | 598.51 | 1.79 | 11.9 |
| 0.6 | 0.2 | 0.2 | 92.37 | 647.7 | 1.3 | 12.21 |
| 0.2 | 0.6 | 0.2 | 176.23 | 535.1 | 2.43 | 11.62 |
| 0.2 | 0.2 | 0.6 | 162.59 | 580.33 | 2.28 | 11.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Liu, X.; Zhang, Z.; Li, G.; Zhang, Y.; Ma, G.; Wang, Z.; Wen, P. A Robust Planning Method for Multi-Village Coupled Rural Micro-Energy Grid Based on Information Gap Decision Theory. Processes 2025, 13, 2881. https://doi.org/10.3390/pr13092881
Wang Y, Liu X, Zhang Z, Li G, Zhang Y, Ma G, Wang Z, Wen P. A Robust Planning Method for Multi-Village Coupled Rural Micro-Energy Grid Based on Information Gap Decision Theory. Processes. 2025; 13(9):2881. https://doi.org/10.3390/pr13092881
Chicago/Turabian StyleWang, Yunjia, Xuefei Liu, Zeya Zhang, Guangyi Li, Yan Zhang, Guozhen Ma, Ziqi Wang, and Peng Wen. 2025. "A Robust Planning Method for Multi-Village Coupled Rural Micro-Energy Grid Based on Information Gap Decision Theory" Processes 13, no. 9: 2881. https://doi.org/10.3390/pr13092881
APA StyleWang, Y., Liu, X., Zhang, Z., Li, G., Zhang, Y., Ma, G., Wang, Z., & Wen, P. (2025). A Robust Planning Method for Multi-Village Coupled Rural Micro-Energy Grid Based on Information Gap Decision Theory. Processes, 13(9), 2881. https://doi.org/10.3390/pr13092881





