Increasing Residence Time in Random Packed Beds of Spheres with a Helical Flow Deflector
Abstract
1. Introduction
2. Methods
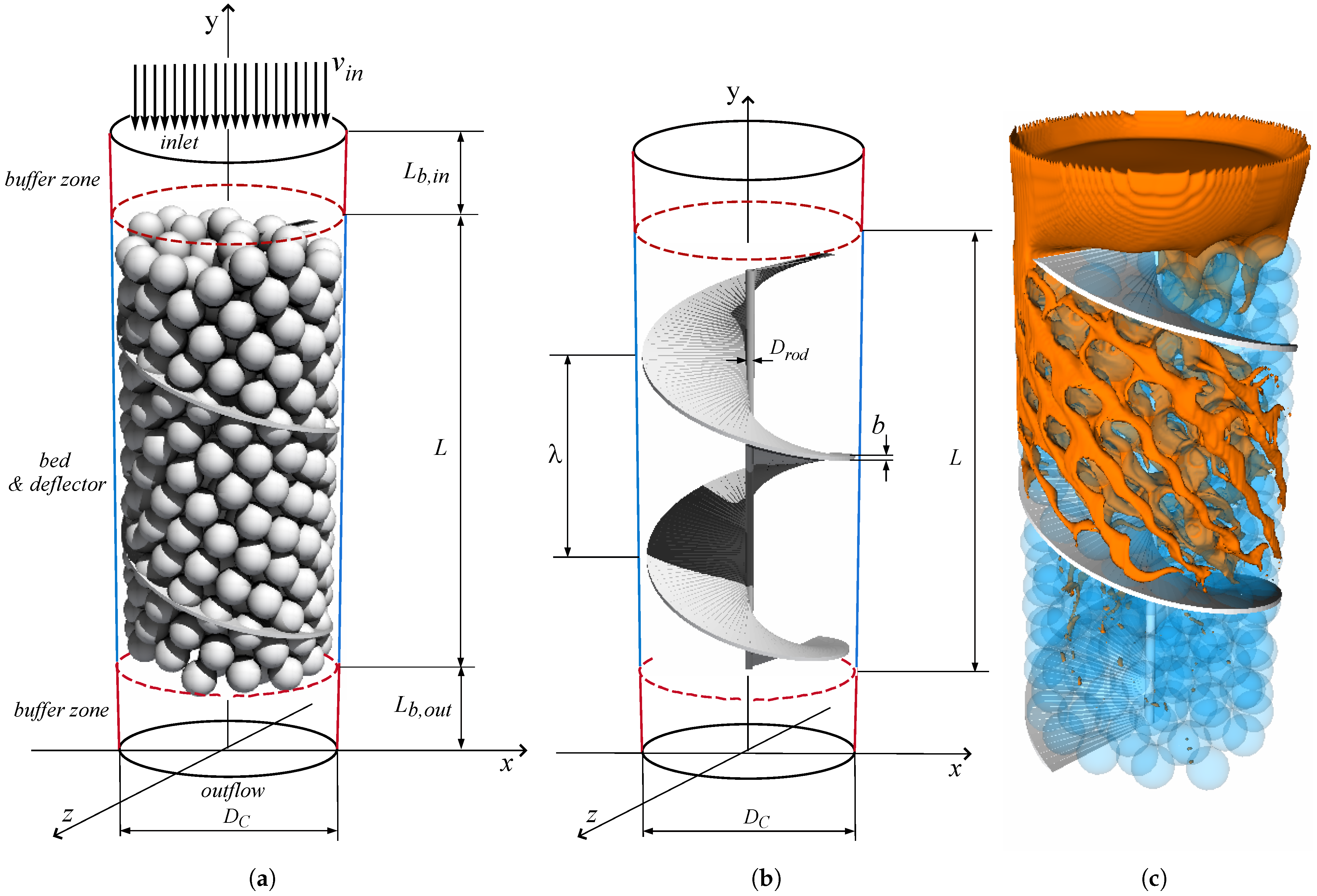
2.1. Flow Configuration
2.2. Generation of the Packed Bed Geometry
2.3. Flow Solver
2.4. Calculation of the Residence Time
3. Results
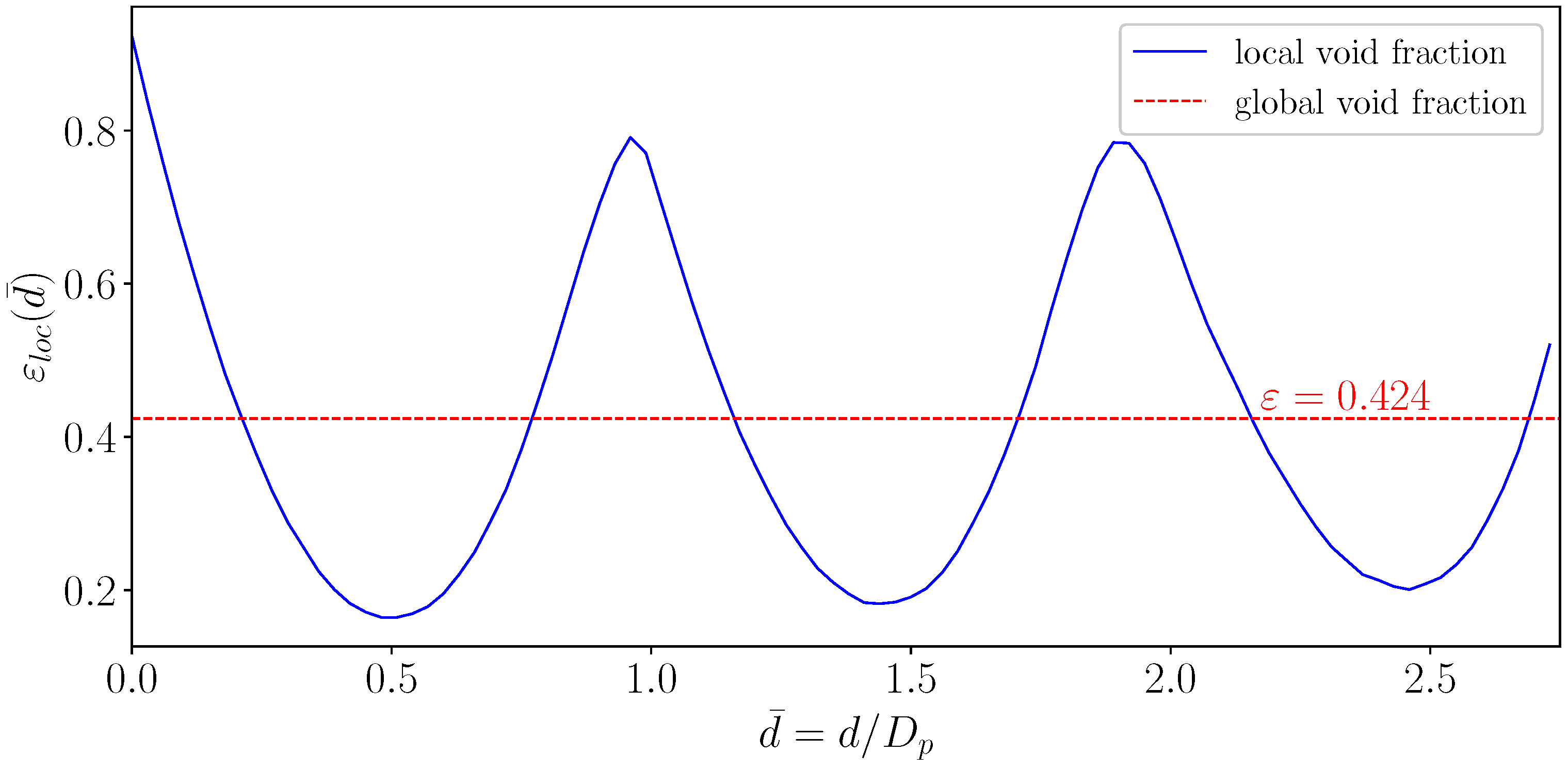
3.1. Packed Bed Generation
3.2. Model Verification
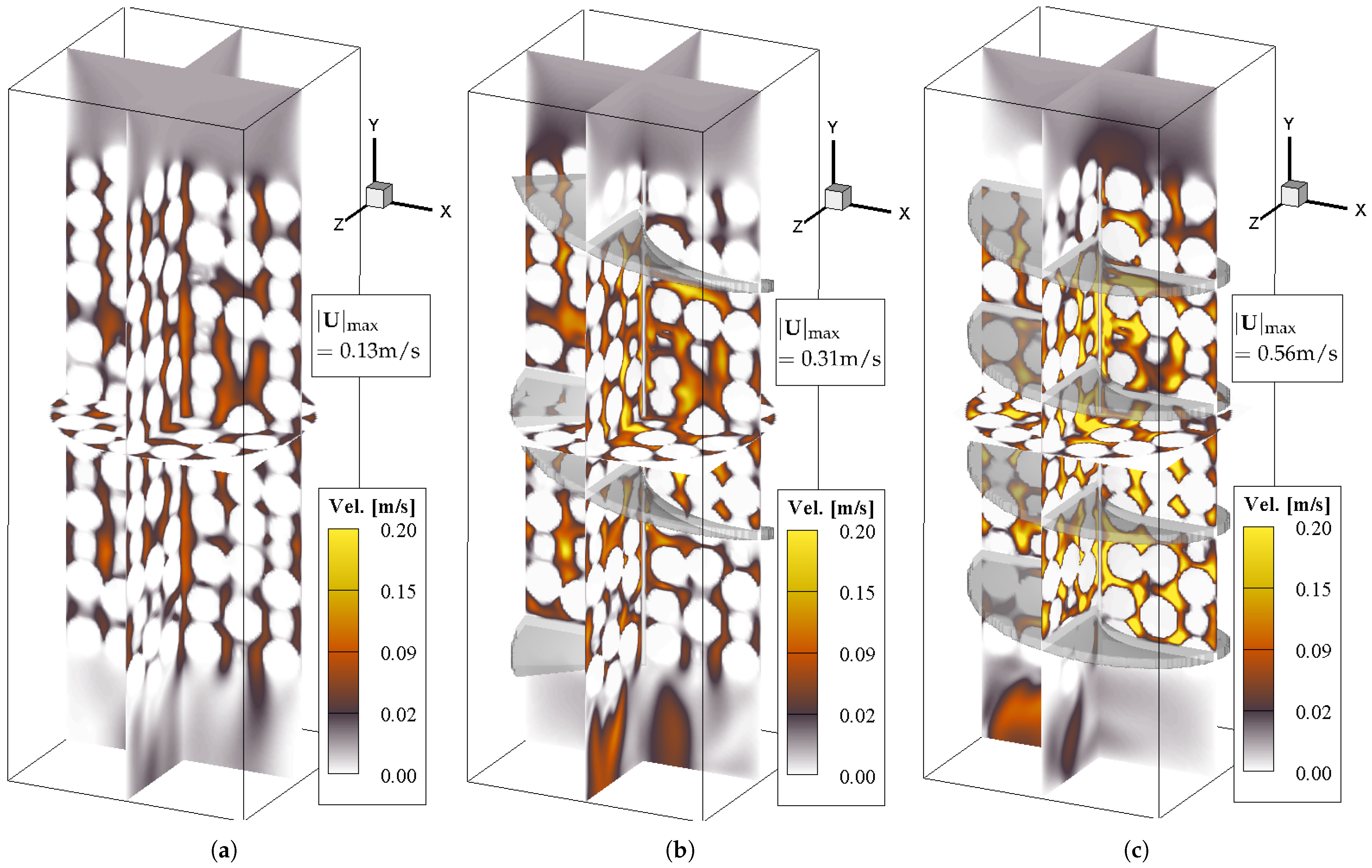
3.3. Calculation of the Flow Velocity Field and the Structure Factor
3.4. Residence Time Analysis (RTD)
4. Discussion
5. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BC | Boundary Condition |
| CFL | Courant–Friedrichs–Lewy |
| IBM | Immersed Boundary Method |
| ICPCG | Incomplete Cholesky Preconditioned Conjugate Gradient |
| MAC | Marker and Cell |
| Probability Density Function | |
| RPB | Random Packed Bed |
| RT | Residence Time |
| RTD | Residence Time Distribution |
| TBR | Trickle Bed Reactor |
| VOF | Volume of Fluid |
References
- Klenov, O.P.; Noskov, A.S. Influence of input conditions on the flow distribution in trickle bed reactors. Chem. Eng. J. 2020, 382, 122806. [Google Scholar] [CrossRef]
- White, J.P.; Chamberlain, T.W.; Bourne, R.A.; Taylor, D.; Brennan, C.; Muller, F.L. Decoupling the relative rate of hydrogen uptake via convection and mass transfer by a single catalytic pellet in a scaled down trickle bed reactor. Chem. Eng. J. 2020, 394, 124290. [Google Scholar] [CrossRef]
- Asimakopoulos, K.; Lezyk, M.; Grimalt-Alemany, A.; Melas, A.; Wen, Z.; Gavala, H.N.; Skiadas, I.V. Temperature effects on syngas biomethanation performed in a trickle bed reactor. Chem. Eng. J. 2020, 393, 124739. [Google Scholar] [CrossRef]
- Guo, R.; Wei, B.; Liu, H.; Shi, X.; Lan, X.; Gao, J. Study on liquid dispersion characteristics in trickle bed reactor based on image processing. Fuel 2023, 351, 128912. [Google Scholar] [CrossRef]
- Liu, M.; Steven Tay, N.; Bell, S.; Belusko, M.; Jacob, R.; Will, G.; Saman, W.; Bruno, F. Review on concentrating solar power plants and new developments in high temperature thermal energy storage technologies. Renew. Sustain. Energy Rev. 2016, 53, 1411–1432. [Google Scholar] [CrossRef]
- Gautam, A.; Saini, R.P. Thermal and hydraulic characteristics of packed bed solar energy storage system having spheres as packing element with pores. J. Energy Storage 2020, 30, 101414. [Google Scholar] [CrossRef]
- Hoffmann, A.; Ausner, I.; Repke, J.U.; Wozny, G. Fluid dynamics in multiphase distillation processes in packed towers. Comput. Chem. Eng. 2005, 29, 1433–1437. [Google Scholar] [CrossRef]
- Li, X.; Yang, X.; Li, H.; Shi, Q.; Gao, X. Significantly enhanced vapor-liquid mass transfer in distillation process based on carbon foam ring random packing. Chem. Eng. Process. Process. Intensif. 2018, 124, 245–254. [Google Scholar] [CrossRef]
- Billet, R. Packed Towers; VCH Verlagsgesellschaft mbH: Weinheim, Germany, 1995. [Google Scholar]
- Maćkowiak, J. Fluid Dynamics of Packed Columns; Springer: Berlin/Heidelberg, Germany,, 2010. [Google Scholar]
- Arthus, L.; Angeli, A.P.; Wolf Maciel, M.R.; Fregolente, L.V. Optimized continuous flow water removal from biodiesel and diesel (B15) using Raschig ring-shaped polyacrylamide/cellulose microfibrils hydrogels in fixed-bed columns. Fuel 2026, 404, 136332. [Google Scholar] [CrossRef]
- Wu, Z.; Guo, Z.; Yang, J.; Wang, Q. Numerical investigation of methane steam reforming in packed bed reactor with internal helical heat fins. Energy 2023, 278, 127988. [Google Scholar] [CrossRef]
- Jurtz, N.; Flaischlen, S.; Scherf, S.C.; Kraume, M.; Wehinger, G.D. Enhancing the Thermal Performance of Slender Packed Beds through Internal Heat Fins. Processes 2020, 8, 1528. [Google Scholar] [CrossRef]
- Xu, Y.H.; Xu, H.Z.; Li, Y.B.; Chu, G.W.; Chen, J.F. Mitigating gas maldistribution in a cross-flow rotating packed bed via optimizing guide baffle structures. Chem. Eng. Process.-Process. Intensif. 2025, 213, 110317. [Google Scholar] [CrossRef]
- Bang, Y.M.; Cho, C.P.; Jung, Y.; Park, S.R.; Kim, J.G.; Park, S. Thermal and flow characteristics of a cylindrical superheated steam generator with helical fins. Energy 2023, 267, 126599. [Google Scholar] [CrossRef]
- Pidaparthi, B.; Missoum, S.; Xu, B.; Li, P. Helical Fins for Concentrated Solar Receivers: Design Optimization and Entropy Analysis. J. Energy Resour. Technol. 2023, 145, 121706. [Google Scholar] [CrossRef]
- Zaboli, M.; Mousavi Ajarostaghi, S.S.; Saedodin, S.; Kiani, B. Hybrid nanofluid flow and heat transfer in a parabolic trough solar collector with inner helical axial fins as turbulator. Eur. Phys. J. Plus 2021, 136, 841. [Google Scholar] [CrossRef]
- Amini, R.; Amini, M.; Jafarinia, A.; Kashfi, M. Numerical investigation on effects of using segmented and helical tube fins on thermal performance and efficiency of a shell and tube heat exchanger. Appl. Therm. Eng. 2018, 138, 750–760. [Google Scholar] [CrossRef]
- Zhang, L.; Du, W.; Wu, J.; Li, Y.; Xing, Y. Fluid flow characteristics for shell side of double-pipe heat exchanger with helical fins and pin fins. Exp. Therm. Fluid Sci. 2012, 36, 30–43. [Google Scholar] [CrossRef]
- Sivalakshmi, S.; Raja, M.; Gowtham, G. Effect of helical fins on the performance of a double pipe heat exchanger. Mater. Today Proc. 2021, 43, 1128–1131. [Google Scholar] [CrossRef]
- Marek, M. Numerical modelling of gas flow in a random packed bed with a helical flow deflector. J. Phys. Conf. Ser. 2024, 2899, 012007. [Google Scholar] [CrossRef]
- Marek, M. Numerical generation of a fixed bed structure. Chem. Process. Eng. 2013, 34, 347–359. [Google Scholar] [CrossRef]
- Chorin, A.J. Numerical solution of the Navier-Stokes equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Marek, M. Numerical simulation of a gas flow in a real geometry of random packed bed of Raschig rings. Chem. Eng. Sci. 2017, 161, 382–393. [Google Scholar] [CrossRef]
- Marek, M. Gas flow maldistribution in random packed beds of non-spherical particles–A CFD study. Chem. Eng. Sci. 2019, 197, 296–305. [Google Scholar] [CrossRef]
- Niegodajew, P.; Durajski, A.P.; Rajca, P.; Gruszka, K.M.; Marek, M. Experimental and numerical study on the orientation distribution of cylindrical particles in random packed beds. Chem. Eng. J. 2022, 432, 134043. [Google Scholar] [CrossRef]
- Suekane, T.; Yokouchi, Y.; Hirai, S. Inertial Flow Structures in a Simple-Packed Bed of Spheres. AIChE J. 2003, 49, 10–17. [Google Scholar] [CrossRef]
- Jaworski, T.; Wajda, A.; Kus, L. Model of Residence Time Distribution, Degree of Mixing and Degree of Dispersion in the Biomass Transport Process on Various Grate Systems. Energies 2023, 16, 5672. [Google Scholar] [CrossRef]
- Marek, M.; Aniszewski, W.; Boguslawski, A. Simplified Volume of Fluid Method (SOF) for two-phase flows. TASK Q. 2008, 12, 255–265. [Google Scholar]
- Fogler, H.S. Elements of Chemical Reaction Engineering, 5th ed.; Prentice Hall: Boston, MA, USA, 2016. [Google Scholar]
- Yang, N.; Xiao, Z.; Liu, H.; Jiang, J.; Liu, F.; Yang, X.; Wang, R. Effect of annulus ratio on the residence time distribution and Péclet number in micro/milli-scale reactors. Can. J. Chem. Eng. 2025, 103, 899–913. [Google Scholar] [CrossRef]
- Gorman, J.M.; Zheng, A.; Sparrow, E.M. Bounding wall effects on fluid flow and pressure drop through packed beds of spheres. Chem. Eng. J. 2019, 373, 519–530. [Google Scholar] [CrossRef]
- von Seckendorff, J.; Achterhold, K.; Pfeiffer, F.; Fischer, R.; Hinrichsen, O. Experimental and numerical analysis of void structure in random packed beds of spheres. Powder Technol. 2021, 380, 613–628. [Google Scholar] [CrossRef]
- Ergun, S. Fluid Flow Through Packed Columns. Chem. Eng. Prog. 1952, 48, 89–92. [Google Scholar]
- Carman, P.C. Fluid flow through granular beds. Trans.-Inst. Chem. Eng. 1937, 15, 150–166. [Google Scholar] [CrossRef]
- Epstein, N. On tortuosity and the tortuosity factor in flow and diffusion through porous media. Chem. Eng. Sci. 1989, 44, 777–779. [Google Scholar] [CrossRef]
- Pisani, L. Simple Expression for the Tortuosity of Porous Media. Transp. Porous Med. 2011, 88, 193–203. [Google Scholar] [CrossRef]
- Duda, A.; Koza, Z.; Matyka, M. Hydraulic tortuosity in arbitrary porous media flow. Phys. Rev. E 2011, 84, 036319. [Google Scholar] [CrossRef] [PubMed]



| Case | Velocity Ratio | Structure Factor | Tortuosity | Reynolds Number |
|---|---|---|---|---|
| no deflector | 2.83 | 0.353 | 1.20 | 38 |
| 3.74 | 0.268 | 1.58 | 51 | |
| 4.90 | 0.204 | 2.08 | 66 | |
| 9.75 | 0.103 | 4.12 | 132 |
| Case | Expected Value | Standard Deviation | Expected Value Gain | Standard Deviation Gain |
|---|---|---|---|---|
| no deflector | 1.42 | 0.42 | – | – |
| 1.86 | 0.74 | 1.3 | 1.8 | |
| 2.39 | 0.83 | 1.7 | 2.0 | |
| 4.44 | 1.30 | 3.1 | 3.1 |
| Case | Inlet Velocity | Skewness | Péclet Number |
|---|---|---|---|
| [m/s] | |||
| no deflector | 0.0177 | 1.43 | 22.7 |
| 0.0134 | 2.23 | 12.3 | |
| 0.0102 | 1.63 | 16.3 | |
| 0.0051 | 0.38 | 23.1 |
| Case | Pressure Drop | Pressure Drop Ratio |
|---|---|---|
| [mPa] | ||
| no deflector | 169 | – |
| 296 | 1.8 | |
| 397 | 2.3 | |
| 729 | 4.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marek, M. Increasing Residence Time in Random Packed Beds of Spheres with a Helical Flow Deflector. Processes 2025, 13, 2828. https://doi.org/10.3390/pr13092828
Marek M. Increasing Residence Time in Random Packed Beds of Spheres with a Helical Flow Deflector. Processes. 2025; 13(9):2828. https://doi.org/10.3390/pr13092828
Chicago/Turabian StyleMarek, Maciej. 2025. "Increasing Residence Time in Random Packed Beds of Spheres with a Helical Flow Deflector" Processes 13, no. 9: 2828. https://doi.org/10.3390/pr13092828
APA StyleMarek, M. (2025). Increasing Residence Time in Random Packed Beds of Spheres with a Helical Flow Deflector. Processes, 13(9), 2828. https://doi.org/10.3390/pr13092828







