1. Introduction
Direct Air Capture (DAC) is a promising carbon dioxide removal (CDR) technology that enables extraction of CO
2 directly from ambient air. The captured CO
2 can be concentrated for sequestration or utilized as feedstock to produce valuable products via green hydrogenation [
1,
2,
3,
4]. Among DAC approaches, Temperature–Vacuum Swing Adsorption (TVSA) using amine-functionalized solid sorbents is particularly attractive due to its high capture efficiency at low CO
2 concentrations [
5,
6,
7]. However, detailed modeling of TVSA-based DAC processes using classical numerical methods is computationally expensive. This high computational cost limits their direct integration into optimization frameworks, thus hindering practical DAC process design and optimization [
8,
9,
10].
To address this challenge, machine-learning-based surrogate models offer a promising alternative by approximating the behavior of computationally expensive numerical simulations with orders-of-magnitude-lower inference times [
11,
12]. The goal of this study is to assess which surrogate modeling method is best suited to describe the adsorption step of the DAC-TVSA process. This is a crucial first step towards developing a complete surrogate model that can replace expensive numerical simulations in optimization frameworks, enabling more efficient DAC process design and control.
Previous attempts to apply artificial neural networks (ANNs) in DAC focused mainly on solvent and sorbent discovery, screening, and design [
13,
14]. However, only a few studies have explored the combination of AI with DAC process modeling. Sipocz et al. [
15] first proposed a purely data-driven surrogate model using ANN for a complete MEA-based capture plant CO
2. More recently, Leperi et al. [
11] proposed a more detailed PSA surrogate model using data-driven ANN, where different multiple ANNs were used to predict state variables in specific bed locations or to predict outlet bed conditions. Young et al. [
16] successfully applied a data-driven ANN surrogate model to perform a detailed global sensitivity analysis of the TVSA process for DAC, which would have required years of computations with traditional numerical methods.
To the best of our knowledge, no previous study has integrated physics-informed neural networks (PINNs) with data-driven models to predict the spatio-temporal evolution of internal states in a DAC-TVSA adsorber. Such integration could significantly reduce training data requirements and enhance prediction accuracy and model generalization.
In this work, we compare two machine learning approaches: traditional data-driven neural networks (data-NNs) and hybrid-physics-informed neural networks (hybrid-PINNs). While standard NNs rely purely on labeled data, hybrid-PINNs incorporate governing physics equations as constraints during training alongside labeled data, potentially reducing the reliance on large datasets and improving model generalization in data-scarce conditions. The study systematically evaluates the performance of these models across different data availability regimes, including extremely low-data conditions, where a curriculum learning strategy is employed to improve model convergence.
The findings serve as a foundation for the development of a full surrogate model, which will replace expensive DAC process steps within an optimization framework, making TVSA-based DAC optimization more computationally efficient.
2. Machine Learning Models
We considered different machine learning techniques to assess their potential as surrogate models to approximate the axial concentration and temperature profiles during the adsorption step for fixed-bed Direct Air Capture: neural networks (NNs) and physics-informed neural networks (PINNs).
2.1. Artificial Neural Networks and PINNs
2.1.1. Feed-Forward Neural Networks
The concept of a neural network emerged in 1943 when Warren McCulloch and Walter Pitts proposed a mathematical model of how neurons work [
17]. This model provided the foundation for understanding computation through interconnected processing units. In 1958, Frank Rosenblatt extended this idea with the development of the single-layer perceptron [
18], which became the simplest form of a neural network (NN) and laid the foundations for modern feed-forward neural networks.
At its core, a neural network is a powerful tool able to approximate complex functions. This remarkable feature is supported by the Universal Approximation Theorem [
19], which states that a sufficiently large neural network, with at least one hidden layer and non-linear activation functions, can approximate any continuous function on a closed interval to any desired level of accuracy.
In general, given a neural network (NN) with
L layers, the resulting approximated function
can be formalized as the composition of
L functions
, such that
where each function
represents a layer of the network,
is the input to the network, and
is the set of parameters (weights and biases) of all layers.
Among the various neural network architectures, the feed-forward neural network (FFNN), also called the multi-layer perceptron (MLP), is one of the most well-known and extensively studied types. The name “feed-forward” reflects its structure: information flows in a single direction from the input layer to the output layer without any feedback loops [
20]. A FFNN consists of multiple layers of interconnected neurons, where each layer performs a linear transformation of the input (via weights and biases) followed by a nonlinear transformation using an activation function. This process enables the network to capture complex patterns in the data.
2.1.2. Physics-Informed Neural Networks
Physics-informed neural networks (PINNs) are a class of neural networks that incorporate physical laws into their training process. PINNs represent an intersection between numerical methods and data-driven machine learning. In fact, numerical methods have been the go-to method for solving systems of partial differential equations by discretizing space and time, often with finite-element, finite-difference or finite-volume methods. Contrary to the mesh-dependent numerical methods, a PINN aims to learn a continuous, mesh-free, solution to the partial differential equations by training a NN. When the PINN is trained, it should satisfy both data (either experimental or numerically obtained) and the governing physical laws. This is achieved by adding a physics-informed loss term to the standard loss function, which enforces the network to satisfy the governing equations of the system, by embedding partial differential equations into the network’s training objective. The most common PINN is a variation on the traditional NN, first introduced by Raissi, M. [
21], in 2019 as a novel method to solve forward and inverse problems involving nonlinear partial differential equations. PINNs have been shown to be particularly effective in solving partial differential equations (PDEs) and other physics-based problems, where the underlying equations are known but difficult to solve analytically or numerically [
22]. PINNs are also particularly useful for solving problems where the amount of data is scarce but the physical laws of the modeled system are well understood.
The mathematical framework of a PINN builds on the traditional NN but introduces physical constraints through additional terms in the loss function. Following the original formalism of Toscano et al. (2025), given a general differential operator
associated with the general boundary condition operator
, both parametrized by
, a general PDE system can be written as
where
is the solution of the PDE in the domain
and its boundary
,
x refers to the spatial–temporal coordinates, and
and
are source terms. Following what was illustrated in the previous section, from Equation (
1), a neural network can be used to approximate the solution
as follows [
23]:
The physics contribution is embedded in the network directly in the loss term
. Thanks to automatic differentiation [
24], the residuals of Equation (
2) can be easily computed during the network training. In fact, given a set of input-training points
and
of sizes
and
, respectively, the physics loss terms can be defined using the residuals of Equation (
2):
where
and
are the designated sets of points where the residuals of the partial differential equations are evaluated, called “collocation points”. The total physics loss is then computed by a direct summing of the two terms or linearly combining them with specified weights. In this way, the PINN is forced to adhere to the governing equations of the system by minimizing the MSE of PDEs residuals, computed using the approximated solution given by the network.
3. Building the PINN-DAC Model
The Direct Air Capture process considered in this work is the adsorption-based technology using solid amine sorbents. A packed bed adsorber designed for DAC is filled with spherical particles with uniform diameter (
) that selectively absorb
. Due to the wide availability of data in the literature, the reference sorbent used in this work is LEWATIT
® VPOC 1065, supplied by LANXESS GmbH, Cologne, Germany [
25]. This sorbent is also considered the benchmark amine-functionalized sorbent for DAC applications due to its commercial availability and its high CO
2 capture capacity at concentrations corresponding to the ppm levels found in ambient air. However, H
2O co-adsorption kinetics and thermodynamics are still not fully understood, and much effort is currently being put into the development of a unified description of the CO
2-H
2O co-adsorption process [
5,
26,
27]. Therefore, the exemplary case study considered in this work will be the non-isothermal dry adsorption of CO
2.
3.1. Problem Statement and Governing Equations
The packed column is fed with a simple gas mixture under ambient conditions, consisting of nitrogen N2 and CO2. The particles do not adsorb N2 and have a finite loading capacity for CO2. The exothermic nature of the adsorption process raises the column temperature during CO2 capture, causing spatial and temporal changes in equilibrium concentration. Initially, at time , an inert gas flows through the adsorption column. At time , CO2 containing the gas mixture is introduced into the column. The following assumptions are made when modeling this system:
The ideal gas law applies;
The system is under constant pressure;
The flow is described by an axially dispersed plug-flow regime;
Gradients in the radial direction are neglected;
The densities, specific heat capacities, thermal conductivities, and axial gas dispersion coefficients are temperature-independent and constant throughout the reactor;
Instantaneous thermal equilibrium is established between the fluid and solid phase;
The gas velocity is constant and equal to the inlet velocity;
The adsorption is limited by internal mass transfer described by the Linear Driving Force approximation (LDF).
Under these assumptions, the CO
2 mass balance can be described by the following PDEs:
where
is the interstitial gas velocity,
is the axial dispersion coefficient,
is the bed porosity,
is the particle density, and
is the mass transfer coefficient from the Linear Driving Force approximation [
28,
29]. The main variables are the gas and solid phase concentrations
c [
] and
q [
], respectively.
The solid equilibrium concentration
is modeled using the non-isothermal Toth isotherm [
30], thanks to its strong resemblance to experimental data [
26,
31,
32]:
The overall energy balance is added considering a negligible gas and adsorbed-phase heat capacity contribution and dominant heat effects due to adsorption:
where
is the heat capacity of the solid,
is the total fluid concentration,
is the heat capacity of the fluid,
is the effective axial thermal conductivity, and
is the adsorption heat. A list of all the parameters used can be found in
Table 1.
Table 1.
Simulation parameters for the Direct Air Capture system.
Table 1.
Simulation parameters for the Direct Air Capture system.
| Variable | Definition | Value | Unit |
|---|
| L | Length of packed bed | 0.1 | m |
| R | Radius of packed bed | 0.001 | m |
| Inlet interstitial gas velocity | 0.1 | m |
| Packed bed porosity | 0.5 | - |
| Particle density [31] | 744 | kg |
| Axial dispersion coefficient | | |
| Feed temperature | 318.15 | K |
| Molar fraction of in feed | 500 | ppm |
| Total pressure | 101,325 | Pa |
| Specific heat capacity particle [31] | 1396 | J |
| Effective axial thermal conductivity | 0.22 | W |
| Heat of adsorption [31] | −70.125 | kJ |
| Linear Driving Force coefficient | 0.005 | |
| Total simulation time | 20,000 | s |
3.1.1. Normalization
The governing equations will be expressed in their non-dimensional form to preserve the generality of the system and facilitate comparisons across different scales. The chosen sets of reference variables will scale both the input and output of the network between zero and one to enhance the learning efficiency and convergence of the neural network.
This normalization minimizes the risk of vanishing or exploding gradients, which are common issues in deep learning models when dealing with variables of vastly different magnitudes [
33].
3.1.2. Boundary Conditions
A Danckwerts boundary condition is applied at the left boundary, while a Neumann boundary condition is used at the right boundary:
along with the non-dimensional initial conditions:
3.2. Data-NN and Hybrid-PINN
To evaluate the neural network approach for constructing a surrogate model, we tested both a data-driven neural network (data-NN) and a hybrid physics-informed neural network (hybrid-PINN).
The data-NN approach focuses solely on minimizing a data-driven loss function, denoted as
, which represents the discrepancy between the solution obtained with the network and the solution obtained by solving Equations (
12)–(
21) via a finite-differences method (FDM). The FDM simulations used for training and validation were derived from a simplified version of a more comprehensive numerical model, which has been validated against independent experimental data from Young et al. (2021) [
26], thereby providing confidence in the physical fidelity of the reference simulations. A summary of this validation is reported in
Appendix A and
Appendix B.
In contrast, the hybrid-PINN combines data-driven learning with physics-based constraints. In this framework, the total loss function
is a combination of two components: the data-driven loss
and the physics-informed loss
. The total composite loss function can be expressed as
where
are weights factor that balances the contribution of the data and physics loss terms. By tuning these parameters, one can adjust the network’s emphasis on fitting the data versus satisfying the physical constraints during training.
The physics loss function, composed of the residuals from the partial differential equations, boundary, and initial condition, is defined as follows:
where
,
, and
represent the residuals associated with the boundary conditions, initial conditions, and PDEs, respectively, evaluated at collocation point
j.
In the specific case of the DAC-PINN investigated in this work, the total loss function was composed of 11 individual loss components:
Three PDE residuals for each field: gaseous CO2, adsorbed CO2, and temperature.
Three initial condition residuals for each field like above.
Four boundary condition residuals: two spatial boundaries for the gas-phase equation and two for the temperature equation.
One data loss component: penalizing the deviation from available data points.
The development of a hybrid-PINN approach, rather than a pure PINN approach
, is motivated by preliminary tests showing that employing a PINN network exclusively tends to converge to trivial solutions that satisfy the PDE system but do not capture the desired physical behavior, as also found in Wu et al. [
34]. Hybrid-PINN modeling provides additional advantages in addressing the challenges posed by standard PINNs, which often struggle to accurately approximate sharp fronts and regions with large gradients [
35,
36].
The FDM simulation provided a uniform distribution of data in the
domain, with resolution provided by time step
s and grid size
. From the data points obtained through the FDM simulation, only a subset was selected for training the models, aiming to balance prediction accuracy and computational cost. Since the optimal balance was not known a priori, a study was conducted to assess the capability of PINNs to enhance prediction accuracy as a function of data availability. The subset was obtained by a uniform random sampling using the NumPy
random module [
37]. Then, the sampled subset was further split into 70% for training and 30% for testing using the scikit-learn
model_selection module [
38]. Model validation was performed exclusively against data from the FDM simulation, which was considered the ground truth.
3.3. Network Construction
The results of the hyperparameters tuning are summarized in
Table 2. A brief discussion on the training routine will be presented, while details regarding other hyperparameters will be excluded for brevity.
3.4. Initial Setup
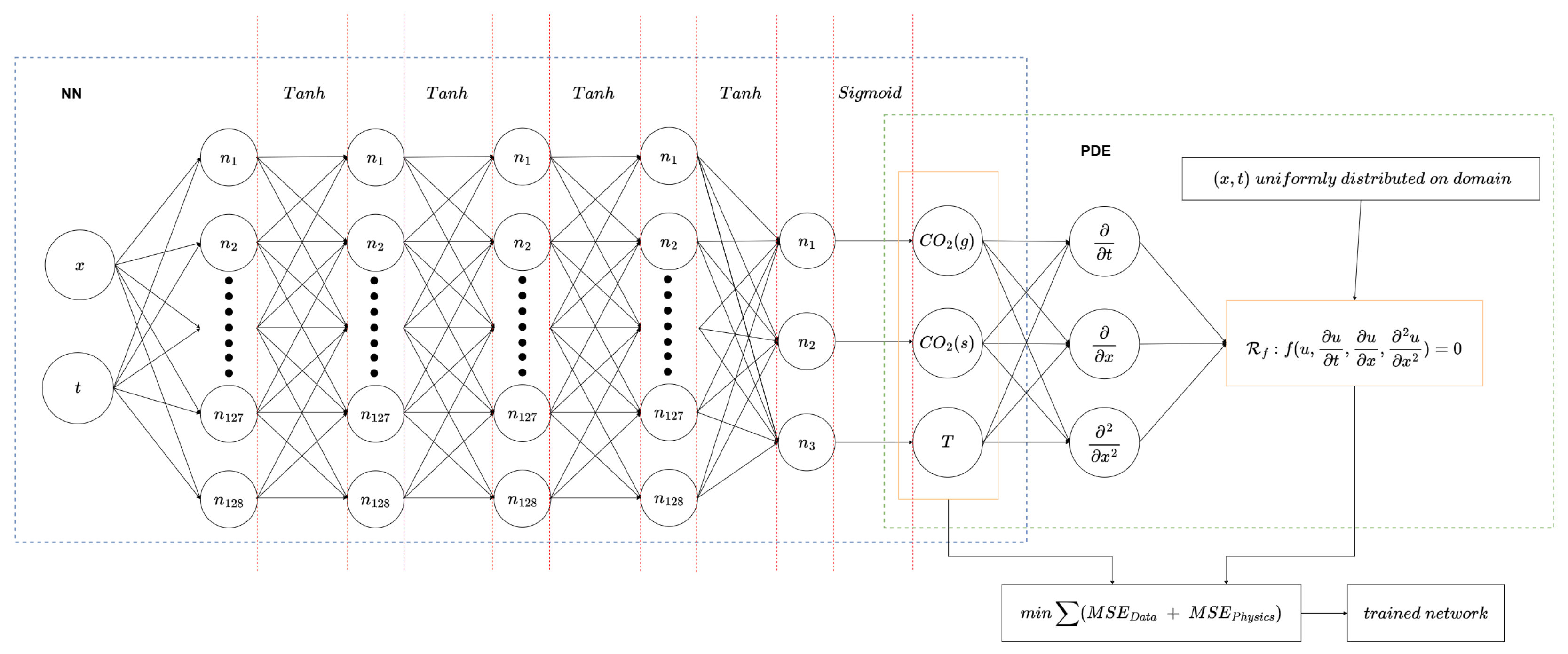
The neural network architecture consists of a total of five layers: one input layer, three hidden layers, and one output layer. The input layer accepts the spatial and temporal coordinates as input features, while the output layer predicts the fields of gaseous and adsorbed CO
2, along with the corresponding temperature field. Each hidden layer comprises 96 neurons, with
tanh activation functions to capture the smooth and non-linear features of the PDEs system, while a
sigmoid activation function is applied to the output layer to ensure that the predicted fields are constrained between 0 and 1, reflecting the physical bounds of the problem. A visual representation of the network architecture can be found in
Figure 1.
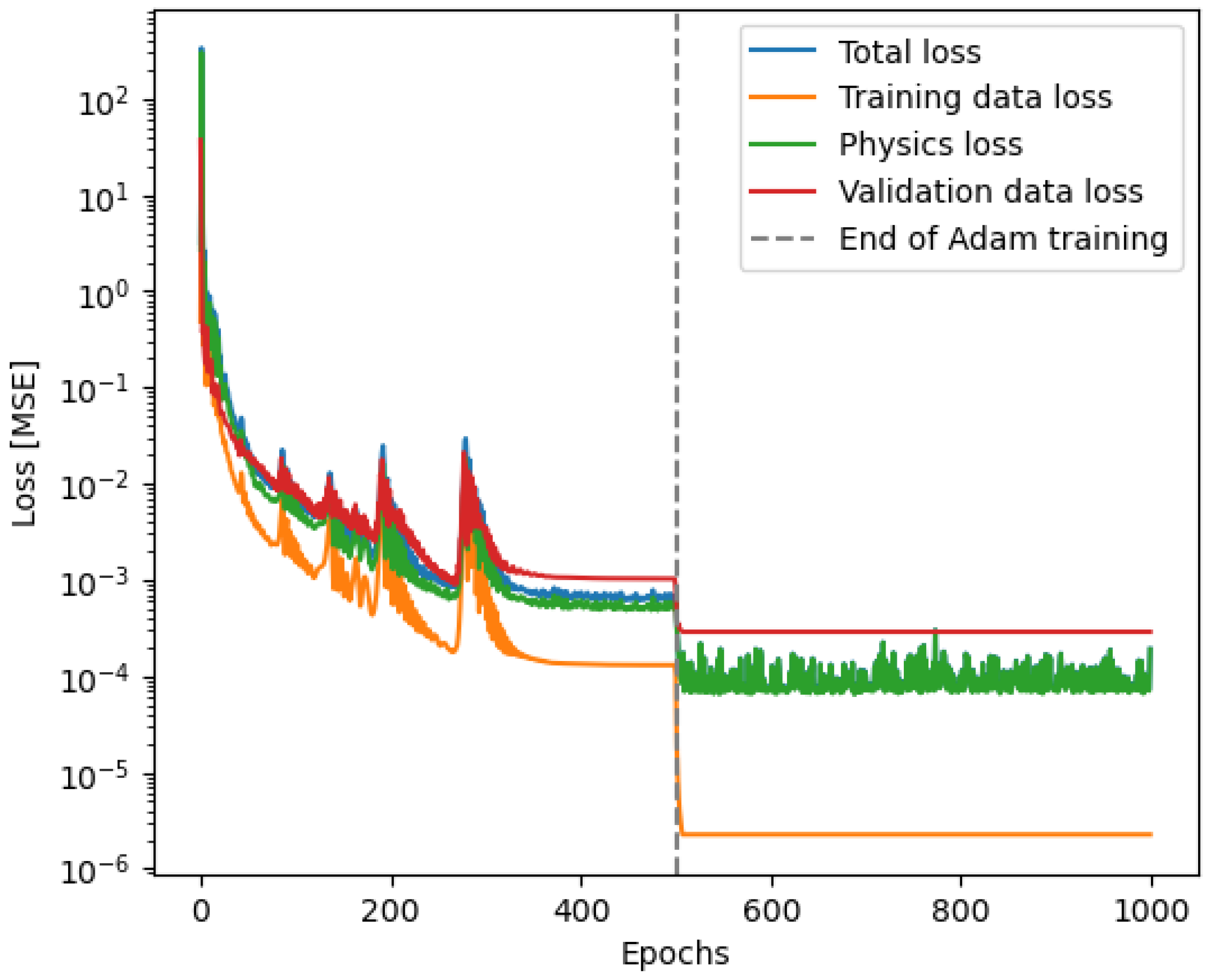
The networks were initially trained using the ADAM optimizer with an initial learning rate of
. A learning rate scheduler was employed to reduce the learning rate by a factor of 2 after 50 epochs without improvement in the validation loss. Training was subject to a maximum number of epochs; however, an early stopping criterion was also implemented to terminate training when the validation loss plateaued. Following this initial training phase, the best-performing model (based on validation loss) was further refined using the L-BFGS optimizer with a learning rate of
. This secondary optimization step aimed to locate a better minimum in the loss landscape, leveraging the L-BFGS algorithm’s quasi-Newton approach to fine-tune the solution near the local minimum found by ADAM. A visual representation of an exemplary test can be found in
Figure 2.
Specifically, the entire work was conducted in Python (version 3.12.9), using PyTorch (version 2.6.0+cu126) [
39] as the primary deep learning framework. All simulations and training were performed on a workstation equipped with an NVIDIA GeForce RTX 4060 Ti GPU (NVIDIA Corporation, Santa Clara, CA, USA) (16 GB memory, CUDA version 12.4, driver version 550.142).
3.4.1. Direct Warm-Start and Curriculum Learning
To enhance the training process of the hybrid-PINN, the knowledge acquired from the data-only training phase was exploited through a warm-start initialization. Specifically, this procedure involved initializing the weights and biases of the hybrid-PINN using those obtained from the data-only model. This approach allowed the hybrid-PINN to start from an already partially trained state, accelerating convergence and improving training stability.
However, this method proved ineffective in cases where the amount of data was significantly scarce. Under such conditions, the hybrid-PINN struggled to converge to a stable solution due to the complexity and strong nonlinearity of the problem. To address this limitation, a tailored approach based on curriculum learning was developed and tested.
Curriculum learning involves gradually increasing the complexity of the training process [
40,
41]. In this work, the curriculum strategy was implemented by progressively introducing the physics-based loss components into the training procedure. Specifically, after the data-only warm-start initialization, the network was first trained using only the initial conditions to anchor the solution at
. Next, the governing PDE residuals were introduced sequentially in a logical order reflecting the underlying physics of the system:
Gas-phase transport equation: The gas phase serves as the primary carrier of the system’s dynamics, driving mass and energy transfer.
Adsorbed-phase mass balance equation: Adsorption depends on the gas-phase transport as the solid uptake is a consequence of gas–solid interactions.
Energy (temperature) equation: The heat release or uptake is driven by adsorption phenomena, making it the last equation to be introduced.
The ordering was chosen to reflect the physical causality of the system: Gas transport drives adsorption, and adsorption drives the thermal response. While heuristic in nature, this hierarchy provides a logical structure for introducing physics constraints.
Finally, the left and right boundary conditions were enforced to refine the solution and ensure consistency across the domain.
3.4.2. Dynamic Weight Scaling: Self-Adaptation and EMA
Effective and efficient training of PINNs still face many challenges, such as the imbalance in the gradient sizes of the different loss components [
42]. This problem occurs when the magnitude of a single loss term in the composite loss function dominates the others. If this happens, the network may only focus on minimizing these larger loss terms, ignoring smaller ones. This can lead to unbalanced training, where some parts of the model do not learn as effectively, making the training process less efficient, especially in the DAC-PINN case where 11 losses need to be balanced (see
Section 3.2). A potential solution to this problem is the introduction of dynamic weighting during the PINN training. Dynamic weighting has shown promising results, with several studies on the subject published in recent years [
43,
44,
45].
During training, we dynamically adjusted the weighting between the data loss and the physics-based loss at each epoch. This was achieved through a combination of Exponential Moving Average (EMA) tracking of the loss values and a Softmax-based normalization scheme. The EMA estimate of the losses was updated as follows:
where the index
j refers to physics and data loss, while
is the smoothing parameter controlling the contribution of the current loss to the moving average. The EMA values are normalized relative to their sum to prevent the losses scale imbalance.
Finally, the weighting coefficients
and
are computed using a Softmax transformation with temperature parameter
:
A visualization of dynamic scaling is shown in
Figure 3.
For the 10 individual physics loss contributions, we employed a self-adaptive physics weights scaling strategy to dynamically balance the different loss components during the training process. Specifically, we introduced learnable logarithmic weights , initialized to zero, for each individual loss term (e.g., PDE residuals, boundary conditions, and initial conditions). The final weights are computed as ensuring positivity and enabling the optimizer to automatically adjust the relative importance of the different terms. The weights are treated as trainable parameters and optimized jointly with the neural network parameters using the ADAM optimizer. Additionally, before applying the weights, each loss component is pre-normalized by a baseline factor to mitigate scale discrepancies across different physical constraints. This approach prevents the dominance of a single loss component and enhances the training stability.
However, applying Dynamic Weight Scaling (DWS) at every epoch during the second-order L-BFGS optimization can interfere with the optimization process. L-BFGS relies on maintaining a history of gradient and step evaluations to approximate the curvature of the loss landscape and guide updates. When the loss weights are dynamically adjusted across epochs, the underlying loss surface is effectively changed, invalidating the gradient history and potentially disrupting the curvature approximation. This can degrade both convergence stability and overall performance.
Nonetheless, empirical tests indicated that properly balancing the loss terms significantly improves model accuracy. Based on these insights, we adopted a hybrid strategy: we applied DWS only once prior to initializing L-BFGS. This pre-scaling step provided a set of static, optimized loss weights, which were then held constant during the L-BFGS training phase. This approach ensured that the loss landscape remained smooth and consistent during L-BFGS while still leveraging the benefits of loss balancing obtained through DWS.
3.4.3. Error Metrics
To assess the predictive performance of our models, we employ the Percentage L1 Relative Error (%L1RE), which provides a normalized measure of the discrepancy between predicted and reference data, enabling error comparisons of the internal profiles across different species.
The Percentage L1 Relative Error (%L1RE) is defined as
where
and
denote the predicted and true values at index
i, respectively. %L1RE is preferred as it preserves the scale of the error without disproportionately emphasizing large deviations. This is particularly important when dealing with localized phenomena or sparse regions of high error, where alternative metrics could amplify the impact of a few large discrepancies and obscure the overall accuracy.
4. Results
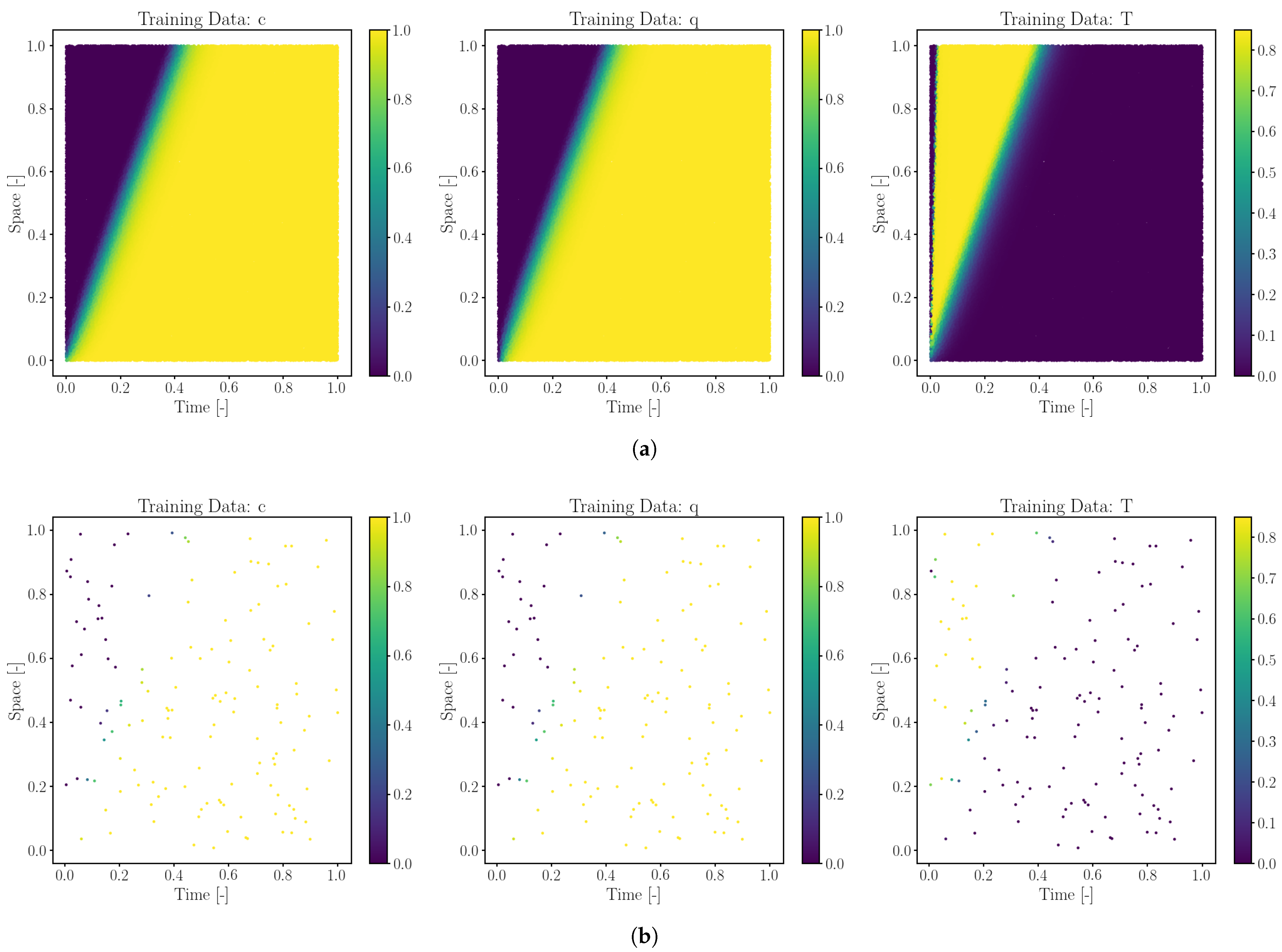
One of the primary objectives of using hybrid-PINNs over traditional neural networks is to reduce the reliance on large datasets, which can be costly and time-consuming to obtain. To evaluate this capability, data-NN and hybrid-PINN were evaluated in four different sets of training points (labeled data) constructed from the results of the numerical simulation, given in
Table 3. These datasets span multiple orders of magnitude, allowing an evaluation of how the model scales with increasing or decreasing labeled data availability. A representative visual representation can be found in
Figure 4.
A summary of the main findings across these regimes is shown in
Figure 5, where the L1 Relative Error (%L1RE) is plotted as a function of the training dataset size. This analysis highlights the trade-off between purely data-driven neural networks and the hybrid-PINN approach. While both methods achieve high accuracy in the large data regime (1%), the performance of the data-driven model deteriorates as labeled data becomes scarce, particularly in the intermediate and low-data regimes. In contrast, the hybrid-PINN effectively leverages physics constraints to maintain predictive accuracy, demonstrating its robustness even when only a minimal fraction (0.001%) of labeled data is available.
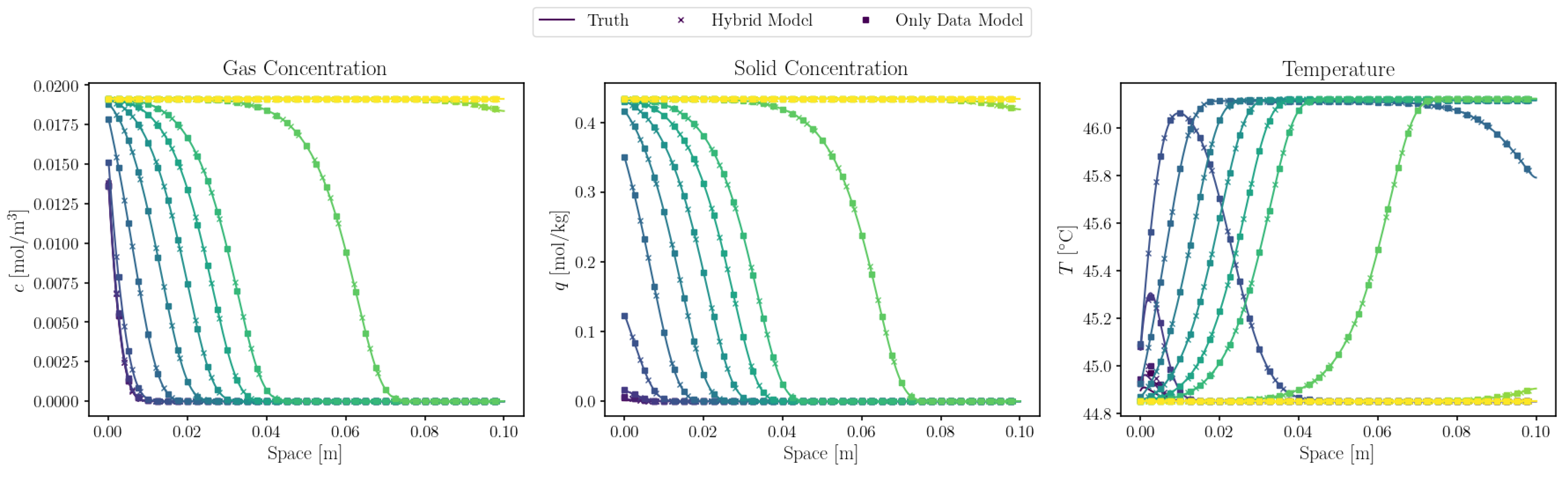
4.1. Large and Intermediate Data Regime
In the large data regime (1% of the total training points), both the purely data-driven neural network and the warmstart-hybrid-PINN achieved very low errors, as illustrated in
Figure 6. The data-driven model alone, having access to a sufficiently large subset of labeled points, manages to learn the system’s behavior with high fidelity. Consequently, the hybrid-PINN approach does not exhibit significant improvements. In scenarios where labeled data is plentiful, the incorporation of physical constraints yields minimal additional benefit as the learning process is already robustly underpinned by the available data.
More interesting differences emerge in the intermediate data regime (0.1% and 0.01% of training points). Here, the data-driven model alone begins to lose accuracy, particularly for the temperature and the solid concentration fields. The warmstart-hybrid-PINN, however, makes better use of limited labeled data by leveraging physics constraints to regularize and guide the solution. As demonstrated in
Figure 7, improvements are visible, especially in the solid-phase concentration and temperature profiles.
4.2. Low-Data Regime: Curriculum Learning
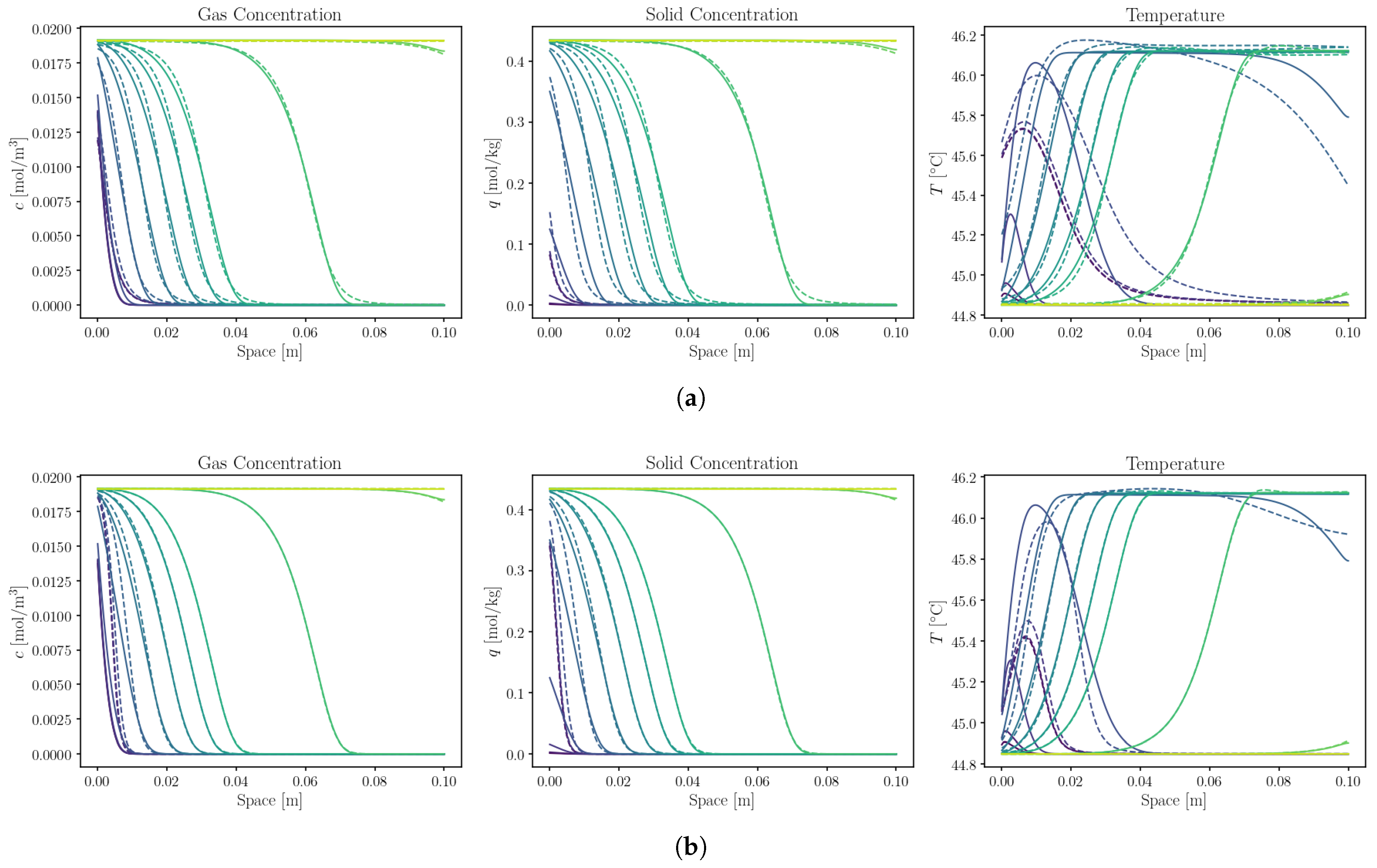
In the low-data regime (below 0.01% of training points),
Figure 5 shows that the warmstart-hybrid-PINN maintains lower L1RE values than the purely data-driven model, mirroring the trend seen at higher data levels. Nevertheless,
Figure 8 indicates that at
0.001% of the training points (roughly 140 samples), neither approach achieves qualitatively acceptable internal profiles. The purely data-driven model (
Figure 8a) underfits the ground truth, while the warmstart-hybrid-PINN (
Figure 8b) still struggles to resolve the three coupled PDEs since 140 labeled points remain insufficient to anchor such a complex model, even with the benefit of physics-informed constraints.
To address this persistent challenge in the low-data regime, the
Curriculum Learning strategy was applied to the hybrid-PINN, yielding significantly reduced L1RE and evidently improved internal profiles, as shown in
Figure 9b. The curriculum-hybrid-PINN approach sequentially introduces each element of the physics-informed network by first anchoring the solution to the initial conditions and then refining step-by-step the prediction incorporating the full set of governing equations and boundary conditions.
This phased training allows the model to stabilize its representations before tackling the full complexity of the coupled PDEs. Consequently, even at 0.001% training data, the curriculum-hybrid-PINN exhibits near intermediate data regime accuracy, closing the gap in gas-phase and solid-phase predictions, where the data-driven baseline (
Figure 9a) struggles with large discrepancies from the ground truth.
The reduced accuracy observed in the temperature predictions can be attributed primarily to the distinct dynamics of this field compared to the gas and solid concentrations. While c and q evolve as traveling fronts with relatively smooth, flat wave profiles, the temperature field is characterized by a localized peak that propagates through the bed. This peak-shaped transient is more challenging to approximate as it requires the network to capture the nonlinear interplay between adsorption kinetics, heat release, and thermal transport. Unlike concentrations, which are governed mainly by advection–dispersion dynamics and, therefore, retain a more uniform profile, the temperature reflects the balance of multiple competing effects: the strongly exothermic adsorption source term, thermal diffusion, and heat exchange with the reactor walls.
Moreover, the smoother, lower-gradient regions of the temperature wave provide a weaker training signal for the network compared to the sharper concentration fronts, further complicating the learning task.
Despite these challenges, the exothermic peak and the traveling thermal wave are both captured with sufficient fidelity for process-level analysis. Nonetheless, these results suggest that temperature fields may benefit from dedicated network representations or task-specific weighting in the training process in order to better accommodate their distinct spatial–temporal patterns.
5. Discussion
The comparison between DAC-PINN and a conventional neural network (NN) revealed several key insights. While the traditional NN demonstrated strong predictive performance when trained on full-domain simulations, its limitations became apparent when extrapolating to regions of the system with little or no training data coverage. In contrast, the hybrid-PINN approach consistently provided better generalization particularly in data-sparse regions.
However, these accuracy gains come at a computational cost. As shown in
Figure 10, training a hybrid-PINN requires an order of magnitude more computational time compared to a traditional NN. The exact increase in training time varies depending on the size of the labeled dataset as the enforcement of physics-informed constraints introduces additional optimization complexity. In particular, the overhead is mainly due to the repeated use of automatic differentiation to compute PDE residuals, as well as their evaluation at a large number of collocation points, both of which increase the cost of each back-propagation step relative to a purely data-driven NN. Among the strategies tested, the curriculum-based training was the most computationally demanding, followed by the hybrid-PINN, with the conventional NN being the most efficient.
Despite this, the added cost is primarily a training-time issue, while inference remains as fast as for a standard NN. This makes the approach practically deployable since, once trained, the model can be used for rapid evaluation in process optimization or control tasks without additional overhead. Furthermore, training cost can be mitigated by techniques such as warm-starting from data-only models or adaptive residual sampling, improving efficiency while retaining the generalization benefits of the hybrid-PINN framework.
Although PINNs have a lot of potential, their current technological state does not yet allow them to compete with traditional high-performance numerical solvers [
46]. Despite these advantages, the overall performance of PINNs often falls short compared to well-established numerical methods. Additionally, most studies on PINNs for simulations without an analytical solution depend on numerical results as truth data for training the network, highlighting the scientific community’s confidence in these mature and thoroughly tested numerical methods. Moreover, the validation in this work relies solely on finite-difference simulations, without direct comparison to experimental data. While this approach is sufficient to demonstrate the capability of the proposed framework under controlled conditions and to isolate numerical effects, it does not yet establish predictive accuracy for physical systems. Future work will, therefore, involve experimental benchmarking, which will be essential to fully assess the applicability of the method to real-world DAC processes.
Nevertheless, several advantages exist in using PINNs over traditional numerical solvers. PINNs can approximate a function across the entire domain, offering a meshless solution. This enables accurate solutions at any point within the domain, without the need to extrapolate between cells and faces. Moreover, once trained,
DAC-PINN can predict concentrations and temperatures at any spatial or temporal point almost instantly, enabling rapid process simulations and optimization. In the context of DAC, such surrogate models can be used to efficiently generate CAPEX–OPEX Pareto fronts in combination with fast sorbent performance evaluations, supporting comprehensive techno-economic evaluations of process configurations [
47,
48]. This approach allows for potential integration, within defined limits and boundaries, into other simulation softwares as a fast alternative to repeatedly solving systems of equations with numerical methods.
The strong performance of this surrogate model suggests that the development of a digital twin for DAC systems with various input parameters using PINNs is a realistic concept, with a multi-input PINN model being currently under development.
6. Conclusions
Overall, our results confirm that hybrid-PINN offer a robust alternative to purely data-driven neural networks when the labeled dataset is limited. While both approaches perform well in the large-data regime (1%), physics constraints add little beyond what abundant data already provides. However, as labeled data availability diminishes (0.1–0.001%), incorporating physics-informed elements becomes increasingly beneficial: hybrid-PINN retains lower error and capture essential dynamics more faithfully. In the extreme low-data regime (0.001%), a curriculum learning strategy was shown to further reduce prediction error by introducing PDE constraints in stages, thereby mitigating model underfitting. Though temperature predictions remain less precise due to small thermal gradients, these discrepancies are minor compared to the overall improvements in gas and solid-phase predictions. Hence, for complex, multi-physics problems under data scarcity, hybrid-PINNs with a curriculum-based approach provide a significant advantage over purely data-driven models.
The modeling of a DAC system using PINNs represents an innovative approach. While significant progress has been made in this field, much of the knowledge is relatively recent, suggesting that this technology will require time to fully mature. One of the key challenges lies in modeling processes involving domains with rapid gradient changes, a difficulty widely acknowledged within the scientific machine learning community. The construction of a digital twin of a CO
2 adsorption system using PINNs is feasible, but the presence of sharp gradients in the domain requires the use of labeled data points to achieve accurate predictions. Notably, this reliance on labeled data is consistent with other adsorption cases reported in the literature (see Wu et al. 2024), where insufficient data can lead to trivial or non-physical solutions, particularly in regions with sparse information. Furthermore, while constructing
DAC-PINN, the importance of normalization and gradient balancing became evident in line with literature findings where unbalanced gradients within the physics-incorporated loss are a well-documented challenge [
49]. The custom loss-balancing algorithm developed for
DAC-PINN addressed this problem, allowing the network to converge to a physically representative and accurate solution.
The strong performance of the surrogate model demonstrates the feasibility of developing a digital twin for DAC systems using physics-informed neural networks (PINNs) across a range of input parameters. Advancing in the digital twin development involves incorporating the initial concentration and temperature profiles as input fields to the model, enabling the evaluation full cyclic operations and the computation cyclic steady-state profiles. A multi-input, initial-condition-aware PINN is currently under development to support this goal.
Author Contributions
Conceptualization, M.G.; methodology, M.G. and M.J.; software, M.G. and M.J.; validation, M.G. and M.J.; formal analysis, M.G. and M.J.; investigation, M.J.; data curation, M.J.; writing—original draft preparation, M.G.; writing—review and editing, M.G., I.R., J.-Y.D., J.B., P.S.O. and M.v.S.A.; visualization, M.G.; supervision, I.R. and M.v.S.A.; project administration, M.G.; funding acquisition, I.R. and M.v.S.A. All authors have read and agreed to the published version of the manuscript.
Funding
We thank Shell Global Solutions International BV for financial support.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PINNs | Physics-Informed Neural Networks |
| NNs | Neural Networks |
| DAC | Direct Air Capture |
| AI | Artificial Intelligence |
| CDR | Carbon Dioxide Removal |
| TVSA | Temperature–Vacuum Swing Adsorption |
| ANN | Artificial Neural Network |
| MEA | Monoethanolamine |
| MLP | Multi-Layer Perceptron |
| FFNN | Feed-Forward Neural Network |
| PDE | Partial Differential Equation |
| MSE | Mean Squared Error |
| FDM | Finite Difference Method |
| EMA | Exponential Moving Average |
| L1RE | L1 Relative Error |
Appendix A. Model Validation
The finite-difference model (FDM) used in this study is a simplified version of a more detailed adsorption–desorption cycle simulator developed by our group for Direct Air Capture (DAC) with temperature–vacuum swing adsorption (TVSA). To establish the fidelity of the model, we benchmarked it against the experimental results reported by Young et al. [
26] for the commercial sorbent Lewatit
® VPOC 1065 under representative DAC conditions.
The baseline case is defined by the cycle parameters and adsorber specifications summarized in
Table A1. The operating steps include adsorption, vacuum, heating, desorption, cooling, and pressurization, with durations and boundary conditions chosen to match those reported in the reference paper.
Table A1.
Baseline case parameters used for model validation.
Table A1.
Baseline case parameters used for model validation.
| Bed length | 0.01 m |
| Bed radius | 0.05 m |
| Bed porosity | 0.40 |
| Particle radius | 0.26 mm |
| Adsorption temperature | 288.15 K |
| Desorption temperature | 373.15 K |
| Relative humidity (feed) | 0.55 |
| Feed velocity | 0.0067 m/s |
| Vacuum pressure | 0.2 bar |
| Dry CO2 capacity | 1.87 g |
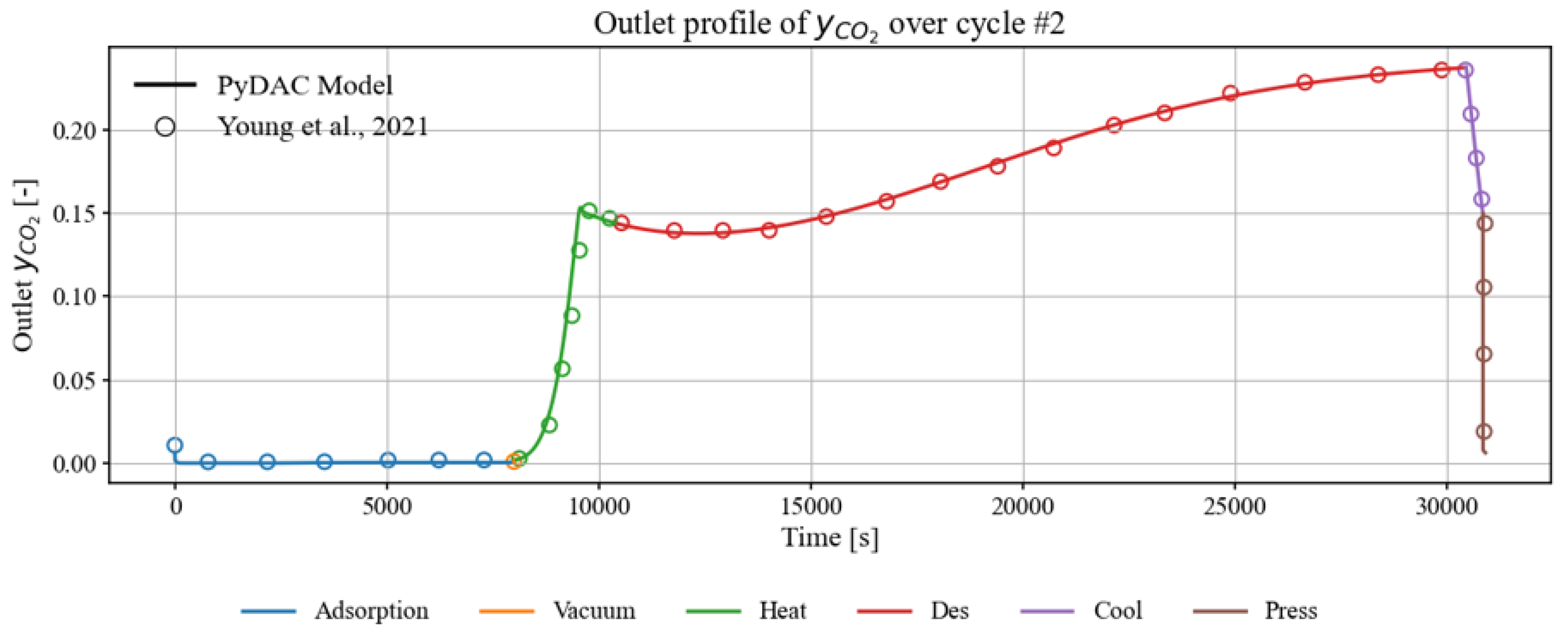
Figure A1 and
Figure A2 show the comparison of the model predictions with the experimental outlet profiles of CO
2 molar fraction and outlet temperature, respectively. The model reproduces both the shape and magnitude of the experimental curves across the adsorption, heating, desorption, and cooling steps, including the CO
2 breakthrough behavior and the thermal response of the bed.
Figure A1.
Comparison between model prediction and data from Young et al. (2021) [
26] for the outlet CO
2 molar fraction over a full TVSA cycle.
Figure A1.
Comparison between model prediction and data from Young et al. (2021) [
26] for the outlet CO
2 molar fraction over a full TVSA cycle.
Figure A2.
Comparison between model prediction and data from Young et al. (2021) [
26] for the outlet temperature profile over a full TVSA cycle.
Figure A2.
Comparison between model prediction and data from Young et al. (2021) [
26] for the outlet temperature profile over a full TVSA cycle.
Appendix B. Feed-Forward Neural Networks
In the feed-forward process, a neuron i with n inputs (state variables) computes its output in the two aforementioned steps:
Weighted Sum and Bias Addition: Each input
is multiplied by a corresponding weight
, and a bias term
is added. The resulting weighted sum
is given by
Nonlinear Activation: The neuron applies an activation function to the weighted sum, such that . This introduces non-linearity, which is crucial for modeling complex data relationships.
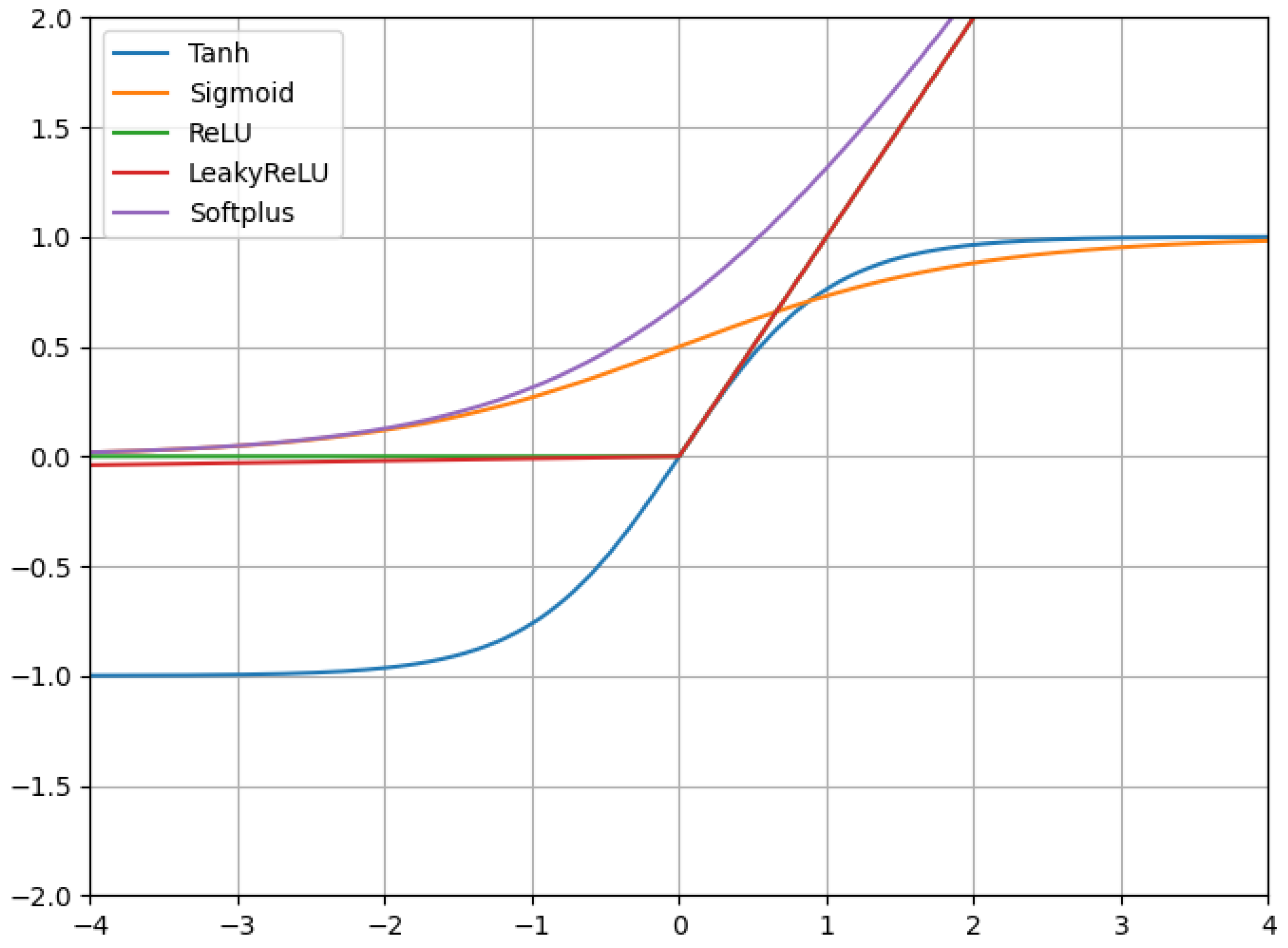
Some examples of activation functions are as follows:
Hyperbolic tangent (Tanh): Outputs values in the range
, making it useful for centered data.
Sigmoid (logistic function): Maps values to the range
, often used for probabilities in binary classification tasks.
Rectified Linear Unit (ReLU): Outputs the input if it is positive, otherwise zero. Widely used for its simplicity and efficiency.
Leaky ReLU: Similar to ReLU but allows a small negative slope for
, addressing the “dying ReLU” problem.
Softplus: A smooth approximation of ReLU, useful when differentiability is important.
A graphical representation of the activation function is shown in
Figure A3.
For a layer consisting of
m neurons, the
lth layer takes the input vector
and computes the output for all neurons in parallel:
where
,
is the matrix containing all the weights of the layer, and
is the bias vector of the layer.
Figure A3.
Graphical representation of the used activation functions.
Figure A3.
Graphical representation of the used activation functions.
Finally, the output of the activation function is passed to the next layer as the input, where the same process of a linear combination followed by a transformation by an activation function is repeated. This procedure will continue until the final output layer is reached [
23]:
where
is the trainable parameters of the network.
A neural network is trained using known output (“truth” data), with the aim of optimizing weights and biases in order to minimize the loss , which represents the difference between the network’s predictions and the truth values. The method used to minimize this loss is called back-propagation, which involves two key steps:
The forward pass: The input data is passed through the network layer by layer, until the final layer where the output is calculated (network prediction), which is then compared to the truth values to calculate the loss.
The backward pass: The network calculates how much each weight contributes to the total loss. This is carried out efficiently using the chain rule of calculus [
50]. The weights are then updated using an optimization algorithm like gradient descent to decrease the loss of the NN.
The most common loss function for NNs is the Mean Squared Error (MSE), as defined in Equation (
A3) [
51]:
where
is the predicted value from the network, and
is the true value. Using this loss function in combination with the chain rule from Calculus, the weights in the network can then be updated relative to their contribution to the loss function. The new weights are then calculated according to Equation (
A4) and the new biases according to Equation (
A5) [
52]:
where
is the learning rate, a small positive number that controls the step size of the updates.
The update of the weights and biases continues until convergence, ideally reaching a point where the loss is minimized.
The downside to this method, and gradient-descent-based optimization methods in general, is that there is no guarantee that at convergence a global minimum is reached. The reason for this is the non-convex nature of the loss landscape, which makes it impossible to prove that the minimum obtained by the iterative updating procedure is indeed the global minimum in the infinite domain [
53,
54,
55].
References
- Ozkan, M.; Nayak, S.P.; Ruiz, A.D.; Jiang, W. Current status and pillars of direct air capture technologies. iScience 2022, 25, 103990. [Google Scholar] [CrossRef]
- Marinič, D.; Likozar, B. Direct air capture multiscale modelling: From capture material optimization to process simulations. J. Clean. Prod. 2023, 408, 137185. [Google Scholar] [CrossRef]
- Zeeshan, M.; Kidder, M.K.; Pentzer, E.; Getman, R.B.; Gurkan, B. Direct air capture of CO2: From insights into the current and emerging approaches to future opportunities. Front. Sustain. 2023, 4, 1167713. [Google Scholar] [CrossRef]
- Erans, M.; Sanz-Pérez, E.S.; Hanak, D.P.; Clulow, Z.; Reiner, D.M.; Mutch, G.A. Direct air capture: Process technology, techno-economic and socio-political challenges. Energy Environ. Sci. 2022, 15, 1360–1405. [Google Scholar] [CrossRef]
- Sabatino, F.; Grimm, A.; Gallucci, F.; van Sint Annaland, M.; Kramer, G.J.; Gazzani, M. A comparative energy and costs assessment and optimization for direct air capture technologies. Joule 2021, 5, 2047–2076. [Google Scholar] [CrossRef]
- Zhu, X.; Xie, W.; Wu, J.; Miao, Y.; Xiang, C.; Chen, C.; Ge, B.; Gan, Z.; Yang, F.; Zhang, M.; et al. Recent advances in direct air capture by adsorption. Chem. Soc. Rev. 2022, 51, 6574–6651. [Google Scholar] [CrossRef] [PubMed]
- Low, M.Y.A.; Barton, L.V.; Pini, R.; Petit, C. Analytical review of the current state of knowledge of adsorption materials and processes for direct air capture. Chem. Eng. Res. Des. 2023, 189, 745–767. [Google Scholar] [CrossRef]
- Ward, A.; Pini, R. Efficient Bayesian Optimization of Industrial-Scale Pressure-Vacuum Swing Adsorption Processes for CO2 Capture. Ind. Eng. Chem. Res. 2022, 61, 13650–13668. [Google Scholar] [CrossRef]
- Ward, A.; Papathanasiou, M.M.; Pini, R. The impact of design and operational parameters on the optimal performance of direct air capture units using solid sorbents. Adsorption 2024, 30, 1829–1848. [Google Scholar] [CrossRef]
- Chung, W.; Kim, J.; Jung, H.; Lee, J.H. Hybrid modeling of vacuum swing adsorption carbon capture process for rapid process-level evaluation of adsorbents. Chem. Eng. J. 2024, 495, 153664. [Google Scholar] [CrossRef]
- Leperi, K.T.; Yancy-Caballero, D.; Snurr, R.Q.; You, F. 110th Anniversary: Surrogate Models Based on Artificial Neural Networks to Simulate and Optimize Pressure Swing Adsorption Cycles for CO2 Capture. Ind. Eng. Chem. Res. 2019, 58, 18241–18252. [Google Scholar] [CrossRef]
- Ye, F.; Ma, S.; Tong, L.; Xiao, J.; Bénard, P.; Chahine, R. Artificial neural network based optimization for hydrogen purification performance of pressure swing adsorption. Int. J. Hydrogen Energy 2019, 44, 5334–5344. [Google Scholar] [CrossRef]
- Jerng, S.E.; Park, Y.J.; Li, J. Machine learning for CO2 capture and conversion: A review. Energy AI 2024, 16, 100361. [Google Scholar] [CrossRef]
- Rahimi, M.; Moosavi, S.M.; Smit, B.; Hatton, T.A. Toward smart carbon capture with machine learning. Cell Rep. Phys. Sci. 2021, 2, 100396. [Google Scholar] [CrossRef]
- Sipöcz, N.; Tobiesen, F.A.; Assadi, M. The use of Artificial Neural Network models for CO2 capture plants. Appl. Energy 2011, 88, 2368–2376. [Google Scholar] [CrossRef]
- Young, J.; Mcilwaine, F.; Smit, B.; Garcia, S.; van der Spek, M. Process-informed adsorbent design guidelines for direct air capture. Chem. Eng. J. 2023, 456, 141035. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Rosenblatt, F. The Perceptron: A Probabilistic Model For Information And Storage In The Brain. Psychol. Rev. 1958, 65, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Bebis, G.; Georgiopoulos, M. Feed-forward neural networks. IEEE Potentials 1994, 13, 27–31. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Cuomo, S.; Di Cola, V.S.; Giampaolo, F.; Rozza, G.; Raissi, M.; Piccialli, F. Scientific Machine Learning Through Physics–Informed Neural Networks: Where we are and What’s Next. J. Sci. Comput. 2022, 92, 88. [Google Scholar] [CrossRef]
- Toscano, J.D.; Oommen, V.; Varghese, A.J.; Zou, Z.; Ahmadi Daryakenari, N.; Wu, C.; Karniadakis, G.E. From PINNs to PIKANs: Recent advances in physics-informed machine learning. Mach. Learn. Comput. Sci. Eng. 2025, 1, 15. [Google Scholar] [CrossRef]
- Güneş Baydin, A.; Pearlmutter, B.A.; Andreyevich Radul, A.; Mark Siskind, J. Automatic differentiation in machine learning: A survey. J. Mach. Learn. Res. 2015, 18, 5595–5637. [Google Scholar]
- LEWATIT® VP OC 1065. Available online: https://lanxess.com/en-us/products-andbrands/products/l/lewatit--vp-oc-1065 (accessed on 25 July 2024).
- Young, J.; García-Díez, E.; Garcia, S.; Van Der Spek, M. The impact of binary water–CO2 isotherm models on the optimal performance of sorbent-based direct air capture processes. Energy Environ. Sci. 2021, 14, 5377–5394. [Google Scholar] [CrossRef]
- Shan, M.; Jin, Y.; Chimani, F.M.; Bhandari, A.A.; Wallmüller, A.; Schöny, G.; Müller, S.; Fuchs, J. Evaluation of CO2/H2O Co-Adsorption Models for the Anion Exchange Resin Lewatit VPOC 1065 under Direct Air Capture Conditions Using a Novel Lab Setup. Separations 2024, 11, 160. [Google Scholar] [CrossRef]
- Glueckauf, E. Formula for Diffusion into Spheres and Their Applications to Chromatography; Technical Report; Atomic Energy Research Establishment: Harwell, UK, 1955. [Google Scholar]
- Sircar, S.; Hufton, J.R. Why does the linear driving force model for adsorption kinetics work? Adsorption 2000, 6, 137–147. [Google Scholar] [CrossRef]
- Duong, D.D. Adsorption Analysis: Equilibria and Kinetics; Imperial College Press: London, UK, 1998; p. 892. [Google Scholar]
- Low, M.Y.A.; Danaci, D.; Azzan, H.; Woodward, R.T.; Petit, C. Measurement of Physicochemical Properties and CO2, N2, Ar, O2, and H2O Unary Adsorption Isotherms of Purolite A110 and Lewatit VP OC 1065 for Application in Direct Air Capture. J. Chem. Eng. Data 2023, 68, 3499–3511. [Google Scholar] [CrossRef]
- Shi, W.; Chen, S.; Xie, R.; Gonzalez-Diaz, A.; Zhang, X.; Wang, T.; Jiang, L. Bi-disperse adsorption model of the performance of amine adsorbents for direct air capture. Chem. Eng. J. 2024, 496, 154090. [Google Scholar] [CrossRef]
- Yu, J.; Spiliopoulos, K. Normalization effects on deep neural networks. Found. Data Sci. 2022, 5, 389–465. [Google Scholar] [CrossRef]
- Wu, Z.; Chen, Y.; Zhang, B.; Ren, J.; Chen, Q.; Wang, H.; He, C. Pressure swing adsorption process modeling using physics-informed machine learning with transfer learning and labeled data. Green Chem. Eng. 2024, 6, 233–248. [Google Scholar] [CrossRef]
- Krishnapriyan, A.S.; Gholami, A.; Zhe, S.; Kirby, R.M.; Mahoney, M.W. Characterizing possible failure modes in physics-informed neural networks. Adv. Neural Inf. Process. Syst. 2021, 32, 26548–26560. [Google Scholar]
- De Florio, M.; Schiassi, E.; Calabrò, F.; Furfaro, R. Physics-Informed Neural Networks for 2nd order ODEs with sharp gradients. J. Comput. Appl. Math. 2024, 436, 115396. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Pedregosa, F.; Michel, V.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Vanderplas, J.; Cournapeau, D.; Pedregosa, F.; Varoquaux, G.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Monaco, S.; Apiletti, D. Training physics-informed neural networks: One learning to rule them all? Results Eng. 2023, 18, 101023. [Google Scholar] [CrossRef]
- Bekele, Y.W. Physics-informed neural networks with curriculum training for poroelastic flow and deformation processes. arXiv 2024, arXiv:2404.13909. [Google Scholar] [CrossRef]
- Wang, S.; Teng, Y.; Perdikaris, P. Understanding and mitigating gradient pathologies in physics-informed neural networks. SIAM J. Sci. Comput. 2020, 43, 3055–3081. [Google Scholar] [CrossRef]
- Li, S.; Feng, X. Dynamic Weight Strategy of Physics-Informed Neural Networks for the 2D Navier–Stokes Equations. Entropy 2022, 24, 1254. [Google Scholar] [CrossRef] [PubMed]
- Deguchi, S.; Asai, M. Dynamic & norm-based weights to normalize imbalance in back-propagated gradients of physics-informed neural networks. J. Phys. Commun. 2023, 7, 075005. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, X.; Feng, X.; Xu, H. An improved physics-informed neural network with adaptive weighting and mixed differentiation for solving the incompressible Navier–Stokes equations. Nonlinear Dyn. 2024, 112, 16113–16134. [Google Scholar] [CrossRef]
- Markidis, S. The Old and the New: Can Physics-Informed Deep-Learning Replace Traditional Linear Solvers? Front. Big Data 2021, 4, 669097. [Google Scholar] [CrossRef]
- Chisăliță, D.A.; Boon, J.; Lücking, L. Adsorbent shaping as enabler for intensified pressure swing adsorption (PSA): A critical review. Sep. Purif. Technol. 2025, 353, 128466. [Google Scholar] [CrossRef]
- Krishnamurthy, S.; Boon, J.; Grande, C.; Lind, A.; Blom, R.; de Boer, R.; Willemsen, H.; de Scheemaker, G. Screening Supported Amine Sorbents in the Context of Post-combustion Carbon Capture by Vacuum Swing Adsorption. Chem. Ing. Tech. 2021, 93, 929–940. [Google Scholar] [CrossRef]
- Rathore, P.; Lei, W.; Frangella, Z.; Lu, L.; Udell, M. Challenges in Training PINNs: A Loss Landscape Perspective. Proc. Mach. Learn. Res. 2024, 235, 42159–42191. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Terven, J.; Cordova-Esparza, D.M.; Ramirez-Pedraza, A.; Chavez-Urbiola, E.A.; Romero-Gonzalez, J.A. Loss Functions and Metrics in Deep Learning. arXiv 2023, arXiv:2307.02694. [Google Scholar] [CrossRef]
- Zhang, J. Gradient Descent based Optimization Algorithms for Deep Learning Models Training. arXiv 2019, arXiv:1903.03614. [Google Scholar] [CrossRef]
- Jentzen, A.; Riekert, A. On the existence of global minima and convergence analyses for gradient descent methods in the training of deep neural networks. J. Mach. Learn. 2021, 1, 141–246. [Google Scholar] [CrossRef]
- Yun, C.; Sra, S.; Jadbabaie, A. Global optimality conditions for deep neural networks. In Proceedings of the 6th International Conference on Learning Representations (ICLR 2018), Vancouver, BC, Canada, 30 April–3 May 2018. Conference Track Proceedings. [Google Scholar]
- Chatterjee, S. Convergence of gradient descent for deep neural networks. arXiv 2022, arXiv:2203.16462. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).