Abstract
High sugar intake from commercial beverages is a public health concern, motivating rapid, user-friendly tools for sugar quantification. We present a compact planar microwave metamaterial sensor that estimates sugar concentration by monitoring resonant frequency shifts induced by dielectric loading. Tests with aqueous glucose solutions demonstrated a wide dynamic range (0 to 12,000 mg/dL), perfect linearity (R2 = 1), and high repeatability. Validation on two commercial beverages showed sensor-predicted sugar contents consistent with their nutrition labels. The method is reagent-free, tolerates opaque samples, and operates under ambient conditions, making it suitable for on-site consumer use as well as regulatory inspection and quality-control applications.
1. Introduction
Beverages with high sugar contents, such as carbonated and isotonic drinks, contribute to caries and obesity and may increase the risk of type 2 diabetes [1,2]. Apovian [3] reported that adding one soft drink (40–50 g sugar) daily could result in a 6.75 kg weight gain within a year. The excessive intake of absorbable carbohydrates may also trigger hepatic lipogenesis and a high glycemic load [1,4,5,6]. While some drinks are sold with nutrition labels, many do not disclose the full list of dissolved compounds. Take, for instance, the drinks sold in fast-food outlets, coffeehouses, and specialty beverage chains. These drinks are often served without full disclosure of their actual ingredients. A sugar level measurement device is therefore essential.
Refractometers are widely used to measure sugar content via the refractive index [7,8,9,10] but face difficulty with opaque liquids such as milk, carbonated soft drinks, and coffee [11]. Other optical methods, such as surface plasmon resonance (SPR) sensors, have been explored [12,13]. However, the results either failed to correlate with concentration [12] or required laborious silver–self-assembled monolayer (silver–SAM) coatings with R2 < 0.95 [13]. Fluorescent probes [14] and chronoamperometry [15] also demand additional reagents. Both of these setups rely on the exploitation of additional chemical reagents for sugar level detection, without which the detection process may be hampered. Also, these methods are usually labor-intensive, with reaction times and analysis requiring several tens of minutes to a few hours, depending on the reagents and protocols employed, since the results of chemical reactions are not instantaneous [16].
Artificial intelligence methods, such as near-infrared spectroscopy (NIRS) with machine learning [11] or impedance spectroscopy with deep learning [17], can achieve high accuracy but require extensive datasets and calibration. Beyond these approaches, a variety of sugar-sensing techniques have been reported in the literature. Enzyme-based electrochemical sensors, particularly glucose oxidase electrodes, are widely used for glucose quantification due to their high sensitivity; however, their reliance on reagents and limited stability restricts broader application [18]. Optical methods such as infrared and Raman spectroscopy can provide detailed compositional information, but their effectiveness is hindered by strong water absorption, sample opacity, and the need for calibration against complex matrices [19]. Chromatographic methods, including high-performance liquid chromatography (HPLC), are considered the gold standard for sugar analysis due to their specificity, yet they are time-intensive and require sample preparation, making them unsuitable for rapid field use [20]. More recently, microwave and radio frequency sensors have been explored for liquid characterization [21], offering reagent-free and rapid testing. However, many of these microwave-based sugar sensors remain limited by a narrow dynamic range.
Sugar quality in beverages is influenced by multiple factors, including temperature, pH, and the presence of other dissolved constituents such as acids, salts, and carbonation. For example, temperature variations can alter sugar solubility and the relaxation dynamics of water–sugar mixtures, thereby affecting the dielectric response at microwave frequencies [22]. Similarly, acidic environments may promote sugar hydrolysis, while carbonation introduces dissolved CO2 that modifies ionic content and pH. From an analytical standpoint, sugar quality is commonly assessed through refractometry, chromatography, or spectroscopic methods, but these techniques are often limited by sample opacity, preparation requirements, or measurement time [9]. These factors highlight the need for a direct, reagent-free sensing approach capable of capturing changes in sugar concentration and quality under realistic beverage conditions.
It is important to note that glucose was chosen in this study due to its known dielectric behavior, although commercial beverages may contain mixtures of glucose, fructose, and sucrose. Due to the structural similarity and polar nature of these sugars, their aqueous solutions exhibit comparable dielectric properties at microwave frequencies, thereby justifying the use of glucose as a representative model for sensor calibration. Moreover, sucrose undergoes hydrolysis in aqueous solution to form equimolar glucose and fructose. Studies have shown that the refractive index versus concentration profile of such hydrolyzed mixtures (invert sugar) closely resembles that of pure sucrose solutions across a wide range of concentrations [23,24].
Microwave planar sensors offer such potential. Unlike refractometers, they rely on dielectric interactions and are unaffected by opacity or color. Thus, even dark beverages (e.g., Coca-Cola) can be analyzed without dilution or reagents, using simple placement on the sensor surface [25]. Moreover, calibration is only performed once using standard glucose solutions to establish the regression model and remove baseline noise from the measurement setup. The same calibration curve can be applied repeatedly for all beverage samples within the session. Yet, most planar microwave sensors are reported for blood glucose monitoring [26,27,28], with limited testing ranges.
Here, we present a compact planar microwave sensor designed for beverage sugar detection. The sensor combines metamaterials on one side with a coplanar waveguide (CPW) transmission line on the other, measured using a portable nano-vector network analyzer (nanoVNA). Fabricated on FR-4 (a flame-retardant glass-reinforced epoxy laminate), it achieves a wide dynamic range (0 to 12,000 mg/dL) with excellent linearity (R2 = 1), surpassing most reported beverage-oriented microwave sensors.
The highlights of this study are as follows: (i) a compact metamaterial-based microwave sensor was designed and fabricated on a low-cost FR-4 substrate; (ii) the sensor demonstrates a wide testing range of 0 to 12,000 mg/dL, which surpasses most reported microwave beverage sensors; (iii) the resonant frequency shifts exhibit excellent linearity with sugar concentration, yielding a coefficient of determination R2 = 1; and (iv) validation using commercial beverages confirms that the sensor can accurately quantify sugar levels in real-world samples without chemical reagents or dilution. These findings establish the proposed device as a promising platform for portable beverage quality assessment.
2. Theoretical Analysis
In our proposed design, a pair of split-ring resonators (SRRs) were adopted to generate resonant effects at the transmission coefficient. An SRR consists of a pair of concentric conducting rings with splits etched at opposite ends. Owing to the inherent inductance L within the rings and the capacitance C formed from the splits and the separations between the rings, an SRR behaves exactly like an LC resonant circuit. The metamaterial exhibits an effective negative magnetic permeability in a narrow band above the resonant frequency [29,30], inhibiting signal propagation at this band and, therefore, producing a transmission dip. While SRR-based metamaterials can be theoretically described in terms of effective negative permeability (μeff) above resonance, it is important to note that in compact sensor implementations this behavior is manifested experimentally as a transmission dip in the S-parameter response. Effective constitutive parameters (εeff, μeff) are typically retrieved from periodic structures using homogenization methods, which are not directly applicable to a single SRR pair. Accordingly, in this work, we interpret the resonant dip in S21 as the experimental signature of the metamaterial response, and we relate shifts in this resonance to changes in the dielectric loading caused by sugar concentration.
In the context of metamaterials, the paired SRRs behave as artificial magnetic resonators. When excited by an incident electromagnetic field, circulating currents are induced within the rings, generating a magnetic dipole moment. At the resonant frequency, the structure exhibits an effective negative magnetic permeability μeff over a narrow band above resonance. This negative response prevents wave propagation, producing the observed transmission dip in S21.
The sensing principle arises because the resonant frequency depends on the equivalent inductance (Leq) and capacitance (Ceq) of the SRRs, where the capacitance is strongly influenced by the dielectric permittivity of the medium surrounding the splits. When a solution with increasing sugar concentration is introduced, the local dielectric constant εr changes, thereby altering Ceq and shifting the resonant frequency. In this way, the metamaterial property (negative μeff and strong field localization at the SRR gaps) directly maps onto a measurable frequency shift in the transmission response. This mechanism provides both high sensitivity and a clear physical interpretation for sugar detection.
In order to constrain the size of the sensor such that it is compact and wieldy enough to be handheld, the essential geometrical parameters of the sensor were first defined. Figure 1 depicts the structure of the proposed circular SRR. The outer radius of the external ring rext and the inner radius of the internal ring rint are set, respectively, to 6 mm and 3 mm, whereas the gaps of the splits g, distance between the rings d, and thickness of the internal ring c are set equally to 1 mm.
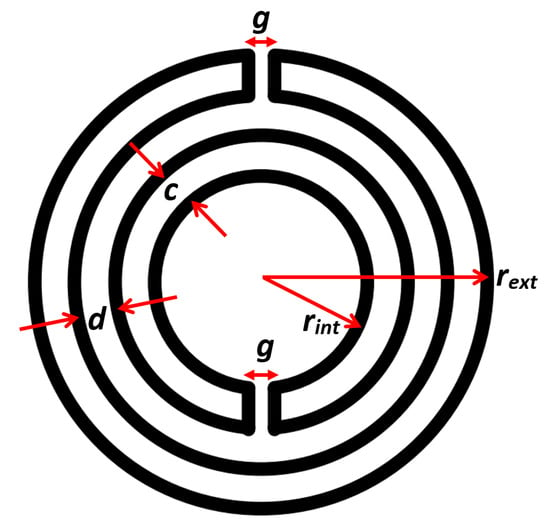
Figure 1.
The geometrical structure of the proposed circular SRR with g = c = d = 1 mm, rint = 3 mm, and rext = 6 mm.
The values of the equivalent inductance Leq and capacitance Ceq are desired for estimating the resonant frequency fr of the SRR structure. These parameters can be found by substituting the predefined parameters into (1) and (2) below [31].
where c0 = 3.0 × 108 m/s is the velocity of the wave in the free space, ε0 = 8.854 × 10−12 F/m is the permittivity of the free space, t = 35 µm is the copper thickness of the metallic rings, and εeff and Z0 are, respectively, the effective permittivity of the medium and characteristic impedance of the CPW transmission line.
The characteristic impedance Z0 can be obtained from [32]
where K(k1) and K(k’1) are the complete elliptic integrals of the first kind. The arguments of the elliptic integrals k1 and k′1 can be solved using a pair of conformal transformations and can be expressed as [33]
where w is the width of the strip and se the gap between the strip and ground plane, as shown in Figure 2. w and se are set, respectively, to 5.5 mm and 0.5 mm.
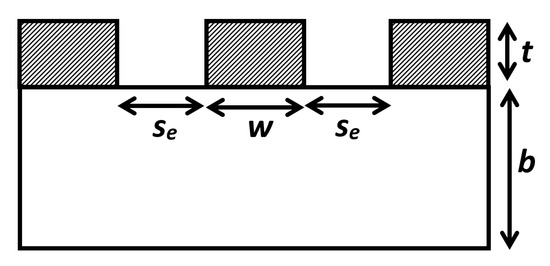
Figure 2.
Cross-section of the coplanar waveguide (CPW). The central copper strip of width w is separated from the ground planes by a gap se. The CPW is fabricated on an FR-4 dielectric substrate (εr = 4.4, tan δ = 0.022, thickness b = 1.6 mm), with air above the substrate.
A simple but accurate expression which relates K(k′1) to K(k1) can be found in [34] as
and
The effective dielectric constant εeff is assumed dispersionless and can be expressed as [34]
Here, arguments k2 and k′2 are given as
where b is the height of the dielectric substrate.
It should be noted that some of the theoretical expressions used in this work are taken from the literature. Specifically, equations referenced in [31,33] were derived by their respective authors, while equations referenced in [32,34] were cited without full derivations provided. For clarity, (1) to (7) follow these sources accordingly, and their use here is consistent with prior applications in planar microwave sensor analysis.
The resonant frequency fr is found to be 2.258 GHz when substituting Leq and Ceq in (1) and (2) into the expression below:
3. The Sensor Design
Figure 3 depicts the complete structure of the planar microwave sensor. The dimensions of the CPW have been parametrically adjusted to approach 50 Ω, so as to match those of the SubMiniature version A (SMA) connectors. The final geometrical parameters of the structure are summarized in Table 1. The proposed design has a size of 30 mm × 50 mm and was fabricated on a flame-retardant FR-4 epoxy laminate substrate which has a thickness of 1.6 mm, dielectric constant of 4.4, and loss tangent of 0.022.
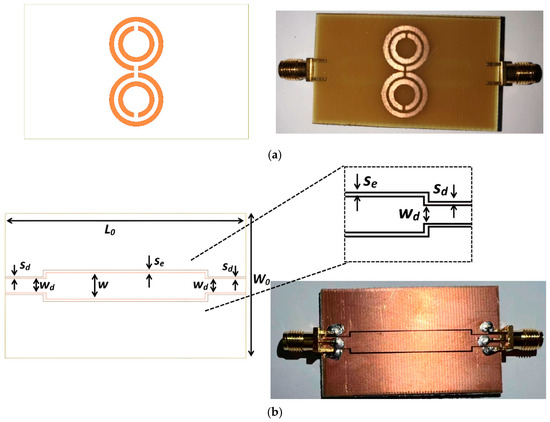
Figure 3.
(a) Top view and (b) bottom view of the proposed planar sensor. An inset has been added in (b) to highlight the finer structural details for better visibility.

Table 1.
The dimensions of the proposed planar sensor (in mm).
The performance of the proposed design was first simulated using Ansoft HFSS v12.1 and was subsequently measured via a Zeenko nanoVNA (model SAA-2, serial number 22060725; manufactured by Zhejiang Zhike Technology Co., Ltd., Hangzhou, Zhejiang, China). Figure 4 and Figure 5 show the transmission coefficients of the unloaded structure at the resonant band. The resonant frequencies obtained from the simulation and measurement results are 2.438 GHz and 2.387 GHz, respectively. Although discrepancies are observed between both results, close inspection evinces that both of them merely differ by approximately 2%. Indeed, it can be seen that the measured value provides a better match with the theoretical fr of 2.258 GHz.
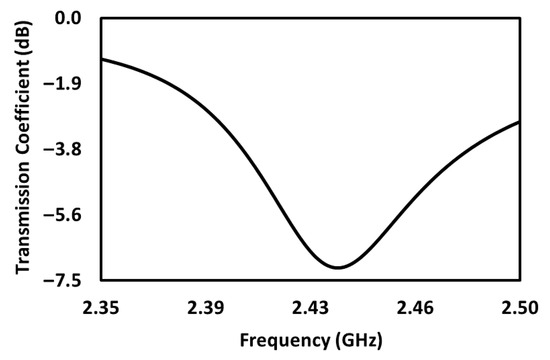
Figure 4.
The simulated result of the unloaded sensor with fr = 2.438 GHz.
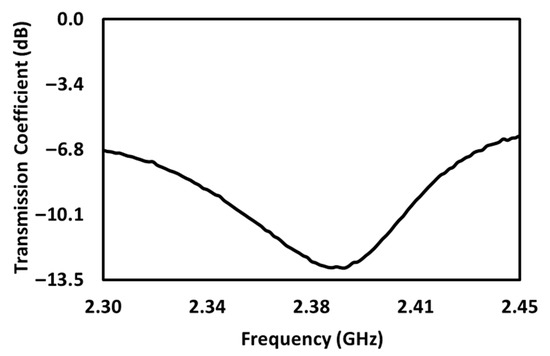
Figure 5.
The measured result of the unloaded sensor with fr = 2.387 GHz.
As can be observed from the simulation result in Figure 6, electric field intensities confined to the center of the paired SRRs are the strongest at fr = 2.387 GHz. That is to say, the field–matter interactions during resonance are at their optimum at this position. It is therefore reasonable to deduce that the highest sensitivity for the sensing mechanism can be achieved when the test sample is placed at the center. In order to correlate the shift in fr with the concentration of sugar in the solution, a beaker filled with 10 mL of distilled water was first deposited at the surface center of the sensor, as shown in Figure 7. For clarity, although nutrition labels typically report sugar in g/100 mL, all concentrations in this study were converted and are consistently expressed in mg/dL for direct comparison. Food-grade D(+) glucose anhydrous (C6H12O6, ≥99.5% purity, 180.16 g/mol, Sigma-Aldrich, St. Louis, MO, USA) was progressively dissolved into distilled water in increments of 0.2 g, with thorough mixing at each step. Glucose was selected due to its well-characterized dielectric properties and frequent use as a model sugar in sensor research. While commercial beverages may contain a mixture of sugars, glucose provides a representative and reproducible basis for validation. The transmission coefficient was measured and recorded for each change in the glucose concentration. Each measurement was conducted three times, and the average was recorded for each concentration level. While minor variations were observed in the amplitude of the transmission coefficient between trials, the resonant frequency remained stable across repetitions, indicating the sensor’s good repeatability. Figure 8 depicts the change in the resonant bands for the disparate glucose concentrations. It can be seen from the figure that fr shifts towards lower frequencies when the concentration of glucose in the solution rises. This phenomenon can be attributed to the increase in the capacitance value as a consequence of the change in the dielectric constant εr. Increasing the glucose concentration tends to increase the dielectric constant εr of its environment. The red shift in fr is therefore to be expected since fr is inversely proportional to the square root of capacitance C, while C is directly proportional to εr.
where td is the thickness of the dielectric substrate. While glucose has a lower static permittivity than water, its dielectric behavior in the microwave regime (~2 GHz to 2.5 GHz) is governed by dynamic molecular interactions rather than static dipole moments alone. At these frequencies, glucose–water mixtures exhibit changes in hydration shell structure, dipolar relaxation times, and the ordering of bound water molecules, which can collectively increase the effective permittivity of the mixture despite glucose’s lower DC permittivity. This counterintuitive trend has been observed in multiple experimental studies using planar microwave sensors [25], where increasing the glucose concentration produced a measurable red shift in the resonant frequency. The consistent red shifts recorded in this work are therefore in agreement with known microwave frequency dielectric behavior. The observed trends are therefore supported by the prior literature and the strong linear correlation between the sugar concentration and resonant frequency in our results. Owing to the variations in loss tangents among different glucose solutions, trackable amplitude changes are also observed in Figure 8 [26]. By plotting fr with respect to the amount of glucose gc added into the solution, a distinct relationship between them can be found, as shown in Figure 9. Each data point in Figure 9 represents the mean of three repeated measurements at the given glucose concentration, with the beaker repositioned between trials. Within the 3.5 MHz frequency resolution of the nanoVNA, no detectable standard deviation was observed, and error bars are therefore not visible. This reflects the instrument’s resolution limit rather than the absence of minor underlying variability. It is apparent from the figure that a simple linear curve, which is mathematically expressed in (10) below, is obtained.
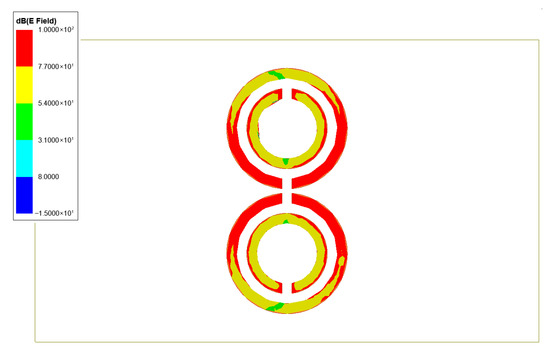
Figure 6.
The electric field density is confined to the vicinity of the outer-ring splits.

Figure 7.
Annotated measurement setup showing the Zeenko nanoVNA (SAA-2), coaxial cables, SMA connectors, sensor board, and beaker placement. Calibration was performed at the SMA connector reference plane using a SOLT kit.
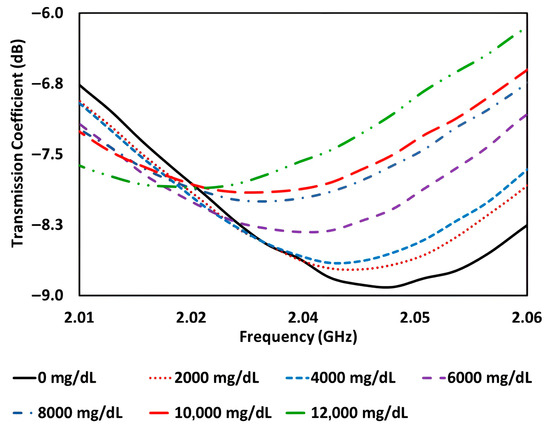
Figure 8.
The measured transmission coefficients of the aqueous solutions with different concentrations of glucose evenly mixed into them.
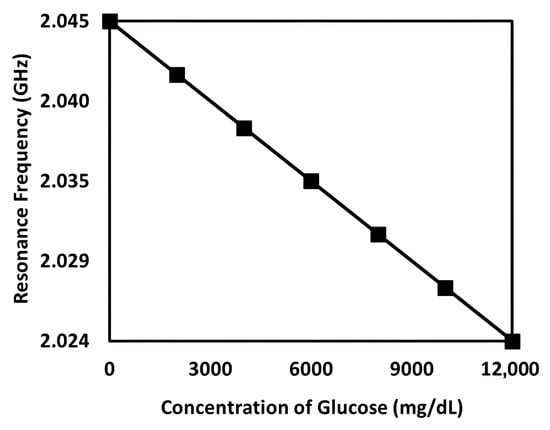
Figure 9.
Relationship between the resonant frequency of the sensor and the glucose concentration in an aqueous solution. Each point represents the mean of three measurements.
Clearly, the amount of glucose in an unknown drink can be easily predicted by employing the inverse linear regression model. The presence of other dissolved compounds such as acids, salts, and carbonation in commercial drinks may subtly influence the dielectric environment. Nevertheless, the sensor demonstrated reliable correlation with the labeled sugar content, suggesting that glucose is the principal contributor to dielectric variation in clear carbonated beverages, particularly those with minimal additional solutes. The dominant effect of sugar on the dielectric behavior of soft drinks can be attributed to its significantly higher concentration compared to other solutes. For instance, Belay and Assefa [22] reported sugar concentrations ranging from 8.62 to 12.3 g/100 mL in major commercial sodas, while non-sugar additives such as dyes, salts, or flavoring agents are typically present at levels below 200 mg/100 mL. Given this disparity, the influence of non-sugar constituents on dielectric or refractive behavior is minimal and does not significantly interfere with the measurement accuracy of the proposed sensor.
4. Measurement Setup and Instrumentation
All S-parameter measurements were performed using a Zeenko nanoVNA (model SAA-2, serial number 22060725), which covers the frequency range from 50 kHz to 3 GHz and is powered via a 5 V USB (1 A max). The sensor board was connected to the analyzer using two ~30 cm male-to-male RF coaxial cables terminated with SMA connectors. The beaker (10 mL) was positioned directly above the paired SRRs, as shown in Figure 7.
Calibration was carried out using a standard short–open–load–through (SOLT) procedure at the SMA connector reference plane immediately before each measurement session. This ensured that cable and connector contributions were removed from the measured S-parameters.
The sweep configuration was set to cover 50 kHz to 3 GHz, with 201 points when using the device’s built-in interface or up to 1024 points when controlled via USB software. The corresponding frequency step was approximately 3.5 MHz in the measurement range of interest (2 to 3 GHz). The output level was at the instrument’s nominal default setting, and default averaging was applied. According to the product specifications, the calibrated dynamic range is approximately 70 dB up to 1.5 GHz and 60 dB up to 3 GHz, which is sufficient for capturing the resonant dip near 2.3 GHz.
Repeatability was verified by repeating each measurement three times, with the beaker repositioned between trials. The resonant frequency remained consistent across all repetitions, while amplitude variations were minor and attributed to background noise. By reporting the instrument model, calibration method, sweep settings, and dynamic range, we ensure reproducibility and enable readers to assess the measurement uncertainty.
5. Results and Discussion
To validate the performance of the proposed sensor, we have selected two carbonated drinks commonly found in Malaysia, namely, Coca-Cola and Anglia Shandy. The nutrition labels for these two beverages are depicted in Figure 10 and Figure 11. As can be seen from the figures, the total sugar in Coca-Cola and Anglia Shandy is 4600 mg/dL and 6000 mg/dL, respectively. The beaker on the sensor was filled with 10 mL of the drinks, and the resonant bands generated at the transmission coefficient are shown in Figure 12. The obtained resonant frequencies for the Coca-Cola and Anglia Shandy measurements are 2.0370 GHz and 2.0345 GHz, respectively. It should be noted that the dielectric constant (εr) and loss tangent (tan δ) of the liquid samples were not measured directly in this work. Instead, the effect of dielectric loading is manifested through the resonance shift and transmission dip (S21) observed in the SRR sensor response. Dedicated dielectric probe or resonant cavity techniques are typically required to extract constitutive parameters, but these are outside the scope of the present study. The focus here is on demonstrating a compact and low-cost sensor, where the resonance frequency shift itself serves as the experimental indicator of sugar concentration. These measurements were also conducted in triplicate. While slight variations in amplitude were observed, the resonant frequencies remained unchanged across all trials. Across all triplicate measurements, the resonant frequencies remained fixed at each concentration level, suggesting high frequency stability under ambient conditions, despite minor amplitude variations caused by background noise. This confirms that the frequency shifts observed between the two drinks are consistent and repeatable. Although the difference may appear small in GHz, the shift from 2.0370 GHz to 2.0345 GHz corresponds to 2.5 MHz—a clear and measurable difference that aligns with the sugar content variation between the beverages. Previous works have demonstrated that MHz level shifts in planar resonators are sufficient to capture subtle dielectric changes in aqueous solutions [35,36]. In particular, dielectric variations arising from solute concentration have been shown to produce shifts on the order of a few MHz, which are resolvable within the frequency resolution of typical vector network analyzers. Thus, the observed shift is both measurable and consistent with reported microwave sensing studies, validating its attribution to the sugar concentration difference between the two beverages. By substituting these values into (10), the sugar concentrations predicted using the proposed sensor are 4571 mg/dL and 6000 mg/dL for the Coca-Cola and Anglia Shandy drinks, respectively. For consistency with the experimental setup, all sugar values from nutrition labels (g/100 mL) are expressed in mg/dL. The values agree exactly with those printed on the nutrition labels of the drinks, thereby corroborating the accuracy of the sensor. Figure 10 and Figure 11 provide the nutritional labels for Coca-Cola and Anglia Shandy, while Figure 12 presents the corresponding resonant frequencies measured using the proposed sensor. The close match between the predicted concentrations from (10) and the labeled sugar contents confirms that the resonant frequency shifts observed in Figure 12 directly correspond to the sugar concentrations reported in Figure 10 and Figure 11. This alignment demonstrates the sensor’s accuracy in validating real beverage samples. It is noteworthy that the measured resonant frequency for the 6000 mg/dL glucose solution was identical, within the instrument’s resolution, to that of Anglia Shandy, which is labeled with the same total sugar content. While Anglia Shandy contains additional non-sugar constituents such as flavorings, preservatives, and carbonation, these are typically present at much lower concentrations than sugar. For example, sodium benzoate and potassium sorbate—common beverage preservatives—have been reported in commercial fruit juice and soft drink samples at levels of 25.8 to 245.1 mg/L (i.e., 2.6 to 24.5 mg per 100 mL) and 1.36 to 158 mg/L (i.e., 0.1 to 15.8 mg per 100 mL), respectively [37]. These ranges are at least an order of magnitude lower than the dominant sugar concentration (6 g per 100 mL), suggesting that the dielectric response is overwhelmingly governed by sugar at such high levels, with other solutes contributing changes smaller than the sensor’s sensitivity threshold. Moreover, the nanoVNA’s frequency resolution (3.5 MHz step size in this study) means that small but non-zero differences in the effective permittivity may remain undetectable in the recorded resonant frequency. Thus, the apparent identical readings reflect both the dominance of sugar in determining dielectric behavior and the resolution limits of the measurement system. While the sensor shows reliable performance in carbonated soft drinks, which are primarily aqueous sugar solutions with minimal interfering solutes, its effectiveness in more complex beverages such as fruit juices, dairy-based drinks, or alcohol remains to be evaluated. These liquids may contain substantial amounts of other polar or non-polar compounds (e.g., proteins, fiber, fats) that could alter the dielectric environment significantly. Future work will focus on extending the sensor’s application to such matrices through either calibration or structural refinement.

Figure 10.
English translation of the nutrition information label of a Coca-Cola beverage.
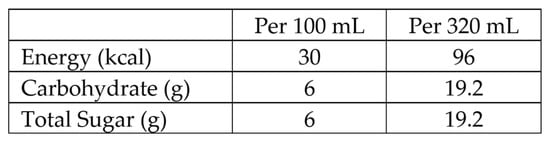
Figure 11.
English translation of the nutrition information label of an Anglia Shandy beverage.
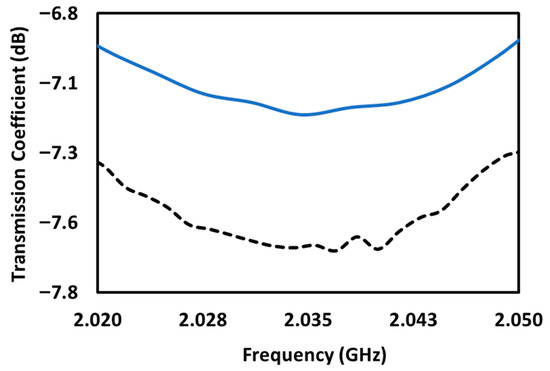
Figure 12.
Transmission coefficient responses of Coca-Cola (solid line, 2.0370 GHz) and Shandy (dashed line, 2.0345 GHz), showing a 2.5 MHz frequency separation.
As mentioned in an earlier section, existing microwave sugar sensors have limitations in their testing ranges. Here, we show a comparison of the performance of some recent microwave sensors with our proposed design in Table 2. The range of sugar concentrations that can be measured using our proposed sensor is from 0 to 12,000 mg/dL. The linearity of the regression remains strong across the full span. Since the shift in fr is directly associated with the sugar concentration in the drink, the coefficient of determination obtained is unity. The glucose concentration range from 0 to 12,000 mg/dL demonstrated a highly linear relationship with the resonant frequency, with a coefficient of determination R2 = 1. While the possibility of nonlinearity at higher concentrations cannot be ruled out, no such effects were observed within the tested range. To ensure consistency, each measurement was performed in triplicate. While inter-device reproducibility was not explored in this work, the strong repeatability observed suggests stable performance. The sensor’s reusability was also examined. After each measurement, the sensor was rinsed with distilled water and allowed to dry at room temperature before reuse. Across three repeated loading–unloading cycles with distilled water and glucose solution, no noticeable drift in the resonant frequency was observed. This indicates good stability and reusability under controlled conditions. Due to the 3.5 MHz frequency step size used in this study, small variations in the resonant frequency may not be detectable, leading to an apparent standard deviation of zero and, consequently, limit of detection (LOD) and limit of quantification (LOQ) values of zero. It should be noted that the apparent zero values for the standard deviation, LOD, and LOQ arise from the 3.5 MHz frequency step size used in this study. Variations smaller than this resolution are not detectable in the recorded data, even though minor fluctuations may exist in practice. As the LOD and LOQ are derived from the standard deviation, they consequently evaluate to zero. This effect reflects the resolution limit of the measurement instrument rather than the absence of underlying variation [10]. While this does not reflect the practical underlying sensor’s resolution, it suggests that the resonant shift is highly stable at the measurement scale used. To provide a more realistic estimate, the standard deviation was estimated to lie within the range of 100 kHz to 150 kHz based on typical frequency fluctuations observed in planar microwave sensor systems. Using this range, the LOD and LOQ were calculated to be approximately 171 mg/dL to 257 mg/dL and 571 mg/dL to 857 mg/dL, respectively. These values provide a realistic estimate of the sensor’s detection capability under typical experimental conditions.

Table 2.
Parametric comparison of various microwave sensors.
To enhance the performance benchmarking of the proposed sensor, statistical analysis was performed by repeating each measurement three times at every concentration level. The mean resonant frequency was reported, while amplitude variations were minor and attributed to background noise. Regression statistics were then computed based on the linear regression model. The root mean square error (RMSE) was found to be approximately 0.0 GHz, and the mean absolute percentage error (MAPE) was 0.0% over the full testing range of 0 to 12,000 mg/dL. Together with the perfect coefficient of determination (R2 = 1), these results confirm the reliability, accuracy, and predictability of the sensor’s linear response. These analyses further validate the robustness, sensitivity, and wide testing range of the proposed sensor, as summarized in Table 2.
It is acknowledged that an exact coefficient of determination (R2 = 1) is rarely achieved in experimental studies. In this case, the result arises because the frequency shifts measured by the nanoVNA fall exactly on the regression line within the instrument’s frequency step size. Thus, while the regression software outputs R2 = 1, this reflects the finite resolution and step size of the measurements rather than an absolute absence of error. In practice, small uncertainties exist due to instrument noise and environmental variations, but these are below the detectable threshold of the setup. Consequently, the reported R2 value should be interpreted as an indication of very high linearity within the limits of measurement resolution.
The sensor’s detection capability is also influenced by its structural design, particularly the dimensions of the split-ring resonators and their proximity to the coplanar waveguide, which directly affect the localized electric field strength and, consequently, the sensitivity.
In addition to the above, we would like to highlight that the sensitivity of the sensor, determined as the slope of the resonant frequency shift against glucose concentration (Figure 9), is approximately 1.75 kHz/(mg/dL). This indicates a measurable and consistent response of the resonant frequency to sugar concentration changes within the studied range. The observed high linearity and repeatability further support the sensor’s reliable sensitivity for aqueous sugar detection, which is the primary focus of this work. Furthermore, the figure of merit (FOM) was evaluated using the unloaded sensor’s response. With a measured full width at half maximum (FWHM) of 94.5 MHz at the resonant frequency of 2.045 GHz (0 mg/dL), the calculated FOM is 0.000309 (mg/dL)−1. This analysis confirms that the sensor exhibits a measurable frequency shift relative to its resonance bandwidth, validating its sensing capability within the tested range.
All measurements in this study were conducted under consistent ambient conditions (~25 °C), which aligns with typical real-world scenarios for beverage testing. This reflects the intended use case of the sensor, where consumers or quality-control personnel are unlikely to employ temperature-controlled environments. Nonetheless, the dielectric properties of aqueous sugar solutions are known to vary with temperature due to changes in molecular relaxation dynamics and viscosity. Such effects can shift the resonant frequency by altering the effective permittivity of the medium. While the present work focuses on demonstrating accuracy and repeatability under standard ambient conditions, future studies will incorporate temperature-controlled experiments to quantify the thermal sensitivity of the sensor. Such evaluations will further extend its applicability to industrial or laboratory environments where temperature fluctuations are significant.
6. Extending the Testing Range
The present sensor demonstrates a linear response to glucose concentrations up to 12,000 mg/dL, which already exceeds most reported microwave beverage sensors. To further extend the testing range, several strategies may be employed. First, the geometrical parameters of the SRRs may be modified to tune the baseline resonant frequency: larger ring radii or narrower gaps lower the resonance and enhance sensitivity to higher dielectric loads, whereas smaller radii and wider gaps increase the resonance, allowing improved resolution at lower concentrations. Second, substrate engineering provides another path. Substrates with lower dielectric loss tangents (e.g., Rogers laminates) would reduce resonance broadening and maintain linearity at higher sugar concentrations, while higher-permittivity substrates could be used to compress the resonance for improved sensitivity at low concentrations. Third, multi-resonant or cascaded SRR designs could be incorporated to cover overlapping frequency windows, thereby enabling detection over wider concentration ranges. Finally, advanced regression models that account for nonlinear responses at very high concentrations could be implemented to extend the effective calibration range without altering the physical design. These approaches suggest clear avenues for extending the applicability of the sensor to broader concentration spans or more complex liquid mixtures.
7. Conclusions
A low-cost, portable metamaterial-based microwave planar sensor was developed for predicting sugar concentrations in beverages. Fabricated on an FR-4 substrate (30 mm × 50 mm × 1.6 mm), the sensor exhibits strong agreement between theoretical, simulated, and measured resonant frequencies. The sensing mechanism relies on frequency shifts induced by dielectric loading, which were shown to correlate linearly with sugar concentration.
Validation against two commercial beverages demonstrated that the sensor could accurately reproduce the labeled sugar contents, confirming its real-world applicability. The device achieved a wide dynamic testing range (0 to 12,000 mg/dL) with excellent linearity (R2 = 1), high repeatability across trials, and good reusability under ambient conditions.
In summary, the proposed sensor is distinguished by its wide dynamic range (0 to 12,000 mg/dL), perfect linearity (R2 = 1), high repeatability, and validated accuracy against the labeled sugar content in commercial beverages. Unlike conventional methods, it operates reagent-free and is unaffected by beverage opacity, enabling rapid and user-friendly sugar concentration detection. These highlights underscore the sensor’s practical potential for consumer, industrial, and quality-control applications.
Although all measurements in this study were conducted at ~25 °C, the dielectric properties of sugar solutions are known to vary with temperature. Future work will therefore incorporate temperature-controlled experiments to quantify thermal sensitivity and extend the sensor’s application to more complex beverage matrices such as juices, dairy-based drinks, and alcoholic solutions.
Author Contributions
Conceptualization, V.D.; validation, K.H.T.; formal analysis, H.N.; data curation, Z.K.C.; writing—original draft, K.H.Y.; writing—review and editing, H.N. and K.W.T.; supervision, N.F.A.R.; project administration, H.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. The APC was partially funded by Universiti Tunku Abdul Rahman.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| CPW | Coplanar Waveguide |
| CSRR | Complementary Split-Ring Resonator |
| FOM | Figure of Merit |
| FWHM | Full Width at Half Maximum |
| LOD | Limit of Detection |
| LOQ | Limit of Quantification |
| MAPE | Mean Absolute Percentage Error |
| RMSE | Root Mean Square Error |
| S11 | Reflection Coefficient (Scattering Parameter) |
| SD | Standard Deviation |
| VNA | Vector Network Analyzer |
References
- Tahmassebi, J.F.; BaniHani, A. Impact of soft drinks to health and economy: A critical review. Eur. Arch. Paediatr. Dent. 2020, 21, 109–117. [Google Scholar] [CrossRef]
- Chi, D.L.; Scott, J.M. Added sugar and dental caries in children: A scientific update and future steps. Dent. Clin. N. Am. 2019, 63, 17–33. [Google Scholar] [CrossRef] [PubMed]
- Apovian, C. Sugar-sweetened soft drinks, obesity, and type 2 diabetes. JAMA 2004, 292, 978–979. [Google Scholar] [CrossRef] [PubMed]
- Hu, F.B.; Malik, V.S. Sugar-sweetened beverages and risk of obesity and type 2 diabetes: Epidemiologic evidence. Physiol. Behav. 2010, 100, 47–54. [Google Scholar] [CrossRef]
- Caprio, S. Calories from soft drinks—Do they matter. N. Engl. J. Med. 2012, 367, 1462–1463. [Google Scholar] [CrossRef]
- Greenwood, D.C.; Threapleton, D.E.; Evans, C.E.; Cleghorn, C.L.; Nykjaer, C.; Woodhead, C.; Burley, V.J. Association between sugar-sweetened and artificially sweetened soft drinks and type 2 diabetes: Systematic review and dose–response metaanalysis of prospective studies. Br. J. Nutr. 2014, 112, 725–734. [Google Scholar] [CrossRef]
- Oti, W.J. Using Refractometer to Determine the Sugar Content in Soft Drinks Commonly Consumed in Abakaliki, Nigeria. IOSR J. Appl. Chem. 2016, 9, 89–91. [Google Scholar]
- Agbazue, V.E.; Ibezim, A.; Ekere, N.R. Assessment of sugar levels in different soft Drinks. Int. J. Chem. Sci. 2014, 12, 327–334. [Google Scholar]
- Ramasami, P.; Jhaumeer-Laulloo, S.; Rondeau, P.; Cadet, F.; Seepujak, H.; Seeruttun, A. Quantification of sugars in soft drinks and fruit juices by density, refractometry, infrared spectroscopy and statistical methods. S. Afr. J. Chem. 2004, 57, 24–27. [Google Scholar]
- Morris, A.S.; Langari, R. Summary of Other Measurements. In Measurement and Instrumentation: Theory and Application; Academic Press: Waltham, MA, USA, 2016; pp. 633–672. [Google Scholar]
- Jiang, W.; Marini, G.; van Berkel, N.; Sarsenbayeva, Z.; Tan, Z.; Luo, C.; He, X.; Dingler, T.; Goncalves, J.; Kawahara, Y.; et al. Probing sucrose contents in everyday drinks using miniaturized near-infrared spectroscopy scanners. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2019, 3, 1–25. [Google Scholar] [CrossRef]
- Yusmawati, W.Y.W.; Chuah, H.P.; Mahmood, M.Y.W. Optical properties and sugar content determination of commercial carbonated drinks using surface plasmon resonance. Am. J. Appl. Sci. 2007, 4, 104. [Google Scholar] [CrossRef]
- Seki, A.; Narita, K.; Watanabe, K. Refractive index measurement in sucrose solution and beverage using surface plasmon resonance sensor based on hetero-core structured fiber optic. Procedia Chem. 2016, 20, 115–117. [Google Scholar] [CrossRef]
- Ashokkumar, P.; Bell, J.; Buurman, M.; Rurack, K. Analytical platform for sugar sensing in commercial beverages using a fluorescent BODIPY “light-up” probe. Sens. Actuators B Chem. 2018, 256, 609–615. [Google Scholar] [CrossRef]
- Cinti, S.; Marrone, R.; Mazzaracchio, V.; Moscone, D.; Arduini, F. Novel bio-lab-on-a-tip for electrochemical glucose sensing in commercial beverages. Biosens. Bioelectron. 2020, 165, 112334. [Google Scholar] [CrossRef]
- Nielsen, S.S. (Ed.) Chapter 6: Carbohydrates. In Food Analysis, 5th ed.; Springer: Cham, Switzerland, 2017; pp. 137–149. [Google Scholar]
- Amarasinghe, C.; Ranasinghe, N. SipBit: A Sensing Platform to Recognize Beverage Type, Volume, and Sugar Content Using Electrical Impedance Spectroscopy and Deep Learning. In Proceedings of the CHI Conference on Human Factors in Computing Systems Extended Abstracts, New Orleans, LA, USA, 9 April–5 May 2022; pp. 1–8. [Google Scholar]
- Wang, J. Electrochemical glucose biosensors. Chem. Rev. 2008, 108, 814–825. [Google Scholar] [CrossRef]
- Ozaki, Y.; Huck, C.; Tsuchikawa, S.; Engelsen, S.B. (Eds.) Near-Infrared Spectroscopy: Theory, Spectral Analysis, Instrumentation, and Applications; Springer Nature: Singapore, 2020. [Google Scholar]
- Swallow, K.W.; Low, N.H. Analysis and quantitation of the carbohydrates in honey using high-performance liquid chromatography. J. Agric. Food Chem. 1990, 38, 1828–1832. [Google Scholar] [CrossRef]
- Kim, H.Y.; Jia, L.L.; Siu, H.L.; Dakulagi, V.; Mazlan, A.U. Microwave Sensor for Sodium Chloride Density Measurement in Aqueous Solutions. J. Eng. Technol. Appl. Phys. 2024, 6, 52–56. [Google Scholar] [CrossRef]
- Belay, A.; Assefa, G. Concentration, wavelength and temperature dependent refractive index of sugar solutions and methods of determination contents of sugar in soft drink beverages using laser lights. J. Lasers Opt. Photonics 2018, 5, 1000187. [Google Scholar]
- Snyder, C.F.; Hattenburg, A.T. Refractive Indices and Densities of Aqueous Solutions of Invert Sugar; NBS Monograph 64, National Bureau of Standards: Gaithersburg, MD, USA; Government Printing Office: Washington, DC, USA, 1963. Available online: https://nvlpubs.nist.gov/nistpubs/Legacy/MONO/nbsmonograph64.pdf (accessed on 4 July 2025).
- Bento, L.S.M. Calculation of refractive index of light in water, glucose, fructose and sucrose solutions. Sugar Ind. 2019, 144, 32–40. [Google Scholar] [CrossRef]
- Odabashyan, L.; Babajanyan, A.; Baghdasaryan, Z.; Kim, S.; Kim, J.; Friedman, B.; Lee, J.-H.; Lee, K. Real-Time Noninvasive Measurement of Glucose Concentration Using a Modified Hilbert Shaped Microwave Sensor. Sensors 2019, 19, 5525. [Google Scholar] [CrossRef] [PubMed]
- Turgul, V.; Kale, I. Permittivity extraction of glucose solutions through artificial neural networks and non-invasive microwave glucose sensing. Sens. Actuators A Phys. 2018, 277, 65–72. [Google Scholar] [CrossRef]
- Saleh, G.; Ateeq, I.S.; Al-Naib, I. Glucose level sensing using single asymmetric split ring resonator. Sensors 2021, 21, 2945. [Google Scholar] [CrossRef]
- Omer, A.E.; Shaker, G.; Safavi-Naeini, S.; Kokabi, H.; Alquié, G.; Deshours, F.; Shubair, R.M. Low-cost portable microwave sensor for non-invasive monitoring of blood glucose level: Novel design utilizing a four-cell CSRR hexagonal configuration. Sci. Rep. 2020, 10, 15200. [Google Scholar] [CrossRef]
- Falcone, F.; Martín, F.; Bonache, J.; Marqués, R.; Lopetegi, T.; Sorolla, M. Left handed coplanar waveguide band pass filters based on bi-layer split ring resonators. IEEE Microw. Wirel. Compon. Lett. 2004, 14, 10–12. [Google Scholar] [CrossRef]
- Baena, J.D.; Bonache, J.; Martín, F.; Sillero, R.M.; Falcone, F.; Lopetegi, T.; Laso, M.A.; Garcia-Garcia, J.; Gil, I.; Portillo, M.F.; et al. Equivalent-circuit models for split-ring resonators and complementary split-ring resonators coupled to planar transmission lines. IEEE Trans. Microw. Theory Tech. 2005, 53, 1451–1461. [Google Scholar] [CrossRef]
- Saha, C.; Siddiqui, J.Y. Versatile CAD formulation for estimation of the resonant frequency and magnetic polarizability of circular split ring resonators. Int. J. RF Microw. Comput.-Aided Eng. 2011, 21, 432–438. [Google Scholar] [CrossRef]
- Bahl, I.; Bhartia, P. Microwave Solid State Circuit Design; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Veyres, C.; Fouad Hanna, V. Extension of the application of conformal mapping techniques to coplanar lines with finite dimensions. Int. J. Electron. Theor. Exp. 1980, 48, 47–56. [Google Scholar] [CrossRef]
- Yeap, K.H.; Lai, K.C.; Lim, S.K.; Low, C.Y. Analysis and comparison of wave propagation in microstrip lines and coplanar waveguides. J. Eng. Sci. Technol. 2017, 12, 1755–1765. [Google Scholar]
- Ebrahimi, A.; Withayachumnankul, W.; Al-Sarawi, S.F.; Abbott, D. Microwave microfluidic sensor for determination of glucose concentration in water. In Proceedings of the 2015 IEEE 15th Mediterranean Microwave Symposium (MMS), Lecce, Italy, 30 November–2 December 2015; pp. 1–3. [Google Scholar]
- Govind, G.; Akhtar, M.J. Metamaterial-inspired microwave microfluidic sensor for glucose monitoring in aqueous solutions. IEEE Sens. J. 2019, 19, 11900–11907. [Google Scholar] [CrossRef]
- Magomya, A.M.; Yebpella, G.G.; Okpaegbe, U.C.; Oko, O.J.; Gambo, S.B. Analysis and health risk assessment of sodium benzoate and potassium sorbate in selected fruit juice and soft drink brands in Nigeria. Int. J. Pharm. Chem. 2020, 5, 54–59. [Google Scholar] [CrossRef]
- Kumari, R.; Patel, P.N.; Yadav, R. An ENG resonator-based microwave sensor for the characterization of aqueous glucose. J. Phys. D Appl. Phys. 2018, 51, 075601. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).