Benchmarking ML Algorithms Against Traditional Correlations for Dynamic Monitoring of Bottomhole Pressure in Nitrogen-Lifted Wells
Abstract
1. Introduction
1.1. The Significance of Predicting Flowing Bottomhole Pressure
1.2. Traditional Prediction Methods
1.3. Machine Learning Models for Predicting BHP
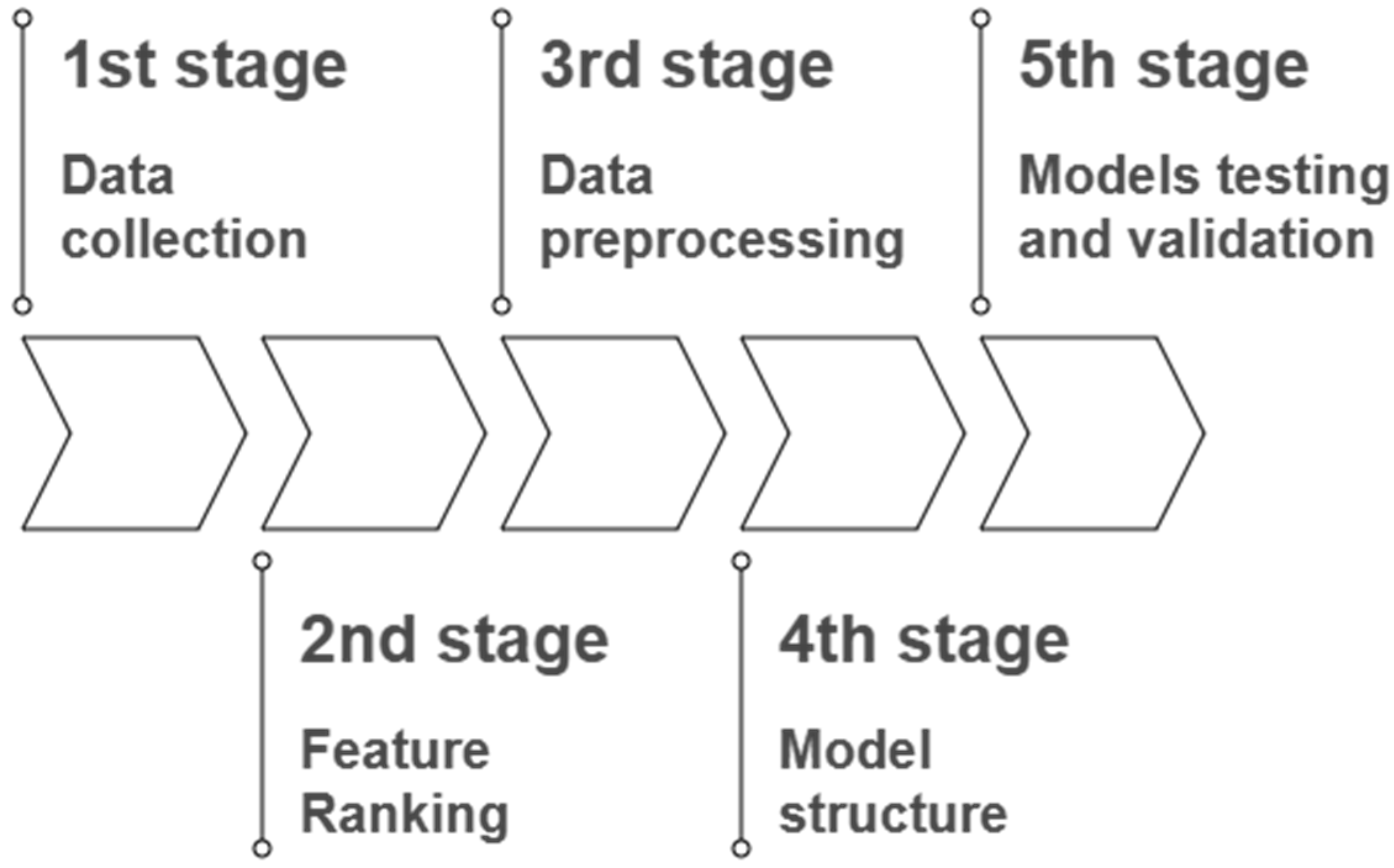
2. Methodology
2.1. Data Collection
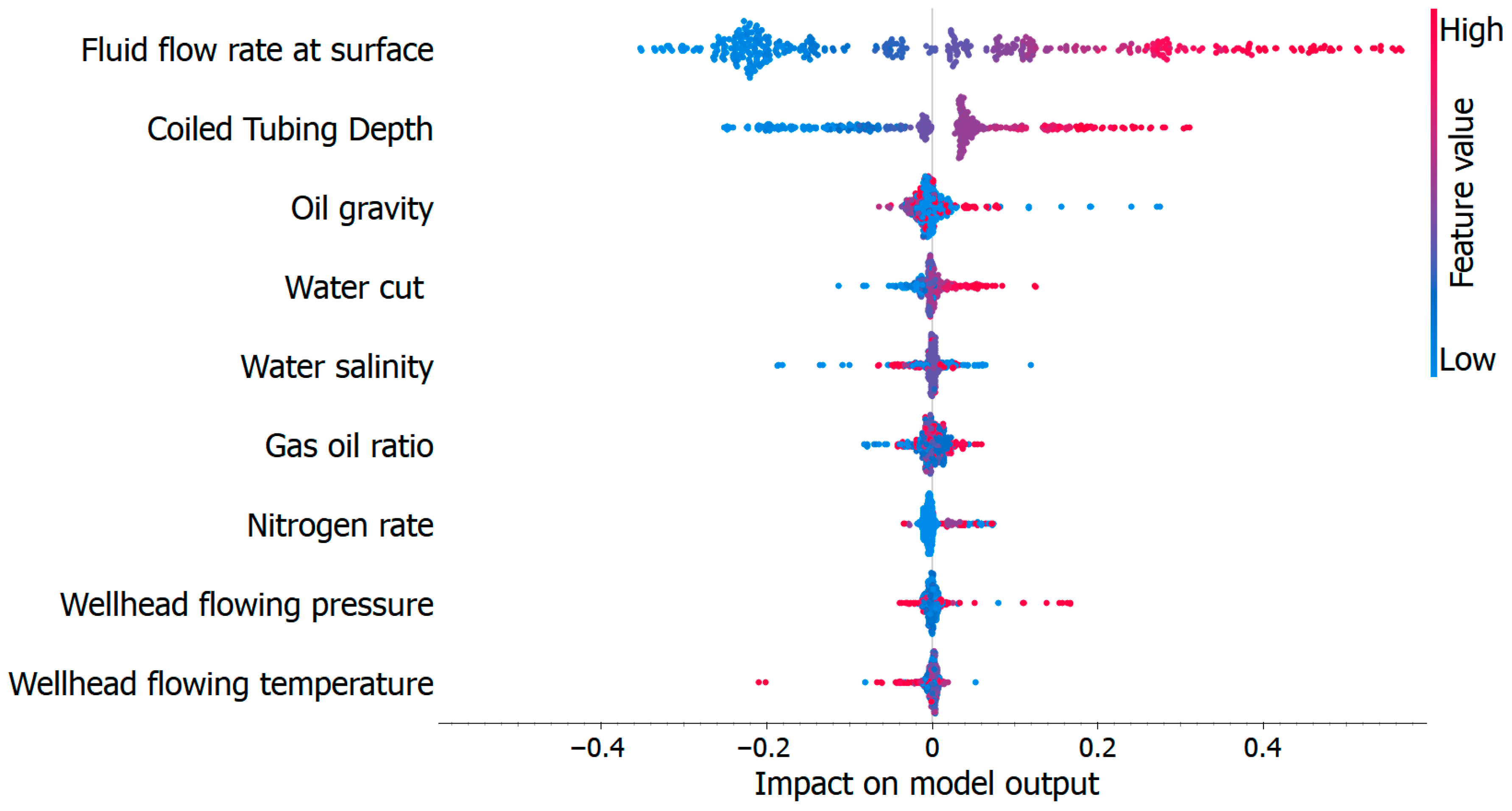
2.2. Feature Ranking
- ▪
- number of paired observations
- ▪
- data values
- ▪
- sum of the product of paired scores
- ▪
- sum of squares
- ▪
- ranks of variables and
- ▪
- covariance of the rank variables
- ▪
- standard deviations of the rank variables
2.3. Data Preprocessing
- ▪
- X is the original (raw) value,
- ▪
- A is the minimum value in the dataset,
- ▪
- B is the maximum value in the dataset,
- ▪
- Y is the normalized value after scaling to the range [0, 1].
2.4. Models Structure
2.4.1. Conventional Predictive Models
2.4.2. Genetic Programming-Based Symbolic Regression
3. Results and Discussion
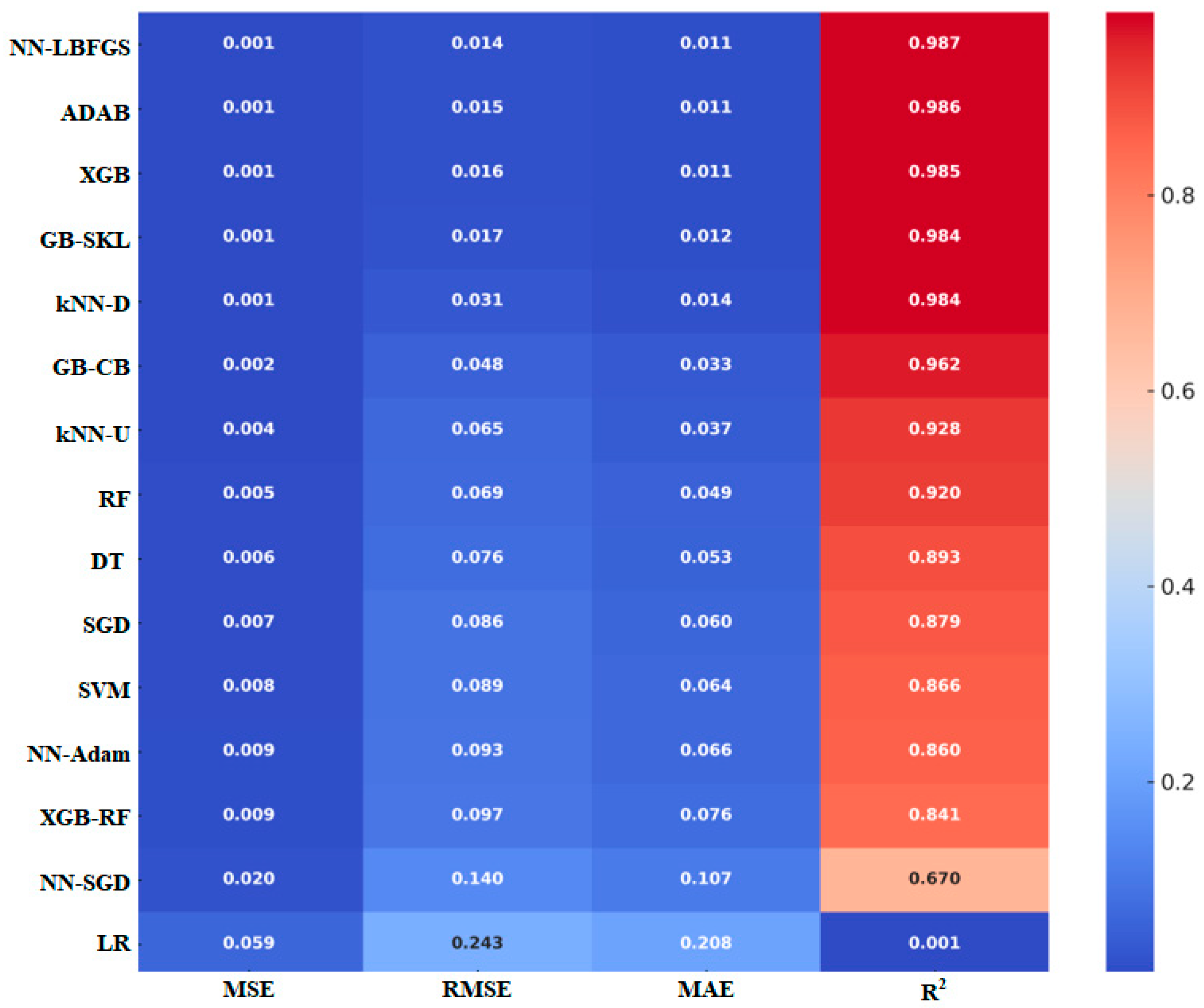
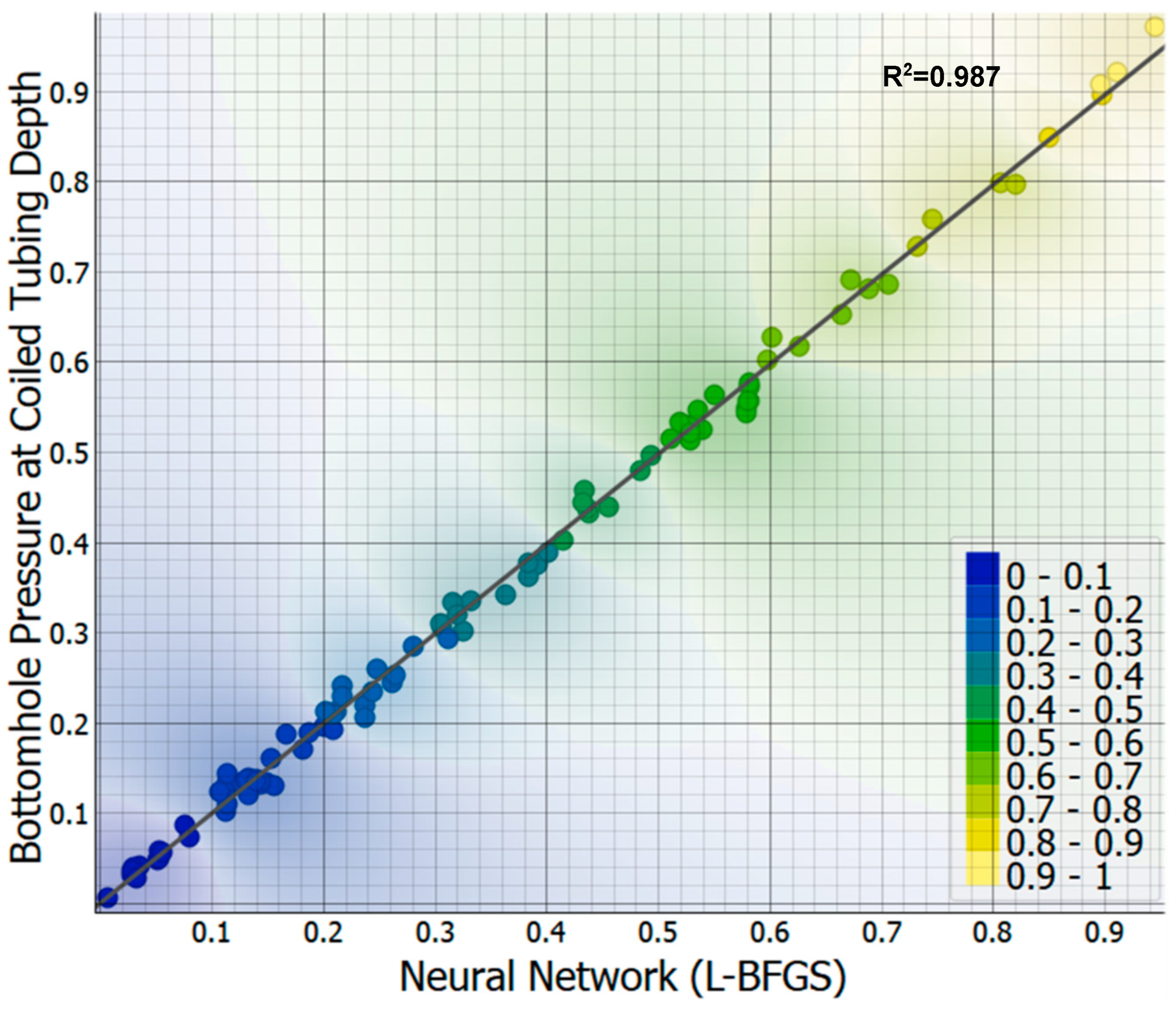
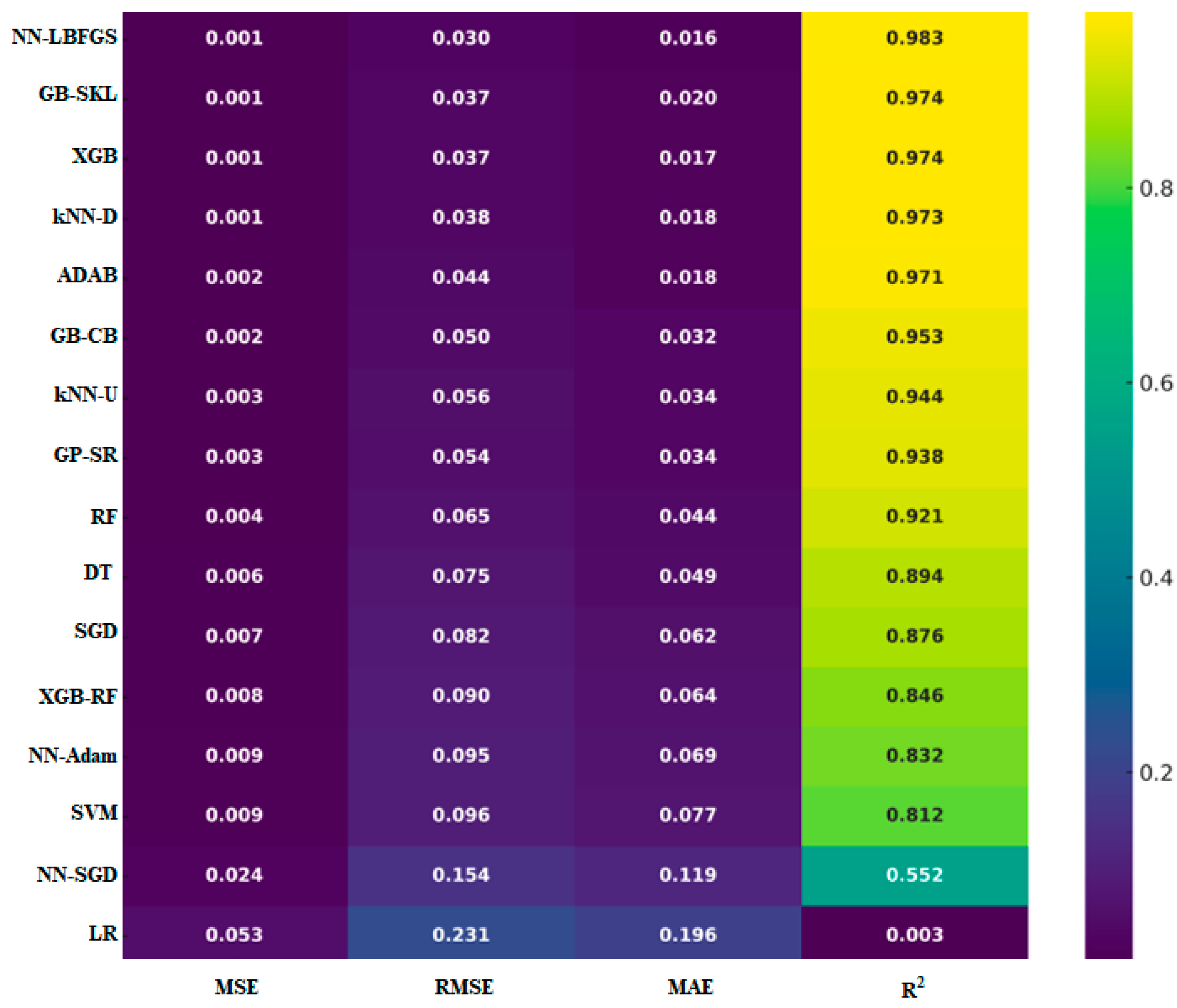
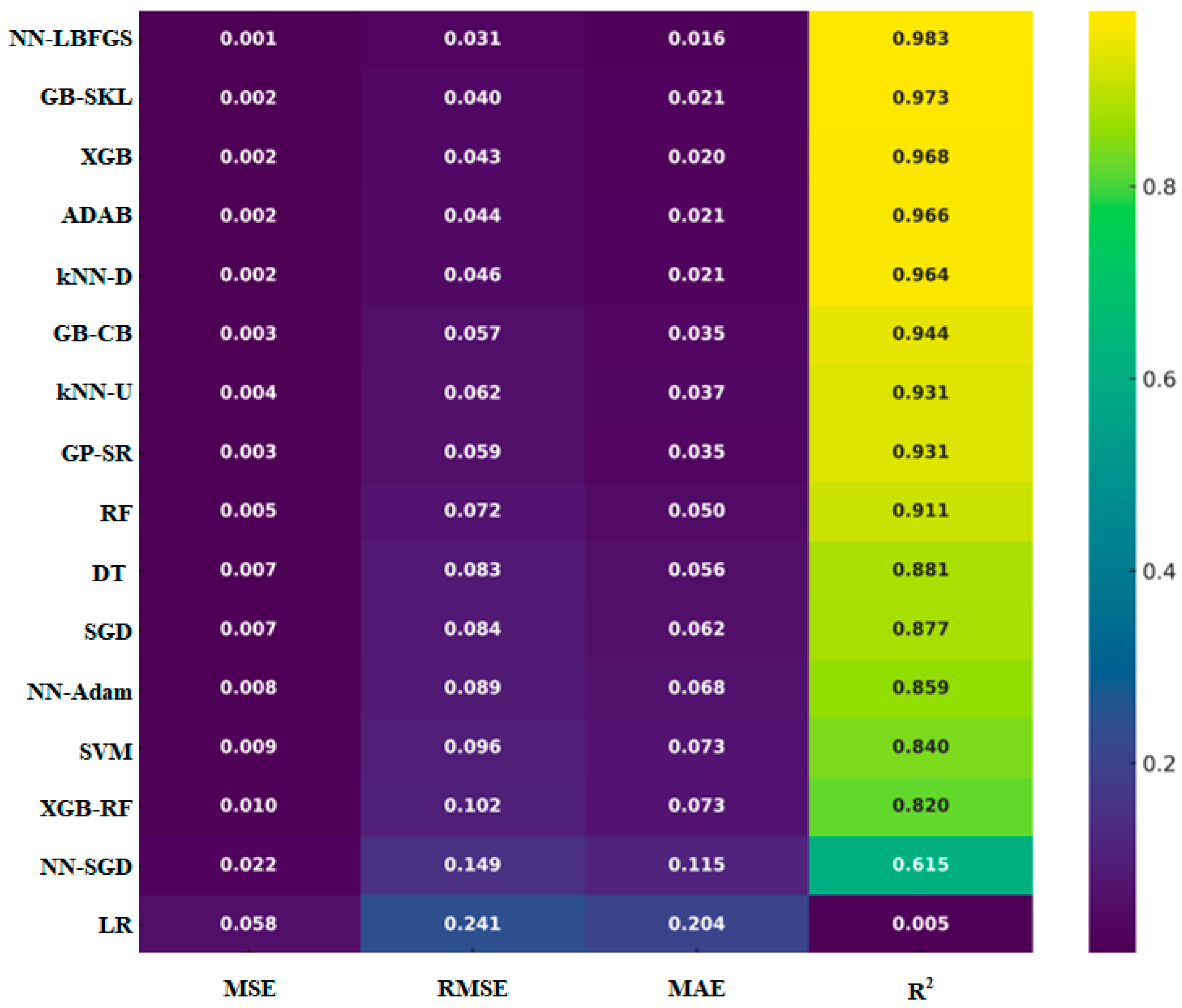
3.1. Model Results
3.2. Model Testing and Validation
3.3. Field Application
3.4. Drawbacks of Machine Learning Techniques in BHP-CTD Forecasting
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AdaBoost | Adaptive Boosting |
| Adam | Adaptive Moment Estimation optimization algorithm |
| BHP | Bottomhole pressure |
| BHP-CT | Bottomhole Pressure at Coiled Tubing Depth |
| CTD | Coiled Tubing Depth |
| DT | Decision Trees |
| FFR-S | Fluid flow rate at surface |
| GB-CB | Gradient Boosting (catboost) |
| GB-SKL | Gradient Boosting (scikit-learn) |
| GOR | Gas–oil ratio |
| GP-SR | Genetic Programming-based Symbolic Regression |
| IQR | Interquartile range |
| kNN-D | K-Nearest Neighbor (By Distances) |
| kNN-U | K-Nearest Neighbor (Uniform) |
| L-BFGS | Limited-memory-Broyden-Fletcher-Goldfarb-Shanno optimization algorithm |
| LR | Linear Regression |
| MAE | Mean absolute error |
| MAPE | Mean absolute percent error |
| ML | Machine learning |
| MSE | Mean square error |
| NN | Neural Network |
| NR | Nitrogen rate |
| OG | Oil gravity |
| r | Pearson’s correlation coefficient |
| R2 | Correlation coefficients |
| RF | Random Forest |
| RMSE | Root mean square error |
| RRSCV | Repeated random sampling cross-validation |
| SGD | Stochastic Gradient Descent |
| SHAP | SHapley Additive exPlanations |
| SVMs | Support Vector Machines |
| WC | Water cut |
| WHP | Wellhead pressure |
| WHT | Wellhead temperature |
| WS | Water salinity |
| XGB | Extreme Gradient Boosting (xgboost) |
| XGB-RF | Extreme Gradient Boosting Random Forest (xgboost) |
| ρ | Spearman’s rank correlation coefficient |
References
- Hashmi, U.I.; Osisanya, S.; Rahman, M.; Ghosh, B.; Subaihi, M.H.; Kuwair, H.F.B.; Fathy, A.; Afagwu, C.; Mahmoud, M. Optimization of Nitrogen Lifting Operation in Horizontal Wells of Carbonate Formation. In International Petroleum Technology Conference; IPTC: Riyadh, Saudi Arabia, 2022. [Google Scholar] [CrossRef]
- Aitken, B.; Livescu, S.; Craig, S. Coiled Tubing Software Models and Field Applications–A Review. J. Pet. Sci. Eng. 2019, 182, 106308. [Google Scholar] [CrossRef]
- Han, G.; Ma, G.; Gao, Y.; Zhang, H.; Ling, K. A New Transient Model to Simulate and Optimize Liquid Unloading with Coiled Tubing Conveyed Gas Lift. J. Pet. Sci. Eng. 2021, 200, 108394. [Google Scholar] [CrossRef]
- Gao, K.; Zhao, Q.; Zhang, X.; Shang, S.; Guan, L.; Li, J.; Xu, N.; Cao, D.; Tao, L.; Yuan, H.; et al. Temperature Field Study of Offshore Heavy Oil Wellbore with Coiled Tubing Gas Lift-Assisted Lifting. Geofluids 2023, 2023, 8936092. [Google Scholar] [CrossRef]
- Zand, N.; Arjmand, Y.; Motamedikia, M.; Pourbahador, M. Economic Equation and Optimization of Artificial Gas Lift with Coil Tubing Based on Dynamic Simulation in One of Iranian Offshore Fields. IJNC 2020, 8, 111–130. [Google Scholar] [CrossRef]
- Michel, G.; Civan, F. Modeling Rapid Multiphase Flow in Wells and Pipelines Under Nonequilibrium and Nonisothermal Conditions. In Proceedings of the Rocky Mountain Oil & Gas Technology Symposium, Denver, CO, USA, 16–18 April 2007; SPE: Richardson, TX, USA, 2007. [Google Scholar] [CrossRef]
- Yudin, E.; Khabibullin, R.; Smirnov, N.; Vodopyan, A.; Goridko, K.; Chigarev, G.; Zamakhov, S. New Applications of Transient Multiphase Flow Models in Wells and Pipelines for Production Management. In Proceedings of the SPE Russian Petroleum Technology Conference, Virtual, 26–29 October 2020; SPE: Richardson, TX, USA, 2020. [Google Scholar] [CrossRef]
- Tyagi, A.; Gupta, A. Machine Learning Based Prediction of Pressure Drop, Liquid-Holdup and Flow Pattern in Multiphase Flows. In SPE EuropEC—Europe Energy Conference featured at the 84th EAGE Annual Conference & Exhibition, Vienna, Austria, 5–8 June 2023; SPE: Richardson, TX, USA, 2023. [Google Scholar] [CrossRef]
- Cremaschi, S.; Kouba, G.E.; Subramani, H.J. Characterization of Confidence in Multiphase Flow Predictions. Energy Fuels 2012, 26, 4034–4045. [Google Scholar] [CrossRef]
- Szalinski, L.; Abdulkareem, L.A.; Da Silva, M.J.; Thiele, S.; Beyer, M.; Lucas, D.; Hernandez Perez, V.; Hampel, U.; Azzopardi, B.J. Comparative Study of Gas–Oil and Gas–Water Two-Phase Flow in a Vertical Pipe. Chem. Eng. Sci. 2010, 65, 3836–3848. [Google Scholar] [CrossRef]
- Al-Qasim, A.S.; Almudairis, F.; Bin Omar, A.; Omair, A. Optimizing Production Facilities Using a Transient Multiphase Flow Simulator. In Proceedings of the ASME 2019 38th International Conference on Ocean, Offshore and Arctic Engineering, Petroleum Technology. Glasgow, Scotland, UK, 9–14 June 2019; American Society of Mechanical Engineers: Glasgow, Scotland, UK, 2019; Volume 8: Polar and Arctic Sciences and Technology. [Google Scholar] [CrossRef]
- Jacobs, T. The New Pathways of Multiphase Flow Modeling. J. Pet. Technol. 2015, 67, 62–68. [Google Scholar] [CrossRef]
- Danielson, T.J. Transient Multiphase Flow: Past, Present, and Future with Flow Assurance Perspective. Energy Fuels 2012, 26, 4137–4144. [Google Scholar] [CrossRef]
- Ye, J.; Guo, L. Multiphase Flow Pattern Recognition in Pipeline–Riser System by Statistical Feature Clustering of Pressure Fluctuations. Chem. Eng. Sci. 2013, 102, 486–501. [Google Scholar] [CrossRef]
- Abubakar, A.; Al-Wahaibi, Y.; Al-Wahaibi, T.; Al-Hashmi, A.; Al-Ajmi, A.; Eshrati, M. Effect of Low Interfacial Tension on Flow Patterns, Pressure Gradients and Holdups of Medium-Viscosity Oil/Water Flow in Horizontal Pipe. Exp. Therm. Fluid Sci. 2015, 68, 58–67. [Google Scholar] [CrossRef]
- Giraudeau, M.; Mureithi, N.W.; Pettigrew, M.J. Two-Phase Flow-Induced Forces on Piping in Vertical Upward Flow: Excitation Mechanisms and Correlation Models. J. Press. Vessel Technol. 2013, 135, 030907. [Google Scholar] [CrossRef]
- Zou, S.; Guo, L.; Xie, C. Fast Recognition of Global Flow Regime in Pipeline-Riser System by Spatial Correlation of Differential Pressures. Int. J. Multiph. Flow 2017, 88, 222–237. [Google Scholar] [CrossRef]
- Ahmadi, M.A.; Galedarzadeh, M.; Shadizadeh, S.R. Low Parameter Model to Monitor Bottom Hole Pressure in Vertical Multiphase Flow in Oil Production Wells. Petroleum 2016, 2, 258–266. [Google Scholar] [CrossRef]
- Pagan, E.; Williams, W.C.; Kam, S.; Waltrich, P.J. A Simplified Model for Churn and Annular Flow Regimes in Small- and Large-Diameter Pipes. Chem. Eng. Sci. 2017, 162, 309–321. [Google Scholar] [CrossRef]
- Kaji, R.; Azzopardi, B.J. The Effect of Pipe Diameter on the Structure of Gas/Liquid Flow in Vertical Pipes. Int. J. Multiph. Flow 2010, 36, 303–313. [Google Scholar] [CrossRef]
- Nydal, O.J. Dynamic Models in Multiphase Flow. Energy Fuels 2012, 26, 4117–4123. [Google Scholar] [CrossRef]
- Zhang, H.-Q.; Sarica, C.; Pereyra, E. Review of High-Viscosity Oil Multiphase Pipe Flow. Energy Fuels 2012, 26, 3979–3985. [Google Scholar] [CrossRef]
- Firouzi, M.; Towler, B.; Rufford, T.E. Developing New Mechanistic Models for Predicting Pressure Gradient in Coal Bed Methane Wells. J. Nat. Gas Sci. Eng. 2016, 33, 961–972. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S.; Sayarpour, M. Simplified Two-Phase Flow Modeling in Wellbores. J. Pet. Sci. Eng. 2010, 72, 42–49. [Google Scholar] [CrossRef]
- Thome, J.R.; Bar-Cohen, A.; Revellin, R.; Zun, I. Unified Mechanistic Multiscale Mapping of Two-Phase Flow Patterns in Microchannels. Exp. Therm. Fluid Sci. 2013, 44, 1–22. [Google Scholar] [CrossRef]
- Sarica, C.; Zhang, H.-Q.; Wilkens, R.J. Sensitivity of Slug Flow Mechanistic Models on Slug Length. J. Energy Resour. Technol. 2011, 133, 043001. [Google Scholar] [CrossRef]
- Meziou, A.; Chaari, M.; Franchek, M.; Borji, R.; Grigoriadis, K.; Tafreshi, R. Low-Dimensional Modeling of Transient Two-Phase Flow in Pipelines. J. Dyn. Syst. Meas. Control 2016, 138, 101008. [Google Scholar] [CrossRef]
- Ali, A.A.; Abdul-Majeed, G.H.; Al-Sarkhi, A. Review of Multiphase Flow Models in the Petroleum Engineering: Classifications, Simulator Types, and Applications. Arab. J. Sci. Eng. 2025, 50, 4413–4456. [Google Scholar] [CrossRef]
- Abdul-Majeed, G.H.; Al-Mashat, A.M. A Unified Correlation for Predicting Slug Liquid Holdup in Viscous Two-Phase Flow for Pipe Inclination from Horizontal to Vertical. SN Appl. Sci. 2019, 1, 71. [Google Scholar] [CrossRef]
- Barnea, D.; Roitberg, E.; Shemer, L. Spatial Distribution of Void Fraction in the Liquid Slug in the Whole Range of Pipe Inclinations. Int. J. Multiph. Flow 2013, 52, 92–101. [Google Scholar] [CrossRef]
- Mikhailov, V.G.; Pashali, A.A. Improvement of Methods for Calculation of Gas-Liquid Slug of Flow in Pipelines. Neftegazov. Delo 2023, 21, 88–95. [Google Scholar] [CrossRef]
- Abdul-Majeed, G.; Al-Sarkhi, A.; Al-Fatlawi, O.F.; Mohmmed, A.O. Empirical Model for Predicting Slug-Pseudo Slug and Slug-Churn Transitions of Upward Air/Water Flow. Geoenergy Sci. Eng. 2025, 246, 213613. [Google Scholar] [CrossRef]
- Pedersen, S.; Durdevic, P.; Yang, Z. Challenges in Slug Modeling and Control for Offshore Oil and Gas Productions: A Review Study. Int. J. Multiph. Flow 2017, 88, 270–284. [Google Scholar] [CrossRef]
- Liang, C.; Xiong, W.; Wang, H.; Wang, Z. Experimental and OLGA Modeling Investigation for Slugging in Underwater Compressed Gas Energy Storage Systems. Appl. Sci. 2023, 13, 9575. [Google Scholar] [CrossRef]
- Rushd, S.; Gazder, U.; Qureshi, H.J.; Arifuzzaman, M. Advanced Machine Learning Applications to Viscous Oil-Water Multi-Phase Flow. Appl. Sci. 2022, 12, 4871. [Google Scholar] [CrossRef]
- Gharieb, A.; Adel Gabry, M.; Algarhy, A.; Elsawy, M.; Darraj, N.; Adel, S.; Taha, M.; Hesham, A. Revealing Insights in Evaluating Tight Carbonate Reservoirs: Significant Discoveries via Statistical Modeling. An In-Depth Analysis Using Integrated Machine Learning Strategies. In Proceedings of the GOTECH, Dubai, United Arab Emirates, 7–9 May 2024; SPE: Richardson, TX, USA, 2024. [Google Scholar] [CrossRef]
- Ahmadi, M.A.; Chen, Z. Machine Learning Models to Predict Bottom Hole Pressure in Multi-phase Flow in Vertical Oil Production Wells. Can. J. Chem. Eng. 2019, 97, 2928–2940. [Google Scholar] [CrossRef]
- Nashed, S.; Moghanloo, R. Hybrid Symbolic Regression and Machine Learning Approaches for Modeling Gas Lift Well Performance. Fluids 2025, 10, 161. [Google Scholar] [CrossRef]
- Hafsa, N.; Rushd, S.; Yousuf, H. Comparative Performance of Machine-Learning and Deep-Learning Algorithms in Predicting Gas–Liquid Flow Regimes. Processes 2023, 11, 177. [Google Scholar] [CrossRef]
- Khan, A.M.; Luo, Y.; Ugarte, E.; Bannikov, D. Physics-Informed Machine Learning for Hydraulic Fracturing—Part I: The Backbone Model. In Proceedings of the SPE Conference at Oman Petroleum & Energy Show, Muscat, Oman, 22–24 April 2024; SPE: Richardson, TX, USA, 2024. [Google Scholar] [CrossRef]
- Nashed, S.; Moghanloo, R. Replacing Gauges with Algorithms: Predicting Bottomhole Pressure in Hydraulic Fracturing Using Advanced Machine Learning. Eng 2025, 6, 73. [Google Scholar] [CrossRef]
- Gharieb, A.; Ibrahim, A.F.; Gabry, M.A.; Elsawy, M.; Algarhy, A.; Darraj, N. Automated Borehole Image Interpretation Using Computer Vision and Deep Learning. SPE J. 2024, 29, 6918–6933. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, Q.; Rong, W.; Zeng, J.; Ren, Y.; Chen, H. Permeability Prediction of Carbonate Reservoir Based on Nuclear Magnetic Resonance (NMR) Logging and Machine Learning. Energies 2024, 17, 1458. [Google Scholar] [CrossRef]
- Thabet, S.; Zidan, H.M.; Elhadidy, A.; Helmy, A.; Yehia, T.; Elnaggar, H.; Elshiekh, M. Prediction of Total Skin Factor in Perforated Wells Using Models Powered by Deep Learning and Machine Learning. In Proceedings of the GOTECH, Dubai, United Arab Emirates, 7–9 May 2024; SPE: Richardson, TX, USA, 2024; p. D011S004R001. [Google Scholar] [CrossRef]
- Hussain, M.; Liu, S.; Ashraf, U.; Ali, M.; Hussain, W.; Ali, N.; Anees, A. Application of Machine Learning for Lithofacies Prediction and Cluster Analysis Approach to Identify Rock Type. Energies 2022, 15, 4501. [Google Scholar] [CrossRef]
- Laalam, A.; Tomomewo, O.S.; Khalifa, H.; Bouabdallah, N.; Ouadi, H.; Tran, T.H.; Perdomo, M.E. Comparative Analysis Between Empirical Correlations and Time Series Models for the Prediction and Forecasting of Unconventional Bakken Wells Production. In Proceedings of the Asia Pacific Unconventional Resources Symposium, Brisbane, Australia, 14–15 November 2023; SPE: Richardson, TX, USA, 2023. [Google Scholar] [CrossRef]
- Thabet, S.A.; Zidan, H.A.; Elhadidy, A.A.; Helmy, A.G.; Yehia, T.A.; Elnaggar, H.; Elshiekh, M. Application of Machine Learning and Deep Learning to Predict Production Rate of Sucker Rod Pump Wells. In Proceedings of the GOTECH, Dubai, United Arab Emirates, 7–9 May 2024; SPE: Richardson, TX, USA, 2024; p. D021S035R001. [Google Scholar] [CrossRef]
- Zhu, R.; Li, N.; Duan, Y.; Li, G.; Liu, G.; Qu, F.; Long, C.; Wang, X.; Liao, Q.; Li, G. Well-Production Forecasting Using Machine Learning with Feature Selection and Automatic Hyperparameter Optimization. Energies 2024, 18, 99. [Google Scholar] [CrossRef]
- Al Selaiti, I.; Mata, C.; Saputelli, L.; Badmaev, D.; Alatrach, Y.; Rubio, E.; Mohan, R.; Quijada, D. Robust Data Driven Well Performance Optimization Assisted by Machine Learning Techniques for Natural Flowing and Gas-Lift Wells in Abu Dhabi. In Proceedings of the SPE Annual Technical Conference and Exhibition, Virtual, 26–29 October 2020; SPE: Richardson, TX, USA, 2020. [Google Scholar] [CrossRef]
- Gharieb, A.; Zidan, H.; Darraj, N. Advancing Recovery: A Data-Driven Approach to Enhancing Artificial Lift Pumps Longevity and Fault Detection in Oil Reservoirs Using Deep Learning, Computer Vision, and Dynamometer Analysis. In Proceedings of the SPE Conference at Oman Petroleum & Energy Show, Muscat, Oman, 12–14 May 2025; SPE: Richardson, TX, USA, 2025. [Google Scholar] [CrossRef]
- Andrade Marin, A.; Al Balushi, I.; Al Ghadani, A.; Al Abri, H.; Al Zaabi, A.K.S.; Dhuhli, K.; Al Hadhrami, I.; Al Hinai, S.H.; Al Aufi, F.M.; Al Bimani, A.A.; et al. Real Time Implementation of ESP Predictive Analytics-Towards Value Realization from Data Science. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 15–18 November 2021; SPE: Richardson, TX, USA, 2021. [Google Scholar] [CrossRef]
- Sheikhi Garjan, Y.; Ghaneezabadi, M. Machine Learning Interpretability Application to Optimize Well Completion in Montney. In Proceedings of the SPE Canada Unconventional Resources Conference, Virtual, 28 September–2 October 2020; SPE: Richardson, TX, USA, 2020. [Google Scholar] [CrossRef]
- Nashed, S.; Lnu, S.; Guezei, A.; Ejehu, O.; Moghanloo, R. Downhole Camera Runs Validate the Capability of Machine Learning Models to Accurately Predict Perforation Entry Hole Diameter. Energies 2024, 17, 5558. [Google Scholar] [CrossRef]
- Tan, C.; Chua, A.; Muniandy, S.; Lee, H.; Chai, P. Optimization of Inflow Control Device Completion Design Using Metaheuristic Algorithms and Supervised Machine Learning Surrogate. In Proceedings of the International Petroleum Technology Conference, Kuala Lumpur, Malaysia, 18–20 February 2025; IPTC: Kuala Lumpur, Malaysia, 2025. [Google Scholar] [CrossRef]
- Sami, N.A. Application of Machine Learning Algorithms to Predict Tubing Pressure in Intermittent Gas Lift Wells. Pet. Res. 2022, 7, 246–252. [Google Scholar] [CrossRef]
- Khan, M.R.; Tariq, Z.; Abdulraheem, A. Application of Artificial Intelligence to Estimate Oil Flow Rate in Gas-Lift Wells. Nat. Resour. Res. 2020, 29, 4017–4029. [Google Scholar] [CrossRef]
- Chen, S.; Jones, C.M.; Dai, B.; Shao, W. Developing Live Oil Property Models with Global Fluid Database Using Symbolic Regression. In Proceedings of the SPWLA 64th Annual Symposium Transactions, Lake Conroe, TX, USA, 10–14 June 2023. [Google Scholar] [CrossRef]
- Abooali, D.; Khamehchi, E. Estimation of Dynamic Viscosity of Natural Gas Based on Genetic Programming Methodology. J. Nat. Gas Sci. Eng. 2014, 21, 1025–1031. [Google Scholar] [CrossRef]
- Gharieb, A.; Gabry, M.A.; Elsawy, M.; Algarhy, A.; Ibrahim, A.F.; Darraj, N.; Sarker, M.R.; Adel, S. Data Analytics and Machine Learning Application for Reservoir Potential Prediction in Vuggy Carbonate Reservoirs Using Conventional Well Logging. In Proceedings of the SPE Western Regional Meeting, Palo Alto, CA, USA, 16–18 April 2024; SPE: Richardson, TX, USA, 2024. [Google Scholar] [CrossRef]
- Han, D.; Kwon, S. Application of Machine Learning Method of Data-Driven Deep Learning Model to Predict Well Production Rate in the Shale Gas Reservoirs. Energies 2021, 14, 3629. [Google Scholar] [CrossRef]
- Thabet, S.A.; Elhadidy, A.A.; Heikal, M.; Taman, A.; Yehia, T.A.; Elnaggar, H.; Mahmoud, O.; Helmy, A. Next-Gen Proppant Cleanout Operations: Machine Learning for Bottom-Hole Pressure Prediction. In Proceedings of the Mediterranean Offshore Conference, Alexandria, Egypt, 20–22 October 2024; SPE: Richardson, TX, USA, 2024. [Google Scholar] [CrossRef]
- Hyoung, J.; Lee, Y.; Han, S. Development of Machine Learning-Based Production Forecasting for Offshore Gas Fields Using a Dynamic Material Balance Equation. Energies 2024, 17, 5268. [Google Scholar] [CrossRef]
- Alakbari, F.S.; Ayoub, M.A.; Awad, M.A.; Ganat, T.; Mohyaldinn, M.E.; Mahmood, S.M. A Robust Pressure Drop Prediction Model in Vertical Multiphase Flow: A Machine Learning Approach. Sci. Rep. 2025, 15, 13420. [Google Scholar] [CrossRef] [PubMed]
- Wan, C.; Zhu, H.; Xiao, S.; Zhou, D.; Bao, Y.; Liu, X.; Han, Z. Prediction of Pressure Drop in Solid-Liquid Two-Phase Pipe Flow for Deep-Sea Mining Based on Machine Learning. Ocean Eng. 2024, 304, 117880. [Google Scholar] [CrossRef]
- Cui, B.; Chen, L.; Zhang, N.; Shchipanov, A.; Demyanov, V.; Rong, C. Review of Different Methods for Identification of Transients in Pressure Measurements by Permanent Downhole Gauges Installed in Wells. Energies 2023, 16, 1689. [Google Scholar] [CrossRef]
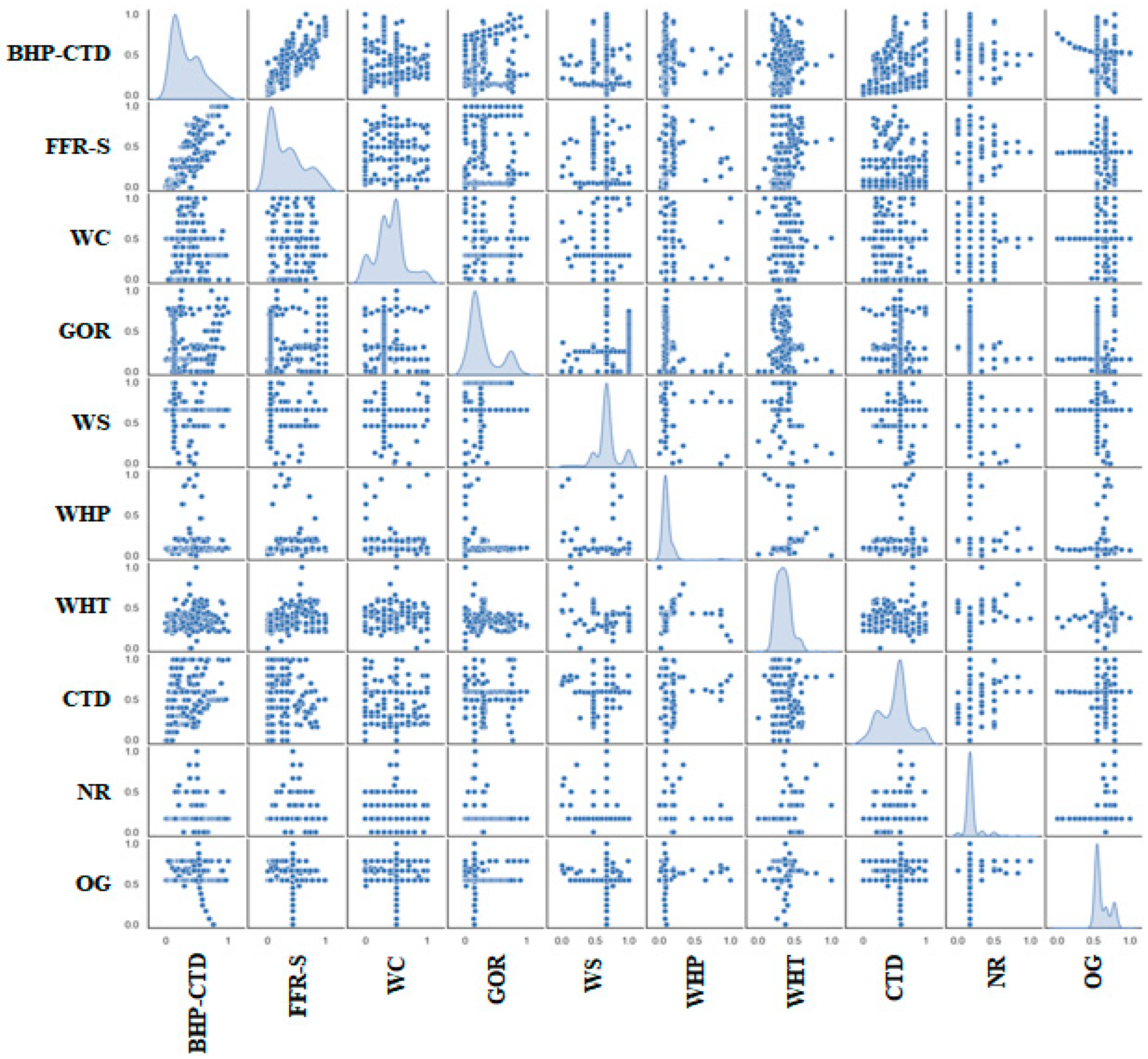
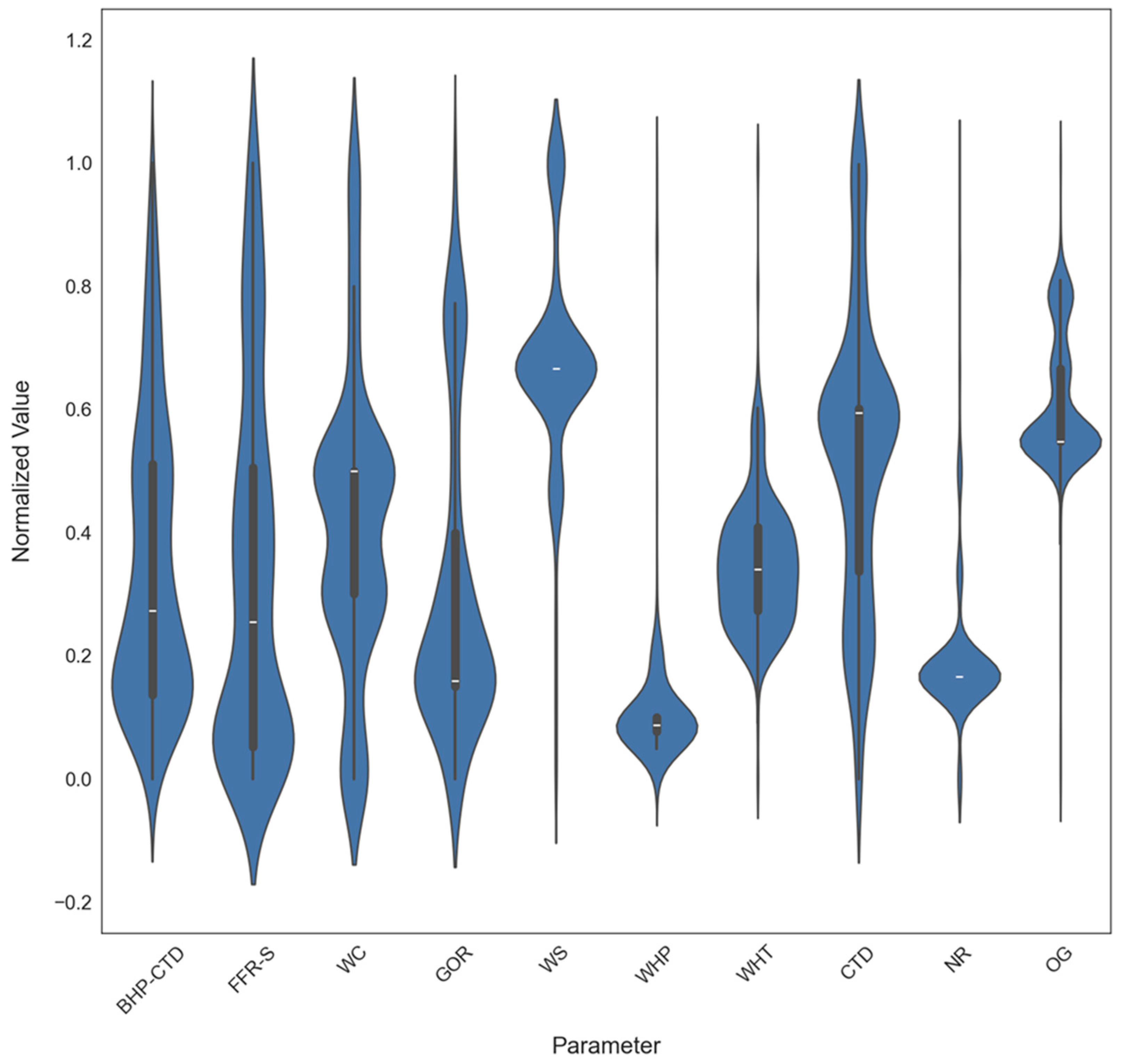
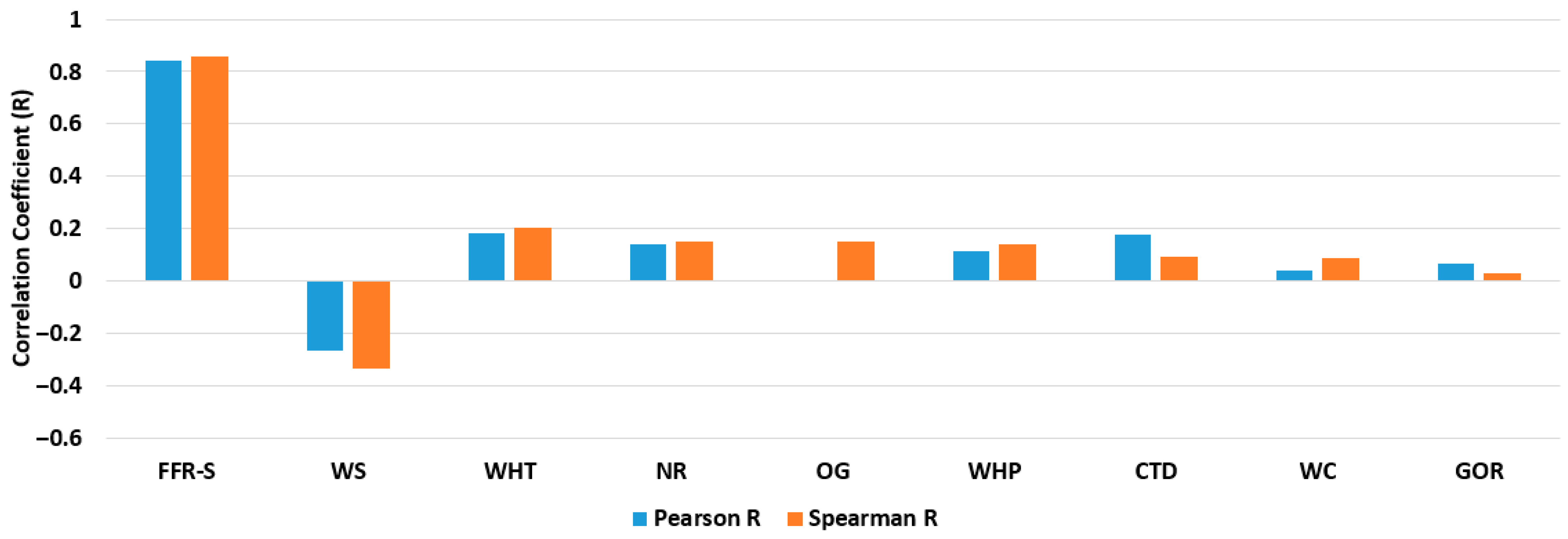
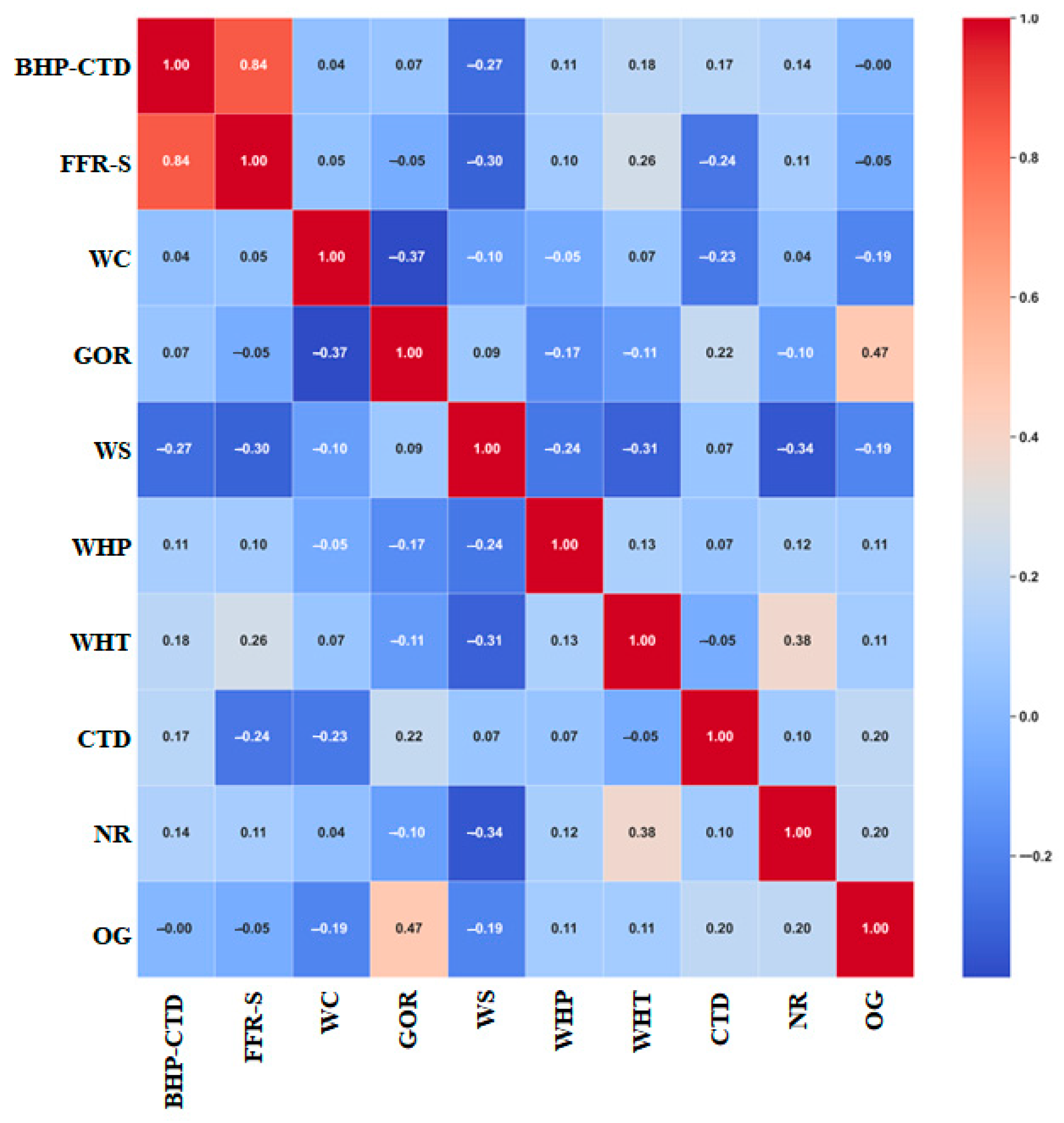
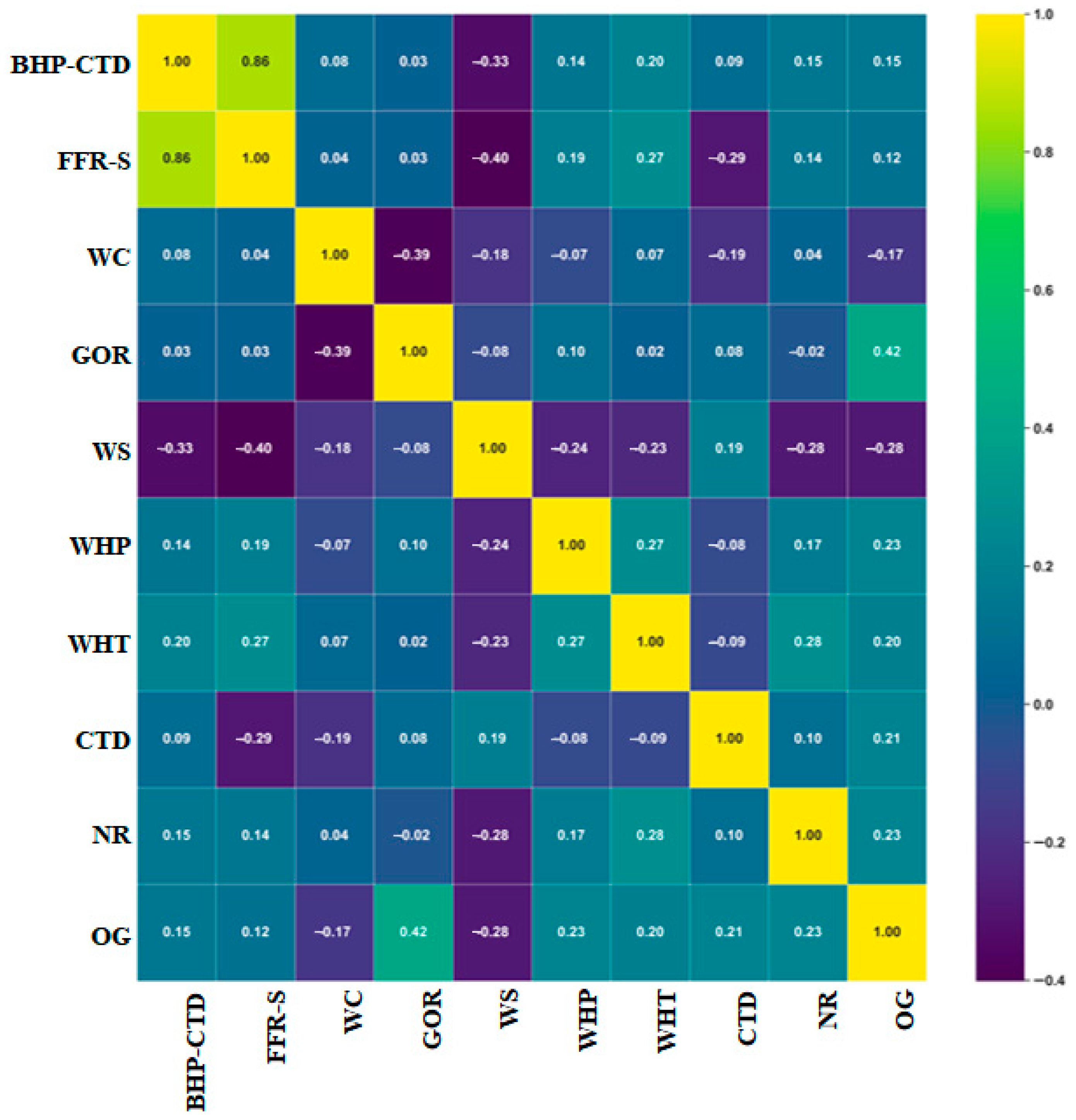
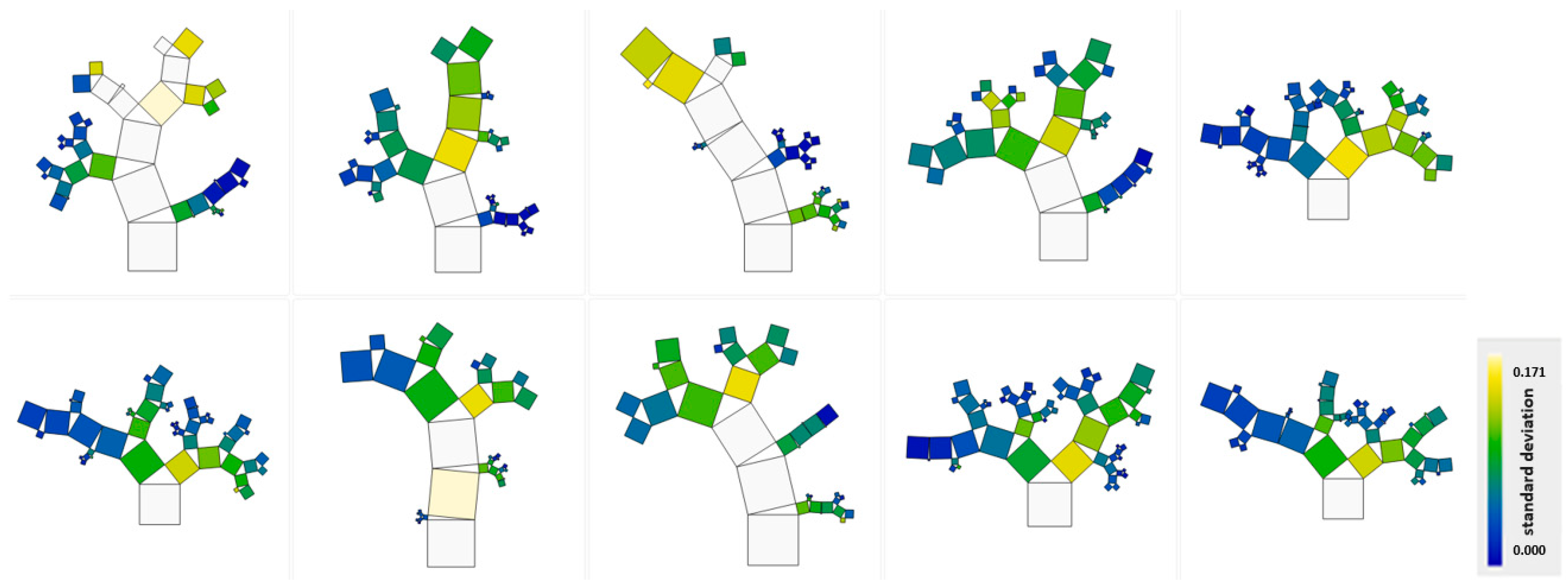
| Parameter | Units | MIN | MAX | AVG | Median |
|---|---|---|---|---|---|
| Bottomhole pressure at coiled tubing depth | psi | 158 | 5942 | 2141 | 1737 |
| Fluid flow rate at surface | stb/d | 80 | 4510 | 1552 | 1210 |
| Water cut | % | 0 | 100 | 41 | 50 |
| Gas–oil ratio | scf/stb | 0 | 2000 | 609 | 319 |
| Water salinity | ppm | 49,995 | 200,000 | 150,941 | 150,000 |
| Wellhead flowing pressure | psi | 13 | 570 | 80 | 62 |
| Wellhead flowing temperature | f | 72 | 160 | 103 | 102 |
| Coiled tubing depth | ft | 3000 | 13,040 | 8250 | 8971 |
| Nitrogen rate | scf/m | 400 | 1000 | 519 | 500 |
| Oil gravity | API | 12 | 54 | 37 | 35 |
| Model | Hyperparameters |
|---|---|
| GB-SKL |
|
| XGB |
|
| XGB-RF |
|
| GB-CB |
|
| ADAB |
|
| RF |
|
| SVMs |
|
| DT |
|
| KNN-D |
|
| KNN-U |
|
| LR |
|
| NN-LBFGS |
|
| NN-Adam |
|
| NN-SGD |
|
| SGD |
|
| Model | Model Parameters |
|---|---|
| GP-SR |
|
| Complexity | Loss | Equation |
|---|---|---|
| 1 | 0.02577 | FFR_S |
| 2 | 0.0204 | sin (FFR_S) |
| 3 | 0.01902 | sin (sin (FFR_S)) |
| 4 | 0.00592 | |
| 6 | 0.00484 | |
| 7 | 0.00447 | (CTD + 0.26175192) (FFRS + 0.12106326) |
| 8 | 0.00429 | sin ((FFRS + 0.112157054) (CTD + 0.32676274)) |
| 10 | 0.00396 | |
| 11 | 0.00364 | |
| 13 | 0.00353 | |
| 14 | 0.00346 | |
| 15 | 0.0034 | |
| 16 | 0.00335 | |
| 17 | 0.00303 | |
| 18 | 0.00296 | |
| 19 | 0.00284 | |
| 20 | 0.00271 |
| Parameter | Units | MIN | MAX | AVG | Median |
|---|---|---|---|---|---|
| Bottomhole pressure at coiled tubing depth | PSI | 851 | 3783 | 2304 | 2522 |
| Fluid flow rate at surface | STB/D | 88 | 3573 | 1437 | 1241 |
| Water cut | % | 0 | 100 | 37 | 30 |
| Gas–oil ratio | SCF/STB | 0 | 1556 | 611 | 500 |
| Water salinity | PPM | 51,000 | 200,000 | 143,451 | 150,000 |
| Wellhead flowing pressure | PSI | 30 | 490 | 97 | 67 |
| Wellhead flowing temperature | F | 90 | 117 | 104 | 107 |
| Coiled tubing depth | FT | 3000 | 13,028 | 8628 | 9002 |
| Nitrogen rate | SCF/M | 400 | 750 | 584 | 600 |
| Oil gravity | API | 22 | 46 | 38 | 35 |
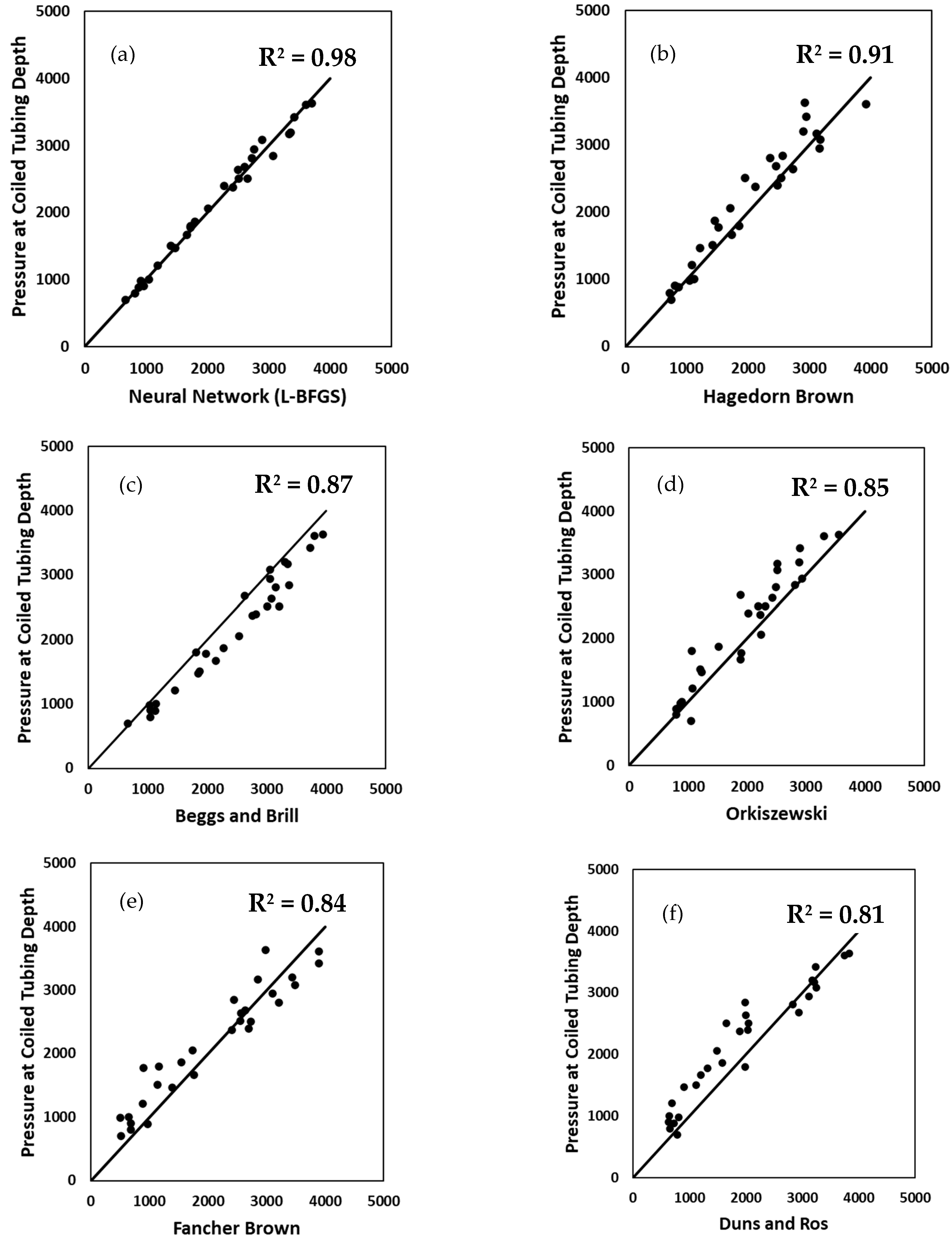
| BHP-CTD Prediction Methods | MSE | RMSE | MAE | R2 |
|---|---|---|---|---|
| Neural Network (L-BFGS) | 9791 | 99 | 76 | 0.98 |
| Hagedorn and Brown | 74,600 | 273 | 212 | 0.91 |
| Beggs and Brill | 107,223 | 327 | 277 | 0.87 |
| Orkiszewski | 117,194 | 342 | 272 | 0.85 |
| Fancher and Brown | 127,148 | 357 | 295 | 0.84 |
| Duns and Ros | 155,331 | 394 | 325 | 0.81 |
| Approach | Advantages | Limitations |
| Machine Learning Models |
|
|
| Empirical Correlations |
|
|
| Mechanistic Models |
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nashed, S.; Moghanloo, R. Benchmarking ML Algorithms Against Traditional Correlations for Dynamic Monitoring of Bottomhole Pressure in Nitrogen-Lifted Wells. Processes 2025, 13, 2820. https://doi.org/10.3390/pr13092820
Nashed S, Moghanloo R. Benchmarking ML Algorithms Against Traditional Correlations for Dynamic Monitoring of Bottomhole Pressure in Nitrogen-Lifted Wells. Processes. 2025; 13(9):2820. https://doi.org/10.3390/pr13092820
Chicago/Turabian StyleNashed, Samuel, and Rouzbeh Moghanloo. 2025. "Benchmarking ML Algorithms Against Traditional Correlations for Dynamic Monitoring of Bottomhole Pressure in Nitrogen-Lifted Wells" Processes 13, no. 9: 2820. https://doi.org/10.3390/pr13092820
APA StyleNashed, S., & Moghanloo, R. (2025). Benchmarking ML Algorithms Against Traditional Correlations for Dynamic Monitoring of Bottomhole Pressure in Nitrogen-Lifted Wells. Processes, 13(9), 2820. https://doi.org/10.3390/pr13092820








