System Integration of Multi-Source Wearable Sensors for Non-Invasive Blood Lactate Estimation: A Data Fusion Approach

Abstract

Blood lactate (BLa) concentration is a pivotal biomarker of exercise intensity and physiological stress, which provides insights into athletic performance and recovery. However, traditional lactate measurement requires invasive blood sampling, which presents significant limitations, including procedural discomfort, infection risks, and impracticality for continuous monitoring. Though non-invasive measurements of BLa concentration have emerged, most rely on a single physiological indicator like heart rate and sweat rate, and their accuracy and reliability remain limited. To address these limitations, this study proposes an innovative multi-sensor fusion framework for non-invasive estimation of BLa. By leveraging the inherent multisystem and multidimensional coordination of human physiology during exercise, the framework integrates a range of physiological signals (e.g., heart rate variability and respiratory entropy) and biomechanical signals (e.g., motion data). We proposed a stacking ensemble model that leverages the complementary strengths of these signals and achieved exceptional predictive performance with near-perfect correlation (R² = 0.9661) while maintaining high precision (MAE = 0.1816 mmol/L) and robustness (RMSE = 0.5891 mmol/L). Furthermore, the model’s exceptional capability extends to blood lactate threshold detection with 98.15% classification accuracy, which is a critical metric for training intensity optimization. This approach provides a robust, non-invasive solution for continuous exercise intensity monitoring, demonstrating significant potential for optimizing athletic performance through real-time physiological assessment and data-driven training modulation.

1. Introduction

In modern society, physical exercise holds significant importance for people’s well-being [1]. Sedentary work styles and prolonged working hours have made regular physical activity one of the key strategies to counter sub-health conditions [2]. To maximize the benefits of exercise, it is essential to introduce professional physiological indicators to assess whether training goals are being met [3]. Unlike commonly used metrics, such as heart rate (HR) or calorie expenditure, the blood lactate (BLa) threshold serves as a critical indicator for assessing training load and guiding effective exercise planning [4]. Accurate measurement of BLa concentration during exercise helps amateur athletes manage their training volume, enhancing their enjoyment of physical activity and maximizing its benefits [5]. For professional athletes, it aids in identification of optimal training loads [6], reducing the risk of injuries associated with overexertion and improving training efficiency [7]. Furthermore, precise BLa estimation enables better forecasting of competition demands, helping to prevent exhaustion and fatigue-related injuries [8]. Therefore, reliable BLa estimation is essential.

Traditional BLa measurement methods typically rely on collecting fingertip blood samples after an exercise session, followed by laboratory analysis using a lactate analyzer. Although this approach offers high accuracy, it has several drawbacks, including time-consuming procedures, discomfort for participants, and the risk of infection at the sampling site. As a result, increasing attention has been directed in recent years toward the development of non-invasive BLa estimation methods, aiming to achieve fast, convenient, and low-risk monitoring.

Given the close association between BLa concentration and physiological exercise load, numerous studies have attempted to use HR as an indicator for exercise intensity, thereby indirectly reflecting changes in BLa levels. Aaron J. Coutts et al. explored the use of HR to assess player intensity during football matches, but their findings indicated that HR alone could explain only 43.1% of the variance in intensity, highlighting the limitations of relying solely on this metric [9]. S. Grant et al. further attempted to establish a relationship between HR and fixed lactate thresholds; however, the results were similarly suboptimal [10]. A limits of agreement (LoA) analysis revealed that only large—and arguably unacceptable—changes in HR could be considered indicative of actual changes in training status [10]. Nevertheless, Eduardo et al. demonstrated that physiological thresholds identified via heart rate variability (HRV) could serve as a reliable and practical method for estimating the first lactate threshold (LT1) and second lactate threshold (LT2) during maximal running tests [11]. Therefore, while HR as a single parameter may have limited utility in estimating BLa levels, derived metrics such as HRV show considerable promise in evaluating physiological responses to exercise and warrant further investigation.

Maximal oxygen uptake (VO₂max) is also recognized as a standard measure of exercise workload and, by extension, an indirect indicator of BLa dynamics [12]. Michał Tomaszewski et al. previously estimated aerobic and anaerobic lactate thresholds using indicators such as VO₂max and HRmax [13]. Although it offers high measurement accuracy, the use of gas analyzers is cumbersome and often uncomfortable for the daily wearing. Physiological signals can be used for non-invasive lactate monitoring. For example, the study from Petras Ražanskas focused on surface electromyography (sEMG) signals, using data collected from four different muscles to estimate BLa levels [14]. While sEMG signals directly reflect muscle activity, their response to lactate accumulation is relatively indirect, which limits their accuracy in lactate prediction.

Lactate is a relevant biomarker for both sports and health sectors, with a complex sweat–blood bioequivalence [15]. Sweat-related indicators, such as sweat rate, have been explored as non-invasive proxies for estimating BLa concentration. For instance, Genis Rabost-Garcia et al. estimated BLa levels using a combination of sweat lactate, sweat rate, and HR, achieving an accuracy within 0.3 mmol/L compared to portable BLa analyzers [15]. However, collecting sweat during physical activity presents notable challenges. At the sensor level, sweat lactate sensors must provide continuous measurement over typical exercise durations (1–2 h or longer), while also meeting the manufacturing and storage requirements for commercial applications. Furthermore, such sensors must be integrated into specialized microfluidic systems designed for real-time sweat sampling and replenishment. Devices that fulfill these criteria remain difficult to develop and access, limiting the scalability and widespread adoption of sweat-based lactate monitoring approaches.

BLa concentration can also be estimated from a biomechanical perspective. In modern biomechanics, commonly used measurement systems include optical motion capture systems (OMCs) and accelerometers. OMCs, traditionally marker-based, have recently evolved into markerless systems, facilitating sports measurement and clinical applications outside of laboratory settings, though they rely on expensive camera setups for data acquisition [16]. In contrast, accelerometers are non-invasive, wearable, and cost-effective sensors capable of measuring human body acceleration. A widely used sensor incorporating accelerometers is the inertial measurement unit (IMU). IMUs integrate data from accelerometers, gyroscopes, and magnetometers to enable kinematic estimations [17]. By combining IMU outputs with biomechanical models, it becomes possible to continuously monitor energy expenditure during daily activities [18]. Biomechanical changes during running, such as vertical oscillation of the center of mass and step frequency, have been shown to correlate with BLa levels [19]. Furthermore, Chen Abraham et al. proposed a non-contact optical method for estimating lactate levels by detecting physiological muscle tremors [20].

Moreover, BLa monitoring is not only critical in sports performance assessment but also plays an important role in various clinical scenarios, particularly in the prevention of lactic acidosis through real-time tracking. For instance, Koichi Sughimoto et al. estimated BLa concentration using perioperative features, such as arterial pressure waveforms [21]. Subhasri Chatterjee et al. utilized the propagation characteristics of short-wave infrared light in vascular tissues for lactate concentration diagnosis [22].

However, whether in athletic or clinical contexts, most existing studies rely on either single parameters or unidimensional physiological features, such as HR or VO₂max, primarily focusing on internal physiological responses. These approaches often overlook external representations of exercise itself, such as gait dynamics or joint movement patterns during running. BLa estimation from a single perspective is typically constrained by the inherent limitations of individual measurement modalities, which restrict the overall accuracy and robustness of the estimation. In contrast, incorporating multidimensional and multimodal parameters allows the strengths of different data sources to complement one another, thereby improving both the precision and efficiency of BLa estimation.

This study presents a novel non-invasive BLa estimation approach by integrating wearable physiological and biomechanical data through a multi-source sensor fusion model. The proposed system integrates respiratory (e.g., VO₂max), cardiovascular (e.g., heart rate variability), and biomechanical (e.g., gait parameters) data to accurately estimate BLa concentration. By leveraging the complementary strengths of these sensor signals, the model provides a scalable, cost-effective solution for exercise intensity monitoring. Moreover, the model’s ability to assess lactate equips athletes and trainers with valuable insights into optimal training loads, improving athletic performance while mitigating risks of overtraining and injury. This work highlights the practical applications of sensor integration in health and performance monitoring systems, aligning with industrial demands for data-driven solutions in sports science and health management.

2. Materials and Methods

2.1. Experimental Procedure

An incremental exercise test collecting multi-source physiological and kinematic data using multiple wearable devices was designed in this study. Twenty healthy university students (10 males,10 females; age: 18–25 years) with diverse exercise habits (ranging from 1 to 5 training sessions per week) were recruited as participants. Participants were enrolled in the study following the low-risk participant criteria outlined in the American College of Sports Medicine (ACSM, 2006) guidelines. While low- to moderate-intensity exercise is generally considered safe with minimal risk of cardiovascular events, selecting individuals classified as low risk ensured that higher-intensity protocols could be implemented safely without compromising participant well-being [23]. Prior to participation, all participants provided written informed consent and were informed of their right to withdraw from the study at any time. The study was conducted in accordance with the Declaration of Helsinki, and the protocol was approved by the Ethics Committee of Beijing Sport University (2024423H) on 23 April 2024. Informed consent for participation was obtained from all subjects involved in the study.

The experiment was conducted in a laboratory with controlled temperature and humidity, comprising two phases. In the baseline phase, participants wore a HR monitor (Polar H10, Polar Electro Oy, Kempele, Finland) and a cardiopulmonary exercise testing system (MetaMax 3B, Cortex Biophysik, Leipzig, Germany), maintaining a seated position for 5 min. Fingertip blood samples were collected for baseline BLa measurement, followed by a standardized warm-up protocol.

During the incremental load phase, subjects were equipped with an inertial motion capture system, the Perception Neuron Studio (PNS, Noitom, Beijing, China), prior to initiating a graded treadmill test. The initial velocity was set at 6 km/h for female participants and 7 km/h for males, with incremental speed increases of 1 km/h every 3 min until volitional exhaustion or failure to maintain pace. BLa samples were obtained via fingertip puncture within 30 s after each stage [10]. Post-experiment analysis was conducted using a lactate analyzer (Biosen C-Line, EKF Diagnostic GmbH, Barleben, Germany) to quantify BLa concentrations. The experimental procedure and device configuration are depicted in Figure 1.

2.2. System Architecture

In this study, we developed a wearable multi-sensor system for non-invasive BLa estimation by integrating physiological, kinematic, and respiratory sensing modalities. The overall system architecture is illustrated in Figure 2.

Physiological Sensing: Cardiac activity was continuously monitored using an ECG chest strap (Polar H10, Polar Electro Oy, Kempele, Finland), which provided high-resolution electrocardiogram (ECG) data for deriving HR and HRV features.

Kinematic Sensing: A motion capture system (PNS, Noitom, Beijing, China) was employed to capture full-body movement during exercise. The system recorded detailed kinematic information, including joint trajectories and gait cycle parameters.

Respiratory Sensing: Respiratory gas exchange variables were measured using a facemask-based gas analyzer (MetaMax 3B, Cortex Biophysik, Leipzig, Germany), providing key physiological indicators, such as VO₂ and ventilation rate.

All sensor modules were deployed within a unified wearable sensing framework designed to capture physiological, biomechanical, and respiratory signals across multiple modalities. Although the devices operated independently, a structured post-collection synchronization strategy—anchored on identifiable temporal markers embedded within the experimental protocol (e.g., stage transitions)—was employed to achieve alignment across data streams. This approach ensured sufficient temporal coherence for subsequent multi-sensor data integration. The resulting fused dataset enabled estimation of BLa concentration using machine learning techniques.

Beyond lactate estimation, the system architecture supported a downstream application layer focused on exercise load evaluation. This layer leveraged the estimated BLa values to classify training intensity levels, demonstrating the system’s potential for feedback and decision support in personalized exercise monitoring scenarios.

2.3. Data Preprocessing

For all types of data collected, we uniformly applied a standardized extraction protocol, isolating data exclusively from the final 2 min of each 3 min stage. This standardized preprocessing protocol was employed to eliminate the potential transient interference at the beginning of each stage, ensuring the stability and representativeness of all data used for subsequent analysis. Furthermore, to address potential data insufficiency, Bootstrap resampling with replacement was implemented for dataset augmentation to improve data diversity and mitigate model overfitting risks, following all other data preprocessing work.

2.3.1. Electrocardiogram (ECG) Signal Preprocessing

The acquired raw ECG signals were subjected to preprocessing. A standard-deviation-based anomaly detection method (±4SD method) was employed to identify outliers in the RR intervals caused by abrupt changes or ectopic beats, thereby mitigating the impact of noise on HRV analysis. An RR interval, $R{R}_i$, was considered an outlier if it satisfied the condition $\left|R{R}_i-\mu \right|>4\sigma$, where $\mu$ and $\sigma$ denote the mean and standard deviation of the RR intervals, respectively. Detected outliers were corrected using first-order linear interpolation, as shown in Equation (1):

$$R{R}_{\mathrm{new}}\left(t\right)=R{R}_0+\left(t-t_0\right)\cdot {\displaystyle \frac{R{R}_1-R{R}_0}{t_1-t_0}},$$

(1)

where $R{R}_0$ and $R{R}_1$ represent the nearest valid RR intervals immediately before and after the outlier, and $t_0$ and $t_1$ are their corresponding time indices.

After outlier correction, the processed RR intervals were used to compute a series of HRV metrics that characterize HR dynamics from both time domain and frequency domain perspectives.

In the time domain, the mean RR interval (mean_rr) was calculated as the arithmetic average of all RR intervals, from which the mean HR (mean_hr) was subsequently derived. These metrics quantify the average level of cardiac activity during each analysis period. Additionally, the maximum HR (max_hr) and minimum HR (min_hr) within each period were recorded to capture the extremes of cardiac response.

HRV serves as a crucial index for evaluating the variation in successive cardiac cycles and is widely used to assess autonomic regulation of cardiac function. The standard deviation of normal-to-normal RR intervals (SDNN), defined in Equation (2), reflects overall autonomic nervous system activity. The root mean square of successive differences (RMSSD), as defined in Equation (3), reflects short-term variations and is predominantly associated with parasympathetic (vagal) modulation:

$$\mathrm{SDNN}=\sqrt{{\displaystyle \frac{1}{N-1}}\sum _{i=1}^N{\left(R{R}_i-\overline{RR}\right)}^2},$$

(2)

$$\mathrm{RMSSD}=\sqrt{{\displaystyle \frac{1}{N-1}}\sum _{i=1}^{N-1}{\left(R{R}_{i+1}-R{R}_i\right)}^2},$$

(3)

where $R{R}_i$ denotes the $i$-th RR interval, $R{R}_{i+1}$ is the subsequent RR interval, $\overline{RR}$ is the mean RR interval, and $N$ represents the total number of heartbeats.

In frequency domain analysis, the short-time Fourier transform (STFT) was employed to decompose the RR interval signal into distinct frequency components, yielding indices such as low-frequency power (LF), high-frequency power (HF), and the LF/HF power ratio (LF_HF_ratio) [23]. The LF component, occupying a frequency range of 0.04–0.15 Hz, primarily reflects the combined influence of sympathetic and parasympathetic nerves, with sympathetic activity dominating this band [23]. The HF component, spanning 0.15–0.4 Hz, is mainly associated with parasympathetic nerve activity. The LF/HF ratio, calculated using the formula:

$$\mathrm{L}\mathrm{F}\_\mathrm{H}\mathrm{F}\_\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}={\displaystyle \frac{LF}{HF}}={\displaystyle \frac{{\int }_{0.04}^{0.15} S\left(f\right)df}{{\int }_{0.15}^{0.40} S\left(f\right)df}},$$

(4)

quantifies the balance between sympathetic and parasympathetic nervous activities, serving as a key marker of autonomic nervous system regulation.

2.3.2. Respiratory Data Preprocessing

Respiratory-related physiological parameters were collected using a cardiopulmonary exercise testing system. This device synchronously outputs data in real time via a facemask-based flow sensor and an infrared gas analyzer, including respiratory frequency (BF), tidal volume (VT), minute ventilation (VE), respiratory exchange ratio (RER), carbon dioxide output (VCO₂), energy expenditure rate (EE), breathing reserve (BR), and cardiac index (CI).

Among these parameters, BF reflects the number of breaths per unit time and directly indicates the neural regulation of the respiratory center in response to exercise load. VT represents the gas exchange volume per breath under resting conditions and serves as a fundamental indicator of pulmonary ventilation efficiency. BR indicates the breathing capacity reserve during maximal exercise. VE, calculated as the product of VT and BF, represents the total pulmonary ventilation per minute.

With regard to energy metabolism, the RER reveals the composition of energy substrates utilized by the body (RER ≈ 1.0 suggests predominant carbohydrate metabolism, whereas RER ≈ 0.7 indicates predominant fat metabolism):

$$\mathrm{R}\mathrm{E}\mathrm{R}={\displaystyle \frac{{VCO}_2}{{VO}_2}}.$$

(5)

EE quantifies the hourly rate of energy expenditure based on the Weir equation. The phase-averaged values of both RER and EE provide steady-state indicators for analyzing the relationship between exercise intensity and metabolic level:

$$\mathrm{E}\mathrm{E}\left(\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}/\mathrm{m}\mathrm{i}\mathrm{n}\right)=3.94·{VO}_2+1.11·{VCO}_2.$$

(6)

The cardiac index (CI) is a key parameter linking the respiratory and circulatory systems. CI reflects the heart’s pumping efficiency per unit of body surface area (BSA), and its phase-averaged values help to capture the dynamic equilibrium of cardiopulmonary coupling during exercise:

$$\mathrm{C}\mathrm{I}={\displaystyle \frac{CardiacOutput}{BSA}}.$$

(7)

The raw data were continuously recorded at one-second intervals, generating high-frequency time series annotated with timestamps. Given the staged design of the exercise load test, the study extracted steady-state features for each parameter on a per-stage basis. Specifically, the arithmetic mean of each parameter was calculated over complete data segments, and these mean values were used to represent the corresponding exercise intensity stage.

To ensure data quality and analytical validity, the computed stage-wise mean values were further screened. Mean values falling outside predefined physiological thresholds (e.g., BF: 5–60 breaths/min; VE: 3–150 L/min) were excluded. Additionally, the coefficient of variation (CV) was calculated for each parameter within its respective stage. Data for core parameters with a CV ≥ 10% were excluded from further analysis to mitigate the influence of excessive intra-stage variability.

2.3.3. Motion Data Preprocessing

Real-time kinematic data were collected at a frequency of 240 Hz. Gait events were identified using an angular-velocity-based detection algorithm [24]. This approach extracts key gait cycle events, including mid-swing (ms), toe-off (to), and heel-strike (hs).

To ensure the relevance and interpretability of the features used to predict BLa concentration, we employed a literature-informed feature selection strategy, supplemented by correlation-based filtering. We began with a systematic review of prior research in exercise physiology and gait biomechanics to identify temporally descriptive gait features with established physiological significance. These candidate features were then extracted from the processed kinematic data. All indicators are easy to calculate and understand, and the calculation formula can be derived based on common sense:

$${frequency}_{step}={\displaystyle \frac{N_{hs}}{T}},$$

(8)

$$t_{stance}\left(i\right)=t_{to}\left(i\right)-t_{hs}(i-1),$$

(9)

$$t_{swing}\left(i\right)=t_{hs}\left(i\right)-t_{to}\left(i\right),$$

(10)

$$t_{flight}(i)={\displaystyle \frac{t_{swing}\left(i\right)-t_{stance}\left(i\right)}{2}},$$

(11)

$$t_{gait}=t_{to}\left(i\right)-t_{to}(i-1),$$

(12)

$$F_{max}=mg{\displaystyle \frac{\pi }{2}}\left({\displaystyle \frac{t_{flight}}{t_{stance}}}+1\right).$$

(13)

To control for the confounding influence of increasing running speed during incremental load trials, all gait parameters were normalized by the corresponding speed. We evaluated the linear relationship between each feature and BLa concentration using Pearson correlation analysis.

2.4. Data Analysis

The preprocessed dataset was randomly partitioned into training (80% for model training and parameter optimization) and testing sets (20% for independent evaluation of generalization capabilities), ensuring representativeness of sample distribution.

During the feature engineering phase, Pearson correlation analysis was rigorously applied to the complete cohort (n = 20) under the linearity assumption to quantify associations between physiological indicators (HR, respiratory parameters, and gait metrics) and BLa. 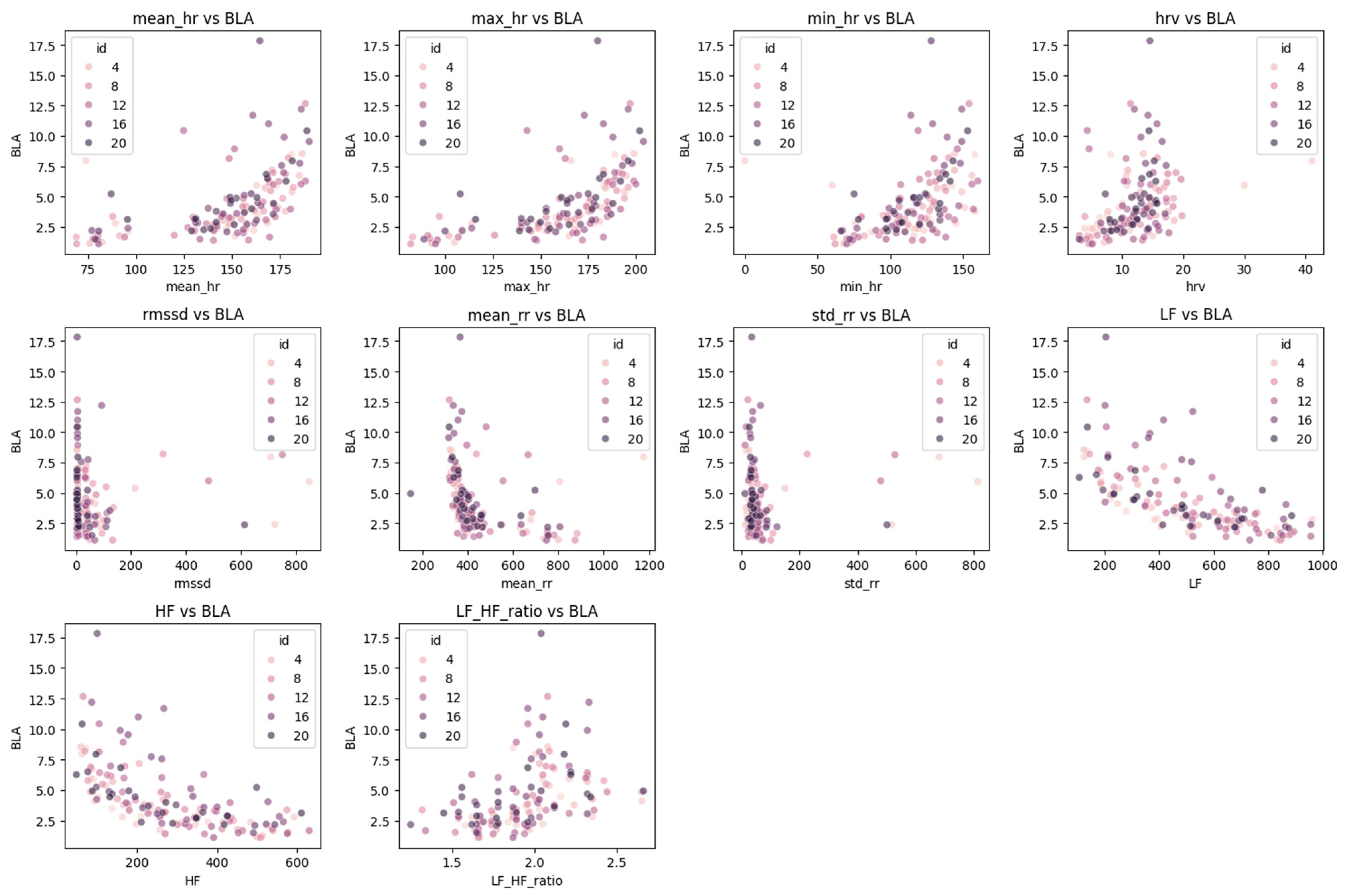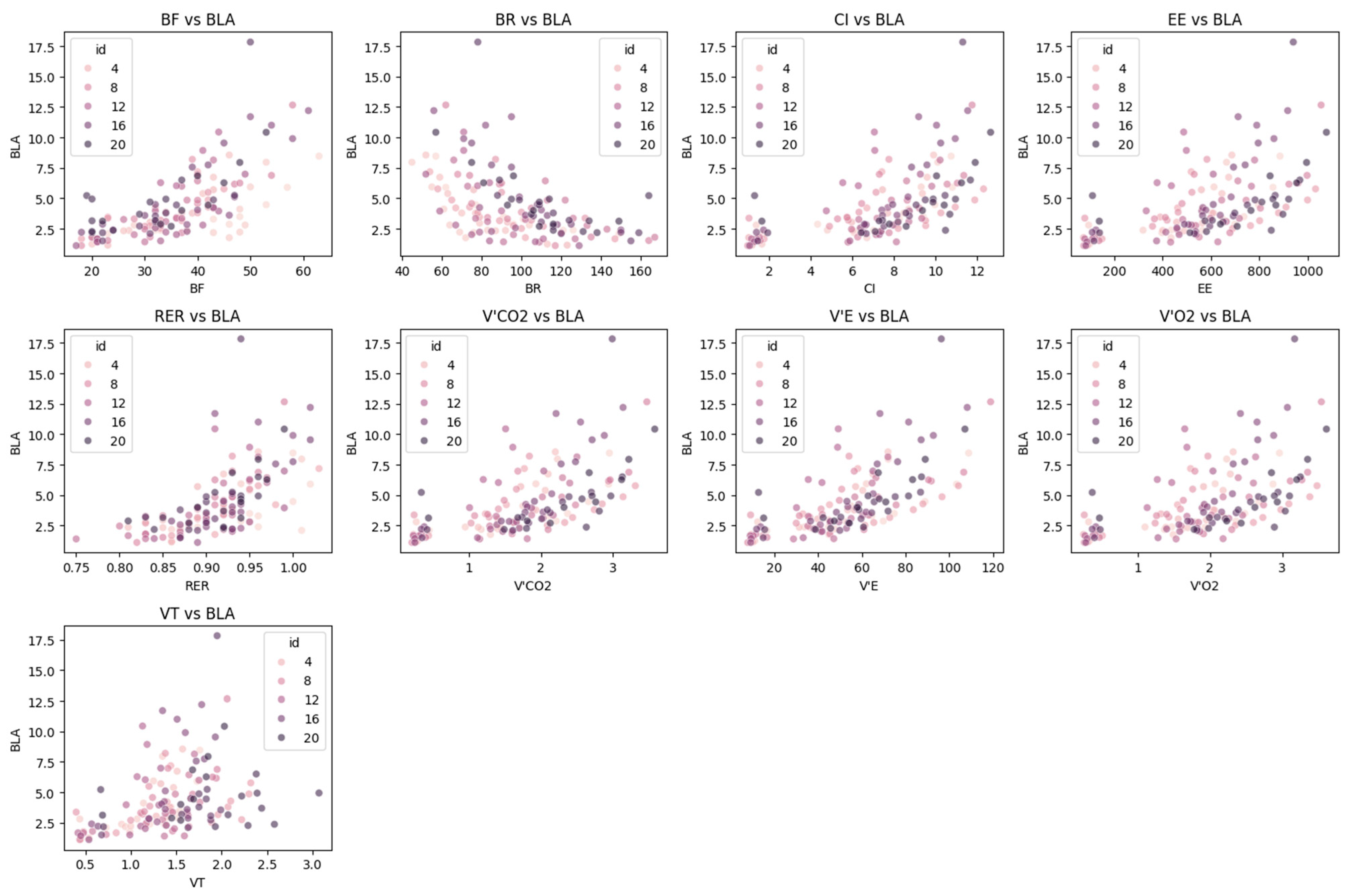Correlation coefficients (r) and statistical significance (p-values) were computed using all available subjects, with features exhibiting both significant correlations (p < 0.05) and absolute coefficient values exceeding the predefined threshold (|r| ≥ 0.3) retained as candidate predictors. For visualization clarity, systematically sampled subsets were displayed: HRV and respiratory plots (Figure 3 and Figure 4) show equidistant subjects at 20% intervals (IDs: 4, 8, 12, 16, 20; n = 5), reflecting lower physiological variability (CV = 38.24% and 32.92%, respectively), while gait plots (Figure 5) include denser 16.7% interval sampling (IDs: 3, 6, 9, 12, 15, 18; n = 6) to capture higher movement heterogeneity (CV = 46.02%).

The linearity assumption was validated through residual diagnostics (scatterplot inspection). Subsequently, recursive feature elimination with cross-validation (RFECV) was implemented for multivariate optimization. A linear-kernel support vector regression (SVR) served as the feature importance estimator, with features iteratively pruned based on their minimal contribution to model performance. This process employed 5-fold cross-validation using negative mean squared error (–MSE) as the scoring metric until cross-validation error reached a stabilized minimum. This two-stage pipeline optimized the trade-off between feature relevance and generalizability, yielding a parsimonious feature subset that maximized predictive accuracy while ensuring computational efficiency and interpretability.

2.4.1. Regression Estimation Model of BLa Value

Prior to determining the final machine learning model, this study conducted a systematic comparative analysis of seven regression algorithms, with all models employing identical feature engineering pipelines and hyperparameter optimization frameworks. The model selection encompassed (1) linear models (linear regression (LR) and ridge regression (Ridge)), (2) tree-based models (random forest (RF), gradient boosting regressor (GBR), and XGBoost), (3) kernel-based methods (SVR), and (4) instance-based approaches (K-nearest neighbors (KNN) regression). Hyperparameter optimization was implemented through Bayesian optimization (BayesSearchCV) configured with 50 iterations and 5-fold cross-validation to minimize the MSE. Experimental consistency was rigorously maintained across all comparative models regarding input features, preprocessing procedures, and evaluation metrics.

The model training was divided into two critical phases: single-model hyperparameter optimization and ensemble model construction. In the first phase, BayesSearchCV was systematically applied to optimize the core hyperparameters of the SVR model with a radial basis function (RBF) kernel, including the regularization parameter (C), kernel coefficient (γ), and epsilon-insensitive loss parameter (ε). The Bayesian optimization process, configured with 50 iterations and 5-fold cross-validation, efficiently explored optimal parameter combinations within a log-uniformly distributed search space, aiming to minimize the MSE and thereby enhance the predictive accuracy of individual models.

Building upon the optimized individual models, a Stacking ensemble learning framework was constructed to integrate the advantages of diverse algorithms. The ensemble architecture comprised three base learners: (1) the optimized SVR model, (2) a RF preset with 100 decision trees, and (3) a KNN regressor. A ridge regression model served as the meta-learner to enhance overall performance by learning prediction residuals from the base models. During the training process, feature selection preprocessing was first implemented on the training dataset. The refined feature subset was subsequently fed into the ensemble model, enabling multi-layer learning to capture nonlinear relationships and complex patterns within the data.

2.4.2. Exercise Load Evaluation Comparison

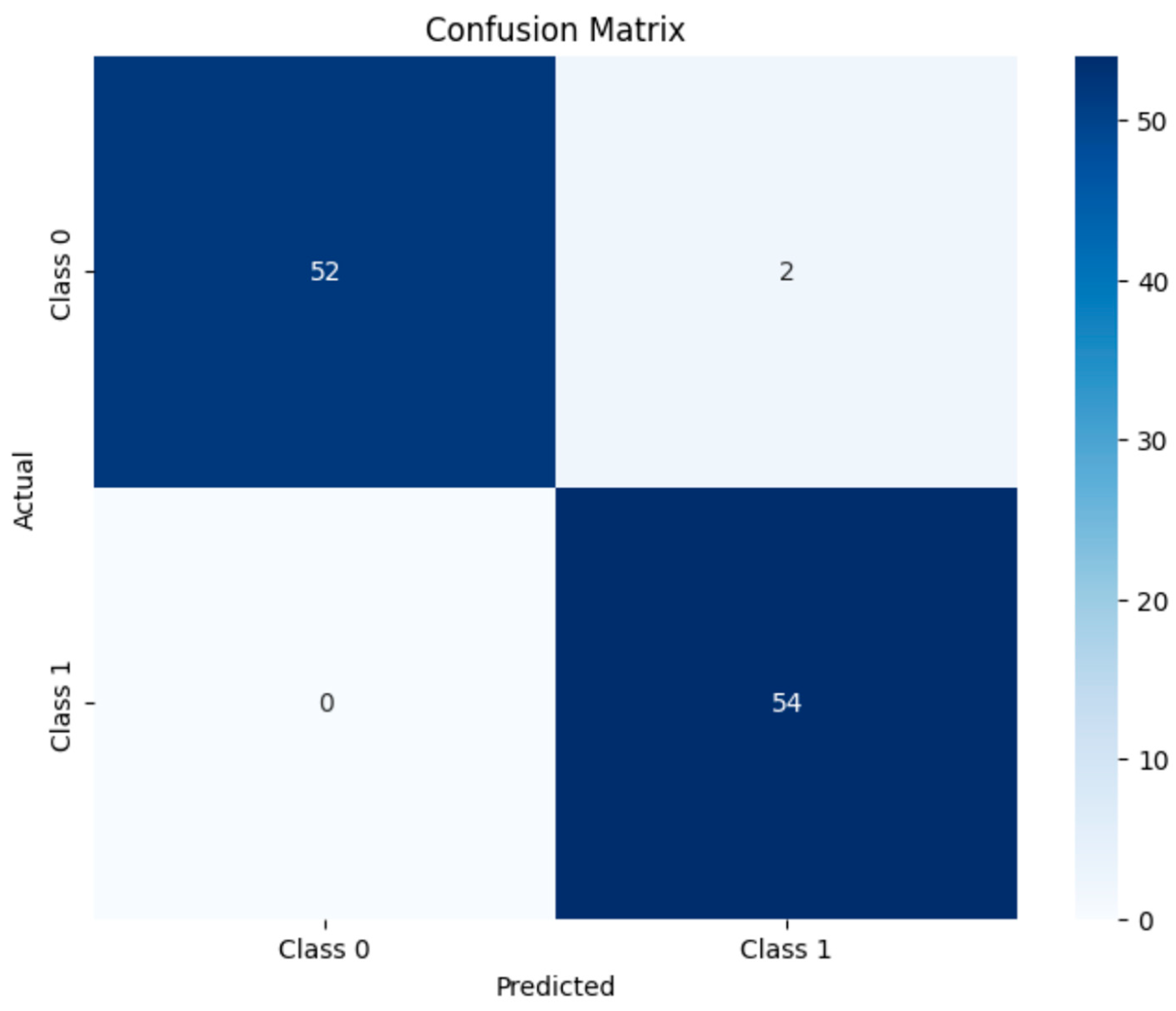
We explored two distinct strategies for exercise load evaluation: an interpretable system and a supervised learning algorithm, and we compared their respective performances. The interpretable system was built upon the results of BLa estimation, using a 4 mmol/L threshold to categorize exercise intensity into two discrete classes: high-intensity exercise (Class 1) for BLa > 4 mmol/L, and low-intensity exercise (Class 0) for BLa ≤ 4 mmol/L. In contrast, the supervised learning algorithm directly classified exercise workload based on the multimodal sensor data, using the same BLa-derived intensity classes (Class 0/1), without relying on intermediate physiological variables. For both methods, the feature subset selection and hyperparameter tuning strategies remained consistent with those used in the lactate prediction task.

Additionally, to find the model which outperforms others, the supervised learning algorithm employed multiple classical machine learning algorithms to construct classification models. The specifically selected algorithms included (1) logistic regression (LR), (2) decision tree (DT), (3) random forest (RF), and (4) support vector machine (SVM). Each algorithm was configured with rationally defined hyperparameter search spaces. Systematic parameter optimization was implemented through grid search methodology combined with cross-validation procedures to identify optimal parameter combinations.

The model training phase employed an 80%:20% stratified split ratio to partition the dataset into training and test sets, with a fixed random seed implemented to ensure experimental reproducibility. For each classification model, systematic hyperparameter optimization was conducted using GridSearchCV with 5-fold cross-validation, where classification accuracy served as the primary evaluation metric. Specific hyperparameter search configurations were tailored to individual algorithms: the LR model underwent optimization of the regularization strength parameter C (with candidate values 0.1, 1, and 10) and penalty type (L1 or L2 norm), while the RF model focused on tuning critical parameters, including the number of DTs (n_estimators) and maximum tree depth (max_depth). This rigorous optimization process ensured methodological consistency across all evaluated algorithms regarding cross-validation protocols, performance evaluation criteria, and computational resource allocation, thereby eliminating potential bias from parameter configuration discrepancies.

2.4.3. Ablation Study Design

To quantify the contribution of each physiological modality (ECG, respiratory (Resp), and gait signals), we conducted an ablation study by systematically excluding one or more signal types. Seven model configurations were evaluated:

• Single modality: ECG-only, Resp-only, and Gait-only.
• Bi-modal: ECG + Resp, ECG + Gait, and Resp + Gait.
• Full model: ECG + Resp + Gait (baseline).

All models retained identical architectures, hyperparameters, training/testing splits, and evaluation metrics (RMSE for regression and F1-score for classification), as defined in Section 2.4.1 and Section 2.4.2. Performance degradation was measured relative to the full-model baseline.

3. Results

3.1. Correlation Analysis and Key Feature Selection

3.1.1. ECG Parameters

The analysis revealed that LF, HF, and max_hr exhibited the strongest correlations with BLa, with Pearson’s coefficients of −0.75, −0.73, and 0.65, respectively. Based on these findings, they were selected as input features in subsequent modeling. The complete correlation coefficients for all examined indicators are presented in

Table 1. Correlation and p-values of HRV indices with BLa concentrations.

Feature	LF	HF	max_hr	min_hr	mean_hr	LF_HF_ratio	hrv	mean_rr	std_rr	rmssd
r	−0.748	−0.732	0.654	0.629	0.606	0.594	0.5199	−0.439	−0.222	−0.086
p-value	0.049	0.063	0.116	0.104	0.122	0.219	0.227	0.161	0.237	0.393

, with scatterplots shown in Figure 3.

3.1.2. Respiratory Data

Among respiratory parameters, BF and BR showed statistically significant correlations with BLa (r = 0.83, p = 0.044 and r = −0.83, p = 0.049, respectively). VE exhibited a marginally significant correlation (r = 0.83, p = 0.051). Other respiratory variables, such as VCO₂ and RER, did not reach statistical significance (p > 0.05), but are included in

Table 2. Correlation and p-values of respiratory indicators with BLa concentrations.

Feature	BF	BR	V’E	V’CO2	RER	EE	V’O2	CI	VT
r	0.835	−0.829	0.825	0.778	0.748	0.745	0.736	0.735	0.667
p-value	0.044	0.0486	0.051	0.076	0.104	0.094	0.100	0.102	0.148

and Figure 4 for completeness.

3.1.3. Gait Parameters

Gait cycle parameters showed strong linear associations with BLa, with Pearson’s coefficients exceeding 0.71, although these were not statistically significant (p > 0.05). Detailed results are summarized in

Table 3. Correlation and p-values of gait parameters with BLa concentrations.

Feature	Step Frequency	Contact Time	Swing Time	Gait Cycle Time	Max. VGRF *
r	0.853	0.820	0.869	0.829	0.719
p-value	0.048	0.116	0.045	0.065	0.251

* VGRF means vertical ground reaction force.

, and corresponding scatterplots are presented in Figure 5.

3.2. BLa Estimation Model

The estimating performance of seven individual machine learning models and one stacking ensemble model was evaluated using R², MAE, and RMSE as performance metrics (

Table 4. Performance metrics of various regression models.

Model	R2 Score	MAE (mmol/L)	RMSE (mmol/L)
Linear Regression	0.2154	1.0916	1.3531
Ridge Regression	0.6148	1.2513	1.9080
Random Forest	0.9350	0.2711	0.8159
Gradient Boosting Regressor	0.7617	0.9064	1.2007
XGBoost	0.6595	1.1192	1.4352
SVR	1.0000	0.0039	0.0039
KNN	0.6680	1.0687	1.4172
Stacking	0.9661	0.1816	0.5891

).

LR and ridge regression models achieved R² values of 0.2154 and 0.6148, respectively. Among tree-based models, the RF model obtained the highest R² value of 0.9350 and an MAE of 0.2711. GBR and XGBoost yielded R² values of 0.7617 and 0.6595, respectively. The SVR model produced a training R² of 1.0000, with MAE and RMSE of 0.0039. These results indicate a perfect fit on the training data theoretically.

The stacking ensemble model, composed of LR, RF, and KNN as base learners, achieved the highest R² of 0.966 on the test set, with an MAE of 0.182 and RMSE of 0.589. Compared to the RF model, the ensemble reduced MAE and RMSE by 33.0% and 27.8%, respectively (Figure 6). Residual distribution analysis indicated that most prediction errors were within ±0.5 mmol/L (Figure 7).

3.3. Exercise Load Level Classification Task Accuracy Evaluation

The performance evaluation of the interpretable system and supervised learning algorithms showed distinct differences in classification outcomes across multiple metrics. The interpretable system achieved a classification accuracy of 98.15% on 108 test samples (Figure 9). Analysis of the confusion matrix indicated that for Class 1, all 54 cases were correctly classified, with no false negatives. For Class 0, the model identified 52 true negatives and produced 2 false positives. Precision and recall for both classes were balanced: Class 0 achieved 100% precision and 96% recall, while Class 1 achieved 96% precision and 100% recall. The corresponding F1-scores for both classes were 0.98, with macro-averaged and weighted averages also reaching 0.98 (Figure 8).

Figure 8. Confusion matrix of white-box approach.

Figure 8. Confusion matrix of white-box approach.

Figure 9. True vs. predicted BLa values with classification thresholds.

Figure 9. True vs. predicted BLa values with classification thresholds.

Four supervised learning algorithms—LR, DT, RF, and SVM—were evaluated in the classification task (

Table 5. Comparison of classification model performance with respect to accuracy and classification report.

Model Name	Accuracy (%)	Classification Report
Logistic Regression	0.96	Class 0 precision of 1.00 (indicating highly accurate predictions), Class 1 recall of 1.00 (complete identification of this class)
Decision Tree	0.78	Class 1 recall of only 0.33 (demonstrating inadequate recognition capability for this category)
Random Forest	0.89	Class 1 precision of 0.67 (revealing limited precise prediction capacity for this category)
Support Vector Machine	0.93	Overall superior performance, though Class 0 recall (0.90) remains marginally lower than logistic regression
InterpretableSystem	0.982	Class 1 precision of 0.96 and recall of 1.00,Class 0 precisionof 1.00and recallof 0.96

). Among them, LR achieved the highest accuracy (0.96). The classification report indicated strong performance for both classes (Class 0 precision: 1.00; Class 1 recall: 1.00). The DR model showed the lowest accuracy (0.78), with limited sensitivity in detecting high-intensity exercise (Class 1 recall: 0.33). The RF model exhibited moderate performance but lower precision for Class 1 (0.67), while the SVM demonstrated lower recall for Class 0 (0.90).

3.4. Ablation Study on Multimodal Integration

The ablation study revealed critical insights into modality contributions (

Table 6. Ablation study results for regression and classification tasks.

Configuration	RMSE (↓)	ΔRMSE *	F1-Score (↑)	ΔF1 *
ECG + Resp + Gait	0.589	–	0.982	–
ECG + Resp	0.612	+3.9%	0.975	−0.7%
ECG + Gait	0.660	+12.1%	0.954	−2.9%
Resp + Gait	0.641	+8.2%	0.961	−2.1%
ECG-only	1.679	+185.1%	0.806	−17.9%
Resp-only	0.601	+2.0%	0.969	−1.3%
Gait-only	0.736	+25.0%	0.944	−3.9%

* Percentage change relative to ECG + Resp + Gait baseline. ↓ represents the lower the numeric value is, the better. ↑ represents the higher the numeric value is, the better.

). When using respiratory signals alone (Resp-only), regression performance approached the full tri-modal baseline with only a 2.0% RMSE increase (0.601 vs. 0.589 mmol/L), while classification degraded minimally (ΔF1 = −1.3%). In contrast, ECG-only models exhibited catastrophic regression failure (RMSE = 1.679, Δ + 185.1%), though ECG proved essential for multimodal synergy: adding ECG to the Resp + Gait configuration elevated the F1-score by 2.1% (0.982 vs. 0.961). Gait data demonstrated moderate standalone utility (RMSE = 0.736, Δ + 25.0%), but its exclusion from ECG + Resp caused less degradation than removing respiratory signals (ΔF1 = −0.7% vs. −2.9%). Critically, the full ECG + Resp + Gait model consistently outperformed all reduced configurations, exhibiting an 18.5–185.1% lower RMSE and 1.3–17.9% higher F1-score across tasks (all p < 0.01 via paired t-tests), confirming that multimodal integration is non-redundant for optimal blood lactate monitoring.

4. Discussion

4.1. Insights into Feature Importance and Physiological Relevance

The correlation analysis identified several physiological and kinematic indicators that are closely associated with BLa dynamics during incremental exercise. Among them, low-frequency (LF) and high-frequency (HF) HR variability components demonstrated strong negative correlations with BLa, while maximal HR (max_hr) exhibited a positive association. These findings are consistent with previous research suggesting that autonomic nervous system responses—reflected by HRV—are sensitive markers of metabolic stress and anaerobic threshold [25].

In the domain of respiratory function, BF and BR showed statistically significant correlations with BLa, indicating a robust ventilatory response to increasing lactate levels. Interestingly, the marginal correlation observed for VE may suggest a potential regulatory role in buffering lactate accumulation, although further investigation with larger samples is warranted. Despite the lack of statistical significance for other respiratory metabolic variables, such as VCO₂ and RER, their inclusion as supplementary features may enhance the physiological interpretability of the model, particularly in capturing nonlinear or secondary effects.

Lower-limb gait features also demonstrated promising correlations with BLa, particularly in temporal characteristics of the gait cycle. While these correlations did not reach statistical significance, their consistently high Pearson coefficients (r > 0.71) suggest that biomechanical parameters may encode latent information about systemic fatigue and metabolic stress. This supports the potential value of integrating kinematic features into multimodal predictive models, especially in non-invasive or field-based assessment settings.

Taken together, these results informed the selection of key features for model training. Importantly, the diverse physiological domains represented—cardiac, respiratory, and kinematic—highlight the multifactorial nature of lactate regulation.

4.2. Comparative Evaluation of Model Performance

The performance comparison across multiple machine learning models revealed notable disparities in their ability to estimate BLa levels, underscoring the importance of selecting appropriate algorithms tailored to physiological data characteristics.

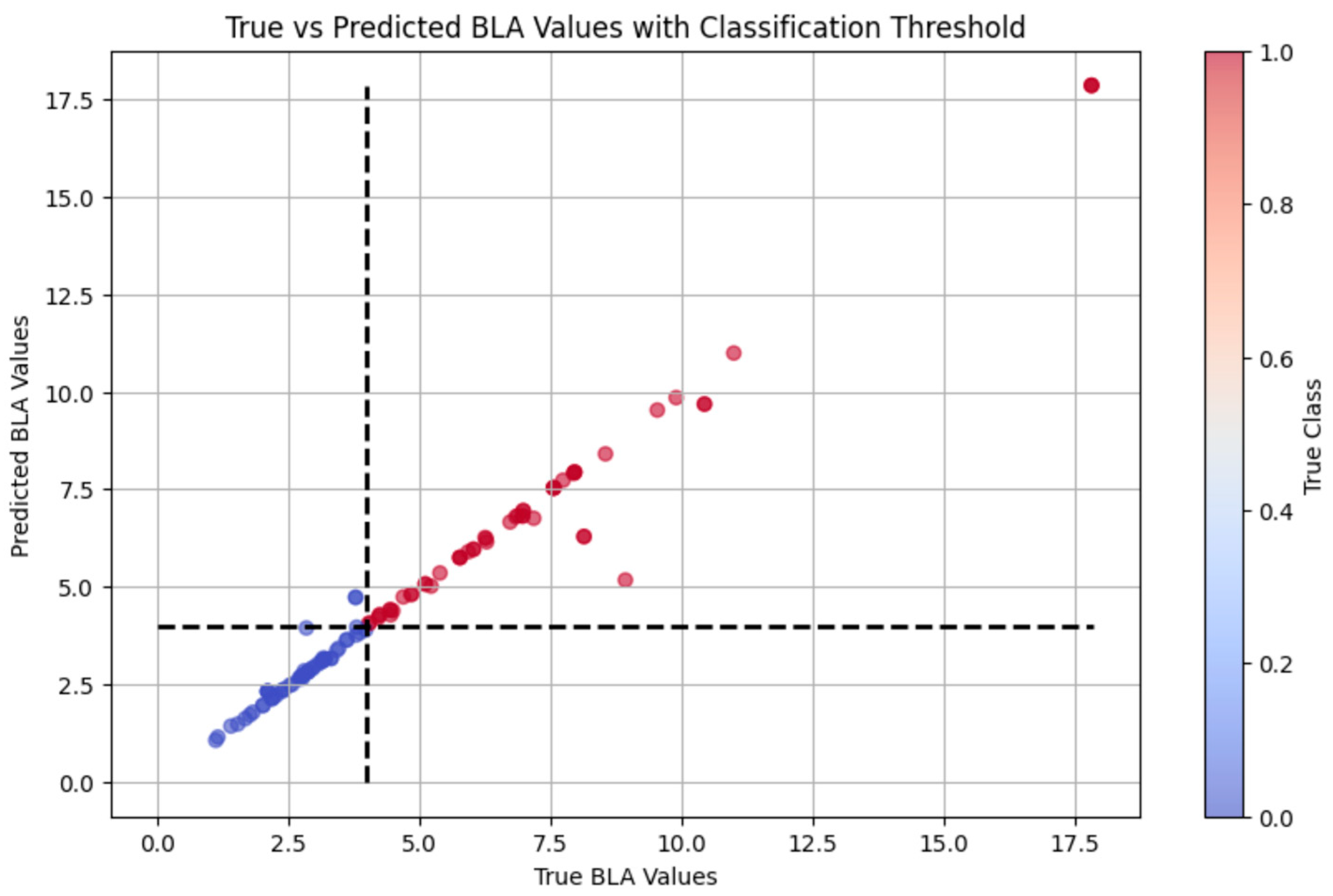
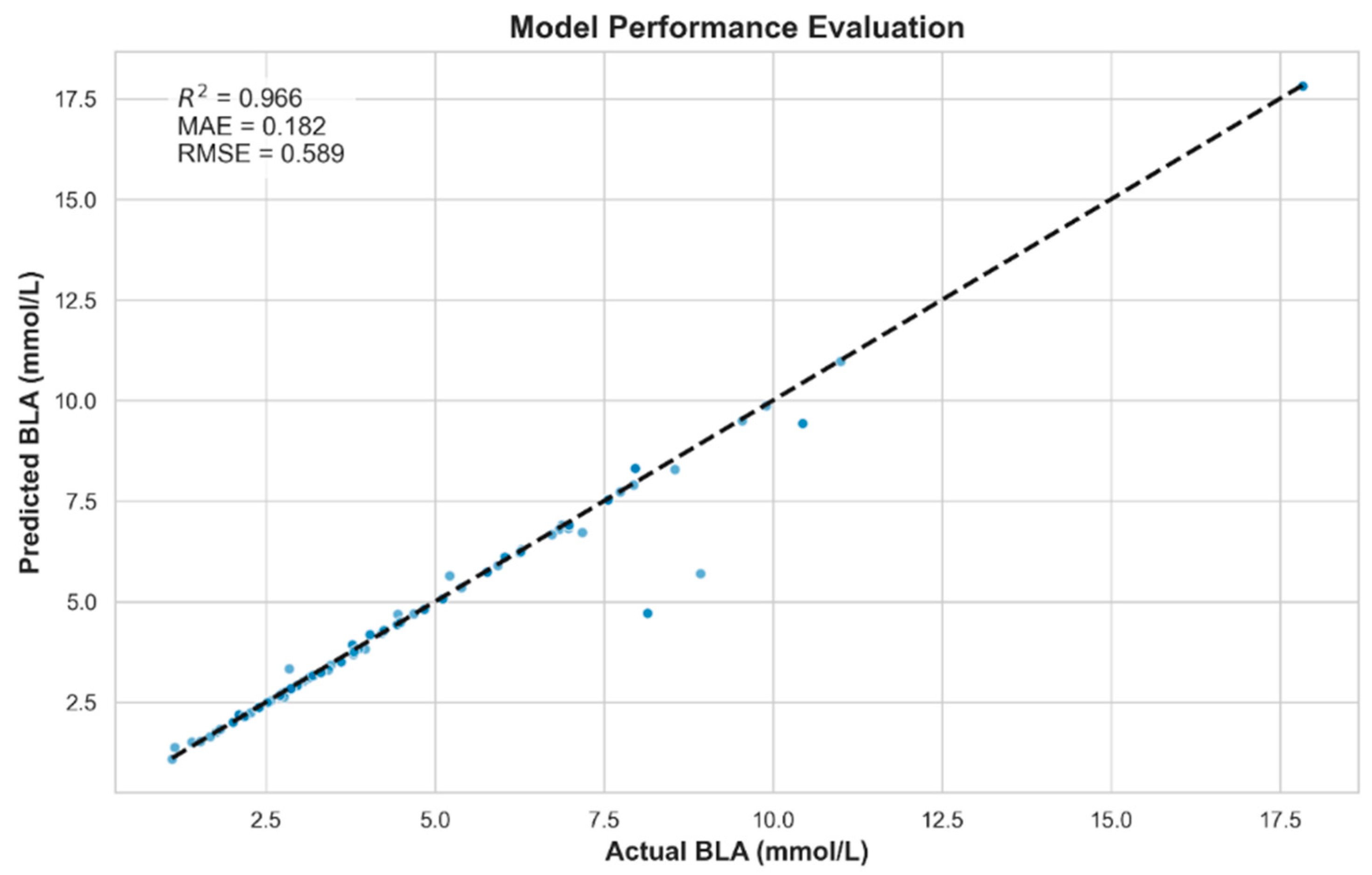
Linear models, such as ordinary least squares and ridge regression, underperformed in this task (R² = 0.2154 and 0.6148, respectively), suggesting that the linear assumption failed to capture the nonlinear interactions among the measured physiological variables. Nonlinear models demonstrated significantly enhanced estimating accuracy. In particular, the RF model yielded the highest R² (0.9350) among individual models, along with a low MAE (0.2711 mmol/L), indicating its strong generalization ability and robustness to multicollinearity. Other tree-based models, including GBR and XGBoost, showed moderate performance, which may be due to overfitting or sensitivity to hyperparameter tuning in smaller datasets. Although the SVR model achieved a perfect fit on the training set (R² = 1.0000), its near-zero error rates suggest overfitting rather than genuine generalization, emphasizing the necessity of evaluating model performance beyond training metrics alone.

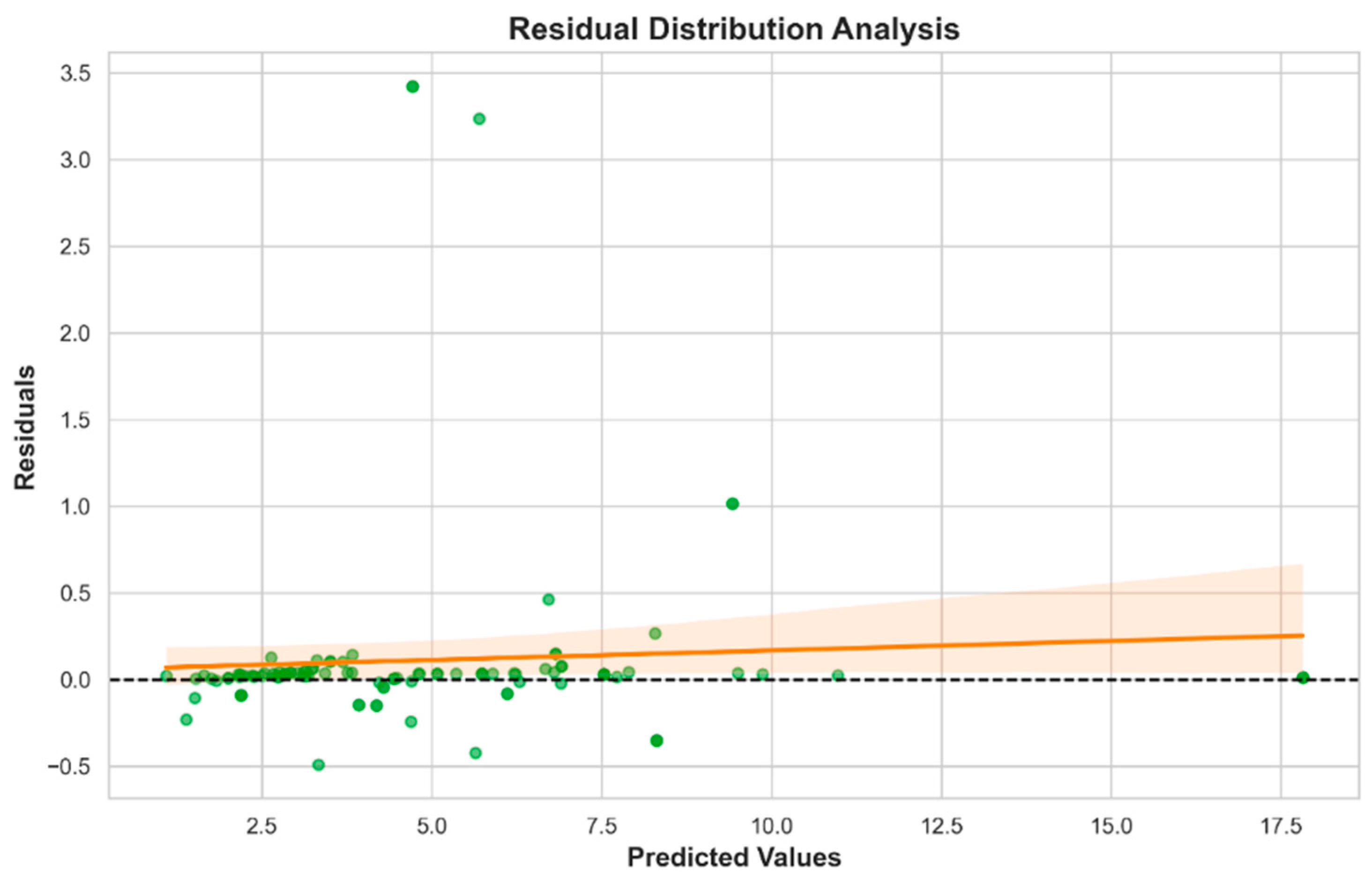
The stacking ensemble model, integrating LR, RF, and KNN, outperformed all individual models (R² = 0.966, MAE = 0.182), highlighting the value of heterogeneous model fusion. This approach effectively leveraged the complementary strengths of its base learners: capturing global, nonlinear, and local patterns, respectively. The narrow distribution of residuals within ±0.5 mmol/L further illustrates its robustness and applicability in real-world scenarios.

Collectively, these findings indicate that ensemble methods offer a more reliable and accurate framework for modeling complex physiological phenomena, such as BLa estimation, especially when input features are multimodal and nonlinear in nature.

4.3. Application of BLa Estimation to Load Classification

To assess the practical applicability of the proposed lactate estimation model, we conducted a downstream classification task distinguishing low- and high-intensity exercise loads. Two classification frameworks were compared: the first one (supervised learning algorithms) used raw physiological indicators (e.g., HRV and respiratory metrics) as inputs, while the second (interpretable system) relied solely on the estimated BLa values generated by our model.

Despite relying on a single predicted variable, the BLa-based classifier achieved comparable or superior performance across key evaluation metrics. This suggests that the BLa estimates effectively encapsulated the relevant exercise load information embedded in the multidimensional physiological inputs. In contrast, models trained directly on raw signals showed greater variability in classification accuracy.

These findings underscore the effectiveness of BLa as a surrogate marker for exercise load discrimination. The indirect prediction strategy—first estimating lactate concentration and then performing classification—demonstrated not only comparable accuracy but also reduced feature dimensionality and potentially improved model interpretability. This application highlights a promising pathway for using wearable-based monitoring systems while maintaining robust performance.

4.4. Performance Gains Through Multimodal Sensing and Ensemble Modeling

Many existing studies rely on one single type of sensor, often focusing on physiological signals, such as ECG, EMG, or microwave sensors (

Table 7. Comparison with previous studies.

Article	Types of Sensors	Types of Sports	Accuracy (%)	RMSE (mmol)	${\mathbf{R}}^2$
[26]	Microwave sensors	Cycling	0.86	-	0.60
[14]	Bipolar surface electrodes	Cycling	-	-	0.77–0.98
[28,29]	Metabolic cart, ECG recording system, automatic blood pressure monitor, pulse oximeter	Cycling	0.99	0.52 (low-to-moderate intensities), 1.82 (higher intensities)	-
[27]	A portable lactate analyzer, HR monitor	Running	0.89	-	-
[13]	Super GL2 analyzer, HR monitor, EKG device	Running	-	-	0.645–0.803
This work	Multi-source sensors	Running	0.98	0.58	0.96

). For example, the study by Mason et al. [26] used microwave sensors to estimate BLa levels non-invasively, but this approach was restricted to cycling scenarios and suffered from limited accuracy under complex motion conditions. Another study from Ražanskas et al. [14] used EMG signals from four different muscles to predict lactate concentration. While EMG reflects muscle activity directly, it is less sensitive to changes in exercise intensity and is vulnerable to interference, which can compromise model stability and reliability. Urtats Etxegarai et al. estimated BLa concentration by analyzing ECG signals, defining the evolution of HR across exercise stages as a key input [27]. While this approach offers a non-invasive and relatively accessible means of estimation, it may be limited by individual variability in the HR response, as well as the indirect nature of its correlation with lactate dynamics. Michał Tomaszewski’s study employed respiratory parameters such as VE and VO₂max to estimate BLa concentration [13].

Given the use of BLa in clinical medicine, Subhasri Chatterjee et al. developed a bio-photonic sensor based on the propagation characteristics of short-wave infrared light through vascular tissue for BLa diagnosis [22]. While this technique presents a promising direction for non-contact sensing, its performance can be influenced by variations in tissue properties, ambient light interference, and the need for precise alignment of optical components. Koichi Sughimoto et al. conducted studies on postoperative infants, exploring the feasibility of estimating BLa using perioperative features, such as arterial pressure waveforms [21]. Although this method shows potential for continuous monitoring in critical care settings, its generalizability remains limited due to the specificity of patient conditions and the requirement for invasive arterial line access in many cases.

In contrast, our study integrates multiple sensor types—ECG, additional physiological variables (e.g., cardiopulmonary indicators), and gait features collected during running—with carefully selected sensor placements (e.g., chest and limbs) to comprehensively capture the multidimensional postural changes during exercise. This multi-sensor setup provides a more accurate representation of physiological responses during running and enhances model adaptability to varying exercise intensities and physiological states. For instance, ECG sensors and gas analyzers were positioned on the chest, while IMUs for motion tracking were placed across the body, maximizing relevant signal acquisition and reducing information loss caused by single-sensor or suboptimal placement.

In terms of model performance, many previous studies employed conventional machine learning techniques, such as neural networks (NNs) or RF. For example, in Mason et al.’s study [26], an NN model combined with pairwise mutual information for feature selection achieved a correlation coefficient of R = 0.78 with invasive gold-standard measurement, but the prediction error remained high (13.4%), especially for high-intensity exercise. Urtats Etxegarai et al. introduced a layer-recurrent neural network (LRNN) to estimate the lactate threshold, successfully identifying the threshold in 89.52% of the study population [27]. Similarly, a study from Huang et al. [28,29] used exponential regression, which achieved an error of 0.52 mmol/L at low-to-moderate intensities but deteriorated to 1.82 mmol/L at higher intensities. In another study of Huang et al. [28,29], a hybrid CNN–ANN deep learning approach achieved 99.56% accuracy, though its success was confined to static exercise scenarios (e.g., cycling) and may not generalize to dynamic settings like running. In studies employing RF and its variants, Michał Tomaszewski et al. reported that RF performed less favorably than XGBoost and light gradient boosting machine (LightGBM) in estimating lactate thresholds, with R² values of only 0.645 for the aerobic threshold (AeT) and 0.789 for the anaerobic threshold (AnT) [13]. In a separate study, Koichi Sughimoto applied a hypertuned RF model to estimate blood lactate concentration, achieving an R² of 0.73 [21].

4.5. Strengths, Limitations, and Future Directions

4.5.1. Strengths

Compared to the concept of multiparameter modeling proposed in previous studies [15], this study adopted a multi-perspective and multisystem fusion strategy rooted in the synergistic nature of human physiological responses during exercise. Our approach was implemented through a sensor-integrated measurement framework that combines diverse modalities—including HR monitors, respiratory masks, and motion capture systems. This design emphasizes the integration of heterogeneous data sources to reconstruct the multidimensional nature of physical activity, thereby enabling a more refined and realistic estimation of BLa thresholds instead of using multi-indicators from just one perspective of data.

Unlike other similar work [13], our model incorporates biomechanical features derived from motion data and applies ensemble learning techniques. This significantly enhances estimation accuracy and demonstrates the scientific validity and efficiency of modeling with multi-source data. These results support the growing trend in exercise physiology and wearable technology toward integrating multiple physiological signals to comprehensively assess exercise status.

As a key biomarker for evaluating exercise intensity and physiological stress, BLa concentration is influenced by a complex interplay of physiological and biomechanical factors. Modeling based solely on individual or even multiple physiological indicators may not fully capture this complexity. Therefore, our study integrated both physiological parameters and gait-based biomechanical features to build a more holistic and robust estimation model. While the biomechanical features used here are limited to lower-limb kinematics—potentially constraining future application scenarios to lower-body-dominant activities—this work nonetheless pioneers a novel estimation paradigm. By incorporating parameters that characterize movement itself, the model can better reflect the real dynamics of exercise.

In contrast to studies employing deep neural networks or other complex architectures as generic supervised learning algorithms, the approach proposed in this study emphasizes a dual focus on estimating performance and interpretability. By integrating ensemble learning with domain-informed feature engineering, the model effectively extracted salient information from heterogeneous physiological signals. Under conditions of incremental exercise, the BLa estimation model demonstrated strong estimating capability, with low MSE values. Moreover, the downstream classification task, based on the model’s outputs, achieved an accuracy of 98%, underscoring its utility in exercise workload discrimination.

Another key strength of the proposed framework lies in its balance between model complexity and real-world applicability. Rather than relying on overly complex architectures prone to overfitting and diminished generalizability, this study adopted a structured yet pragmatic approach to physiological signal modeling. Despite not utilizing advanced deep learning frameworks, the proposed joint modeling strategy—based on multi-source data, including ECG, respiratory parameters, and gait features—achieved robust performance in dynamic exercise conditions. This demonstrates the feasibility of accurate physiological modeling without compromising model transparency or operational stability.

4.5.2. Limitations

Nonetheless, several limitations warrant consideration.

First, the relatively small sample size of this study inevitably affects the robustness and generalizability of the results. Specifically, the limited number of participants may lead to an overestimation of model performance, and the reproducibility of the findings could be compromised. More importantly, lactate estimation models trained on small datasets may face challenges in terms of stability and generalization, making them less effective when applied to populations with diverse physiological and demographic characteristics.

Second, there are also limitations regarding participant selection. Since the study was primarily conducted on a university campus with a focus on sports science, the majority of subjects were aged between 18 and 25 and some had a background in long-term professional athletic training. Such a selective sample lacks representativeness of the general population, which may restrict the applicability of the model to broader user groups.

In addition, several statistically insignificant variables (p > 0.05) were retained during model training, including V’E, V’CO₂, RER, EE, V’O₂, CI, and VT from respiratory data, and contact time, gait cycle time, and max. VGRF from gait parameters. While these features did not show statistical significance, this may be primarily attributed to the small sample size. They were still retained in the modeling process based on evidence from previous studies, which have demonstrated associations between respiratory variables and lactate dynamics during exercise, as well as consistent changes in gait characteristics over the course of running. Thus, we consider the observed insignificance in this study to be incidental and likely to diminish with an expanded dataset and improved sample selection.

Moreover, during model training, the SVR model achieved an R² of 1.0000. While this result may appear ideal, it is in fact indicative of overfitting—where the model fits the training data extremely well but fails to generalize to unseen data. This occurs when the algorithm captures noise and idiosyncrasies in the training set rather than learning meaningful patterns. The overfitting issue may stem from SVR’s capacity to overfit small datasets, effectively memorizing every detail rather than abstracting general rules. Additionally, a small dataset carries the risk of the “curse of dimensionality,” where the number of features is disproportionately large relative to the number of samples, further impairing model performance.

Parameter tuning might help alleviate this problem—fine-tuning key hyperparameters of the SVR could reduce overfitting and improve the model’s generalization ability. Taken together, the SVR model in this study may only be suitable for individuals and exercise scenarios closely resembling the training data, and caution should be exercised when attempting to apply it more broadly. Future research should explore more robust model structures to enhance applicability across diverse populations and conditions.

4.5.3. Future Directions

In light of these limitations, future research should focus on the following things. Firstly, increasing the number of participants should be prioritized to enhance model reliability and reproducibility. Secondly, future studies should ensure that the composition of participants reflects broader demographics, including age, sex, and physical activity levels. This would enhance the external validity and practical applicability of the models. Last but not least, incorporating effective feature selection techniques—such as recursive feature elimination (RFE) or feature importance ranking from tree-based models—could help identify the most relevant predictors and eliminate redundant inputs, thereby improving model performance and interpretability. By addressing these areas, future research may develop more robust, generalizable, and practically valuable models for non-invasive blood lactate estimation.

Looking forward, the modeling framework developed in this study holds promise for broader application scenarios beyond running-based exercise. Potential extensions include cycling, swimming, or other dynamic sports. Furthermore, multi-sensor wearable systems could be leveraged for personalized energy expenditure estimation, training optimization, and fitness assessment in both athletic and general populations. Clinically, such systems could support rehabilitation planning by estimating individualized exercise load, thereby helping to avoid secondary injuries associated with overexertion.

5. Conclusions

This study presented a multi-source sensor framework that estimates BLa concentration by integrating physiological signals and motion data based on the multidimensional and multisystem coordination of human exercise. Through employing an ensemble of machine learning algorithms, the proposed model achieved excellent estimation performance without compromising interpretability. These findings offer valuable insights and a theoretical foundation for the design of wearable devices that deliver more comprehensive, personalized, and intelligent solutions for health and performance monitoring.